| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
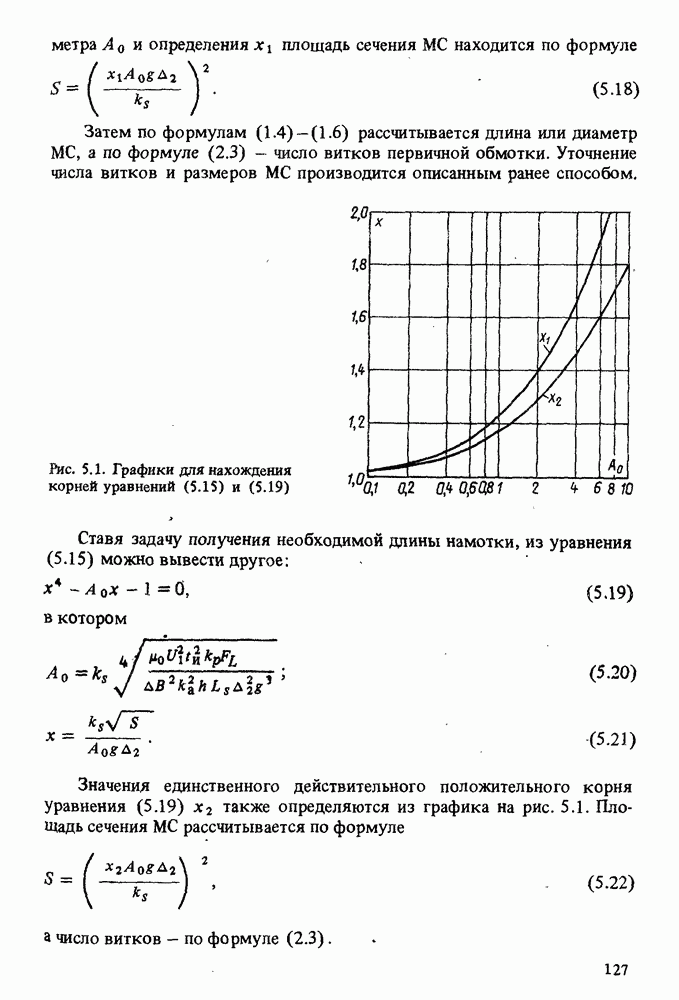
4.3. ДИНАМИЧЕСКИЕ ЕМКОСТИ
Замена распределенных емкостей обмоток ИТ сосредоточенными основана на том же энергетическом принципе, что и расчет индуктивностей рассеяния. Если известны геометрия обмоток и распределение напряжения на них, то можно вычислить энергию электрического поля, сосредоточенного между соответствующими элементами конструкции ИТ. Приравнивая энергию, рассчитанную таким образом, энергии

выраженной через сосредоточенную емкость и напряжение на первичной обмотке, можно определить сосредоточенную емкость как энергетически эквивалентную распределенной, приведенную к напряжению первичной обмотки.
Определенная таким образом емкостьносит название динамической емкости.
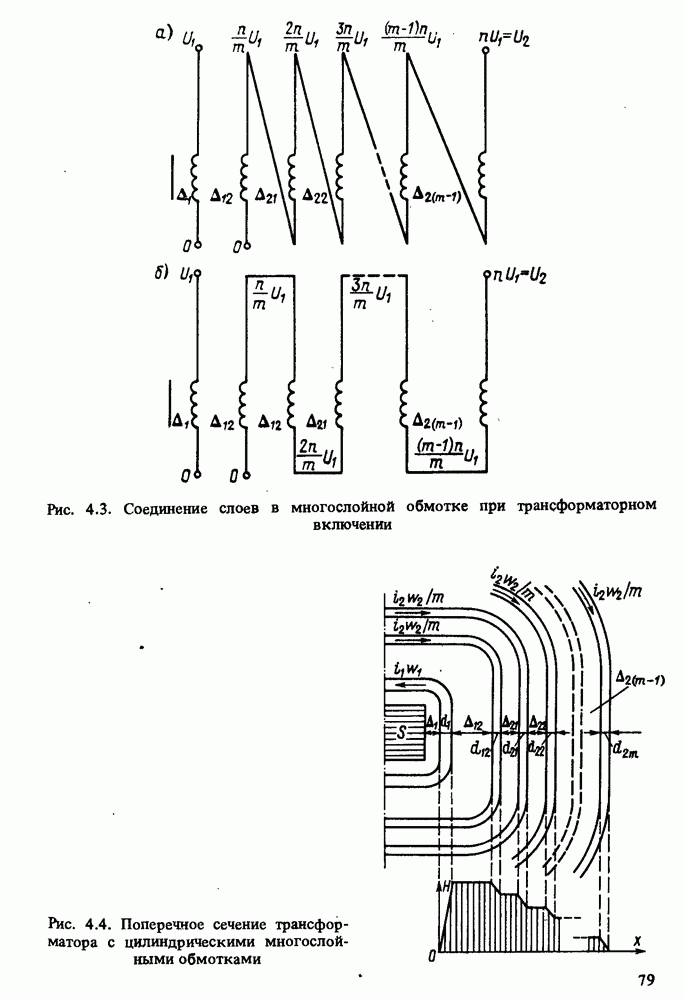
Вычислим динамические емкости ИТ с многослойными цилиндрическими обмотками, слои которых соединены по схемам на рис. 4.3 и 4.5, полагая, как это обычно и бывает на практике, что МС и начало первичной и вторичной обмоток имеют нулевой потенциал. Если бы между первичной обмоткой и МС действовало постоянное напряжение, то при  что обычно выполняется в ИТ, электрическое поле в изоляционном промежутке Д) было бы практически однородным. По этой причине первичная обмотка и МС могли бы рассматриваться как эквипотенциальные поверхности конденсатора с параллельными пластинами. Емкость такого конденсатора выражается известной формулой
что обычно выполняется в ИТ, электрическое поле в изоляционном промежутке Д) было бы практически однородным. По этой причине первичная обмотка и МС могли бы рассматриваться как эквипотенциальные поверхности конденсатора с параллельными пластинами. Емкость такого конденсатора выражается известной формулой

где  — относительная диэлектрическая проницаемость материала изоляции.
— относительная диэлектрическая проницаемость материала изоляции.
Однако, вследствие того что на первичной обмотке ИТ импульсное напряжение, она не может рассматриваться как эквипотенциальная поверхность. Поэтому при расчете емкости необходимо учитывать распределение напряжения в обмотке, имеющее сложный пространственно-временной характер, который обусловлен распределенным характером индуктивности, емкости, сопротивления обмотки, и взаимной индуктивности витков [8]. Картина распределения напряжения непрерывно меняется во времени — до тех пор, пока не закончится
формирование фронта импульса, и только после этого напряжение линейно распределится вдоль обмотки. Однако с целью упрощения вычисления емкости принимают линейное распределение напряжения [2, 3, 7]. Оправданием такому предположению служит то обстоятельство, что другими способами не удается представить распределенную емкость в виде сосредоточенной. С другой стороны, накопленный опыт проектирования ИТ с МС показывает, что такой подход не сопровождается чрезмерно грубыми ошибками.

Рис. 4.7. Первичная обмотка ИТ
При равенстве потенциалов начала первичной обмотки и МС напряжение по длине обмотки равномерно нарастает от нуля в начале обмотки до  как показано на рис. 4.7. На расстоянии
как показано на рис. 4.7. На расстоянии  от начала обмотки
от начала обмотки  Элементарная емкость участка обмотки
Элементарная емкость участка обмотки 

а энергия, сосредоточенная в элементарной емкости, —

Полная энергия, сосредоточенная в пространстве между первичной обмоткой и МС, при этом составит

Из последнего выражения можно найти динамическую емкость первичной обмотки

Таким образом, динамическая емкость первичной обмотки в три раза меньше статической емкости.
Определим теперь динамическую емкость между обмотками для трансформаторного включения обмоток по схемам на рис. 4.3. (Эта емкость складывается из емкости между первичной обмоткой и первым слоем вторичной, а также емкости между слоями вторичной обмотки.) При этом возможны два способа включения вторичной обмотки:
направление намотки вторичной обмотки совпадает с направлением намотки первичной, и напряжения на первичной и вторичной
совпадают по фазе; такое включение обмоток будет в дальнейшем называться согласным;
направление намотки вторичной обмотки противоположно направлению намотки первичной, и напряжения на первичной и вторичной обмотках находятся в противофазе; такое включение обмоток будет в дальнейшем называться встречным.

Рис. 4.8. Первичный слой многослойной обмотки ИТ
Способы включения обмоток существенно влияют на распределение напряжения между ними. Обращаясь к рис. 4.8, можно определить, что при согласном и встречном включении напряжение между обмотками при  изменяется по закону
изменяется по закону

где знак "минус” соответствует согласному, а знак "плюс” — встречному включению обмоток.
При 

В частном случае, когда  напряжение
напряжение  и при согласном включении обмоток в пространстве между ними электрическая энергия не запасается, динамическая емкость между обмотками отсутствует.
и при согласном включении обмоток в пространстве между ними электрическая энергия не запасается, динамическая емкость между обмотками отсутствует.
Составляя выражение для энергии, сосредоточенной в пространстве между первичной и вторичной обмотками, по аналогии с ранее рассмотренным, имеем: при 

или

Из формул (4.12) и (4.13) видно, что при встречном включении обмоток и любых соотношениях значений пят междуобмоточная емкость всегда больше емкости при согласном включении. При обоих видах включения и  с увеличением коэффициента трансформации междуобмоточная емкость быстро возрастает примерно пропорционально
с увеличением коэффициента трансформации междуобмоточная емкость быстро возрастает примерно пропорционально 
Определим далее междуслоевую емкость вторичной обмотки. Из схемы трансформатора (рис. 4.3, а) видно, что во всех изоляционных промежутках вторичной обмотки действует одинаковое по высоте обмотки напряжение  Поэтому в произвольно взятом промежутке энергия электрического поля
Поэтому в произвольно взятом промежутке энергия электрического поля

или

Полная емкость вторичной обмотки при этом

а общая динамическая емкость трансформатора —

при 

при 
В схеме трансформатора на рис. 4.3, б во всех изоляционных промежутках вторичной обмотки действует изменяющееся по длине намотки напряжение. Нетрудно найти, что закон изменения напряжения выражается формулой

Согласно изложенной выше методике определения динамической
емкости

и общая динамическая емкость трансформатора

при 
Создается впечатление, что схема на рис. 4.3, б хуже, чем схема на рис. 4.3, а, так как отличается большей емкостью вторичной обмотки. В действительности, однако, это не так. Поскольку максимальное напряжение, действующее между слоями вторичной обмотки в схеме на рис. 4.3, а, вдвое выше, чем в схеме на рис. 4.3, б, все изоляционные промежутки вторичной обмотки в схеме на рис. 4.3, б для обеспечения равной электрической прочности также должны быть удвоены по размеру. Поэтому динамическая емкость такого трансформатора в действительности несколько меньше емкости трансформатора по схеме на рис. 4.3, а.
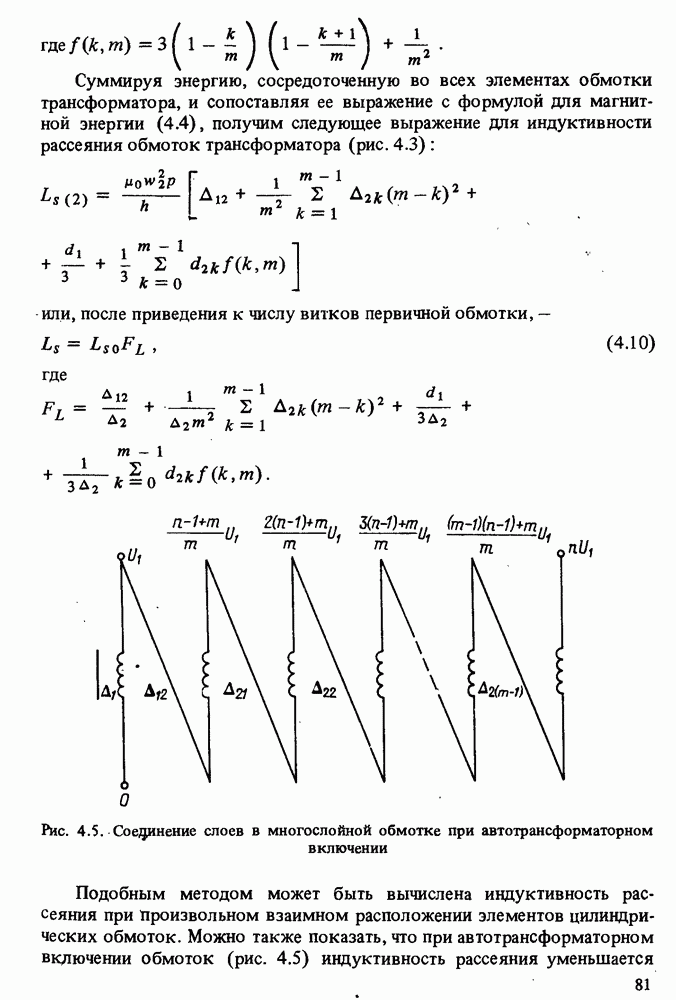
Пользуясь изложенной методикой, нетрудно показать, что при автотрансформаторном согласном включении обмоток по схеме на рис. 4.5 (встречное включение обмоток автотрансформатора не имеет смысла) динамические емкости при  выразятся следующими формулами:
выразятся следующими формулами:

или

Подобным образом могут быть рассчитаны динамические емкости при любом включении слоев цилиндрических обмоток.
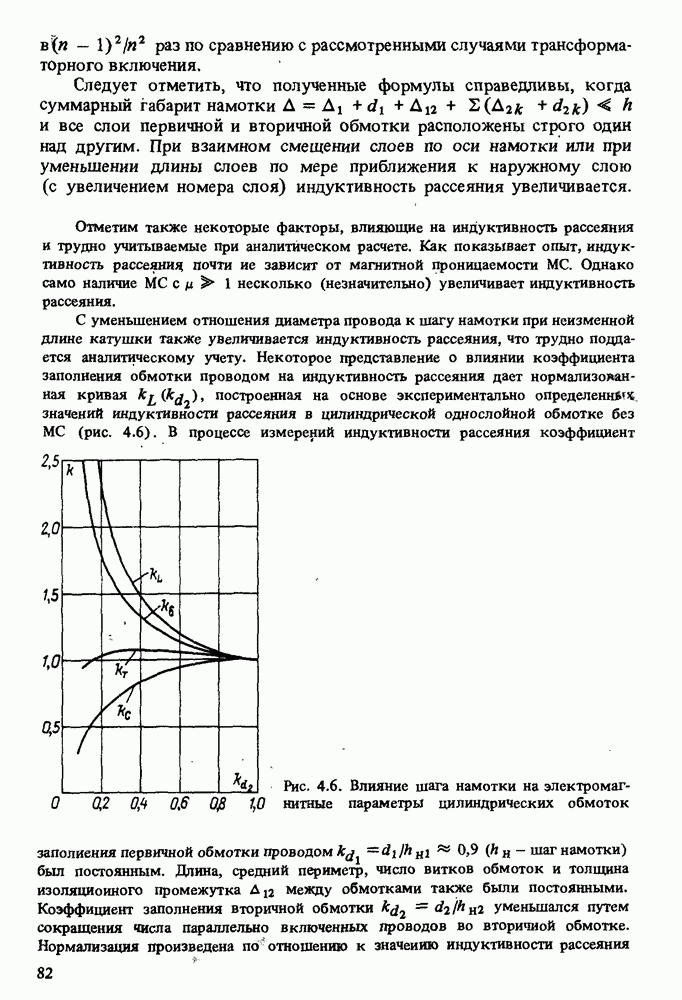
При уменьшении отношения диаметра провода к шагу намотки уменьшается емкость обмотки. Представление о степени этого уменьшения дает кривая  на рис. 4.6. На том же графике построена кривая
на рис. 4.6. На том же графике построена кривая  показывающая, что при изменении шага намотки произведение
показывающая, что при изменении шага намотки произведение  остается практически постоянным.
остается практически постоянным.
Таким образом, изменение шага намотки не приводит к существенному изменению высокочастотной постоянной времени трансформатора  и по этой причине не вызывает дополнительного удлинения фронта импульса. Однако с изменением шага намотки резко изменяется отношение
и по этой причине не вызывает дополнительного удлинения фронта импульса. Однако с изменением шага намотки резко изменяется отношение  определяющее коэффициент затухания трансформаторной цепи в (кривая
определяющее коэффициент затухания трансформаторной цепи в (кривая  на рис. 4.6).
на рис. 4.6).
В связи с тем что параметр 8 существенно влияет на характер переходного процесса в трансформаторной цепи, изменение искажений импульса в зависимости от шага намотки связано именно с изменением  . С другой стороны, рациональным выбором шага намотки можно получить необходимое значение 8 без существенного увеличения постоянной времени.
. С другой стороны, рациональным выбором шага намотки можно получить необходимое значение 8 без существенного увеличения постоянной времени.
Формулы для расчета динамической емкости обмоток также удобно привести к толщине главной изоляции обмоток. Если сделать такое приведение для суммарной емкости ИТ со схемой на рис. 4.3, а, эту емкость можно выразить формулой

где после формальных преобразований величина

представляет собой динамическую емкость между обмотками простейшего идеализированного ИТ с однослойными цилиндрическими первичной и вторичнои обмотками при  .
.
Множитель

в рассматриваемом случае  является коэффициентом, учитывающим конструктивные и схемные особенности обмоток.
является коэффициентом, учитывающим конструктивные и схемные особенности обмоток.
Точно так же, как и при расчете индуктивности рассеяния мощных высоковольтных ИТ, формула (4.23) имеет и самостоятельное значение, поскольку в этих ИТ междуобмоточная емкость намного больше других емкостей обмоток.
Обращает на себя внимание то, что в отличие от индуктивности рассеяния динамическая емкость обмоток пропорциональна объему МС.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА ПЕРВАЯ. ИМПУЛЬСНЫЙ ТРАНСФОРМАТОР В УСТАНОВКАХ ИМПУЛЬСНОЙ ЭЛЕКТРОЭНЕРГЕТИКИ
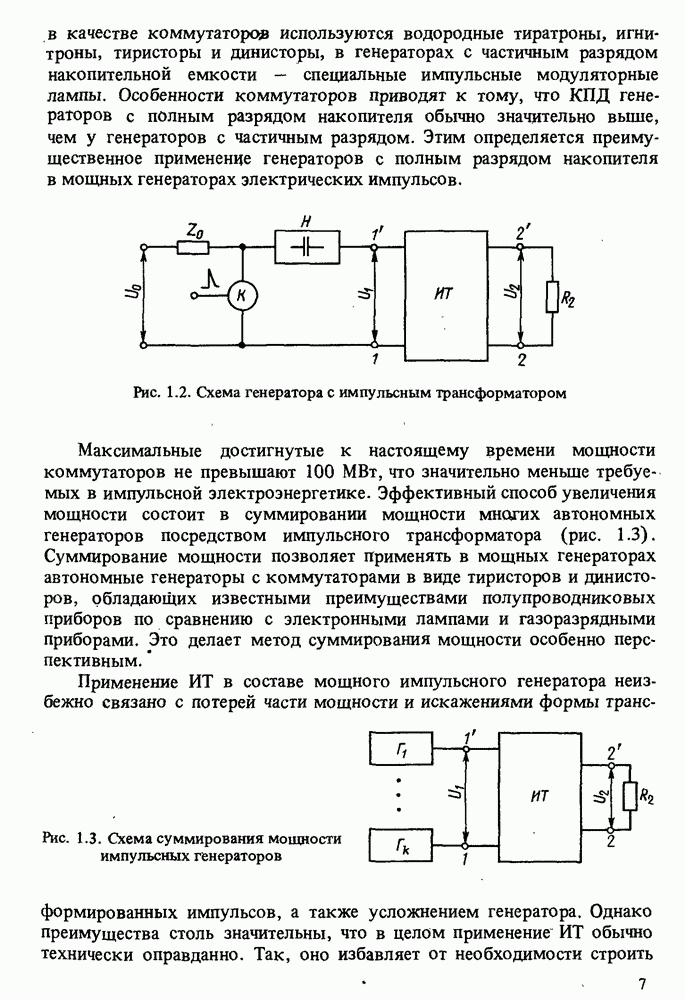
- 1.2. ГЕНЕРАТОРЫ МОЩНЫХ ЭЛЕКТРИЧЕСКИХ ИМПУЛЬСОВ
- 1.3. ПОТРЕБИТЕЛИ ИМПУЛЬСНОЙ ЭНЕРГИИ
- 1.4. ТРЕБОВАНИЯ К ИМПУЛЬСНОМУ ТРАНСФОРМАТОРУ
- 1.5. ОБЩИЕ КОНСТРУКТИВНЫЕ СХЕМЫ И КЛАССИФИКАЦИЯ ИМПУЛЬСНЫХ ТРАНСФОРМАТОРОВ
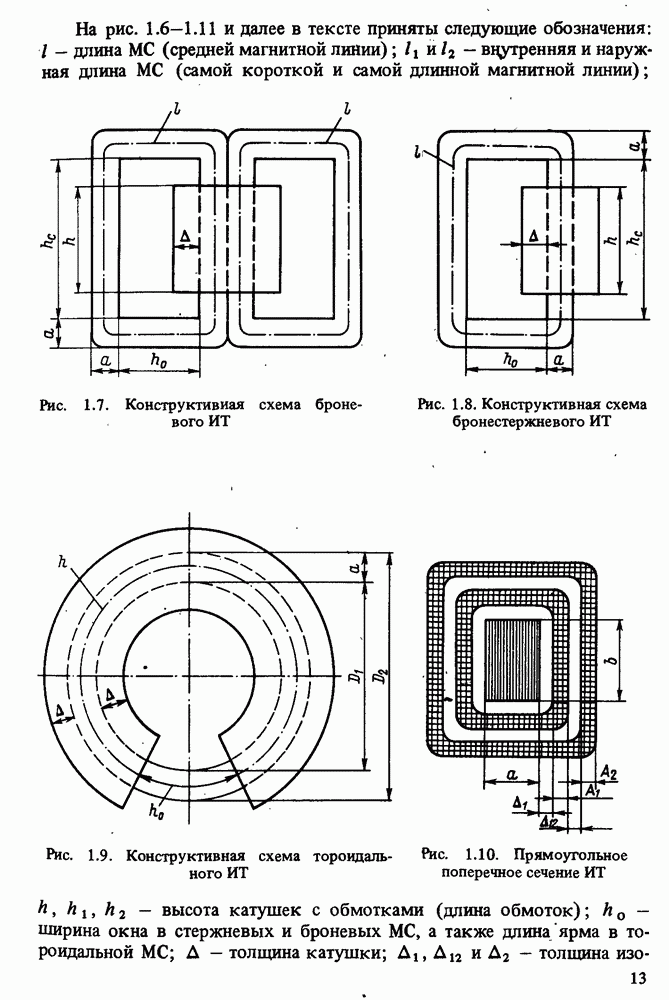
- 1.6. ИСХОДНЫЕ ДАННЫЕ ДЛЯ ПРОЕКТИРОВАНИЯ ИМПУЛЬСНОГО ТРАНСФОРМАТОРА
- ГЛАВА ВТОРАЯ. ЭЛЕКТРОМАГНИТНЫЕ ПРОЦЕССЫ В МАГНИТНОЙ СИСТЕМЕ
- 2.1. ОБЩИЕ СВЕДЕНИЯ О ТРАНСФОРМАТОРАХ С МАГНИТНОЙ СИСТЕМОЙ
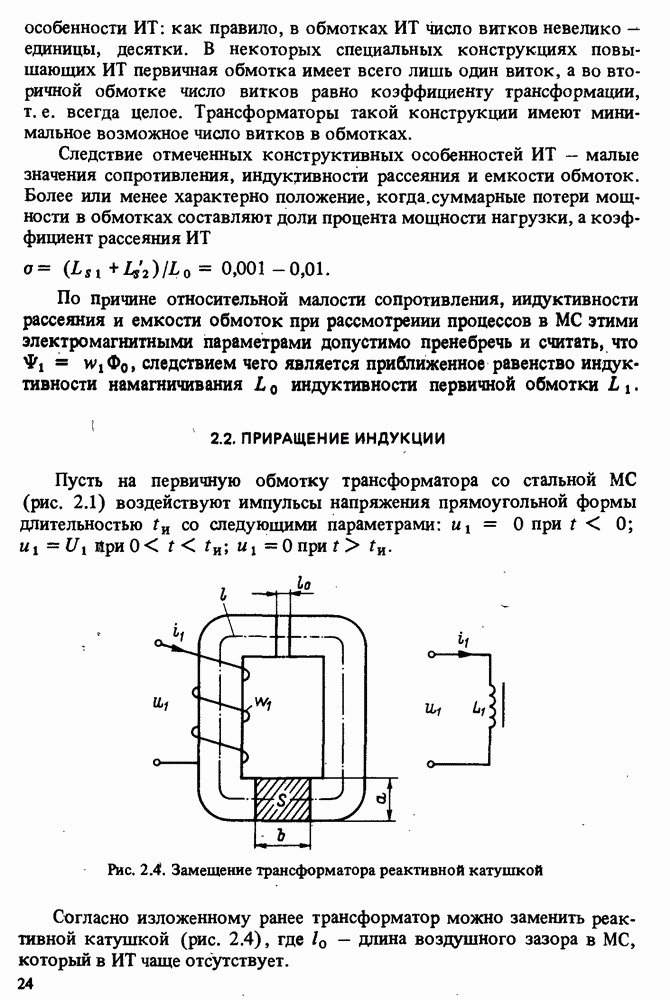
- 2.2. ПРИРАЩЕНИЕ ИНДУКЦИИ
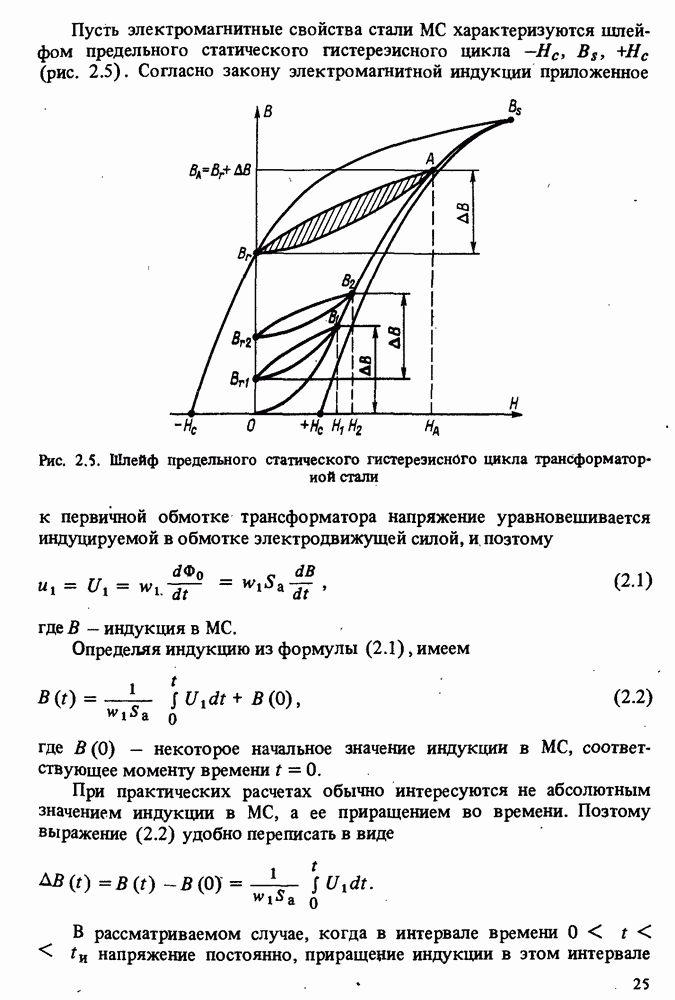
- 2.3. МЕТОДЫ УМЕНЬШЕНИЯ ОСТАТОЧНОЙ ИНДУКЦИИ
- 2.4. ПОТЕРИ ЭНЕРГИИ
- 2.5. МАГНИТНЫЕ МАТЕРИАЛЫ
- 2.6. ИЗМЕРЕНИЕ ХАРАКТЕРИСТИК МАГНИТНЫХ МАТЕРИАЛОВ
- ГЛАВА ТРЕТЬЯ. РАСЧЕТ ЭЛЕКТРОМАГНИТНЫХ ПАРАМЕТРОВ СХЕМЫ ЗАМЕЩЕНИЯ ПО ЗАДАННЫМ ИСКАЖЕНИЯМ ФОРМЫ ИМПУЛЬСА
- 3.1. СХЕМА ЗАМЕЩЕНИЯ ИМПУЛЬСНОГО ТРАНСФОРМАТОРА
- 3.2. СХЕМА ЗАМЕЩЕНИЯ ТРАНСФОРМАТОРНОЙ ЦЕПИ
- 3.3. ИСКАЖЕНИЯ ФРОНТА ИМПУЛЬСА
- 3.4. ИСКАЖЕНИЯ ВЕРШИНЫ ИМПУЛЬСА
- 3.5. ИСКАЖЕНИЯ СРЕЗА ИМПУЛЬСА
- 3.6. ЭНЕРГИЯ В РЕАКТИВНЫХ ЭЛЕМЕНТАХ ТРАНСФОРМАТОРНОЙ ЦЕПИ
- 3.7. РАСЧЕТ ЭЛЕКТРОМАГНИТНЫХ ПАРАМЕТРОВ СХЕМЫ ЗАМЕЩЕНИЯ
- 3.8. КРИТЕРИЙ ОСУЩЕСТВИМОСТИ ИМПУЛЬСНОГО ТРАНСФОРМАТОРА
- 3.9. КОРРЕКЦИЯ ИСКАЖЕНИЙ ФОРМЫ ИМПУЛЬСА
- ГЛАВА ЧЕТВЕРТАЯ. ЭЛЕКТРОМАГНИТНЫЕ ПАРАМЕТРЫ ОБМОТОК
- 4.1. СВЯЗЬ МЕЖДУ ЭЛЕКТРОМАГНИТНЫМИ И КОНСТРУКТИВНЫМИ ПАРАМЕТРАМИ. ИНДУКТИВНОСТЬ НАМАГНИЧИВАНИЯ
- 4.2. ИНДУКТИВНОСТЬ РАССЕЯНИЯ
- 4.3. ДИНАМИЧЕСКИЕ ЕМКОСТИ
- 4.4. СОПРОТИВЛЕНИЕ
- 4.5. ЦИЛИНДРИЧЕСКИЕ ОБМОТКИ
- 4.6. СПИРАЛЬНЫЕ ОБМОТКИ
- 4.7. КОНИЧЕСКИЕ ОБМОТКИ
- 4.8. ОБМОТКИ МОЩНЫХ ВЫСОКОВОЛЬТНЫХ ИМПУЛЬСНЫХ ТРАНСФОРМАТОРОВ
- 4.9. ВЫБОР ИЗОЛЯЦИИ И ПРОВОДОВ
- ГЛАВА ПЯТАЯ. ОСНОВЫ ПРОЕКТИРОВАНИЯ
- 5.2. МИНИМАЛЬНЫЙ ОБЪЕМ МАГНИТНОЙ СИСТЕМЫ
- 5.3. ВЫБОР КОНСТРУКЦИИ
- 5.4. КОНСТРУКТИВНЫЙ РАСЧЕТ
- 5.5. РАСЧЕТ МЕХАНИЧЕСКИХ СИЛ В ОБМОТКАХ
- 5.6. РАСЧЕТ ТЕПЛОВОГО РЕЖИМА
- 5.7. ОЦЕНКА ТЕХНИКО-ЭКОНОМИЧЕСКИХ И ФУНКЦИОНАЛЬНЫХ ПОКАЗАТЕЛЕЙ
- 5.8. О МАШИННОМ ПРОЕКТИРОВАНИИ
- ГЛАВА ШЕСТАЯ. ИМПУЛЬСНЫЕ ТРАНСФОРМАТОРЫ СО СТЕРЖНЕВОЙ МАГНИТНОЙ СИСТЕМОЙ
- 6.1. ОСНОВНЫЕ СВЕДЕНИЯ О СТЕРЖНЕВЫХ МАГНИТНЫХ СИСТЕМАХ
- 6.2. КОНСТРУКЦИИ ИМПУЛЬСНЫХ ТРАНСФОРМАТОРОВ СО СТЕРЖНЕВОЙ МАГНИТНОЙ СИСТЕМОЙ
- 6.4. МОЩНЫЙ ВЫСОКОВОЛЬТНЫЙ ИМПУЛЬСНЫЙ ТРАНСФОРМАТОР С ВИТОЙ НЕРАЗРЕЗНОЙ МАГНИТНОЙ СИСТЕМОЙ
- 6.5. ИМПУЛЬСНЫЙ ТРАНСФОРМАТОР СРЕДНЕЙ МОЩНОСТИ С РАЗРЕЗНОЙ МАГНИТНОЙ СИСТЕМОЙ
- ГЛАВА СЕДЬМАЯ. ИМПУЛЬСНЫЕ ТРАНСФОРМАТОРЫ С ТОРОИДАЛЬНОЙ МАГНИТНОЙ СИСТЕМОЙ
- 7.2. ИМПУЛЬСНЫЕ ТРАНСФОРМАТОРЫ С ВЕРТИКАЛЬНО УСТАНОВЛЕННОЙ МАГНИТНОЙ СИСТЕМОЙ
- 7.3. ИМПУЛЬСНЫЕ ТРАНСФОРМАТОРЫ С ГОРИЗОНТАЛЬНО УСТАНОВЛЕННОЙ МАГНИТНОЙ СИСТЕМОЙ
- ГЛАВА ВОСЬМАЯ. ИМПУЛЬСНЫЕ ТРАНСФОРМАТОРЫ С ОДНИМ ВИТКОМ В ПЕРВИЧНОЙ ОБМОТКЕ
- 8.2. РАСЧЕТ КОНСТРУКТИВНЫХ ПАРАМЕТРОВ
- 8.3. КОНСТРУКЦИИ
- 8.4. ПРИМЕР РАСЧЕТА МОЩНОГО ВЫСОКОВОЛЬТНОГО ОДНОВИТКОВОГО ИМПУЛЬСНОГО ТРАНСФОРМАТОРА
- 8.5. ОЦЕНКА ФУНКЦИОНАЛЬНЫХ И ТЕХНИКО-ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ
- ГЛАВА ДЕВЯТАЯ. ИМПУЛЬСНЫЕ ТРАНСФОРМАТОРЫ БЕЗ МАГНИТНОЙ СИСТЕМЫ
- 9.2. ИСКАЖЕНИЯ ФОРМЫ ИМПУЛЬСА
- 9.3. РАСЧЕТ КОНСТРУКТИВНЫХ ПАРАМЕТРОВ
- 9.4. ПРИМЕРЫ ПРИМЕНЕНИЯ И РАСЧЕТА
- СПИСОК ЛИТЕРАТУРЫ