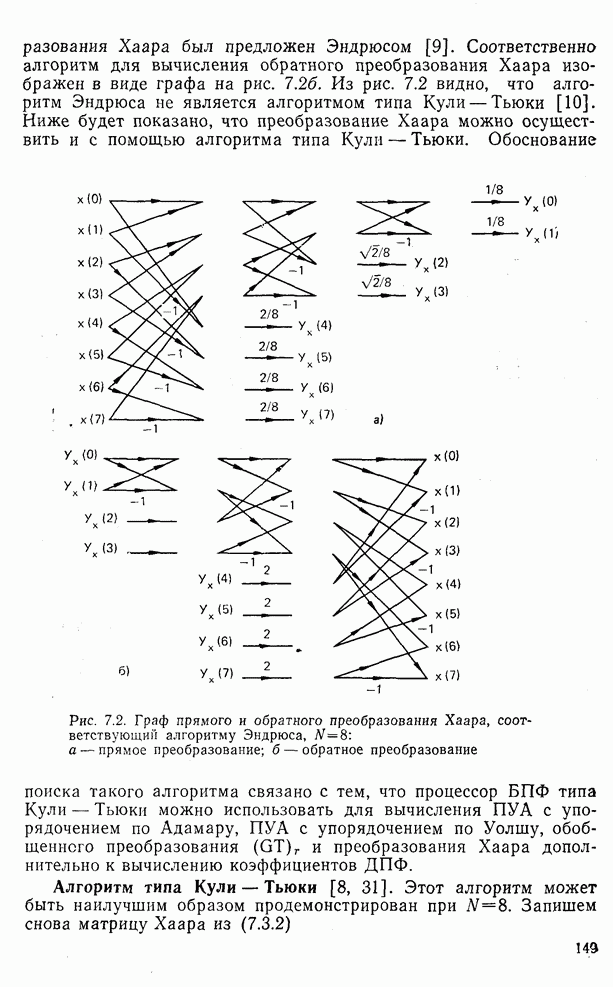
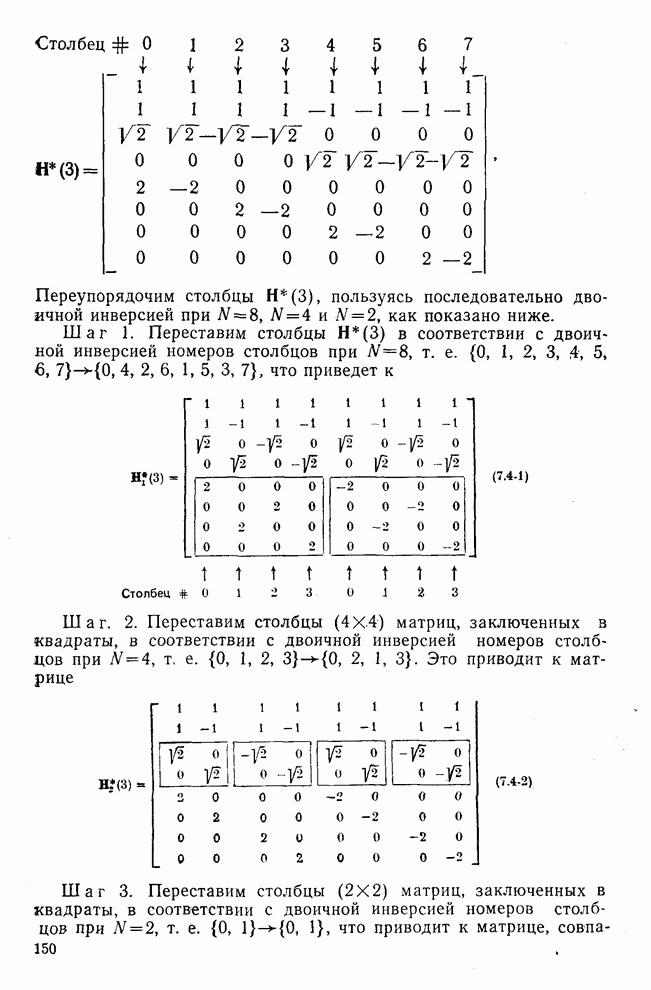
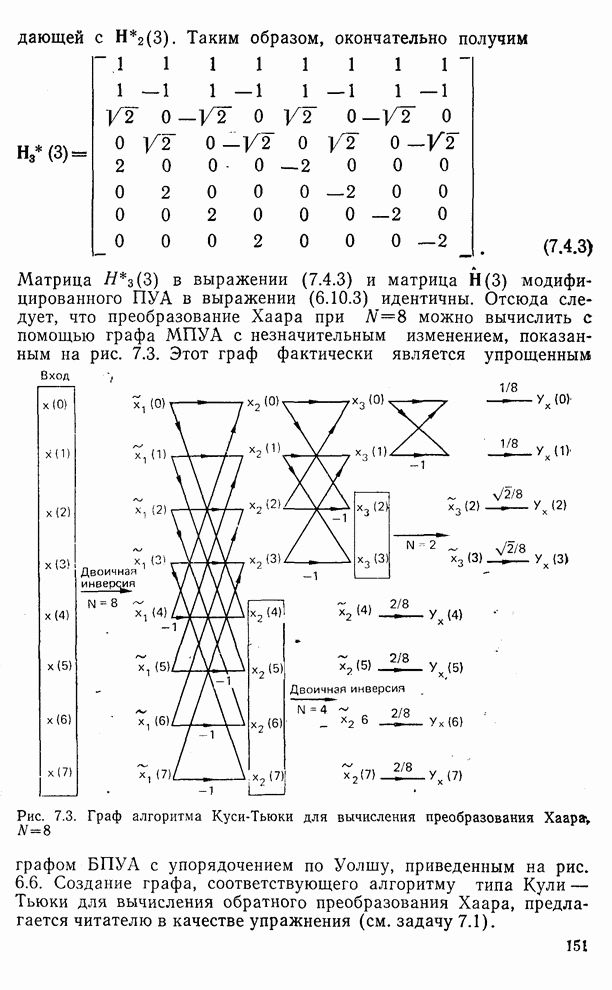
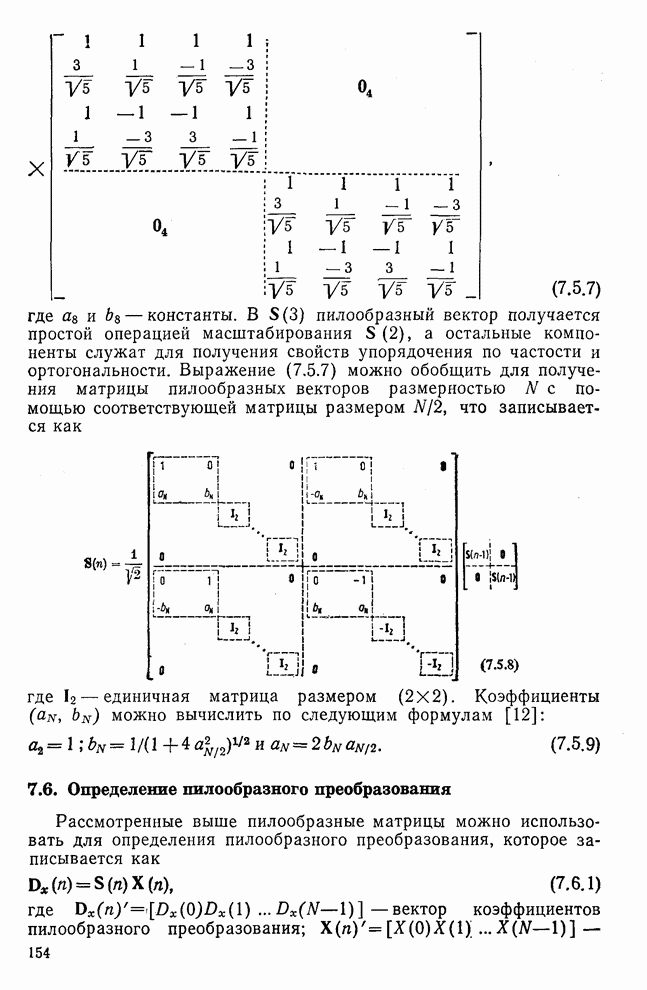
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
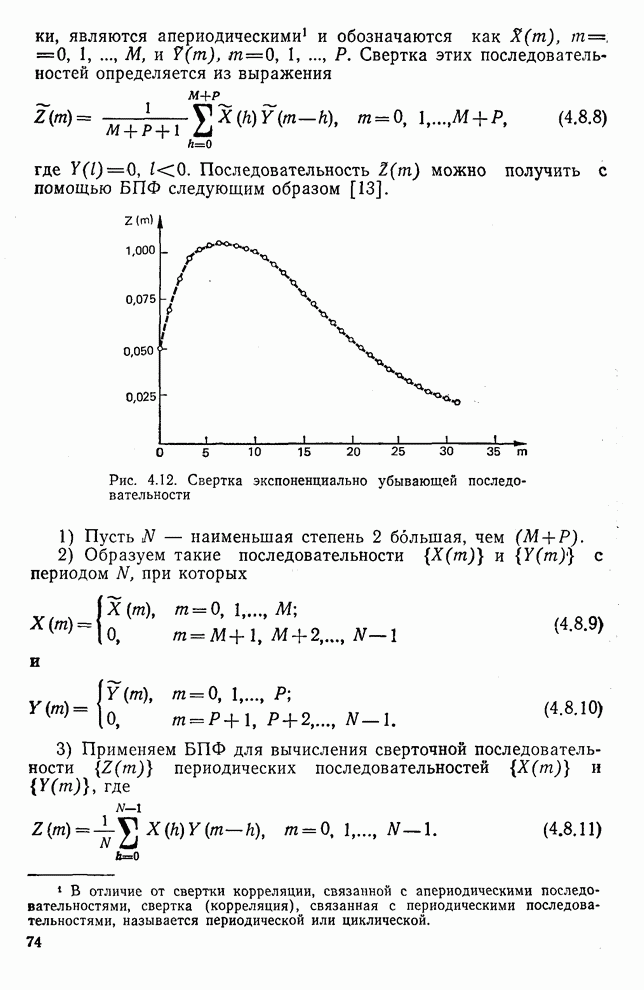
8.4. Субоптимальная винеровская фильтрация
Исходя из того, что  не зависит от вида ортогонального преобразования I, можно свободно выбирать вид преобразования, стремясь при этом сократить число вычислительных операций, связанных с осуществлением фильтрации.
не зависит от вида ортогонального преобразования I, можно свободно выбирать вид преобразования, стремясь при этом сократить число вычислительных операций, связанных с осуществлением фильтрации.
Число операций умножения, связанных с выполнением винеровской фильтрации [см. формулу (8.3.6)], в соответствии со структурной схемой, приведенной на рис. 8.1, сведено в табл. 8.4.1. Основным препятствием для осуществления фильтрации в реальном масштабе времени является то, что число требуемых операций умножения пропорционально  .
.
Таблица 8.4.1. Количество умножений при оптимальной винеровской фильтрации
Таким образом, в качестве компромиссного решения рассмотрим возможность использования матриц фильтра, содержащих относительно большое число нулей. С помощью таких матриц операция фильтрации  (см. рис. 8.1) может быть выполнена при меньшем числе умножений. Основной целью расчета фильтра, конечно, остается получение среднеквадратичной ошибки, близкой к среднеквадратичной ошибке оптимального фильтра.
(см. рис. 8.1) может быть выполнена при меньшем числе умножений. Основной целью расчета фильтра, конечно, остается получение среднеквадратичной ошибки, близкой к среднеквадратичной ошибке оптимального фильтра.
Задача расчета субоптимального винеровского фильтра может быть сформулирована как задача оптимизации, в которой матрица фильтра А выбирается исходя из минимизации [см. выражение (8.3.20)]

при ограничении, заключающемся в том, что определенные выбранные элементы матрицы А равняются нулю. Рассмотрим следующие возможные случаи.
1. Ограничим А классом диагональных матриц. Этот класс фильтров рассматривается в § 8.6.
2. Рассчитаем фильтр, матрица которого содержит два отличных от нуля элемента в строке; дополнительные элементы будем добавлять до тех пор, пока не получим требуемое качество по критерию минимума среднеквадратичной ошибки.
Однако такой подход быстро становится чрезвычайно сложным.
3. Получим матрицу субоптимального фильтра из матрицы оптимального фильтра, оставляя только те элементы, которые имеют относительно большую величину. Все остальные элементы приравняем к нулю.
В качестве примера рассмотрим третий случай реализации субоптимального фильтра.
Пример субоптимальной фильтрации. Рассмотрим случай оценки случайного сигнала в присутствии шума по среднеквадратичному критерию, когда ковариационные матрицы сигнала и шума определяются следующим выражением:
 (8.4.1)
(8.4.1)
и
 (8.4.2)
(8.4.2)
где  теплицева матрица [см. выражение (7.7.10)]. Ковариационная матрица
теплицева матрица [см. выражение (7.7.10)]. Ковариационная матрица  соответствует марковскому процессу первого порядка,
соответствует марковскому процессу первого порядка,  — белому шуму.
— белому шуму.
Для определения влияния ортогональных преобразований на структуру соответствующей матрицы фильтра вычислим матрицы фильтра для тождественного и дискретного косинусного преобразований, пользуясь уравнением (8.3.14) при  и
и  . Так как
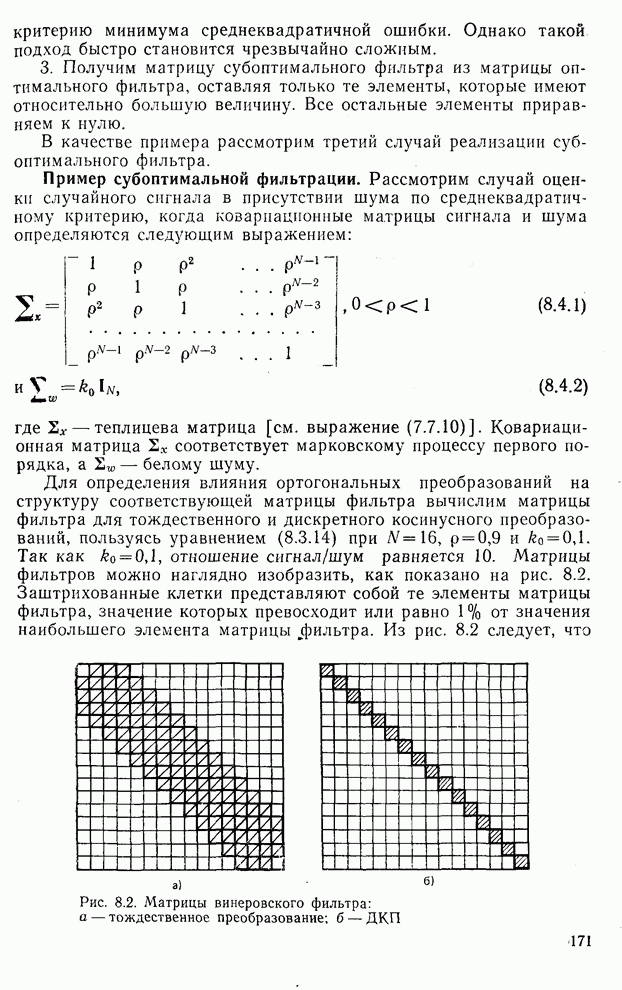
. Так как  , отношение сигнал/шум равняется 10. Матрицы фильтров можно наглядно изобразить, как показано на рис. 8.2. Заштрихованные клетки представляют собой те элементы матрицы фильтра, значение которых превосходит или равно
, отношение сигнал/шум равняется 10. Матрицы фильтров можно наглядно изобразить, как показано на рис. 8.2. Заштрихованные клетки представляют собой те элементы матрицы фильтра, значение которых превосходит или равно  от значения наибольшего элемента матрицы
от значения наибольшего элемента матрицы  . Из рис. 8.2 следует, что применение дискретного косинусного преобразования позволяет получить матрицу для соответствующего фильтра, содержащую значительно меньшее число элементов с относительно большими значениями.
. Из рис. 8.2 следует, что применение дискретного косинусного преобразования позволяет получить матрицу для соответствующего фильтра, содержащую значительно меньшее число элементов с относительно большими значениями.

Рис. 8.2. Матрицы винеровского фильтра: a — тождественное преобразование; б — ДКП
Рассмотрим теперь пример, касающийся среднеквадратичной ошибки, получающейся в результате субоптимальной винеровской фильтрации. Для этого рассмотрим фильтр с использованием ПУА, упорядоченным по Уолшу, и ПУА, упорядоченным по Адамару, при  и
и  . Отношение сигнал/шум выбирается равным единице, т. е.
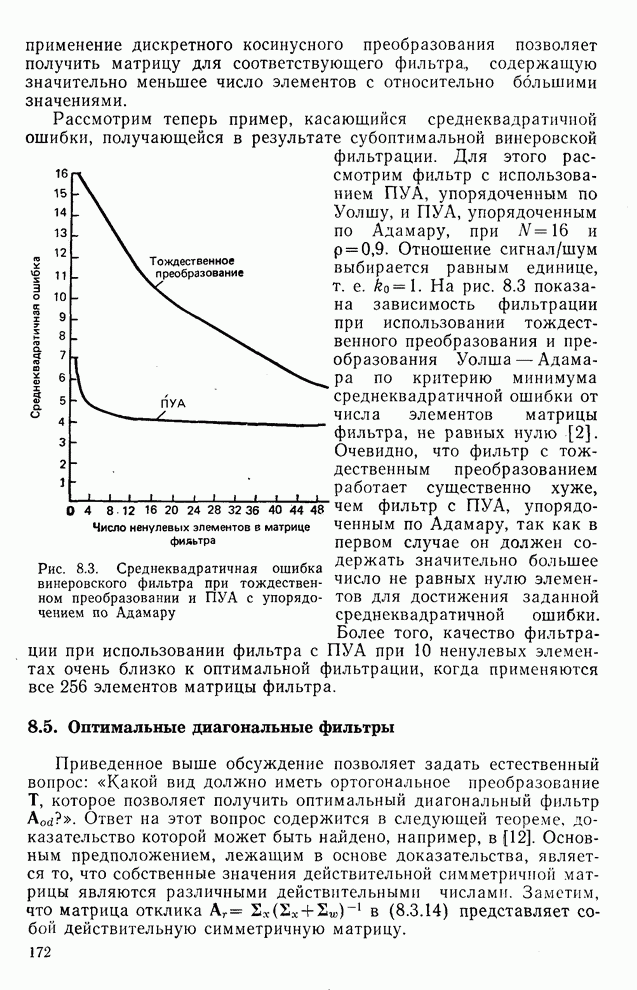
. Отношение сигнал/шум выбирается равным единице, т. е.  . На рис. 8.3 показана зависимость фильтрации при использовании тождественного преобразования и преобразования Уолша — Адамара по критерию минимума среднеквадратичной ошибки от числа элементов матрицы фильтра, не равных нулю [2]. Очевидно, что фильтр с тождественным преобразованием работает существенно хуже, чем фильтр с ПУА, упорядоченным по Адамару, так как в первом случае он должен содержать значительно большее число не равных нулю элементов для достижения заданной среднеквадратичной ошибки. Более того, качество фильтрации при использовании фильтра с ПУА при 10 ненулевых элементах очень близко к оптимальной фильтрации, когда применяются все 256 элементов матрицы фильтра.
. На рис. 8.3 показана зависимость фильтрации при использовании тождественного преобразования и преобразования Уолша — Адамара по критерию минимума среднеквадратичной ошибки от числа элементов матрицы фильтра, не равных нулю [2]. Очевидно, что фильтр с тождественным преобразованием работает существенно хуже, чем фильтр с ПУА, упорядоченным по Адамару, так как в первом случае он должен содержать значительно большее число не равных нулю элементов для достижения заданной среднеквадратичной ошибки. Более того, качество фильтрации при использовании фильтра с ПУА при 10 ненулевых элементах очень близко к оптимальной фильтрации, когда применяются все 256 элементов матрицы фильтра.

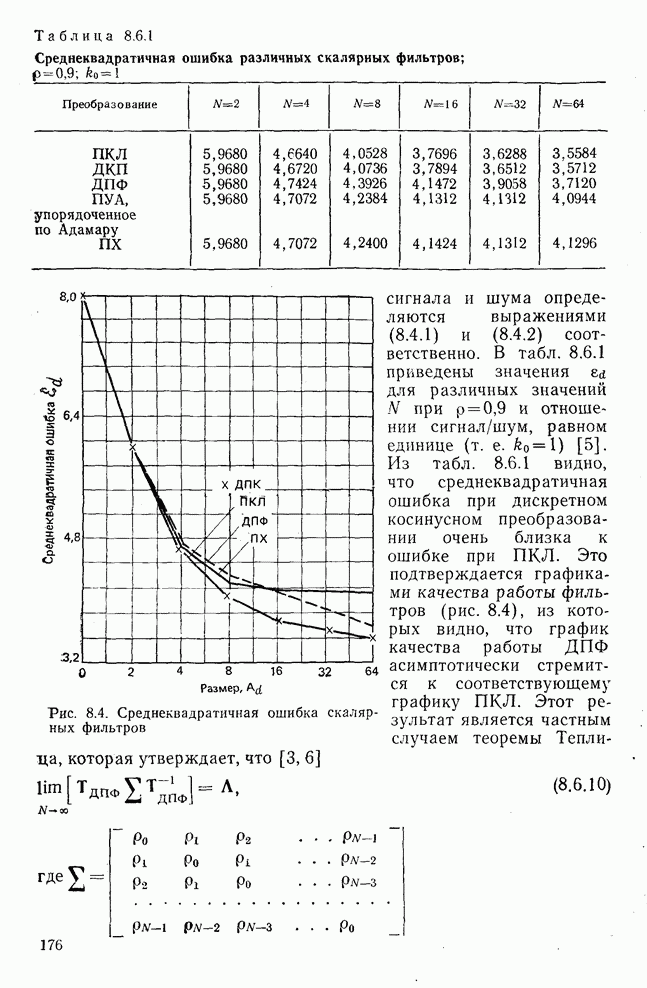
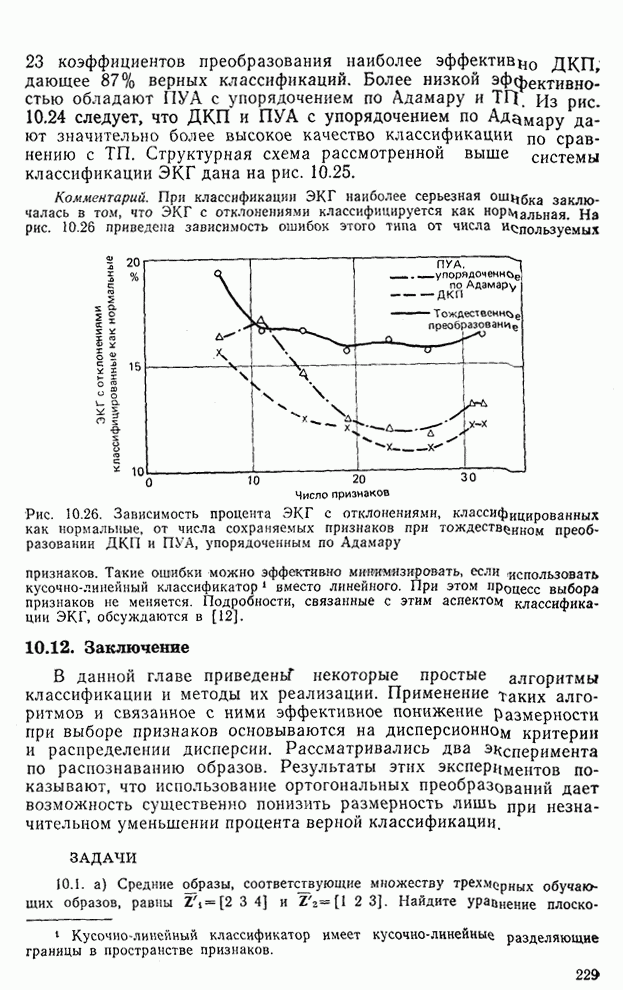
Рис. 8.3. Среднеквадратичная ошибка винеровского фильтра при тождественном преобразовании и ПУА с упорядочением по Адамару
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ АВТОРОВ
- ГЛАВА 1. Введение
- 1.1. Общие замечания
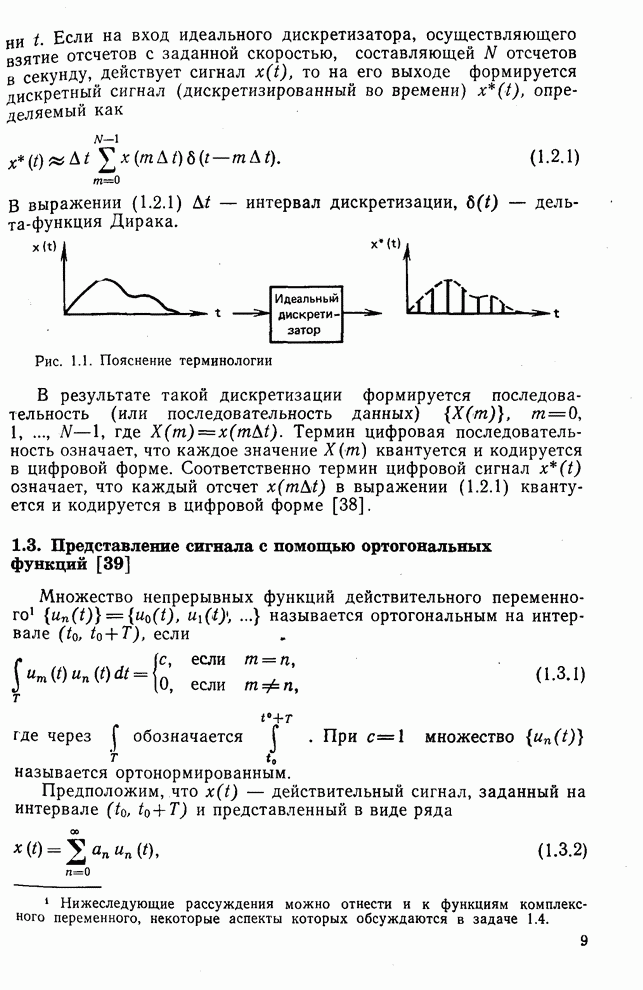
- 1.2. Терминология
- 1.3. Представление сигнала с помощью ортогональных функций [39]
- 1.4. Содержание книги
- ЗАДАЧИ
- ГЛАВА 2. Фурье-представление сигналов
- 2.1. Фурье-представление
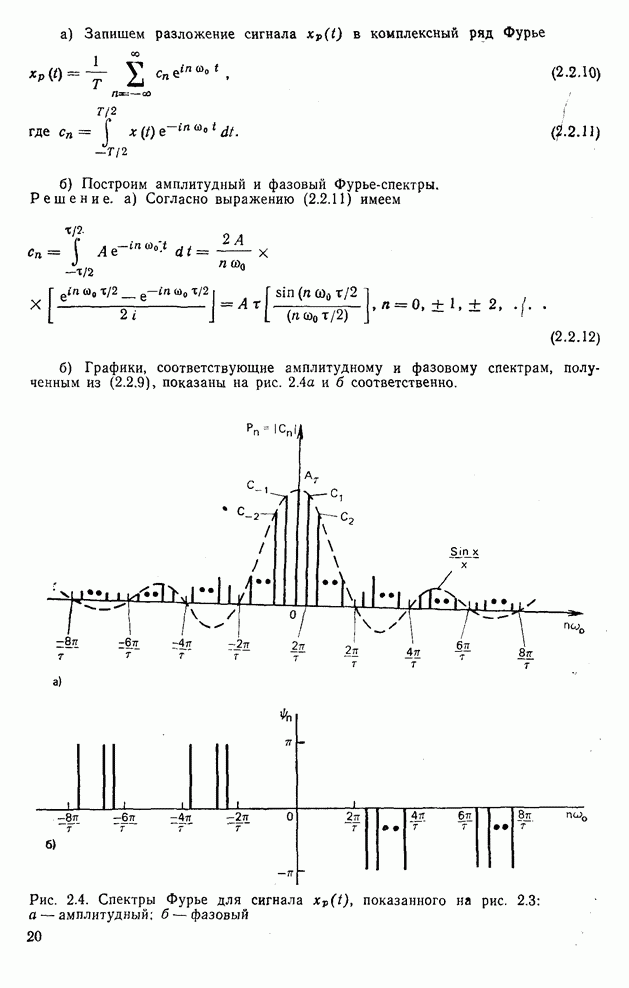
- 2.2. Спектр мощности, амплитудный и фазовый спектры
- 2.3. Преобразование Фурье
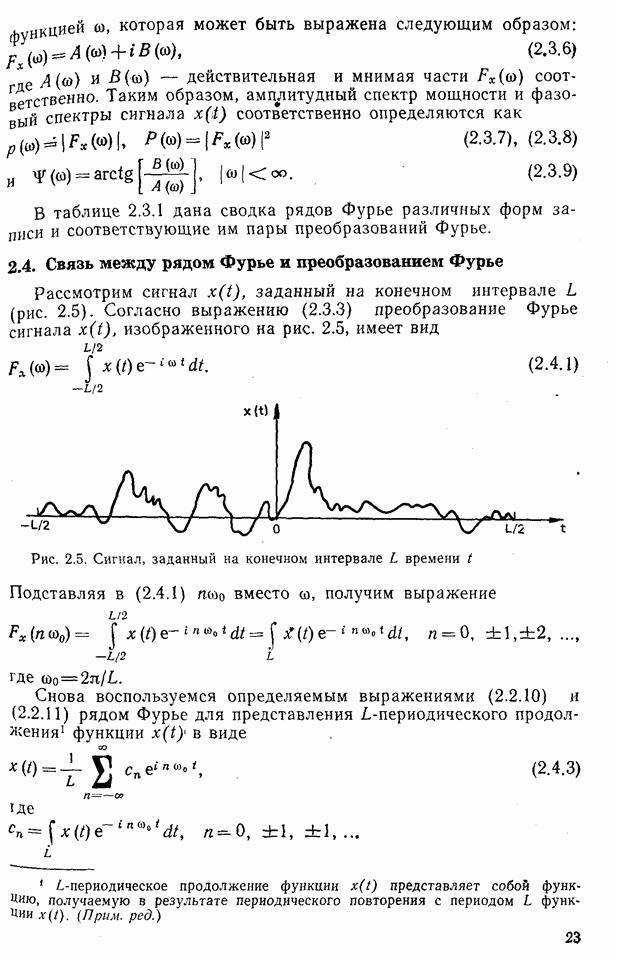
- 2.4. Связь между рядом Фурье и преобразованием Фурье
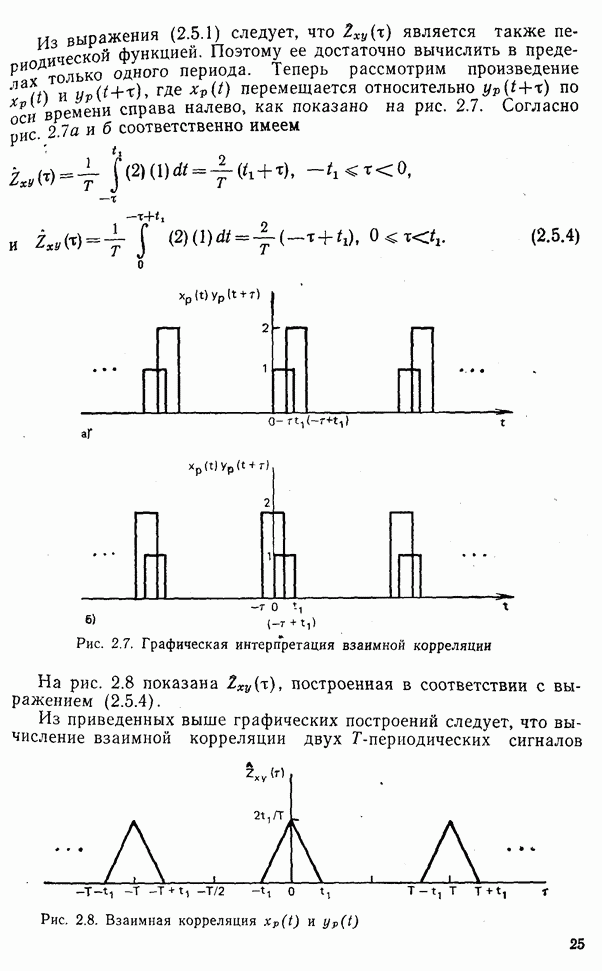
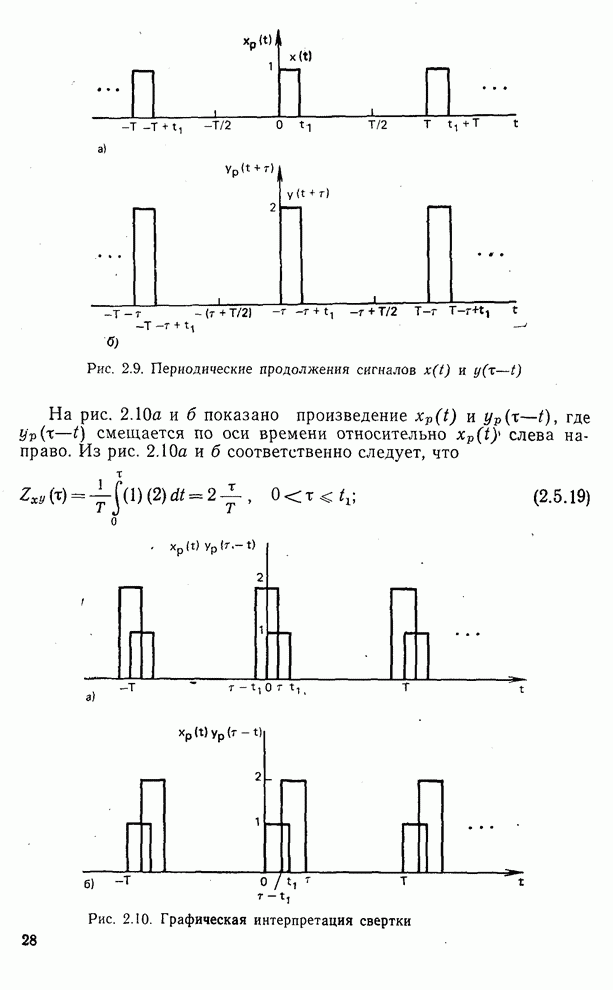
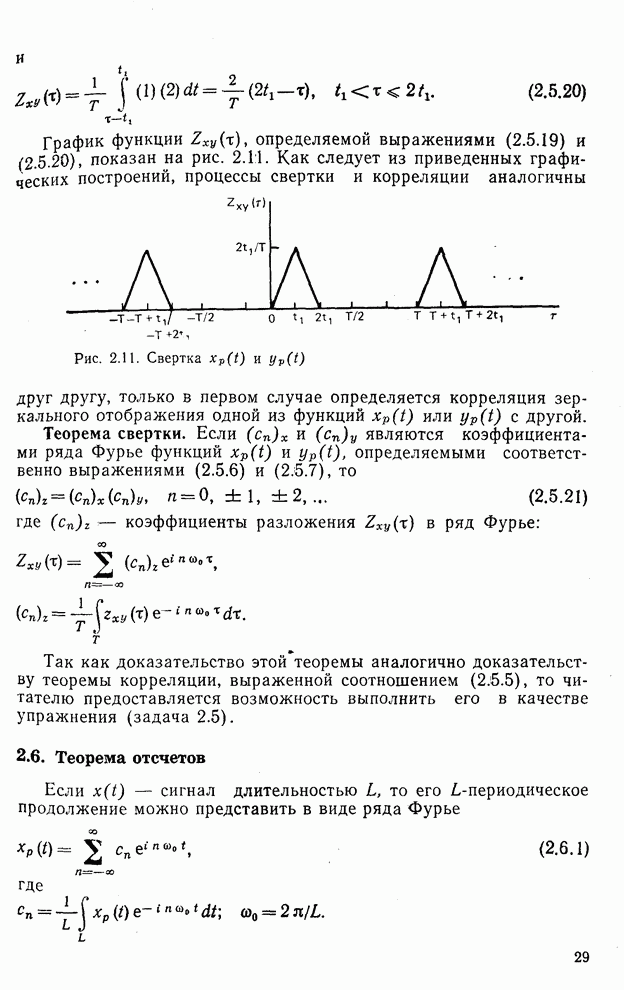
- 2.5. Взаимная корреляция, автокорреляция и свертка
- 2.6. Теорема отсчетов
- 2.7. Заключение
- ЗАДАЧИ
- ГЛАВА 3. Фурье-представление временных последовательностей
- 3.1. Определение дискретного преобразования Фурье
- 3.2. Свойства ДПФ
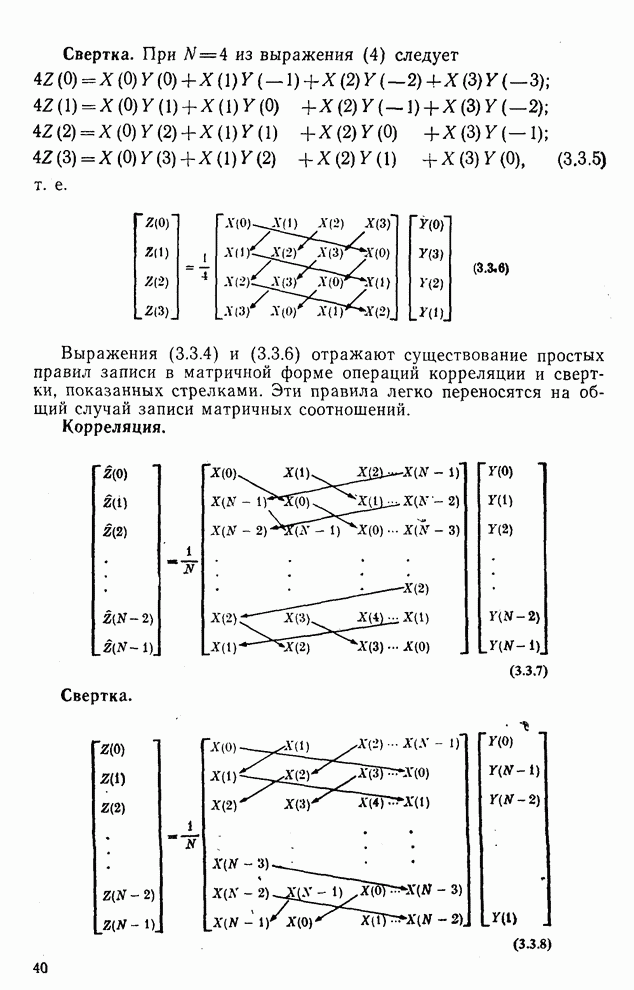
- 3.3. Матричное представление корреляции и свертки
- 3.4. Соотношение между ДПФ, преобразованием Фурье и рядом Фурье
- 3.5. Спектр мощности, амплитудный и фазовый спектры
- 3.6. Двумерное ДПФ
- 3.7. Мгновенный спектр Фурье
- 3.8. Заключение
- ЗАДАЧИ 3.1.
- ГЛАВА 4. Быстрое преобразование Фурье
- 4.1. Постановка задачи
- 4.2. Обоснование поиска алгоритма
- 4.3. Основа для вывода алгоритма
- 4.4. Вывод алгоритма
- 4.5. Численные примеры
- 4.6. Перестановка данных
- 4.7. Объем вычислений и памяти
- 4.8. Некоторые приложения
- 4.9. Заключение
- Приложение 4.1
- ЗАДАЧИ
- ГЛАВА 5. Класс ортогональных функций
- 5.1. Определение частости
- 5.2. Обозначение непрерывных и дискретных функций
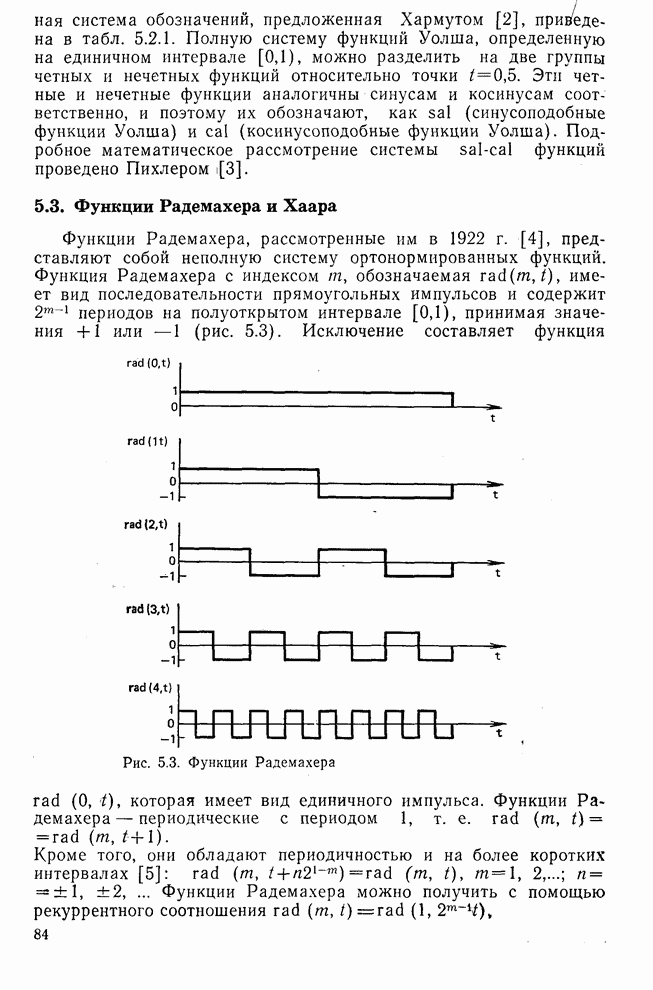
- 5.3. Функции Радемахера и Хаара
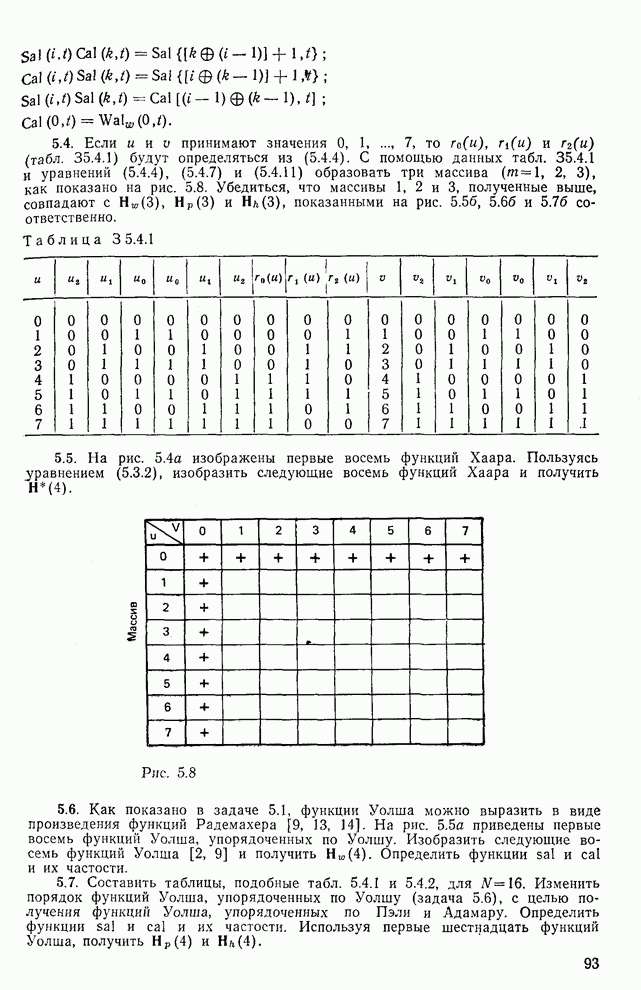
- 5.4. Функции Уолша
- 5.5. Заключение
- Приложение 5.1. Код Грея
- ЗАДАЧИ
- ГЛАВА 6. Преобразование Уолша—Адамара
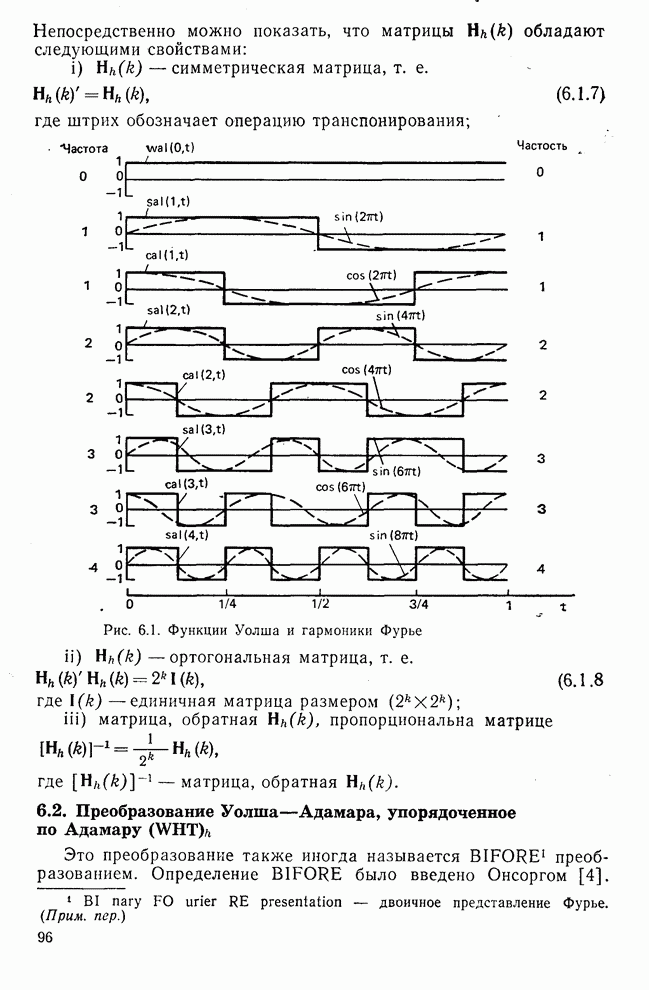
- 6.1. Представление сигналов в виде ряда Уолша
- 6.2. Преобразование Уолша—Адамара, упорядоченное по Адамару
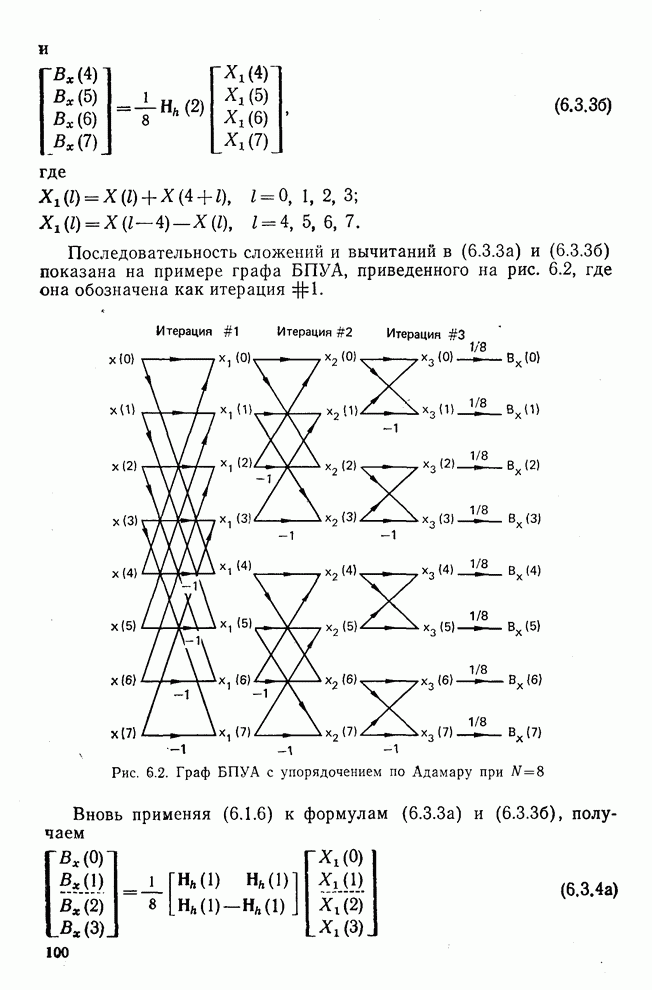
- 6.3. Быстрое преобразование Уолша-Адамара, упорядоченное по Адамару (БПУА)
- 6.4. Преобразование Уолша—Адамара, упорядоченное по Уолшу
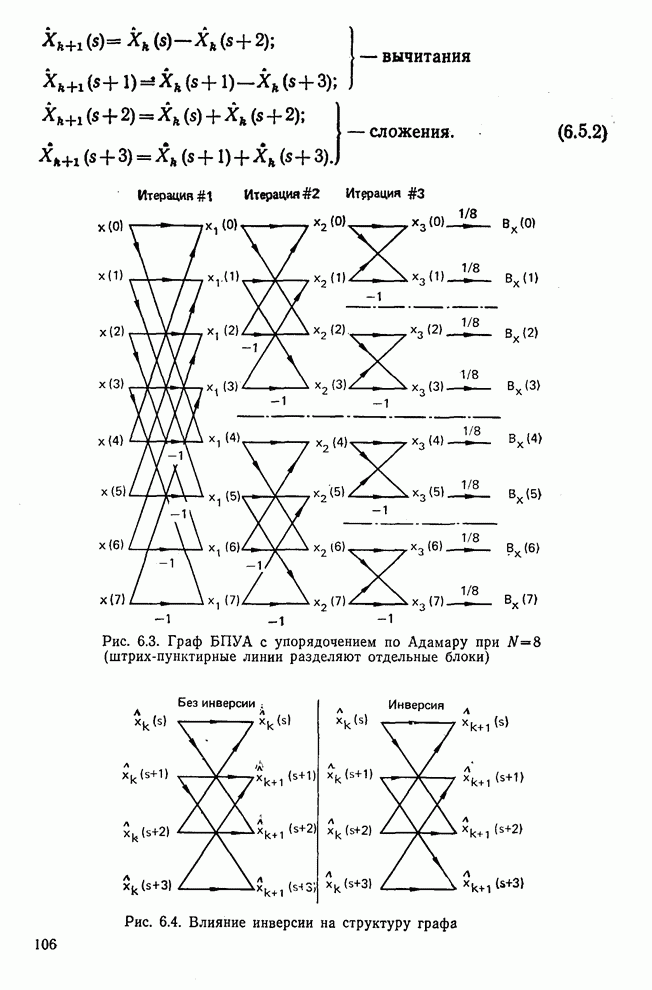
- 6.5. Быстрое преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.6. Циклический и диадический сдвиги
- 6.7. Спектр ПУА с упорядочением по Уолшу [10—12]
- 6.8. Спектр ПУА с упорядочением по Адамару [4, 13]
- 6.9. Физическая интерпретация энергетического спектра ПУА с упорядочением по Адамару [13]
- 6.10. Модифицированное преобразование Уолша—Адамара МПУА)
- 6.11. Циклическая и диадическая корреляция (свертка)
- 6.12. Многомерные преобразования Уолша—Адамара с упорядочением по Адамару и по Уолшу
- 6.13. Заключение
- ПРИЛОЖЕНИЕ 6.1
- ЗАДАЧИ
- ГЛАВА 7. Различные ортогональные преобразования
- 7.1. Факторизация матриц
- 7.2. Обобщенное преобразование [4, 5]
- 7.3. Преобразование Хаара [ПХ]
- 7.4. Алгоритмы для вычисления преобразования Хаара (ПХ)
- 7.5. Пилообразные матрицы
- 7.6. Определение пилообразного преобразования
- 7.7. Дискретное косинусное преобразование (ДКП)
- 7.8. Двумерные преобразования
- 7.9. Заключение
- ПРИЛОЖЕНИЕ 7.1. Кронекеровское произведение матриц
- ПРИЛОЖЕНИЕ 7.2 Факторизация матриц
- ЗАДАЧИ
- ГЛАВА 8. Обобщенная винеровская фильтрация
- 8.1. Некоторые основные матричные операции
- 8.2. Математическая модель [2]
- 8.3. Расчет фильтра
- 8.4. Субоптимальная винеровская фильтрация
- 8.5. Оптимальные диагональные фильтры
- 8.6. Субоптимальные диагональные фильтры [2—4]
- 8.7. Двумерная винеровская фильтрация
- 8.8. Заключение
- ПРИЛОЖЕНИЕ 8.1. Терминология и определения
- ЗАДАЧИ
- ГЛАВА 9. Сжатие данных
- 9.1. Поиск оптимального преобразования
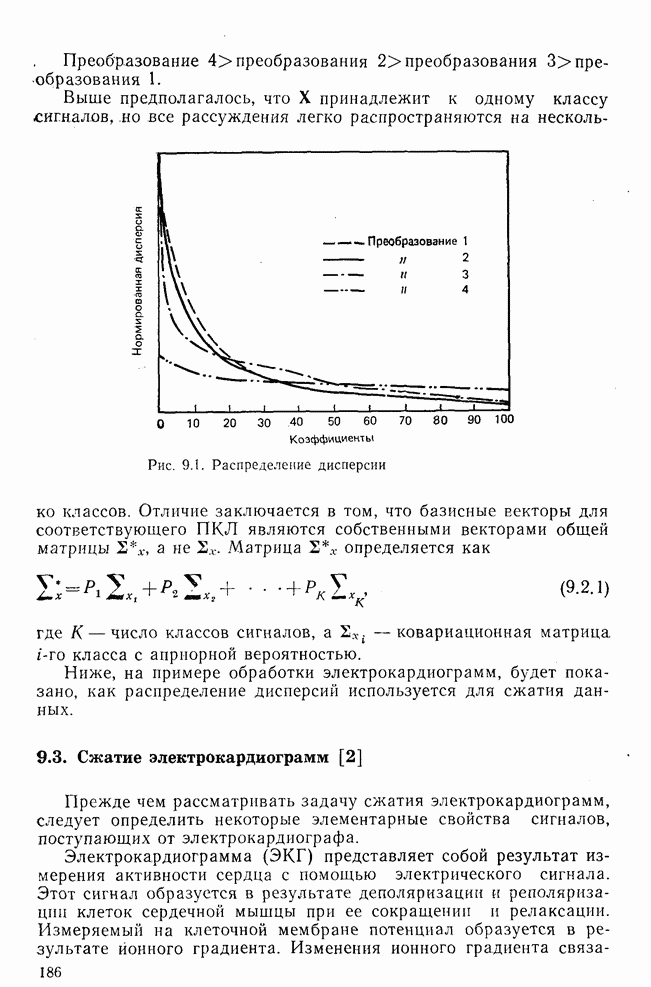
- 9.2. Дисперсионный критерий и распределение дисперсии [1]
- 9.3. Сжатие электрокардиограмм [2]
- 9.4. Основные понятия сжатия изображений
- 9.5. Примеры сжатия изображений
- 9.6. Дополнительные соображения
- 9.7. Заключение
- ПРИЛОЖЕНИЕ 9.1. Множители Лагранжа [9]
- ЗАДАЧИ
- ГЛАВА 10. Выбор признаков и распознавание образов
- 10.1. Введение
- 10.2. Принцип обучения
- 10.3. d-мерные образы
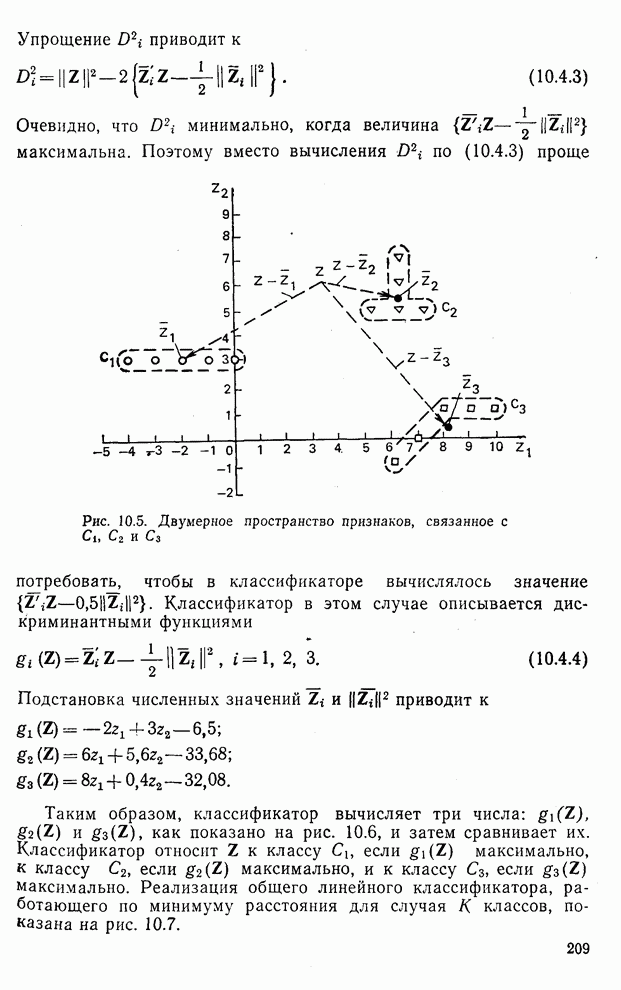
- 10.4. Задача трех классов
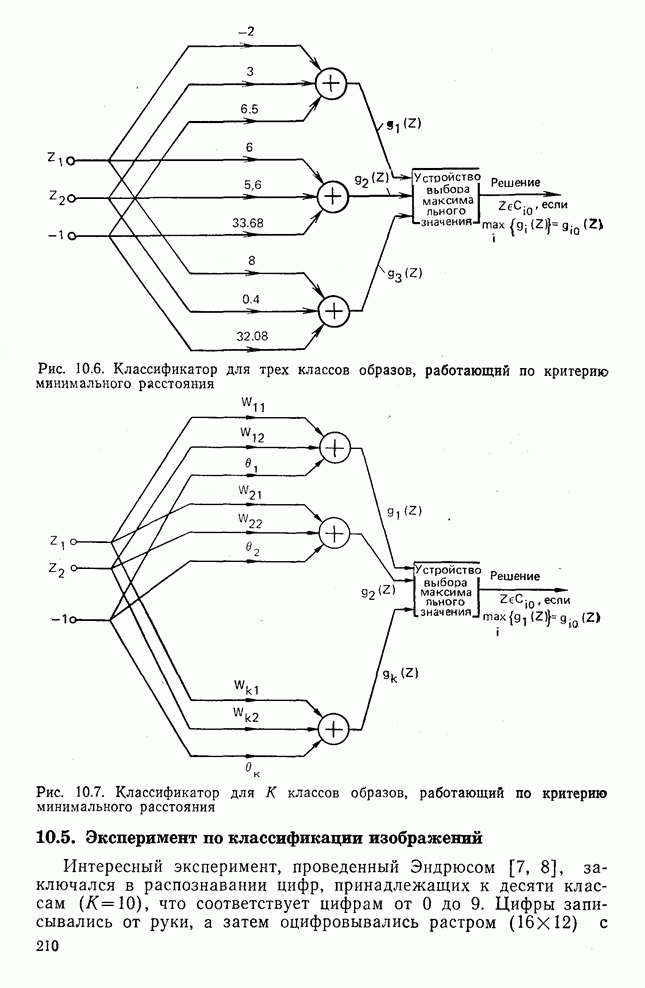
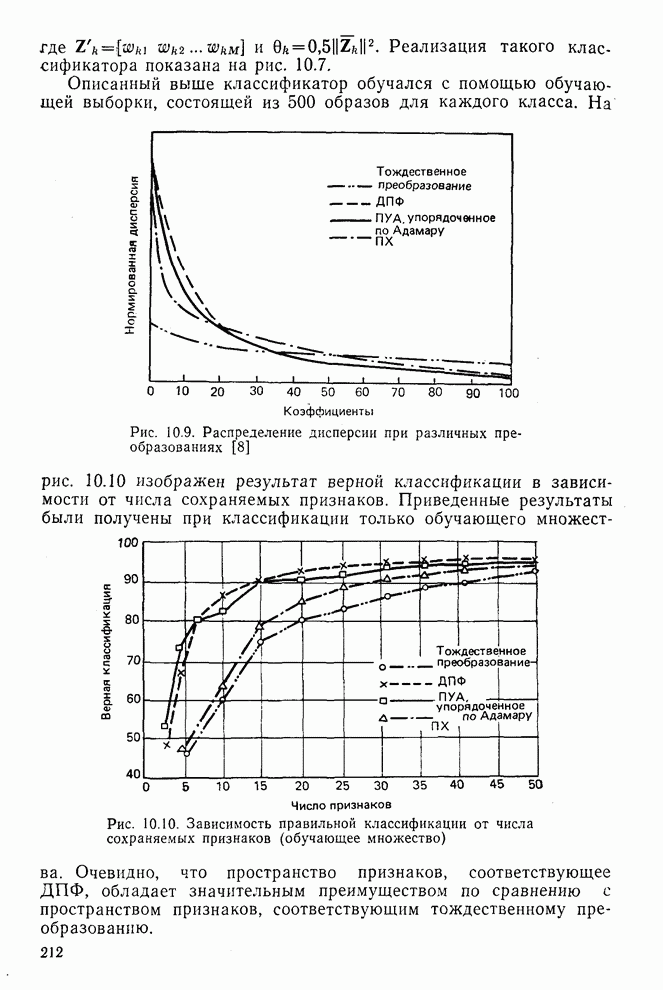
- 10.5. Эксперимент по классификации изображений
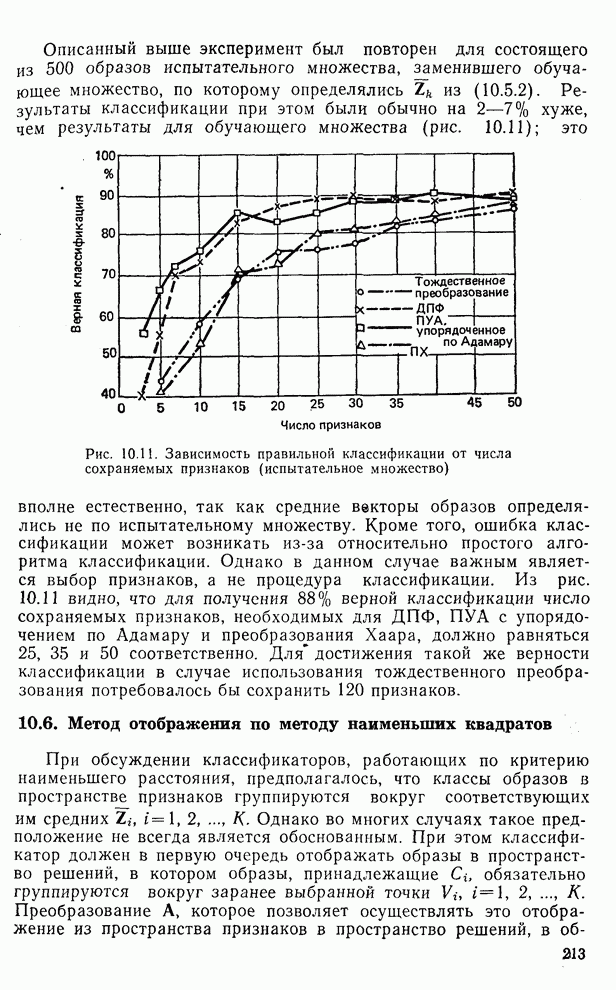
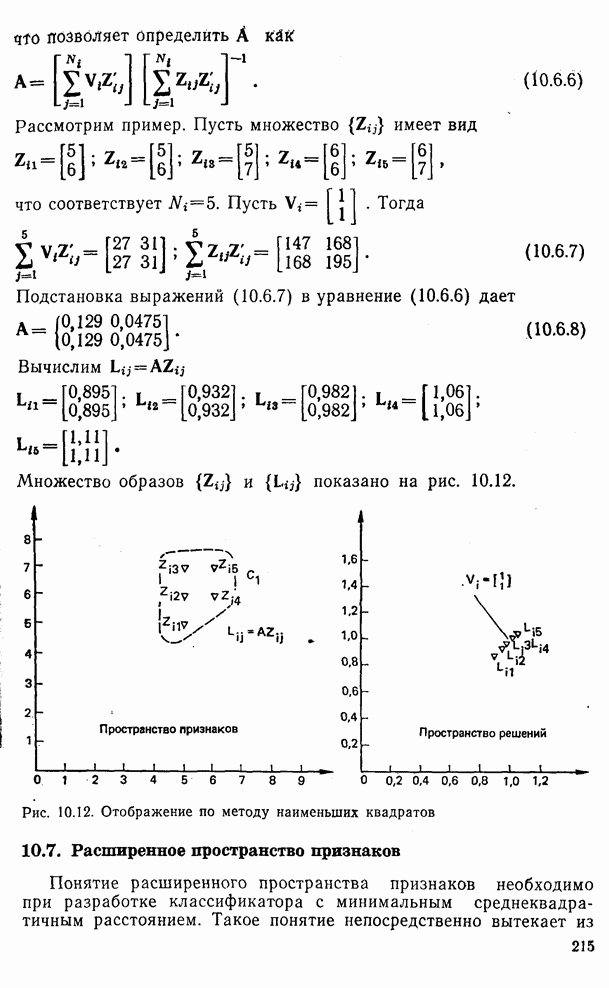
- 10.6. Метод отображения по методу наименьших квадратов
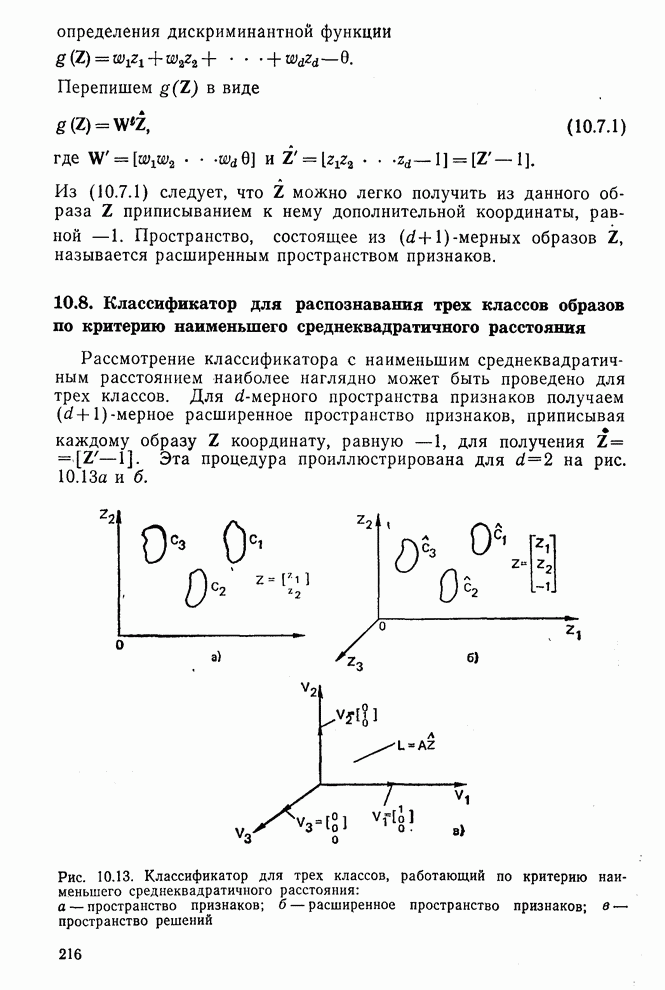
- 10.7. Расширенное пространство признаков
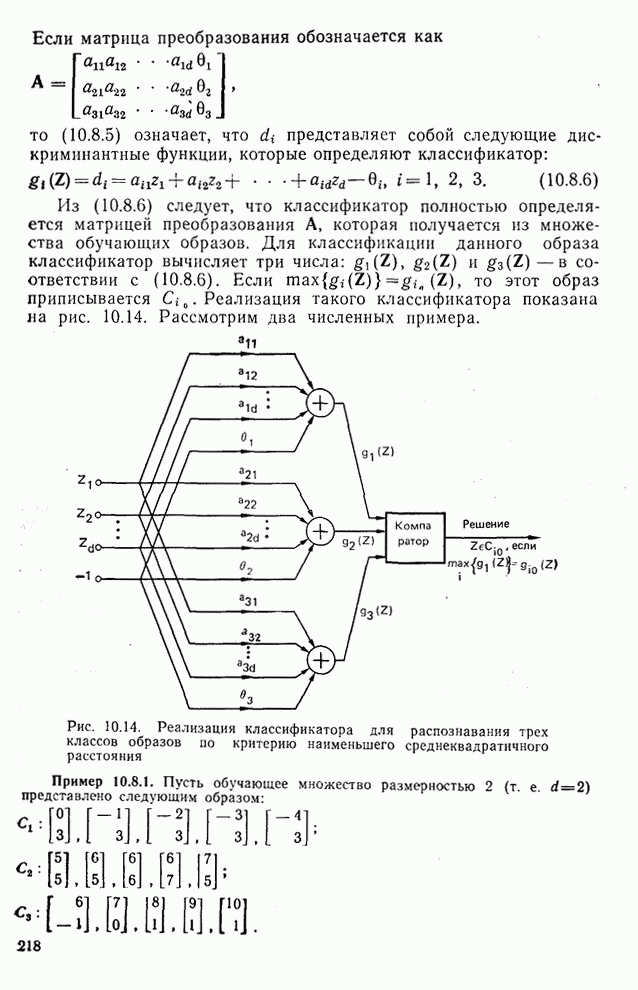
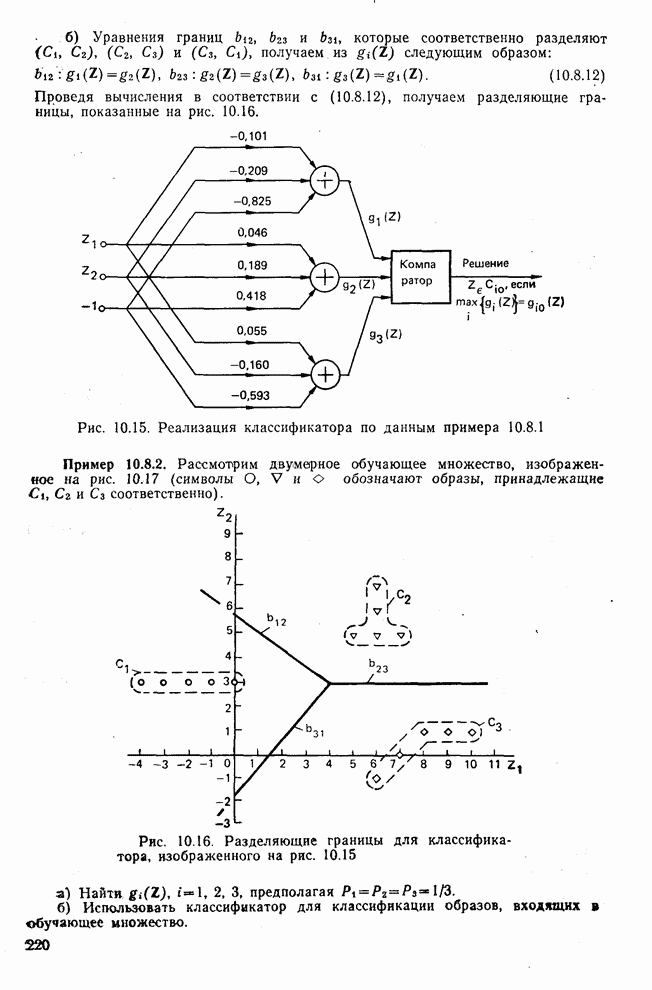
- 10.8. Классификатор для распознавания трех классов образов по критерию наименьшего среднеквадратичного расстояния
- 10.9. Классификатор для распознавания К классов образов по критерию наименьшего среднеквадратичного расстояния [9-11]
- 10.10. Квадратичные классификаторы [2]
- 10.11. Эксперимент по классификации ЭКГ
- 10.12. Заключение
- ЗАДАЧИ
- СПИСОК ЛИТЕРАТУРЫ