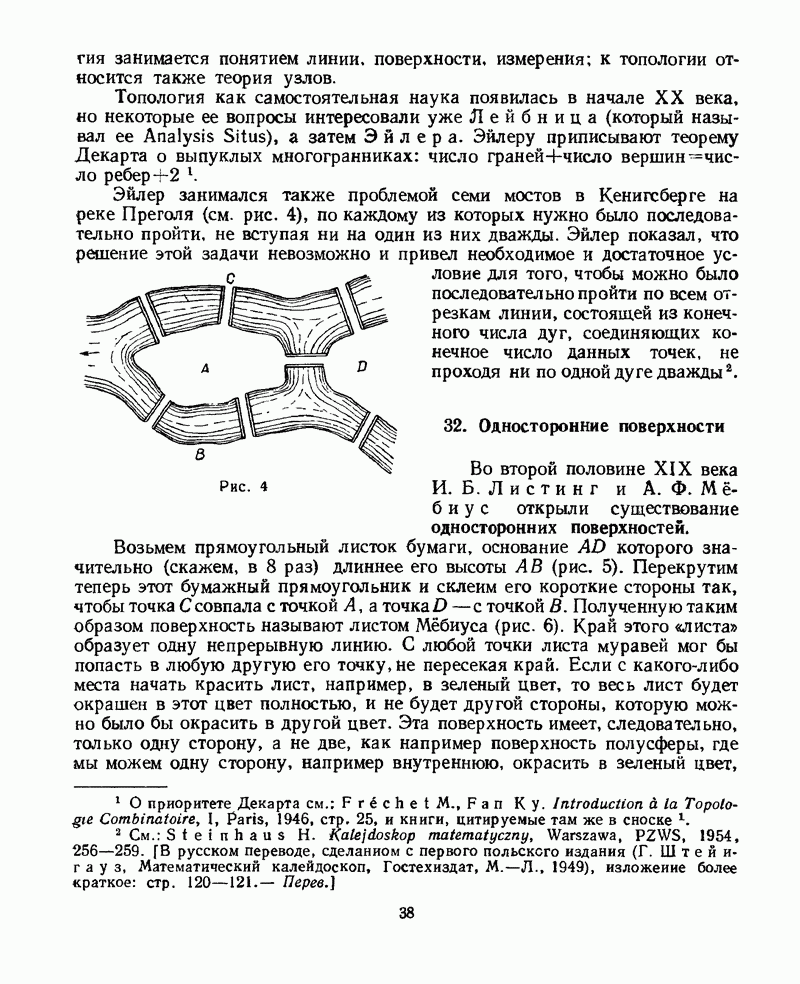
11. Несчетные множества

Возникает вопрос, счетно ли множество всех действительных чисел. Оказывается, можно доказать, что оно несчетно. Можно ли доказательство несчетности множества всех действительных чисел излагать в средней школе? Это зависит от того, что знают учащиеся о действительных числах.

Если, например, им известен факт, что каждое действительное число имеет одно и только одно представление в виде бесконечной десятичной дроби, в которой бесконечно много цифр отлично от 9, то доказательство несчетности множества всех действительных чисел можно вывести из более общего утверждения, что для любой бесконечной последовательности действительных чисел

существует действительное число х, не совпадающее ни с одним из членов этой последовательности. Вот доказательство этой теоремы.

Пусть

— представления чисел их, в виде бесконечных десятичных дробей, каждая из которых содержит бесконечно много цифр, отличных от 9. Здесь — целые числа.

Определим теперь бесконечную последовательность цифр следующим образом. Пусть для данного натурального числа будет наименьшей цифрой, отличной от и от 9. Очевидно, что имеется не меньше 8 цифр, отличных от и от 9. Таким образом, получим:

Бесконечная десятичная дробь

будет, следовательно, представлять некоторое действительное число х, такое, что и будет содержать бесконечно много цифр, отличных от 9. При этом хфип при так как для любого натурального числа дроби, представляющие и содержащие бесконечно много цифр, отличных от 9, отличаются в цифре.

Наша теорема доказана. Из нее сразу же вытекает, что множество всех действительных чисел не может быть счетным

Учащиеся средней школы знают о существовании взаимно однозначного соответствия между действительными числами и точками прямой.

Положение точки на прямой может быть определено с помощью действительного числа, определяющего расстояние этой точки от заданной точки О на прямой, причем расстояния точек, находящихся вправо от точки О (расположенной на горизонтальной прямой), считают положительными, а находящихся влево от точки О — отрицательными.

Ввиду наличия взаимно однозначного соответствия между действительными числами и точками прямой, из теоремы о несчетности множества всех действительных чисел следует теорема о несчетности множества всех точек прямой. Теорему эту можно легко доказать также и геометрически, исходя из так называемой аксиомы Асколи: Если бесконечная последовательность отрезков, из которых каждый, начиная со второго, целиком содержится в предшествующем ему отрезке, то существует (по меньшей мере одна) точка, общая всем этим отрезкам.

Допустим, что множество всех точек прямой Р — счетно; мы можем в таком случае расположить их в бесконечную последовательность

Очевидно, что можно построить отрезок не содержащий точки Далее, можно построить отрезок являющийся частью отрезка и не содержащий точки Для этого достаточно разделить отрезок на три равные части и взять в качестве ту, которая ни внутри, ни на конце не содержит точки (если этим свойством обладает не одна часть то выберем, скажем, самую левую). Затем так же строим отрезок являющийся частью отрезка и не содержащий точки

По аксиоме Асколи существует точка , общая всем отрезкам Эта точка не совпадает ни с одной точкой последовательности (6), так как при любом натуральном точка лежит на отрезке и, наоборот, точка (как это следует из способа построения отрезка не лежит на отрезке Предположение, что последовательность (6) содержит все точки прямой Р, ведет, следовательно, к противоречию. Следовательно, множество всех точек прямой является несчетным.