31. Топология

Топологическим пространством называют всякое множество М. любому подмножеству которого поставлено произвольным способом в соответствие некоторое подмножество множества М, такое, что для любых подмножеств множества М были выполнены условия (1), (2) и (3).

Метрическое пространство М становится топологическим пространством, если замыкание множества являющегося подмножеством множества М, определить как множество всех точек множества М, обладающих тем свойством, что для любого положительного числа существует по меньшей мере одна точка множества (не обязательно отличная от ), расстояние которой от меньше

Несмотря на свою общность, понятие метрического пространства нашло много применений в математическом анализе.

Перейдем теперь к топология. Это раздел геометрии, изучающий свойства формы и взаимного расположения фигур. Это наука о таких свойствах геометрических объектов, которые не исчезают при взаимно однозначных и непрерывных в обе стороны преобразованиях этих объектов, т. е. свойствах, которые не исчезнут при произвольном изгибе и растяжении или сжатии фигуры без разрывов и склеиваний в каком-либо месте. В частности, топология

занимается понятием линии, поверхности, измерения; к топологии относится также теория узлов.

Топология как самостоятельная наука появилась в начале XX века, но некоторые ее вопросы интересовали уже Лейбница (который называл ее Analysis Situs), а затем Эйлера. Эйлеру приписывают теорему Декарта о выпуклых многогранниках: число граней -число вершин число ребер

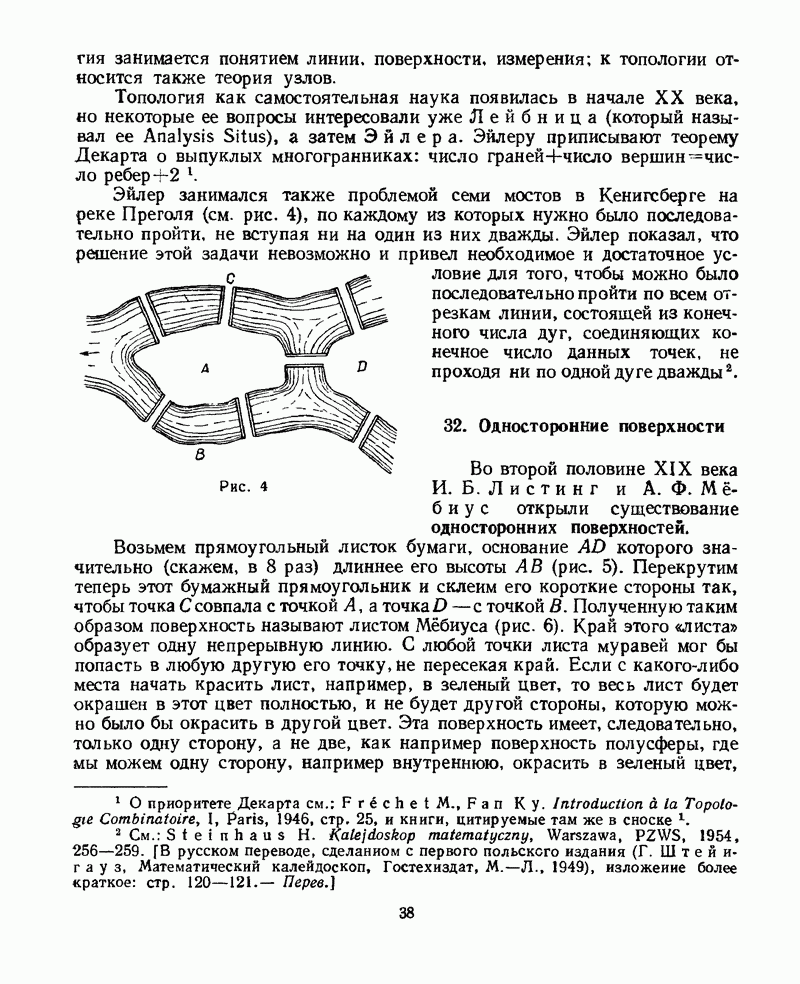
Эйлер занимался также проблемой семи мостов в Кенигсберге на реке Преголя (см. рис. 4), по каждому из которых нужно было последовательно пройти, не вступая ни на один из них дважды. Эйлер показал, что решение этой задачи невозможно и привел необходимое и достаточное условие для того, чтобы можно было последовательно пройти по всем отрезкам линии, состоящей из конечного числа дуг, соединяющих конечное число данных точек, не проходя ни по одной дуге дважды.

Рис. 4