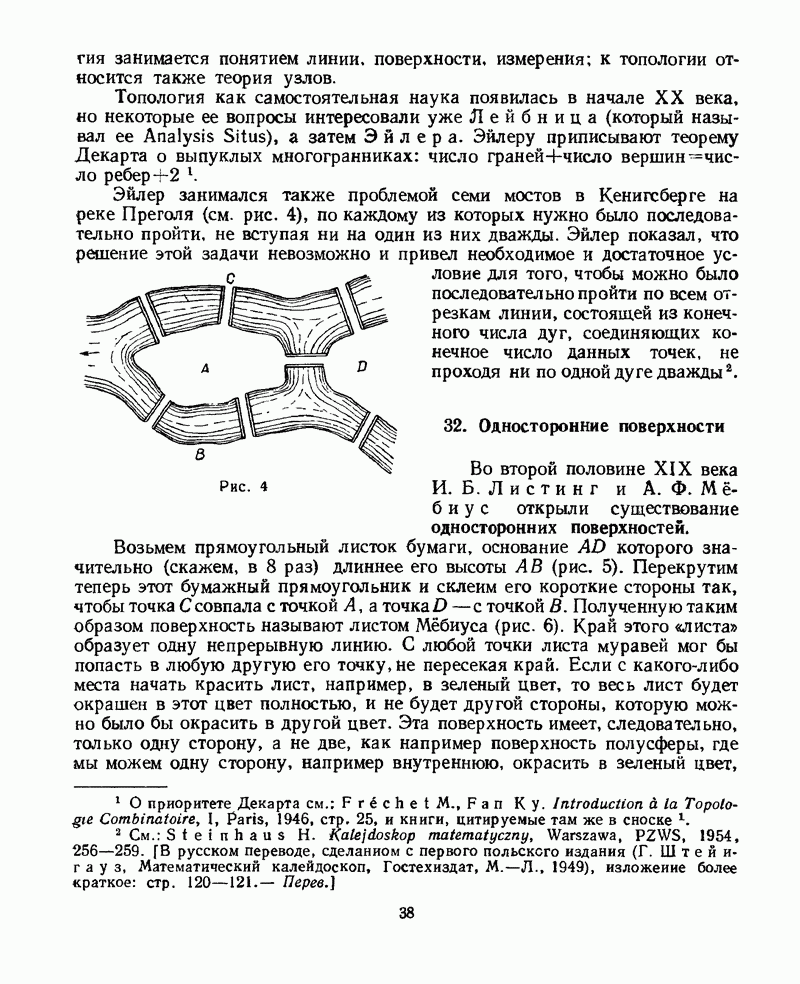
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
23. Принцип математической индукции
Можно доказать, что если для данного упорядоченного множества справедлив принцип трансфинитной индукции, то это множество должно быть вполне упорядоченным.
Что же касается принципа обычной математической индукции, то легко доказать, что он равносилен утверждению  что множество всех натуральных чисел, упорядоченное по их величине, является вполне упорядоченным.
что множество всех натуральных чисел, упорядоченное по их величине, является вполне упорядоченным.
Действительно, допустим, что утверждение  справедливо. В этом случае из определения вполне упорядоченного множества следует, что в каждом непустом множестве натуральных чисел имеется наименьшее число. Пусть теперь будет дано такое утверждение Т (в котором говорится о натуральном числе
справедливо. В этом случае из определения вполне упорядоченного множества следует, что в каждом непустом множестве натуральных чисел имеется наименьшее число. Пусть теперь будет дано такое утверждение Т (в котором говорится о натуральном числе  которое справедливо для числа
которое справедливо для числа  и для которого из справедливости утверждения Т для какого-либо натурального числа
и для которого из справедливости утверждения Т для какого-либо натурального числа  вытекает его справедливость для числа
вытекает его справедливость для числа 
Если бы существовало натуральное число х, для которого утверждение Т не имело бы силы, то множество  всех таких чисел было бы непустым и в силу утверждения
всех таких чисел было бы непустым и в силу утверждения  в нем имелось бы наименьшее число
в нем имелось бы наименьшее число  . Это число
. Это число  было бы натуральным числом, для которого утверждение Т не имело бы
было бы натуральным числом, для которого утверждение Т не имело бы
силы, и из условия относительно утверждения Т (что оно справедливо для числа 1) следовало бы, что  Утверждение Т было бы, следовательно, справедливо для натурального числа
Утверждение Т было бы, следовательно, справедливо для натурального числа  что, по смыслу условия, принятого для утверждения Т, влечет за собой его справедливость для числа
что, по смыслу условия, принятого для утверждения Т, влечет за собой его справедливость для числа  что противоречит предположению. Утверждение Т должно быть, следовательно, справедливо для любого натурального числа. Мы доказали таким образом, что из утверждения
что противоречит предположению. Утверждение Т должно быть, следовательно, справедливо для любого натурального числа. Мы доказали таким образом, что из утверждения  вытекает принцип математической индукции.
вытекает принцип математической индукции.
Допустим теперь справедливость принципа математической индукции. Пусть  есть некоторое произвольное непустое множество натуральных чисел. Допустим, что в множестве
есть некоторое произвольное непустое множество натуральных чисел. Допустим, что в множестве  нет наименьшего числа. Очевидно, что в таком случае число 1 не принадлежит множеству
нет наименьшего числа. Очевидно, что в таком случае число 1 не принадлежит множеству 
Обозначим через Т утверждение (в котором говорится о натуральном числе  «Ни одно натуральное число, меньшее или равное
«Ни одно натуральное число, меньшее или равное  не принадлежит множеству
не принадлежит множеству  Утверждение Т очевидным образом справедливо для числа
Утверждение Т очевидным образом справедливо для числа  Если утверждение Т справедливо для натурального числа
Если утверждение Т справедливо для натурального числа  то оно имеет силу и для числа
то оно имеет силу и для числа  так как в противном случае число
так как в противном случае число  было бы, как легко видеть, наименьшим числом множества
было бы, как легко видеть, наименьшим числом множества  что противоречит предположению о том, что множество не имеет наименьшего числа.
что противоречит предположению о том, что множество не имеет наименьшего числа.
Следовательно, на основании принципа индукции утверждение Т справедливо для любого натурального числа  . Но в таком случае из утверждения Т вытекает, что множество
. Но в таком случае из утверждения Т вытекает, что множество  является пустым, что противоречит предположению.
является пустым, что противоречит предположению.
Итак, допущение, что существует непустое множество натуральных чисел, не содержащее наименьшего числа, приводит к противоречию. Мы доказали, таким образом, что из принципа математической индукции вытекает, что множество всех натуральных чисел, упорядоченное по их величине, является вполне упорядоченным.
Тем самым мы доказали, что утверждение  равносильно принципу математической индукции.
равносильно принципу математической индукции.
| << Предыдущий параграф | Следующий параграф >> |
- ОТ ИЗДАТЕЛЬСТВА
- От редакции польского издания
- ГЛАВА I. О МНОЖЕСТВАХ И ИХ СВОЙСТВАХ
- 2. Равенство множеств
- 4. Пустое множество
- 5. Конечные множества
- 6. Равночисленные множества
- 7. Взаимно однозначное соответствие
- 8. Равномощные множества
- 9. Счетные множества
- 10. Сумма множеств
- 11. Несчетные множества
- 12. Континуум-гипотеза
- 13. Непересекающиеся множества
- 14. Сравнение мощностей бесконечных множеств
- 15. Аксиома выбора
- 16. Алгебра множеств
- 17. Упорядоченные множества
- 18. Подобные упорядоченные множества
- 19. Плотные упорядоченные множества. Сечения. Щели
- 20. Заполнение щелей
- 21. Вполне упорядоченные множества
- 22. Принцип трансфинитной индукции
- 23. Принцип математической индукции
- 24. Функции
- 25. Декартово произведение
- 26. Метрические пространства
- 27. Евклидовы пространства
- 28. Борелевские множества
- 29. Открытые и замкнутые множества
- 30. Производное множество и замыкание множества
- 31. Топология
- 32. Односторонние поверхности
- 33. Проблема четырех красок
- ГЛАВА II. О КОНГРУЭНТНОСТИ МНОЖЕСТВ. КОНГРУЭНТНОСТЬ МНОЖЕСТВ ПРИ КОНЕЧНОМ РАЗБИЕНИИ
- 2. Движения множеств
- 3. Конгруэнтность множеств при конечном разбиении
- 4. Преобразования сжатия