| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ПРИЛОЖЕНИЕ Б
МАТЕМАТИЧЕСКИЙ ОБЗОР
Для того чтобы понять изложенный в этой книге материал, необходимо иметь некоторые познания в области алгебры и тригонометрии. Кроме того, полезно, хотя и не столь необходимо, уметь выполнять кое-какие действия с комплексными числами и производными (которые рассматриваются в разделе математического анализа). Это приложение содержит кратчайшее изложение основных положений алгебры комплексных чисел и дифференциального исчисления. Ни в коем случае не предполагается, что оно может заменить собой учебник. Для самообразования в области математики рекомендуем книгу: D. Kleppner, N. Ramsey. Quick Calculus (John Wiley  Sons, 1972).
Sons, 1972).
Комплексные числа
Комплексное число представляется в следующей форме:

где а и  -действительные числа, a i представляет собой корень квадратный из — 1 (вместо i в остальных частях книги использован символ j для того, чтобы не возникало путаницы с обозначением малосигнального тока); а называют действительной частью комплексного числа, а
-действительные числа, a i представляет собой корень квадратный из — 1 (вместо i в остальных частях книги использован символ j для того, чтобы не возникало путаницы с обозначением малосигнального тока); а называют действительной частью комплексного числа, а  -мнимой. Для обозначения комплексных чисел используют иногда жирный шрифт или подчеркивают символ жирной линией. Во всех остальных случаях, когда нет специальных обозначений, предполагается, что вы сами знаете, когда перед вами комплексное число!
-мнимой. Для обозначения комплексных чисел используют иногда жирный шрифт или подчеркивают символ жирной линией. Во всех остальных случаях, когда нет специальных обозначений, предполагается, что вы сами знаете, когда перед вами комплексное число!
Комплексные числа, так же как и действительные, можно складывать, вычитать, умножать:

Все эти действия выполняются просто в том смысле, что i рассматривается как величина, на которую умножена мнимая часть, а все остальные - простая арифметика. Отметим, что  (это используется в примере с умножением), а операция деления упрощается путем умножения числителя и знаменателя на сопряженное комплексное число, которое получается при изменении знака мнимой части на противоположный. Иногда сопряженное комплексное число отмечают звездочкой.
(это используется в примере с умножением), а операция деления упрощается путем умножения числителя и знаменателя на сопряженное комплексное число, которое получается при изменении знака мнимой части на противоположный. Иногда сопряженное комплексное число отмечают звездочкой.

Модуль комплексного числа равен

Для того чтобы определить модуль комплексного числа, нужно умножить это число на сопряженное и взять квадратный корень от произведения. Модуль произведения (или частного) двух комплексных чисел представляет собой просто произведение (или частное) их модулей.

Рис. Б.1.
Для действительной и мнимой частей комплексного числа иногда используется следующая запись:

Для того чтобы получить действительную или мнимую часть, нужно записать число в виде а  взять а или
взять а или  . При этом может потребоваться выполнить умножение или деление, так как комплексное число может быть весьма запутанным.
. При этом может потребоваться выполнить умножение или деление, так как комплексное число может быть весьма запутанным.
Для представления комплексных чисел иногда используют комплексную плоскость. Она представляет собой такую же плоскость, как и плоскость с координатами  . При изображении комплексного числа действительная часть берется как координата
. При изображении комплексного числа действительная часть берется как координата  , а мнимая - как у, т. е. на этой плоскости используются оси ДЕЙСТВИТЕЛЬНАЯ
, а мнимая - как у, т. е. на этой плоскости используются оси ДЕЙСТВИТЕЛЬНАЯ  и МНИМАЯ (у), как показано на рис.
и МНИМАЯ (у), как показано на рис.  . Используя эту аналогию, иногда комплексные числа записывают с помощью координат
. Используя эту аналогию, иногда комплексные числа записывают с помощью координат  :
:

Как и обычные точки с координатами  , комплексные числа можно представлять в полярных координатах; это представление называют тригонометрическим. Например, число
, комплексные числа можно представлять в полярных координатах; это представление называют тригонометрическим. Например, число  можно записать и так (рис.
можно записать и так (рис.  ):
):

где  .
.
Если учесть, что

(это выражение, известное под названием формулы Эйлера, нетрудно получить, если представить экспоненциальную функцию в виде ряда Тейлора), то получим показательную форму записи:

т. e. модуль комплексного числа R и угол  - это просто полярные координаты точки, представляющей число на комплексной плоскости. Показательная (или полярная) форма представления удобна для выполнения операций умножения (или деления) комплексных чисел-модули чисел перемножаются (делятся), а углы-аргументы складываются (вычитаются):
- это просто полярные координаты точки, представляющей число на комплексной плоскости. Показательная (или полярная) форма представления удобна для выполнения операций умножения (или деления) комплексных чисел-модули чисел перемножаются (делятся), а углы-аргументы складываются (вычитаются):

И наконец, для того чтобы перейти от представления в полярных координатах к представлению в прямоугольных координатах, следует просто воспользоваться формулой Эйлера:

т. е.  .
.
Для того чтобы умножить комплексное число на экспоненциальную функцию, необходимо просто выполнить соответствующие операции умножения:

Дифференциальное исчисление
Начнем с понятия функции  , т. е. формулы, которая для каждого значения
, т. е. формулы, которая для каждого значения  позволяет найти значение
позволяет найти значение  Функция
Функция  является однозначной, если каждому значению
является однозначной, если каждому значению  она ставит в соответствие единственное значение у. Понятие функции
она ставит в соответствие единственное значение у. Понятие функции  иллюстрирует график, представленный на рис. Б.З. Производная у по
иллюстрирует график, представленный на рис. Б.З. Производная у по  определяется углом наклона графика у к оси
определяется углом наклона графика у к оси  . Если вы проведете касательную к графику функции в некоторой точке, то наклон касательной в этой точке и есть dy/dx, т. е. производная сама по себе представляет функцию, так как ее значение определено в каждой точке.
. Если вы проведете касательную к графику функции в некоторой точке, то наклон касательной в этой точке и есть dy/dx, т. е. производная сама по себе представляет функцию, так как ее значение определено в каждой точке.

Рис. Б.2.

Рис. Б.3.
На рис. Б.3. наклон в точке (1,1) определяется значением 2, а в точке начала координат он нулевой (немного ниже сказано, как вычисляется производная).
Пользуясь математическими терминами, можно сказать, что производная - это предел, к которому стремится отношение приращения у  к приращению
к приращению  , когда
, когда  стремится к нулю. Процитируем песенку, которую когда-то сочинили по этому поводу в Гарвардском университете (авторы Том Лехрер и Льюис Бранском):
стремится к нулю. Процитируем песенку, которую когда-то сочинили по этому поводу в Гарвардском университете (авторы Том Лехрер и Льюис Бранском):

Дифференцирование - это прямая операция, и для основных функций составлены стандартные таблицы производных. Ниже приводятся основные правила нахождения производных (и и  -это функции
-это функции  ):
):
Некоторые производные


Последнее правило представляет собой правило дифференцирования сложной функции, оно распространяется на цепочку из любого числа функций и очень полезно для вычисления производных.
Иногда функцию дифференцируют, чтобы определить значение производной в некоторой точке. В других случаях требуется найти минимум или максимум функции. Так как в точке экстремума производная равна нулю, то найденную производную приравнивают к нулю и разрешают полученное уравнение относительно  . Рассмотрите следующие примеры:
. Рассмотрите следующие примеры:

| << Предыдущий параграф | Следующий параграф >> |
- ГЛАВА 11. МИКРОПРОЦЕССОРЫ
- ВНИМАТЕЛЬНЫЙ ВЗГЛЯД НА МП 68008
- 11.01. Регистры, память и ввод-вывод
- 11.02. Система команд и способы адресации
- 11.03. Представление команд на машинном языке
- 11.04. Сигналы магистрали
- ПРИМЕР ЗАКОНЧЕННОЙ РАЗРАБОТКИ: АНАЛОГОВЫЙ УСРЕДНИТЕЛЬ СИГНАЛОВ
- 11.05. Разработка схемы
- 11.06. Программирование: определение задачи
- 11.07. Программирование: детали
- 11.08. Характеристики
- 11.09. Некоторые дополнительные соображения
- МИКРОСХЕМЫ АППАРАТНОЙ ПОДДЕРЖКИ МИКРОПРОЦЕССОРА
- 11.10. Микросхемы средней степени интеграции
- 11.11. Периферийные БИС
- 11.12. Запоминающие устройства
- 11.13. Другие микропроцессоры
- 11.14. Эмуляторы, системы проектирования, логические анализаторы и макетные платы
- ГЛАВА 12. КОНСТРУИРОВАНИЕ ЭЛЕКТРОННЫХ СХЕМ
- МЕТОД ПРОТОТИПОВ
- 12.01. Макетные платы («самолеты»)
- 12.02. Прототипы платы печатной схемы (ПС)
- 12.03. Платы под монтаж накруткой
- ПЕЧАТНЫЕ ПЛАТЫ
- 12.04. Изготовление плат печатного монтажа
- 12.05. Проектирование плат с печатным монтажом
- 12.06. Монтаж плат ПС
- 12.07. Несколько дополнительных соображений по поводу плат ПС
- 12.08. Передовая техника
- КОНСТРУИРОВАНИЕ ПРИБОРОВ
- 12.09. Установка схемных плат в приборы
- 12.10. Оформление
- 12.11. Замечания по конструкции
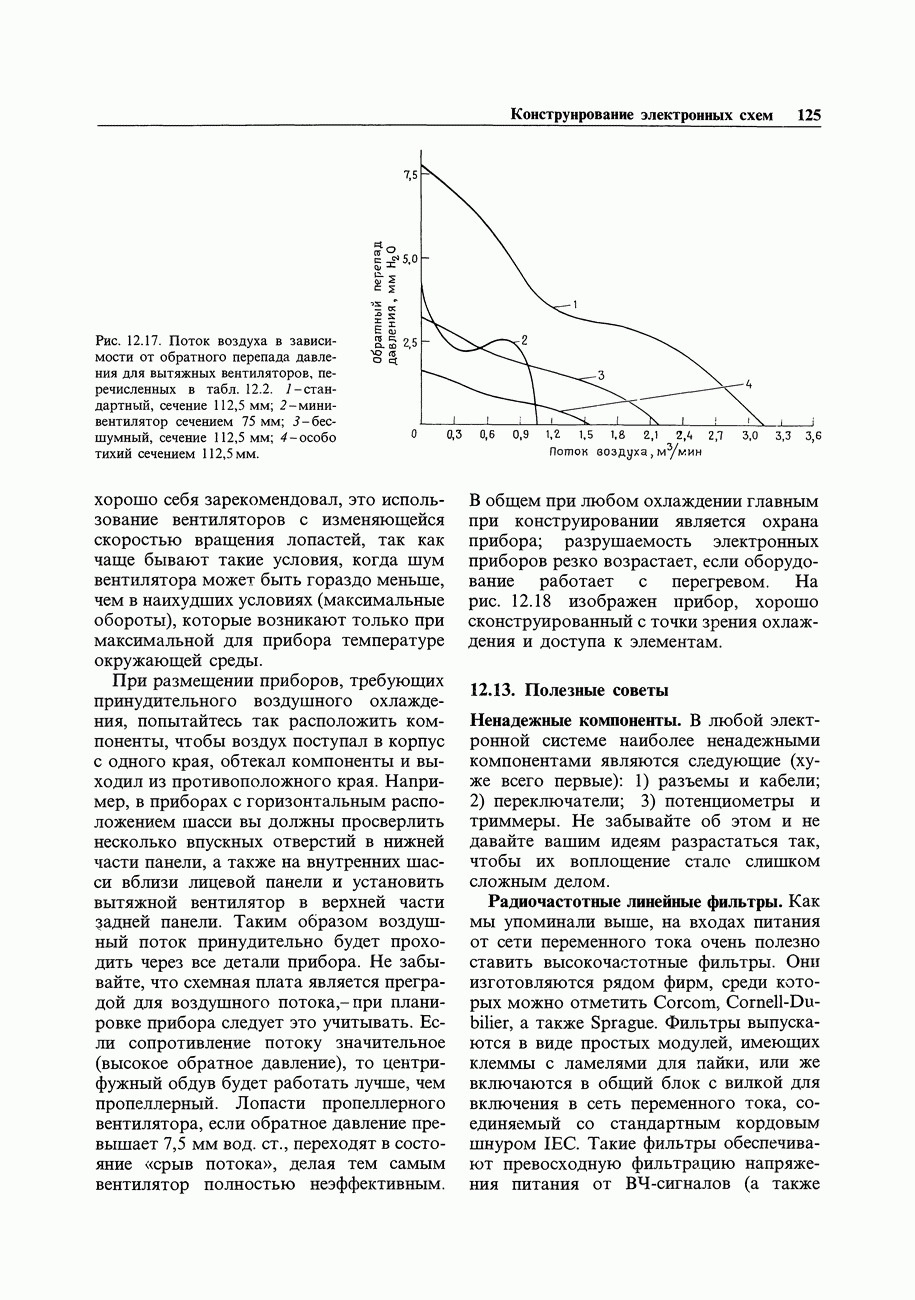
- 12.12. Охлаждение
- 12.13. Полезные советы
- 12.14. Где доставать компоненты
- ГЛАВА 13. ВЫСОКОЧАСТОТНЫЕ И БЫСТРОДЕЙСТВУЮЩИЕ ПРИБОРЫ
- 13.01. Транзисторный усилитель на высоких частотах в первом приближении
- 13.02. Высокочастотные усилители: модели для переменного тока
- 13.03. Пример высокочастотных расчетов
- 13.04. Примеры высокочастотных усилителей
- 13.05. Пример проектирования широкополосной схемы
- 13.06. Уточненные модели схем по переменному току
- 13.07. Последовательнопараллельные пары
- 13.08. Модульные усилители
- ЭЛЕМЕНТЫ ВЫСОКОЧАСТОТНЫХ СХЕМ
- 13.09. Соединительные линии
- 13.10. Отрезки линий, согласующие устройства и трансформаторы
- 13.11. Резонансные усилители
- 13.12. Элементы ВЧ-схем
- 13.13. Измерение амплитуды и мощности
- РАДИОСВЯЗЬ: АМ
- 13.14. Некоторые принципы связи
- 13.15. Амплитудная модуляция
- 13.16. Супергетеродинный приемник
- ПЕРЕДОВЫЕ МЕТОДЫ МОДУЛЯЦИИ
- 13.17. Метод одной боковой полосы (SSB)
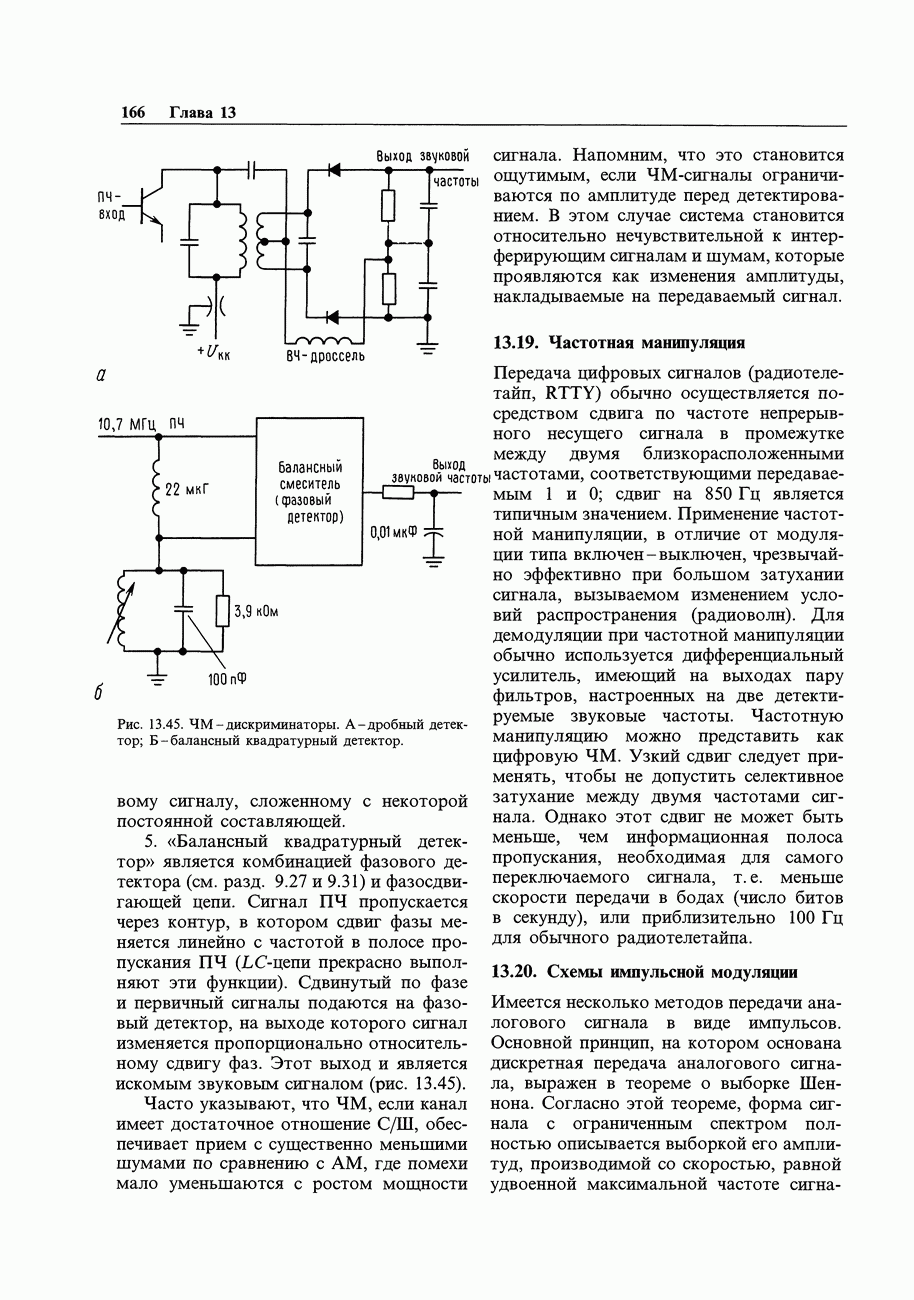
- 13.18. Частотная модуляция
- 13.19. Частотная манипуляция
- 13.20. Схемы импульсной модуляции
- СПЕЦИФИЧЕСКИЕ ОСОБЕННОСТИ РАДИОЧАСТОТНЫХ СХЕМ
- 13.21. Специальные методы конструирования
- 13.22. Экзотические ВЧ-усилители и устройства
- БЫСТРОДЕЙСТВУЮЩИЕ КЛЮЧИ
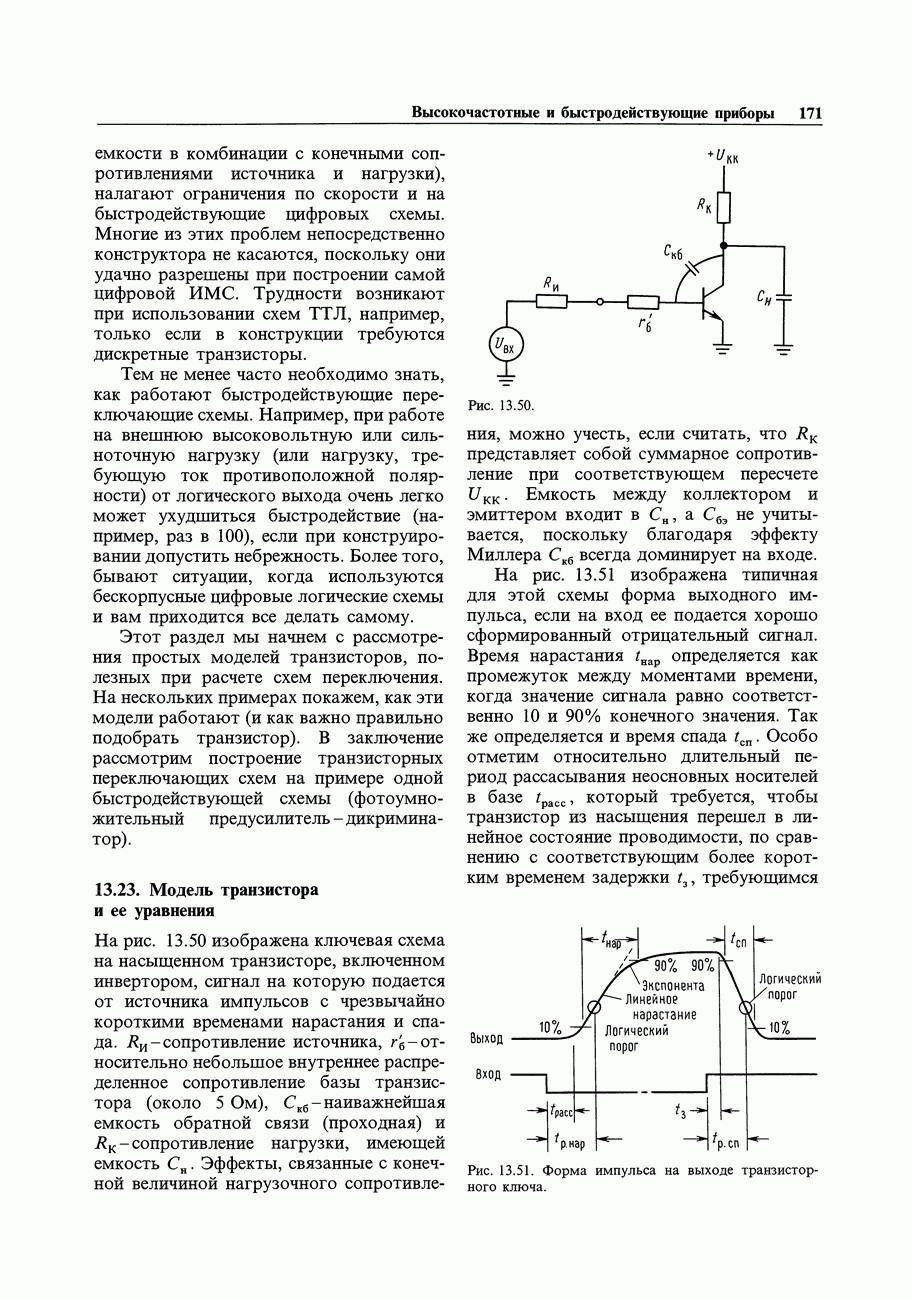
- 13.23. Модель транзистора и ее уравнения
- 13.24. Устройства аналогового моделирования
- НЕСКОЛЬКО ПРИМЕРОВ БЫСТРОДЕЙСТВУЮЩИХ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 13.25. Высоковольтный усилитель
- 13.26. Усилитель с «открытым коллектором» при работе на шину
- 13.27. Пример схемы: предусилитель для фотоумножителя
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ГЛАВА 14. ПРОЕКТИРОВАНИЕ МАЛОМОЩНЫХ УСТРОЙСТВ
- 14.01. Прикладные задачи с малым потреблением мощности
- ИСТОЧНИКИ ПИТАНИЯ
- 14.02. Типы батарей
- 14.03. Включаемые в розетку блоки питания
- 14.04. Солнечные элементы
- 14.05. Сигнальные токи
- ВЫКЛЮЧЕНИЕ ИСТОЧНИКА ПИТАНИЯ И МИКРОМОЩНЫЕ СТАБИЛИЗАТОРЫ
- 14.06. Выключение источника питания
- 14.07. Микромощные стабилизаторы
- 14.08. Опорное напряжение земли
- 14.09. Микромощные источники эталонного напряжения и датчики температуры
- 14.10. Проблемы проектирования микромощных линейных схем
- 14.11. Пример проектирования линейной схемы на дискретных элементах
- 14.12. Микромощные операционные усилители
- 14.13. Микромощные компараторы
- 14.14. Микромощные таймеры и генераторы
- ПРОЕКТИРОВАНИЕ ЦИФРОВЫХ МИКРОМОЩНЫХ УСТРОЙСТВ
- 14.15. КМОП-семейства
- 14.16. Обеспечение работы КМОП-схем в маломощном режиме
- 14.17. Микромощные микропроцессоры и периферийные устройства
- 14.18. Пример проектирования на микропроцессоре: регистратор данных типа «градус-день»
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ГЛАВА 15. ИЗМЕРЕНИЯ И ОБРАБОТКА СИГНАЛОВ
- ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 15.01. Температура
- 15.02. Уровень излучения
- 15.03. Деформация и смещение
- 15.04. Ускорение, давление, сила, скорость
- 15.05. Магнитное поле
- 15.06. Вакуумные манометры
- 15.07. Детекторы элементарных частиц
- 15.08. Щупы, используемые в биологии и химии
- ЭТАЛОНЫ ТОЧНЫХ ВЕЛИЧИН И ПРЕЦИЗИОННЫЕ ИЗМЕРЕНИЯ
- 15.09. Эталоны частоты
- 15.10. Измерения частоты, периода и временных интервалов
- 15.11. Эталоны напряжения и сопротивления и их измерение
- МЕТОДЫ СУЖЕНИЯ ПОЛОСЫ ПРОПУСКАНИЯ
- 15.12. Отношение сигнал/шум
- 15.13. Усреднение сигнала и многоканальное усреднение
- 15.14. Получение периодического сигнала
- 15.15. Обнаружение путем захвата
- 15.16. Амплитудный анализ импульсов
- 15.17. Преобразователи времени в амплитуду
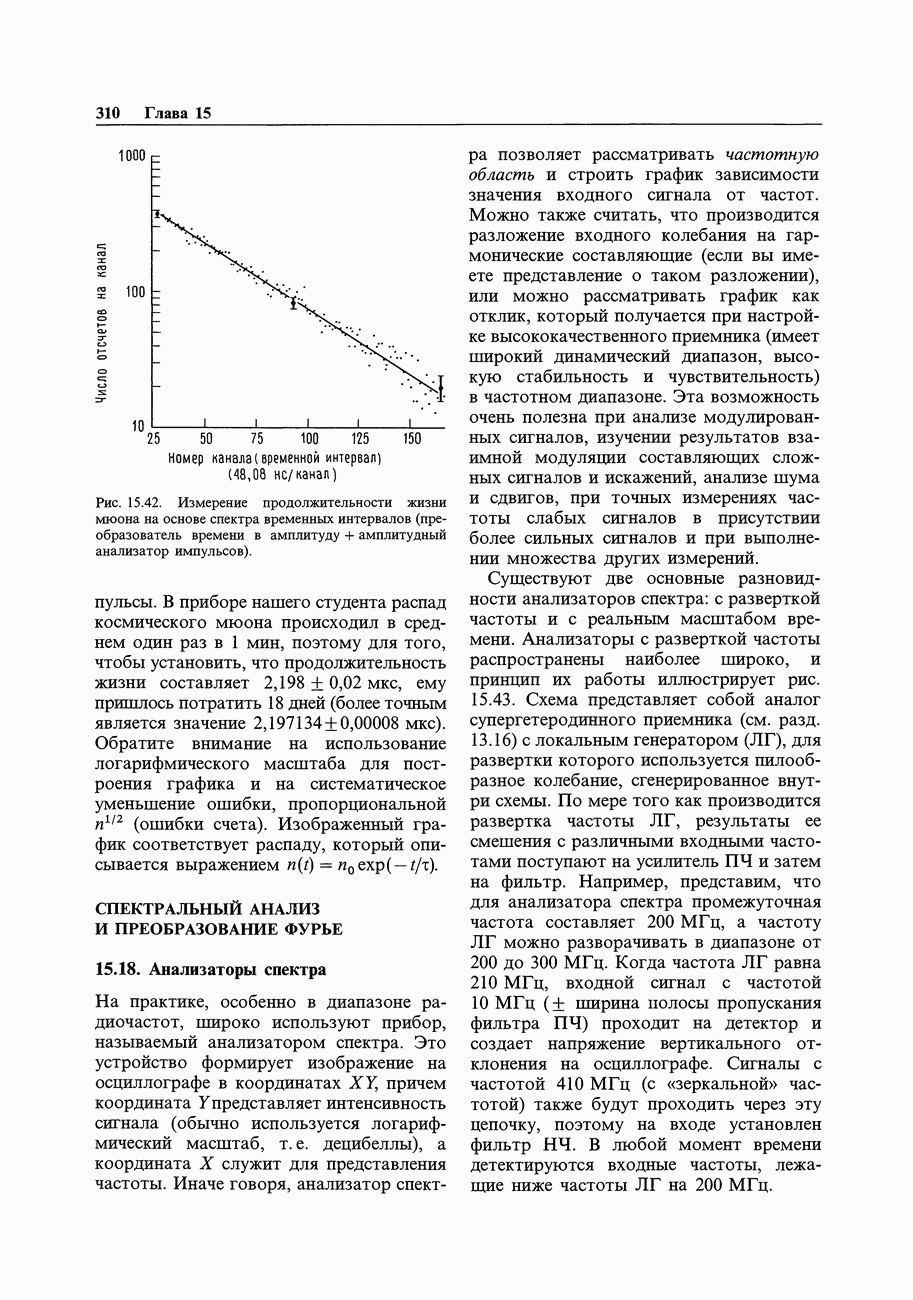
- СПЕКТРАЛЬНЫЙ АНАЛИЗ И ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 15.18. Анализаторы спектра
- 15.19. Автономный спектральный анализ
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ПРИЛОЖЕНИЕ А
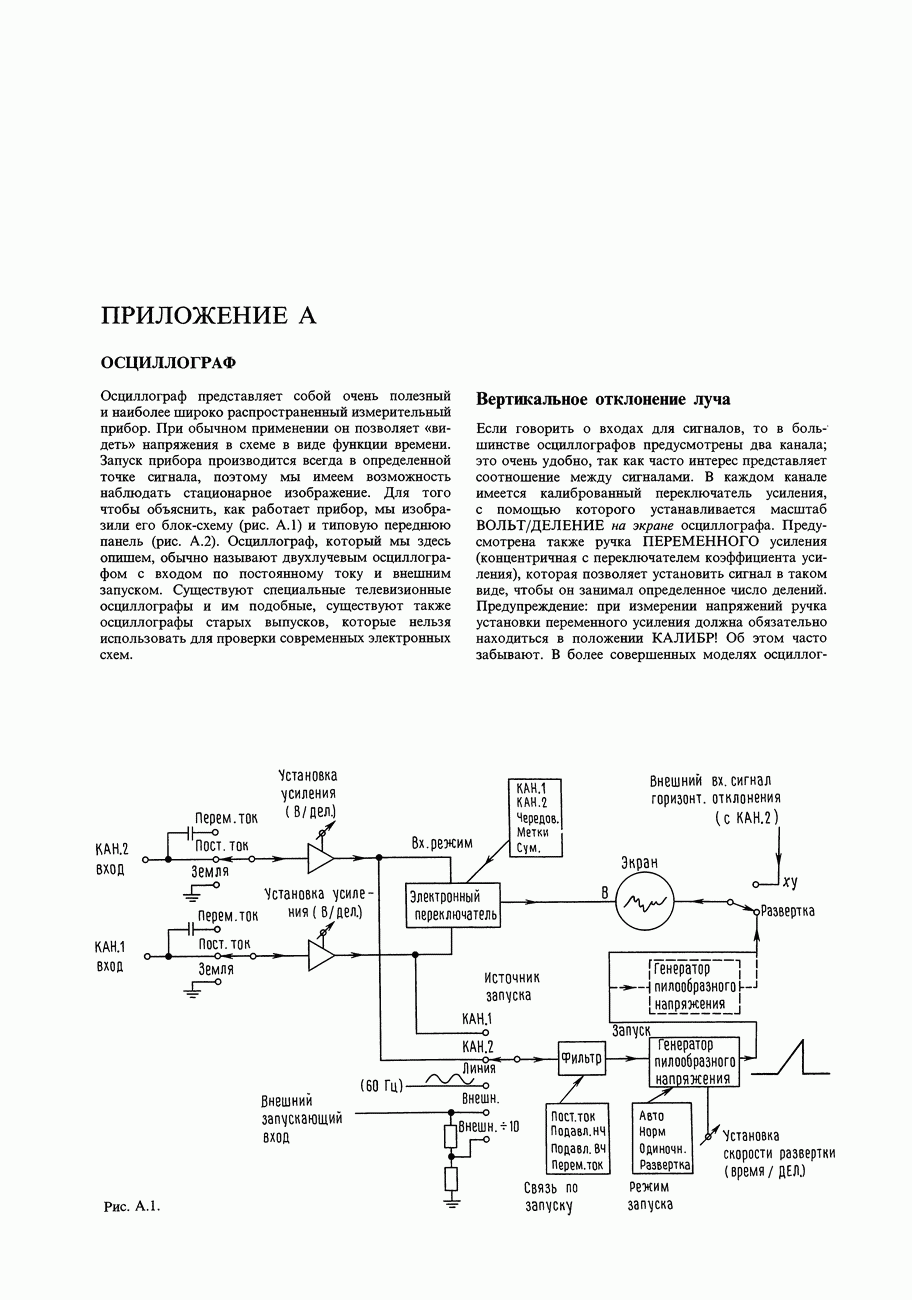
- ОСЦИЛЛОГРАФ
- ПРИЛОЖЕНИЕ Б
- МАТЕМАТИЧЕСКИЙ ОБЗОР
- ПРИЛОЖЕНИЕ В. ЦВЕТНАЯ МАРКИРОВКА РЕЗИСТОРОВ С ДОПУСКОМ 5%
- ПРИЛОЖЕНИЕ Г. ПРЕЦИЗИОННЫЕ РЕЗИСТОРЫ С ДОПУСКОМ 1%
- ПРИЛОЖЕНИЕ Д. КАК РИСОВАТЬ ПРИНЦИПИАЛЬНЫЕ СХЕМЫ
- ПРИЛОЖЕНИЕ Е. НАГРУЗОЧНЫЕ ЛИНИИ
- ПРИЛОЖЕНИЕ Ж. НАСЫЩЕНИЕ ТРАНЗИСТОРА
- ПРИЛОЖЕНИЕ З. LС-ФИЛЬТРЫ БАТТЕРВОРТА
- ПРИЛОЖЕНИЕ И. ЖУРНАЛЫ И ПЕРИОДИЧЕСКИЕ ИЗДАНИЯ ПО ЭЛЕКТРОНИКЕ
- ПРИЛОЖЕНИЕ К. ПРЕФИКСЫ В СЕРИЙНЫХ НОМЕРАХ ИС
- ПРИЛОЖЕНИЕ Л. ТЕХНИЧЕСКИЕ ПАСПОРТА НА ЭЛЕМЕНТЫ ЭЛЕКТРОННЫХ СХЕМ
- БИБЛИОГРАФИЯ