| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
15.10. Измерения частоты, периода и временных интервалов
Оказывается, что измерять частоту и период колебаний с высокой степенью точности на редкость просто - для этого достаточно иметь генератор эталонной частоты и несложную цифровую схему.
Измерение частоты.
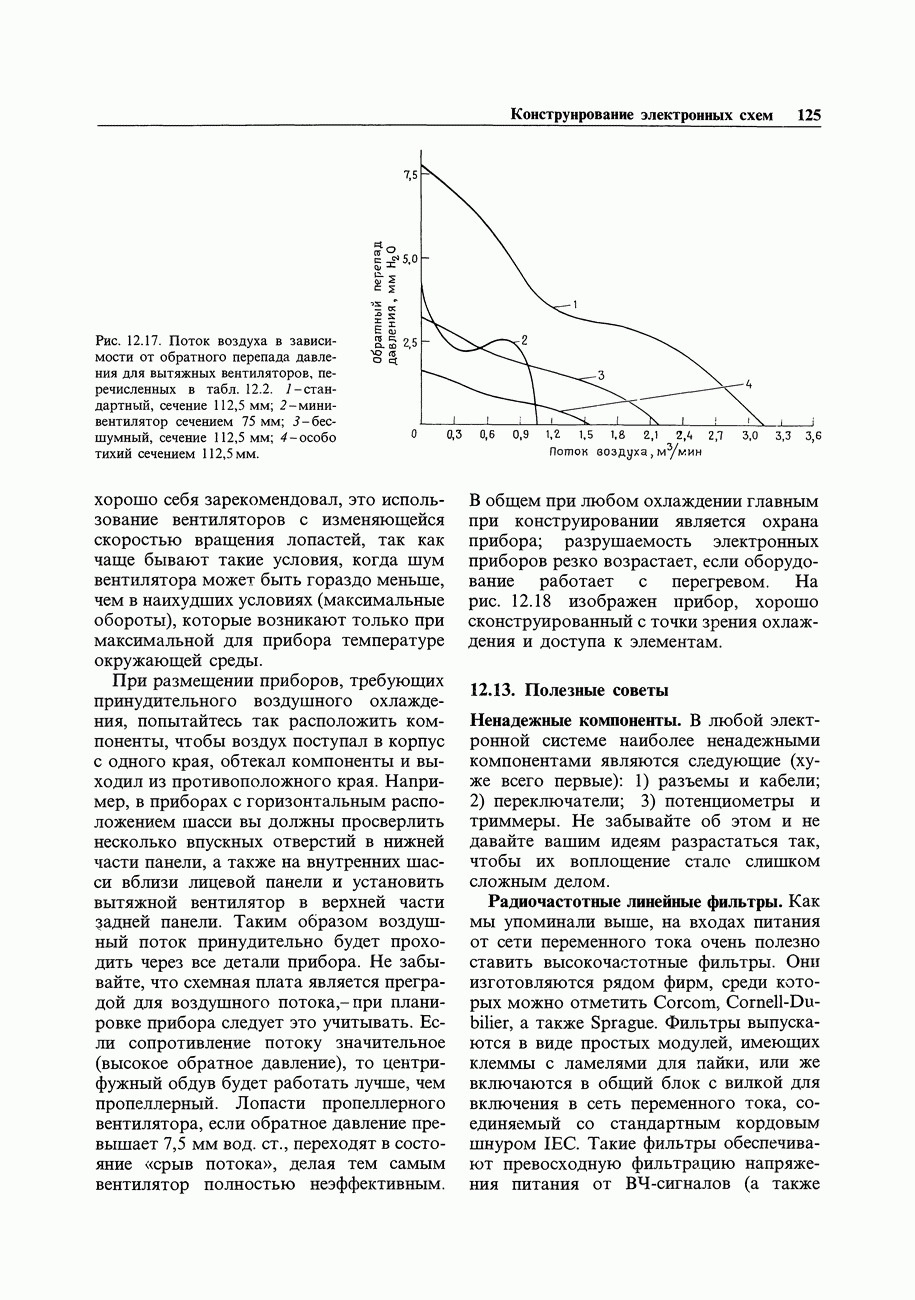
На рис. 15.25 показана основная схема счетчика частоты. Триггер Шмитта преобразует аналоговый входной сигнал в логические уровни, после этого производится стробирование вторым импульсом, получаемым от кварцевого генератора с делителем, длительность которого точно равна 1 с. Частота в герцах определяется числом импульсов, зафиксированным многоразрядным двоично-десятичным счетчиком. Между интервалами счета полезно зафиксировать полученное число и произвести сброс счетчика.На практике времязадающую схему можно построить так, чтобы можно было выбирать короткие и длинные интервалы: 0,1, 1, 10 с. Можно также устранить интервал длительностью 1 с между измерениями.

Рис. 15.25. Схема измерения частоты с помощью счетчика.
Схема может быть усовершенствована: можно включить регулируемый предусилитель с перестраиваемым уровнем срабатывания и гистерезисом и панель, на которую поступает выход дискриминатора и с помощью которой можно контролировать уровень срабатывания на осциллографе; выход двоично-десятичного счетчика можно подключить к ЭВМ или регистрирующему устройству, может быть предусмотрена возможность для подключения внешнего генератора в тех случаях, когда имеется прецизионный эталон; полезно предусмотреть возможность ручного старт-стопного режима при простом счете (суммировании).
Микроволновые счетчики. Используя современные цифровые интегральные схемы, можно работать с частотами порядка  . В частности, фирма
. В частности, фирма  Logic выпускает серию счетчиков с чрезвычайно высоким быстродействием - до
Logic выпускает серию счетчиков с чрезвычайно высоким быстродействием - до  . На более высоких частотах можно использовать гетеродинный метод для смешения микроволнового входного сигнала с частотой счета, или так называемый метод переходного генератора, при котором входной сигнал «захватывается» по фазе
. На более высоких частотах можно использовать гетеродинный метод для смешения микроволнового входного сигнала с частотой счета, или так называемый метод переходного генератора, при котором входной сигнал «захватывается» по фазе  гармоникой ГУН, затем частота ГУН измеряется и умножается на п.
гармоникой ГУН, затем частота ГУН измеряется и умножается на п.
Ошибка при счете  . Недостаток представленной счетной схемы состоит в том, что на низких частотах нельзя обеспечить высокую точность из-за того, что при счете имеет место ошибка, равная
. Недостаток представленной счетной схемы состоит в том, что на низких частотах нельзя обеспечить высокую точность из-за того, что при счете имеет место ошибка, равная  Например, если частота сигнала равна приблизительно 10 Гц, а время стробирования составляет 1 с, то результат будет правильным только на 10%, так как вы получите или 9, или 10, или 11. Можно производить измерение на более длинном интервале времени, но вам понадобится целый день, чтобы получить приличную точность (определяемую отношением
Например, если частота сигнала равна приблизительно 10 Гц, а время стробирования составляет 1 с, то результат будет правильным только на 10%, так как вы получите или 9, или 10, или 11. Можно производить измерение на более длинном интервале времени, но вам понадобится целый день, чтобы получить приличную точность (определяемую отношением  ), а если бы частота сигнала была равна, например, 1 МГц, то для проведения измерений потребовалась бы всего одна секунда. Существует несколько способов решения этой задачи: измерение периода (вместо частоты), использование методов интерполяции, использование ФАПЧ с умножением частоты.
), а если бы частота сигнала была равна, например, 1 МГц, то для проведения измерений потребовалась бы всего одна секунда. Существует несколько способов решения этой задачи: измерение периода (вместо частоты), использование методов интерполяции, использование ФАПЧ с умножением частоты.
Два первых способа мы рассмотрим в следующих разделах, так как на самом деле их нельзя отнести к непосредственным измерениям частоты.
На рис. 15.26 показано применение схемы ФАПЧ для измерения частоты методом «увеличения разрешающей способности с помощью умножения частоты». Стандартная схема ФАПЧ синтезирует частоту, которая превосходит частоту входного сигнала, скажем, точно в 100 раз, затем такой сигнал поступает на счетчик, работу которого мы описали выше. На точность этого метода накладывает ограничение «дребезг фазы» в фазовом детекторе и компенсационные параметры петли.

Рис. 15.26. Увеличение разрешающей способности при измерениях низких частот с помощью схемы ФАПЧ.
Например, если сигнал, имеющий частоту 100 Гц, умножается на 1000, время счета составляет 1 с, а дребезг в фазовом детекторе оценивается величиной 1% за цикл (3,6°) или  , то точность измерения будет определяться отношением
, то точность измерения будет определяться отношением  , хотя разрешающая способность оценивается отношением
, хотя разрешающая способность оценивается отношением  .
.
А теперь мы скажем несколько слов о двух других способах повышения точности при измерении частоты: речь идет об измерениях периода и о методе интерполяции при измерениях временных интервалов.
Измерение периода («обратный счет»).
Один из способов повышения разрешающей способности при измерении низких частот состоит в том, что входной сигнал (или некоторая его часть) используется для стробирования часов. На рис. 15.27 показана стандартная схема такого счетчика периода. Число периодов измерения обычно можно задавать с помощью переключателя в виде одной из степеней основания 10 (1, 10, 100 и т.д.). Обычно число периодов выбирают так, чтобы измерения занимали удобный отрезок времени, как правило 1 с, а полученный за это время результат должен содержать около семи значащих цифр. Само собой разумеется, результат будет измеряться в единицах времени, а не частоты, поэтому необходимо выполнить обратный пересчет для получения искомого значения. Для того чтобы выполнить преобразование, не нужно даже уметь делить, так как в современных счетчиках используют микропроцессоры, предназначенные для выполнения преобразования периода в частоту.

Рис. 15.27. Схема измерения периода.
Отметим, что точность измерений периода существенно зависит от стабильности срабатывания триггера Шмитта и от отношения сигнал/шум. Сказанное иллюстрирует рис. 15.28.
Основное достоинство метода «обратного счета» состоит в том, что он обеспечивает постоянное разрешение  для заданной продолжительности измерения независимо от входной частоты. С помощью графика, изображенного на рис. 15.29, можно сравнить разрешающую способность частотного и периодического (обратного счета) методов измерения частоты при продолжительности измерения, равной 1 с, и при использовании таймера с частотой 10 МГц. График, соответствующий методу периода, на самом деле должен представлять собой слегка волнистую линию, так как обычно приходится иметь дело с приближениями к степени числа 10 для осредняемого числа периодов.
для заданной продолжительности измерения независимо от входной частоты. С помощью графика, изображенного на рис. 15.29, можно сравнить разрешающую способность частотного и периодического (обратного счета) методов измерения частоты при продолжительности измерения, равной 1 с, и при использовании таймера с частотой 10 МГц. График, соответствующий методу периода, на самом деле должен представлять собой слегка волнистую линию, так как обычно приходится иметь дело с приближениями к степени числа 10 для осредняемого числа периодов.

Рис. 15.28.
Но даже этот недостаток отходит в область предания с появлением «умных» счетчиков» на микропроцессорах (например, дешевый счетчик фирмы Hewlett-Packard типа  ), которые обеспечивают плавную регулировку времени стробирования; они сами знают, по какому числу периодов производилось осреднение, и самостоятельно выполняют деление результата на нужное число. Кроме того, они сами определяют, когда необходимо перейти от режима измерений периода к режиму прямого измерения частоты. Такое переключение выполняется в том случае, когда входная частота превышает частоту таймера и позволяет получать оптимальное разрешение при любой частоте входных сигналов.
), которые обеспечивают плавную регулировку времени стробирования; они сами знают, по какому числу периодов производилось осреднение, и самостоятельно выполняют деление результата на нужное число. Кроме того, они сами определяют, когда необходимо перейти от режима измерений периода к режиму прямого измерения частоты. Такое переключение выполняется в том случае, когда входная частота превышает частоту таймера и позволяет получать оптимальное разрешение при любой частоте входных сигналов.
Еще одно достоинство метода измерений частоты по периоду состоит в возможности внешнего управления временем стробирования. Это достоинство проявляется, например, когда возникает необходимость измерить частоту короткого тонового импульса. В этом случае простой счетчик частоты даст неправильный результат, так как его интервал стробирования не совпадает с импульсом.

Рис. 15.29. Разрешающая способность для счетчиков частоты и периода.

Рис. 15.30. Сравнение частот с высоким разрешением.
Метод счета периода позволяет стробировать измерения извне и даже за счет высокой разрешающей способности выполнять измерения в различных точках импульса.
Возникает вопрос: можно ли получить более высокую разрешающую способность, чем  (для периодических измерений) или
(для периодических измерений) или  (для частотного счетчика) при относительной ошибке по частоте, равной
(для частотного счетчика) при относительной ошибке по частоте, равной  для интервала счета 77 Оказывается, можно. На практике применяют несколько хитроумных схем. Некоторые из них мы рассмотрим в следующем подразделе (посвященном измерению временных интервалов), а сейчас, просто для того чтобы показать, как можно этого добиться, мы приводим рис. 15.30, который иллюстрирует метод измерения частоты 1 МГц-генератора с разрешающей способностью
для интервала счета 77 Оказывается, можно. На практике применяют несколько хитроумных схем. Некоторые из них мы рассмотрим в следующем подразделе (посвященном измерению временных интервалов), а сейчас, просто для того чтобы показать, как можно этого добиться, мы приводим рис. 15.30, который иллюстрирует метод измерения частоты 1 МГц-генератора с разрешающей способностью  при продолжительности измерений, равной 1 с. Неизвестная частота смешивается со стабильной эталонной частотой, имеющей небольшой сдвиг относительно 1,0 МГц, например, 1,000001 МГц (для этого можно использовать схему ФАПЧ). На выходе смесителя получаем частоту, равную сумме, и частоту, равную разности. Пропустив сигнал через фильтр НЧ, получим частоту 1 Гц, которая определяет разность частот двух генераторов. Ее нетрудно измерить с помощью счетчика периода, разрешающая способность при этом будет определяться отношением
при продолжительности измерений, равной 1 с. Неизвестная частота смешивается со стабильной эталонной частотой, имеющей небольшой сдвиг относительно 1,0 МГц, например, 1,000001 МГц (для этого можно использовать схему ФАПЧ). На выходе смесителя получаем частоту, равную сумме, и частоту, равную разности. Пропустив сигнал через фильтр НЧ, получим частоту 1 Гц, которая определяет разность частот двух генераторов. Ее нетрудно измерить с помощью счетчика периода, разрешающая способность при этом будет определяться отношением  при продолжительности измерений, равной 1 с. Иными словами, мы измерили частоту 1 МГц с точностью до
при продолжительности измерений, равной 1 с. Иными словами, мы измерили частоту 1 МГц с точностью до  за 1 с.
за 1 с.
Этот метод измерения предполагает, что в схеме обеспечено хорошее отношение сигнал/шум; на практике приходится беспокоиться об уровне низкочастотного шума, времени установления фильтра и т. п., и фактическая разрешающая способность определяется отношением  за 1 с. Но и такая разрешающая способность значительно лучше, чем при использовании счетчика частоты (или при счете периода). Кроме того, точность будет ниже, чем разрешающая способность, если точность эталонного генератора хуже, чем
за 1 с. Но и такая разрешающая способность значительно лучше, чем при использовании счетчика частоты (или при счете периода). Кроме того, точность будет ниже, чем разрешающая способность, если точность эталонного генератора хуже, чем  (такую точность при современном уровне технологии получить можно, но это не просто). При желании эту схему можно рассматривать как схему для сравнения отношения частот двух генераторов.
(такую точность при современном уровне технологии получить можно, но это не просто). При желании эту схему можно рассматривать как схему для сравнения отношения частот двух генераторов.

Рис. 15.31. Измерение временных интервалов.
Измерение временных интервалов.
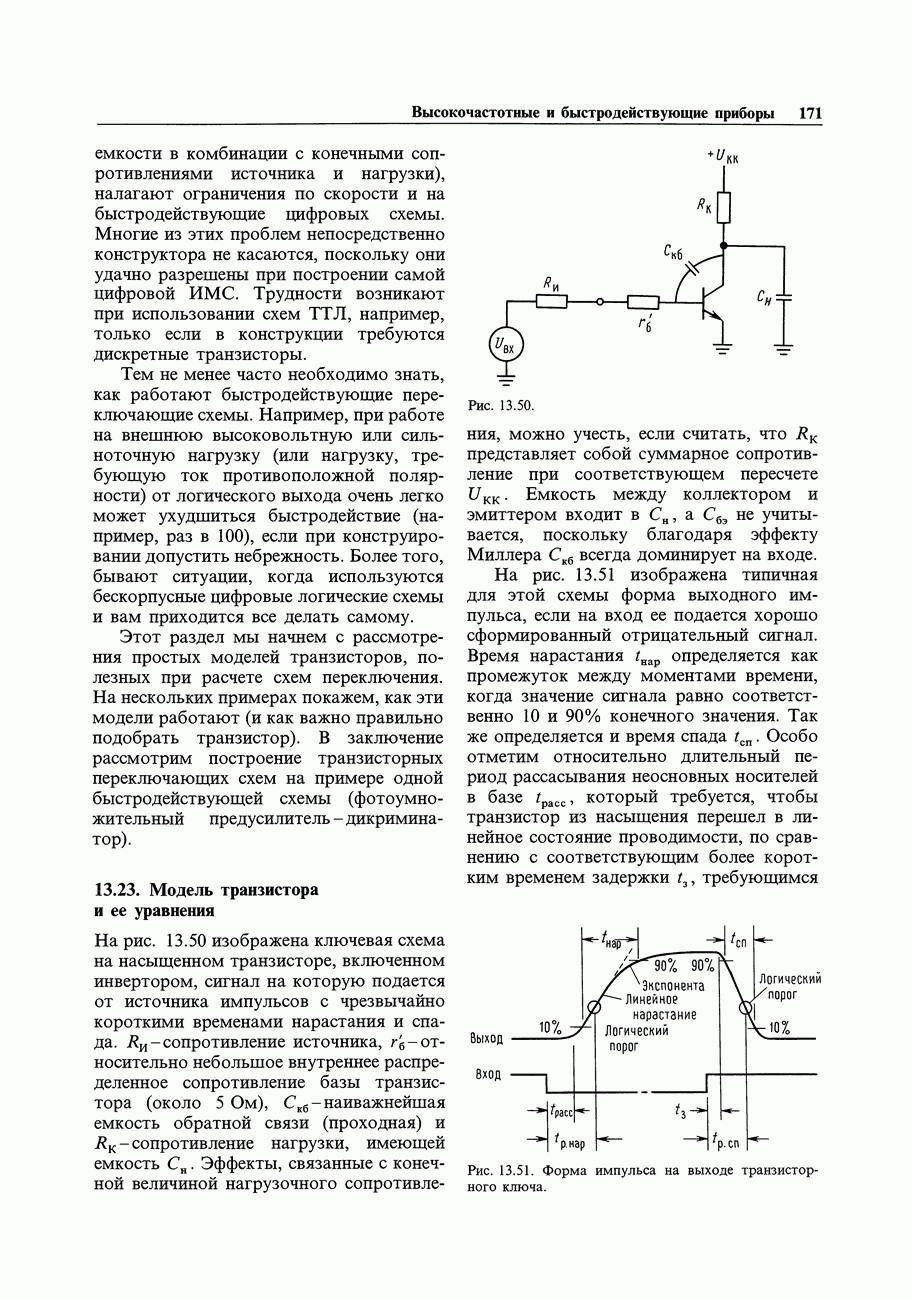
Простейшее изменение в схеме счетчика периода позволяет измерять интервалы времени между событиями. Рис. 15.31 иллюстрирует сказанное. На практике желательно, чтобы в схему был включен синхронизатор, как показано на второй схеме, для предотвращения действия небольших импульсов помехи. Очевидно, что самое хорошее разрешение получается при работе генератора на максимально возможной частоте. Имеющиеся в продаже счетчики используют эталонную частоту порядка 500 МГц, а во внутренней схеме ФАПЧ используется стабильный кварцевый генератор с частотой 5 или 10 МГц. Эталон 500 МГц обеспечивает разрешение 2 нс.Как уже упоминалось выше, существуют приемы, с помощью которых можно преодолеть ограничение по разрешающей способности, присущее методу обратного счета, при измерении временных интервалов. Для этого используют дополнительную информацию о точках, в которых входной сигнал пересекает нулевой уровень по отношению к сигналу - эталону. В схеме сравнения частот двух генераторов, которую мы привели выше, используется та же самая информация, но в неявном виде.

Рис. 15.32. Линейная интерполяция (при измерении временных интервалов),  Гтакт
Гтакт  .
.
На эти схемы должен подаваться чистый сигнал с очень низким уровнем шума. В коммерческих приборах используют два интерполяционных метода: линейную интерполяцию и верньерную интерполяцию.
Линейная интерполяция. Допустим, требуется измерить интервал времени между стартовым и стоповым импульсами, показанными на рис. 15.32. Вы измеряете число импульсов синхронизации n за время m, как показано на временной диаграмме (при наличии синхронизатора вы начнете и закончите счет по первому синхронизирующему импульсу, поступающему после соответствующего изменения входного сигнала). Для того чтобы улучшить разрешение, вам нужно знать только длительность интервалов  , определяющих задержку синхронизирующих импульсов относительно каждого входного импульса. Если используемый в системе таймер работает с максимальной приемлемой для счета скоростью, то для того, чтобы измерить нужные нам интервалы времени, их нужно расширить. Для этого прибегают к помощи треугольного импульса, имеющего разные углы наклона: на искомых интервалах конденсатор накапливает заряд, а затем разряжается со скоростью, равной небольшой доле скорости заряда, например 1/1000, при этом искомый интервал увеличивается в 1000 раз. На расширенных интервалах подсчитывается число синхронизирующих импульсов
, определяющих задержку синхронизирующих импульсов относительно каждого входного импульса. Если используемый в системе таймер работает с максимальной приемлемой для счета скоростью, то для того, чтобы измерить нужные нам интервалы времени, их нужно расширить. Для этого прибегают к помощи треугольного импульса, имеющего разные углы наклона: на искомых интервалах конденсатор накапливает заряд, а затем разряжается со скоростью, равной небольшой доле скорости заряда, например 1/1000, при этом искомый интервал увеличивается в 1000 раз. На расширенных интервалах подсчитывается число синхронизирующих импульсов  . Окончательно искомый интервал времени определяется из следующего выражения:
. Окончательно искомый интервал времени определяется из следующего выражения:

которое явно свидетельствует об улучшении разрешения. Точность этого метода ограничена точностью интерполяторов и часов, используемых в системе. Примером приборов такого типа служит счетчик типа  фирмы Hewlett-Packard, который отображает 9 цифр (значение частоты или времени) за секунду счета.
фирмы Hewlett-Packard, который отображает 9 цифр (значение частоты или времени) за секунду счета.
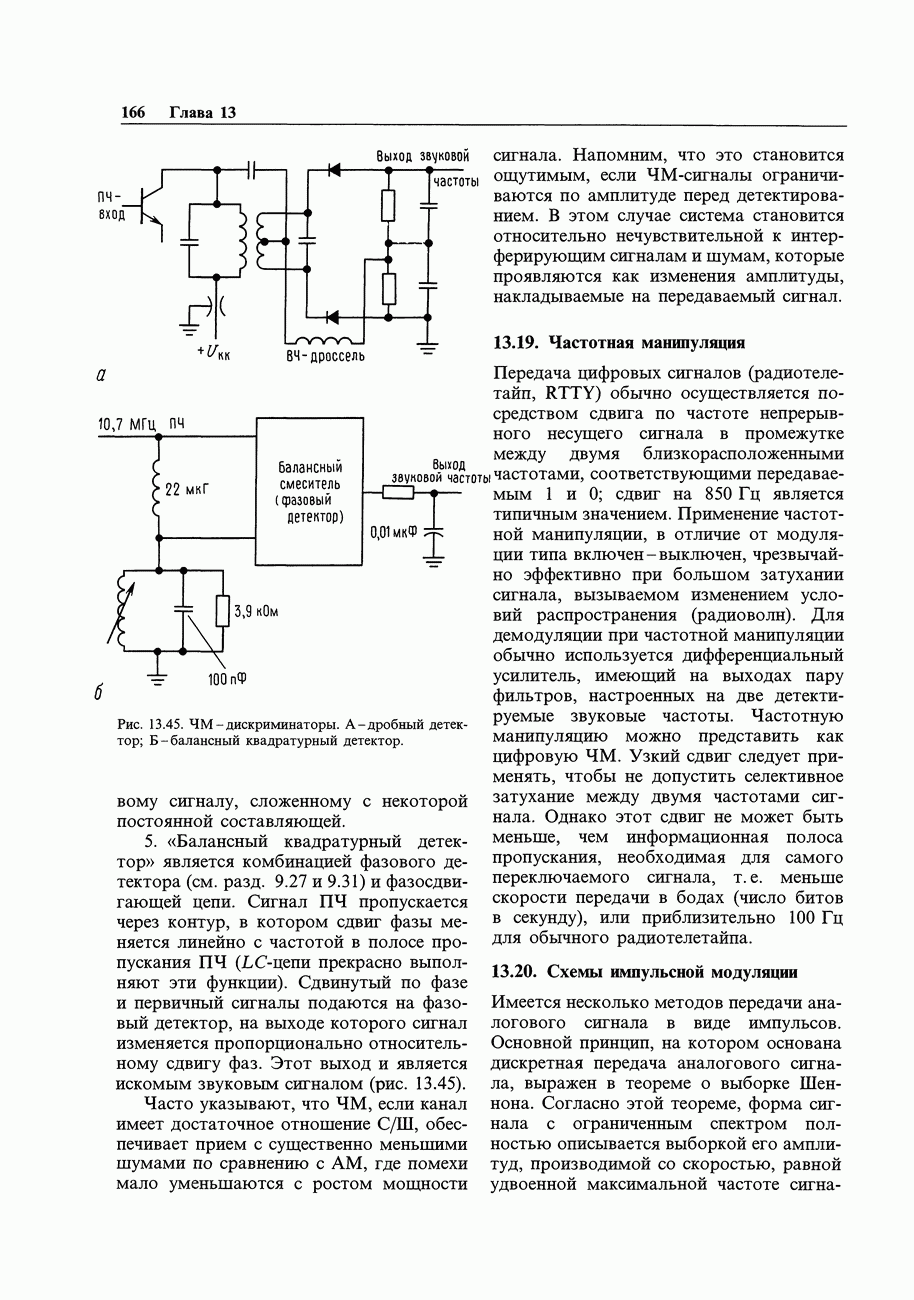
Верньерная интерполяция. Верньерная интерполяция представляет собой цифровой метод, который позволяет определить, в какой момент периода синхронизации появился входной импульс. На рис. 15.33 показаны временные диаграммы, соответствующие этому методу. Используются три времязадающие схемы: главные эталонные часы, работающие непрерывно с периодом  , равным, например, 5 не; входной импульс СТАРТ запускает второй генератор, период которого больше, чем период эталонного генератора в
, равным, например, 5 не; входной импульс СТАРТ запускает второй генератор, период которого больше, чем период эталонного генератора в  ) раз (для нашего примера мы взяли
) раз (для нашего примера мы взяли  входной импульс СТОП запускает третий генератор с таким же периодом, как и второй запускаемый генератор. Быстродействующая схема следит за тем, когда произойдет совпадение импульсов запущенных генераторов и главных часов, и подсчитывает число импульсов
входной импульс СТОП запускает третий генератор с таким же периодом, как и второй запускаемый генератор. Быстродействующая схема следит за тем, когда произойдет совпадение импульсов запущенных генераторов и главных часов, и подсчитывает число импульсов  , которые проходят до момента совпадения. Арифметический подсчет представлен вместе с диаграммами; интервал между импульсами СТАРТ и СТОП определяется с точностью до
, которые проходят до момента совпадения. Арифметический подсчет представлен вместе с диаграммами; интервал между импульсами СТАРТ и СТОП определяется с точностью до  длительности импульса главных часов.
длительности импульса главных часов.
В счетчике типа  фирмы Hewlett-Packard используется этот метод,
фирмы Hewlett-Packard используется этот метод,  не,
не,  Разрешение при измерении временных интервалов определяется величиной 20 не. Этот же метод можно использовать для измерения периодов, так как период представляет собой не что иное, как продолжительность одного цикла входного колебания.
Разрешение при измерении временных интервалов определяется величиной 20 не. Этот же метод можно использовать для измерения периодов, так как период представляет собой не что иное, как продолжительность одного цикла входного колебания.
В этом случае только что описанный счетчик дает разрешение по частоте до 11 цифр за 1 с!
Осреднение по временному интервалу. Существует третий способ улучшения разрешения при измерении временных интервалов, он состоит в многократном повторении измерений и определении среднего значения. Ошибка счета, равная  , при этом усредняется, и результат стремится к реальной величине интервала при условии, что скорость повторения импульсов СТАРТ непропорциональна скорости главных часов (таймера). В некоторых счетчиках для того, чтобы наверняка избежать такого соотношения, используют «подпрыгивающие часы».
, при этом усредняется, и результат стремится к реальной величине интервала при условии, что скорость повторения импульсов СТАРТ непропорциональна скорости главных часов (таймера). В некоторых счетчиках для того, чтобы наверняка избежать такого соотношения, используют «подпрыгивающие часы».
Спектральный анализ.
В связи с измерениями частоты следует упомянуть и такой мощный метод, как спектральный анализ, с помощью которого анализируются сигналы в частотной области. Анализаторы спектра измеряют частоту (особенно они незаменимы, когда требуется определить частоту слабого сигнала на фоне более сильных сигналов), а кроме этого выполняют и многие другие функции. Мы рассмотрим их в разд. 15.18.
Рис. 15.33. Верньерная интерполяция (при измерении временных интервалов)  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ГЛАВА 11. МИКРОПРОЦЕССОРЫ
- ВНИМАТЕЛЬНЫЙ ВЗГЛЯД НА МП 68008
- 11.01. Регистры, память и ввод-вывод
- 11.02. Система команд и способы адресации
- 11.03. Представление команд на машинном языке
- 11.04. Сигналы магистрали
- ПРИМЕР ЗАКОНЧЕННОЙ РАЗРАБОТКИ: АНАЛОГОВЫЙ УСРЕДНИТЕЛЬ СИГНАЛОВ
- 11.05. Разработка схемы
- 11.06. Программирование: определение задачи
- 11.07. Программирование: детали
- 11.08. Характеристики
- 11.09. Некоторые дополнительные соображения
- МИКРОСХЕМЫ АППАРАТНОЙ ПОДДЕРЖКИ МИКРОПРОЦЕССОРА
- 11.10. Микросхемы средней степени интеграции
- 11.11. Периферийные БИС
- 11.12. Запоминающие устройства
- 11.13. Другие микропроцессоры
- 11.14. Эмуляторы, системы проектирования, логические анализаторы и макетные платы
- ГЛАВА 12. КОНСТРУИРОВАНИЕ ЭЛЕКТРОННЫХ СХЕМ
- МЕТОД ПРОТОТИПОВ
- 12.01. Макетные платы («самолеты»)
- 12.02. Прототипы платы печатной схемы (ПС)
- 12.03. Платы под монтаж накруткой
- ПЕЧАТНЫЕ ПЛАТЫ
- 12.04. Изготовление плат печатного монтажа
- 12.05. Проектирование плат с печатным монтажом
- 12.06. Монтаж плат ПС
- 12.07. Несколько дополнительных соображений по поводу плат ПС
- 12.08. Передовая техника
- КОНСТРУИРОВАНИЕ ПРИБОРОВ
- 12.09. Установка схемных плат в приборы
- 12.10. Оформление
- 12.11. Замечания по конструкции
- 12.12. Охлаждение
- 12.13. Полезные советы
- 12.14. Где доставать компоненты
- ГЛАВА 13. ВЫСОКОЧАСТОТНЫЕ И БЫСТРОДЕЙСТВУЮЩИЕ ПРИБОРЫ
- 13.01. Транзисторный усилитель на высоких частотах в первом приближении
- 13.02. Высокочастотные усилители: модели для переменного тока
- 13.03. Пример высокочастотных расчетов
- 13.04. Примеры высокочастотных усилителей
- 13.05. Пример проектирования широкополосной схемы
- 13.06. Уточненные модели схем по переменному току
- 13.07. Последовательнопараллельные пары
- 13.08. Модульные усилители
- ЭЛЕМЕНТЫ ВЫСОКОЧАСТОТНЫХ СХЕМ
- 13.09. Соединительные линии
- 13.10. Отрезки линий, согласующие устройства и трансформаторы
- 13.11. Резонансные усилители
- 13.12. Элементы ВЧ-схем
- 13.13. Измерение амплитуды и мощности
- РАДИОСВЯЗЬ: АМ
- 13.14. Некоторые принципы связи
- 13.15. Амплитудная модуляция
- 13.16. Супергетеродинный приемник
- ПЕРЕДОВЫЕ МЕТОДЫ МОДУЛЯЦИИ
- 13.17. Метод одной боковой полосы (SSB)
- 13.18. Частотная модуляция
- 13.19. Частотная манипуляция
- 13.20. Схемы импульсной модуляции
- СПЕЦИФИЧЕСКИЕ ОСОБЕННОСТИ РАДИОЧАСТОТНЫХ СХЕМ
- 13.21. Специальные методы конструирования
- 13.22. Экзотические ВЧ-усилители и устройства
- БЫСТРОДЕЙСТВУЮЩИЕ КЛЮЧИ
- 13.23. Модель транзистора и ее уравнения
- 13.24. Устройства аналогового моделирования
- НЕСКОЛЬКО ПРИМЕРОВ БЫСТРОДЕЙСТВУЮЩИХ ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ
- 13.25. Высоковольтный усилитель
- 13.26. Усилитель с «открытым коллектором» при работе на шину
- 13.27. Пример схемы: предусилитель для фотоумножителя
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ГЛАВА 14. ПРОЕКТИРОВАНИЕ МАЛОМОЩНЫХ УСТРОЙСТВ
- 14.01. Прикладные задачи с малым потреблением мощности
- ИСТОЧНИКИ ПИТАНИЯ
- 14.02. Типы батарей
- 14.03. Включаемые в розетку блоки питания
- 14.04. Солнечные элементы
- 14.05. Сигнальные токи
- ВЫКЛЮЧЕНИЕ ИСТОЧНИКА ПИТАНИЯ И МИКРОМОЩНЫЕ СТАБИЛИЗАТОРЫ
- 14.06. Выключение источника питания
- 14.07. Микромощные стабилизаторы
- 14.08. Опорное напряжение земли
- 14.09. Микромощные источники эталонного напряжения и датчики температуры
- 14.10. Проблемы проектирования микромощных линейных схем
- 14.11. Пример проектирования линейной схемы на дискретных элементах
- 14.12. Микромощные операционные усилители
- 14.13. Микромощные компараторы
- 14.14. Микромощные таймеры и генераторы
- ПРОЕКТИРОВАНИЕ ЦИФРОВЫХ МИКРОМОЩНЫХ УСТРОЙСТВ
- 14.15. КМОП-семейства
- 14.16. Обеспечение работы КМОП-схем в маломощном режиме
- 14.17. Микромощные микропроцессоры и периферийные устройства
- 14.18. Пример проектирования на микропроцессоре: регистратор данных типа «градус-день»
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ГЛАВА 15. ИЗМЕРЕНИЯ И ОБРАБОТКА СИГНАЛОВ
- ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 15.01. Температура
- 15.02. Уровень излучения
- 15.03. Деформация и смещение
- 15.04. Ускорение, давление, сила, скорость
- 15.05. Магнитное поле
- 15.06. Вакуумные манометры
- 15.07. Детекторы элементарных частиц
- 15.08. Щупы, используемые в биологии и химии
- ЭТАЛОНЫ ТОЧНЫХ ВЕЛИЧИН И ПРЕЦИЗИОННЫЕ ИЗМЕРЕНИЯ
- 15.09. Эталоны частоты
- 15.10. Измерения частоты, периода и временных интервалов
- 15.11. Эталоны напряжения и сопротивления и их измерение
- МЕТОДЫ СУЖЕНИЯ ПОЛОСЫ ПРОПУСКАНИЯ
- 15.12. Отношение сигнал/шум
- 15.13. Усреднение сигнала и многоканальное усреднение
- 15.14. Получение периодического сигнала
- 15.15. Обнаружение путем захвата
- 15.16. Амплитудный анализ импульсов
- 15.17. Преобразователи времени в амплитуду
- СПЕКТРАЛЬНЫЙ АНАЛИЗ И ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 15.18. Анализаторы спектра
- 15.19. Автономный спектральный анализ
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
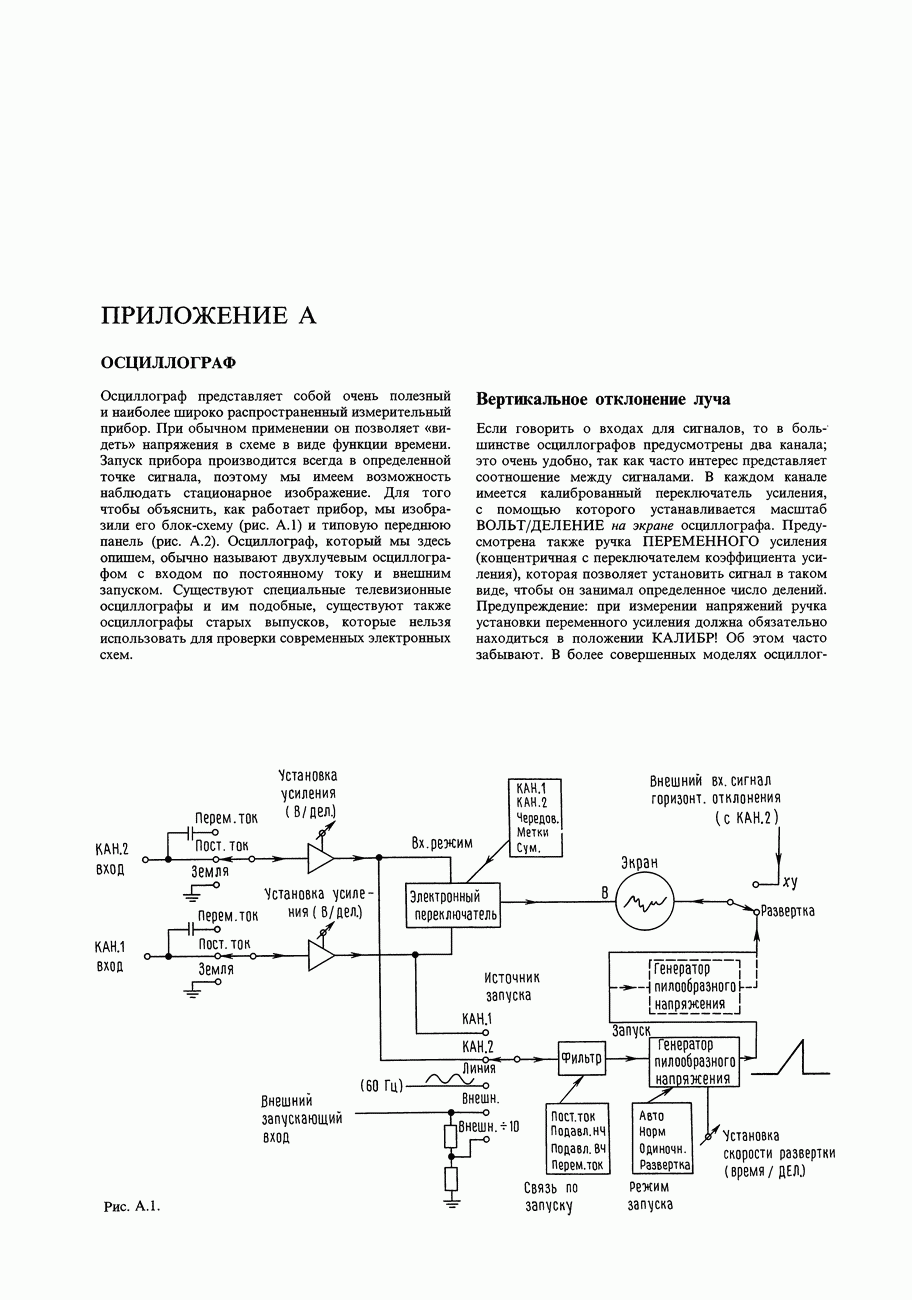
- ПРИЛОЖЕНИЕ А
- ОСЦИЛЛОГРАФ
- ПРИЛОЖЕНИЕ Б
- МАТЕМАТИЧЕСКИЙ ОБЗОР
- ПРИЛОЖЕНИЕ В. ЦВЕТНАЯ МАРКИРОВКА РЕЗИСТОРОВ С ДОПУСКОМ 5%
- ПРИЛОЖЕНИЕ Г. ПРЕЦИЗИОННЫЕ РЕЗИСТОРЫ С ДОПУСКОМ 1%
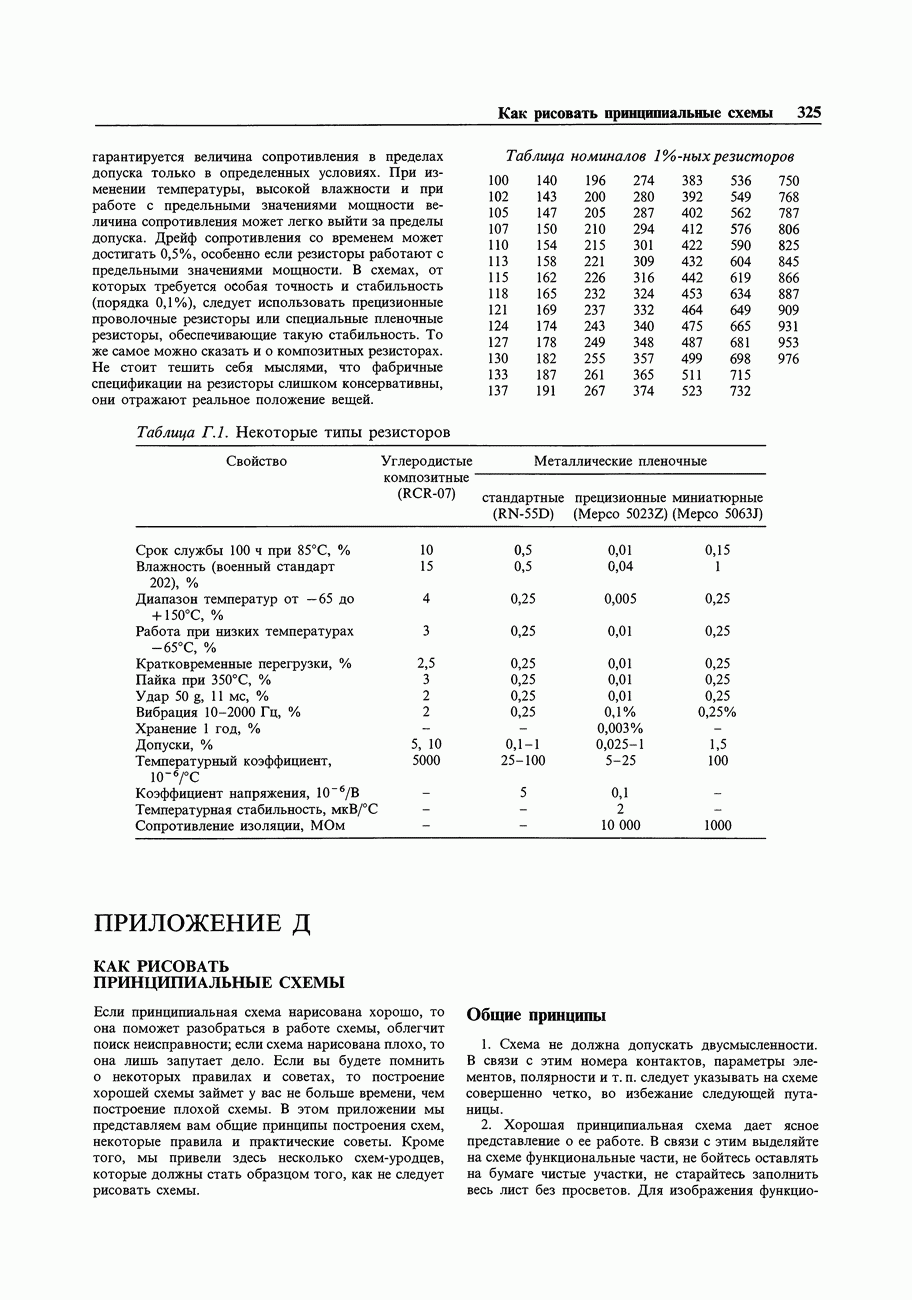
- ПРИЛОЖЕНИЕ Д. КАК РИСОВАТЬ ПРИНЦИПИАЛЬНЫЕ СХЕМЫ
- ПРИЛОЖЕНИЕ Е. НАГРУЗОЧНЫЕ ЛИНИИ
- ПРИЛОЖЕНИЕ Ж. НАСЫЩЕНИЕ ТРАНЗИСТОРА
- ПРИЛОЖЕНИЕ З. LС-ФИЛЬТРЫ БАТТЕРВОРТА
- ПРИЛОЖЕНИЕ И. ЖУРНАЛЫ И ПЕРИОДИЧЕСКИЕ ИЗДАНИЯ ПО ЭЛЕКТРОНИКЕ
- ПРИЛОЖЕНИЕ К. ПРЕФИКСЫ В СЕРИЙНЫХ НОМЕРАХ ИС
- ПРИЛОЖЕНИЕ Л. ТЕХНИЧЕСКИЕ ПАСПОРТА НА ЭЛЕМЕНТЫ ЭЛЕКТРОННЫХ СХЕМ
- БИБЛИОГРАФИЯ