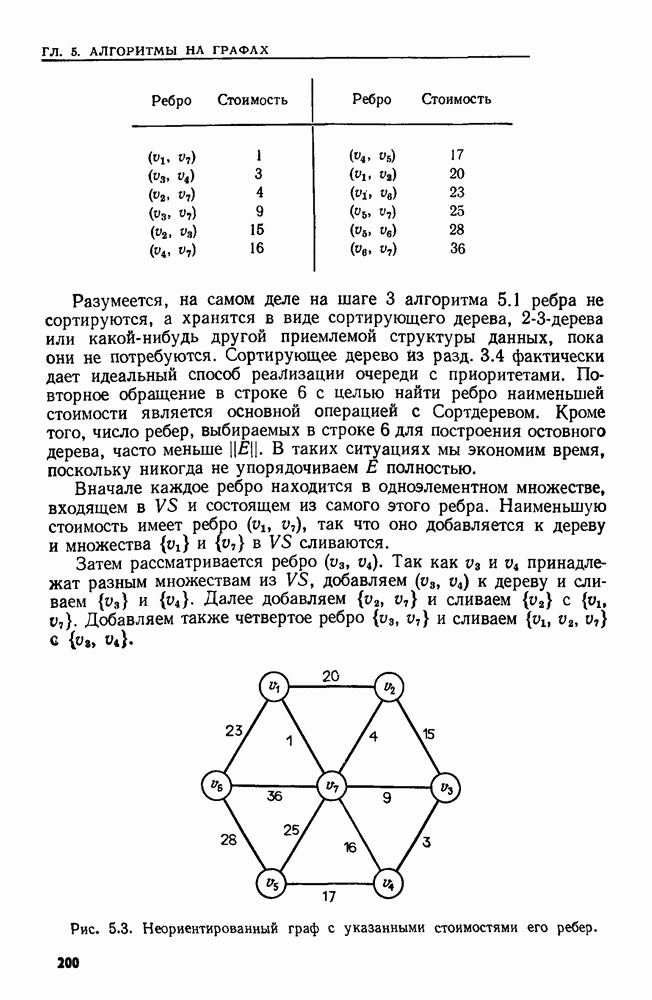
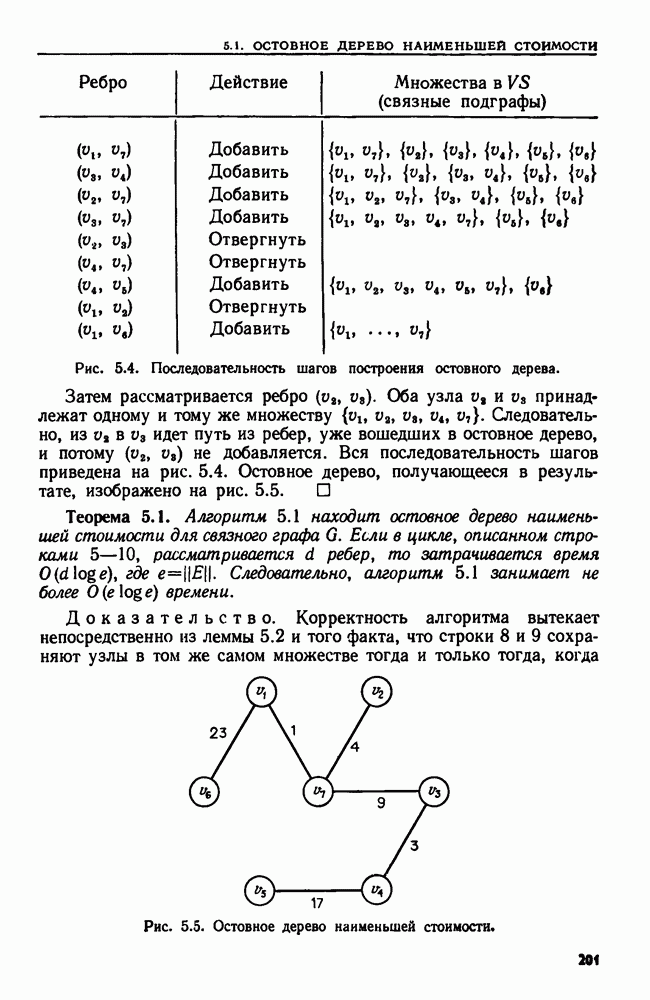
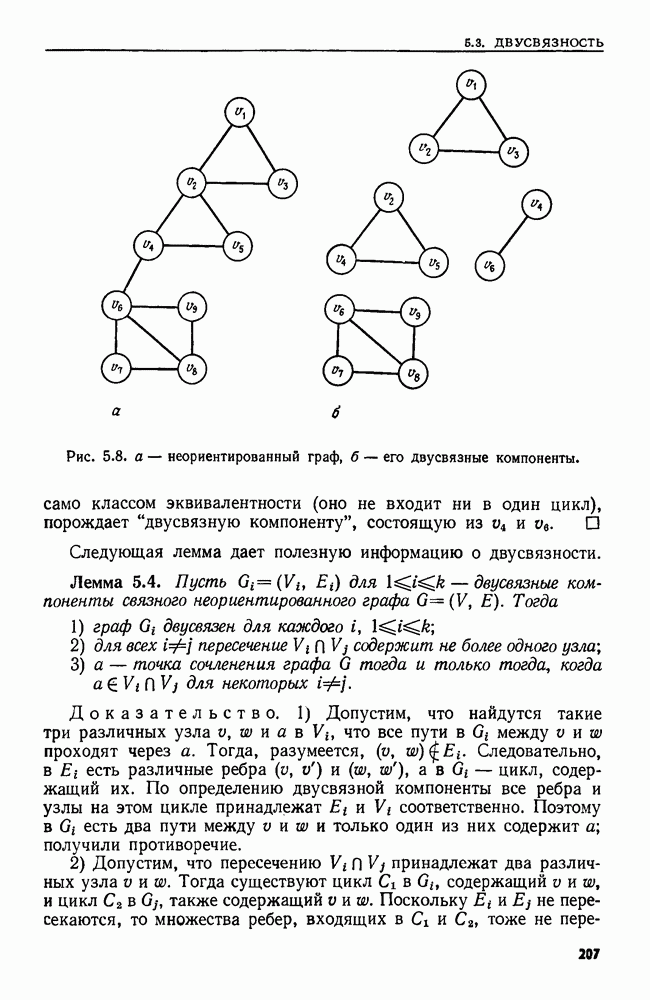
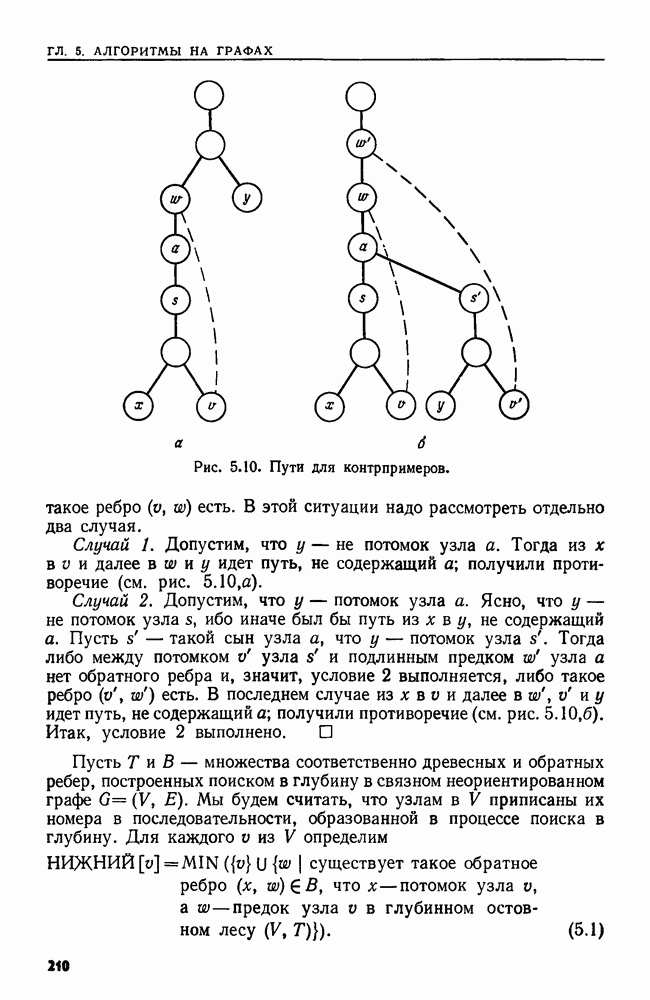
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.6. РАЗДЕЛЯЙ И ВЛАСТВУЙ
Для решения той или иной задачи ее часто разбивают на части, находят их решения и затем из них получают решение всей задачи. Этот прием, особенно если его применять рекурсивно, часто приводит к эффективному решению задачи, подзадачи которой представляют собой ее меньшие версии. Проиллюстрируем эту технику на двух примерах, сопровождаемых анализом получающихся рекуррентных уравнений.
Рассмотрим задачу о нахождении наибольшего и наименьшего элементов множества  содержащего
содержащего  элементов. Для простоты будем считать, что
элементов. Для простоты будем считать, что  есть степень числа 2. Очевидный путь поиска наибольшего и наименьшего элементов состоит в том, чтобы искать их по отдельности. Например, следующая процедура находит наибольший элемент множества
есть степень числа 2. Очевидный путь поиска наибольшего и наименьшего элементов состоит в том, чтобы искать их по отдельности. Например, следующая процедура находит наибольший элемент множества  произведя
произведя  сравнений его
сравнений его
элементов:

Аналогично можно найти наименьший из остальных  элементов, произведя
элементов, произведя  сравнений. Итак, видим, что для нахождения наибольшего и наименьшего элементов при потребуется
сравнений. Итак, видим, что для нахождения наибольшего и наименьшего элементов при потребуется  сравнений.
сравнений.
Применяя прием "разделяй и властвуй", мы разбили бы множество  на два подмножества
на два подмножества  по
по  элементов в каждом. Тогда описанный выше алгоритм нашел бы наибольший и наименьший элементы в каждой из двух половин с помощью рекурсии. Наибольший и наименьший элементы множества
элементов в каждом. Тогда описанный выше алгоритм нашел бы наибольший и наименьший элементы в каждой из двух половин с помощью рекурсии. Наибольший и наименьший элементы множества  можно было бы определить, произведя еще два сравнения — наибольших элементов в
можно было бы определить, произведя еще два сравнения — наибольших элементов в  и наименьших элементов в них. Сформулируем этот алгоритм более точно.
и наименьших элементов в них. Сформулируем этот алгоритм более точно.
Алгоритм 2.3. Нахождение наибольшего и наименьшего элементов множества
Вход. Множество  из
из  элементов, где
элементов, где  степень числа 2,2.
степень числа 2,2.
Выход. Наибольший и наименьший элементы множества 
Метод. К множеству  применяется рекурсивная процедура MAXMIN. Она имеет один аргумент представляющий собой множество
применяется рекурсивная процедура MAXMIN. Она имеет один аргумент представляющий собой множество  такое, что
такое, что  при некотором
при некотором  и вырабатывает пару
и вырабатывает пару  где а — наибольший и
где а — наибольший и  наименьший элементы в
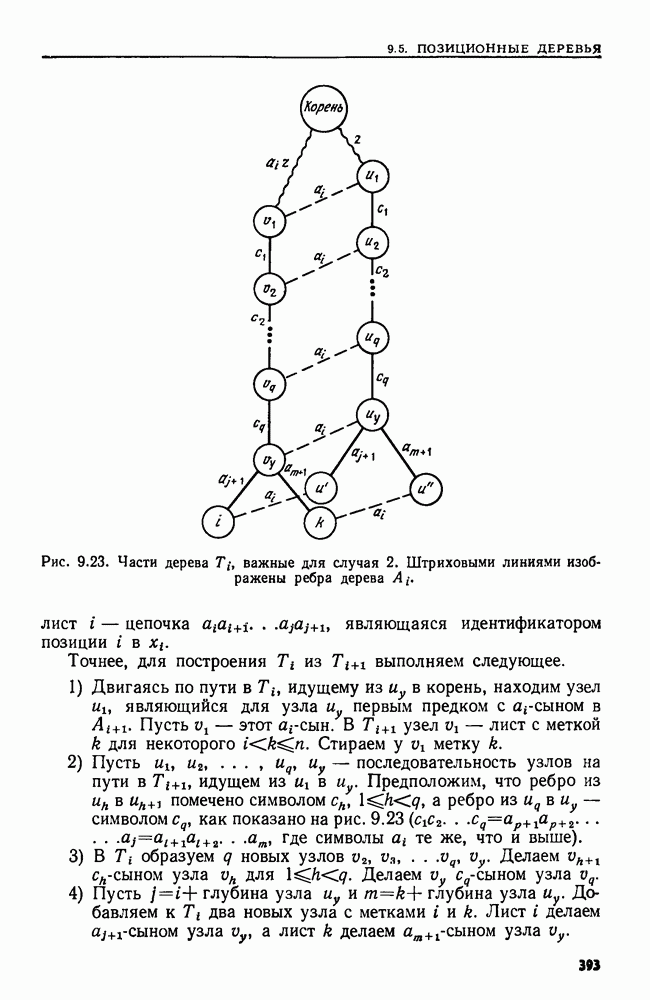
наименьший элементы в  Процедура MAXMIN приведена на рис. 2.12.
Процедура MAXMIN приведена на рис. 2.12.
Заметим, что сравнения элементов множества  происходят только на шаге 3, где сравниваются два элемента множества
происходят только на шаге 3, где сравниваются два элемента множества  из которых оно состоит, и на шаге 7, где сравниваются
из которых оно состоит, и на шаге 7, где сравниваются  с
с  Пусть
Пусть  число сравнений элементов множества
число сравнений элементов множества  которые надо произвести в процедуре MAXMIN, чтобы найти наибольший и наименьший элементы
которые надо произвести в процедуре MAXMIN, чтобы найти наибольший и наименьший элементы  -элементного множества. Ясно, что
-элементного множества. Ясно, что  Если
Если  то
то  общее число сравнений, произведенных в двух вызовах процедуры MAXMIN (строки 5 и 6), работающей на множествах размера
общее число сравнений, произведенных в двух вызовах процедуры MAXMIN (строки 5 и 6), работающей на множествах размера  и еще два сравнения в
и еще два сравнения в

Рис. 2.12. Процедура для нахождения  и MIN.
и MIN.
строке 7. Таким образом,

Решением рекуррентных уравнений (2.2) служит функция  Легко проверить, что эта функция удовлетворяет (2.2) при
Легко проверить, что эта функция удовлетворяет (2.2) при  и если она удовлетворяет (2.2) при
и если она удовлетворяет (2.2) при  где 2, то
где 2, то

т. е. она удовлетворяет (2.2) при  Таким образом, индукцией по
Таким образом, индукцией по  доказано, что
доказано, что  удовлетворяет (2.2), если
удовлетворяет (2.2), если  есть степень числа 2.
есть степень числа 2.
Можно показать, что для одновременного нахождения наибольшего и наименьшего элементов  -элементного множества надо сделать не менее
-элементного множества надо сделать не менее  сравнений его элементов. Следовательно, алгоритм 2.3 оптимален в смысле числа сравнений между элементами из
сравнений его элементов. Следовательно, алгоритм 2.3 оптимален в смысле числа сравнений между элементами из  когда
когда  есть степень числа 2.
есть степень числа 2.
В предыдущем примере прием "разделяй и властвуй" позволил уменьшить количество сравнений лишь в фиксированное число раз. В следующем примере мы с помощью этого приема уменьшим даже порядок роста сложности алгоритма.
Рассмотрим умножение двух  -разрядных двоичных чисел. Традиционный метод требует
-разрядных двоичных чисел. Традиционный метод требует  битовых операций. В методе,
битовых операций. В методе,

Рис. 2.13. Разбиение цепочек, представленных в виде двоичных чисел.
изложенном ниже, достаточно уже порядка  т. е. примерно пиьа битовых операций.
т. е. примерно пиьа битовых операций.
Пусть х и у — два  -разрядных двоичных числа. Снова будем считать для простоты, что
-разрядных двоичных числа. Снова будем считать для простоты, что  есть степень числа 2. Разобьем х и у на две равные части, как показано на рис. 2.13. Если рассматривать каждую из этих частей как
есть степень числа 2. Разобьем х и у на две равные части, как показано на рис. 2.13. Если рассматривать каждую из этих частей как  -разрядное число, то можно представить произведение чисел х и у в виде
-разрядное число, то можно представить произведение чисел х и у в виде

Равенство (2.3) дает способ вычисления произведения х и у с помощью четырех умножений  -разрядных чисел и нескольких сложений и сдвигов (умножений на степень числа 2). Произведение
-разрядных чисел и нескольких сложений и сдвигов (умножений на степень числа 2). Произведение  чисел х и у также можно вычислить по следующей программе:
чисел х и у также можно вычислить по следующей программе:

На время забудем, что из-за переноса  могут иметь
могут иметь  разрядов, и предположим, что они состоят лишь из
разрядов, и предположим, что они состоят лишь из  разрядов. Наша схема для умножения двух
разрядов. Наша схема для умножения двух  -разрядных чисел требует только трех умножений
-разрядных чисел требует только трех умножений  -разрядных чисел и нескольких сложений и сдвигов. Для вычисления произведений
-разрядных чисел и нескольких сложений и сдвигов. Для вычисления произведений  можно применять эту программу рекурсивно. Сложения и сдвиги занимают
можно применять эту программу рекурсивно. Сложения и сдвиги занимают  времени. Следовательно, временная сложность умножения двух
времени. Следовательно, временная сложность умножения двух  -разрядных чисел ограничена сверху функцией
-разрядных чисел ограничена сверху функцией

где  постоянная, отражающая сложение и сдвиги в выражениях, входящих в (2.4). Решение рекуррентных уравнений (2.5) ограничено сверху функцией
постоянная, отражающая сложение и сдвиги в выражениях, входящих в (2.4). Решение рекуррентных уравнений (2.5) ограничено сверху функцией

На самом деле можно показать, что в (2.5)

Доказательство проведем индукцией по  где
где  степень числа 2. Базис, т. е. случай
степень числа 2. Базис, т. е. случай  тривиален. Если функция
тривиален. Если функция  удовлетворяет (2.5) при
удовлетворяет (2.5) при  то
то

так что она удовлетворяет (2.5) и при  Отсюда следует, что
Отсюда следует, что  Заметим, что попытка использовать в индукции
Заметим, что попытка использовать в индукции  вместо
вместо  не проходит.
не проходит.
Для завершения описания алгоритма умножения мы должны учесть, что числа  вообще говоря, имеют
вообще говоря, имеют  разрядов, и поэтому произведение
разрядов, и поэтому произведение  нельзя вычислить непосредственным рекурсивным применением нашего алгоритма к задаче размера
нельзя вычислить непосредственным рекурсивным применением нашего алгоритма к задаче размера  Вместо этого надо записать
Вместо этого надо записать  в виде
в виде  где
где  или 1. Аналогично запишем
или 1. Аналогично запишем  в виде
в виде  Тогда произведение
Тогда произведение  можно представить в виде
можно представить в виде

Слагаемое Ьгйг вычисляется с помощью рекурсивного применения нашего алгоритма умножения к задаче размера  Остальные умножения в (2.6) можно сделать за время
Остальные умножения в (2.6) можно сделать за время  поскольку они содержат в качестве одного из аргументов либо единственный бит
поскольку они содержат в качестве одного из аргументов либо единственный бит  или
или  либо степень числа 2.
либо степень числа 2.
Пример 2.6. Этот асимптотически быстрый алгоритм умножения целых чисел можно применять не только к двоичным, но и к десятичным числам. Проиллюстрируем это на примере:

Заметим, что алгоритм, основанный на (2.4), заменял одно умножение тремя сложениями и вычитанием (ср. с (2.3)). Почему такая замена приводит к асимптотической эффективности, можно
интуитивно объяснить тем, что умножение выполнить труднее, чем сложение, и для достаточно больших  любое фиксированное число
любое фиксированное число  -разрядных сложений требует меньше времени, чем
-разрядных сложений требует меньше времени, чем  -разрядное умножение, независимо от того, какой из (известных) алгоритмов применяется. Вначале кажется, что уменьшение числа
-разрядное умножение, независимо от того, какой из (известных) алгоритмов применяется. Вначале кажется, что уменьшение числа  -разрядных произведений с четырех до трех может уменьшить общее время в лучшем случае на 25%. Однако соотношения (2.4) применяются рекурсивно для вычисления
-разрядных произведений с четырех до трех может уменьшить общее время в лучшем случае на 25%. Однако соотношения (2.4) применяются рекурсивно для вычисления  -разрядных,
-разрядных,  -разрядных и т. д. произведений. Эти
-разрядных и т. д. произведений. Эти  -процентные уменьшения объединяются и дают в результате асимптотическое улучшение временной сложности.
-процентные уменьшения объединяются и дают в результате асимптотическое улучшение временной сложности.
Временная сложность процедуры определяется числом и размером подзадач и в меньшей степени работой, необходимой для разбиения данной задачи на подзадачи. Так как рекуррентные уравнения вида (2.2) и (2.5) часто возникают при анализе рекурсивных алгоритмов типа "разделяй и властвуй", рассмотрим решение таких уравнений в общем виде.
Теорема 2.1. Пусть  и с — неотрицательные постоянные. Решение рекуррентных уравнений
и с — неотрицательные постоянные. Решение рекуррентных уравнений

где  степень числа с, имеет вид,
степень числа с, имеет вид,

Доказательство. Если  степень числа в, то
степень числа в, то

Если  то сходится и, следовательно,
то сходится и, следовательно, 
Если  то каждым членом этого ряда будет 1, а всего в нем
то каждым членом этого ряда будет 1, а всего в нем  членов. Поэтому
членов. Поэтому  Наконец, если
Наконец, если  то
то

что составляет  или
или 
Из теоремы 2.1 вытекает, что разбиение задачи размера  (за линейное время) на две подзадачи размера
(за линейное время) на две подзадачи размера  дает алгоритм сложности
дает алгоритм сложности  Если бы подзадач было 3, 4 или 8, то получился бы алгоритм сложности порядка
Если бы подзадач было 3, 4 или 8, то получился бы алгоритм сложности порядка  или
или  соответственно.
соответственно.
С другой стороны, разбиение задачи на 4 подзадачи размера  дает алгоритм сложности
дает алгоритм сложности  а на 9 и 16 — порядка
а на 9 и 16 — порядка  и
и  соответственно. Поэтому асимптотически более быстрый алгоритм умножения целых чисел можно было бы получить, если бы удалось так разбить исходные целые числа на 4 части, чтобы суметь выразить исходное умножение через 8 или менее меньших умножений. Другой тип рекуррентных соотношений возникает в случае, когда работа по разбиению задачи не пропорциональна ее размеру. Некоторые типы рекуррентных соотношений вынесены в упражнения.
соответственно. Поэтому асимптотически более быстрый алгоритм умножения целых чисел можно было бы получить, если бы удалось так разбить исходные целые числа на 4 части, чтобы суметь выразить исходное умножение через 8 или менее меньших умножений. Другой тип рекуррентных соотношений возникает в случае, когда работа по разбиению задачи не пропорциональна ее размеру. Некоторые типы рекуррентных соотношений вынесены в упражнения.
Если  не является степенью числа с, то обычно можно вложить задачу размера
не является степенью числа с, то обычно можно вложить задачу размера  в задачу размера
в задачу размера  где
где  наименьшая степень числа с, большая или равная
наименьшая степень числа с, большая или равная  Поэтому порядки роста, указанные в теореме 2.1, сохраняются для любого
Поэтому порядки роста, указанные в теореме 2.1, сохраняются для любого  На практике часто можно разработать рекурсивные алгоритмы, разбивающие задачи произвольного размера на с равных частей, где с велико, насколько возможно. Эти алгоритмы, как правило, эффективнее (на постоянный множитель) тех, которые получаются путем представления размера входа в виде ближайшей сверху степени числа с.
На практике часто можно разработать рекурсивные алгоритмы, разбивающие задачи произвольного размера на с равных частей, где с велико, насколько возможно. Эти алгоритмы, как правило, эффективнее (на постоянный множитель) тех, которые получаются путем представления размера входа в виде ближайшей сверху степени числа с.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- МОДЕЛИ ВЫЧИСЛЕНИЙ
- 1.1. АЛГОРИТМЫ И ИХ СЛОЖНОСТИ
- 1.2. МАШИНЫ С ПРОИЗВОЛЬНЫМ ДОСТУПОМ К ПАМЯТИ
- 1.3. ВЫЧИСЛИТЕЛЬНАЯ СЛОЖНОСТЬ РАМ-ПРОГРАММ
- 1.4. МОДЕЛЬ С ХРАНИМОЙ ПРОГРАММОЙ
- 1.5. МОДИФИКАЦИЯ РАМ
- 1.6. ПРОСТЕЙШАЯ МОДЕЛЬ ВЫЧИСЛЕНИЙ: МАШИНА ТЬЮРИНГА
- 1.7. СВЯЗЬ МАШИН ТЬЮРИНГА И РАМ
- 1.8. ЯЗЫК ВЫСОКОГО УРОВНЯ — УПРОЩЕННЫЙ АЛГОЛ
- 2. РАЗРАБОТКА ЭФФЕКТИВНЫХ АЛГОРИТМОВ
- 2.1. СТРУКТУРЫ ДАННЫХ: СПИСКИ, ОЧЕРЕДИ И СТЕКИ
- 2.2. ПРЕДСТАВЛЕНИЯ МНОЖЕСТВ
- 2.3. ГРАФЫ
- 2.4. ДЕРЕВЬЯ
- 2.5. РЕКУРСИЯ
- 2.6. РАЗДЕЛЯЙ И ВЛАСТВУЙ
- 2.7. БАЛАНСИРОВКА
- 2.8. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
- 2.9. ЭПИЛОГ
- 3. СОРТИРОВКА И ПОРЯДКОВЫЕ СТАТИСТИКИ
- 3.1. ЗАДАЧА СОРТИРОВКИ
- 3.2. ЦИФРОВАЯ СОРТИРОВКА
- 3.3. СОРТИРОВКА С ПОМОЩЬЮ СРАВНЕНИЙ
- 3.4. СОРТДЕРЕВОМ — УПОРЯДОЧЕНИЕ С ПОМОЩЬЮ O(n log n) СРАВНЕНИЙ
- 3.5. БЫСТРСОРТ — УПОРЯДОЧЕНИЕ ЗА СРЕДНЕЕ ВРЕМЯ O(n log n)
- 3.6. ПОРЯДКОВЫЕ СТАТИСТИКИ
- 3.7. СРЕДНЕЕ ВРЕМЯ ДЛЯ ПОРЯДКОВЫХ СТАТИСТИК
- 4. СТРУКТУРЫ ДАННЫХ ДЛЯ ЗАДАЧ, КАСАЮЩИХСЯ РАБОТЫ С МНОЖЕСТВАМИ
- 4.2. МЕТОД РАССТАНОВКИ
- 4.3. ДВОИЧНЫЙ ПОИСК
- 4.4. ДЕРЕВЬЯ ДВОИЧНОГО ПОИСКА
- 4.5. ОПТИМАЛЬНЫЕ ДЕРЕВЬЯ ДВОИЧНОГО ПОИСКА
- 4.6. ПРОСТОЙ АЛГОРИТМ ДЛЯ НАХОЖДЕНИЯ ОБЪЕДИНЕНИЯ НЕПЕРЕСЕКАЮЩИХСЯ МНОЖЕСТВ
- 4.7. ДРЕВОВИДНЫЕ СТРУКТУРЫ ДЛЯ ЗАДАЧИ ОБЪЕДИНИТЬ — НАЙТИ
- 4.8. ПРИЛОЖЕНИЯ И ОБОБЩЕНИЯ АЛГОРИТМА ОБЪЕДИНИТЬ — НАЙТИ
- 4.9. СХЕМЫ СБАЛАНСИРОВАННЫХ ДЕРЕВЬЕВ
- 4.10. СЛОВАРИ И ОЧЕРЕДИ С ПРИОРИТЕТАМИ
- 4.11. СЛИВАЕМЫЕ ДЕРЕВЬЯ
- 4.12. СЦЕПЛЯЕМЫЕ ОЧЕРЕДИ
- 4.13. РАЗБИЕНИЕ
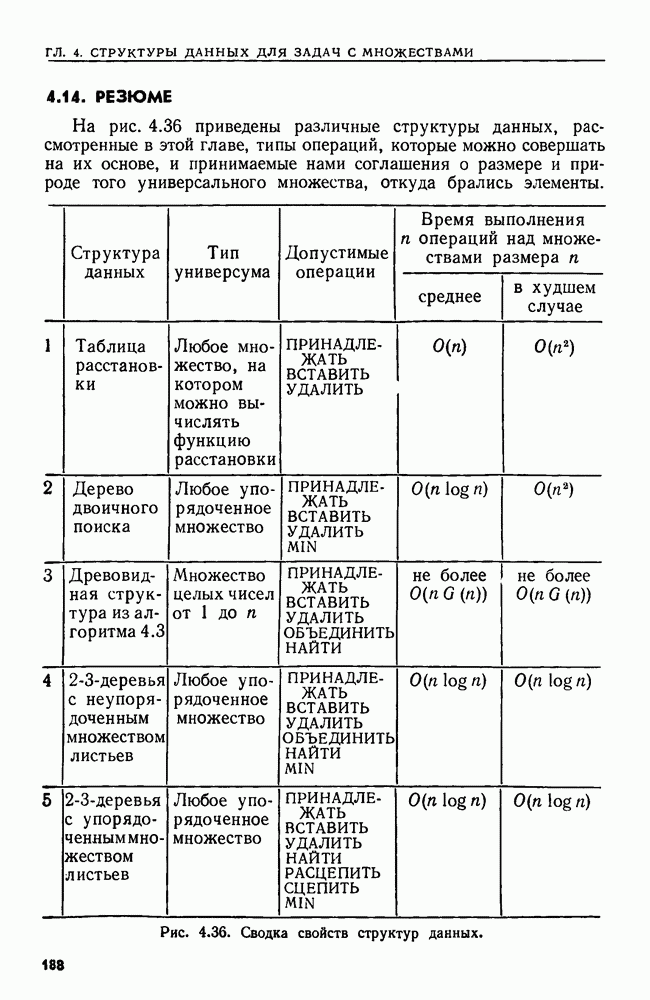
- 4.14. РЕЗЮМЕ
- 5. АЛГОРИТМЫ НА ГРАФАХ
- 5.1. ОСТОВНОЕ ДЕРЕВО НАИМЕНЬШЕЙ СТОИМОСТИ
- 5.2. МЕТОД ПОИСКА В ГЛУБИНУ
- 5.3. ДВУСВЯЗНОСТЬ
- 5.4. ПОИСК В ГЛУБИНУ В ОРИЕНТИРОВАННОМ ГРАФЕ
- 5.5. СИЛЬНАЯ СВЯЗНОСТЬ
- 5.6. ЗАДАЧИ НАХОЖДЕНИЯ ПУТЕЙ
- 5.7. АЛГОРИТМ ТРАНЗИТИВНОГО ЗАМЫКАНИЯ
- 5.8. АЛГОРИТМ НАХОЖДЕНИЯ КРАТЧАЙШЕГО ПУТИ
- 5.9. ЗАДАЧИ О ПУТЯХ И УМНОЖЕНИЕ МАТРИЦ
- 5.10. ЗАДАЧИ С ОДНИМ ИСТОЧНИКОМ
- 5.11. ДОМИНАТОРЫ В ОРИЕНТИРОВАННЫХ АЦИКЛИЧЕСКИХ ГРАФАХ: КОМБИНИРОВАНИЕ ПОНЯТИЙ
- 6. УМНОЖЕНИЕ МАТРИЦ И СВЯЗАННЫЕ С НИМ ОПЕРАЦИИ
- 6.2. АЛГОРИТМ ШТРАССЕНА ДЛЯ УМНОЖЕНИЯ МАТРИЦ
- 6.3. ОБРАЩЕНИЕ МАТРИЦ
- 6.4. НВП-РАЗЛОЖЕНИЕ МАТРИЦЫ
- 6.5. ПРИЛОЖЕНИЯ НВП-РАЗЛОЖЕНИЯ
- 6.6. УМНОЖЕНИЕ БУЛЕВЫХ МАТРИЦ
- 7. БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ И ЕГО ПРИЛОЖЕНИЯ
- 7.2. АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 7.3. БПФ ПРИ ИСПОЛЬЗОВАНИИ БИТОВЫХ ОПЕРАЦИЙ
- 7.4. ПРОИЗВЕДЕНИЕ ПОЛИНОМОВ
- 7.5. АЛГОРИТМ ШЕНХАГЕ — ШТРАССЕНА ДЛЯ УМНОЖЕНИЯ ЦЕЛЫХ ЧИСЕЛ
- 8. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД ЦЕЛЫМИ ЧИСЛАМИ И ПОЛИНОМАМИ
- 8.1. АНАЛОГИИ МЕЖДУ ЦЕЛЫМИ ЧИСЛАМИ И ПОЛИНОМАМИ
- 8.2. УМНОЖЕНИЕ И ДЕЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ
- 8.3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ПОЛИНОМОВ
- 8.4. МОДУЛЬНАЯ АРИФМЕТИКА
- 8.5. МОДУЛЬНАЯ АРИФМЕТИКА ПОЛИНОМОВ И ВЫЧИСЛЕНИЕ ИХ ЗНАЧЕНИЙ
- 8.6. ПРИМЕНЕНИЕ КИТАЙСКОЙ ТЕОРЕМЫ ОБ ОСТАТКАХ
- 8.7. КИТАЙСКАЯ ТЕОРЕМА ОБ ОСТАТКАХ И ИНТЕРПОЛЯЦИЯ ПОЛИНОМОВ
- 8.8. НАИБОЛЬШИЕ ОБЩИЕ ДЕЛИТЕЛИ И АЛГОРИТМ ЕВКЛИДА
- 8.9. АСИМПТОТИЧЕСКИ БЫСТРЫЙ АЛГОРИТМ НАХОЖДЕНИЯ НОД ПОЛИНОМОВ
- 8.10. НОД ЦЕЛЫХ ЧИСЕЛ
- 8.11. ЕЩЕ РАЗ О ПРИМЕНЕНИИ КИТАЙСКОЙ ТЕОРЕМЫ ОБ ОСТАТКАХ
- 8.12. РАЗРЕЖЕННЫЕ ПОЛИНОМЫ
- 9. АЛГОРИТМЫ ИДЕНТИФИКАЦИИ
- 9.1. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ВЫРАЖЕНИЯ
- 9.2. РАСПОЗНАВАНИЕ ОБРАЗОВ, ЗАДАВАЕМЫХ РЕГУЛЯРНЫМИ ВЫРАЖЕНИЯМИ
- 9.3. РАСПОЗНАВАНИЕ ПОДЦЕПОЧЕК
- 9.4. ДВУСТОРОННИЙ ДЕТЕРМИНИРОВАННЫЙ МАГАЗИННЫЙ АВТОМАТ
- 9.5. ПОЗИЦИОННЫЕ ДЕРЕВЬЯ И ИДЕНТИФИКАТОРЫ ПОЗИЦИЙ
- 10. NP-ПОЛНЫЕ ЗАДАЧИ
- 10.1. НЕДЕТЕРМИНИРОВАННЫЕ МАШИНЫ ТЬЮРИНГА
- 10.2. КЛАССЫ …
- 10.3. ЯЗЫКИ И ЗАДАЧИ
- 10.4. NP-ПОЛНОТА ЗАДАЧИ ВЫПОЛНИМОСТИ
- 10.5. ЕЩЕ НЕСКОЛЬКО NP-ПОЛНЫХ ЗАДАЧ
- 10.6. ЗАДАЧИ С ПОЛИНОМИАЛЬНО ОГРАНИЧЕННОЙ ПАМЯТЬЮ
- 11. НЕКОТОРЫЕ ДОКАЗУЕМО ТРУДНО РАЗРЕШИМЫЕ ЗАДАЧИ
- 11.2. ИЕРАРХИЯ ПО ЕМКОСТНОЙ СЛОЖНОСТИ ДЛЯ ДЕТЕРМИНИРОВАННЫХ МАШИН ТЬЮРИНГА
- 11.3. ЗАДАЧА, ТРЕБУЮЩАЯ ЭКСПОНЕНЦИАЛЬНЫХ ВРЕМЕНИ И ПАМЯТИ
- 11.4. НЕЭЛЕМЕНТАРНАЯ ЗАДАЧА
- 12. НИЖНИЕ ОЦЕНКИ ЧИСЛА АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ
- 12.2. ЕЩЕ РАЗ О НЕВЕТВЯЩИХСЯ ПРОГРАММАХ
- 12.3. МАТРИЧНАЯ ФОРМУЛИРОВКА ЗАДАЧ
- 12.4. НИЖНЯЯ ГРАНИЦА ДЛЯ ЧИСЛА УМНОЖЕНИЙ, СВЯЗАННАЯ С РАНГОМ ПО СТРОКАМ
- 12.5. НИЖНЯЯ ГРАНИЦА ДЛЯ ЧИСЛА УМНОЖЕНИЙ, СВЯЗАННАЯ С РАНГОМ ПО СТОЛБЦАМ
- 12.6. ГРАНИЦА ДЛЯ ЧИСЛА УМНОЖЕНИЙ, СВЯЗАННАЯ С РАССМОТРЕНИЕМ СТРОК И СТОЛБЦОВ
- 12.7. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА