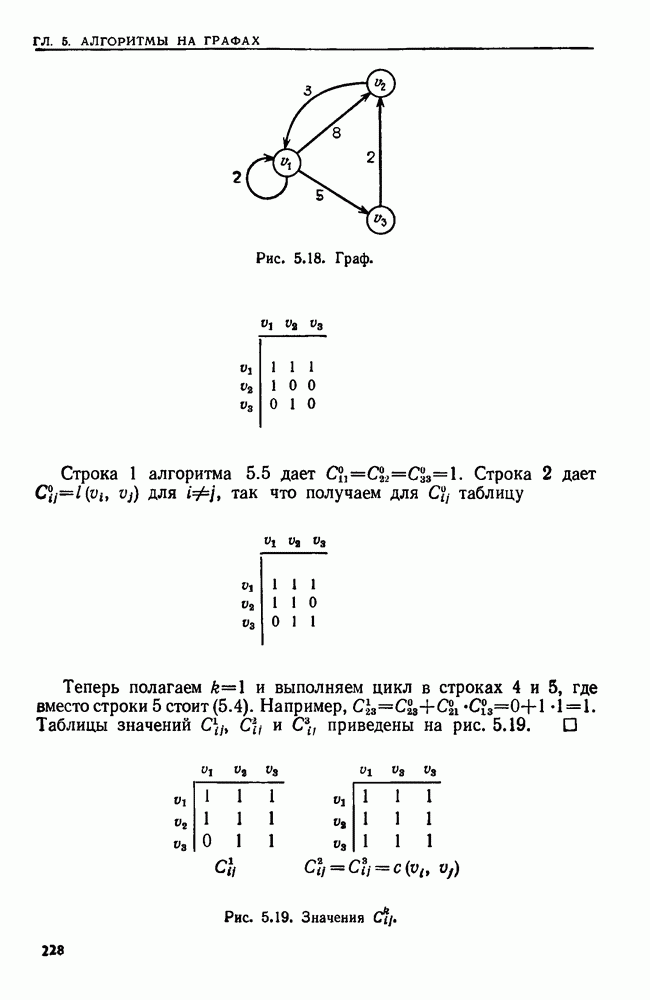
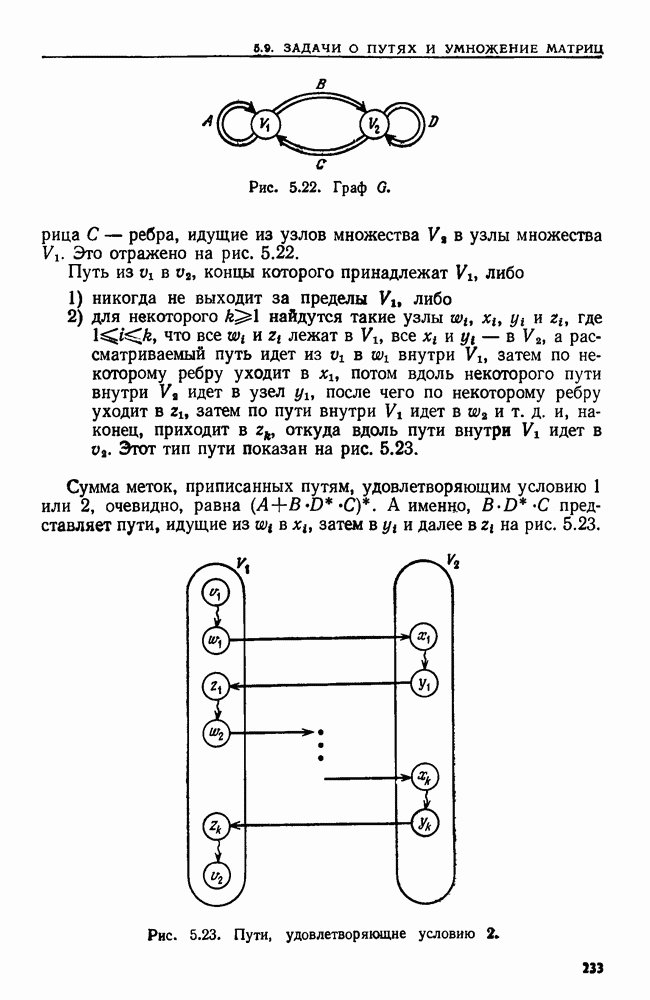
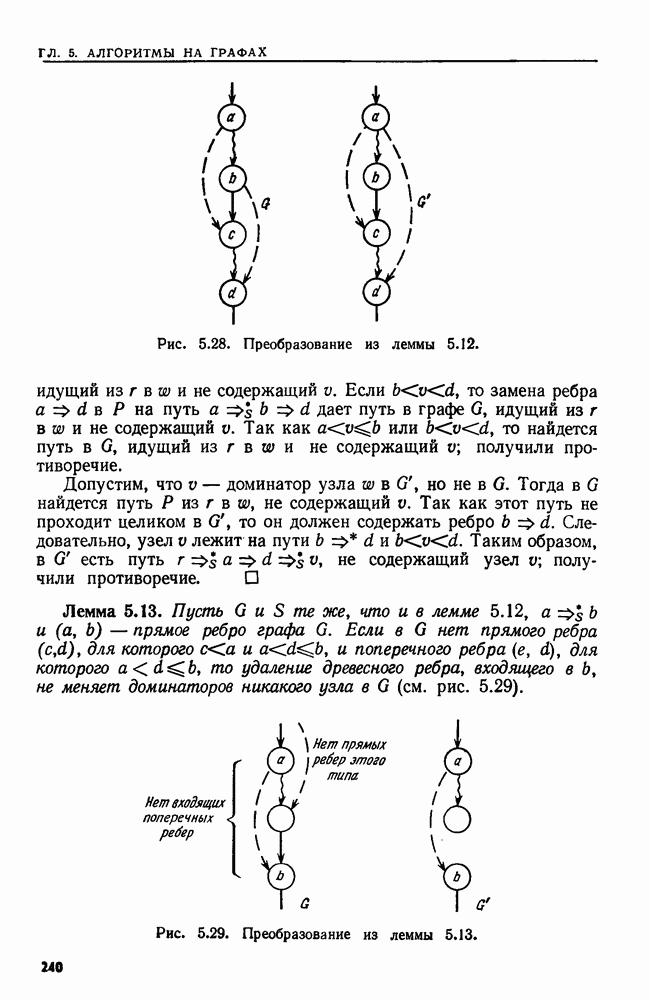
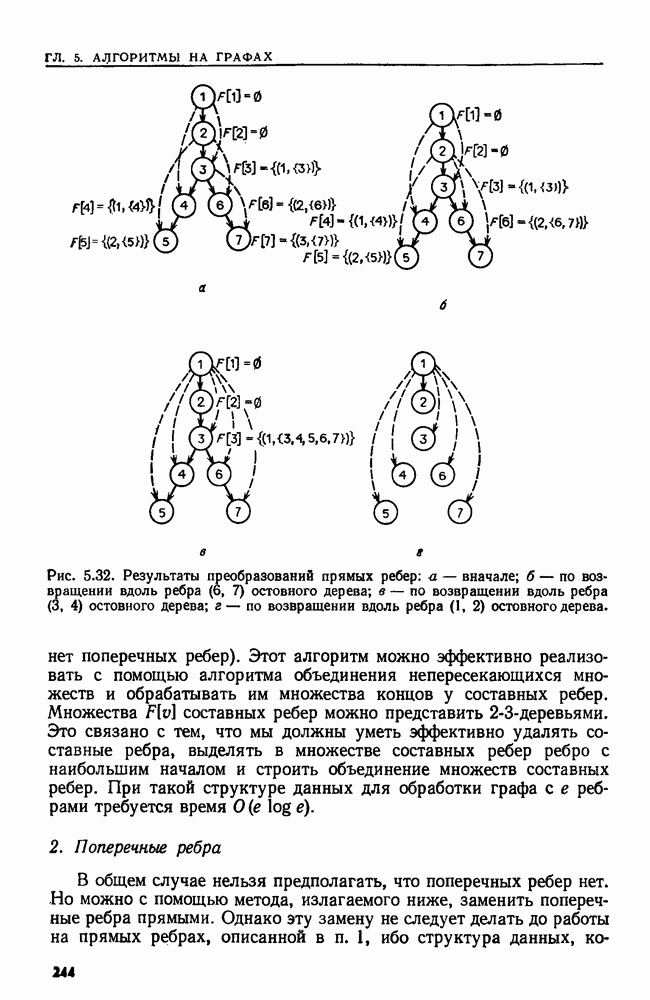
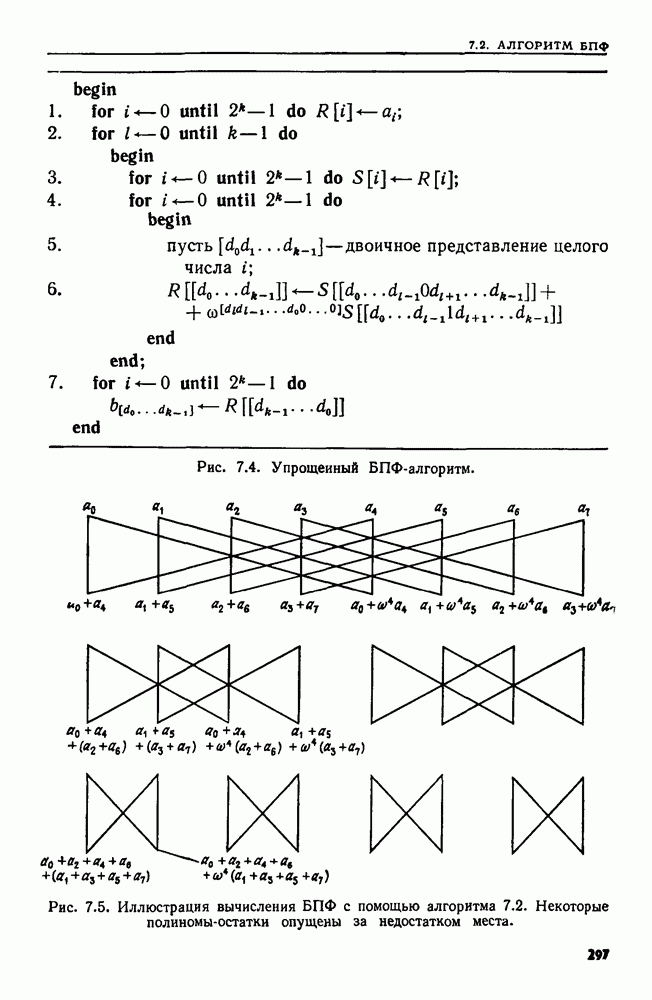
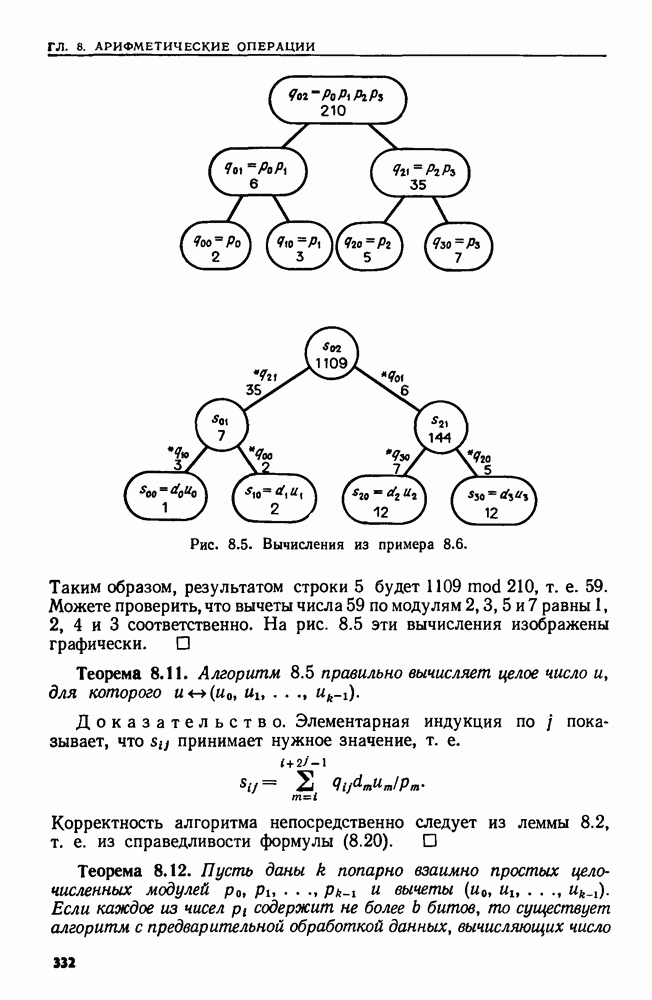
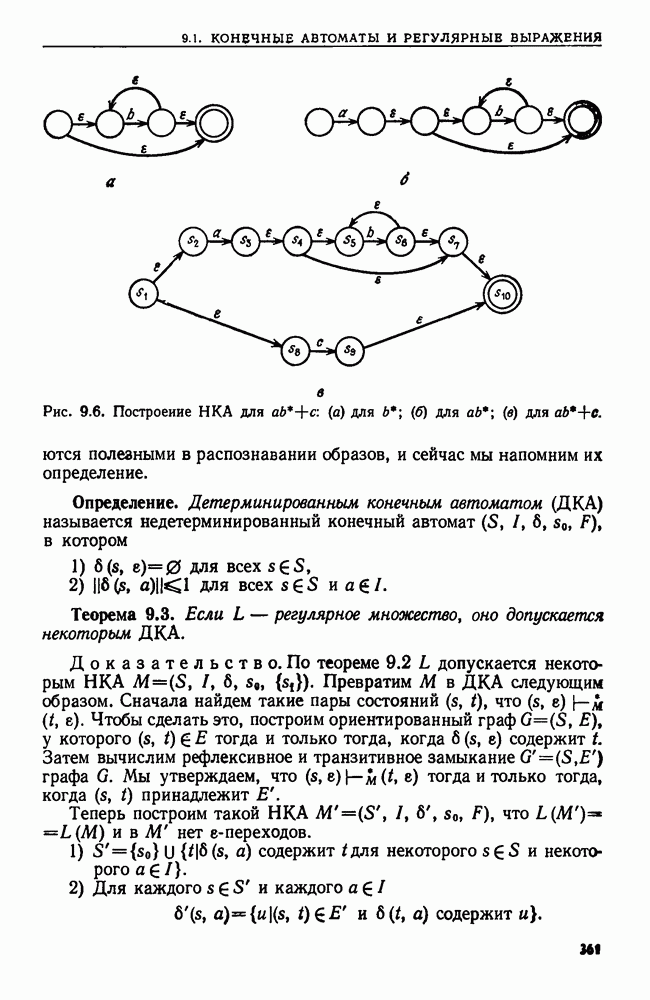
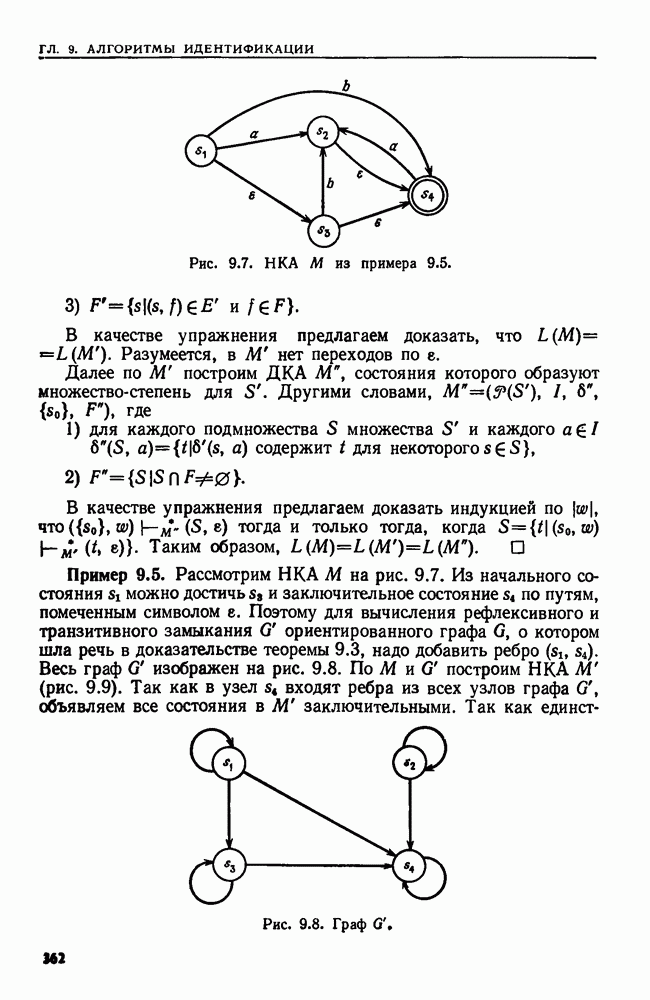
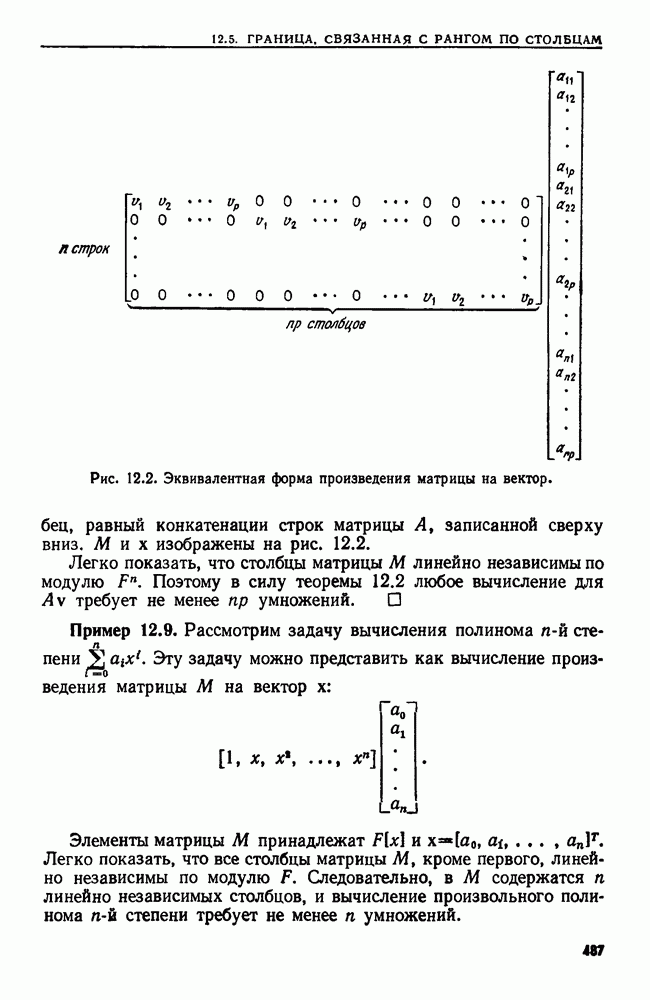
| << Предыдущий параграф | Следующий параграф >> |
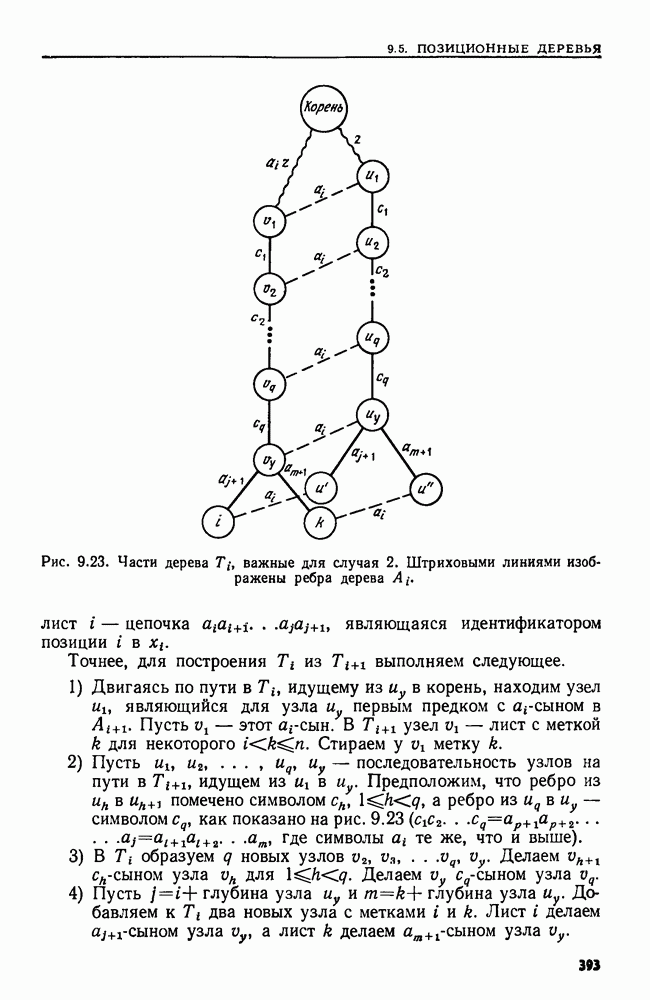
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.4. НВП-РАЗЛОЖЕНИЕ МАТРИЦЫ
Один из эффективных методов решения системы линейных уравнений состоит в применении так называемого НВП-разложения.
Определение. НВ-разложением  -матрицы А,
-матрицы А,  , называется представление ее в виде
, называется представление ее в виде  где
где  нормированная нижняя треугольная
нормированная нижняя треугольная  -матрица, a U - верхняя треугольная
-матрица, a U - верхняя треугольная  -матрица.
-матрица.
Уравнение  где А — это
где А — это  -матрица,
-матрица,  -мерный вектор-столбец неизвестных,
-мерный вектор-столбец неизвестных,  -мерный вектор-столбец, можно решить, сначала НВ-разложив А в произведение
-мерный вектор-столбец, можно решить, сначала НВ-разложив А в произведение  в предположении, что это возможно. Затем представим
в предположении, что это возможно. Затем представим  в виде
в виде  Чтобы получить решение х, решим сначала
Чтобы получить решение х, решим сначала  относительно у, а затем
относительно у, а затем  относительно х.
относительно х.
Трудность применения этого метода заключается в том, что у матрицы А может не быть НВ-разложения, даже если она невырож-денна. Например, матрица

невырожденна,  нее нет НВ-разложения. Однако если матрица А невырожденна, то найдется такая матрица перестановки
нее нет НВ-разложения. Однако если матрица А невырожденна, то найдется такая матрица перестановки  что
что  имеет НВ-разложение. Изложим алгоритм, который по любой невырожденной матрице А находит такие матрицы
имеет НВ-разложение. Изложим алгоритм, который по любой невырожденной матрице А находит такие матрицы  что
что  Матрицы
Матрицы  образуют НВП-разложение 2) матрицы
образуют НВП-разложение 2) матрицы 
Алгоритм 6.1. НВП-разложение
Вход. Невырожденная  -матрица
-матрица  степень числа 2.
степень числа 2.
Выход. Матрицы  для которых
для которых  причем
причем  нормированная нижняя треугольная матрица,
нормированная нижняя треугольная матрица,  верхняя треугольная и
верхняя треугольная и  матрица перестановки.
матрица перестановки.
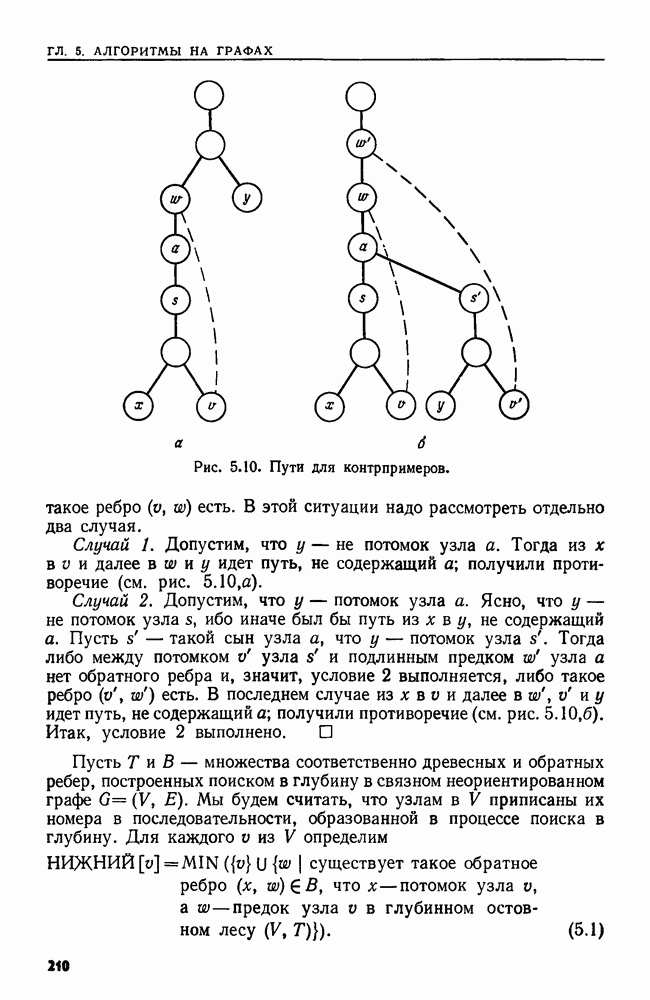
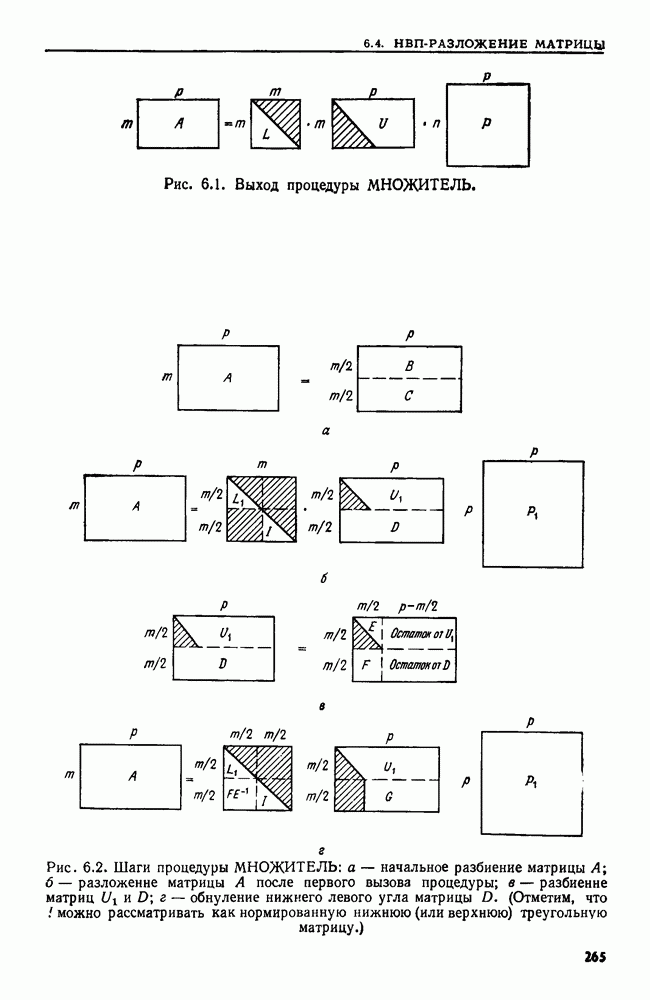
Метод. Вызываем процедуру  где
где  рекурсивная процедура, показанная на рис. 6.4. При описании этой процедуры используются диаграммы на рис.
рекурсивная процедура, показанная на рис. 6.4. При описании этой процедуры используются диаграммы на рис.  где затемненная область матрицы представляет ту ее часть, о которой известно, что она состоит из одних нулей.
где затемненная область матрицы представляет ту ее часть, о которой известно, что она состоит из одних нулей.
Каждый рекурсивный вызов процедуры МНОЖИТЕЛЬ происходит на  -подматрице А
-подматрице А  -матрицы
-матрицы  При каждом вызове
При каждом вызове  есть степень числа 2 и Выходом этой процедуры являются три матрицы
есть степень числа 2 и Выходом этой процедуры являются три матрицы  показанные на рис. 6.1.
показанные на рис. 6.1.
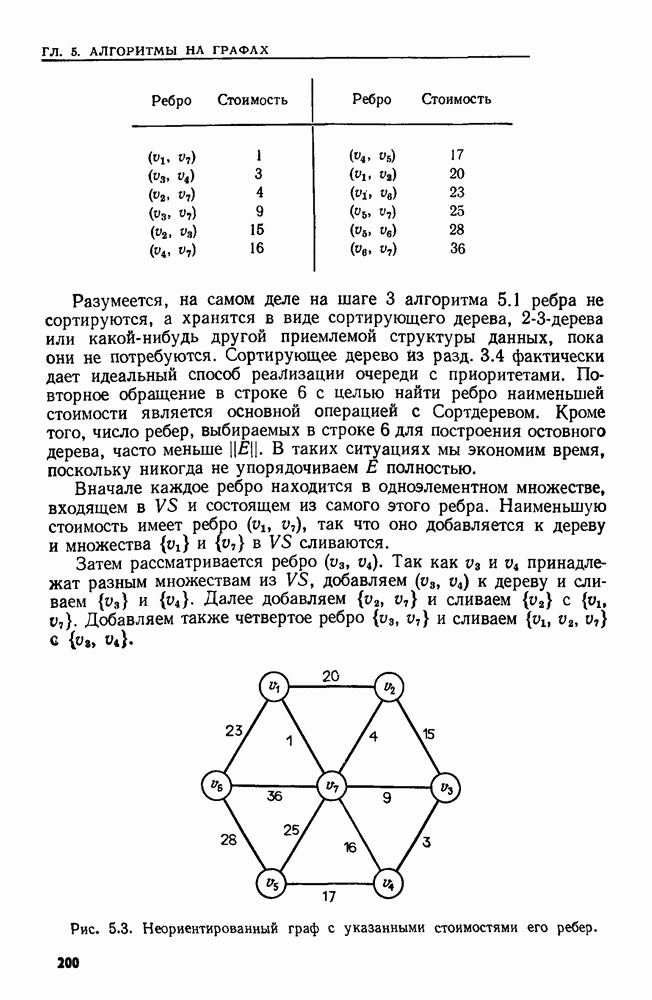
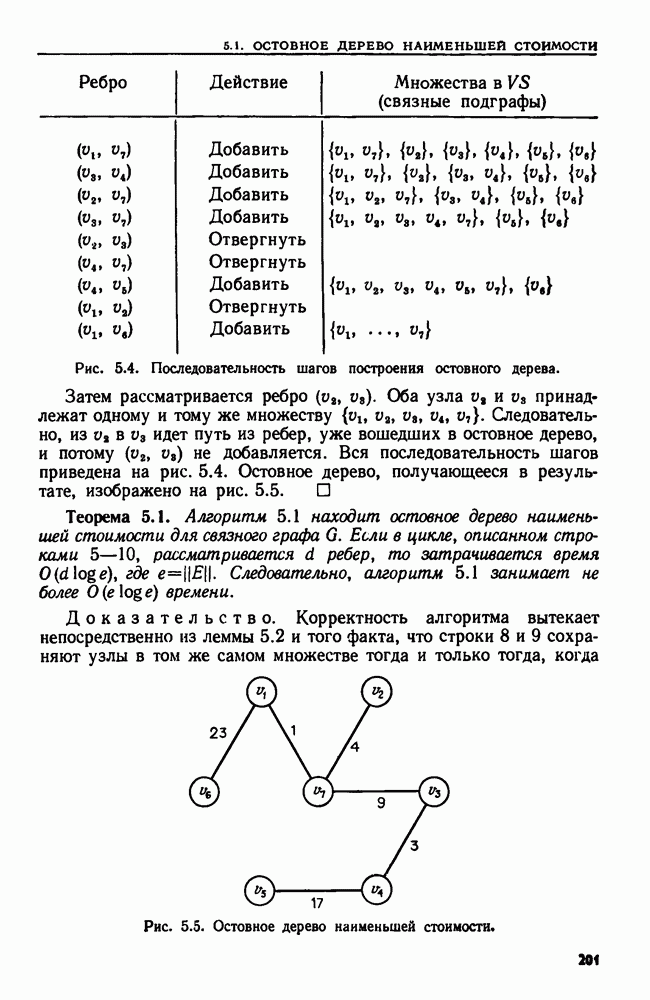
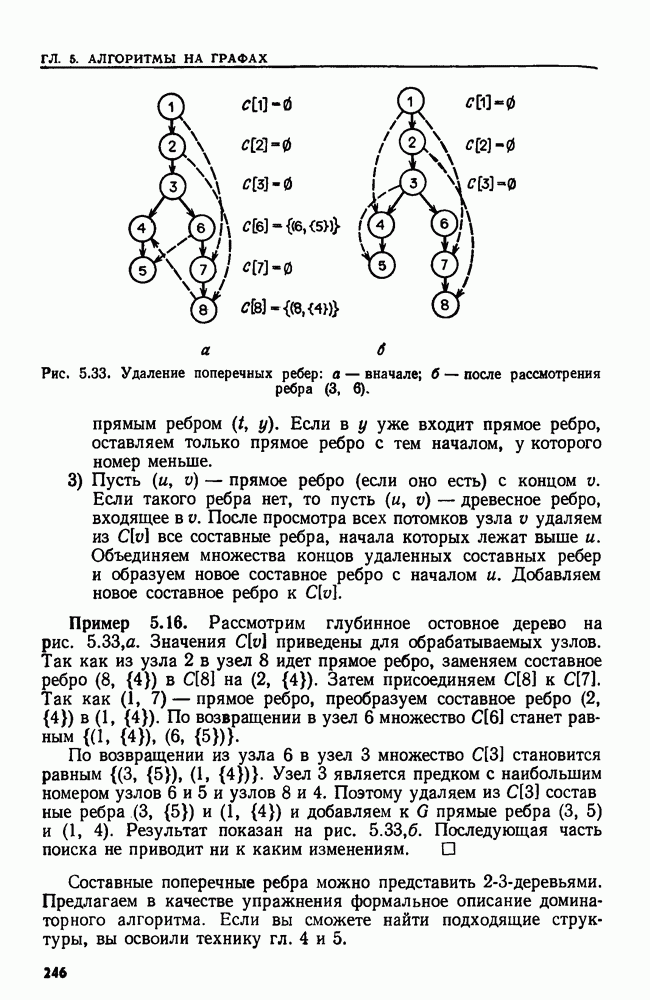
Пример 6.3. Найдем НВП-разложение матрицы


(кликните для просмотра скана)

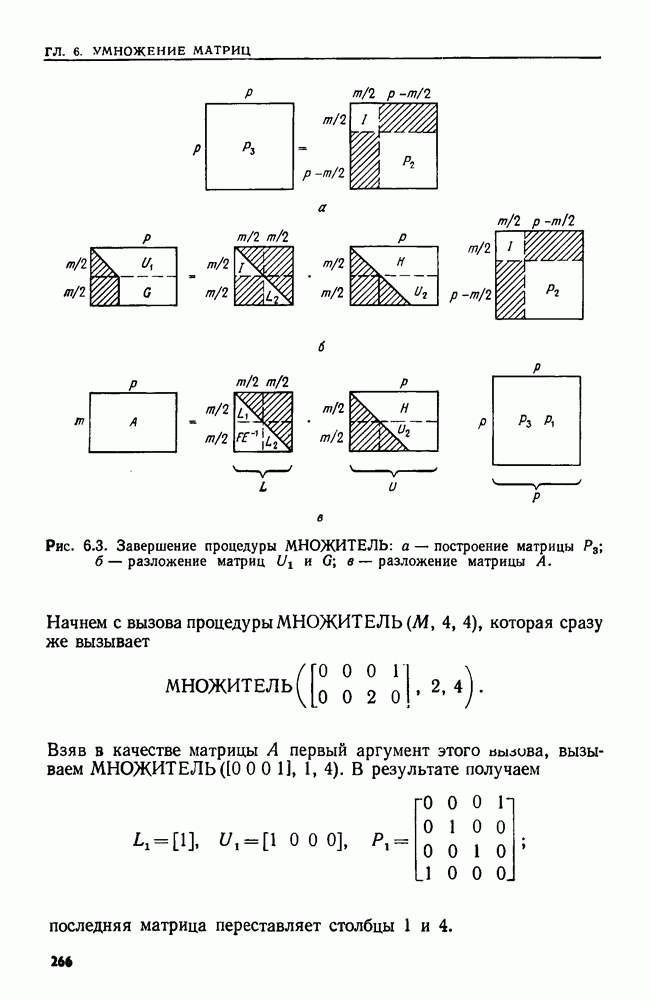
Рис. 6.3. Завершение процедуры  а — построение матрицы
а — построение матрицы  ; б - разложение матриц
; б - разложение матриц  в — разложение матрицы А.
в — разложение матрицы А.
Начнем с вызова процедуры  ), которая сразу же вызывает
), которая сразу же вызывает

Взяв в качестве матрицы А первый аргумент этого иылива, вызываем МНОЖИТЕЛЬ результате получаем

последняя матрица переставляет столбцы 1 и 4.
(см. скан)
Рис. 6.4. (см. скан) Процедура 
В строке 7 вычисляем
ГО

В строке 8 имеем  , так что после выполнения строки
, так что после выполнения строки  Строка 10 дает
Строка 10 дает  ; следовательно, после строки 11 будет
; следовательно, после строки 11 будет

В строке 12

а в строке 13

Таким образом, МНОЖИТЕЛЬ выдает

Теперь возвращаемся к вызову  в строке 6, причем роль
в строке 6, причем роль  играют соответственно
играют соответственно  В строке 7 вычисляем
В строке 7 вычисляем

в строке 8

так что после выполнения строки 9

и в строке 10

Предлагаем читателю проверить, что  ) выдает
) выдает

Таким образом, в строке  а в строке 13
а в строке 13

Следовательно, в строках 14—16 вычисляем

Теперь приступим к доказательству корректности алгоритма 6.1.
Теорема 6.3. Для любой невырожденной матрицы А алгоритм 6.1 вычисляет такие матрицы  что
что 
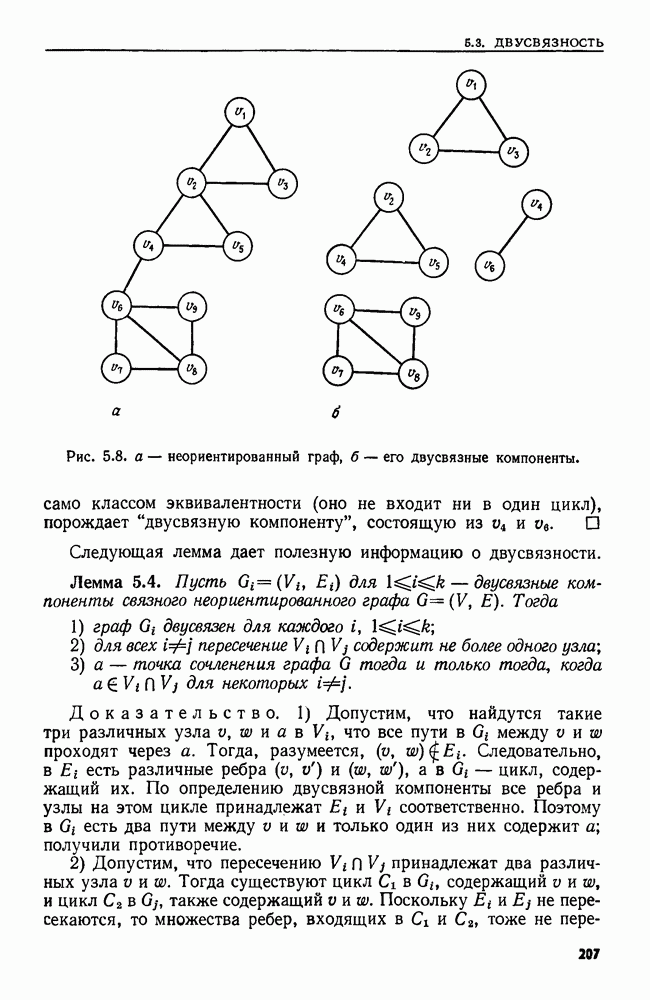
Доказательство. Детали, необходимые для доказательства того, что различные разложения, изображенные на рис. 6.2 и 6.3, корректны, оставляем в качестве упражнения. Покажем лишь, что
1) в строке 2 процедуры МНОЖИТЕЛЬ всегда можно найти ненулевой столбец и
2) в строке 9 всегда существует 
Пусть А будет  -матрицей. Покажем индукцией по
-матрицей. Покажем индукцией по  где
где  степень числа 2, что если А имеет ранг
степень числа 2, что если А имеет ранг  то МНОЖИТЕЛЬ вычислит такие
то МНОЖИТЕЛЬ вычислит такие  что
что  нижняя треугольная матрица, верхняя треугольная матрица и матрица перестановки рангов
нижняя треугольная матрица, верхняя треугольная матрица и матрица перестановки рангов  соответственно. Кроме того, первые
соответственно. Кроме того, первые  столбцов матрицы
столбцов матрицы  образуют подматрицу ранга
образуют подматрицу ранга  Если
Если  то в А должен быть ненулевой элемент, так что базис индукции выполняется. Допустим, что
то в А должен быть ненулевой элемент, так что базис индукции выполняется. Допустим, что  Так как А имеет
Так как А имеет  столбцов и ранг
столбцов и ранг  то каждая из матриц
то каждая из матриц  появляющихся в строке 5, имеет
появляющихся в строке 5, имеет  столбцов и ранг
столбцов и ранг  По предположению индукции вызов процедуры МНОЖИТЕЛЬ в строке 6 выдает требуемые матрицы
По предположению индукции вызов процедуры МНОЖИТЕЛЬ в строке 6 выдает требуемые матрицы  причем первые
причем первые  столбцов матрицы
столбцов матрицы  образуют матрицу ранга
образуют матрицу ранга  Поэтому матрица
Поэтому матрица  необходимая в строке 9, существует.
необходимая в строке 9, существует.
Из рис. 6.2,г видно, что матрица А равна произведению трех матриц, у одной из которых в верхней части стоит  а в нижней
а в нижней  Ранг этой матрицы должен быть
Ранг этой матрицы должен быть  ибо матрица А имеет ранг
ибо матрица А имеет ранг  Поэтому
Поэтому  имеет ранг
имеет ранг  Поскольку первые
Поскольку первые  столбцов матрицы
столбцов матрицы  состоят из нулей,
состоят из нулей,  получается из
получается из  вычеркиванием ее первых
вычеркиванием ее первых  столбцов, то ранг матрицы
столбцов, то ранг матрицы  также равен
также равен  Следовательно, по предположению индукции вызов процедуры МНОЖИТЕЛЬ в строке 11 дает нужные
Следовательно, по предположению индукции вызов процедуры МНОЖИТЕЛЬ в строке 11 дает нужные  Отсюда непосредственно вытекает доказываемое утверждение.
Отсюда непосредственно вытекает доказываемое утверждение. 
Прежде чем переходить к анализу времени работы, заметим, что матрицу перестановки можно представить в виде такого массива  что
что  тогда и только тогда, когда 1 в столбце
тогда и только тогда, когда 1 в столбце  стоит в строке
стоит в строке  Поэтому две
Поэтому две  -матрицы перестановок можно перемножить за время
-матрицы перестановок можно перемножить за время  положив
положив  При таком представлении можно вычислить за время
При таком представлении можно вычислить за время  также и обращение матрицы перестановки.
также и обращение матрицы перестановки.
Теорема 6.4. Пусть для каждого  можно умножить две
можно умножить две  -матрицы за такое время
-матрицы за такое время  что при некотором
что при некотором  неравенство
неравенство
 выполняется для всех
выполняется для всех  Тогда найдется такая постоянная
Тогда найдется такая постоянная  что алгоритм 6.1 тратит не более
что алгоритм 6.1 тратит не более  времени для любой невырожденной матрицы.
времени для любой невырожденной матрицы.
Доказательство. Применим алгоритм 6.1 к  -матрице. Пусть
-матрице. Пусть  время, требуемое для выполнения процедуры
время, требуемое для выполнения процедуры  где А — это
где А — это  -матрица,
-матрица,  В силу строк 1—4 этой процедуры
В силу строк 1—4 этой процедуры  для некоторой постоянной
для некоторой постоянной  Рекурсивные вызовы в строках 6 и 11 занимают
Рекурсивные вызовы в строках 6 и 11 занимают  времени каждый. В каждой из строк 7 и 13 вычисляется матрица, обратная к матрице перестановки (что занимает
времени каждый. В каждой из строк 7 и 13 вычисляется матрица, обратная к матрице перестановки (что занимает  времени), и произвольная матрица умножается на матрицу перестановки. Это умножение просто переставляет столбцы первой матрицы. Представляя матрицу перестановки в виде массива
времени), и произвольная матрица умножается на матрицу перестановки. Это умножение просто переставляет столбцы первой матрицы. Представляя матрицу перестановки в виде массива  видим, что
видим, что  столбец первой матрицы становится
столбец первой матрицы становится  столбцом произведения. Таким образом, произведение можно найти за время
столбцом произведения. Таким образом, произведение можно найти за время  и тем самым строки 7 и 13 выполняются за время
и тем самым строки 7 и 13 выполняются за время 
Строка 9 тратит  времени на вычисление
времени на вычисление  (в силу теоремы 6.2); такое же время требуется для вычисления
(в силу теоремы 6.2); такое же время требуется для вычисления  Так как матрица
Так как матрица  имеет не более
имеет не более  строк и не более
строк и не более  столбцов, то произведение
столбцов, то произведение  можно вычислить за время
можно вычислить за время 
Заметим, что  делится на
делится на  так как тип являются степенями числа
так как тип являются степенями числа  Легко видеть, что остальные шаги занимают
Легко видеть, что остальные шаги занимают  времени в худшем случае. Таким образом, получили рекуррентные соотношения
времени в худшем случае. Таким образом, получили рекуррентные соотношения

где  постоянные.
постоянные.
В силу условия теоремы и равенствам  справедливо неравенство
справедливо неравенство  Поэтому можно объединить второе и третье слагаемые в (6.5). Для некоторой постоянной
Поэтому можно объединить второе и третье слагаемые в (6.5). Для некоторой постоянной 

Из (6.6) выводим 

Из условия теоремы вытекает, что  Поэтому
Поэтому

Так как сумма в правой части сходится и  существует такая постоянная
существует такая постоянная  что
что  Для алгоритма
Для алгоритма  значит,
значит, 
Следствие. НВП-разложение любой невырожденной  -мат-рицы можно найти за
-мат-рицы можно найти за  шагов.
шагов.
Доказательство. В силу теорем 6.1, 6.3 и 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
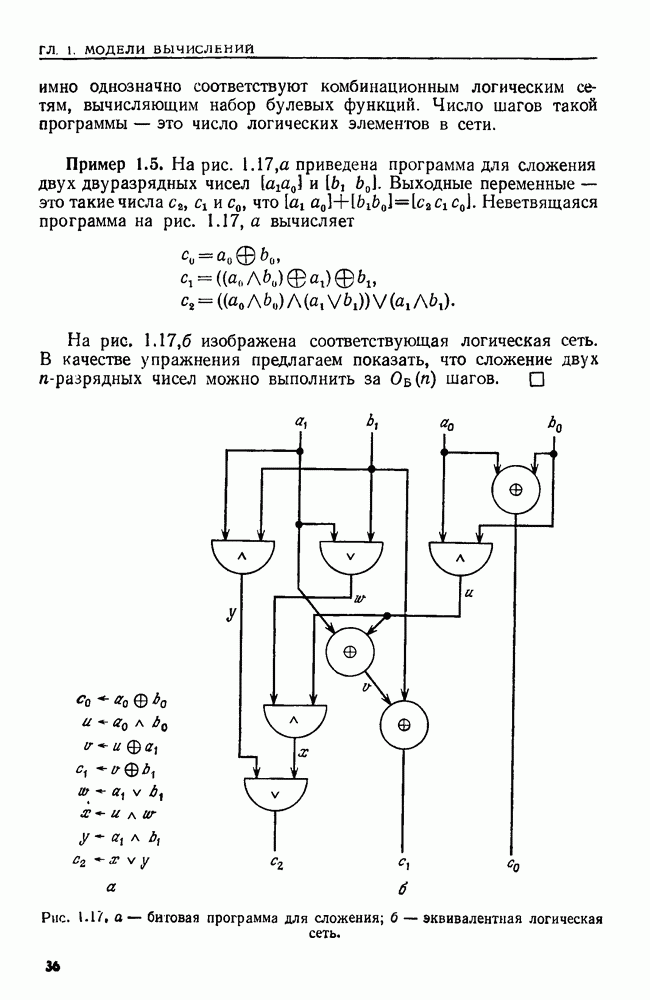
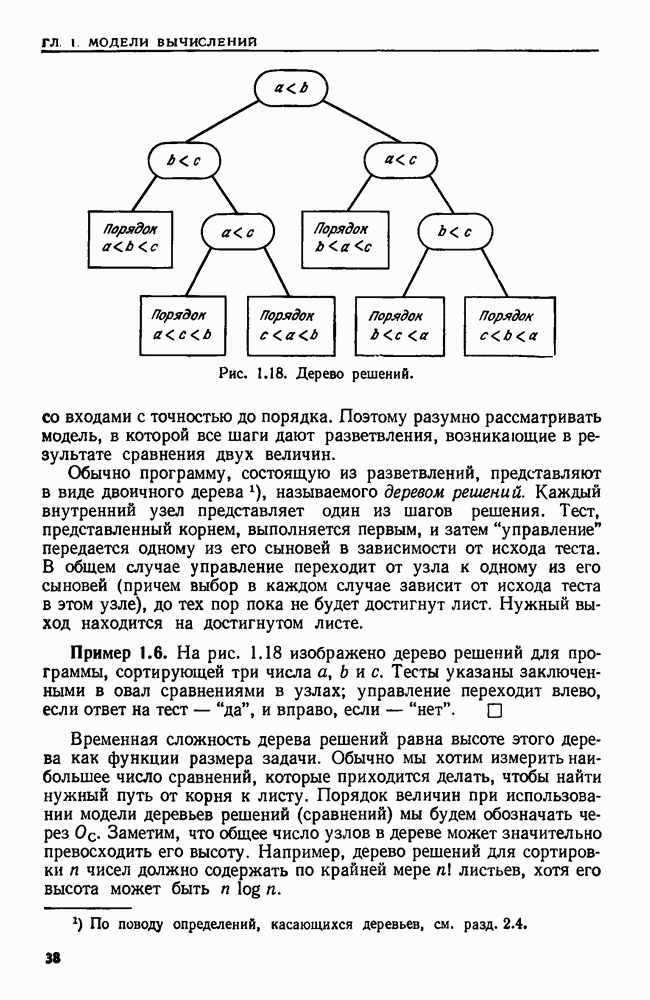
- МОДЕЛИ ВЫЧИСЛЕНИЙ
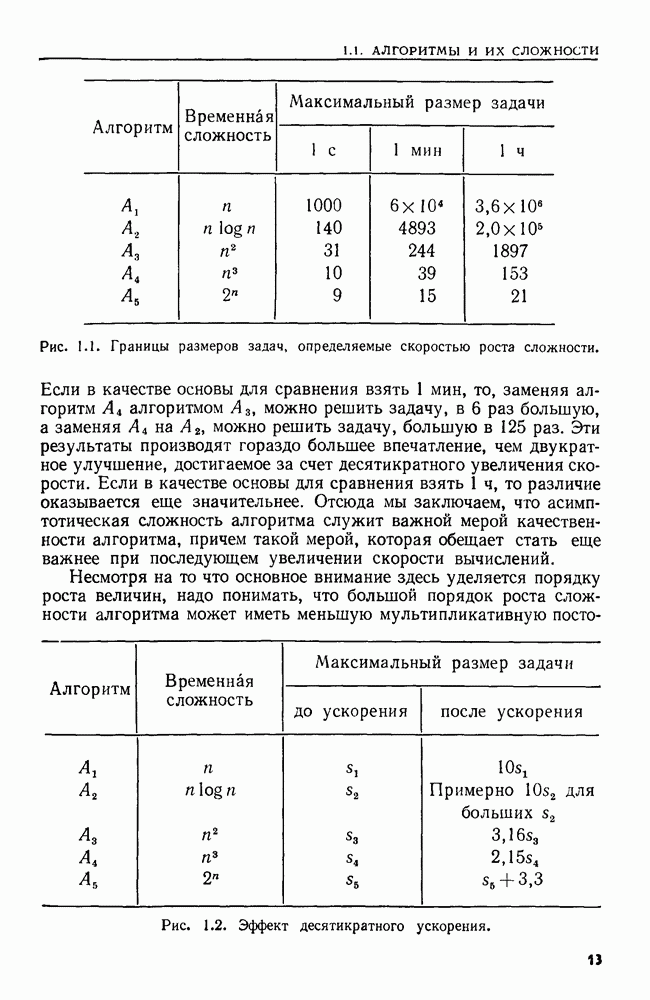
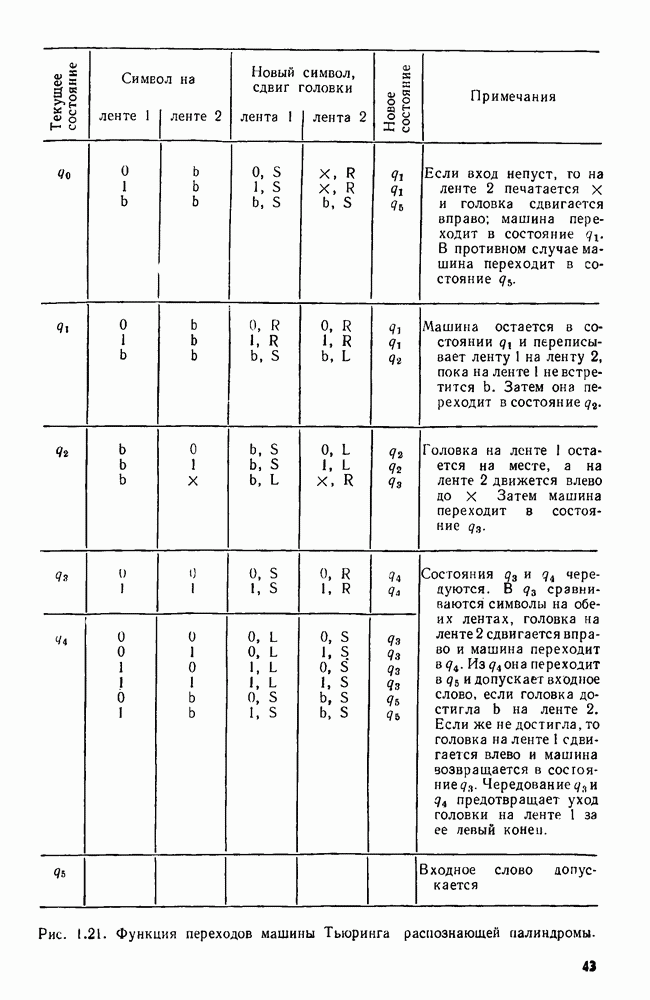
- 1.1. АЛГОРИТМЫ И ИХ СЛОЖНОСТИ
- 1.2. МАШИНЫ С ПРОИЗВОЛЬНЫМ ДОСТУПОМ К ПАМЯТИ
- 1.3. ВЫЧИСЛИТЕЛЬНАЯ СЛОЖНОСТЬ РАМ-ПРОГРАММ
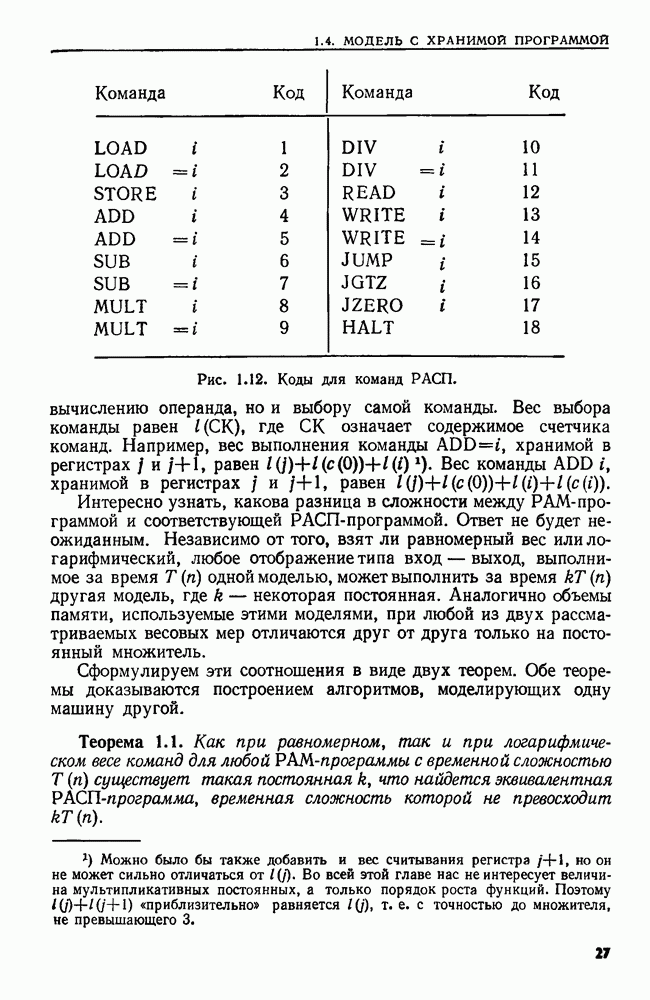
- 1.4. МОДЕЛЬ С ХРАНИМОЙ ПРОГРАММОЙ
- 1.5. МОДИФИКАЦИЯ РАМ
- 1.6. ПРОСТЕЙШАЯ МОДЕЛЬ ВЫЧИСЛЕНИЙ: МАШИНА ТЬЮРИНГА
- 1.7. СВЯЗЬ МАШИН ТЬЮРИНГА И РАМ
- 1.8. ЯЗЫК ВЫСОКОГО УРОВНЯ — УПРОЩЕННЫЙ АЛГОЛ
- 2. РАЗРАБОТКА ЭФФЕКТИВНЫХ АЛГОРИТМОВ
- 2.1. СТРУКТУРЫ ДАННЫХ: СПИСКИ, ОЧЕРЕДИ И СТЕКИ
- 2.2. ПРЕДСТАВЛЕНИЯ МНОЖЕСТВ
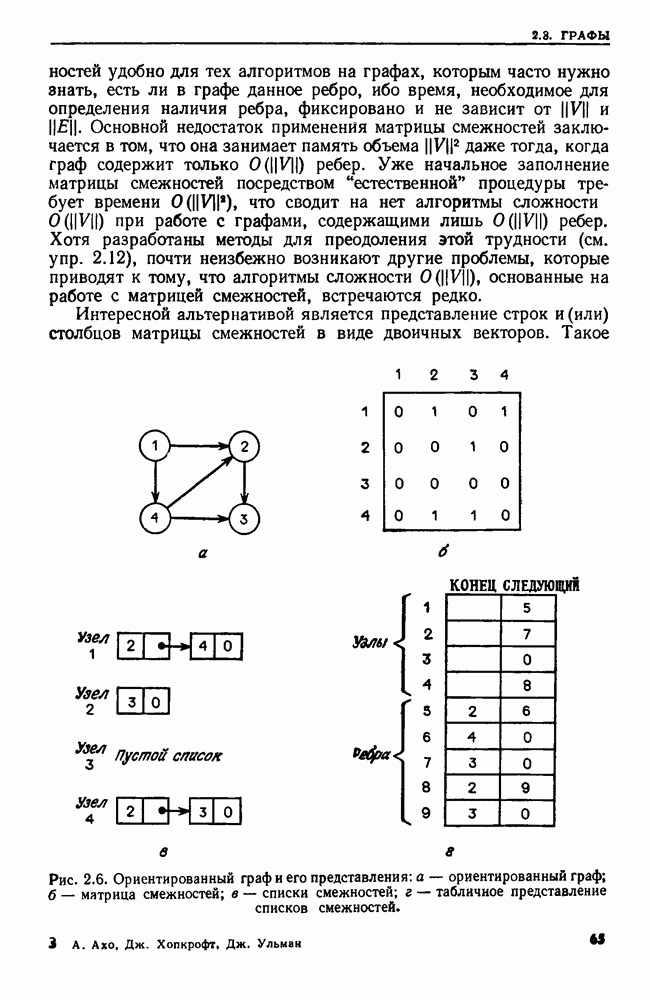
- 2.3. ГРАФЫ
- 2.4. ДЕРЕВЬЯ
- 2.5. РЕКУРСИЯ
- 2.6. РАЗДЕЛЯЙ И ВЛАСТВУЙ
- 2.7. БАЛАНСИРОВКА
- 2.8. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
- 2.9. ЭПИЛОГ
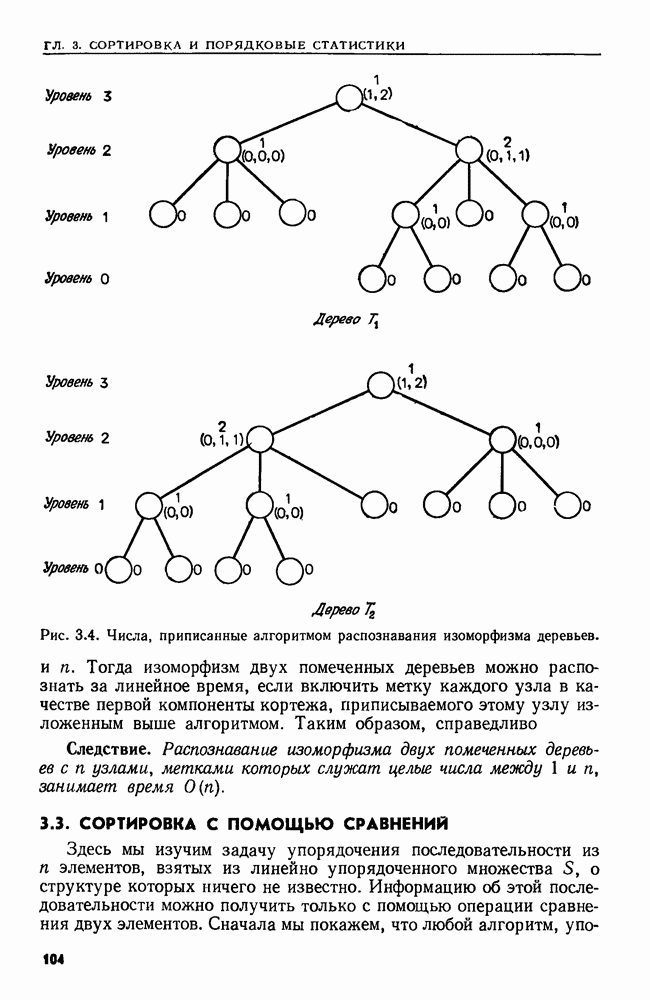
- 3. СОРТИРОВКА И ПОРЯДКОВЫЕ СТАТИСТИКИ
- 3.1. ЗАДАЧА СОРТИРОВКИ
- 3.2. ЦИФРОВАЯ СОРТИРОВКА
- 3.3. СОРТИРОВКА С ПОМОЩЬЮ СРАВНЕНИЙ
- 3.4. СОРТДЕРЕВОМ — УПОРЯДОЧЕНИЕ С ПОМОЩЬЮ O(n log n) СРАВНЕНИЙ
- 3.5. БЫСТРСОРТ — УПОРЯДОЧЕНИЕ ЗА СРЕДНЕЕ ВРЕМЯ O(n log n)
- 3.6. ПОРЯДКОВЫЕ СТАТИСТИКИ
- 3.7. СРЕДНЕЕ ВРЕМЯ ДЛЯ ПОРЯДКОВЫХ СТАТИСТИК
- 4. СТРУКТУРЫ ДАННЫХ ДЛЯ ЗАДАЧ, КАСАЮЩИХСЯ РАБОТЫ С МНОЖЕСТВАМИ
- 4.2. МЕТОД РАССТАНОВКИ
- 4.3. ДВОИЧНЫЙ ПОИСК
- 4.4. ДЕРЕВЬЯ ДВОИЧНОГО ПОИСКА
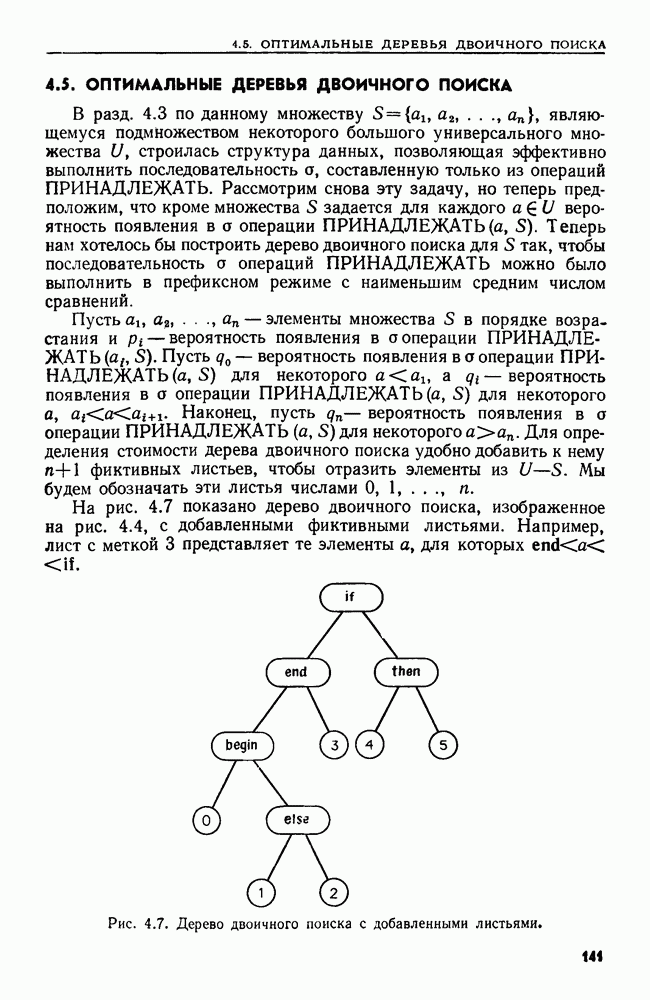
- 4.5. ОПТИМАЛЬНЫЕ ДЕРЕВЬЯ ДВОИЧНОГО ПОИСКА
- 4.6. ПРОСТОЙ АЛГОРИТМ ДЛЯ НАХОЖДЕНИЯ ОБЪЕДИНЕНИЯ НЕПЕРЕСЕКАЮЩИХСЯ МНОЖЕСТВ
- 4.7. ДРЕВОВИДНЫЕ СТРУКТУРЫ ДЛЯ ЗАДАЧИ ОБЪЕДИНИТЬ — НАЙТИ
- 4.8. ПРИЛОЖЕНИЯ И ОБОБЩЕНИЯ АЛГОРИТМА ОБЪЕДИНИТЬ — НАЙТИ
- 4.9. СХЕМЫ СБАЛАНСИРОВАННЫХ ДЕРЕВЬЕВ
- 4.10. СЛОВАРИ И ОЧЕРЕДИ С ПРИОРИТЕТАМИ
- 4.11. СЛИВАЕМЫЕ ДЕРЕВЬЯ
- 4.12. СЦЕПЛЯЕМЫЕ ОЧЕРЕДИ
- 4.13. РАЗБИЕНИЕ
- 4.14. РЕЗЮМЕ
- 5. АЛГОРИТМЫ НА ГРАФАХ
- 5.1. ОСТОВНОЕ ДЕРЕВО НАИМЕНЬШЕЙ СТОИМОСТИ
- 5.2. МЕТОД ПОИСКА В ГЛУБИНУ
- 5.3. ДВУСВЯЗНОСТЬ
- 5.4. ПОИСК В ГЛУБИНУ В ОРИЕНТИРОВАННОМ ГРАФЕ
- 5.5. СИЛЬНАЯ СВЯЗНОСТЬ
- 5.6. ЗАДАЧИ НАХОЖДЕНИЯ ПУТЕЙ
- 5.7. АЛГОРИТМ ТРАНЗИТИВНОГО ЗАМЫКАНИЯ
- 5.8. АЛГОРИТМ НАХОЖДЕНИЯ КРАТЧАЙШЕГО ПУТИ
- 5.9. ЗАДАЧИ О ПУТЯХ И УМНОЖЕНИЕ МАТРИЦ
- 5.10. ЗАДАЧИ С ОДНИМ ИСТОЧНИКОМ
- 5.11. ДОМИНАТОРЫ В ОРИЕНТИРОВАННЫХ АЦИКЛИЧЕСКИХ ГРАФАХ: КОМБИНИРОВАНИЕ ПОНЯТИЙ
- 6. УМНОЖЕНИЕ МАТРИЦ И СВЯЗАННЫЕ С НИМ ОПЕРАЦИИ
- 6.2. АЛГОРИТМ ШТРАССЕНА ДЛЯ УМНОЖЕНИЯ МАТРИЦ
- 6.3. ОБРАЩЕНИЕ МАТРИЦ
- 6.4. НВП-РАЗЛОЖЕНИЕ МАТРИЦЫ
- 6.5. ПРИЛОЖЕНИЯ НВП-РАЗЛОЖЕНИЯ
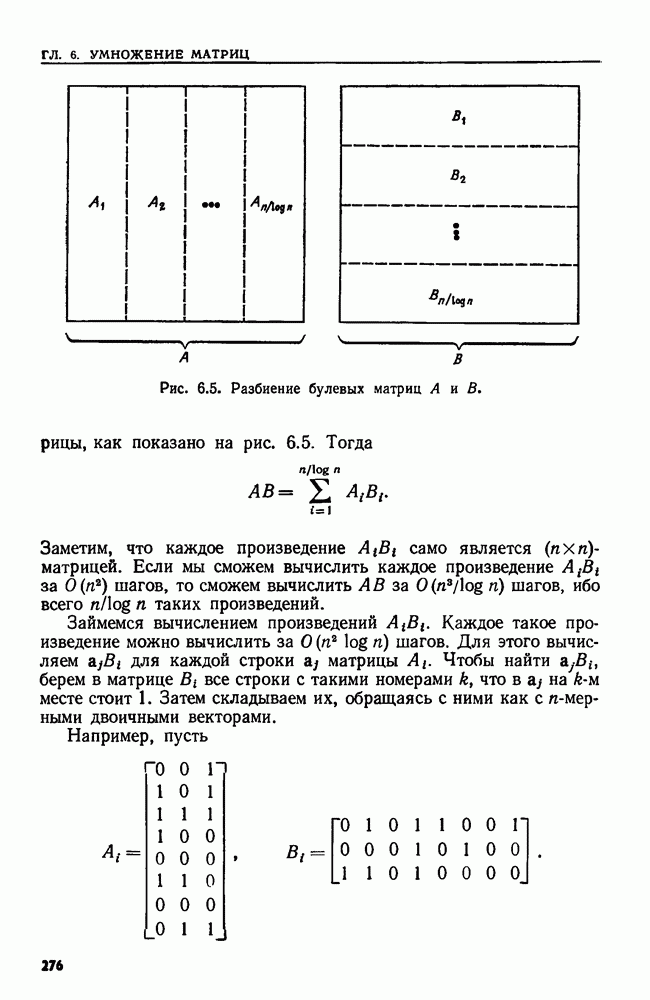
- 6.6. УМНОЖЕНИЕ БУЛЕВЫХ МАТРИЦ
- 7. БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ И ЕГО ПРИЛОЖЕНИЯ
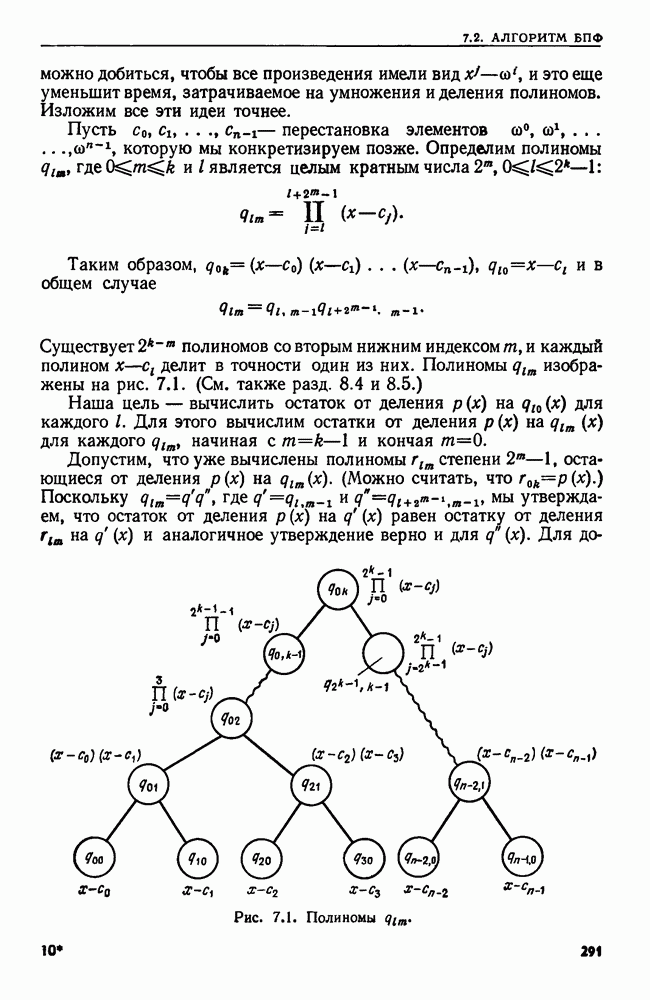
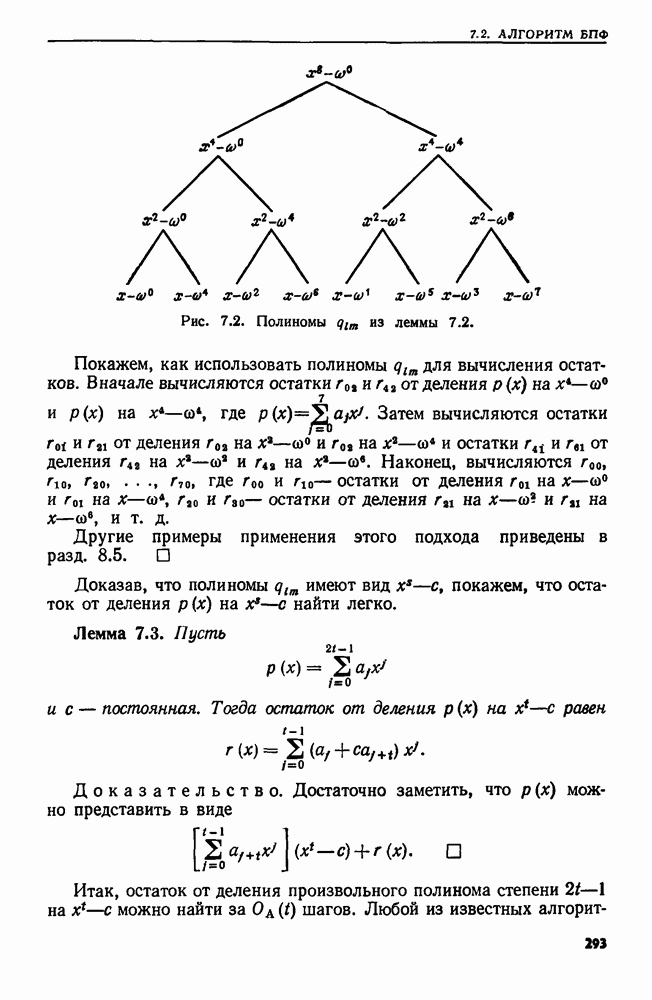
- 7.2. АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 7.3. БПФ ПРИ ИСПОЛЬЗОВАНИИ БИТОВЫХ ОПЕРАЦИЙ
- 7.4. ПРОИЗВЕДЕНИЕ ПОЛИНОМОВ
- 7.5. АЛГОРИТМ ШЕНХАГЕ — ШТРАССЕНА ДЛЯ УМНОЖЕНИЯ ЦЕЛЫХ ЧИСЕЛ
- 8. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД ЦЕЛЫМИ ЧИСЛАМИ И ПОЛИНОМАМИ
- 8.1. АНАЛОГИИ МЕЖДУ ЦЕЛЫМИ ЧИСЛАМИ И ПОЛИНОМАМИ
- 8.2. УМНОЖЕНИЕ И ДЕЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ
- 8.3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ПОЛИНОМОВ
- 8.4. МОДУЛЬНАЯ АРИФМЕТИКА
- 8.5. МОДУЛЬНАЯ АРИФМЕТИКА ПОЛИНОМОВ И ВЫЧИСЛЕНИЕ ИХ ЗНАЧЕНИЙ
- 8.6. ПРИМЕНЕНИЕ КИТАЙСКОЙ ТЕОРЕМЫ ОБ ОСТАТКАХ
- 8.7. КИТАЙСКАЯ ТЕОРЕМА ОБ ОСТАТКАХ И ИНТЕРПОЛЯЦИЯ ПОЛИНОМОВ
- 8.8. НАИБОЛЬШИЕ ОБЩИЕ ДЕЛИТЕЛИ И АЛГОРИТМ ЕВКЛИДА
- 8.9. АСИМПТОТИЧЕСКИ БЫСТРЫЙ АЛГОРИТМ НАХОЖДЕНИЯ НОД ПОЛИНОМОВ
- 8.10. НОД ЦЕЛЫХ ЧИСЕЛ
- 8.11. ЕЩЕ РАЗ О ПРИМЕНЕНИИ КИТАЙСКОЙ ТЕОРЕМЫ ОБ ОСТАТКАХ
- 8.12. РАЗРЕЖЕННЫЕ ПОЛИНОМЫ
- 9. АЛГОРИТМЫ ИДЕНТИФИКАЦИИ
- 9.1. КОНЕЧНЫЕ АВТОМАТЫ И РЕГУЛЯРНЫЕ ВЫРАЖЕНИЯ
- 9.2. РАСПОЗНАВАНИЕ ОБРАЗОВ, ЗАДАВАЕМЫХ РЕГУЛЯРНЫМИ ВЫРАЖЕНИЯМИ
- 9.3. РАСПОЗНАВАНИЕ ПОДЦЕПОЧЕК
- 9.4. ДВУСТОРОННИЙ ДЕТЕРМИНИРОВАННЫЙ МАГАЗИННЫЙ АВТОМАТ
- 9.5. ПОЗИЦИОННЫЕ ДЕРЕВЬЯ И ИДЕНТИФИКАТОРЫ ПОЗИЦИЙ
- 10. NP-ПОЛНЫЕ ЗАДАЧИ
- 10.1. НЕДЕТЕРМИНИРОВАННЫЕ МАШИНЫ ТЬЮРИНГА
- 10.2. КЛАССЫ …
- 10.3. ЯЗЫКИ И ЗАДАЧИ
- 10.4. NP-ПОЛНОТА ЗАДАЧИ ВЫПОЛНИМОСТИ
- 10.5. ЕЩЕ НЕСКОЛЬКО NP-ПОЛНЫХ ЗАДАЧ
- 10.6. ЗАДАЧИ С ПОЛИНОМИАЛЬНО ОГРАНИЧЕННОЙ ПАМЯТЬЮ
- 11. НЕКОТОРЫЕ ДОКАЗУЕМО ТРУДНО РАЗРЕШИМЫЕ ЗАДАЧИ
- 11.2. ИЕРАРХИЯ ПО ЕМКОСТНОЙ СЛОЖНОСТИ ДЛЯ ДЕТЕРМИНИРОВАННЫХ МАШИН ТЬЮРИНГА
- 11.3. ЗАДАЧА, ТРЕБУЮЩАЯ ЭКСПОНЕНЦИАЛЬНЫХ ВРЕМЕНИ И ПАМЯТИ
- 11.4. НЕЭЛЕМЕНТАРНАЯ ЗАДАЧА
- 12. НИЖНИЕ ОЦЕНКИ ЧИСЛА АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ
- 12.2. ЕЩЕ РАЗ О НЕВЕТВЯЩИХСЯ ПРОГРАММАХ
- 12.3. МАТРИЧНАЯ ФОРМУЛИРОВКА ЗАДАЧ
- 12.4. НИЖНЯЯ ГРАНИЦА ДЛЯ ЧИСЛА УМНОЖЕНИЙ, СВЯЗАННАЯ С РАНГОМ ПО СТРОКАМ
- 12.5. НИЖНЯЯ ГРАНИЦА ДЛЯ ЧИСЛА УМНОЖЕНИЙ, СВЯЗАННАЯ С РАНГОМ ПО СТОЛБЦАМ
- 12.6. ГРАНИЦА ДЛЯ ЧИСЛА УМНОЖЕНИЙ, СВЯЗАННАЯ С РАССМОТРЕНИЕМ СТРОК И СТОЛБЦОВ
- 12.7. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА