| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
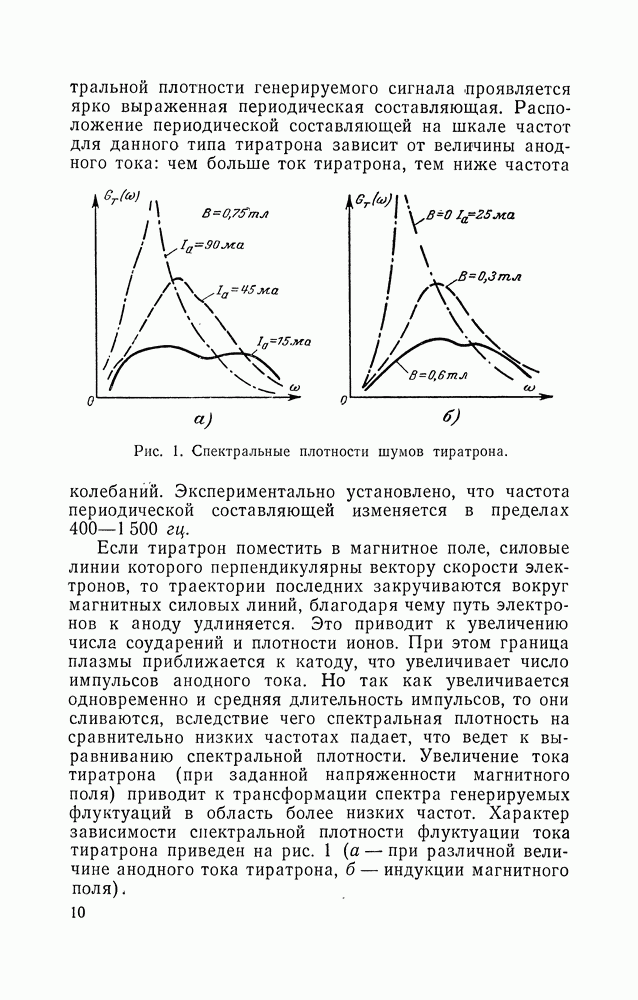
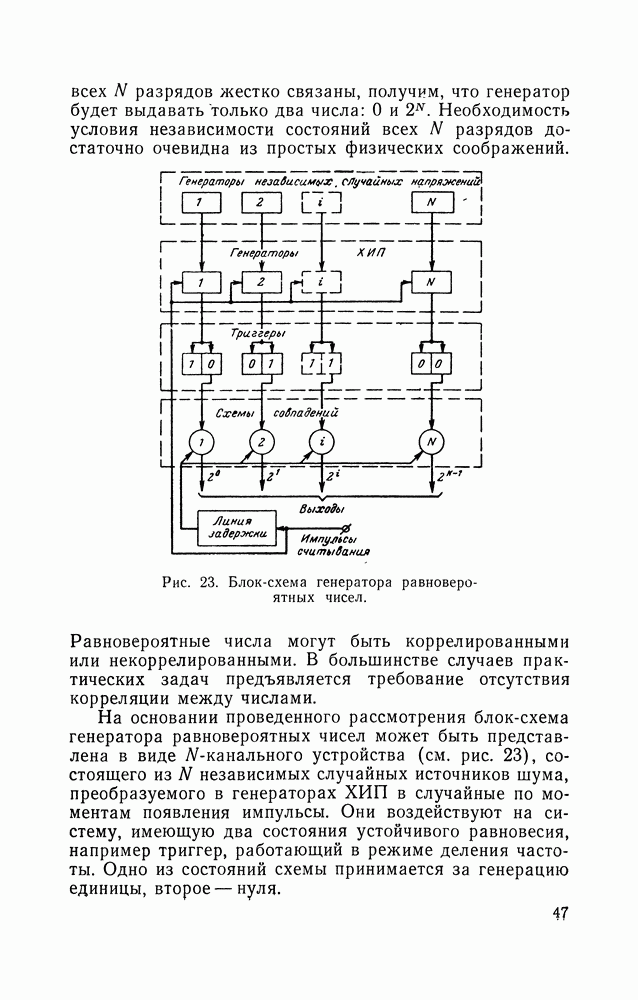
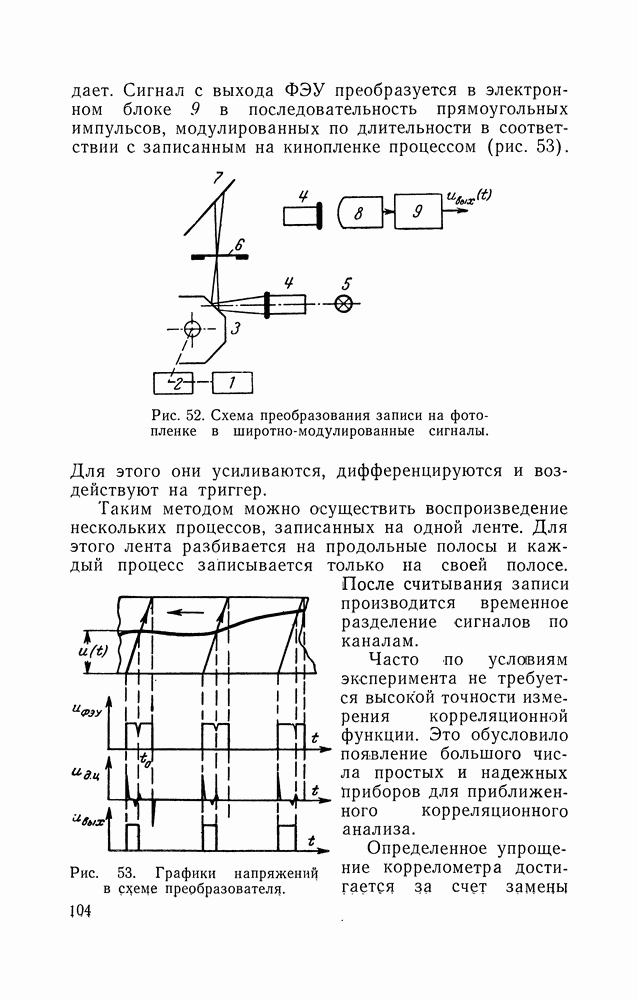
10. ПОЛУЧЕНИЕ ИНФРАНИЗКОЧАСТОТНЫХ ФЛУКТУАЦИИ С ЗАДАННОЙ КОРРЕЛЯЦИОННОЙ ФУНКЦИЕЙ
Инфранизкочастотные флуктуации с требуемой корреляционной функцией можно получить, пропуская через фильтр нижних частот случайный сигнал с постоянной в пределах его полосы пропускания спектральной плотностью.
Спектральная плотность сигнала на выходе линейной системы  связана с спектральной плотностью сигнала на его входе
связана с спектральной плотностью сигнала на его входе  и частотной характеристикой фильтра
и частотной характеристикой фильтра  соотношением
соотношением

Если предположить, что в пределах полосы пропускания фильтра  то
то

будет определяться только значением спектральной плотности входного сигнала на нулевой частоте и параметрами формирующего фильтра. В свою очередь спектральная плотность функционально связана с корреляционной функцией, поэтому, использовав выражение

можно однозначно связать параметры формирующего фильтра с параметрами корреляционной функции.
Таким образом, задача отыскания схемы, необходимой для формирования флуктуаций с заданной корреляционной функцией, сводится к определению по формуле (43) модуля частотой характеристики фильтра, а по ней — набора элементарных звеньев, соединение которых обеспечит получение необходимой частотной характеристики. Конечно, при этом допускается методическая ошибка, связанная с идеализацией исходного сигнала. Ниже мы оценим величину этой ошибки.
Формирующие фильтры могут быть пассивными и активными. Наиболее важными недостатками пассивных фильтров являются высокое выходное сопротивление и трудность обеспечения плавной регулировки всех параметров с целью получения необходимой корреляционной функции флуктуаций. Активные фильтры, созданные на базе усилителей постоянного тока, лишены этих недостатков и позволяют плавно регулировать и достаточно просто задавать требуемые параметры флуктуаций.
Наиболее часто встречающиеся на практике корреляционные функции описываются выражениями:

Можно найти весьма большое количество схем активных фильтров для формирования случайных сигналов с такими корреляционными функциями. Рассмотрим наиболее простые реализации таких фильтров.
1. Фильтр для формирования флуктуаций с корреляционной функцией (44). Подставив в формулу (43) выражение для корреляционной функции (44), получим:

Частотной характеристикой такого вида обладает фильтр, схема которого изображена на рис. 31. Квадрат модуля его частотной характеристики будет:

где

Приравняв (47) и (48), получим:

Связь между требуемыми параметрами корреляционной функции и фильтра будет определяться равенствами


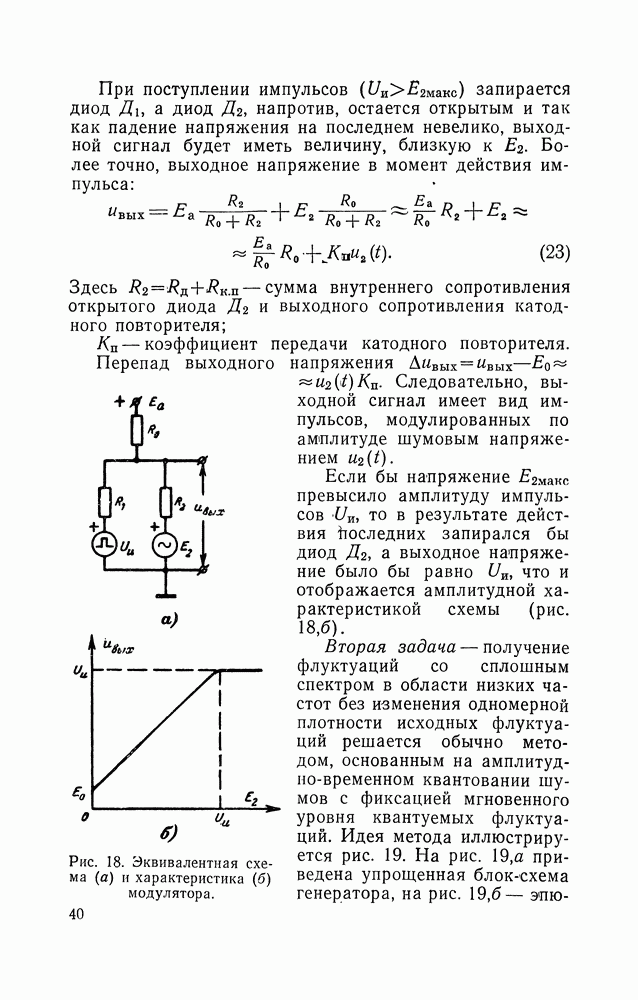
Рис. 31. Активный фильтр для получения сигнала с корреляционной функцией 
Если  заданы, то двумя параметрами фильтра
заданы, то двумя параметрами фильтра  определяются два параметра корреляционной функции
определяются два параметра корреляционной функции  Величину а можно задавать, устанавливая заранее проградуированные значения
Величину а можно задавать, устанавливая заранее проградуированные значения  Более просто это сделать, использовав источник постоянного напряжения. В самом деле, если на вход фильтра подать постоянное напряжение
Более просто это сделать, использовав источник постоянного напряжения. В самом деле, если на вход фильтра подать постоянное напряжение  на выходе фильтра установится напряжение
на выходе фильтра установится напряжение

Изменяя  и наблюдая
и наблюдая  легко задать требуемое значение а.
легко задать требуемое значение а.
Подставив в (49) значение  полученное из (51), найдем:
полученное из (51), найдем:

Значение второго параметра флуктуаций  можно задать регулировкой
можно задать регулировкой  но для этого необходимо иметь семейство кривых
но для этого необходимо иметь семейство кривых  для различных значений
для различных значений  и проградуированный резистор
и проградуированный резистор  Если в качестве исходного используется случайный телеграфный сигнал, для которого на основании
Если в качестве исходного используется случайный телеграфный сигнал, для которого на основании  то, регулируя
то, регулируя  или
или  можно однозначно задавать
можно однозначно задавать 
Таким образом, при наличии двух номограмм  Ыусл) и
Ыусл) и  для заданного значения
для заданного значения  весь процес настройки генератора сводится к двум операциям:
весь процес настройки генератора сводится к двум операциям:
изменяя  и наблюдая напряжение на выходе фильтра, устанавливается требуемое значение а;
и наблюдая напряжение на выходе фильтра, устанавливается требуемое значение а;
по номограмме для  определяется требуемое значение А, которое и устанавливается в генераторе.
определяется требуемое значение А, которое и устанавливается в генераторе.
Конечно, установку требуемого значения дисперсии
генерируемого сигнала можно осуществить и с помощью калиброванного делителя напряжения, но это усложняет генератор и неизбежно увеличивает его выходное сопротивление.

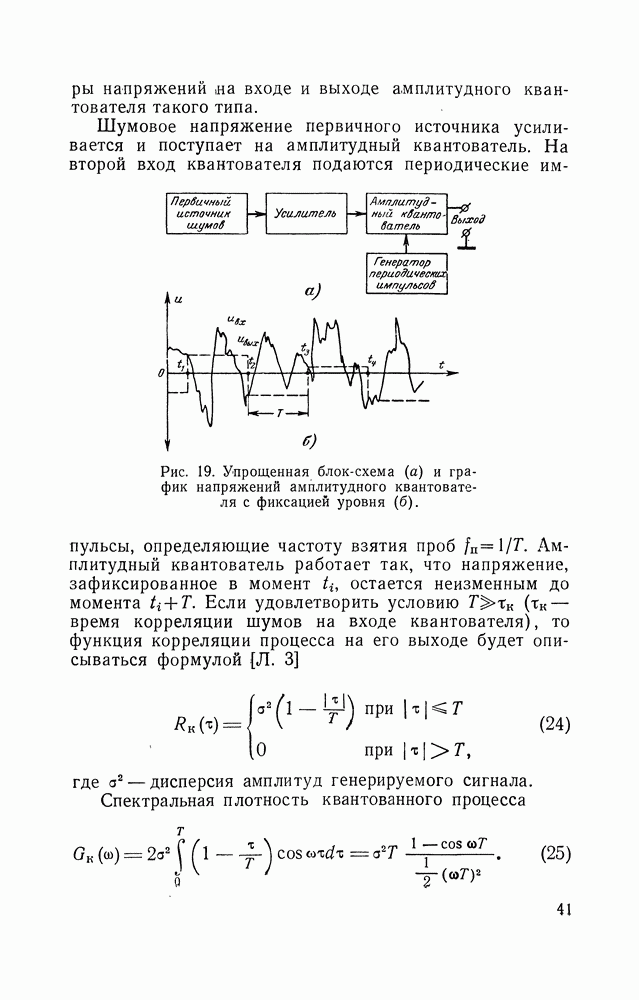
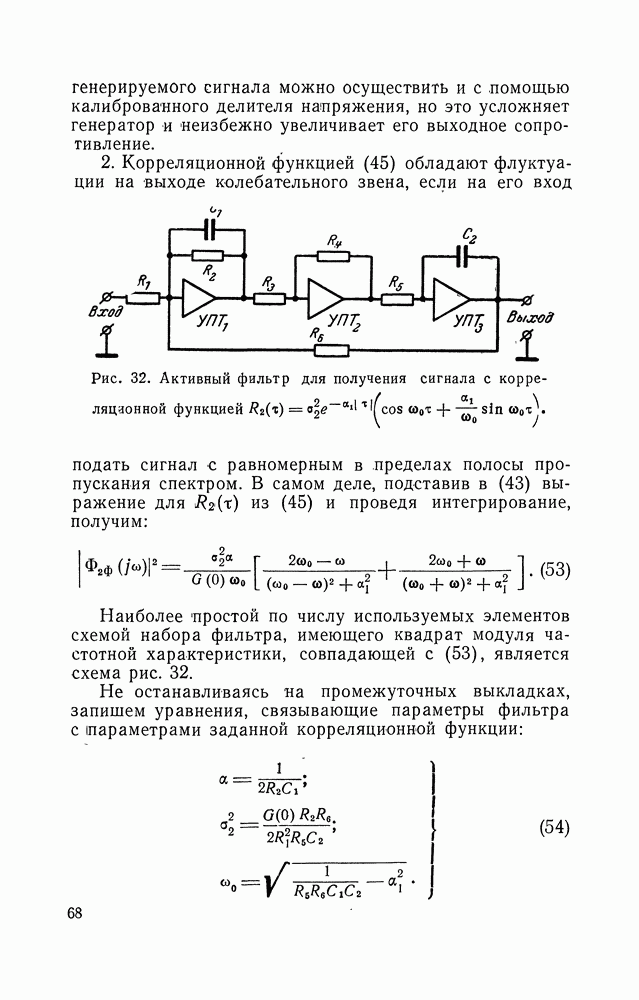
Рис. 32. Активный фильтр для получения сигнала с корре-ляцаонной функцией 
2. Корреляционной функцией (45) обладают флуктуации на выходе колебательного звена, если на его вход подать сигнал с равномерным в пределах полосы пропускания спектром. В самом деле, подставив в (43) выражение для  из (45) и проведя интегрирование, получим:
из (45) и проведя интегрирование, получим:

Наиболее простой по числу используемых элементов схемой набора фильтра, имеющего квадрат модуля частотной характеристики, совпадающей с (53), является схема рис. 32.
Не останавливаясь на промежуточных выкладках, запишем уравнения, связывающие параметры фильтра с параметрами заданной корреляционной функции:

Таким образом, для трех параметров корреляционной функции имеются три уравнения. Схема содержит шесть резисторов. Процесс настройки оказывается наиболее простым, если регулируемыми сделать резисторы  Установку требуемых значений сопротивлений можно производить, как и в первом случае, подавая на вход фильтра постоянное напряжение. Все расчетные формулы целесообразно представить в виде номограмм, построенных для требуемых значений
Установку требуемых значений сопротивлений можно производить, как и в первом случае, подавая на вход фильтра постоянное напряжение. Все расчетные формулы целесообразно представить в виде номограмм, построенных для требуемых значений  Использование этих номограмм окажется целесообразным, если фильтр реализован как отдельное устройство. В том же случае, когда используется набор фильтра на блоках модели постоянного тока, требуемые параметры легко определить из уравнений (54), разрешив их относительно
Использование этих номограмм окажется целесообразным, если фильтр реализован как отдельное устройство. В том же случае, когда используется набор фильтра на блоках модели постоянного тока, требуемые параметры легко определить из уравнений (54), разрешив их относительно 
Для формирования флуктуаций с корреляционной функцией (46) удобно использовать фильтр, который является последовательным соединением (рис. 33) только что рассмотренного фильтра и активного форсирующего звена с частотной характеристикой

где

Частотная характеристика всего фильтра:

Квадрат модуля частотной характеристики фильтра, который позволил бы формировать флуктуации с корреляционной функцией (46), будет определяться формулой

Можно показать, что фильтр, изображенный на рис. 33, будет иметь требуемую для решения поставленной задачи частотную характеристику только в том случае, если удовлетворено условие согласования:

где

Подставив в (57) значение  из (59), можно определить квадрат модуля частотной характеристики, приравняв его выражению (58), найти связь между параметрами фильтра и корреляционной функции формируемых флуктуаций.
из (59), можно определить квадрат модуля частотной характеристики, приравняв его выражению (58), найти связь между параметрами фильтра и корреляционной функции формируемых флуктуаций.

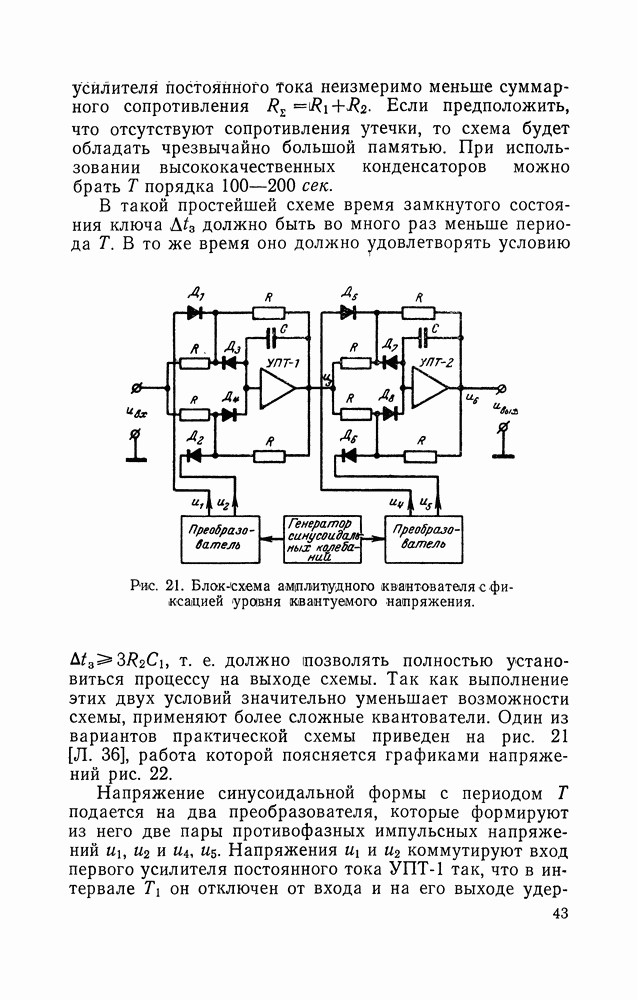
Рис. 33. Активный фильтр для получения сигнала с корреляционной функцией 
При этом  будут связаны с параметрами фильтра выражениями (54). Величина дисперсии флуктуаций будет определяться формулой
будут связаны с параметрами фильтра выражениями (54). Величина дисперсии флуктуаций будет определяться формулой

В качестве регулируемых параметров фильтра удобно принять:  -для задания
-для задания  — для задания
— для задания  а условие согласования (59) удовлетворять, изменяя Как и в первых двух случаях, задать требуемые значения параметров флуктуаций можно, используя источник постоянного напряжения, подключаемый к соответствующим точкам схемы. По приведенным формулам легко могут быть рассчитаны номограммы для настройки фильтров.
а условие согласования (59) удовлетворять, изменяя Как и в первых двух случаях, задать требуемые значения параметров флуктуаций можно, используя источник постоянного напряжения, подключаемый к соответствующим точкам схемы. По приведенным формулам легко могут быть рассчитаны номограммы для настройки фильтров.
При использовании в фильтрах типовых усилителей постоянного тока нельзя получить флуктуации, спектр которых шире 100 гц. Для формирования более широкополосных флуктуаций применяют пассивные  -фильтры. Для формирования флуктуаций с корреляционной функцией
-фильтры. Для формирования флуктуаций с корреляционной функцией  наиболее простым является
наиболее простым является  -фильтр
-фильтр
(рис. 34,а). Параметры флуктуаций связаны с параметрами фильтра формулами

Флуктуации с корреляционной функцией (45) можно сформулировать с помощью  -фильтра (рис. 34,б). Для него связь параметров будет определяться формулами
-фильтра (рис. 34,б). Для него связь параметров будет определяться формулами

Для получения флуктуаций, имеющих корреляционную функцию (46), необходимо последовательно с  -фильтром включить звено с частотной характеристикой вида (55). Однако из пассивных элементов получить цепь с такой частотной характеристикой невозможно. Приближение к цепи с корреляционной функцией типа (46) дает схема, изображенная на рис. 34,е. Для развязки звеньев фильтра между ними включен усилитель с коэффициентом передачи
-фильтром включить звено с частотной характеристикой вида (55). Однако из пассивных элементов получить цепь с такой частотной характеристикой невозможно. Приближение к цепи с корреляционной функцией типа (46) дает схема, изображенная на рис. 34,е. Для развязки звеньев фильтра между ними включен усилитель с коэффициентом передачи  Частотная характеристика фильтра, состоящего
Частотная характеристика фильтра, состоящего  описывается формулой
описывается формулой

где коэффициент передачи по постоянному току: 

Если взять  то
то

При выборе элементов форсирующей цепочки необходимо учесть, условие согласования (59),
в соответствии с которым должно удовлетворяться равенство

Дисперсия флуктуаций на выходе фильтра при выполнении равенства (64) приближенно равна:

Параметры  будут определяться равенствами (63).
будут определяться равенствами (63).
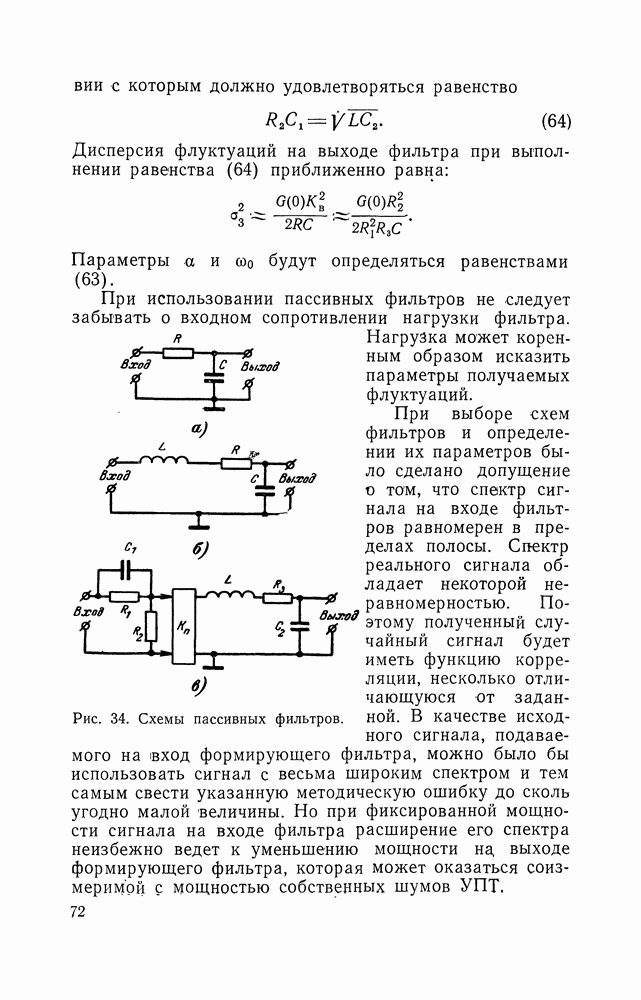
При использовании пассивных фильтров не следует забывать о входном сопротивлении нагрузки фильтра.
Нагрузка может коренным образом исказить параметры получаемых флуктуаций.

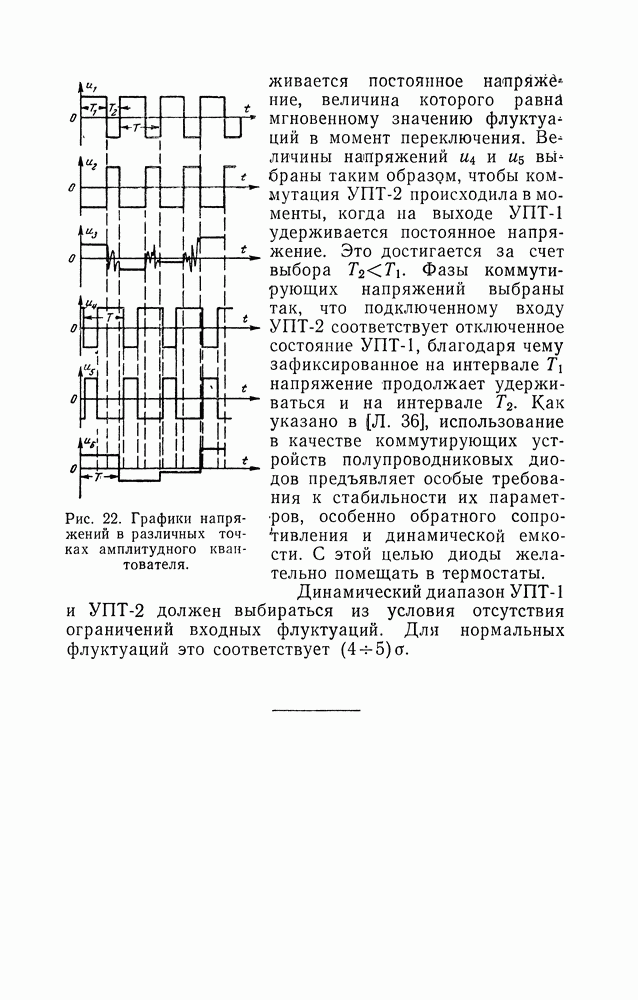
Рис. 34. Схемы пассивных фильтров.
При выборе схем фильтров и определении их параметров было сделано допущение о том, что спектр сигнала на входе фильтров равномерен в пределах полосы. Сгсектр реального сигнала обладает некоторой неравномерностью. Поэтому полученный случайный сигнал будет иметь функцию корреляции, несколько отличающуюся от заданной. В качестве исходного сигнала, подаваемого на вход формирующего фильтра, можно было бы использовать сигнал с весьма широким спектром и тем самым свести указанную методическую ошибку до сколь угодно малой величины. Но при фиксированной мощности сигнала на входе фильтра расширение его спектра неизбежно ведет к уменьшению мощности на, выходе формирующего фильтра, которая может оказаться соизмеримой с мощностью собственных шумов УПТ.
В любом случае необходимо оценить методическую погрешность, связанную с идеализацией входного сигнала. В качестве меры методической ошибки удобно принять отношение:

где  -корреляционная функция при идеализации входного сигнала;
-корреляционная функция при идеализации входного сигнала;  -корреляционная функция полученного сигнала.
-корреляционная функция полученного сигнала.
Найдем методические погрешности для случая, когда в качестве входного используется случайный телеграфный сигнал со спектральной плотностью (19). При использовании фильтра, приведенного на рис. 33, корреляционная функция сигнала на его выходе может быть найдена извыражения 00

Опустив вычисления, связанные с применением теории вычетов, запишем конечный результат:

При идеализации входного сигнала функция корреляции имеет вид

Подставив в (65) выражения (66) и (67), получим:

где

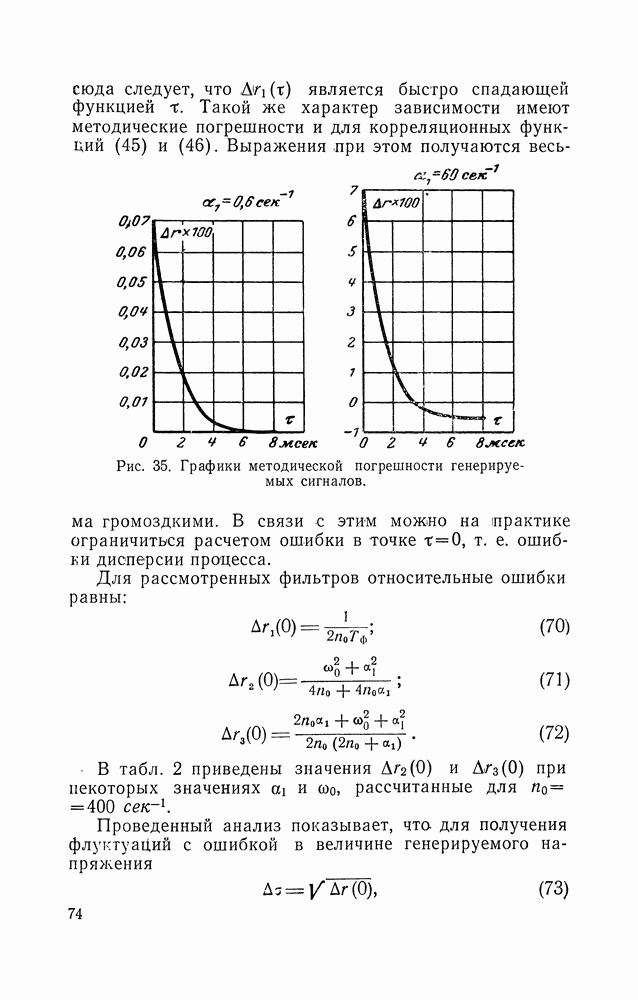
На рис. 35 приведены зависимости, рассчитанные по формуле (68) для  и двух значений а.
и двух значений а.
Отсюда следует, что  является быстро спадающей функцией
является быстро спадающей функцией  Такой же характер зависимости имеют методические погрешности и для корреляционных функций (45) и (46). Выражения при этом получаются весьма громоздкими.
Такой же характер зависимости имеют методические погрешности и для корреляционных функций (45) и (46). Выражения при этом получаются весьма громоздкими.

Рис. 35. Графики методической погрешности генерируемых сигналов.
В связи с этим можно на практике ограничиться расчетом ошибки в точке  т. е. ошибки дисперсии процесса.
т. е. ошибки дисперсии процесса.
Для рассмотренных фильтров относительные ошибки равны:

В табл. 2 приведены значения  при некоторых значениях
при некоторых значениях  рассчитанные для
рассчитанные для 
Проведенный анализ показывает, что для получения флуктуаций с ошибкой в величине генерируемого напряжения

не превышающий 5%, спектр на входе фильтра должен быть в 30—100 раз шире его полосы пропускания.
Таблица 2

| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА ПЕРВАЯ. ГЕНЕРИРОВАНИЕ ИМПУЛЬСНЫХ И НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ СИГНАЛОВ СО СПЛОШНЫМ СПЕКТРОМ В ОБЛАСТИ НИЗКИХ ЧАСТОТ
- 1. КРАТКИЕ СВЕДЕНИЯ О ПЕРВИЧНЫХ ИСТОЧНИКАХ СЛУЧАЙНЫХ НАПРЯЖЕНИЙ
- 2. ПОЛУЧЕНИЕ НИЗКОЧАСТОТНЫХ ФЛУКТУАЦИИ ПУТЕМ СИНХРОННОГО ДЕТЕКТИРОВАНИЯ УЗКОПОЛОСНЫХ ШУМОВ
- 3. ГЕНЕРИРОВАНИЕ КВАЗИСЛУЧАЙНЫХ ИНФРАНИЗКОЧАСТОТНЫХ СИГНАЛОВ
- 4. ГЕНЕРИРОВАНИЕ СЛУЧАЙНЫХ ПО МОМЕНТАМ ПОЯВЛЕНИЯ (ПУАССОНОВСКИХ) ИМПУЛЬСОВ
- 5. ГЕНЕРИРОВАНИЕ СЛУЧАЙНЫХ ПО ДЛИТЕЛЬНОСТИ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ
- 6. ГЕНЕРИРОВАНИЕ ПЕРИОДИЧЕСКИХ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ СО СЛУЧАЙНОЙ АМПЛИТУДОЙ
- ГЛАВА ВТОРАЯ. ГЕНЕРИРОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ С ЗАДАННЫМИ СТАТИСТИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ
- 7. СПОСОБЫ ПОЛУЧЕНИЯ СЛУЧАЙНЫХ НАПРЯЖЕНИЙ С РАВНОВЕРОЯТНЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ АМПЛИТУД
- 8. ИСПОЛЬЗОВАНИЕ НЕЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ ПОЛУЧЕНИЯ НАПРЯЖЕНИЙ С ЗАДАННЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ МГНОВЕННЫХ ЗНАЧЕНИЙ
- 9. ПОЛУЧЕНИЕ НАПРЯЖЕНИЯ С ЗАДАННОЙ ОДНОМЕРНОЙ ПЛОТНОСТЬЮ ВЕРОЯТНОСТЕЙ МЕТОДОМ ЗАДАНИЯ ВЕРОЯТНОСТЕЙ СОСТЯНИЙ КАНАЛОВ
- 10. ПОЛУЧЕНИЕ ИНФРАНИЗКОЧАСТОТНЫХ ФЛУКТУАЦИИ С ЗАДАННОЙ КОРРЕЛЯЦИОННОЙ ФУНКЦИЕЙ
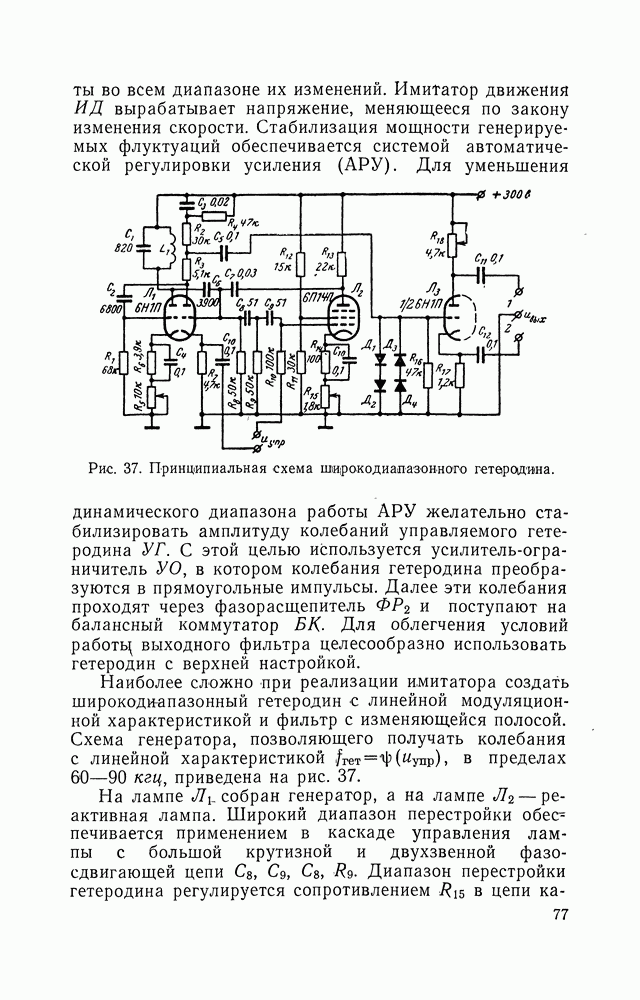
- 11. ИМИТАЦИЯ СИГНАЛОВ ДОППЛЕРОВСКИХ НАВИГАЦИОННЫХ СИСТЕМ
- ГЛАВА ТРЕТЬЯ. СТАБИЛИЗАЦИЯ И ИЗМЕРЕНИЕ ОСНОВНЫХ ПАРАМЕТРОВ СЛУЧАЙНЫХ СИГНАЛОВ
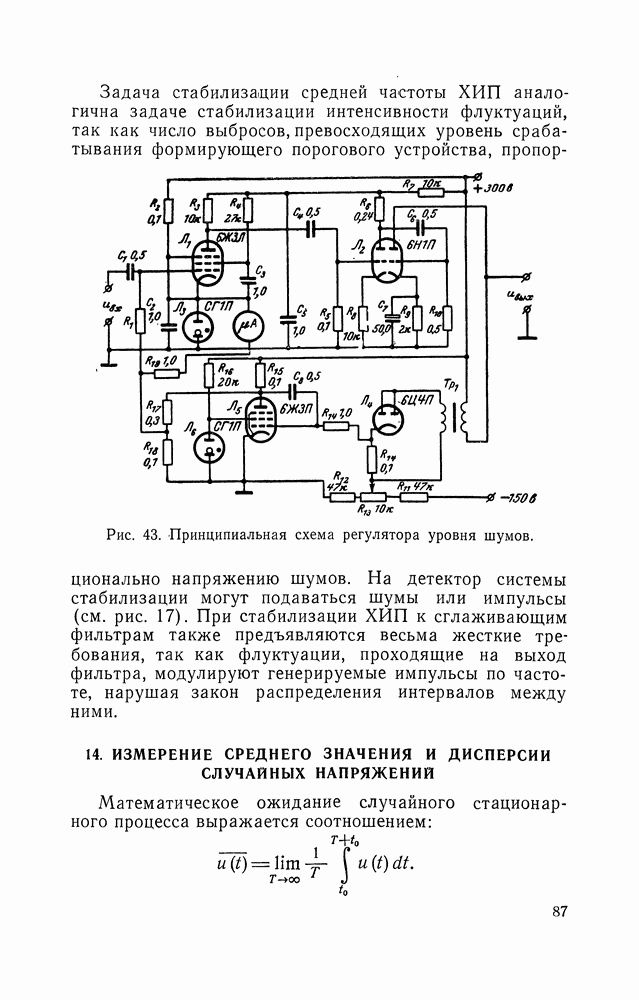
- 13. СПОСОБЫ СТАБИЛИЗАЦИИ МОЩНОСТИ ФЛУКТУАЦИЙ
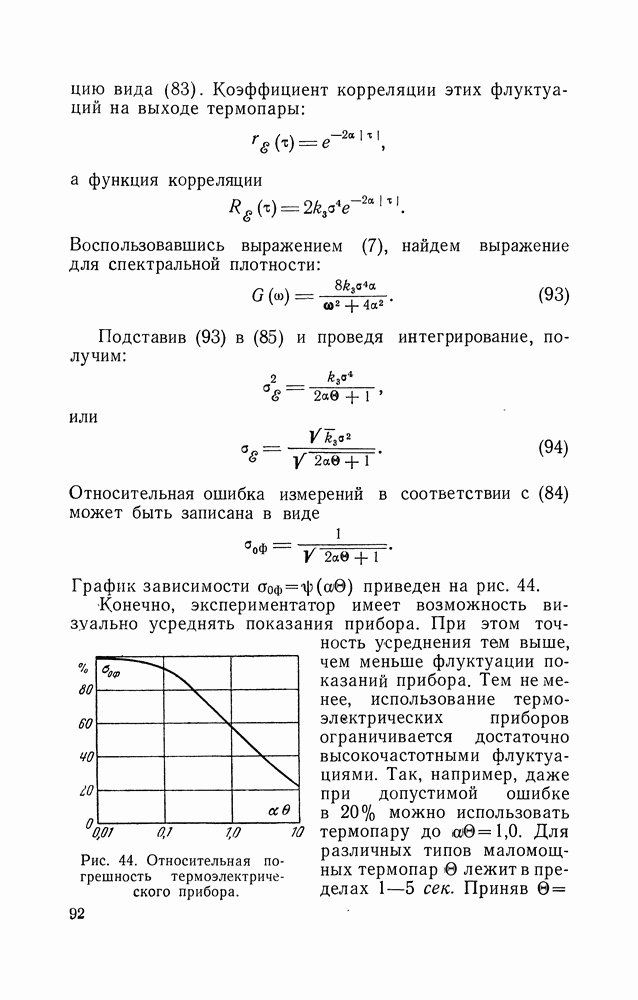
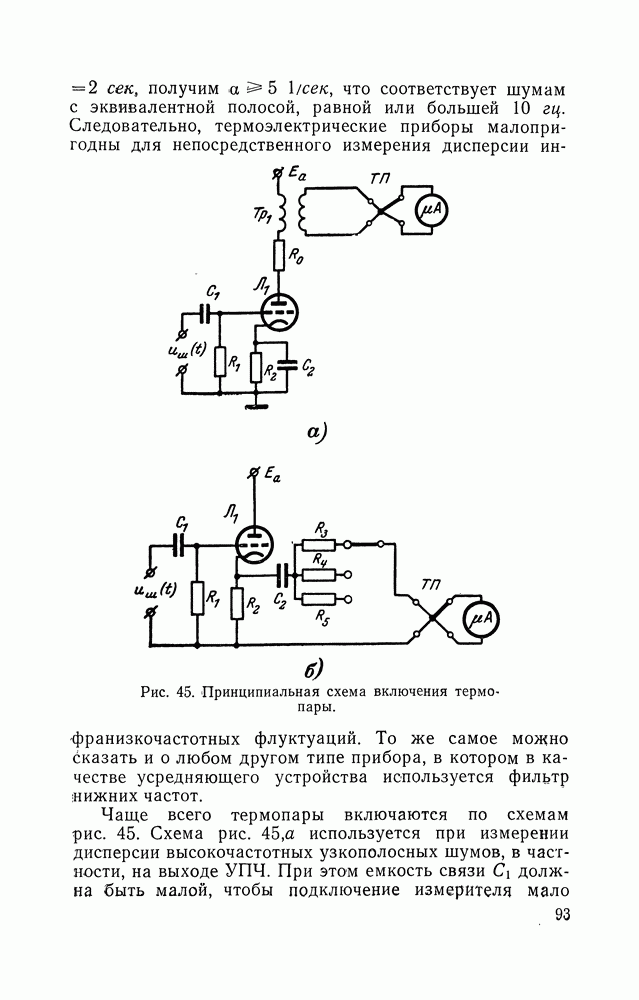
- 14. ИЗМЕРЕНИЕ СРЕДНЕГО ЗНАЧЕНИЯ И ДИСПЕРСИИ СЛУЧАЙНЫХ НАПРЯЖЕНИЙ
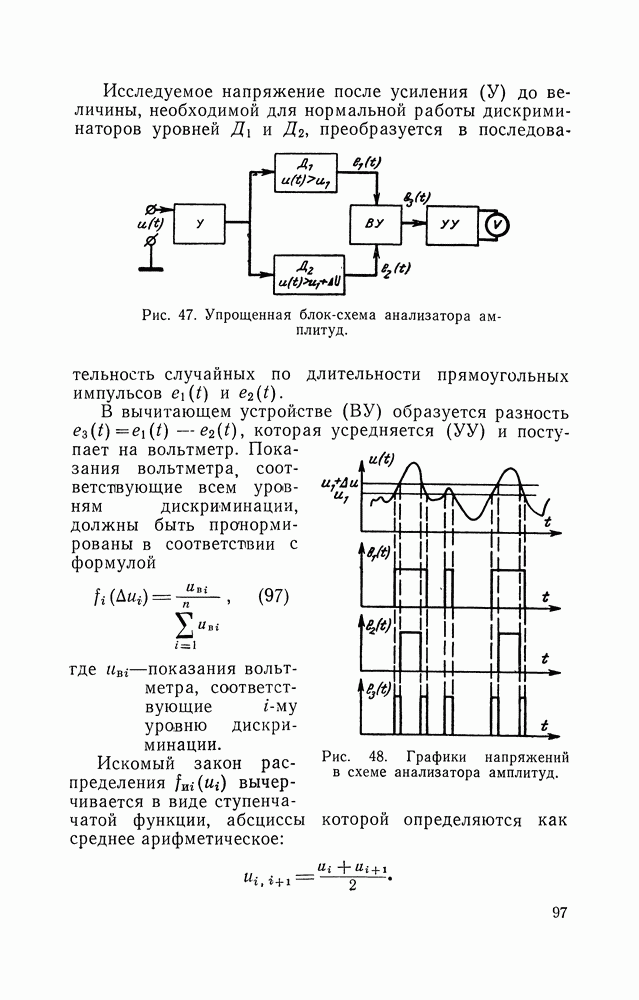
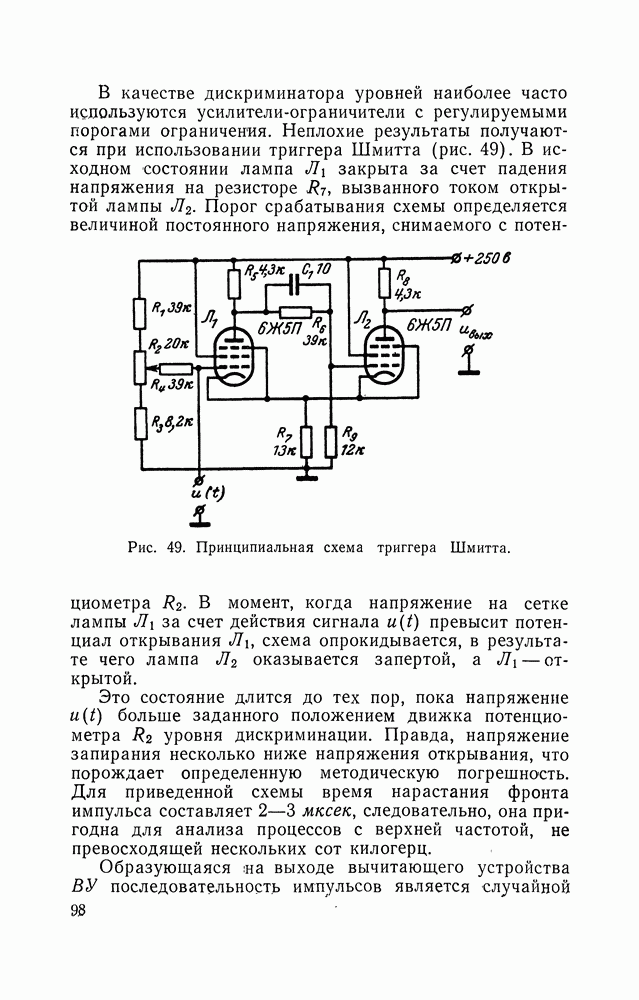
- 15. ОПРЕДЕЛЕНИЕ ОДНОМЕРНЫХ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ
- 16 КОРРЕЛОМЕТРЫ И СПЕКТРОАНАЛИЗАТОРЫ