| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
14. ИЗМЕРЕНИЕ СРЕДНЕГО ЗНАЧЕНИЯ И ДИСПЕРСИИ СЛУЧАЙНЫХ НАПРЯЖЕНИЙ
Математическое ожидание случайного стационарного процесса выражается соотношением:

Определение  сводится к достаточно длительному интегрированию процесса и умножению на
сводится к достаточно длительному интегрированию процесса и умножению на 
Очень часто вместо интегрирования применяют операцию усреднения с помощью фильтров нижних частот и, в частности,  -цепочек. Полоса пропускания фильтра нижних частот должна быть достаточно узкой, чтобы измеряемая постоянная составляющая существенно превышала случайные составляющие, попадающие на выход фильтра. При использовании в качестве усредняющего устройства фильтра нижних частот дисперсия сигнала на его выходе
-цепочек. Полоса пропускания фильтра нижних частот должна быть достаточно узкой, чтобы измеряемая постоянная составляющая существенно превышала случайные составляющие, попадающие на выход фильтра. При использовании в качестве усредняющего устройства фильтра нижних частот дисперсия сигнала на его выходе  и будет определять методическую погрешность измерений. В качестве меры ошибки измерений в соответствии с (74) удобно принять величину
и будет определять методическую погрешность измерений. В качестве меры ошибки измерений в соответствии с (74) удобно принять величину

Величина  по своему физическому смыслу является среднеквадратическим значением флуктуаций на выходе сглаживающего фильтра:
по своему физическому смыслу является среднеквадратическим значением флуктуаций на выходе сглаживающего фильтра:

При решении задач статистической динамики на моделях постоянного тока возникает необходимость измерения математических ожиданий процессов, имеющих большое время корреляции. Использовать фильтры нижних частот для усреднения таких процессов практически невозможно, поэтому оценку математического ожидания получают путем интегрирования в течение некоторого времени  Относительная дисперсия оценки математического ожидания определяется по формуле
Относительная дисперсия оценки математического ожидания определяется по формуле 

где  -коэффициент корреляции флуктуационной составляющей процесса.
-коэффициент корреляции флуктуационной составляющей процесса.
Казалось бы, что при известной функции корреляции нет нужды производить измерение первых двух
моментов, которые полностью определяют его, а при неизвестной функции корреляции нельзя оценить точность измерений. Однако, как показывают расчеты, при времени измерений (интегрирования), значительно превосходящем время корреляции процесса, дисперсия оценки мало зависит от вида корреляционной функции флуктуаций и определяется только временем корреляции. Кроме того, спектральная плотность случайного напряжения на входе интегратора, как правило, полностью определяется передаточной функцией фильтра, с выхода которого поступают флуктуации на вход прибора. Другими словами, флуктуации на входе фильтра, как правило, могут отождествляться с белым шумом и коэффициент корреляции оказывается с достаточной для практики точностью определен. Если флуктуации имеют функцию корреляции вида  подставив (83) в (86), легко получить:
подставив (83) в (86), легко получить:

Так как практически всегда удовлетворяется условие  для оценки точности результатов измерения можно использовать приближенную формулу
для оценки точности результатов измерения можно использовать приближенную формулу

Для получения достаточно точных результатов необходимо брать большое время интегрирования. Так, если приемлемым является значение  то
то  и при
и при  сек.
сек.
В процессе моделирования приходится сталкиваться с процессами, имеющими время корреляции, измеряемое десятками секунд. Поэтому целесообразно наряду с усреднением по времени применять усреднение по ансамблю. Дисперсия оценки убывает обратно пропорционально числу проведенных измерений.
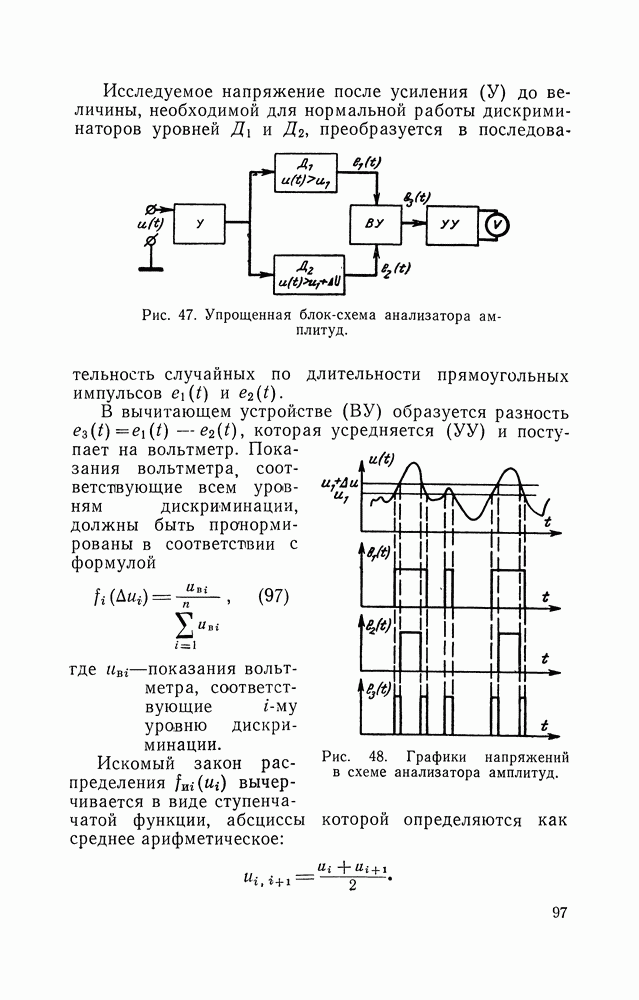
Для измерения мощности случайного стационарного процесса в соответствии с формулой

необходимо осуществив две операции: возвести в квадрат исследуемое напряжение и проинтегрировать напряжение, поступающее с выхода квадратора.
Квадратичной характеристикой обладают все тепловые и термоэлектрические приборы, которые имеют достаточно большую постоянную времени (порядка единиц секунд) и поэтому одновременно с операцией возведения в квадрат осуществляют операцию усреднения. Если случайный процесс имеет отличное от нуля среднее значение, то его дисперсия может быть вычислена по формуле 

Перед измерением мощности случайного сигнала желательно исключить среднее значение и тем самым облегчить условия работы измерителя, полнее использовать его динамический диапазон.
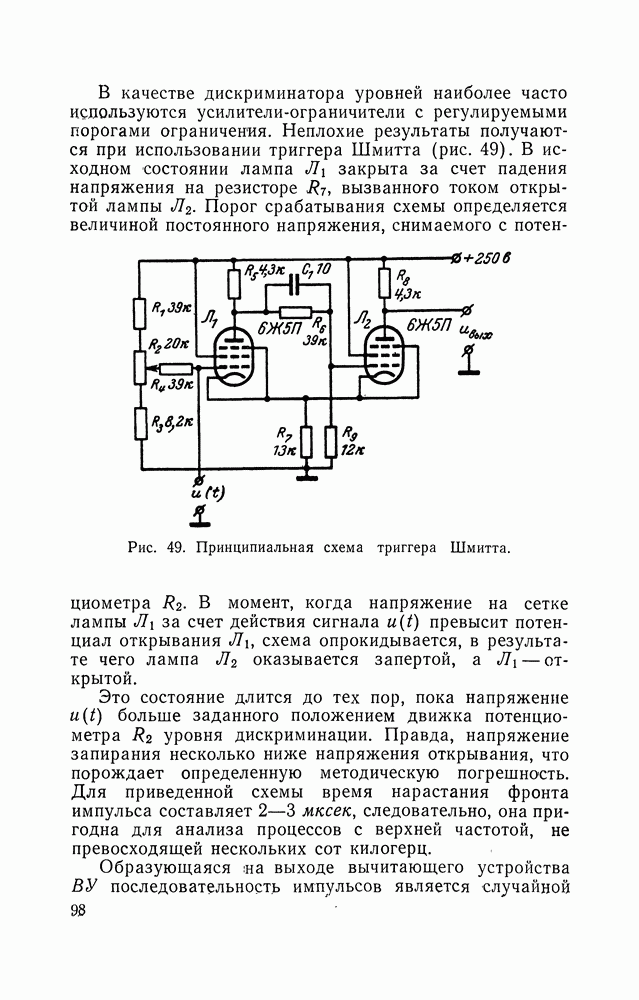
Тем же дифференциальным уравнением, что и термоэлектрические приборы, описываются измерители мощности, основанные на использовании нелинейного устройства для возведения измеряемого напряжения в квадрат, с усреднением  -фильтром. В связи с этим остановимся на теории термоэлектрического измерителя мощности
-фильтром. В связи с этим остановимся на теории термоэлектрического измерителя мощности  . В основе термоэлектрического метода измерения мощности сигналов, в том числе и случайных, лежит линейная зависимость между э. д. с. термопары 8 и температурой спая
. В основе термоэлектрического метода измерения мощности сигналов, в том числе и случайных, лежит линейная зависимость между э. д. с. термопары 8 и температурой спая 

где  постоянная, определяемая используемыми металлами.
постоянная, определяемая используемыми металлами.
Температура описывается дифференциальным уравнением

где  постоянная времени термопары.
постоянная времени термопары.
Э. д. с. термопары наряду с постоянной составляющей, пропорциональной мощности измеряемого процесса  имеет флуктуационную составляющую, которая является методической ошибкой измерений. Найдем дисперсию этой ошибки в предположении, что каждое из фиксируемых показаний прибора принимается за
имеет флуктуационную составляющую, которая является методической ошибкой измерений. Найдем дисперсию этой ошибки в предположении, что каждое из фиксируемых показаний прибора принимается за
истинное, т. е. экспериментатор не осуществляет визуального усреднения показаний. Уравнение (90) с учетом (89) можно переписать для э. д. с. термопары 

где 
Э. д. с. термопары прикладывается к магнитоэлектрическому прибору и вызывает отклонение его стрелки на угол  Магнитоэлектрический прибор является инерционной системой, но с этим можно не считаться, так как его инерционность, как правило, значительно ниже инерционности термопары. Таким образом, задача отыскания дисперсии ошибки измерений сводится к отысканию дисперсии флуктуаций на выходе инерционного звена, характеризующего тепловую инерцию термопары.
Магнитоэлектрический прибор является инерционной системой, но с этим можно не считаться, так как его инерционность, как правило, значительно ниже инерционности термопары. Таким образом, задача отыскания дисперсии ошибки измерений сводится к отысканию дисперсии флуктуаций на выходе инерционного звена, характеризующего тепловую инерцию термопары.
Если на входе квадратора действуют флуктуации с корреляционной функцией  то функция корреляции напряжения на его выходе будет равна
то функция корреляции напряжения на его выходе будет равна  :
:

где  — коэффициент корреляции флуктуаций э. д. с. на входе термопары.
— коэффициент корреляции флуктуаций э. д. с. на входе термопары.
Найдем выражение для относительной ошибки измерений в предположении, что случайный процесс на входе термопары не содержит постоянной составляющей. Квадрат постоянной составляющей напряжения на выходе термопары можно определить, положив в выражении 

откуда величина

есть полезная составляющая сигнала.
Известно, что уравнению (91) соответствует фильтр с частотной характеристикой

Рассмотрим в качестве примера случай, когда флуктуации на входе термопары имеют корреляционную
функцию вида (83). Коэффициент корреляции этих флуктуаций на выходе термопары:

а функция корреляции

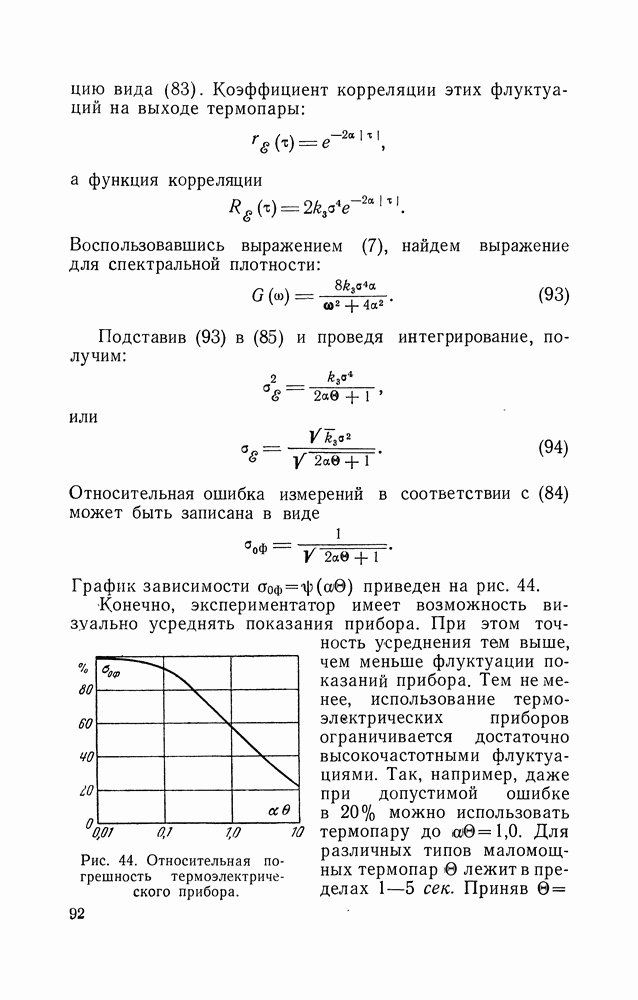
Воспользовавшись выражением (7), найдем выражение для спектральной плотности:

Подставив (93) в (85) и проведя интегрирование, получим:

или

Относительная ошибка измерений в соответствии с (84) может быть записана в виде

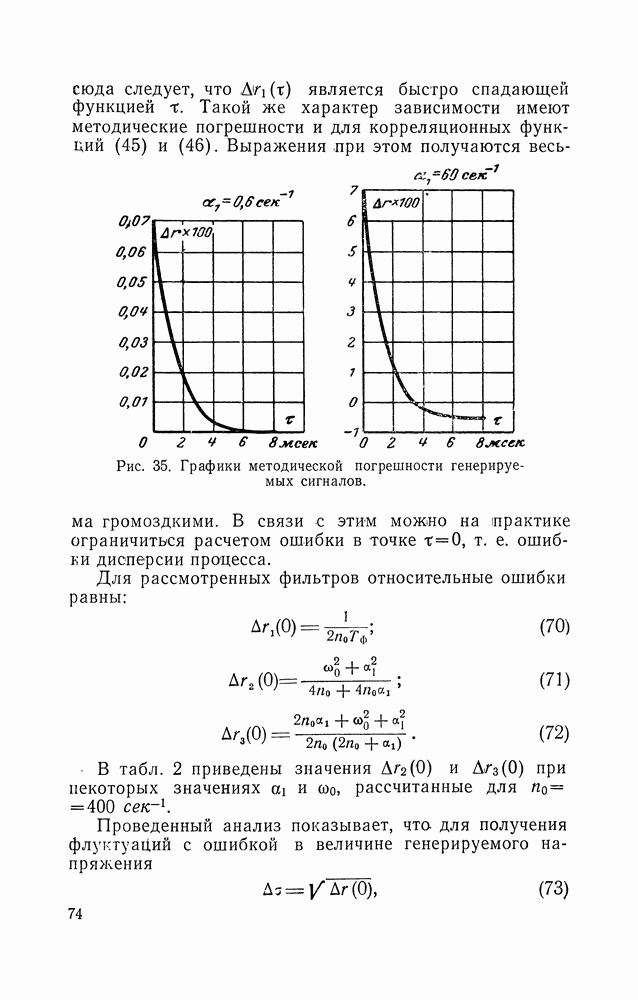
График зависимости  приведен на рис. 44.
приведен на рис. 44.
Конечно, экспериментатор имеет возможность визуально усреднять показания прибора. При этом точность усреднения тем выше, чем меньше флуктуации показаний прибора. Тем не менее, использование термоэлектрических приборов ограничивается достаточно высокочастотными флуктуациями. Так, например, даже при допустимой ошибке в 20% можно использовать термопару до  Для различных типов маломощных термопар в лежит в пределах 1—5 сек.
Для различных типов маломощных термопар в лежит в пределах 1—5 сек.

Рис. 44. Относительная погрешность термоэлектрического прибора.
Приняв  получим а
получим а  что соответствует шумам с эквивалентной полосой, равной или большей 10 гц. Следовательно, термоэлектрические приборы малопригодны для непосредственного измерения дисперсии инфранизкочастотных флуктуаций.
что соответствует шумам с эквивалентной полосой, равной или большей 10 гц. Следовательно, термоэлектрические приборы малопригодны для непосредственного измерения дисперсии инфранизкочастотных флуктуаций.

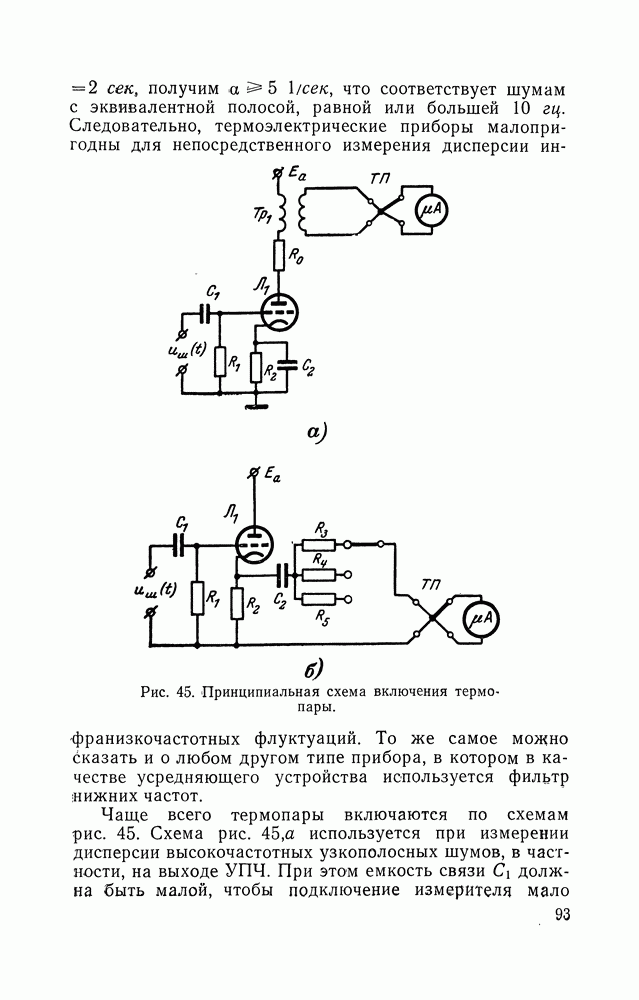
Рис. 45. Принципиальная схема включения термопары.
То же самое можно сказать и о любом другом типе прибора, в котором в качестве усредняющего устройства используется фильтр нижних частот.
Чаще всего термопары включаются по схемам рис. 45. Схема рис. 45,а используется при измерении дисперсии высокочастотных узкополосных шумов, в частности, на выходе УПЧ. При этом емкость связи  должна быть малой, чтобы подключение измерителя мало
должна быть малой, чтобы подключение измерителя мало
влияло на настройку усилителя промежуточной частоты. Схема, приведенная на рис. 45,б, применяется для измерения дисперсии низкочастотных шумов. Резисторы  подбираемые экспериментально, выполняют; роль ограничительных по току сопротивдений. Хотя они и снижают чувствительность схемы, их включение необходимо. Дело в том, что термопары весьма чувствительны к перегрузкам. В момент включения, а особенно в случае неожиданных выключений анодного напряжения, в прогретой схеме возникает скачок разрядного тока: (в схеме рис. 45,б) и э. д. с. (в схеме рис. 45,а). Термопара при этом может перегореть.
подбираемые экспериментально, выполняют; роль ограничительных по току сопротивдений. Хотя они и снижают чувствительность схемы, их включение необходимо. Дело в том, что термопары весьма чувствительны к перегрузкам. В момент включения, а особенно в случае неожиданных выключений анодного напряжения, в прогретой схеме возникает скачок разрядного тока: (в схеме рис. 45,б) и э. д. с. (в схеме рис. 45,а). Термопара при этом может перегореть.
В том случае, если плотность вероятностей и спектральная плотность флуктуаций в процессе эксперимента не меняются, а регулируемым параметром является только дисперсия флуктуаций, термопару целесообразно использовать только в процессе градуировки электронного вольтметра. Предварительно с помощью синусоидальных колебаний градуируется измерительный прибор, т. е. снимается градуированная кривая:

где  показания микроамперметра;
показания микроамперметра;
 эффективное напряжение подаваемого на вход прибора градуировочного синусоидального напряжения.
эффективное напряжение подаваемого на вход прибора градуировочного синусоидального напряжения.
Затем электронный вольтметр градуируется по шумам т. е. снимается зависимость его показаний

от интенсивности шумов. В дальнейшем термопара отключается и установка требуемых значений а производится по электронному вольтметру.
При исследовании статистической динамики той или иной системы на электронной модели возникает необходимость измерения математического ожидания и дисперсии инфранизкочастотных флуктуаций. Для измерения целесообразно использовать блоки самой модели, собранные по схеме рис. 46. Входной сигнал измерителя может быть представлен в виде

где  — полезная составляющая сигнала, в общем случае изменяющаяся во времени, отклонения от которой и рассматриваются в качестве подлежащих измерению флуктуаций
— полезная составляющая сигнала, в общем случае изменяющаяся во времени, отклонения от которой и рассматриваются в качестве подлежащих измерению флуктуаций 
Для проведения измерений необходимо тем или иным способом скомпенсировать сигнал.

Рис. 46. Блок-схема измерения среднего значения и дисперсии инфранизкочастотных флуктуаций.
Если он не изменяется во времени, то компенсацию можно осуществить подключением внешнего источника постоянного напряжения. Иногда при моделировании сигнал  удается скомпенсировать за счет создания параллельного, не подверженного воздействию помех, канала. Тогда на вход прибора подается разность выходных сигналов опорной и изучаемой систем.
удается скомпенсировать за счет создания параллельного, не подверженного воздействию помех, канала. Тогда на вход прибора подается разность выходных сигналов опорной и изучаемой систем.
После компенсации полезного сигнала  измеряемые флуктуации поступают на вход делителя напряжения с коэффициентом передачи
измеряемые флуктуации поступают на вход делителя напряжения с коэффициентом передачи  и далее на интегратор. В результате интегрирования сигнала в течение времени
и далее на интегратор. В результате интегрирования сигнала в течение времени  выходное напряжение интегратора достигнет величины:
выходное напряжение интегратора достигнет величины:

откуда для оценки математического ожидания исследуемого процесса получим:

Для определения среднеквадратического отклонения сигнал с выхода схемы компенсации подается на схему квадратора, в качестве которого может быть использован блок произведений. Возведенный с
коэффициентом  в квадрат, сигнал проходит через блок делений напряжения, имеющий коэффициент передачи
в квадрат, сигнал проходит через блок делений напряжения, имеющий коэффициент передачи  Средний квадрат измеряемого процесса:
Средний квадрат измеряемого процесса:

Коэффициенты  должны выбираться так, чтобы за время интегрирования
должны выбираться так, чтобы за время интегрирования  напряжений
напряжений  оказались близкими к максимально допустимым для данного типа интегратора. В этом случае ошибки самого интегратора будут оказывать минимальное влияние на точность измерений.
оказались близкими к максимально допустимым для данного типа интегратора. В этом случае ошибки самого интегратора будут оказывать минимальное влияние на точность измерений.
При измерении слабых флуктуаций, когда эффективное напряжение на входе квадратора не превышает 2— 3 в, целесообразно осуществить усиление измеряемого сигнала перед возведением его в квадрат, так как стандартные блоки произведений работают тем точнее, чем большее напряженеи подается на их входы.
Рассмотренная выше схема может быть очень просто реализована на любой нелинейной модели постоянного тока.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА ПЕРВАЯ. ГЕНЕРИРОВАНИЕ ИМПУЛЬСНЫХ И НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ СИГНАЛОВ СО СПЛОШНЫМ СПЕКТРОМ В ОБЛАСТИ НИЗКИХ ЧАСТОТ
- 1. КРАТКИЕ СВЕДЕНИЯ О ПЕРВИЧНЫХ ИСТОЧНИКАХ СЛУЧАЙНЫХ НАПРЯЖЕНИЙ
- 2. ПОЛУЧЕНИЕ НИЗКОЧАСТОТНЫХ ФЛУКТУАЦИИ ПУТЕМ СИНХРОННОГО ДЕТЕКТИРОВАНИЯ УЗКОПОЛОСНЫХ ШУМОВ
- 3. ГЕНЕРИРОВАНИЕ КВАЗИСЛУЧАЙНЫХ ИНФРАНИЗКОЧАСТОТНЫХ СИГНАЛОВ
- 4. ГЕНЕРИРОВАНИЕ СЛУЧАЙНЫХ ПО МОМЕНТАМ ПОЯВЛЕНИЯ (ПУАССОНОВСКИХ) ИМПУЛЬСОВ
- 5. ГЕНЕРИРОВАНИЕ СЛУЧАЙНЫХ ПО ДЛИТЕЛЬНОСТИ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ
- 6. ГЕНЕРИРОВАНИЕ ПЕРИОДИЧЕСКИХ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ СО СЛУЧАЙНОЙ АМПЛИТУДОЙ
- ГЛАВА ВТОРАЯ. ГЕНЕРИРОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ С ЗАДАННЫМИ СТАТИСТИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ
- 7. СПОСОБЫ ПОЛУЧЕНИЯ СЛУЧАЙНЫХ НАПРЯЖЕНИЙ С РАВНОВЕРОЯТНЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ АМПЛИТУД
- 8. ИСПОЛЬЗОВАНИЕ НЕЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ ПОЛУЧЕНИЯ НАПРЯЖЕНИЙ С ЗАДАННЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ МГНОВЕННЫХ ЗНАЧЕНИЙ
- 9. ПОЛУЧЕНИЕ НАПРЯЖЕНИЯ С ЗАДАННОЙ ОДНОМЕРНОЙ ПЛОТНОСТЬЮ ВЕРОЯТНОСТЕЙ МЕТОДОМ ЗАДАНИЯ ВЕРОЯТНОСТЕЙ СОСТЯНИЙ КАНАЛОВ
- 10. ПОЛУЧЕНИЕ ИНФРАНИЗКОЧАСТОТНЫХ ФЛУКТУАЦИИ С ЗАДАННОЙ КОРРЕЛЯЦИОННОЙ ФУНКЦИЕЙ
- 11. ИМИТАЦИЯ СИГНАЛОВ ДОППЛЕРОВСКИХ НАВИГАЦИОННЫХ СИСТЕМ
- ГЛАВА ТРЕТЬЯ. СТАБИЛИЗАЦИЯ И ИЗМЕРЕНИЕ ОСНОВНЫХ ПАРАМЕТРОВ СЛУЧАЙНЫХ СИГНАЛОВ
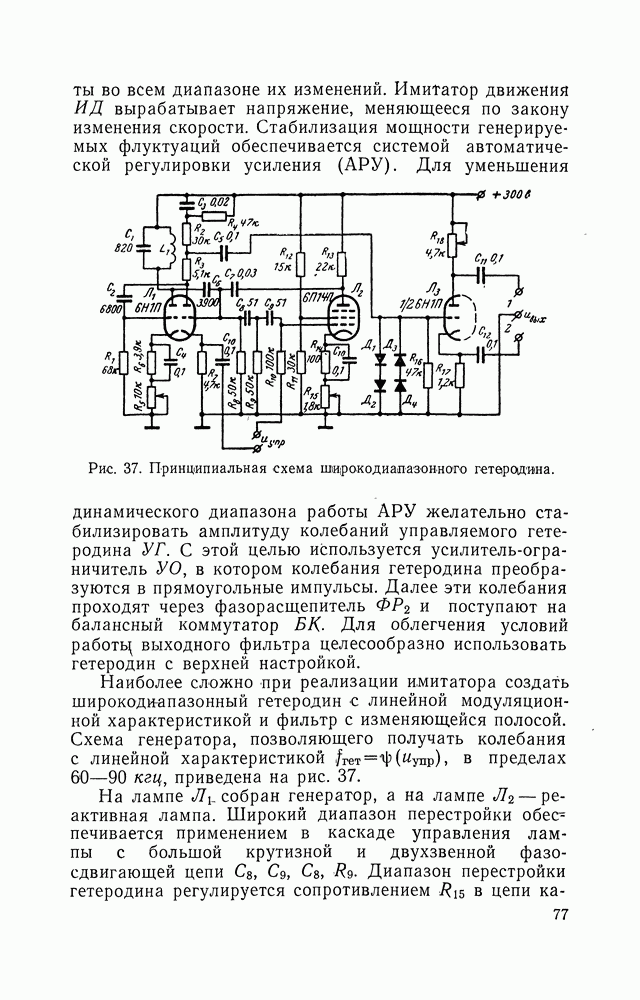
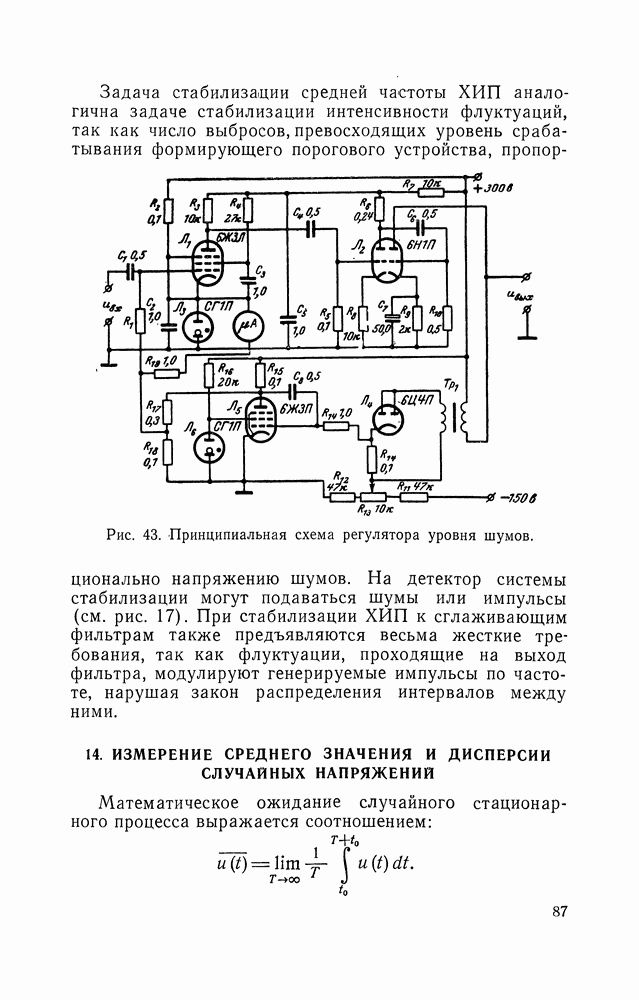
- 13. СПОСОБЫ СТАБИЛИЗАЦИИ МОЩНОСТИ ФЛУКТУАЦИЙ
- 14. ИЗМЕРЕНИЕ СРЕДНЕГО ЗНАЧЕНИЯ И ДИСПЕРСИИ СЛУЧАЙНЫХ НАПРЯЖЕНИЙ
- 15. ОПРЕДЕЛЕНИЕ ОДНОМЕРНЫХ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ
- 16 КОРРЕЛОМЕТРЫ И СПЕКТРОАНАЛИЗАТОРЫ