| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. ГЕНЕРИРОВАНИЕ КВАЗИСЛУЧАЙНЫХ ИНФРАНИЗКОЧАСТОТНЫХ СИГНАЛОВ
Генерирование случайных сигналов связано с непрерывным контролем их параметров. Если для высокочастотных сигналов эта задача решается сравнительно просто, то положение коренным образом меняется, когда речь идет о генерировании низкочастотных и особенно инфранизкочастотных флуктуаций. Дело в том, что измерение любого параметра случайного сигнала требует времени, на 2—3 порядка превышающего время корреляции последнего. В связи с этим непрерывный контроль параметров инфранизкочастотных сигналов оказывается практически невозможным, а точность их задания в генераторе — низкой. Поэтому поиск методов замены чисто случайных сигналов квазислучайными, где указанная задача решается очень просто, является весьма актуальной задачей. Удовлетворительное техническое решение найдено для получения квазислучайных низкочастотных флуктуаций 
Низкочастотный случайный сигнал с равномерной в интервале  спектральной плотностью можно представить в виде суммы большого количества синусоидальных сигналов, равномерно распределенных по шкале частот, имеющих амплитуды
спектральной плотностью можно представить в виде суммы большого количества синусоидальных сигналов, равномерно распределенных по шкале частот, имеющих амплитуды  и случайные фазы
и случайные фазы  . Подобное представление становится точным в том случае, если интервалы между составляющими До и их амплитуды стремить к нулю, а
. Подобное представление становится точным в том случае, если интервалы между составляющими До и их амплитуды стремить к нулю, а  распределить равномерно в интервале
распределить равномерно в интервале  . В эксперименте нет необходимости осуществлять подобный предельный переход и вместо сигнала со сплошным спектром можно использовать сигнал с дискретным спектром. Для того чтобы подобная замена была правомочной, необходимо, чтобы сигнал с дискретным спектром удовлетворял по крайней мере двум условиям: 1) в пределах полосы пропускания исследуемой системы должно быть минимум 5—10 синусоидальных составляющих; 2) функции взаимной
. В эксперименте нет необходимости осуществлять подобный предельный переход и вместо сигнала со сплошным спектром можно использовать сигнал с дискретным спектром. Для того чтобы подобная замена была правомочной, необходимо, чтобы сигнал с дискретным спектром удовлетворял по крайней мере двум условиям: 1) в пределах полосы пропускания исследуемой системы должно быть минимум 5—10 синусоидальных составляющих; 2) функции взаимной
корреляции составляющих должны быть равны нулю. Генерируемый сигнал можно представить как

Как первое, так и второе условия будут удовлетворены, если каждая составляющая будет генерироваться независимым генератором. Однако такой генератор будет чрезвычайно громоздким. В то же время условие отсутствия взаимной корреляции будет автоматически выполняться, если составляющие сигнала (10) будут иметь некратные частоты. Достигнуть этого можно, использовав генератор, состоящий из  синусно-косинусных потенциометров, питаемых от стабильного источника напряжения
синусно-косинусных потенциометров, питаемых от стабильного источника напряжения  (левая часть рис.
(левая часть рис.  Вращение движков потенциометров осуществляется мотором через редуктор, состоящий из последовательных ступеней с коэффициентом редукции каждой ступени, равным
Вращение движков потенциометров осуществляется мотором через редуктор, состоящий из последовательных ступеней с коэффициентом редукции каждой ступени, равным  Коэффициент редукции должен представлять собой правильную дробь, например
Коэффициент редукции должен представлять собой правильную дробь, например  .
.
Сигналы на выходах сумматоров будут представлять собой колебания, описываемые уравнениями

Как синусная, так и косинусная составляющие являются периодическими функциями времени. Однако при большом числе составляющих  и практически используемых скоростях вращения движков потенциометров (порядка нескольких единиц оборотов в секунду) период повторения для суммарного сигнала, получаемого с каждой группы (потенциометров, оказывается очень большим и на ограниченном отрезке времени можно рассматривать его как сумму синусоидальных (коси-нусоидальных) колебаний, имеющих случайные и независимые фазы. Использовать непосредственно колебания (11) нельзя, так как составляющие оказываются распределенными по шкале частот, неравномерно. В самом
и практически используемых скоростях вращения движков потенциометров (порядка нескольких единиц оборотов в секунду) период повторения для суммарного сигнала, получаемого с каждой группы (потенциометров, оказывается очень большим и на ограниченном отрезке времени можно рассматривать его как сумму синусоидальных (коси-нусоидальных) колебаний, имеющих случайные и независимые фазы. Использовать непосредственно колебания (11) нельзя, так как составляющие оказываются распределенными по шкале частот, неравномерно. В самом
деле, если принять, что частота вращения первого вала  то частота напряжения, генерируемого
то частота напряжения, генерируемого  каналом генератора
каналом генератора  По шкале частот сигналы будут разнесены на неодинаковые интервалы:
По шкале частот сигналы будут разнесены на неодинаковые интервалы:

Неравномерность спектра и ограниченность числа составляющих является большим недостатком генератора. Поэтому целесообразно с сигналом произвести определенные нелинейные функциональные преобразования. Можно предложить много различных видов таких преобразований. При их выборе следует обеспечить равномерность распределения составляющих спектра по шкале частот и равенство амплитуд. Например, сигнал  можно преобразовать следующим образом:
можно преобразовать следующим образом:

Из (12) видно, что  будет иметь составляющие на частотах:
будет иметь составляющие на частотах:

Все составляющие  встретятся по
встретятся по  разу, если
разу, если

при любых значениях  в пределах от
в пределах от  до
до  Неравенство (12а) выполняется указанным выше способом выбора
Неравенство (12а) выполняется указанным выше способом выбора 
Не будут совпадать по частотам и составляющие вида  Число членов, имеющих суммарные
Число членов, имеющих суммарные
и разностные частоты, определяется формулой

Общее число составляющих

Амплитуды  составляющих будут равны
составляющих будут равны  и всех остальных
и всех остальных  . Преобразование сигнала в соответствии с выражением (12) позволяет получить весьма большое число составляющих (по сравнению с исходном сигналом). Но неравномерное распределение их по шкале частот является недостатком метода. Добиться равномерности распределения составляющих можно, использовав в каждой ступени переменное редукционное число
. Преобразование сигнала в соответствии с выражением (12) позволяет получить весьма большое число составляющих (по сравнению с исходном сигналом). Но неравномерное распределение их по шкале частот является недостатком метода. Добиться равномерности распределения составляющих можно, использовав в каждой ступени переменное редукционное число  Но как правильный выбор редукционных чисел, так и реализация такого редуктора связаны с большими практическими трудностями. Равномерности спектра можно достигнуть, использовав преобразование вида
Но как правильный выбор редукционных чисел, так и реализация такого редуктора связаны с большими практическими трудностями. Равномерности спектра можно достигнуть, использовав преобразование вида

Можно показать, что при 

Сигнал, преобразованный в соответствии с (12в), будет иметь

составляющих с одинаковой амплитудой, равномерно распределенных в пределах от

до

Конечно, в силу невозможности идеально выполнить заданное функциональное преобразование спектр выходного сигнала будет значительно богаче составляющими, чем это следует из выражения (126). Но те преобразования, которые заданы формулой (12в), могут выполняться с ошибкой, не превышающей 1—3%. Такой же порядок величины будут иметь и амплитуды паразитных составляющих.

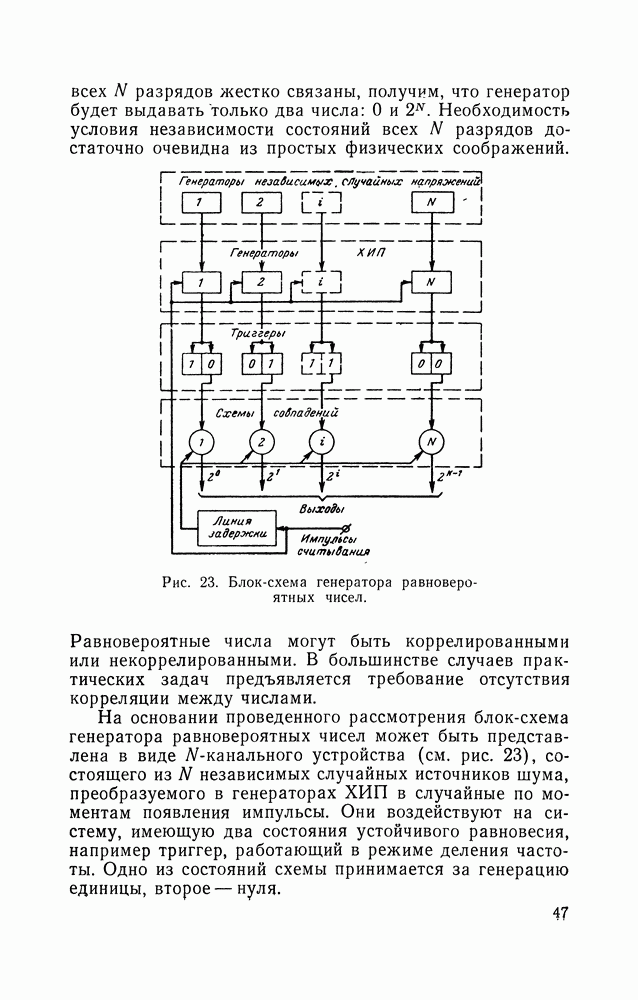
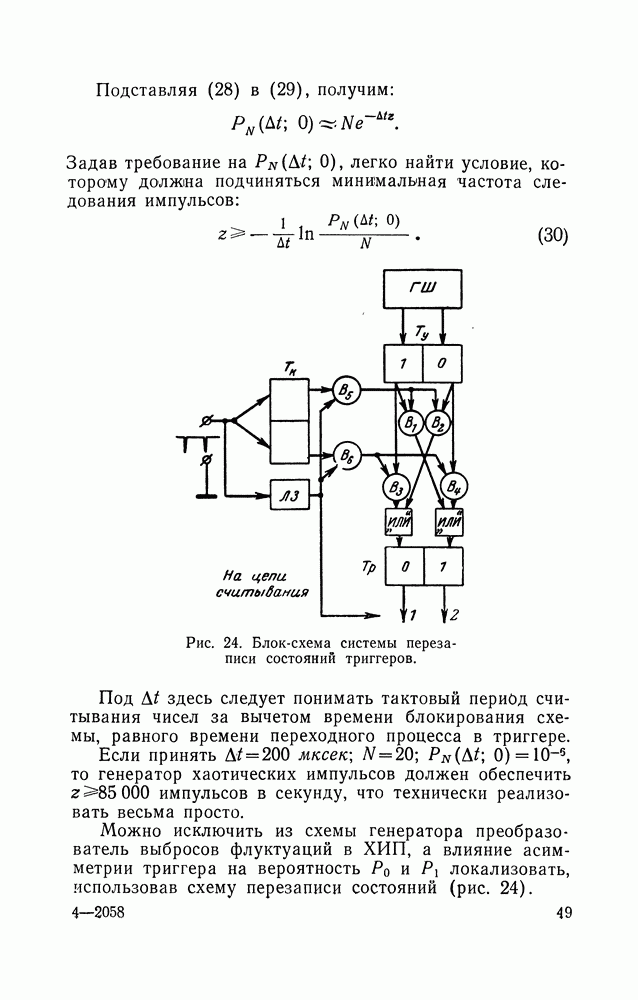
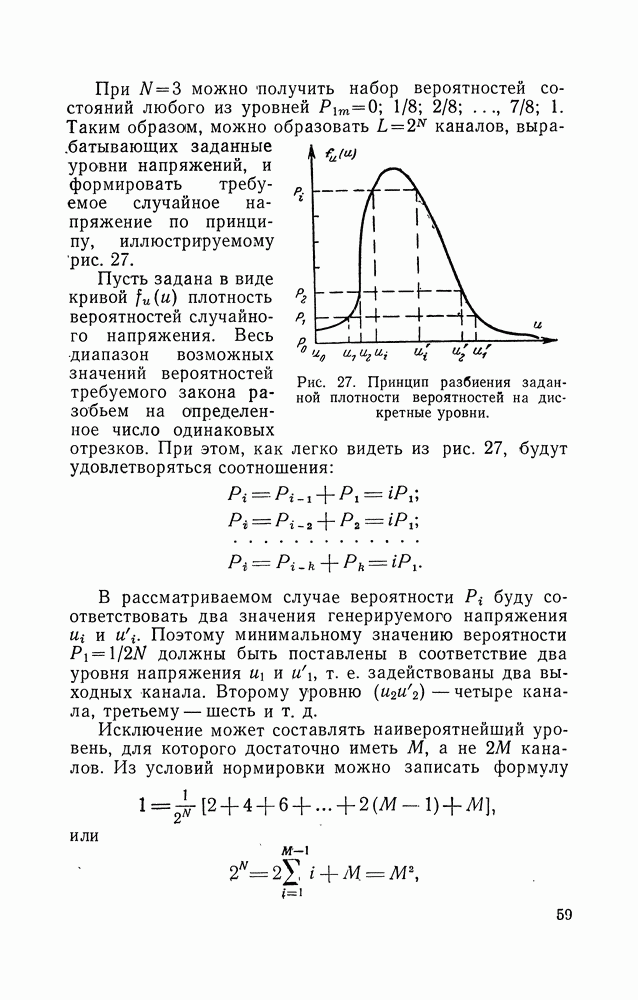
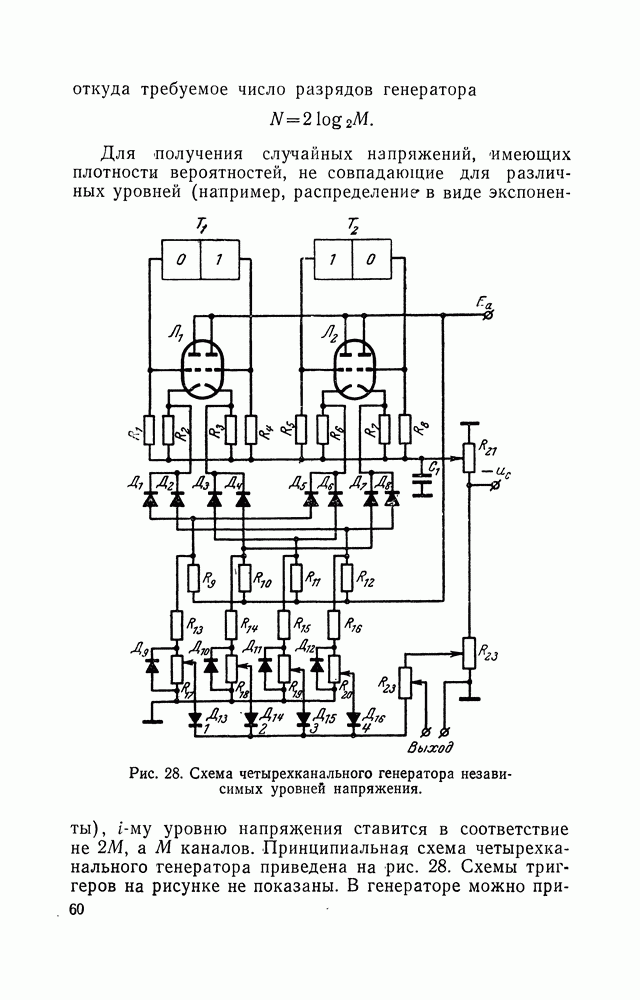
Рис. 8. Блок-схема генератора квазислучайного непрерывного сигнала.
Схема генератора, позволяющего получать сигнал, соответствующий (12в), приведена на рис. 8. Генератор получается достаточно сложным, но эта сложность окупается тем, что все параметры сигнала могут быть заданы с требуемой точностью и отсутствуют цепи стабилизации случайных параметров. Регулируя число оборотов в генераторе, можно в широких пределах изменять ширину спектра, при этом, конечно, будет меняться и интервал между составляющими. В рассмотренном генераторе можно получить инфранизкочастотные сигналы без каких бы то ни было ограничений в сторону уменьшения частот, что чрезвычайно важно при имитации весьма низкочастотных случайных сигналов, таких, например, как фединг коротковолновых радиосигналов.
Укажем еще на одну возможность, которой располагает рассмотренный метод генерации квазислучайного сигнала. Если на потенциометры подать не постоянное, а синусоидальное напряжение с частотой  то спектр сигнала будет смещен на частоту питающего
то спектр сигнала будет смещен на частоту питающего
напряжения. Рассмотрим одну из составляющих сигнала, например косинусную:

Полученное выражение показывает, что сигнал будет представлять квазигармоническое колебание, имеющее симметричный относительно  спектр, ширина которого
спектр, ширина которого

В тех случаях, когда по условиям эксперимента необходимо получить весьма узкополосные шумы, указанный метод может оказаться полезным.
Питание потенциометров сигналом, изменяющимся по тому или иному закону, эквивалентно операции идеального умножения этого закона на закон, по которому намотаны потенциометры. Поэтому устройство рассмотренного выше типа можно использовать для получения сигналов с весьма сложными характеристиками спектра выходного сигнала. В частности, если потенциометры питать случайными сигналами, можно получать нестационарные флуктуации.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА ПЕРВАЯ. ГЕНЕРИРОВАНИЕ ИМПУЛЬСНЫХ И НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ СИГНАЛОВ СО СПЛОШНЫМ СПЕКТРОМ В ОБЛАСТИ НИЗКИХ ЧАСТОТ
- 1. КРАТКИЕ СВЕДЕНИЯ О ПЕРВИЧНЫХ ИСТОЧНИКАХ СЛУЧАЙНЫХ НАПРЯЖЕНИЙ
- 2. ПОЛУЧЕНИЕ НИЗКОЧАСТОТНЫХ ФЛУКТУАЦИИ ПУТЕМ СИНХРОННОГО ДЕТЕКТИРОВАНИЯ УЗКОПОЛОСНЫХ ШУМОВ
- 3. ГЕНЕРИРОВАНИЕ КВАЗИСЛУЧАЙНЫХ ИНФРАНИЗКОЧАСТОТНЫХ СИГНАЛОВ
- 4. ГЕНЕРИРОВАНИЕ СЛУЧАЙНЫХ ПО МОМЕНТАМ ПОЯВЛЕНИЯ (ПУАССОНОВСКИХ) ИМПУЛЬСОВ
- 5. ГЕНЕРИРОВАНИЕ СЛУЧАЙНЫХ ПО ДЛИТЕЛЬНОСТИ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ
- 6. ГЕНЕРИРОВАНИЕ ПЕРИОДИЧЕСКИХ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ СО СЛУЧАЙНОЙ АМПЛИТУДОЙ
- ГЛАВА ВТОРАЯ. ГЕНЕРИРОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ С ЗАДАННЫМИ СТАТИСТИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ
- 7. СПОСОБЫ ПОЛУЧЕНИЯ СЛУЧАЙНЫХ НАПРЯЖЕНИЙ С РАВНОВЕРОЯТНЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ АМПЛИТУД
- 8. ИСПОЛЬЗОВАНИЕ НЕЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ ПОЛУЧЕНИЯ НАПРЯЖЕНИЙ С ЗАДАННЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ МГНОВЕННЫХ ЗНАЧЕНИЙ
- 9. ПОЛУЧЕНИЕ НАПРЯЖЕНИЯ С ЗАДАННОЙ ОДНОМЕРНОЙ ПЛОТНОСТЬЮ ВЕРОЯТНОСТЕЙ МЕТОДОМ ЗАДАНИЯ ВЕРОЯТНОСТЕЙ СОСТЯНИЙ КАНАЛОВ
- 10. ПОЛУЧЕНИЕ ИНФРАНИЗКОЧАСТОТНЫХ ФЛУКТУАЦИИ С ЗАДАННОЙ КОРРЕЛЯЦИОННОЙ ФУНКЦИЕЙ
- 11. ИМИТАЦИЯ СИГНАЛОВ ДОППЛЕРОВСКИХ НАВИГАЦИОННЫХ СИСТЕМ
- ГЛАВА ТРЕТЬЯ. СТАБИЛИЗАЦИЯ И ИЗМЕРЕНИЕ ОСНОВНЫХ ПАРАМЕТРОВ СЛУЧАЙНЫХ СИГНАЛОВ
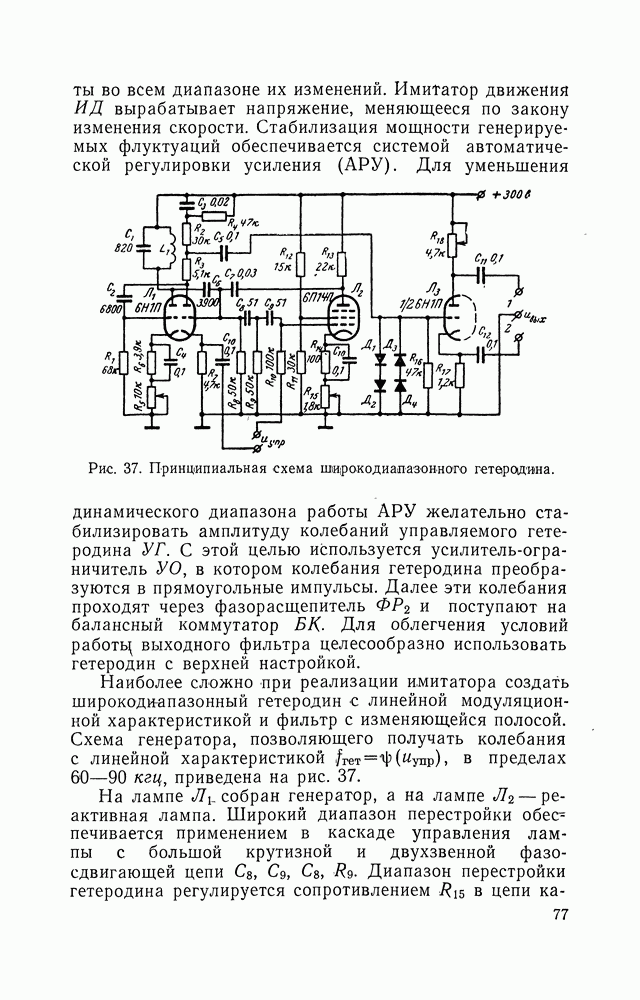
- 13. СПОСОБЫ СТАБИЛИЗАЦИИ МОЩНОСТИ ФЛУКТУАЦИЙ
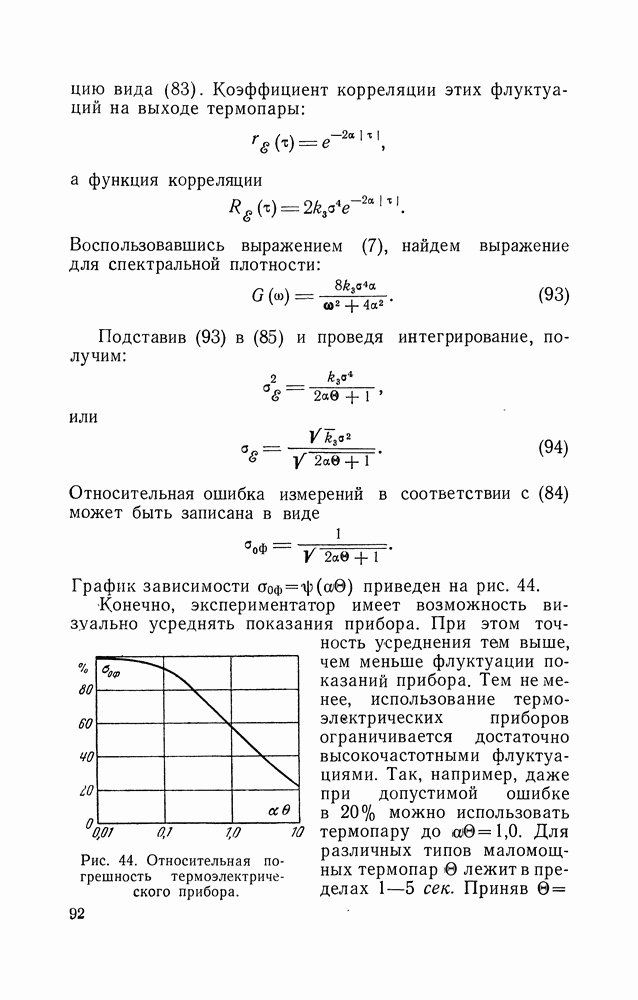
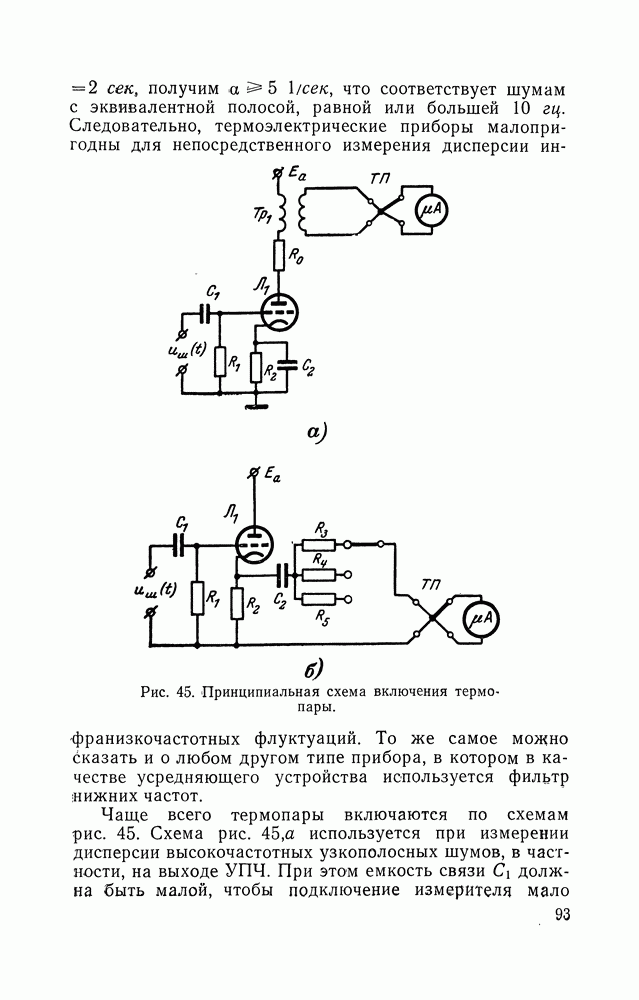
- 14. ИЗМЕРЕНИЕ СРЕДНЕГО ЗНАЧЕНИЯ И ДИСПЕРСИИ СЛУЧАЙНЫХ НАПРЯЖЕНИЙ
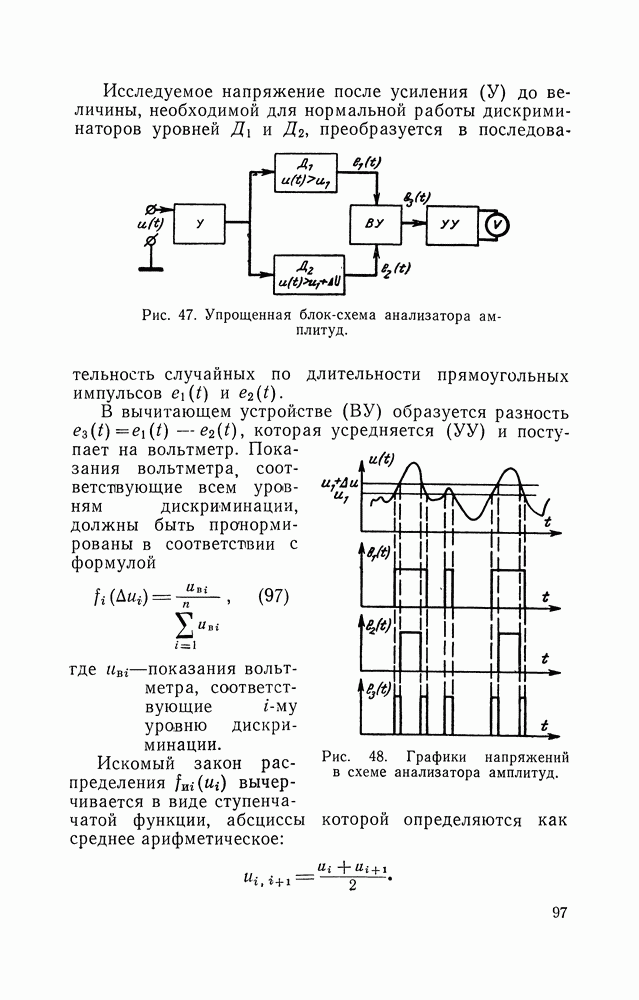
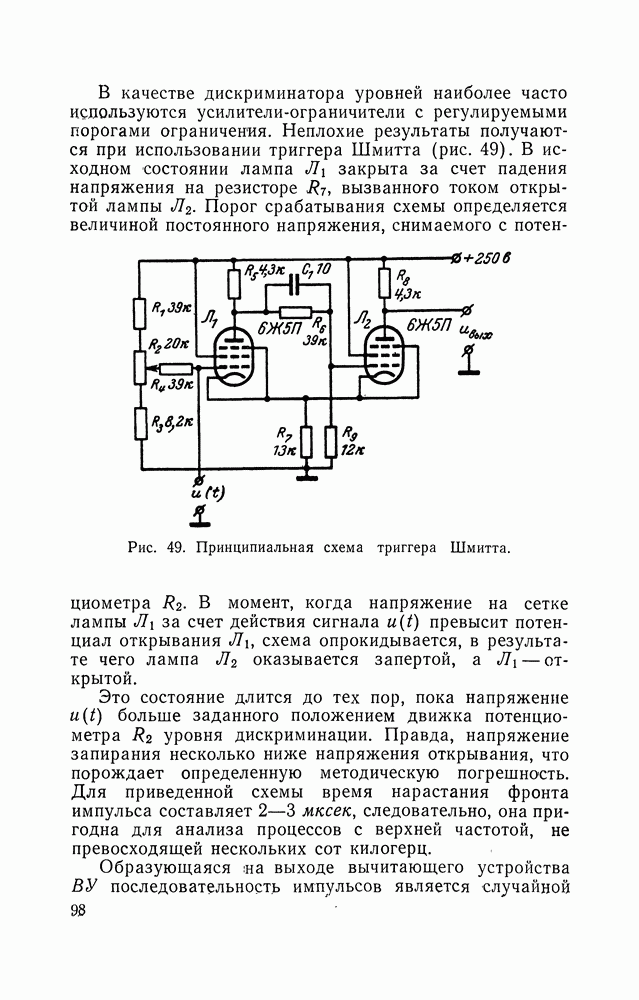
- 15. ОПРЕДЕЛЕНИЕ ОДНОМЕРНЫХ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ
- 16 КОРРЕЛОМЕТРЫ И СПЕКТРОАНАЛИЗАТОРЫ