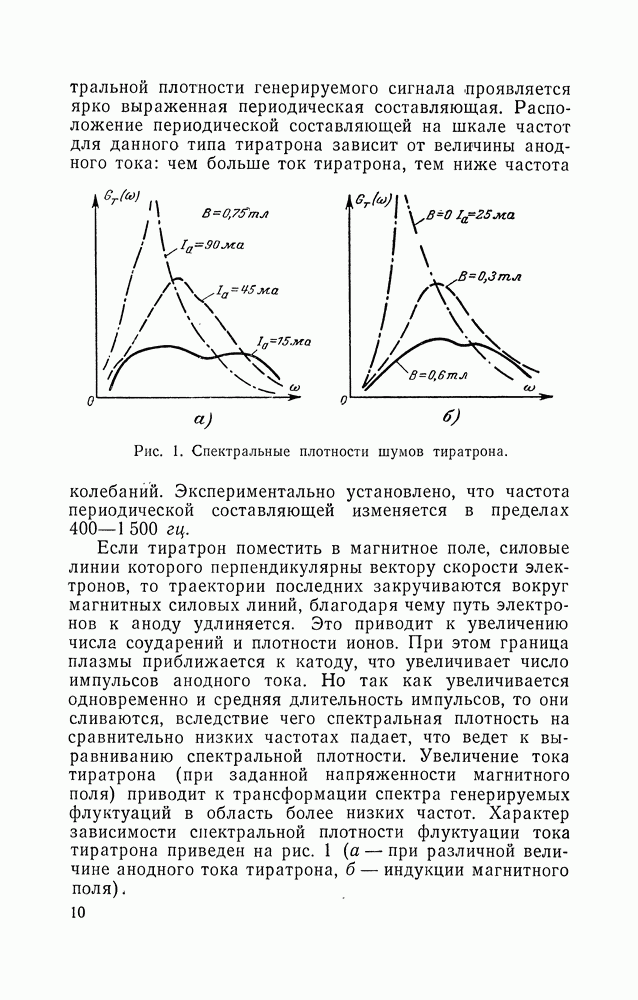
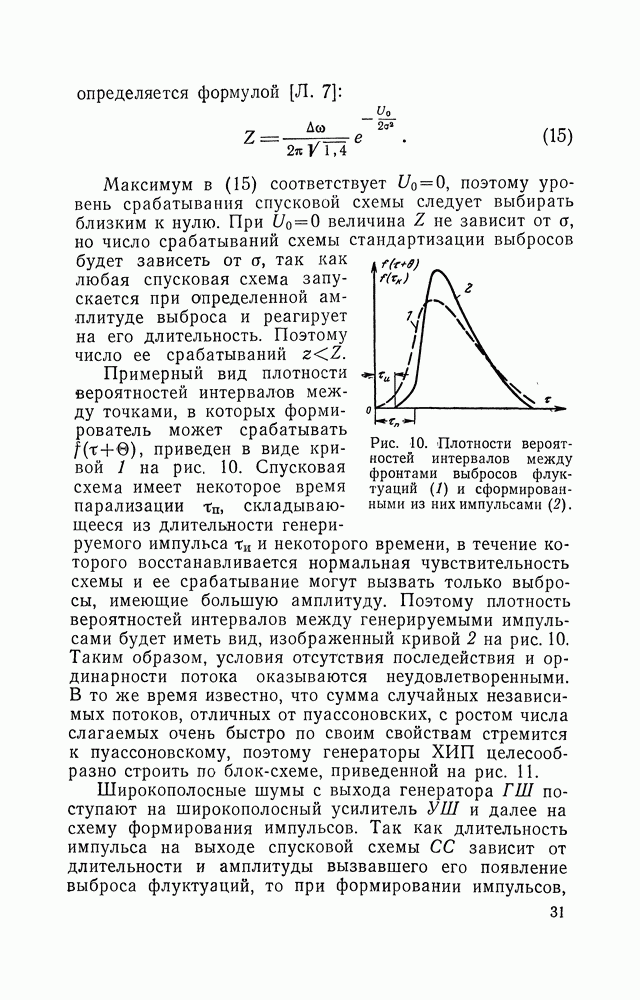
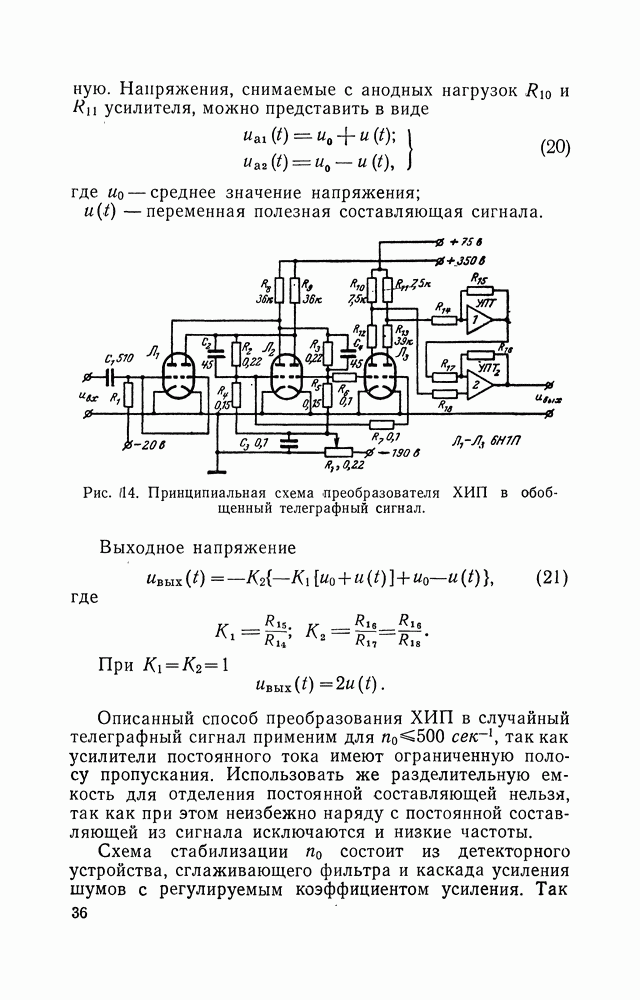
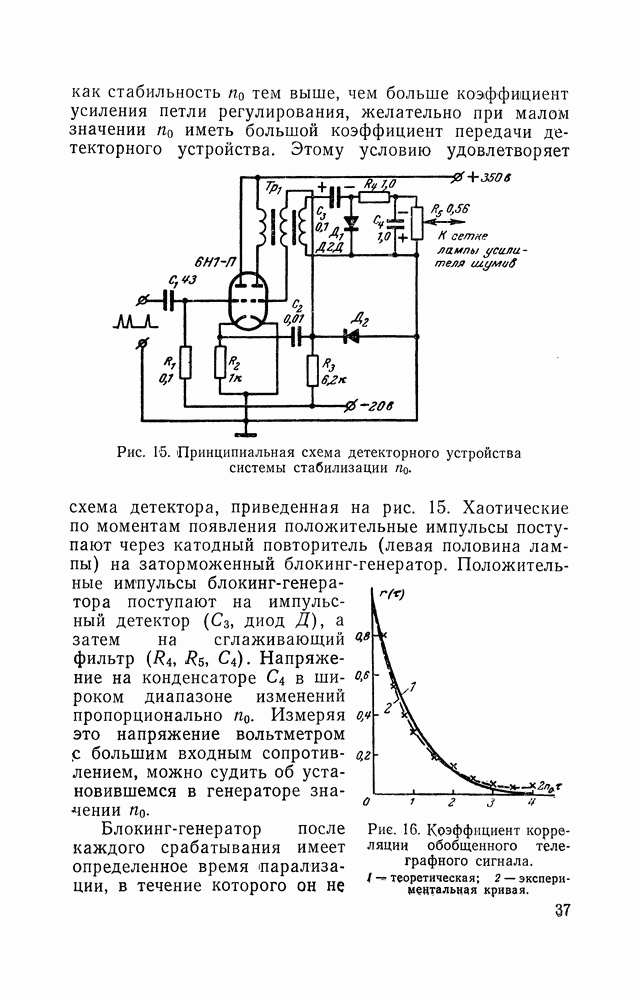
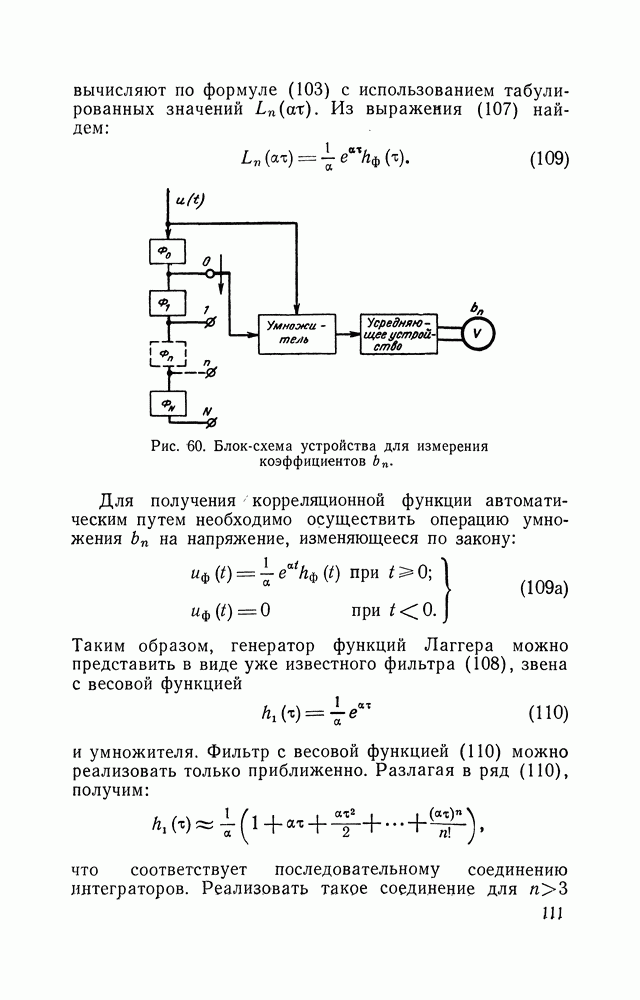
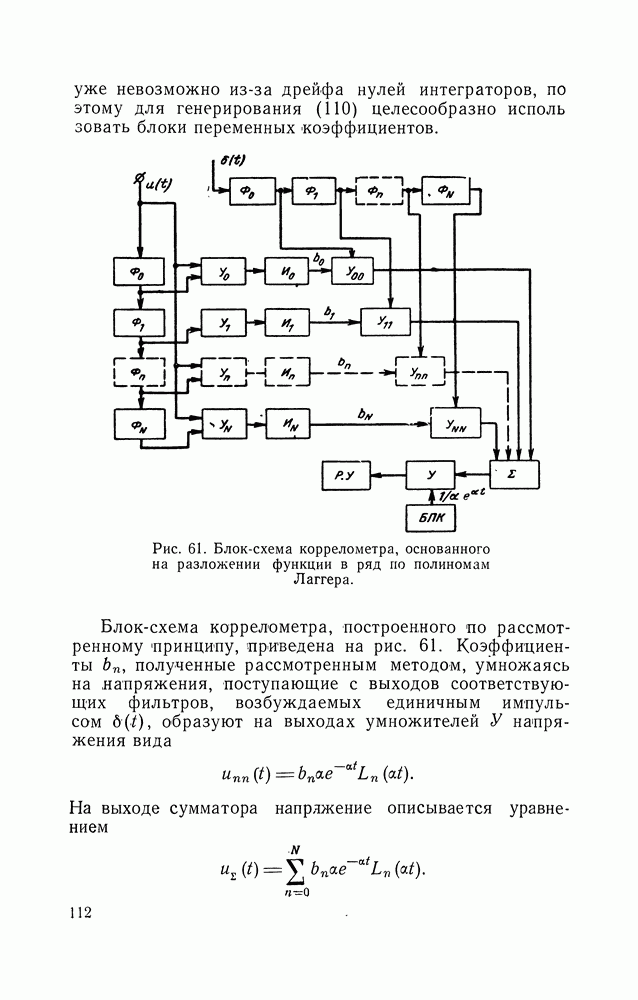
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8. ИСПОЛЬЗОВАНИЕ НЕЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ ПОЛУЧЕНИЯ НАПРЯЖЕНИЙ С ЗАДАННЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ МГНОВЕННЫХ ЗНАЧЕНИЙ
Для получения напряжений с заданной плотностью вероятностей амплитуд мгновенных значений широко используются нелинейные преобразования случайных сигналов. Исходными, как правило, являются сигналы с равновероятным или нормальным распределениями амплитуд. Особенно перспективным метод нелинейных преобразований стал в связи с внедрением в практику проведения исследований моделей постоянного тока, располагающих набором легко перестраиваемых нелинейностей.
В теории вероятностей обычно рассматривается задача нахождения плотности вероятностей флуктуаций, прошедших через нелинейный элемент.
Рассмотрим обратную задачу  . Пусть известны плотности вероятностей исходного сигнала
. Пусть известны плотности вероятностей исходного сигнала  и требуемая плотность вероятностей Надо найти уравнение нелинейного элемента, осуществляющего требуемое преобразование случайного сигнала, т. е. функцию
и требуемая плотность вероятностей Надо найти уравнение нелинейного элемента, осуществляющего требуемое преобразование случайного сигнала, т. е. функцию

Вероятности пребывания обоих сигналов в интервалах  одинаковы, поэтому
одинаковы, поэтому  откуда
откуда

Наиболее простым нелинейное преобразование оказывается в том случае, если в качестве исходного используется равномерно распределенный сигнал, т. е. когда

В теории вероятностей доказывается теорема (см., например,  согласно которой случайная величина
согласно которой случайная величина  связанная со случайной величиной
связанная со случайной величиной  имеющей плотность вероятностей
имеющей плотность вероятностей  соотношением
соотношением

является равномерно распределенной в интервале  По физическому смыслу
По физическому смыслу  является монотонно возрастающей функцией у и всегда может быть найдена функция
является монотонно возрастающей функцией у и всегда может быть найдена функция  а обратная функция
а обратная функция

выражается соотношением (36). В самом деле, в силу равномерности распределения у в интервале  случайная величина
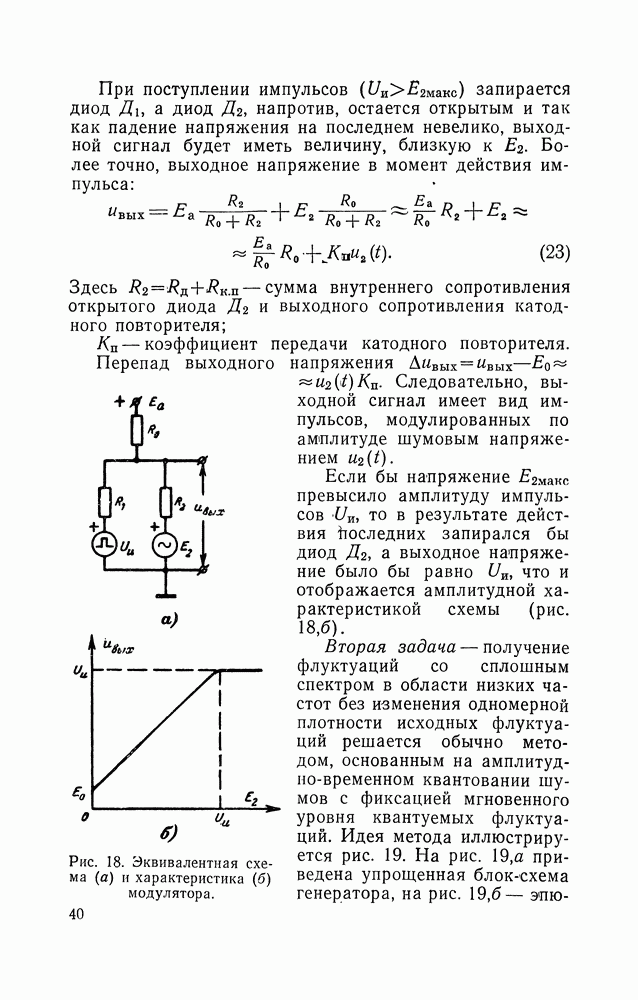
случайная величина  распределена в том же интервале и ее интегральный закон распределения удовлетворяет соотношению
распределена в том же интервале и ее интегральный закон распределения удовлетворяет соотношению

откуда с учетом (37)

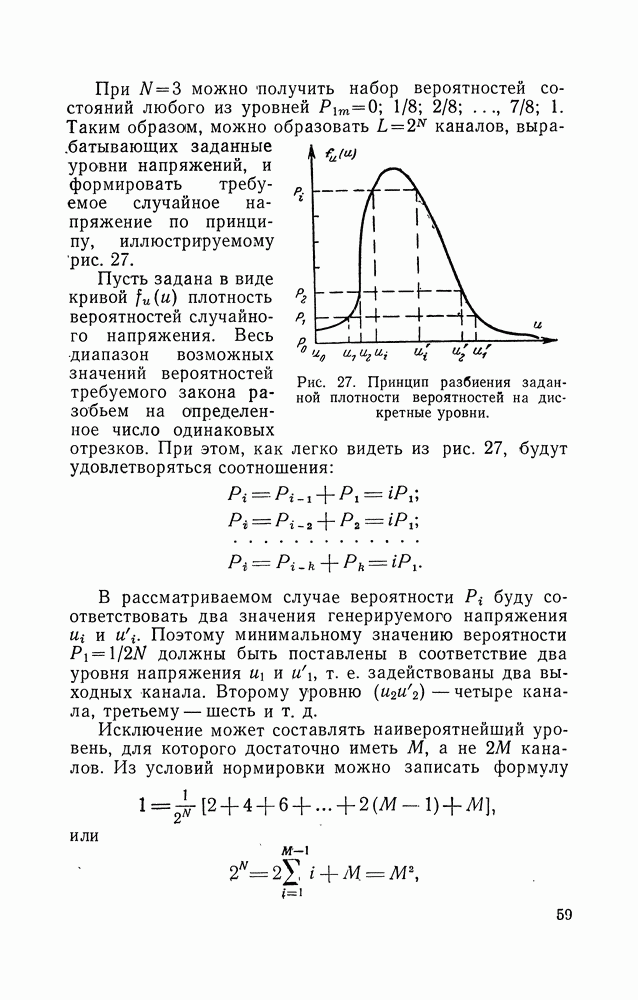
Найдем уравнения нелинейных элементов для некоторых наиболее типичных плотностей вероятностей.
1. Показательный закон

откуда уравнение нелинейного звена

2. Закон Коши

3. Релеевское распределение

откуда

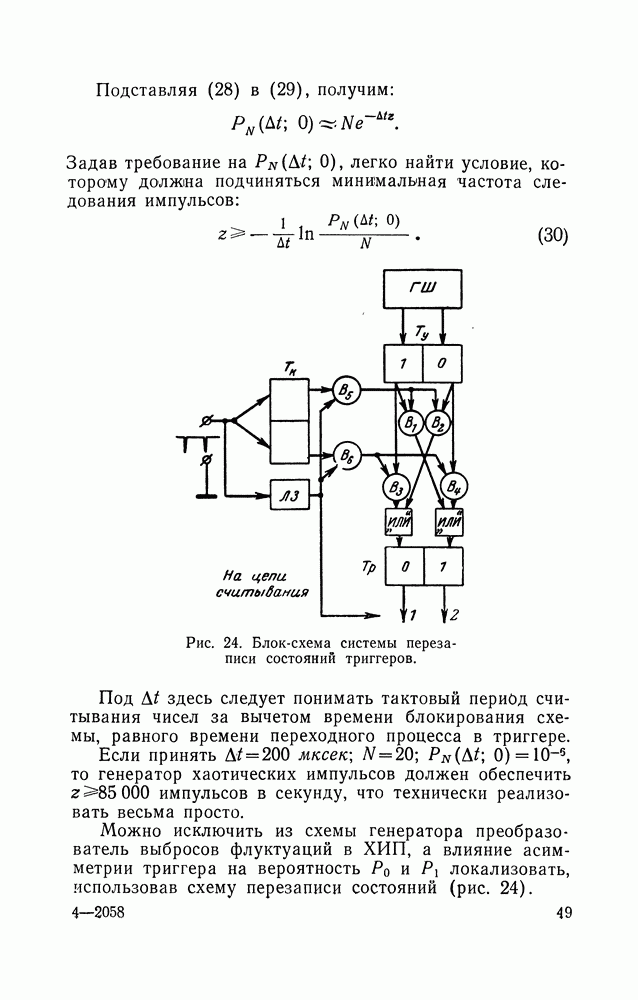
Так как диапазон изменений входных напряжений для нелинейных преобразователей всегда превосходит  то необходимо выбрать соответствующим образом масштаб уравнений нелинейных преобразователей.
то необходимо выбрать соответствующим образом масштаб уравнений нелинейных преобразователей.
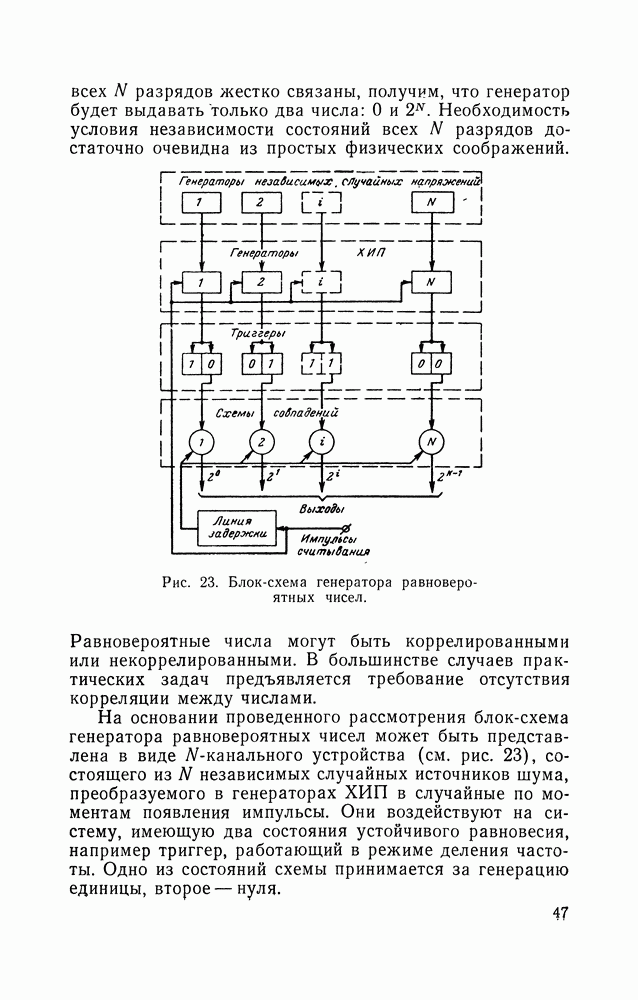
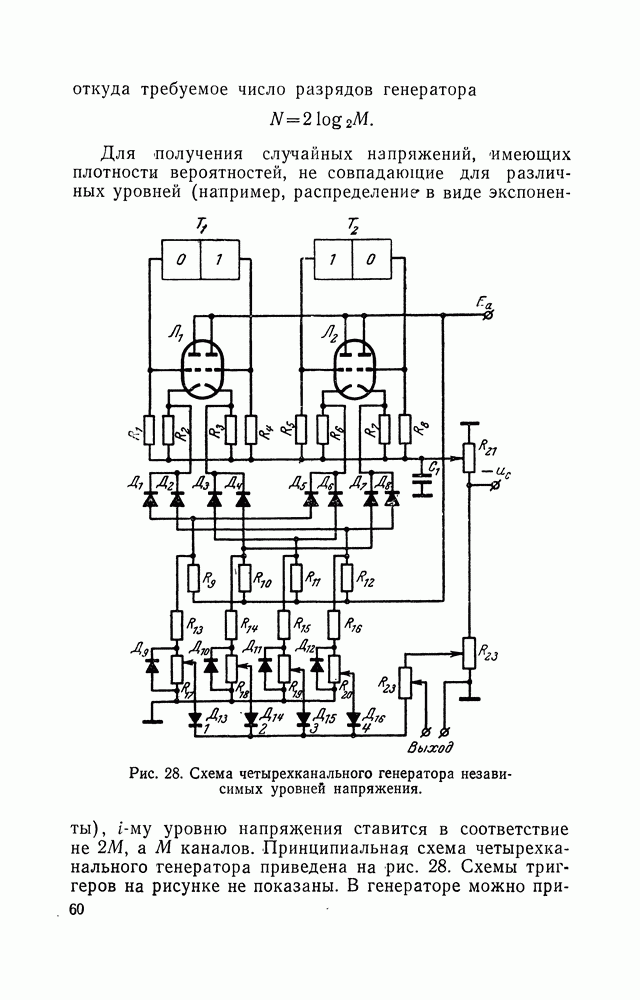
Устройство генераторов равновероятных напряжений, основанных на преобразовании равновероятных чисел в напряжение, оказывается достаточно сложным. В то же время получение напряжений с нормальным законом распределения амплитуд осуществляется значительно
более простыми средствами. Поэтому определенный интерес может представлять преобразование напряжений с нормальным законом распределения амплитуд в напряжения с другим законом распределения. Так, равномерно распределенный симметричный относительно нуля сигнал с функцией распределения

можно получить путем преобразования вида (35):

Согласование масштаба флуктуаций можно считать удовлетворенным, если принять  Тогда
Тогда

где

| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА ПЕРВАЯ. ГЕНЕРИРОВАНИЕ ИМПУЛЬСНЫХ И НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ СИГНАЛОВ СО СПЛОШНЫМ СПЕКТРОМ В ОБЛАСТИ НИЗКИХ ЧАСТОТ
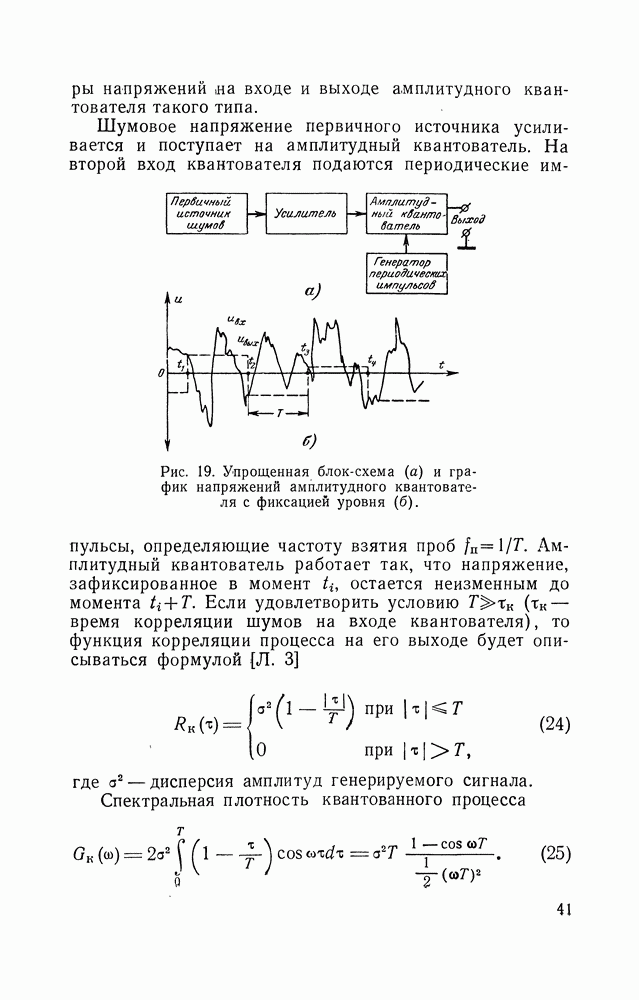
- 1. КРАТКИЕ СВЕДЕНИЯ О ПЕРВИЧНЫХ ИСТОЧНИКАХ СЛУЧАЙНЫХ НАПРЯЖЕНИЙ
- 2. ПОЛУЧЕНИЕ НИЗКОЧАСТОТНЫХ ФЛУКТУАЦИИ ПУТЕМ СИНХРОННОГО ДЕТЕКТИРОВАНИЯ УЗКОПОЛОСНЫХ ШУМОВ
- 3. ГЕНЕРИРОВАНИЕ КВАЗИСЛУЧАЙНЫХ ИНФРАНИЗКОЧАСТОТНЫХ СИГНАЛОВ
- 4. ГЕНЕРИРОВАНИЕ СЛУЧАЙНЫХ ПО МОМЕНТАМ ПОЯВЛЕНИЯ (ПУАССОНОВСКИХ) ИМПУЛЬСОВ
- 5. ГЕНЕРИРОВАНИЕ СЛУЧАЙНЫХ ПО ДЛИТЕЛЬНОСТИ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ
- 6. ГЕНЕРИРОВАНИЕ ПЕРИОДИЧЕСКИХ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ СО СЛУЧАЙНОЙ АМПЛИТУДОЙ
- ГЛАВА ВТОРАЯ. ГЕНЕРИРОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ С ЗАДАННЫМИ СТАТИСТИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ
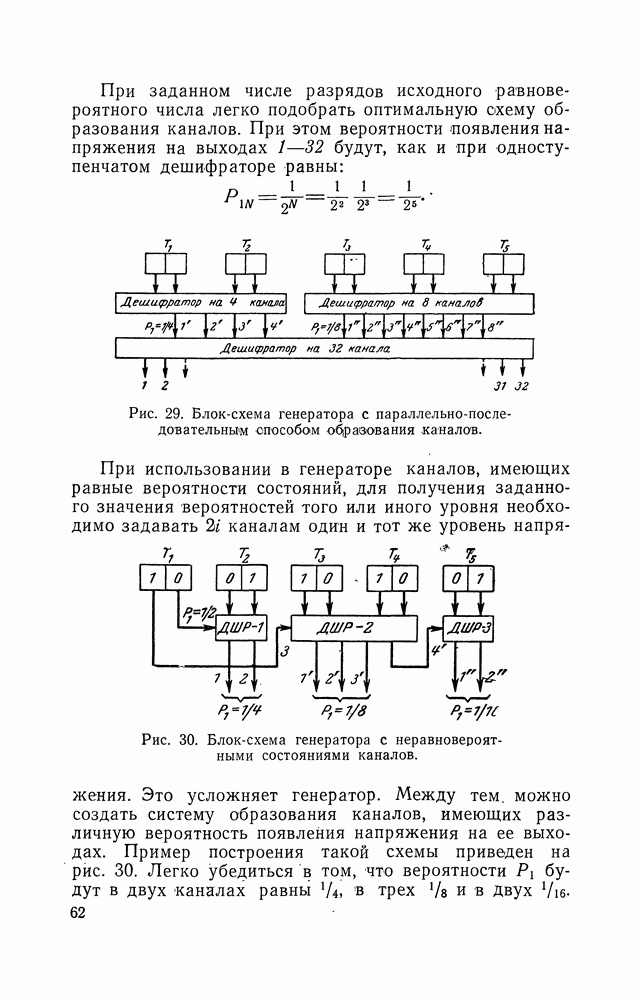
- 7. СПОСОБЫ ПОЛУЧЕНИЯ СЛУЧАЙНЫХ НАПРЯЖЕНИЙ С РАВНОВЕРОЯТНЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ АМПЛИТУД
- 8. ИСПОЛЬЗОВАНИЕ НЕЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ ПОЛУЧЕНИЯ НАПРЯЖЕНИЙ С ЗАДАННЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ МГНОВЕННЫХ ЗНАЧЕНИЙ
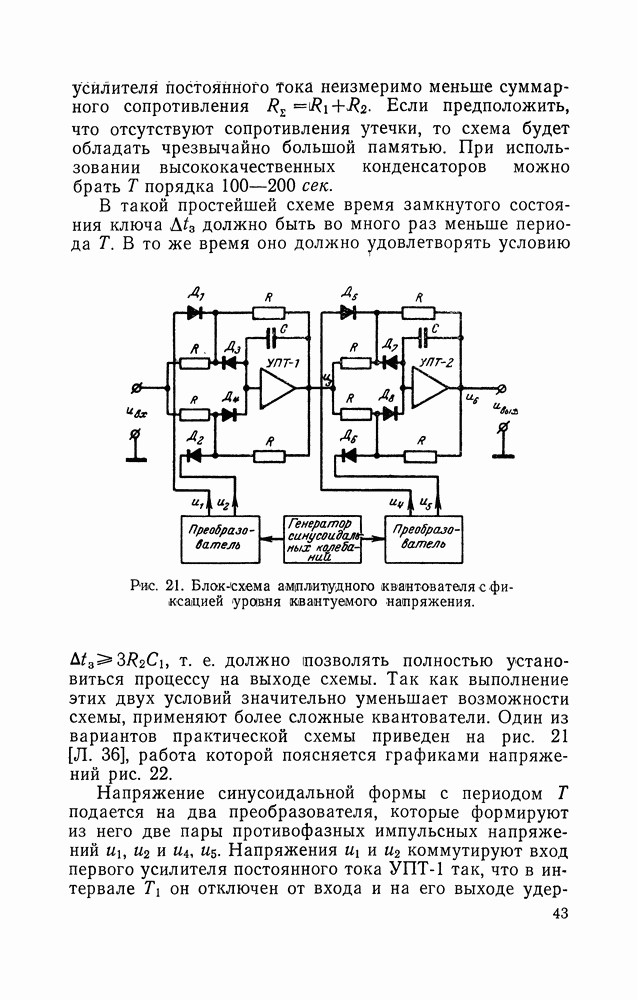
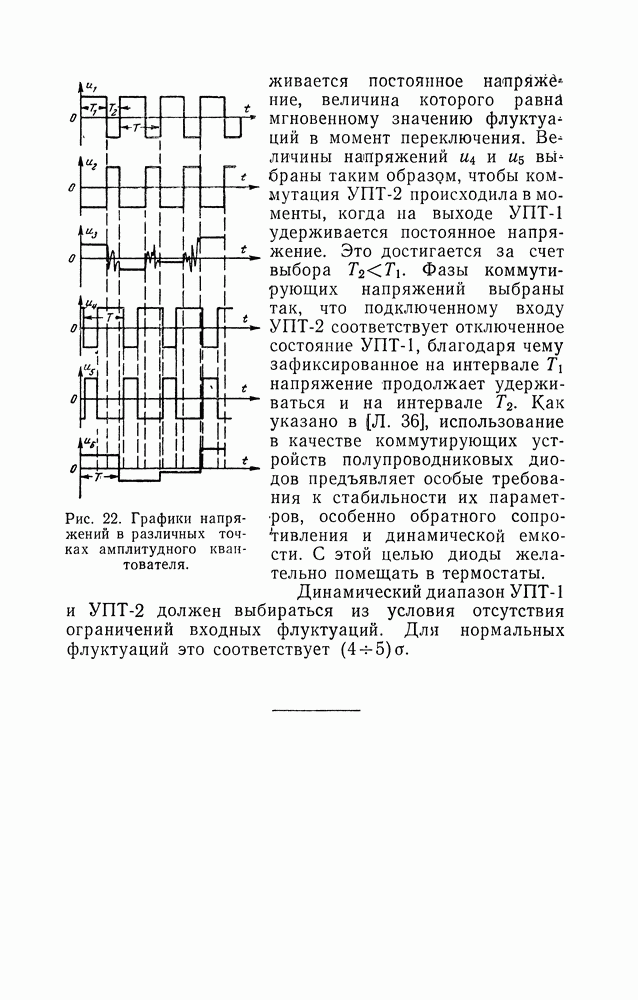
- 9. ПОЛУЧЕНИЕ НАПРЯЖЕНИЯ С ЗАДАННОЙ ОДНОМЕРНОЙ ПЛОТНОСТЬЮ ВЕРОЯТНОСТЕЙ МЕТОДОМ ЗАДАНИЯ ВЕРОЯТНОСТЕЙ СОСТЯНИЙ КАНАЛОВ
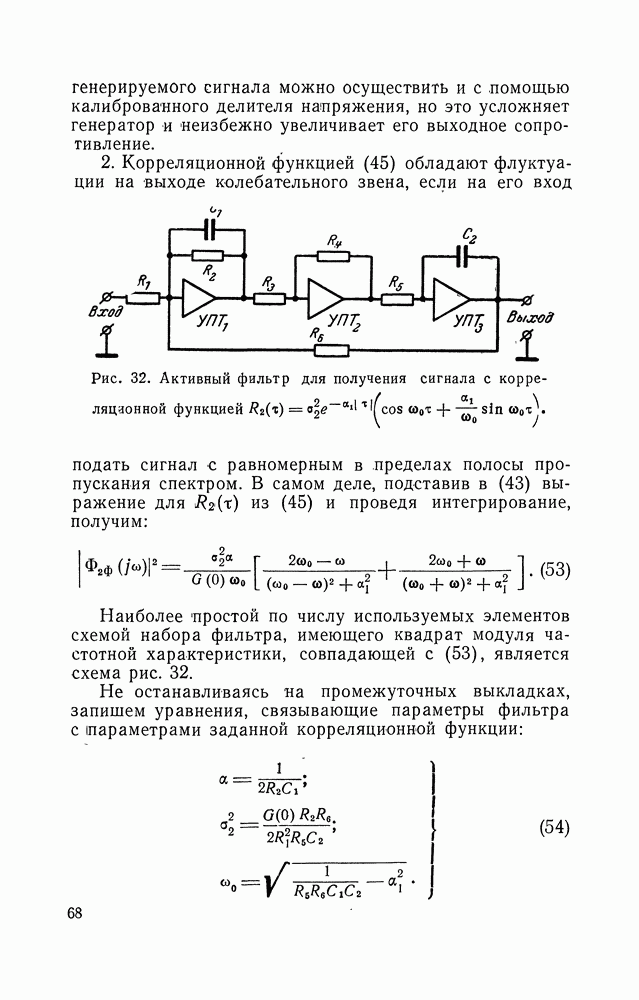
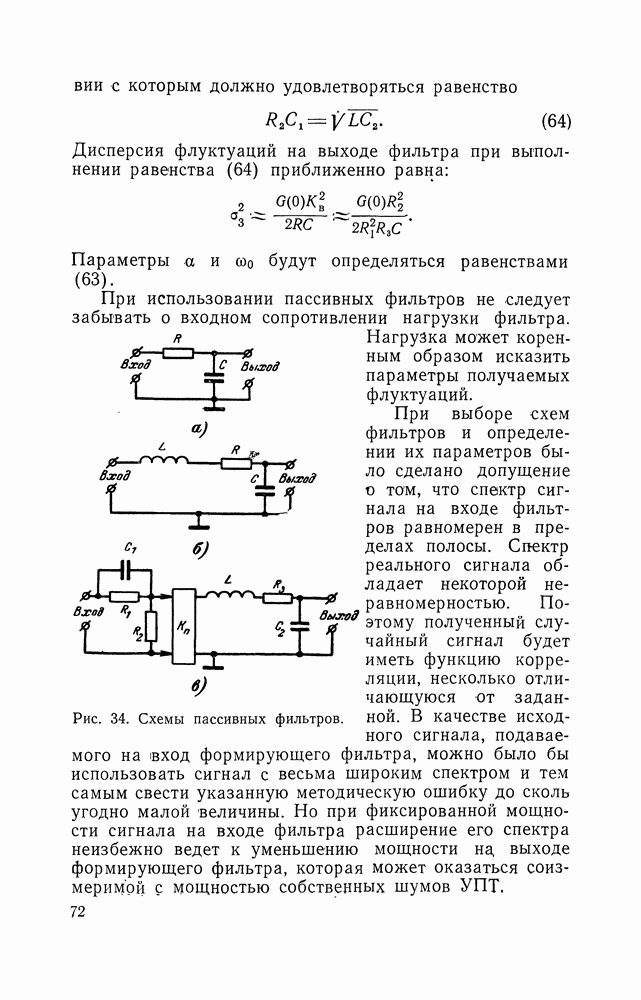
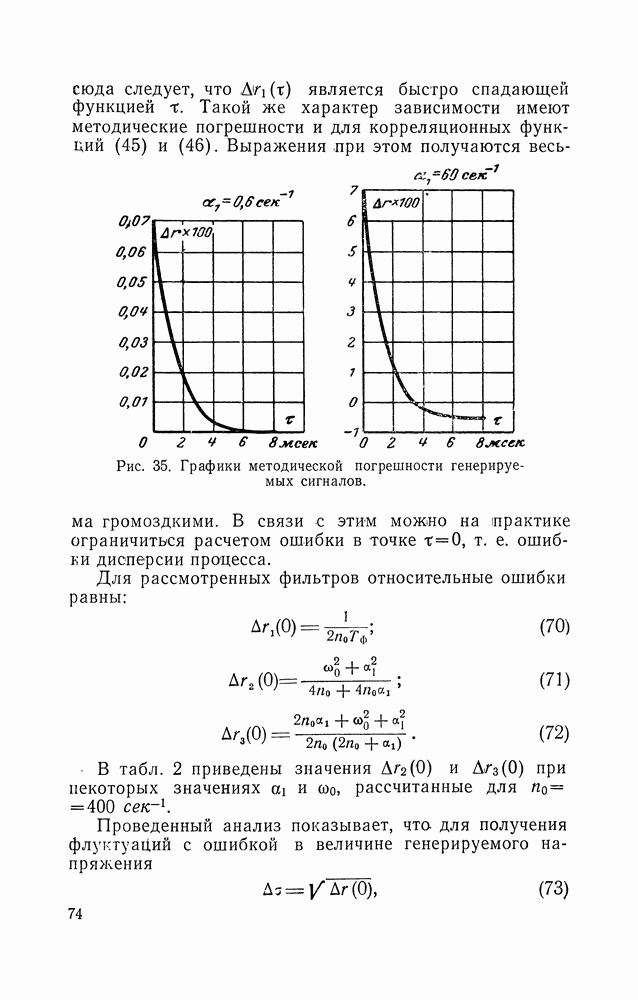
- 10. ПОЛУЧЕНИЕ ИНФРАНИЗКОЧАСТОТНЫХ ФЛУКТУАЦИИ С ЗАДАННОЙ КОРРЕЛЯЦИОННОЙ ФУНКЦИЕЙ
- 11. ИМИТАЦИЯ СИГНАЛОВ ДОППЛЕРОВСКИХ НАВИГАЦИОННЫХ СИСТЕМ
- ГЛАВА ТРЕТЬЯ. СТАБИЛИЗАЦИЯ И ИЗМЕРЕНИЕ ОСНОВНЫХ ПАРАМЕТРОВ СЛУЧАЙНЫХ СИГНАЛОВ
- 13. СПОСОБЫ СТАБИЛИЗАЦИИ МОЩНОСТИ ФЛУКТУАЦИЙ
- 14. ИЗМЕРЕНИЕ СРЕДНЕГО ЗНАЧЕНИЯ И ДИСПЕРСИИ СЛУЧАЙНЫХ НАПРЯЖЕНИЙ
- 15. ОПРЕДЕЛЕНИЕ ОДНОМЕРНЫХ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ
- 16 КОРРЕЛОМЕТРЫ И СПЕКТРОАНАЛИЗАТОРЫ