| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
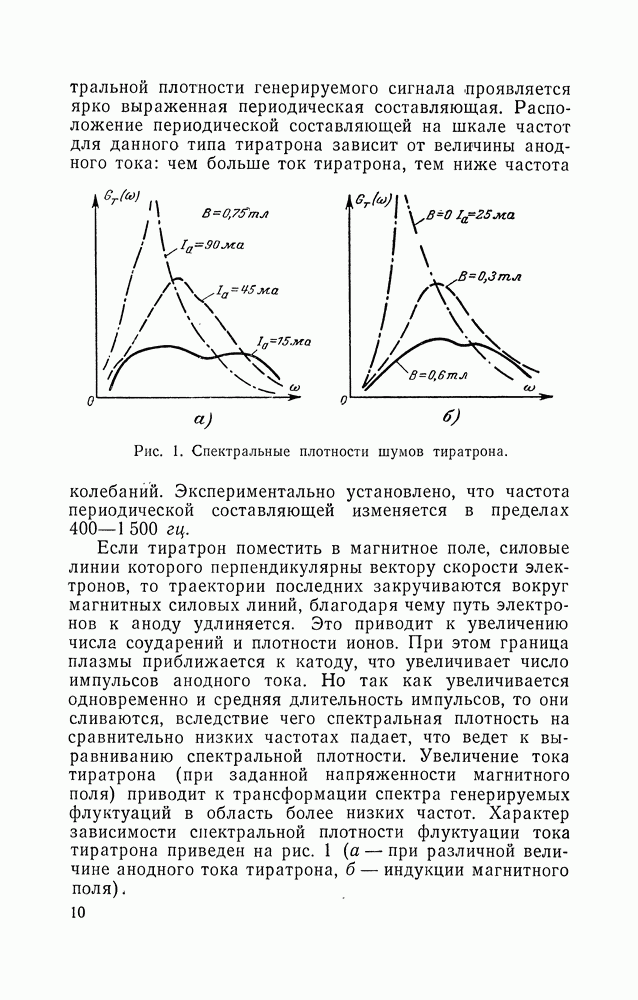
ГЛАВА ВТОРАЯ. ГЕНЕРИРОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ С ЗАДАННЫМИ СТАТИСТИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ
7. СПОСОБЫ ПОЛУЧЕНИЯ СЛУЧАЙНЫХ НАПРЯЖЕНИЙ С РАВНОВЕРОЯТНЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ АМПЛИТУД
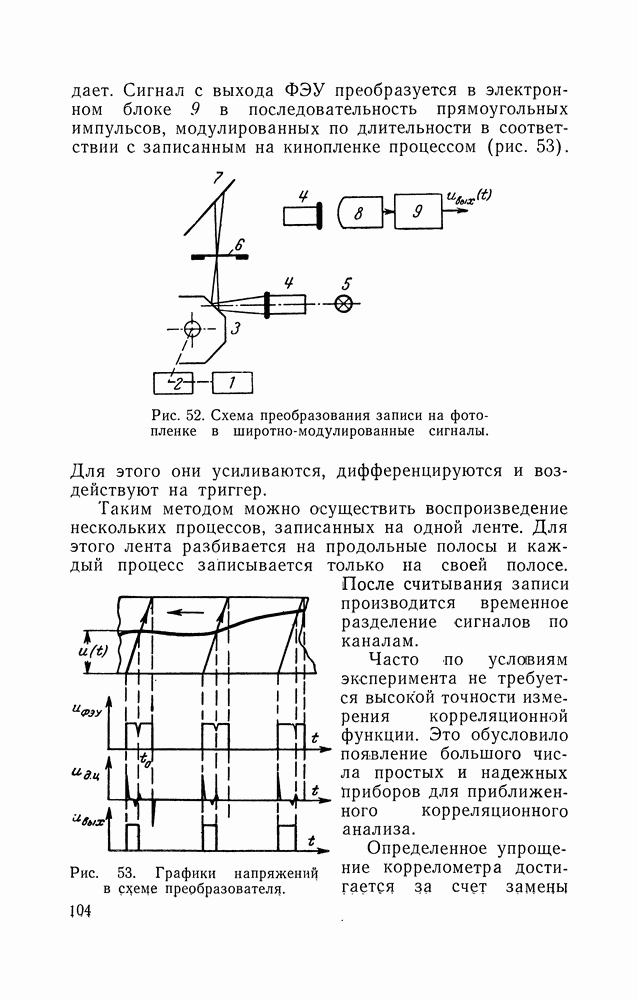
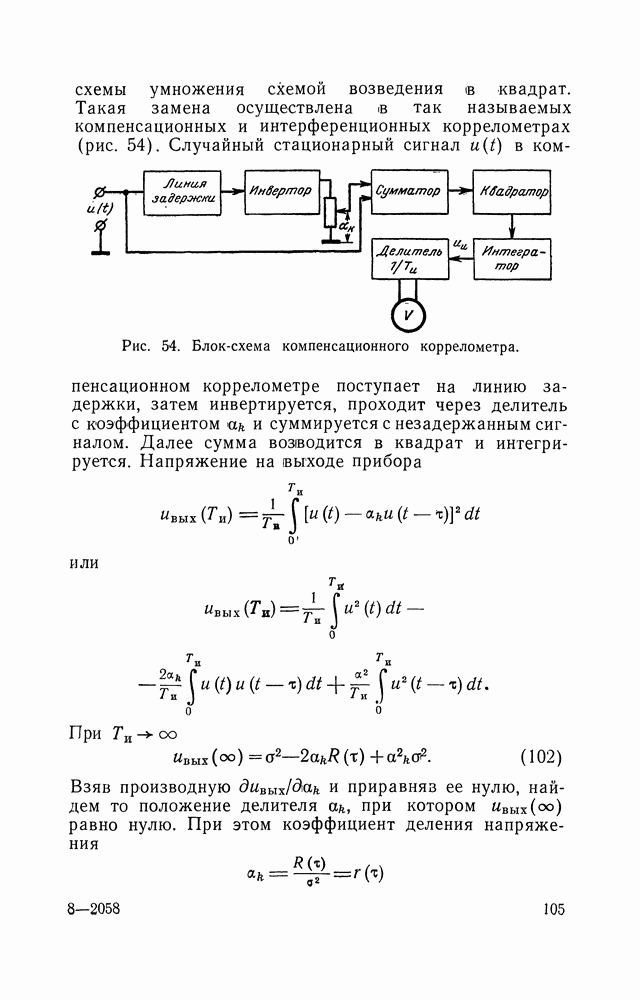
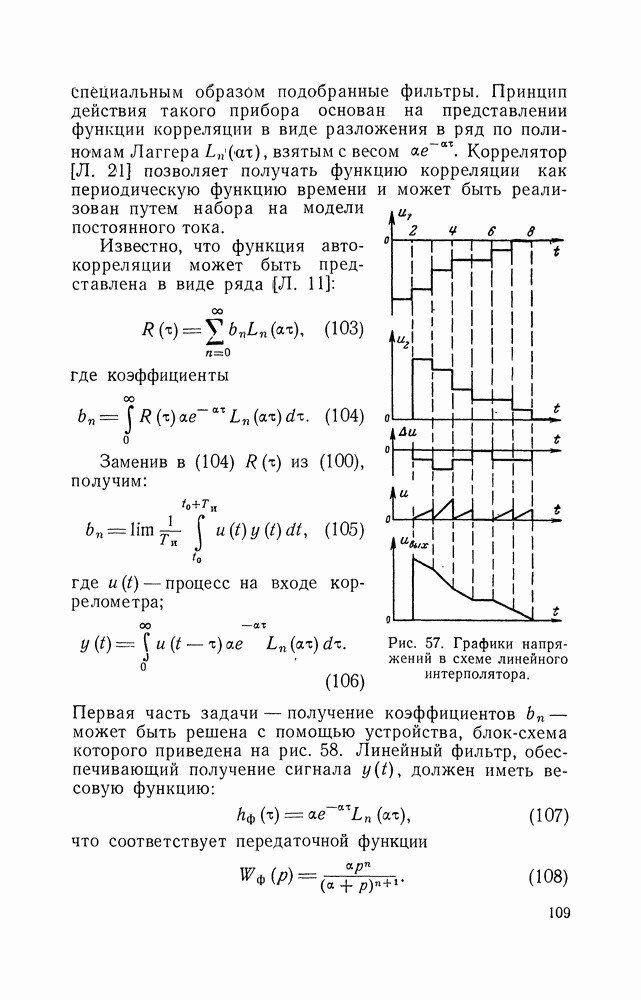
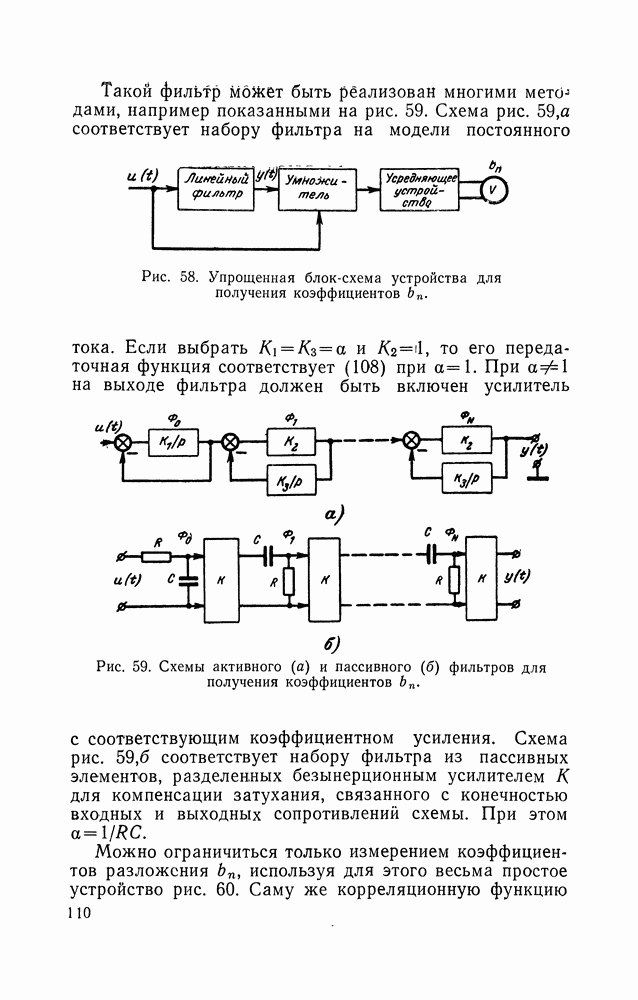
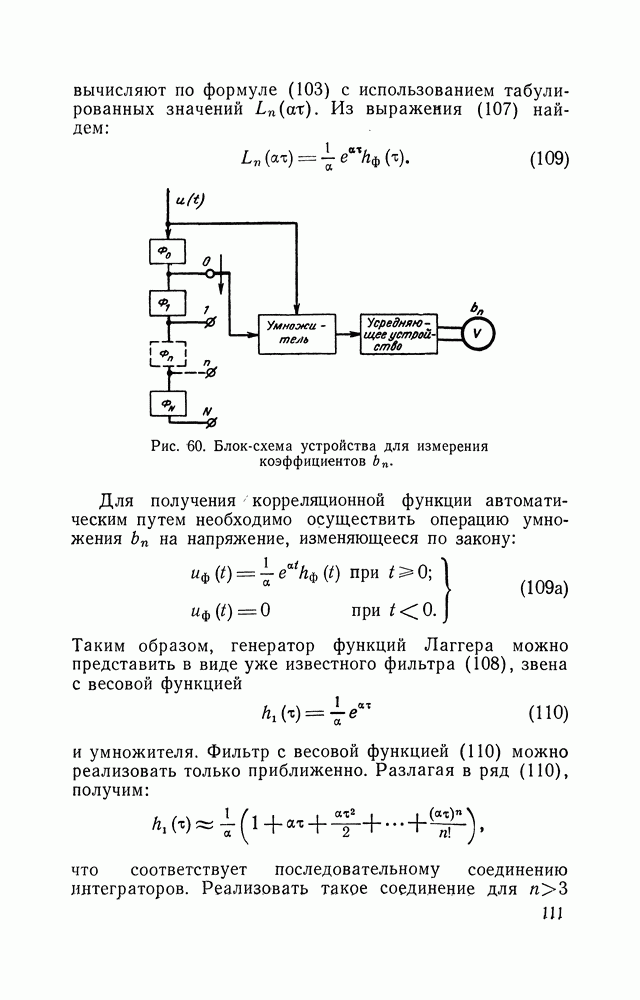
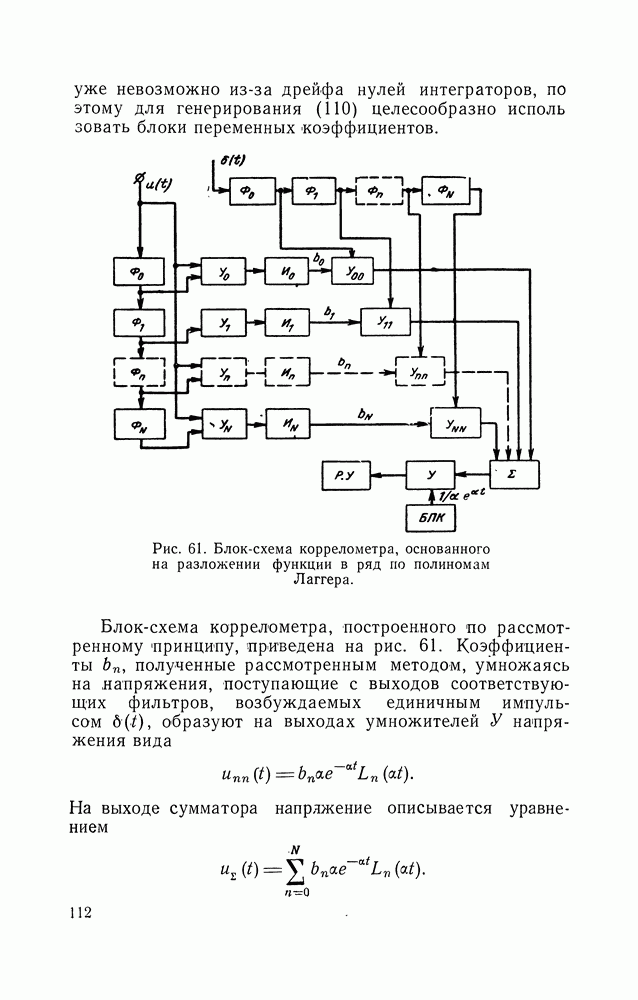
Случайные напряжения с равновероятным распределением амплитуд играют заметную роль при моделировании различных процессов. Равновероятные напряжения наиболее просто преобразуются в напряжения с любым другим заданным законом распределения путем пропускания их через нелинейные устройства. Методы непосредственного генерирования напряжений с заданными плотностями вероятностей, за исключением нормальных флуктуаций, разработаны слабо. В то же время методы генерации случайных чисел с заданными законами распределения разработаны хорошо, поэтому целесообразно получать напряжения с заданным законом распределения путем использования преобразования число — аналог.
Часто для получения чисел с заданным законом распределения используются цифровые машины, работающие по определенной программе. Однако наиболее универсальным, простым и экономичным является способ генерирования случайных чисел с помощью специальных генераторов. В основе получения чисел с любым заданным законом распределения лежат преобразования равновероятных двоичных чисел, для которых вероятность появления каждого целого числа (от  ) одинакова. Особенностью равновероятных чисел является
) одинакова. Особенностью равновероятных чисел является
равенство вероятностей появления  во всех
во всех  разрядах двоичного числа:
разрядах двоичного числа:

Это соотношение можно доказать. Пусть генерируются  -разрядные равновероятные числа. В любом из чисел в
-разрядные равновероятные числа. В любом из чисел в  разрядах будет зафиксирована единица, а в
разрядах будет зафиксирована единица, а в  нуль. Число
нуль. Число  случайная величина, принимающая значения
случайная величина, принимающая значения  Ровно
Ровно  единиц будет содержать
единиц будет содержать  чисел. Единиц во всем ансамбле равновероятных чисел от
чисел. Единиц во всем ансамбле равновероятных чисел от  до
до  будет:
будет:

где  число сочетаний из
число сочетаний из  по
по 
В каждом разряде единицы встретятся  раз. Вероятность появления единицы в
раз. Вероятность появления единицы в  разряде равна отношению числа тех комбинаций, у которых в
разряде равна отношению числа тех комбинаций, у которых в  разряде будет фиксироваться единица, к общему числу всех возможных комбинаций:
разряде будет фиксироваться единица, к общему числу всех возможных комбинаций:

Но в силу условия несовместимости состояний  и
и  откуда непосредственно следует (27).
откуда непосредственно следует (27).
Таким образом, задача генерации равновероятных чисел сводится к получению  одноразрядных двоичных чисел с равновероятным появлением 1 и 0. Однако это условие является необходимым, но недостаточным. Если между состоянием
одноразрядных двоичных чисел с равновероятным появлением 1 и 0. Однако это условие является необходимым, но недостаточным. Если между состоянием  разрядов будет существовать статистическая связь, то числа не получатся равновероятными. В самом деле, допустив, что состояния
разрядов будет существовать статистическая связь, то числа не получатся равновероятными. В самом деле, допустив, что состояния
всех  разрядов жестко связаны, получим, что генератор будет выдавать только два числа:
разрядов жестко связаны, получим, что генератор будет выдавать только два числа:  и
и  Необходимость условия независимости состояний всех
Необходимость условия независимости состояний всех  разрядов достаточно очевидна из простых физических соображений.
разрядов достаточно очевидна из простых физических соображений.

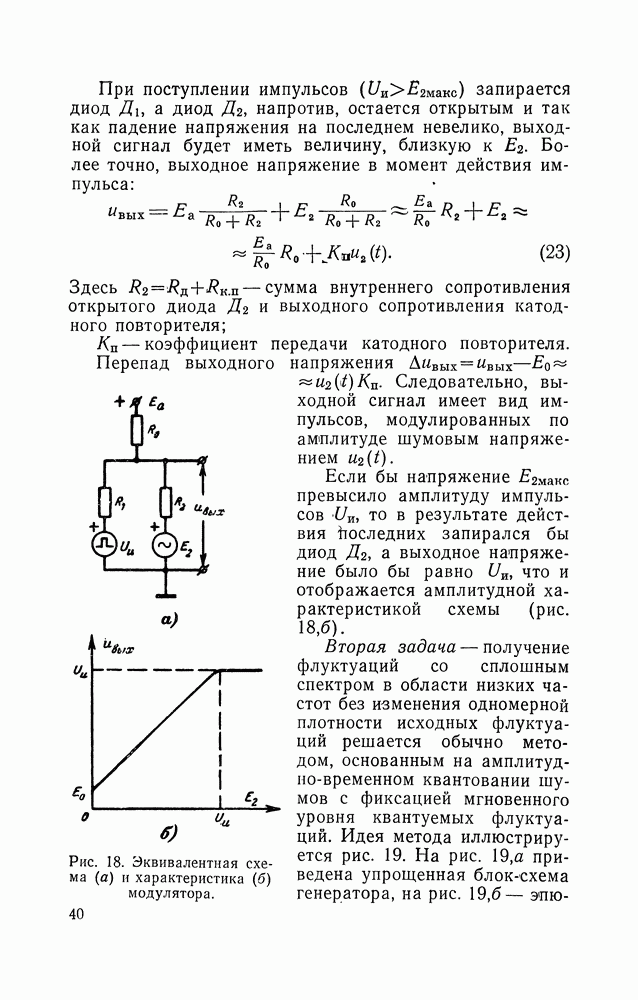
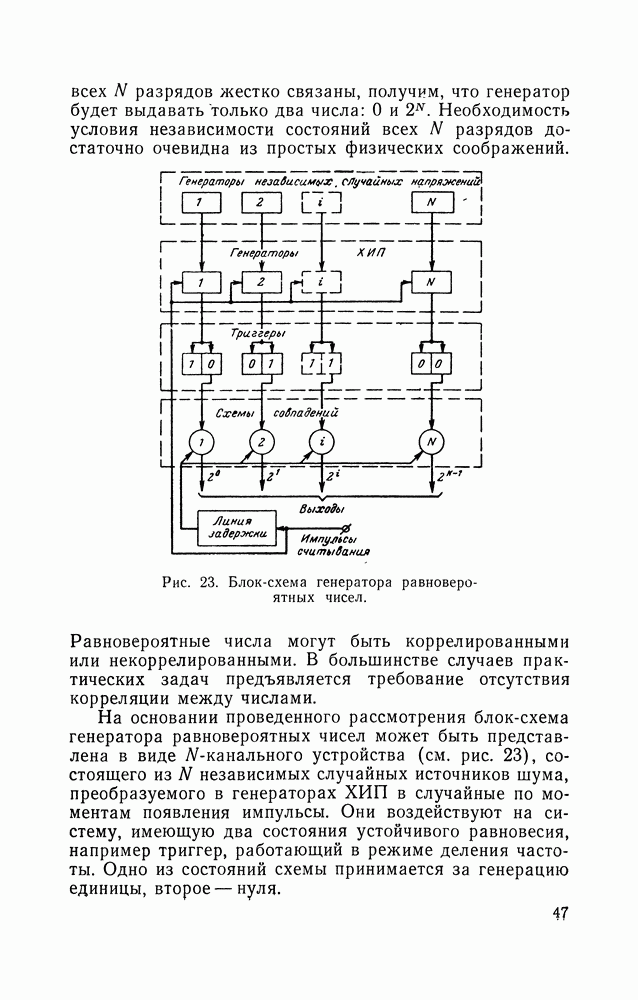
Рис. 23. Блок-схема генератора равновероятных чисел.
Равновероятные числа могут быть коррелированными или некоррелированными. В большинстве случаев практических задач предъявляется требование отсутствия корреляции между числами.
На основании проведенного рассмотрения блок-схема генератора равновероятных чисел может быть представлена в виде  -канального устройства (см. рис. 23), состоящего из
-канального устройства (см. рис. 23), состоящего из  независимых случайных источников шума, преобразуемого в генераторах ХИП в случайные по моментам появления импульсы. Они воздействуют на систему, имеющую два состояния устойчивого равновесия, например триггер, работающий в режиме деления частоты. Одно из состояний схемы принимается за генерацию единицы, второе — нуля.
независимых случайных источников шума, преобразуемого в генераторах ХИП в случайные по моментам появления импульсы. Они воздействуют на систему, имеющую два состояния устойчивого равновесия, например триггер, работающий в режиме деления частоты. Одно из состояний схемы принимается за генерацию единицы, второе — нуля.
Непосредственное использование флуктуаций для переключения состояний триггеров недопустимо, так как уровни срабатываний его плеч всегда различны и условие (27) не удовлетворяется. Поэтому и необходимо предварительно преобразовать выбросы флуктуаций в короткие импульсы такой амплитуды, при которой каждый импульс вызывал бы перевод триггера в новое устойчивое состояние равновесия. Перед считыванием числа с триггера за время, несколько превосходящее время переходного процесса в нем, цепи запусков триггеров разрываются. После считывания процесс возобновляется.
Условие (27) будет полностью удовлетворяться в рассматриваемой схеме, но условие независимости каждого  двоичного числа от
двоичного числа от  требует, чтобы с вероятностью, сколь угодно близкой к единице, каждый из
требует, чтобы с вероятностью, сколь угодно близкой к единице, каждый из  триггеров хотя бы один раз переменил устойчивое состояние равновесия в течение одного тактового периода. Рассмотрим, как это условие удовлетворяется при использовании импульсов, подчиняющихся закону Пуассона. Степень выполнения условия независимости чисел удобно характеризовать вероятностью события, состоящего в том, что все
триггеров хотя бы один раз переменил устойчивое состояние равновесия в течение одного тактового периода. Рассмотрим, как это условие удовлетворяется при использовании импульсов, подчиняющихся закону Пуассона. Степень выполнения условия независимости чисел удобно характеризовать вероятностью события, состоящего в том, что все  триггеров за один тактовый период сменят хотя бы один раз состояния равновесия. Найдем эту вероятность.
триггеров за один тактовый период сменят хотя бы один раз состояния равновесия. Найдем эту вероятность.
Вероятность события, состоящего в том, что  триггер не сменит состояния равновесия за время
триггер не сменит состояния равновесия за время  будет определяться формулой
будет определяться формулой

где  средняя частота хаотических импульсов.
средняя частота хаотических импульсов.
Состояния всех  триггеров не зависят друг от друга, поэтому вероятность события, состоящего в том, что хотя бы один из
триггеров не зависят друг от друга, поэтому вероятность события, состоящего в том, что хотя бы один из  триггеров за время
триггеров за время  не сменит состояния равновесия, подчиняется биноминальному закону и равна:
не сменит состояния равновесия, подчиняется биноминальному закону и равна:

В любом случае должно удовлетворяться условие  поэтому приближенно можно принять:
поэтому приближенно можно принять:

Подставляя (28) в (29), получим:

Задав требование на  легко найти условие, которому должна подчиняться минимальная частота следования импульсов:
легко найти условие, которому должна подчиняться минимальная частота следования импульсов:


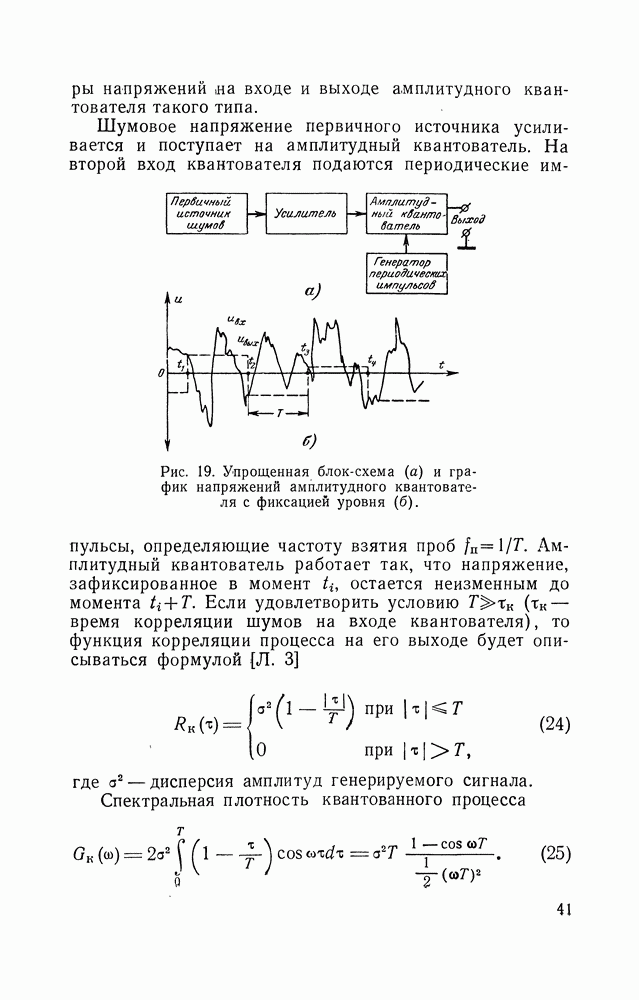
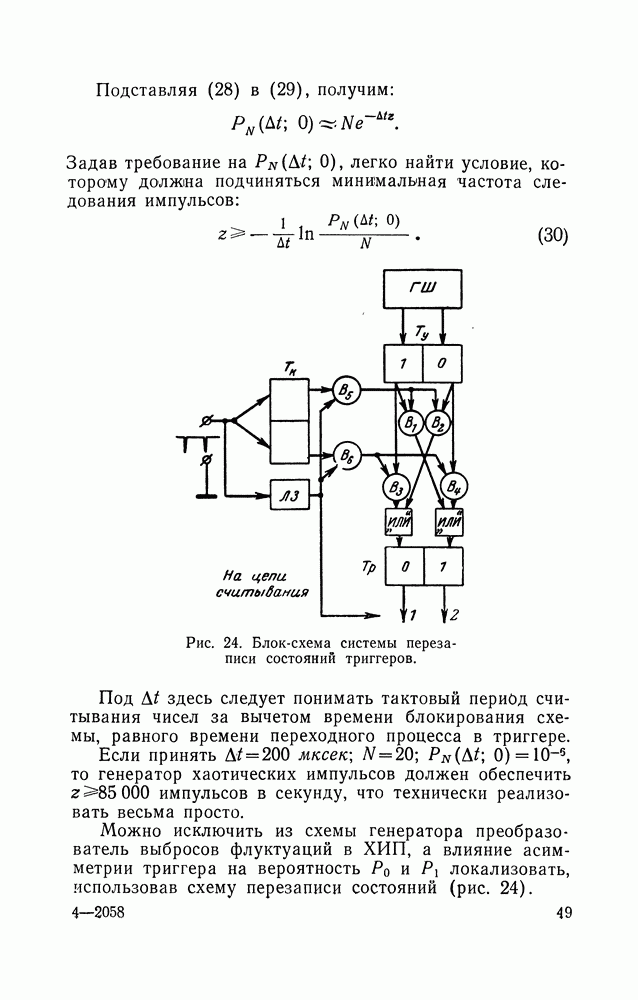
Рис. 24. Блок-схема системы перезаписи состояний триггеров.
Под  здесь следует понимать тактовый период считывания чисел за вычетом времени блокирования схемы, равного времени переходного процесса в триггере.
здесь следует понимать тактовый период считывания чисел за вычетом времени блокирования схемы, равного времени переходного процесса в триггере.
Если принять  то генератор хаотических импульсов должен обеспечить
то генератор хаотических импульсов должен обеспечить  импульсов в секунду, что технически реализовать весьма просто.
импульсов в секунду, что технически реализовать весьма просто.
Можно исключить из схемы генератора преобразователь выбросов флуктуаций в ХИП, а влияние асимметрии триггера на вероятность  локализовать, использовав схему перезаписи состояний (рис. 24).
локализовать, использовав схему перезаписи состояний (рис. 24).
Коммутирующее напряжение, представляющее собой периодические биполярные импульсы, со скважностью, равной двум, и частотой, равной частоте считывания, коммутируют вентили. Благодаря этому перезапись состояний с исходного триггера  на разрядный
на разрядный  в один тактовый период производится через вентили.
в один тактовый период производится через вентили.  а в следующий период — через вентили
а в следующий период — через вентили  Легко убедиться, что независимо от соотношения вероятностей состояний триггера
Легко убедиться, что независимо от соотношения вероятностей состояний триггера  состояния триггера
состояния триггера  будут равновероятными.
будут равновероятными.

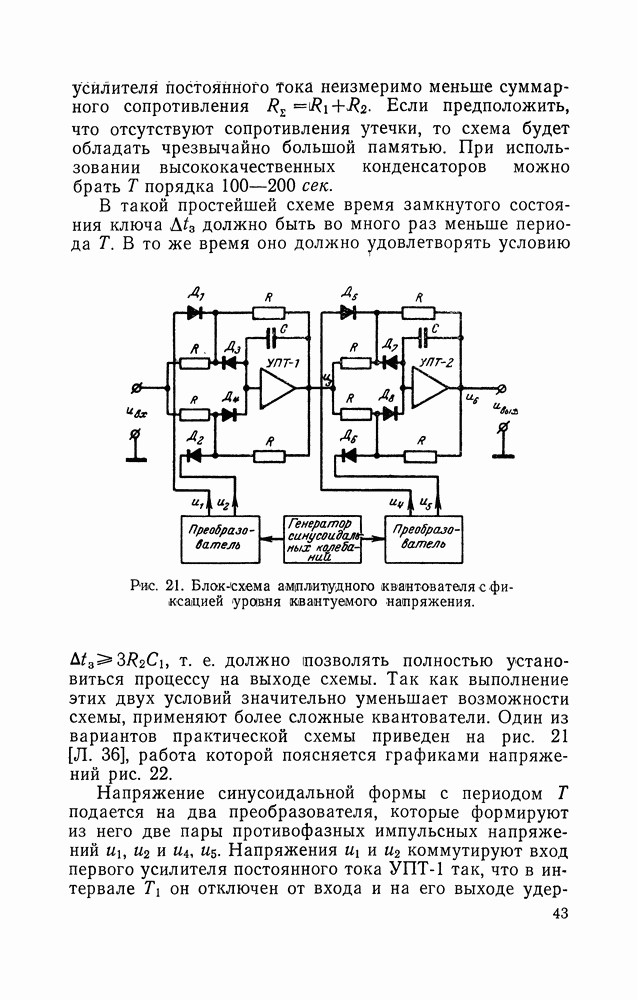
Рис. 25. Графики напряжений в генераторе равновероятных интервалов времени.
Линия задержки  необходима для того, чтобы успели установиться процессы в триггерах.
необходима для того, чтобы успели установиться процессы в триггерах.
Из сопоставления схем рис. 23 и 24 видно, что схема генератора с использованием преобразователей выбросов флуктуаций в ХИП значительно проще по числу используемых элементов и, что особенно важно, по регулировке. Не обязательно, чтобы случайные по моментам появления импульсы строго подчинялись закону Пуассона. Достаточно удовлетворить одно условие: тактовый период генерируемых чисел должен существенно (в 10— 15 раз) превосходить средний период следования случайных импульсов.
В основе второго способа получения равновероятных чисел лежит использование равновероятных случайных отрезков времени, получаемых сопоставлением моментов появления пуассоновских и периодических импульсов. Метод иллюстрируется временными диаграммами рис. 25. Здесь  периодическая последовательность импульсов (период
периодическая последовательность импульсов (период  пуассоновские импульсы.
пуассоновские импульсы.
Пусть моменты появления периодических импульсов служат началом отсчета временных интервалов 
Длительности этих интервалов являются случайными величинами, заключенными в интервале  по мере роста средней частоты случайных импульсов более вероятными становятся короткие интервалы. Однако если использовать только те интервалы
по мере роста средней частоты случайных импульсов более вероятными становятся короткие интервалы. Однако если использовать только те интервалы  которые образованы в результате попадания в период
которые образованы в результате попадания в период  одного и только одного случайного импульса, то эти интервалы будут подчиняться равновероятному закону. В приведенной на рис. 25 реализации сигналов указанлому условию удовлетворяет только интервал То, что интервалы, подобные интервалу подчиняются равновероятному закону, следует из самой природы явления: один и только один импульс в силу независимости моментов появления периодических и случайных последовательностей может появиться с равной вероятностью в любой точке интервала
одного и только одного случайного импульса, то эти интервалы будут подчиняться равновероятному закону. В приведенной на рис. 25 реализации сигналов указанлому условию удовлетворяет только интервал То, что интервалы, подобные интервалу подчиняются равновероятному закону, следует из самой природы явления: один и только один импульс в силу независимости моментов появления периодических и случайных последовательностей может появиться с равной вероятностью в любой точке интервала 
Выбирая из последовательности интервалов  интервалы, подобные и преобразуя их тем или иным методом в двоичные числа, можно решить поставленную задачу. Получаемые таким образом числа будут появляться на выходе генератора не в каждый период следования регулярной последовательности импульсов.
интервалы, подобные и преобразуя их тем или иным методом в двоичные числа, можно решить поставленную задачу. Получаемые таким образом числа будут появляться на выходе генератора не в каждый период следования регулярной последовательности импульсов.
Генератор будет работать как бы с перебоями. Чтобы число «холостых» периодов было минимальным, необходимо, чтобы вероятность появления одного и только одного импульса в интервале была максимальной. Указанная вероятность

имеет максимум при  При этом
При этом

т. е. только примерно одна треть циклов работы генератора будет рабочими. Апериодичность генерируемых чисел является большим недостатком метода.
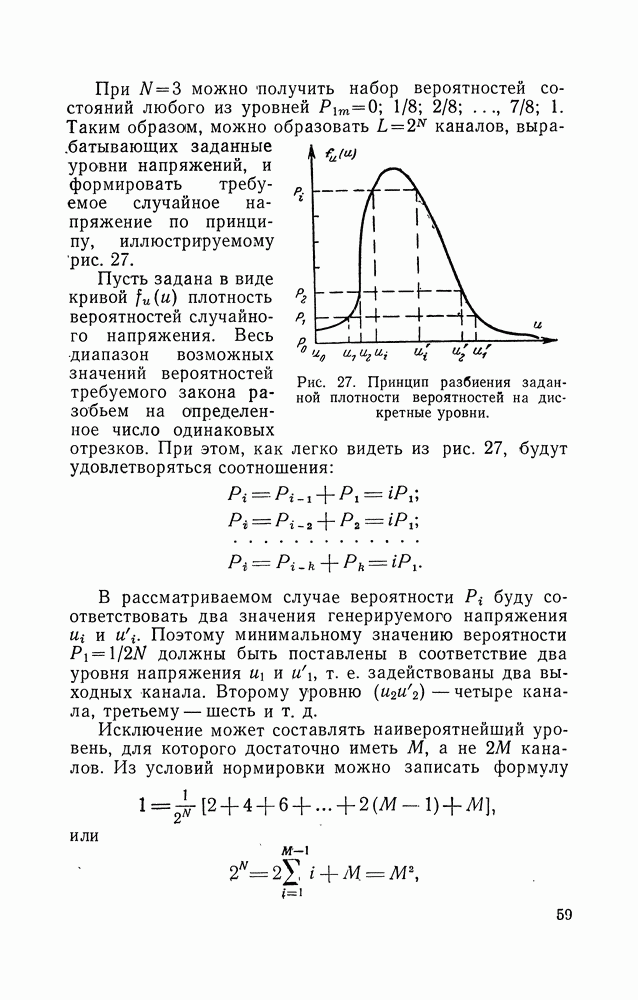
При конструировании генератора равновероятных чисел (как и чисел с любым другим законом распределения) необходимо решить вопрос об оптимальном числе разрядов (каналов) в генераторе. Напряжение, полученное путем преобразования число — аналог, будет иметь дискретное распределение с шагом по шкале амплитуд:

Шаг квантования получаемого напряжения Может выбираться из различных соображений, например из соответствия дисперсии требуемого закона дисперсии генерируемого напряжения.
Оценим методическую ошибку по дисперсии для генераторов равновероятных напряжений,  использующих в качестве исходного сигнала набор из
использующих в качестве исходного сигнала набор из  равновероятных чисел с дальнейшим их преобразованием типа число — аналог. Ошибку будем искать для закона распределения, определяемого выражением
равновероятных чисел с дальнейшим их преобразованием типа число — аналог. Ошибку будем искать для закона распределения, определяемого выражением

Математическое ожидание для такого закона при непрерывном изменении и в указанных пределах;  а дисперсия
а дисперсия 
Пусть дешифратор, преобразующий двоичное число в напряжение, построен так, что максимальное значение напряжения равно 1 в, а минимальное — нулю. В процессе работы единицы в разрядах будут фиксироваться с вероятностью  поэтому для значения математического ожидания напряжения можно записать:
поэтому для значения математического ожидания напряжения можно записать:

Таким образом, если "веса" разрядов в дешифраторе выбирать по закону

то генератор будет свободен от методической ошибки по математическому ожиданию. Дисперсия напряжения, обусловленного работой  разряда генератора, на выходе дешифратора будет равна:
разряда генератора, на выходе дешифратора будет равна:

где

В силу независимости напряжений, поступающих на выход дешифратора по всем  его разрядам, для дисперсии полного напряжения можно записать:
его разрядам, для дисперсии полного напряжения можно записать:

Учитывая, что

получим:

Естественно, что при 

Методическую погрешность, связанную с дискретностью уровней напряжения, можно оценить относительной ошибкой:

Значения  для различных значений
для различных значений  приведены в табл. 1. Отсюда следует, что по выбранному критерию дискретное напряжение от непрерывного отличается мало уже при
приведены в табл. 1. Отсюда следует, что по выбранному критерию дискретное напряжение от непрерывного отличается мало уже при 
Оценка методической погрешности для других законов распределения весьма сложна.
Таблица 1 (см. скан)
Однако для широкого класса законов распределения, а именно для законов, имеющих один максимум (нормального, релеевского, экспоненциального и т. д.), дисперсия оказывается меньше дисперсии равновероятного закона. Следовательно, можно предположить, что и методическая погрешность, вызванная дискретностью генерируемыхуровнбй, не превзойдет аналогичной погрешности, рассчитанной для равновероятного закона.
Если исходные числа независимы, то полученное напряжение будет иметь функцию корреляции и спектральную плотность, определяемые выражениями (25) и (26) соответственно. Если же числа коррелированы, то функция корреляции напряжения будет, естественно, определяться функцией корреляции чисел. Задавая вероятности событий, состоящих в смене знаков напряжения от такта к такту считывания чисел, можно получить напряжения с любой функцией корреляции. Вся сложность состоит в задании вероятностей переходов триггеров из одного устойчивого состояния равновесия в другое.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА ПЕРВАЯ. ГЕНЕРИРОВАНИЕ ИМПУЛЬСНЫХ И НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ СИГНАЛОВ СО СПЛОШНЫМ СПЕКТРОМ В ОБЛАСТИ НИЗКИХ ЧАСТОТ
- 1. КРАТКИЕ СВЕДЕНИЯ О ПЕРВИЧНЫХ ИСТОЧНИКАХ СЛУЧАЙНЫХ НАПРЯЖЕНИЙ
- 2. ПОЛУЧЕНИЕ НИЗКОЧАСТОТНЫХ ФЛУКТУАЦИИ ПУТЕМ СИНХРОННОГО ДЕТЕКТИРОВАНИЯ УЗКОПОЛОСНЫХ ШУМОВ
- 3. ГЕНЕРИРОВАНИЕ КВАЗИСЛУЧАЙНЫХ ИНФРАНИЗКОЧАСТОТНЫХ СИГНАЛОВ
- 4. ГЕНЕРИРОВАНИЕ СЛУЧАЙНЫХ ПО МОМЕНТАМ ПОЯВЛЕНИЯ (ПУАССОНОВСКИХ) ИМПУЛЬСОВ
- 5. ГЕНЕРИРОВАНИЕ СЛУЧАЙНЫХ ПО ДЛИТЕЛЬНОСТИ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ
- 6. ГЕНЕРИРОВАНИЕ ПЕРИОДИЧЕСКИХ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ СО СЛУЧАЙНОЙ АМПЛИТУДОЙ
- ГЛАВА ВТОРАЯ. ГЕНЕРИРОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ С ЗАДАННЫМИ СТАТИСТИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ
- 7. СПОСОБЫ ПОЛУЧЕНИЯ СЛУЧАЙНЫХ НАПРЯЖЕНИЙ С РАВНОВЕРОЯТНЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ АМПЛИТУД
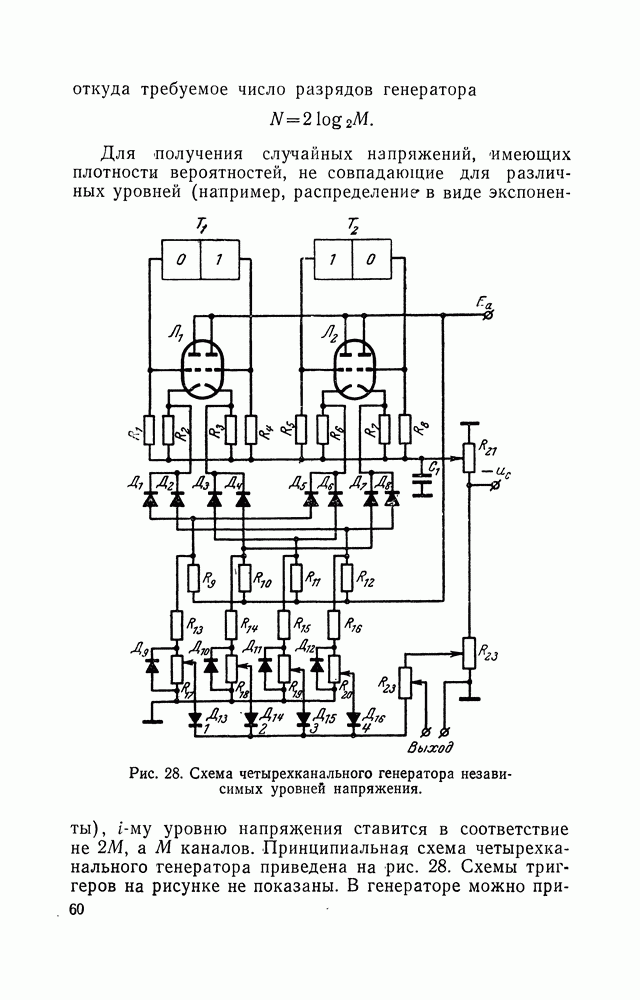
- 8. ИСПОЛЬЗОВАНИЕ НЕЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ ПОЛУЧЕНИЯ НАПРЯЖЕНИЙ С ЗАДАННЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ МГНОВЕННЫХ ЗНАЧЕНИЙ
- 9. ПОЛУЧЕНИЕ НАПРЯЖЕНИЯ С ЗАДАННОЙ ОДНОМЕРНОЙ ПЛОТНОСТЬЮ ВЕРОЯТНОСТЕЙ МЕТОДОМ ЗАДАНИЯ ВЕРОЯТНОСТЕЙ СОСТЯНИЙ КАНАЛОВ
- 10. ПОЛУЧЕНИЕ ИНФРАНИЗКОЧАСТОТНЫХ ФЛУКТУАЦИИ С ЗАДАННОЙ КОРРЕЛЯЦИОННОЙ ФУНКЦИЕЙ
- 11. ИМИТАЦИЯ СИГНАЛОВ ДОППЛЕРОВСКИХ НАВИГАЦИОННЫХ СИСТЕМ
- ГЛАВА ТРЕТЬЯ. СТАБИЛИЗАЦИЯ И ИЗМЕРЕНИЕ ОСНОВНЫХ ПАРАМЕТРОВ СЛУЧАЙНЫХ СИГНАЛОВ
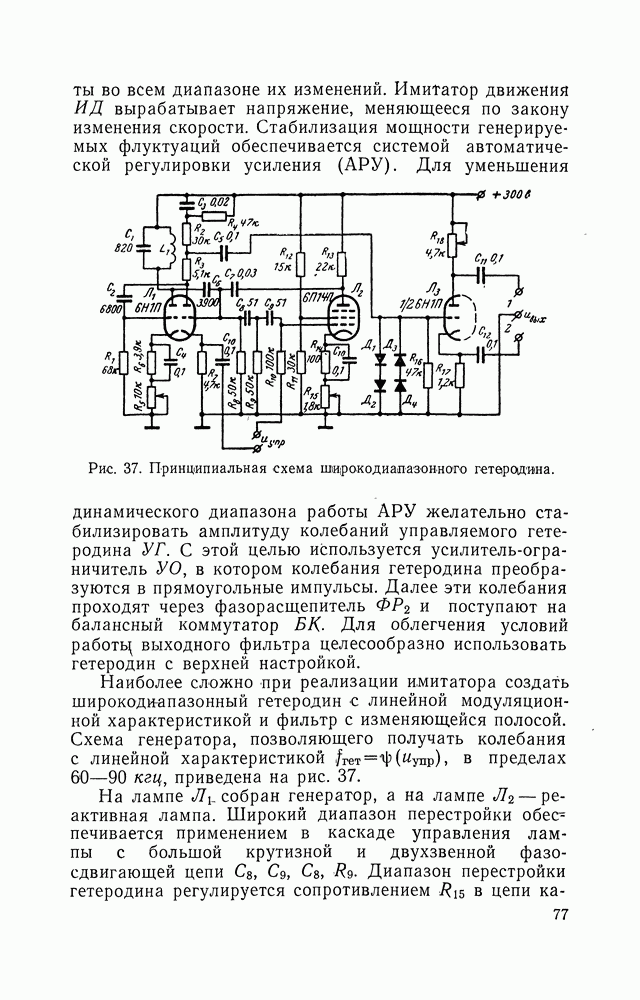
- 13. СПОСОБЫ СТАБИЛИЗАЦИИ МОЩНОСТИ ФЛУКТУАЦИЙ
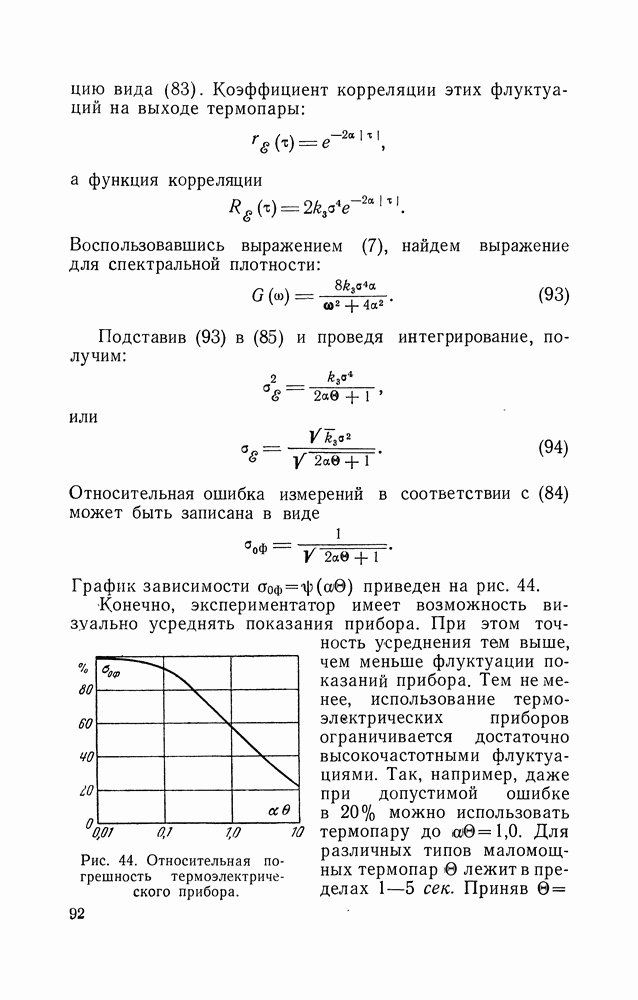
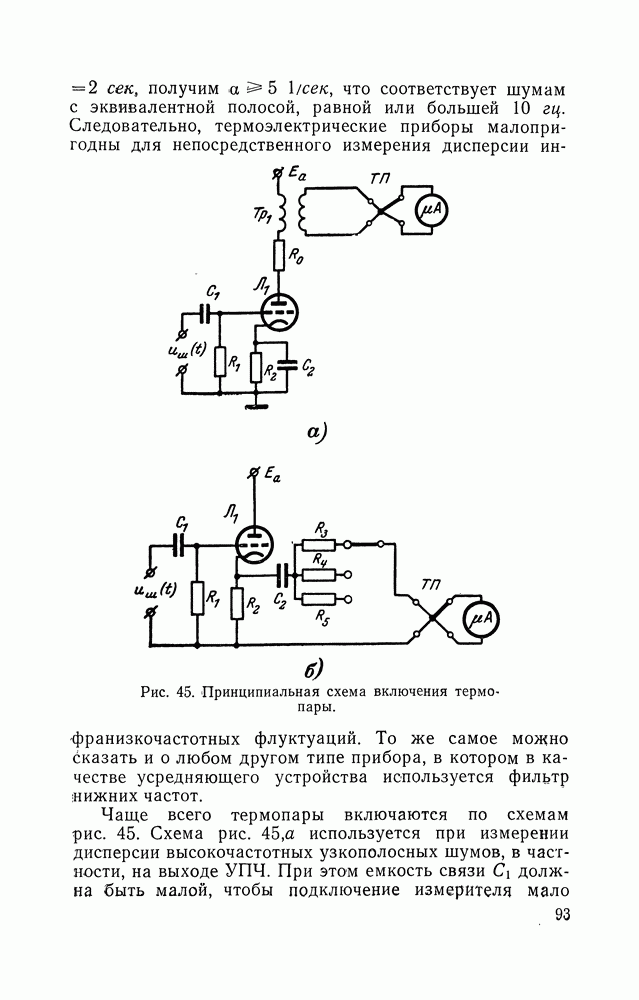
- 14. ИЗМЕРЕНИЕ СРЕДНЕГО ЗНАЧЕНИЯ И ДИСПЕРСИИ СЛУЧАЙНЫХ НАПРЯЖЕНИЙ
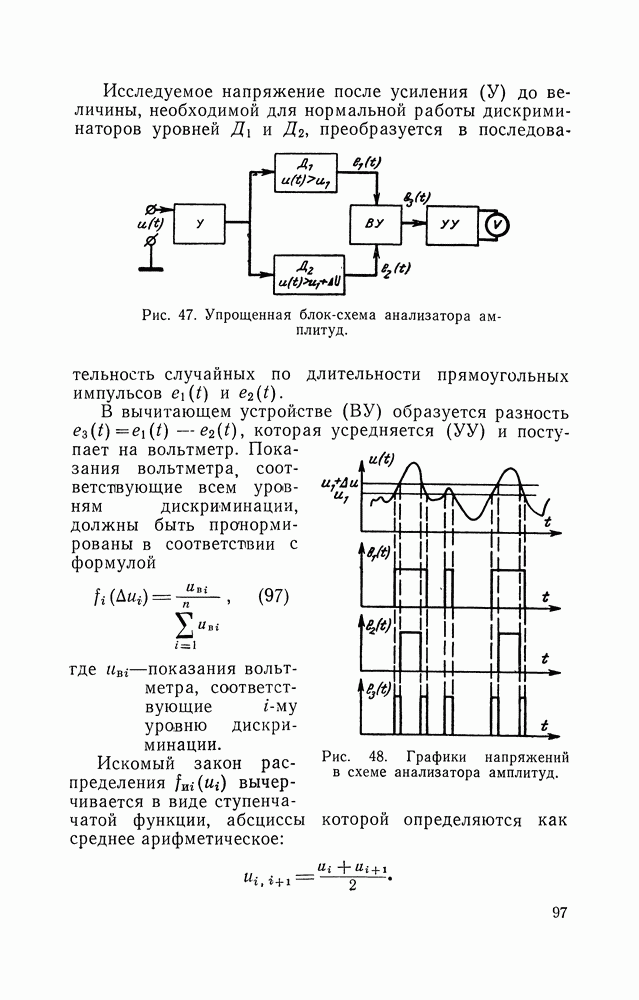
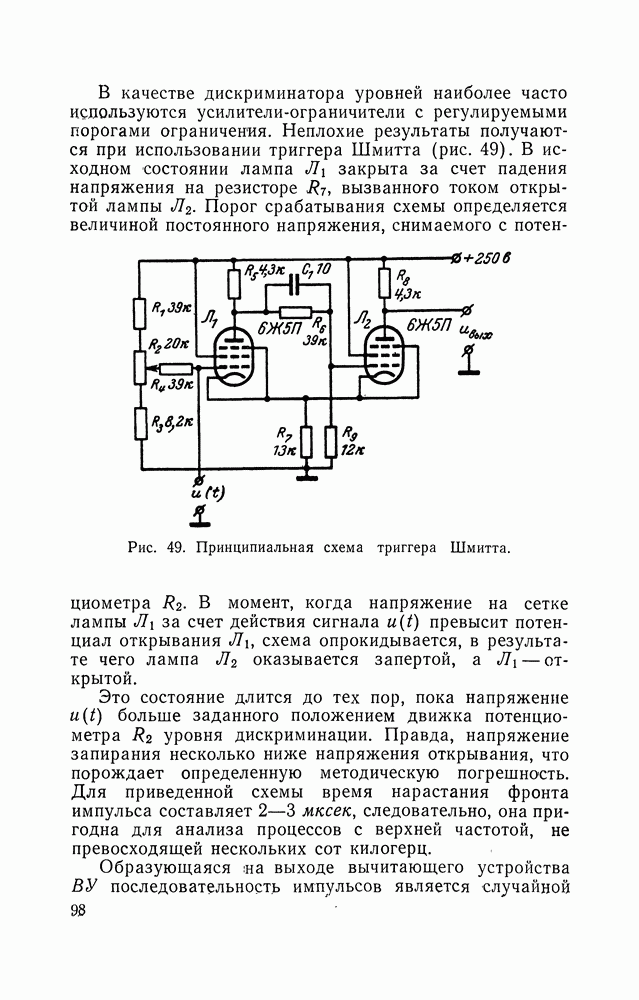
- 15. ОПРЕДЕЛЕНИЕ ОДНОМЕРНЫХ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ
- 16 КОРРЕЛОМЕТРЫ И СПЕКТРОАНАЛИЗАТОРЫ