| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. Метод ломаных.
Это простейший численный метод. В практике вычислений он употребляется очень редко из-за невысокой точности. Но на его примере удобно пояснить способы построения и исследования численных методов.
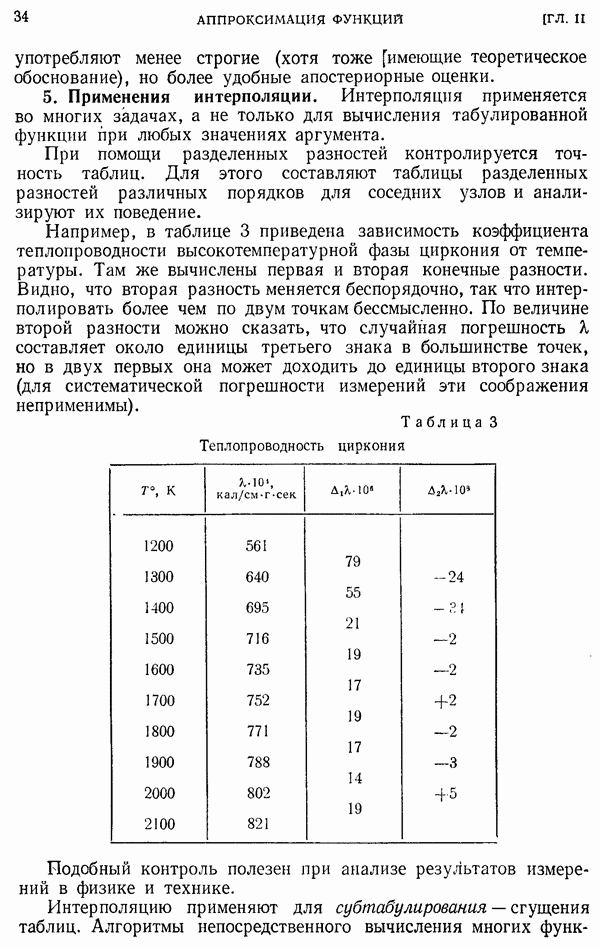
Рассмотрим задачу Коши (7) и выберем на отрезке  некоторую сетку
некоторую сетку  значений аргумента так, чтобы выполнялись соотношения
значений аргумента так, чтобы выполнялись соотношения  (сетка может быть неравномерной). Разлагая решение и
(сетка может быть неравномерной). Разлагая решение и  по формуле Тейлора на интервале сетки
по формуле Тейлора на интервале сетки  и обозначая и
и обозначая и  получим
получим

Стоящие в правой части производные можно найти, дифференцируя уравнение (7) требуемое число раз:

и т. д. В принципе, если  имеет
имеет  непрерывные производные по совокупности аргументов, то в разложении (13) можно удержать члены вплоть до
непрерывные производные по совокупности аргументов, то в разложении (13) можно удержать члены вплоть до 
Однако использовать для расчетов формулу (13) с большим числом членов невыгодно. Во-первых, даже при сравнительно простой правой части выражения для производных могут оказаться громоздкими. Во-вторых, если правая часть известна лишь приближенно, то находить ее производные нежелательно. В простейшем случае, подставляя (14) в (13) и ограничиваясь только первым членом разложения, получим схему ломаных 

Поскольку при такой замене можно найти только приближенные значения искомой функции в узлах, то будем обозначать эти значения через  в отличие от точных значений
в отличие от точных значений  Для численного расчета по схеме ломаных достаточно задать начальное значение
Для численного расчета по схеме ломаных достаточно задать начальное значение  . Затем по формуле (15) последовательно вычисляем величины
. Затем по формуле (15) последовательно вычисляем величины 
Геометрическая интерпретация этой схемы дана на рис. 41, где изображено поле интегральных кривых. Использование только первого члена формулы Тейлора означает движение не по интегральной кривой, а по касательной к ней.
На каждом шаге мы заново находим касательную; следовательно, траектория движежения будет ломаной линией.
Исследуем сходимость метода ломаных, предполагая правую часть  непрерывной и ограниченной вместе со своими первыми производными:
непрерывной и ограниченной вместе со своими первыми производными:  (отсюда следует, что
(отсюда следует, что  ).
).
Рассмотрим погрешность приближенного решения  Вычитая (15) из (13), получим соотношение, связывающее погрешности в соседних узлах сетки:
Вычитая (15) из (13), получим соотношение, связывающее погрешности в соседних узлах сетки:

(члены более высокого порядка малости здесь опущены). Последовательно применяя рекуррентное соотношение (16), выразим погрешность на произвольном шаге через погрешность начальных данных

Отсюда нетрудно дать асимптотическую оценку погрешности. Заметим, что при малых шагах сетки

причем в качестве верхнего предела интеграла молено взять  , ибо ошибка при этом остается в пределах общей точности преобразований. Аналогично преобразуя второй член (17), получим
, ибо ошибка при этом остается в пределах общей точности преобразований. Аналогично преобразуя второй член (17), получим

Здесь  — непрерывная функция, дающая в каждом узле
— непрерывная функция, дающая в каждом узле  величину шага
величину шага  в качестве такой, функции можно выбрать линейный сплайн.
в качестве такой, функции можно выбрать линейный сплайн.

Рис. 41.
Рассмотрим структуру погрешности (18). Первое слагаемое справа связано с погрешностью начального значения  которая умножается на ограниченную (благодаря ограниченности производных) величину. Начальное значение можно задать точно и считать, что
которая умножается на ограниченную (благодаря ограниченности производных) величину. Начальное значение можно задать точно и считать, что  . Остановимся на втором слагаемом. Оно обусловлено тем членом формулы Тейлора (13), который был отброшен при выводе схемы ломаных (15). Оценим это слагаемое сверху; заменяя все функции под интегралами их модулями и вынося
. Остановимся на втором слагаемом. Оно обусловлено тем членом формулы Тейлора (13), который был отброшен при выводе схемы ломаных (15). Оценим это слагаемое сверху; заменяя все функции под интегралами их модулями и вынося  за знак интеграла, получим
за знак интеграла, получим

где

Таким образом, при  приближенное решение сходится к точному равномерно (на ограниченном отрезке
приближенное решение сходится к точному равномерно (на ограниченном отрезке  с первым порядком точности.
с первым порядком точности.
Замечание 1. Оценка погрешности (19) является мажорантной. Для функций со знакопеременными производными эта оценка может быть сильно завышена по сравнению с асимптотической оценкой (18).
Замечание 2. Экспоненциальный член в оценке (18) характеризует расхождение интегральных кривых (см. рис. 41); если он очень велик, то исходная задача Коши плохо обусловлена.
Пример. Проинтегрируем по схеме Эйлера задачу Коши для уравнения (3):

В таблице 18 даны численные решения  полученные на сетках с шагами
полученные на сетках с шагами  столбик
столбик  будет пояснен в п. 10. Приведено также точное решение
будет пояснен в п. 10. Приведено также точное решение  вычисленное методом Пикара (см. пример в п. 3). Видно, что схема Эйлера для получения удовлетворительной точности требует гораздо более малого шага, чем использованный здесь.
вычисленное методом Пикара (см. пример в п. 3). Видно, что схема Эйлера для получения удовлетворительной точности требует гораздо более малого шага, чем использованный здесь.
Таблица 18

Ограничимся только написанными членами, так как уже они обеспечивают четвертый порядок точности. Для вычисления решения в следующей точке запишем дифференциальное уравнение в интегральной форме

и подставим в него интерполяционный многочлен (28). Получим формулу Адамса для переменного шага

Эта формула имеет четвертый порядок точности. Если отбросить последнее слагаемое, получим формулу третьего порядка точности. Аналогично получаются формулы низших порядков. Формула первого порядка совпадает со схемой ломаных.
Чаще пользуются менее громоздким вариантом формулы (30), рассчитанным на постоянный шаг интегрирования. Вместо разделенных разностей вводят конечные разности  приблизительно равные
приблизительно равные  производной в точке
производной в точке  и получают
и получают

Остаточный член этой формулы равен 
Метод без изменений переносится на системы уравнений первого порядка типа (25).
Чтобы начать расчет методом Адамса, недостаточно знать  . Для начала расчета по формуле (30) надо знать величину решения в четырех точках
. Для начала расчета по формуле (30) надо знать величину решения в четырех точках  (а при формуле
(а при формуле  порядка точности в
порядка точности в  точках). Поэтому надо вычислить недостающие значения
точках). Поэтому надо вычислить недостающие значения  каким-либо другим методом — методом Рунге — Кутта, или разложением по формуле Тейлора (13)-(14) с достаточно большим числом членов. При работе на ЭВМ это вдвое увеличивает объем программы. Кроме того, формулы (30) громоздки, а несложные формулы (31) рассчитаны только на постоянный шаг и требуют нестандартных действий при смене шага: надо перейти к формулам (30), сделать по ним четыре шага и снова вернуться (21), равномерно сходится к точному решению с погрешностью
каким-либо другим методом — методом Рунге — Кутта, или разложением по формуле Тейлора (13)-(14) с достаточно большим числом членов. При работе на ЭВМ это вдвое увеличивает объем программы. Кроме того, формулы (30) громоздки, а несложные формулы (31) рассчитаны только на постоянный шаг и требуют нестандартных действий при смене шага: надо перейти к формулам (30), сделать по ним четыре шага и снова вернуться (21), равномерно сходится к точному решению с погрешностью  т. е. двучленная схема Рунге—Кутта имеет второй порядок точности.
т. е. двучленная схема Рунге—Кутта имеет второй порядок точности.
Формула (21) имеет неплохую точность и нередко используется в численных расчетах.

Рис. 42.

Рис. 43.
При этом обычно полагают либо  либо
либо  В первом случае получается схема особенно простого вида
В первом случае получается схема особенно простого вида

Ее смысл поясняется рис. 42. Сначала делаем половинный шаг по схеме ломаных, находя  Затем в найденной точке определяем наклон интегральной кривой
Затем в найденной точке определяем наклон интегральной кривой  Поэтому наклону определяем приращение функции на целом шаге
Поэтому наклону определяем приращение функции на целом шаге 
Геометрическая интерпретация второго случая

изображена на рис. 43. Здесь мы сначала грубо вычисляем по схеме ломаных значение функции  и наклбн интегральной кривой
и наклбн интегральной кривой  в новой точке. Затем находим средний наклон на шаге
в новой точке. Затем находим средний наклон на шаге  и по нему уточняем значение
и по нему уточняем значение  Схемы подобного типа нередко называют «предиктор — корректор».
Схемы подобного типа нередко называют «предиктор — корректор».
Таблица 19

В таблице 19 приведен численный расчет по схеме (22) того же примера, который рассмотрен в таблице 18 (п.5). Из таблицы видно, что схема второго порядка точности дает существенно лучшие результаты, чем схема ломаных; уже расчет на грубой сетке с  можно считать удовлетворительным.
можно считать удовлетворительным.
Методом Рунге—Кутта можно строить схемы различного порядка точности. Например, схема ломаных (15) есть схема Рунге—Кутта первого порядка точности. Наиболее употребительны схемы четвертого порядка точности, образующие семейство четырехчленных схем. Приведем без вывода ту из них, которая записана в большинстве стандартных программ ЭВМ:

(при величинах  и шаге h следует также ставить индекс сетки
и шаге h следует также ставить индекс сетки  , но для простоты записи мы его опускаем).
, но для простоты записи мы его опускаем).
Формулы более высокого порядка точности практически не употребляются. Пятичленные формулы имеют всего лишь четвертый порядок точности; шестичленные имеют шестой порядок, но слишком громоздки. Кроме того, высокий порядок реализуется лишь при наличии у правой части непрерывных производных соответствующего порядка.
Схемы Рунге—Кутта имеют ряд важных достоинств. 1) Все они (кроме схемы ломаных) имеют хорошую точность. 2) Они являются явными, т. е. значение  вычисляется по ранее найденным значениям за определенное число действий по определенным формулам. 3) Все схемы допускают расчет переменным шагом; значит, нетрудно уменьшить шаг там, где функция быстро меняется, и увеличить его в обратном случае. 4) Для начала расчета достаточно выбрать сетку
вычисляется по ранее найденным значениям за определенное число действий по определенным формулам. 3) Все схемы допускают расчет переменным шагом; значит, нетрудно уменьшить шаг там, где функция быстро меняется, и увеличить его в обратном случае. 4) Для начала расчета достаточно выбрать сетку  и задать значение
и задать значение  далее вычисления идут по одним и тем же формулам. Все эти свойства схем очень ценны при расчетах на ЭВМ.
далее вычисления идут по одним и тем же формулам. Все эти свойства схем очень ценны при расчетах на ЭВМ.
На случай систем уравнений схемы Рунге—Кутта легко переносятся, как во всех других методах, при помощи формальной замены у, f(х, у) на у, f(x, у). Нетрудно произвести покомпонентную запись этих схем. Например, для системы двух уравнений

обозначая через у, z приближенные значения функций  запишем аналогичную (24) четырехчленную схему следующим образом:
запишем аналогичную (24) четырехчленную схему следующим образом:

где

Напомним, что именно эта схема четвертого порядка точности (разумеется, записанная для системы произвольного числа уравнений) лежит в основе большинства стандартных программ численного решения задачи Коши на ЭВМ.
Замечание. Погрешности различных схем Рунге—Кутта связаны с максимумами модулей соответствующих производных  громоздкими выражениями типа (18)-(19). Наглядное представление о величине этих погрешностей можно получить в одном частном случае, когда
громоздкими выражениями типа (18)-(19). Наглядное представление о величине этих погрешностей можно получить в одном частном случае, когда  При этом дифференциальное уравнение сводится к квадратуре, а все схемы численного интегрирования переходят в квадратурные формулы. Легко убедиться, что схема (22) переходит в формулу средних (4.16), схема
При этом дифференциальное уравнение сводится к квадратуре, а все схемы численного интегрирования переходят в квадратурные формулы. Легко убедиться, что схема (22) переходит в формулу средних (4.16), схема  формулу трапеций (4.7) с шагом h, а схема (24) — в формулу Симпсона (4.11) с шагом
формулу трапеций (4.7) с шагом h, а схема (24) — в формулу Симпсона (4.11) с шагом  Напомним, что мажоранты остаточных членов этих формул на равномерной сетке с указанными шагами соответственно равны
Напомним, что мажоранты остаточных членов этих формул на равномерной сетке с указанными шагами соответственно равны

Численные коэффициенты в остаточных членах (27) малы; это является одной из причин хорошей точности схем Рунге—Кутта.
Какими из формул Рунге—Кутта целесообразно пользоваться в каждом конкретном случае и как выбирать шаг сетки?
Если правая часть дифференциального уравнения непрерывна и ограничена вместе со своими четвертыми производными (и эти производные не слишком велики), то хорошие результаты дает схема четвертого порядка (24) благодаря очень малому коэффициенту в остаточном члене и быстрому возрастанию точности при уменьшении шага. Если же правая часть не имеет указанных производных, то предельный порядок точности этой схемы не может реализоваться. Тогда не худшие (хотя, по-видимому, и не лучшие) результаты дают схемы меньшего порядка точности, равного порядку имеющихся производных; например, для двукратно непрерывно дифференцируемых правых частей — несложные схемы (21)-(23).
Шаг сетки следует выбирать настолько малым, чтобы обеспечить требуемую точность расчета; других ограничивающих шаг условий в методе Рунге—Кутта нет. Но выражения остаточных членов типа. (18)-(19) слишком громоздки; поэтому априорными оценками точности для выбора шага в практических расчетах не пользуются. Удобнее делать расчеты со сгущением сетки, давая апостериорную оценку точности (подробнее это будет рассмотрено в п. 11).
Встречаются важные задачи, в которых функции являются достаточно гладкими, но настолько быстро меняющимися, что схемы Рунге—Кутта как низкого, так и высокого порядка точности требуют неприемлемо малого шага для получения удовлетворительного результата. Такие задачи требуют использования (а нередко — разработки) специальных методов, ориентированных на данный узкий класс, задач.
| << Предыдущий параграф | Следующий параграф >> |
- ГЛАВА I. ЧТО ТАКОЕ ЧИСЛЕННЫЕ МЕТОДЫ?
- § 2. Приближенный анализ
- 2. Структура погрешности.
- 3. Корректность.
- ГЛАВА II. АППРОКСИМАЦИЯ ФУНКЦИЙ
- § 1. Интерполирование
- 2. Линейная интерполяция.
- 3. Интерполяционный многочлен Ньютона.
- 4. Погрешность многочлена Ньютона.
- 5. Применения интерполяции.
- 6. Интерполяционный многочлен Эрмита.
- 7. Сходимость интерполяции.
- 8. Нелинейная интерполяция.
- 9. Интерполяция сплайнами.
- 10. Монотонная интерполяция.
- 11. Многомерная интерполяция.
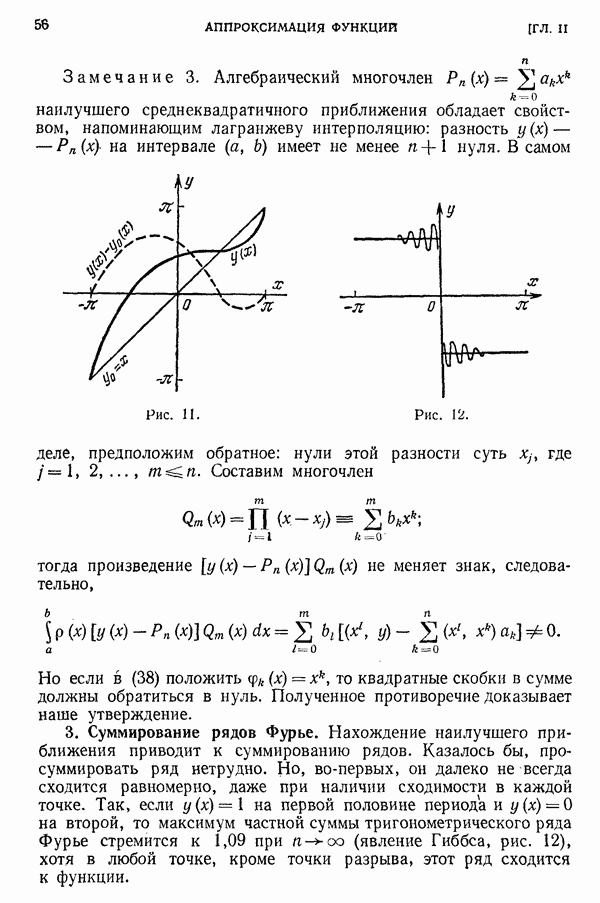
- § 2. Среднеквадратичное приближение
- 2. Линейная аппроксимация.
- 3. Суммирование рядов Фурье.
- 4. Метод наименьших квадратов.
- 5. Нелинейная аппроксимация.
- § 3. Равномерное приближение
- 2. Нахождение равномерного приближения.
- ЗАДАЧИ
- ГЛАВА III. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
- 1. Полиномиальные формулы.
- 2. Простейшие формулы.
- 3. Метод Рунге — Ромберга.
- 4. Квазиравномерные сетки.
- 5. Быстропеременные функции.
- 6. Регуляризация дифференцирования.
- ЗАДАЧИ
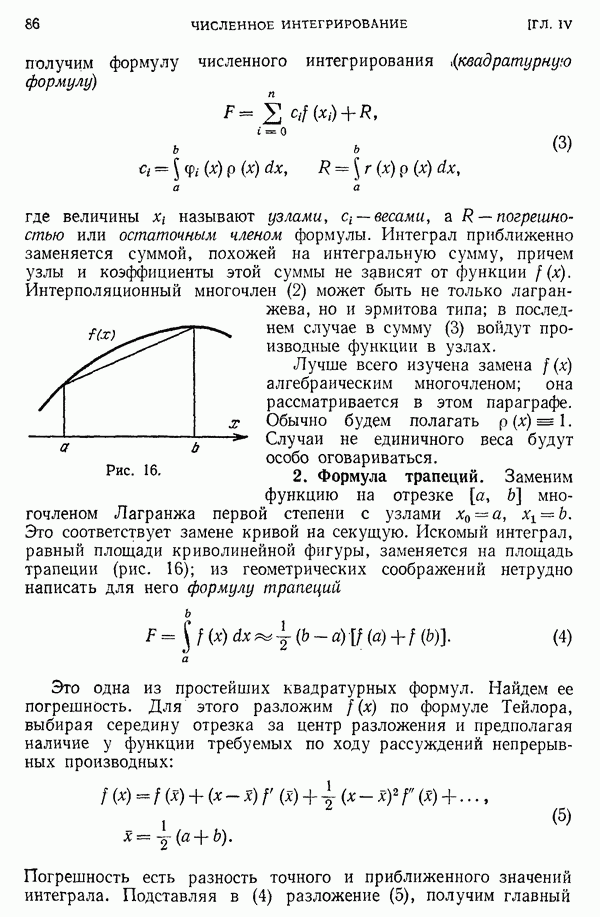
- ГЛАВА IV. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
- § 1. Полиномиальная аппроксимация
- 2. Формула трапеций.
- 3. Формула Симпсона.
- 4. Формула средних.
- 5. Формула Эйлера.
- 6. Процесс Эйткена.
- 7. Формулы Гаусса — Кристоффеля.
- 8. Формулы Маркова.
- 9. Сходимость квадратурных формул.
- § 2. Нестандартные формулы
- 2 Нелинейные формулы.
- 3. Метод Филона.
- 4. Переменный предел интегрирования.
- 5. Несобственные интегралы.
- § 3. Кратные интегралы
- 2. Последовательное интегрирование.
- § 4. Метод статистических испытаний
- 2. Разыгрывание случайной величины.
- 3. Вычисление интеграла.
- 4. Уменьшение дисперсии.
- 5. Кратные интегралы.
- ЗАДАЧИ
- ГЛАВА V. СИСТЕМЫ УРАВНЕНИЙ
- § 1. Линейные системы
- 2. Метод исключения Гаусса.
- 3. Определитель и обратная матрица
- 4. О других прямых методах.
- 5. Прогонка.
- 6. Метод квадратного корня.
- 7. Плохо обусловленные системы.
- § 2. Уравнение с одним неизвестным
- 2. Дихотомия (деление пополам).
- 3. Удаление корней.
- 4. Метод простых итераций.
- 5. Метод Ньютона.
- 6. Процессы высоких порядков.
- 7. Метод секущих [48].
- 8. Метод парабол.
- 9. Метод квадрирования.
- § 3. Системы нелинейных уравнений
- 2. Метод Ньютона.
- 3. Методы спуска.
- 4. Итерационные методы решения линейных систем
- ЗАДАЧИ
- ГЛАВА VI. АЛГЕБРАИЧЕСКАЯ ПРОБЛЕМА СОБСТВЕННЫХ ЗНАЧЕНИЙ
- § 1. Проблема и простейшие методы
- 2. Устойчивость.
- 3. Метод интерполяции.
- 4. Трехдиагольные матрицы.
- 5. Почти треугольные матрицы.
- 6. Обратные итерации.
- § 2. Эрмитовы матрицы
- 2. Прямой метод вращений.
- 3. Итерационный метод вращений.
- § 3. Неэрмитовы матрицы
- 2. Итерационные методы.
- 3. Некоторые частные случаи.
- § 4. Частичная проблема собственных значений
- 2. Метод линеаризации.
- 3. Степенной метод (счет на установление)
- 4. Обратные итерации со сдвигом.
- ЗАДАЧИ
- ГЛАВА VII. ПОИСК МИНИМУМА
- § 1. Минимум функции одного переменного
- 2. Золотое сечение.
- 3. Метод парабол.
- 4. Стохастические задачи.
- § 2. Минимум функции многих переменных
- 2. Спуск по координатам.
- 3. Наискорейший спуск.
- 4. Метод оврагов.
- 5. Сопряженные направления.
- 6. Случайный поиск.
- § 3. Минимум в ограниченной области
- 2. Метод штрафных функций.
- 3. Линейное программирование.
- 4. Симплекс-метод
- 5. Регуляризация линейного программирования.
- § 4. Минимизация функционала
- 2. Метод пробных функций.
- 3. Метод Ритца.
- ЗАДАЧИ
- ГЛАВА VIII. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 1. Задача Коши
- 2. Методы решения.
- 3. Метод Пикара.
- 4. Метод малого параметра.
- 5. Метод ломаных.
- 7. Метод Адамса.
- 8. Неявные схемы.
- 9. Специальные методы.
- 10. Особые точки.
- 11. Сгущение сетки.
- § 2. Краевые задачи
- 2. Метод стрельбы (называемый также баллистическим).
- 3. Уравнения высокого порядка
- 4. Разностный метод; линейные задачи.
- 5. Разностный метод; нелинейные задачи.
- 6. Метод Галеркина.
- 7. Разрывные коэффициенты.
- § 3. Задачи на собственные значения
- 2. Метод стрельбы.
- 3. Фазовый метод.
- 5. Метод дополненного вектора.
- 6. Метод Галеркина.
- ЗАДАЧИ
- ГЛАВА IX. УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ
- 2. Точные методы решения.
- 3. Автомодельность и подобие.
- 4. Численные методы.
- § 2. Аппроксимация
- 2. Явные и неявные схемы.
- 3. Невязка.
- 4. Методы составления схем.
- 5. Аппроксимация и ее порядок.
- § 3. Устойчивость
- 2. Основные понятия.
- 4. Метод разделения переменных.
- 5. Метод энергетических неравенств.
- 6. Операторные неравенства.
- § 4. Сходимость
- 2. Оценки точности.
- 3. Сравнение схем на тестах.
- ЗАДАЧИ
- ГЛАВА X. УРАВНЕНИЕ ПЕРЕНОСА
- 2. Схемы бегущего счета.
- 3. Геометрическая интерпретация устойчивости.
- 4. Многомерное уравнение.
- 5. Перенос с поглощением.
- 6. Монотонность схем.
- 7. Диссипативные схемы.
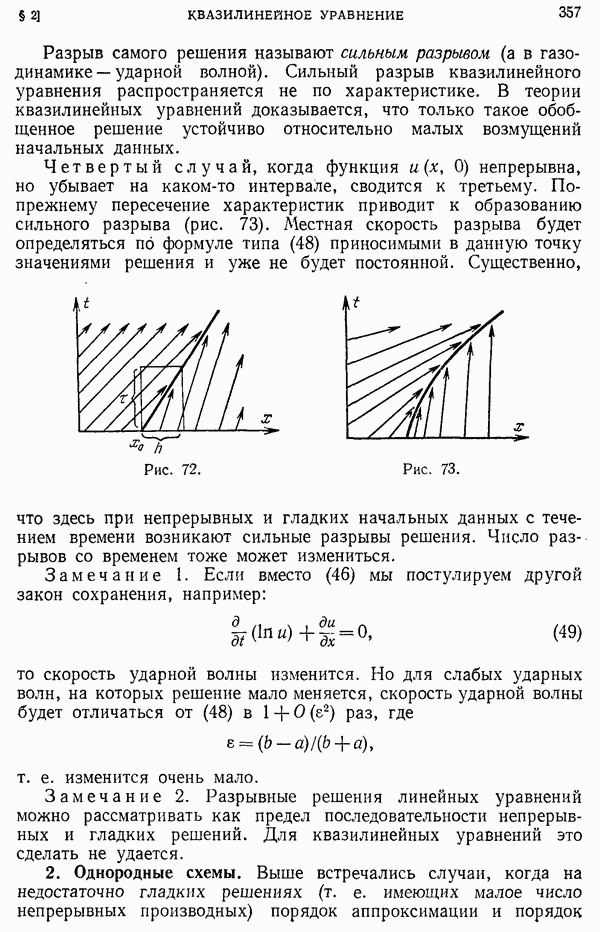
- § 2. Квазилинейное уравнение
- 2. Однородные схемы.
- 3. Псевдовязкость.
- 4. Ложная сходимость.
- 5. Консервативные схемы.
- ЗАДАЧИ
- ГЛАВА XI. ПАРАБОЛИЧЕСКИЕ УРАВНЕНИЯ
- § 1. Одномерные уравнения
- 3. Асимптотическая устойчивость неявной схемы.
- 4. Монотонность.
- 5. Явные схемы.
- 6. Наилучшая схема.
- 7. Криволинейные координаты.
- 8. Квазилинейное уравнение.
- § 2. Многомерное уравнение
- 2. Продольно-поперечная схема
- 3. Локально-одномерный метод.
- 4. Метод Монте-Карло.
- ЗАДАЧИ
- ГЛАВА XII. ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ
- § 1. Счет на установление
- 2. Оптимальный шаг.
- 3. Чебышевский набор шагов.
- § 2. Вариационные и вариационно-разностные методы
- 2. Стационарные разностные схемы.
- 3. Прямые методы решения.
- 4. Итерационные методы.
- ЗАДАЧИ
- ГЛАВА XIII. ГИПЕРБОЛИЧЕСКИЕ УРАВНЕНИЯ
- § 1. Волновое уравнение
- 2. Неявная схема.
- 3. Двуслойная акустическая схема.
- 4. Инварианты.
- 5. Явная многомерная схема.
- 6. Факторизованные схемы.
- § 2. Одномерные уравнения газодинамики
- 2. Псевдовязкость.
- 3. Схема «крест».
- 4. Неявная консервативная схема.
- 5. О других схемах.
- ЗАДАЧИ
- ГЛАВА XIV. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
- § 1. Корректно поставленные задачи
- 2. Разностный метод.
- 5. Метод Галеркина
- § 2. Некорректные задачи
- 2. Вариационный метод регуляризации.
- 3. Уравнение Эйлера.
- 4. Некоторые приложения.
- 5. Разностные схемы.
- ЗАДАЧИ
- ГЛАВА XV. СТАТИСТИЧЕСКАЯ ОБРАБОТКА ЭКСПЕРИМЕНТА
- 2. Величина и доверительный интервал.
- 3. Сравнение величин.
- 4. Нахождение стохастической зависимости.
- ЗАДАЧИ
- ПРИЛОЖЕНИЕ. ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ
- ЛИТЕРАТУРА