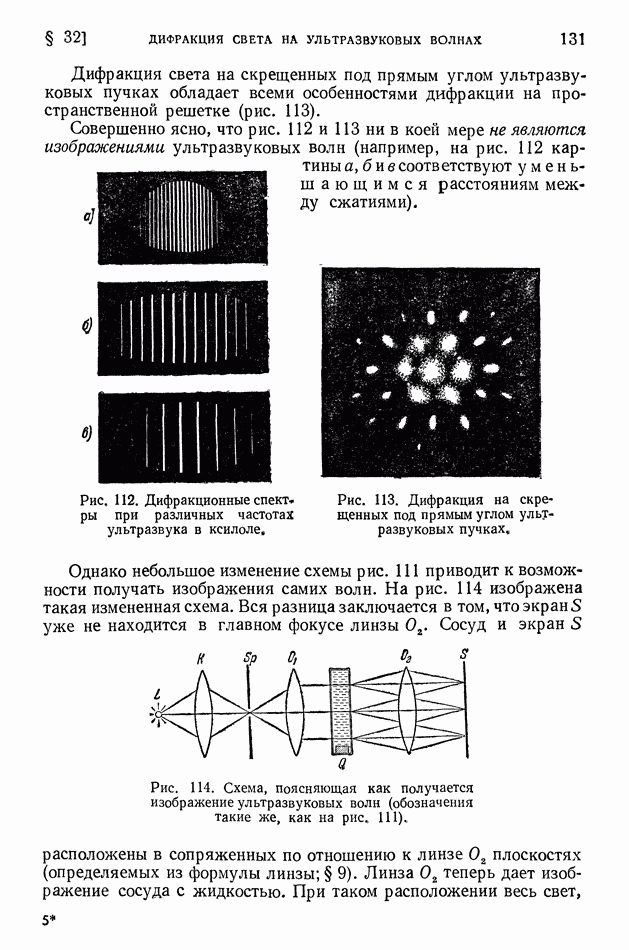
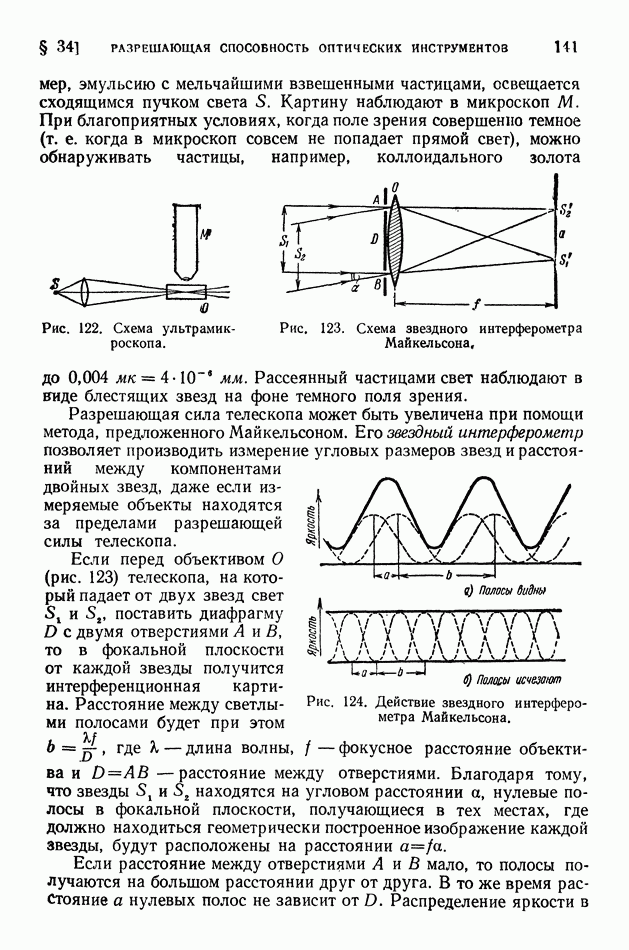
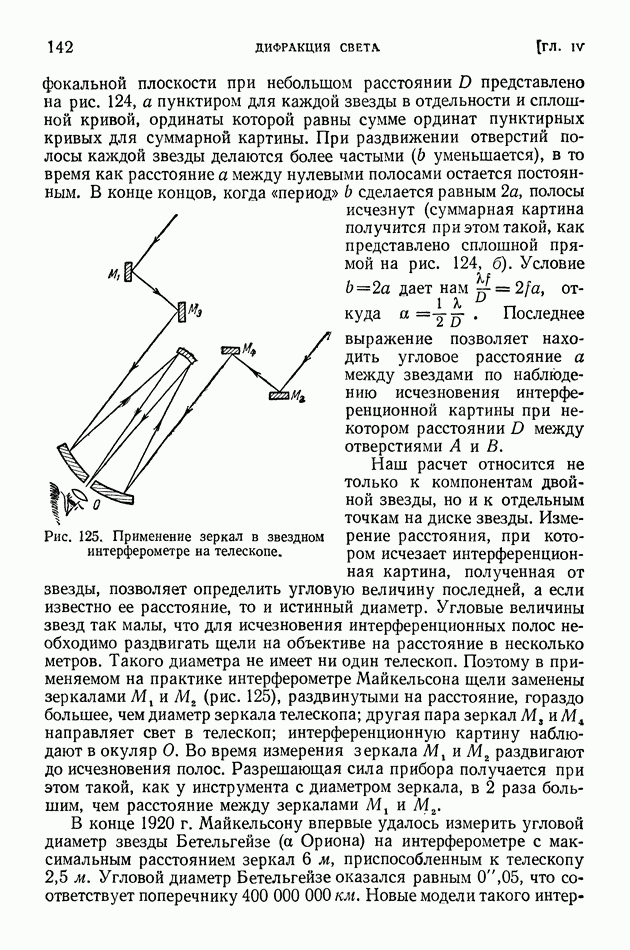
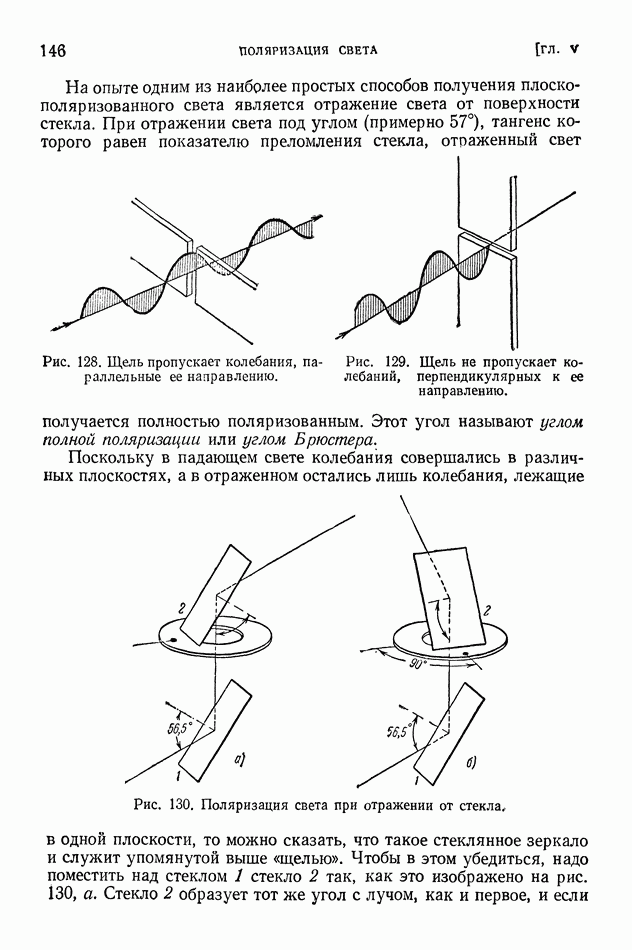
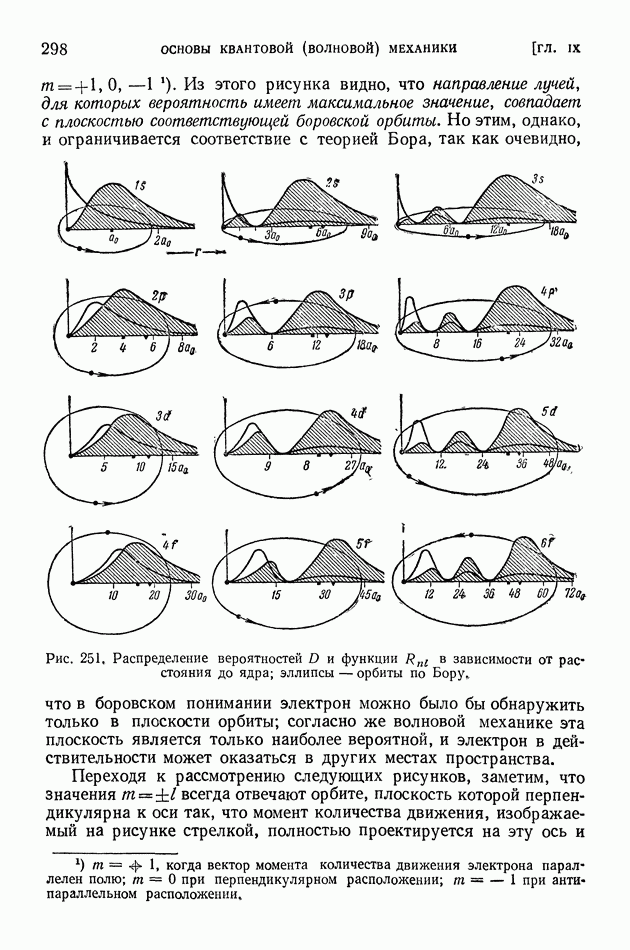
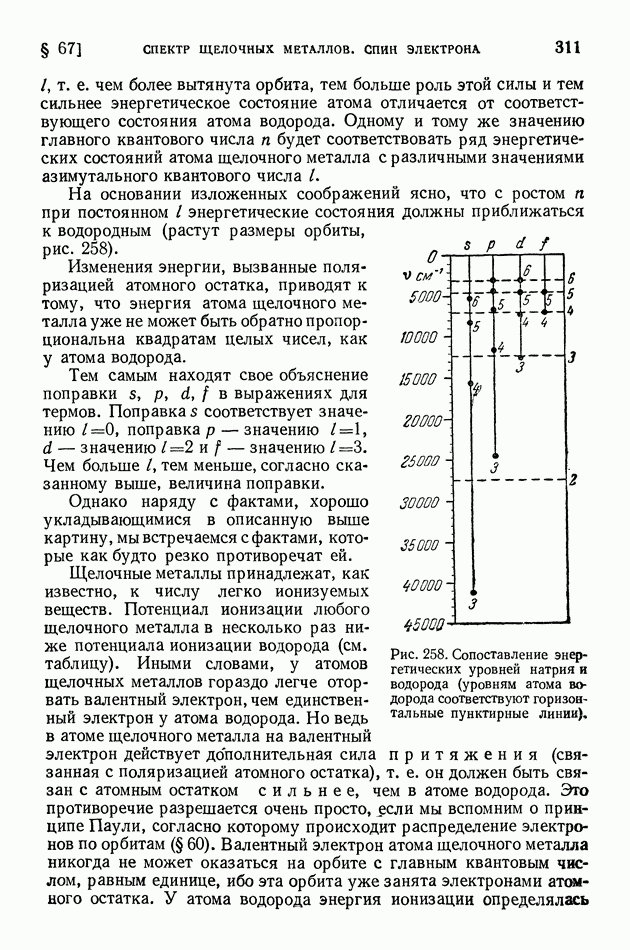
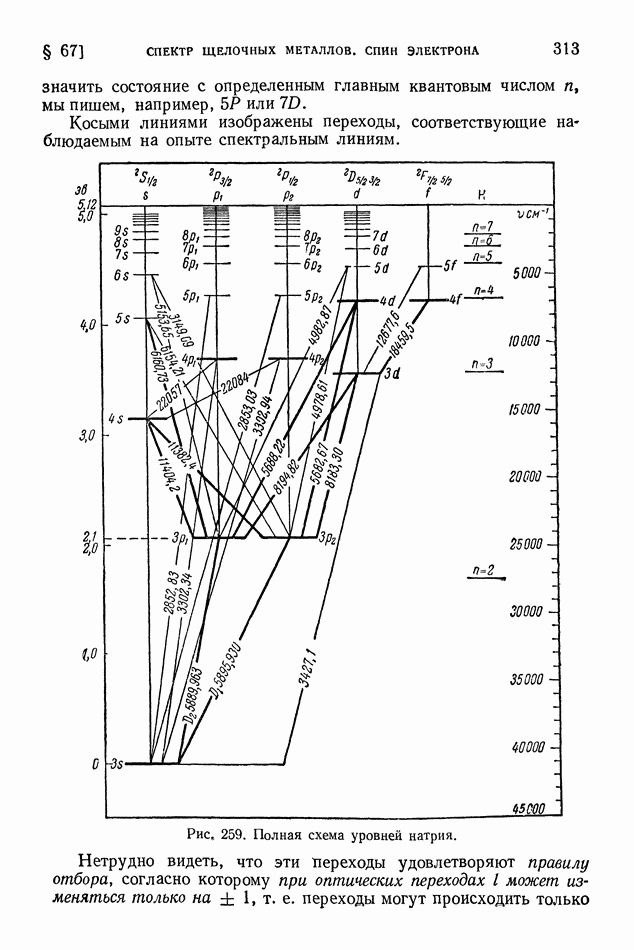
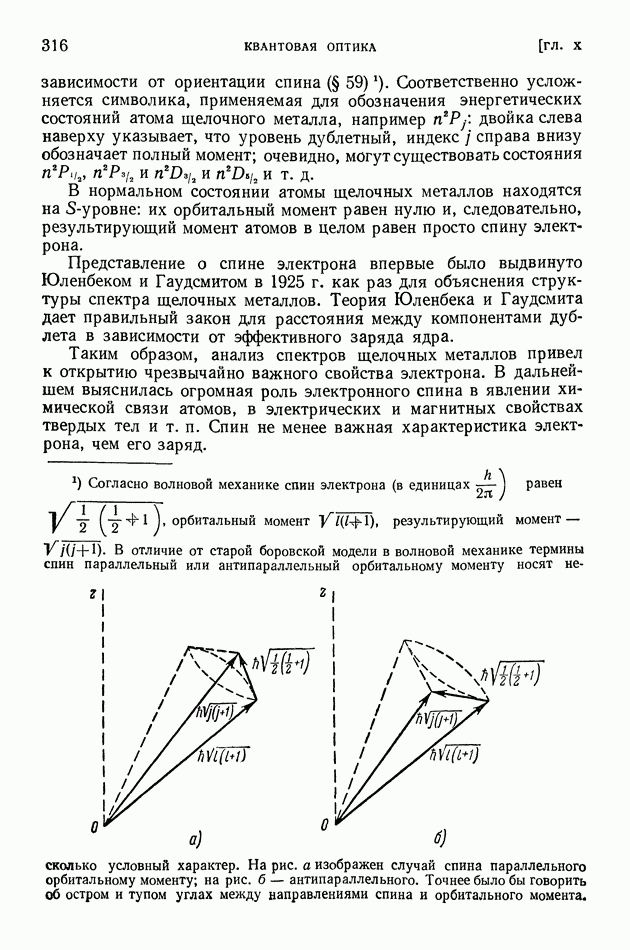
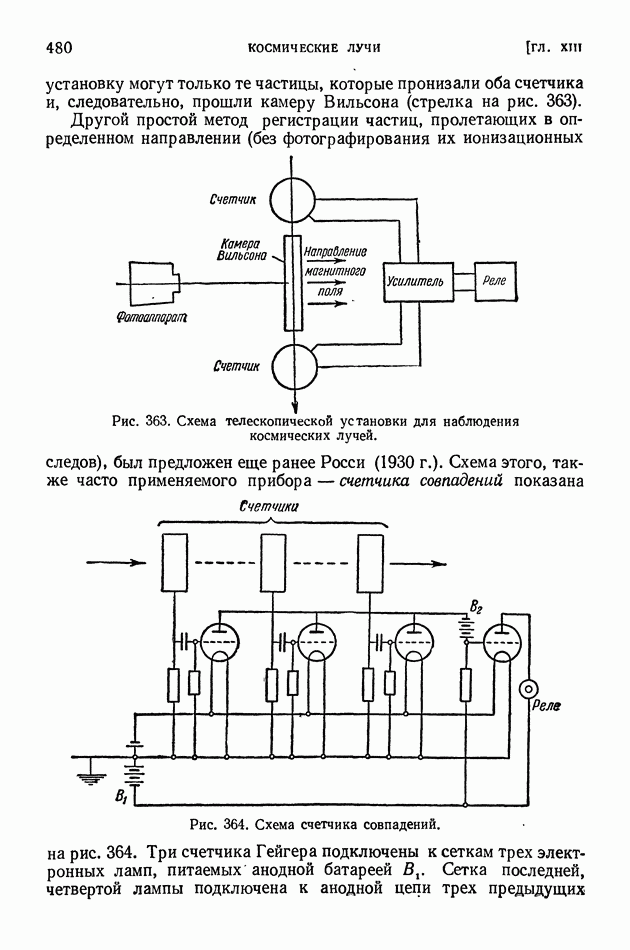
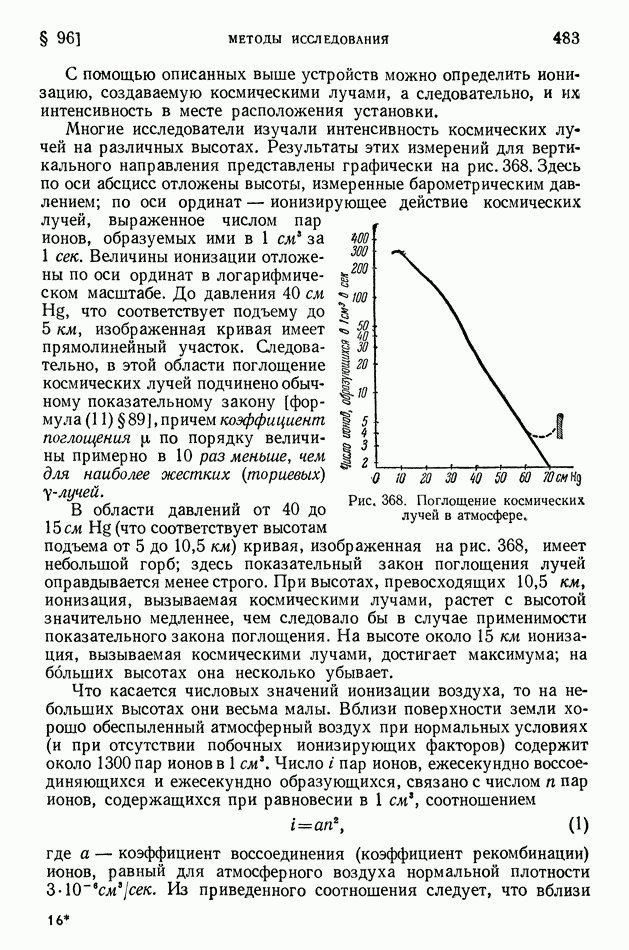
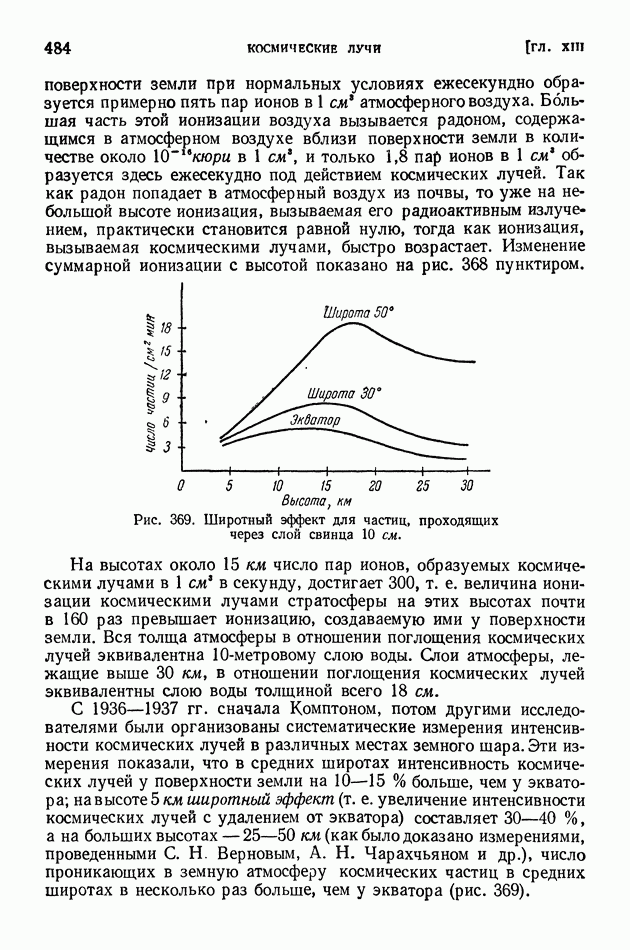
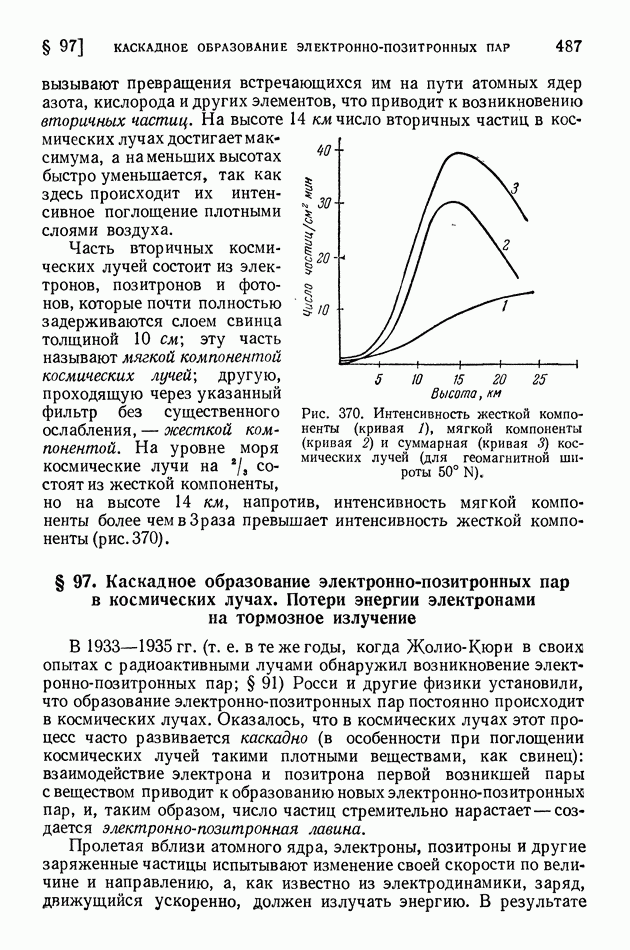
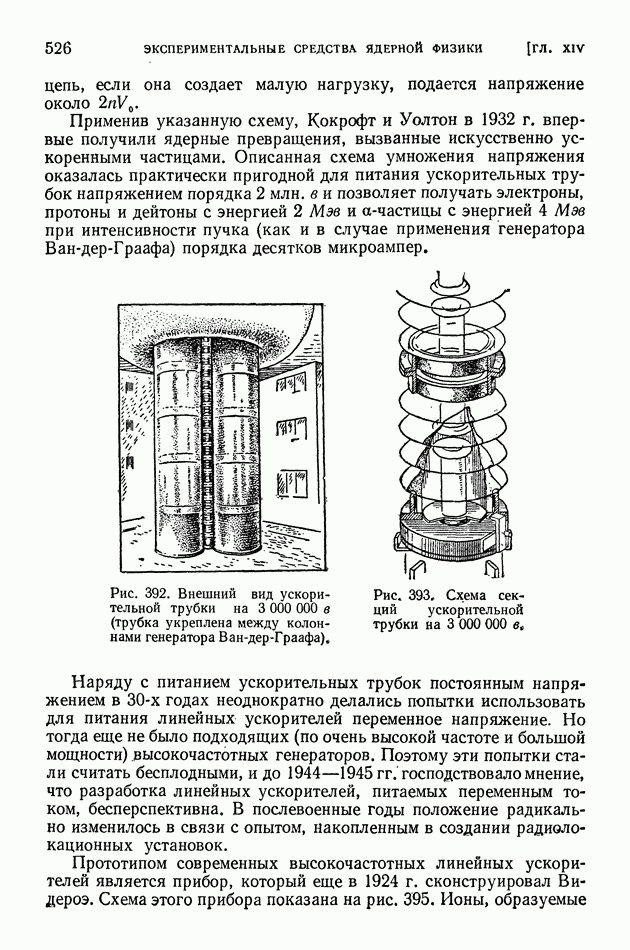
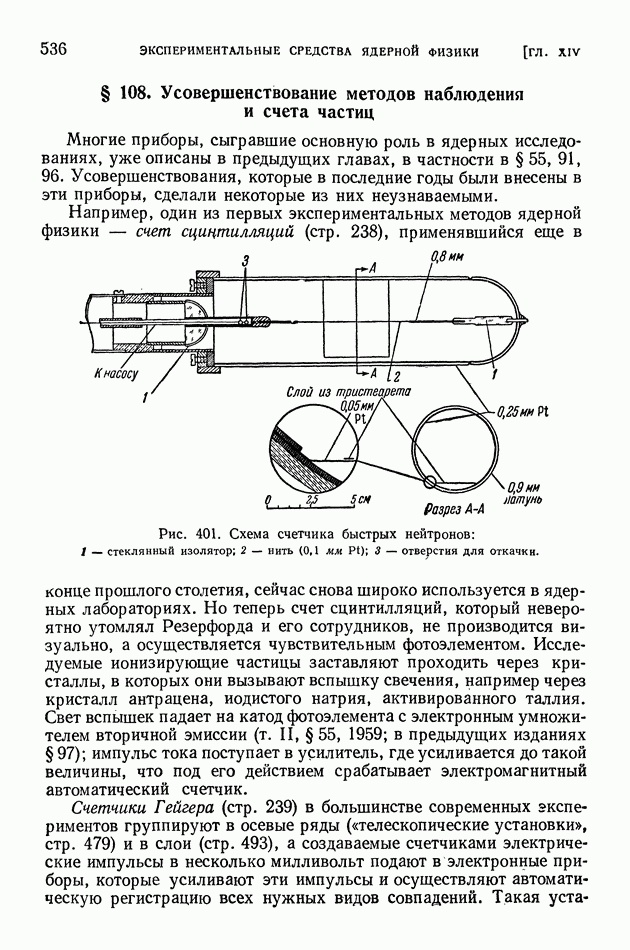
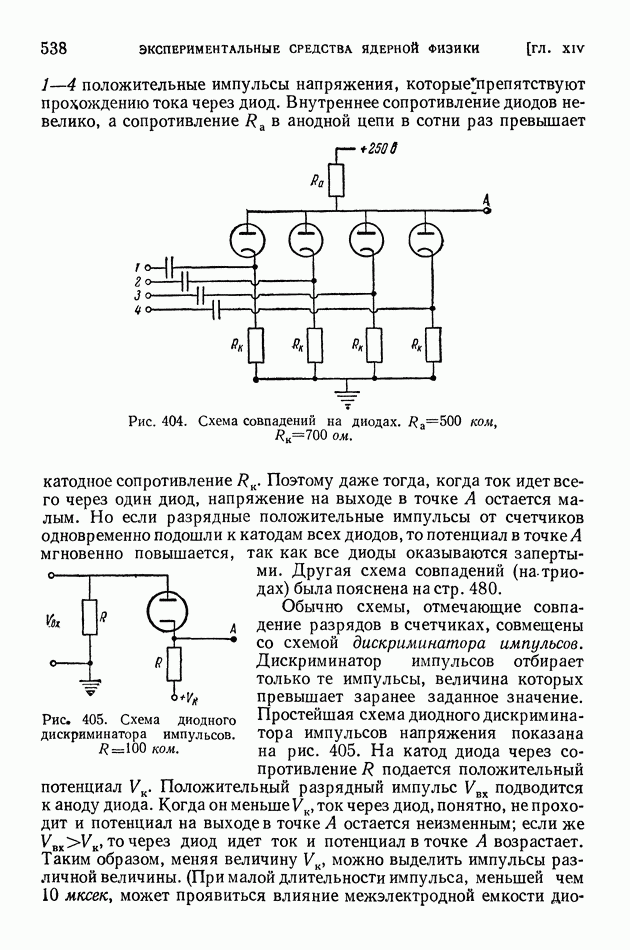
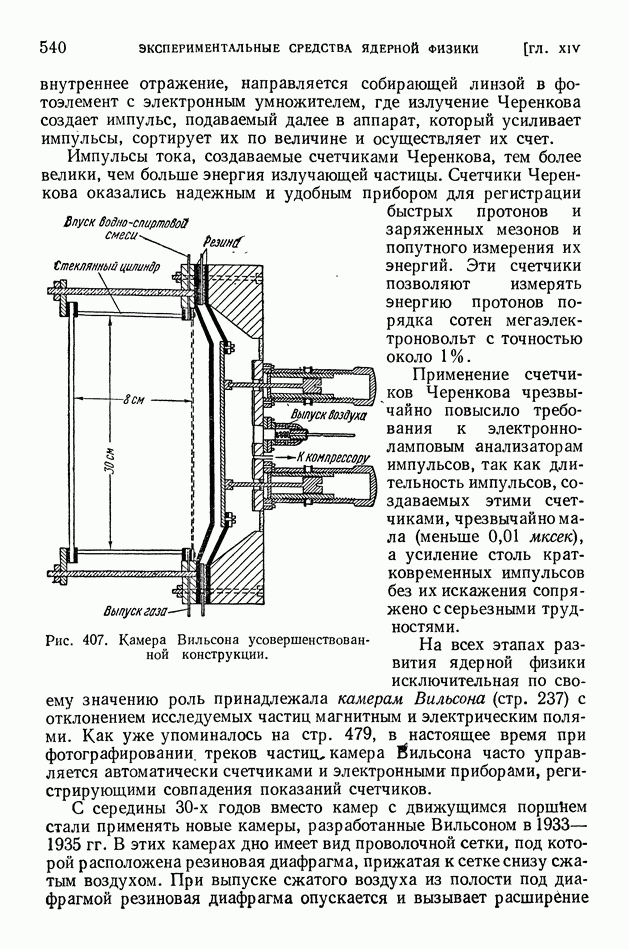
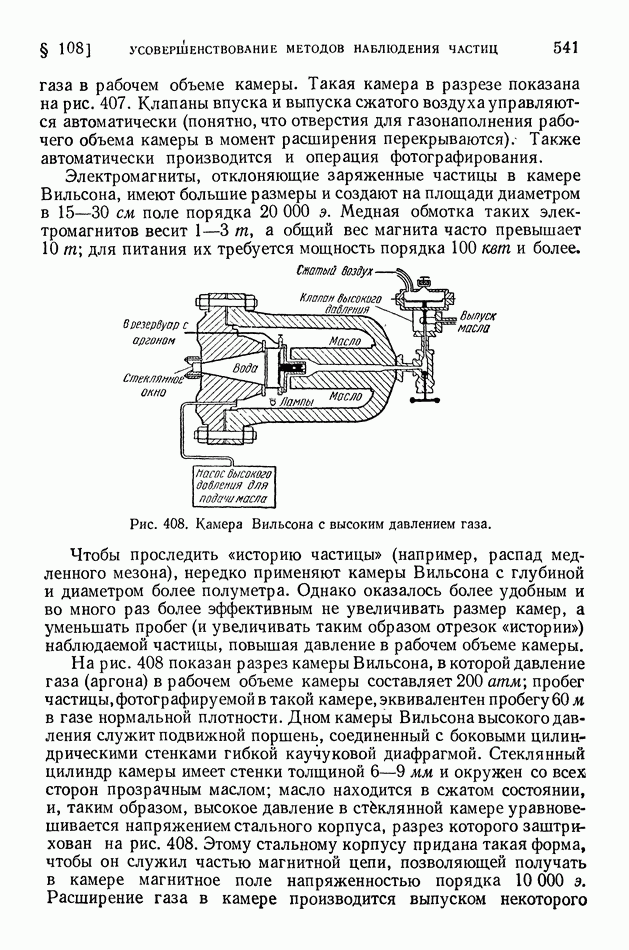
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 116. Энергия отделения частиц и анализ возможного хода ядерной реакции
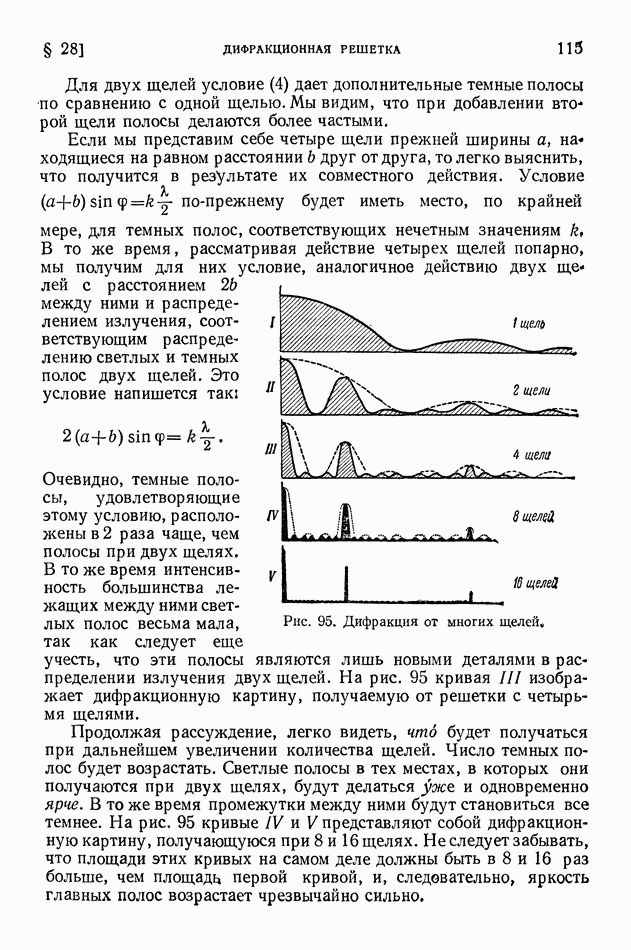
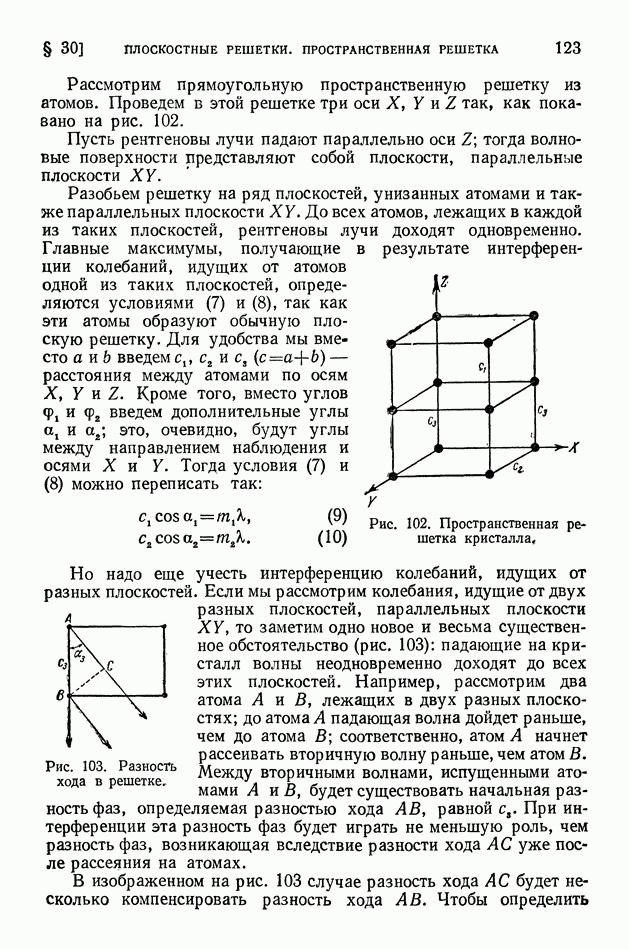
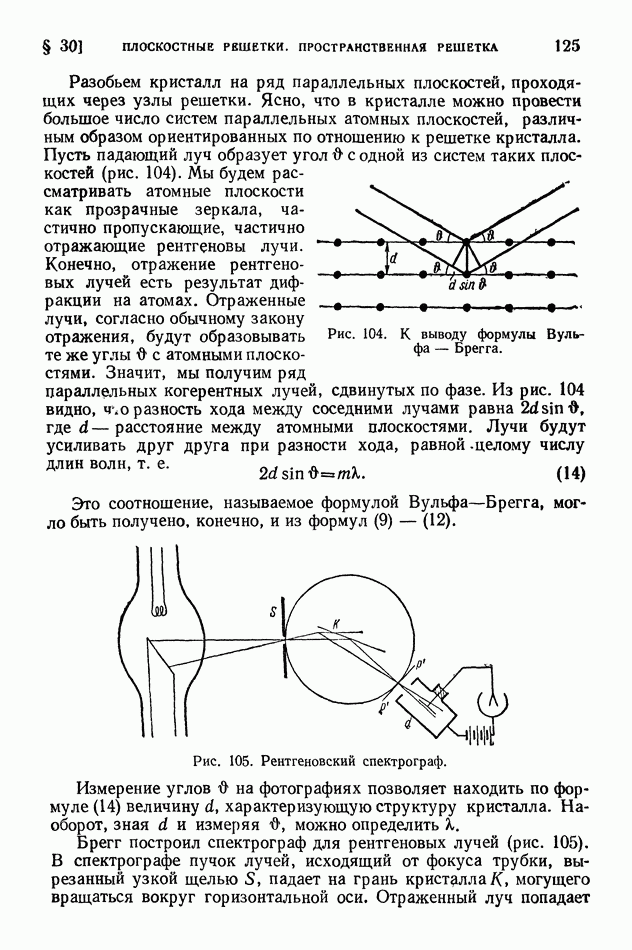
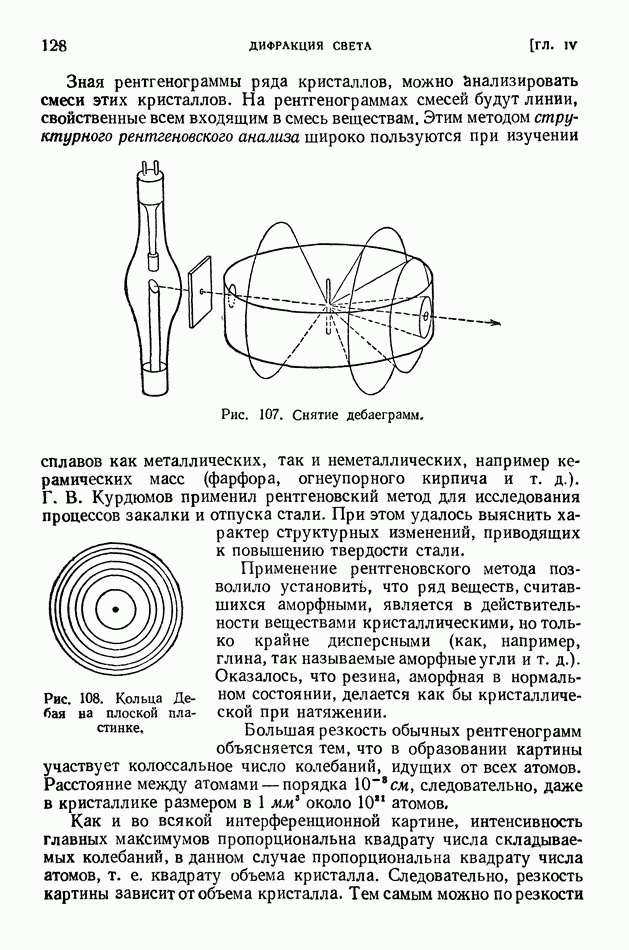
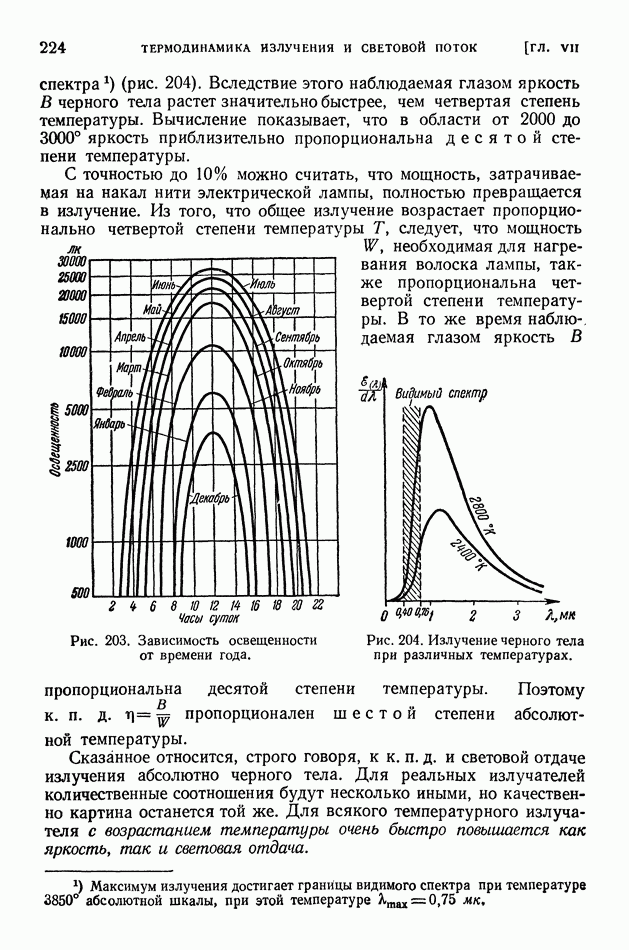
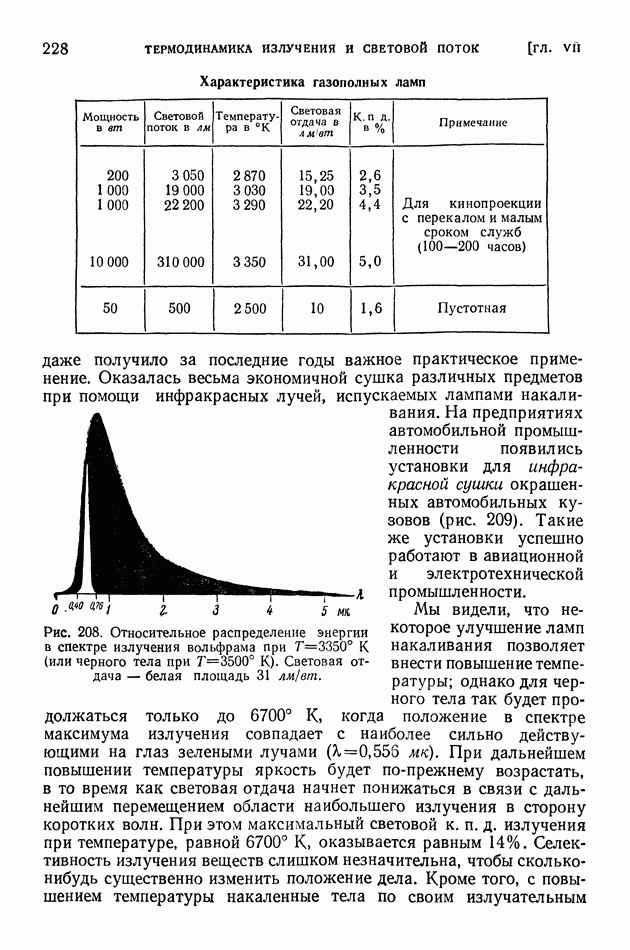
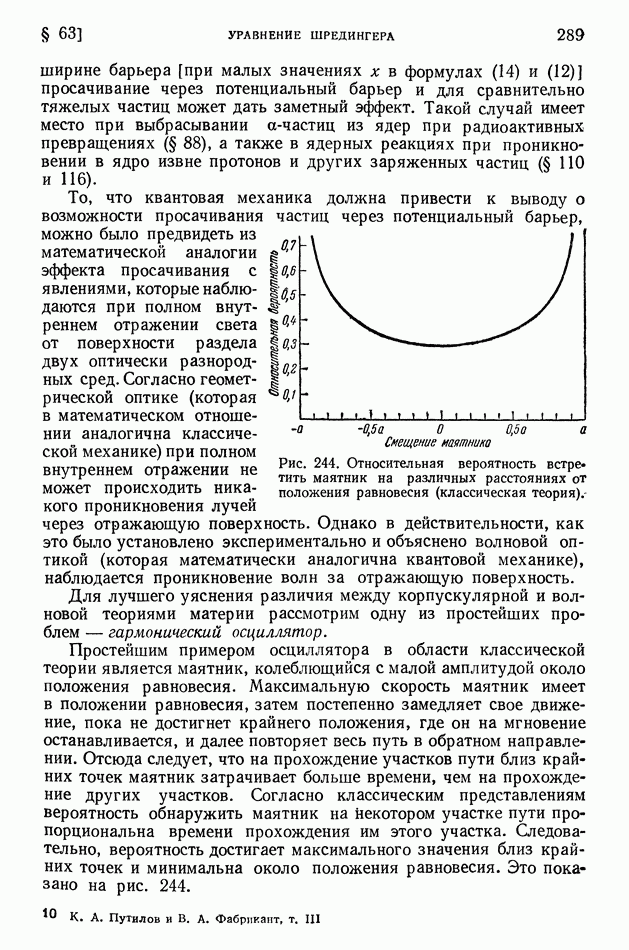
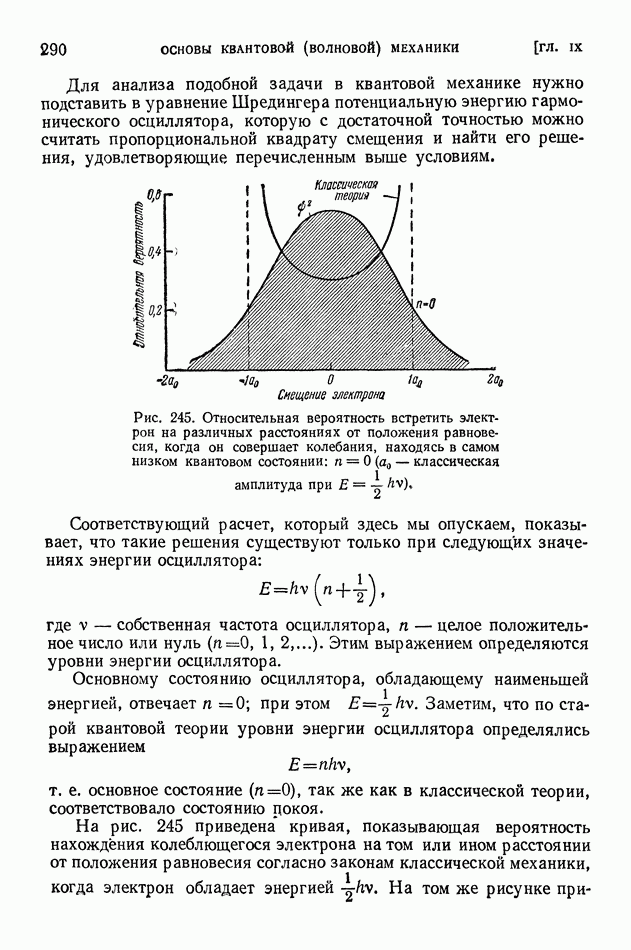
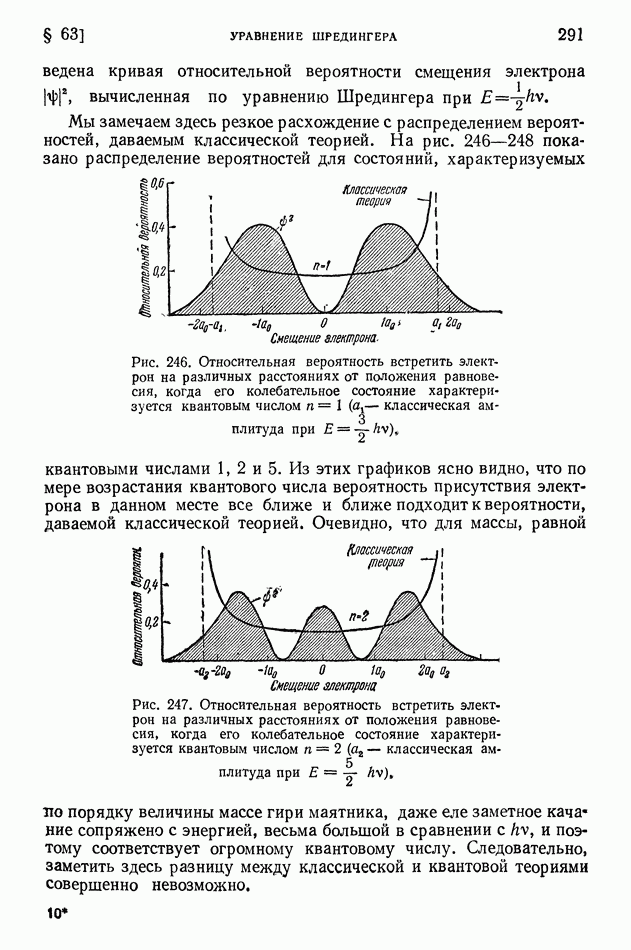
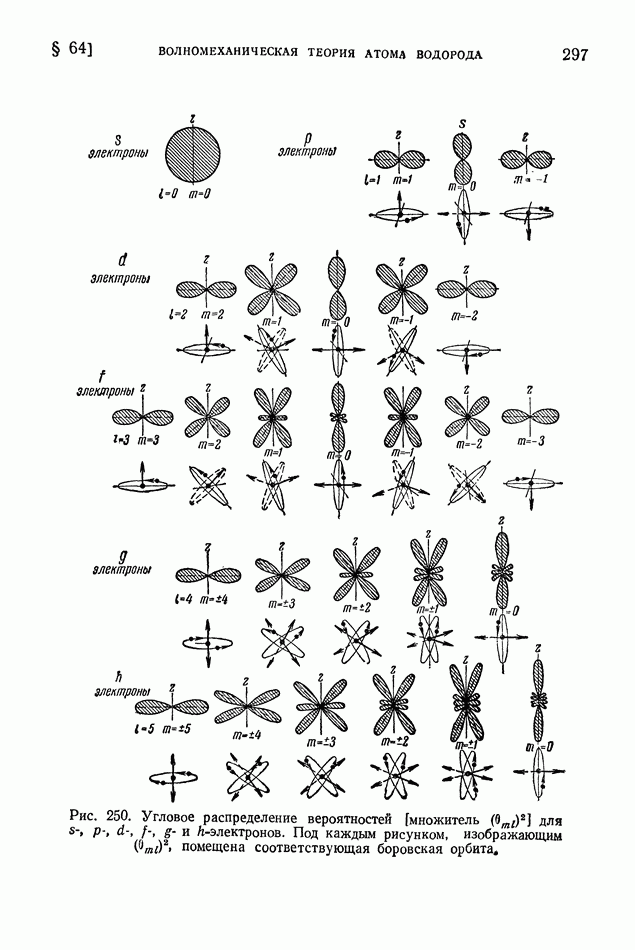
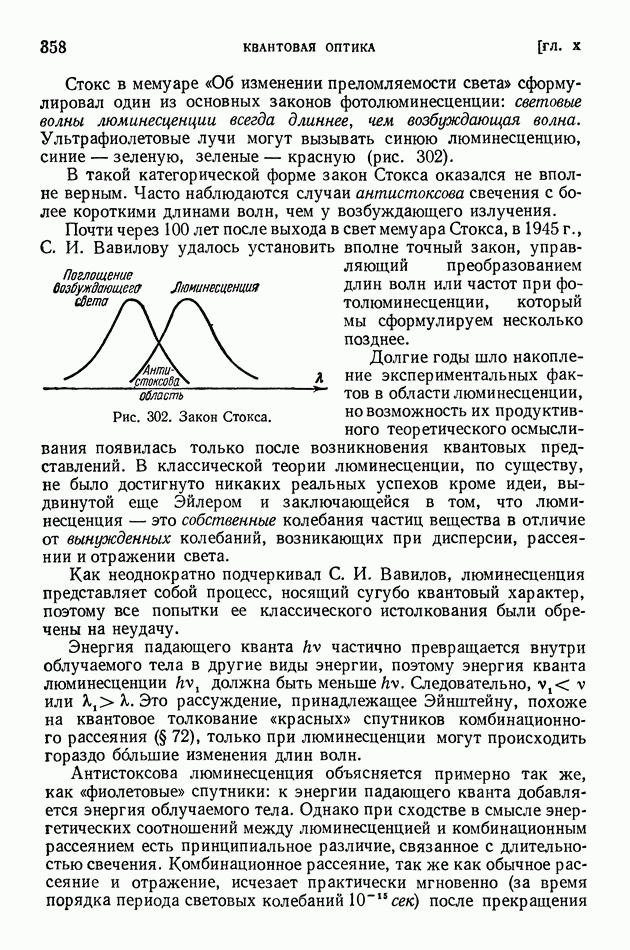
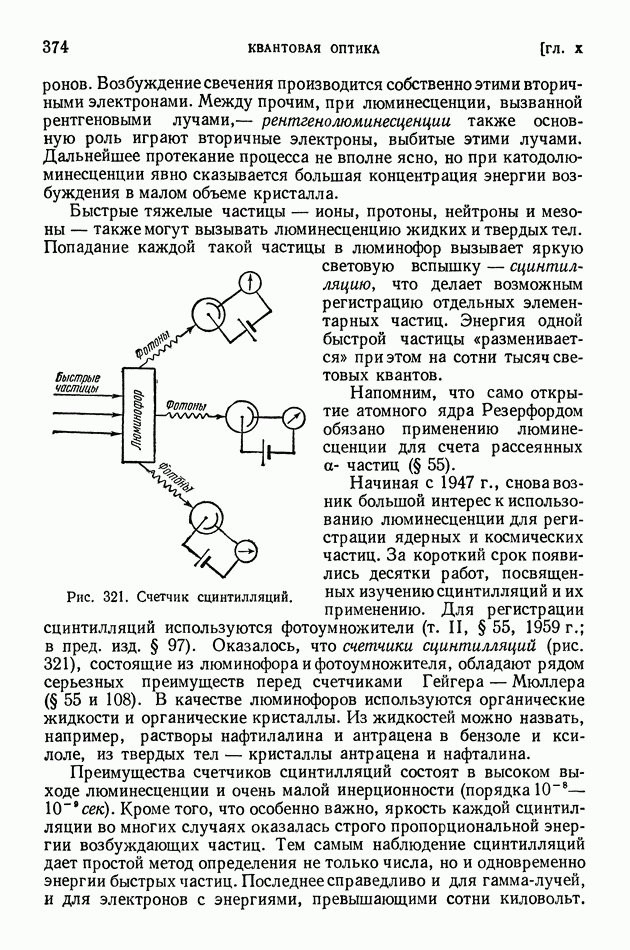
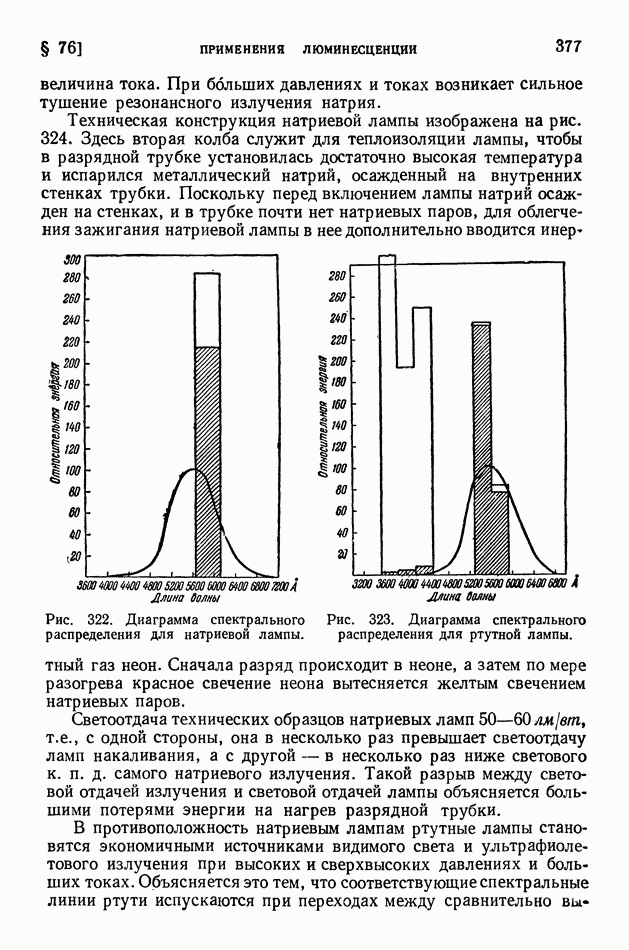
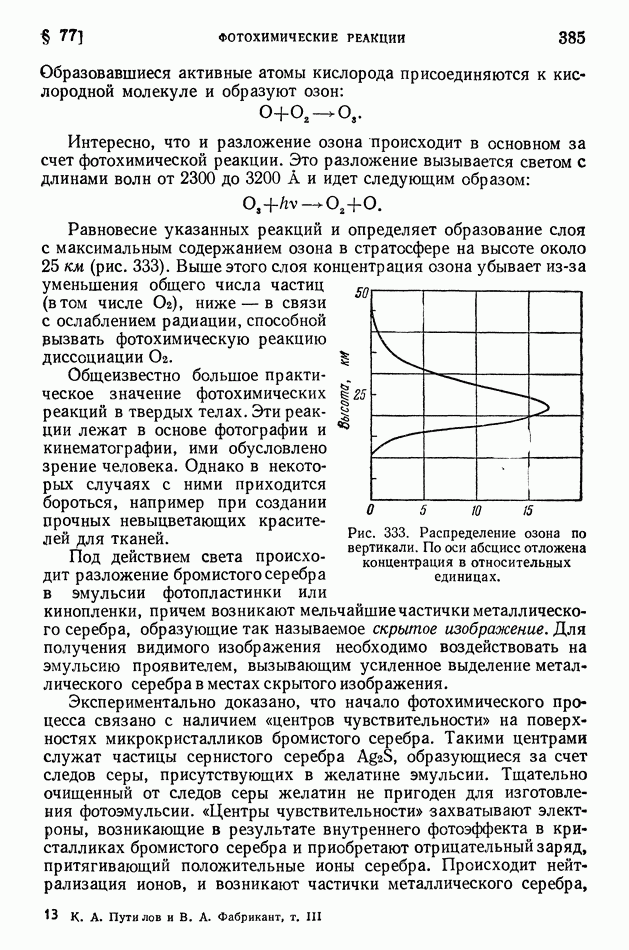
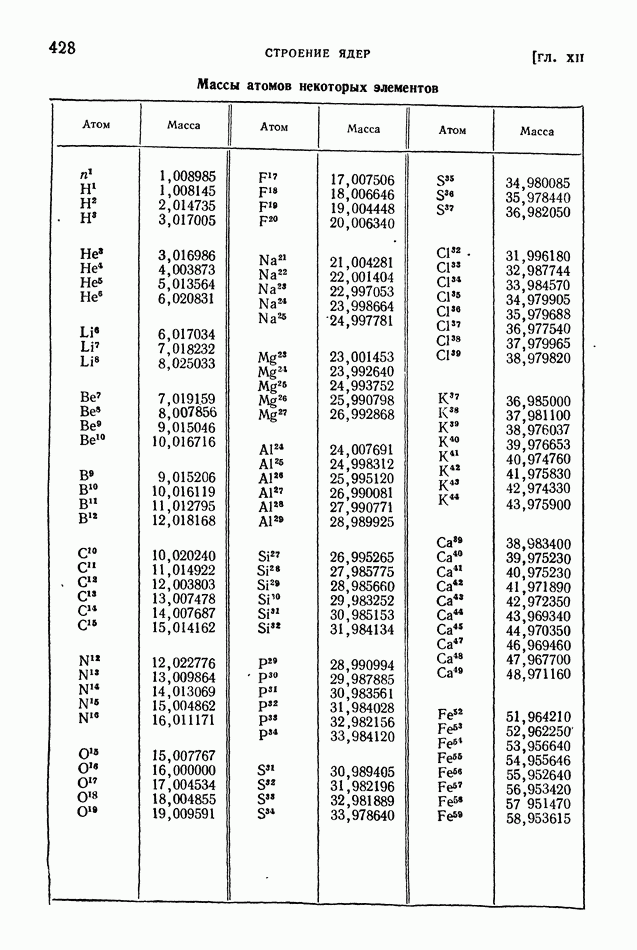
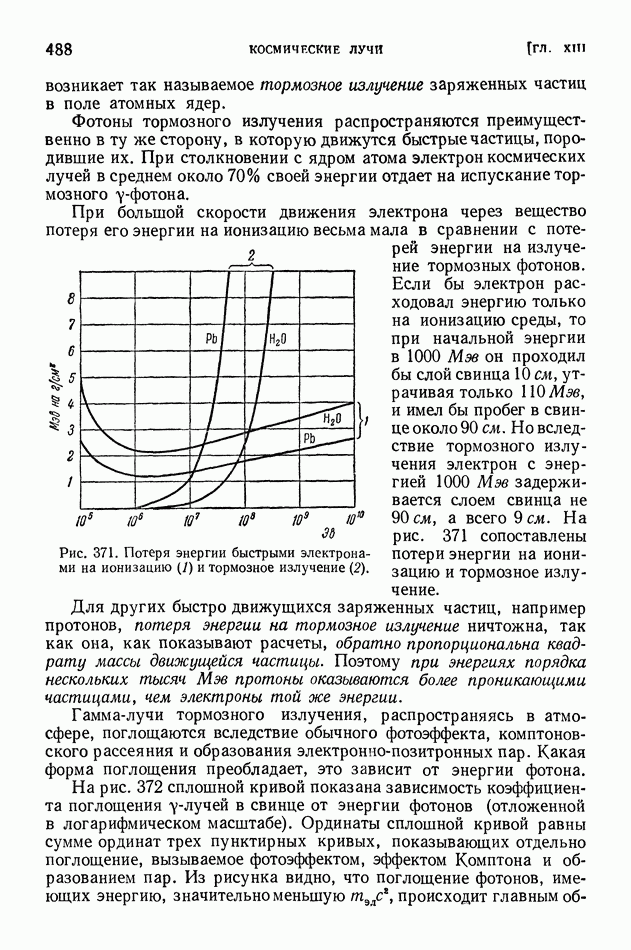
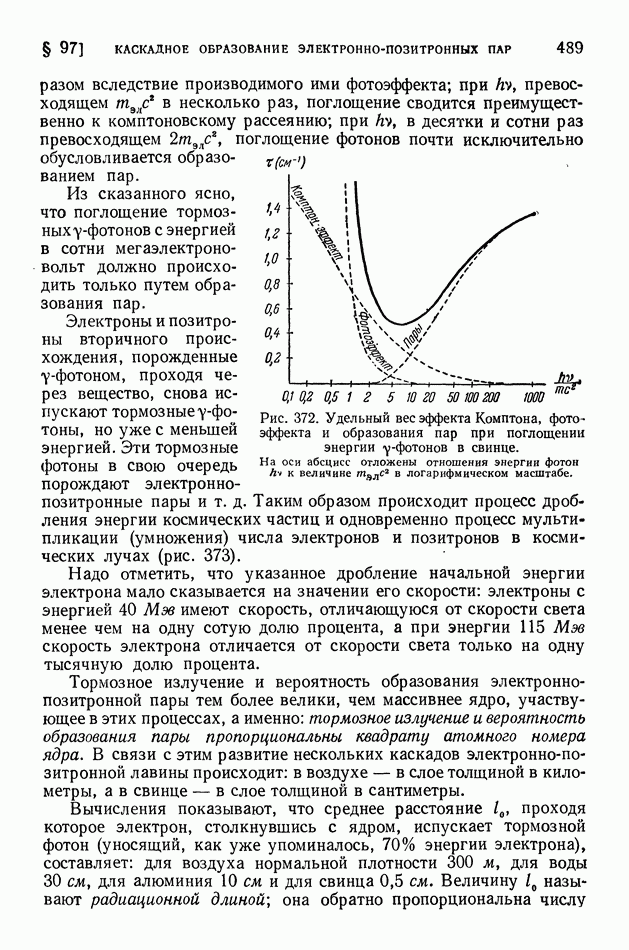
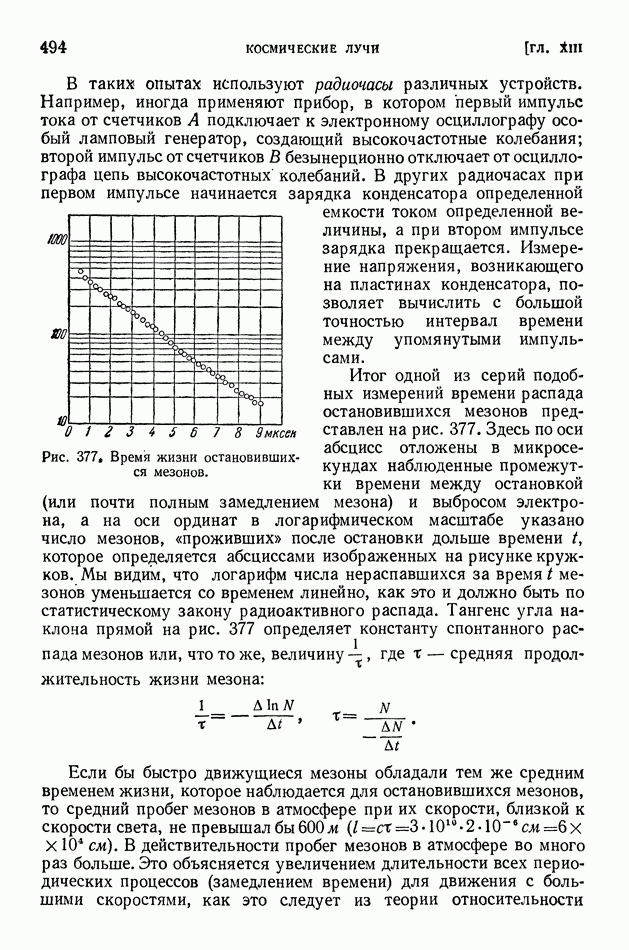
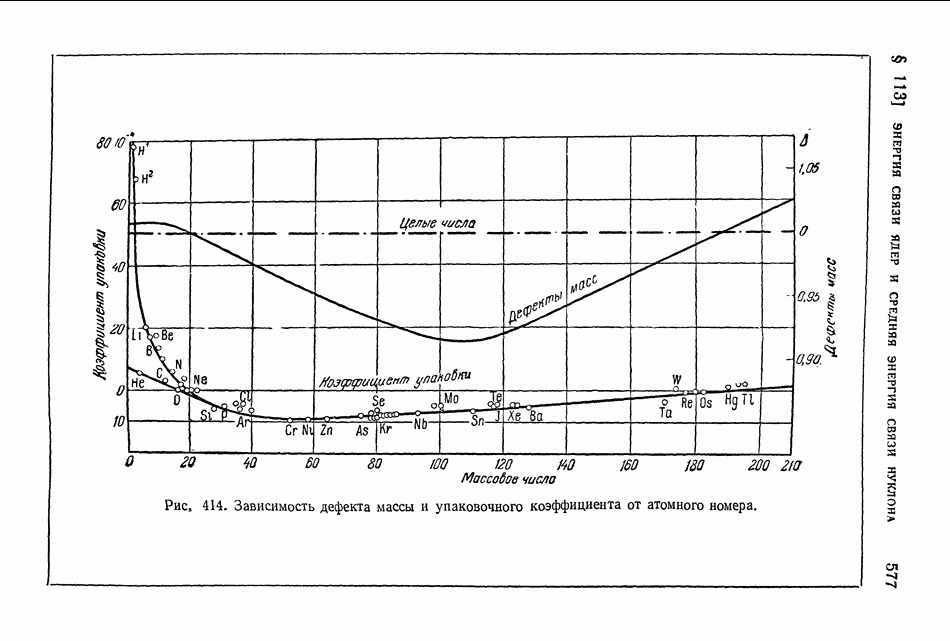
Ядро тем более «прочно», чем больше средняя энергия связи нуклонов в ядре. В разных ядрах средние энергии связи нуклона мало различаются (рис. 413 на стр. 574), поэтому «прочность» разных ядер более или менее одинакова. Вместе с тем в ядерных реакциях различные ядра ведут себя совершенно неодинаково? некоторые ядра легко подвергаются превращениям, другие, напротив, оказываются весьма устойчивыми; в одних случаях из возбужденного ядра выбрасываются нейтроны, в других — протоны, или дейтоны, или альфа-частицы.
Чем это объясняется? Если не средняя энергия связи нуклонов в ядре, то какая же именно величина определяет поведение ядра в реакции?
Очевидно, что в ядерных реакциях в первую очередь отщепляются нуклоны, находящиеся на верхних энергетических уровнях; их называют последними нуклонами. Чтобы осуществить отщепление от ядра частицы а (нуклона, дейтона или альфа-частицы), нужно затратить энергию  которую называют энергией отделения или (для нуклонов) энергией связи последнего нуклона. Она вычисляется как разность энергий ядра после отделения частицы а (в сумме с собственной энергией этой частицы) и до отделения частицы, причем ядра сопоставляются в их основных состояниях:
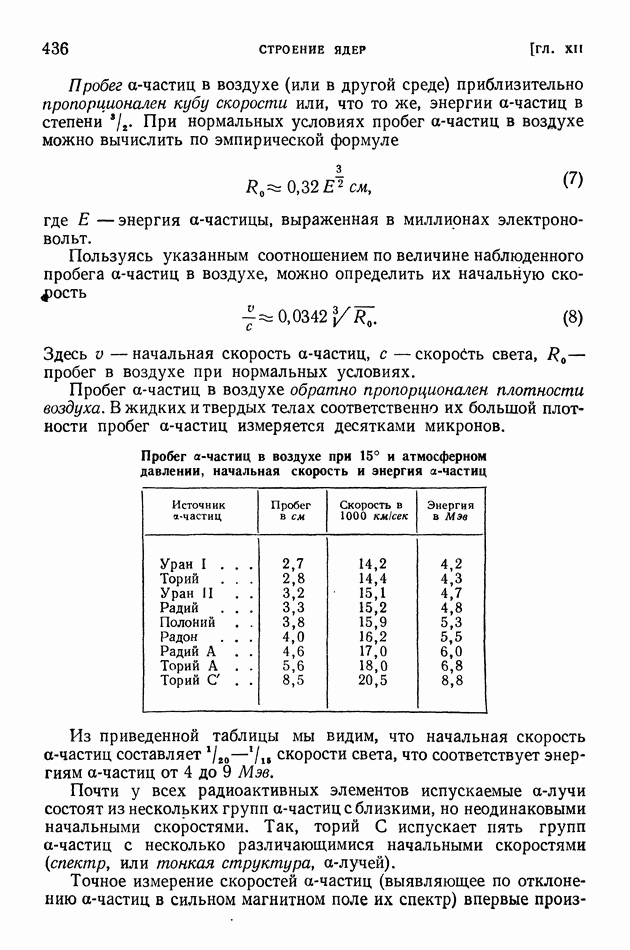
которую называют энергией отделения или (для нуклонов) энергией связи последнего нуклона. Она вычисляется как разность энергий ядра после отделения частицы а (в сумме с собственной энергией этой частицы) и до отделения частицы, причем ядра сопоставляются в их основных состояниях:

Здесь  энергия внутренней связи отделяемой частицы (для нуклонов
энергия внутренней связи отделяемой частицы (для нуклонов  для дейтонов и альфа-частиц
для дейтонов и альфа-частиц 
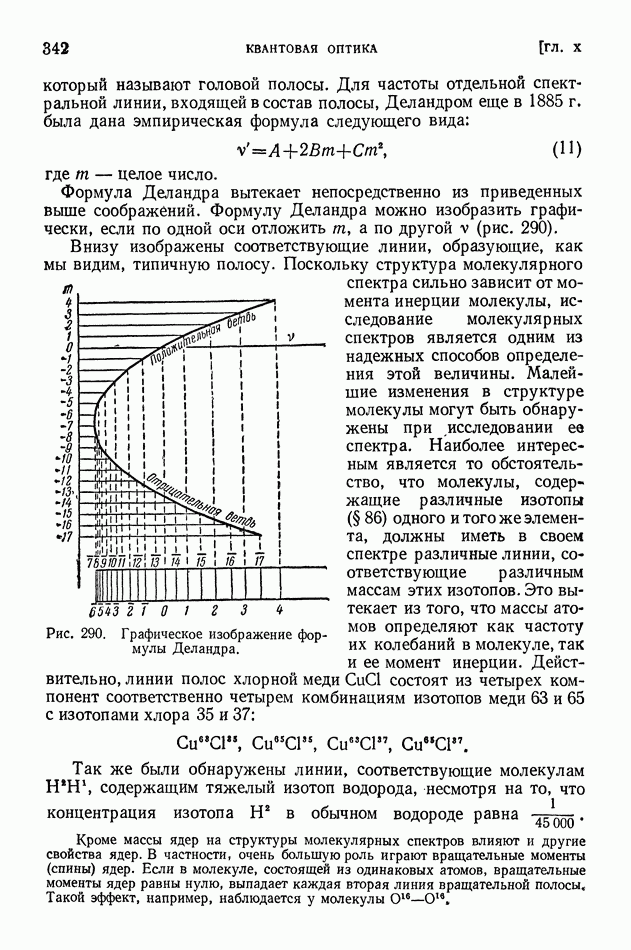
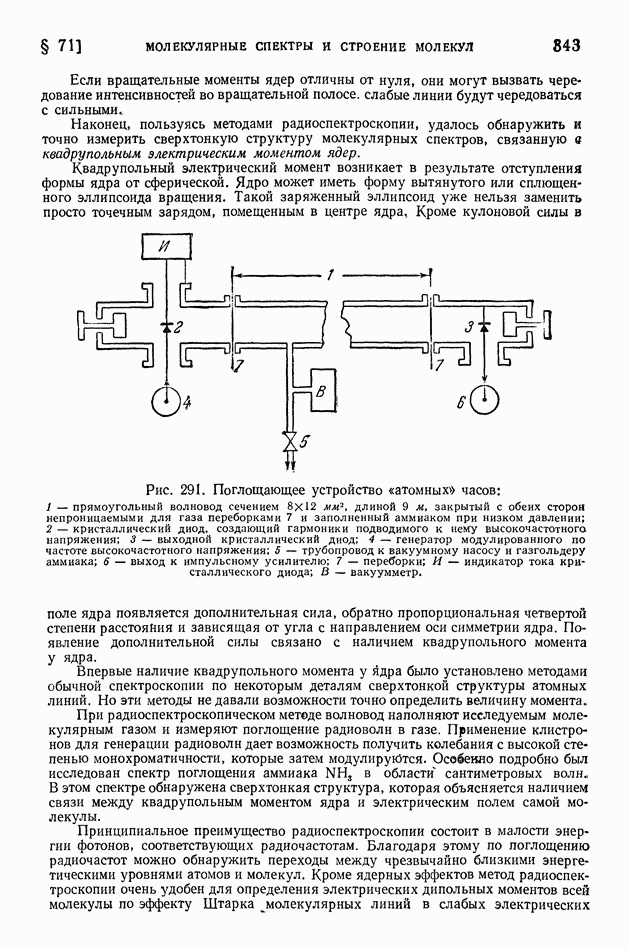
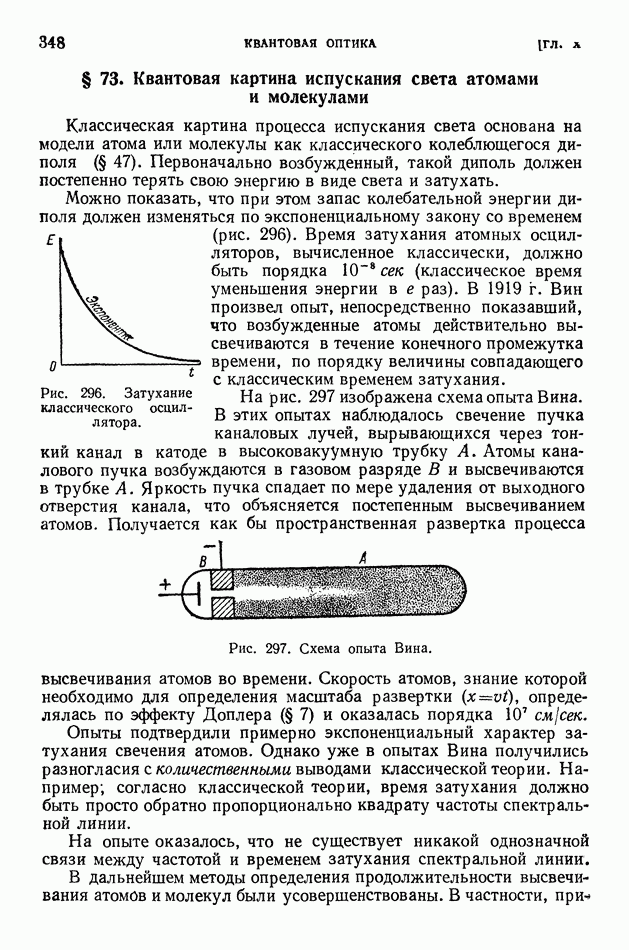
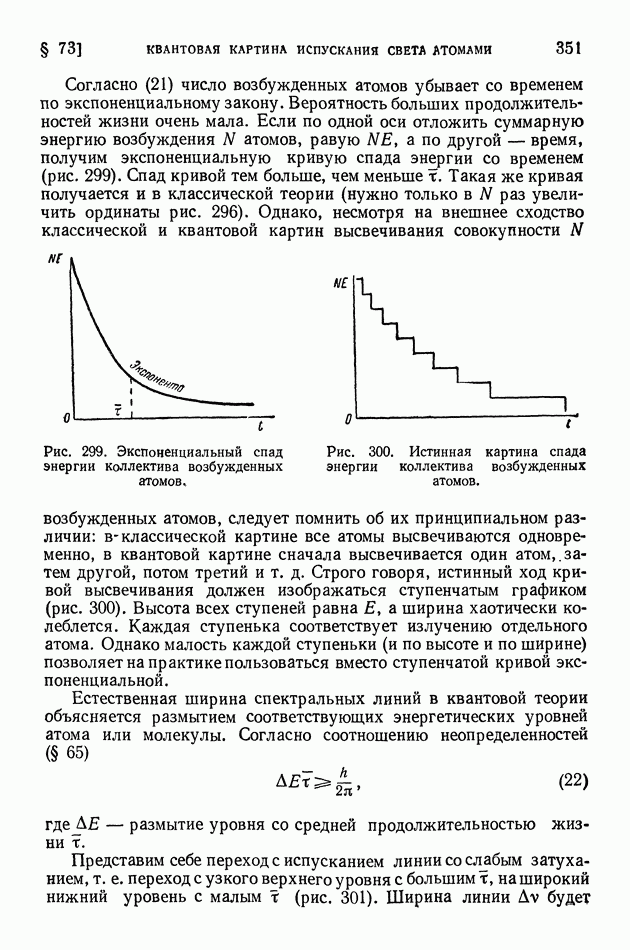
Об энергии отделения  уже было упомянуто в § 110 (на стр. 550), но величина эта столь важна для анализа энергетически возможного хода ядерных реакций, что необходимо рассмотреть ее подробнее.
уже было упомянуто в § 110 (на стр. 550), но величина эта столь важна для анализа энергетически возможного хода ядерных реакций, что необходимо рассмотреть ее подробнее.
Энергия отделения нуклонов (энергия связи последнего нейтрона  и последнего протона
и последнего протона  для одних ядер оказывается значительно меньше средней энергии связи, а для других, напротив, больше средней энергии связи.
для одних ядер оказывается значительно меньше средней энергии связи, а для других, напротив, больше средней энергии связи.
Что связь последнего нуклона часто оказывается меньше средней, это понятно: чем выше энергетический уровень, на
котором находится нуклон, тем меньшую энергию нужно ему сообщить, чтобы его положительная кинетическая энергия сравнялась по абсолютной величине с отрицательной потенциальной энергией и чтобы вследствие этого нуклон мог оторваться от ядра.
Истинная энергия связи нуклона с ядром полностью определяется высотой занятого им уровня энергии. Если бы можно было осуществить удаление нуклона из ядра, не изменяя энергетического состояния других нуклонов ядра (подобно отрыву периферического электрона при ионизации атома), то энергия отделения нуклона была бы равна истинной энергии связи этого нуклона с ядром (т. е. взятой с обратным знаком сумме его потенциальной и кинетической энергий). Но энергия отделения — это мера эффективной связи, и обычно она больше истинной связи.
Отщепление нуклона от ядра происходит совсем не так, как отщепление атомного электрона. Уровни энергии электронов в атоме отстоят друг от друга на величину, превышающую работу отрыва периферического электрона. Поэтому отщепление слабо связанного периферического электрона не оказывает влияния на состояние движения остающихся электронов и затрата работы на ионизацию атома равна истинной энергии связи отщепляемого электрона.
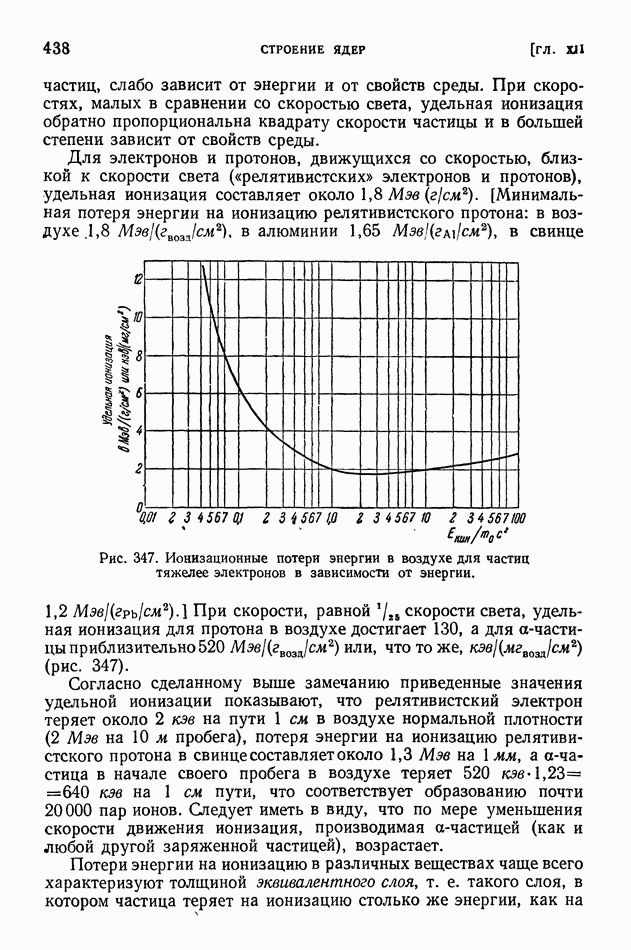
В противоположность этому энергия связи любого нуклона в ядре столь велика, что она в десятки раз превышает «энергетическое расстояние» между уровнями энергии нуклонов ядра. Поэтому дополнительная энергия, сообщенная одному нуклону, распределяется между остальными нуклонами раньше, чем этот нуклон успеет покинуть ядро. Кроме того, и в основном состоянии ядра энергия внутриядерного движения сильно зависит, как это было пояснено в предыдущем параграфе, от состава ядра. Поэтому реальная затрата энергии на удаление нуклона из ядра больше, чем работа, потребная для преодоления связи отщепляемого нуклона с ядром, на величину энергии, которая расходуется вследствие перераспределения остающихся нуклонов по новым энергетическим состояниям. (У некоторых легких ядер энергия отделения в 1,5-2 и даже 3 раза превышает истинную и среднюю энергию связи нуклона в ядре.)
Может оказаться, что размещение нуклонов по энергетическим уровням в ядре, которое утратило один нуклон, будет более выгодным, чем существовавшее ранее. В этом случае процесс перераспределения нуклонов по новым уровням содействует отщеплению нуклона и энергия отделения нуклона оказывается меньше истинной связи этого нуклона с ядром, а для неустойчивых ядер может даже оказаться отрицательной.
Следует иметь в виду, что минимальная («пороговая») энергия, необходимая для фактического удаления заряженной частицы из ядра, больше энергии отделения этой частицы. Действительно, ведь энергия отделения указывает затрату энергии на отщепление при условии, чтобы вне ядра отщепленная частица находилась в покое. Но когда положительно заряженная частица, имеющая заряд  удалена из ядра, заряд которого был
удалена из ядра, заряд которого был  и стал
и стал  то она вследствие кулоновского отталкивания со стороны ядра («скатываясь с кулоновского барьера») приобретает кинетическую энергию, равную потенциальной энергии отталкивания между частицей и ядром, которую можно приближенно считать равной высоте кулоновского барьера для этой частицы
то она вследствие кулоновского отталкивания со стороны ядра («скатываясь с кулоновского барьера») приобретает кинетическую энергию, равную потенциальной энергии отталкивания между частицей и ядром, которую можно приближенно считать равной высоте кулоновского барьера для этой частицы  .
.
Высота кулоновского барьера для протонов и дейтонов
(см. скан)
Стало быть, пороговая затрата энергии на удаление заряженной частицы из ядра (с перевалом через кулоновский барьер) равна

При вычислении высоты кулоновского барьера обычно применяют эмпирическую формулу для радиусов ядер:

Тогда

где для протонов и дейтонов  а для альфа-частиц
а для альфа-частиц 
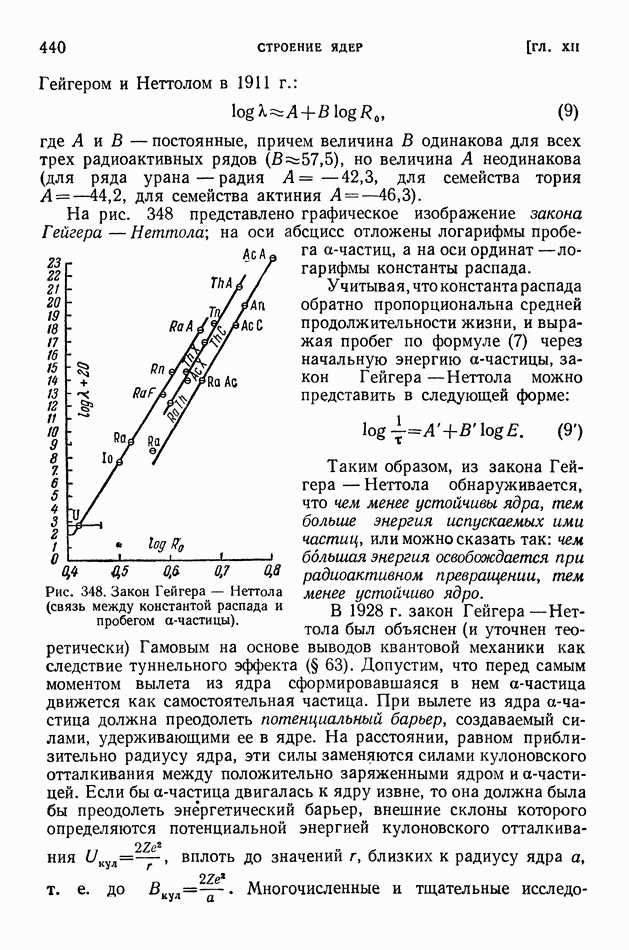
Таблицы величин  для всевозможных стабильных и нестабильных ядер служат основным средством анализа энергетически возможного хода ядерных реакций. Эти таблицы составляют по значениям атомных масс, по полным энергиям связи и по экспериментальным данным изученных ядерных превращений.
для всевозможных стабильных и нестабильных ядер служат основным средством анализа энергетически возможного хода ядерных реакций. Эти таблицы составляют по значениям атомных масс, по полным энергиям связи и по экспериментальным данным изученных ядерных превращений.
В качестве примера проанализируем возможные виды распада возбужденного ядра Для этого согласно (40) сопоставим полные энергии связи, выраженные  мегаэлектроновольтах, следующих ядер в их основных состояниях:
мегаэлектроновольтах, следующих ядер в их основных состояниях:

Получаем:

Следовательно, если энергия возбуждения ядра  меньше
меньше  ядро будет отдавать ее, испуская
ядро будет отдавать ее, испуская  фотон. При облучении
фотон. При облучении  -фотонами с
-фотонами с  будет наблюдаться фоторасщепление ядра с выбросом нейтронов и протонов. Таким образом, значение энергии
будет наблюдаться фоторасщепление ядра с выбросом нейтронов и протонов. Таким образом, значение энергии  является порогом фотоядерной реакции для изотопа серы
является порогом фотоядерной реакции для изотопа серы  При энергиях возбуждения ядра
При энергиях возбуждения ядра  порядка
порядка  может происходить выброс альфа-частицы, а при возбуждениях, превышающих
может происходить выброс альфа-частицы, а при возбуждениях, превышающих  более вероятен выброс дейтона. Если ядру
более вероятен выброс дейтона. Если ядру  была сообщена избыточная энергия
была сообщена избыточная энергия  то наиболее вероятным является сначала выброс дейтона, сразу понижающий энергию возбуждения примерно в 2 раза, а вслед за этим выброс еще одной частицы (чтобы установить, какой именно, нужно аналогичным образом проанализировать получающееся ядро
то наиболее вероятным является сначала выброс дейтона, сразу понижающий энергию возбуждения примерно в 2 раза, а вслед за этим выброс еще одной частицы (чтобы установить, какой именно, нужно аналогичным образом проанализировать получающееся ядро  для этого ядра
для этого ядра  следовательно, за дейтоном будет выброшен: протон, а не нейтрон); оставшаяся избыточная энергия будет отдана у-излучением.
следовательно, за дейтоном будет выброшен: протон, а не нейтрон); оставшаяся избыточная энергия будет отдана у-излучением.
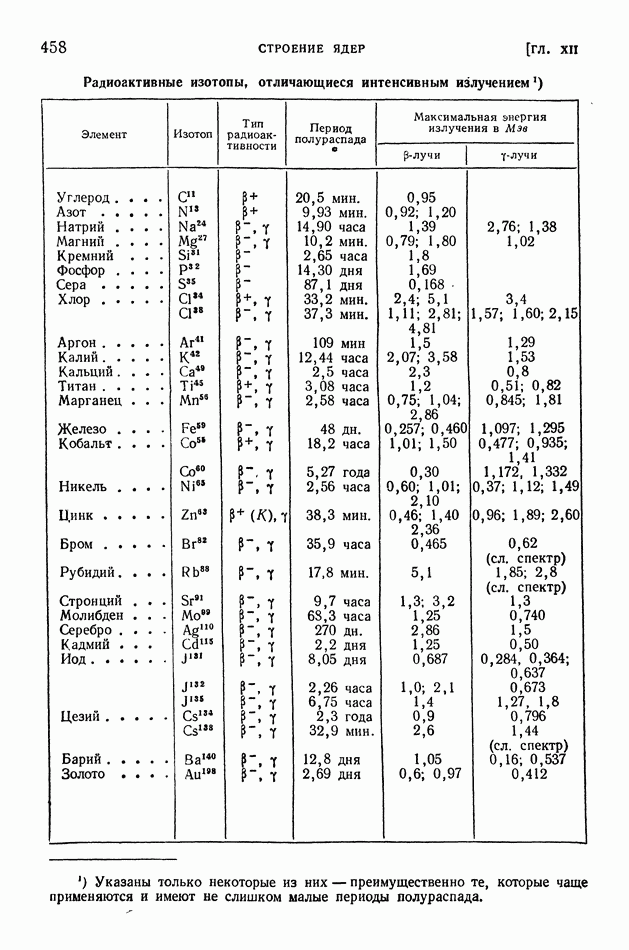
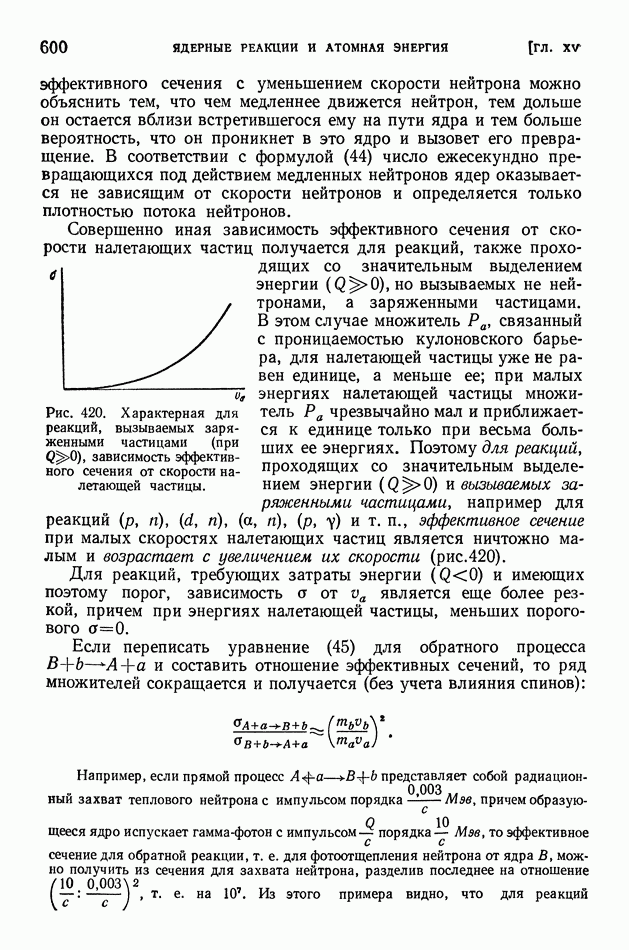
В качестве второго примера проанализируем, какие реакции могут быть вызваны при поглощении медленного нейтрона ядром  . Энергия отделения нейтрона для ядра
. Энергия отделения нейтрона для ядра  равна
равна  Это означает, что когда медленный нейтрон захватывается ядром
Это означает, что когда медленный нейтрон захватывается ядром  то составное ядро
то составное ядро  получается не в основном, а в возбужденном состоянии и с энергией возбуждения
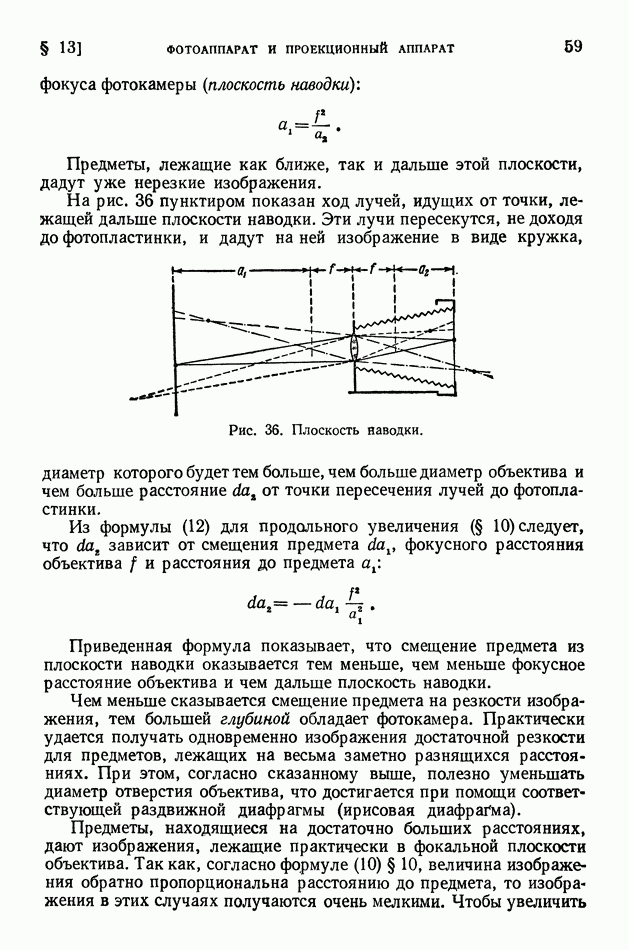
получается не в основном, а в возбужденном состоянии и с энергией возбуждения  Если эта энергия возбуждения будет отдана у-излучением» то Для удаления нейтрона из ядра
Если эта энергия возбуждения будет отдана у-излучением» то Для удаления нейтрона из ядра  перешедшего в основное состояние, необходимо сообщить ему энергию
перешедшего в основное состояние, необходимо сообщить ему энергию  Но очевидно, что кроме у-излучения составное ядро может испускать обратно поглощенный нейтрон. Возможен также выброс протона, так как энергия отделения протона от ядра
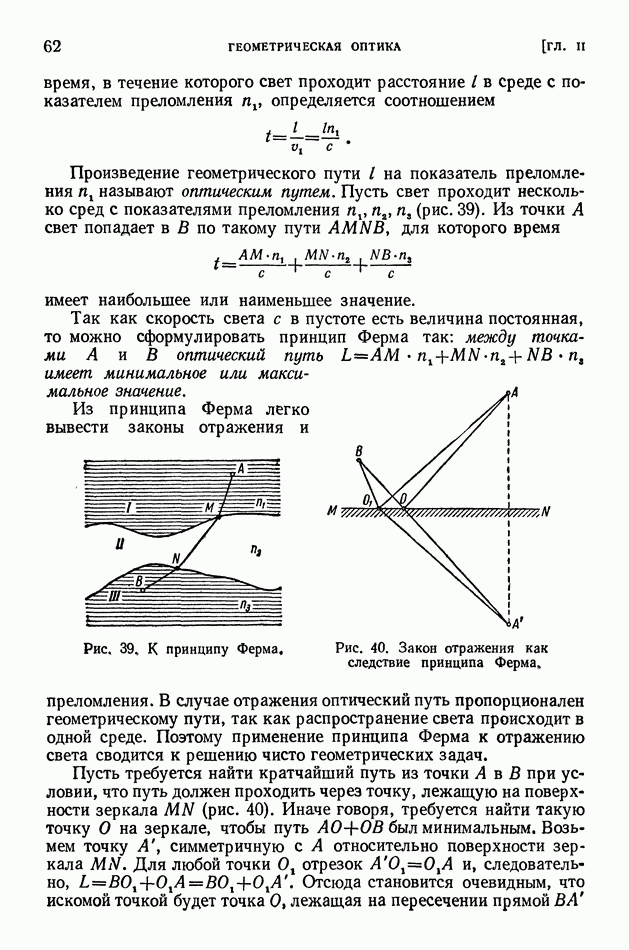
Но очевидно, что кроме у-излучения составное ядро может испускать обратно поглощенный нейтрон. Возможен также выброс протона, так как энергия отделения протона от ядра  равна
равна  Следовательно, при энергии возбуждения
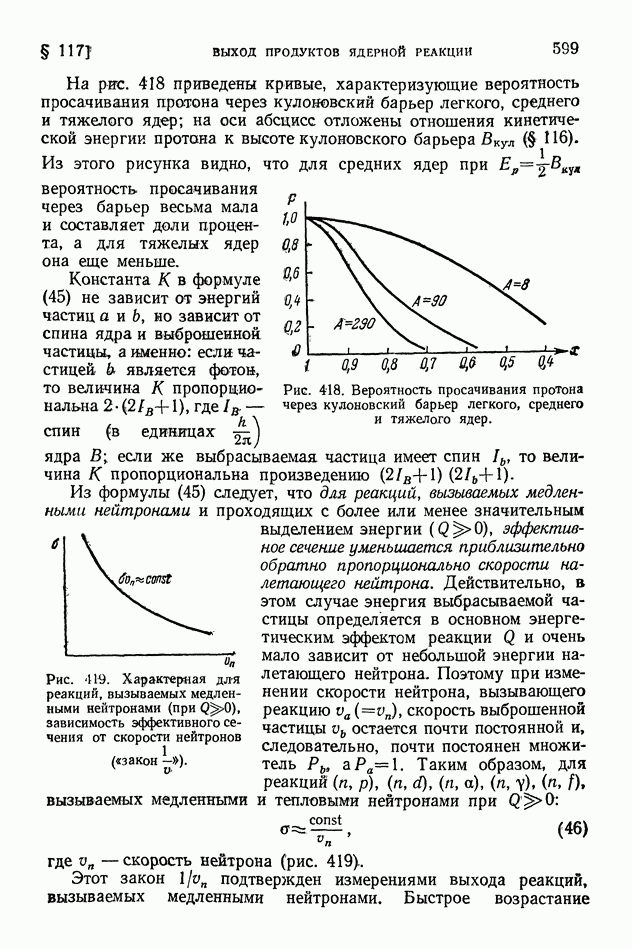
Следовательно, при энергии возбуждения  имеется некоторая вероятность просачивания протона через кулоновский барьер, высота которого в этом случае
имеется некоторая вероятность просачивания протона через кулоновский барьер, высота которого в этом случае  согласно формуле (42), равна Вкул
согласно формуле (42), равна Вкул  И действительно, поглощение тепловых нейтронов азотом
И действительно, поглощение тепловых нейтронов азотом  приводит как к у-излучению с
приводит как к у-излучению с  и к выбросу протонов (последнее является результатом туннельного эффекта).
и к выбросу протонов (последнее является результатом туннельного эффекта).
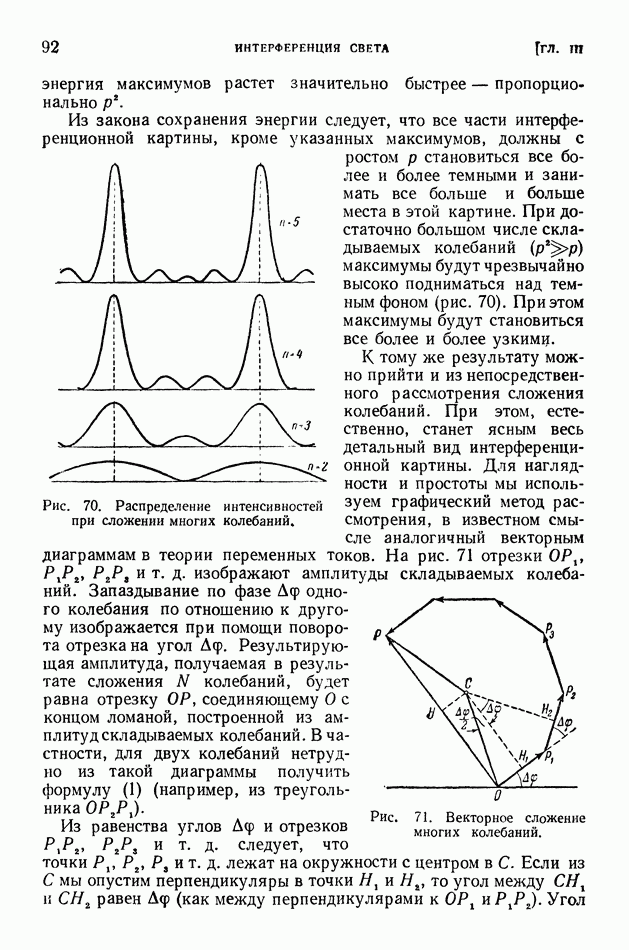
Для выброса протона из ядра  («с перевалом» через кулоновский барьер) нужна энергия
(«с перевалом» через кулоновский барьер) нужна энергия  Поэтому выброс протонов резко возрастает при энергии поглощаемого нейтрона, равной (в системе центра масс)
Поэтому выброс протонов резко возрастает при энергии поглощаемого нейтрона, равной (в системе центра масс)  [или в лабораторной системе, согласно формуле (6) § 110, при энергии
[или в лабораторной системе, согласно формуле (6) § 110, при энергии 
Многие составные ядра совершенно неустойчивы и поэтому не могут быть получены в их основных состояниях. Для таких ядер энергии отделения определяют по энергетическому балансу реакций, в которых они участвуют, а если необходимых экспериментальных данных нет, то ориентировочные значения  вычисляют, руководствуясь формулой
вычисляют, руководствуясь формулой 
Если сопоставлять ядра, пользуясь формулой (34), то становятся понятными следующие правила:
1) Превышение числа нейтронов в ядре над числом протонов приводит к уменьшению энергии отделения нейтронов и к увеличению энергии отделения протонов (в тяжелых ядрах каждый избыточный нейтрон сказывается в уменьшении  приблизительно на
приблизительно на 
2) Степень заполнения высших энергетических уровней нуклонов в ядре вносит в энергию отделения вклад Д:

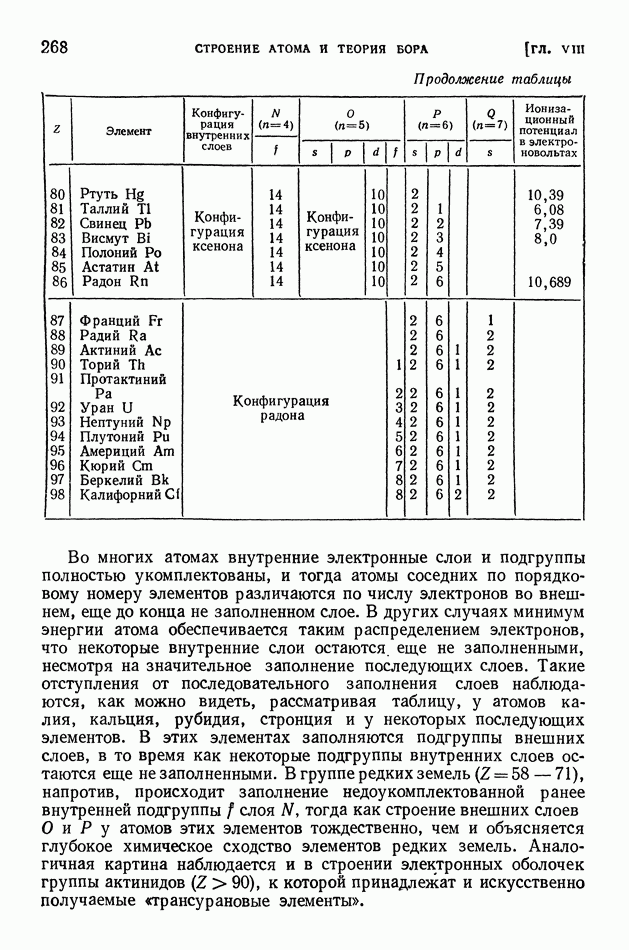
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ЧЕТВЕРТАЯ. ОПТИКА
- § 2. Электромагнитная теория света
- § 3. Скорость света
- § 4. Опыт Майкельсона
- § 5. Отрицательный результат опыта Майкельсона и теория относительности
- § 6. Некоторые замечания о теории относительности
- § 7. Явление Доплера для световых волн
- ГЛАВА II. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- § 8. Законы отражения и преломления света
- § 9. Линза
- § 10. Оптические системы
- § 11. Глаз как оптическая система
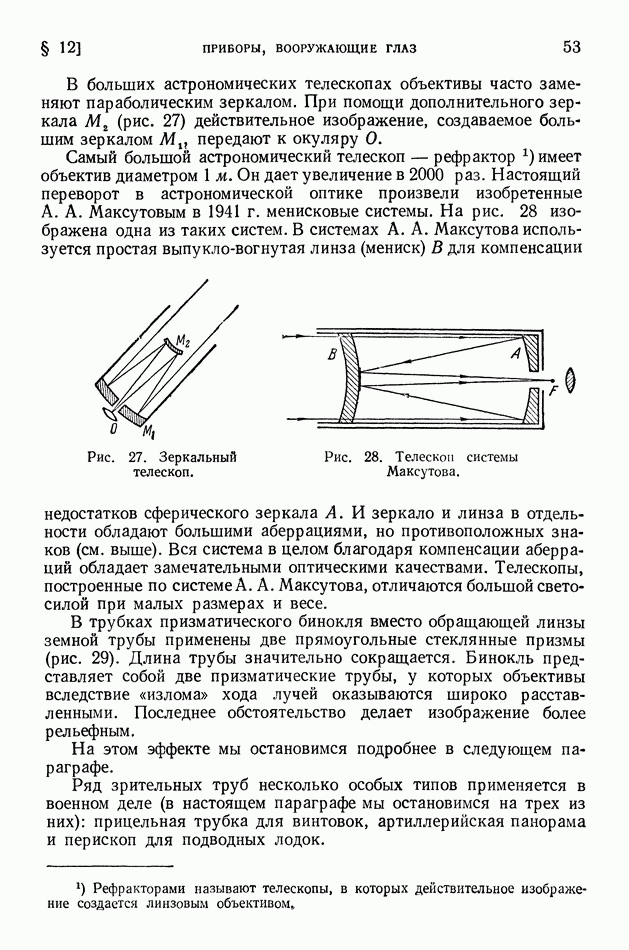
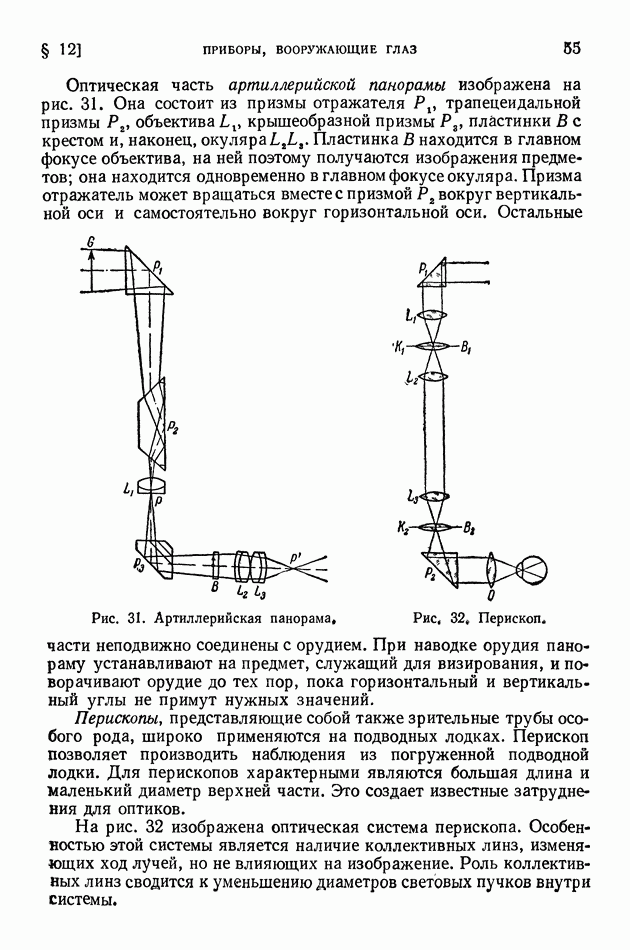
- § 12. Приборы, вооружающие глаз
- § 13. Фотоаппарат и проекционный аппарат
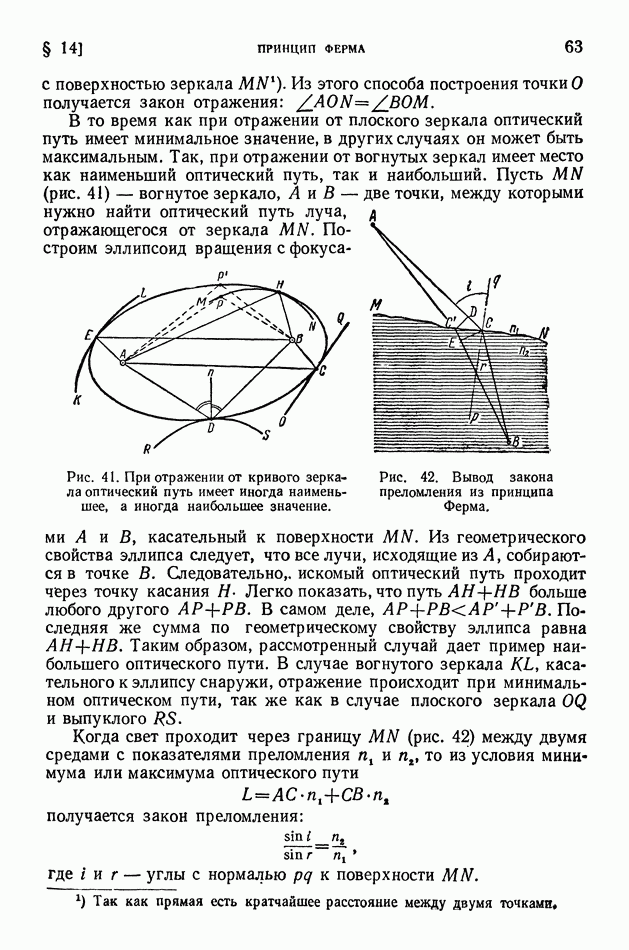
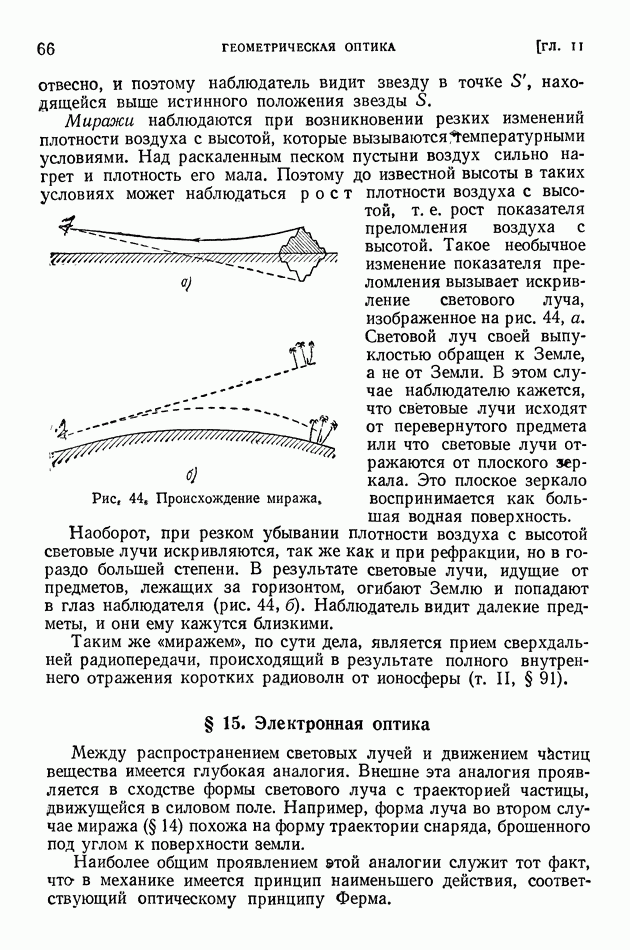
- § 14. Принцип Ферма
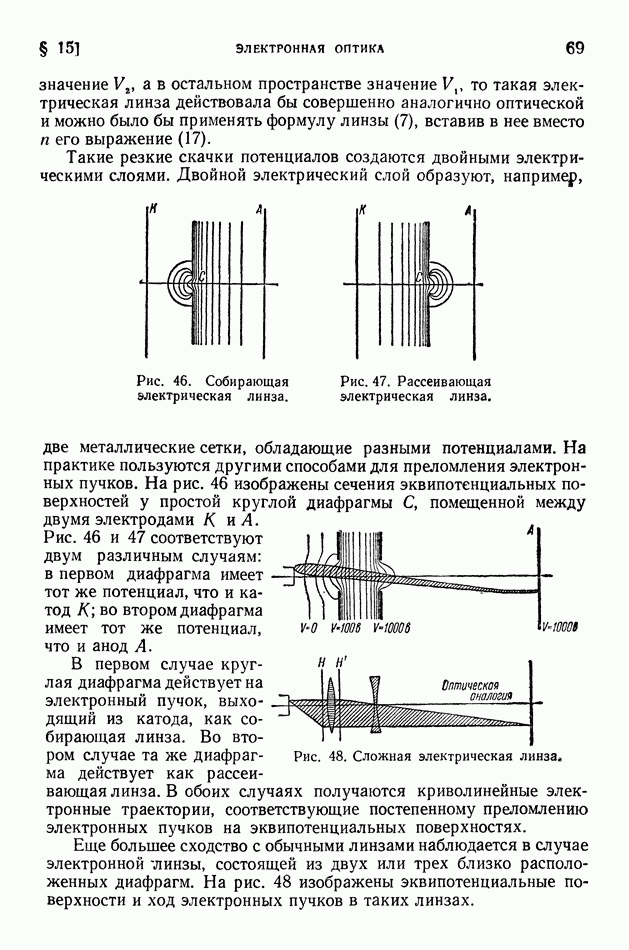
- § 15. Электронная оптика
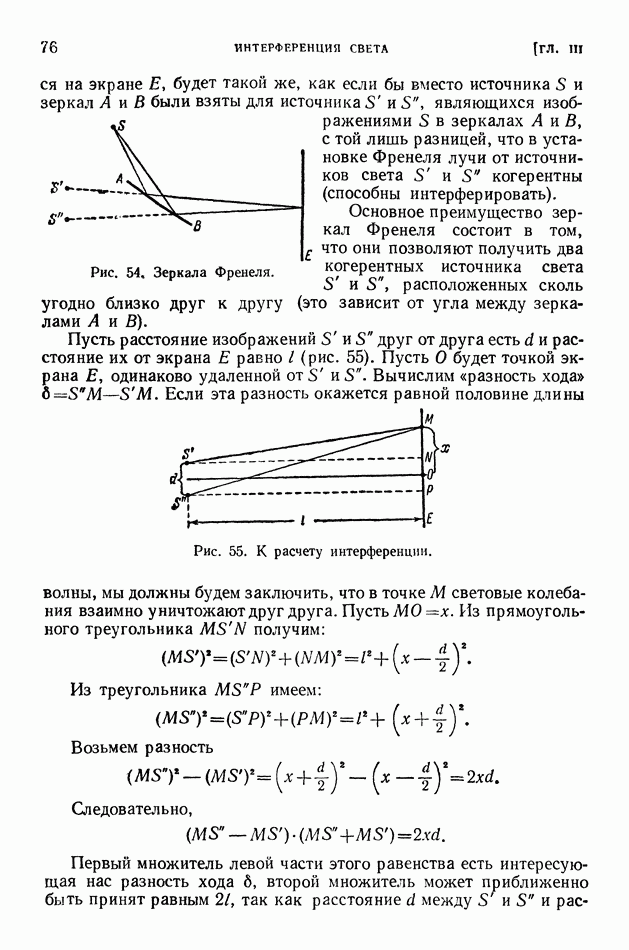
- ГЛАВА III. ИНТЕРФЕРЕНЦИЯ СВЕТА
- § 16. Принцип суперпозиции. Когерентность
- § 17. Зеркала Френеля
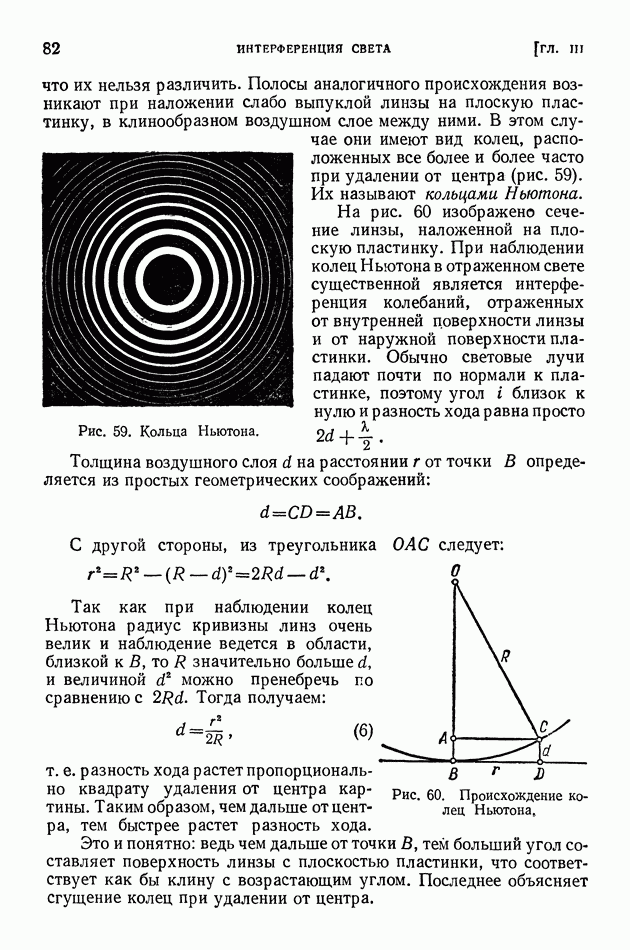
- § 18. Цвета тонких пленок. Полосы равной толщины
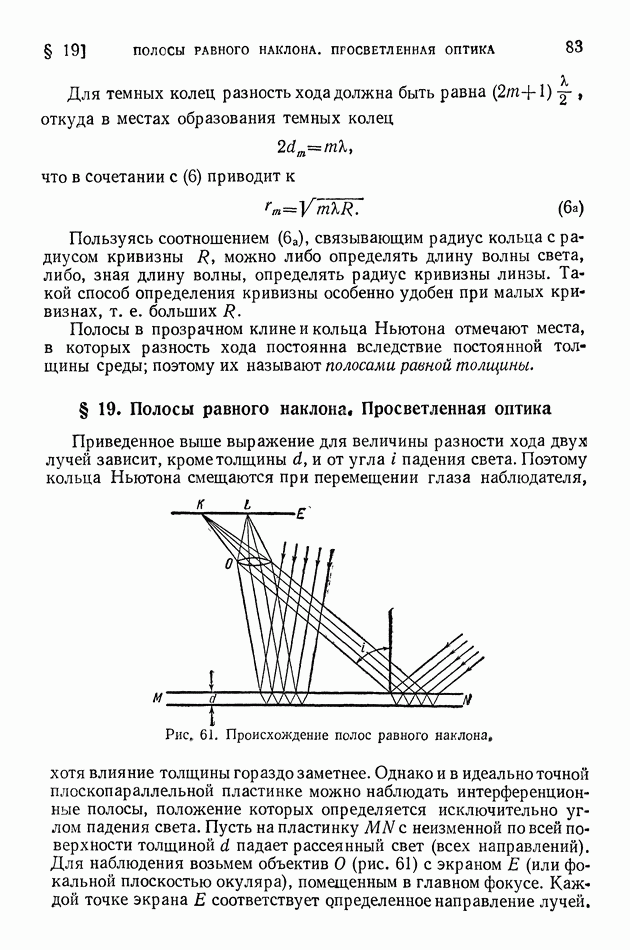
- § 19. Полосы равного наклона. Просветленная оптика
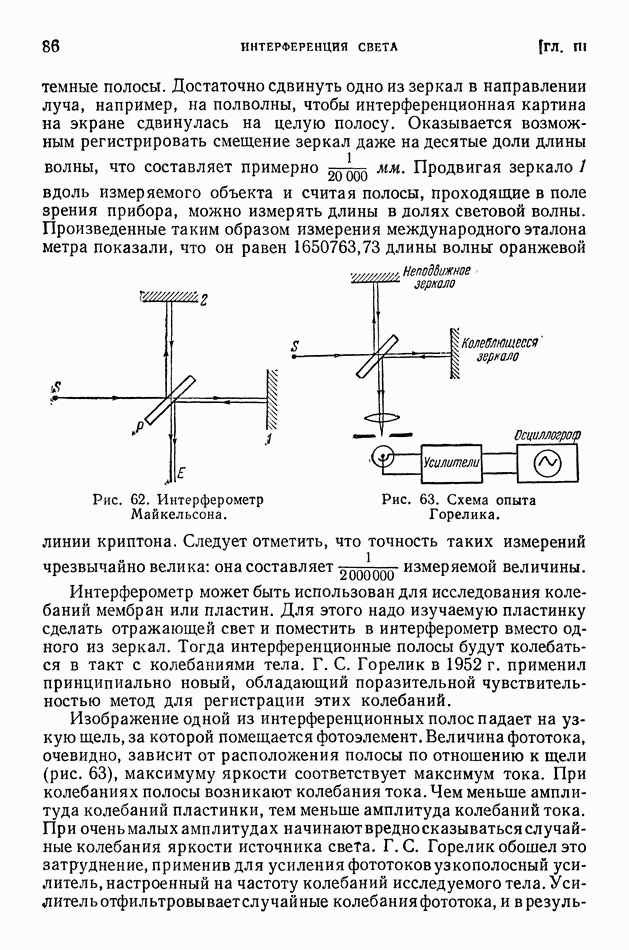
- § 20. Интерферометры
- § 21. Интерференционное измерение технических мер длины
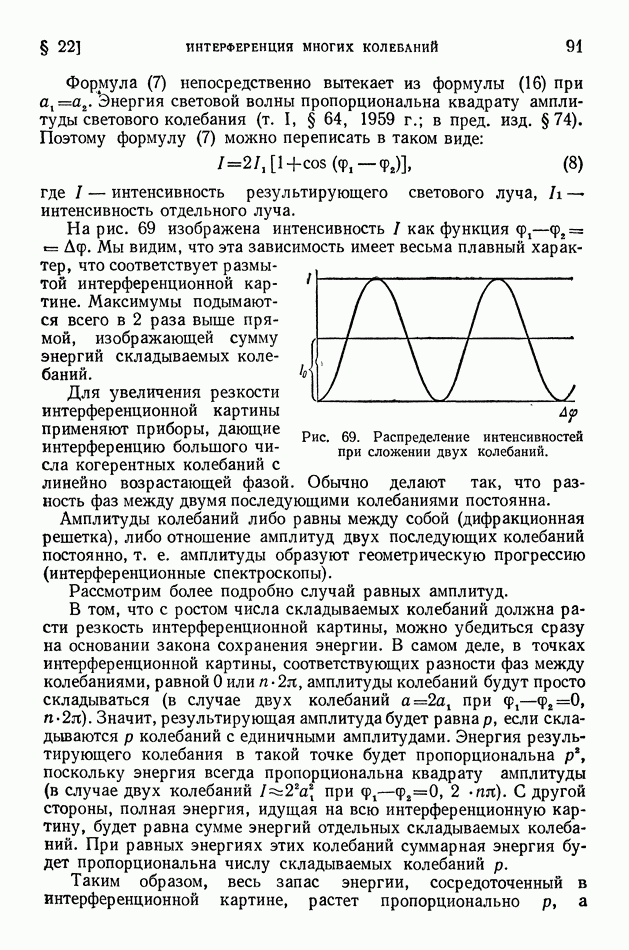
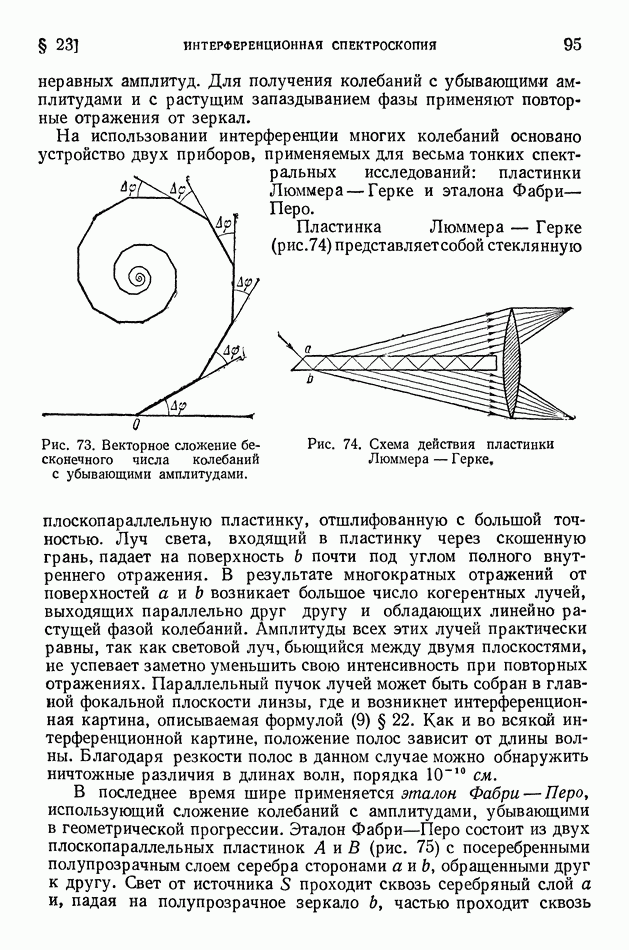
- § 22. Интерференция многих колебаний
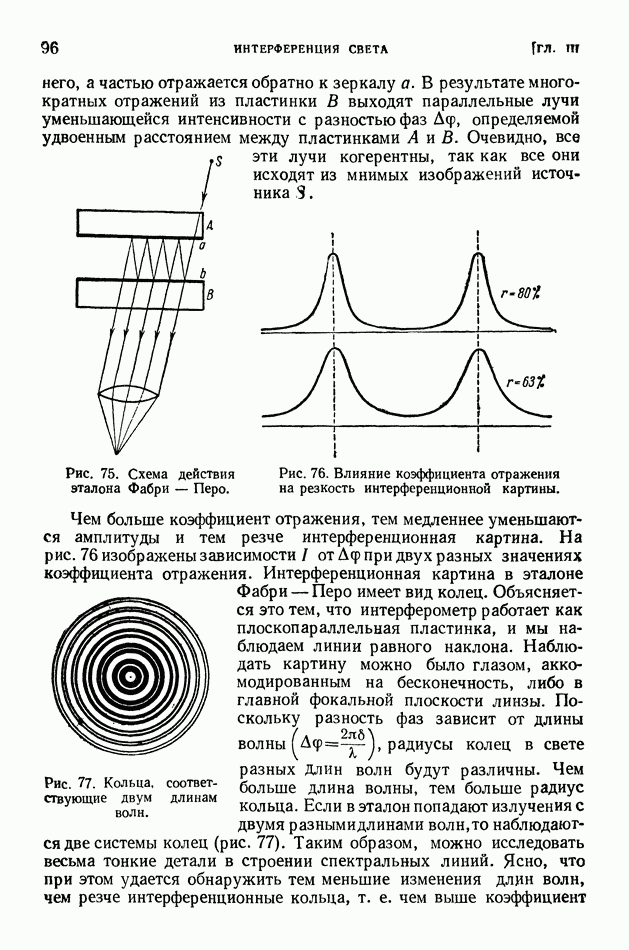
- § 23. Интерференционная спектроскопия
- ГЛАВА IV. ДИФРАКЦИЯ СВЕТА
- § 24. Явление дифракции. Опыт Френеля
- § 25. Принцип Гюйгенса-Френеля
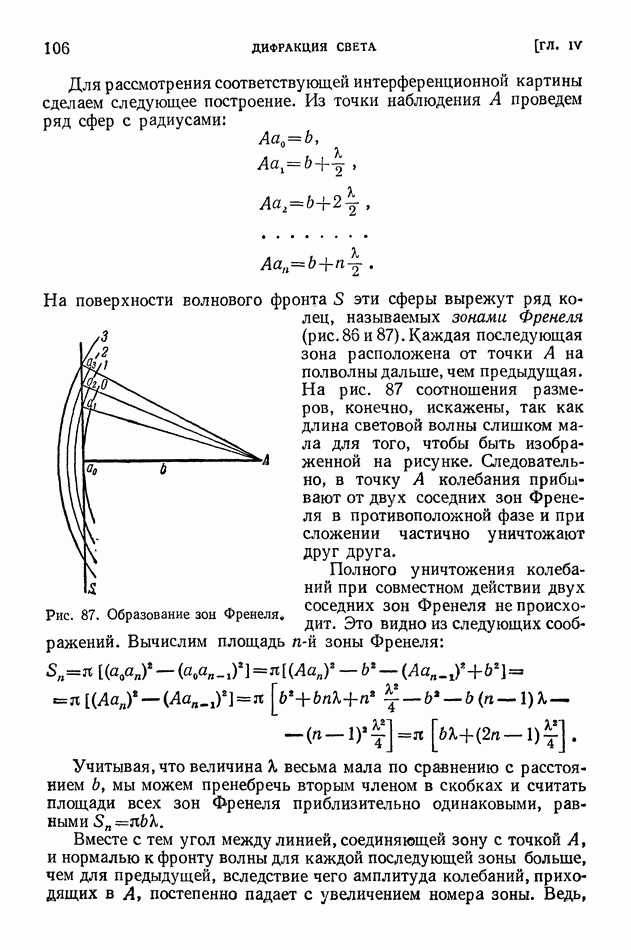
- § 26. Метод зон Френеля
- § 27. Дифракция от узкой щели
- § 28. Дифракционная решетка
- § 29. Дифракционный спектр. Решетки Роуланда и эшелон Майкельсона
- § 30. Плоскостные решетки. Пространственная решетка
- § 31. Структурный рентгеновский анализ
- § 32. Дифракция света на ультразвуковых волнах
- § 33. Дифракция от мелких частиц
- § 34. Разрешающая способность оптических инструментов. Звездный интерферометр
- ГЛАВА V. ПОЛЯРИЗАЦИЯ СВЕТА
- § 35. Поляризация света
- § 36. Двойное лучепреломление
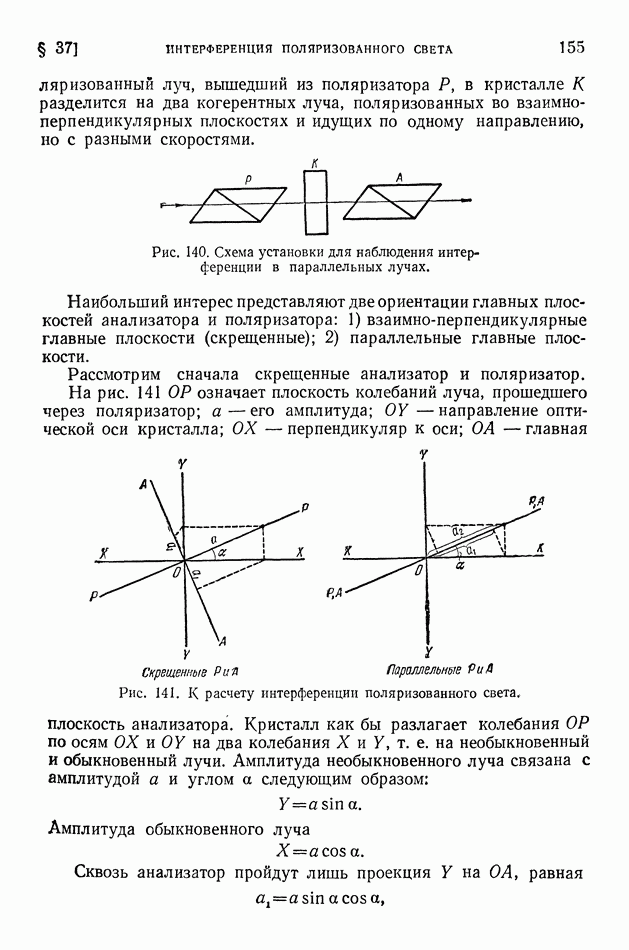
- § 37. Интерференция поляризованного света
- § 38. Оптический метод исследования упругих натяжений. Эффект Керра
- § 39. Вращение плоскости поляризации. Эллиптическая поляризация
- ГЛАВА VI. ДИСПЕРСИЯ, ПОГЛОЩЕНИЕ И ИЗЛУЧЕНИЕ СВЕТА
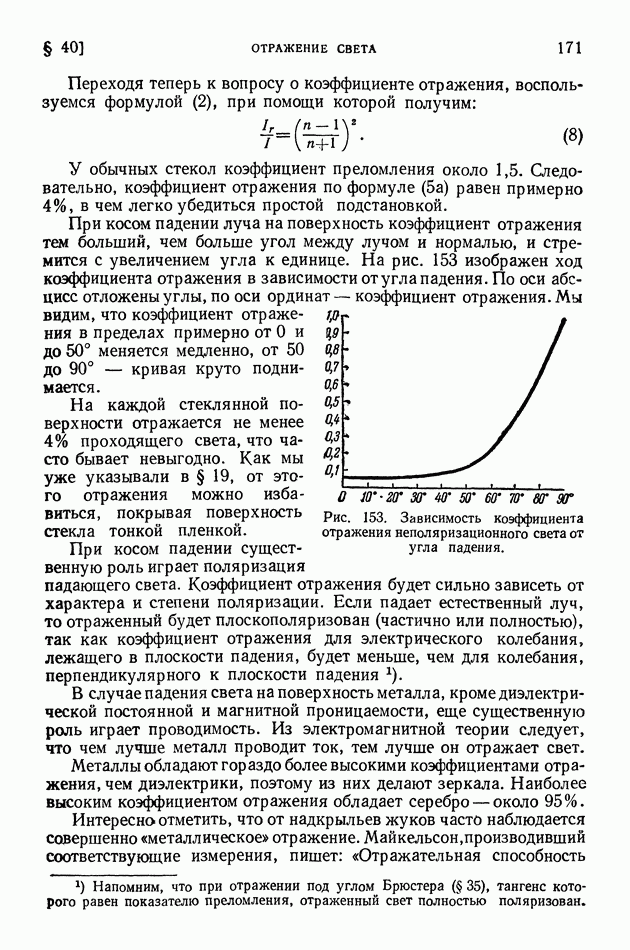
- § 40. Отражение света
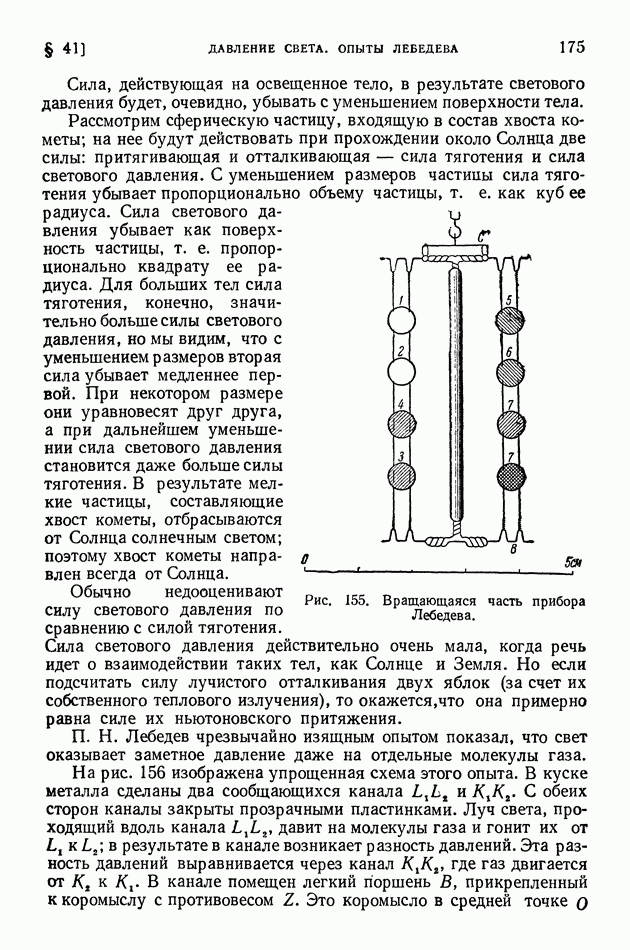
- § 41. Давление света. Опыты Лебедева
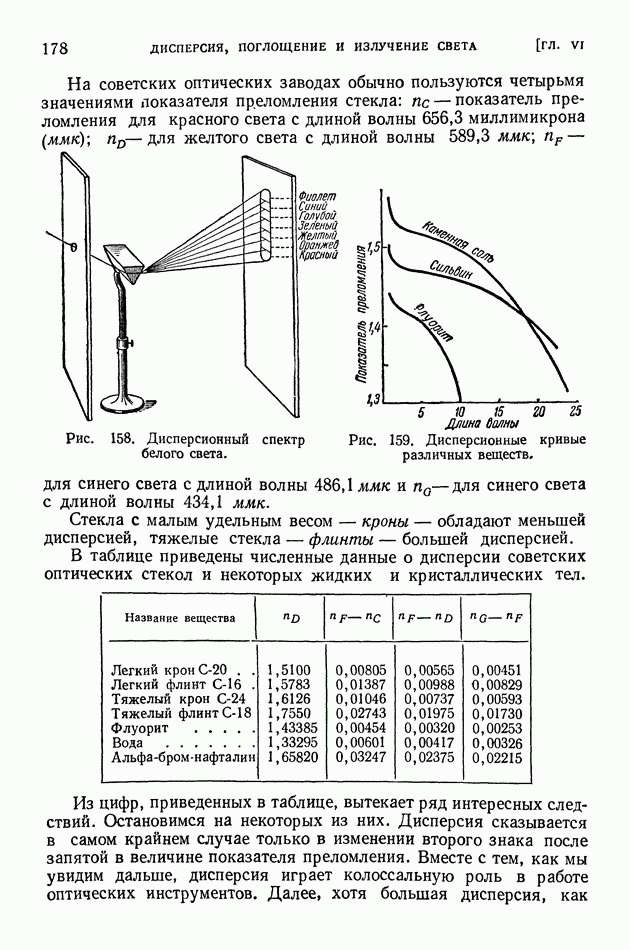
- § 42. Дисперсия. Опыты Ньютона
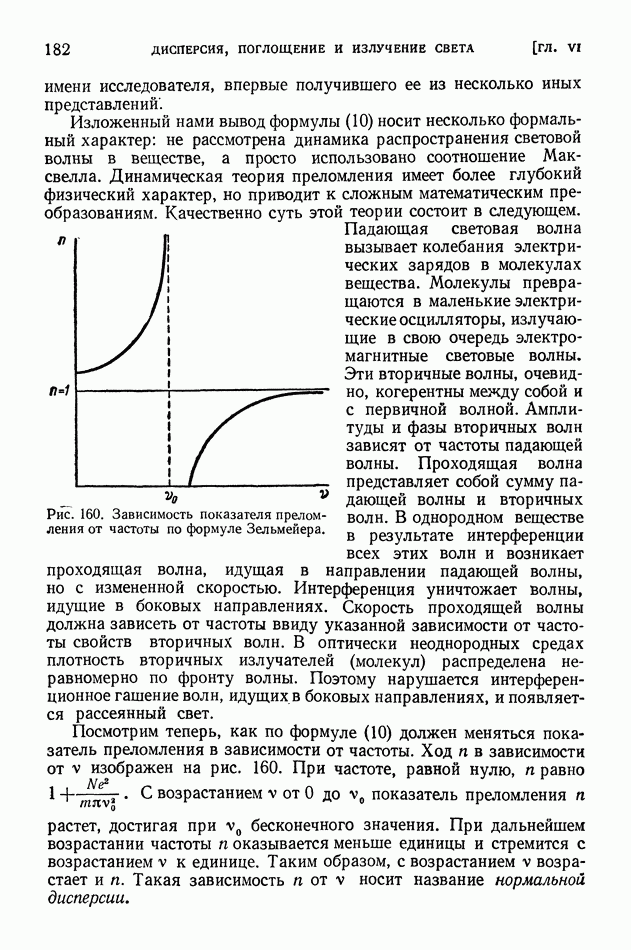
- § 43. Молекулярная теория дисперсии
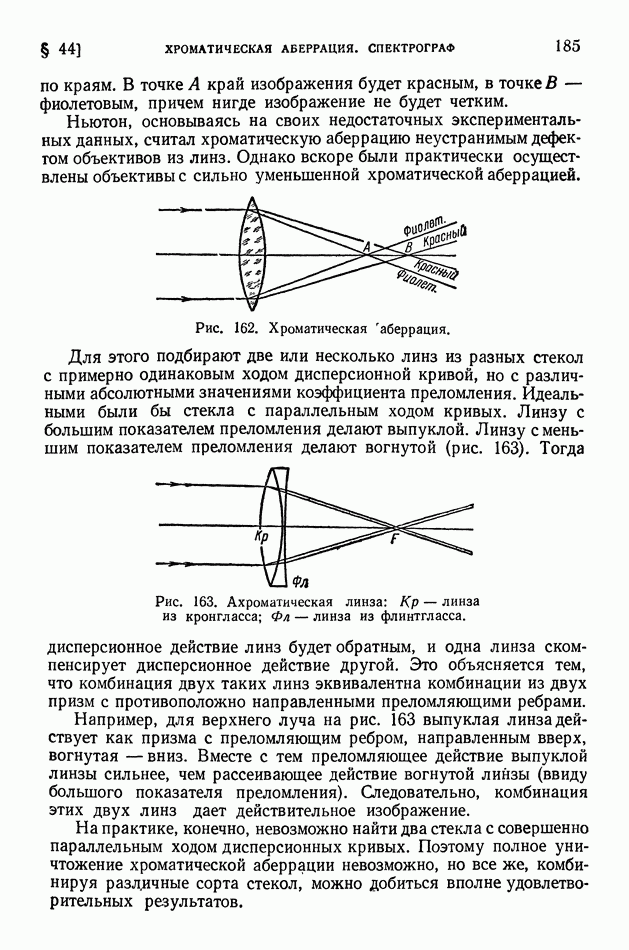
- § 44. Хроматическая аберрация. Спектрограф
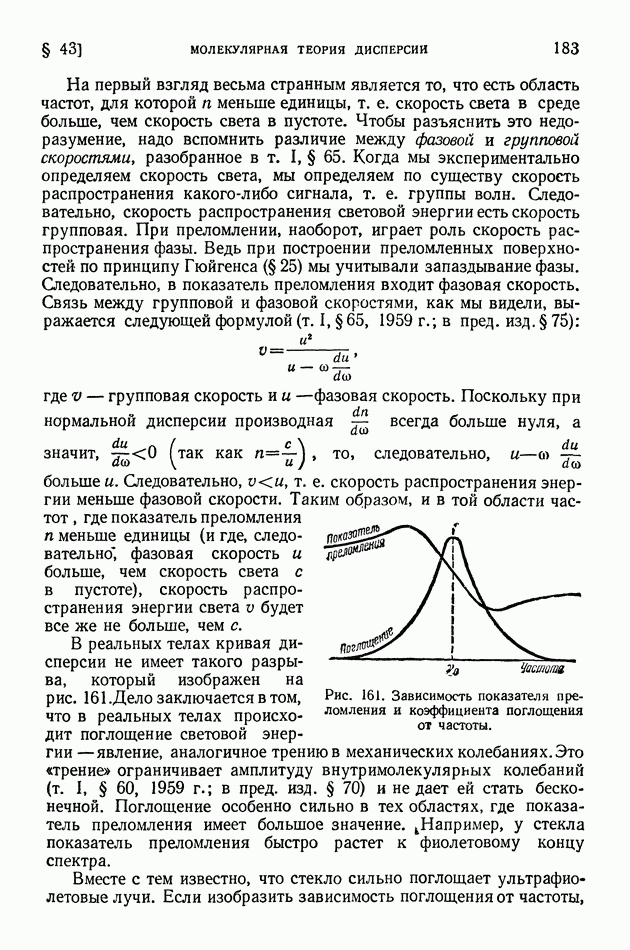
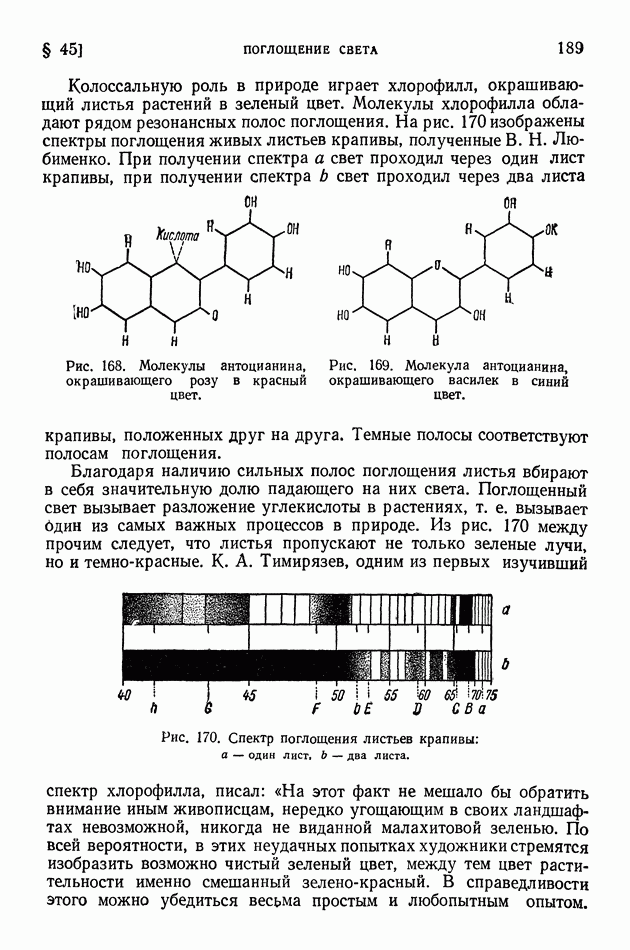
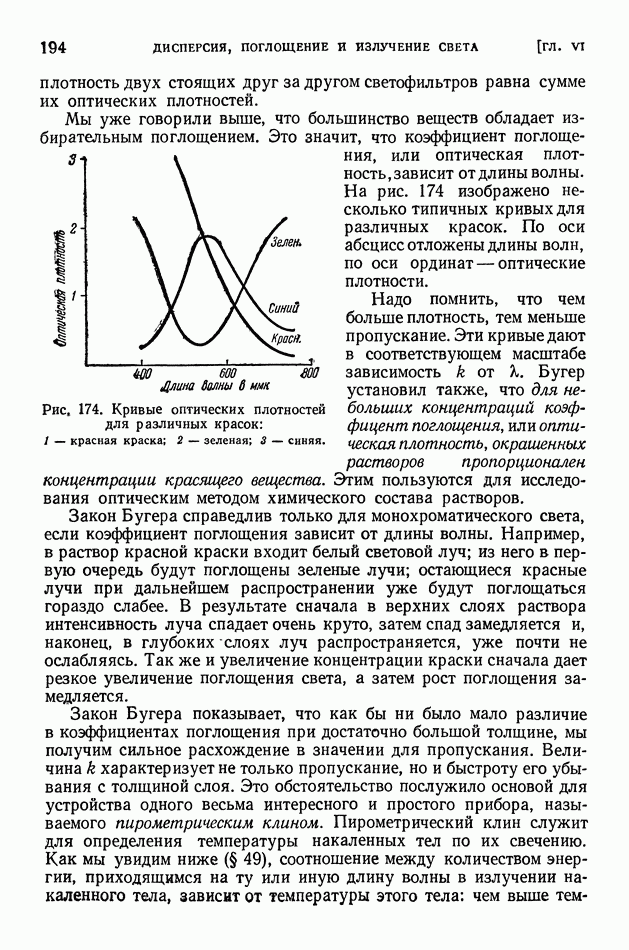
- § 45. Поглощение света
- § 46. Закон Бугера. Опыты Вавилова
- § 47. Атом как элементарный излучатель света
- § 48. Эффект Вавилова — Черенкова
- ГЛАВА VII. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ И СВЕТОВОЙ ПОТОК
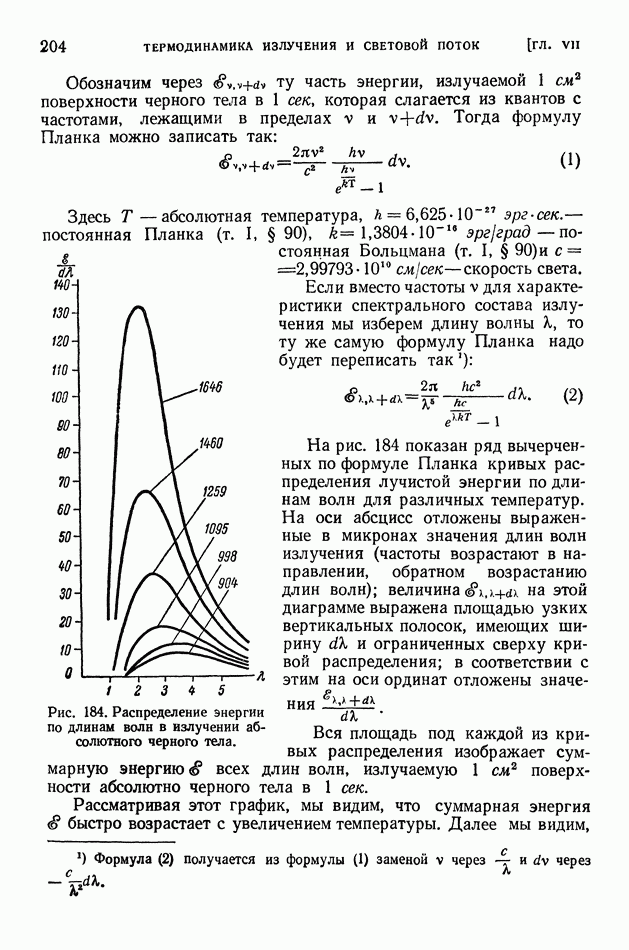
- § 49. Излучение черного тела. Формула Планка. Закон Вина
- § 50. Излучение нечерных тел. Законы Кирхгофа
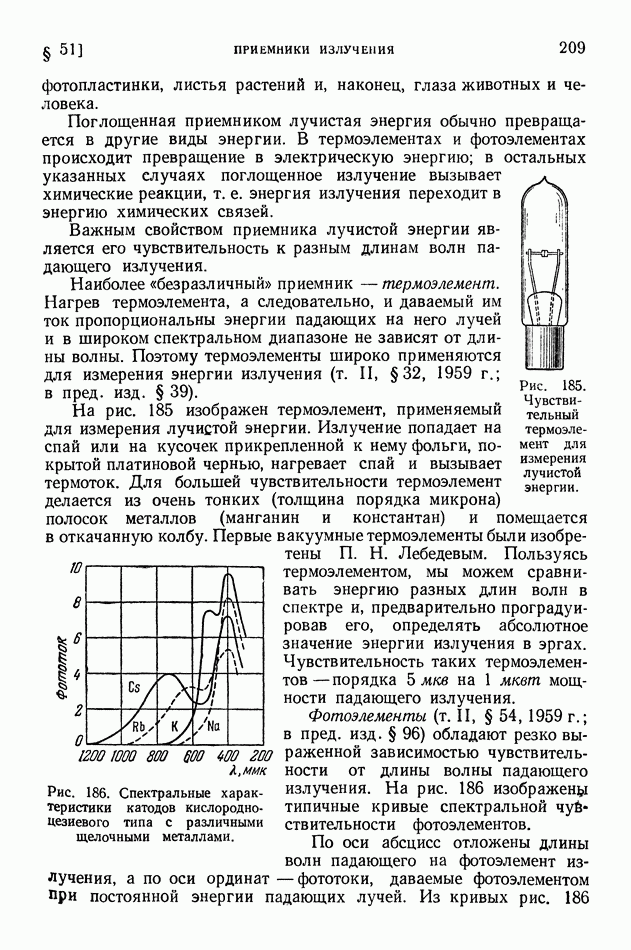
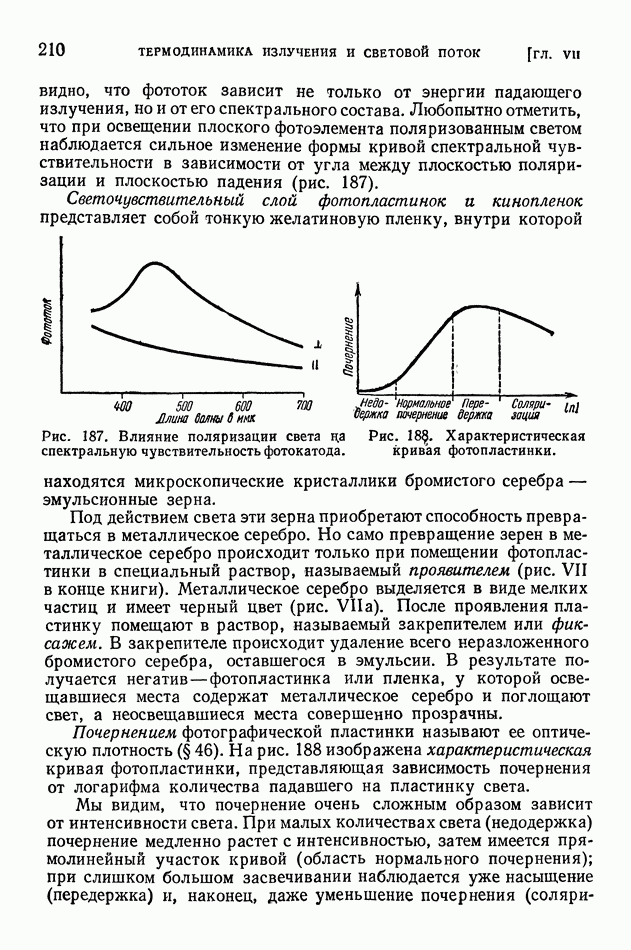
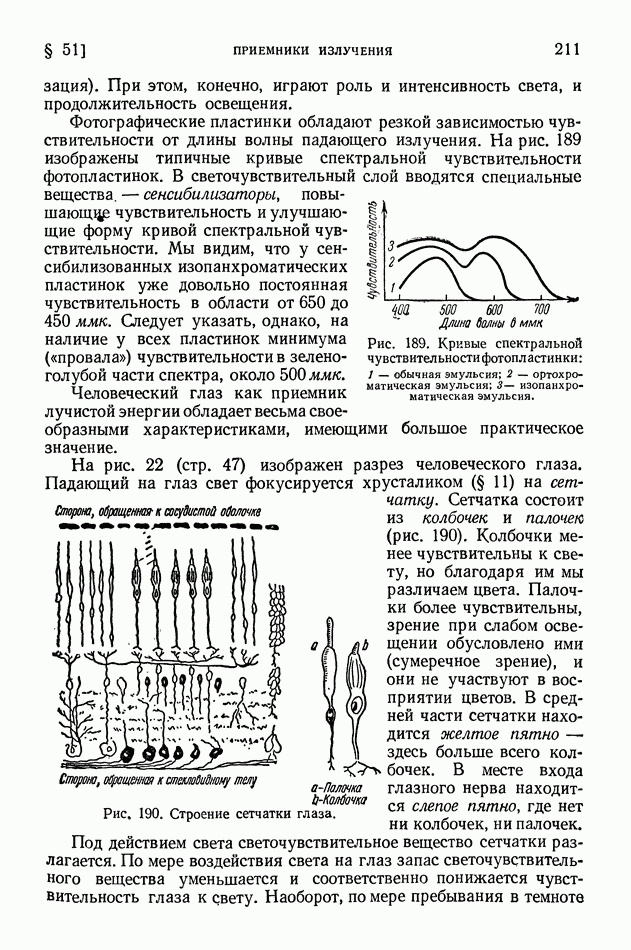
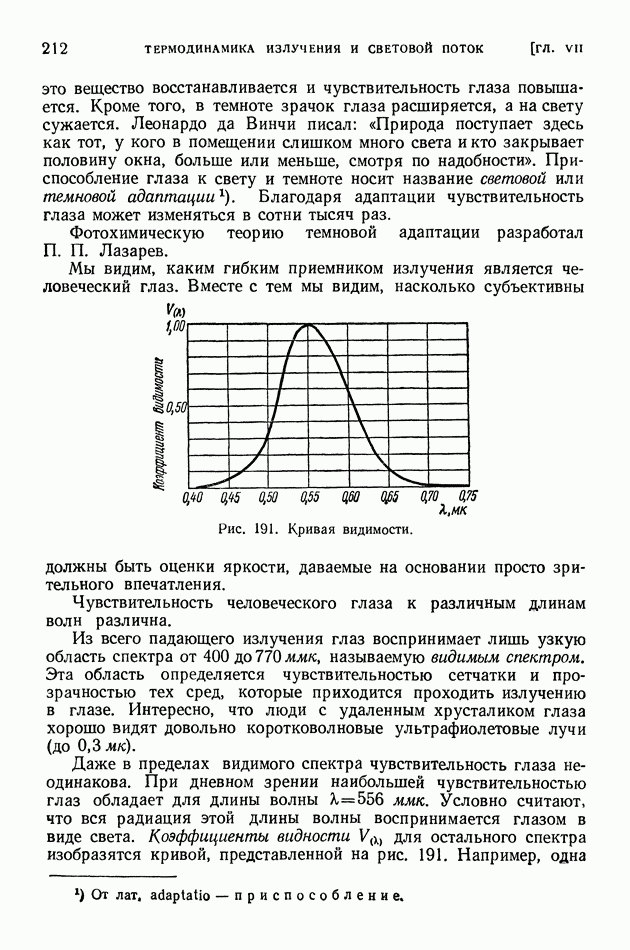
- § 51. Приемники излучения
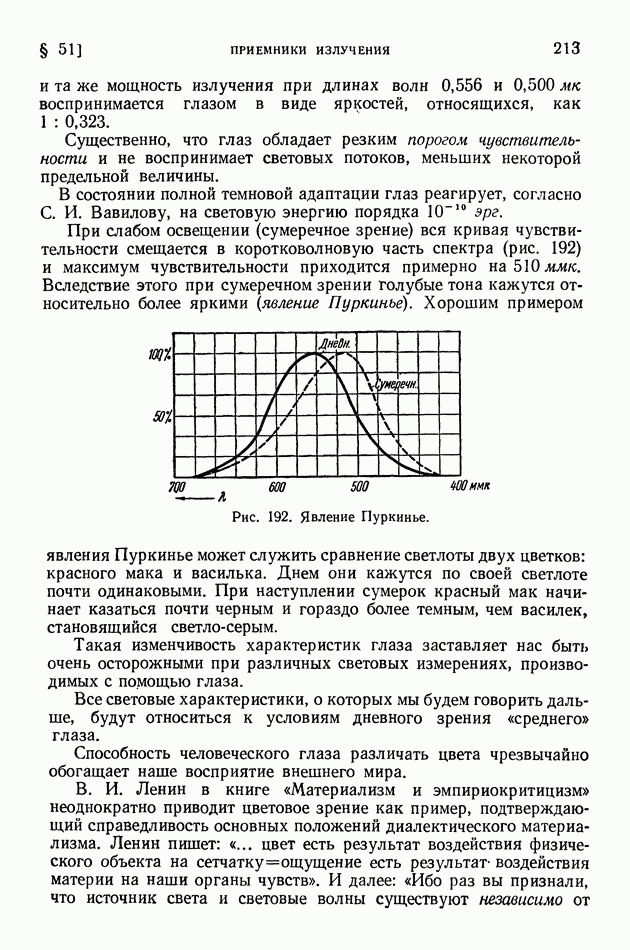
- § 52. Световые величины и их измерения
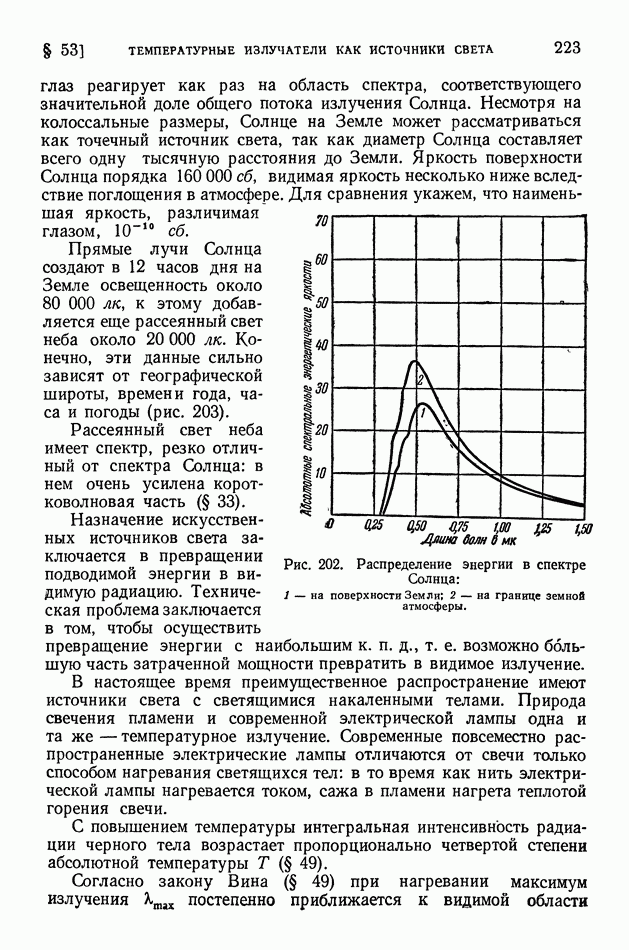
- § 53 Температурные излучатели как источники света
- ЧАСТЬ ПЯТАЯ. АТОМНАЯ ФИЗИКА
- ГЛАВА VIII. СТРОЕНИЕ АТОМА И ТЕОРИЯ БОРА
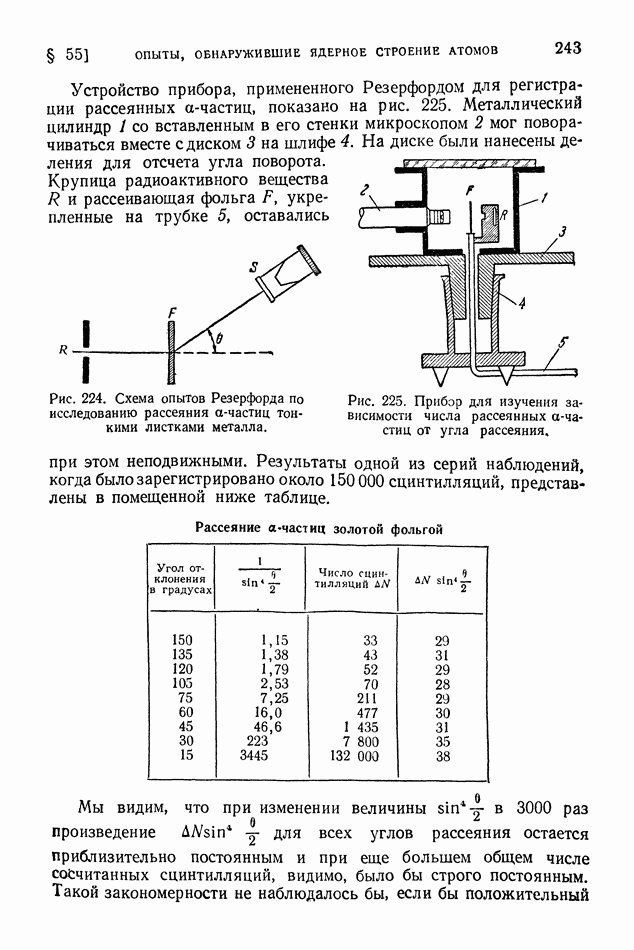
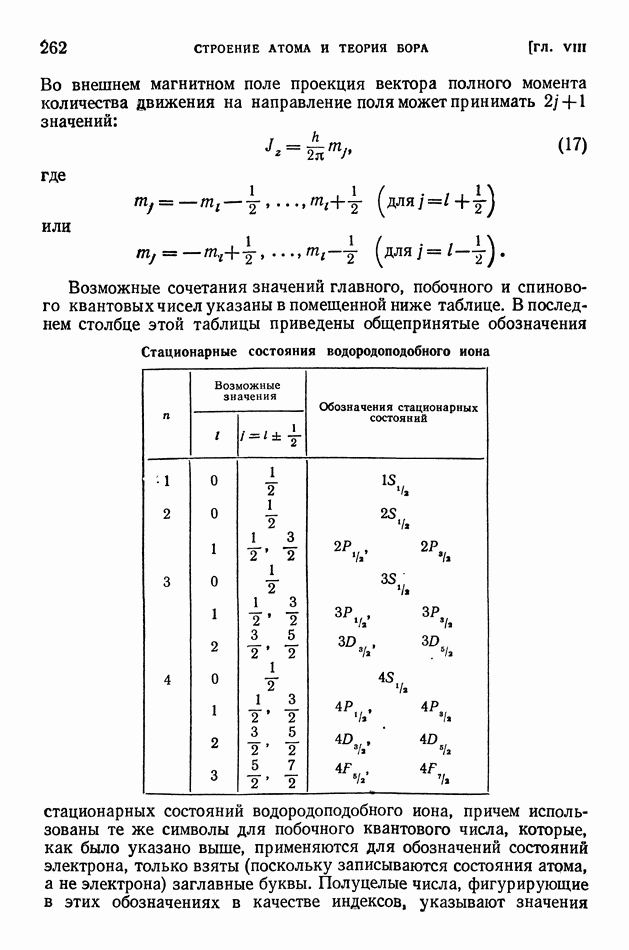
- § 55. Опыты, обнаружившие ядерное строение атомов
- § 56. Противоречие между фактическим строением атомов и выводами классической электродинамики. Строение линейчатых спектров
- § 57. Опытные основания теории квантов в первые годы ее развития
- § 58. Теория Бора. Происхождение спектра водорода
- § 59. Квантовые числа
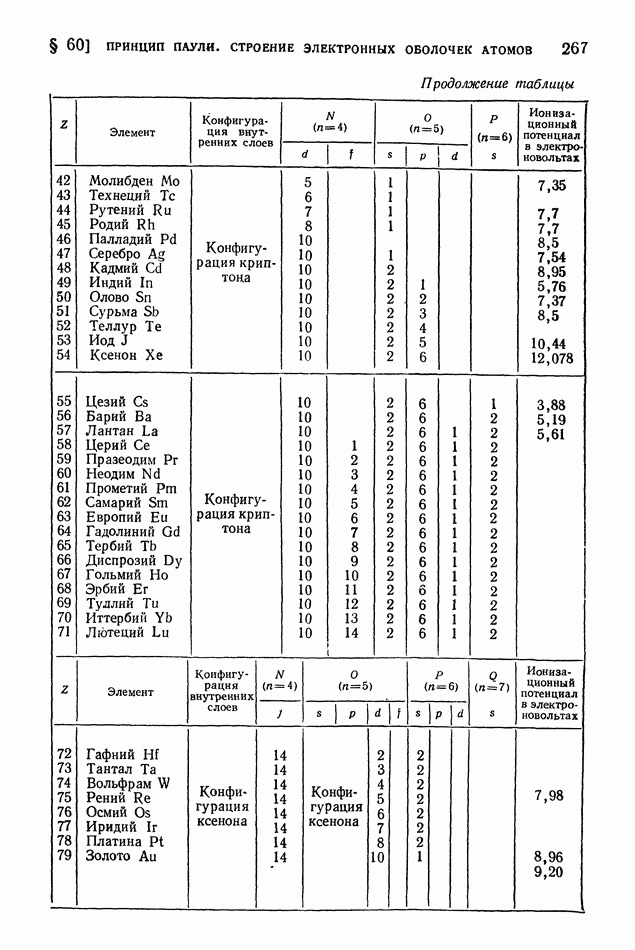
- § 60. Принцип Паули. Строение электронных оболочек атомов
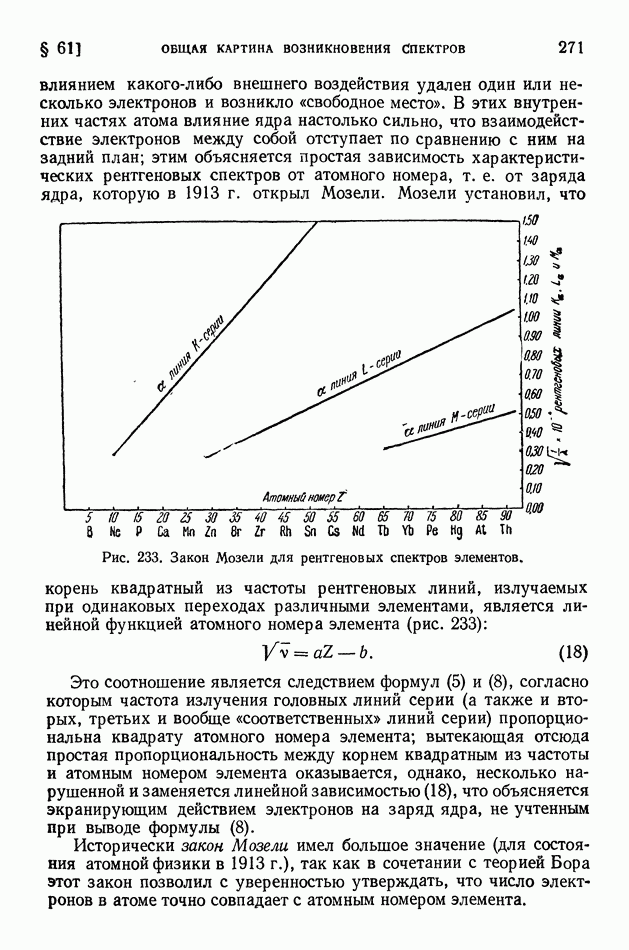
- § 61. Общая картина возникновения спектров
- ГЛАВА IX. ОСНОВЫ КВАНТОВОЙ (ВОЛНОВОЙ) МЕХАНИКИ
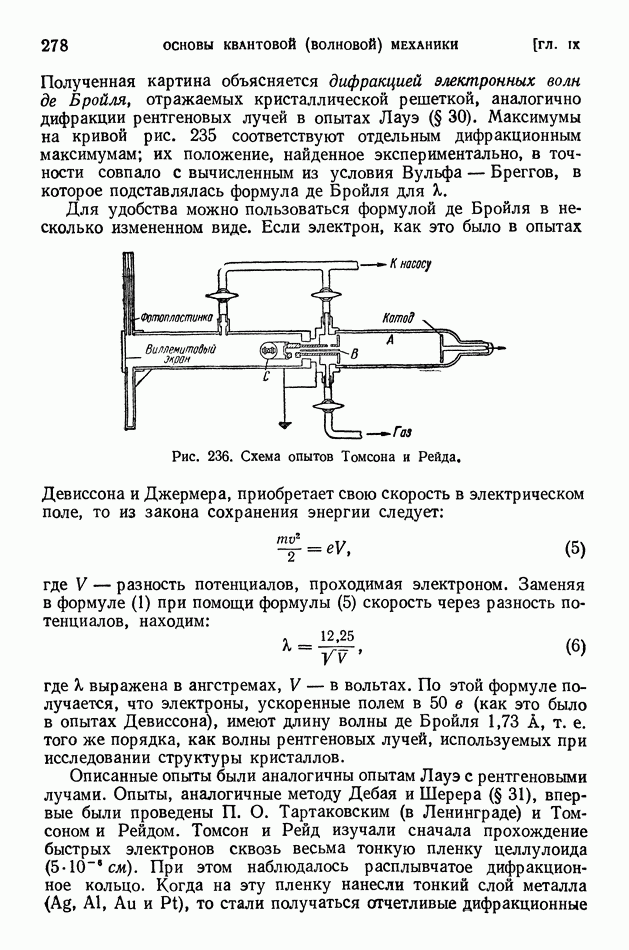
- § 62. Волновые свойства частиц. Формула де Бройля. Дифракция электронов
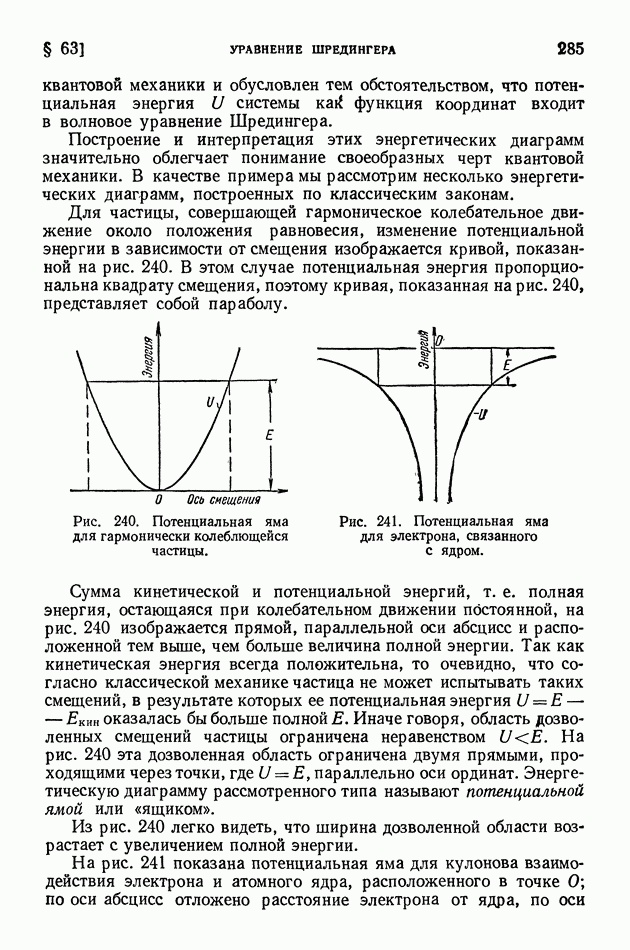
- § 63. Уравнение Шредингера. Просачивание через энергетический барьер. Нулевая энергия
- § 64. Волномеханическая теория атома водорода
- § 65. Соотношение неопределенностей и его разные трактовки
- ГЛАВА X. КВАНТОВАЯ ОПТИКА
- § 66. Развитие квантовой оптики
- § 67. Спектр щелочных металлов. Спин электрона
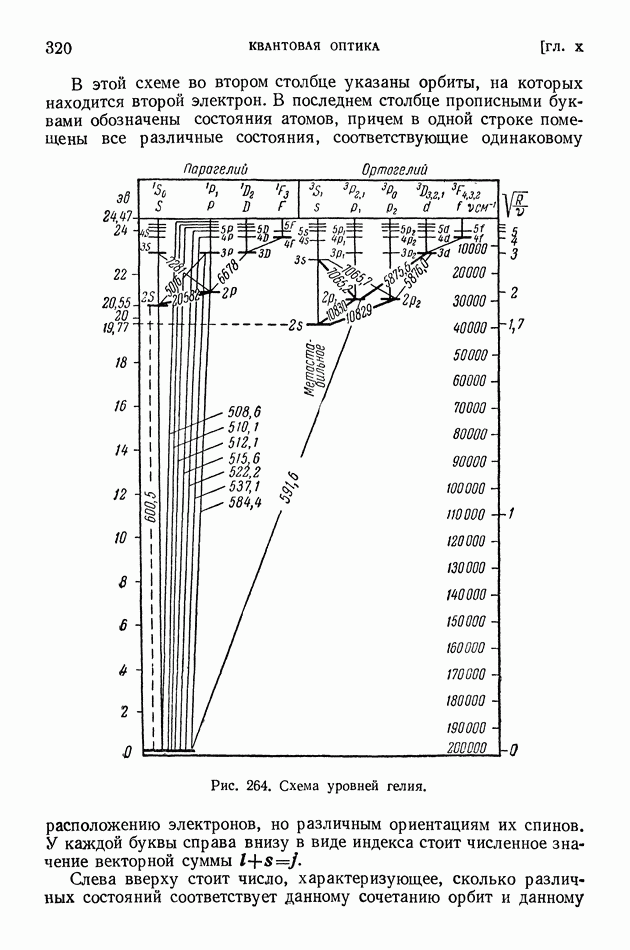
- § 68. Спектр гелия. Символика спектральных термов
- § 69. Сверхтонкая структура спектральных линий
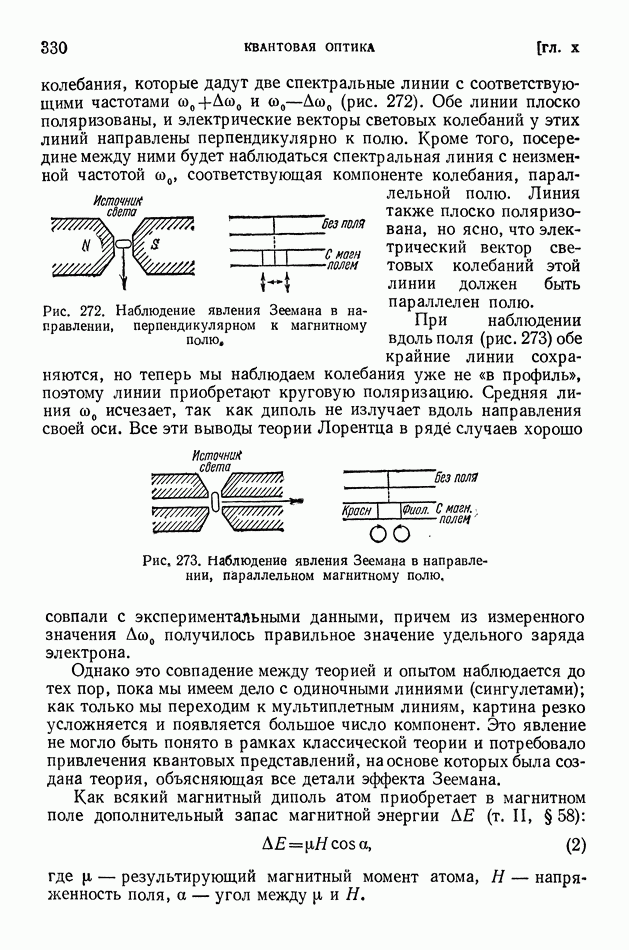
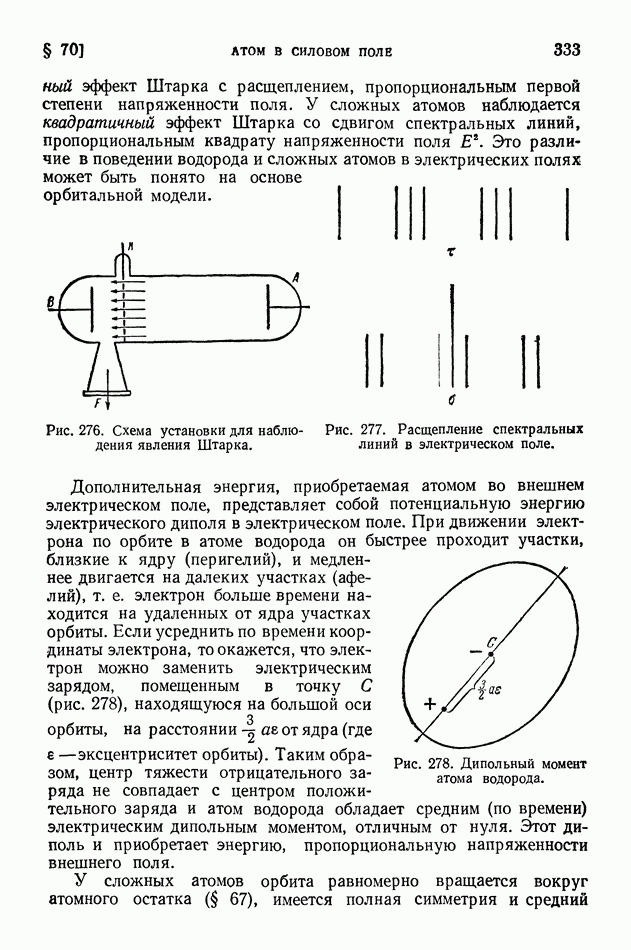
- § 70. Атом в силовом поле
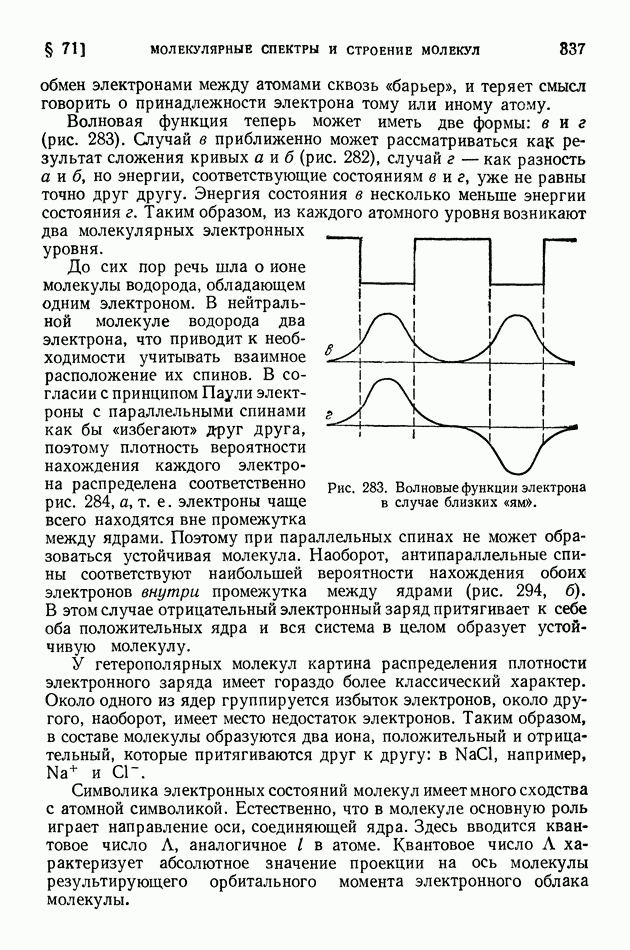
- § 71. Молекулярные спектры и строение молекул
- § 72. Комбинационное рассеяние света
- § 73. Квантовая картина испускания света атомами и молекулами
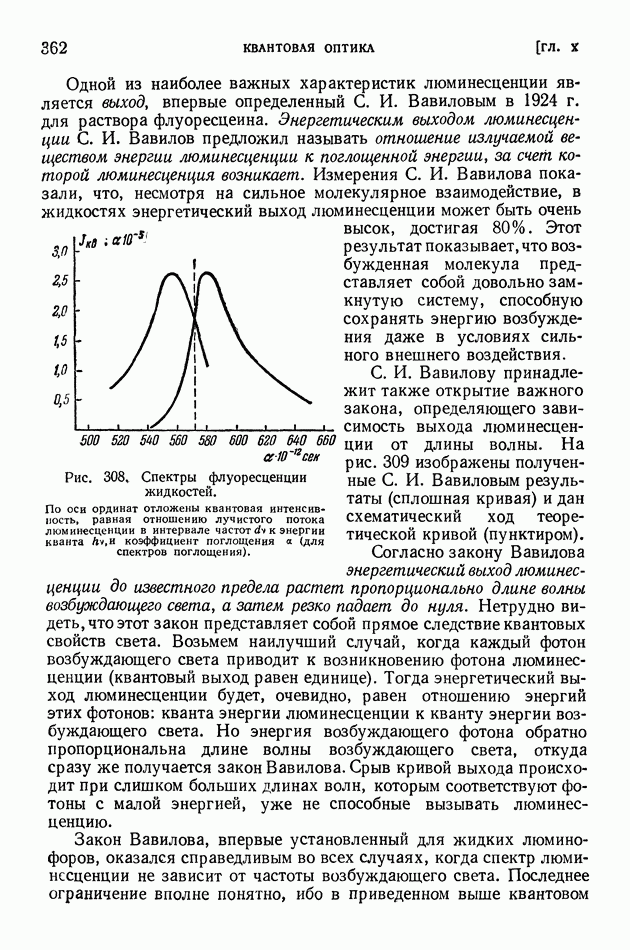
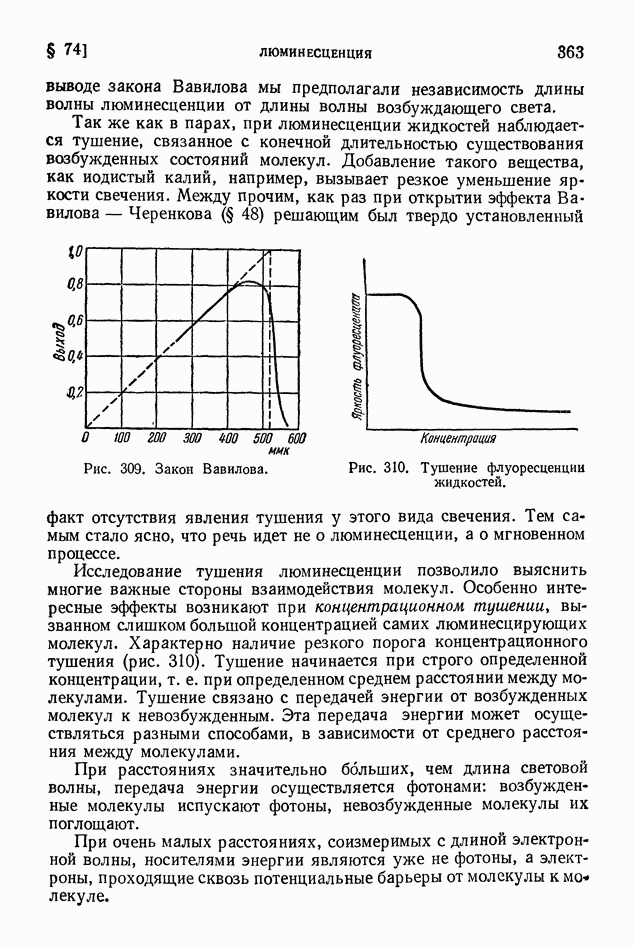
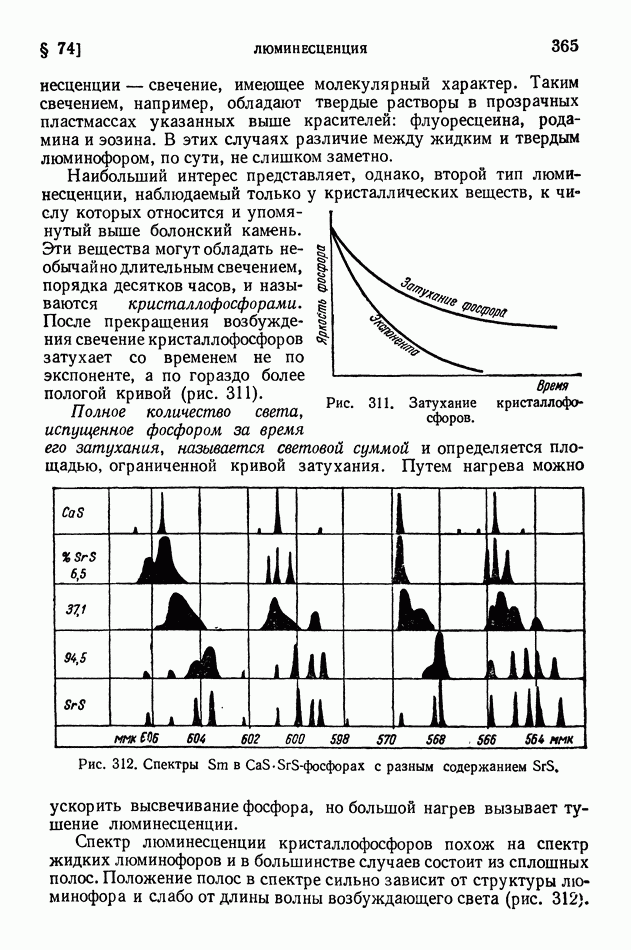
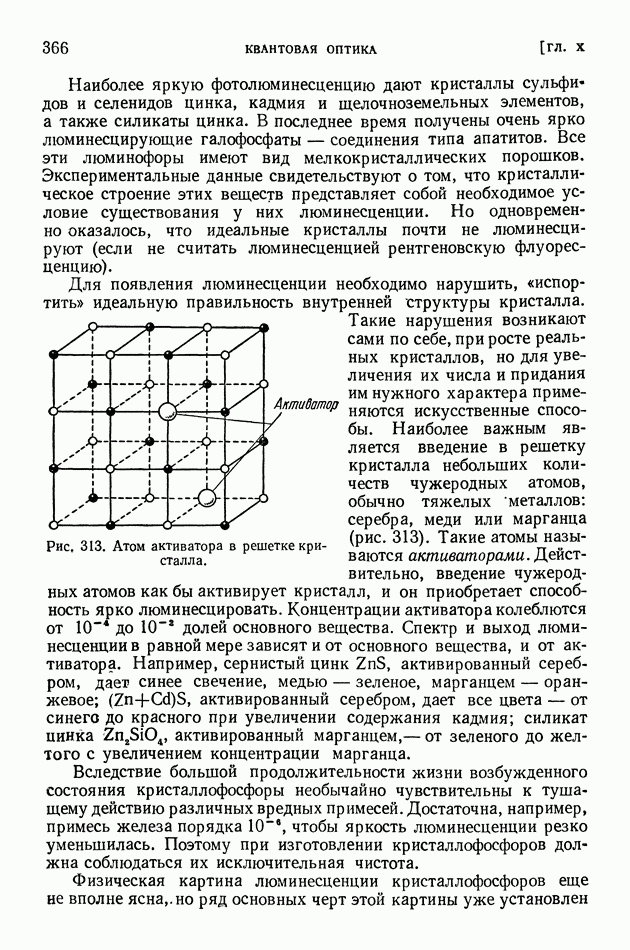
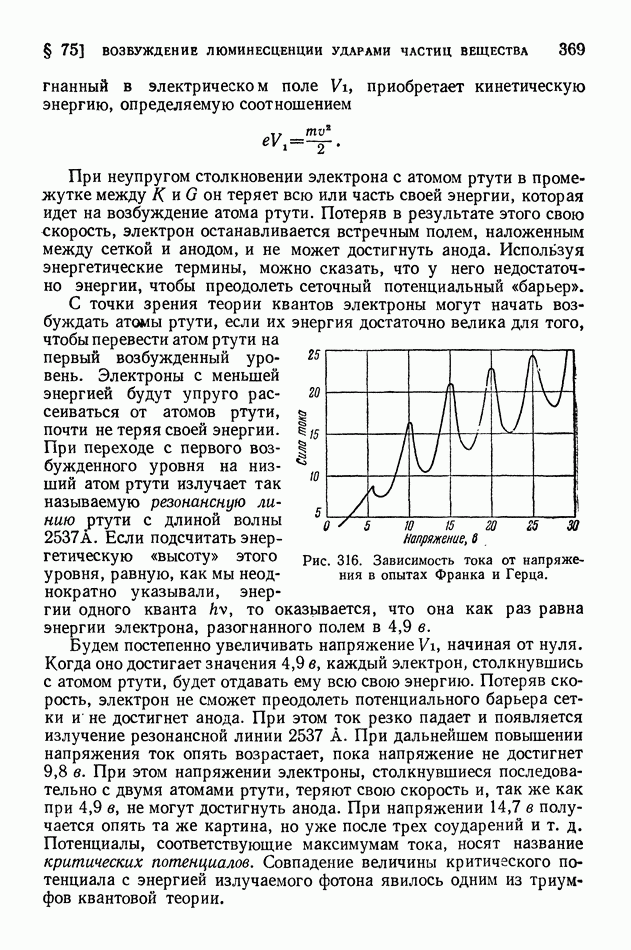
- § 74. Люминесценция
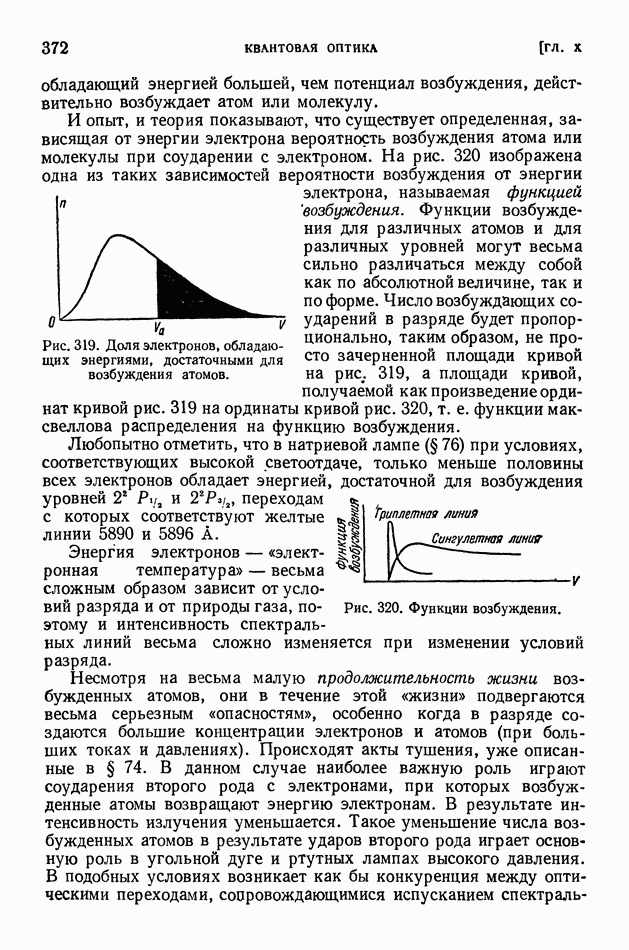
- § 75. Возбуждение люминесценции ударами частиц вещества
- § 76. Применения люминесценции
- § 77. Фотохимические реакции
- ГЛАВА XI. ЗАКОН ПРОПОРЦИОНАЛЬНОСТИ МАССЫ И ЭНЕРГИИ И РЕЛЯТИВИСТСКИЕ СООТНОШЕНИЯ
- § 78. Закон пропорциональности массы и энергии
- § 79. Предварительные замечания о релятивистских эффектах. Зависимость массы от скорости
- § 80. Корпускулярные свойства фотонов. Явление Комптона
- § 81. Вывод закона Эйнштейна сложения скоростей из закона пропорциональности массы и энергии и законов сохранения энергии или количества движения
- § 82. Две трактовки закона пропорциональности массы и энергии и уточнение закона тяготения
- § 83. Красное смещение спектральных линий. Поперечный эффект Доплера
- § 84. Влияние гравитационного поля на скорость света в вакууме и показатель преломления вакуума
- ЧАСТЬ ШЕСТАЯ. ЯДЕРНАЯ ФИЗИКА
- § 85. Заряд и масса ядра. Масс-спектральный анализ
- § 86. Состав ядер. Изотопы. Атомные единицы массы и энергии
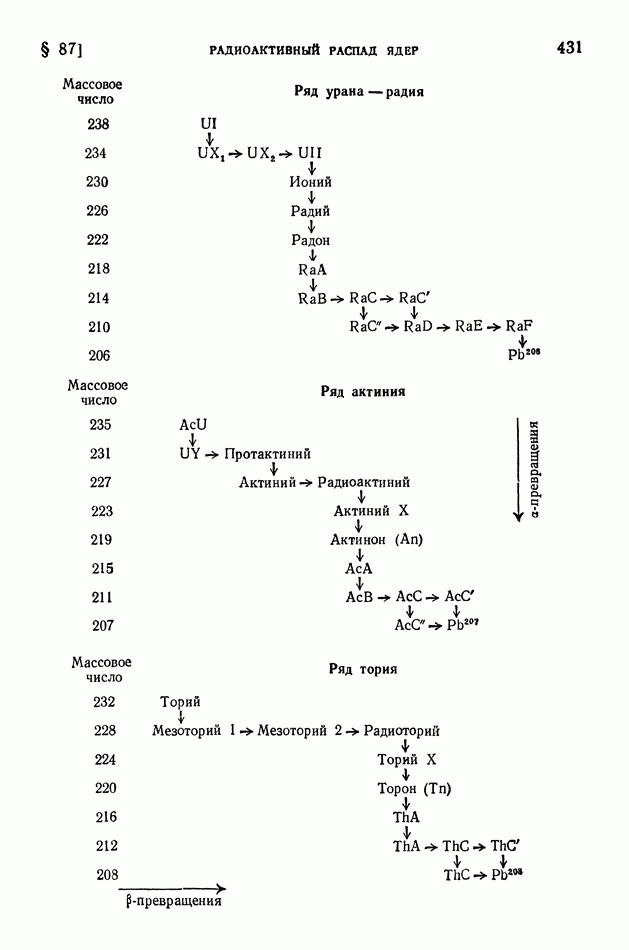
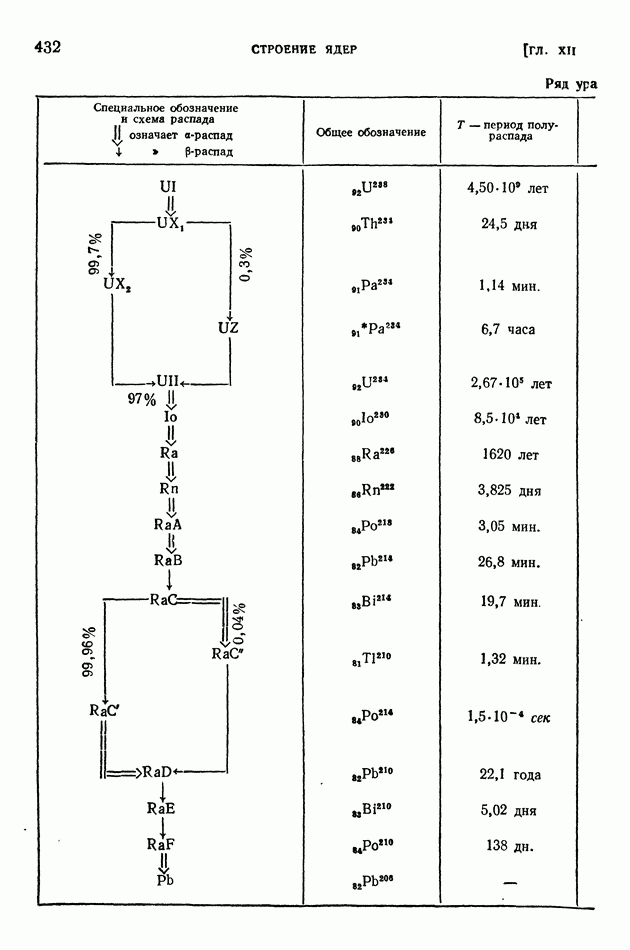
- § 87. Радиоактивный распад ядер. Закон радиоактивного смещения. Изомеры
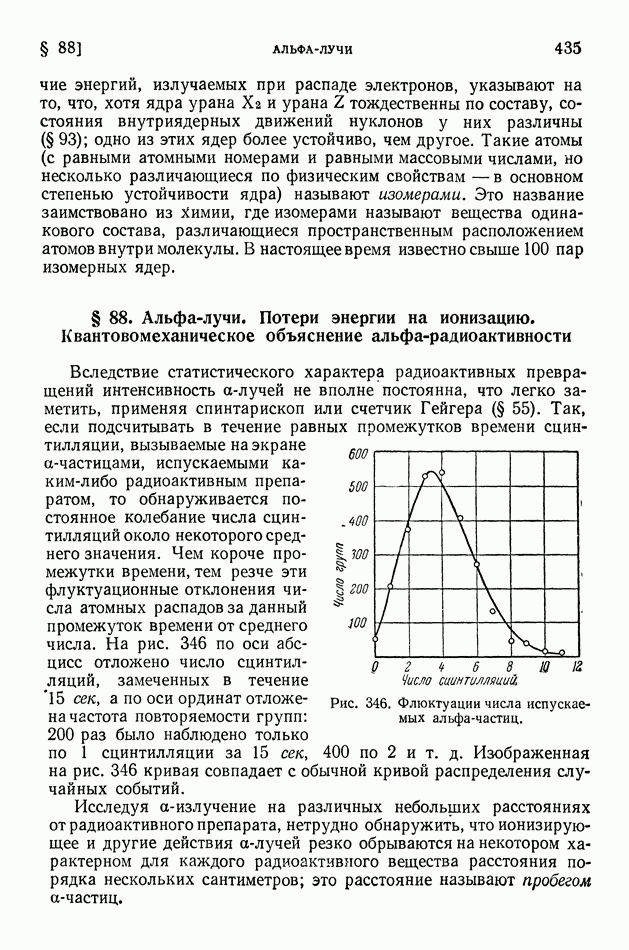
- § 88. Альфа-лучи. Потери энергии на ионизацию. Квантовомеханическое объяснение альфа-радиоактивности
- § 89. Бета- и гамма-лучи
- § 90. Искусственное расщепление ядер. Открытие нейтрона
- § 91. Открытие позитрона. Взаимопревращение фотонов определенной энергии и электронно-позитронных пар
- § 92. Индуцированная позитронная и электронная радиоактивность. Фоторасщепление ядер, K-захват
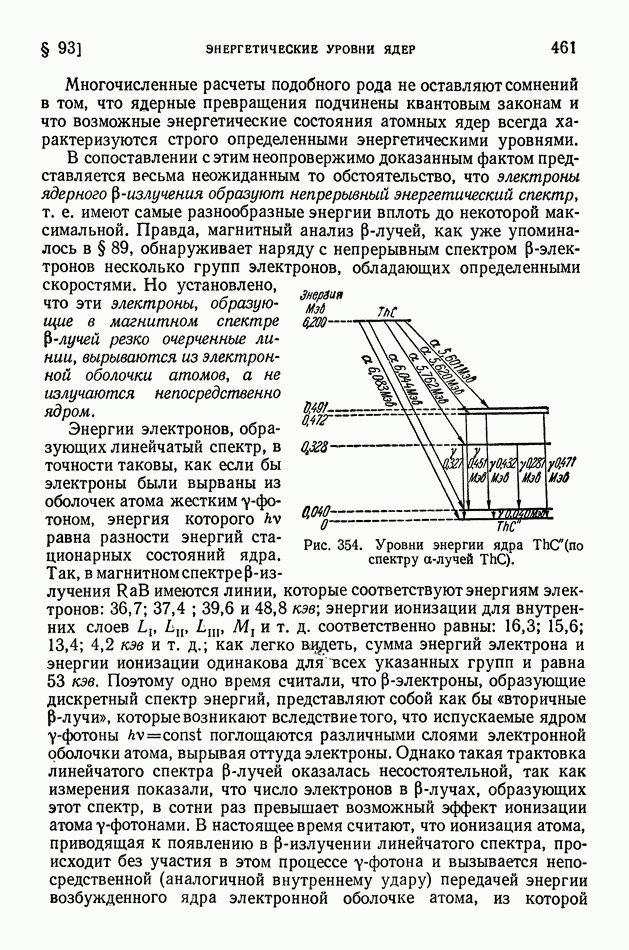
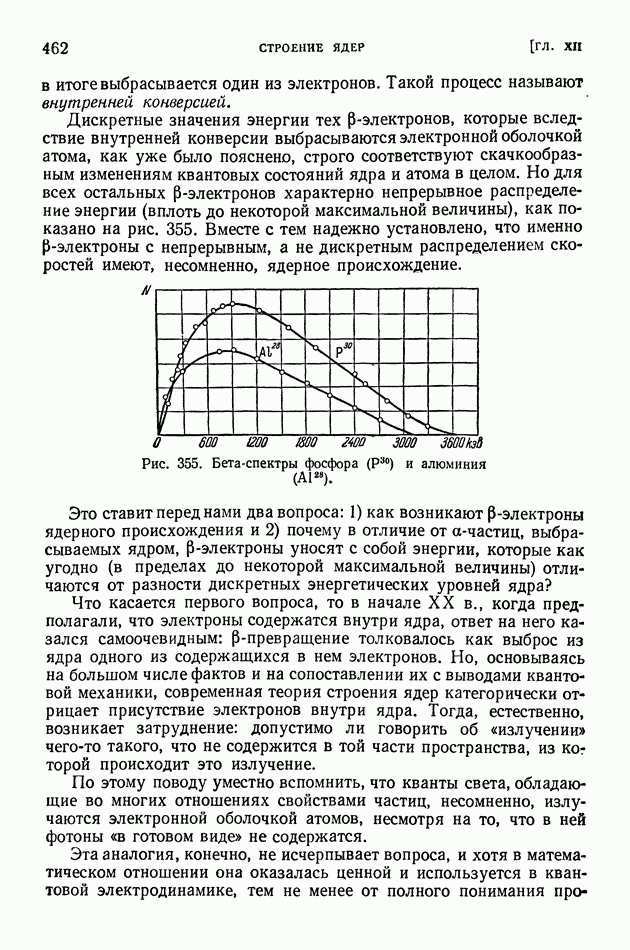
- § 93. Энергетические уровни ядер. Внутренняя конверсия. Нейтрино
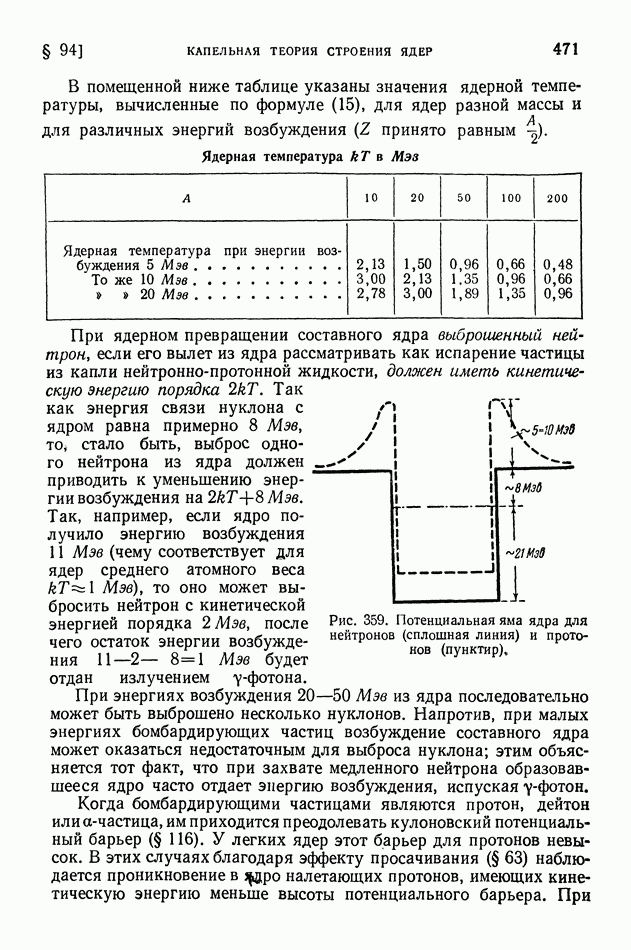
- § 94. Капельная теория строения ядер
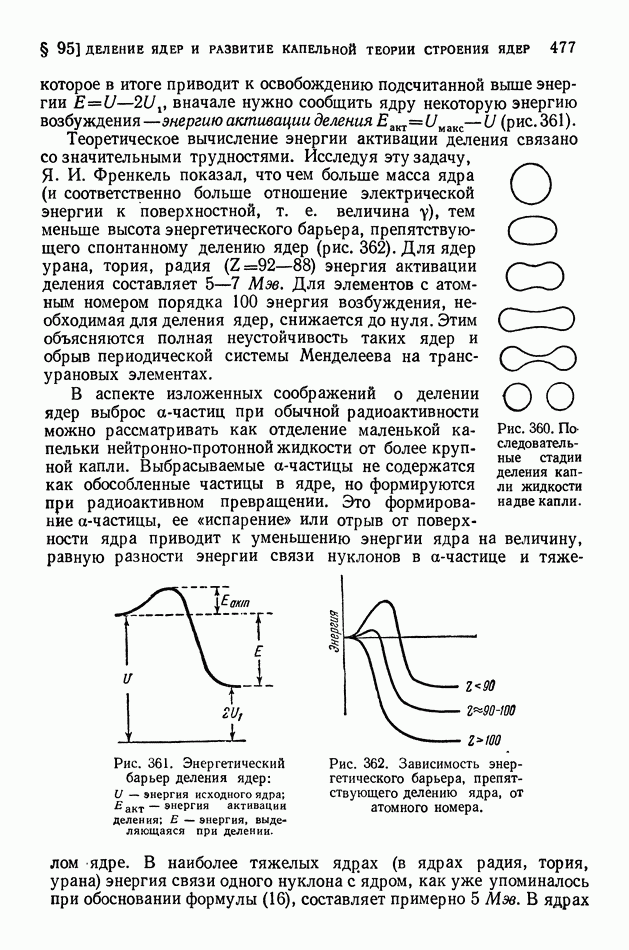
- § 95. Деление ядер и развитие капельной теории строения ядер
- ГЛАВА XIII. КОСМИЧЕСКИЕ ЛУЧИ
- § 96. Методы исследования и первые итоги изучения космических лучей
- § 97. Каскадное образование электронно-позитронных пар в космических лучах. Потери энергии электронами на тормозное излучение
- § 98. «мю»-мезоны. Зависимость времени жизни неустойчивых частиц от скорости движения
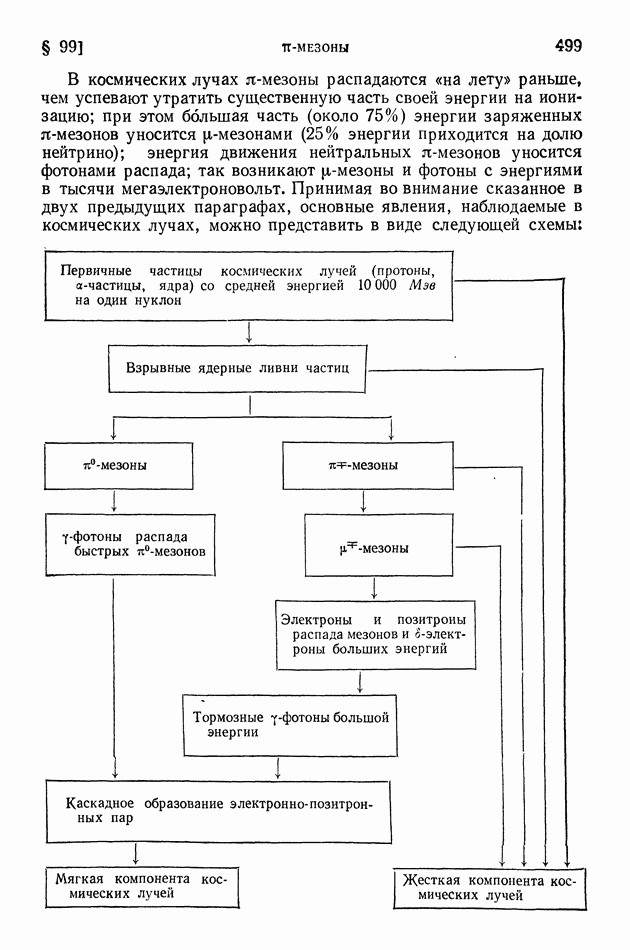
- § 99. «пи»-мезоны
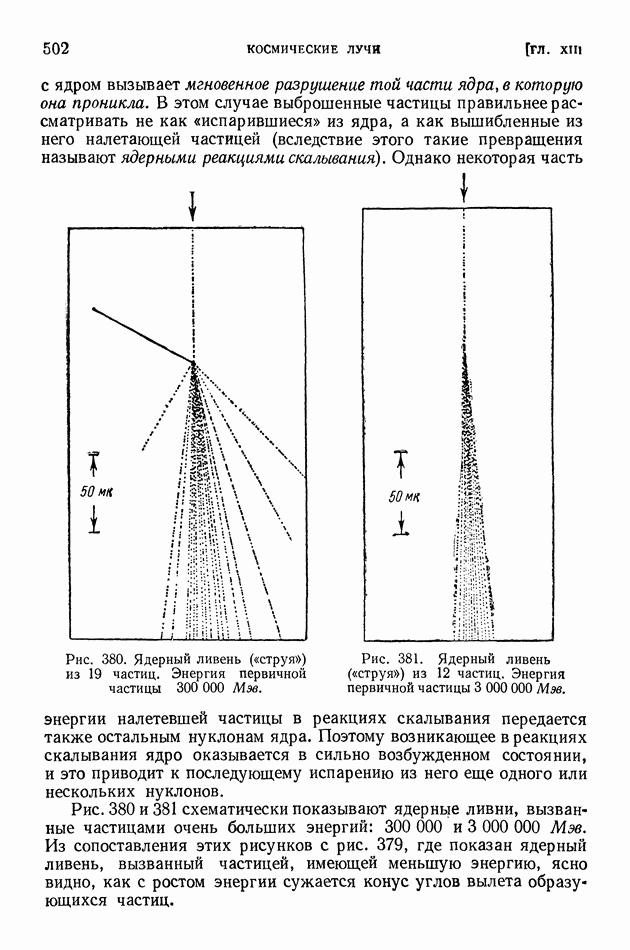
- § 100. Взрывные ядерные ливни и их каскадное развитие в космических лучах
- § 101. Корпускулярный и энергетический спектр космических лучей. Происхождение космического излучения
- ГЛАВА XIV. ЭКСПЕРИМЕНТАЛЬНЫЕ СРЕДСТВА ЯДЕРНОЙ ФИЗИКИ
- § 102. Циклотроны
- § 103. Фазотроны
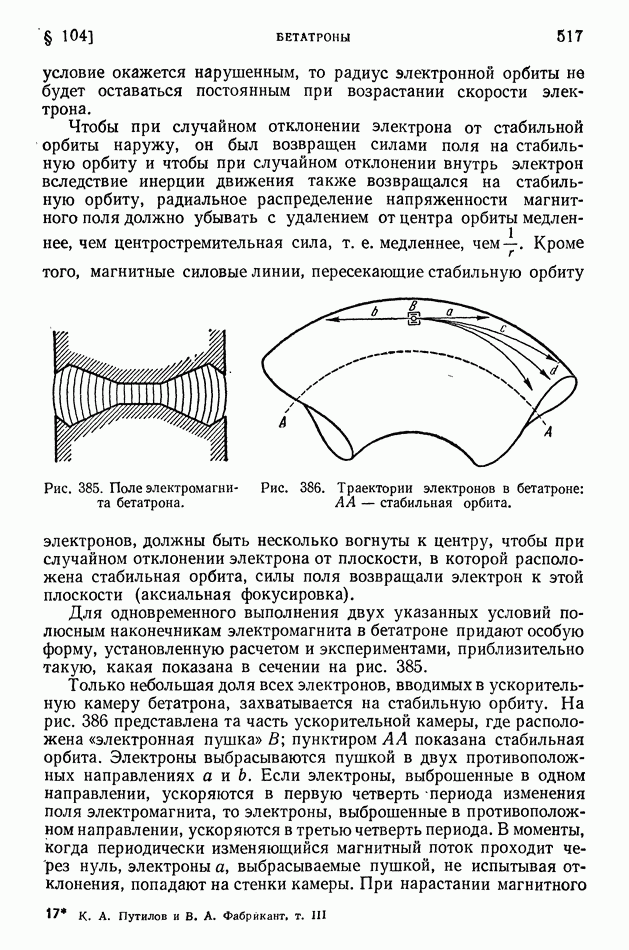
- § 104. Бетатроны
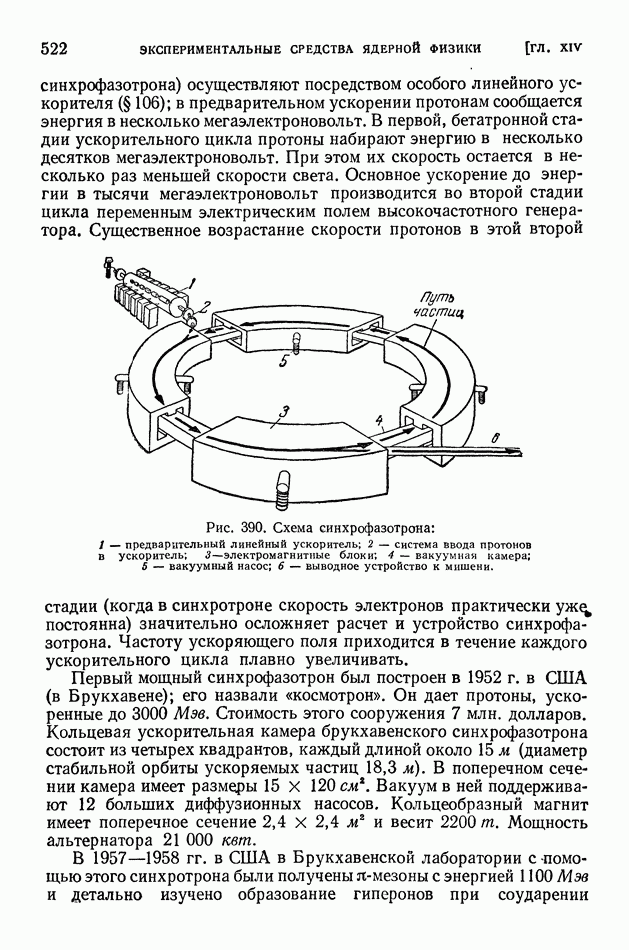
- § 105. Синхротроны и синхрофазотроны
- § 106. Линейные ускорители электронов и ионов
- § 107. Лабораторные источники нейтронов. Замедлители нейтронов в ядерных реакторах
- § 108. Усовершенствование методов наблюдения и счета частиц
- ГЛАВА XV. ЯДЕРНЫЕ РЕАКЦИИ И АТОМНАЯ ЭНЕРГИЯ
- § 109. Основные виды и обозначения ядерных реакций. Конкурирующие процессы в ядерных реакциях
- § 110. Энергетический эффект, энергия возбуждения и порог ядерных реакций
- § 111. Превращения элементарных частиц
- § 112. Ядерные силы
- § 113. Энергия связи ядер и средняя энергия связи нуклона
- § 114. Полуэмпирическая формула для энергии ядерной связи и для атомных энергий и масс
- § 115. Взаимосвязь энергии и строения ядер. Внутриядерное движение нуклонов и нуклонные оболочки. Спины и магнитные моменты ядер
- § 116. Энергия отделения частиц и анализ возможного хода ядерной реакции
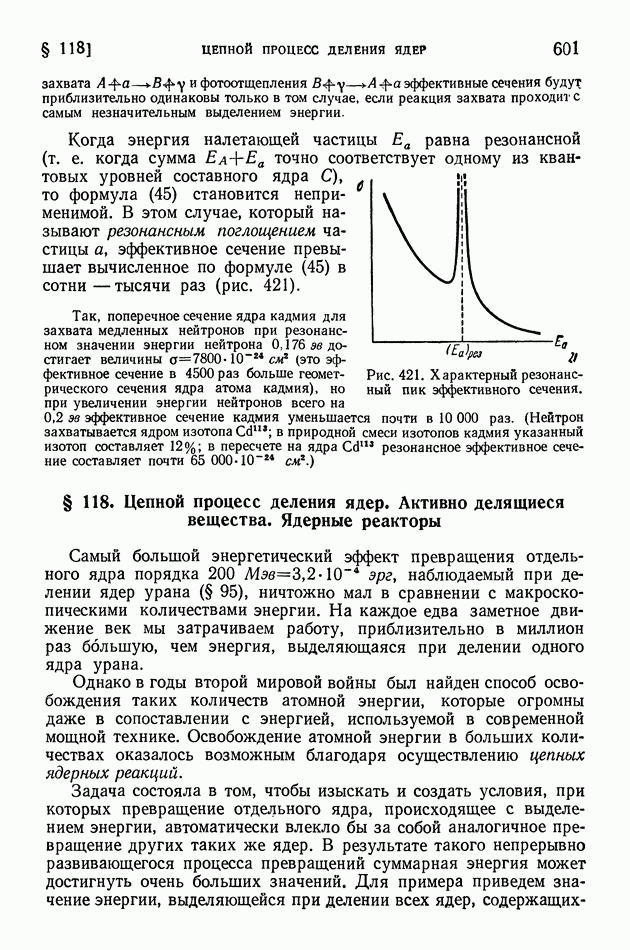
- § 117. Выход продуктов ядерной реакции. Эффективные сечения. Резонансные явления
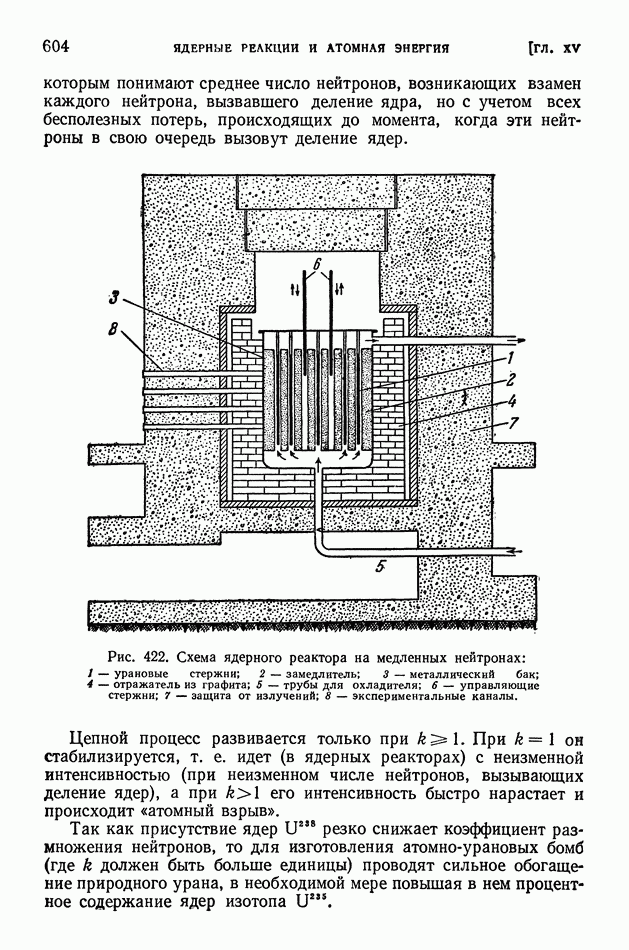
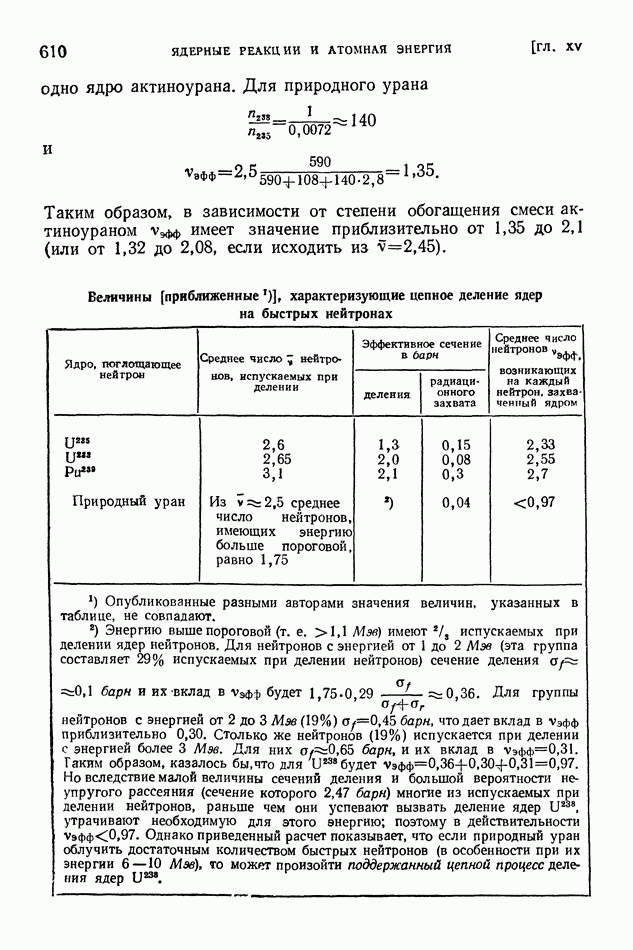
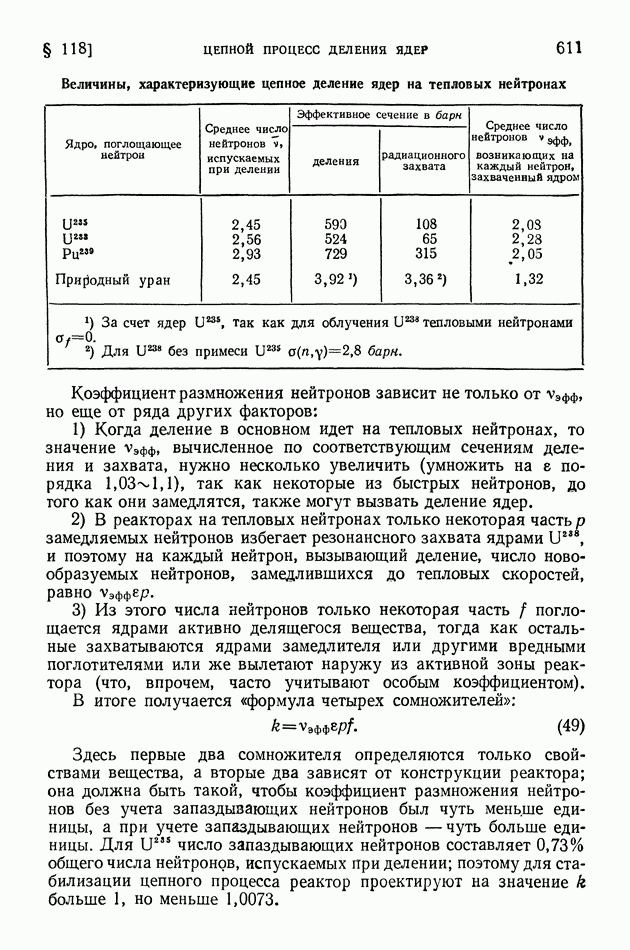
- § 118. Цепной процесс деления ядер. Активно делящиеся вещества. Ядерные реакторы
- § 119. Термоядерные реакции
- § 120. Применение ядерных реакций
- § 121. Ядерные реакции в звездах