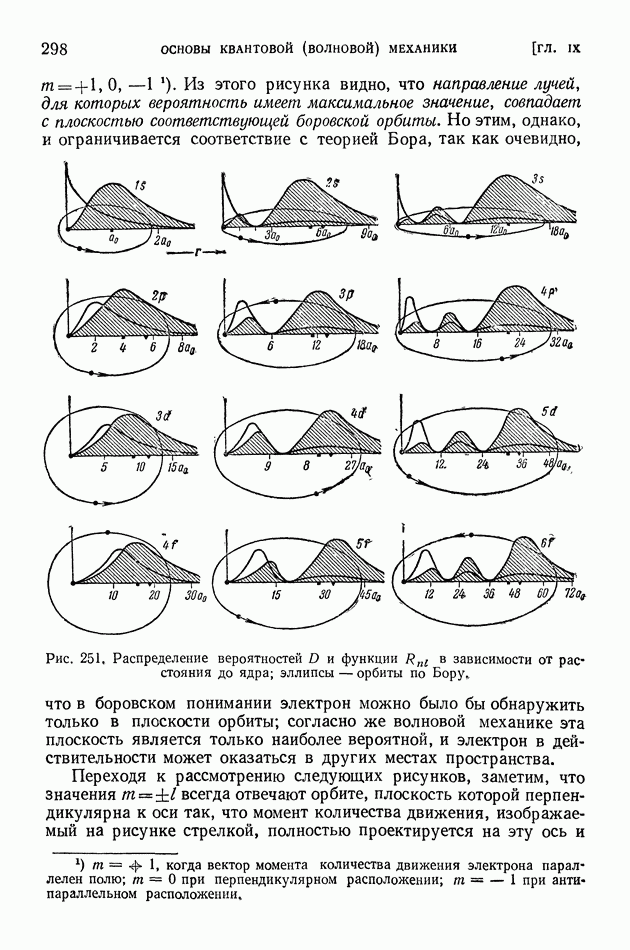
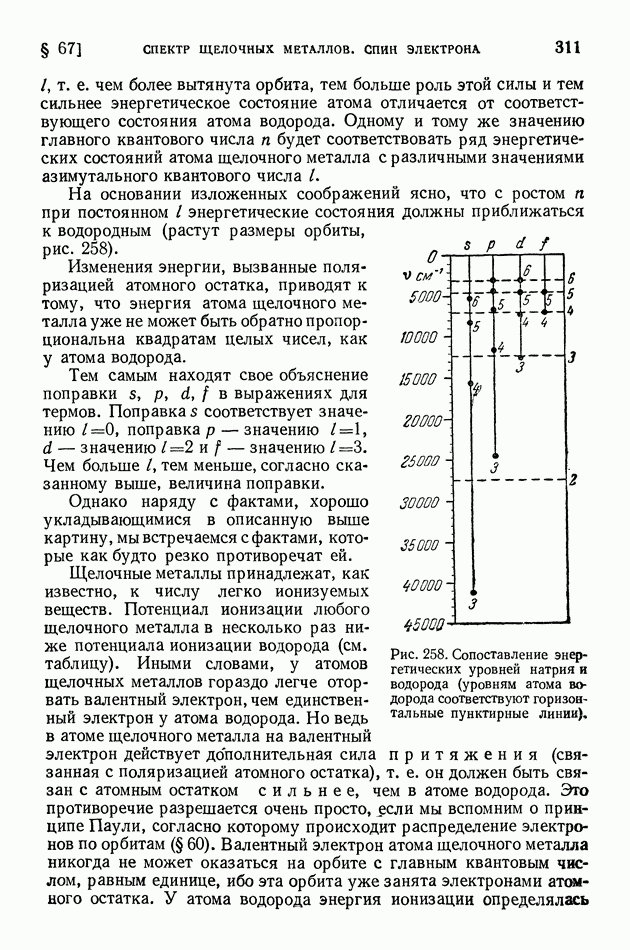
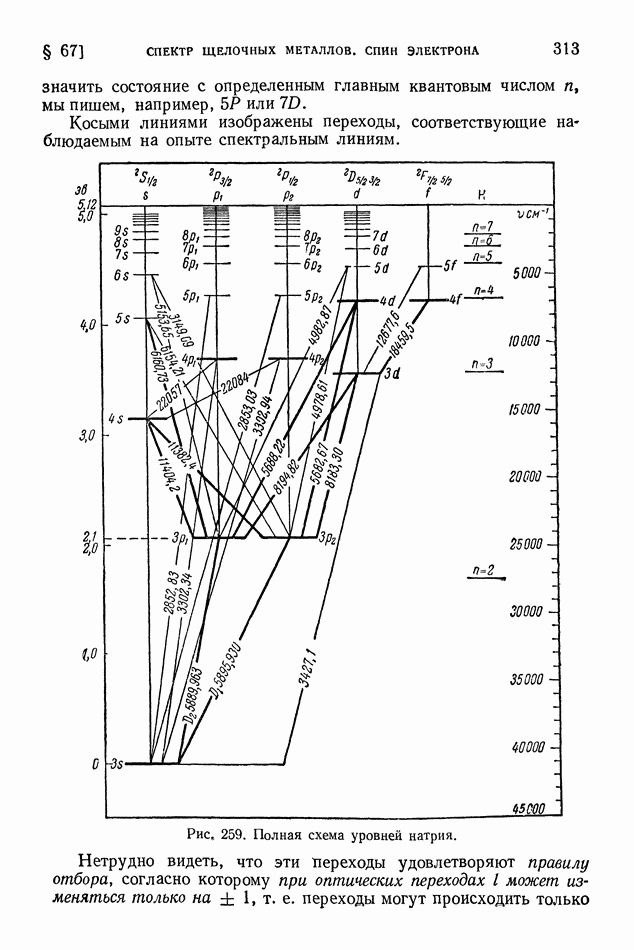
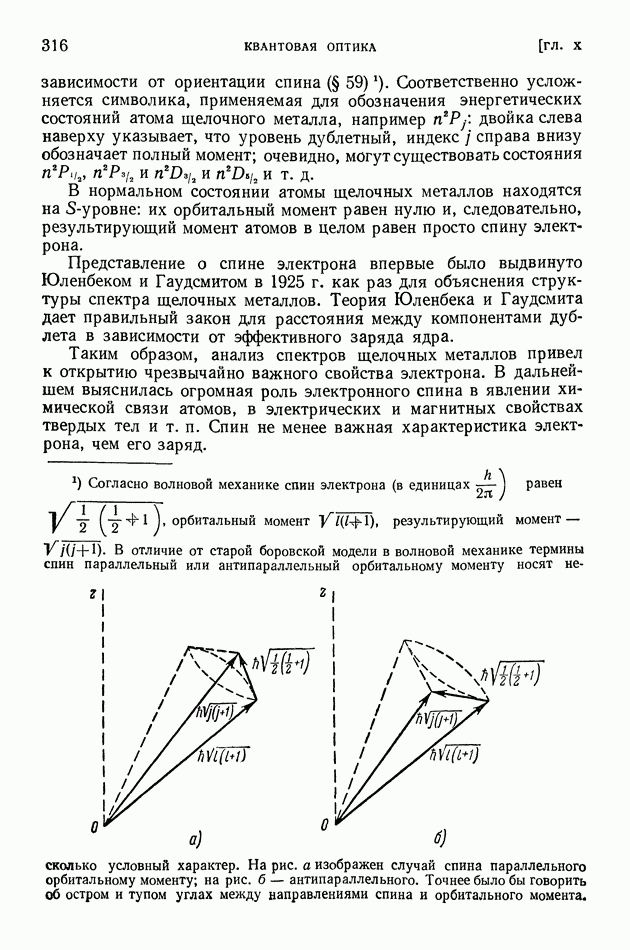
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 82. Две трактовки закона пропорциональности массы и энергии и уточнение закона тяготения
По теории Эйнштейна, гравитационное поле представляет собой проявление особых свойств пространства, которое, как предполагается, тем существеннее отличается от евклидова пространства, чем больше масса близрасположенных тел Согласно этим представлениям, развитым в общей теории относительности, все величины, характеризующие гравитационное поле (напряженность, потенциал, энергия тяготения), имеют только геометрический смысл, в отличие от аналогичных величин, характеризующих электромагнитное поле. Придерживаясь указанной концепции, величину  в законе пропорциональности массы и энергии нужно понимать как совокупность всех видов энергии, кроме энергии тяготения. В соответствии с этим тогда и масса тела, перемещаемого без ускорения в гравитационном поле, считается неизменяющейся.
в законе пропорциональности массы и энергии нужно понимать как совокупность всех видов энергии, кроме энергии тяготения. В соответствии с этим тогда и масса тела, перемещаемого без ускорения в гравитационном поле, считается неизменяющейся.
Но допустима (т. е. не приводит ни к каким противоречиям, а, напротив, во многих случаях оказывается даже более удобной) иная трактовка закона
пропорциональности массы и энергии, а именно трактовка этого закона как совершенно универсального, охватывающего все виды энергии, включая и энергию тяготения. При такой трактовке закона  нужно учитывать гравитационное изменение
нужно учитывать гравитационное изменение  массы тела, определяемое Соотношением
массы тела, определяемое Соотношением  где
где  потенциал тяготения и
потенциал тяготения и  подациальная энергия тяготения.
подациальная энергия тяготения.
Действительно если  масса тела при
масса тела при  энергия тела без учета потенциальной энергии тяготения,
энергия тела без учета потенциальной энергии тяготения,  масса того же тела (при той же его скорости и при тех же значениях других параметров его состояния), когда оно находится в поле тяготения в месте, где потенциал равен
масса того же тела (при той же его скорости и при тех же значениях других параметров его состояния), когда оно находится в поле тяготения в месте, где потенциал равен  и
и  полная энергия этого тела с учетом потенциальной энергии тяготения, то из разности соотношений
полная энергия этого тела с учетом потенциальной энергии тяготения, то из разности соотношений  получаем
получаем  или, что то же,
или, что то же,

Поскольку потенциал тяготения отрицателен  т. е. поскольку для удаления тела из гравитационного поля (без изменения скорости тела) к телу должна быть подведена энергия, а с
т. е. поскольку для удаления тела из гравитационного поля (без изменения скорости тела) к телу должна быть подведена энергия, а с  и соответствующая масса, то
и соответствующая масса, то  т. е. масса тела
т. е. масса тела  вне поля тяготения больше, чем масса того же тела при потенциале тяготения
вне поля тяготения больше, чем масса того же тела при потенциале тяготения  Для зависимости массы от потенциала поля из (18) получаем:
Для зависимости массы от потенциала поля из (18) получаем:

Потенциальную энергию взаимодействия двух тел мы представляем себе как величину взаимную, относящуюся к обоим взаимодействующим телам. Однако, рассматривая смещение двух взаимодействующих тел относительно их общего центра масс, можно расчленить "энергию взаимодействия на части, каждая из которых сопряжена с одним из взаимодействующих тел. Действительно, представим себе, что сила взаимного тяготения тел преодолевается едва превышающей ее силой отталкивания, изменяющейся с расстоянием по тому же закону, что и сила тяготения. Работа, производимая этой силой отталкивания при удалении тел на бесконечно большое расстояние друг от друга, численно равна интересующей нас потенциальной энергии. Ускорения, приобретаемые телами, обратно пропорциональны массам тел, поэтому и пути, проходимые телами за любой промежуток времени, будут тоже обратно пропорциональны массам тел. Но так как в любой момент времени силы, заставляющие тела удаляться друг от друга, равны, то, стало быть, и работы, производимые этими силами, будут также обратно пропорциональны массам тел:  Отсюда
Отсюда

Сумма указанных работ  взятая с обратным знаком, равна потенциальной энергии взаимодействия рассматриваемых тел. Мы видим, таким образом, что энергия взаимодействия двух тел слагается из двух частей, физически сопряженных с каждым из взаимодействующих тел и пропорциональных отношению массы другого тела к сумме масс.
взятая с обратным знаком, равна потенциальной энергии взаимодействия рассматриваемых тел. Мы видим, таким образом, что энергия взаимодействия двух тел слагается из двух частей, физически сопряженных с каждым из взаимодействующих тел и пропорциональных отношению массы другого тела к сумме масс.
В частном случае, когда масса одного тела крайне мала в сравнении с массой другого тела, почти вся энергия взаимодействия должна считаться присущей телу с малой массой.
Учитывая сказанное, рассмотрим, как должен быть записан ньютонов закон тяготения, чтобы он в явной форме представлял изменение силы тяготения в зависимости от расстояния.
Согласно ньютонову закону тяготения потенциальная энергия тела малой массы  в гравитационном радиальном поле, создаваемом телом большой массы
в гравитационном радиальном поле, создаваемом телом большой массы 
равна

где  расстояние
расстояние  от центра массы тела
от центра массы тела  гравитационная постоянная» равная в абсолютной системе единиц
гравитационная постоянная» равная в абсолютной системе единиц 
При перемещении тела в гравитационном поле масса тела изменяется  закону
закону

где  поэтому
поэтому

или при 

Следовательно, сила тяготения

В геометрической теории тяготения, развитой Эйнштейном и составляющей сущность общей теории относительности, не приходится рассматривать энергию и силу тяготения, и в соответствии с этим масса тела, перемещающегося в гравитационном поле, считается неизменной (если, разумеется, неизменна скорость). Для величины, соответствующей ускорению в поле тяготения  Эйнштейном была получена (в 1915 г.) формула, которая, несмотря на различие трактовок, может быть выведена, что легко видеть, из формулы (19):
Эйнштейном была получена (в 1915 г.) формула, которая, несмотря на различие трактовок, может быть выведена, что легко видеть, из формулы (19):

где  Эту величину а, имеющую размерность длины, называют гравитационным радиусом массы
Эту величину а, имеющую размерность длины, называют гравитационным радиусом массы  Гравитационный радиус точечной массы, равной массе Солнца, составляет
Гравитационный радиус точечной массы, равной массе Солнца, составляет  Земли — около
Земли — около 
Вычислим ускорение, создаваемое гравитационным полем электрона. В атом случае нужно учесть, что масса электрона полностью или частично обусловлена его электрическим полем и поэтому должна считаться распределенной в пространстве с плотностью  Внутри сферического слоя, между поверхностью электрона, имеющего радиус а, и сферой радиуса
Внутри сферического слоя, между поверхностью электрона, имеющего радиус а, и сферой радиуса  заключена масса
заключена масса 

где  полная масса покоя электрона),
полная масса покоя электрона),
Потенциал тяготения, создаваемый массой, равномерно распделенной вне сферы радиуса  всюду внутри этой сферы постоянен (т. I, § 33, 1959 г.; в пред. изд. § 39).
всюду внутри этой сферы постоянен (т. I, § 33, 1959 г.; в пред. изд. § 39).
Подставляя значение  в формулу (19) или (19) вместо
в формулу (19) или (19) вместо  находим, что отклонение гравитационного поля электрона от обычного ньютонова выражения определяется формулой
находим, что отклонение гравитационного поля электрона от обычного ньютонова выражения определяется формулой

где а — гравитационный радиус электрона

Учитывая, что классический электромагнитный радиус электрона  предыдущую формулу можно переписать так:
предыдущую формулу можно переписать так:

Это уравнение (при его трактовке, принятой в общей теории относительности) в точности совпадает с уравнением, коюрое было получено Шварцшильдом
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ЧЕТВЕРТАЯ. ОПТИКА
- § 2. Электромагнитная теория света
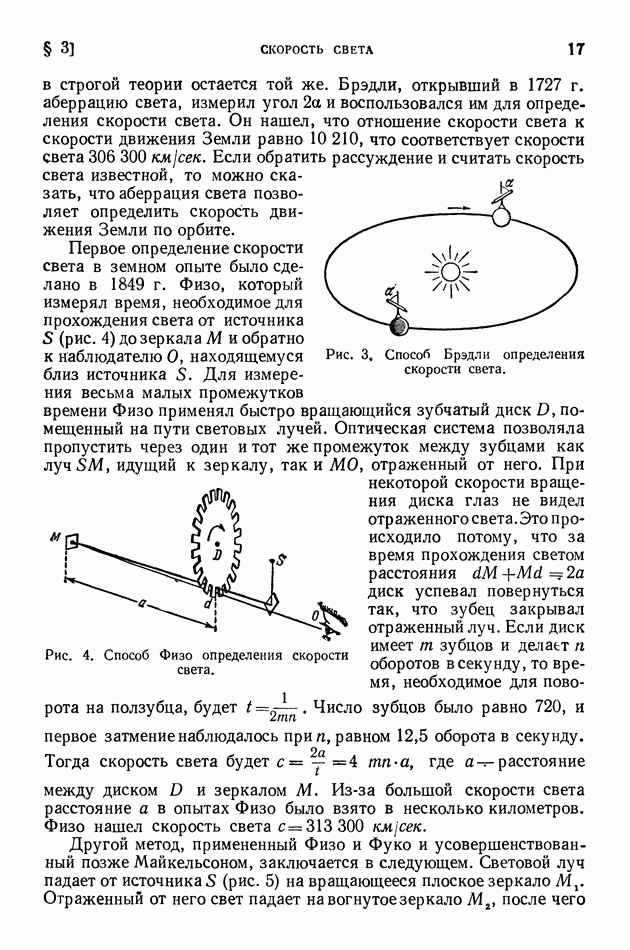
- § 3. Скорость света
- § 4. Опыт Майкельсона
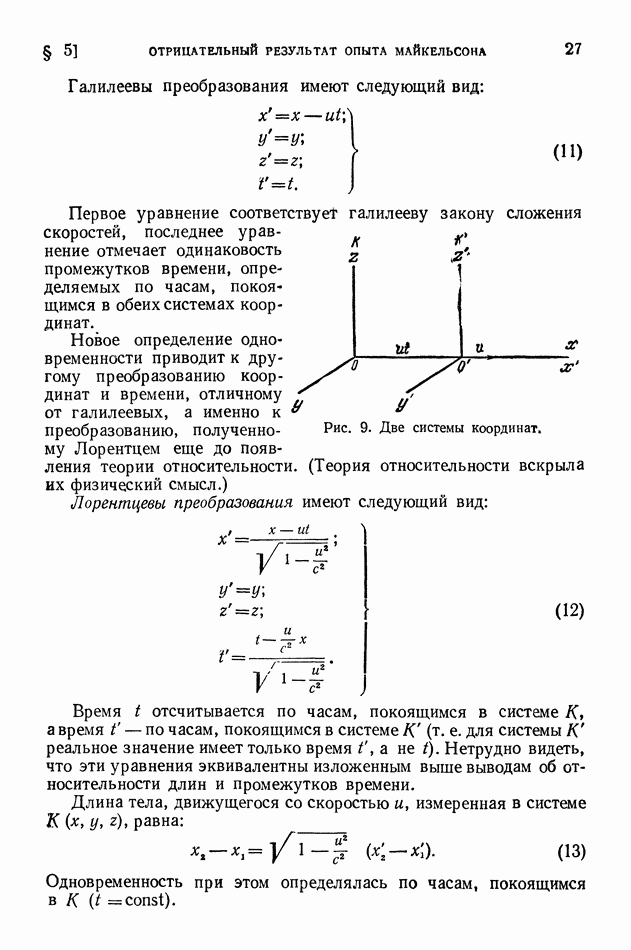
- § 5. Отрицательный результат опыта Майкельсона и теория относительности
- § 6. Некоторые замечания о теории относительности
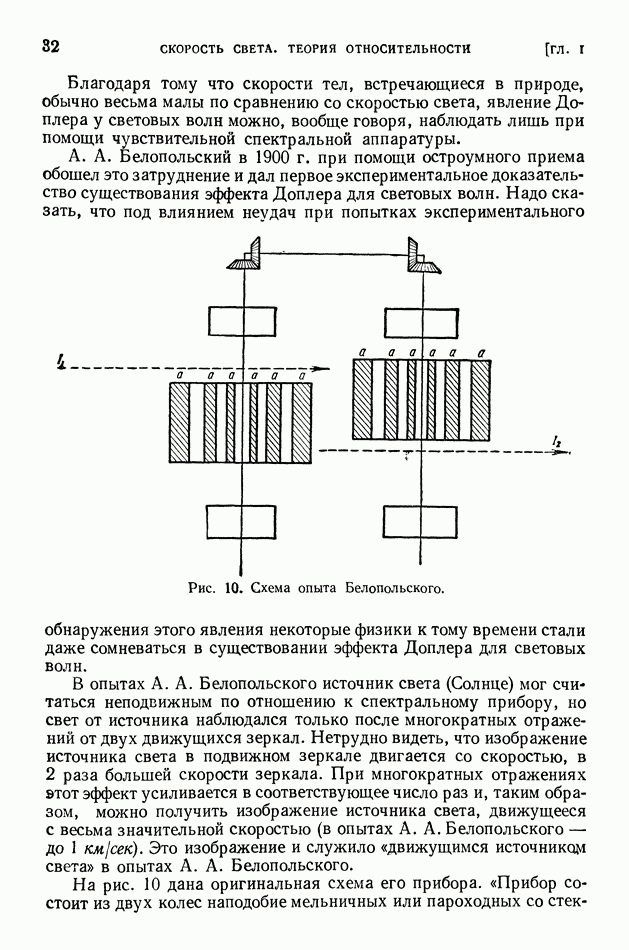
- § 7. Явление Доплера для световых волн
- ГЛАВА II. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
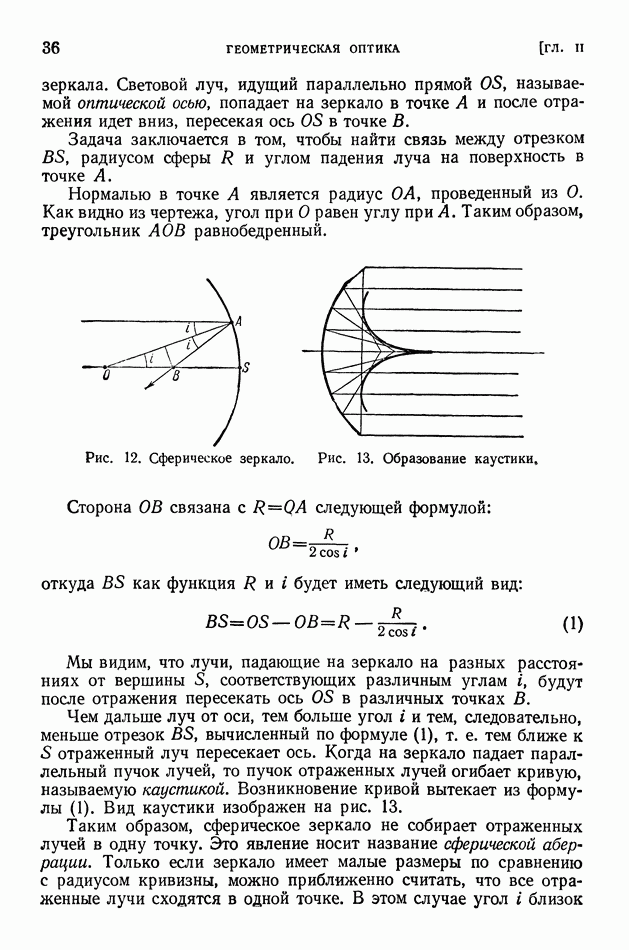
- § 8. Законы отражения и преломления света
- § 9. Линза
- § 10. Оптические системы
- § 11. Глаз как оптическая система
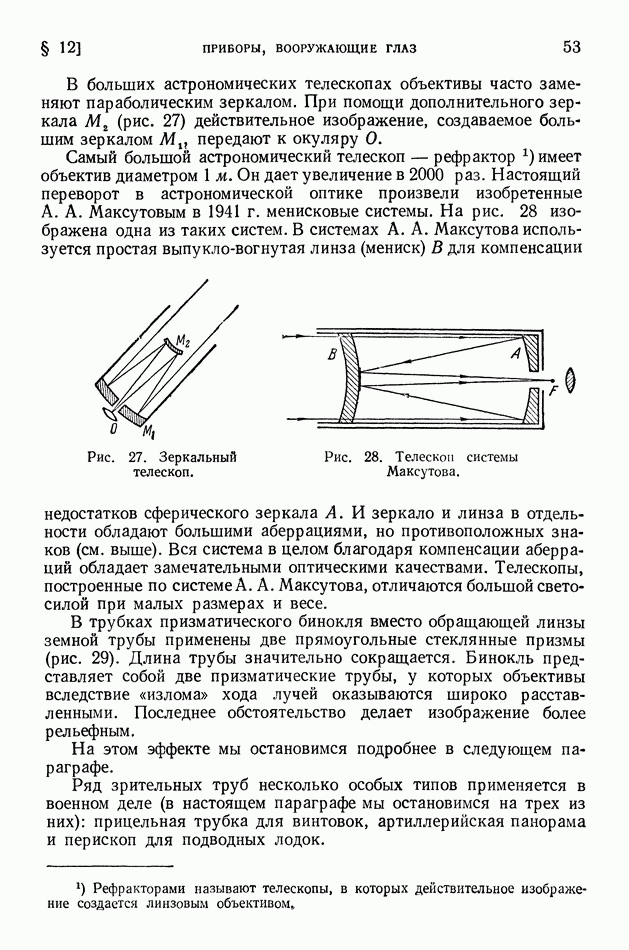
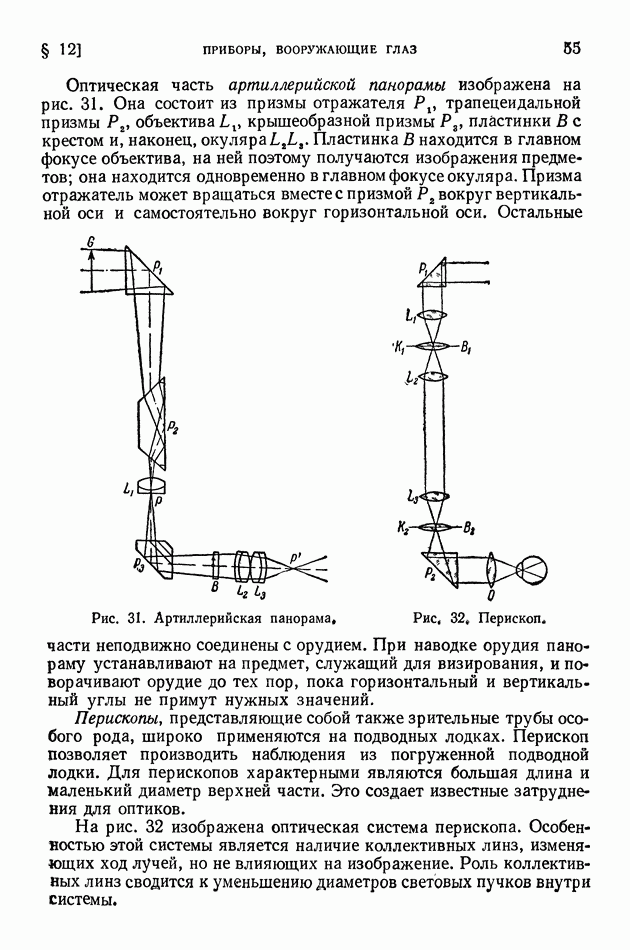
- § 12. Приборы, вооружающие глаз
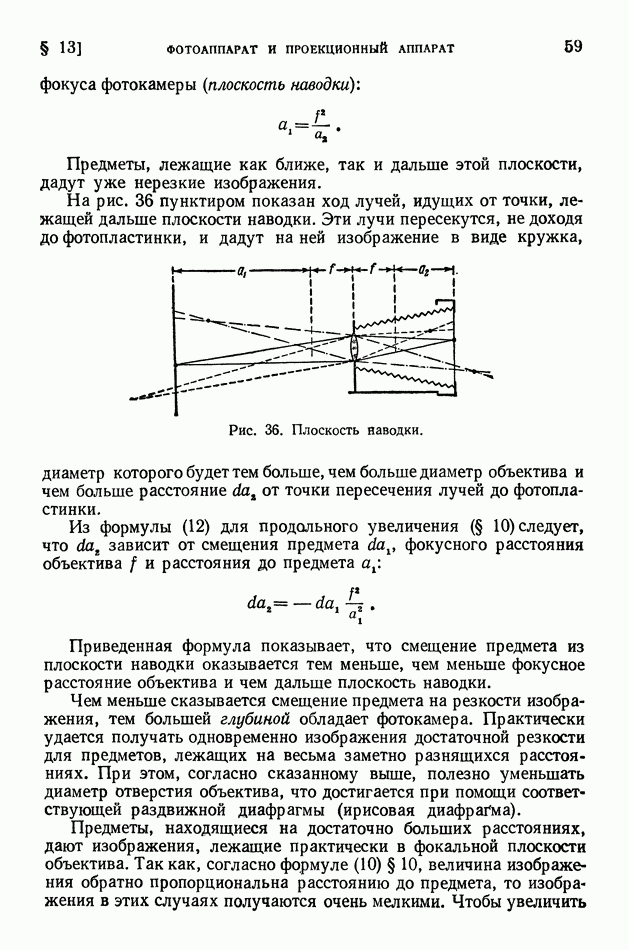
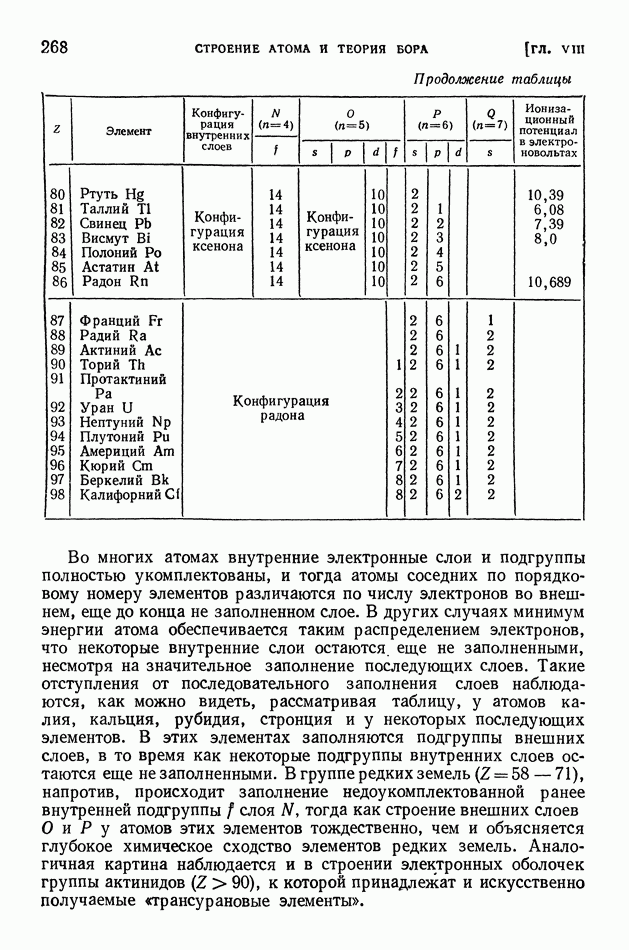
- § 13. Фотоаппарат и проекционный аппарат
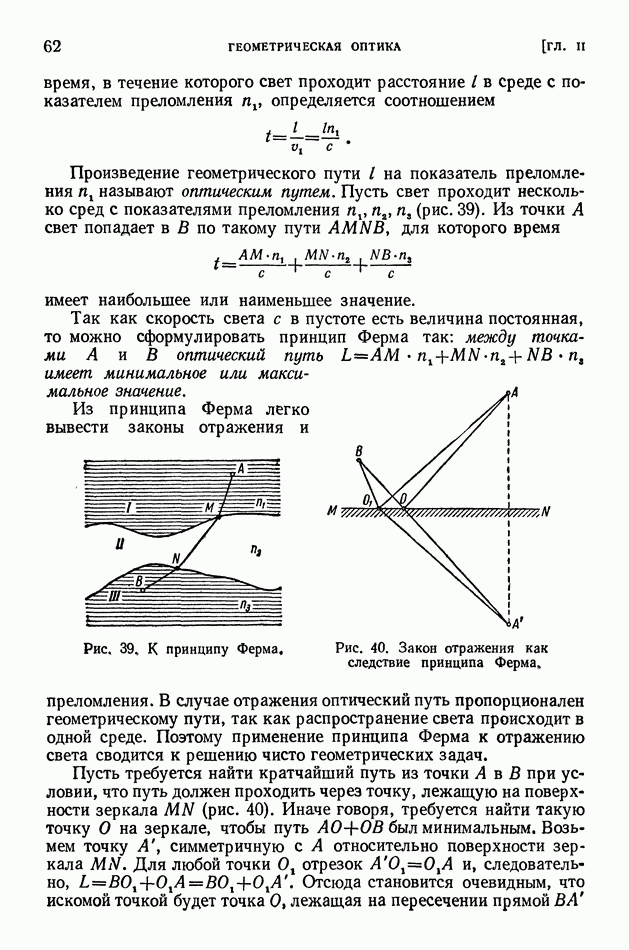
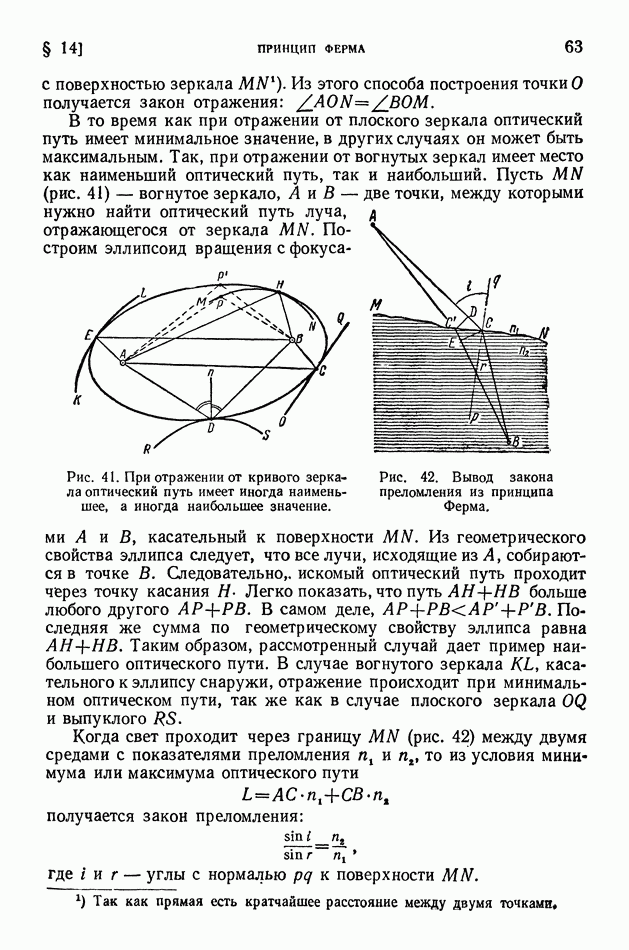
- § 14. Принцип Ферма
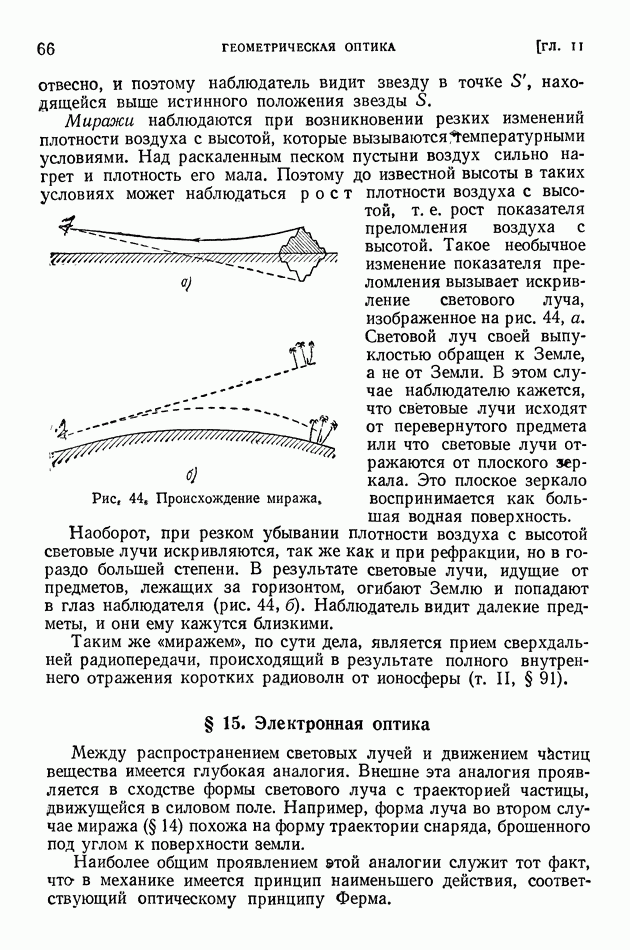
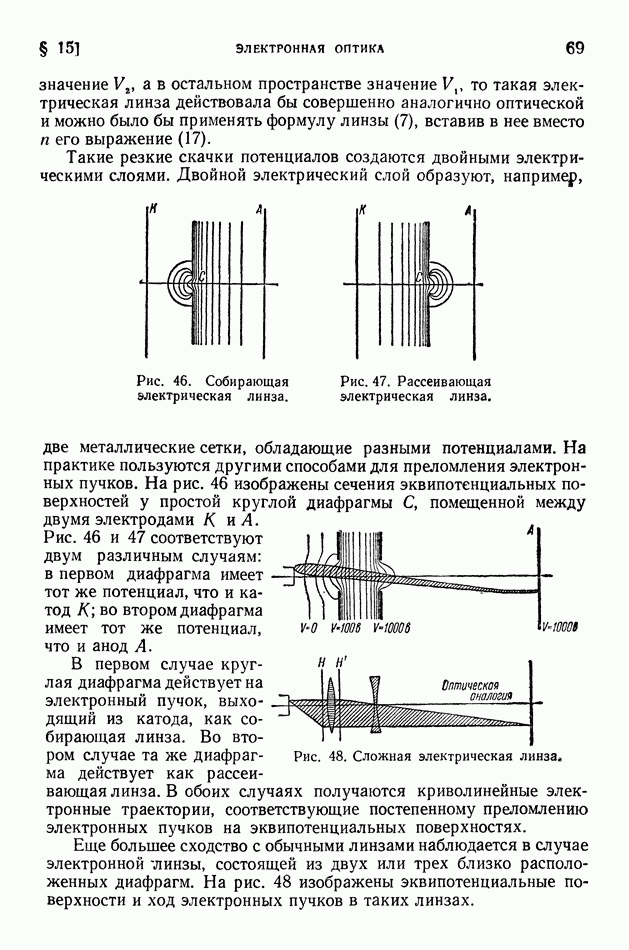
- § 15. Электронная оптика
- ГЛАВА III. ИНТЕРФЕРЕНЦИЯ СВЕТА
- § 16. Принцип суперпозиции. Когерентность
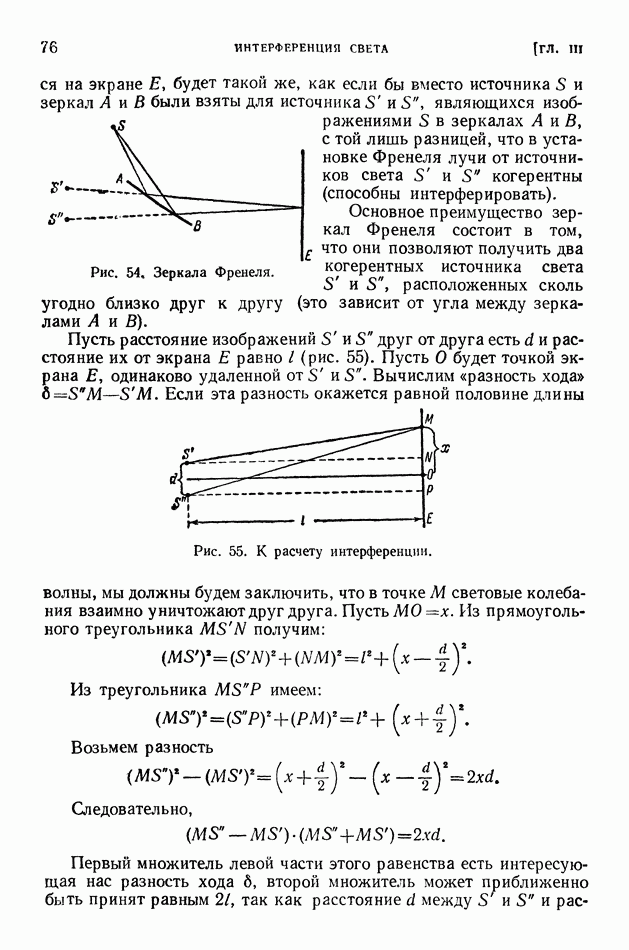
- § 17. Зеркала Френеля
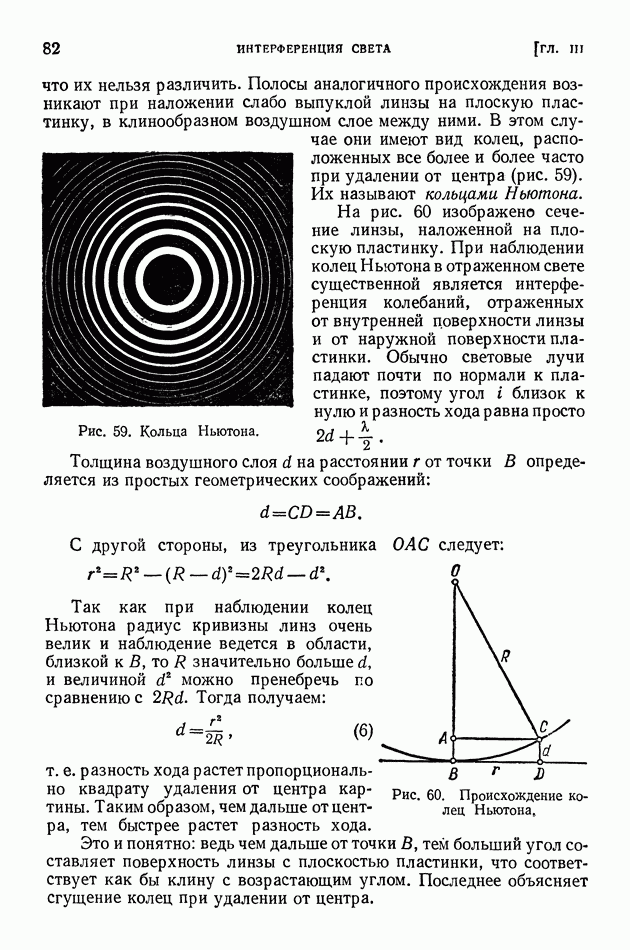
- § 18. Цвета тонких пленок. Полосы равной толщины
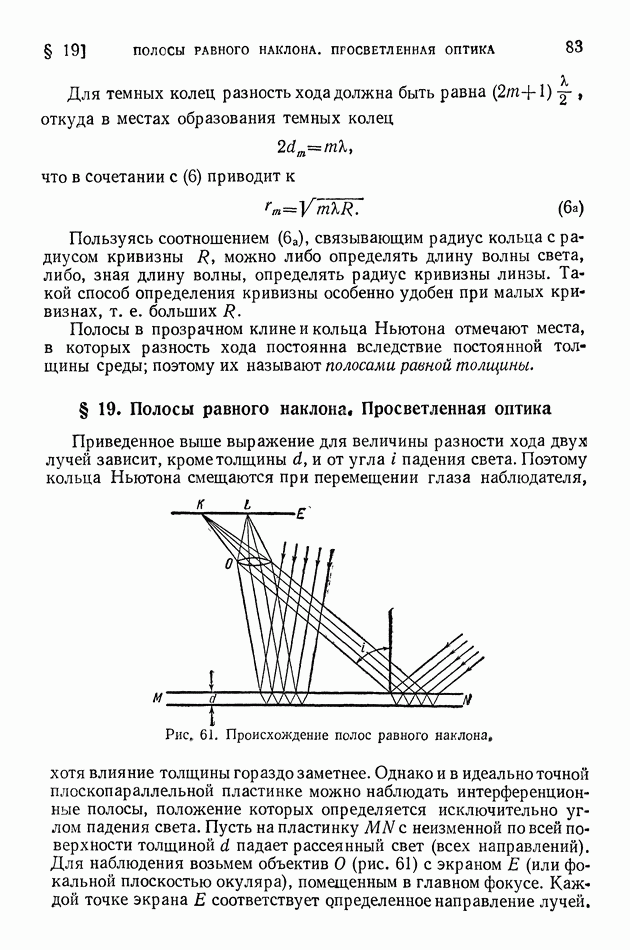
- § 19. Полосы равного наклона. Просветленная оптика
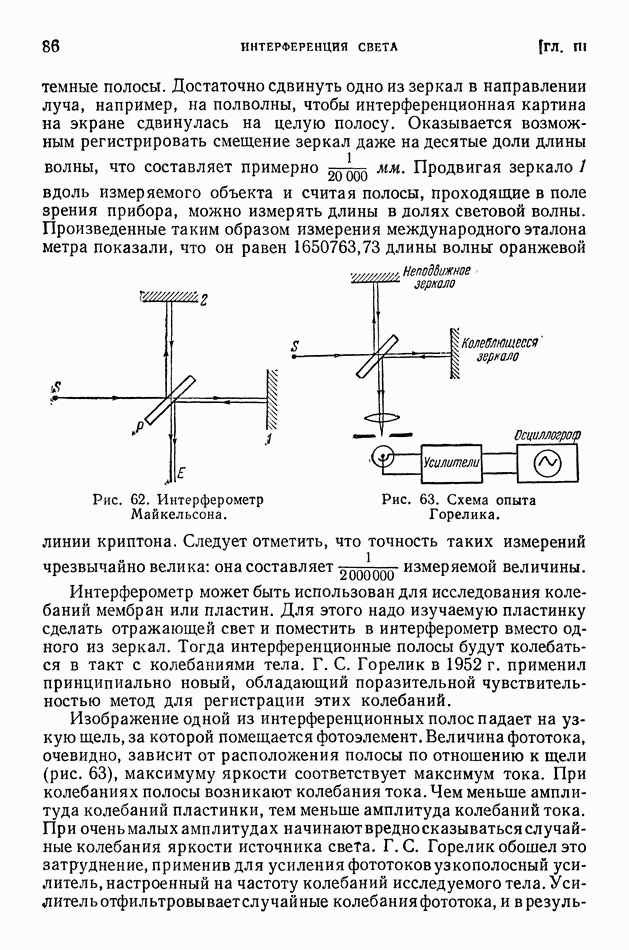
- § 20. Интерферометры
- § 21. Интерференционное измерение технических мер длины
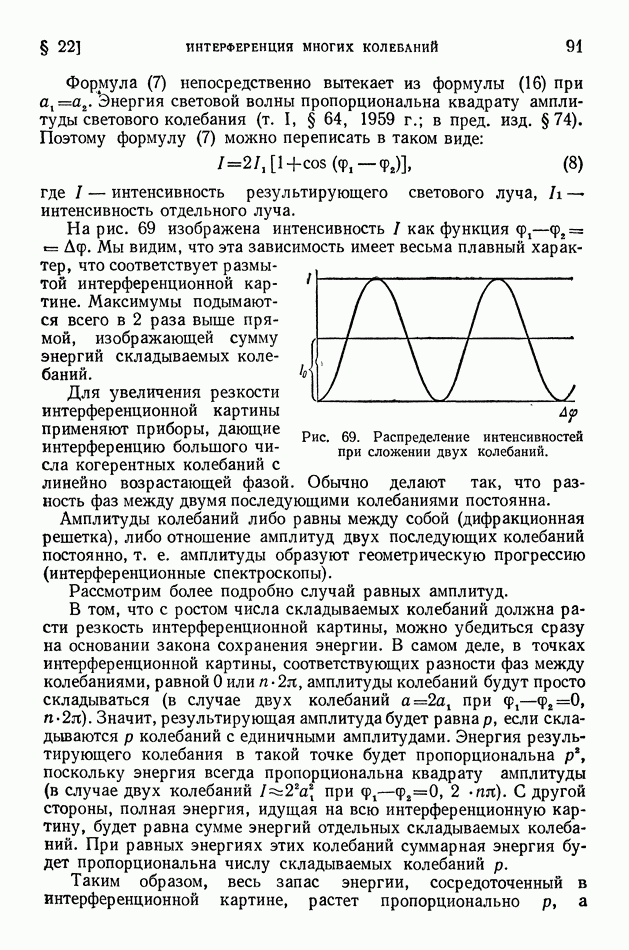
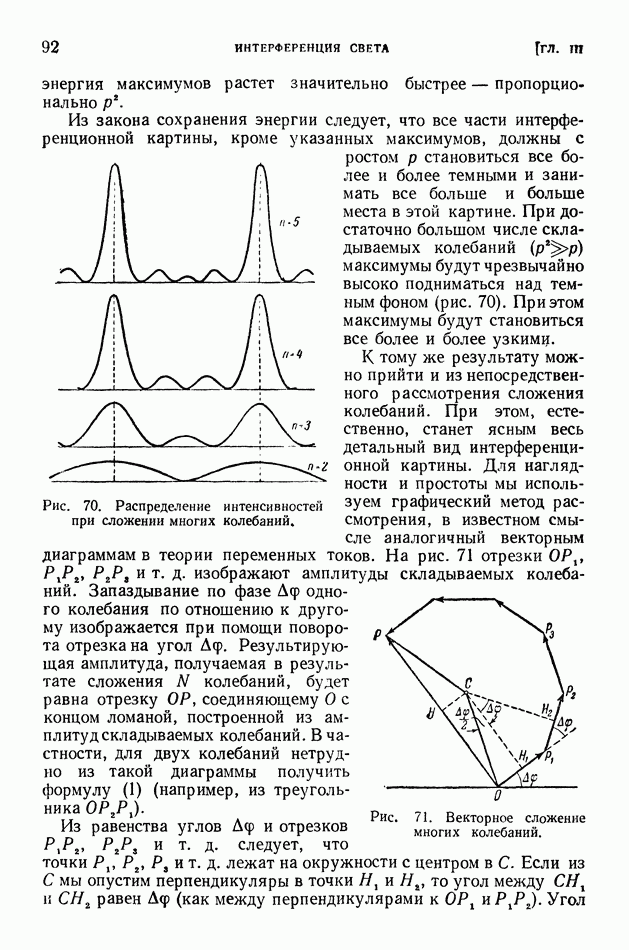
- § 22. Интерференция многих колебаний
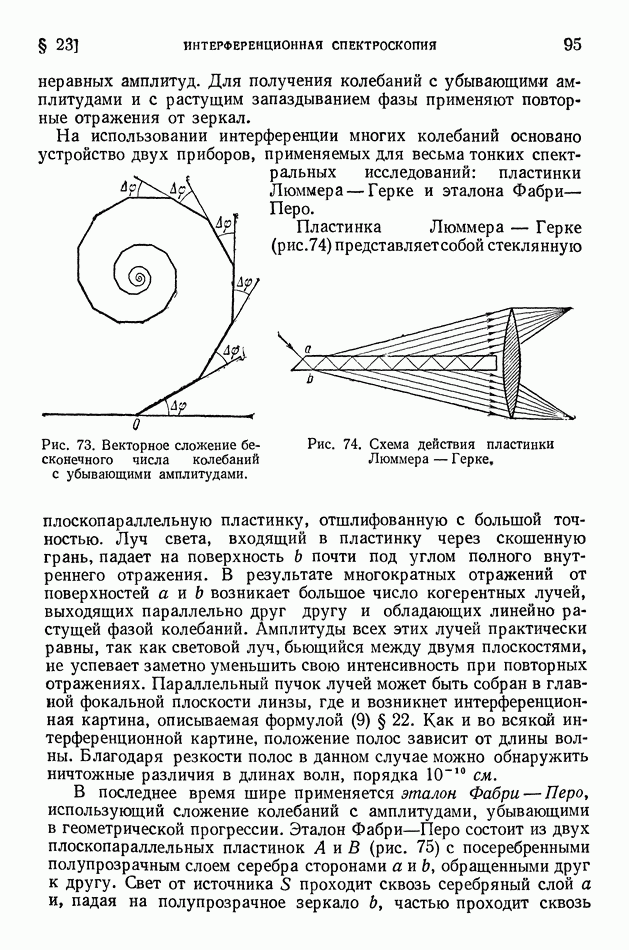
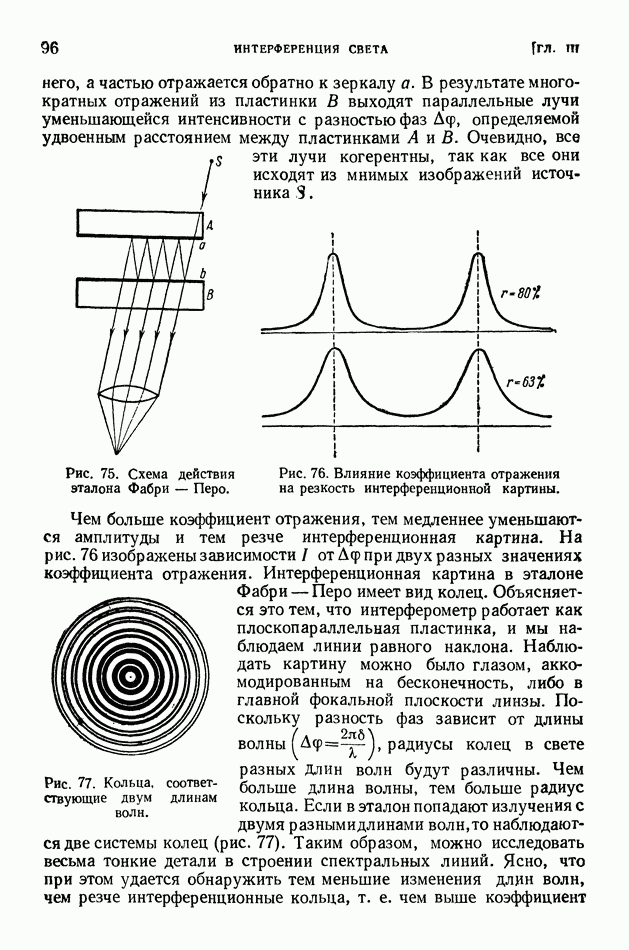
- § 23. Интерференционная спектроскопия
- ГЛАВА IV. ДИФРАКЦИЯ СВЕТА
- § 24. Явление дифракции. Опыт Френеля
- § 25. Принцип Гюйгенса-Френеля
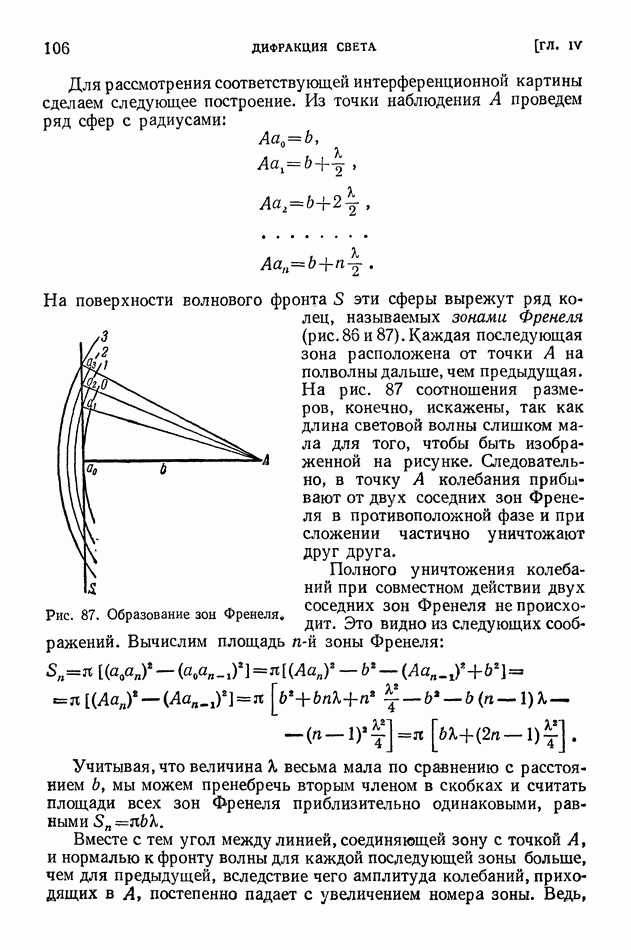
- § 26. Метод зон Френеля
- § 27. Дифракция от узкой щели
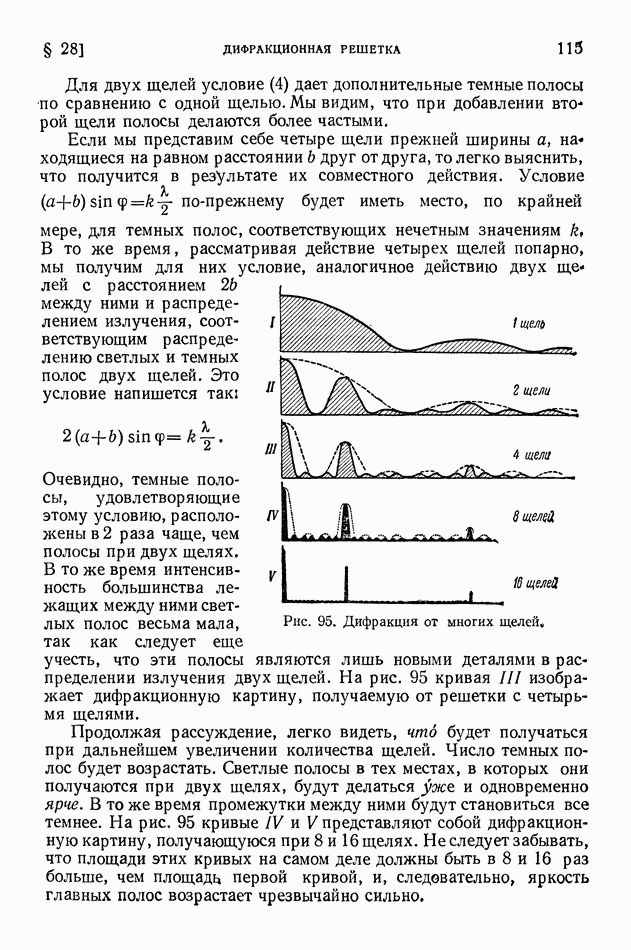
- § 28. Дифракционная решетка
- § 29. Дифракционный спектр. Решетки Роуланда и эшелон Майкельсона
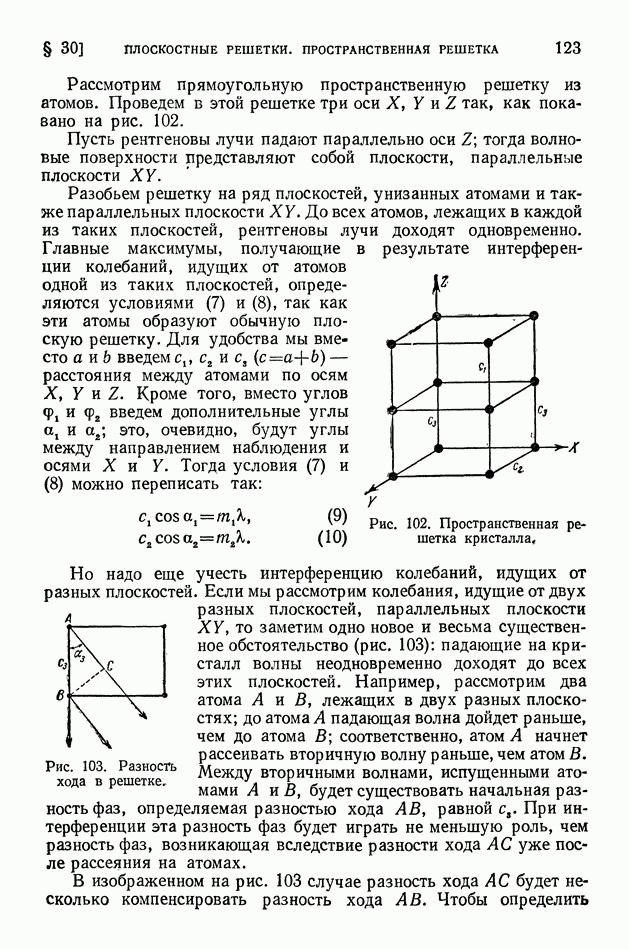
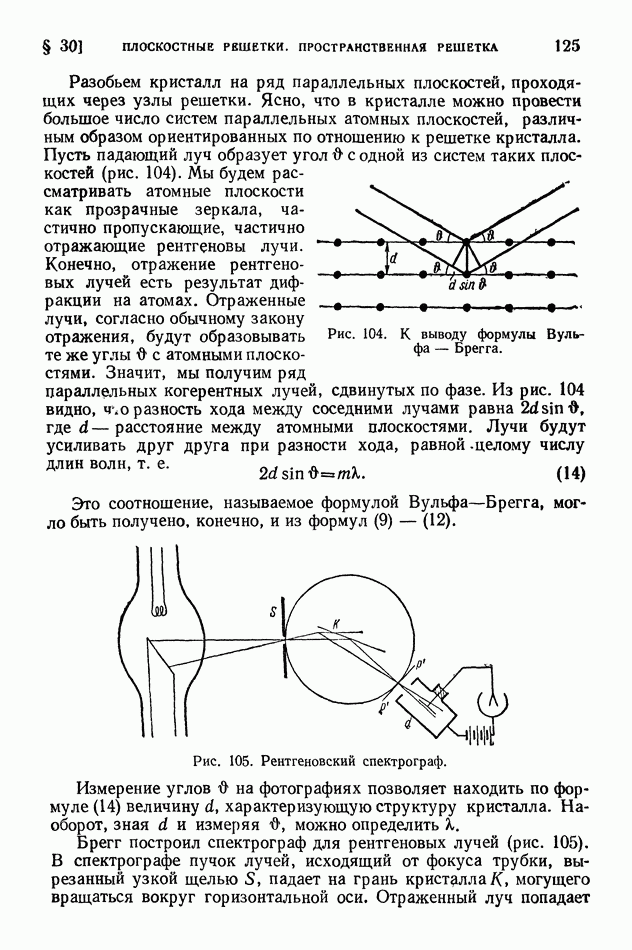
- § 30. Плоскостные решетки. Пространственная решетка
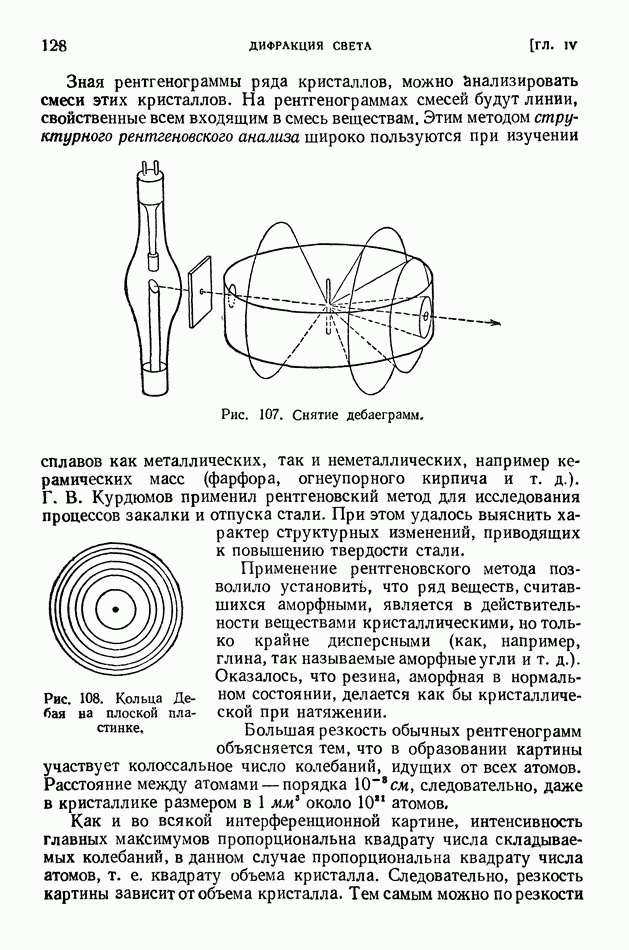
- § 31. Структурный рентгеновский анализ
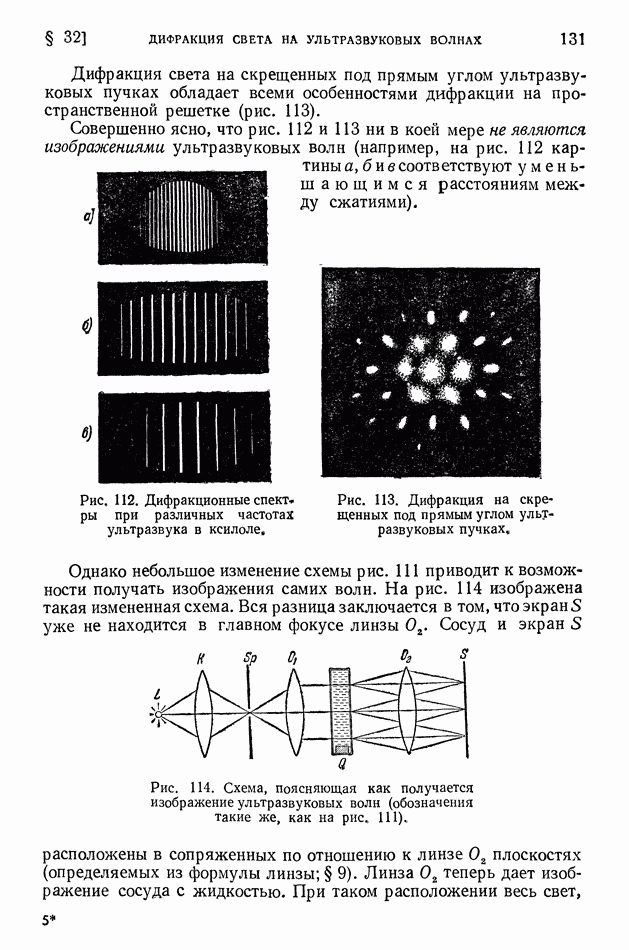
- § 32. Дифракция света на ультразвуковых волнах
- § 33. Дифракция от мелких частиц
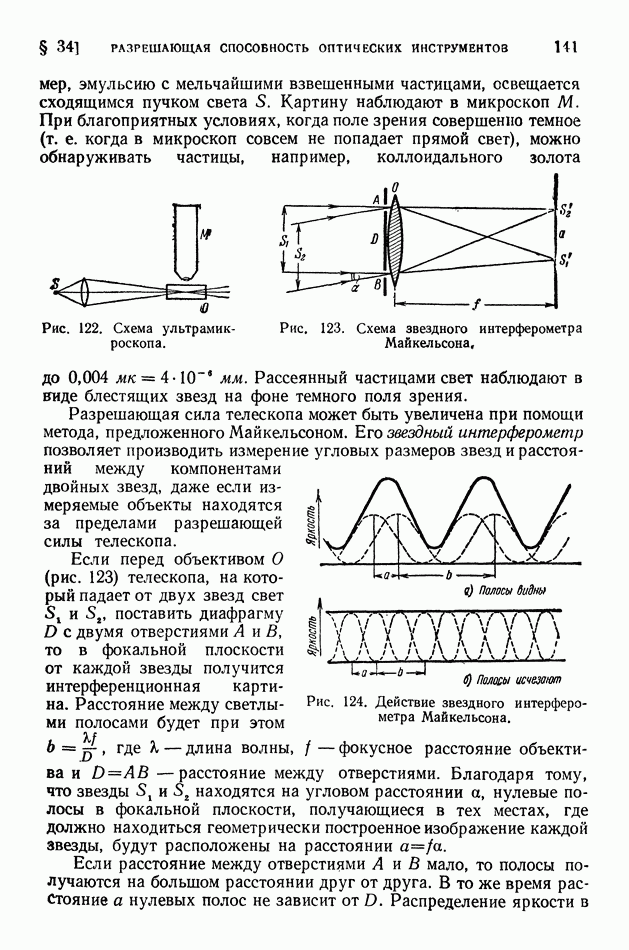
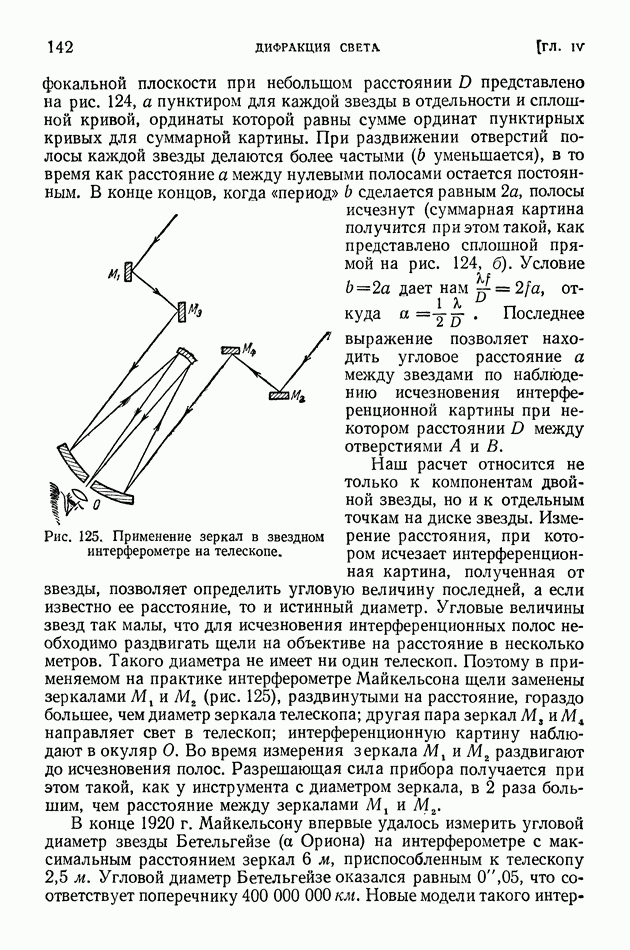
- § 34. Разрешающая способность оптических инструментов. Звездный интерферометр
- ГЛАВА V. ПОЛЯРИЗАЦИЯ СВЕТА
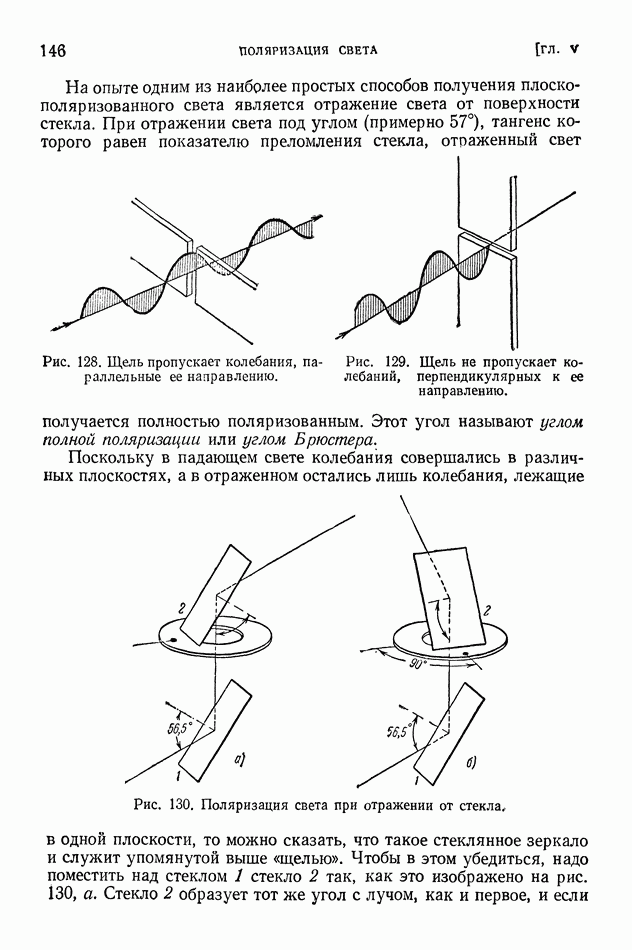
- § 35. Поляризация света
- § 36. Двойное лучепреломление
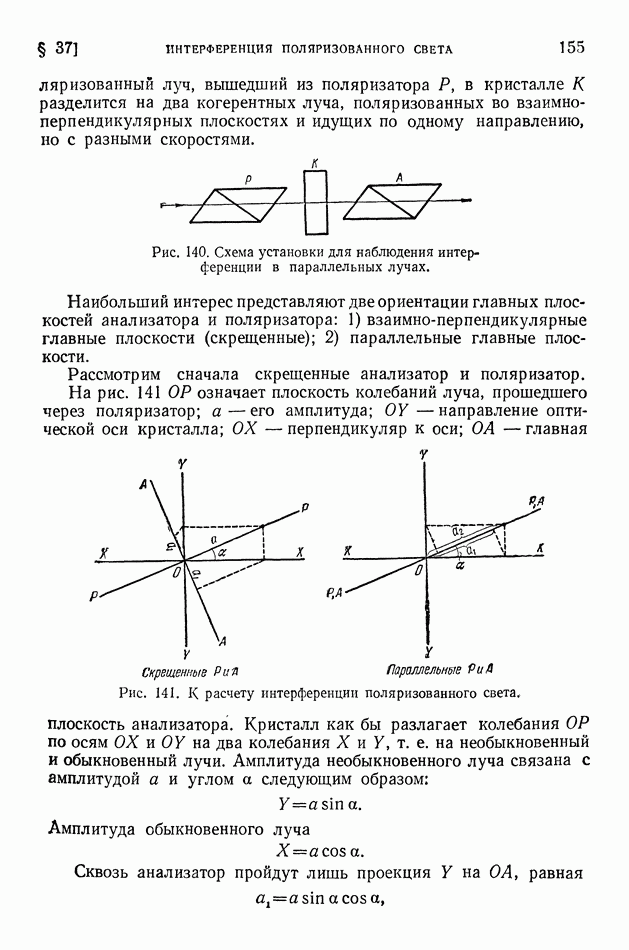
- § 37. Интерференция поляризованного света
- § 38. Оптический метод исследования упругих натяжений. Эффект Керра
- § 39. Вращение плоскости поляризации. Эллиптическая поляризация
- ГЛАВА VI. ДИСПЕРСИЯ, ПОГЛОЩЕНИЕ И ИЗЛУЧЕНИЕ СВЕТА
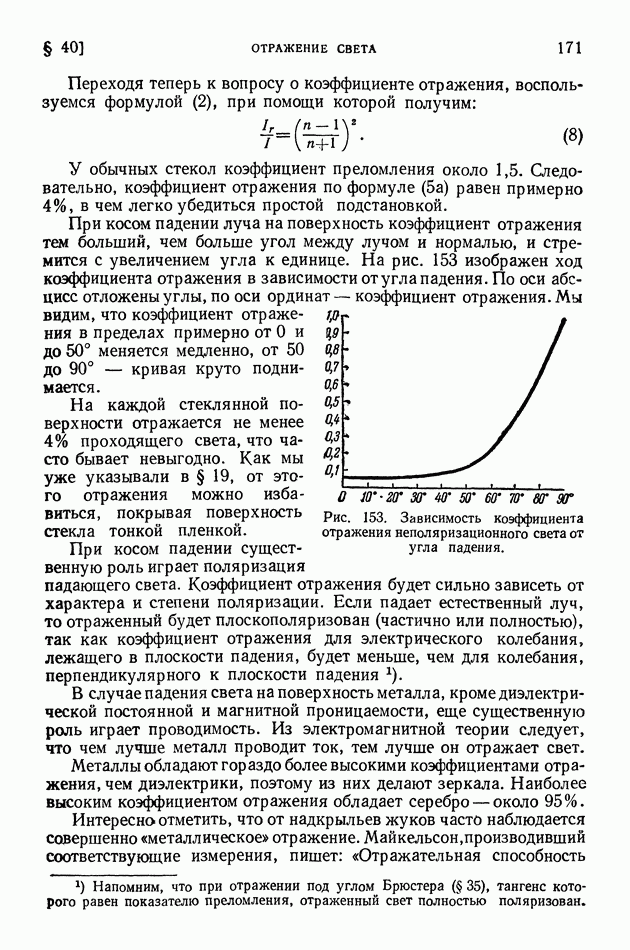
- § 40. Отражение света
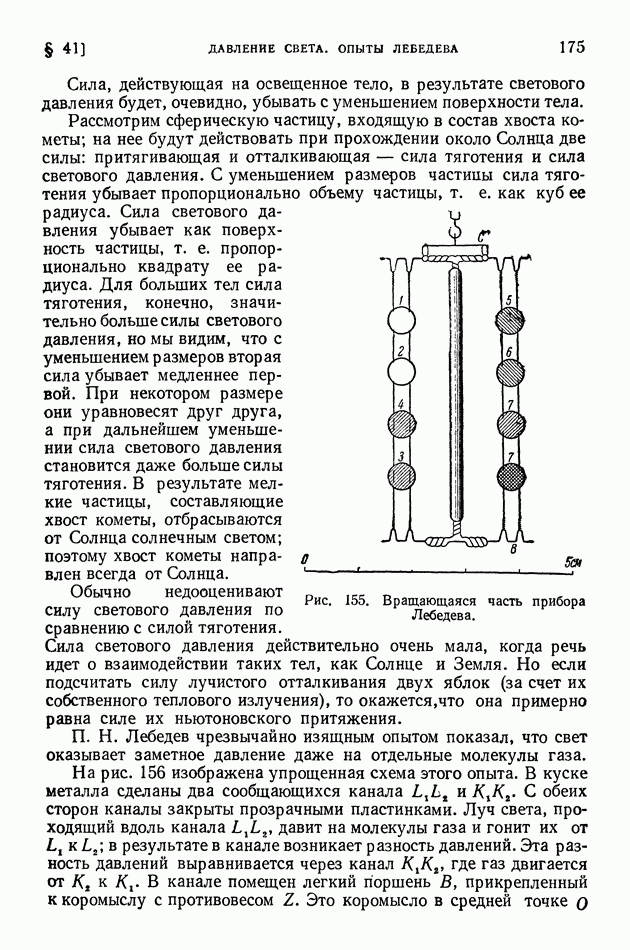
- § 41. Давление света. Опыты Лебедева
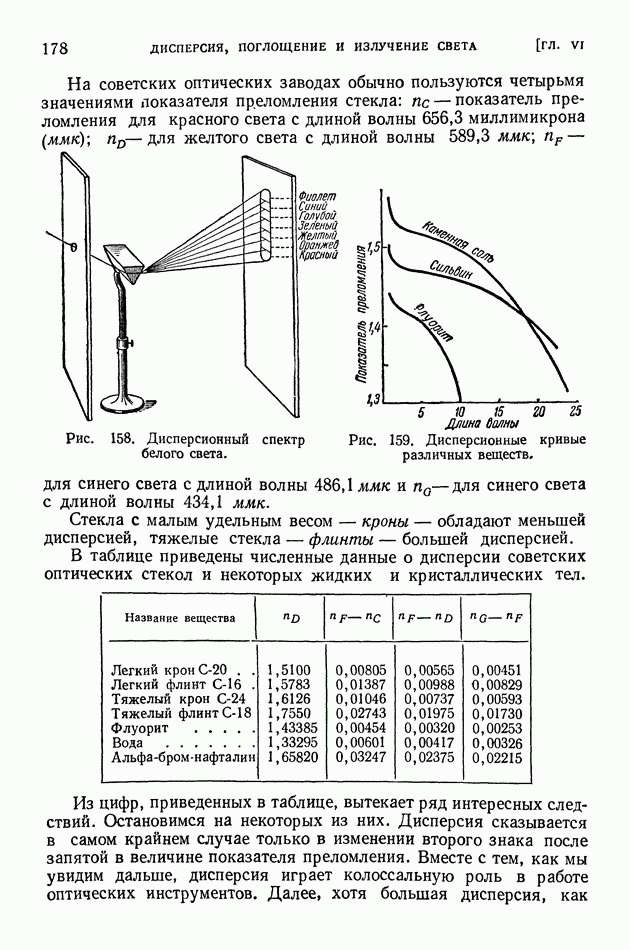
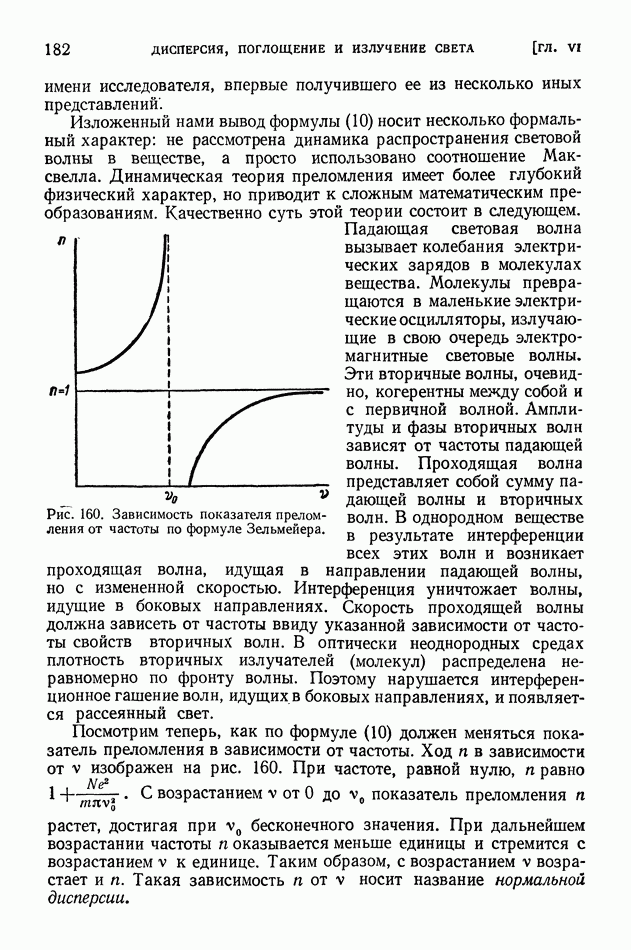
- § 42. Дисперсия. Опыты Ньютона
- § 43. Молекулярная теория дисперсии
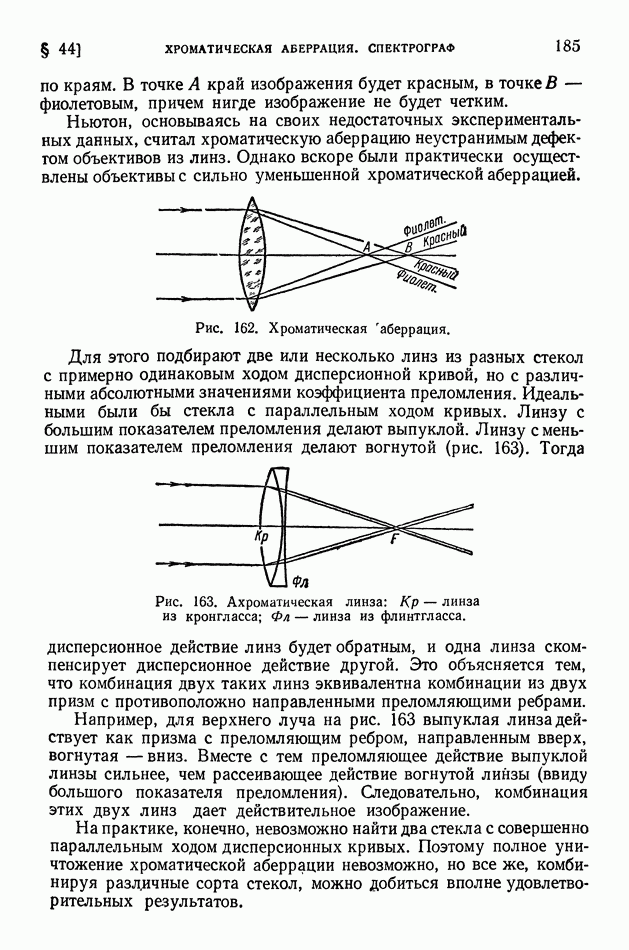
- § 44. Хроматическая аберрация. Спектрограф
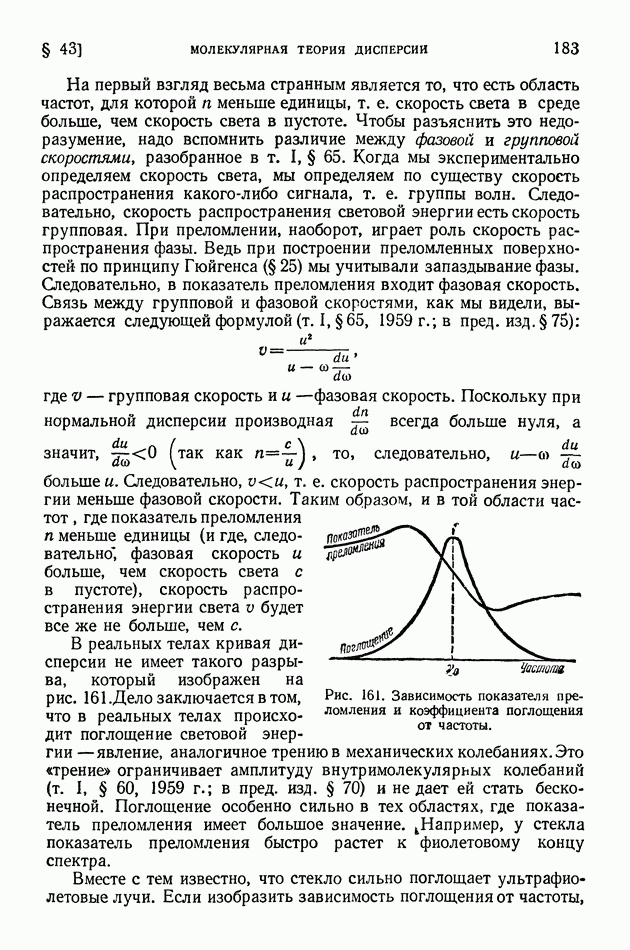
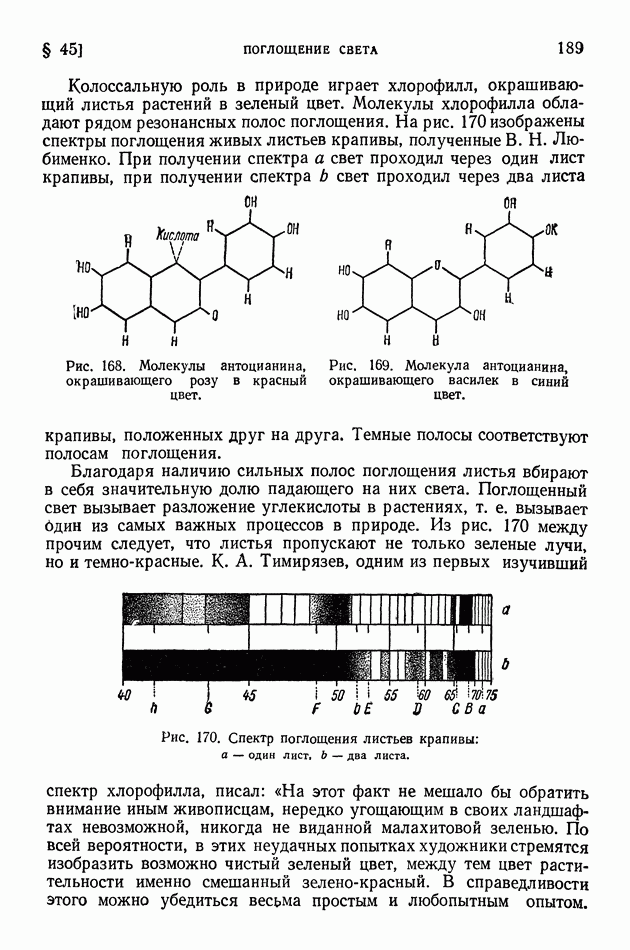
- § 45. Поглощение света
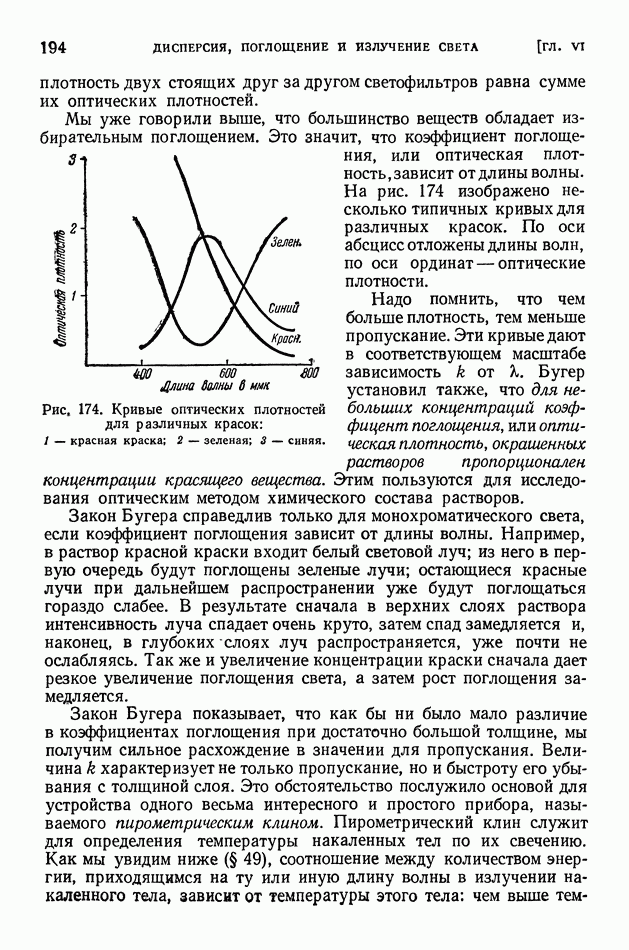
- § 46. Закон Бугера. Опыты Вавилова
- § 47. Атом как элементарный излучатель света
- § 48. Эффект Вавилова — Черенкова
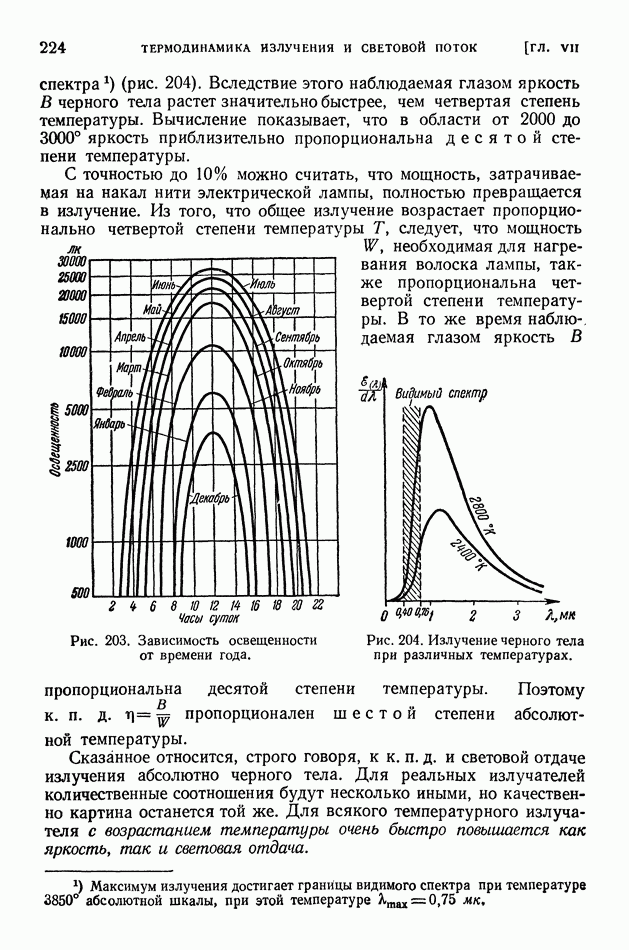
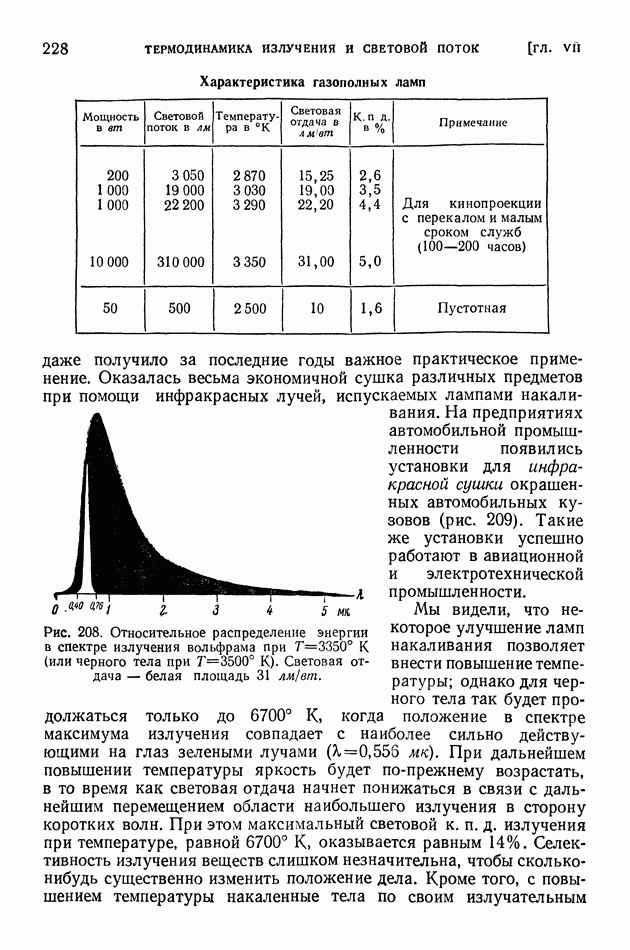
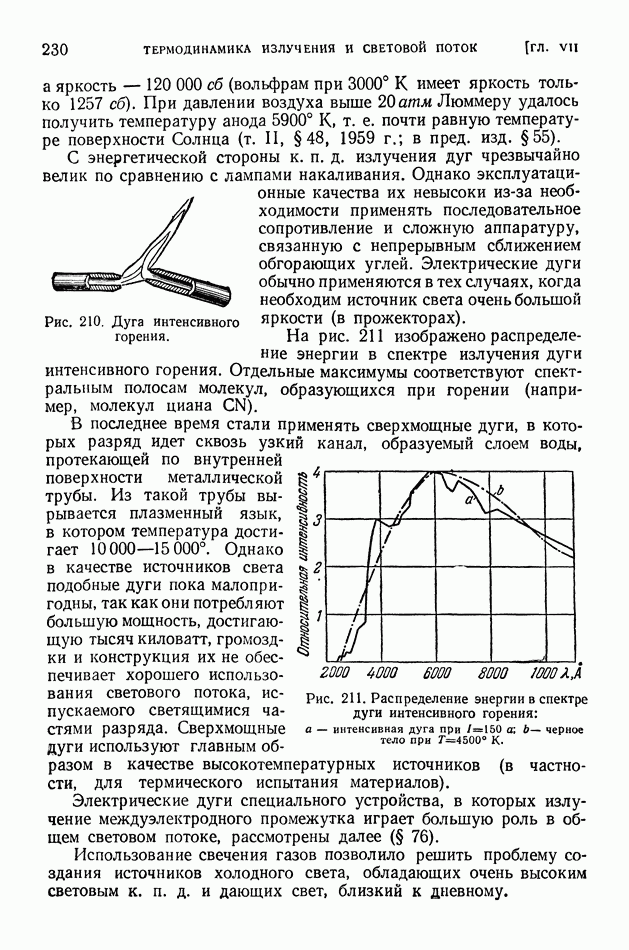
- ГЛАВА VII. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ И СВЕТОВОЙ ПОТОК
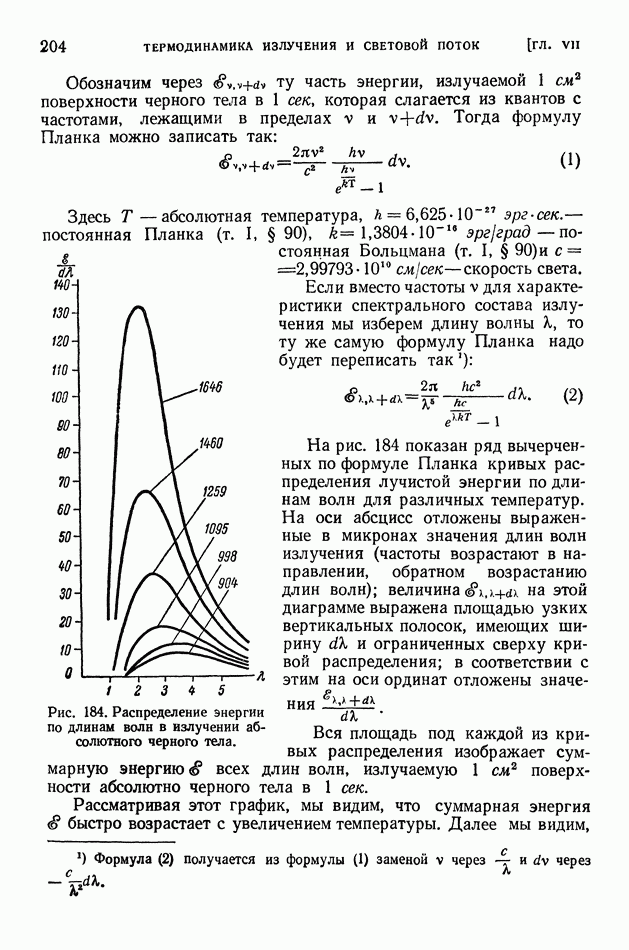
- § 49. Излучение черного тела. Формула Планка. Закон Вина
- § 50. Излучение нечерных тел. Законы Кирхгофа
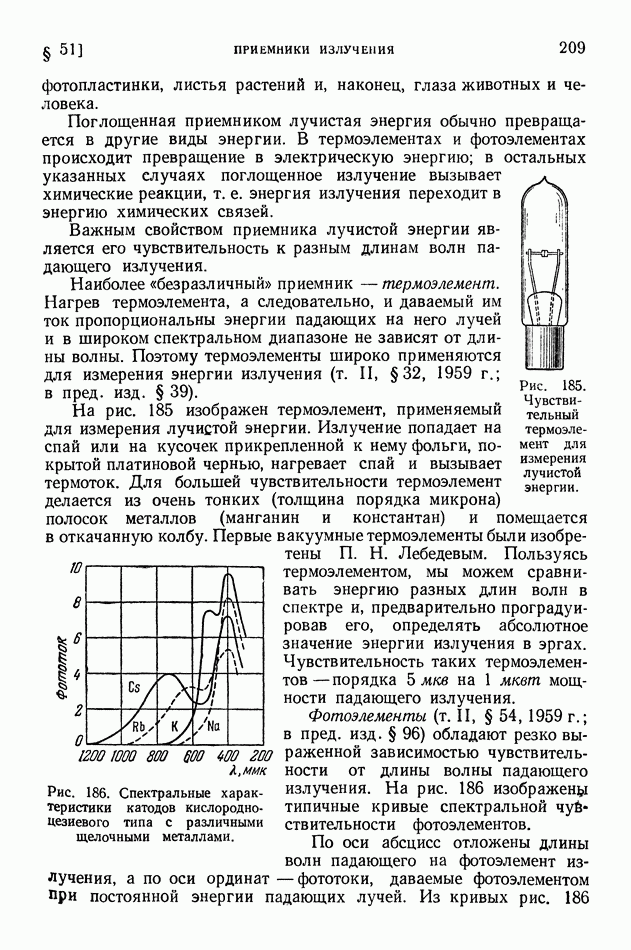
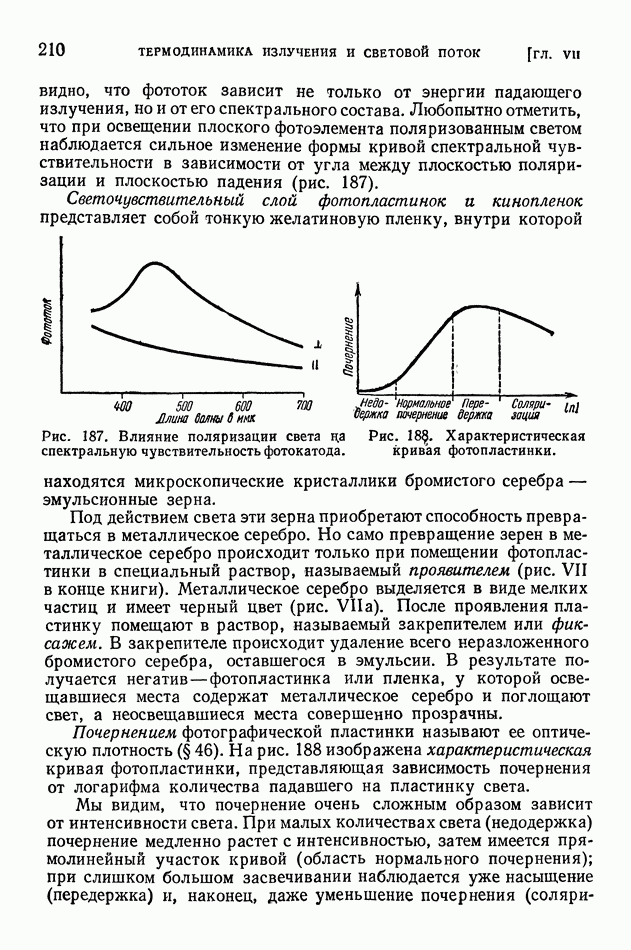
- § 51. Приемники излучения
- § 52. Световые величины и их измерения
- § 53 Температурные излучатели как источники света
- ЧАСТЬ ПЯТАЯ. АТОМНАЯ ФИЗИКА
- ГЛАВА VIII. СТРОЕНИЕ АТОМА И ТЕОРИЯ БОРА
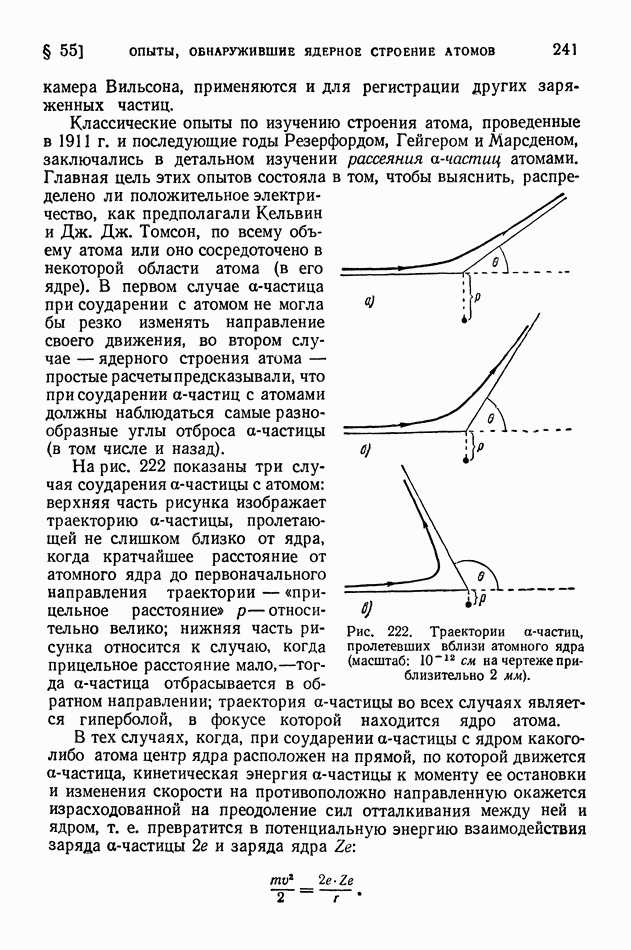
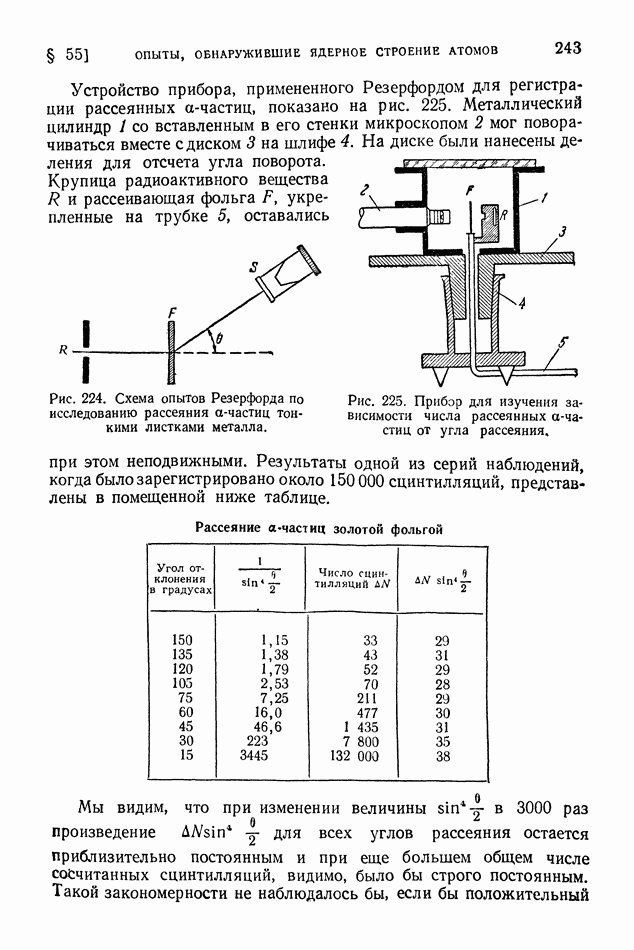
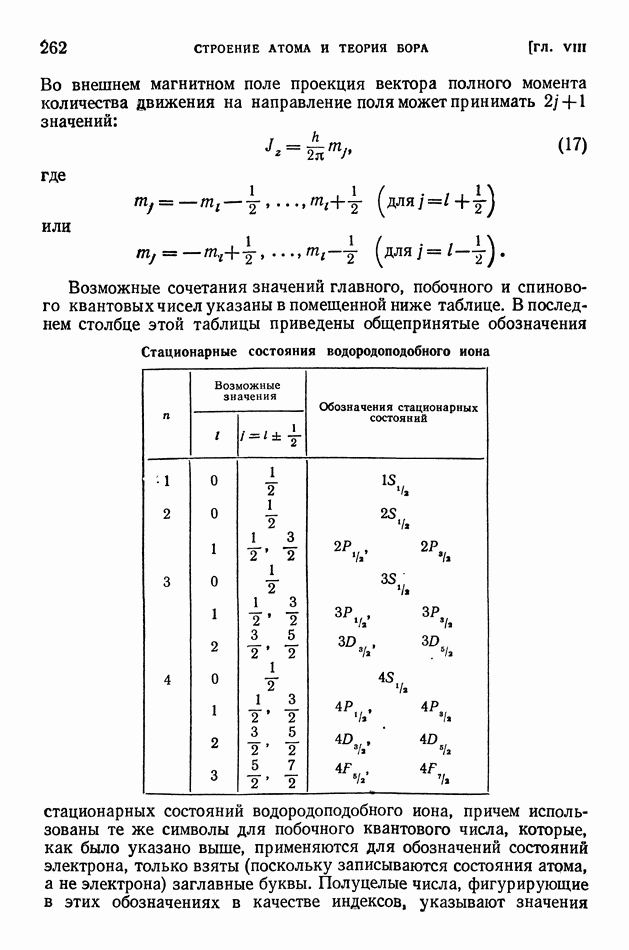
- § 55. Опыты, обнаружившие ядерное строение атомов
- § 56. Противоречие между фактическим строением атомов и выводами классической электродинамики. Строение линейчатых спектров
- § 57. Опытные основания теории квантов в первые годы ее развития
- § 58. Теория Бора. Происхождение спектра водорода
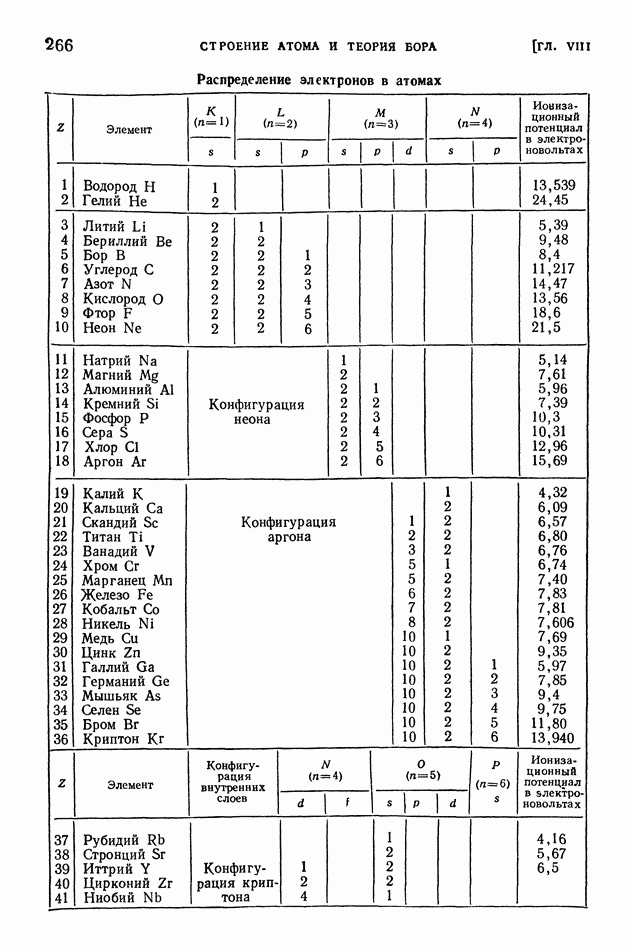
- § 59. Квантовые числа
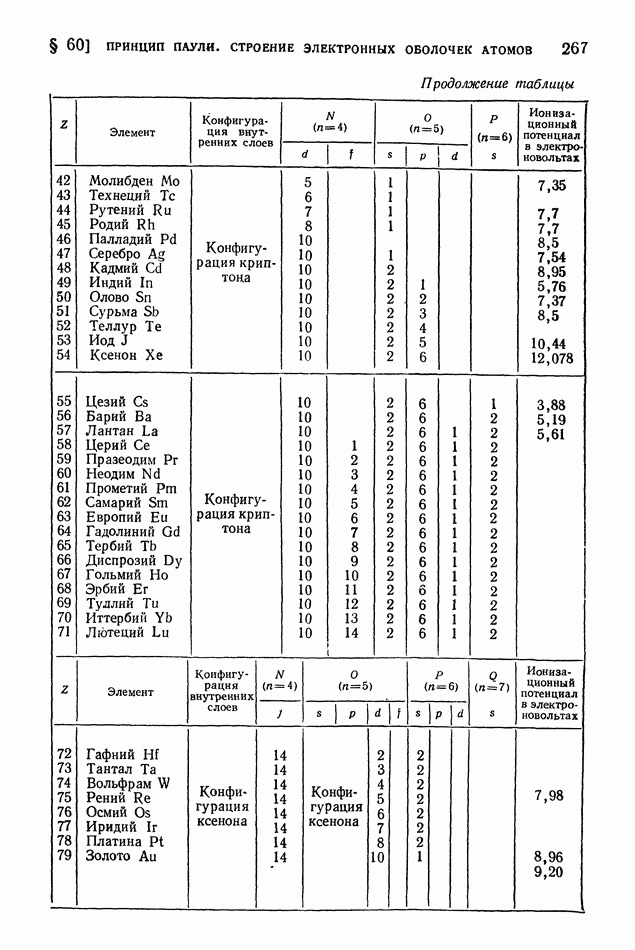
- § 60. Принцип Паули. Строение электронных оболочек атомов
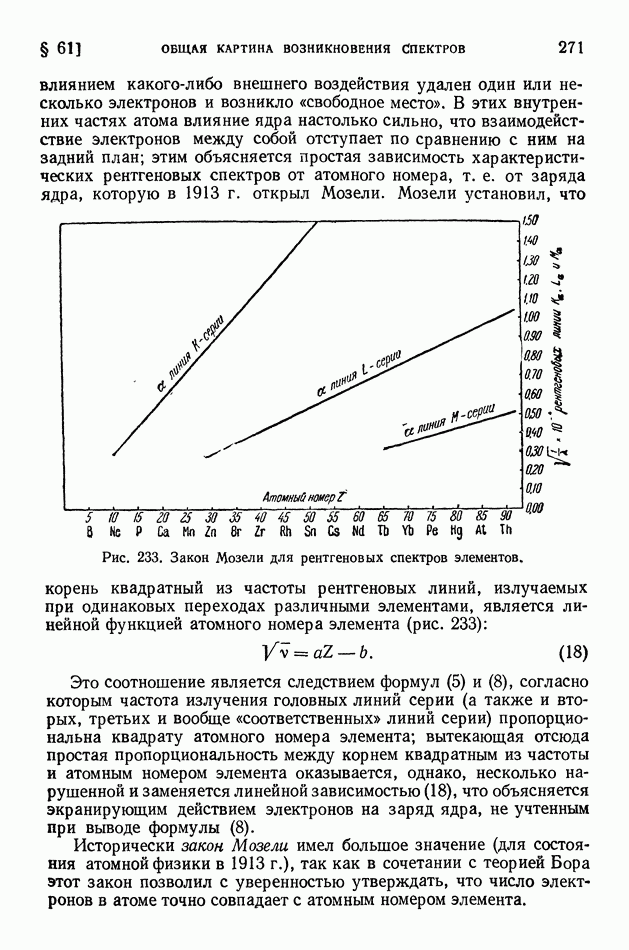
- § 61. Общая картина возникновения спектров
- ГЛАВА IX. ОСНОВЫ КВАНТОВОЙ (ВОЛНОВОЙ) МЕХАНИКИ
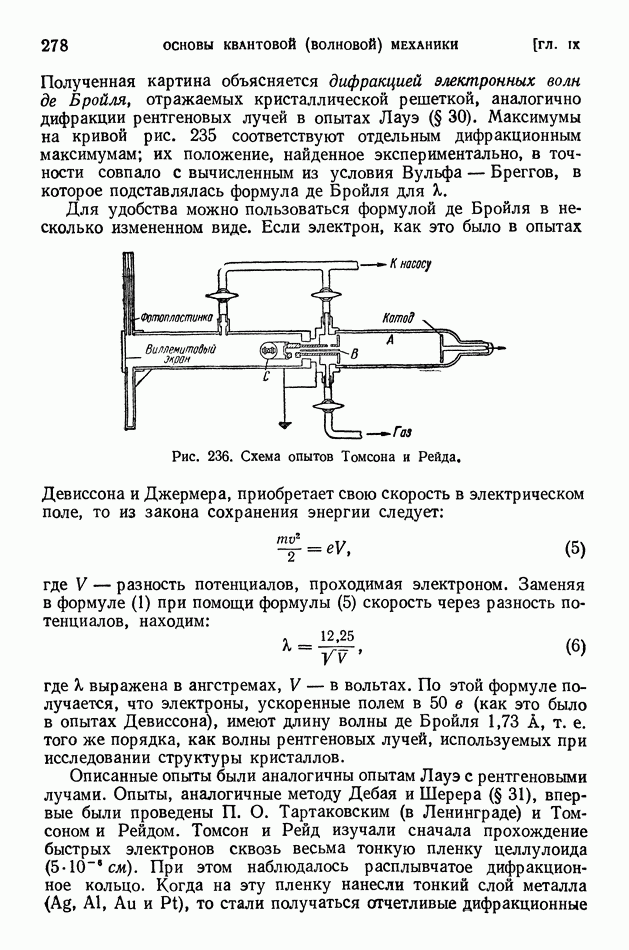
- § 62. Волновые свойства частиц. Формула де Бройля. Дифракция электронов
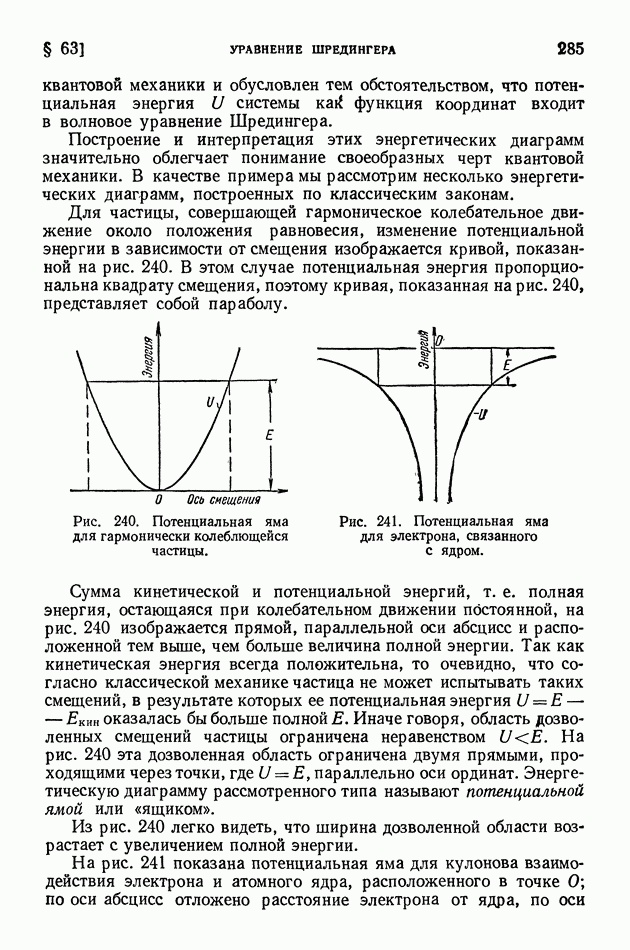
- § 63. Уравнение Шредингера. Просачивание через энергетический барьер. Нулевая энергия
- § 64. Волномеханическая теория атома водорода
- § 65. Соотношение неопределенностей и его разные трактовки
- ГЛАВА X. КВАНТОВАЯ ОПТИКА
- § 66. Развитие квантовой оптики
- § 67. Спектр щелочных металлов. Спин электрона
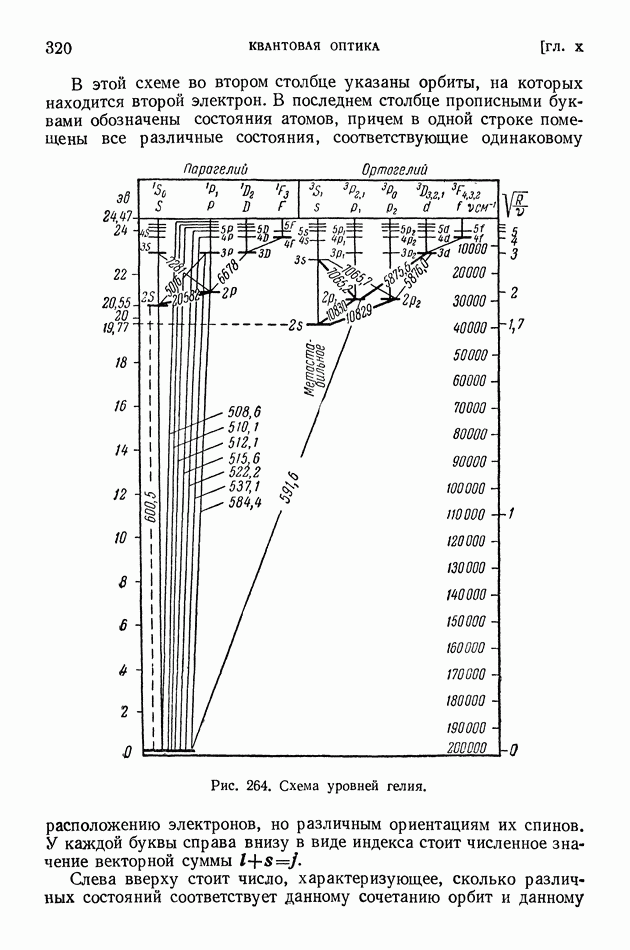
- § 68. Спектр гелия. Символика спектральных термов
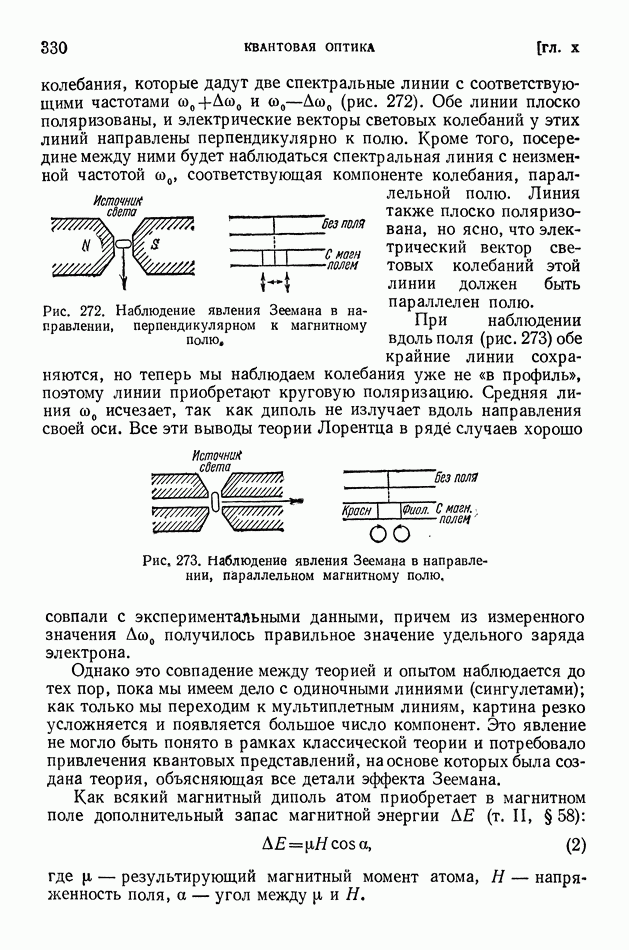
- § 69. Сверхтонкая структура спектральных линий
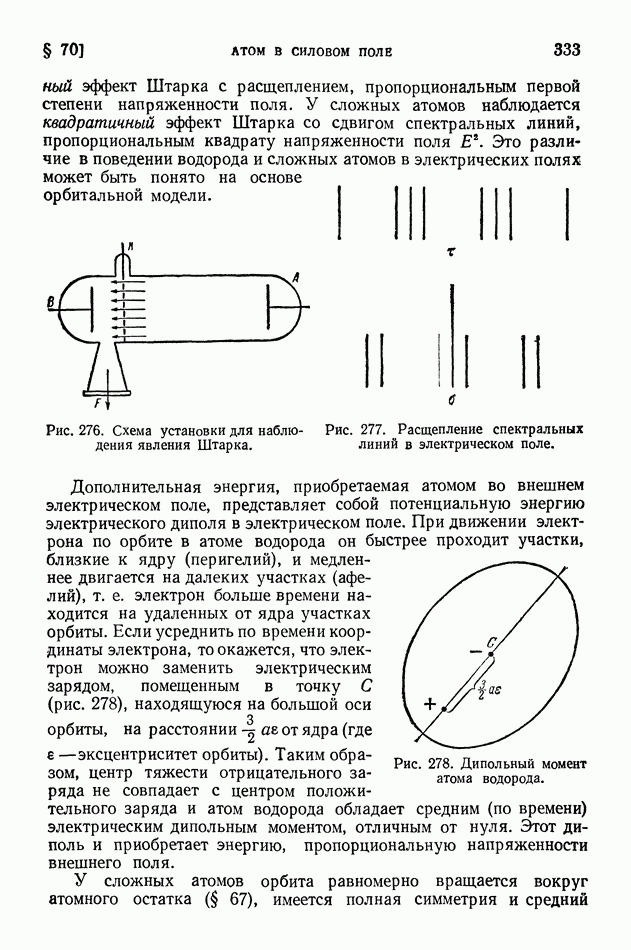
- § 70. Атом в силовом поле
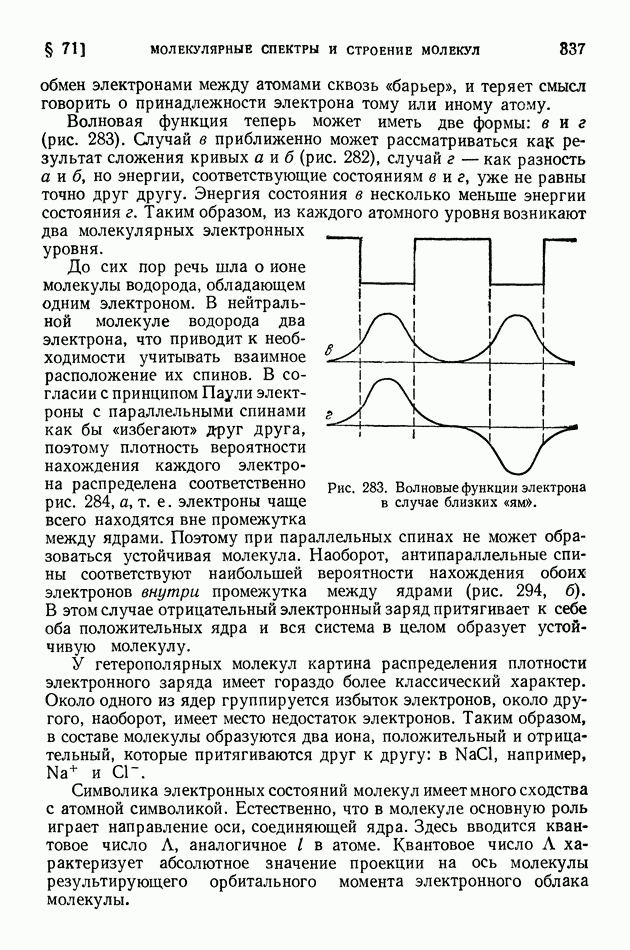
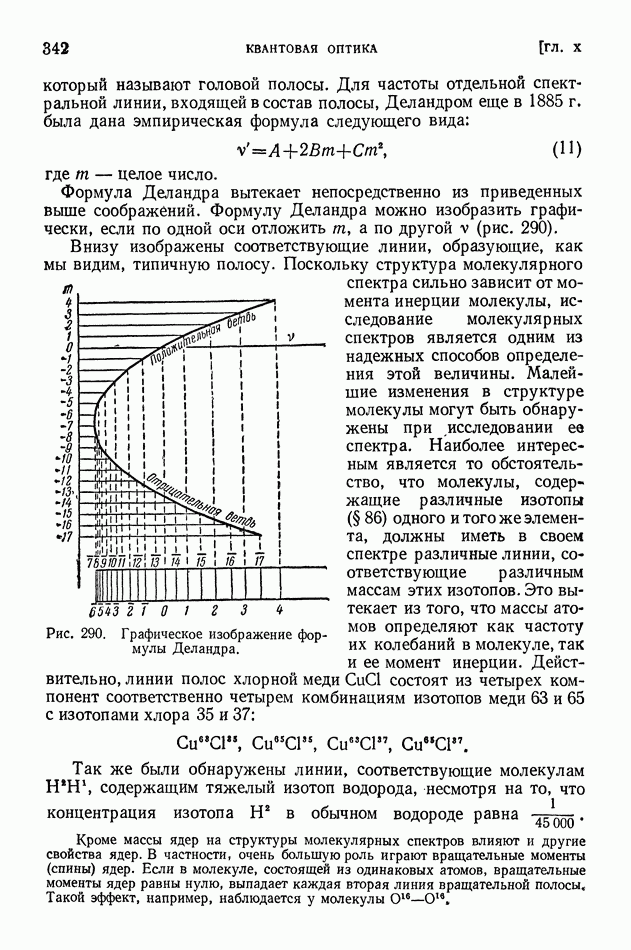
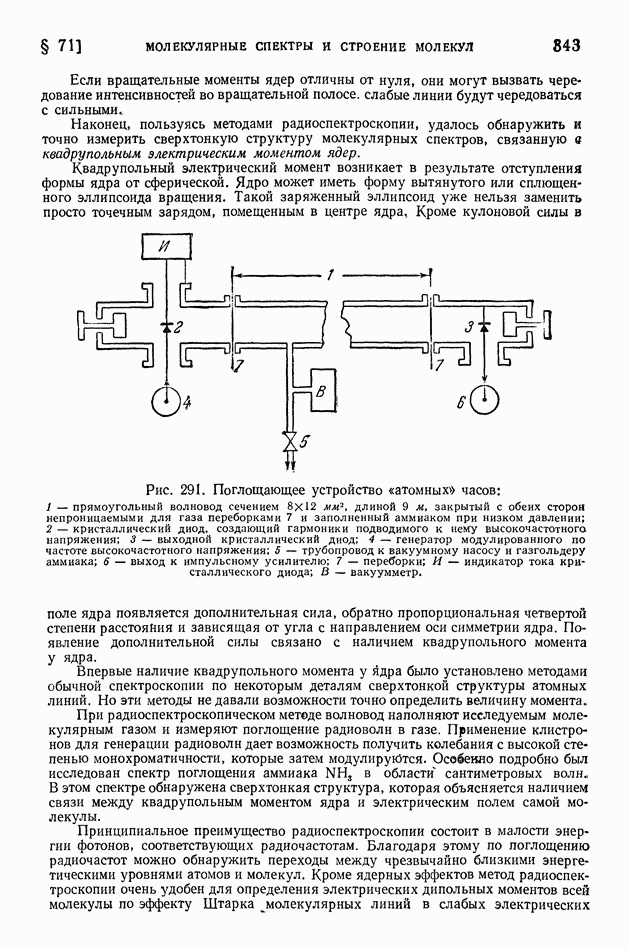
- § 71. Молекулярные спектры и строение молекул
- § 72. Комбинационное рассеяние света
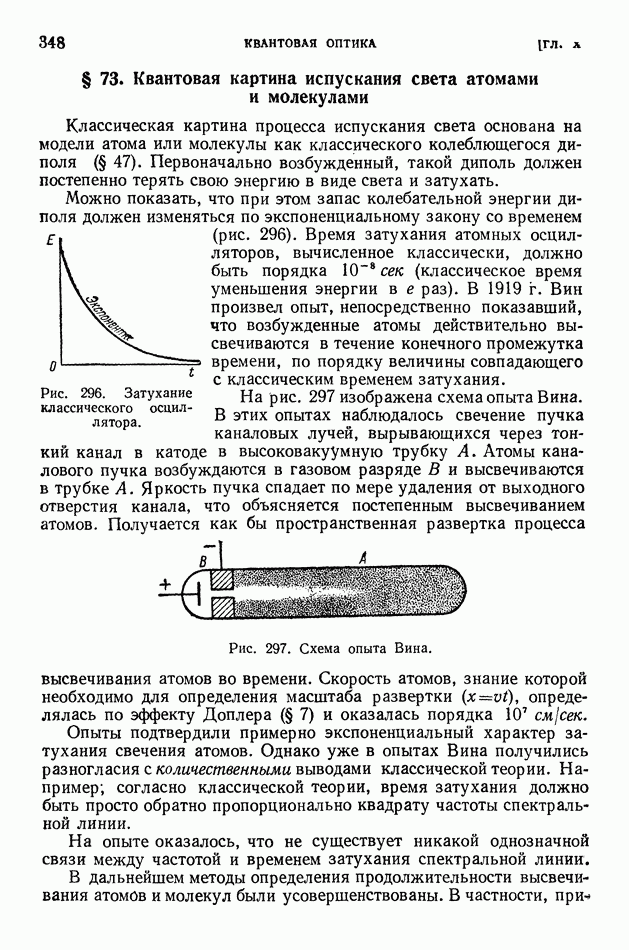
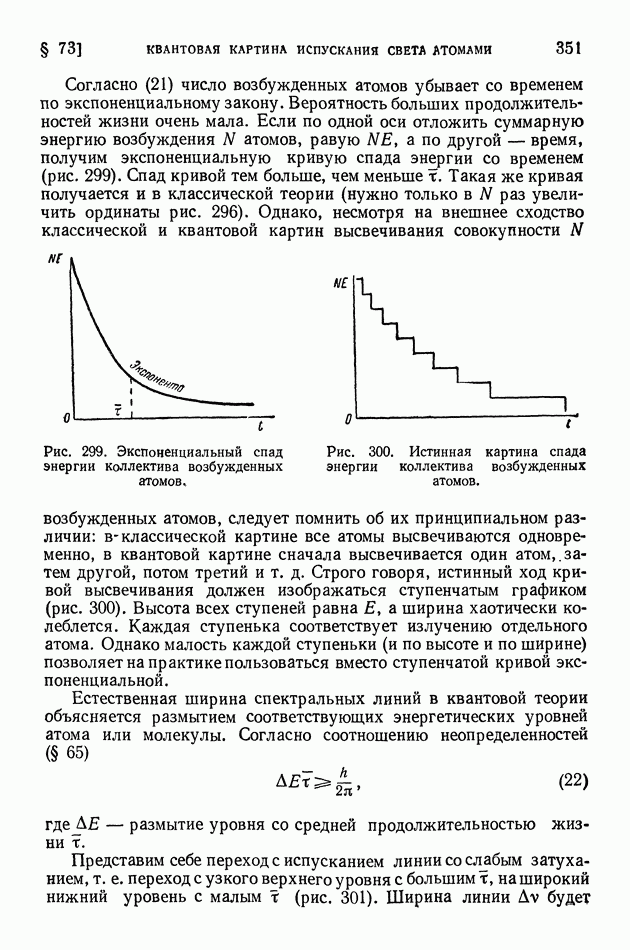
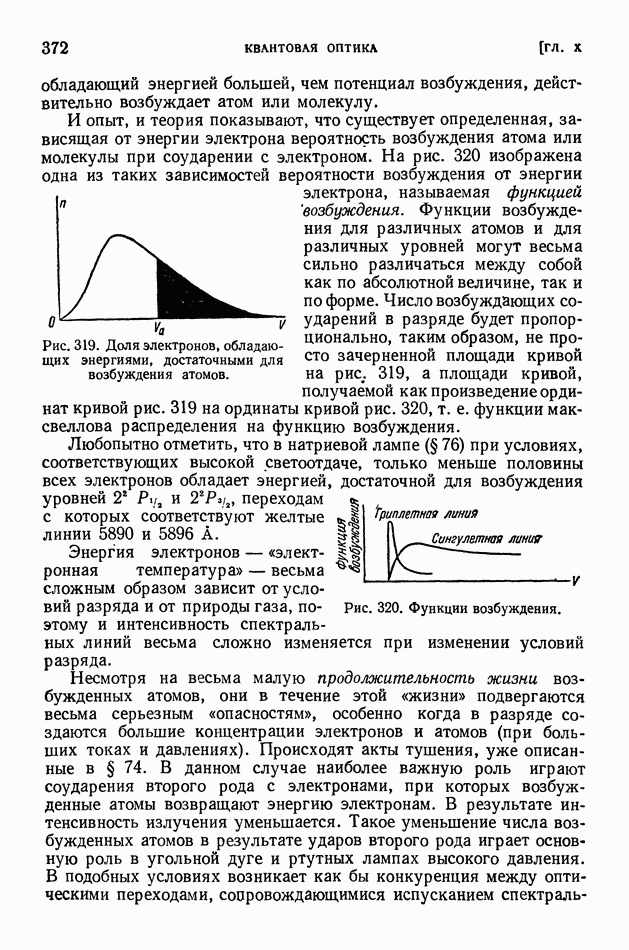
- § 73. Квантовая картина испускания света атомами и молекулами
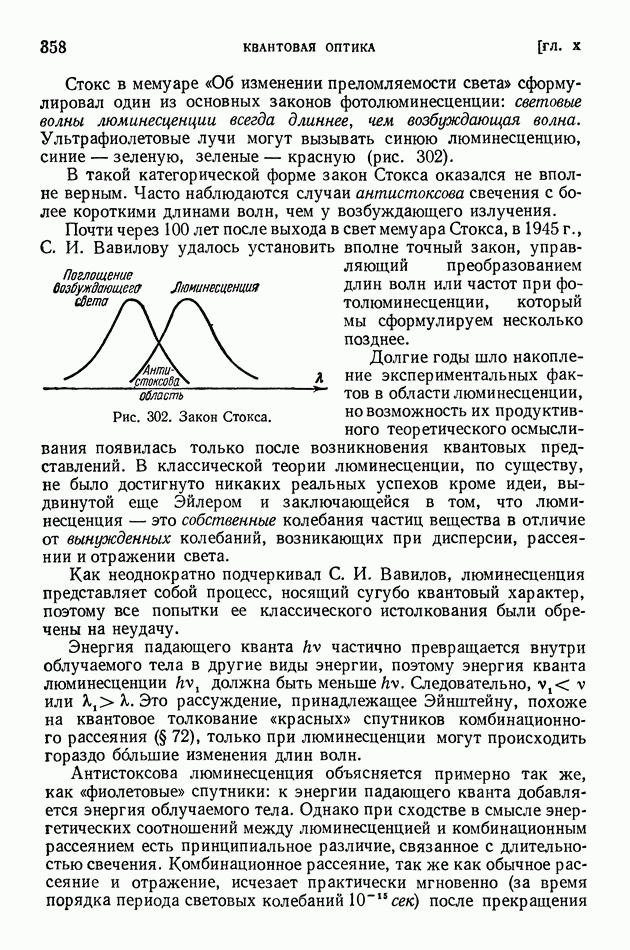
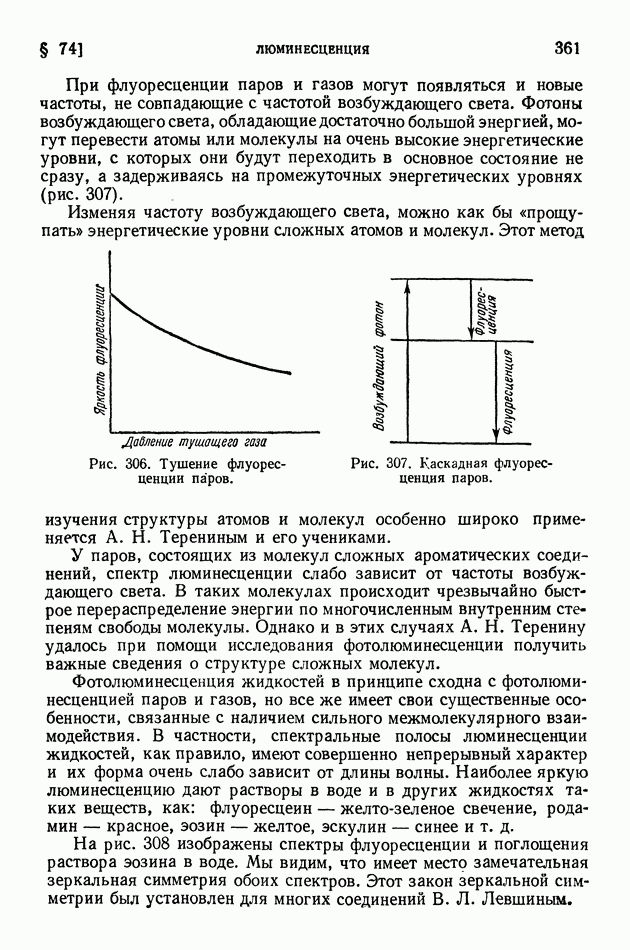
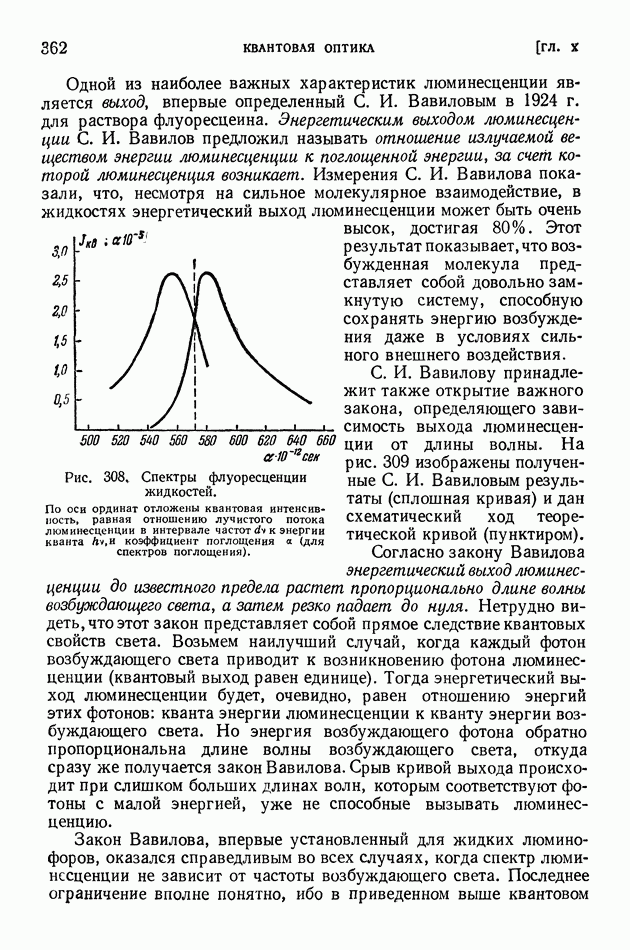
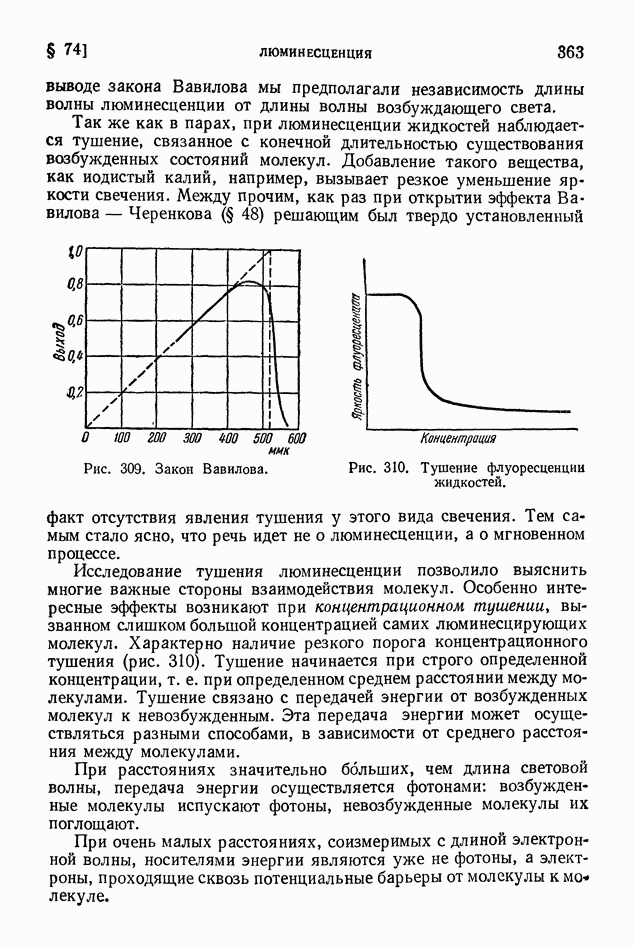
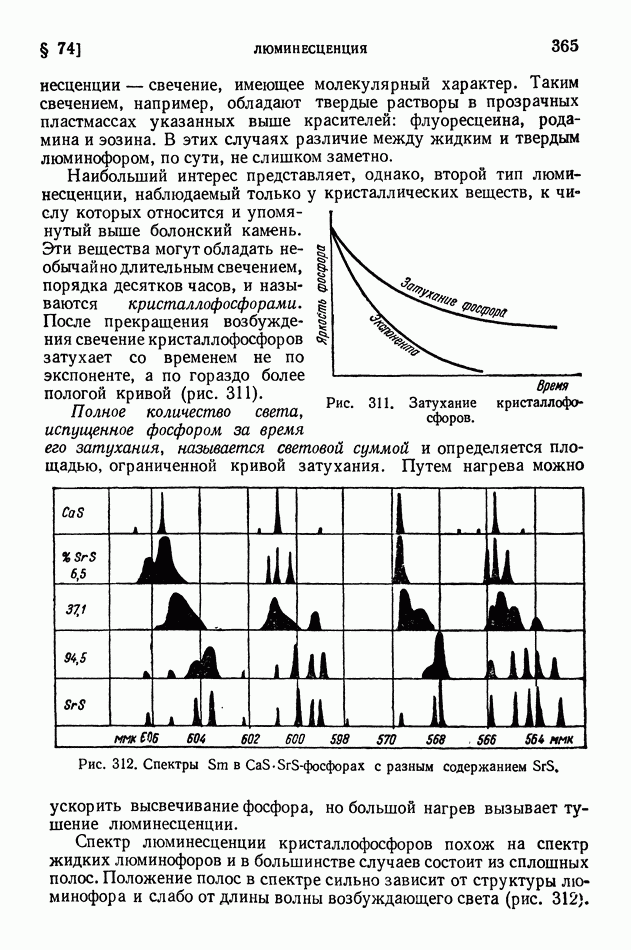
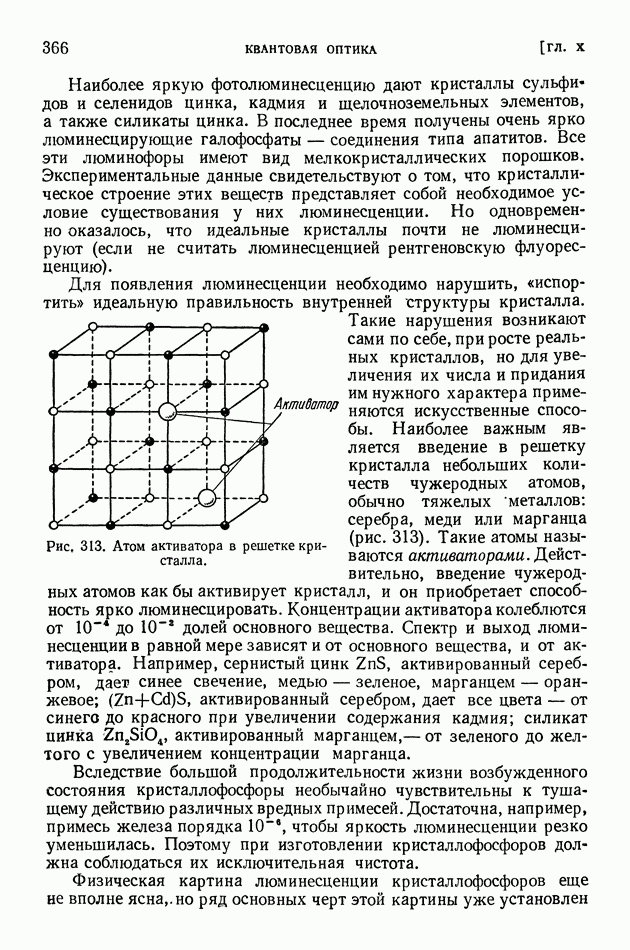
- § 74. Люминесценция
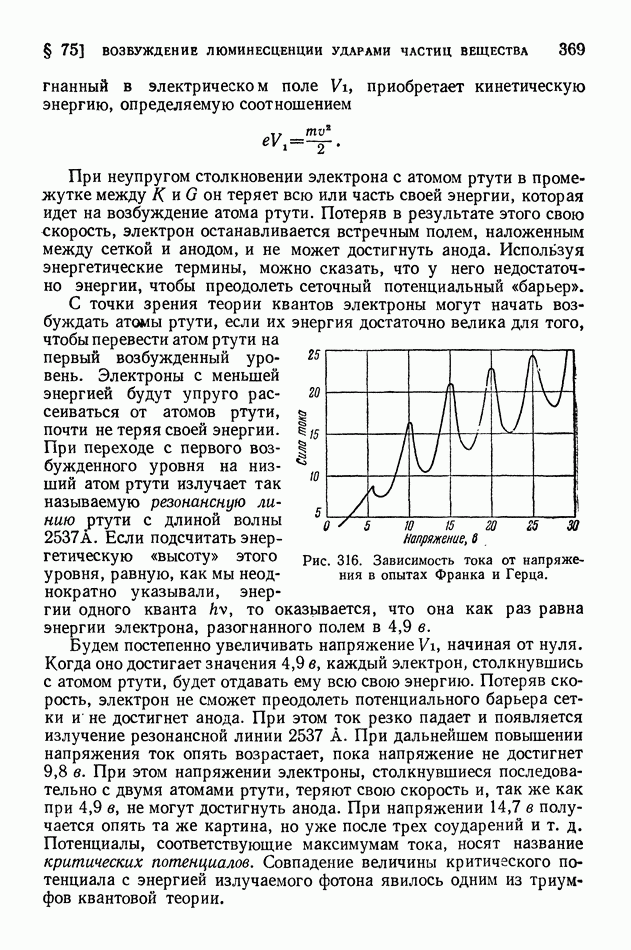
- § 75. Возбуждение люминесценции ударами частиц вещества
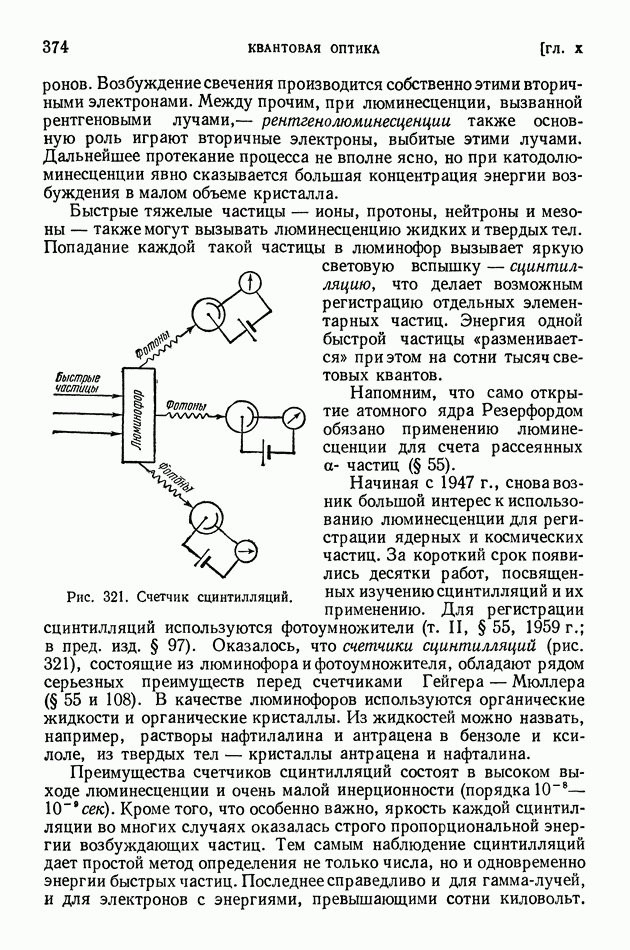
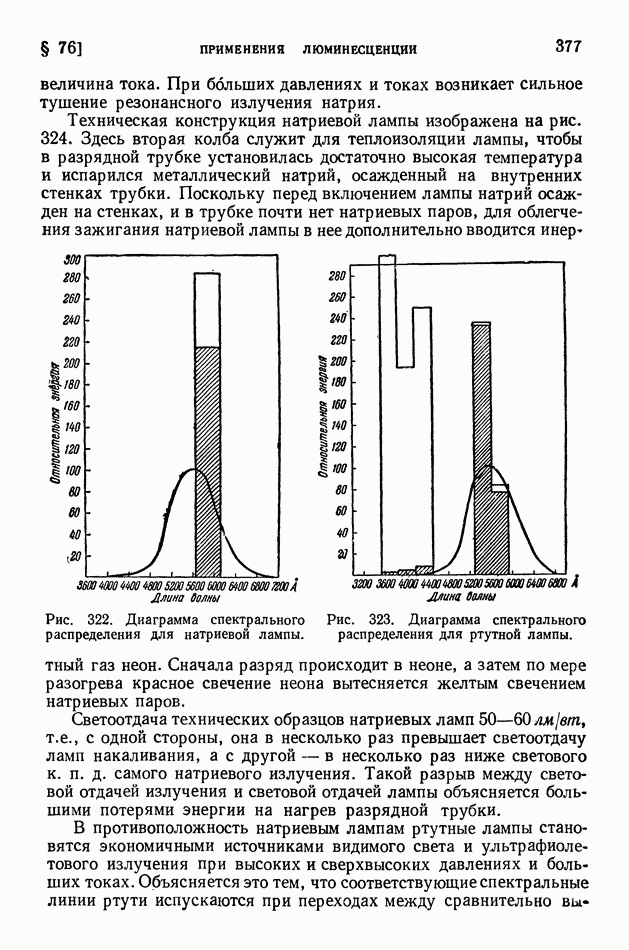
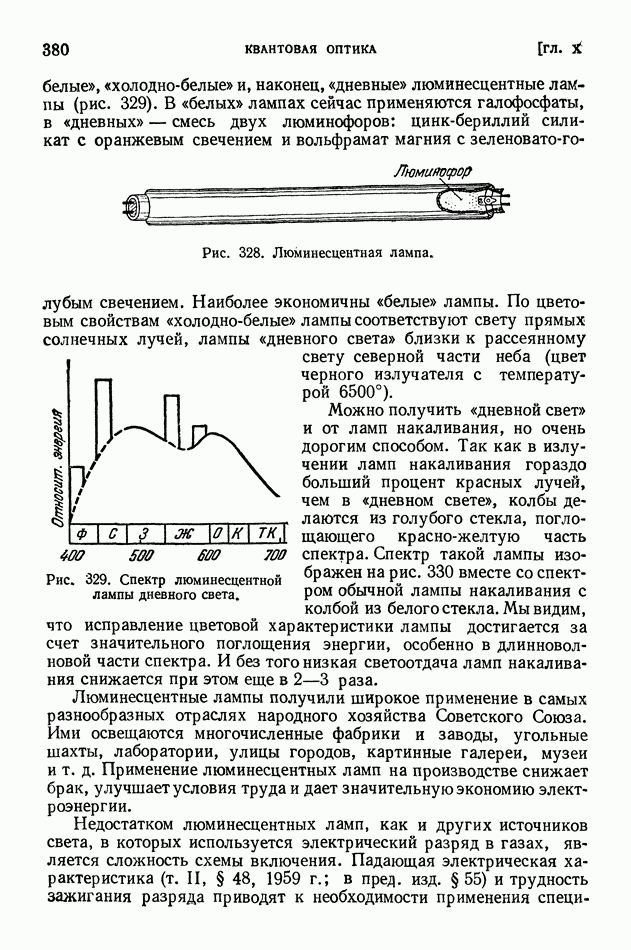
- § 76. Применения люминесценции
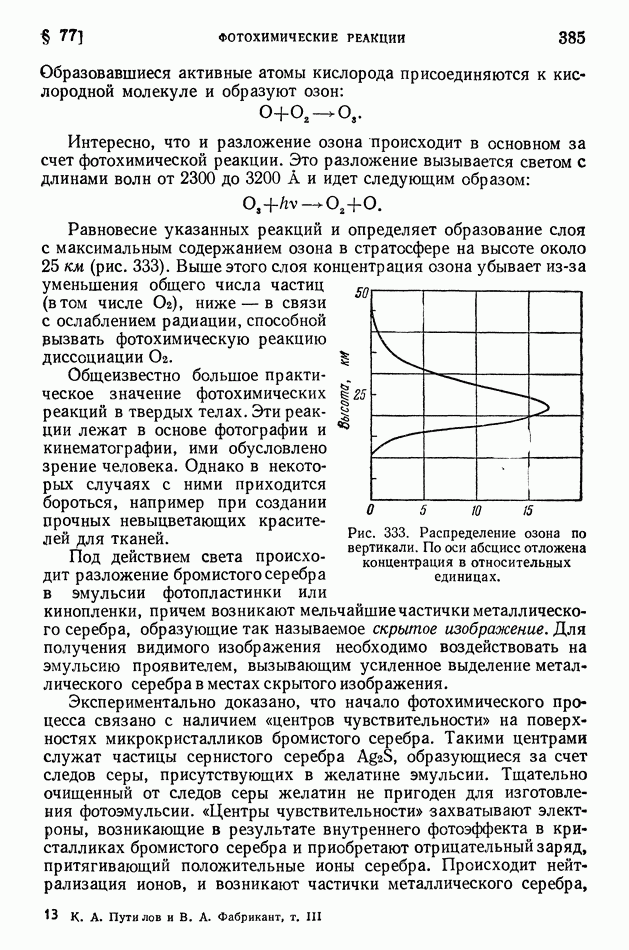
- § 77. Фотохимические реакции
- ГЛАВА XI. ЗАКОН ПРОПОРЦИОНАЛЬНОСТИ МАССЫ И ЭНЕРГИИ И РЕЛЯТИВИСТСКИЕ СООТНОШЕНИЯ
- § 78. Закон пропорциональности массы и энергии
- § 79. Предварительные замечания о релятивистских эффектах. Зависимость массы от скорости
- § 80. Корпускулярные свойства фотонов. Явление Комптона
- § 81. Вывод закона Эйнштейна сложения скоростей из закона пропорциональности массы и энергии и законов сохранения энергии или количества движения
- § 82. Две трактовки закона пропорциональности массы и энергии и уточнение закона тяготения
- § 83. Красное смещение спектральных линий. Поперечный эффект Доплера
- § 84. Влияние гравитационного поля на скорость света в вакууме и показатель преломления вакуума
- ЧАСТЬ ШЕСТАЯ. ЯДЕРНАЯ ФИЗИКА
- § 85. Заряд и масса ядра. Масс-спектральный анализ
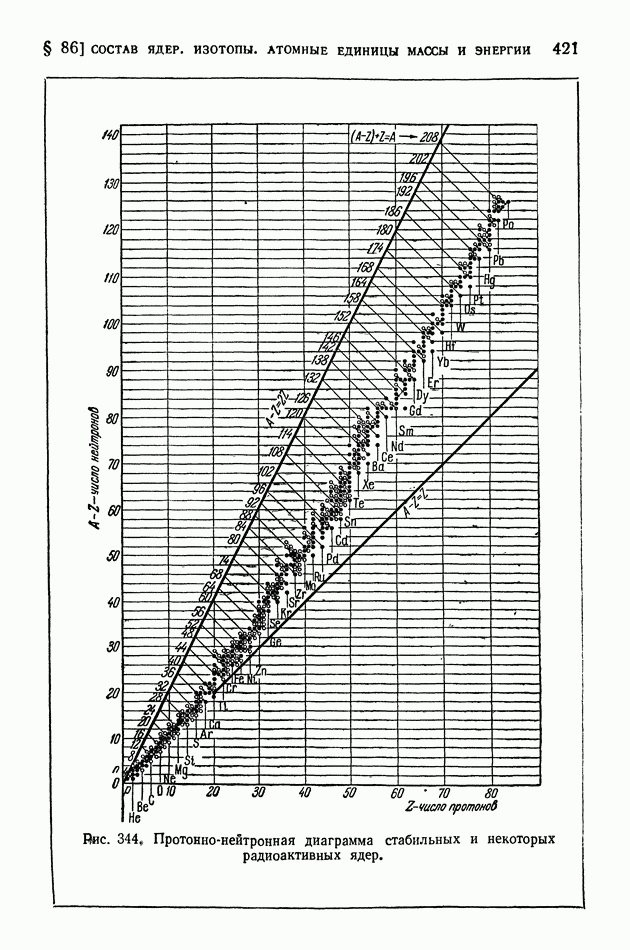
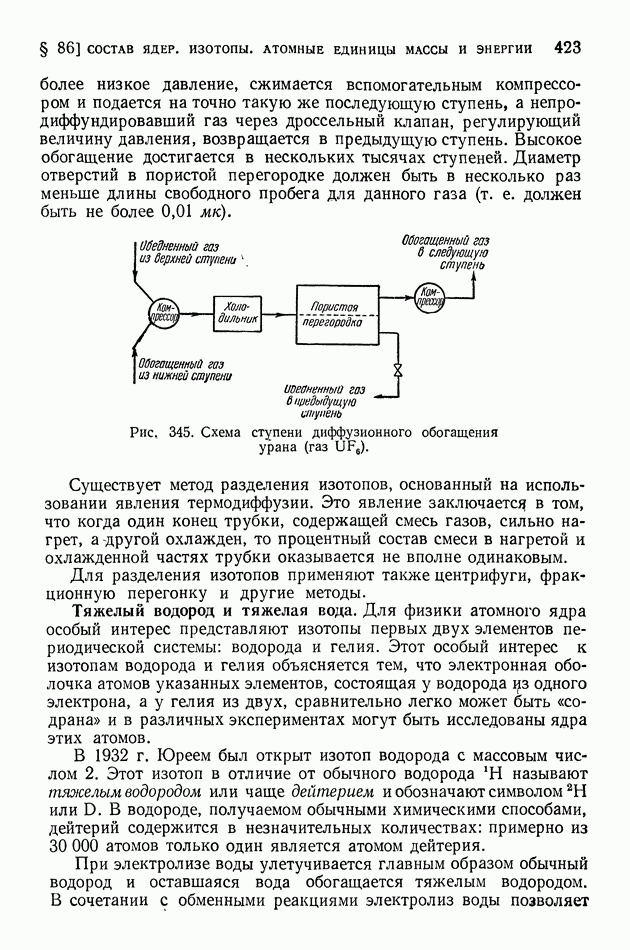
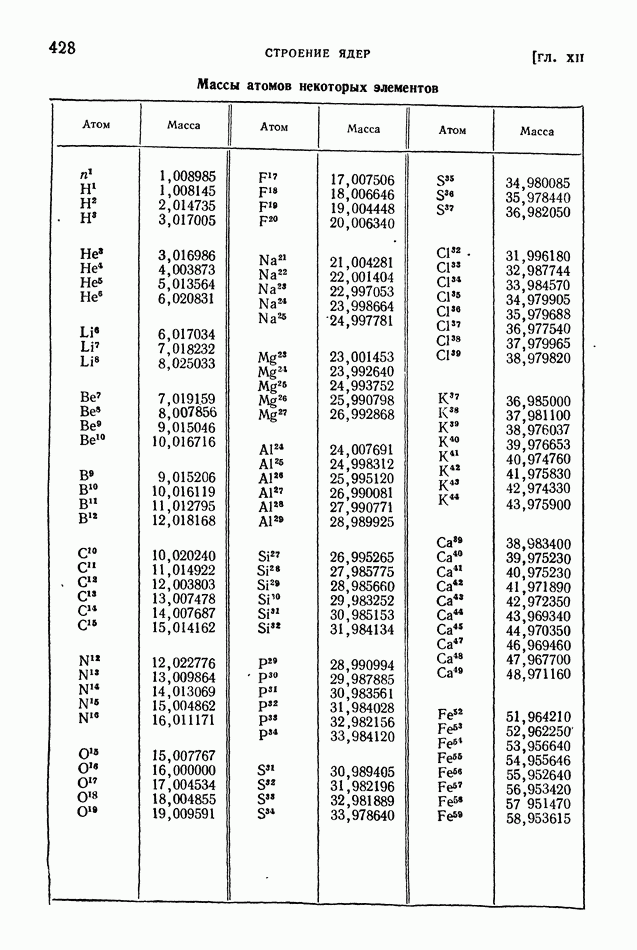
- § 86. Состав ядер. Изотопы. Атомные единицы массы и энергии
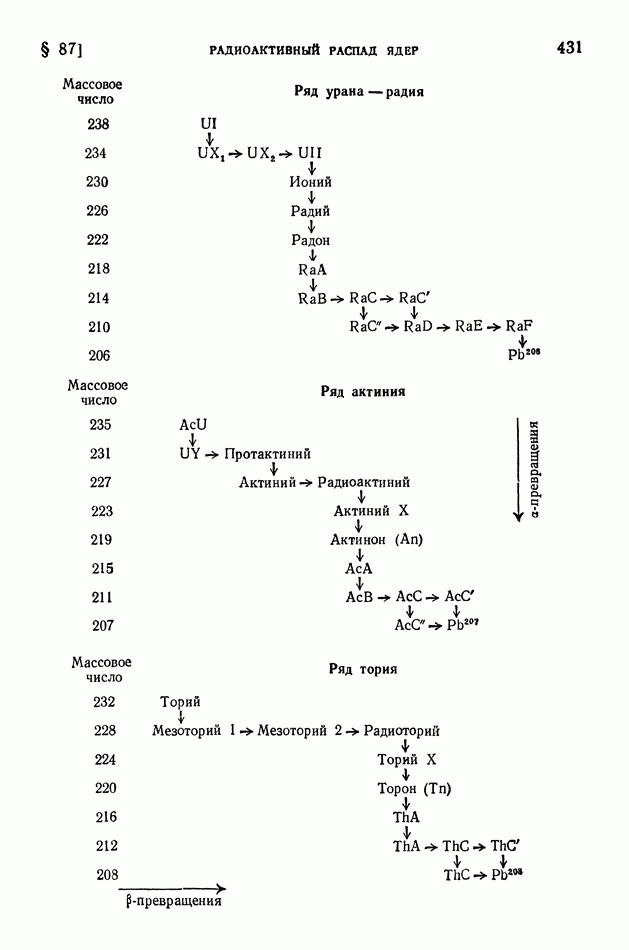
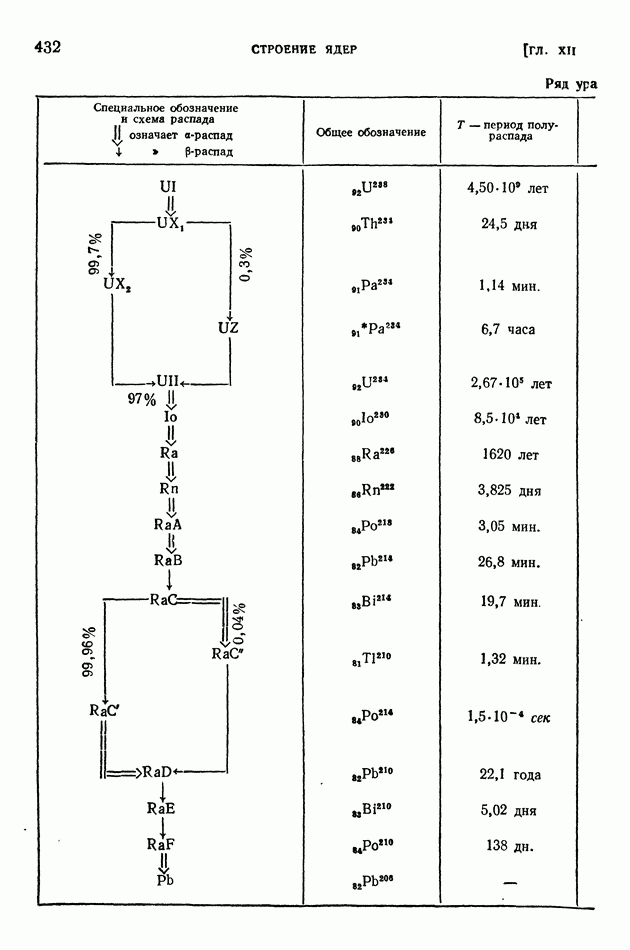
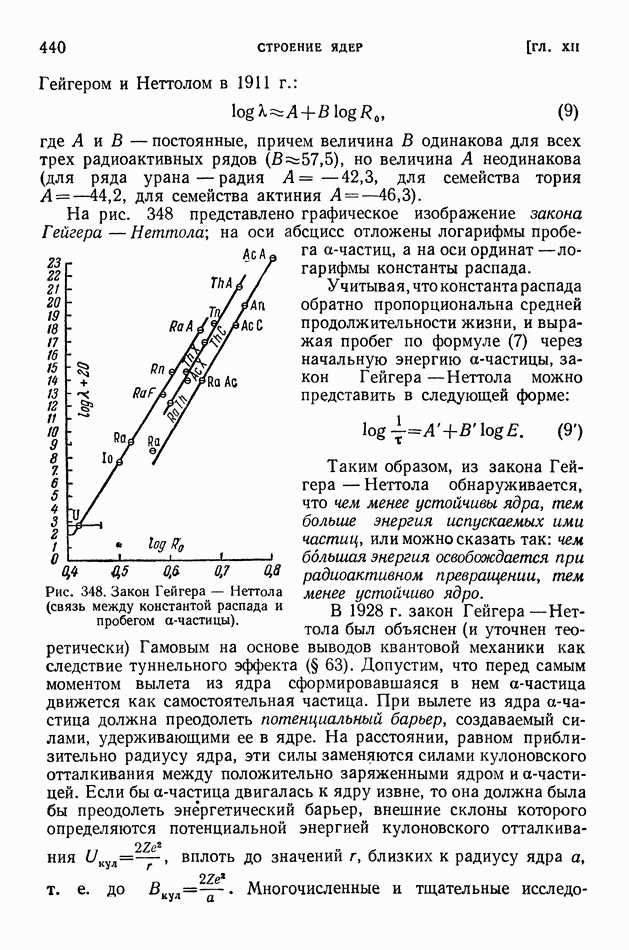
- § 87. Радиоактивный распад ядер. Закон радиоактивного смещения. Изомеры
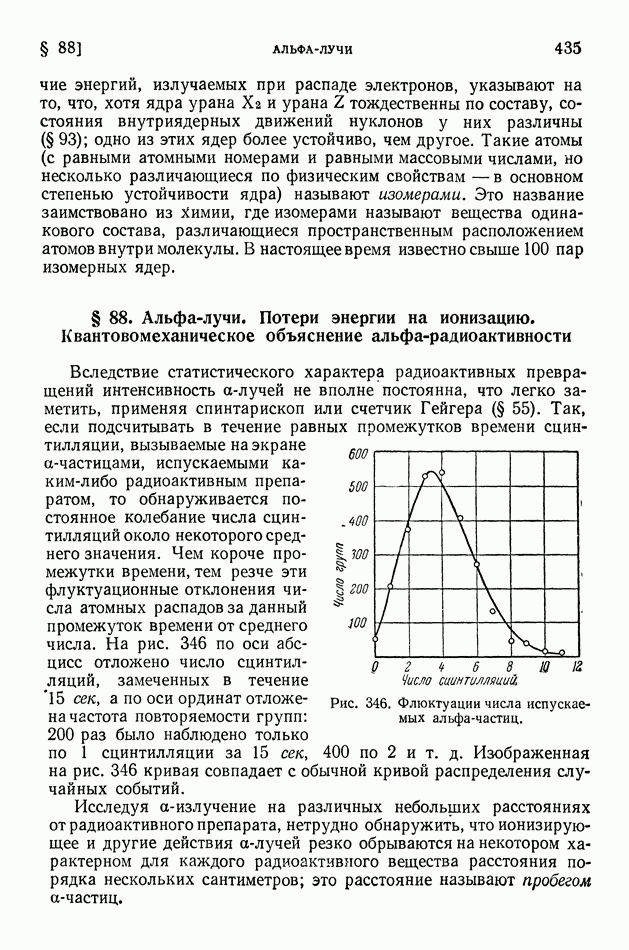
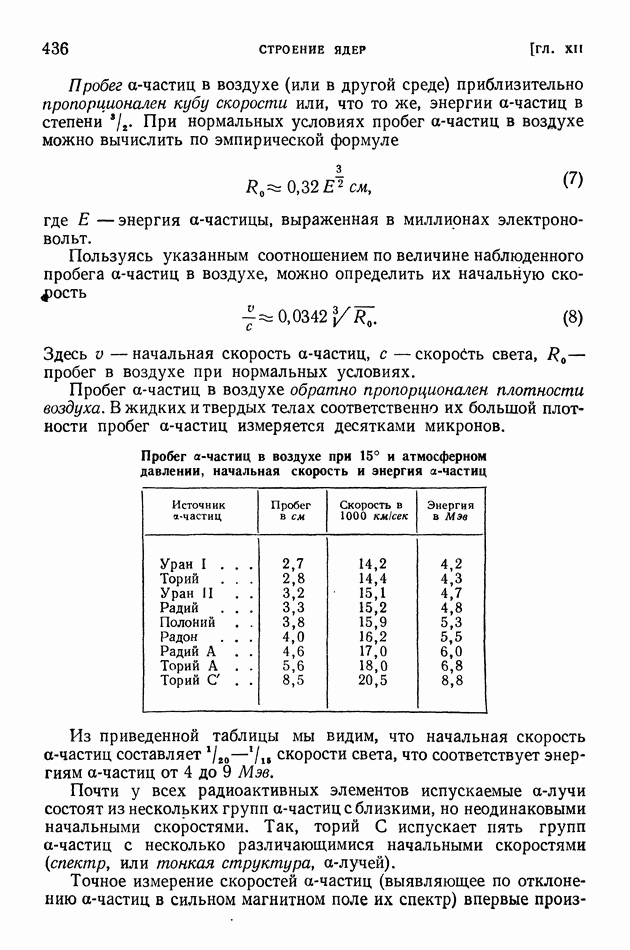
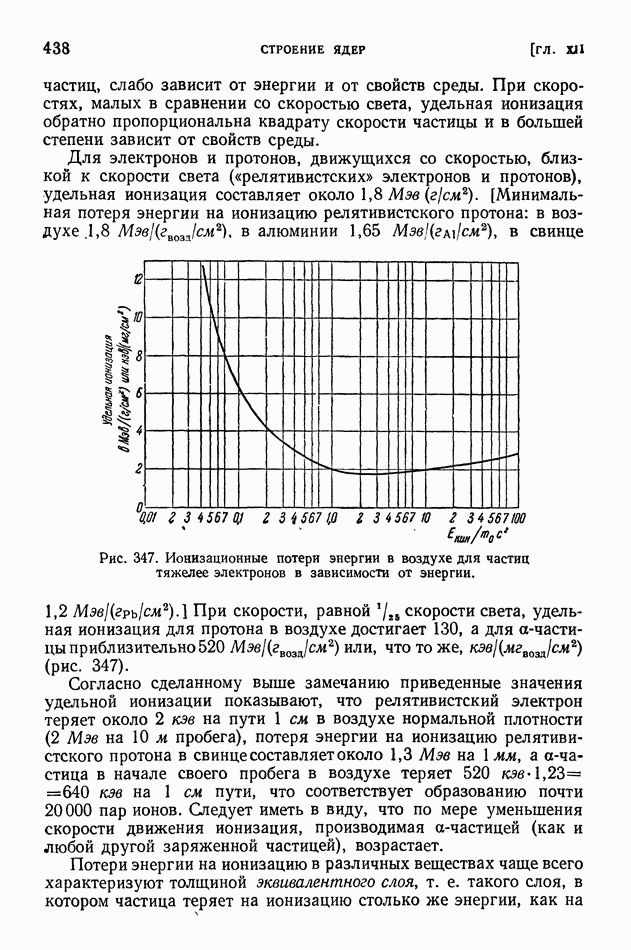
- § 88. Альфа-лучи. Потери энергии на ионизацию. Квантовомеханическое объяснение альфа-радиоактивности
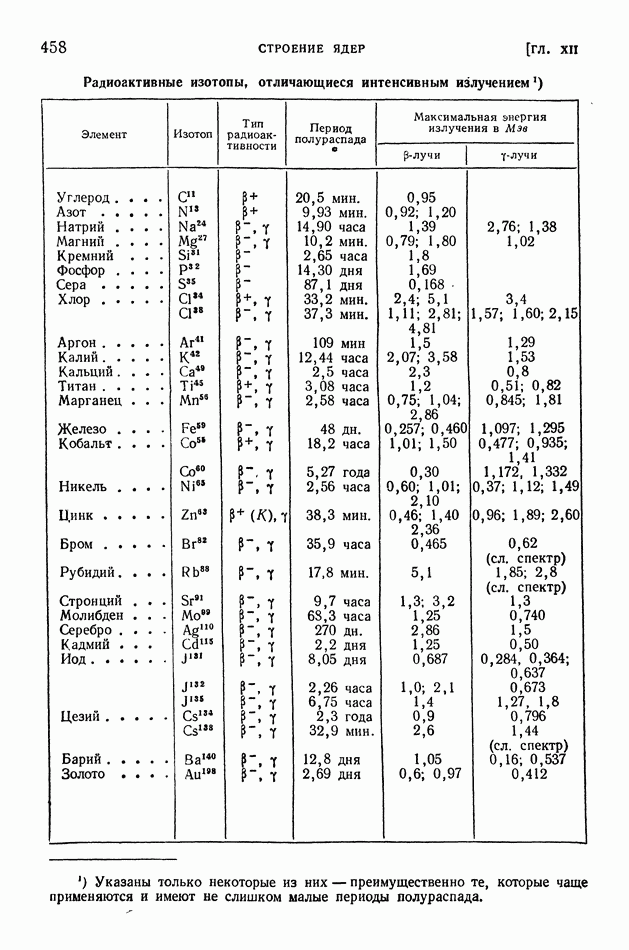
- § 89. Бета- и гамма-лучи
- § 90. Искусственное расщепление ядер. Открытие нейтрона
- § 91. Открытие позитрона. Взаимопревращение фотонов определенной энергии и электронно-позитронных пар
- § 92. Индуцированная позитронная и электронная радиоактивность. Фоторасщепление ядер, K-захват
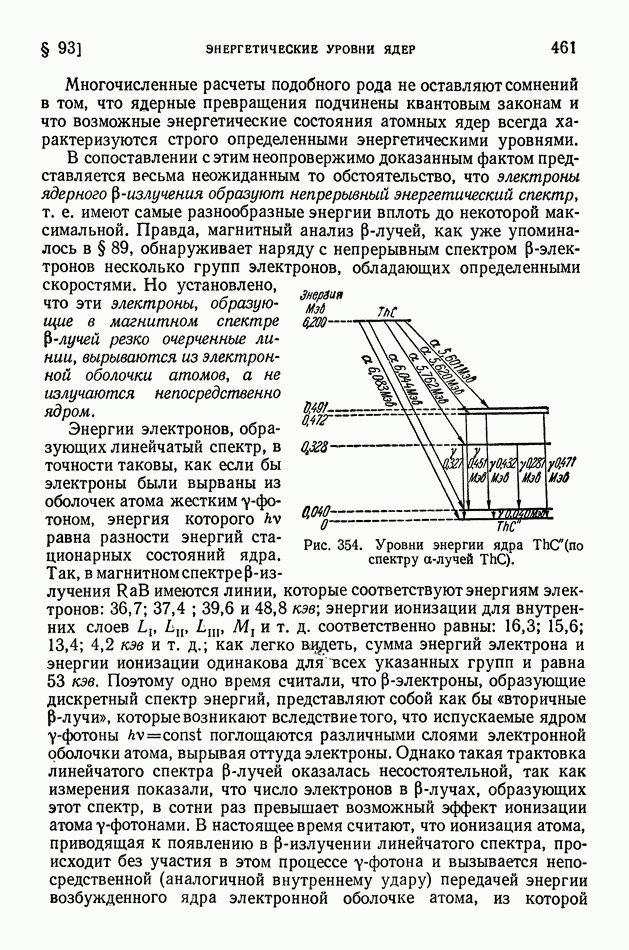
- § 93. Энергетические уровни ядер. Внутренняя конверсия. Нейтрино
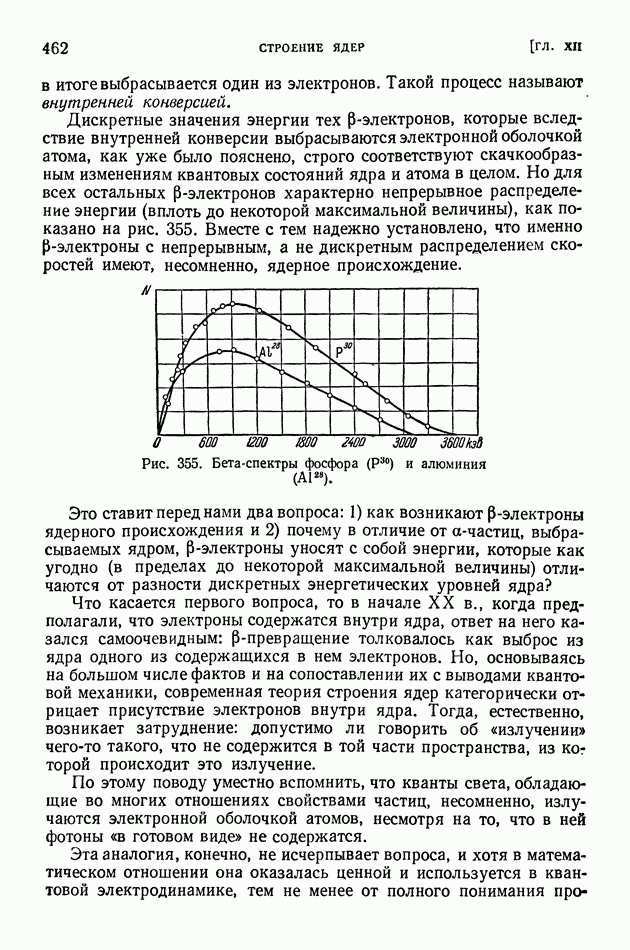
- § 94. Капельная теория строения ядер
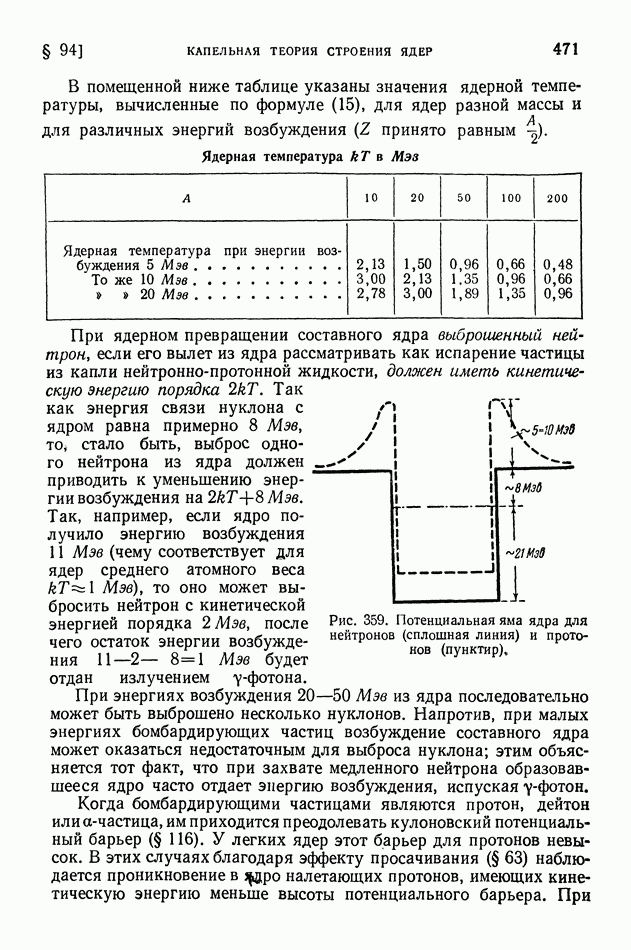
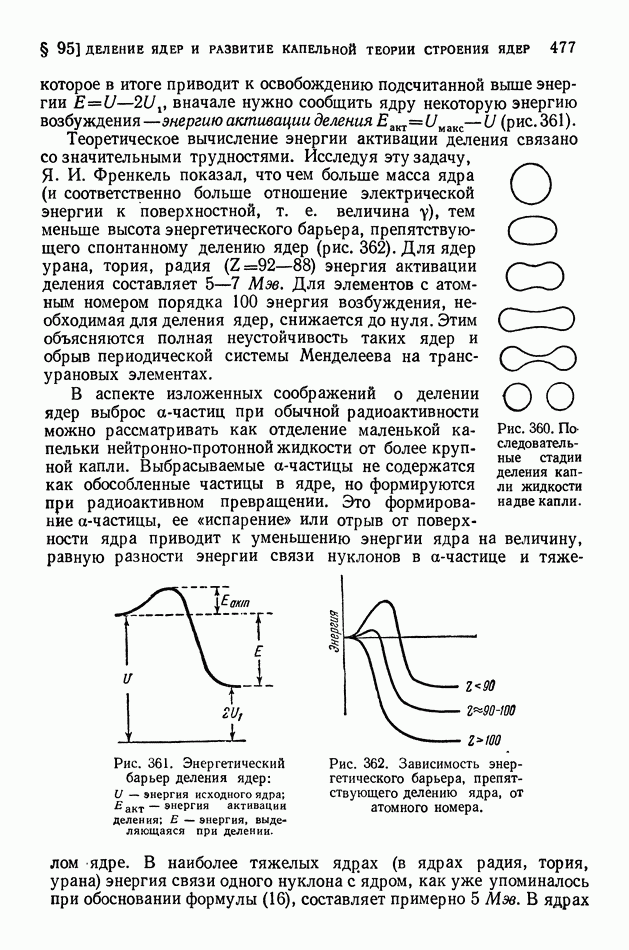
- § 95. Деление ядер и развитие капельной теории строения ядер
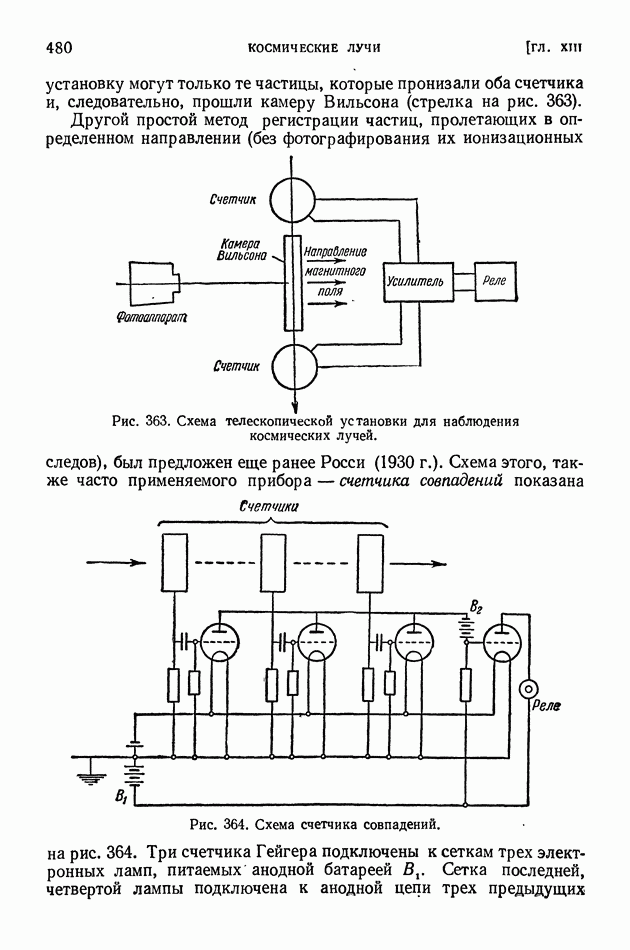
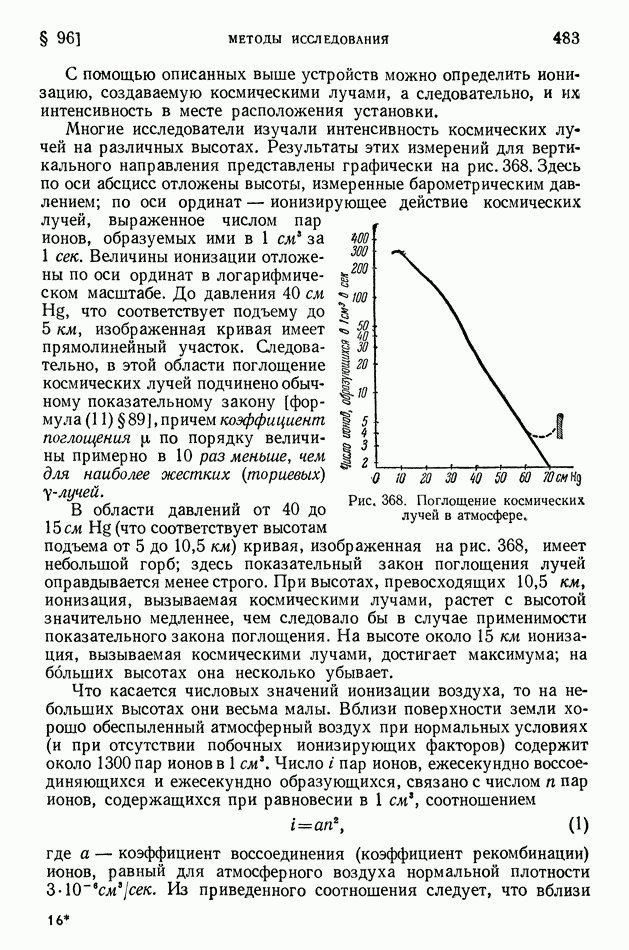
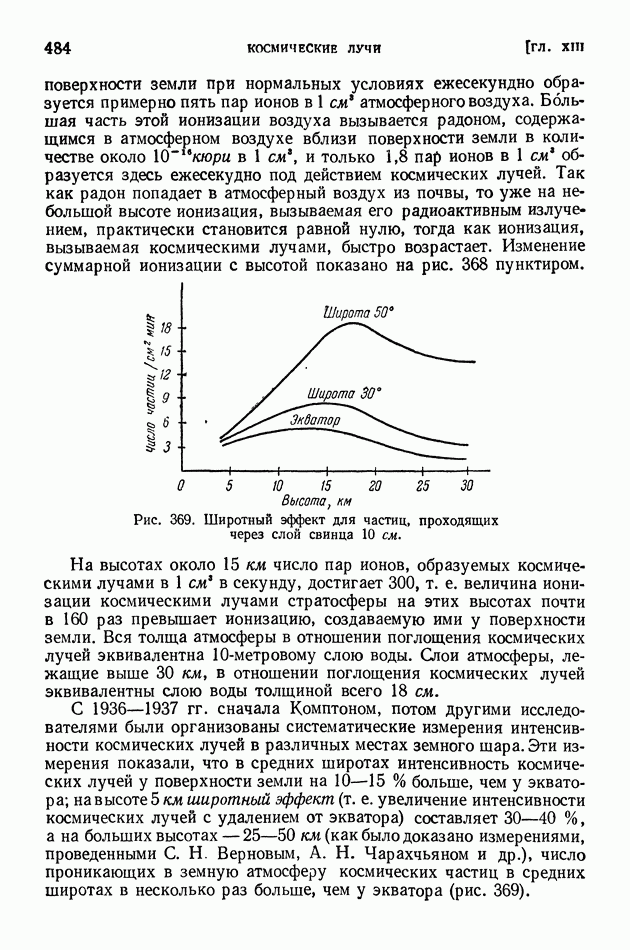
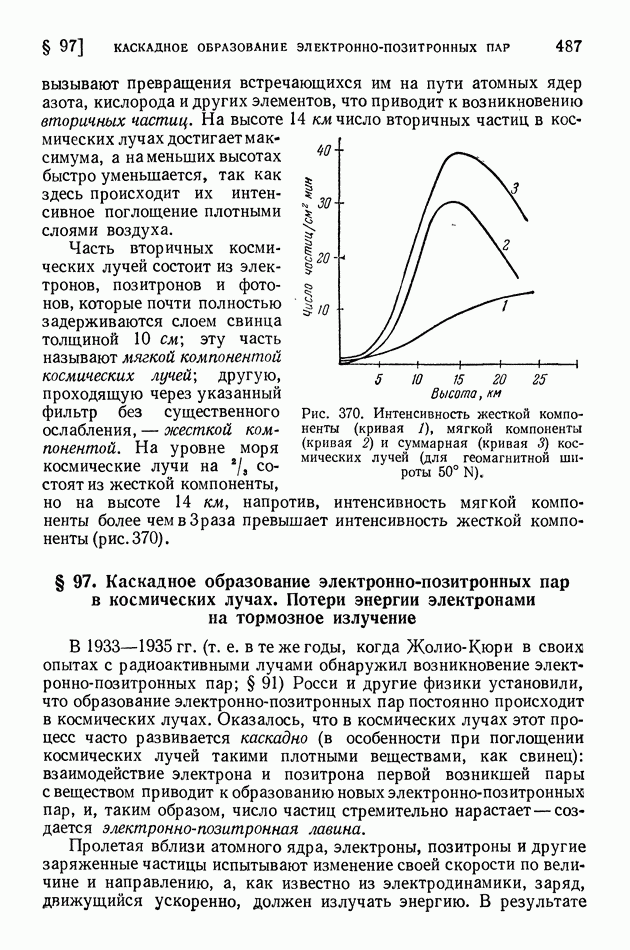
- ГЛАВА XIII. КОСМИЧЕСКИЕ ЛУЧИ
- § 96. Методы исследования и первые итоги изучения космических лучей
- § 97. Каскадное образование электронно-позитронных пар в космических лучах. Потери энергии электронами на тормозное излучение
- § 98. «мю»-мезоны. Зависимость времени жизни неустойчивых частиц от скорости движения
- § 99. «пи»-мезоны
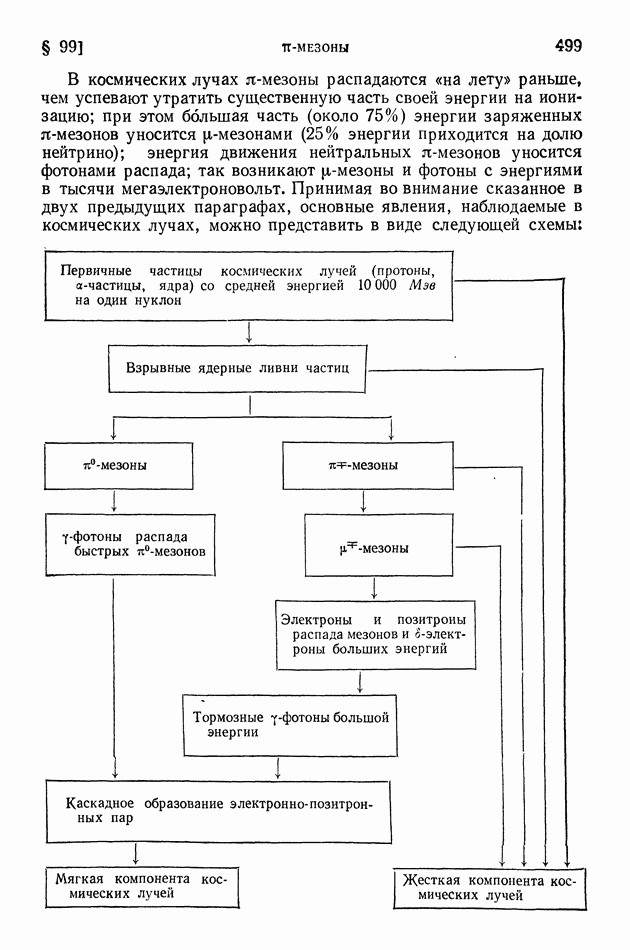
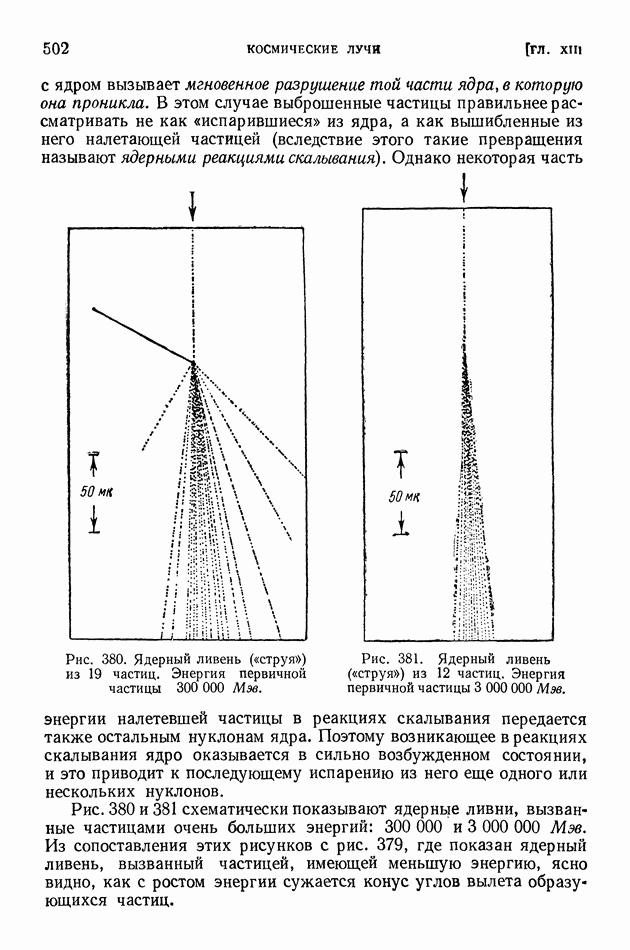
- § 100. Взрывные ядерные ливни и их каскадное развитие в космических лучах
- § 101. Корпускулярный и энергетический спектр космических лучей. Происхождение космического излучения
- ГЛАВА XIV. ЭКСПЕРИМЕНТАЛЬНЫЕ СРЕДСТВА ЯДЕРНОЙ ФИЗИКИ
- § 102. Циклотроны
- § 103. Фазотроны
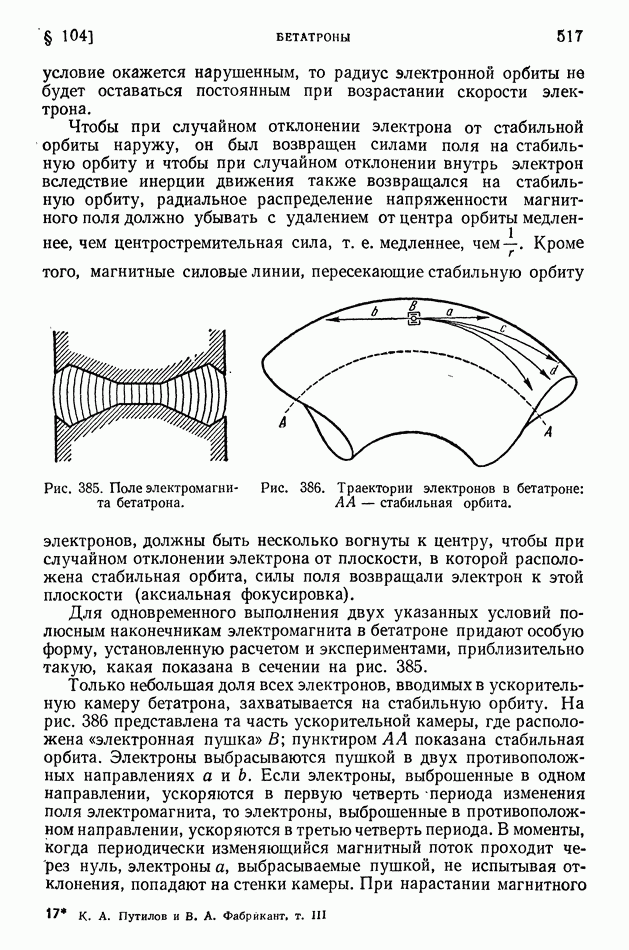
- § 104. Бетатроны
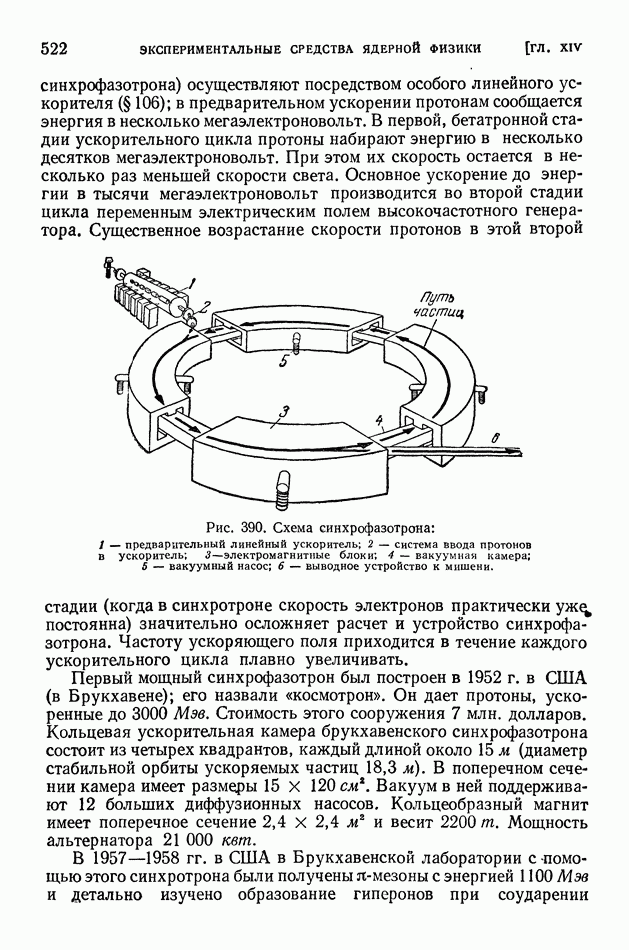
- § 105. Синхротроны и синхрофазотроны
- § 106. Линейные ускорители электронов и ионов
- § 107. Лабораторные источники нейтронов. Замедлители нейтронов в ядерных реакторах
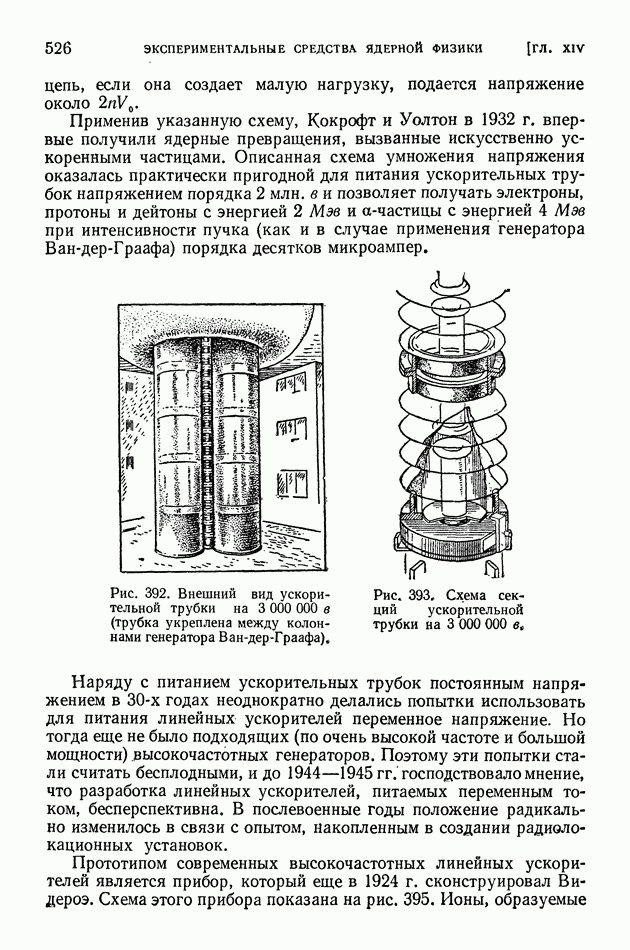
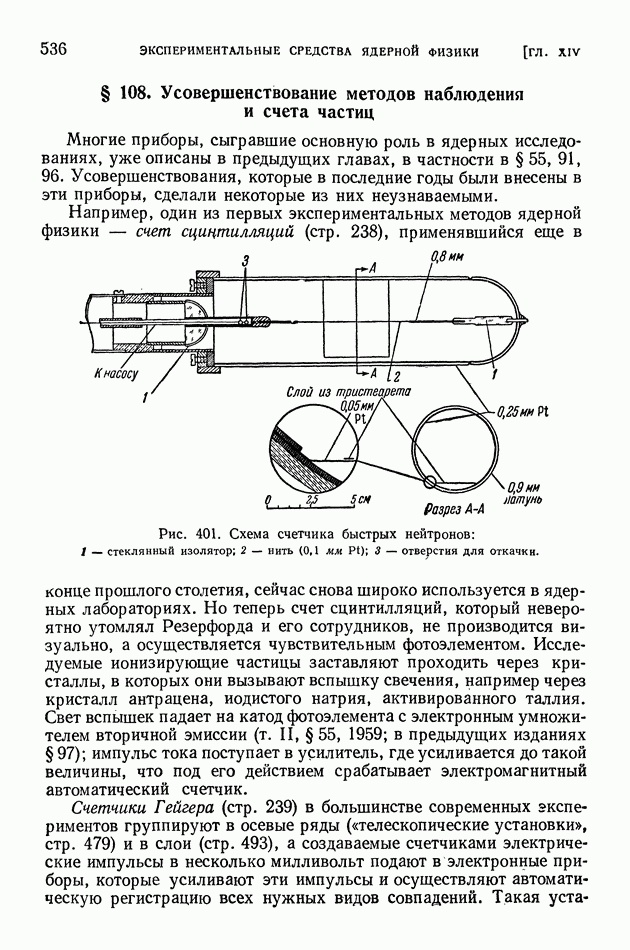
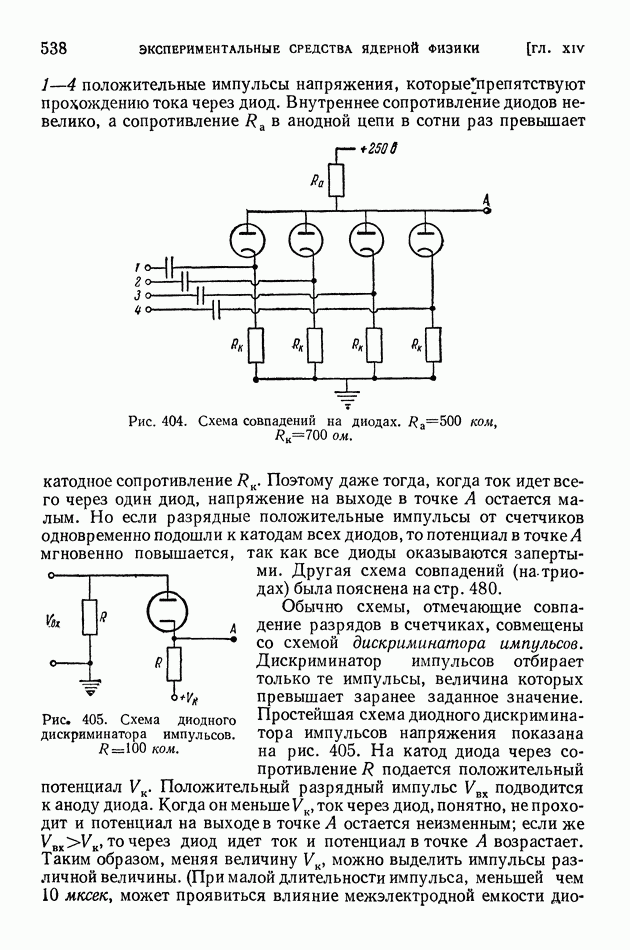
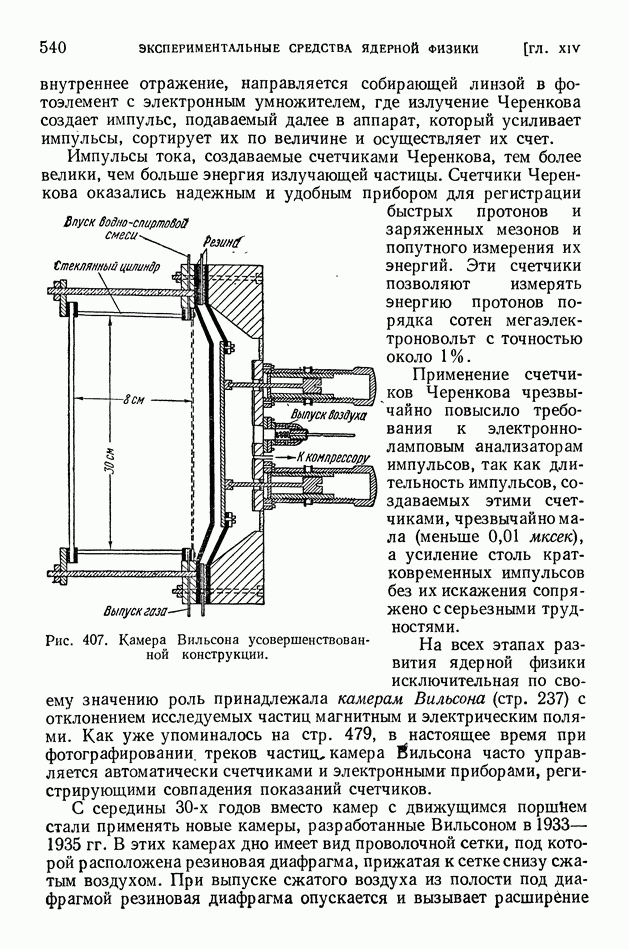
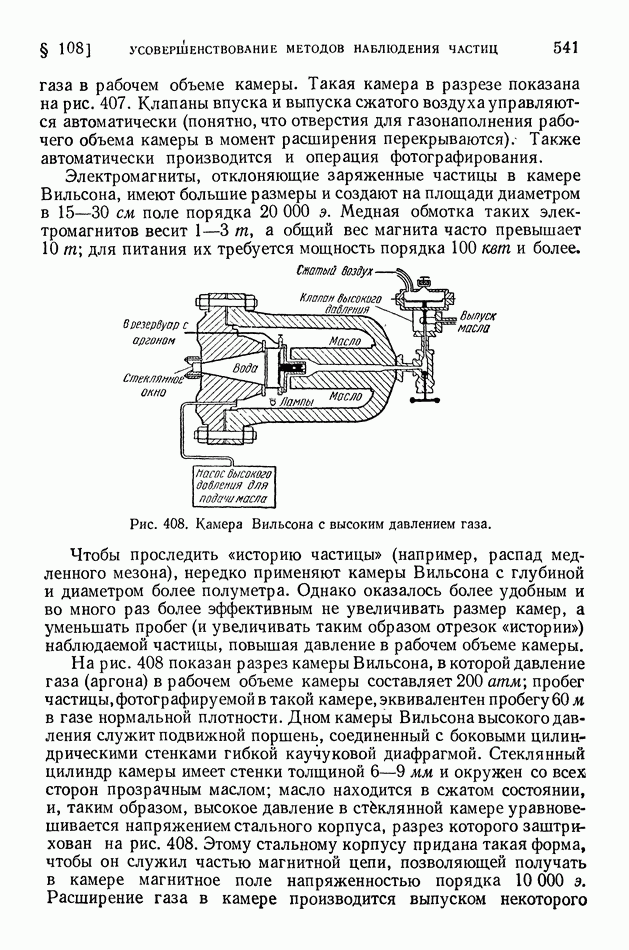
- § 108. Усовершенствование методов наблюдения и счета частиц
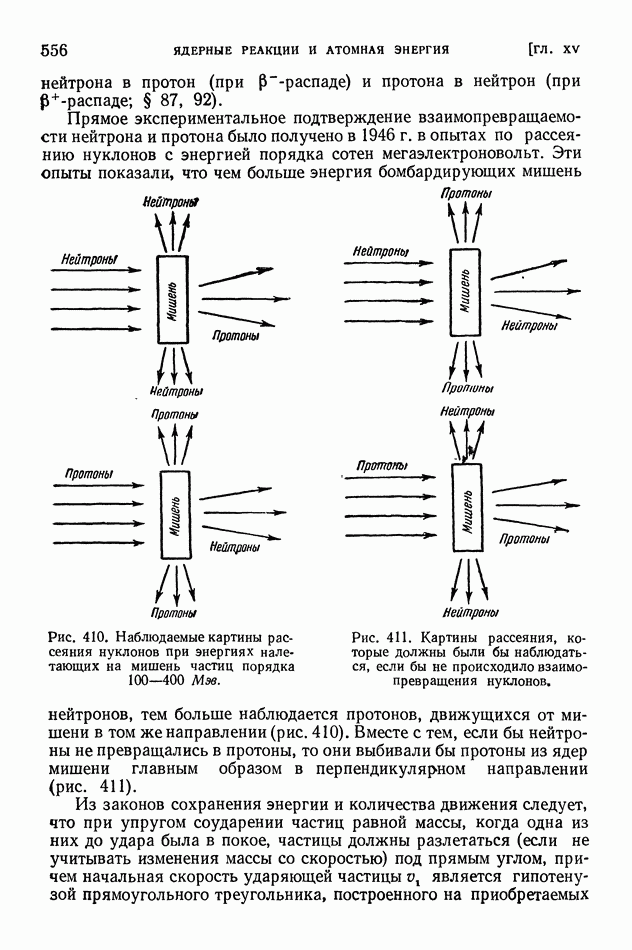
- ГЛАВА XV. ЯДЕРНЫЕ РЕАКЦИИ И АТОМНАЯ ЭНЕРГИЯ
- § 109. Основные виды и обозначения ядерных реакций. Конкурирующие процессы в ядерных реакциях
- § 110. Энергетический эффект, энергия возбуждения и порог ядерных реакций
- § 111. Превращения элементарных частиц
- § 112. Ядерные силы
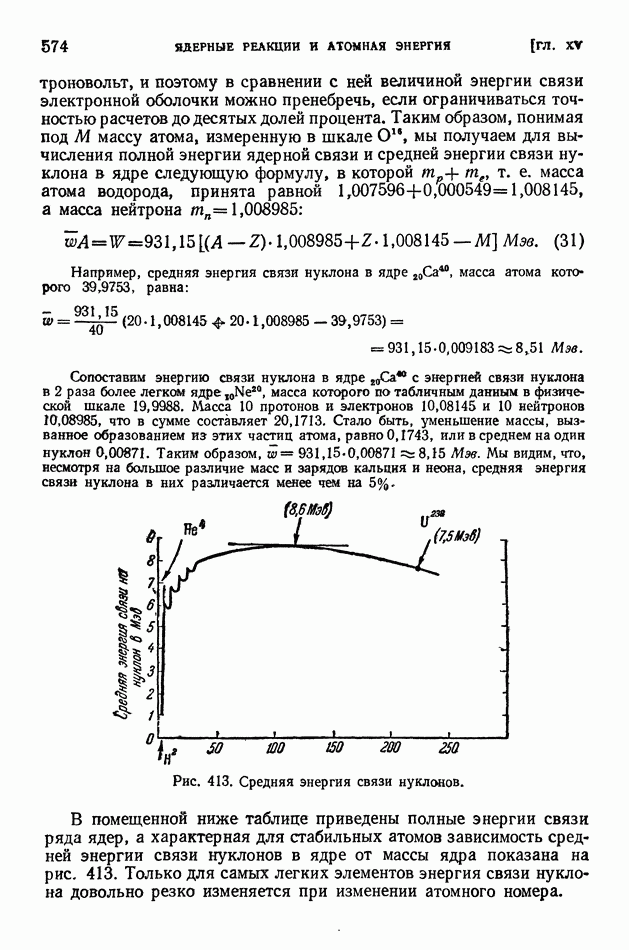
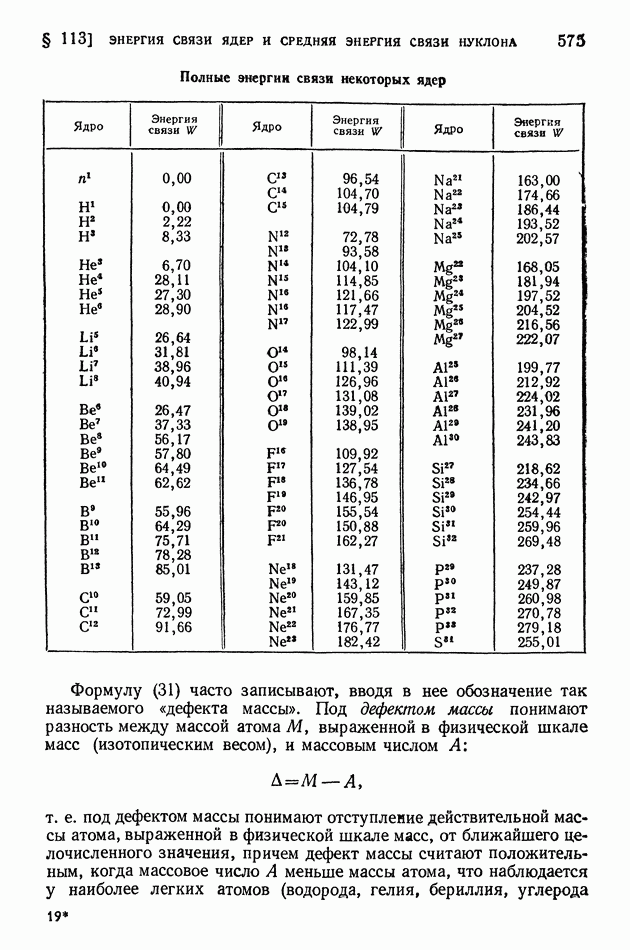
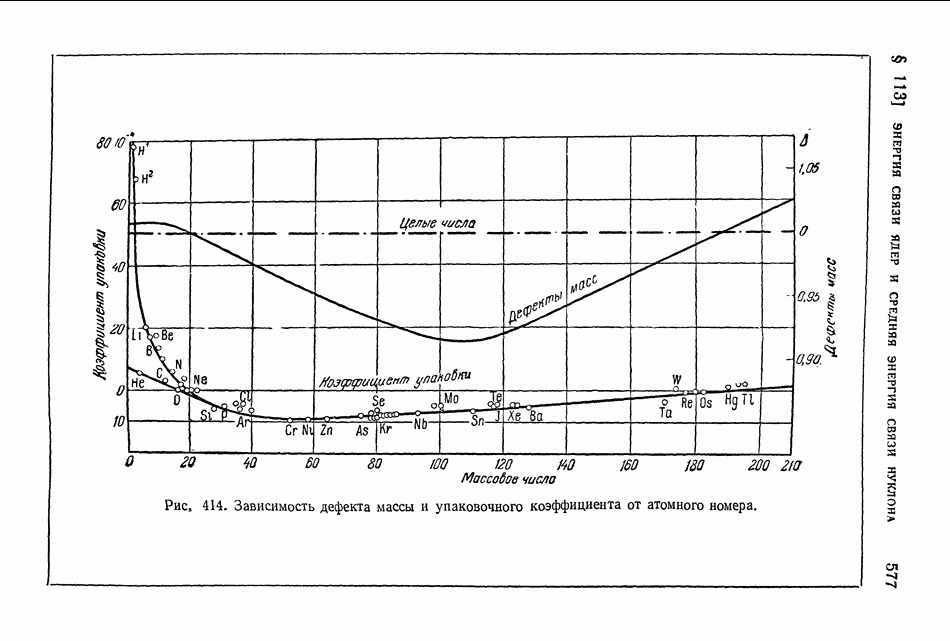
- § 113. Энергия связи ядер и средняя энергия связи нуклона
- § 114. Полуэмпирическая формула для энергии ядерной связи и для атомных энергий и масс
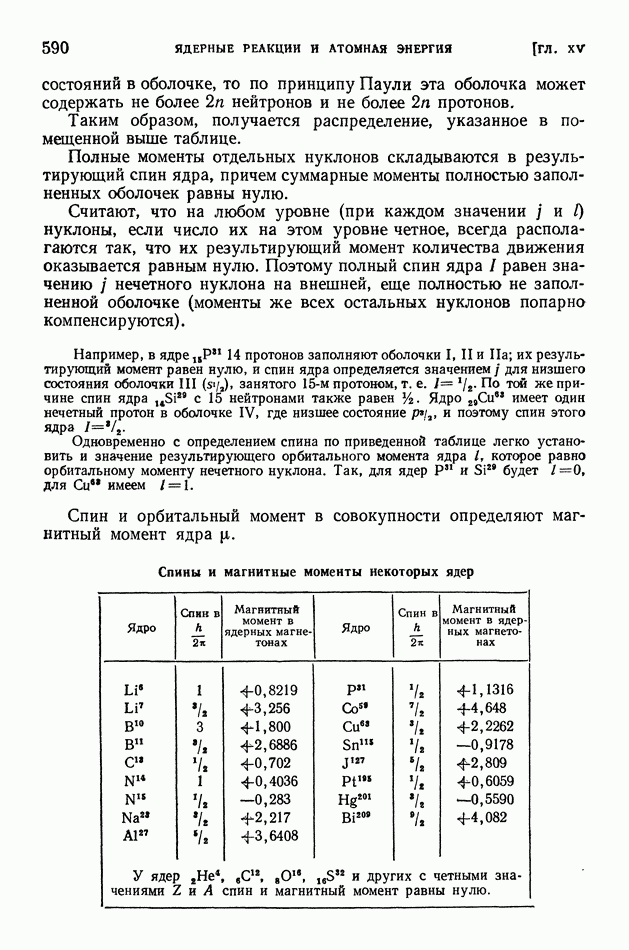
- § 115. Взаимосвязь энергии и строения ядер. Внутриядерное движение нуклонов и нуклонные оболочки. Спины и магнитные моменты ядер
- § 116. Энергия отделения частиц и анализ возможного хода ядерной реакции
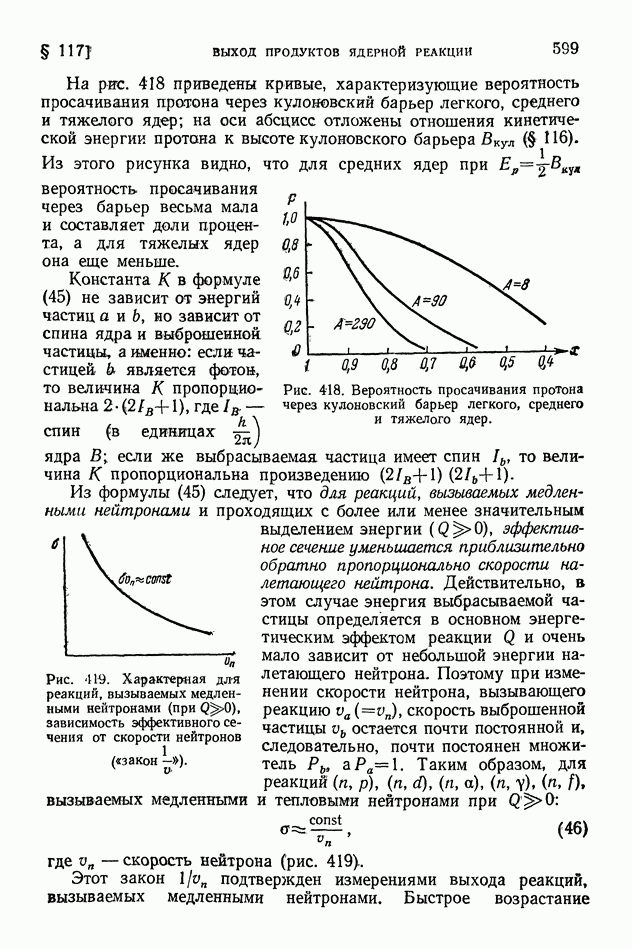
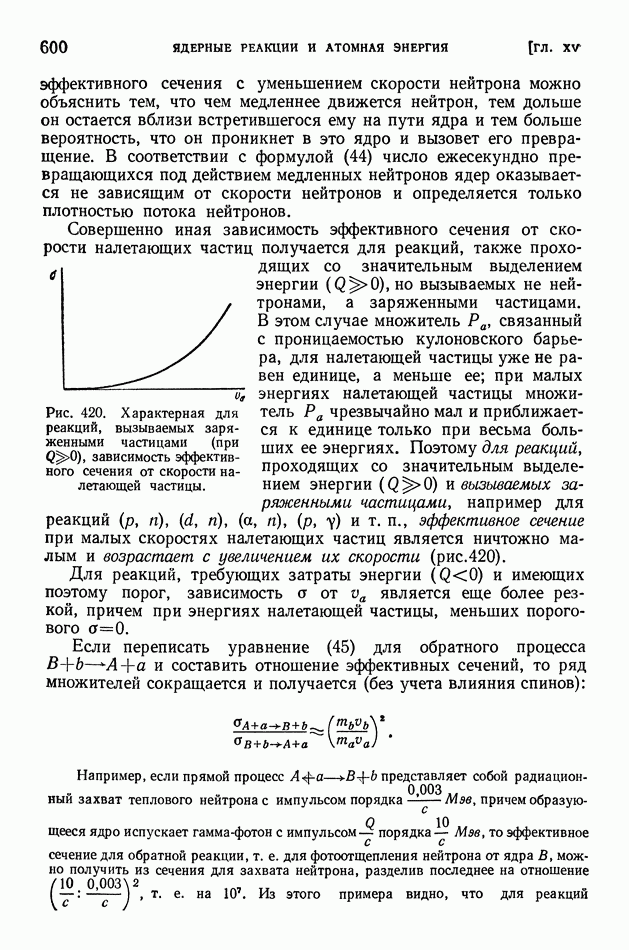
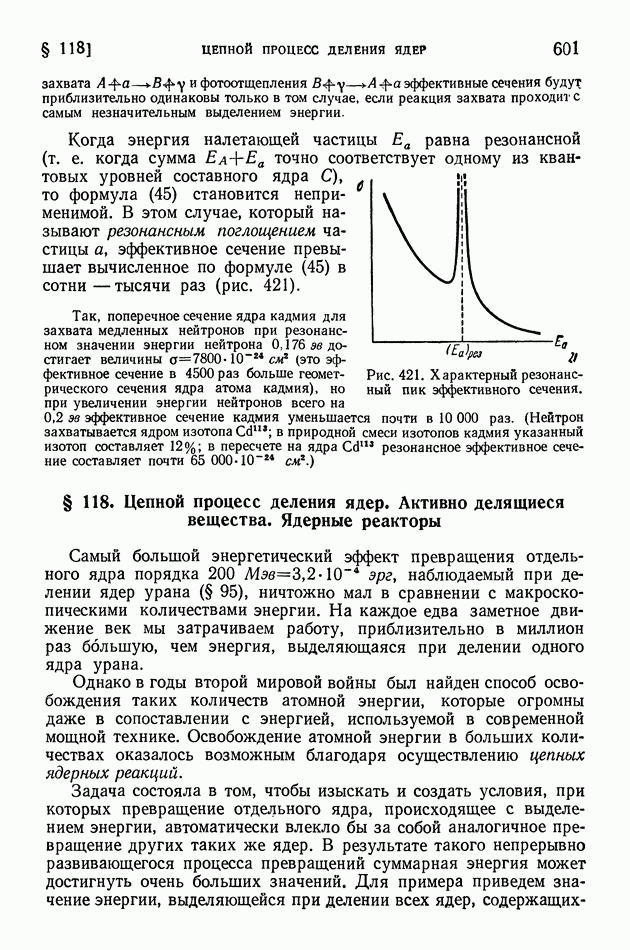
- § 117. Выход продуктов ядерной реакции. Эффективные сечения. Резонансные явления
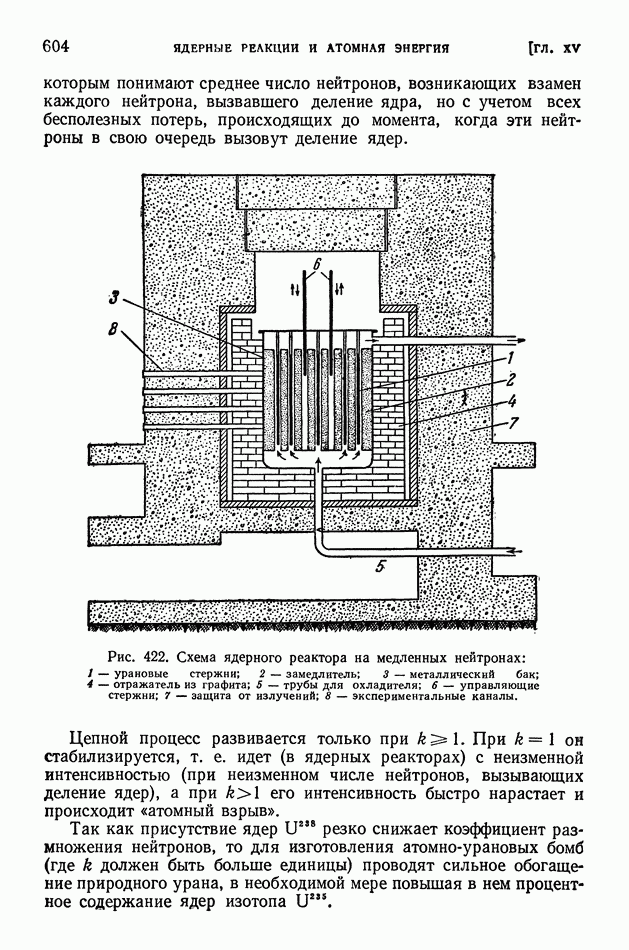
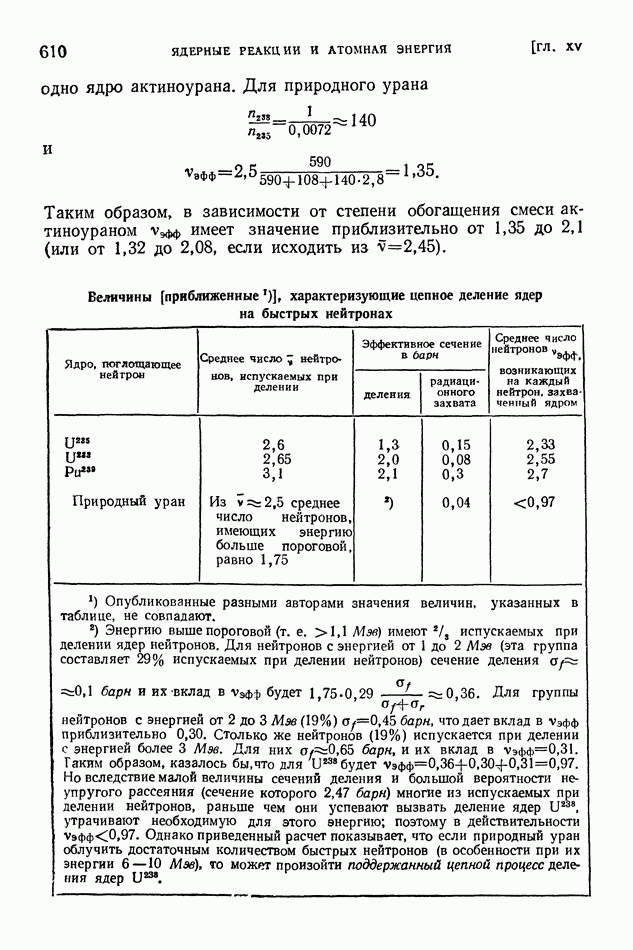
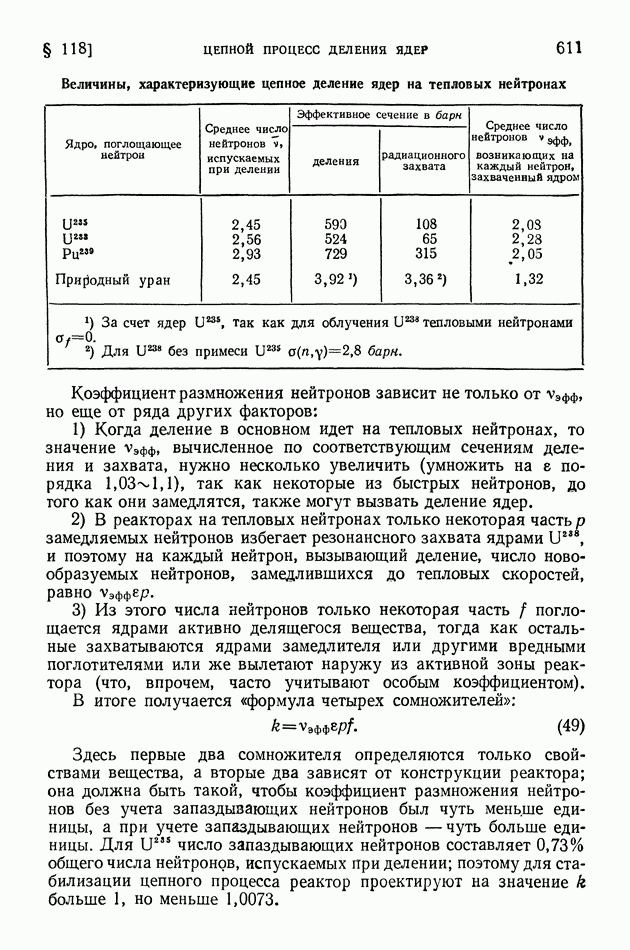
- § 118. Цепной процесс деления ядер. Активно делящиеся вещества. Ядерные реакторы
- § 119. Термоядерные реакции
- § 120. Применение ядерных реакций
- § 121. Ядерные реакции в звездах