| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
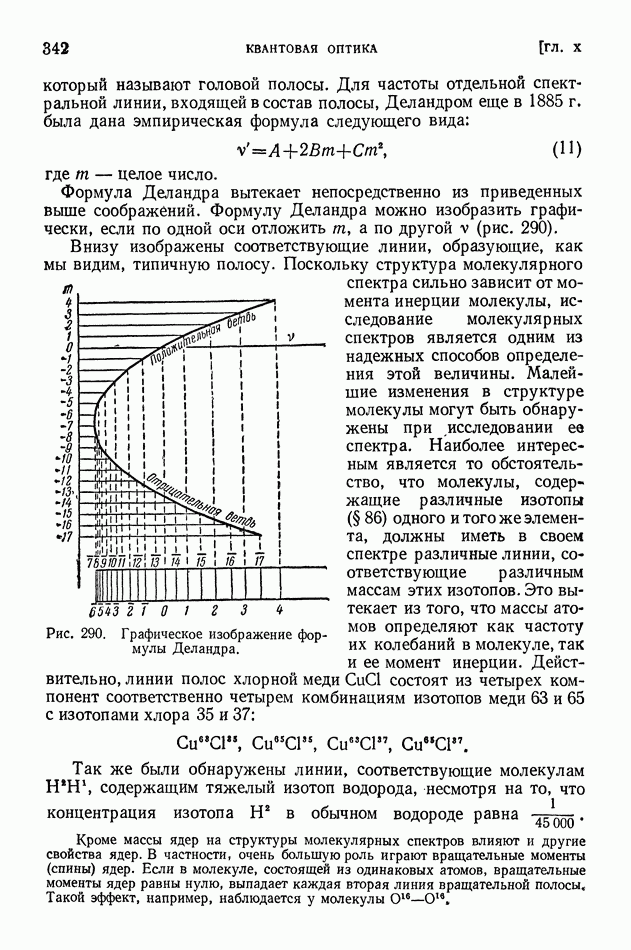
ГЛАВА II. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
§ 8. Законы отражения и преломления света
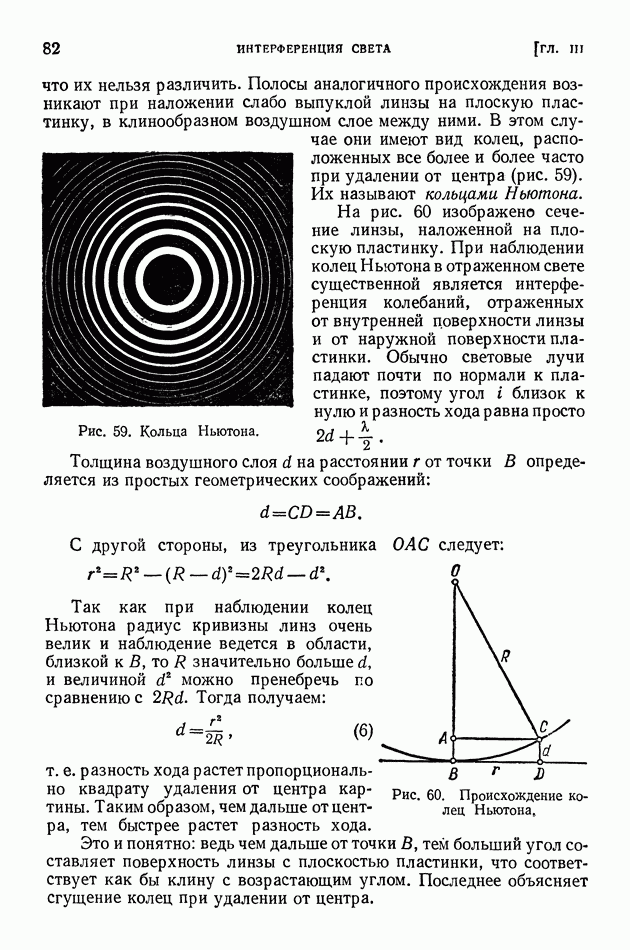
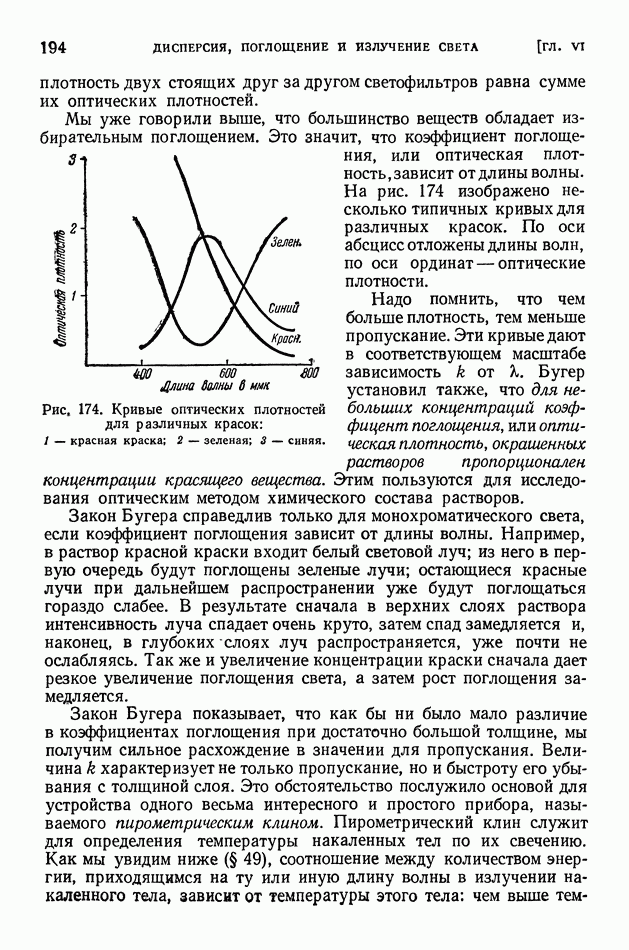
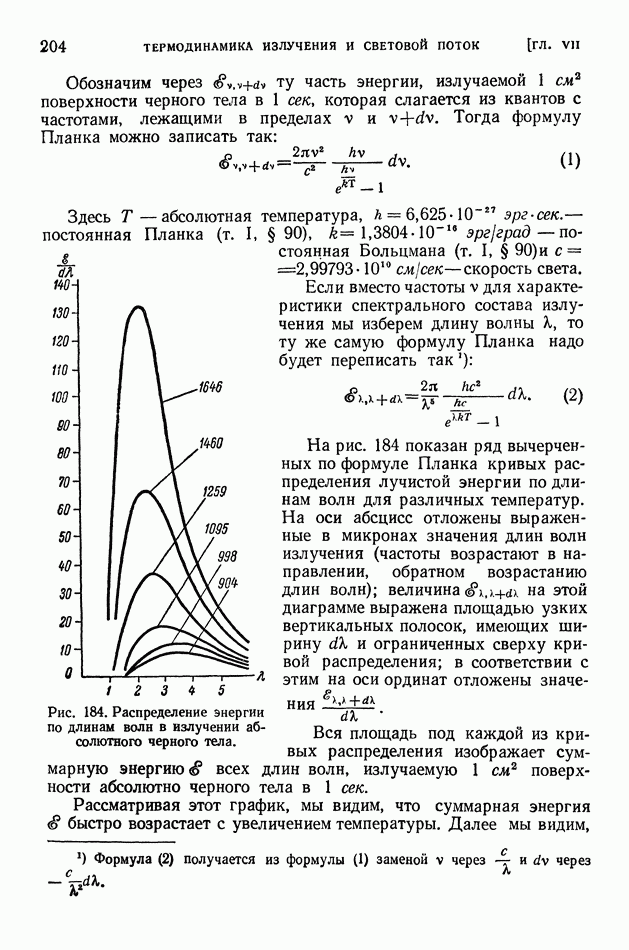
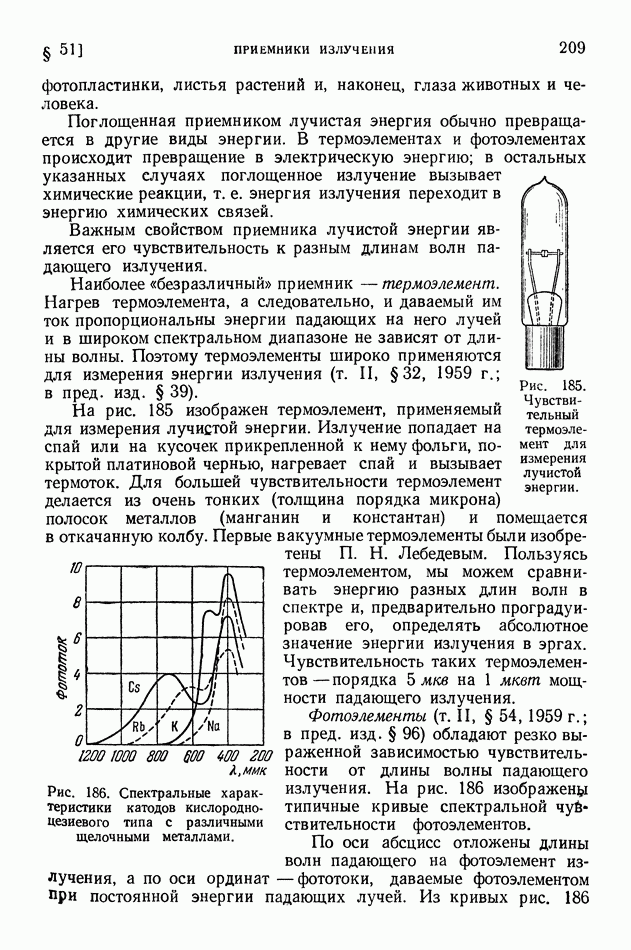
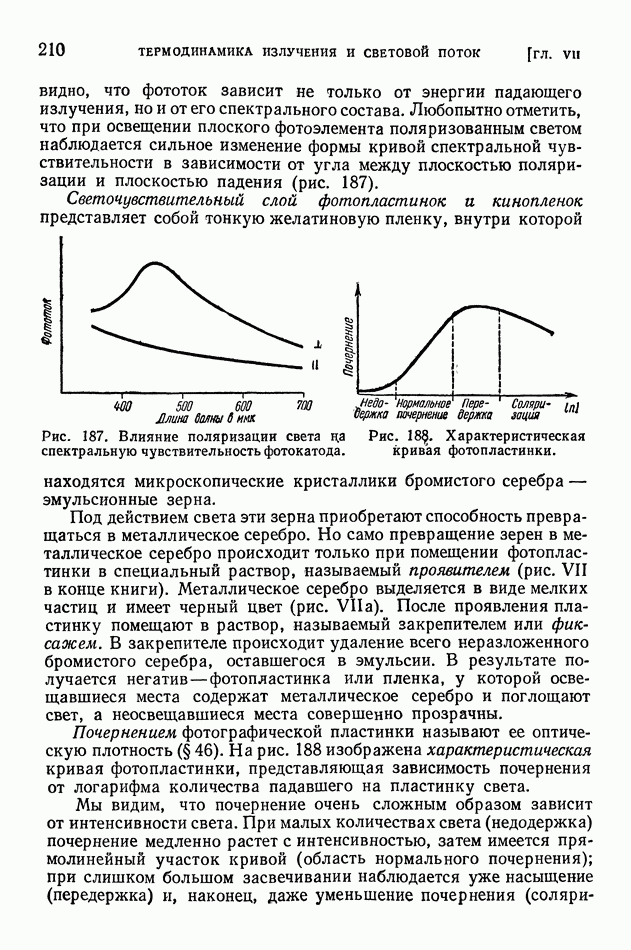
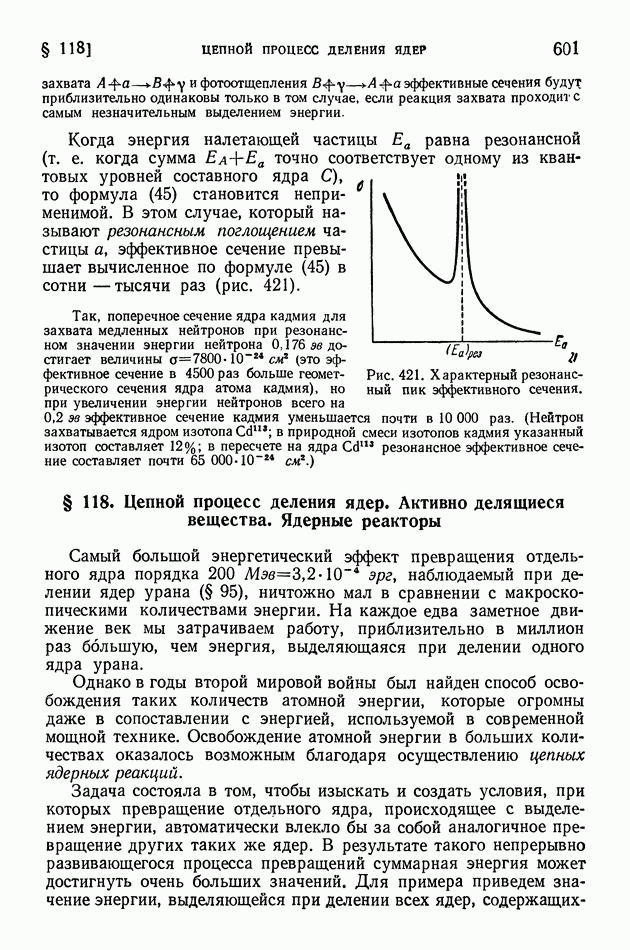
Основным отличием геометрической оптики является то, что в ней рассматривают распространение световых лучей без каких-либо предположений об их природе. Каждый световой луч представляет собой линию (бесконечно тонкую), вдоль которой распространяется лучистая энергия. Ниже, в волновой оптике, мы увидим, что такое представление о свете не всегда может дать объяснение наблюдаемым явлениям. Однако для объяснения обширного класса явлений и конструирования многих весьма важных приборов это упрощенное представление вполне достаточно.
К числу самых простых явлений, разбираемых в геометрической оптике, принадлежит отражение света от зеркал.
Отражение света от зеркал подчиняется двум законам, открытым опытным путем:
Лучу падающий на поверхностьу нормаль к поверхности в точке падения и лучу отраженный от поверхности, лежат в одной плоскости, называемой плоскостью падения.

Рис. 11. Отражение света.
Угол между падающим лучом и нормалью к поверхности в точке падения (угол падения) равен углу между отраженным лучом и той же нормалью (угол отражения) (рис, 11).
Пользуясь этими двумя законами отражения света, можно объяснить все явления, наблюдаемые при отражении пучка световых лучей от зеркал самой сложной формы.
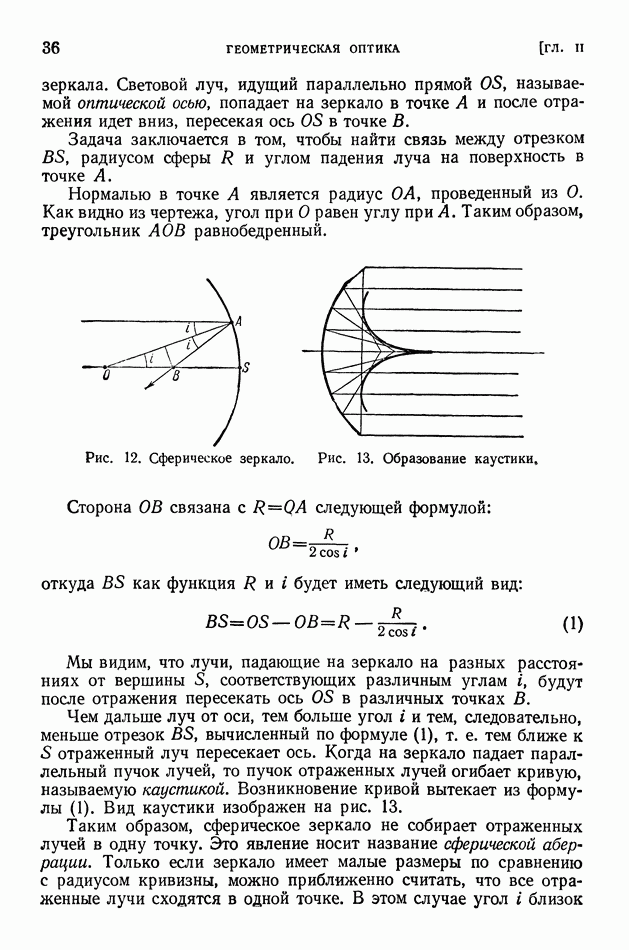
Разберем случай отражения параллельного светового пучка от вогнутого сферического зеркала. На рис. 12 дуга окружности представляет собой сечение сферического зеркала, точка  - центр
- центр
зеркала. Световой луч, идущий параллельно прямой  называемой оптической осью, попадает на зеркало в точке А и после отражения идет вниз, пересекая ось
называемой оптической осью, попадает на зеркало в точке А и после отражения идет вниз, пересекая ось  в точке В.
в точке В.
Задача заключается в том, чтобы найти связь между отрезком  радиусом сферы
радиусом сферы  и углом падения луча на поверхность в точке А.
и углом падения луча на поверхность в точке А.
Нормалью в точке А является радиус  проведенный из О. Как видно из чертежа, угол при О равен углу при
проведенный из О. Как видно из чертежа, угол при О равен углу при  Таким образом, треугольник
Таким образом, треугольник  равнобедренный.
равнобедренный.

Рис. 12. Сферическое зеркало.

Рис. 13. Образование каустики
Сторона  связана с
связана с  следующей формулой:
следующей формулой:

откуда  как функция
как функция  будет иметь следующий вид:
будет иметь следующий вид:

Мы видим, что лучи, падающие на зеркало на разных расстояниях от вершины  соответствующих различным углам будут после отражения пересекать ось
соответствующих различным углам будут после отражения пересекать ось  в различных точках В.
в различных точках В.
Чем дальше луч от оси, тем больше угол  и тем, следовательно, меньше отрезок
и тем, следовательно, меньше отрезок  вычисленный по формуле (1), т. е. тем ближе к 5 отраженный луч пересекает ось. Когда на зеркало падает параллельный пучок лучей, то пучок отраженных лучей огибает кривую, называемую каустикой. Возникновение кривой вытекает из формулы (1). Вид каустики изображен на рис. 13.
вычисленный по формуле (1), т. е. тем ближе к 5 отраженный луч пересекает ось. Когда на зеркало падает параллельный пучок лучей, то пучок отраженных лучей огибает кривую, называемую каустикой. Возникновение кривой вытекает из формулы (1). Вид каустики изображен на рис. 13.
Таким образом, сферическое зеркало не собирает отраженных лучей в одну точку. Это явление носит название сферической аберрации. Только если зеркало имеет малые размеры по сравнению с радиусом кривизны, можно приближенно считать, что все отраженные лучи сходятся в одной точке. В этом случае угол  близок
близок
к нулю, косинус практически равен единице, и формула (1) приобретает следующий вид:

В этом случае  обозначают буквой
обозначают буквой  и называют главным фокусным расстоянием зеркала. Сферическая аберрация считается отрицательной, если крайние лучи пересекают ось ближе главного фокусного расстояния (сферическое зеркало), и положительной — если дальше фокуса (выпукло-вогнутая линза).
и называют главным фокусным расстоянием зеркала. Сферическая аберрация считается отрицательной, если крайние лучи пересекают ось ближе главного фокусного расстояния (сферическое зеркало), и положительной — если дальше фокуса (выпукло-вогнутая линза).
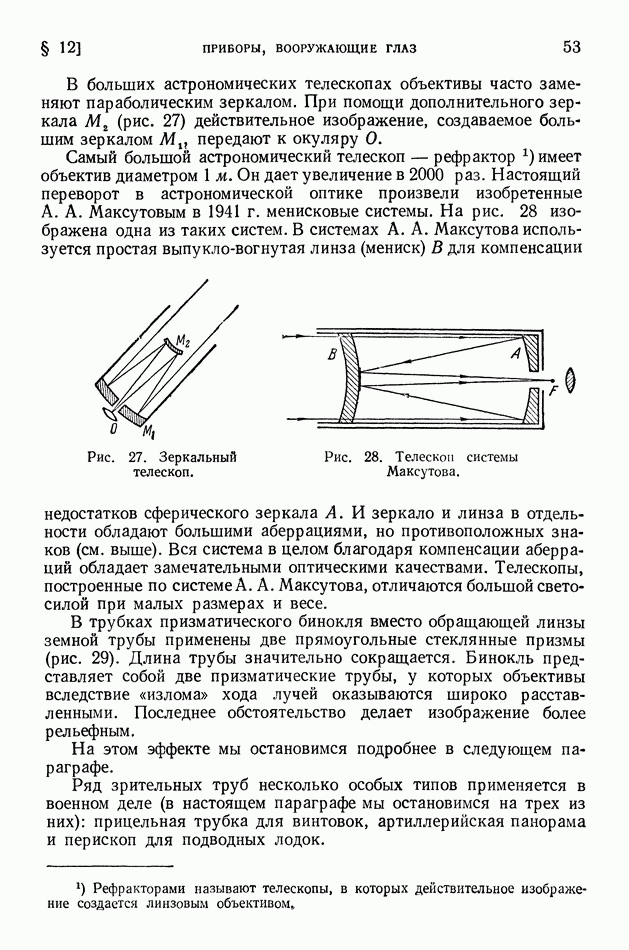
Применение сферических зеркал крайне ограничено ввиду только что описанных свойств. Вогнутые зеркала обычно применяют или для получения изображения звезд, — в этом случае на зеркало падает параллельный пучок лучей, и он должен быть сведен в точку, — или для получения параллельного пучка лучей, — в этом случае в главном фокусе зеркала помещают точечный источник света, и от зеркала отражается параллельный пучок (рис. 14).

Рис. 14. Прожектор.
Из формулы (1) ясно, что для этих целей пригодны лишь малые сферические зеркала, улавливающие весьма малые количества света. Ввиду этого от сферических зеркал отказались и пользуются параболическими зеркалами. Из геометрических свойств параболы легко доказать, что параболоид вращения собирает все лучи, падающие параллельно оси, в одну точку (фокус параболоида). Следовательно, лучи, исходящие из источника, помещенного в фокусе, после отражения от параболоида делаются параллельными оси. Этими свойствами обладает параболоид любых размеров. Во всех телескопах и прожекторах стоят параболические зеркала, причем их величина часто достигает нескольких метров в поперечнике.
При переходе света из одной среды в Другую происходит преломление световых лучей (рис. 15). Преломление световых лучей подчиняется двум следующим законам:
Луч, падающий на преломляющую поверхность, нормаль к поверхности в точке падения и преломленный луч лежат в одной плоскости Синус угла падения  (рис. 15) между падающим лучом и нормалью относится к синусу угла преломления
(рис. 15) между падающим лучом и нормалью относится к синусу угла преломления  между преломленным лучом и нормалью, как скорость света в первой среде
между преломленным лучом и нормалью, как скорость света в первой среде  к скорости света во второй среде
к скорости света во второй среде 

или, вводя показатель преломления  равный
равный 

Для обычных стекол 1,5. Пользуясь формулой (2) и первым законом преломления, можно объяснить все явления, происходящие при преломлении света на самых сложных поверхностях.

Рис. 15. Преломление света,
Из формулы (2) видно, что при  угол
угол  всегда больше угла
всегда больше угла  т. е. преломленный луч при переходе из менее плотной в более плотную среду приближается к нормали.
т. е. преломленный луч при переходе из менее плотной в более плотную среду приближается к нормали.
При обратном направлении луча — из более плотной среды в менее плотную — картина будет обратная. Если на рис. 15 считать направление светового луча обратным, то угол  будет углом падения, а угол
будет углом падения, а угол  углом преломления.
углом преломления.
Увеличивая угол  мы можем дойти до такого угла
мы можем дойти до такого угла  при котором
при котором

станет равным единице. Тогда

и

Преломленный луч будет скользить вдоль границы раздела. Для углов падения, больших  мы получим следующее противоречивое соотношение:
мы получим следующее противоречивое соотношение:

Это соотношение, конечно, не удовлетворится ни при одйом  Преломленного луча вообще не будет. Опыт показывает, что действительно при падении лучей на границу раздела под углами с нормалью, большими, чем угол
Преломленного луча вообще не будет. Опыт показывает, что действительно при падении лучей на границу раздела под углами с нормалью, большими, чем угол  свет не проходит сквозь поверхность, а полностью отражается. Это явление, наблюдаемое при переходе света из более плотной среды в менее плотную, называют полным внутренним отражением.
свет не проходит сквозь поверхность, а полностью отражается. Это явление, наблюдаемое при переходе света из более плотной среды в менее плотную, называют полным внутренним отражением.
Предельный угол  определяется простой формулой:
определяется простой формулой:

Для обычных стекол  угол
угол  равен примерно 42
равен примерно 42
Геометрическая оптика не совсем точно описывает явление полного внутреннего ртражения. На самом деле наблюдается проникновение света во вторую среду. Однако это явление может быть объяснено только при учете волновых свойств света.
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ЧЕТВЕРТАЯ. ОПТИКА
- § 2. Электромагнитная теория света
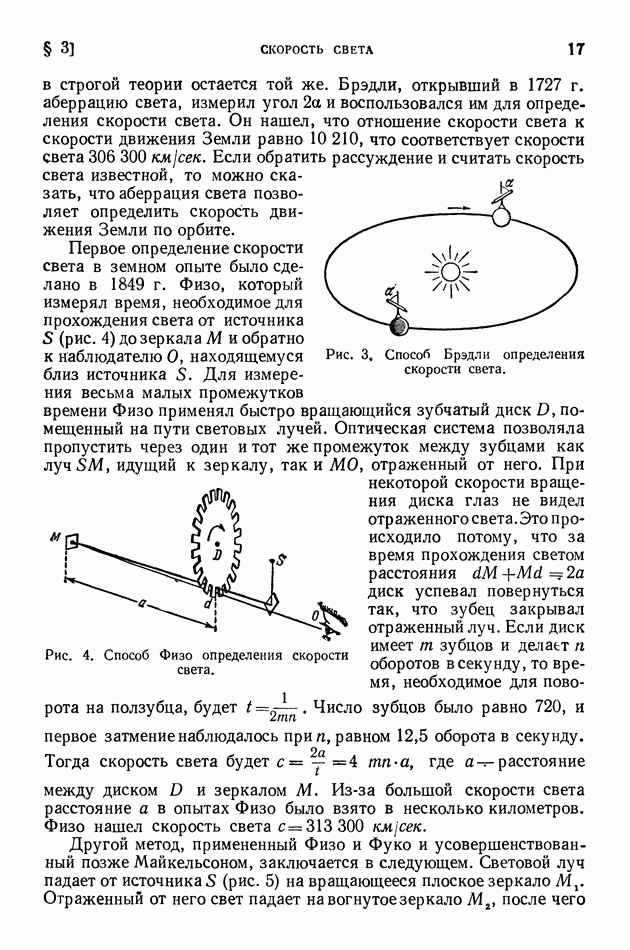
- § 3. Скорость света
- § 4. Опыт Майкельсона
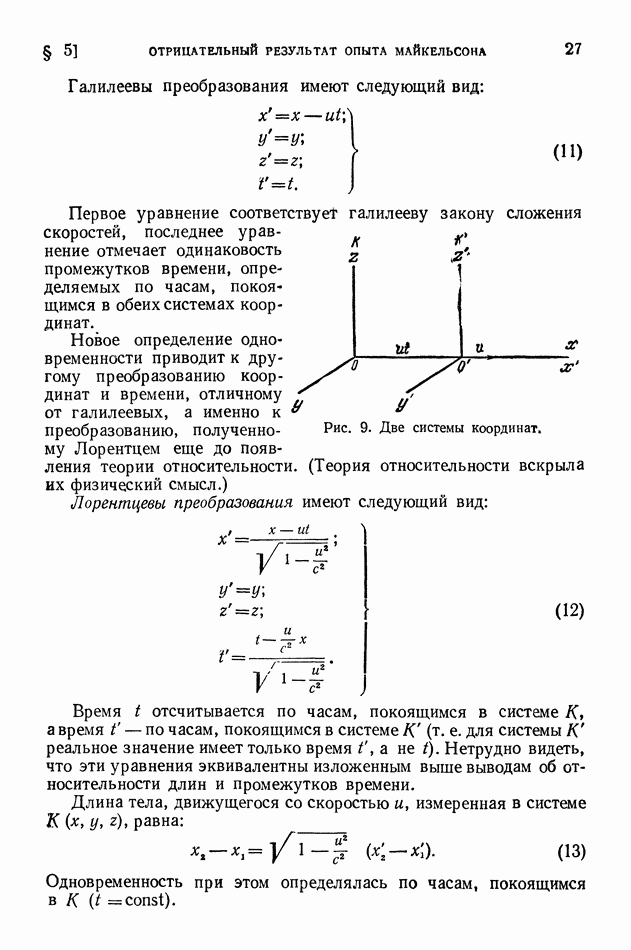
- § 5. Отрицательный результат опыта Майкельсона и теория относительности
- § 6. Некоторые замечания о теории относительности
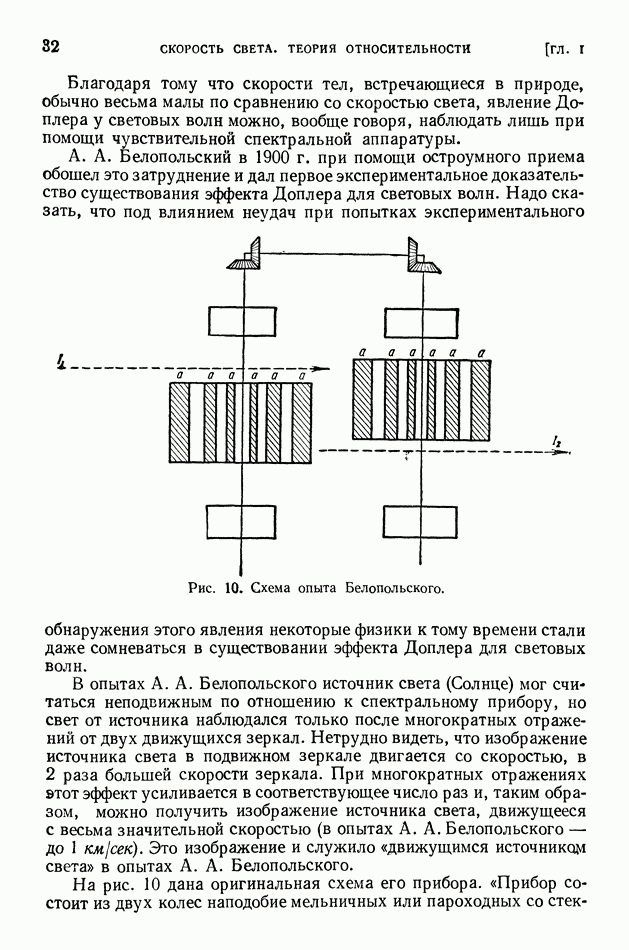
- § 7. Явление Доплера для световых волн
- ГЛАВА II. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- § 8. Законы отражения и преломления света
- § 9. Линза
- § 10. Оптические системы
- § 11. Глаз как оптическая система
- § 12. Приборы, вооружающие глаз
- § 13. Фотоаппарат и проекционный аппарат
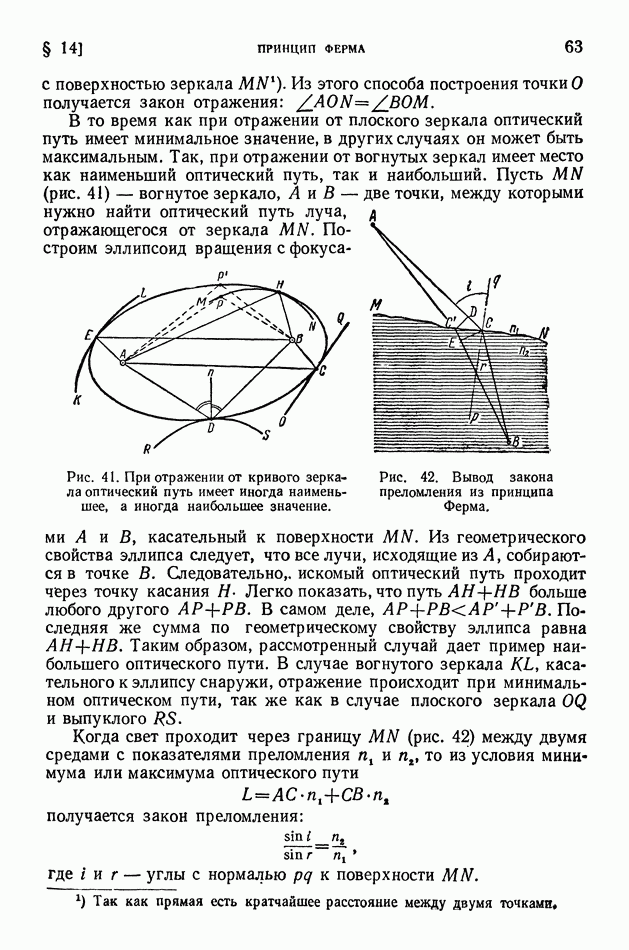
- § 14. Принцип Ферма
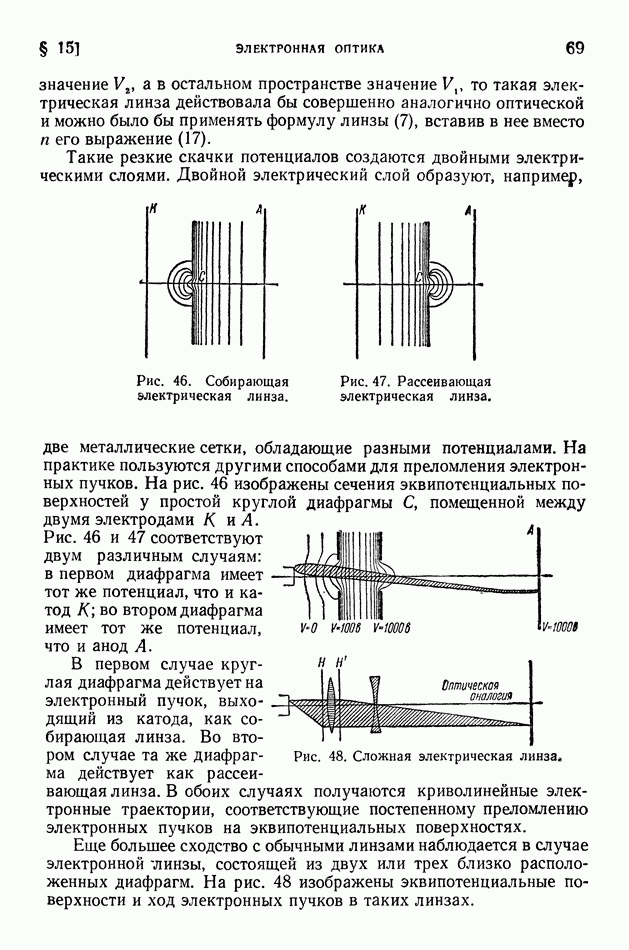
- § 15. Электронная оптика
- ГЛАВА III. ИНТЕРФЕРЕНЦИЯ СВЕТА
- § 16. Принцип суперпозиции. Когерентность
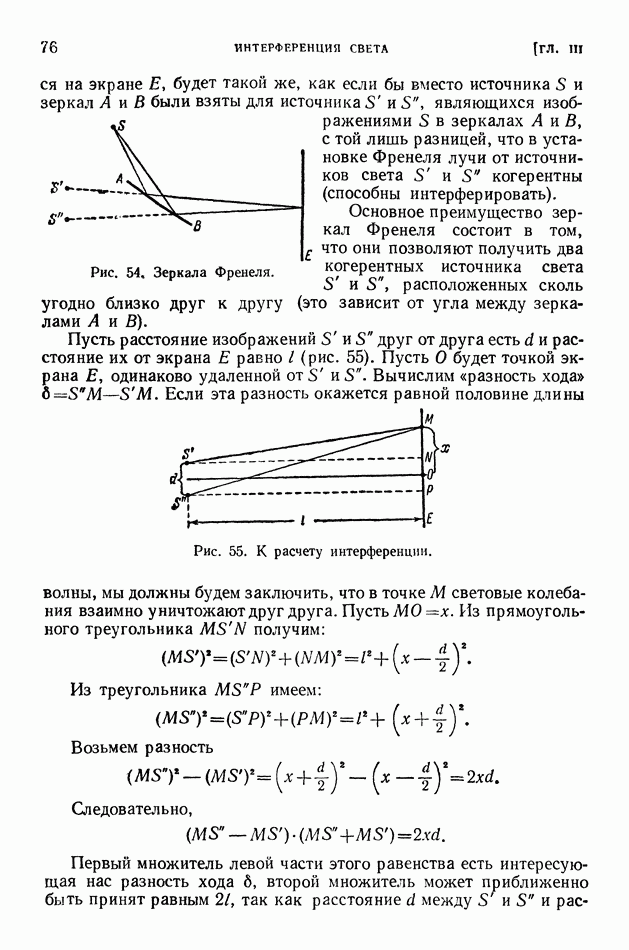
- § 17. Зеркала Френеля
- § 18. Цвета тонких пленок. Полосы равной толщины
- § 19. Полосы равного наклона. Просветленная оптика
- § 20. Интерферометры
- § 21. Интерференционное измерение технических мер длины
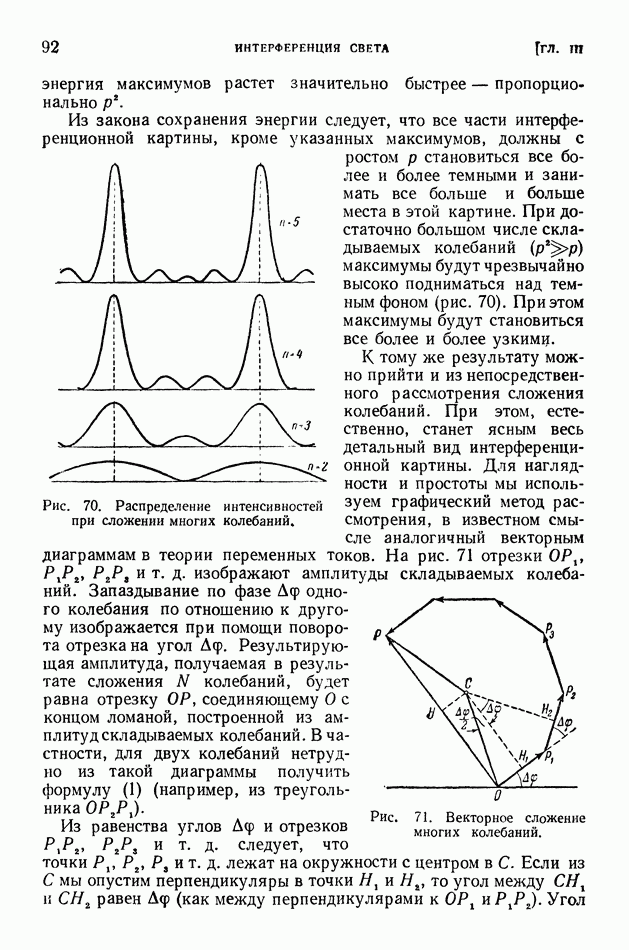
- § 22. Интерференция многих колебаний
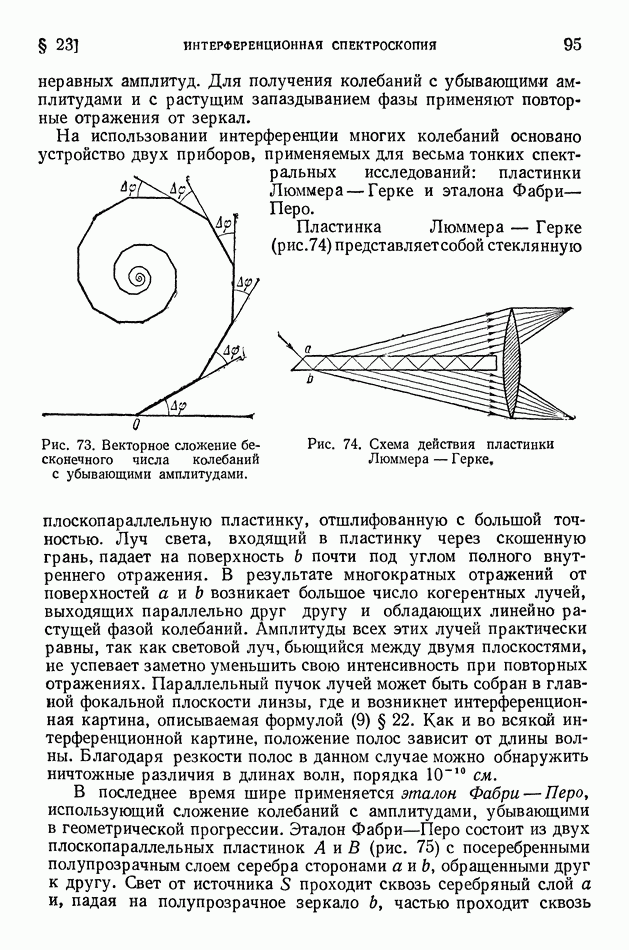
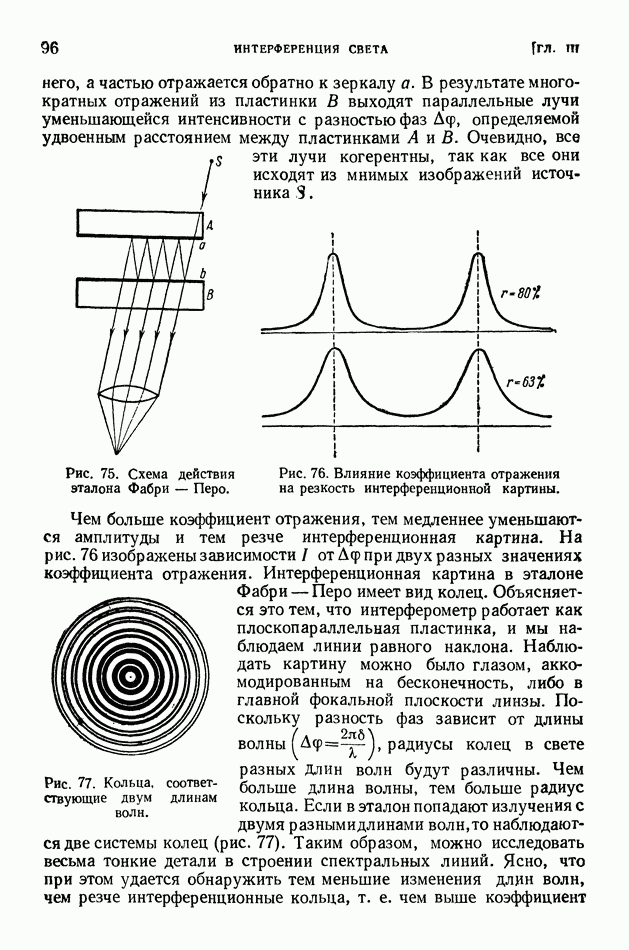
- § 23. Интерференционная спектроскопия
- ГЛАВА IV. ДИФРАКЦИЯ СВЕТА
- § 24. Явление дифракции. Опыт Френеля
- § 25. Принцип Гюйгенса-Френеля
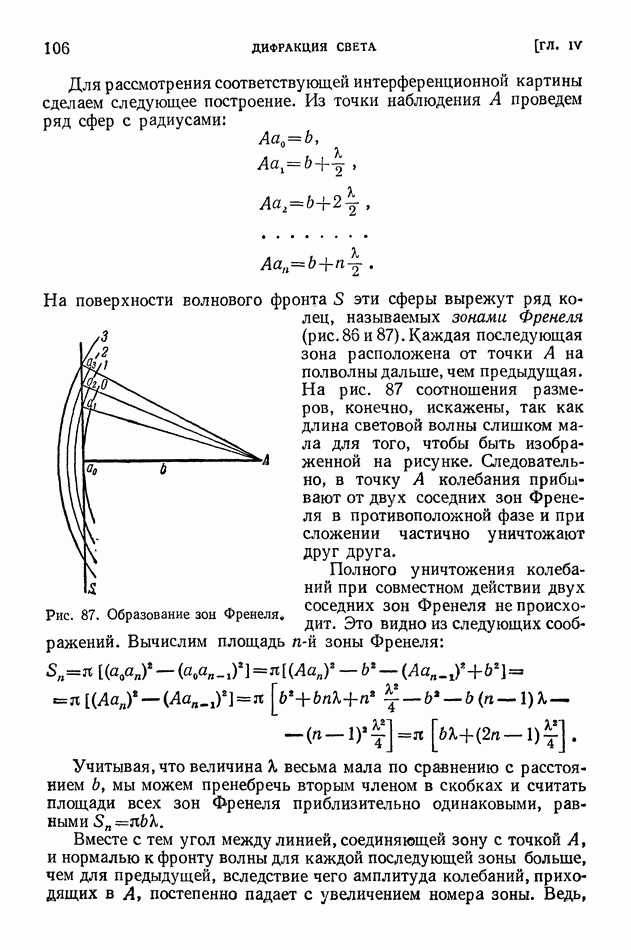
- § 26. Метод зон Френеля
- § 27. Дифракция от узкой щели
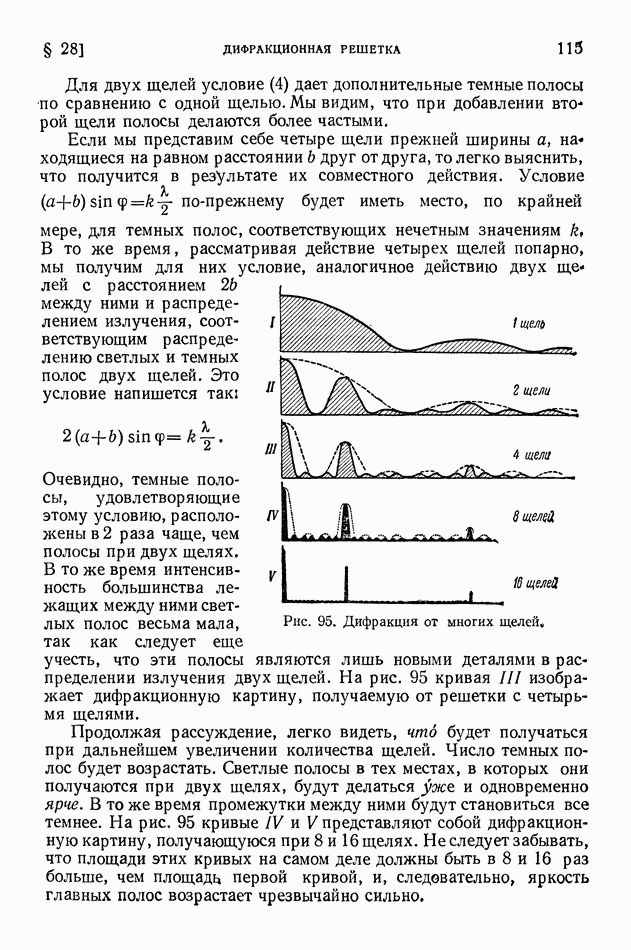
- § 28. Дифракционная решетка
- § 29. Дифракционный спектр. Решетки Роуланда и эшелон Майкельсона
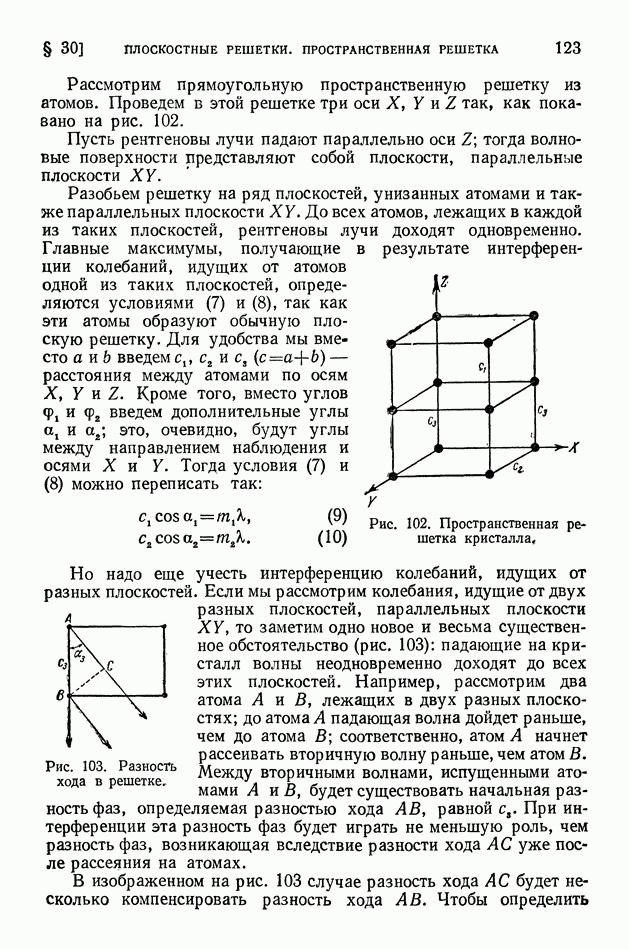
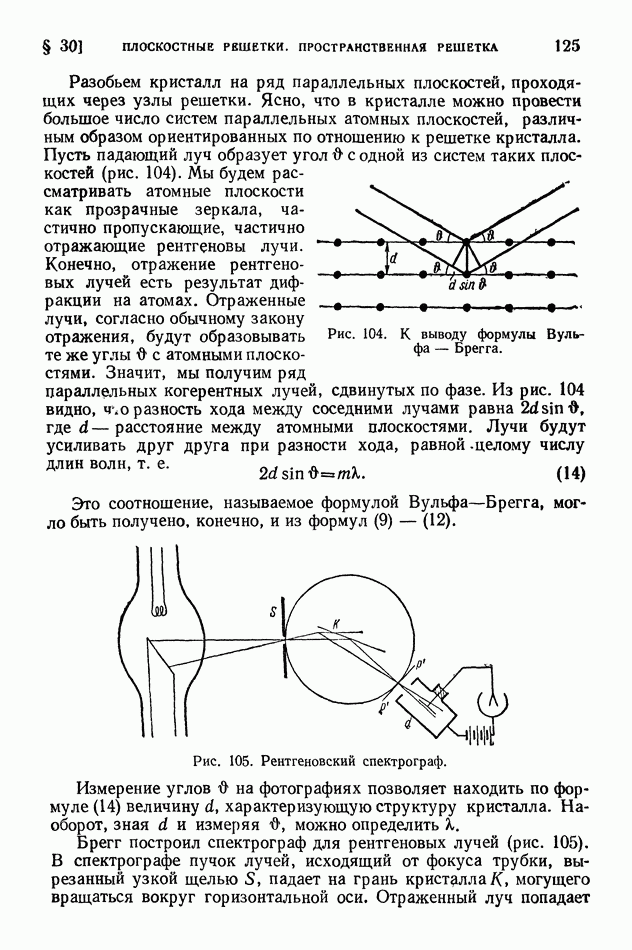
- § 30. Плоскостные решетки. Пространственная решетка
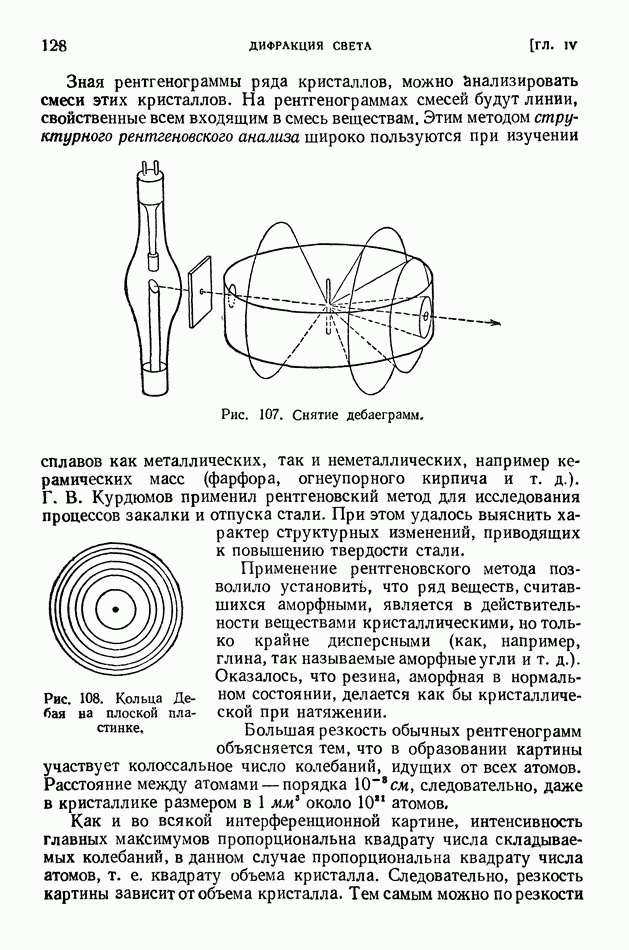
- § 31. Структурный рентгеновский анализ
- § 32. Дифракция света на ультразвуковых волнах
- § 33. Дифракция от мелких частиц
- § 34. Разрешающая способность оптических инструментов. Звездный интерферометр
- ГЛАВА V. ПОЛЯРИЗАЦИЯ СВЕТА
- § 35. Поляризация света
- § 36. Двойное лучепреломление
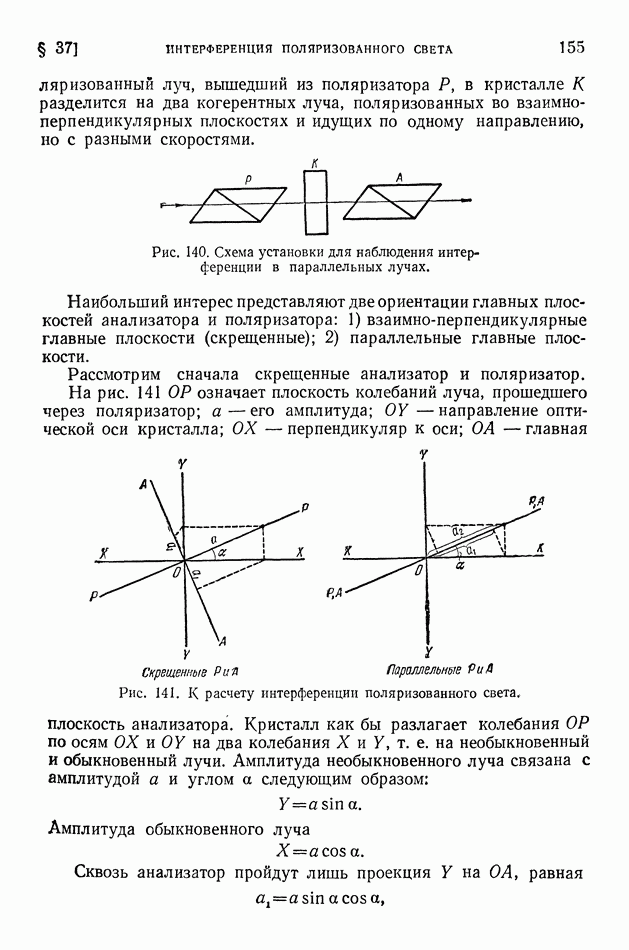
- § 37. Интерференция поляризованного света
- § 38. Оптический метод исследования упругих натяжений. Эффект Керра
- § 39. Вращение плоскости поляризации. Эллиптическая поляризация
- ГЛАВА VI. ДИСПЕРСИЯ, ПОГЛОЩЕНИЕ И ИЗЛУЧЕНИЕ СВЕТА
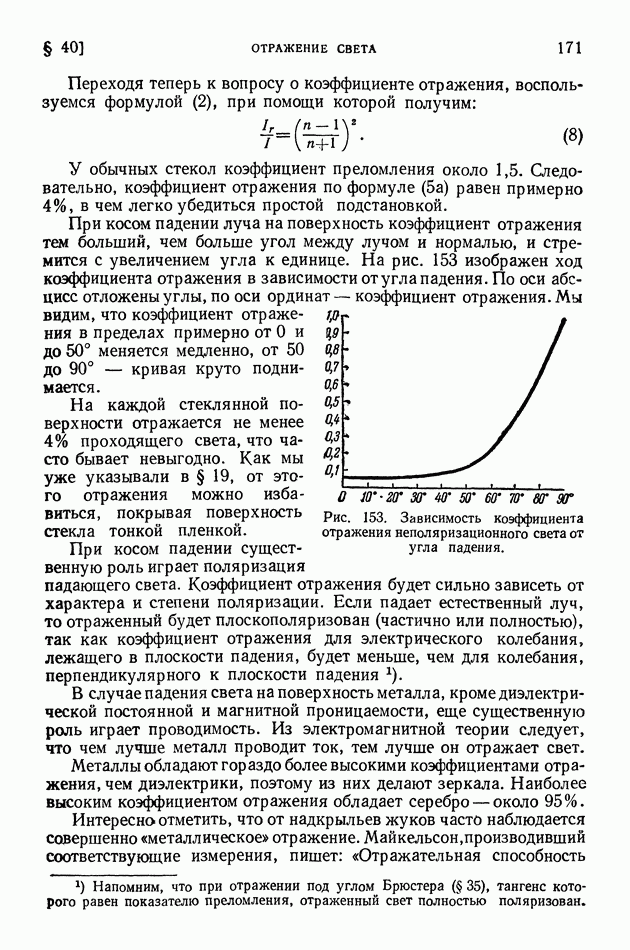
- § 40. Отражение света
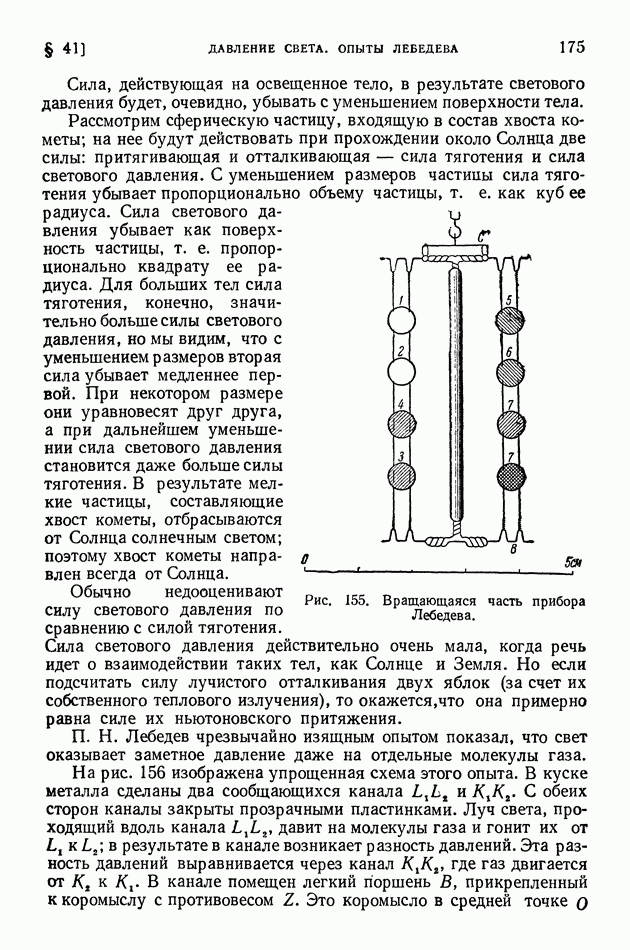
- § 41. Давление света. Опыты Лебедева
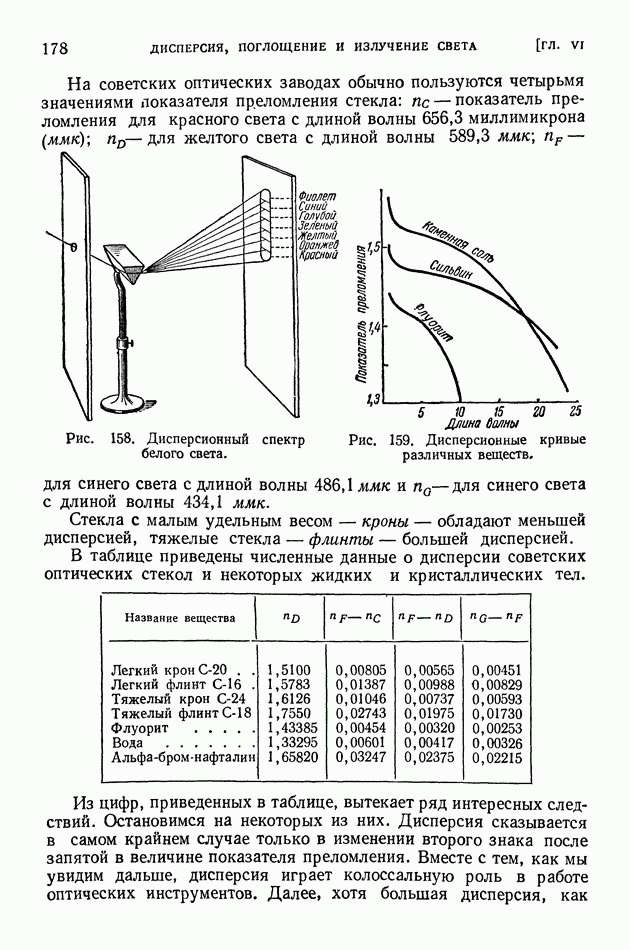
- § 42. Дисперсия. Опыты Ньютона
- § 43. Молекулярная теория дисперсии
- § 44. Хроматическая аберрация. Спектрограф
- § 45. Поглощение света
- § 46. Закон Бугера. Опыты Вавилова
- § 47. Атом как элементарный излучатель света
- § 48. Эффект Вавилова — Черенкова
- ГЛАВА VII. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ И СВЕТОВОЙ ПОТОК
- § 49. Излучение черного тела. Формула Планка. Закон Вина
- § 50. Излучение нечерных тел. Законы Кирхгофа
- § 51. Приемники излучения
- § 52. Световые величины и их измерения
- § 53 Температурные излучатели как источники света
- ЧАСТЬ ПЯТАЯ. АТОМНАЯ ФИЗИКА
- ГЛАВА VIII. СТРОЕНИЕ АТОМА И ТЕОРИЯ БОРА
- § 55. Опыты, обнаружившие ядерное строение атомов
- § 56. Противоречие между фактическим строением атомов и выводами классической электродинамики. Строение линейчатых спектров
- § 57. Опытные основания теории квантов в первые годы ее развития
- § 58. Теория Бора. Происхождение спектра водорода
- § 59. Квантовые числа
- § 60. Принцип Паули. Строение электронных оболочек атомов
- § 61. Общая картина возникновения спектров
- ГЛАВА IX. ОСНОВЫ КВАНТОВОЙ (ВОЛНОВОЙ) МЕХАНИКИ
- § 62. Волновые свойства частиц. Формула де Бройля. Дифракция электронов
- § 63. Уравнение Шредингера. Просачивание через энергетический барьер. Нулевая энергия
- § 64. Волномеханическая теория атома водорода
- § 65. Соотношение неопределенностей и его разные трактовки
- ГЛАВА X. КВАНТОВАЯ ОПТИКА
- § 66. Развитие квантовой оптики
- § 67. Спектр щелочных металлов. Спин электрона
- § 68. Спектр гелия. Символика спектральных термов
- § 69. Сверхтонкая структура спектральных линий
- § 70. Атом в силовом поле
- § 71. Молекулярные спектры и строение молекул
- § 72. Комбинационное рассеяние света
- § 73. Квантовая картина испускания света атомами и молекулами
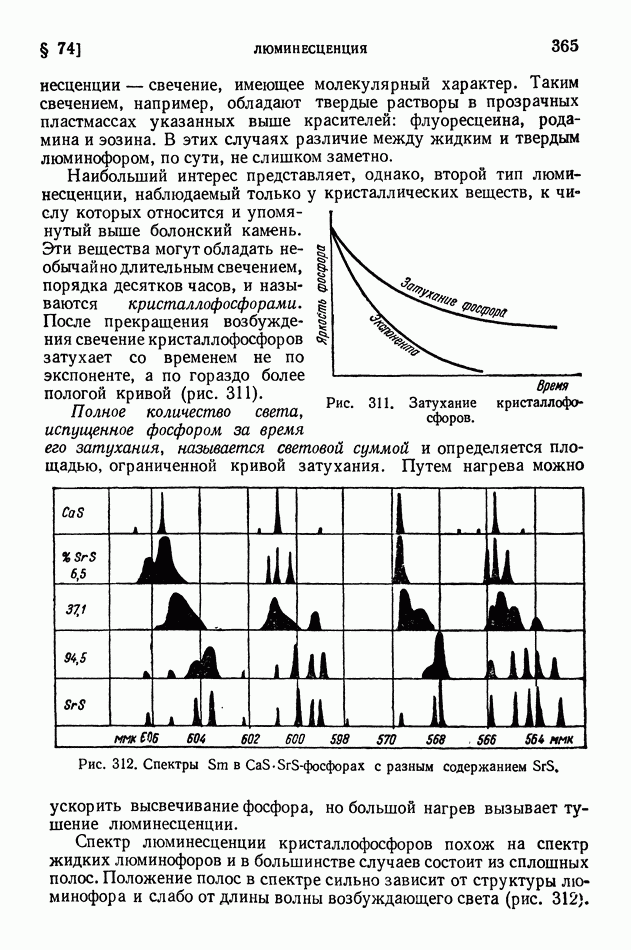
- § 74. Люминесценция
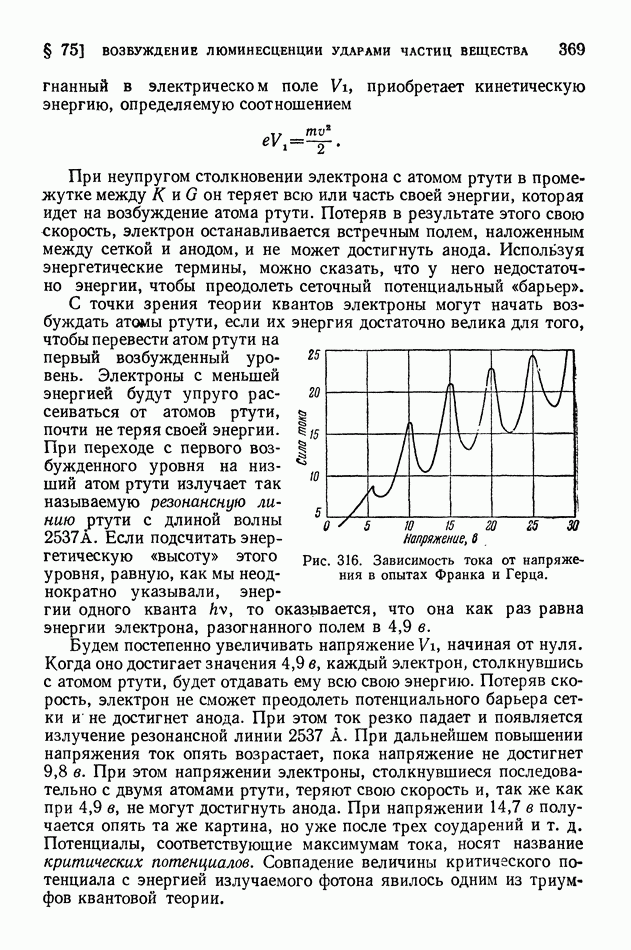
- § 75. Возбуждение люминесценции ударами частиц вещества
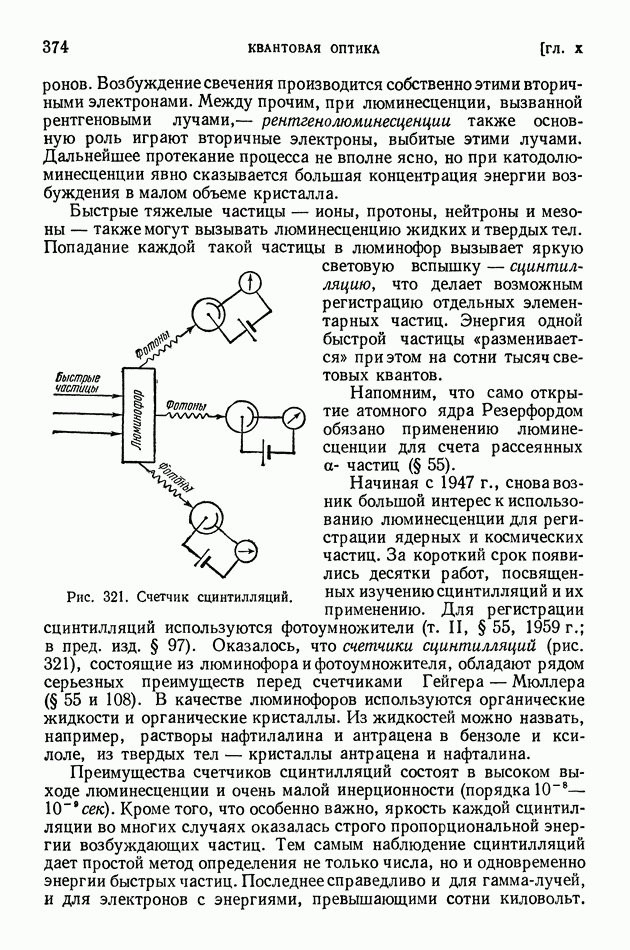
- § 76. Применения люминесценции
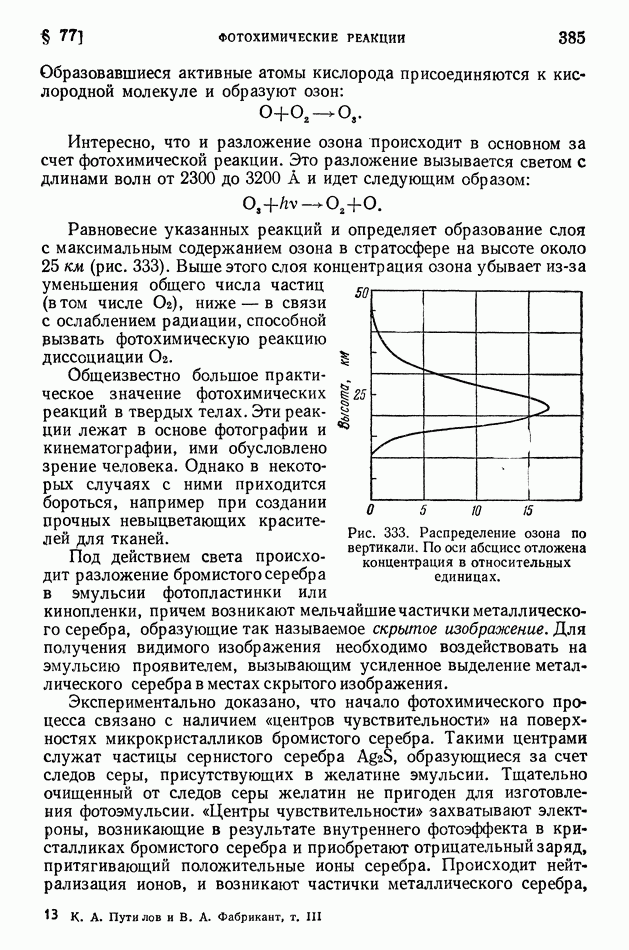
- § 77. Фотохимические реакции
- ГЛАВА XI. ЗАКОН ПРОПОРЦИОНАЛЬНОСТИ МАССЫ И ЭНЕРГИИ И РЕЛЯТИВИСТСКИЕ СООТНОШЕНИЯ
- § 78. Закон пропорциональности массы и энергии
- § 79. Предварительные замечания о релятивистских эффектах. Зависимость массы от скорости
- § 80. Корпускулярные свойства фотонов. Явление Комптона
- § 81. Вывод закона Эйнштейна сложения скоростей из закона пропорциональности массы и энергии и законов сохранения энергии или количества движения
- § 82. Две трактовки закона пропорциональности массы и энергии и уточнение закона тяготения
- § 83. Красное смещение спектральных линий. Поперечный эффект Доплера
- § 84. Влияние гравитационного поля на скорость света в вакууме и показатель преломления вакуума
- ЧАСТЬ ШЕСТАЯ. ЯДЕРНАЯ ФИЗИКА
- § 85. Заряд и масса ядра. Масс-спектральный анализ
- § 86. Состав ядер. Изотопы. Атомные единицы массы и энергии
- § 87. Радиоактивный распад ядер. Закон радиоактивного смещения. Изомеры
- § 88. Альфа-лучи. Потери энергии на ионизацию. Квантовомеханическое объяснение альфа-радиоактивности
- § 89. Бета- и гамма-лучи
- § 90. Искусственное расщепление ядер. Открытие нейтрона
- § 91. Открытие позитрона. Взаимопревращение фотонов определенной энергии и электронно-позитронных пар
- § 92. Индуцированная позитронная и электронная радиоактивность. Фоторасщепление ядер, K-захват
- § 93. Энергетические уровни ядер. Внутренняя конверсия. Нейтрино
- § 94. Капельная теория строения ядер
- § 95. Деление ядер и развитие капельной теории строения ядер
- ГЛАВА XIII. КОСМИЧЕСКИЕ ЛУЧИ
- § 96. Методы исследования и первые итоги изучения космических лучей
- § 97. Каскадное образование электронно-позитронных пар в космических лучах. Потери энергии электронами на тормозное излучение
- § 98. «мю»-мезоны. Зависимость времени жизни неустойчивых частиц от скорости движения
- § 99. «пи»-мезоны
- § 100. Взрывные ядерные ливни и их каскадное развитие в космических лучах
- § 101. Корпускулярный и энергетический спектр космических лучей. Происхождение космического излучения
- ГЛАВА XIV. ЭКСПЕРИМЕНТАЛЬНЫЕ СРЕДСТВА ЯДЕРНОЙ ФИЗИКИ
- § 102. Циклотроны
- § 103. Фазотроны
- § 104. Бетатроны
- § 105. Синхротроны и синхрофазотроны
- § 106. Линейные ускорители электронов и ионов
- § 107. Лабораторные источники нейтронов. Замедлители нейтронов в ядерных реакторах
- § 108. Усовершенствование методов наблюдения и счета частиц
- ГЛАВА XV. ЯДЕРНЫЕ РЕАКЦИИ И АТОМНАЯ ЭНЕРГИЯ
- § 109. Основные виды и обозначения ядерных реакций. Конкурирующие процессы в ядерных реакциях
- § 110. Энергетический эффект, энергия возбуждения и порог ядерных реакций
- § 111. Превращения элементарных частиц
- § 112. Ядерные силы
- § 113. Энергия связи ядер и средняя энергия связи нуклона
- § 114. Полуэмпирическая формула для энергии ядерной связи и для атомных энергий и масс
- § 115. Взаимосвязь энергии и строения ядер. Внутриядерное движение нуклонов и нуклонные оболочки. Спины и магнитные моменты ядер
- § 116. Энергия отделения частиц и анализ возможного хода ядерной реакции
- § 117. Выход продуктов ядерной реакции. Эффективные сечения. Резонансные явления
- § 118. Цепной процесс деления ядер. Активно делящиеся вещества. Ядерные реакторы
- § 119. Термоядерные реакции
- § 120. Применение ядерных реакций
- § 121. Ядерные реакции в звездах