| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
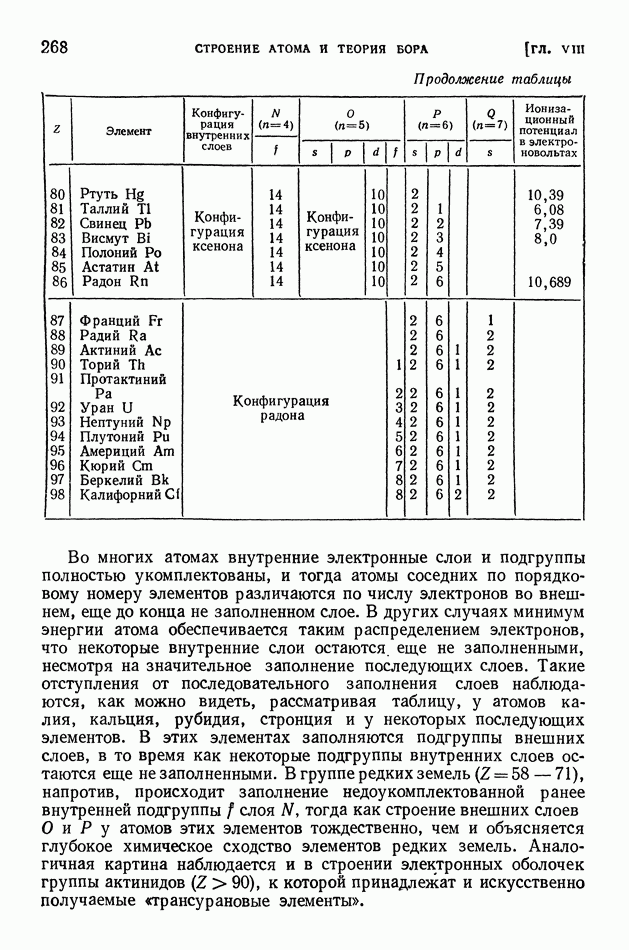
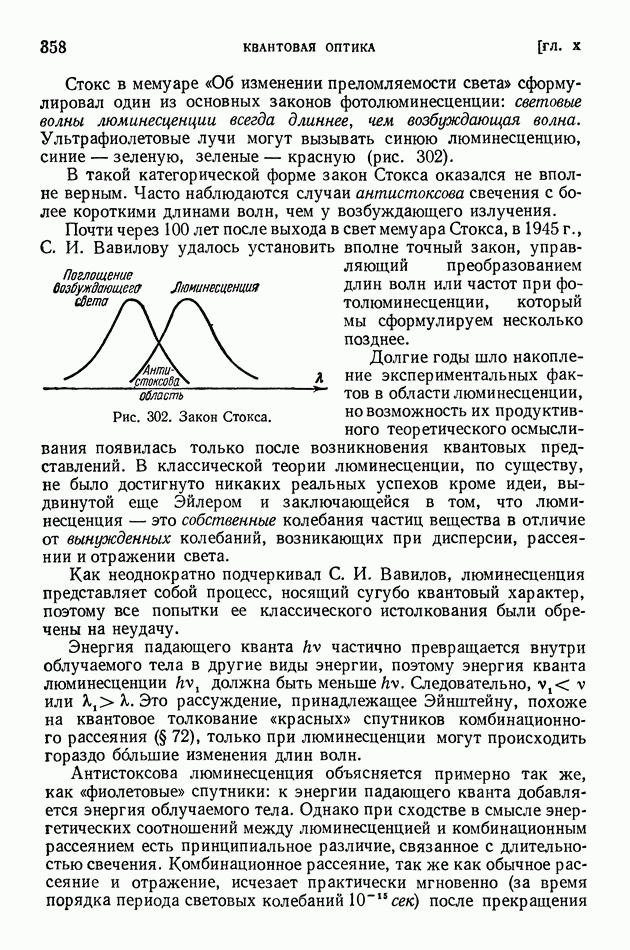
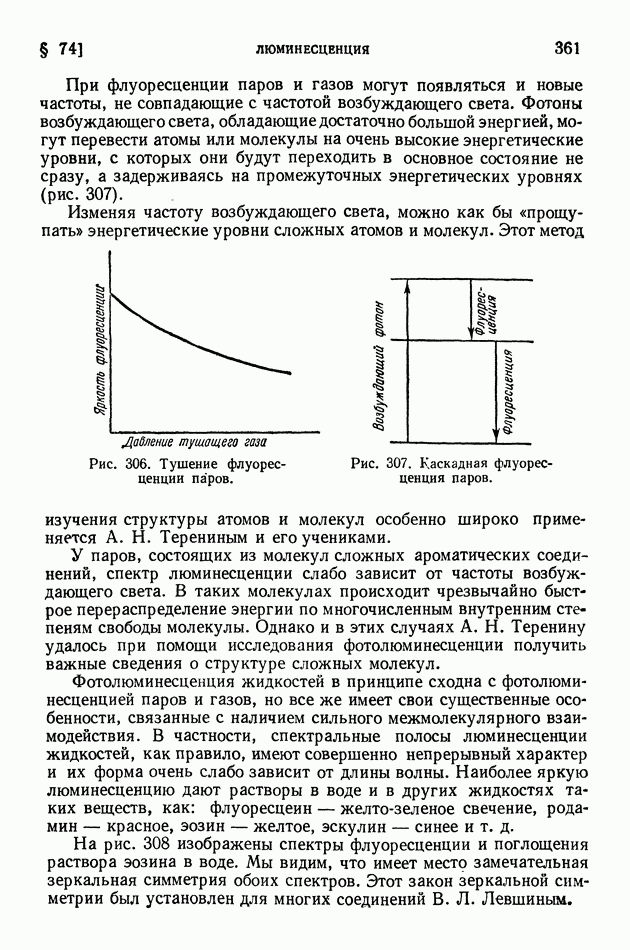
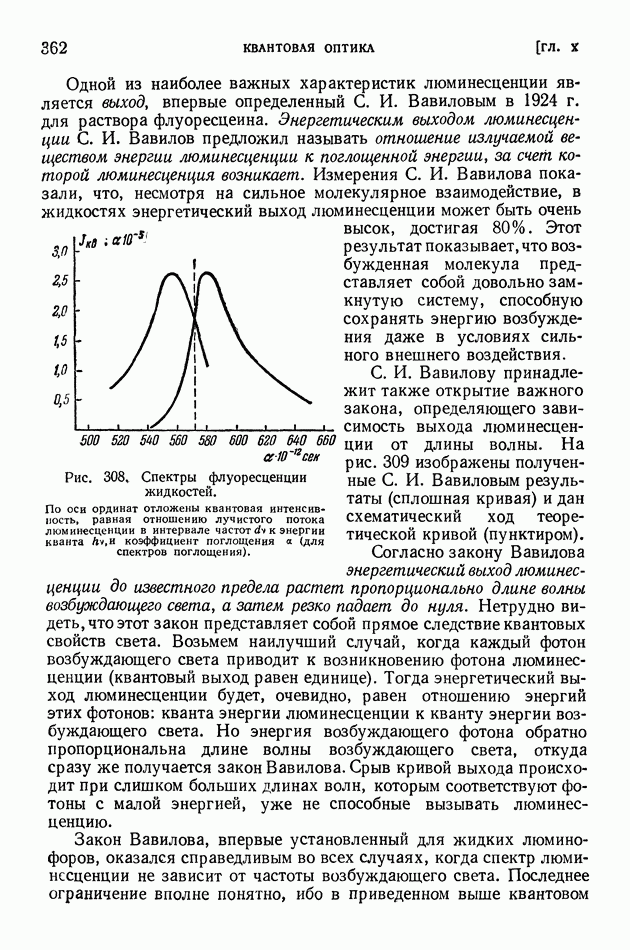
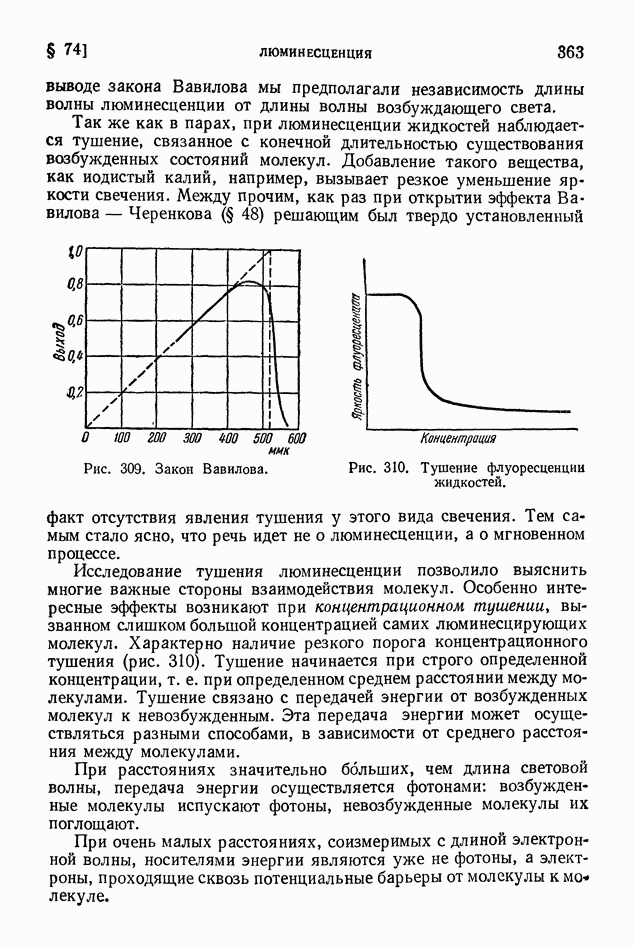
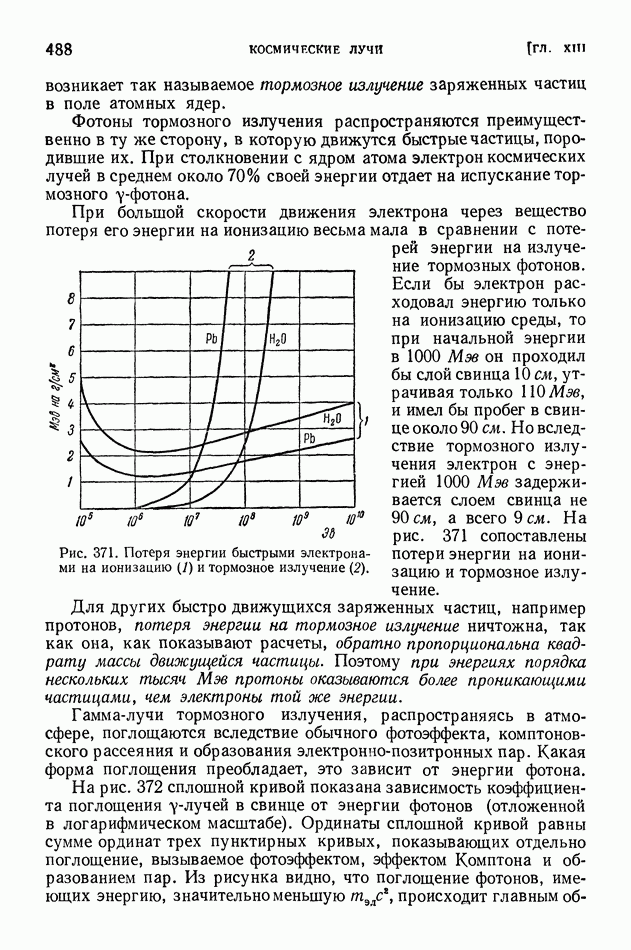
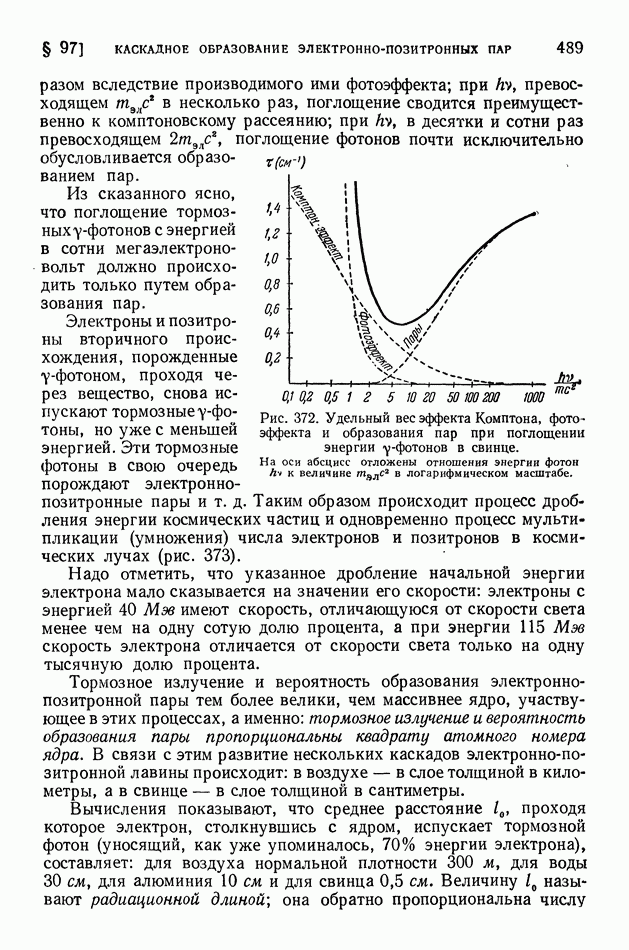
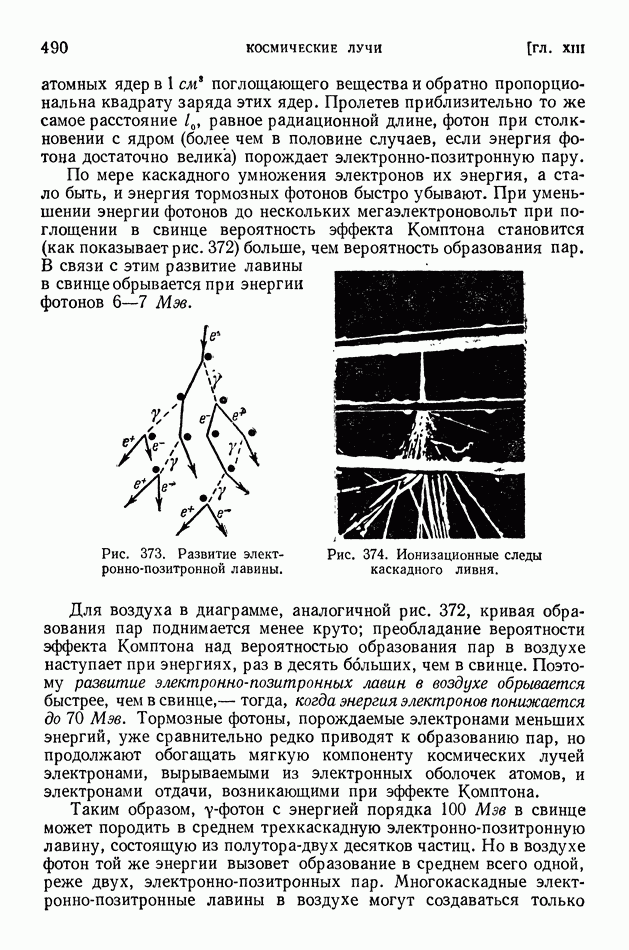
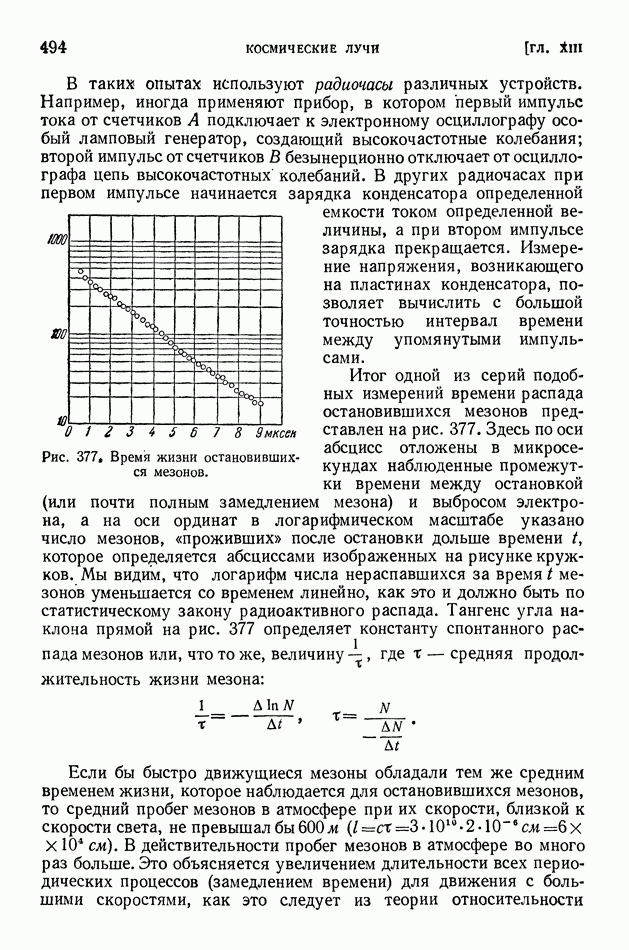
§ 63. Уравнение Шредингера. Просачивание через энергетический барьер. Нулевая энергия
В предыдущем параграфе при описании опытов с дифракцией электронов мы ограничились указанием, что электроны ведут себя как волны с длиной волны, определяемой формулой де Бройля.
Однако, как известно, волна характеризуется не только своей длиной, но и амплитудой, а также пропорциональной квадрату амплитуды интенсивностью. Какой же физический смысл имеют эти понятия в случае электронной волны?
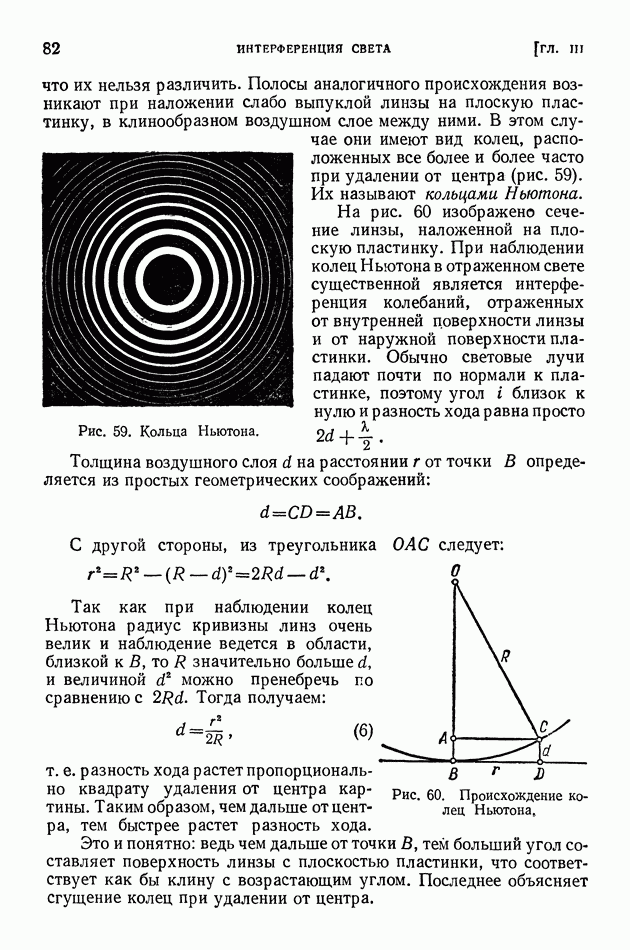
Обратимся снова к опыту по дифракции электронов. Пусть через тонкую металлическую пластинку проходят электроны (опыт Томсона). Тогда на фотографической пластинке зафиксируется система дифракционных колец. Почернение пластинки в каждом месте определяется интенсивностью падающей туда электронной волны. Но вместе с тем очевидно, что почернение пропорционально числу попадающих в это место пластинки электронов. Для проявления волновых свойств электронов нет необходимости, чтобы пучок содержал большое число совместно движущихся электронов. В соответствии с этим изменим теперь условия опыта так, чтобы
электроны по одному проходили через рассеиватель, и будем регистрировать возникающую при этом картину. Оказывается, что отдельные электроны попадают в различные точки., разбросанные по всей пластинке. Только после попадания на пластинку достаточного количества электронов обнаруживается, что они распределены по пластинке неравномерно. Наибольшее число попаданий будет в тех местах, которые соответствовали дифракционным максимумам в опыте с интенсивным пучком электронов. В местах, отвечающих дифракционным минимумам, попаданий либо совсем не будет, либо будет очень мало.

Рис. 239. Дифракционные кольца, образуемые электронами, проходящими через тонкую металлическую пластинку: а — картина, получающаяся после прохождения нескольких электронов; б - после прохождения интенсивного пучка,
Когда через рассеиватель проходит друг за другом достаточно большое число электронов, хотя бы и через значительные промежутки времени, то возникает полная система дифракционных колец (рис. 239). Однако заранее невозможно предсказать, в какое место пластинки попадет отдельный электрон. Это приводит нас к вероятностной трактовке величины интенсивности электронной волны.
Пусть нас интересует вероятность пребывания электрона в некотором объеме пространства с координатами  Эта вероятность будет равна
Эта вероятность будет равна  где
где  амплитуда электронной волны. Таким образом,
амплитуда электронной волны. Таким образом,  определяет вероятность попадания электрона в определенный объем пространства
определяет вероятность попадания электрона в определенный объем пространства  В случае достаточно интенсивных пучков электронов
В случае достаточно интенсивных пучков электронов  определяет вероятность попадания каждого электрона, в определенное место пространства, и мы приходим к прежнему пониманию
определяет вероятность попадания каждого электрона, в определенное место пространства, и мы приходим к прежнему пониманию  как средней плотности частиц.
как средней плотности частиц.
Итак, в противоположность классической механике в квантовой механике мы не можем точно указать, по какой траектории будет
двигаться электрон. Мы можем только вычислить вероятность нахождения электрона в определенном месте пространства в данный момент времени.
Амплитуда электронной волны называемая также волновой функцией, зависит от пространственных координат и (в общем случае) от времени.
Рассмотрим теперь вопрос о том, как находить волновую функцию в различных конкретных случаях. Как известно [формула (5), § 2], уравнение для монохроматической электромагнитной волны, имеющей длину X, записывается в виде

По мысли Шредингера, этому же уравнению удовлетворяет амплитуда электронной волны, длина которой определяется формулой де Бройля  где
где  импульс электрона (то). Подставляя это значение X в уравнение (7), получим:
импульс электрона (то). Подставляя это значение X в уравнение (7), получим:

Так как кинетическая энергия частицы 

Полученное уравнение справедливо для свободного электрона, на который никакие силы не действуют. Если же электрон движется в некотором силовом поле, то нужно еще учесть его потенциальную энергию. Так как полная энергия электрона  в этом случае равна
в этом случае равна

где  потенциальная энергия, то
потенциальная энергия, то

и уравнение (8) принимает вид

Уравнение (9) носит название амплитудного уравнения Шредингера.
В применении к электрону, движущемуся в атоме, различное строение атомов разных элементов сказывается в неодинаковой зависимости потенциальной энергии от координат электрона. Решения уравнения Шредингера для конкретных случаев дают амплитуду электронной волны  как функцию координат. Квадрат волновой функции
как функцию координат. Квадрат волновой функции  умноженный на элемент объема, определяет согласно сказанному выше вероятность нахождения электрона в соответствующих частях атома.
умноженный на элемент объема, определяет согласно сказанному выше вероятность нахождения электрона в соответствующих частях атома.
Ряд существенных выводов можно сделать даже не решая уравнения Шредингера, а только исследуя условия существования непрерывных, однозначных и конечных решений этого уравнения. Поскольку квадрат функции  имеет смысл вероятности пребывания частицы в единице объема для того места пространства, которое определяется координатами
имеет смысл вероятности пребывания частицы в единице объема для того места пространства, которое определяется координатами  то требования конечности, однозначности и непрерывности функции
то требования конечности, однозначности и непрерывности функции  являются совершенно естественными.
являются совершенно естественными.
Наложение указанных условий на волновую функцию  часто приводит к тому, что уравнение Шредингера имеет решение не при всех значениях полной энергии а только для дискретного ряда ее значений.
часто приводит к тому, что уравнение Шредингера имеет решение не при всех значениях полной энергии а только для дискретного ряда ее значений.
Так, если уравнение (9) применить к задаче атома водорода, подставив в него вместо  кулоновскую энергию взаимодействия электрона и ядра, то окажется, что уравнение (9) имеет непрерывные, всюду конечные и однозначные решения только при таких значениях полной энергии, которые получаются для стационарных состояний по теории Бора.
кулоновскую энергию взаимодействия электрона и ядра, то окажется, что уравнение (9) имеет непрерывные, всюду конечные и однозначные решения только при таких значениях полной энергии, которые получаются для стационарных состояний по теории Бора.
Таким образом, уравнение Шредингера по своим математическим свойствам уже содержит в себе условия квантования, которые в теории Бора приходилось постулировать. (Почему уравнение Шредингера приводит во многих случаях к дискретности ряда возможных состояний движения, пояснено в § 64.)
Для исследования какой-нибудь молекулярной или атомной проблемы часто прежде всего строят энергетическую диаграмму. Для этого по оси ординат откладывают потенциальную энергию системы, а по оси абсцисс — какую-либо характеризующую ее координату. Такова, например, кривая зависимости энергии взаимного притяжения или отталкивания двух атомов от расстояния между ними. Подобный подход к решению задач является характерным для
квантовой механики и обусловлен тем обстоятельством, что потенциальная энергия  системы
системы  функция координат входит в волновое уравнение Шредингера.
функция координат входит в волновое уравнение Шредингера.
Построение и интерпретация этих энергетических диаграмм значительно облегчает понимание своеобразных черт квантовой механики. В качестве примера мы рассмотрим несколько энергетических диаграмм, построенных по классическим законам.
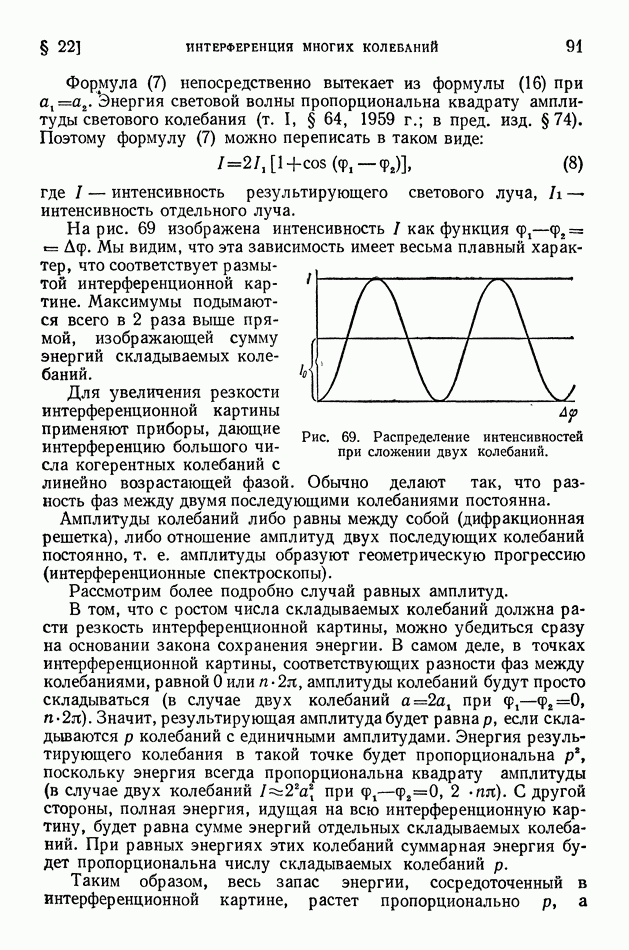
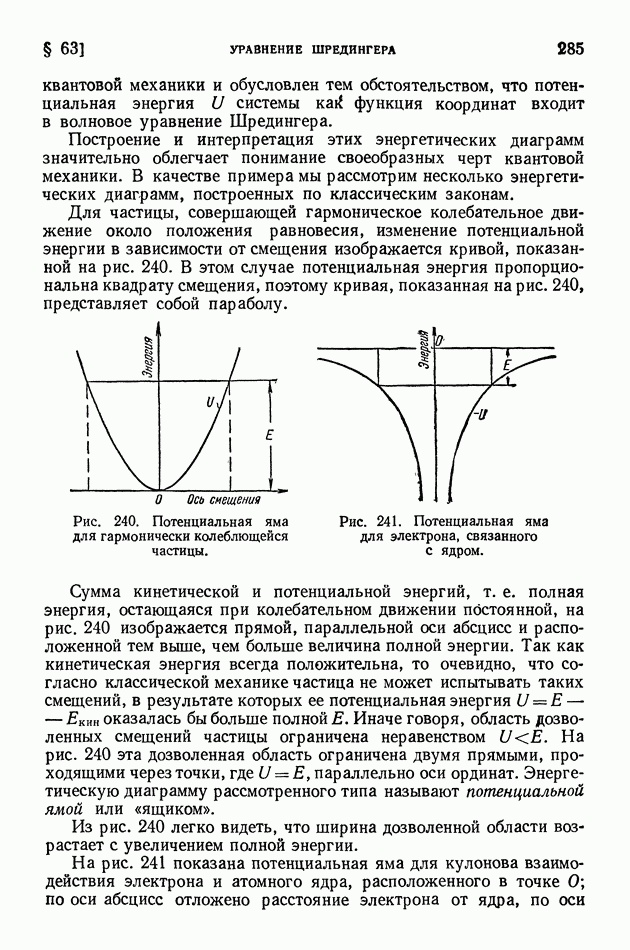
Для частицы, совершающей гармоническое колебательное движение около положения равновесия, изменение потенциальной энергии в зависимости от смещения изображается кривой, показанной на рис. 240. В этом случае потенциальная энергия пропорциональна квадрату смещения, поэтому кривая, показанная на рис. 240, представляет собой параболу.

Рис. 240. Потенциальная яма для гармонически колеблющейся частицы.

Рис. 241. Потенциальная яма для электрона, связанного с ядром.
Сумма кинетической и потенциальной энергий, т. е. полная энергия, остающаяся при колебательном движении постоянной, на рис. 240 изображается прямой, параллельной оси абсцисс и расположенной тем выше, чем больше величина полной энергии. Так как кинетическая энергия всегда положительна, то очевидно, что согласно классической механике частица не может испытывать таких смещений, в результате которых ее потенциальная энергия  оказалась бы больше полной
оказалась бы больше полной  Иначе говоря, область дозволенных смещений частицы ограничена неравенством
Иначе говоря, область дозволенных смещений частицы ограничена неравенством  На рис. 240 эта дозволенная область ограничена двумя прямыми, проходящими через точки, где
На рис. 240 эта дозволенная область ограничена двумя прямыми, проходящими через точки, где  параллельно оси ординат. Энергетическую диаграмму рассмотренного типа называют потенциальной ямой или «ящиком».
параллельно оси ординат. Энергетическую диаграмму рассмотренного типа называют потенциальной ямой или «ящиком».
Из рис. 240 легко видеть, что ширина дозволенной области возрастает с увеличением полной энергии.
На рис. 241 показана потенциальная яма для кулонова взаимодействия электрона и атомного ядра, расположенного в точке  по оси абсцисс отложено расстояние электрона от ядра, по оси
по оси абсцисс отложено расстояние электрона от ядра, по оси
ординат — значения потенциальной энергии. В отличие от предыдущего случая, где потенциальная энергия была величиной положительной, в данном случае потенциальная энергия отрицательна. Так же как и на диаграммах атомных уровней энергии (рис. 229 на стр. 256), верхняя прямая соответствует нулевой полной энергии, т. е. бесконечно большому расстоянию между электроном и ядром. Значения потенциальной энергии, как отрицательные, отложены вниз от этого нулевого уровня энергии. Подобная диаграмма для двух точечных зарядов, потенциальная энергия которых при их сближении стремится к минус бесконечности, изображает бездонную яму. Понимая под  алгебраические величины, по-прежнему можно утверждать, что область дозволенных движений с точки зрения классической механики ограничивается неравенством
алгебраические величины, по-прежнему можно утверждать, что область дозволенных движений с точки зрения классической механики ограничивается неравенством  как
как  О всегда). До тех пор пока полная энергия
О всегда). До тех пор пока полная энергия  остается отрицательной, максимальное удаление электрона от ядра ограничено, как показано на рисунке; напротив, при положительной полной энергии электрон уже не связан с ядром и может уйти от ядра на любое расстояние по некоторой гиперболической орбите.
остается отрицательной, максимальное удаление электрона от ядра ограничено, как показано на рисунке; напротив, при положительной полной энергии электрон уже не связан с ядром и может уйти от ядра на любое расстояние по некоторой гиперболической орбите.

Рис. 242. Прямоугольная потенциальная яма.
По классической механике все частицы в мире движутся в области, для которой  Очевидно, что в каком бы направлении ни двигалась частица, она рано или поздно достигнет поверхности, на которой
Очевидно, что в каком бы направлении ни двигалась частица, она рано или поздно достигнет поверхности, на которой  и от нее повернет обратно. В волновой механике это положение становится несправедливым и существует отличная от нуля вероятность проникновения частицы в область
и от нее повернет обратно. В волновой механике это положение становится несправедливым и существует отличная от нуля вероятность проникновения частицы в область 
Для того чтобы пояснить возникающие здесь закономерности, применим уравнение Шредингера к одномерному движению частицы, находящейся в прямоугольной потенциальной яме, изображенной на рис. 242. Как видно из этого рисунка, потенциальная энергия частицы в области  равна нулю, а в областях
равна нулю, а в областях  равна постоянной величине
равна постоянной величине 
Так как мы рассматриваем одномерное движение, то волновая функция будет зависеть только от одной координаты х, и для области —  получим уравнение
получим уравнение

Его общее решение можно записать в следующем виде;

где  постоянные.
постоянные.
Рассмотрим теперь, что дает уравнение Шредингера в областях  Так как здесь
Так как здесь  то уравнение Шредингера имеет вид
то уравнение Шредингера имеет вид

Общее его решение будет

где  постоянные. Это легко проверить, подставив (13) в уравнение (12).
постоянные. Это легко проверить, подставив (13) в уравнение (12).
Из вида решения (13) следует, что при  второй его член также стремится к бесконечности. Если же
второй его член также стремится к бесконечности. Если же  то в бесконечность обращается первый член. Так как неограниченное возрастание и
то в бесконечность обращается первый член. Так как неограниченное возрастание и  на больших расстояниях от ямы противоречит физическому смыслу и условию конечности
на больших расстояниях от ямы противоречит физическому смыслу и условию конечности  при любых значениях аргументов, то мы должны приравнять коэффициент
при любых значениях аргументов, то мы должны приравнять коэффициент  нулю для случая движения в области справа от ямы, а коэффициент С для области слева. Следовательно, движение по обе стороны от ямы описывается только экспоненциально убывающими функциями. Если
нулю для случая движения в области справа от ямы, а коэффициент С для области слева. Следовательно, движение по обе стороны от ямы описывается только экспоненциально убывающими функциями. Если  достаточно велико, то функция
достаточно велико, то функция  убывает очень быстро при проникновении в «запрещенную» классической механикой область
убывает очень быстро при проникновении в «запрещенную» классической механикой область 

Рис. 243.
Полную картину изменения волновой функции  при некотором
при некотором  с расстоянием х мы получим, соединяя все три ее части вместе так, чтобы при
с расстоянием х мы получим, соединяя все три ее части вместе так, чтобы при  функция
функция  и ее первая производная оставались непрерывными. Из этого условия можно определить значение постоянных
и ее первая производная оставались непрерывными. Из этого условия можно определить значение постоянных  входящих в полученные нами решения, а также уровни энергии частицы в рассматриваемой яме. В результате мы получим следующую картину: в области
входящих в полученные нами решения, а также уровни энергии частицы в рассматриваемой яме. В результате мы получим следующую картину: в области  волновая функция имеет вид синусоиды, а по обеим сторонам от этой области — убывающей экспоненциальной кривой, простирающейся до бесконечности (рис. 243, а). Рис. 243, б показывает изменение вероятности
волновая функция имеет вид синусоиды, а по обеим сторонам от этой области — убывающей экспоненциальной кривой, простирающейся до бесконечности (рис. 243, а). Рис. 243, б показывает изменение вероятности 
Таким образом, в волновой механике разделение на дозволенные и запрещенные области исчезает, так как  есть вероятность нахождения частицы на любом расстоянии от ямы в интервале
есть вероятность нахождения частицы на любом расстоянии от ямы в интервале  В рассмотренном нами случае ямы с бесконечно широкими стенками эта вероятность при достаточно больших х является очень малой, но тем не менее конечной величиной и будет стремиться к нулю только при
В рассмотренном нами случае ямы с бесконечно широкими стенками эта вероятность при достаточно больших х является очень малой, но тем не менее конечной величиной и будет стремиться к нулю только при 
Рассмотрим теперь ту же потенциальную яму, но со стенками конечной ширины. Поведение частицы за пределами классической границы определяется величиной  убывающей как
убывающей как 
Если за единицу длины выбрать ангстрем, а за единицу энергии — электроновольт, то для величины  получим:
получим:

Отсюда следует, что чем больше расстоянием, масса частицы и разность между глубиной ямы и полной энергией, тем меньше будет величина  пропорциональная
пропорциональная  Например, если
Например, если  то
то

Если ширина стенок ямы равна  то величина
то величина  представляет собой вероятность нахождения частицы вне ямы, т. е. вероятность прохождения частицы через потенциальный барьер, образованный стенками ямы. Это явление получило название эффекта просачивания или туннельного эффекта. Им объясняются некоторые явления, которые оставались непонятными с точки зрения классической физики. Так, например, эффектом просачивания объясняются неожиданно большие плотности тока при холодной эмиссии электронов из металлов (т. II, § 45, 1959; в предыдущих изданиях § 52). По классической теории, электронная эмиссия не должна наблюдаться, когда напряжение, приложенное к металлу, недостаточно велико для того, чтобы электроны могли преодолеть потенциальный барьер, определяемый работой выхода электронов. В действительности наблюдаются значительные плотности тока холодной эмиссии при напряжениях, несравненно меньших того, которое, казалось бы, необходимо для вырывания электронов; это есть следствие эффекта просачивания, что подтвердилось сопоставлением волномеханических расчетов с результатами опытов.
представляет собой вероятность нахождения частицы вне ямы, т. е. вероятность прохождения частицы через потенциальный барьер, образованный стенками ямы. Это явление получило название эффекта просачивания или туннельного эффекта. Им объясняются некоторые явления, которые оставались непонятными с точки зрения классической физики. Так, например, эффектом просачивания объясняются неожиданно большие плотности тока при холодной эмиссии электронов из металлов (т. II, § 45, 1959; в предыдущих изданиях § 52). По классической теории, электронная эмиссия не должна наблюдаться, когда напряжение, приложенное к металлу, недостаточно велико для того, чтобы электроны могли преодолеть потенциальный барьер, определяемый работой выхода электронов. В действительности наблюдаются значительные плотности тока холодной эмиссии при напряжениях, несравненно меньших того, которое, казалось бы, необходимо для вырывания электронов; это есть следствие эффекта просачивания, что подтвердилось сопоставлением волномеханических расчетов с результатами опытов.
По формуле (14) для протонов вследствие их значительной массы получается, как мы видели, ничтожно малое значение вероятности просачивания через потенциальный барьер. Таким образом, классический принципиальный запрет проникновения через барьер при энергии частиц, меньшей высоты барьера, заменяется для протонов не менее эффективным практическим запретом, еще более резко выраженным для частиц, тяжелее протонов.
Именно по этой причине неудовлетворительность классической механики не была обнаружена ранее. Однако при крайне малой
ширине барьера [при малых значениях х в формулах (14) и (12)] просачивание через потенциальный барьер и для сравнительно тяжелых частиц может дать заметный эффект. Такой случай имеет место при выбрасывании  -частиц из ядер при радиоактивных превращениях (§ 88), а также в ядерных реакциях при проникновении в ядро извне протонов и других заряженных частиц (§ 110 и 116).
-частиц из ядер при радиоактивных превращениях (§ 88), а также в ядерных реакциях при проникновении в ядро извне протонов и других заряженных частиц (§ 110 и 116).
То, что квантовая механика должна привести к выводу о возможности просачивания частиц через потенциальный барьер, можно было предвидеть из математической аналогии эффекта просачивания с явлениями, которые наблюдаются при полном внутреннем отражении света от поверхности раздела двух оптически разнородных сред. Согласно геометрической оптике (которая в математическом отношении аналогична классической механике) при полном внутреннем отражении не может происходить никакого проникновения лучей через отражающую поверхность. Однако в действительности, как это было установлено экспериментально и объяснено волновой оптикой (которая математически аналогична квантовой механике), наблюдается проникновение волн за отражающую поверхность.

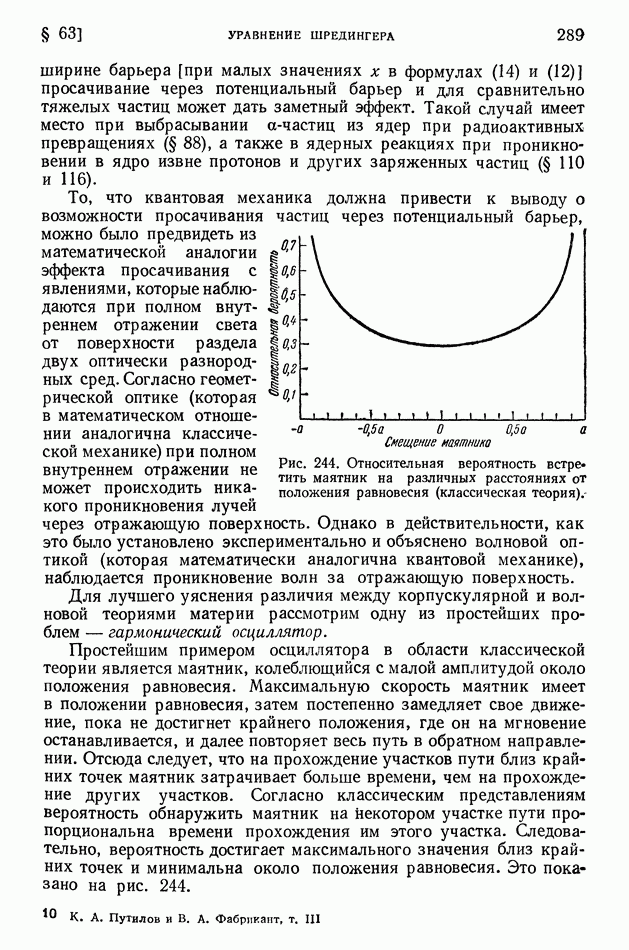
Рис. 244. Относительная вероятность встретить маятник на различных расстояниях от положения равновесия (классическая теория).
Для лучшего уяснения различия между корпускулярной и волновой теориями материи рассмотрим одну из простейших проблем — гармонический осциллятор.
Простейшим примером осциллятора в области классической теории является маятник, колеблющийся с малой амплитудой около положения равновесия. Максимальную скорость маятник имеет в положении равновесия, затем постепенно замедляет свое движение, пока не достигнет крайнего положения, где он на мгновение останавливается, и далее повторяет весь путь в обратном направлении. Отсюда следует, что на прохождение участков пути близ крайних точек маятник затрачивает больше времени, чем на прохождение других участков. Согласно классическим представлениям вероятность обнаружить маятник на некотором участке пути пропорциональна времени прохождения им этого участка. Следовательно, вероятность достигает максимального значения близ крайних точек и минимальна около положения равновесия. Это показано на рис. 244.
Для анализа подобной задачи в квантовой механике нужно подставить в уравнение Шредингера потенциальную энергию гармонического осциллятора, которую с достаточной точностью можно считать пропорциональной квадрату смещения и найти его решения, удовлетворяющие перечисленным выше условиям.

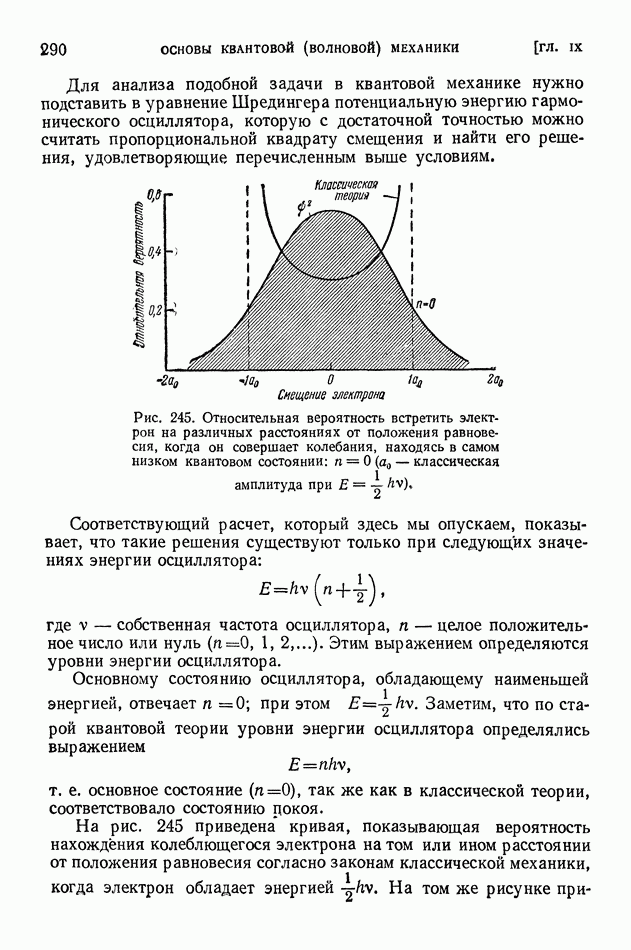
Рис. 245. Относительная вероятность встретить электрон на различных расстояниях от положения равновесия, когда он совершает колебания, находясь в самом низком квантовом состоянии:  классическая амплитуда при
классическая амплитуда при 
Соответствующий расчет, который здесь мы опускаем, показывает, что такие решения существуют только при следующих значениях энергии осциллятора:

где  собственная частота осциллятора,
собственная частота осциллятора,  целое положительное число или нуль
целое положительное число или нуль  Этим выражением определяются уровни энергии осциллятора.
Этим выражением определяются уровни энергии осциллятора.
Основному состоянию осциллятора, обладающему наименьшей энергией, отвечает  при этом Заметим, что по старой квантовой теории уровни энергии осциллятора определялись выражением
при этом Заметим, что по старой квантовой теории уровни энергии осциллятора определялись выражением

т. е. основное состояние  так же как в классической теории, соответствовало состоянию цокоя.
так же как в классической теории, соответствовало состоянию цокоя.
На рис. 245 приведена кривая, показывающая вероятность нахождения колеблющегося электрона на том или ином расстоянии от положения равновесия согласно законам классической механики, когда электрон обладает энергией На том же рисунке
приведена кривая относительной вероятности смещения электрона  вычисленная по уравнению Шредингера при
вычисленная по уравнению Шредингера при 
Мы замечаем здесь резкое расхождение с распределением вероятностей, даваемым классической теорией. На рис. 246—248 показано распределение вероятностей для состояний, характеризуемых квантовыми числами 1, 2 и 5.

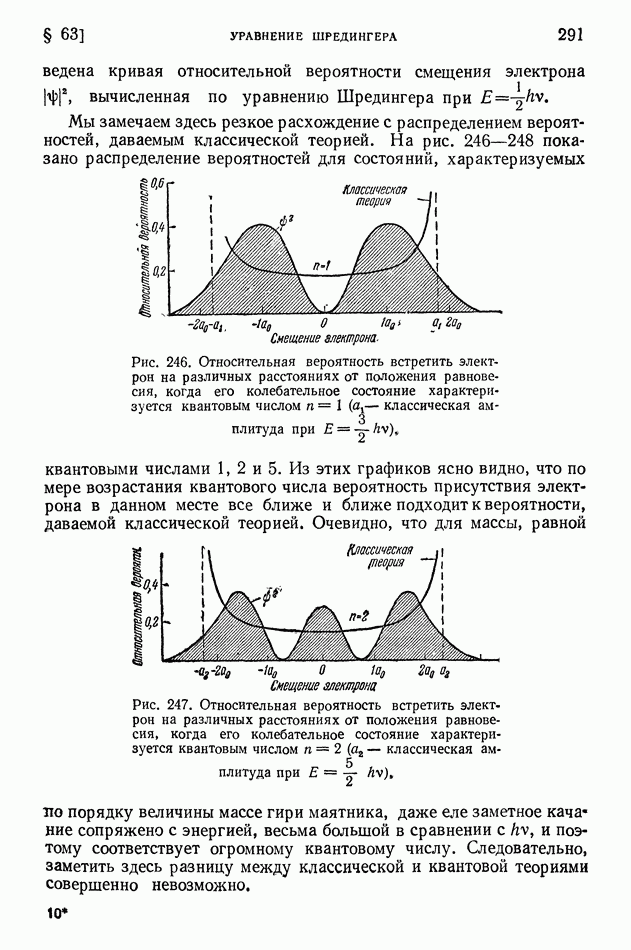
Рис. 246. Относительная вероятность встретить электрон на различных расстояниях от положения равновесия, когда его колебательное состояние характеризуется квантовым числом  классическая амплитуда при
классическая амплитуда при 
Из этих графиков ясно видно, что по мере возрастания квантового числа вероятность присутствия электрона в данном месте все ближе и ближе подходит к вероятности, даваемой классической теорией.

Рис. 247. Относительная вероятность встретить электрон на различных расстояниях от положения равновесия, когда его колебательное состояние характеризуется квантовым числом  (а — классическая амплитуда при
(а — классическая амплитуда при 
Очевидно, что для массы, равной по порядку величины массе гири маятника, даже еле заметное качание сопряжено с энергией, весьма большой в сравнении с  и поэтому соответствует огромному квантовому числу. Следовательно, заметить здесь разницу между классической и квантовой теориями совершенно невозможно.
и поэтому соответствует огромному квантовому числу. Следовательно, заметить здесь разницу между классической и квантовой теориями совершенно невозможно.
Наоборот, в осцилляторах атомных размеров для не слишком больших квантовых чисел классическая теория даже приближенно не дает правильной картины колебаний.
Вывод волновой механики о существовании нулевой энергии осцилляторов оказался важным для правильного понимания некоторых молекулярных явлений.

Рис. 248. Относительная вероятность встретить электрон на различных расстояниях от положения равновесия, когда его колебательное состояние характеризуется квантовым числом  классическая амплитуда при
классическая амплитуда при 
Нулевая энергия осцилляторов  — число осцилляторов) сказывается не только при температурах, близких к абсолютному нулю, где термодинамические
— число осцилляторов) сказывается не только при температурах, близких к абсолютному нулю, где термодинамические  в основе своей — статистические) свойства тел определяются тепловым законом Нернста и где происходит вырождение газов, но косвенно проявляется и при нормальных температурах, обусловливая происхождение дисперсионных сил связи в кристаллах (т. I, § 130, 1959; в предыдущих изданиях § 124).
в основе своей — статистические) свойства тел определяются тепловым законом Нернста и где происходит вырождение газов, но косвенно проявляется и при нормальных температурах, обусловливая происхождение дисперсионных сил связи в кристаллах (т. I, § 130, 1959; в предыдущих изданиях § 124).
| << Предыдущий параграф | Следующий параграф >> |
- ЧАСТЬ ЧЕТВЕРТАЯ. ОПТИКА
- § 2. Электромагнитная теория света
- § 3. Скорость света
- § 4. Опыт Майкельсона
- § 5. Отрицательный результат опыта Майкельсона и теория относительности
- § 6. Некоторые замечания о теории относительности
- § 7. Явление Доплера для световых волн
- ГЛАВА II. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- § 8. Законы отражения и преломления света
- § 9. Линза
- § 10. Оптические системы
- § 11. Глаз как оптическая система
- § 12. Приборы, вооружающие глаз
- § 13. Фотоаппарат и проекционный аппарат
- § 14. Принцип Ферма
- § 15. Электронная оптика
- ГЛАВА III. ИНТЕРФЕРЕНЦИЯ СВЕТА
- § 16. Принцип суперпозиции. Когерентность
- § 17. Зеркала Френеля
- § 18. Цвета тонких пленок. Полосы равной толщины
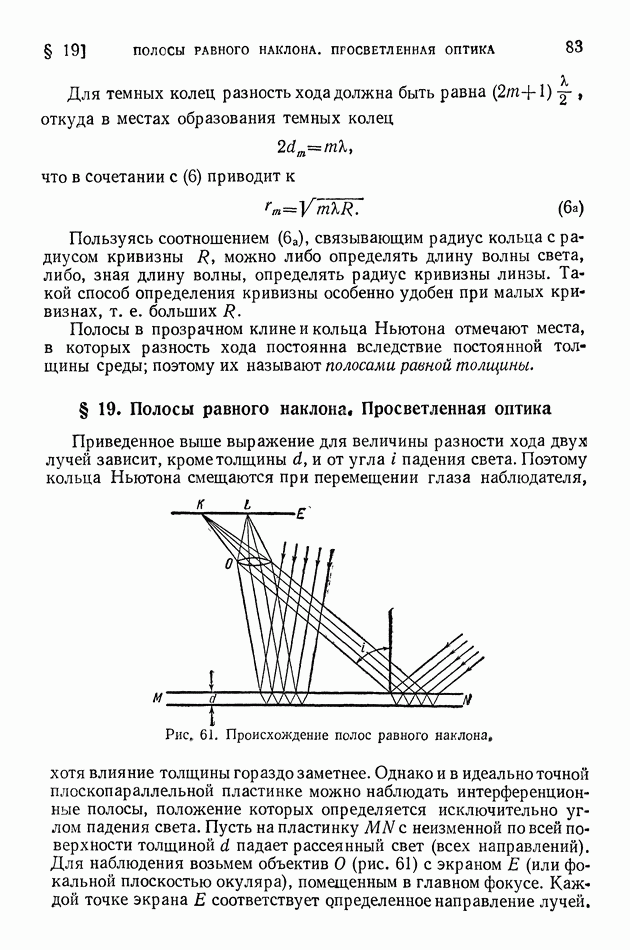
- § 19. Полосы равного наклона. Просветленная оптика
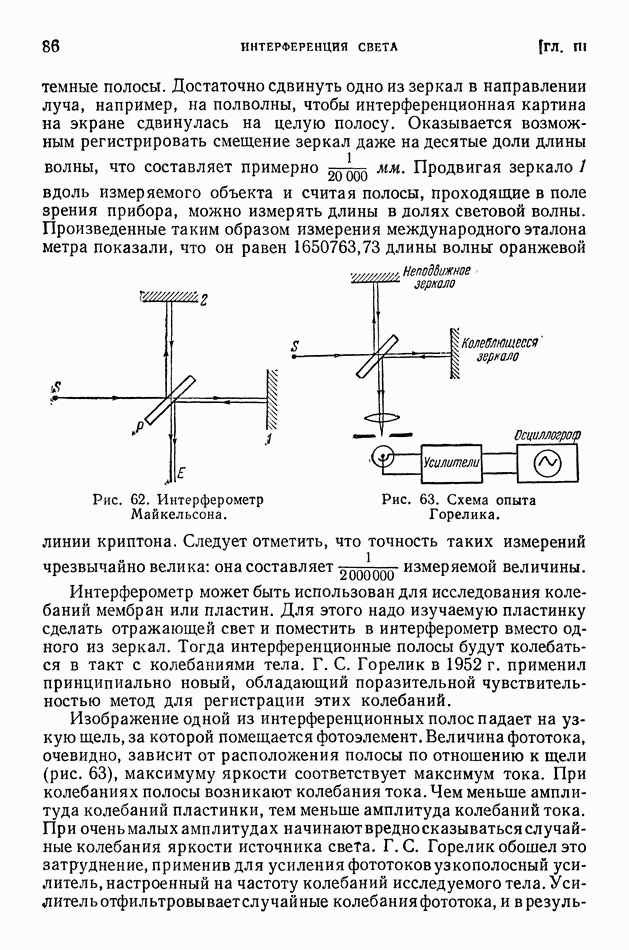
- § 20. Интерферометры
- § 21. Интерференционное измерение технических мер длины
- § 22. Интерференция многих колебаний
- § 23. Интерференционная спектроскопия
- ГЛАВА IV. ДИФРАКЦИЯ СВЕТА
- § 24. Явление дифракции. Опыт Френеля
- § 25. Принцип Гюйгенса-Френеля
- § 26. Метод зон Френеля
- § 27. Дифракция от узкой щели
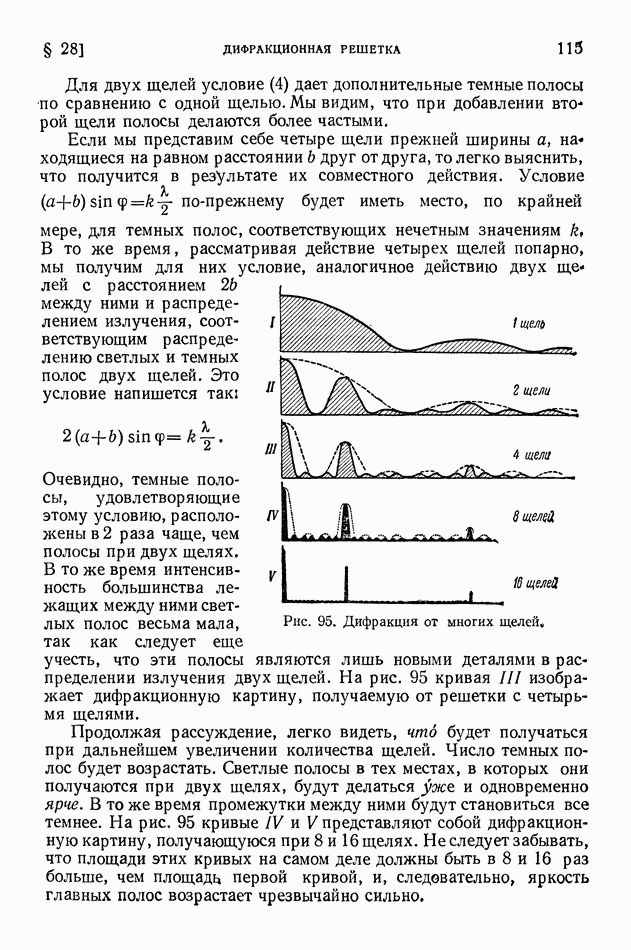
- § 28. Дифракционная решетка
- § 29. Дифракционный спектр. Решетки Роуланда и эшелон Майкельсона
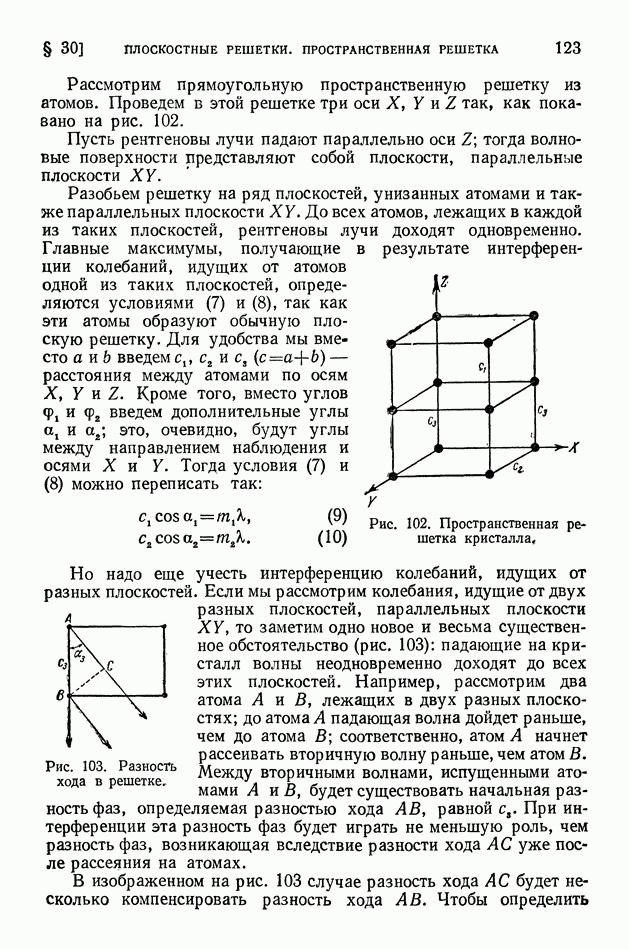
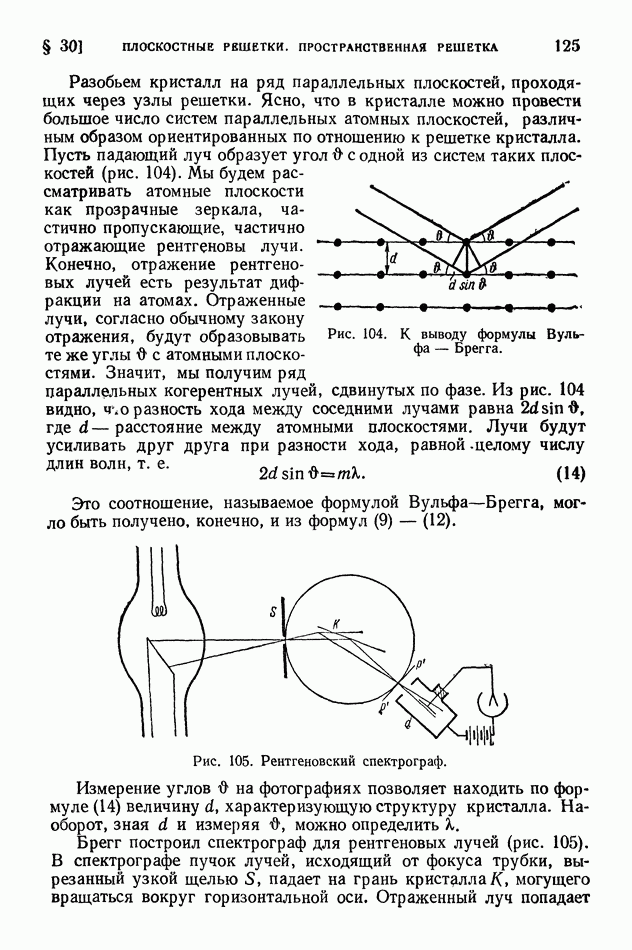
- § 30. Плоскостные решетки. Пространственная решетка
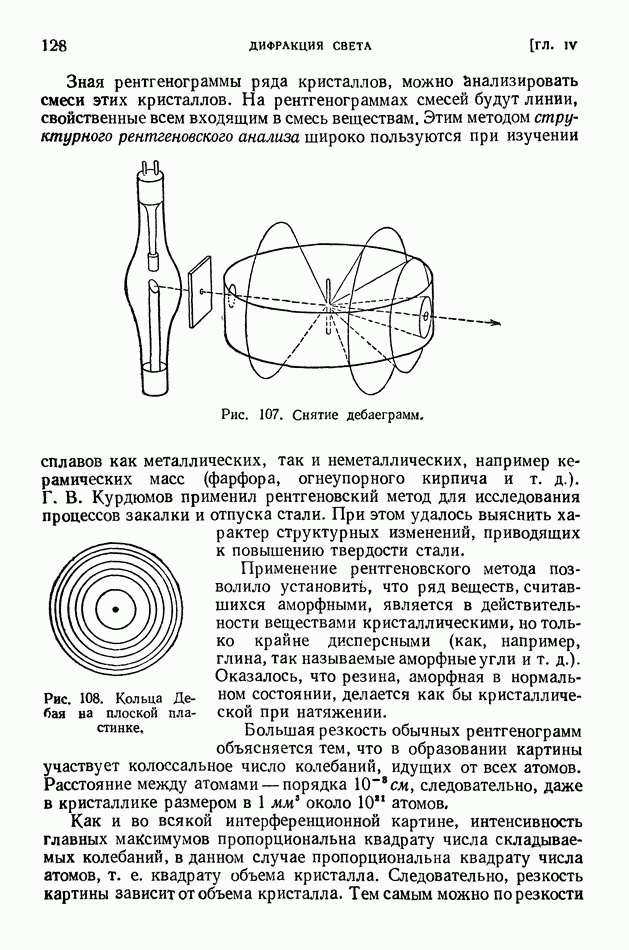
- § 31. Структурный рентгеновский анализ
- § 32. Дифракция света на ультразвуковых волнах
- § 33. Дифракция от мелких частиц
- § 34. Разрешающая способность оптических инструментов. Звездный интерферометр
- ГЛАВА V. ПОЛЯРИЗАЦИЯ СВЕТА
- § 35. Поляризация света
- § 36. Двойное лучепреломление
- § 37. Интерференция поляризованного света
- § 38. Оптический метод исследования упругих натяжений. Эффект Керра
- § 39. Вращение плоскости поляризации. Эллиптическая поляризация
- ГЛАВА VI. ДИСПЕРСИЯ, ПОГЛОЩЕНИЕ И ИЗЛУЧЕНИЕ СВЕТА
- § 40. Отражение света
- § 41. Давление света. Опыты Лебедева
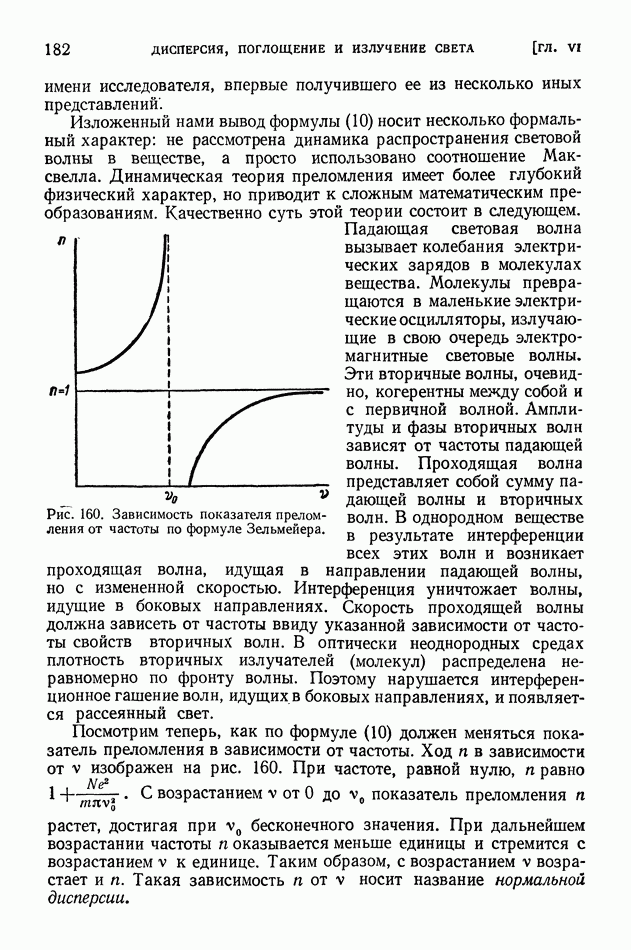
- § 42. Дисперсия. Опыты Ньютона
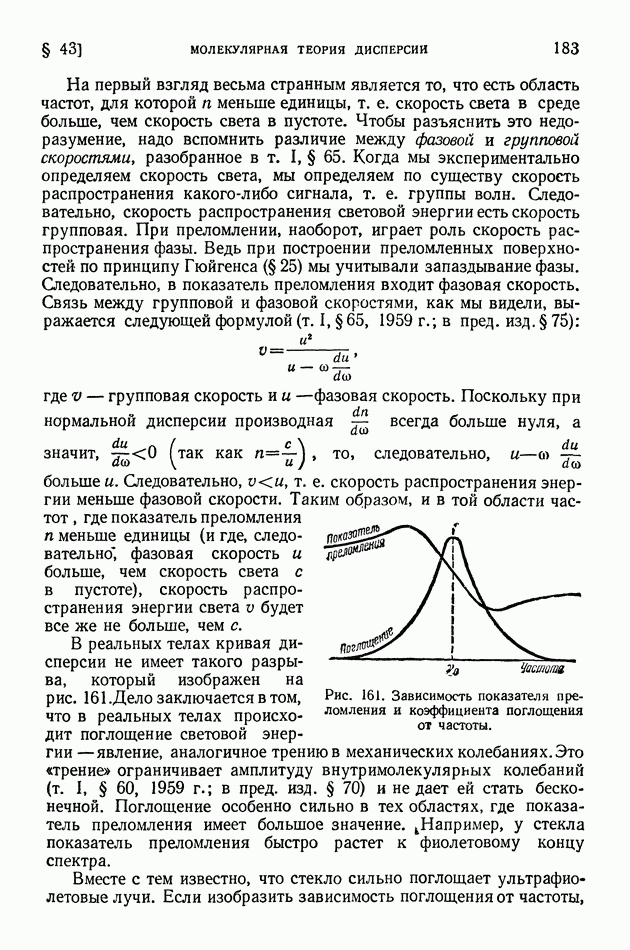
- § 43. Молекулярная теория дисперсии
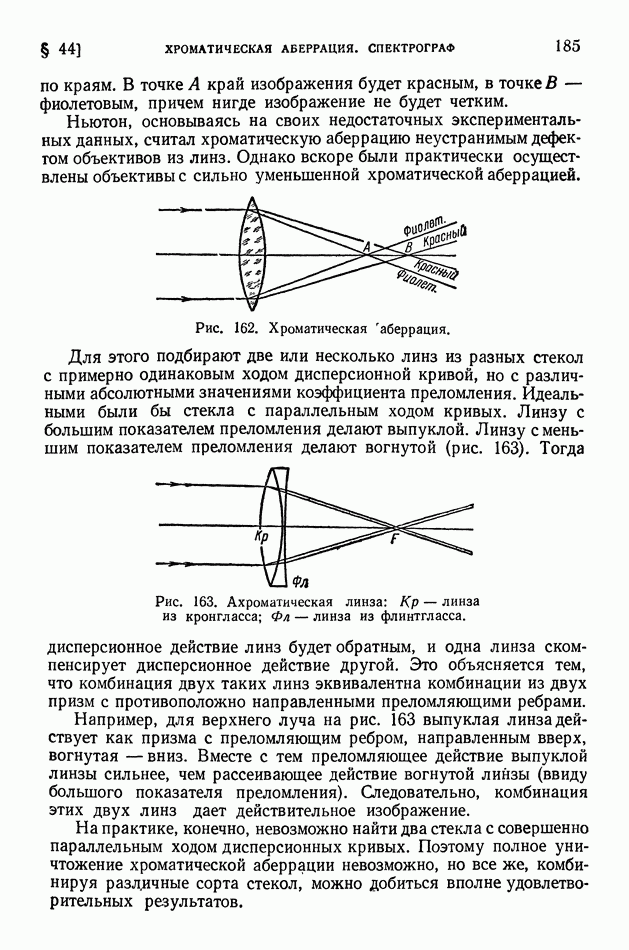
- § 44. Хроматическая аберрация. Спектрограф
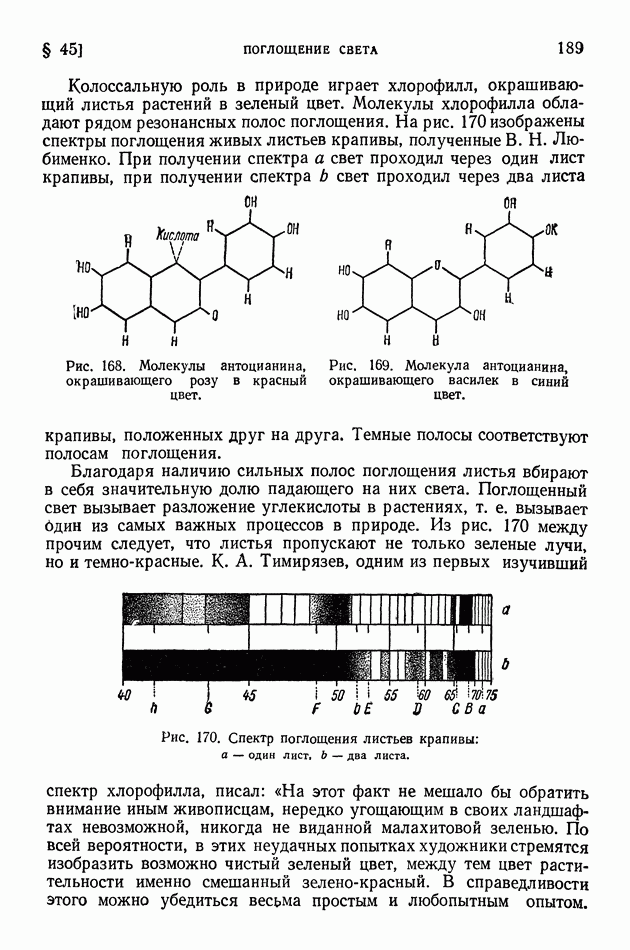
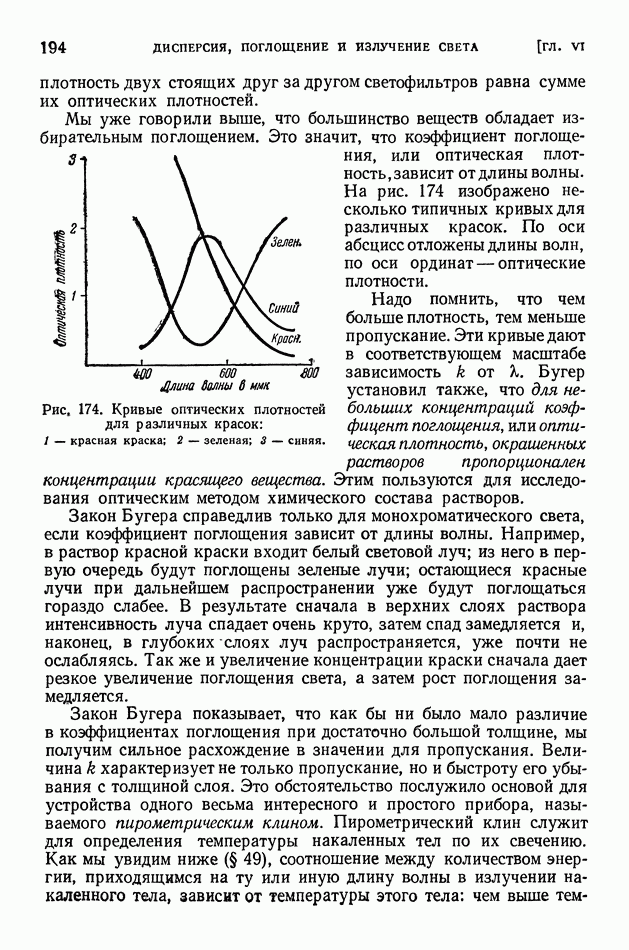
- § 45. Поглощение света
- § 46. Закон Бугера. Опыты Вавилова
- § 47. Атом как элементарный излучатель света
- § 48. Эффект Вавилова — Черенкова
- ГЛАВА VII. ТЕРМОДИНАМИКА ИЗЛУЧЕНИЯ И СВЕТОВОЙ ПОТОК
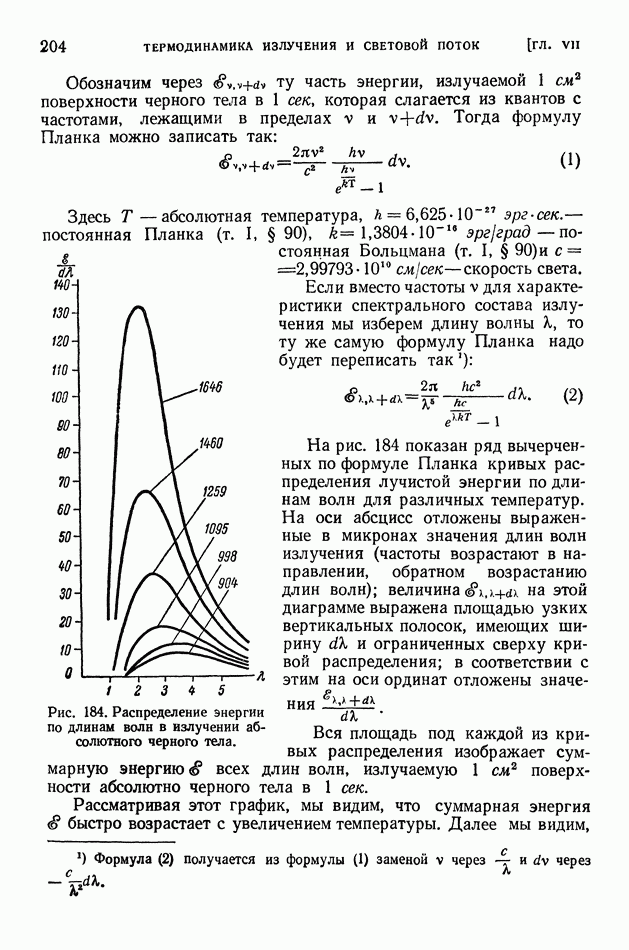
- § 49. Излучение черного тела. Формула Планка. Закон Вина
- § 50. Излучение нечерных тел. Законы Кирхгофа
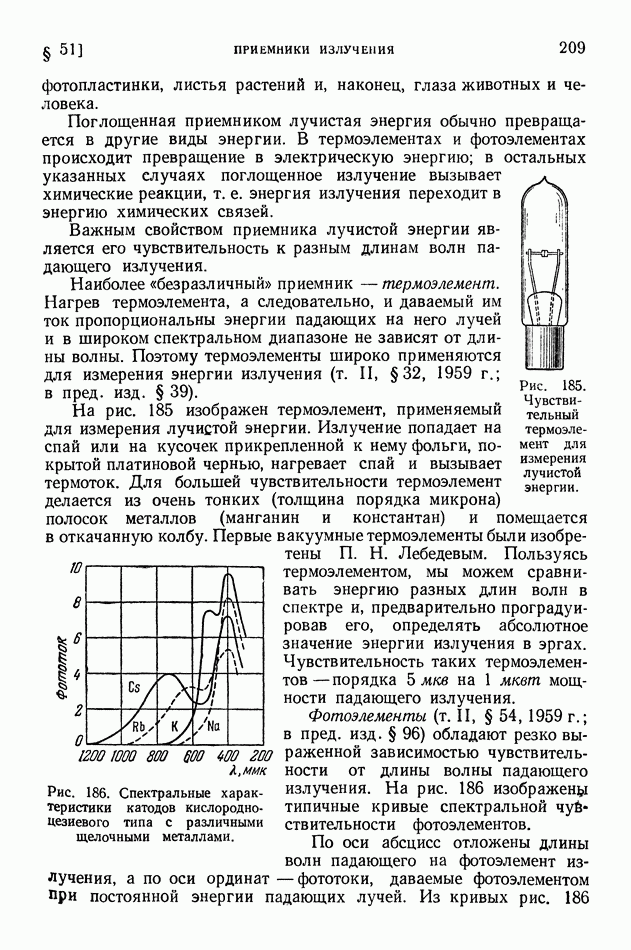
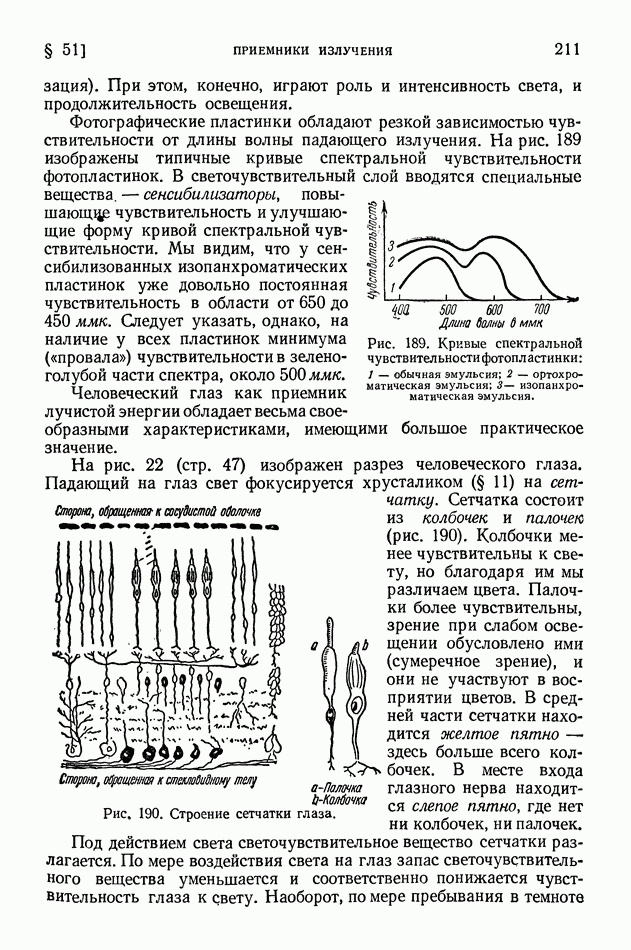
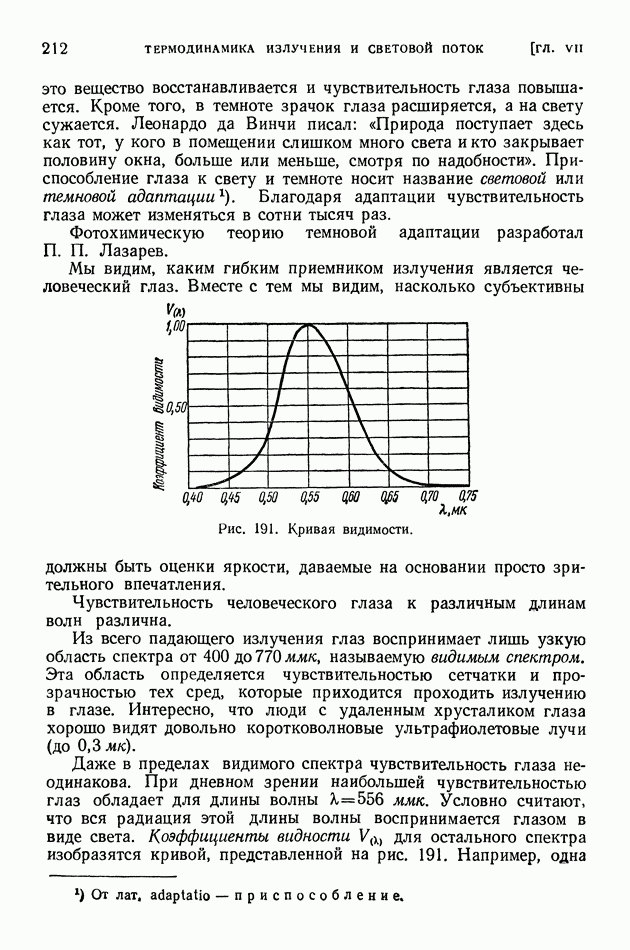
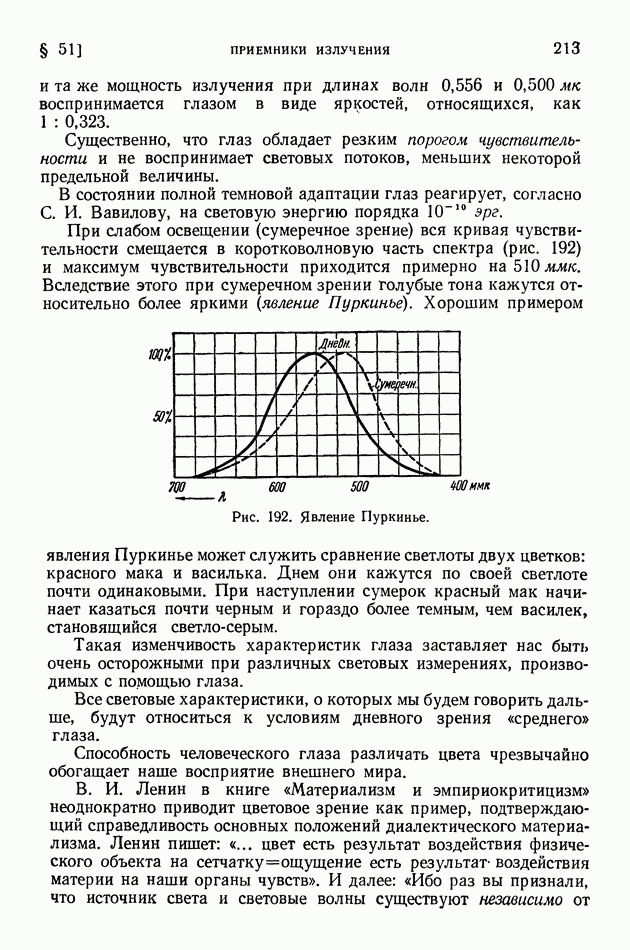
- § 51. Приемники излучения
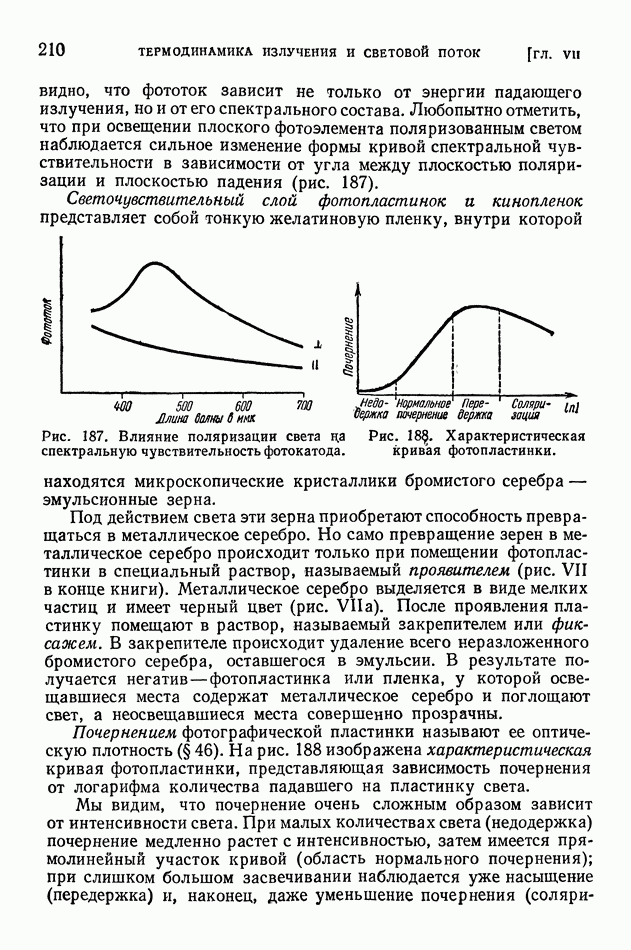
- § 52. Световые величины и их измерения
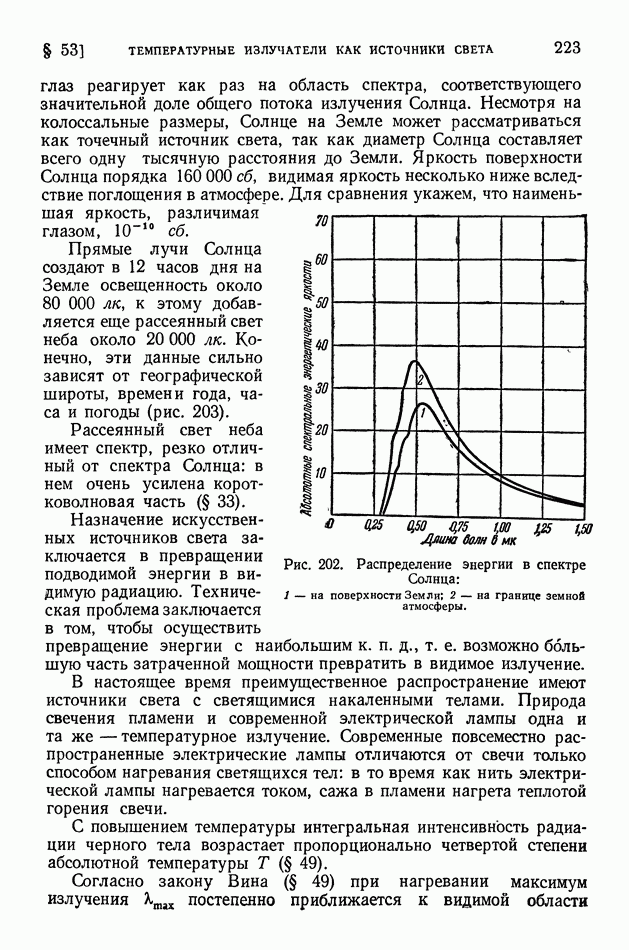
- § 53 Температурные излучатели как источники света
- ЧАСТЬ ПЯТАЯ. АТОМНАЯ ФИЗИКА
- ГЛАВА VIII. СТРОЕНИЕ АТОМА И ТЕОРИЯ БОРА
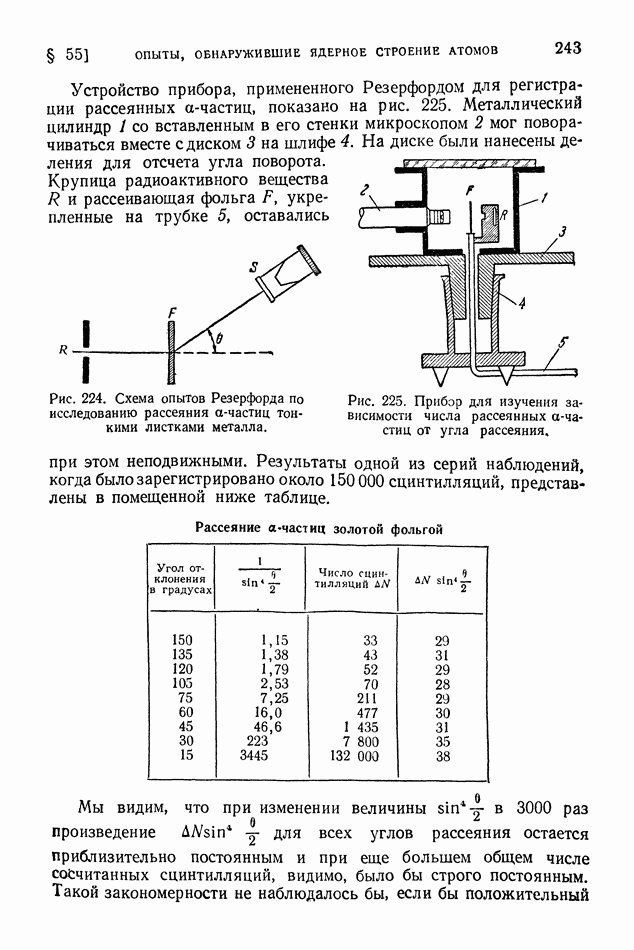
- § 55. Опыты, обнаружившие ядерное строение атомов
- § 56. Противоречие между фактическим строением атомов и выводами классической электродинамики. Строение линейчатых спектров
- § 57. Опытные основания теории квантов в первые годы ее развития
- § 58. Теория Бора. Происхождение спектра водорода
- § 59. Квантовые числа
- § 60. Принцип Паули. Строение электронных оболочек атомов
- § 61. Общая картина возникновения спектров
- ГЛАВА IX. ОСНОВЫ КВАНТОВОЙ (ВОЛНОВОЙ) МЕХАНИКИ
- § 62. Волновые свойства частиц. Формула де Бройля. Дифракция электронов
- § 63. Уравнение Шредингера. Просачивание через энергетический барьер. Нулевая энергия
- § 64. Волномеханическая теория атома водорода
- § 65. Соотношение неопределенностей и его разные трактовки
- ГЛАВА X. КВАНТОВАЯ ОПТИКА
- § 66. Развитие квантовой оптики
- § 67. Спектр щелочных металлов. Спин электрона
- § 68. Спектр гелия. Символика спектральных термов
- § 69. Сверхтонкая структура спектральных линий
- § 70. Атом в силовом поле
- § 71. Молекулярные спектры и строение молекул
- § 72. Комбинационное рассеяние света
- § 73. Квантовая картина испускания света атомами и молекулами
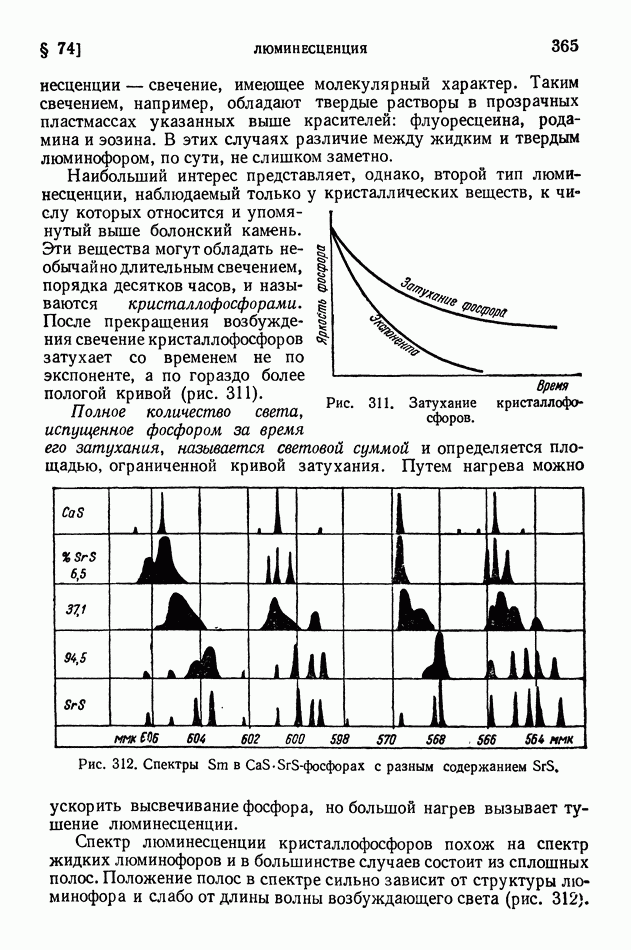
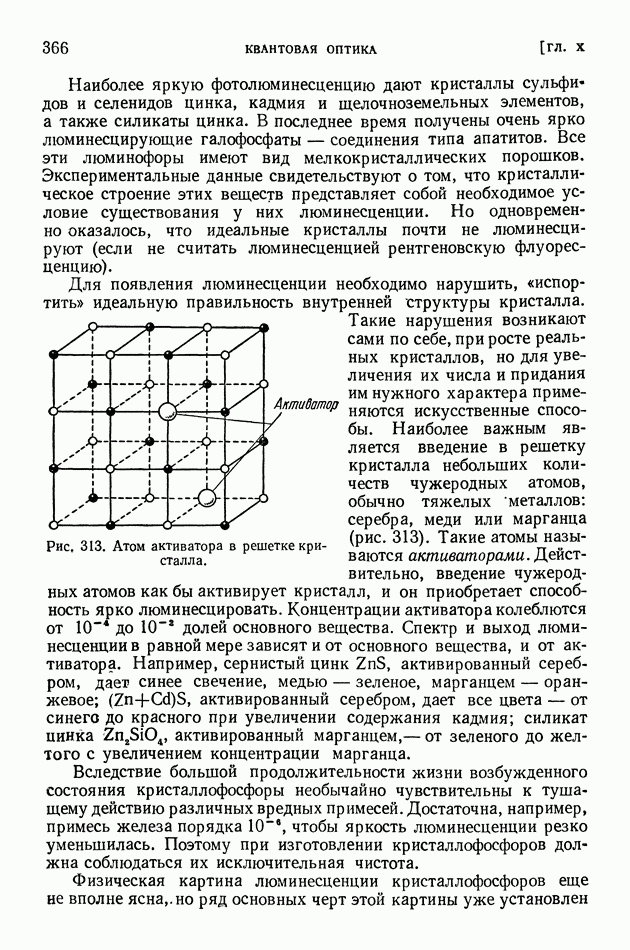
- § 74. Люминесценция
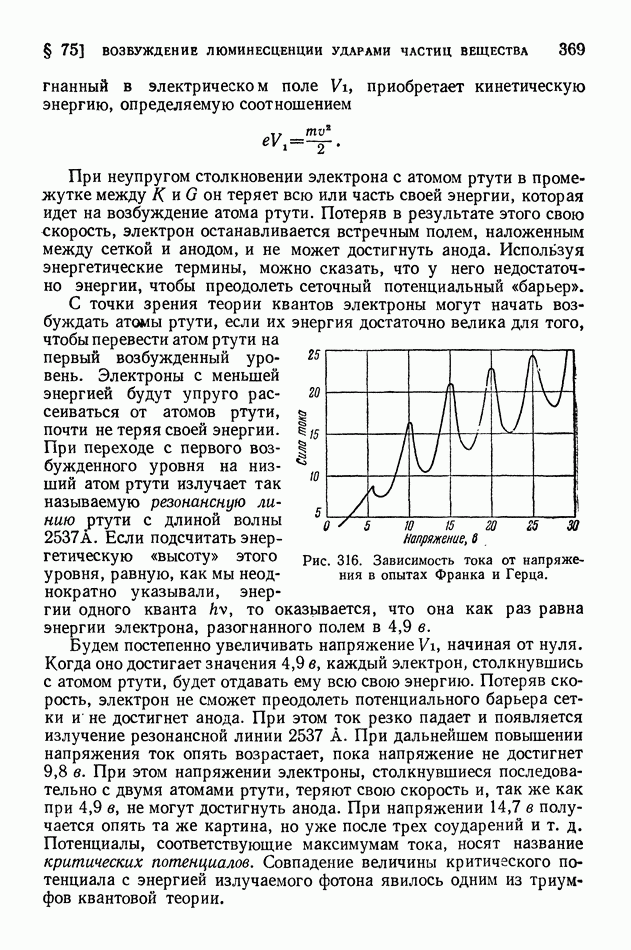
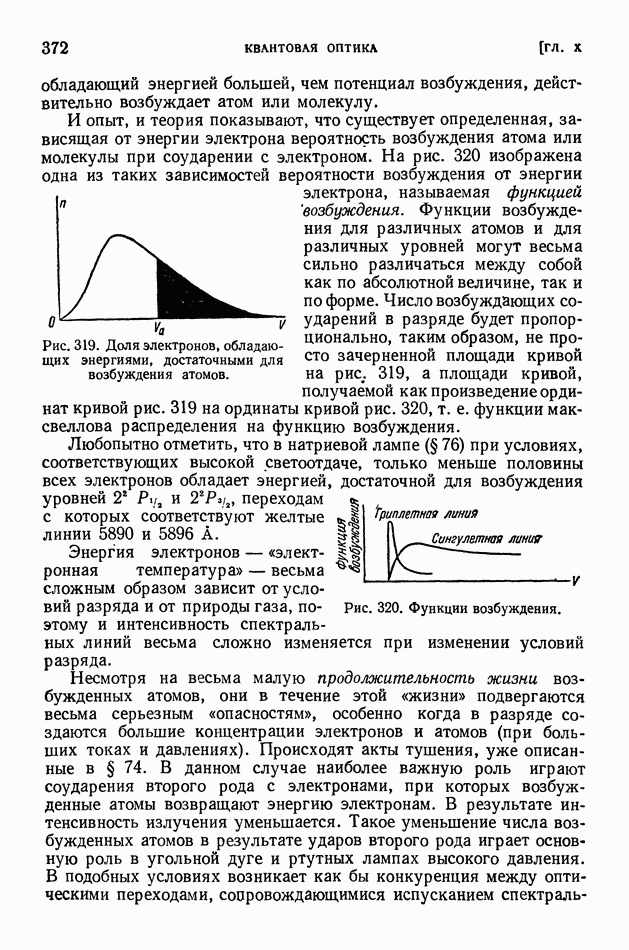
- § 75. Возбуждение люминесценции ударами частиц вещества
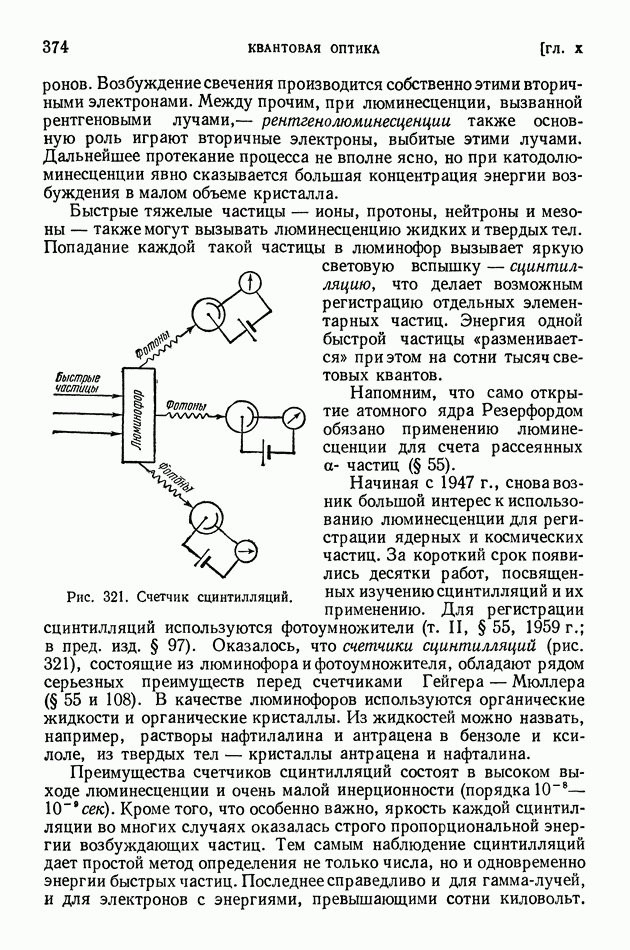
- § 76. Применения люминесценции
- § 77. Фотохимические реакции
- ГЛАВА XI. ЗАКОН ПРОПОРЦИОНАЛЬНОСТИ МАССЫ И ЭНЕРГИИ И РЕЛЯТИВИСТСКИЕ СООТНОШЕНИЯ
- § 78. Закон пропорциональности массы и энергии
- § 79. Предварительные замечания о релятивистских эффектах. Зависимость массы от скорости
- § 80. Корпускулярные свойства фотонов. Явление Комптона
- § 81. Вывод закона Эйнштейна сложения скоростей из закона пропорциональности массы и энергии и законов сохранения энергии или количества движения
- § 82. Две трактовки закона пропорциональности массы и энергии и уточнение закона тяготения
- § 83. Красное смещение спектральных линий. Поперечный эффект Доплера
- § 84. Влияние гравитационного поля на скорость света в вакууме и показатель преломления вакуума
- ЧАСТЬ ШЕСТАЯ. ЯДЕРНАЯ ФИЗИКА
- § 85. Заряд и масса ядра. Масс-спектральный анализ
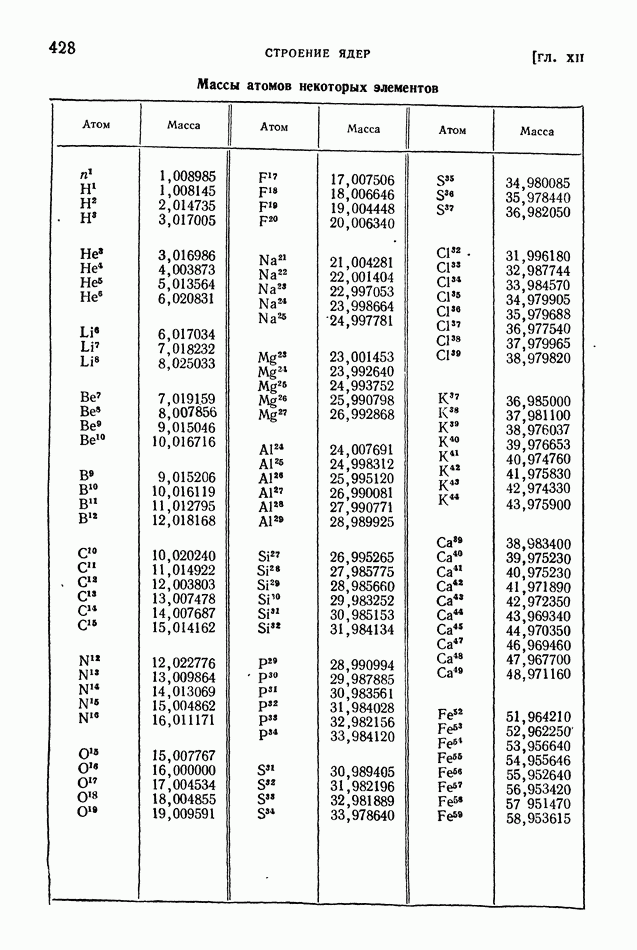
- § 86. Состав ядер. Изотопы. Атомные единицы массы и энергии
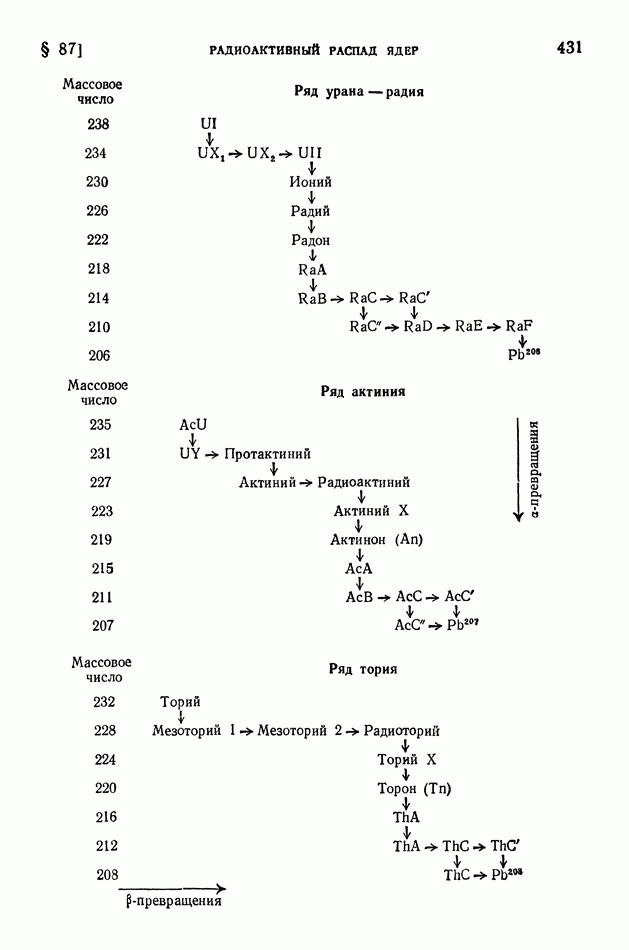
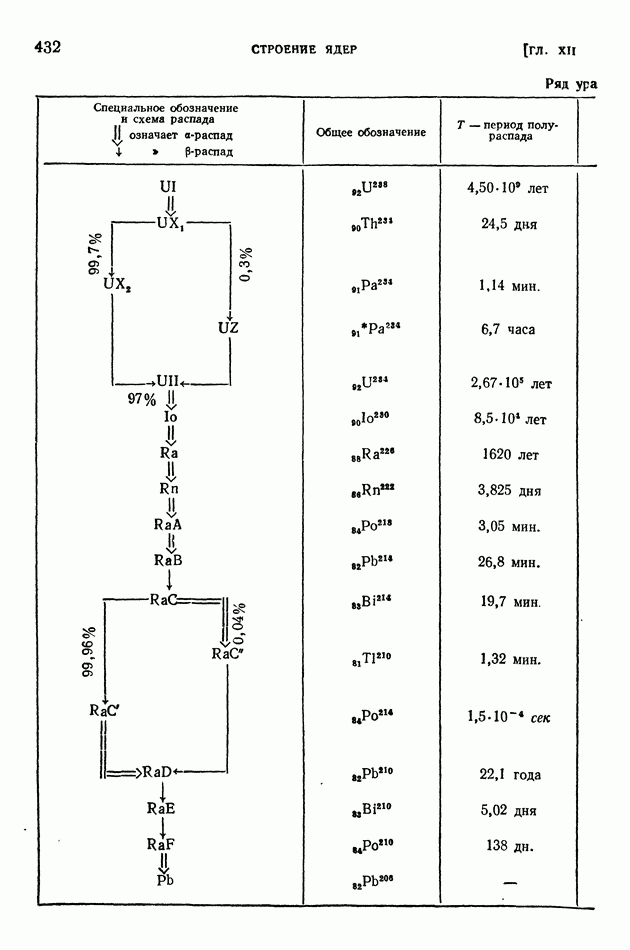
- § 87. Радиоактивный распад ядер. Закон радиоактивного смещения. Изомеры
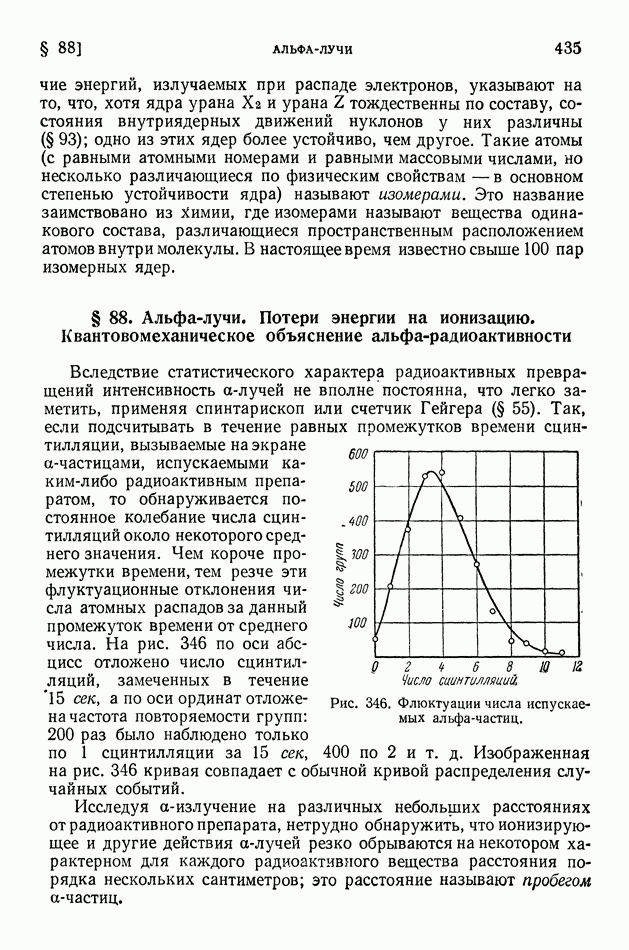
- § 88. Альфа-лучи. Потери энергии на ионизацию. Квантовомеханическое объяснение альфа-радиоактивности
- § 89. Бета- и гамма-лучи
- § 90. Искусственное расщепление ядер. Открытие нейтрона
- § 91. Открытие позитрона. Взаимопревращение фотонов определенной энергии и электронно-позитронных пар
- § 92. Индуцированная позитронная и электронная радиоактивность. Фоторасщепление ядер, K-захват
- § 93. Энергетические уровни ядер. Внутренняя конверсия. Нейтрино
- § 94. Капельная теория строения ядер
- § 95. Деление ядер и развитие капельной теории строения ядер
- ГЛАВА XIII. КОСМИЧЕСКИЕ ЛУЧИ
- § 96. Методы исследования и первые итоги изучения космических лучей
- § 97. Каскадное образование электронно-позитронных пар в космических лучах. Потери энергии электронами на тормозное излучение
- § 98. «мю»-мезоны. Зависимость времени жизни неустойчивых частиц от скорости движения
- § 99. «пи»-мезоны
- § 100. Взрывные ядерные ливни и их каскадное развитие в космических лучах
- § 101. Корпускулярный и энергетический спектр космических лучей. Происхождение космического излучения
- ГЛАВА XIV. ЭКСПЕРИМЕНТАЛЬНЫЕ СРЕДСТВА ЯДЕРНОЙ ФИЗИКИ
- § 102. Циклотроны
- § 103. Фазотроны
- § 104. Бетатроны
- § 105. Синхротроны и синхрофазотроны
- § 106. Линейные ускорители электронов и ионов
- § 107. Лабораторные источники нейтронов. Замедлители нейтронов в ядерных реакторах
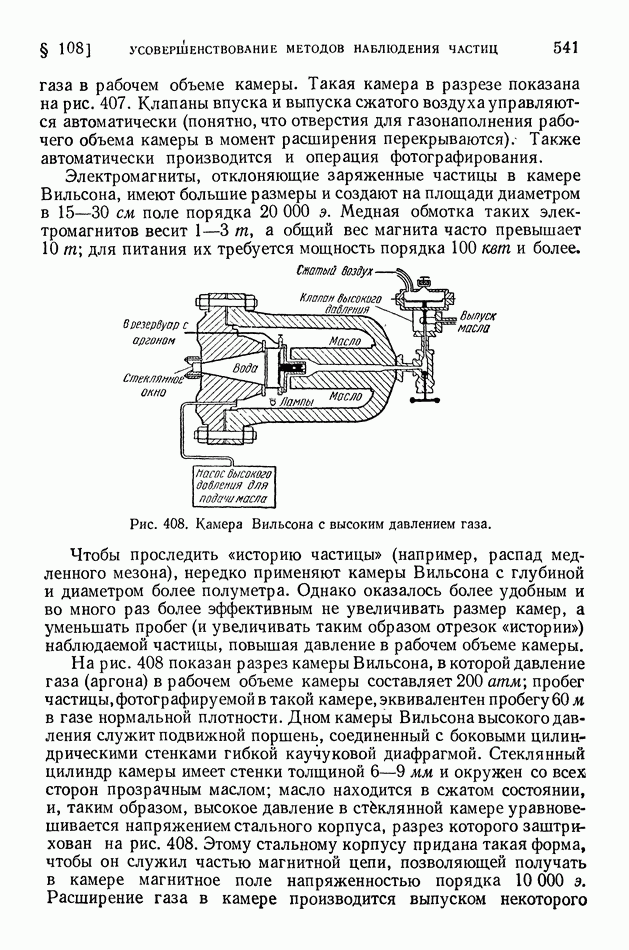
- § 108. Усовершенствование методов наблюдения и счета частиц
- ГЛАВА XV. ЯДЕРНЫЕ РЕАКЦИИ И АТОМНАЯ ЭНЕРГИЯ
- § 109. Основные виды и обозначения ядерных реакций. Конкурирующие процессы в ядерных реакциях
- § 110. Энергетический эффект, энергия возбуждения и порог ядерных реакций
- § 111. Превращения элементарных частиц
- § 112. Ядерные силы
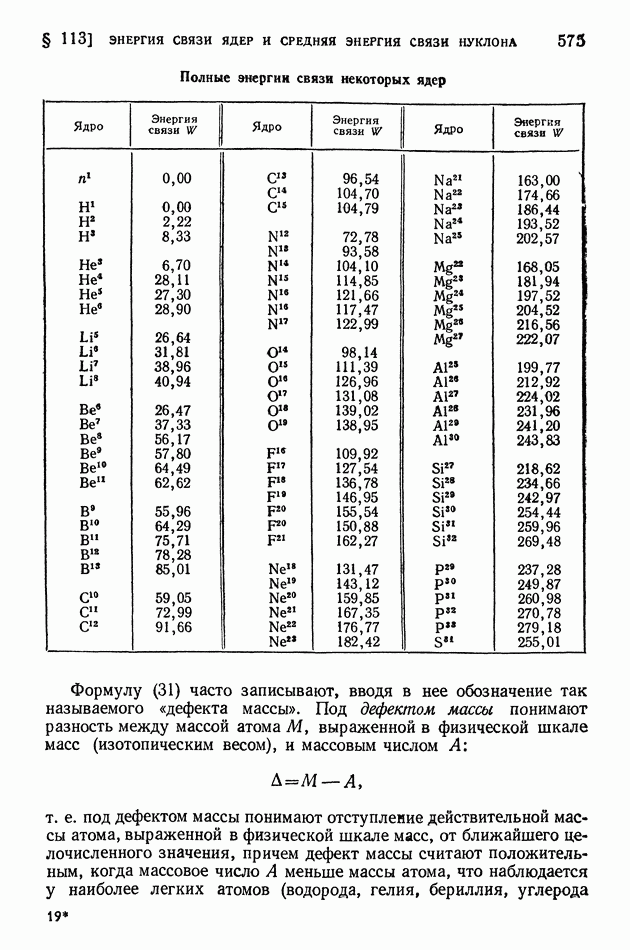
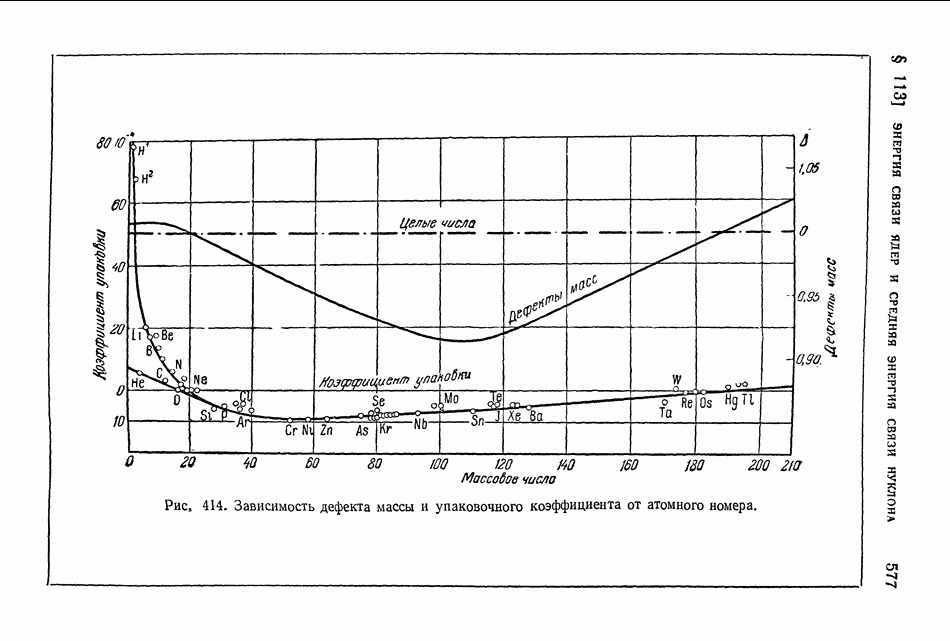
- § 113. Энергия связи ядер и средняя энергия связи нуклона
- § 114. Полуэмпирическая формула для энергии ядерной связи и для атомных энергий и масс
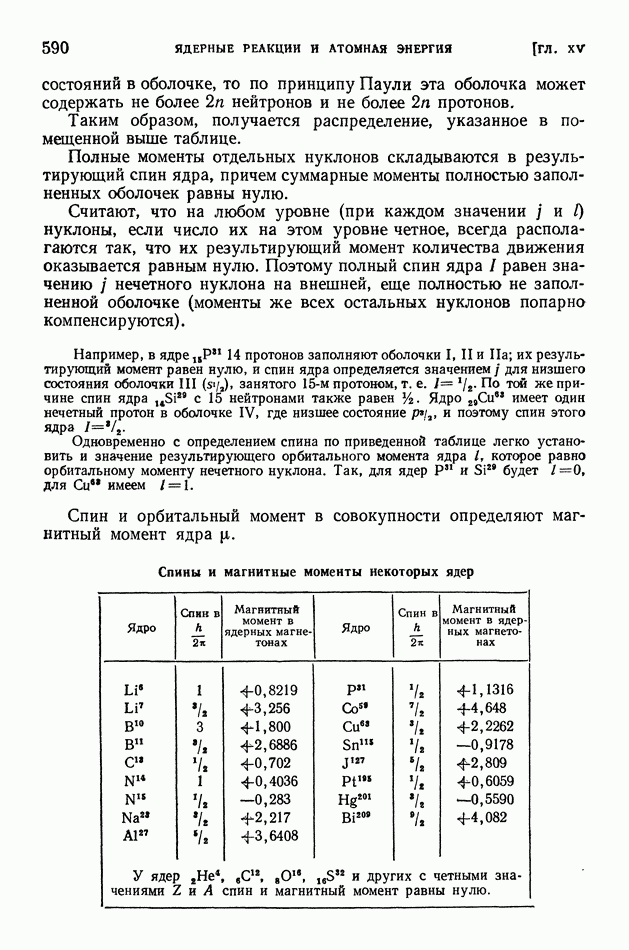
- § 115. Взаимосвязь энергии и строения ядер. Внутриядерное движение нуклонов и нуклонные оболочки. Спины и магнитные моменты ядер
- § 116. Энергия отделения частиц и анализ возможного хода ядерной реакции
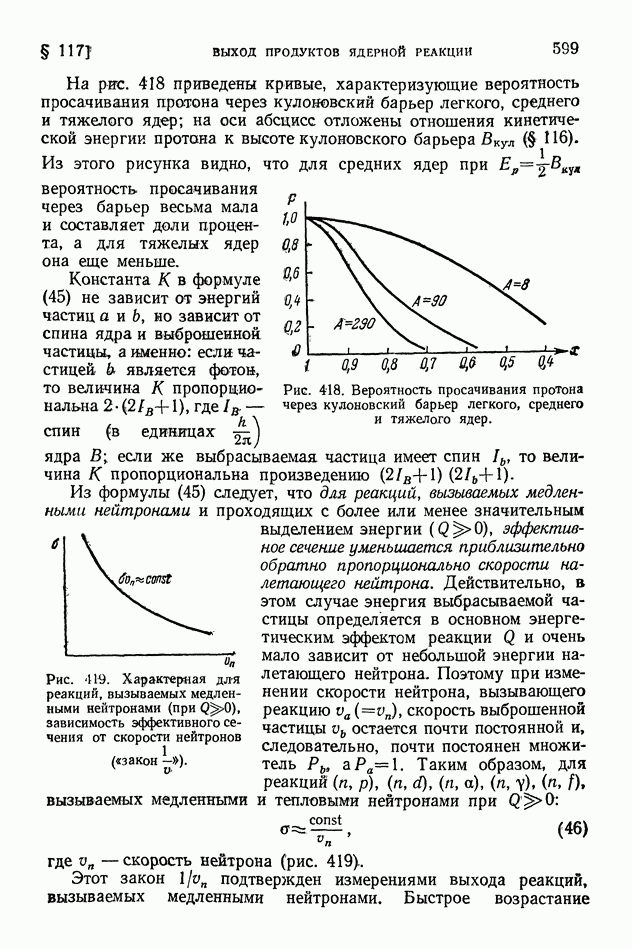
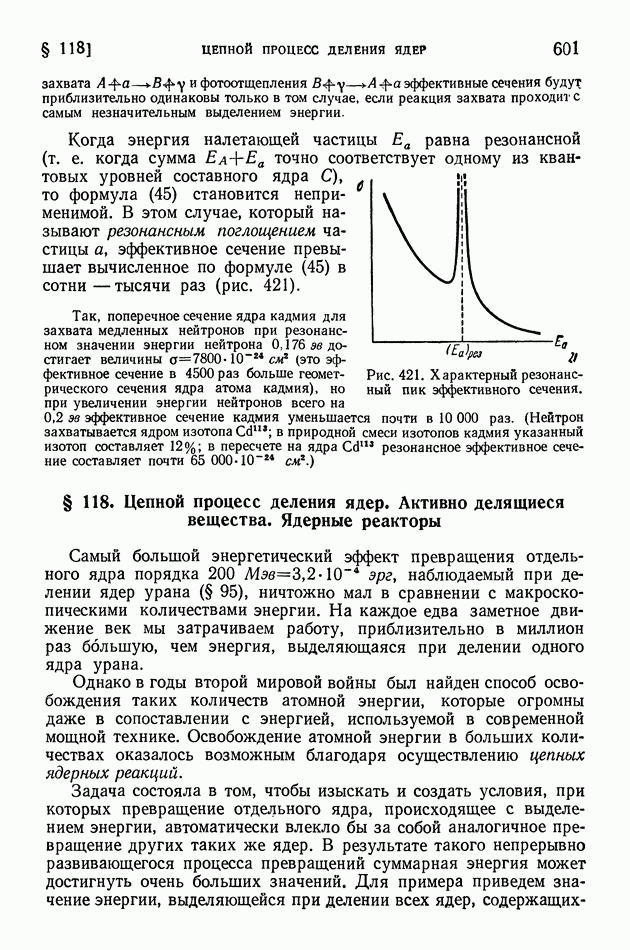
- § 117. Выход продуктов ядерной реакции. Эффективные сечения. Резонансные явления
- § 118. Цепной процесс деления ядер. Активно делящиеся вещества. Ядерные реакторы
- § 119. Термоядерные реакции
- § 120. Применение ядерных реакций
- § 121. Ядерные реакции в звездах