| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Гипербола и ее асимптоты.
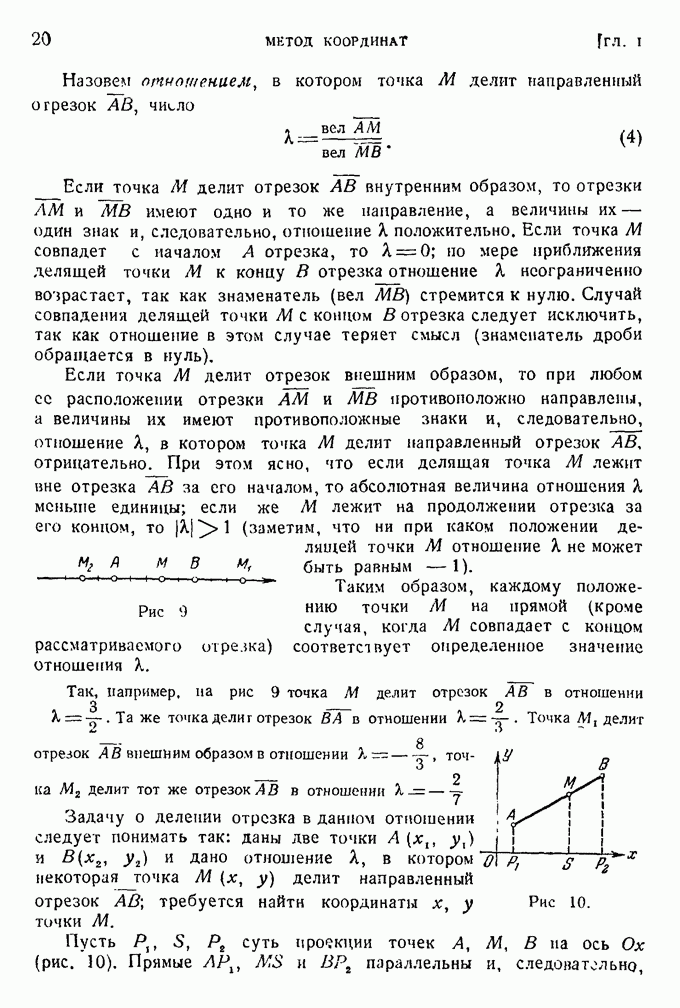
Гиперболой называется геометрическое место точек, разность расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (эта постоянная должна быть положительной и меньше расстояния между фокусами).
Обозначим эту постоянную через 2а, расстояние между фокусами через  и выберем оси координат так же, как и в § 3. Пусть
и выберем оси координат так же, как и в § 3. Пусть  — произвольная точка гиперболы.
— произвольная точка гиперболы.
По определению гиперболы

В правой части равенства нужно выбрать знак плюс, если  и знак минус, если
и знак минус, если 
Так как  то последнее равенство можно записать в виде:
то последнее равенство можно записать в виде:

Это и есть уравнение гиперболы в выбранной системе координат.
Освобождаясь в этом уравнении от радикалов (как и в § 3), можно привести уравнение к простейшему виду.
Перенося первый радикал в правую часть равенства и возводя обе части в квадрат, после очевидных преобразований получим:

Возведя еще раз обе части равенства в квадрат, сделав приведение подобных членов и разделив на свободный член, получим:

Так как  , то величина
, то величина  положительна. Обозначая ее через
положительна. Обозначая ее через  , т. е. полагая
, т. е. полагая

получим каноническое уравнение гиперболы.

Исследуем форму гиперболы.
1) Симметрии гиперболы. Так как уравнение (3) содержит только квадраты текущих координат, то оси координат являются осями симметрии гиперболы (см. аналогичное утверждение для эллипса). Ось симметрии гиперболы, на которой располагаются фокусы, называется фокальной осью. Точка пересечения осей симметрии — центр симметрии — называется центром гиперболы. Для гиперболы, заданной уравнением (3), фокальная ось совпадает с осью Ох, а центром является начало координат.
2) Точки пересечения с осями симметрии. Найдем точки пересечения гиперболы с осями симметрии — вершины гиперболы. Полагая в ураннении  найдем абсциссы точек пересечения гиперболы с осью
найдем абсциссы точек пересечения гиперболы с осью 

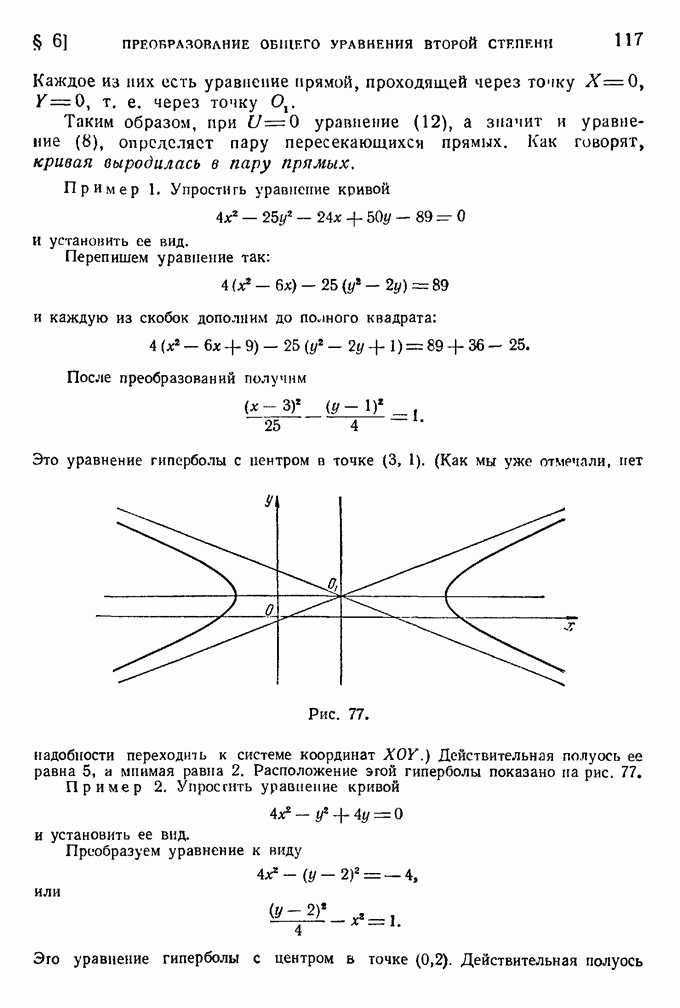
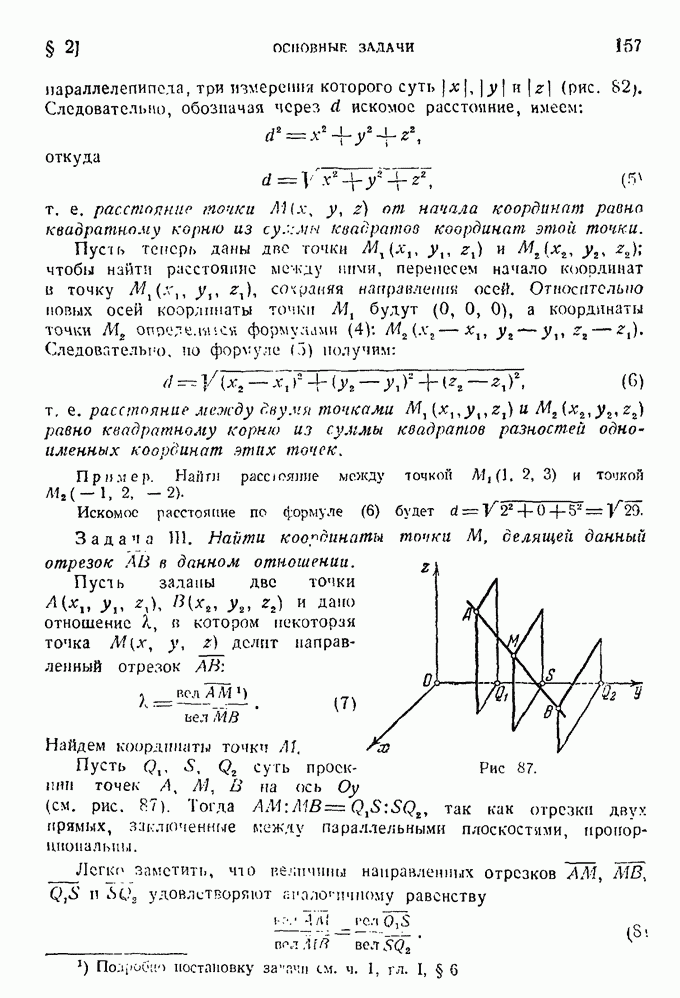
Следовательно, точки  являются вершинами гиперболы (рис. 51); расстояние между ними равно 2а. Чтобы найти точки пересечения с осью Оу, положим в уравнении
являются вершинами гиперболы (рис. 51); расстояние между ними равно 2а. Чтобы найти точки пересечения с осью Оу, положим в уравнении  Получим для определения ординат этих точек уравнение
Получим для определения ординат этих точек уравнение

откуда

т. е. для у мы получили мнимые значения; это означает, что ось Оу не пересекает гиперболы.

Рис. 51.
В соответствии с этим ось симметрии, пересекающая гиперболу, называется действительной осью симметрии (фокальной осью), ось симметрии, которая не пересекает гиперболы, называется мнимой осью симметрии. Для гиперболы, заданной уравнением (3), действительной осью симметрии является ось  , мнимой осью симметрии — ось
, мнимой осью симметрии — ось  Отрезок
Отрезок  соединяющий вершины гиперболы, а также его длина 2а называются действительной осью гиперболы. Если на мнимой оси симметрии гиперболы отложить в обе стороны от ее центра О отрезки ОБ, и
соединяющий вершины гиперболы, а также его длина 2а называются действительной осью гиперболы. Если на мнимой оси симметрии гиперболы отложить в обе стороны от ее центра О отрезки ОБ, и  длиною b, то отрезок
длиною b, то отрезок  а также его длина
а также его длина  называются мнимой осью гиперболы. Величины а и b называются соответственно действительной и мнимой полуосями гиперболы.
называются мнимой осью гиперболы. Величины а и b называются соответственно действительной и мнимой полуосями гиперболы.
3) Форма гиперболы. При исследовании формы гиперболы достаточно рассматривать положительные значения х и у, потому что кривая симметрично расположена относительно осей координат.
Так как из уравнения (3) следует, что 1, то  может изменяться от а до Когда
может изменяться от а до Когда  увеличивается от а до
увеличивается от а до  то У тоже увеличивается от 0 до
то У тоже увеличивается от 0 до  Кривая имеет форму, изображенную на рис. 51. Она располагается вне полосы, ограниченной прямыми
Кривая имеет форму, изображенную на рис. 51. Она располагается вне полосы, ограниченной прямыми  и состоит из двух отдельных ветвей. Для любой точки М одной из этих ветвей
и состоит из двух отдельных ветвей. Для любой точки М одной из этих ветвей  (правая ветвь), для любой точки М другой ветви
(правая ветвь), для любой точки М другой ветви  (левая ветвь).
(левая ветвь).
4) Асимптоты гиперболы. Чтобы более ясно представить себе вид гиперболы, рассмотрим две прямые линии, тесно с нею связанные — так называемые асимптоты.
Предполагая х и у положительными, разрешим уравнение (3) гиперболы относительно ординаты у:


Сопоставим уравнение  с уравнением прямой линии
с уравнением прямой линии  называя соответствующими две точки
называя соответствующими две точки  расположенные соответственно на этой прямой и на гиперболе и имеющие одну и ту же абсциссу
расположенные соответственно на этой прямой и на гиперболе и имеющие одну и ту же абсциссу  (рис. 51). Очевидно, и разность Y — у ординат соответствующих точек выражает расстояние между ними, т. е.
(рис. 51). Очевидно, и разность Y — у ординат соответствующих точек выражает расстояние между ними, т. е. 
Покажем, что при неограниченном возрастании  расстояние MN, убивая, стремится к нулю. В самом деле,
расстояние MN, убивая, стремится к нулю. В самом деле,

откуда

После упрощения получим:

Из последней формулы мы усматриваем, что при неограниченном возрастании абсциссы  расстояние MN убывает и стремится к нулю. Отсюда следует, что когда точка М, двигаясь по гиперболе в первом квадранте, удаляется в бесконечность, то ее расстояние до прямой
расстояние MN убывает и стремится к нулю. Отсюда следует, что когда точка М, двигаясь по гиперболе в первом квадранте, удаляется в бесконечность, то ее расстояние до прямой  уменьшается и стремится к нулю. То же обстоятельство будет иметь место при движении точки М по гиперболе в третьем квадранте (вследствие симметрии относительно начала координат О).
уменьшается и стремится к нулю. То же обстоятельство будет иметь место при движении точки М по гиперболе в третьем квадранте (вследствие симметрии относительно начала координат О).
Наконец, вследствие симметрии гиперболы относительно оси Оу мы получим вторую прямую  симметрично расположенную с прямой
симметрично расположенную с прямой  к которой также будет неограниченно приближаться точка М при движении по гиперболе и удалении в бесконечность (во втором и четвертом квадрантах).
к которой также будет неограниченно приближаться точка М при движении по гиперболе и удалении в бесконечность (во втором и четвертом квадрантах).
Эти две прямые линии носят название асимптот гиперболы, они, как мы видели, имеют уравнения:

Очевидно, асимптоты гиперболы располагаются по диагоналям прямоугольника, одна сторона которого параллельна оси Ох и равна 2а, другая — параллельна оси Оу и равна  а центр лежит в начале координат (см. рис. 51).
а центр лежит в начале координат (см. рис. 51).
При вычерчивании гиперболы по ее уравнению рекомендуется предварительно построить ее асимптоты.
Равносторонняя гипербола. В случае  гипербола называется равносторонней; ее уравнение получается из (3) и имеет вид:
гипербола называется равносторонней; ее уравнение получается из (3) и имеет вид:

Очевидно, угловые коэффициенты асимптот  для равносторонней гиперболы будут
для равносторонней гиперболы будут  Следовательно, асимптоты равносторонней гиперболы перпендикулярны между собой и делят пополам углы между ее осями симметрии.
Следовательно, асимптоты равносторонней гиперболы перпендикулярны между собой и делят пополам углы между ее осями симметрии.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- ГЛАВА I. МЕТОД КООРДИНАТ
- § 2. Координаты на прямой линии.
- § 3. Расстояние между двумя точками на прямой линии.
- § 4. Прямоугольные координаты на плоскости.
- § 5. Расстояние между двумя точками на плоскости.
- § 6. Деление отрезка в данном отношении.
- § 7. Угол между двумя осями.
- § 8. Основные положения теории проекций.
- § 9. Проекции направленного отрезка на оси координат.
- § 10. Площадь треугольника.
- § 11. Полярные координаты.
- Упражнения
- ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ
- § 1. Составление уравнений заданных линий.
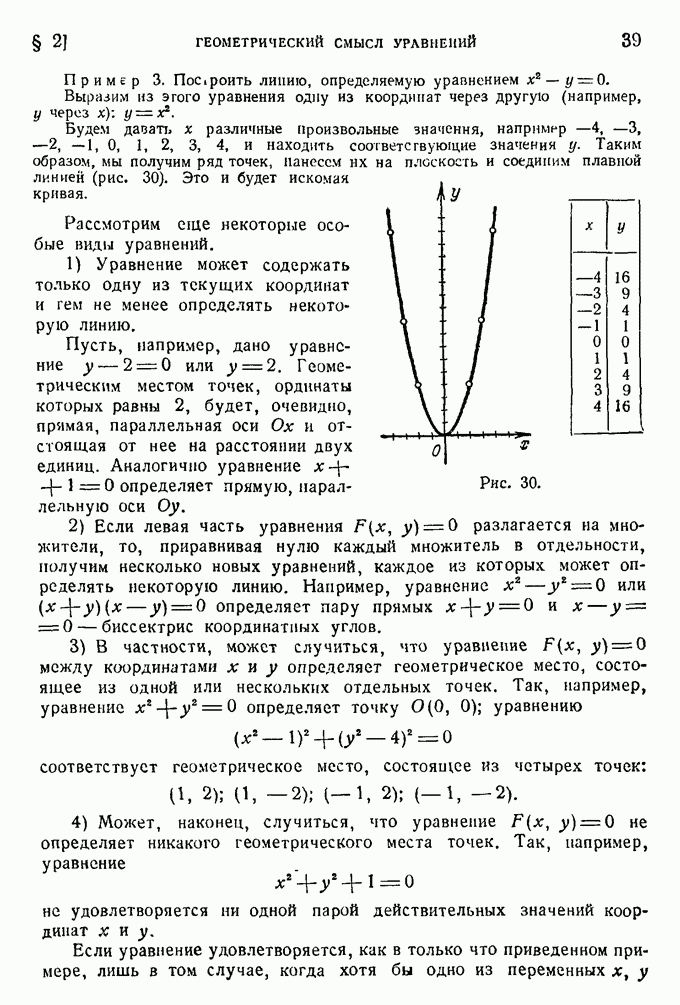
- § 2. Геометрический смысл уравнений.
- § 3. Две основные задачи.
- § 4. Пересечение двух линий.
- § 5. Параметрические уравнения линий.
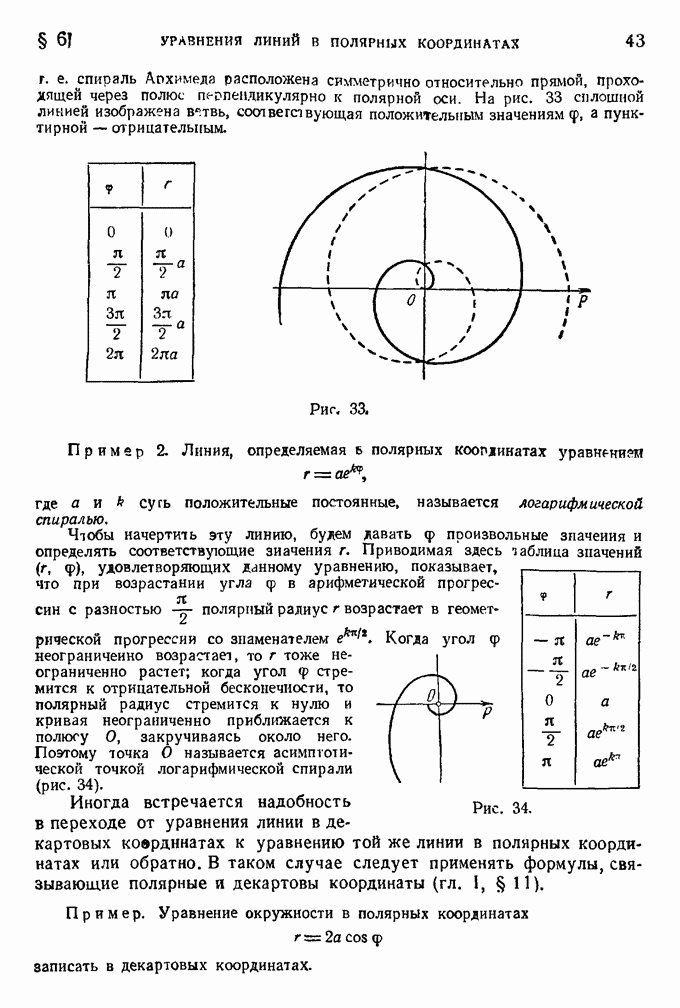
- § 6. Уравнения линий в полярных координатах.
- ГЛАВА III. ПРЯМАЯ ЛИНИЯ
- § 1. Угловой коэффициент прямой.
- § 2. Уравнение прямой линии с угловым коэффициентом.
- § 3. Геометрический смысл уравнения первой степени между двумя переменными.
- § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0.
- § 5. Уравнение прямой линии в отрезках.
- § 6. Построение прямой линии по ее уравнению.
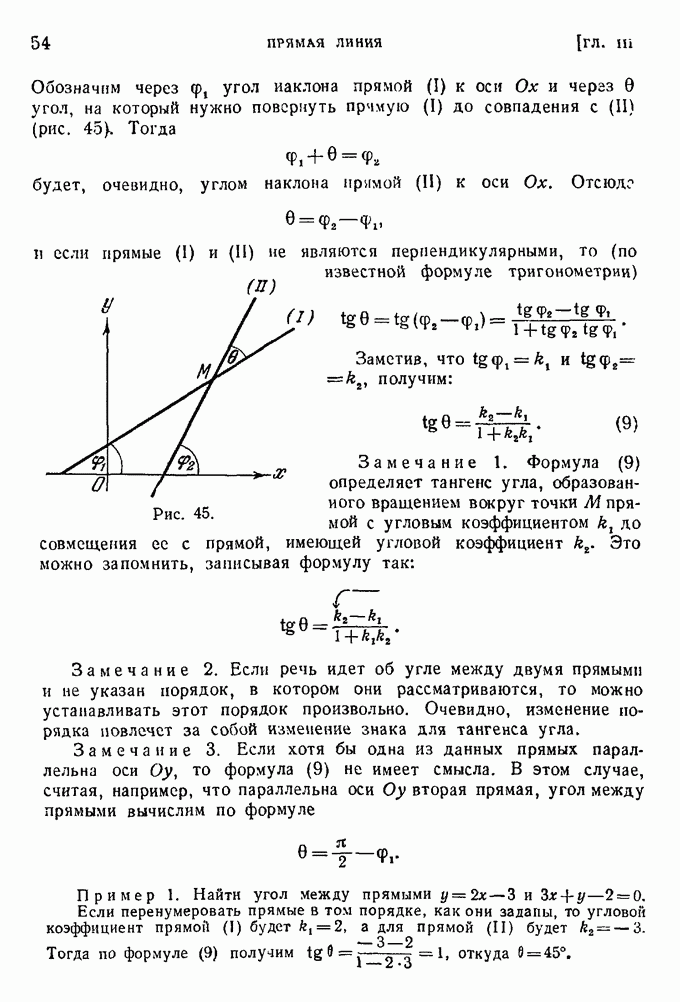
- § 7. Угол между двумя прямыми.
- § 8. Условия параллельности и перпендикулярности двух прямых.
- § 9. Уравнение прямой, проходящей через данную точку в данном направлении.
- § 10. Взаимное расположение двух прямых на плоскости.
- § 11. Уравнение пучка прямых.
- § 12. Уравнение прямой, проходящей через две данные точки.
- § 13. Условие, при котором три данные точки лежат на одной прямой.
- § 14. Нормальное уравнение прямой линии.
- § 15. Приведение общего уравнения первой степени к нормальному виду.
- § 16. Расстояние от дайной точки до данной прямой.
- § 17. Уравнение прямой в полярной системе координат.
- Упражнения
- ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ
- § 2. Окружность.
- § 3. Эллипс.
- § 4. Гипербола и ее асимптоты.
- § 5. Парабола.
- § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки.
- § 7. Эллипс, гипербола и парабола как конические сечения.
- § 8. Эксцентриситет и директрисы эллипса.
- § 9. Эксцентриситет и директрисы гиперболы.
- § 10. Эксцентриситет и директриса параболы.
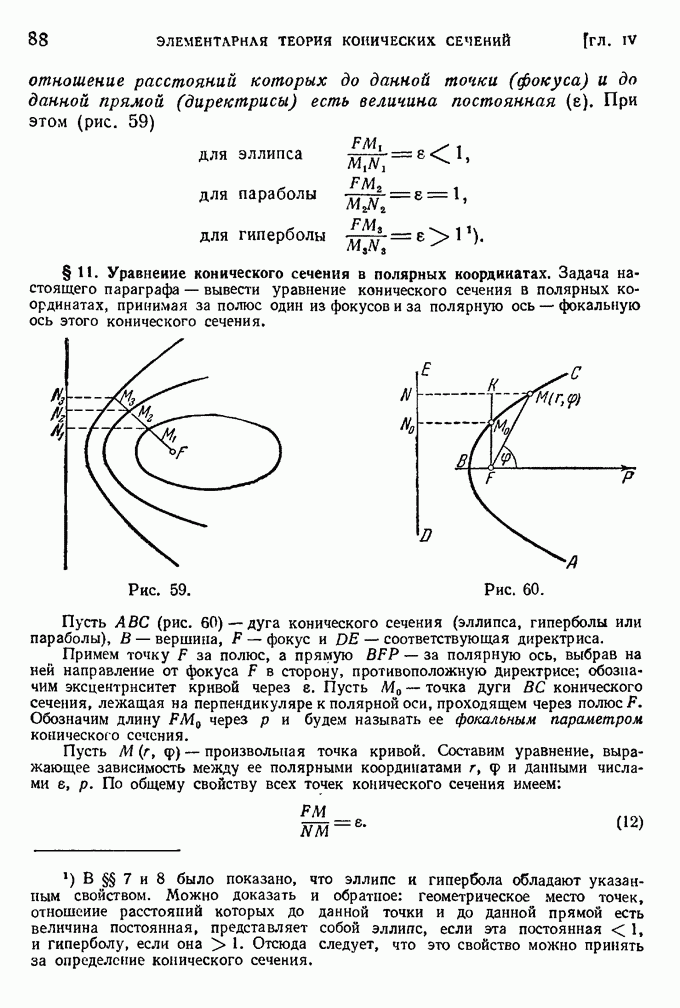
- § 11. Уравнение конического сечения в полярных координатах.
- § 12. Диаметры зллипса. Сопряженные диаметры.
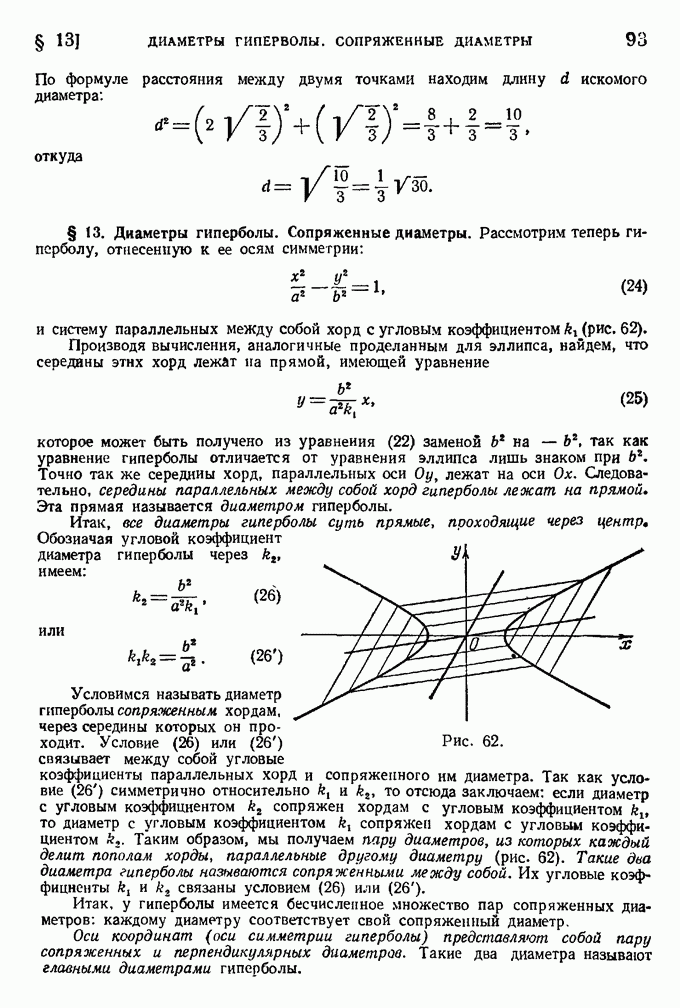
- § 13. Диаметры гиперболы. Сопряженные диаметры.
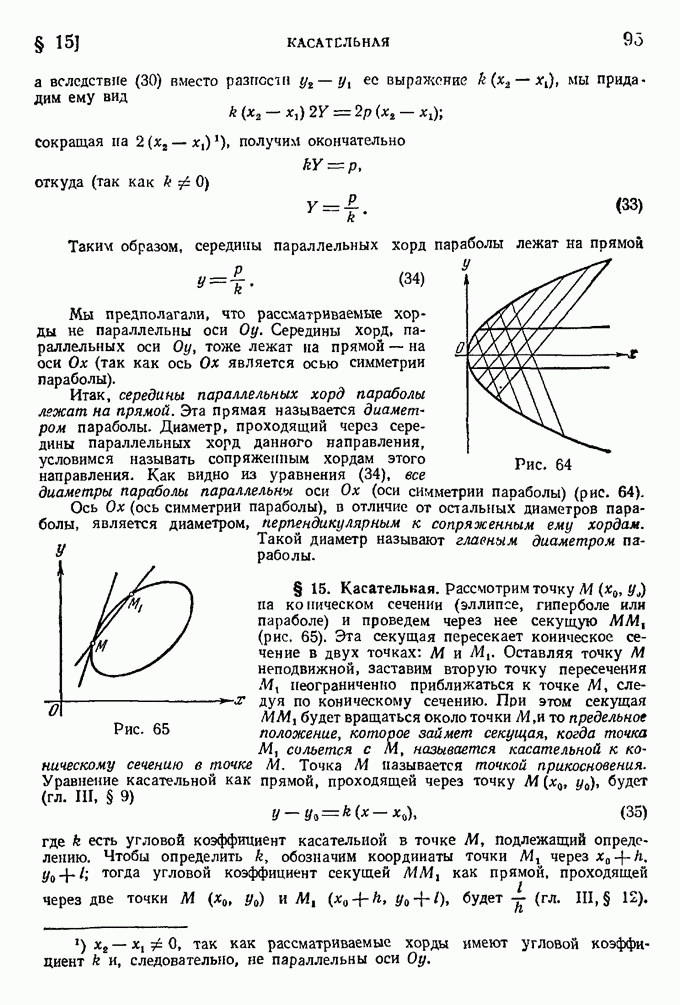
- § 14. Диаметры параболы.
- § 15. Касательная.
- § 16. Эллипс как проекция окружности.
- § 17. Параметрические уравнения эллипса.
- Упражнения
- ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ
- § 2. Перенос начала координат.
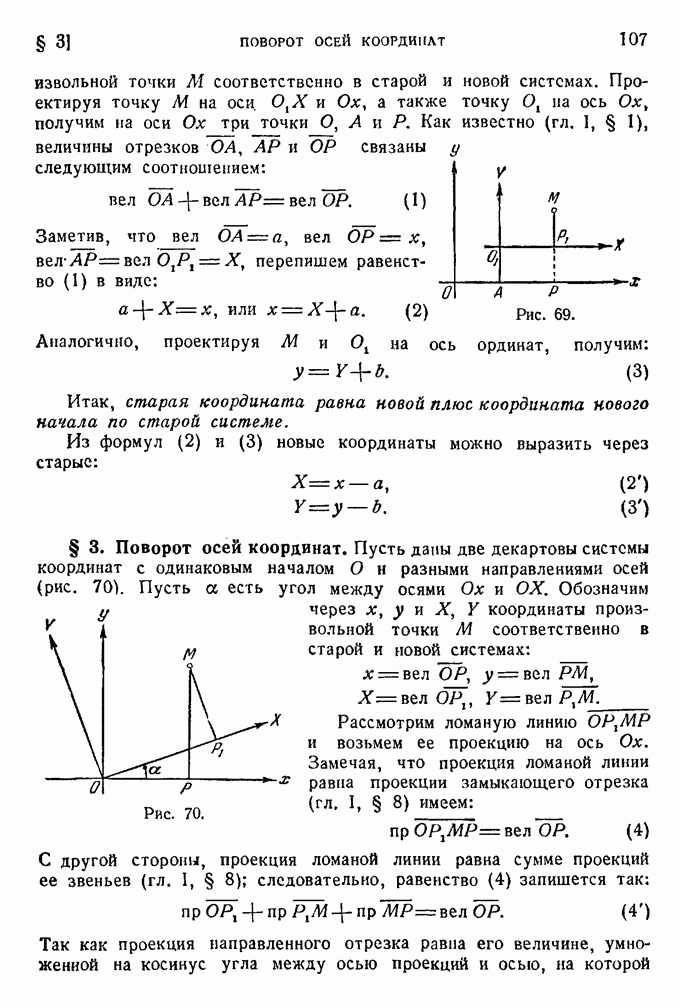
- § 3. Поворот осей координат.
- § 4. Общий случай.
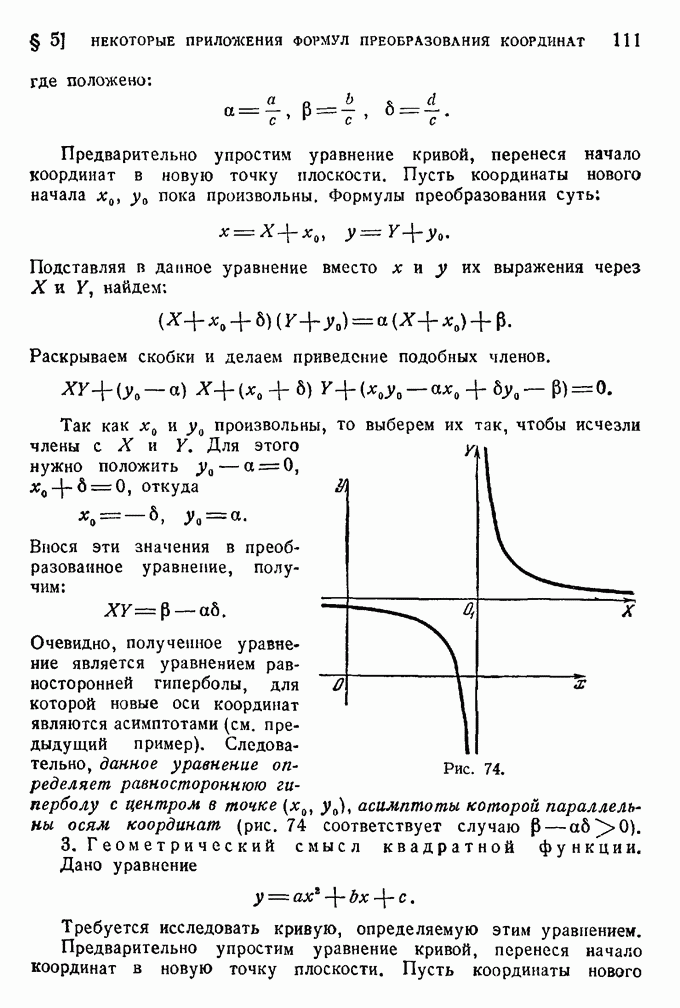
- § 5. Некоторые приложения формул преобразования координат.
- § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных.
- § 7. Преобразование общего уравнения второй степени.
- § 8. Классификация линий.
- Упражнения
- ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА
- § 2. Однородная система двух уравнений с тремя неизвестными.
- § 3. Определители 3-го порядка.
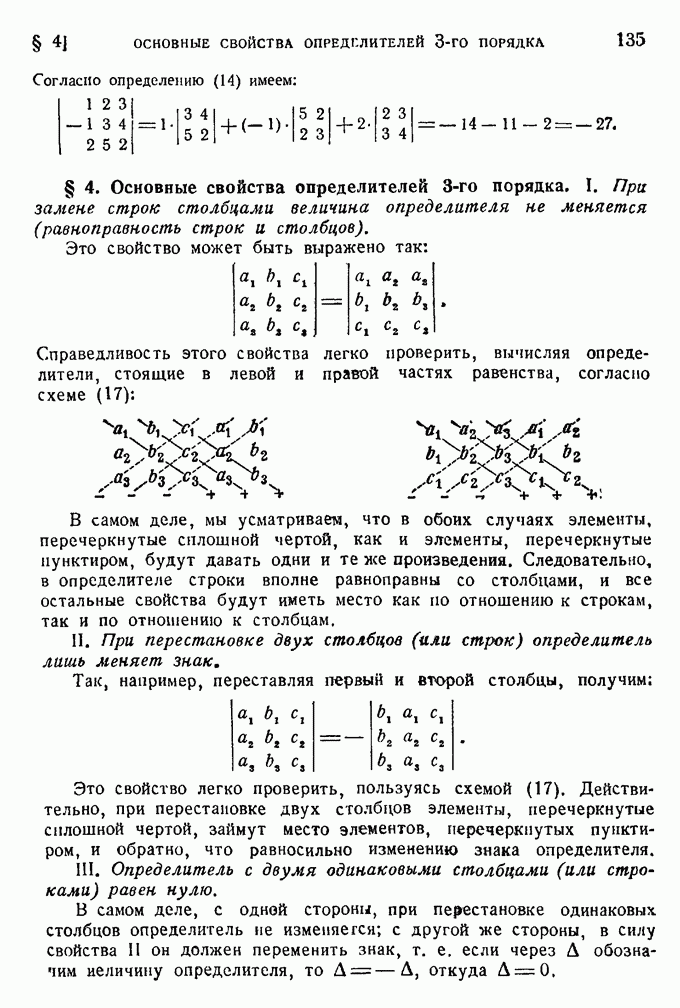
- § 4. Основные свойства определителей 3-го порядка.
- § 5. Система трех уравнений первой степени с тремя неизвестными.
- § 6. Однородная система.
- § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными.
- § 8. Некоторые приложения определителей к аналитической геометрии.
- Упражнения
- ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
- § 2. Основные задачи.
- § 3. Основные положения теории проекций в пространстве.
- § 4. Вычисление угла между двумя осями в пространстве.
- Упражнения
- ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
- § 2. Сложение векторов.
- § 3. Вычитание векторов.
- § 4. Умножение вектора на число.
- § 5. Проекции вектора.
- § 6. Действия над векторами, заданными своими проекциями.
- § 7. Скалярное произведение векторов.
- § 8. Основные свойства скалярного произведения.
- § 9. Скалярное произведение векторов, заданных проекциями.
- § 10. Направление вектора.
- § 11. Векторное произведение.
- § 12. Основные свойства векторного произведения.
- § 13. Векторное произведение векторов, заданных проекциями.
- § 14. Векторно-скалярное произведение.
- § 15. Векторно-скалярное произведение в проекциях.
- § 16. Двойное векторное произведение.
- Упражнения
- ГЛАВА III. ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ
- § 1. Уравнение поверхности.
- § 2. Геометрический смысл уравнений.
- § 3. Две основные задачи.
- § 4. Сфера.
- § 5. Цилиндрические поверхности.
- § 6. Уравнения линии в пространстве.
- § 7. Пересечение трех поверхностей.
- Упражнения
- ГЛАВА IV. ПЛОСКОСТЬ
- § 1. Нормальное уравнение плоскости.
- § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду.
- § 3. Исследование общего уравнения плоскости.
- § 4. Уравнение плоскости в отрезках.
- § 5. Уравнение плоскости, проходящей через данную точку.
- § 6. Уравнение плоскости, проходящей через три данные точки.
- § 7. Угол между двумя плоскостями.
- § 8. Условия параллельности и перпендикулярности двух плоскостей.
- § 9. Точка пересечения трех плоскостей.
- § 10. Расстояние от точки до плоскости.
- Упражнения
- ГЛАВА V. ПРЯМАЯ ЛИНИЯ
- § 1. Уравнения прямой линии.
- § 2. Прямая как линия пересечения двух плоскостей. Общие уравнения прямой.
- § 3. Угол между двумя прямыми линиями.
- § 4. Условия параллельности и перпендикулярности двух прямых.
- § 5. Уравнения прямой, проходящей через две данные точки.
- § 6. Угол между прямой и плоскостью.
- § 7. Условия параллельности и перпендикулярности прямой и плоскости.
- § 8. Уравнение пучка плоскостей.
- § 9. Пересечение прямой с плоскостью.
- § 10. Условие, при котором две прямые лежат в одной плоскости.
- Упражнения
- ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА
- § 1. Классификация поверхностей.
- § 2. Цилиндрические поверхности (общий случай).
- § 3. Конические поверхности.
- § 4. Поверхности вращения.
- § 5. Эллипсоид.
- § 6. Однополостный гиперболоид.
- § 7. Двуполостный гиперболоид.
- § 8. Эллиптический параболоид.
- § 9. Гиперболический параболоид.
- § 10. Конус 2-го порядка.
- § 11. Цилиндры 2-го порядка.
- § 12. Прямолинейные образующие поверхностей 2-го порядка. Конструкции В. Г. Шухова.
- Упражнения
- Ответы