| << Предыдущий параграф | Следующий параграф >> |
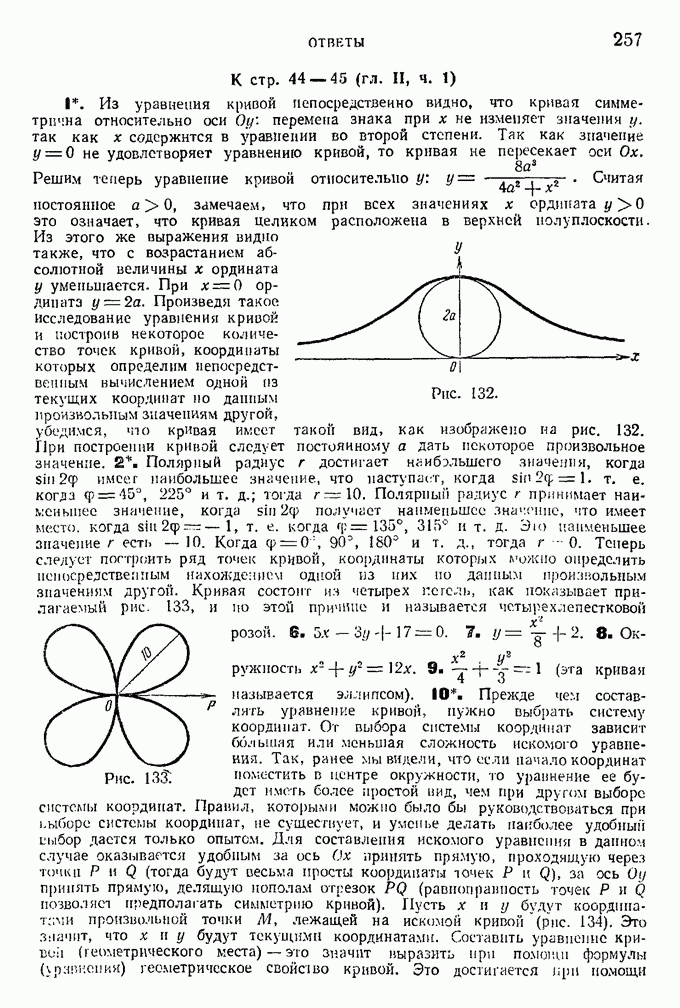
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных.
Общее уравнение  степени между двумя переменными, не содержащее их произведения, имеет вид:
степени между двумя переменными, не содержащее их произведения, имеет вид:

где коэффициенты А и С одновременно не равны нулю, так как в иротивном случае уравнение превратилось бы в уравнение  степени.
степени.
Посмотрим, какие кривые определяются этим уравнением при различных значениях его коэффициентов.
Случай I. Коэффициенты при  одного знака. Можно считать, что они положительны, так как если бы они были отрицательными, то, умножив обе части уравнения на
одного знака. Можно считать, что они положительны, так как если бы они были отрицательными, то, умножив обе части уравнения на  мы
мы
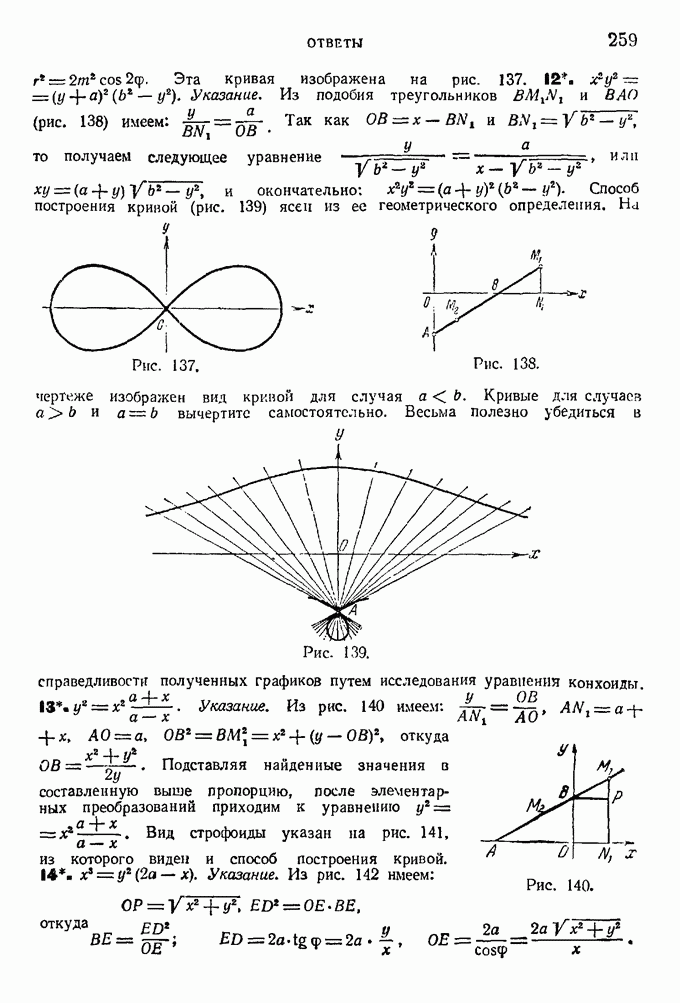
сделали бы их положительными. Перепишем уравнение (8) следующим образом:

Дополним выражения в скобках до полных квадратов. Для этого к левой и правой частям уравнения прибавим  уравнение примет вид:
уравнение примет вид:

или

Перенесем начало координат в точку  Тогда по формулам (2) и (3) (§ 2)
Тогда по формулам (2) и (3) (§ 2)

где  - координаты в новых осях. Обозначим правую часть уравнения (9) через
- координаты в новых осях. Обозначим правую часть уравнения (9) через 

В результате уравнение (9) примет вид:

Пусть  разделив обе части уравнения (10) на U, получим:
разделив обе части уравнения (10) на U, получим:

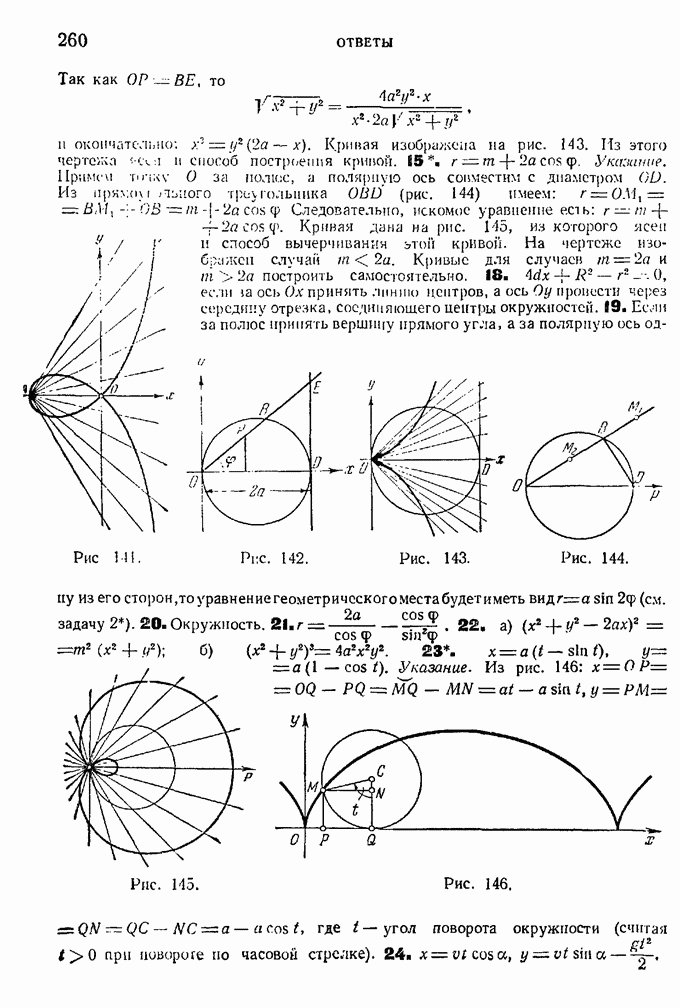
Введя обозначения и  что возможно, так как А,
что возможно, так как А,
С и U положительны, будем иметь

Это есть уравнение эллипса. Следовательно, в данном случае уравнение (10), а значит и уравнение (8), определяет эллипс (в частности, при  — окружность). Центр этого эллипса имеет координаты — и
— окружность). Центр этого эллипса имеет координаты — и  системе координат
системе координат  а его оси параллельны осям коардинат.
а его оси параллельны осям коардинат.
Если  то уравнение (10) будет иметь вид
то уравнение (10) будет иметь вид  Оно определяет только одну точку
Оно определяет только одну точку  так как при любых
так как при любых
других значениях переменных левая часть уравнения положительна. Возвращаясь к уравнению (8), видим, что ему удовлетворяют координаты только одной точки  .
.
Наконец, если  то правая часть уравнения (10) отрицательна, в то время как оба члена левой части при любых значениях X и Y неотрицательны. Следовательно, нет ни одной точки, координаты которой удовлетворяли бы уравнению (10), а значит и уравнению (8). В этом случае уравнение не определяет никакой линии.
то правая часть уравнения (10) отрицательна, в то время как оба члена левой части при любых значениях X и Y неотрицательны. Следовательно, нет ни одной точки, координаты которой удовлетворяли бы уравнению (10), а значит и уравнению (8). В этом случае уравнение не определяет никакой линии.
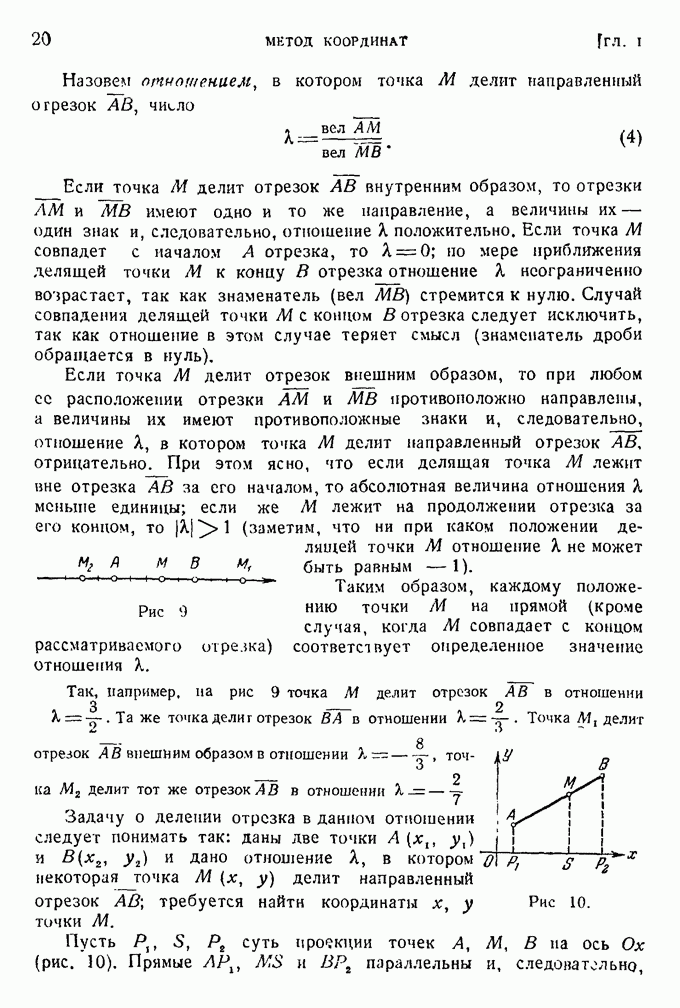
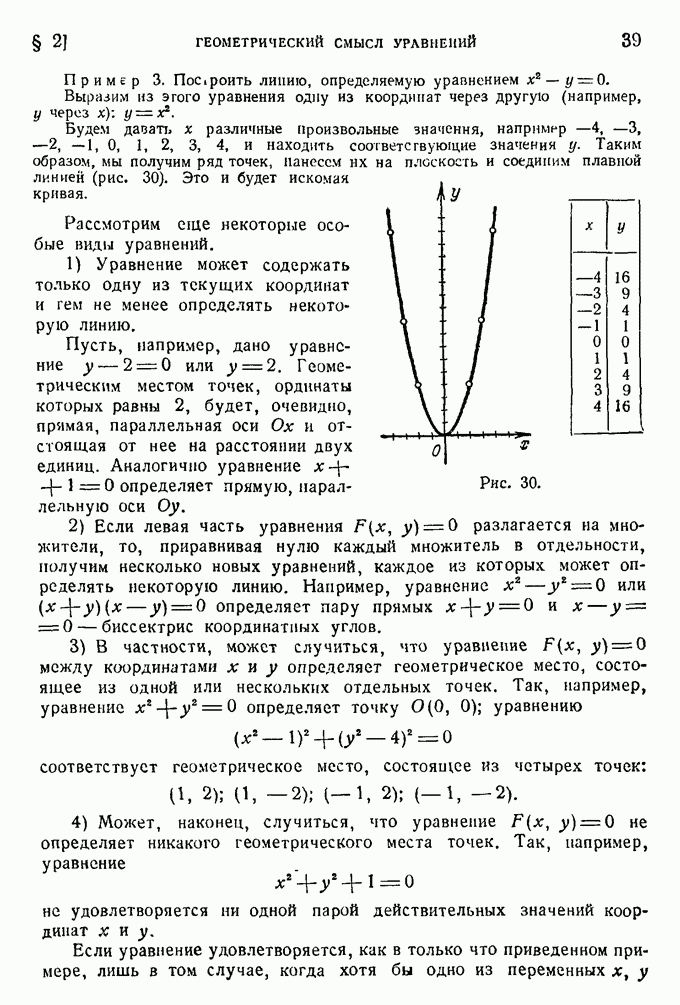
Пример. Упростить уравнение кривой

и установить ее вид.
Перепишем уравнение так:

Дополняя выражения в скобках до полных квадратов, получим

или, после преобразований,

Перенесем начало координат в точку  волагая
волагая  будем иметь
будем иметь

Это есть уравнение эллипса.
Центр его лежит в точке  , а полуоси равны 3 и 2 (рис. 76).
, а полуоси равны 3 и 2 (рис. 76).

Рис. 76.
Заметим, что обычно нет надобности писать уравнение эллипса в системе координат ХОУ. Лучше оставить его в виде  . В этой форме записи сразу видны координаты центра эллипса.
. В этой форме записи сразу видны координаты центра эллипса.
Случай II. Коэффициенты А и С уравнения (8) имеют разные знаки. Для определенности положим, что  . Как и в случае I, приведем уравнение (8) к виду:
. Как и в случае I, приведем уравнение (8) к виду:

Перенесем начало координат в точку  и обозначим правую часть уравнения (11) через U. После этого в системе
и обозначим правую часть уравнения (11) через U. После этого в системе
координат ХОУ уравнение (11) примет вид

где

Пусть U отлично от нули. Разделив обе части уравнения (12) на U, получим:

Если  то можно ввести обозначения (напомним, что по условию
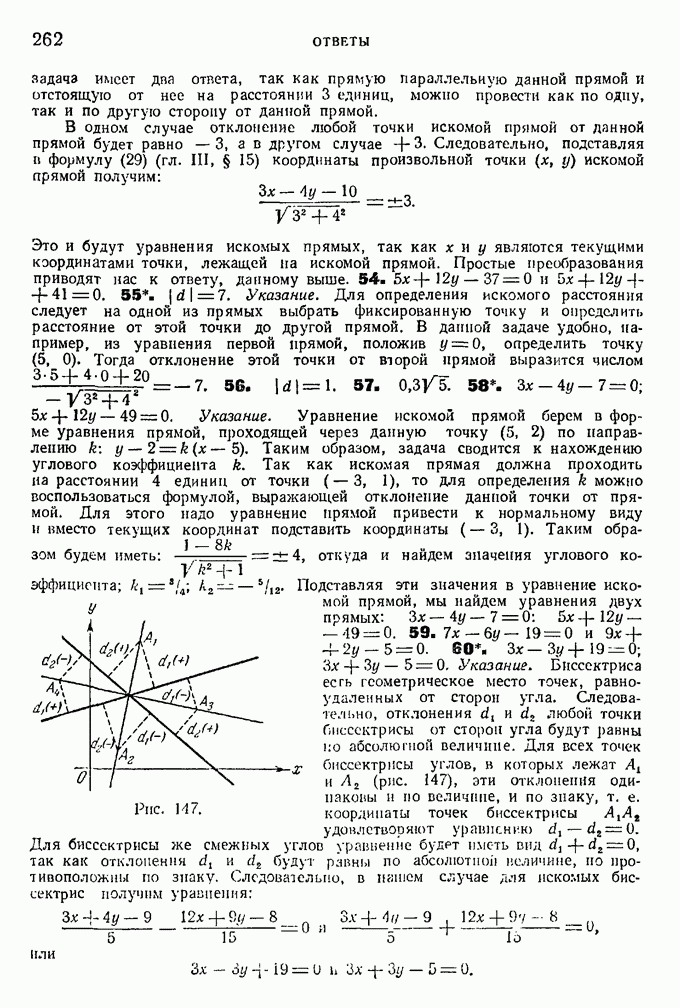
то можно ввести обозначения (напомним, что по условию  ):
):

После этого уравнение примет вид:

Это уравнение гиперболы, действительная ось которой лежит на оси  а мнимая на оси О, У.
а мнимая на оси О, У.
Если же  то, обозначая
то, обозначая

придем к уравнению

Это тоже уравнение гиперболы. Только действительная ось ее лежит на оси  , а мнимая — на оси
, а мнимая — на оси 
Итак, в рассматриваемом случае уравнение (8) определяет гиперболу с центром в точке  Действительная ось ее будет параллельна оси Ох или оси Оу в зависимости от знака U. Пусть
Действительная ось ее будет параллельна оси Ох или оси Оу в зависимости от знака U. Пусть  . В этом случае уравнение (12) представится так:
. В этом случае уравнение (12) представится так:

Полагая  перепишем его в таком виде:
перепишем его в таком виде:

или

По это уравнение распадается на два уравнения первой степени:

Каждое из них есть уравнение прямой, проходящей через точку  , т. е. через точку
, т. е. через точку  . Таким образом, при
. Таким образом, при  уравнение (12), а значит и уравнение (8), определяет пару пересекающихся прямых. Как говорят, кривая выродилась в пару прямых.
уравнение (12), а значит и уравнение (8), определяет пару пересекающихся прямых. Как говорят, кривая выродилась в пару прямых.
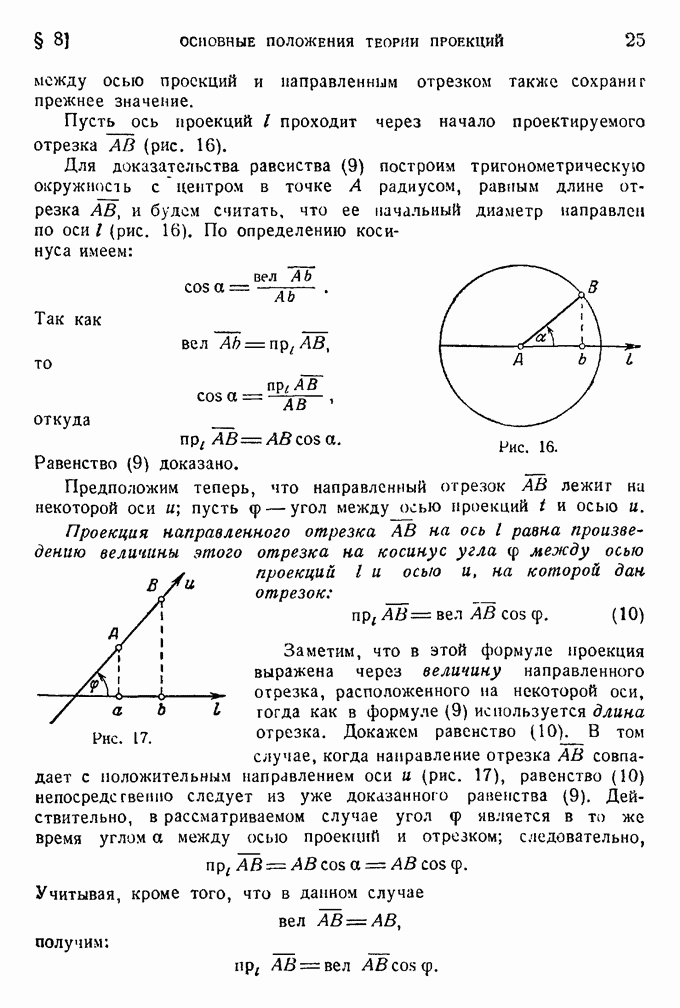
Пример 1. Упростить уравнение кривой

и установить ее вид.
Перепишем уравнение так:

и каждую из скобок дополним до полного квадрата:

После преобразований получим

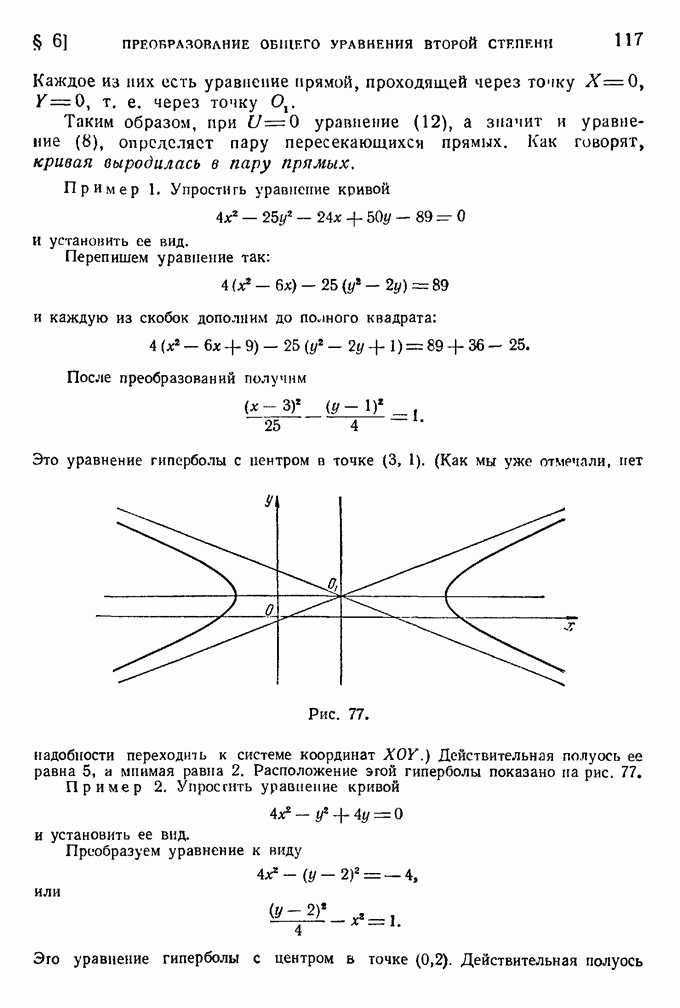
Это уравнение гиперболы с центром в точке (3, 1). (Как мы уже отмечали, нет надобности переходить к системе координат ХОУ.)

Рис. 77.
Действительная полуось ее равна 5, а мнимая равна 2. Расположение этой гиперболы показано на рис. 77. Пример 2. Упростить уравнение кривой

и установить ее вид.
Преобразуем уравнение к виду

или

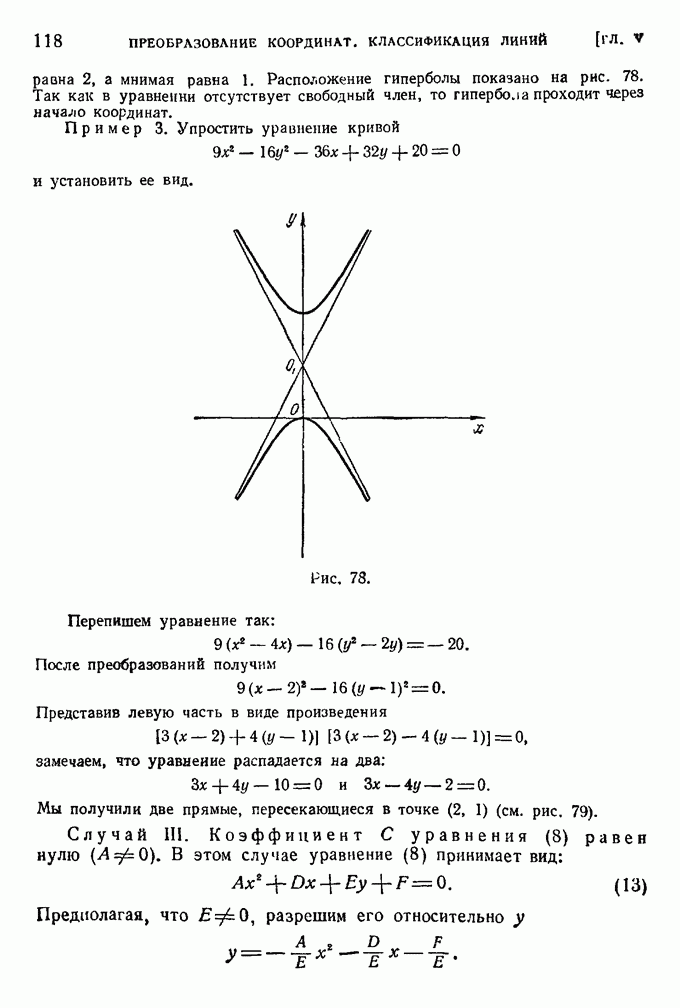
Это уравнение гиперболы с центром в точке (0,2). Действительная полуось
равна 2, а мнимая равна 1. Расположение гиперболы показано на рис. 78. Так как в уравнении отсутствует свободный член, то гипербола проходит через начало координат.
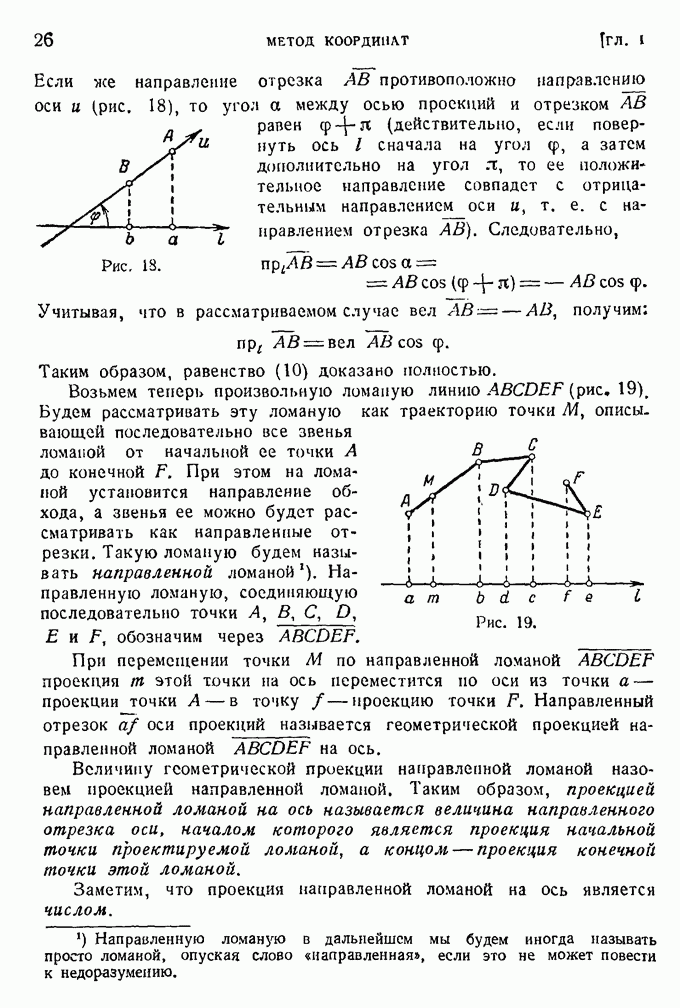
Пример 3. Упростить уравнение кривой

и установить ее вид.

Рис. 78.
Перепишем уравнение так:

После преобразований получим

Представив левую часть в виде произведения

замечаем, что уравнение распадается на два:

Мы получили две прямые, пересекающиеся в точке (2, 1) (см. рис. 79).
Случай III. Коэффициент С уравнения (8) равен нулю  ). В этом случае уравнение (8) принимает вид:
). В этом случае уравнение (8) принимает вид:

Предполагая, что  разрешим его относительно у
разрешим его относительно у

Введем обозначения:

Наше уравнение запишется так:

Преобразуем его к виду

или

Перенесем начало координат в точку  Полагая
Полагая  получим уравнение
получим уравнение

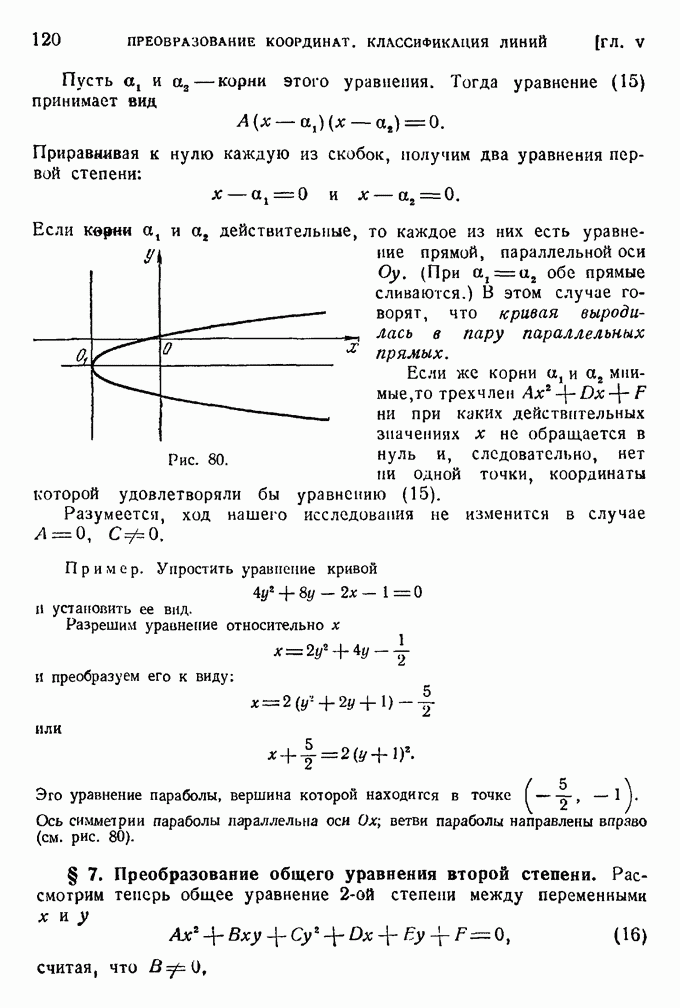
Это есть уравнение параболы.

Рис. 79.
Вершина ее находится в точке  а ось симметрии лежит на оси
а ось симметрии лежит на оси  и, следовательно, параллельна первоначальной оси
и, следовательно, параллельна первоначальной оси 
Заметим, что уравнение (14) было рассмотрено в § 5, где приведение его к простейшему виду производилось иным способом.
Если в уравнении  то оно примет вид:
то оно примет вид:

т. е. будет содержать только одно переменное 
Пусть а, и  корни этого уравнения. Тогда уравнение (15) принимает вид
корни этого уравнения. Тогда уравнение (15) принимает вид

Приравнивая к нулю каждую из скобок, получим два уравнения первой степени:

Если корни  и
и  действительные, то каждое из них есть уравнение прямой, параллельной оси
действительные, то каждое из них есть уравнение прямой, параллельной оси  (При
(При  обе прямые сливаются.) В этом случае говорят, что кривая выродилась в пару параллельных прямых.
обе прямые сливаются.) В этом случае говорят, что кривая выродилась в пару параллельных прямых.

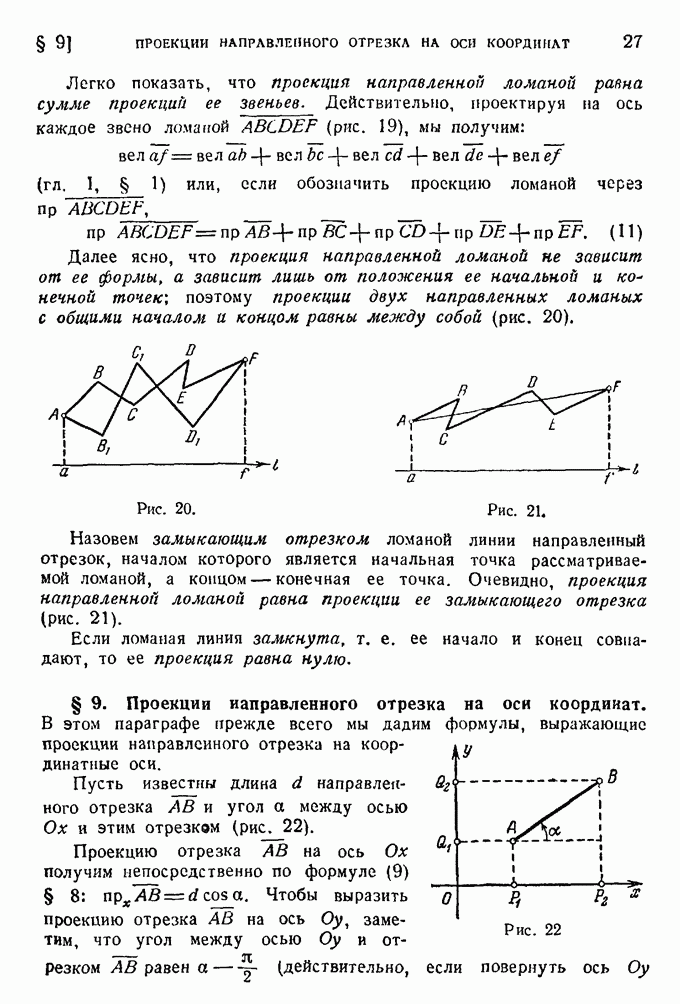
Рис. 80.
Если же корни  мнимые, то трехчлен
мнимые, то трехчлен  ни при каких действительных значениях
ни при каких действительных значениях  не обращается в нуль и, следовательно, нет
не обращается в нуль и, следовательно, нет  одной точки, координаты которой удовлетворяли бы уравнению (15).
одной точки, координаты которой удовлетворяли бы уравнению (15).
Разумеется, ход нашего исследования не изменится в случае 
Пример. Упростить уравнение кривой

Н установить ее вид.
Разрешим уравнение относительно 

И преобразуем его к виду:

или

Это уравнение параболы, вершина которой находится в точке 
Ось симметрии параболы параллельна оси  ветви параболы направлены вправо (см. рис. 80).
ветви параболы направлены вправо (см. рис. 80).
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- ГЛАВА I. МЕТОД КООРДИНАТ
- § 2. Координаты на прямой линии.
- § 3. Расстояние между двумя точками на прямой линии.
- § 4. Прямоугольные координаты на плоскости.
- § 5. Расстояние между двумя точками на плоскости.
- § 6. Деление отрезка в данном отношении.
- § 7. Угол между двумя осями.
- § 8. Основные положения теории проекций.
- § 9. Проекции направленного отрезка на оси координат.
- § 10. Площадь треугольника.
- § 11. Полярные координаты.
- Упражнения
- ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ
- § 1. Составление уравнений заданных линий.
- § 2. Геометрический смысл уравнений.
- § 3. Две основные задачи.
- § 4. Пересечение двух линий.
- § 5. Параметрические уравнения линий.
- § 6. Уравнения линий в полярных координатах.
- ГЛАВА III. ПРЯМАЯ ЛИНИЯ
- § 1. Угловой коэффициент прямой.
- § 2. Уравнение прямой линии с угловым коэффициентом.
- § 3. Геометрический смысл уравнения первой степени между двумя переменными.
- § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0.
- § 5. Уравнение прямой линии в отрезках.
- § 6. Построение прямой линии по ее уравнению.
- § 7. Угол между двумя прямыми.
- § 8. Условия параллельности и перпендикулярности двух прямых.
- § 9. Уравнение прямой, проходящей через данную точку в данном направлении.
- § 10. Взаимное расположение двух прямых на плоскости.
- § 11. Уравнение пучка прямых.
- § 12. Уравнение прямой, проходящей через две данные точки.
- § 13. Условие, при котором три данные точки лежат на одной прямой.
- § 14. Нормальное уравнение прямой линии.
- § 15. Приведение общего уравнения первой степени к нормальному виду.
- § 16. Расстояние от дайной точки до данной прямой.
- § 17. Уравнение прямой в полярной системе координат.
- Упражнения
- ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ
- § 2. Окружность.
- § 3. Эллипс.
- § 4. Гипербола и ее асимптоты.
- § 5. Парабола.
- § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки.
- § 7. Эллипс, гипербола и парабола как конические сечения.
- § 8. Эксцентриситет и директрисы эллипса.
- § 9. Эксцентриситет и директрисы гиперболы.
- § 10. Эксцентриситет и директриса параболы.
- § 11. Уравнение конического сечения в полярных координатах.
- § 12. Диаметры зллипса. Сопряженные диаметры.
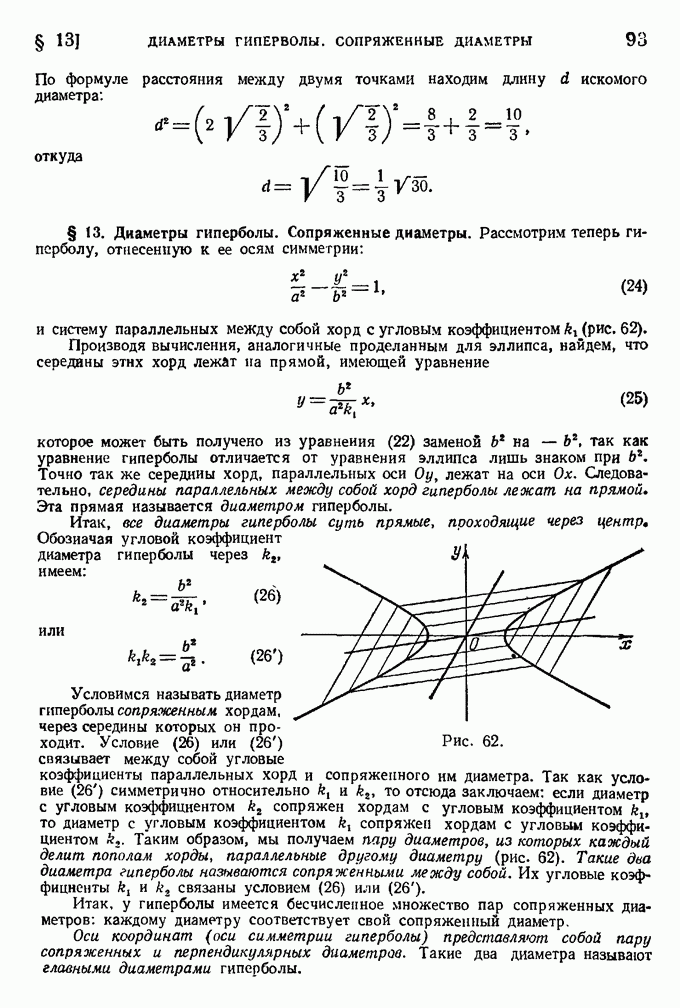
- § 13. Диаметры гиперболы. Сопряженные диаметры.
- § 14. Диаметры параболы.
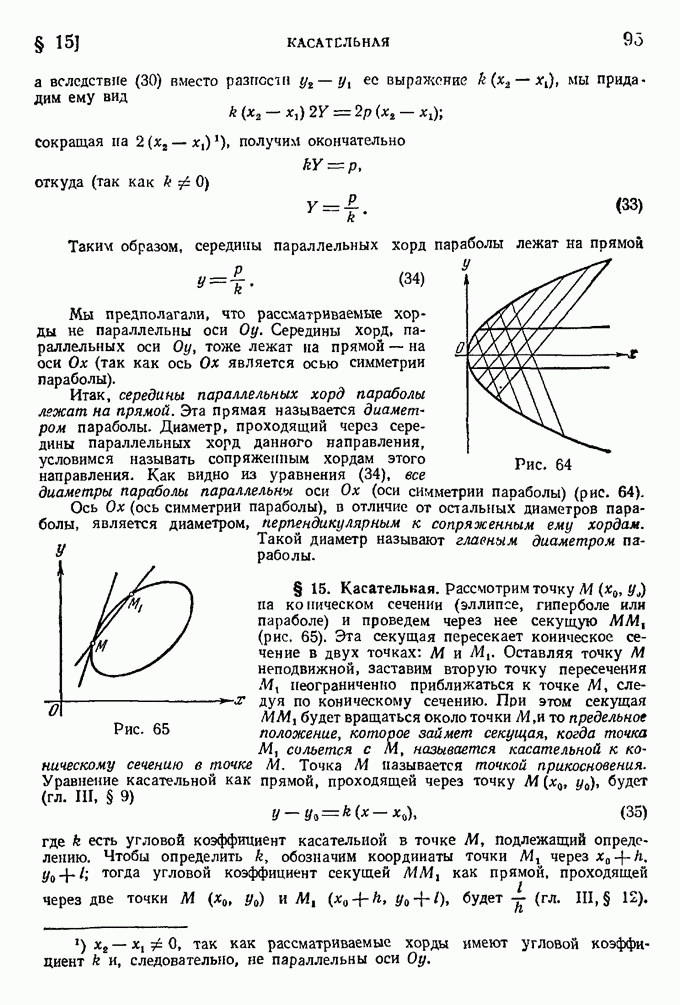
- § 15. Касательная.
- § 16. Эллипс как проекция окружности.
- § 17. Параметрические уравнения эллипса.
- Упражнения
- ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ
- § 2. Перенос начала координат.
- § 3. Поворот осей координат.
- § 4. Общий случай.
- § 5. Некоторые приложения формул преобразования координат.
- § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных.
- § 7. Преобразование общего уравнения второй степени.
- § 8. Классификация линий.
- Упражнения
- ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА
- § 2. Однородная система двух уравнений с тремя неизвестными.
- § 3. Определители 3-го порядка.
- § 4. Основные свойства определителей 3-го порядка.
- § 5. Система трех уравнений первой степени с тремя неизвестными.
- § 6. Однородная система.
- § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными.
- § 8. Некоторые приложения определителей к аналитической геометрии.
- Упражнения
- ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
- § 2. Основные задачи.
- § 3. Основные положения теории проекций в пространстве.
- § 4. Вычисление угла между двумя осями в пространстве.
- Упражнения
- ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
- § 2. Сложение векторов.
- § 3. Вычитание векторов.
- § 4. Умножение вектора на число.
- § 5. Проекции вектора.
- § 6. Действия над векторами, заданными своими проекциями.
- § 7. Скалярное произведение векторов.
- § 8. Основные свойства скалярного произведения.
- § 9. Скалярное произведение векторов, заданных проекциями.
- § 10. Направление вектора.
- § 11. Векторное произведение.
- § 12. Основные свойства векторного произведения.
- § 13. Векторное произведение векторов, заданных проекциями.
- § 14. Векторно-скалярное произведение.
- § 15. Векторно-скалярное произведение в проекциях.
- § 16. Двойное векторное произведение.
- Упражнения
- ГЛАВА III. ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ
- § 1. Уравнение поверхности.
- § 2. Геометрический смысл уравнений.
- § 3. Две основные задачи.
- § 4. Сфера.
- § 5. Цилиндрические поверхности.
- § 6. Уравнения линии в пространстве.
- § 7. Пересечение трех поверхностей.
- Упражнения
- ГЛАВА IV. ПЛОСКОСТЬ
- § 1. Нормальное уравнение плоскости.
- § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду.
- § 3. Исследование общего уравнения плоскости.
- § 4. Уравнение плоскости в отрезках.
- § 5. Уравнение плоскости, проходящей через данную точку.
- § 6. Уравнение плоскости, проходящей через три данные точки.
- § 7. Угол между двумя плоскостями.
- § 8. Условия параллельности и перпендикулярности двух плоскостей.
- § 9. Точка пересечения трех плоскостей.
- § 10. Расстояние от точки до плоскости.
- Упражнения
- ГЛАВА V. ПРЯМАЯ ЛИНИЯ
- § 1. Уравнения прямой линии.
- § 2. Прямая как линия пересечения двух плоскостей. Общие уравнения прямой.
- § 3. Угол между двумя прямыми линиями.
- § 4. Условия параллельности и перпендикулярности двух прямых.
- § 5. Уравнения прямой, проходящей через две данные точки.
- § 6. Угол между прямой и плоскостью.
- § 7. Условия параллельности и перпендикулярности прямой и плоскости.
- § 8. Уравнение пучка плоскостей.
- § 9. Пересечение прямой с плоскостью.
- § 10. Условие, при котором две прямые лежат в одной плоскости.
- Упражнения
- ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА
- § 1. Классификация поверхностей.
- § 2. Цилиндрические поверхности (общий случай).
- § 3. Конические поверхности.
- § 4. Поверхности вращения.
- § 5. Эллипсоид.
- § 6. Однополостный гиперболоид.
- § 7. Двуполостный гиперболоид.
- § 8. Эллиптический параболоид.
- § 9. Гиперболический параболоид.
- § 10. Конус 2-го порядка.
- § 11. Цилиндры 2-го порядка.
- § 12. Прямолинейные образующие поверхностей 2-го порядка. Конструкции В. Г. Шухова.
- Упражнения
- Ответы