| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 162. Сдвиг фаз между током и напряжением.
Проделаем
следующий опыт. Возьмем описанный в § 153 осциллограф с двумя петлями и включим
его в цепь так (рис. 305,а), чтобы петля 1 была включена в цепь последовательно
с конденсатором, а петля 2 параллельно этому конденсатору. Очевидно, что
кривая, получаемая от петли 1, изображает форму тока, проходящего через
конденсатор, а от петли 2 дает форму напряжения между обкладками конденсатора
(точками ![]() и
и
![]() ),
потому что в этой петле осциллографа ток в каждый момент времени пропорционален
напряжению. Опыт показывает, что в этом случае кривые тока и напряжения смещены
по фазе, причем ток опережает по фазе напряжение на четверть периода (на
),
потому что в этой петле осциллографа ток в каждый момент времени пропорционален
напряжению. Опыт показывает, что в этом случае кривые тока и напряжения смещены
по фазе, причем ток опережает по фазе напряжение на четверть периода (на ![]() ). Если бы мы
заменили конденсатор катушкой с большой индуктивностью (рис. 305,б), то
оказалось бы, что ток отстает по фазе от напряжения на четверть периода (на
). Если бы мы
заменили конденсатор катушкой с большой индуктивностью (рис. 305,б), то
оказалось бы, что ток отстает по фазе от напряжения на четверть периода (на ![]() ). Наконец, таким
же образом можно было бы показать, что в случае активного сопротивления
напряжение и ток совпадают по фазе (рис. 305,в).
). Наконец, таким
же образом можно было бы показать, что в случае активного сопротивления
напряжение и ток совпадают по фазе (рис. 305,в).

Рис. 305. Опыт по обнаружению сдвига фаз между током и напряжением: слева – схема опыта, справа – результаты
В
общем случае, когда участок цепи содержит не только активное, но и реактивное
(емкостное, индуктивное или и то и другое) сопротивление, напряжение между
концами этого участка сдвинуто по фазе относительно тока, причем сдвиг фаз
лежит в пределах от ![]() до
до ![]() и определяется соотношением между
активным и реактивным сопротивлениями данного участка цепи.
и определяется соотношением между
активным и реактивным сопротивлениями данного участка цепи.
В чем заключается физическая причина наблюдаемого сдвига фаз между током и напряжением?
Если в цепь не входят конденсаторы и катушки, т. е. емкостным и индуктивным сопротивлениями цепи можно пренебречь по сравнению с активным, то ток следует за напряжением, проходя одновременно с ним через максимумы и нулевые значения, как это показано на рис. 305,в.
Если
цепь имеет заметную индуктивность ![]() , то при прохождении по ней
переменного тока в цепи возникает э. д. с. самоиндукции. Эта э. д. с. по
правилу Ленца направлена так, что она стремится препятствовать тем изменениям
магнитного поля (а следовательно, и изменениям тока, создающего это поле),
которые вызывают э. д. с. индукции. При нарастании тока э. д. с. самоиндукции
препятствует этому нарастанию, и потому ток позже достигает максимума, чем в
отсутствие самоиндукции. При убывании тока э. д. с. самоиндукции стремится
поддерживать ток и нулевые значения тока будут достигнуты в более поздний
момент, чем в отсутствие самоиндукции. Таким образом, при наличии индуктивности
ток отстает по фазе от тока в отсутствие индуктивности, а следовательно,
отстает по фазе от своего напряжения.
, то при прохождении по ней
переменного тока в цепи возникает э. д. с. самоиндукции. Эта э. д. с. по
правилу Ленца направлена так, что она стремится препятствовать тем изменениям
магнитного поля (а следовательно, и изменениям тока, создающего это поле),
которые вызывают э. д. с. индукции. При нарастании тока э. д. с. самоиндукции
препятствует этому нарастанию, и потому ток позже достигает максимума, чем в
отсутствие самоиндукции. При убывании тока э. д. с. самоиндукции стремится
поддерживать ток и нулевые значения тока будут достигнуты в более поздний
момент, чем в отсутствие самоиндукции. Таким образом, при наличии индуктивности
ток отстает по фазе от тока в отсутствие индуктивности, а следовательно,
отстает по фазе от своего напряжения.
Если
активным сопротивлением цепи ![]() можно пренебречь по сравнению с ее
индуктивным сопротивлением
можно пренебречь по сравнению с ее
индуктивным сопротивлением ![]() , то отставание тока от напряжения
по времени равно
, то отставание тока от напряжения
по времени равно ![]() (сдвиг фаз равен
(сдвиг фаз равен ![]() ), т. е. максимум
), т. е. максимум
![]() совпадает
с
совпадает
с ![]() , как
это показано на рис. 305,б. Действительно, в этом случае напряжение на активном
сопротивлении
, как
это показано на рис. 305,б. Действительно, в этом случае напряжение на активном
сопротивлении ![]() ,
ибо
,
ибо ![]() ,
и, следовательно, все внешнее напряжение
,
и, следовательно, все внешнее напряжение ![]() уравновешивается э. д. с. индукции,
которая противоположна ему по направлению:
уравновешивается э. д. с. индукции,
которая противоположна ему по направлению: ![]() . Таким образом, максимум
. Таким образом, максимум ![]() совпадает с
максимумом
совпадает с
максимумом ![]() ,
т. е. наступает в тот момент, когда
,
т. е. наступает в тот момент, когда ![]() изменяется быстрее всего, а это
бывает, когда
изменяется быстрее всего, а это
бывает, когда ![]() .
Наоборот, в момент, когда
.
Наоборот, в момент, когда ![]() проходит через максимальное
значение, изменение тока наименьшее
проходит через максимальное
значение, изменение тока наименьшее ![]() , т. е. в этот момент
, т. е. в этот момент ![]() .
.
Если
активное сопротивление цепи ![]() не настолько мало, чтобы им можно
было пренебречь, то часть внешнего напряжения
не настолько мало, чтобы им можно
было пренебречь, то часть внешнего напряжения ![]() падает на сопротивлении
падает на сопротивлении ![]() , а остальная
часть уравновешивается э. д. с. самоиндукции:
, а остальная
часть уравновешивается э. д. с. самоиндукции: ![]() . В этом случае максимум
. В этом случае максимум ![]() отстоит от
максимума
отстоит от
максимума ![]() по
времени меньше, чем на
по
времени меньше, чем на ![]() (сдвиг фаз меньше
(сдвиг фаз меньше ![]() ), как это
изображено на рис. 306. Расчет показывает, что в этом случае отставание по фазе
), как это
изображено на рис. 306. Расчет показывает, что в этом случае отставание по фазе
![]() может
быть вычислено по формуле
может
быть вычислено по формуле
![]() . (162.1)
. (162.1)
При
![]() имеем
имеем ![]() и
и ![]() , как это
объяснено выше.
, как это
объяснено выше.

Рис. 306. Сдвиг фаз между током и напряжением в цепи, содержащей активное и индуктивное сопротивления
Если
цепь состоит из конденсатора емкости ![]() , а активным сопротивлением можно
пренебречь, то обкладки конденсатора, присоединенные к источнику тока с
напряжением
, а активным сопротивлением можно
пренебречь, то обкладки конденсатора, присоединенные к источнику тока с
напряжением ![]() ,
заряжаются и между ними возникает напряжение
,
заряжаются и между ними возникает напряжение ![]() . Напряжение на конденсаторе
. Напряжение на конденсаторе ![]() следует за
напряжением источника тока
следует за
напряжением источника тока ![]() практически мгновенно, т. е.
достигает максимума одновременно с
практически мгновенно, т. е.
достигает максимума одновременно с ![]() и обращается в нуль, когда
и обращается в нуль, когда ![]() .
.
Зависимость
между током ![]() и
напряжением
и
напряжением ![]() в
этом случае показана на рис. 307,а. На рис. 307,б условно изображен процесс
перезарядки конденсатора, связанный с появлением переменного тока в цепи.
в
этом случае показана на рис. 307,а. На рис. 307,б условно изображен процесс
перезарядки конденсатора, связанный с появлением переменного тока в цепи.

Рис. 307. а) Сдвиг фаз между напряжением и током в цепи с емкостным сопротивлением в отсутствие активного сопротивления. б) Процесс перезарядки конденсатора в цепи переменного тока
Когда
конденсатор заряжен до максимума (т. е. ![]() , а следовательно, и
, а следовательно, и ![]() имеют
максимальное значение), ток
имеют
максимальное значение), ток ![]() и вся энергия цепи есть
электрическая энергия заряженного конденсатора (точка
и вся энергия цепи есть
электрическая энергия заряженного конденсатора (точка ![]() на рис. 307,а). При
уменьшении напряжения
на рис. 307,а). При
уменьшении напряжения ![]() конденсатор начинает разряжаться и
в цепи появляется ток; он направлен от обкладки 1 к обкладке 2, т. е. навстречу
напряжению
конденсатор начинает разряжаться и
в цепи появляется ток; он направлен от обкладки 1 к обкладке 2, т. е. навстречу
напряжению ![]() .
Поэтому на рис. 307,а он изображен как отрицательный (точки лежат ниже оси
времени). К моменту времени
.
Поэтому на рис. 307,а он изображен как отрицательный (точки лежат ниже оси
времени). К моменту времени ![]() конденсатор полностью разряжен (
конденсатор полностью разряжен (![]() и
и ![]() ), а ток достигает
максимального значения (точка
), а ток достигает
максимального значения (точка ![]() ); электрическая энергия равна нулю,
и вся энергия сводится к энергии магнитного поля, создаваемого током. Далее,
напряжение
); электрическая энергия равна нулю,
и вся энергия сводится к энергии магнитного поля, создаваемого током. Далее,
напряжение ![]() меняет
знак, и ток начинает ослабевать, сохраняя прежнее направление. Когда
меняет
знак, и ток начинает ослабевать, сохраняя прежнее направление. Когда ![]() (и
(и ![]() ) достигнет
максимума, вся энергия вновь станет электрической, и ток
) достигнет
максимума, вся энергия вновь станет электрической, и ток ![]() (точка
(точка ![]() ). В дальнейшем
). В дальнейшем ![]() (и
(и ![]() ) начинает
убывать, конденсатор разряжается, ток нарастает, имея теперь направление от
обкладки 2 к обкладке 1, т. е. положительное; ток доходит до максимума в
момент, когда
) начинает
убывать, конденсатор разряжается, ток нарастает, имея теперь направление от
обкладки 2 к обкладке 1, т. е. положительное; ток доходит до максимума в
момент, когда ![]() (точка
(точка
![]() ) и т.
д. Из рис. 307,а видно, что ток раньше, чем напряжение, достигает максимума и
проходит через нуль, т. е. ток опережает напряжение по фазе.
) и т.
д. Из рис. 307,а видно, что ток раньше, чем напряжение, достигает максимума и
проходит через нуль, т. е. ток опережает напряжение по фазе.
Если
активным сопротивлением цепи ![]() нельзя пренебречь по сравнению с
емкостным
нельзя пренебречь по сравнению с
емкостным ![]() ,
то ток опережает напряжение по времени меньше, чем на
,
то ток опережает напряжение по времени меньше, чем на ![]() (сдвиг фаз меньше
(сдвиг фаз меньше ![]() , рис. 308). Для
этого случая, как показывает расчет, сдвиг фаз
, рис. 308). Для
этого случая, как показывает расчет, сдвиг фаз ![]() может быть вычислен по формуле
может быть вычислен по формуле
![]() . (162.2)
. (162.2)
При
![]() имеем
имеем ![]() и
и ![]() , как это
объяснено выше.
, как это
объяснено выше.

Рис. 308. Сдвиг фаз между током и напряжением в цепи, содержащей активное и емкостное сопротивления
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- Глава I. Электрические заряды
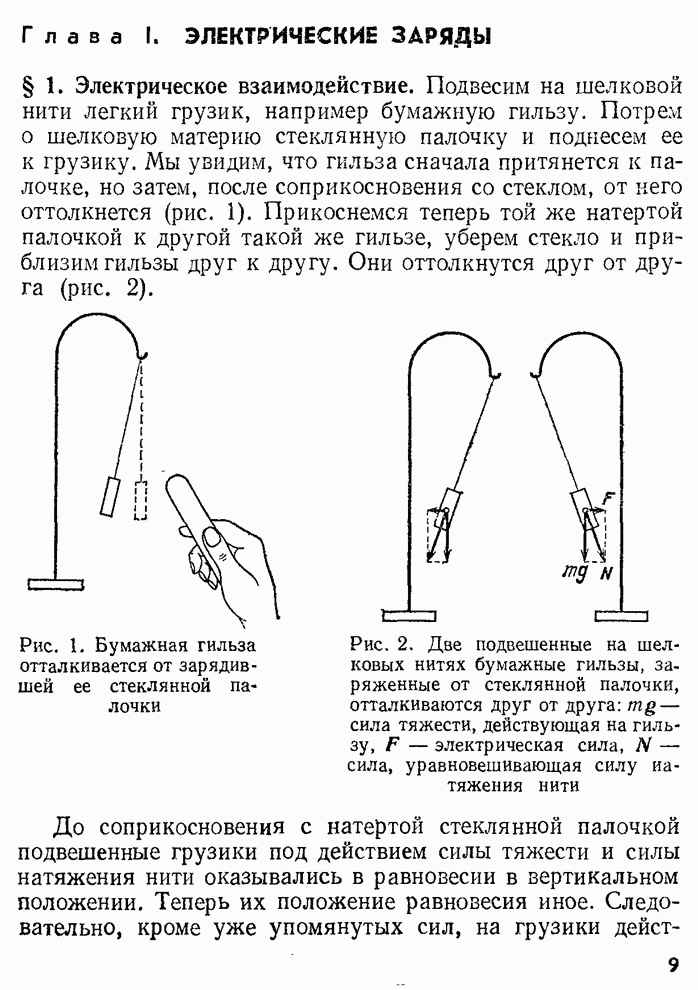
- § 1. Электрическое взаимодействие.
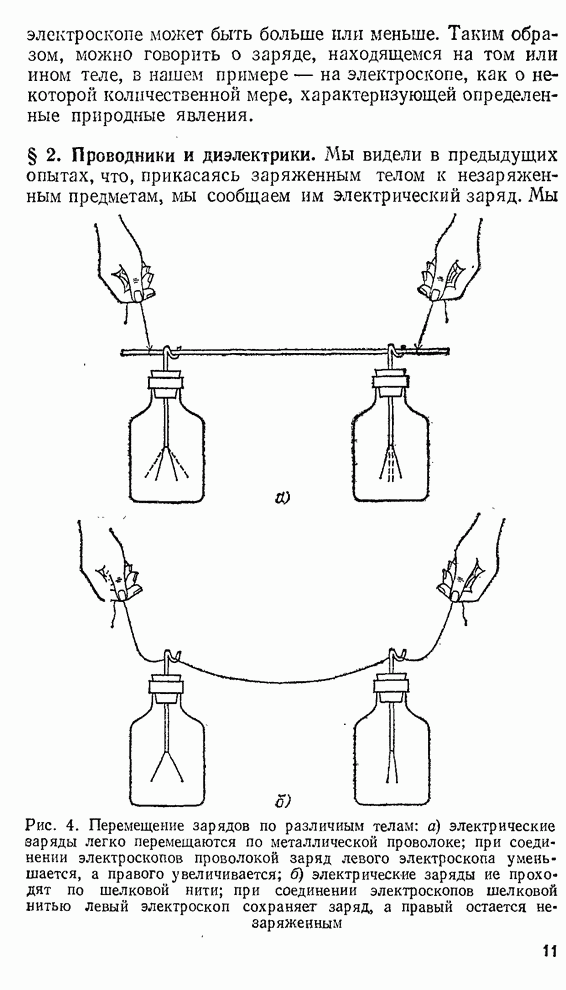
- § 2. Проводники и диэлектрики.
- § 3. Разделение тел на проводники и диэлектрики
- § 4. Положительные и отрицательные заряды
- § 5. Что происходит при электризации?
- § 6. Электронная теория.
- § 7. Электризация трением.
- § 8. Электризация через влияние.
- § 9. Электризация под действием света.
- § 10. Закон Кулона.
- § 11. Единица заряда.
- Глава II. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- § 12. Действие электрического заряда на окружающие тела.
- § 13. Понятие об электрическом поле.
- § 14. Напряженность электрического поля.
- § 15. Сложение полей.
- § 16. Электрическое поле в диэлектриках и в проводниках.
- § 17. Графическое изображение полей.
- § 18. Основные особенности электрических карт.
- § 19. Применение метода линий поля к задачам электростатики.
- § 20. Работа при перемещении заряда в электрическом поле.
- § 21. Разность потенциалов (электрическое напряжение).
- § 22. Эквипотенциальные поверхности.
- § 23. В чем смысл введения разности потенциалов?
- § 24. Условия равновесия зарядов в проводниках.
- § 25. Электрометр.
- § 26. В чем различие между электрометром и электроскопом?
- § 27. Соединение с Землей.
- § 28. Измерение разности потенциалов в воздухе. Электрический зонд.
- § 29. Электрическое поле Земли.
- § 30. Простейшие электрические поля.
- § 31. Распределение зарядов в проводнике. Клетка Фарадея.
- § 32. Поверхностная плотность заряда.
- § 33. Конденсаторы.
- § 34. Различные типы конденсаторов.
- § 35. Параллельное и последовательное соединение конденсаторов.
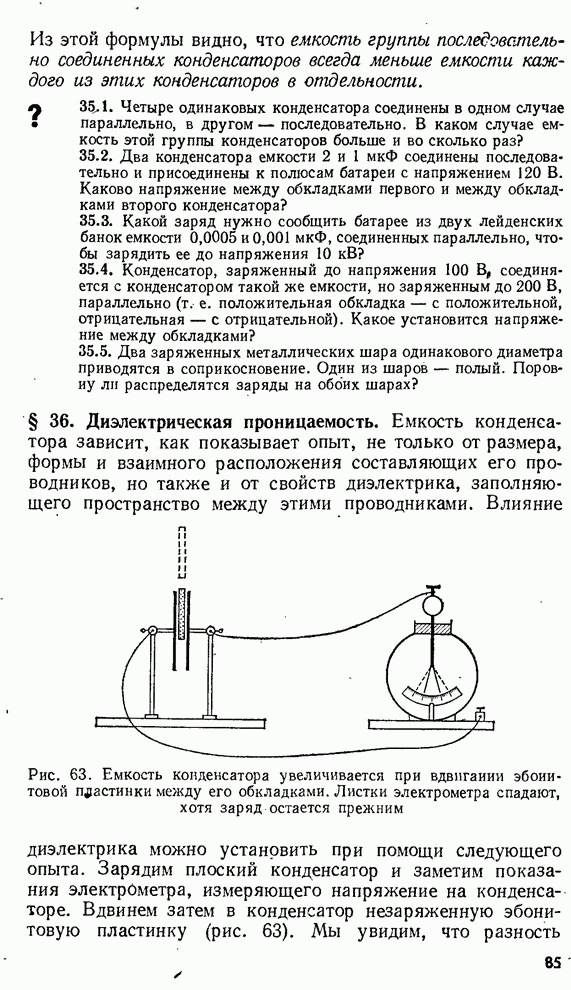
- § 36. Диэлектрическая проницаемость.
- § 37. Почему электрическое поле ослабляется внутри диэлектрика?
- § 38. Энергия заряженных тел. Энергия электрического поля.
- Глава III. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 39. Электрический ток и электродвижущая сила.
- § 40. Признаки электрического тока.
- § 41. Направление тока.
- § 42. Сила тока.
- § 43. «Скорость электрического тока» и скорость движения носителей заряда.
- § 44. Гальванометр.
- § 45. Распределение напряжения в проводнике с током.
- § 46. Закон Ома.
- § 47. Сопротивление проводов.
- § 48. Зависимость сопротивления от температуры.
- § 49. Сверхпроводимость.
- § 50. Последовательное и параллельное соединение проводников.
- § 51. Реостаты.
- § 52. Распределение напряжения в цепи.
- § 53. Вольтметр.
- § 54. Каким должно быть сопротивление вольтметра и амперметра?
- § 55. Шунтирование измерительных приборов.
- Глава IV. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА
- § 56. Нагревание током. Закон Джоуля-Ленца.
- § 57. Работа, совершаемая электрическим током.
- § 58. Мощность электрического тока.
- § 59. Контактная сварка.
- § 60. Электрические нагревательные приборы. Электрические печи.
- § 61. Понятие о расчете нагревательных приборов.
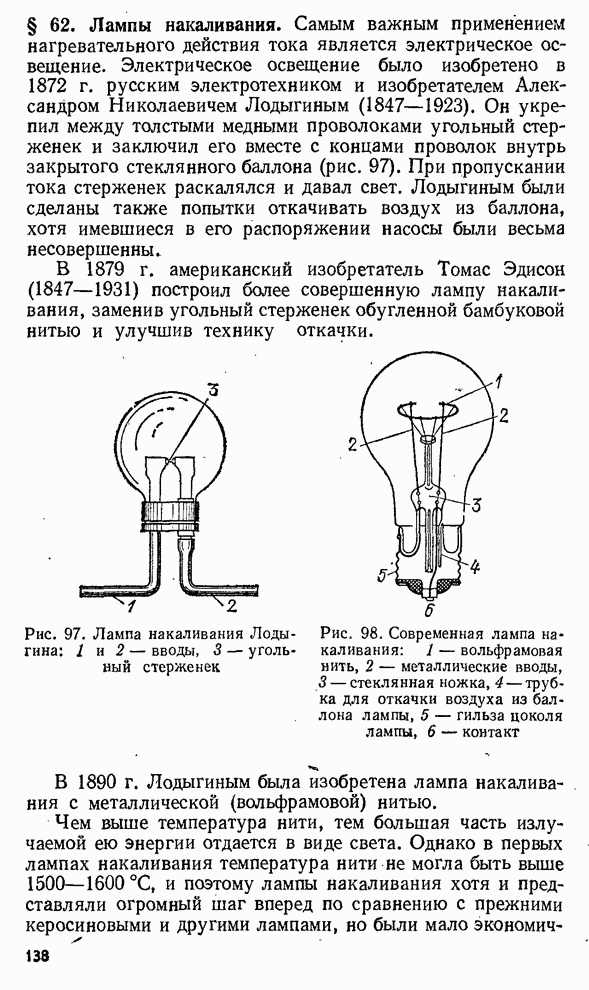
- § 62. Лампы накаливания.
- § 63. Короткое замыкание.
- § 64. Электрическая проводка.
- Глава V. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ЭЛЕКТРОЛИТЫ
- § 65. Первый закон Фарадея.
- § 66. Второй закон Фарадея.
- § 67. Ионная проводимость электролитов.
- § 68. Движение ионов в электролитах.
- § 69. Элементарный электрический заряд.
- § 70. Первичные и вторичные процессы при электролизе.
- § 71. Электролитическая диссоциация.
- § 72. Градуировка амперметров при помощи электролиза.
- § 73. Технические применения электролиза.
- Глава VI. ХИМИЧЕСКИЕ И ТЕПЛОВЫЕ ГЕНЕРАТОРЫ ТОКА
- § 74. Введение. Открытие Вольты.
- § 75. Правило Вольты. Гальванический элемент.
- § 76. Как возникают э. д. с. и ток в гальваническом элементе?
- § 77. Поляризация электродов.
- § 78. Деполяризация в гальванических элементах.
- § 79. Аккумуляторы.
- § 80. Закон Ома для замкнутой цепи.
- § 81. Напряжение на зажимах источника тока и э. д. с.
- § 82. Соединение источников тока.
- § 83. Термоэлементы.
- § 84. Термоэлементы в качестве генераторов.
- § 85. Измерение температуры с помощью термоэлементов.
- Глава VII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ МЕТАЛЛЫ
- § 86. Электронная проводимость металлов.
- § 87. Строение металлов.
- § 88. Причина электрического сопротивления.
- § 89. Работа выхода.
- § 90. Испускание электронов накаленными телами.
- Глава VIII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ГАЗЫ
- § 91. Самостоятельная и несамостоятельная проводимость газов.
- § 92. Несамостоятельная проводимость газа.
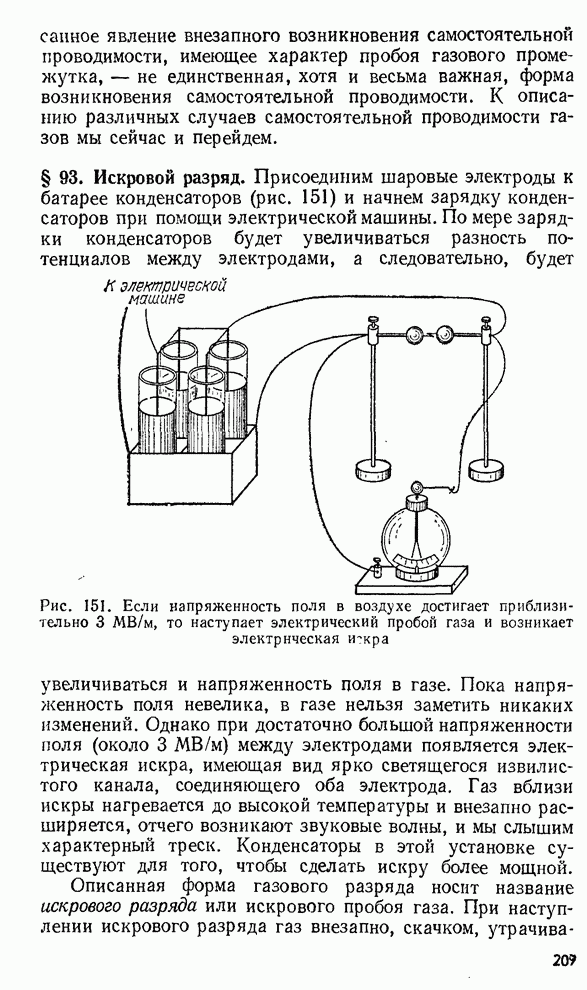
- § 93. Искровой разряд.
- § 94. Молния.
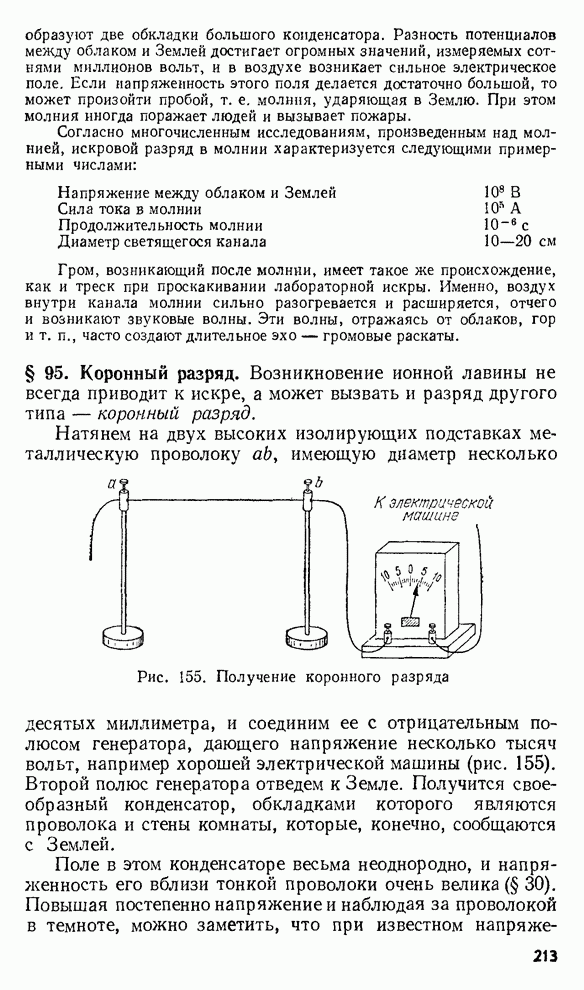
- § 95. Коронный разряд.
- § 96. Применения коронного разряда.
- § 97. Громоотвод.
- § 98. Электрическая дуга.
- § 99. Применения дугового разряда.
- § 100. Тлеющий разряд.
- § 101. Что происходит при тлеющем разряде?
- § 102. Катодные лучи.
- § 103. Природа катодных лучей.
- § 104. Каналовые лучи.
- § 105. Электронная проводимость в высоком вакууме.
- § 106. Электронные лампы.
- § 107. Электроннолучевая трубка.
- Глава IX. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ПОЛУПРОВОДНИКИ
- § 108. Природа электрического тока в полупроводниках.
- § 109. Движение электронов в полупроводниках.
- § 110. Полупроводниковые выпрямители.
- § 111. Полупроводниковые фотоэлементы.
- Глава X. ОСНОВНЫЕ МАГНИТНЫЕ ЯВЛЕНИЯ
- § 112. Естественные и искусственные магниты.
- § 113. Полюсы магнита и его нейтральная зона.
- § 114. Магнитное действие электрического тока.
- § 115. Магнитные действия токов и постоянных магнитов.
- § 116. Происхождение магнитного поля постоянных магнитов.
- § 117. Гипотеза Ампера об элементарных электрических токах.
- Глава XI. МАГНИТНОЕ ПОЛЕ
- § 118. Магнитное поле и его проявления. Магнитная индукция.
- § 119. Магнитный момент. Единица магнитной индукции.
- § 120. Измерение магнитной индукции поля с помощью магнитной стрелки.
- § 121. Сложение магнитных полей.
- § 122. Линии магнитного поля.
- § 123. Приборы для измерения магнитной индукции.
- Глава XII. МАГНИТНЫЕ ПОЛЯ ЭЛЕКТРИЧЕСКИХ ТОКОВ
- § 124. Магнитное поле прямолинейного проводника и кругового витка с током.
- § 125. Магнитное поле соленоида. Эквивалентность соленоида и полосового магнита.
- § 126. Магнитное поле внутри соленоида. Напряженность магнитного поля.
- § 127. Магнитное поле движущихся зарядов.
- Глава XIII. МАГНИТНОЕ ПОЛЕ ЗЕМЛИ
- § 128. Магнитное поле Земли.
- § 129. Элементы земного магнетизма.
- § 130. Магнитные аномалии и магнитная разведка полезных ископаемых.
- § 131. Изменение элементов земного магнетизма с течением времени. Магнитные бури.
- Глава XIV. СИЛЫ, ДЕЙСТВУЮЩИЕ В МАГНИТНОМ ПОЛЕ НА ПРОВОДНИКИ С ТОКОМ
- § 132. Введение.
- § 133. Действие магнитного поля на прямолинейный проводник с током. Правило левой руки.
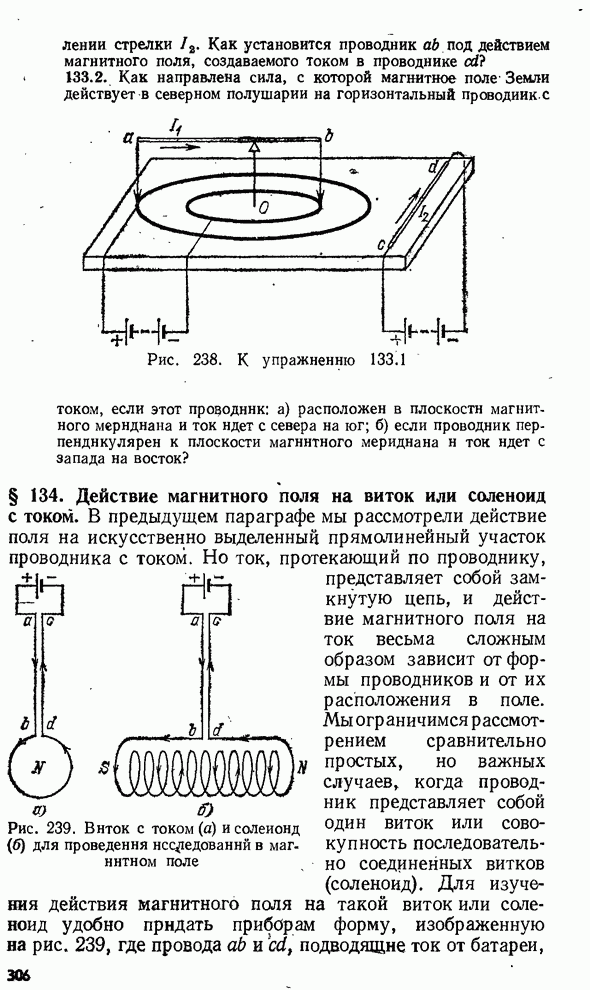
- § 134. Действие магнитного поля на виток или соленоид с током.
- § 135. Гальванометр, основанный на взаимодействии магнитного поля и тока.
- § 136. Сила Лоренца.
- § 137. Сила Лоренца и полярные сияния.
- Глава XV. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
- § 138. Условия возникновения индукционного тока.
- § 139. Направление индукционного тока. Правило Ленца.
- § 140. Основной закон электромагнитной индукции.
- § 141. Электродвижущая сила индукции.
- § 142. Электромагнитная индукция и сила Лоренца.
- § 143. Индукционные токи в массивных проводниках. Токи Фуко.
- Глава XVI. МАГНИТНЫЕ СВОЙСТВА ТЕЛ
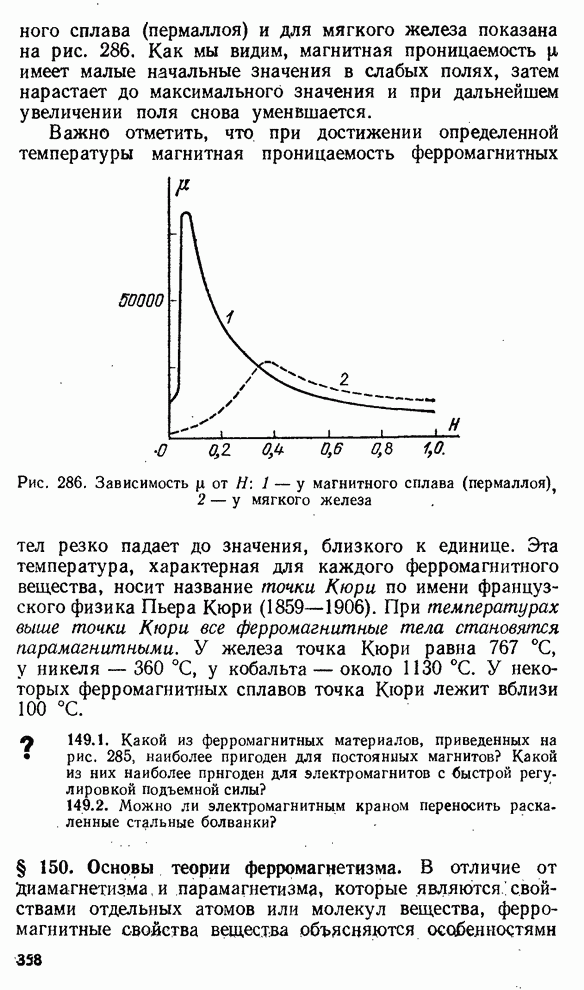
- § 144. Магнитная проницаемость железа.
- § 145. Магнитная проницаемость различных веществ. Вещества парамагнитные и диамагнитные.
- § 146. Движение парамагнитных и диамагнитных тел в магнитном поле. Опыты Фарадея.
- § 147. Молекулярная теория магнетизма.
- § 148. Магнитная защита.
- § 149. Особенности ферромагнитных тел.
- § 150. Основы теории ферромагнетизма.
- Глава XVII. ПЕРЕМЕННЫЙ ТОК
- § 151. Постоянная и переменная электродвижущая сила.
- § 152. Опытное исследование формы переменного тока. Осциллограф.
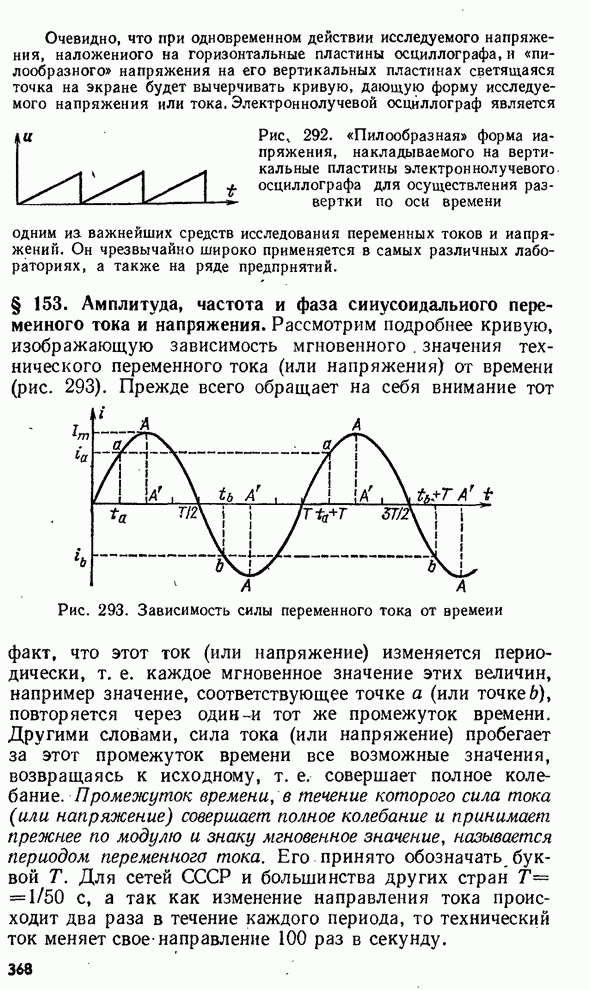
- § 153. Амплитуда, частота и фаза синусоидального переменного тока и напряжения.
- § 154. Сила переменного тока.
- § 155. Амперметры и вольтметры переменного тока.
- § 156. Самоиндукция.
- § 157. Индуктивность катушки.
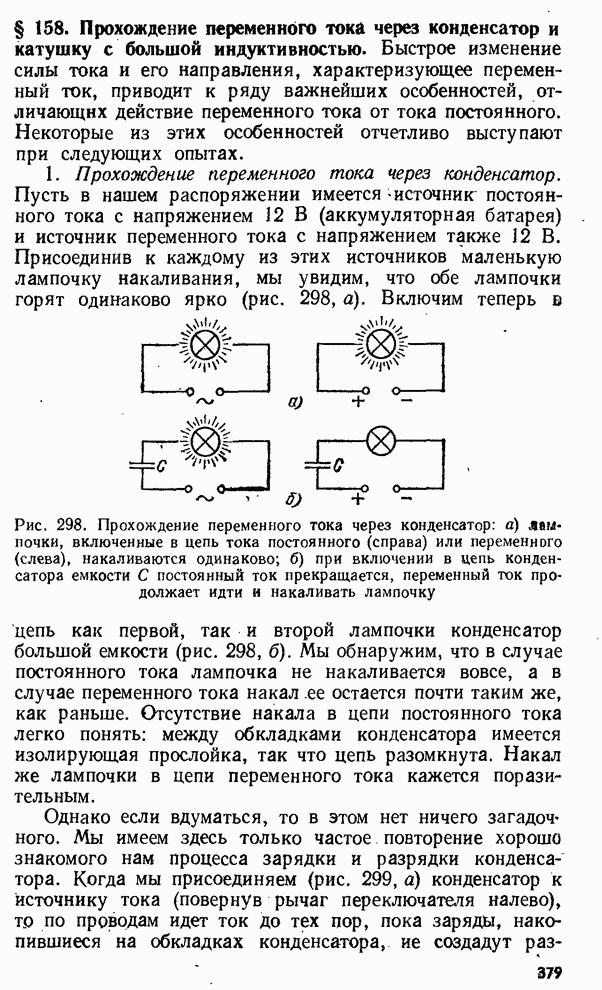
- § 158. Прохождение переменного тока через конденсатор и катушку с большой индуктивностью.
- § 159. Закон Ома для переменного тока. Емкостное и индуктивное сопротивления.
- § 160. Сложение токов при параллельном включении сопротивлений в цепь переменного тока.
- § 161. Сложение напряжений при последовательном соединении сопротивлений в цепи переменного тока.
- § 162. Сдвиг фаз между током и напряжением.
- § 163. Мощность переменного тока.
- § 164. Трансформаторы.
- § 165. Централизованное производство и распределение электрической энергии.
- § 166. Выпрямление переменного тока.
- Глава XVIII. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ: ГЕНЕРАТОРЫ, ДВИГАТЕЛИ, ЭЛЕКТРОМАГНИТЫ
- § 167. Генераторы переменного тока.
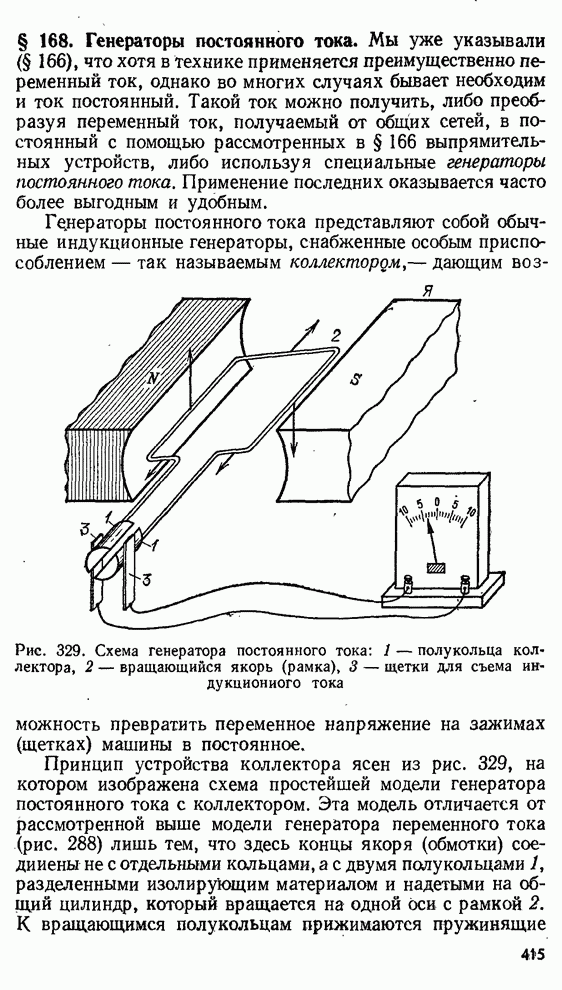
- § 168. Генераторы постоянного тока.
- § 169. Генераторы с независимым возбуждением и с самовозбуждением.
- § 170. Трехфазный ток.
- § 171. Трехфазный электродвигатель.
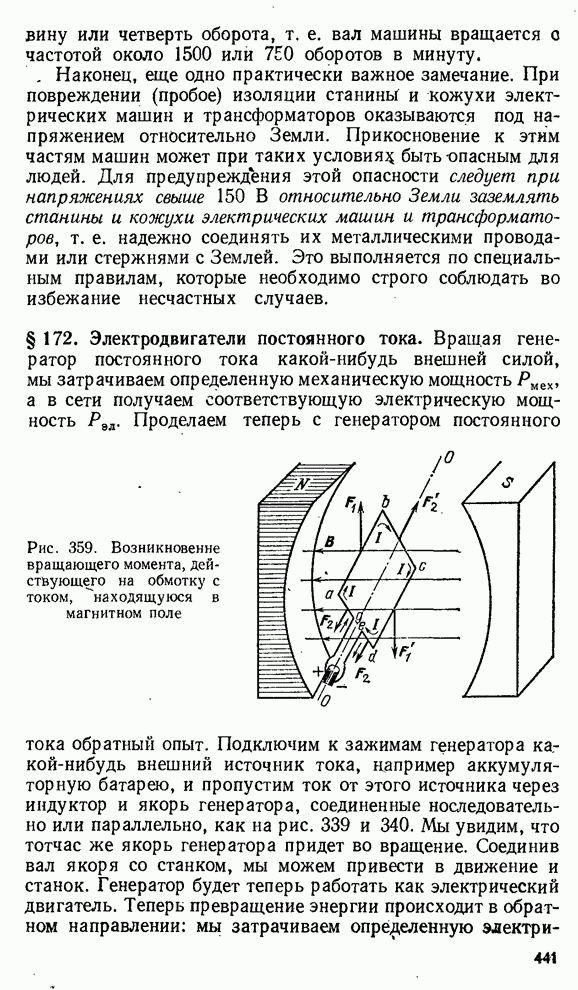
- § 172. Электродвигатели постоянного тока.
- § 173. Основные рабочие характеристики и особенности двигателей постоянного тока с параллельным и последовательным возбуждением.
- § 174. Коэффициент полезного действия генератора и двигателя.
- § 175. Обратимость электрических генераторов постоянного тока.
- § 176. Электромагниты.
- § 177. Применение электромагнитов.
- § 178. Реле и их применения в технике и автоматике.
- Ответы и решения к упражнениям
- Приложения
- Предметный указатель
- Таблицы