| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 160. Сложение токов при параллельном включении сопротивлений в цепь переменного тока.
Включим
в цепь переменного тока две параллельные ветви, содержащие активные
сопротивления ![]() и
и
![]() и
амперметры
и
амперметры ![]() и
и
![]() ,
измеряющие токи
,
измеряющие токи ![]() и
и ![]() в этих ветвях (рис. 301). Третий
амперметр А измеряет ток в неразветвленной цепи. Положим сначала, что оба
сопротивления
в этих ветвях (рис. 301). Третий
амперметр А измеряет ток в неразветвленной цепи. Положим сначала, что оба
сопротивления ![]() и
и
![]() представляют
собой лампочки накаливания или реостаты, индуктивным сопротивлением которых
можно пренебречь по сравнению с их активным сопротивлением (рис. 301,а). Тогда,
так же как и в случае постоянного тока, мы убедимся в том, что показание
амперметра
представляют
собой лампочки накаливания или реостаты, индуктивным сопротивлением которых
можно пренебречь по сравнению с их активным сопротивлением (рис. 301,а). Тогда,
так же как и в случае постоянного тока, мы убедимся в том, что показание
амперметра ![]() равно
сумме показаний амперметров
равно
сумме показаний амперметров ![]() и
и ![]() , т. е.
, т. е. ![]() . Если сопротивления
. Если сопротивления ![]() и
и ![]() представляют
собой реостаты, то, изменяя их сопротивления, мы можем как угодно изменять
каждый из токов
представляют
собой реостаты, то, изменяя их сопротивления, мы можем как угодно изменять
каждый из токов ![]() и
и ![]() , но равенство
, но равенство ![]() всегда будет сохраняться.
То же будет иметь место и в том случае, если мы заменим оба реостата
конденсаторами, т. е. если оба сопротивления будут емкостными (рис. 301,б), или
в том случае, если оба сопротивления являются индуктивными, т. е. реостаты заменены
катушками с железным сердечником, индуктивное сопротивление которых настолько
больше активного, что последним можно пренебречь (рис. 301,в).
всегда будет сохраняться.
То же будет иметь место и в том случае, если мы заменим оба реостата
конденсаторами, т. е. если оба сопротивления будут емкостными (рис. 301,б), или
в том случае, если оба сопротивления являются индуктивными, т. е. реостаты заменены
катушками с железным сердечником, индуктивное сопротивление которых настолько
больше активного, что последним можно пренебречь (рис. 301,в).

Рис. 301. Сопротивления в параллельных ветвях цепи переменного тока одинаковы по своей природе
Таким образом, если сопротивления параллельных ветвей одинаковы по своей природе, то ток в неразветвленной цепи равен сумме токов в отдельных ветвях. Это справедливо, конечно, и в том случае, когда имеются не две ветви, а любое их число.
Заменим
теперь в одной из ветвей (рис. 302,а и б) активное сопротивление емкостным
(конденсатором) или индуктивным (катушкой с большой индуктивностью и малым
активным сопротивлением). Опыт дает в этом случае результат, кажущийся на
первый взгляд странным: ток в неразветвленной цепи ![]() оказывается меньшим, чем
сумма токов в обеих ветвях:
оказывается меньшим, чем
сумма токов в обеих ветвях: ![]() . Если, например, ток в одной ветви
равен 3 А, а в другой – 4 А, то амперметр в неразветвленной цепи покажет не ток
7 А, как мы ожидали бы, а только ток 5 А, или 3 А, или 2 А и т. д. Ток
. Если, например, ток в одной ветви
равен 3 А, а в другой – 4 А, то амперметр в неразветвленной цепи покажет не ток
7 А, как мы ожидали бы, а только ток 5 А, или 3 А, или 2 А и т. д. Ток ![]() будет меньше
суммы токов
будет меньше
суммы токов ![]() и
и
![]() и
тогда, когда сопротивление одной ветви емкостное, а другой – индуктивное (рис.
302,в).
и
тогда, когда сопротивление одной ветви емкостное, а другой – индуктивное (рис.
302,в).

Рис. 302. Сопротивления в параллельных ветвях переменного тока различны по своей природе
Таким образом, если сопротивления параллельных ветвей различны по своей природе, то ток в неразветвленной цепи меньше суммы токов в отдельных ветвях.
Чтобы разобраться в этих явлениях, заменим в схемах на рис. 301 и 302 амперметры осциллографами и запишем форму кривой тока в каждой из параллельных ветвей. Оказывается, что токи разной природы в каждой из ветвей не совпадают по фазе ни друг с другом, ни с током в неразветвленной цепи. В частности, ток в цепи с активным сопротивлением опережает по фазе на четверть периода ток в цепи с емкостным сопротивлением и отстает по фазе на четверть периода от тока в цепи с индуктивным сопротивлением.
В
этом случае кривые, изображающие форму тока в неразветвленной цепи и в
какой-нибудь из ветвей, расположены относительно друг друга так, как кривые 1 и
2 на рис. 294. В общем же случае, в зависимости от соотношения между активным и
емкостным (или индуктивным) сопротивлениями каждой из ветвей, сдвиг фаз между
током в этой ветви и неразветвленным током может иметь любое значение от нуля
до ![]() .
Следовательно, при смешанном сопротивлении разность фаз между токами в
параллельных ветвях цепи может иметь любое значение между нулем и
.
Следовательно, при смешанном сопротивлении разность фаз между токами в
параллельных ветвях цепи может иметь любое значение между нулем и ![]() .
.
Это несовпадение фаз токов в параллельных ветвях с сопротивлениями, различными по своей природе, и является причиной тех явлений, о которых было сказано в начале этого параграфа. Действительно, для мгновенных значений токов, т. е. для тех значений, которые эти токи имеют в один и тот же момент времени, соблюдается известное правило:
![]() .
.
Но для амплитуд (или действующих значений) этих токов это правило не соблюдается, потому что результат сложения двух синусоидальных токов или иных двух величин, изменяющихся по закону синуса, зависит от разности фаз между складываемыми величинами.
В самом деле, предположим для простоты, что амплитуды складываемых токов одинаковы, а разность фаз между ними равна нулю. Тогда мгновенное значение суммы двух токов будет равно просто удвоенному значению мгновенного значения одного из складываемых токов, т. е. форма результирующего тока будет представлять собой синусоиду с тем же периодом и фазой, но с удвоенной амплитудой. Если амплитуды складываемых токов различны (рис. 303,а), то сумма их представляет собой синусоиду с амплитудой, равной сумме амплитуд складываемых токов. Это имеет место, когда разность фаз между складываемыми токами равна нулю, например когда сопротивления в обеих параллельных ветвях одинаковы по своей природе.

Рис. 303. Сложение двух
синусоидальных переменных токов. Складываемые токи: а) совпадают по фазе (![]() ); б)
противоположны по фазе, т. е. сдвинуты во времени на половину периода (
); б)
противоположны по фазе, т. е. сдвинуты во времени на половину периода (![]() ); в) сдвинуты во
времени на четверть периода (
); в) сдвинуты во
времени на четверть периода (![]() )
)
Рассмотрим
теперь другой крайний случай, когда складываемые токи, имея равные амплитуды,
противоположны по фазе, т. е. разность фаз между ними равна ![]() . В этом случае мгновенные
значения складываемых токов равны по модулю, но противоположны по направлению.
Поэтому их алгебраическая сумма будет постоянно равна нулю. Таким образом, при
сдвиге фаз на
. В этом случае мгновенные
значения складываемых токов равны по модулю, но противоположны по направлению.
Поэтому их алгебраическая сумма будет постоянно равна нулю. Таким образом, при
сдвиге фаз на ![]() между
токами в обеих ветвях, несмотря на наличие токов в каждой из параллельных
ветвей, в неразветвленной цепи тока не будет. Если амплитуды обоих смещенных на
между
токами в обеих ветвях, несмотря на наличие токов в каждой из параллельных
ветвей, в неразветвленной цепи тока не будет. Если амплитуды обоих смещенных на
![]() токов
различны, то мы получим результирующий ток с той же частотой, но с амплитудой,
равной разности амплитуд складываемых токов; по фазе этот ток совпадает с
током, имеющим большую амплитуду (рис. 303,б). Практически этот случай имеет
место тогда, когда в одной из ветвей имеется емкостное, а в другой –
индуктивное сопротивление.
токов
различны, то мы получим результирующий ток с той же частотой, но с амплитудой,
равной разности амплитуд складываемых токов; по фазе этот ток совпадает с
током, имеющим большую амплитуду (рис. 303,б). Практически этот случай имеет
место тогда, когда в одной из ветвей имеется емкостное, а в другой –
индуктивное сопротивление.
В
общем случае при сложении двух синусоидальных токов одной и той же частоты со
сдвигом фаз мы получаем всегда синусоидальный ток той же частоты с амплитудой,
которая в зависимости от разности фаз ![]() имеет промежуточное значение между
разностью амплитуд складываемых токов и их суммой. Для примера на рис. 303,в
показано графическое сложение двух токов с разностью фаз
имеет промежуточное значение между
разностью амплитуд складываемых токов и их суммой. Для примера на рис. 303,в
показано графическое сложение двух токов с разностью фаз ![]() . С помощью циркуля легко
убедиться в том, что каждая ордината результирующей кривой
. С помощью циркуля легко
убедиться в том, что каждая ордината результирующей кривой ![]() действительно
представляет собой алгебраическую сумму ординат кривых
действительно
представляет собой алгебраическую сумму ординат кривых ![]() и
и ![]() с одинаковой абсциссой,
т. е. для того же момента времени.
с одинаковой абсциссой,
т. е. для того же момента времени.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- Глава I. Электрические заряды
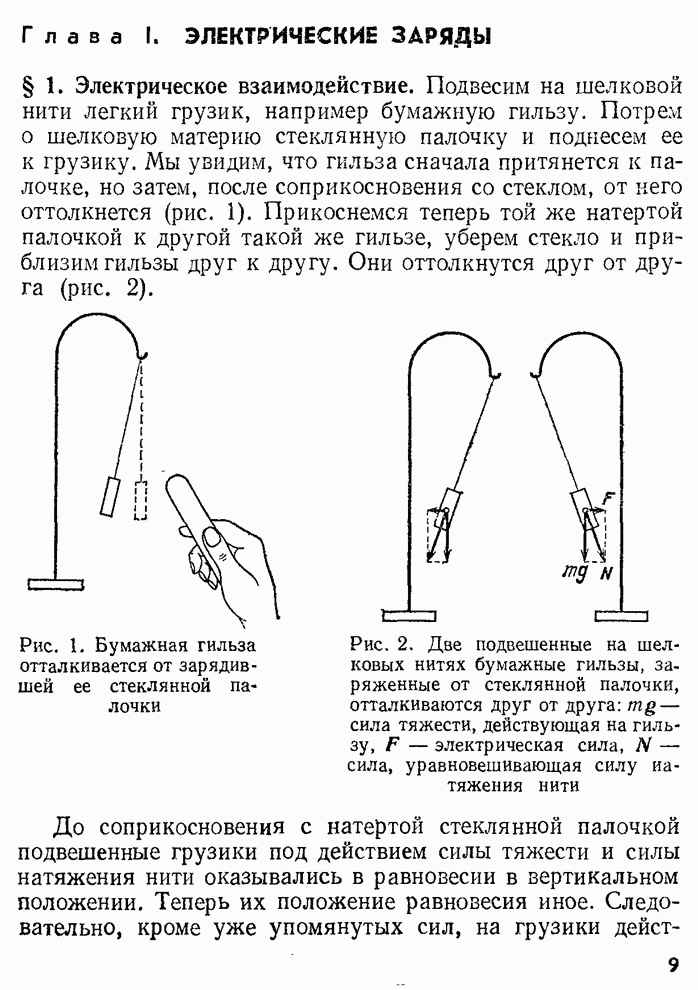
- § 1. Электрическое взаимодействие.
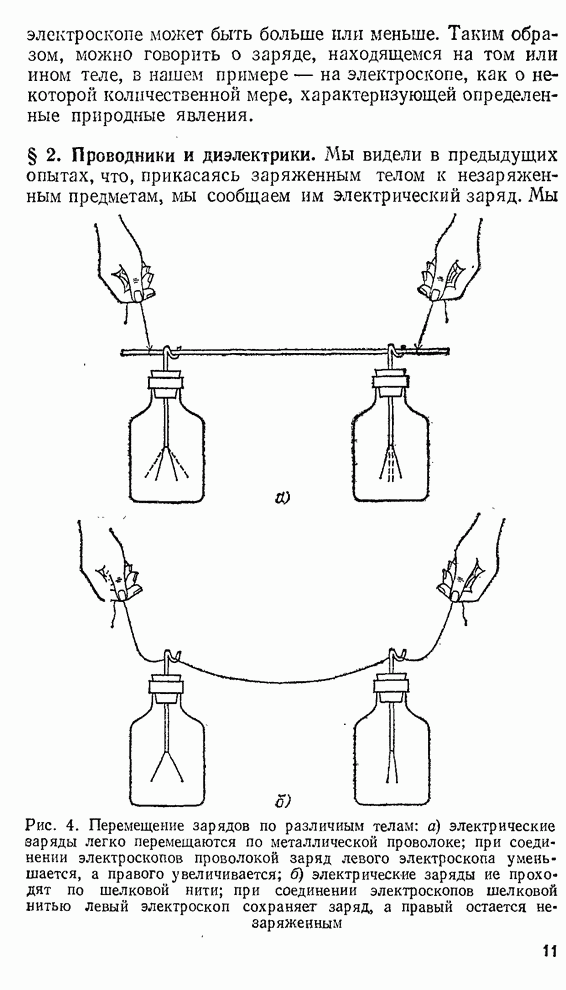
- § 2. Проводники и диэлектрики.
- § 3. Разделение тел на проводники и диэлектрики
- § 4. Положительные и отрицательные заряды
- § 5. Что происходит при электризации?
- § 6. Электронная теория.
- § 7. Электризация трением.
- § 8. Электризация через влияние.
- § 9. Электризация под действием света.
- § 10. Закон Кулона.
- § 11. Единица заряда.
- Глава II. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- § 12. Действие электрического заряда на окружающие тела.
- § 13. Понятие об электрическом поле.
- § 14. Напряженность электрического поля.
- § 15. Сложение полей.
- § 16. Электрическое поле в диэлектриках и в проводниках.
- § 17. Графическое изображение полей.
- § 18. Основные особенности электрических карт.
- § 19. Применение метода линий поля к задачам электростатики.
- § 20. Работа при перемещении заряда в электрическом поле.
- § 21. Разность потенциалов (электрическое напряжение).
- § 22. Эквипотенциальные поверхности.
- § 23. В чем смысл введения разности потенциалов?
- § 24. Условия равновесия зарядов в проводниках.
- § 25. Электрометр.
- § 26. В чем различие между электрометром и электроскопом?
- § 27. Соединение с Землей.
- § 28. Измерение разности потенциалов в воздухе. Электрический зонд.
- § 29. Электрическое поле Земли.
- § 30. Простейшие электрические поля.
- § 31. Распределение зарядов в проводнике. Клетка Фарадея.
- § 32. Поверхностная плотность заряда.
- § 33. Конденсаторы.
- § 34. Различные типы конденсаторов.
- § 35. Параллельное и последовательное соединение конденсаторов.
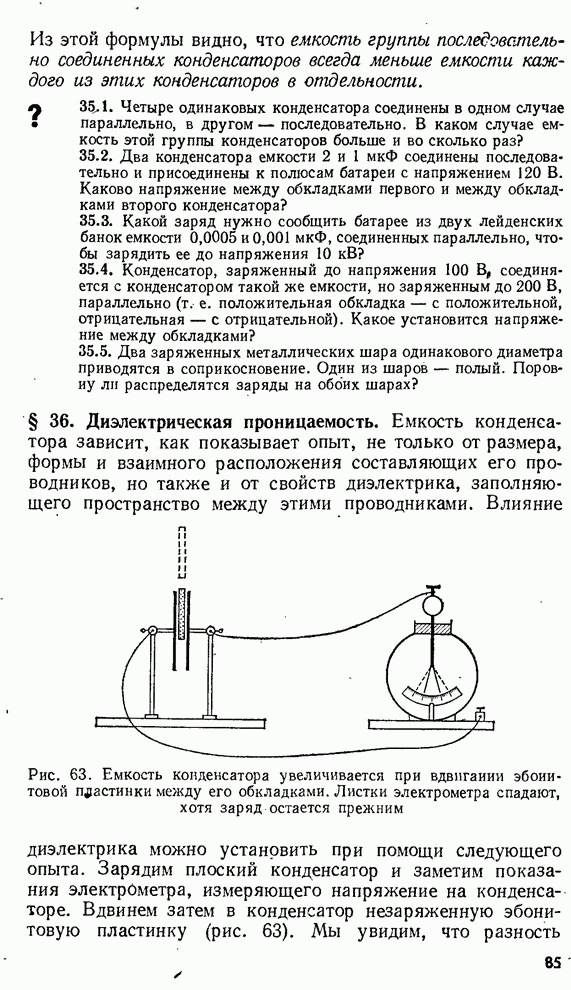
- § 36. Диэлектрическая проницаемость.
- § 37. Почему электрическое поле ослабляется внутри диэлектрика?
- § 38. Энергия заряженных тел. Энергия электрического поля.
- Глава III. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 39. Электрический ток и электродвижущая сила.
- § 40. Признаки электрического тока.
- § 41. Направление тока.
- § 42. Сила тока.
- § 43. «Скорость электрического тока» и скорость движения носителей заряда.
- § 44. Гальванометр.
- § 45. Распределение напряжения в проводнике с током.
- § 46. Закон Ома.
- § 47. Сопротивление проводов.
- § 48. Зависимость сопротивления от температуры.
- § 49. Сверхпроводимость.
- § 50. Последовательное и параллельное соединение проводников.
- § 51. Реостаты.
- § 52. Распределение напряжения в цепи.
- § 53. Вольтметр.
- § 54. Каким должно быть сопротивление вольтметра и амперметра?
- § 55. Шунтирование измерительных приборов.
- Глава IV. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА
- § 56. Нагревание током. Закон Джоуля-Ленца.
- § 57. Работа, совершаемая электрическим током.
- § 58. Мощность электрического тока.
- § 59. Контактная сварка.
- § 60. Электрические нагревательные приборы. Электрические печи.
- § 61. Понятие о расчете нагревательных приборов.
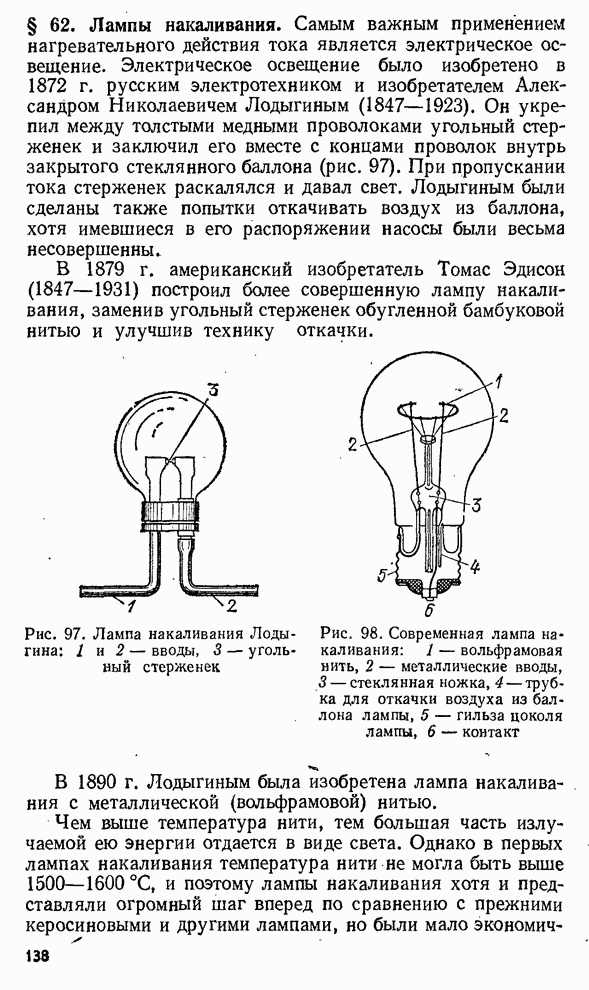
- § 62. Лампы накаливания.
- § 63. Короткое замыкание.
- § 64. Электрическая проводка.
- Глава V. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ЭЛЕКТРОЛИТЫ
- § 65. Первый закон Фарадея.
- § 66. Второй закон Фарадея.
- § 67. Ионная проводимость электролитов.
- § 68. Движение ионов в электролитах.
- § 69. Элементарный электрический заряд.
- § 70. Первичные и вторичные процессы при электролизе.
- § 71. Электролитическая диссоциация.
- § 72. Градуировка амперметров при помощи электролиза.
- § 73. Технические применения электролиза.
- Глава VI. ХИМИЧЕСКИЕ И ТЕПЛОВЫЕ ГЕНЕРАТОРЫ ТОКА
- § 74. Введение. Открытие Вольты.
- § 75. Правило Вольты. Гальванический элемент.
- § 76. Как возникают э. д. с. и ток в гальваническом элементе?
- § 77. Поляризация электродов.
- § 78. Деполяризация в гальванических элементах.
- § 79. Аккумуляторы.
- § 80. Закон Ома для замкнутой цепи.
- § 81. Напряжение на зажимах источника тока и э. д. с.
- § 82. Соединение источников тока.
- § 83. Термоэлементы.
- § 84. Термоэлементы в качестве генераторов.
- § 85. Измерение температуры с помощью термоэлементов.
- Глава VII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ МЕТАЛЛЫ
- § 86. Электронная проводимость металлов.
- § 87. Строение металлов.
- § 88. Причина электрического сопротивления.
- § 89. Работа выхода.
- § 90. Испускание электронов накаленными телами.
- Глава VIII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ГАЗЫ
- § 91. Самостоятельная и несамостоятельная проводимость газов.
- § 92. Несамостоятельная проводимость газа.
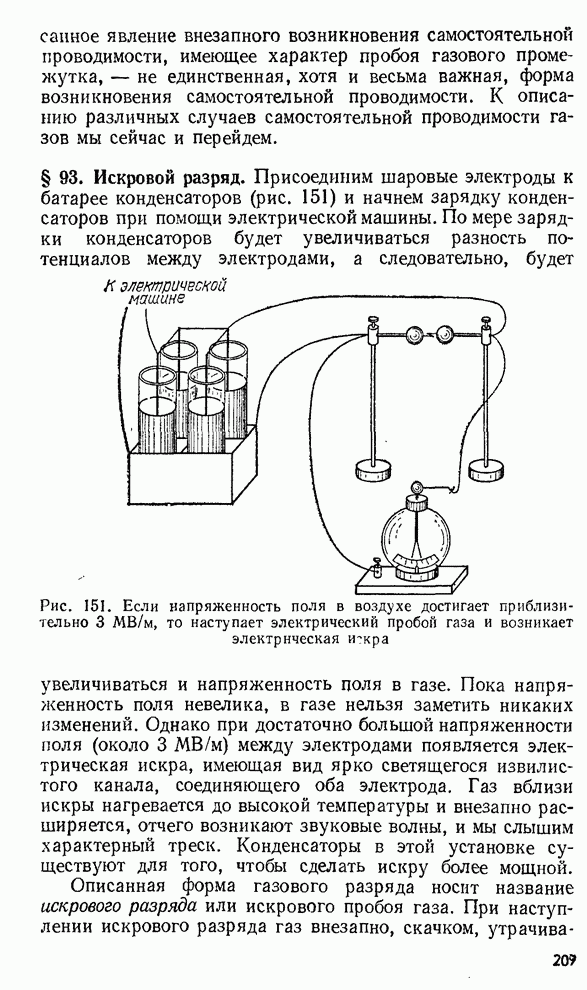
- § 93. Искровой разряд.
- § 94. Молния.
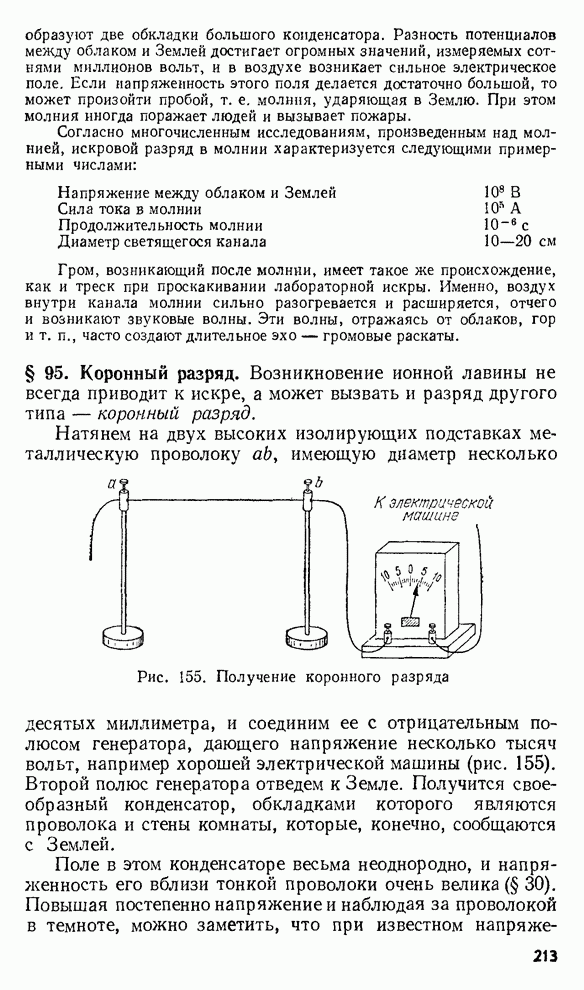
- § 95. Коронный разряд.
- § 96. Применения коронного разряда.
- § 97. Громоотвод.
- § 98. Электрическая дуга.
- § 99. Применения дугового разряда.
- § 100. Тлеющий разряд.
- § 101. Что происходит при тлеющем разряде?
- § 102. Катодные лучи.
- § 103. Природа катодных лучей.
- § 104. Каналовые лучи.
- § 105. Электронная проводимость в высоком вакууме.
- § 106. Электронные лампы.
- § 107. Электроннолучевая трубка.
- Глава IX. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ПОЛУПРОВОДНИКИ
- § 108. Природа электрического тока в полупроводниках.
- § 109. Движение электронов в полупроводниках.
- § 110. Полупроводниковые выпрямители.
- § 111. Полупроводниковые фотоэлементы.
- Глава X. ОСНОВНЫЕ МАГНИТНЫЕ ЯВЛЕНИЯ
- § 112. Естественные и искусственные магниты.
- § 113. Полюсы магнита и его нейтральная зона.
- § 114. Магнитное действие электрического тока.
- § 115. Магнитные действия токов и постоянных магнитов.
- § 116. Происхождение магнитного поля постоянных магнитов.
- § 117. Гипотеза Ампера об элементарных электрических токах.
- Глава XI. МАГНИТНОЕ ПОЛЕ
- § 118. Магнитное поле и его проявления. Магнитная индукция.
- § 119. Магнитный момент. Единица магнитной индукции.
- § 120. Измерение магнитной индукции поля с помощью магнитной стрелки.
- § 121. Сложение магнитных полей.
- § 122. Линии магнитного поля.
- § 123. Приборы для измерения магнитной индукции.
- Глава XII. МАГНИТНЫЕ ПОЛЯ ЭЛЕКТРИЧЕСКИХ ТОКОВ
- § 124. Магнитное поле прямолинейного проводника и кругового витка с током.
- § 125. Магнитное поле соленоида. Эквивалентность соленоида и полосового магнита.
- § 126. Магнитное поле внутри соленоида. Напряженность магнитного поля.
- § 127. Магнитное поле движущихся зарядов.
- Глава XIII. МАГНИТНОЕ ПОЛЕ ЗЕМЛИ
- § 128. Магнитное поле Земли.
- § 129. Элементы земного магнетизма.
- § 130. Магнитные аномалии и магнитная разведка полезных ископаемых.
- § 131. Изменение элементов земного магнетизма с течением времени. Магнитные бури.
- Глава XIV. СИЛЫ, ДЕЙСТВУЮЩИЕ В МАГНИТНОМ ПОЛЕ НА ПРОВОДНИКИ С ТОКОМ
- § 132. Введение.
- § 133. Действие магнитного поля на прямолинейный проводник с током. Правило левой руки.
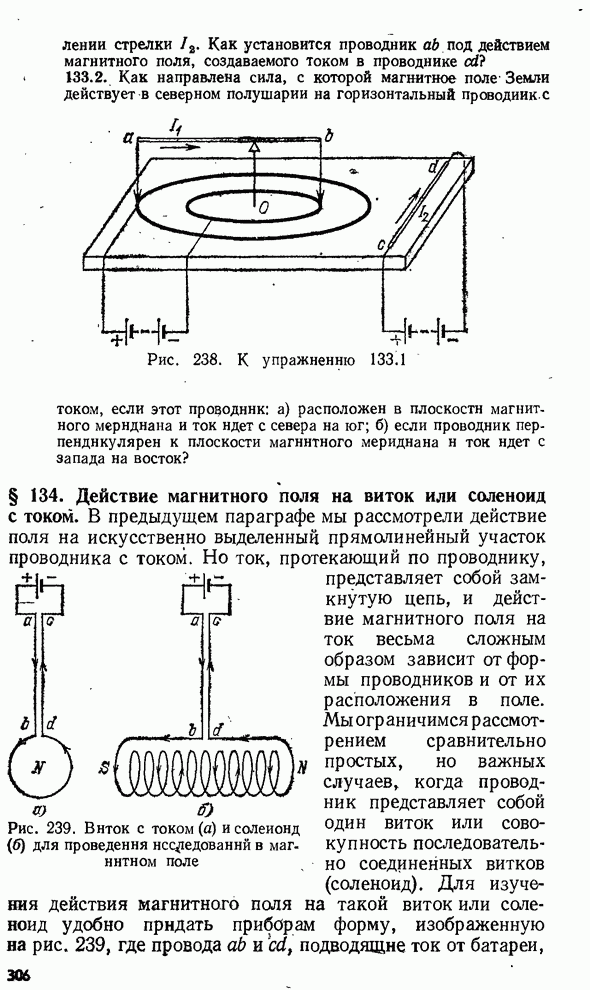
- § 134. Действие магнитного поля на виток или соленоид с током.
- § 135. Гальванометр, основанный на взаимодействии магнитного поля и тока.
- § 136. Сила Лоренца.
- § 137. Сила Лоренца и полярные сияния.
- Глава XV. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
- § 138. Условия возникновения индукционного тока.
- § 139. Направление индукционного тока. Правило Ленца.
- § 140. Основной закон электромагнитной индукции.
- § 141. Электродвижущая сила индукции.
- § 142. Электромагнитная индукция и сила Лоренца.
- § 143. Индукционные токи в массивных проводниках. Токи Фуко.
- Глава XVI. МАГНИТНЫЕ СВОЙСТВА ТЕЛ
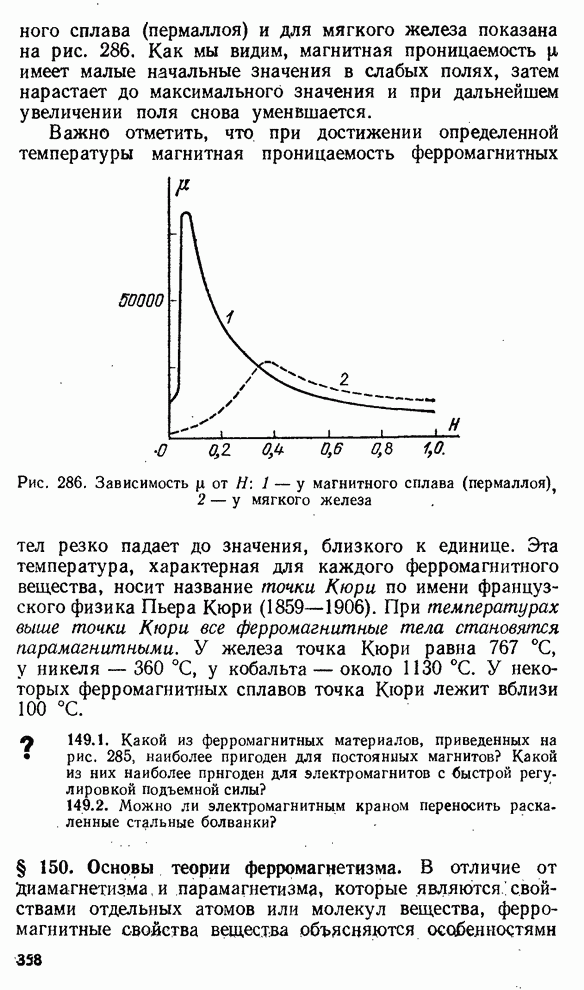
- § 144. Магнитная проницаемость железа.
- § 145. Магнитная проницаемость различных веществ. Вещества парамагнитные и диамагнитные.
- § 146. Движение парамагнитных и диамагнитных тел в магнитном поле. Опыты Фарадея.
- § 147. Молекулярная теория магнетизма.
- § 148. Магнитная защита.
- § 149. Особенности ферромагнитных тел.
- § 150. Основы теории ферромагнетизма.
- Глава XVII. ПЕРЕМЕННЫЙ ТОК
- § 151. Постоянная и переменная электродвижущая сила.
- § 152. Опытное исследование формы переменного тока. Осциллограф.
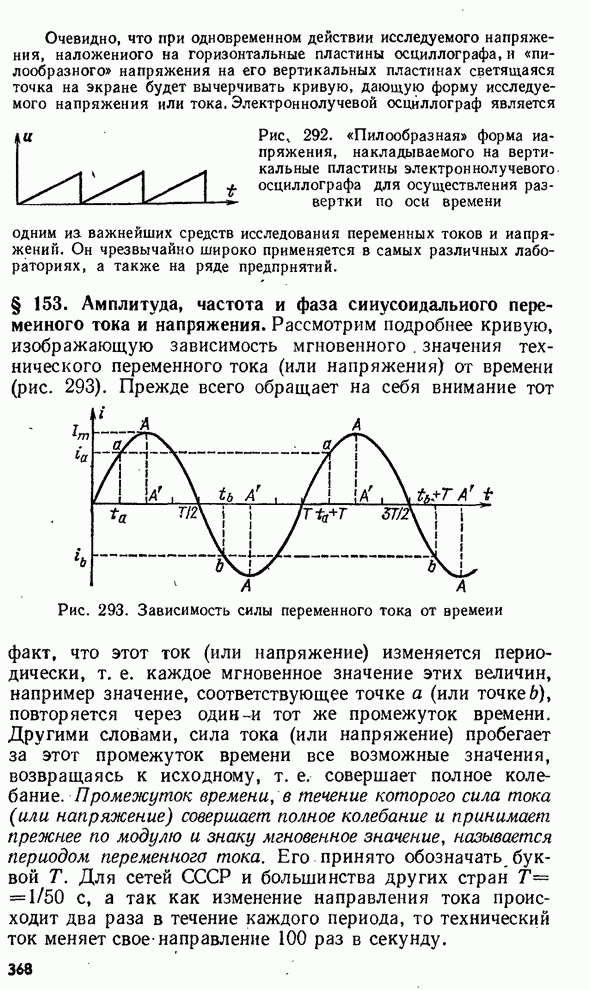
- § 153. Амплитуда, частота и фаза синусоидального переменного тока и напряжения.
- § 154. Сила переменного тока.
- § 155. Амперметры и вольтметры переменного тока.
- § 156. Самоиндукция.
- § 157. Индуктивность катушки.
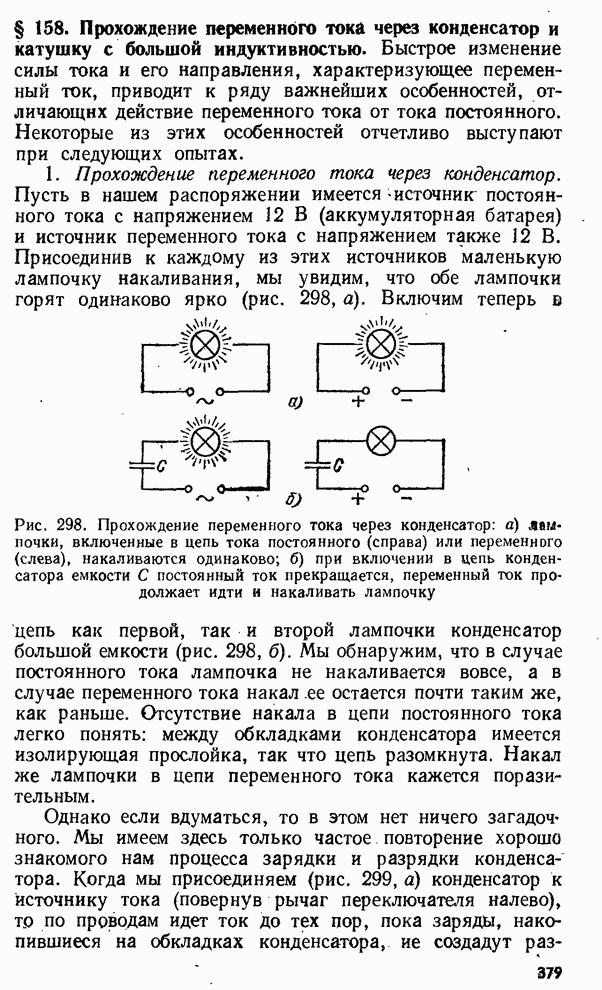
- § 158. Прохождение переменного тока через конденсатор и катушку с большой индуктивностью.
- § 159. Закон Ома для переменного тока. Емкостное и индуктивное сопротивления.
- § 160. Сложение токов при параллельном включении сопротивлений в цепь переменного тока.
- § 161. Сложение напряжений при последовательном соединении сопротивлений в цепи переменного тока.
- § 162. Сдвиг фаз между током и напряжением.
- § 163. Мощность переменного тока.
- § 164. Трансформаторы.
- § 165. Централизованное производство и распределение электрической энергии.
- § 166. Выпрямление переменного тока.
- Глава XVIII. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ: ГЕНЕРАТОРЫ, ДВИГАТЕЛИ, ЭЛЕКТРОМАГНИТЫ
- § 167. Генераторы переменного тока.
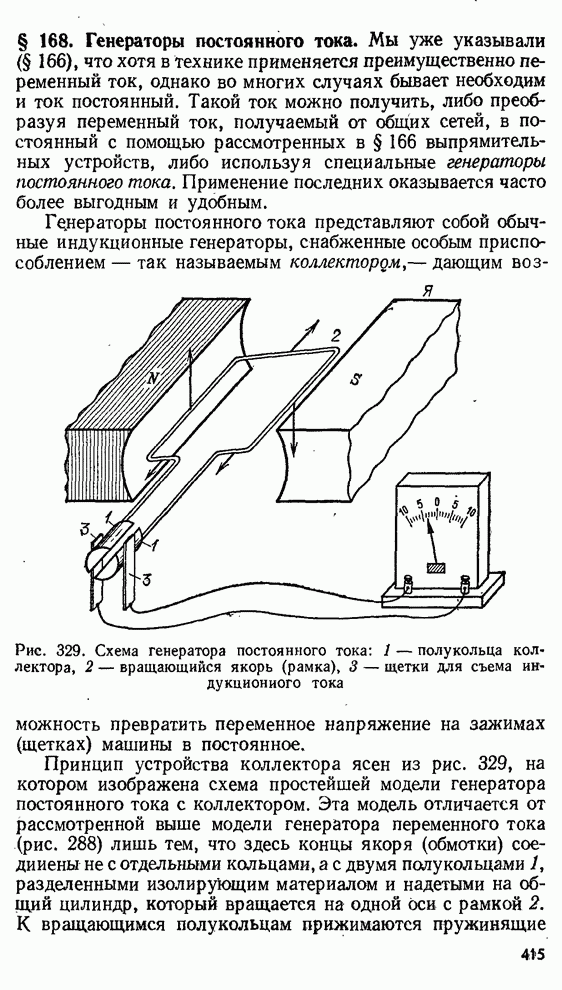
- § 168. Генераторы постоянного тока.
- § 169. Генераторы с независимым возбуждением и с самовозбуждением.
- § 170. Трехфазный ток.
- § 171. Трехфазный электродвигатель.
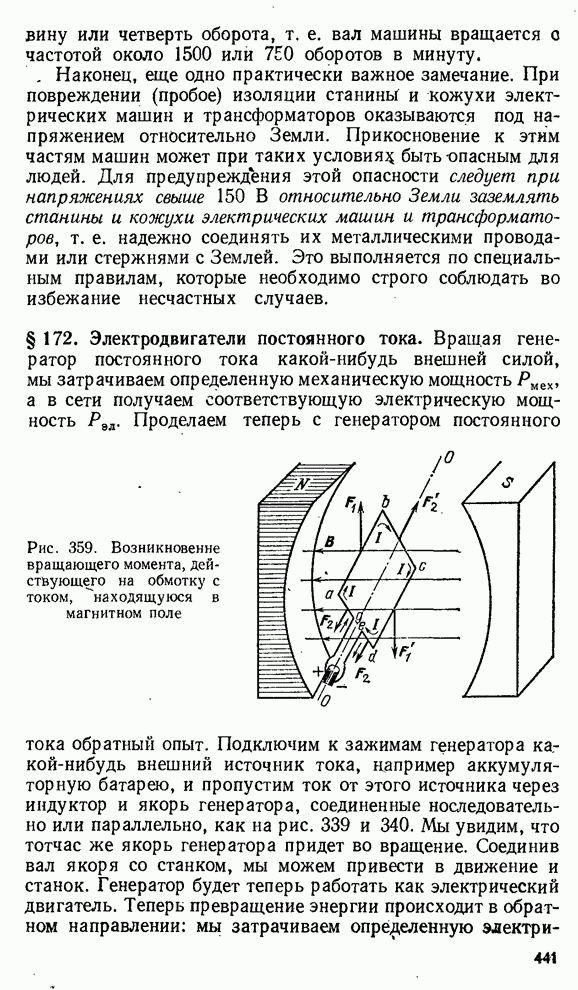
- § 172. Электродвигатели постоянного тока.
- § 173. Основные рабочие характеристики и особенности двигателей постоянного тока с параллельным и последовательным возбуждением.
- § 174. Коэффициент полезного действия генератора и двигателя.
- § 175. Обратимость электрических генераторов постоянного тока.
- § 176. Электромагниты.
- § 177. Применение электромагнитов.
- § 178. Реле и их применения в технике и автоматике.
- Ответы и решения к упражнениям
- Приложения
- Предметный указатель
- Таблицы