| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
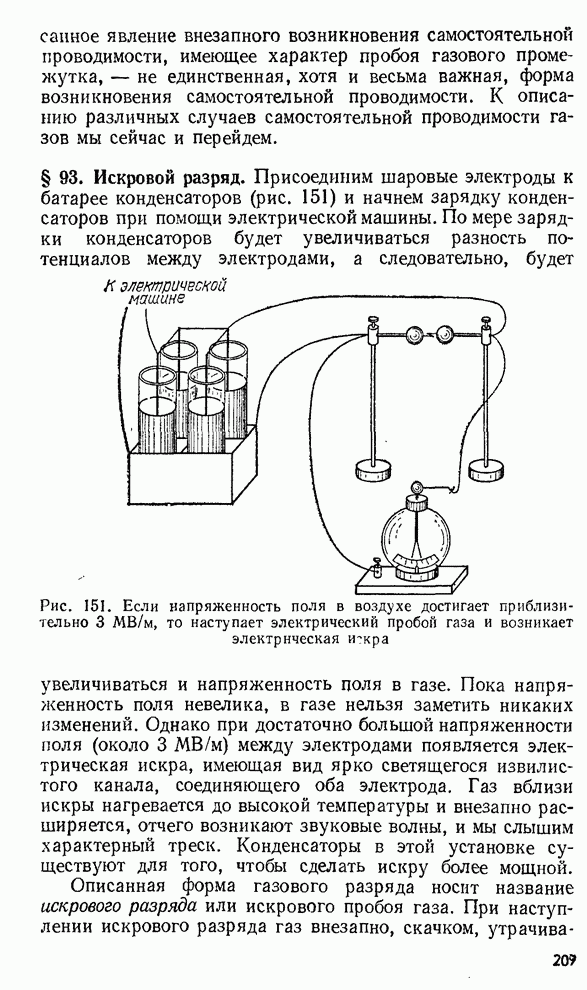
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
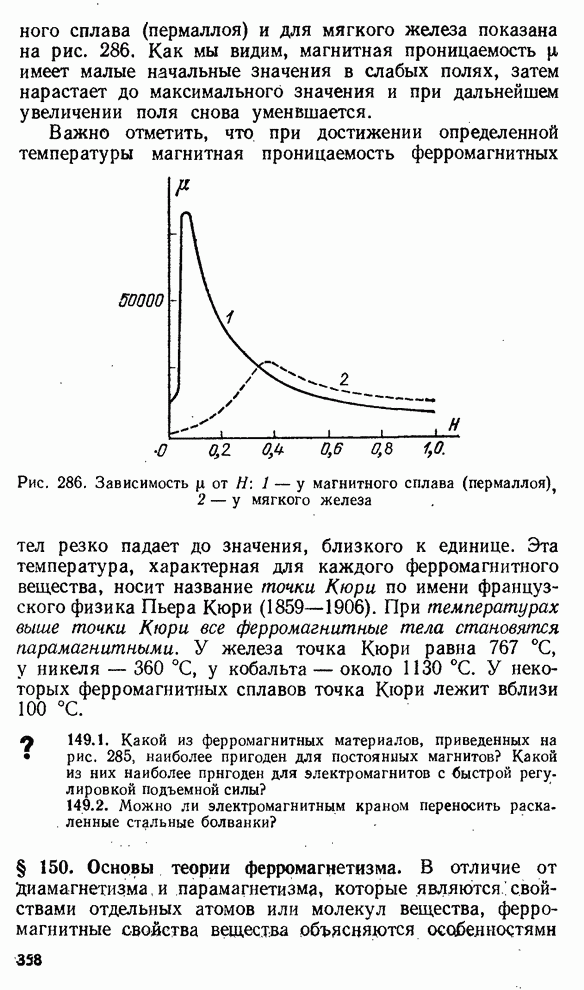
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
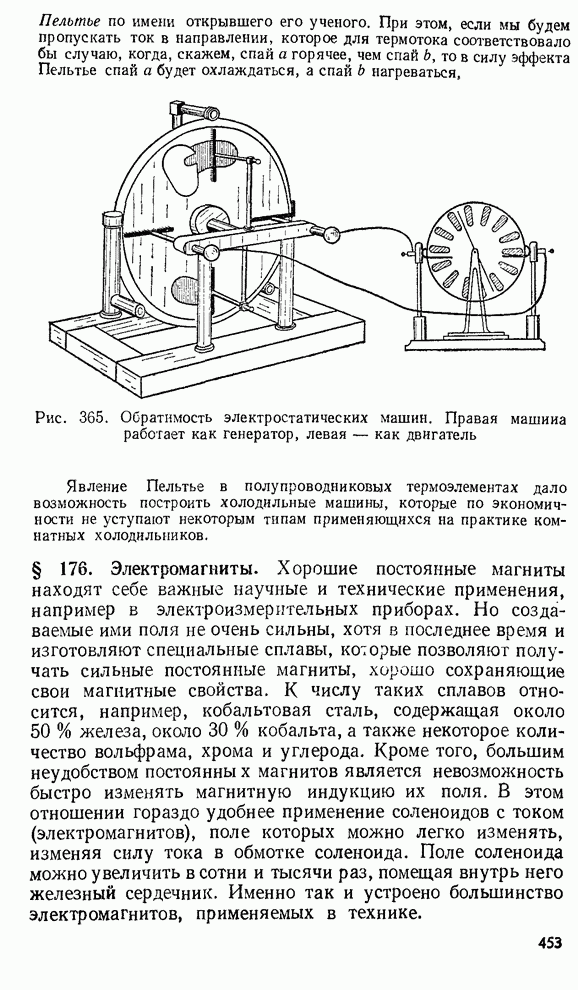
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 22. Эквипотенциальные поверхности.
Подобно тому как мы графически изображаем линиями напряженность электрического поля, можно изобразить и разность потенциалов (напряжение).
Вообразим поверхность, для любой пары точек которой разность потенциалов равна нулю. Такая поверхность называется эквипотенциальной поверхностью или поверхностью равного потенциала. Пересекаясь с плоскостью чертежа, эта поверхность образует некоторую линию – эквипотенциальную линию. Согласно формуле (21.1), при перемещении заряда вдоль такой поверхности (или линии) работа электрических сил равна нулю. Это может быть только в том случае, если направление перемещения все время перпендикулярно к действующей силе, а значит, эквипотенциальная поверхность в любой точке перпендикулярна к линиям поля. И обратно, всякая поверхность, перпендикулярная в любой точке к линиям поля, есть эквипотенциальная поверхность, так как перемещение заряда вдоль этой поверхности вследствие перпендикулярности силы и перемещения не будет сопровождаться работой электрических сил.
На чертеже мы изображаем не эквипотенциальные поверхности, а лишь их сечение плоскостью чертежа, т. е. эквипотенциальные линии. С их помощью мы получаем наглядное представление о том, как изменяется разность потенциалов в данном поле. Их удобно чертить таким образом, чтобы разность потенциалов для любых двух соседних линий была одна и та же, например 1 В. Для того чтобы эту разность потенциалов показать на чертеже, мы выберем произвольную эквипотенциальную линию, отметим ее цифрой 0 и будем проставлять возле всех остальных цифры 1, 2, 3 и т. д., указывающие разность потенциалов в вольтах между точками данной эквипотенциальной линии и линии, выбранной нами за нулевую. При этом выбор нулевой линии (нулевой поверхности) совершенно произволен, так как физический смысл имеет только разность потенциалов для двух каких-либо поверхностей (§ 21), а эта разность, очевидно, не зависит от выбора нулевой поверхности.
Рассмотрим в качестве примера поле точечного положительного заряда. В этом случае линии поля – радиальные прямые, и поэтому эквипотенциальные поверхности – концентрические сферы, которые в каждой точке перпендикулярны к линиям поля. Эквипотенциальные линии – концентрические окружности, изображенные на рис. 40,а. При построении этого чертежа за нулевую линию была выбрана произвольная окружность и затем построены окружности с разностью потенциалов (относительно нулевой окружности) 1, 2, 3 и т. д. вольт. На рис. 40,б показаны построенные таким образом эквипотенциальные линии точечного отрицательного заряда.

Рис. 40. Карта эквипотенциальных поверхностей точечного заряда: а) заряд положительный; б) заряд отрицательный
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- Глава I. Электрические заряды
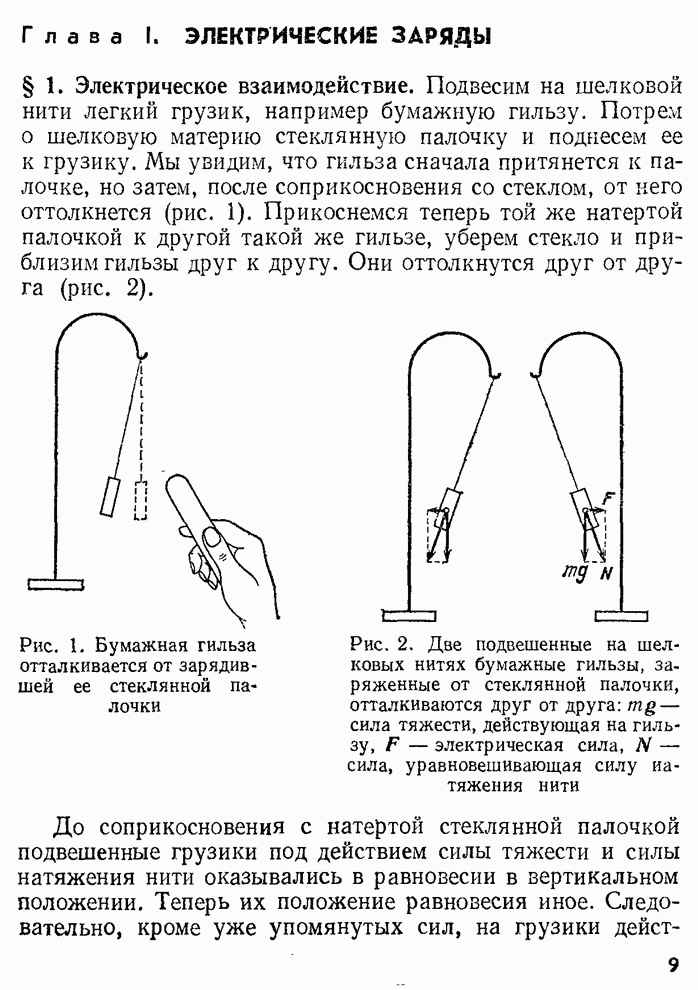
- § 1. Электрическое взаимодействие.
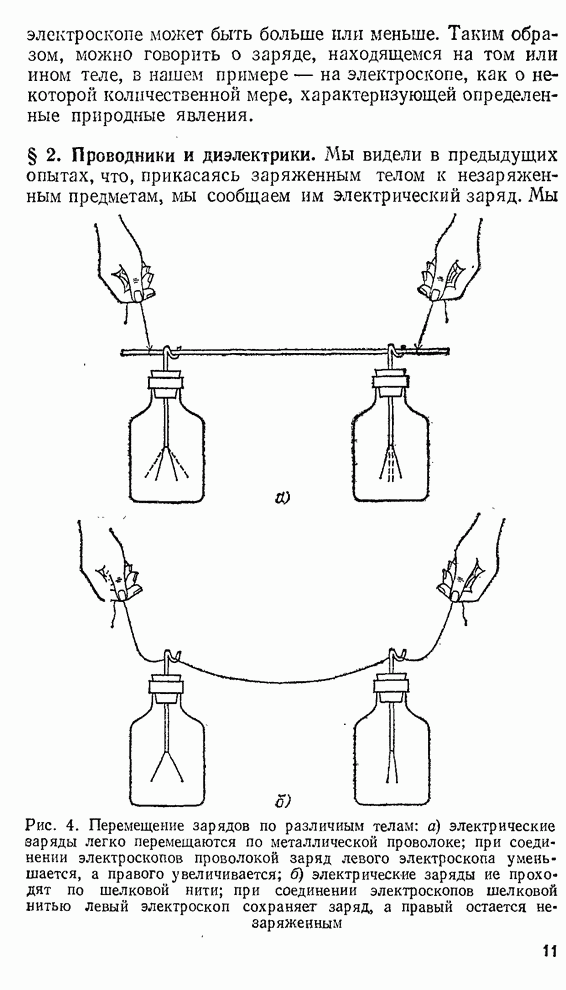
- § 2. Проводники и диэлектрики.
- § 3. Разделение тел на проводники и диэлектрики
- § 4. Положительные и отрицательные заряды
- § 5. Что происходит при электризации?
- § 6. Электронная теория.
- § 7. Электризация трением.
- § 8. Электризация через влияние.
- § 9. Электризация под действием света.
- § 10. Закон Кулона.
- § 11. Единица заряда.
- Глава II. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- § 12. Действие электрического заряда на окружающие тела.
- § 13. Понятие об электрическом поле.
- § 14. Напряженность электрического поля.
- § 15. Сложение полей.
- § 16. Электрическое поле в диэлектриках и в проводниках.
- § 17. Графическое изображение полей.
- § 18. Основные особенности электрических карт.
- § 19. Применение метода линий поля к задачам электростатики.
- § 20. Работа при перемещении заряда в электрическом поле.
- § 21. Разность потенциалов (электрическое напряжение).
- § 22. Эквипотенциальные поверхности.
- § 23. В чем смысл введения разности потенциалов?
- § 24. Условия равновесия зарядов в проводниках.
- § 25. Электрометр.
- § 26. В чем различие между электрометром и электроскопом?
- § 27. Соединение с Землей.
- § 28. Измерение разности потенциалов в воздухе. Электрический зонд.
- § 29. Электрическое поле Земли.
- § 30. Простейшие электрические поля.
- § 31. Распределение зарядов в проводнике. Клетка Фарадея.
- § 32. Поверхностная плотность заряда.
- § 33. Конденсаторы.
- § 34. Различные типы конденсаторов.
- § 35. Параллельное и последовательное соединение конденсаторов.
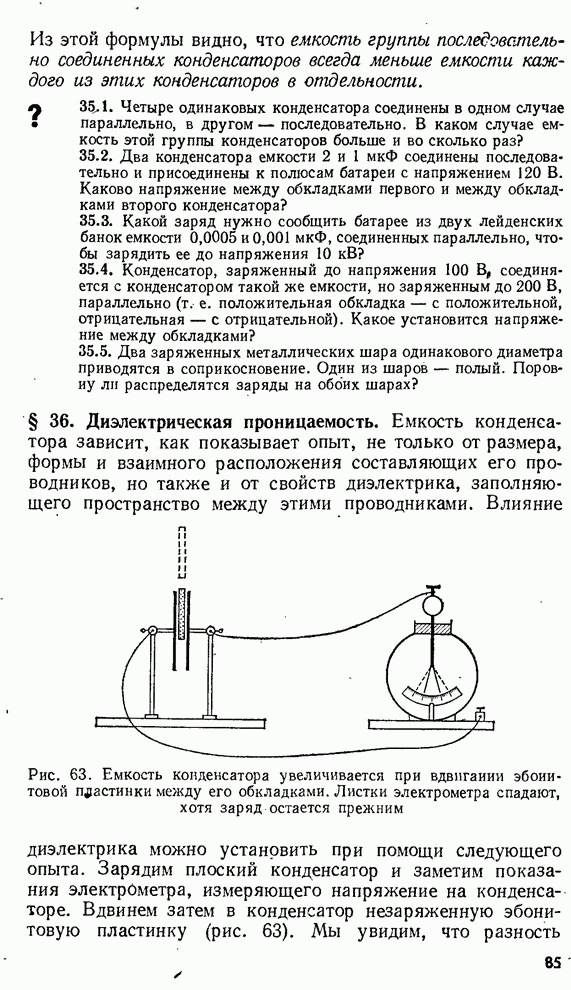
- § 36. Диэлектрическая проницаемость.
- § 37. Почему электрическое поле ослабляется внутри диэлектрика?
- § 38. Энергия заряженных тел. Энергия электрического поля.
- Глава III. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 39. Электрический ток и электродвижущая сила.
- § 40. Признаки электрического тока.
- § 41. Направление тока.
- § 42. Сила тока.
- § 43. «Скорость электрического тока» и скорость движения носителей заряда.
- § 44. Гальванометр.
- § 45. Распределение напряжения в проводнике с током.
- § 46. Закон Ома.
- § 47. Сопротивление проводов.
- § 48. Зависимость сопротивления от температуры.
- § 49. Сверхпроводимость.
- § 50. Последовательное и параллельное соединение проводников.
- § 51. Реостаты.
- § 52. Распределение напряжения в цепи.
- § 53. Вольтметр.
- § 54. Каким должно быть сопротивление вольтметра и амперметра?
- § 55. Шунтирование измерительных приборов.
- Глава IV. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА
- § 56. Нагревание током. Закон Джоуля-Ленца.
- § 57. Работа, совершаемая электрическим током.
- § 58. Мощность электрического тока.
- § 59. Контактная сварка.
- § 60. Электрические нагревательные приборы. Электрические печи.
- § 61. Понятие о расчете нагревательных приборов.
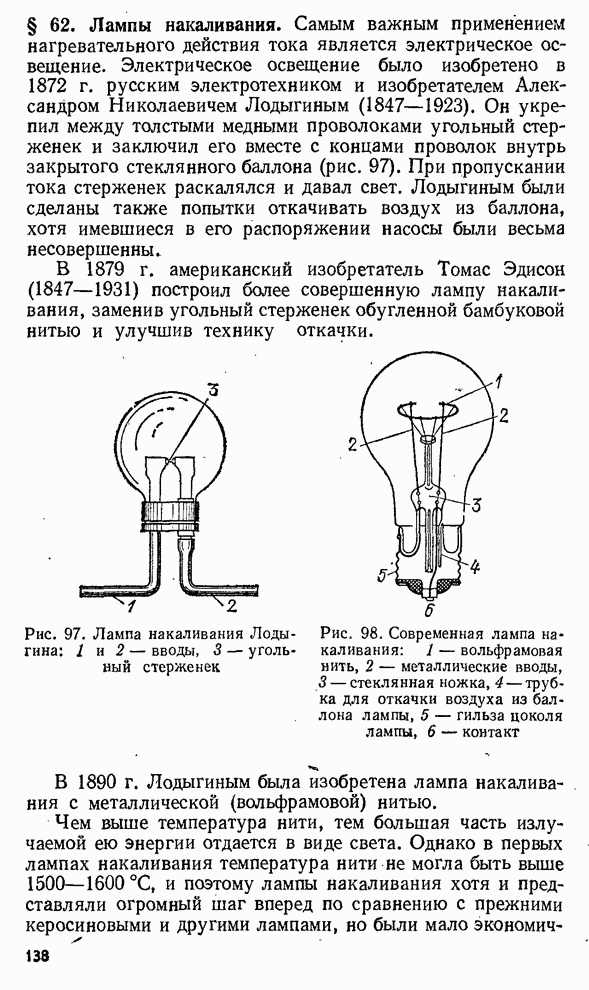
- § 62. Лампы накаливания.
- § 63. Короткое замыкание.
- § 64. Электрическая проводка.
- Глава V. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ЭЛЕКТРОЛИТЫ
- § 65. Первый закон Фарадея.
- § 66. Второй закон Фарадея.
- § 67. Ионная проводимость электролитов.
- § 68. Движение ионов в электролитах.
- § 69. Элементарный электрический заряд.
- § 70. Первичные и вторичные процессы при электролизе.
- § 71. Электролитическая диссоциация.
- § 72. Градуировка амперметров при помощи электролиза.
- § 73. Технические применения электролиза.
- Глава VI. ХИМИЧЕСКИЕ И ТЕПЛОВЫЕ ГЕНЕРАТОРЫ ТОКА
- § 74. Введение. Открытие Вольты.
- § 75. Правило Вольты. Гальванический элемент.
- § 76. Как возникают э. д. с. и ток в гальваническом элементе?
- § 77. Поляризация электродов.
- § 78. Деполяризация в гальванических элементах.
- § 79. Аккумуляторы.
- § 80. Закон Ома для замкнутой цепи.
- § 81. Напряжение на зажимах источника тока и э. д. с.
- § 82. Соединение источников тока.
- § 83. Термоэлементы.
- § 84. Термоэлементы в качестве генераторов.
- § 85. Измерение температуры с помощью термоэлементов.
- Глава VII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ МЕТАЛЛЫ
- § 86. Электронная проводимость металлов.
- § 87. Строение металлов.
- § 88. Причина электрического сопротивления.
- § 89. Работа выхода.
- § 90. Испускание электронов накаленными телами.
- Глава VIII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ГАЗЫ
- § 91. Самостоятельная и несамостоятельная проводимость газов.
- § 92. Несамостоятельная проводимость газа.
- § 93. Искровой разряд.
- § 94. Молния.
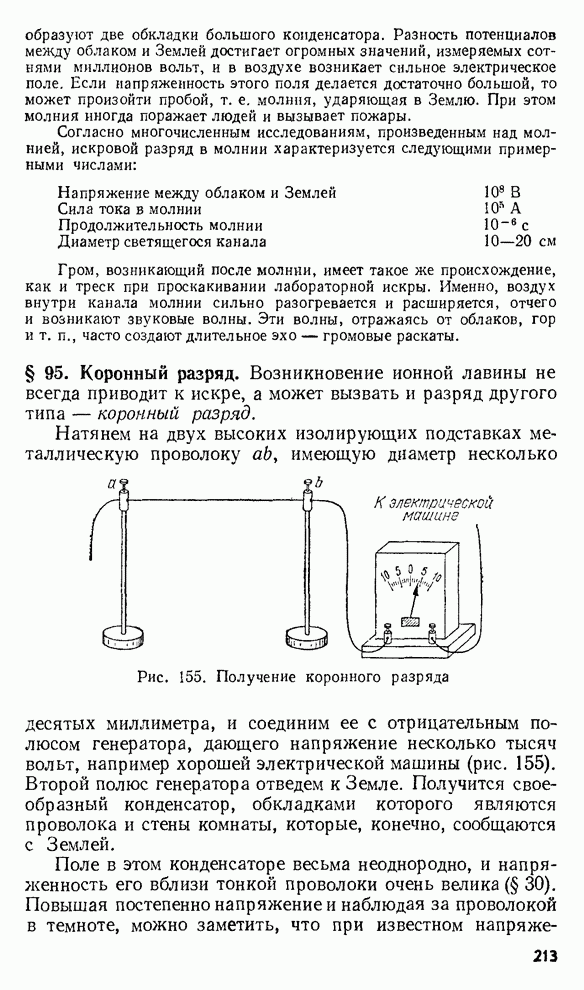
- § 95. Коронный разряд.
- § 96. Применения коронного разряда.
- § 97. Громоотвод.
- § 98. Электрическая дуга.
- § 99. Применения дугового разряда.
- § 100. Тлеющий разряд.
- § 101. Что происходит при тлеющем разряде?
- § 102. Катодные лучи.
- § 103. Природа катодных лучей.
- § 104. Каналовые лучи.
- § 105. Электронная проводимость в высоком вакууме.
- § 106. Электронные лампы.
- § 107. Электроннолучевая трубка.
- Глава IX. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ПОЛУПРОВОДНИКИ
- § 108. Природа электрического тока в полупроводниках.
- § 109. Движение электронов в полупроводниках.
- § 110. Полупроводниковые выпрямители.
- § 111. Полупроводниковые фотоэлементы.
- Глава X. ОСНОВНЫЕ МАГНИТНЫЕ ЯВЛЕНИЯ
- § 112. Естественные и искусственные магниты.
- § 113. Полюсы магнита и его нейтральная зона.
- § 114. Магнитное действие электрического тока.
- § 115. Магнитные действия токов и постоянных магнитов.
- § 116. Происхождение магнитного поля постоянных магнитов.
- § 117. Гипотеза Ампера об элементарных электрических токах.
- Глава XI. МАГНИТНОЕ ПОЛЕ
- § 118. Магнитное поле и его проявления. Магнитная индукция.
- § 119. Магнитный момент. Единица магнитной индукции.
- § 120. Измерение магнитной индукции поля с помощью магнитной стрелки.
- § 121. Сложение магнитных полей.
- § 122. Линии магнитного поля.
- § 123. Приборы для измерения магнитной индукции.
- Глава XII. МАГНИТНЫЕ ПОЛЯ ЭЛЕКТРИЧЕСКИХ ТОКОВ
- § 124. Магнитное поле прямолинейного проводника и кругового витка с током.
- § 125. Магнитное поле соленоида. Эквивалентность соленоида и полосового магнита.
- § 126. Магнитное поле внутри соленоида. Напряженность магнитного поля.
- § 127. Магнитное поле движущихся зарядов.
- Глава XIII. МАГНИТНОЕ ПОЛЕ ЗЕМЛИ
- § 128. Магнитное поле Земли.
- § 129. Элементы земного магнетизма.
- § 130. Магнитные аномалии и магнитная разведка полезных ископаемых.
- § 131. Изменение элементов земного магнетизма с течением времени. Магнитные бури.
- Глава XIV. СИЛЫ, ДЕЙСТВУЮЩИЕ В МАГНИТНОМ ПОЛЕ НА ПРОВОДНИКИ С ТОКОМ
- § 132. Введение.
- § 133. Действие магнитного поля на прямолинейный проводник с током. Правило левой руки.
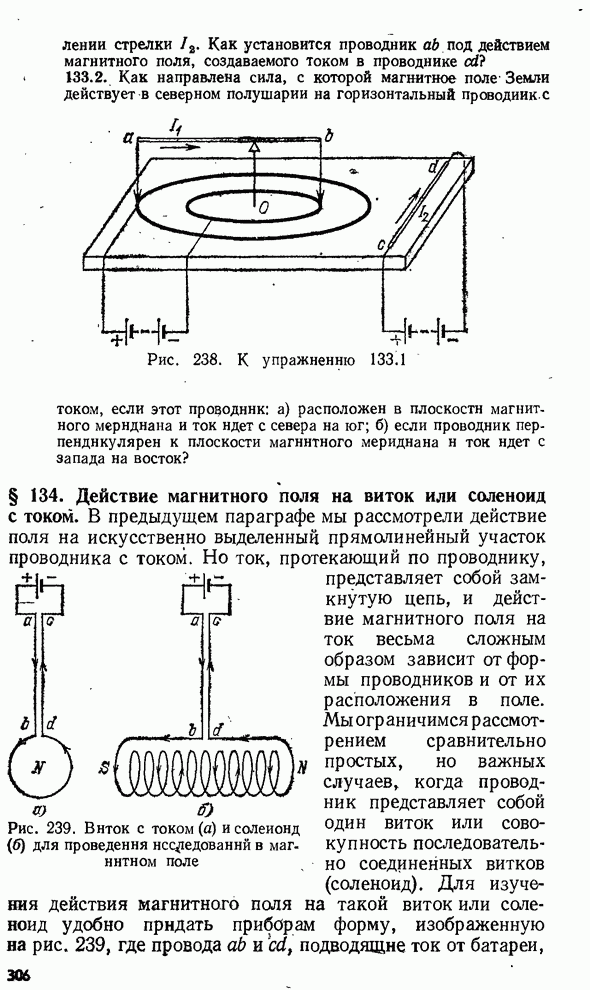
- § 134. Действие магнитного поля на виток или соленоид с током.
- § 135. Гальванометр, основанный на взаимодействии магнитного поля и тока.
- § 136. Сила Лоренца.
- § 137. Сила Лоренца и полярные сияния.
- Глава XV. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
- § 138. Условия возникновения индукционного тока.
- § 139. Направление индукционного тока. Правило Ленца.
- § 140. Основной закон электромагнитной индукции.
- § 141. Электродвижущая сила индукции.
- § 142. Электромагнитная индукция и сила Лоренца.
- § 143. Индукционные токи в массивных проводниках. Токи Фуко.
- Глава XVI. МАГНИТНЫЕ СВОЙСТВА ТЕЛ
- § 144. Магнитная проницаемость железа.
- § 145. Магнитная проницаемость различных веществ. Вещества парамагнитные и диамагнитные.
- § 146. Движение парамагнитных и диамагнитных тел в магнитном поле. Опыты Фарадея.
- § 147. Молекулярная теория магнетизма.
- § 148. Магнитная защита.
- § 149. Особенности ферромагнитных тел.
- § 150. Основы теории ферромагнетизма.
- Глава XVII. ПЕРЕМЕННЫЙ ТОК
- § 151. Постоянная и переменная электродвижущая сила.
- § 152. Опытное исследование формы переменного тока. Осциллограф.
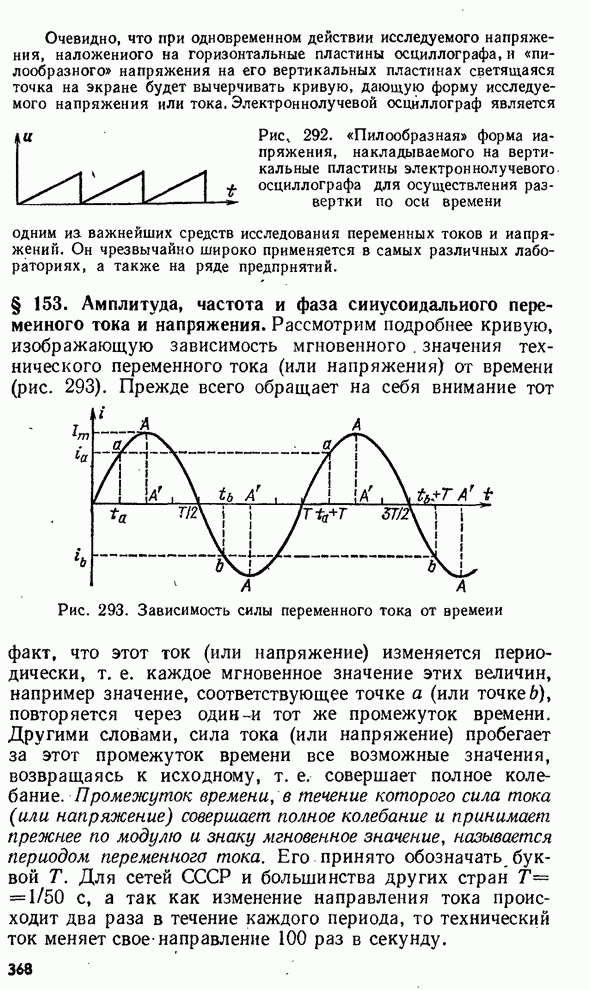
- § 153. Амплитуда, частота и фаза синусоидального переменного тока и напряжения.
- § 154. Сила переменного тока.
- § 155. Амперметры и вольтметры переменного тока.
- § 156. Самоиндукция.
- § 157. Индуктивность катушки.
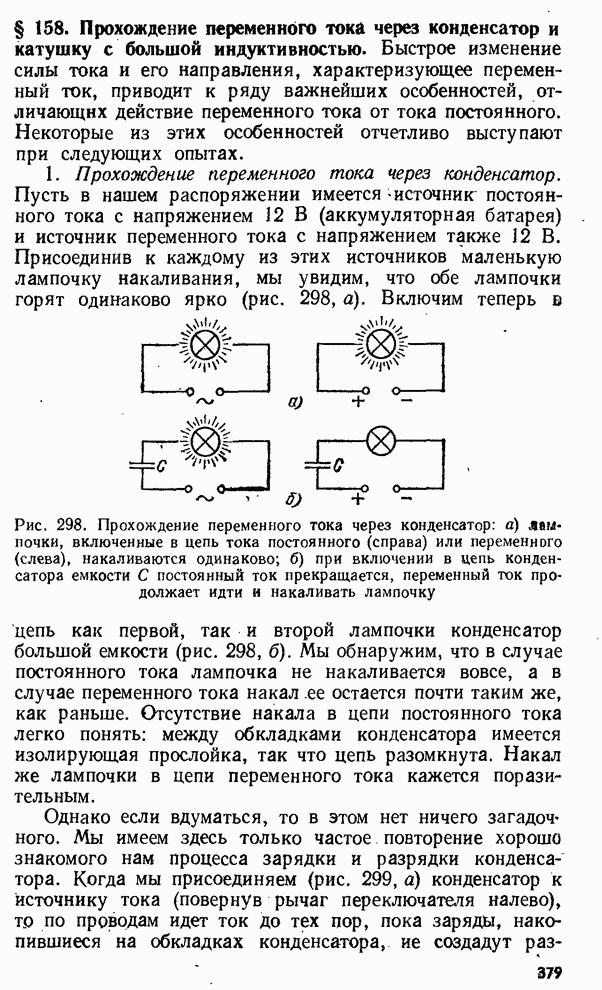
- § 158. Прохождение переменного тока через конденсатор и катушку с большой индуктивностью.
- § 159. Закон Ома для переменного тока. Емкостное и индуктивное сопротивления.
- § 160. Сложение токов при параллельном включении сопротивлений в цепь переменного тока.
- § 161. Сложение напряжений при последовательном соединении сопротивлений в цепи переменного тока.
- § 162. Сдвиг фаз между током и напряжением.
- § 163. Мощность переменного тока.
- § 164. Трансформаторы.
- § 165. Централизованное производство и распределение электрической энергии.
- § 166. Выпрямление переменного тока.
- Глава XVIII. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ: ГЕНЕРАТОРЫ, ДВИГАТЕЛИ, ЭЛЕКТРОМАГНИТЫ
- § 167. Генераторы переменного тока.
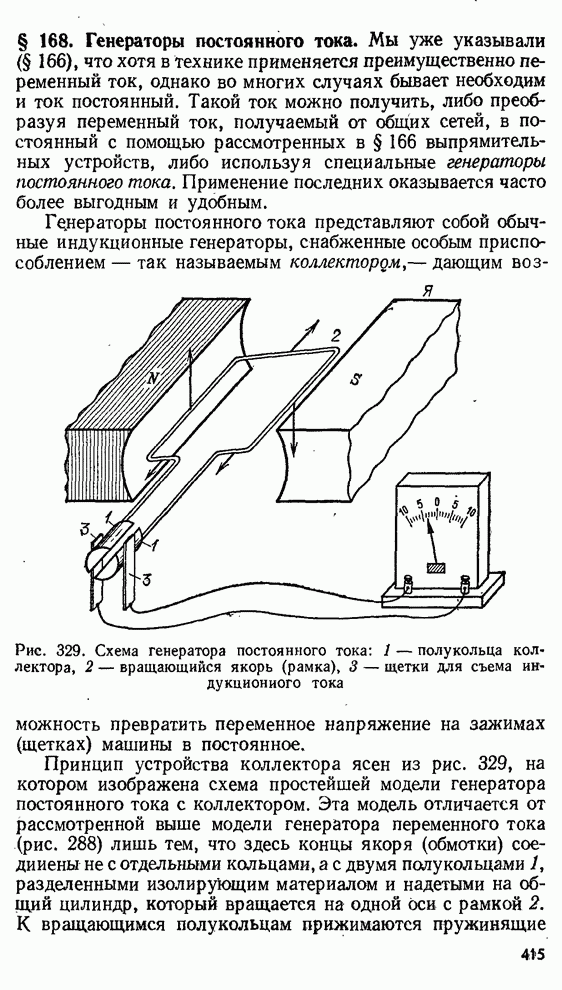
- § 168. Генераторы постоянного тока.
- § 169. Генераторы с независимым возбуждением и с самовозбуждением.
- § 170. Трехфазный ток.
- § 171. Трехфазный электродвигатель.
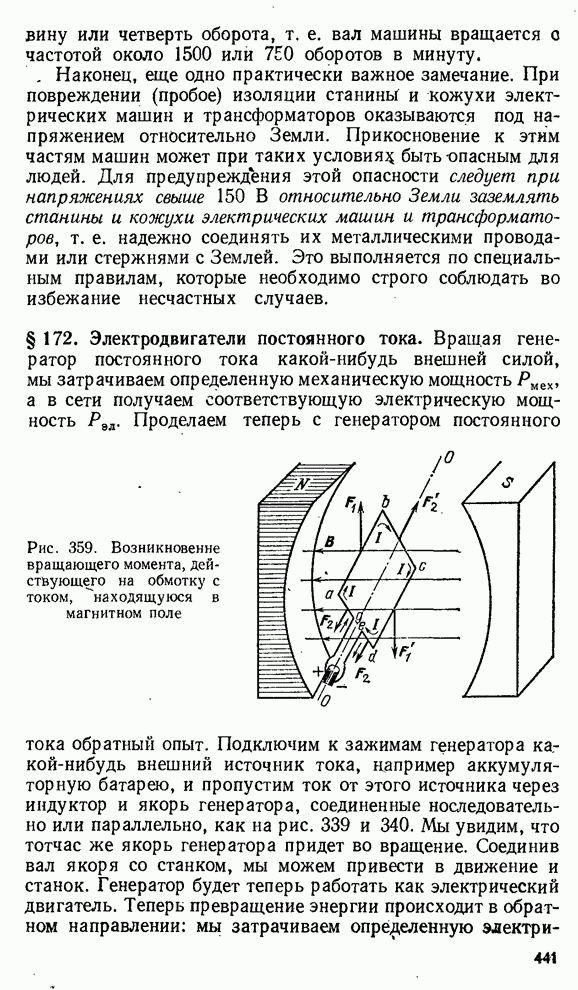
- § 172. Электродвигатели постоянного тока.
- § 173. Основные рабочие характеристики и особенности двигателей постоянного тока с параллельным и последовательным возбуждением.
- § 174. Коэффициент полезного действия генератора и двигателя.
- § 175. Обратимость электрических генераторов постоянного тока.
- § 176. Электромагниты.
- § 177. Применение электромагнитов.
- § 178. Реле и их применения в технике и автоматике.
- Ответы и решения к упражнениям
- Приложения
- Предметный указатель
- Таблицы