| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.2. Когерентные структуры и гидродинамическая неустойчивость
Возникновение когерентных структур в струйных течениях обусловлено гидродинамической неустойчивостью этих течений. В начальных участках осесимметричных струй следует различать три вида неустойчивости.
А. При начальном ламинарном пограничном слое на срезе сопла в слое смешения  формируется по существу двумерная пространственная неустойчивость Кельвина-Гельмгольца с характеристиками, которые
формируется по существу двумерная пространственная неустойчивость Кельвина-Гельмгольца с характеристиками, которые
хорошо описываются линейной теорией пространственной неустойчивости [1.44]. При этом максимальному коэффициенту пространственного усиления осесимметричных возмущений соответствует число Струхаля  же значение справедливо и для смешения плоской струи. Результаты линейной теории весьма удовлетворительно согласуются с экспериментом. В частности, эксперименты подтверждают зависимость
же значение справедливо и для смешения плоской струи. Результаты линейной теории весьма удовлетворительно согласуются с экспериментом. В частности, эксперименты подтверждают зависимость  которая следует из предыдущего выражения, если учесть, что в ламинарном пограничном слое
которая следует из предыдущего выражения, если учесть, что в ламинарном пограничном слое  .
.
В ряде экспериментов, однако, получаются значения  отличающиеся от теоретических, что обычно объясняют влиянием начальных условий (профили скорости и интенсивности пульсаций, акустические возмущения и вибрации сопла). На нелинейной стадии развития этих возмущений было обнаружено [1.36] образование вихревых сгустков, их последующее взаимодействие и попарное слияние.
отличающиеся от теоретических, что обычно объясняют влиянием начальных условий (профили скорости и интенсивности пульсаций, акустические возмущения и вибрации сопла). На нелинейной стадии развития этих возмущений было обнаружено [1.36] образование вихревых сгустков, их последующее взаимодействие и попарное слияние.
При теоретическом исследовании линейной устойчивости слоя смешения (неустойчивость Кельвина-Гельмгольца) в качестве исходного задается профиль скорости в виде гиперболического тангенса, характерный для сформировавшегося ламинарного слоя смешения. Между тем в выходном сечении формируется ламинарный пограничный слой Блаузиуса, для которого характерна неустойчивость Толмина-Шлихтинга. Однако в теориях линейной устойчивости слоя смешения перестроение профиля скорости от пограничного слоя Блаузиуса до струйного профиля скорости никак не учитывается.
При начальном турбулентном пограничном слое на срезе сопла и масштабе турбулентности, довольно малом по сравнению с длиной волны максимально усиленной моды, можно ожидать появления того же типа неустойчивости, что и при начальном ламинарном пограничном слое [1.13,1.18, 1.29]. Тогда начальный профиль скорости будут определять характеристики нестационарных волн. Возникающие при этом пространственно усиливающиеся волновые компоненты на нелинейной стадии развития приведут к образованию турбулентных кольцевых вихрей, что и наблюдается в эксперименте.
Однако возможность расчета характеристик неустойчивости турбулентного слоя смешения по начальному осредненному профилю скорости подвергается сомнению [1.34] на том основании, что здесь очень велики пульсации скорости, и осредненный профиль скорости не может характеризовать неустойчивость. Тем не менее основные механизмы развития и взаимодействия когерентных структур в струе как при ламинарном, так и при турбулентном пограничном слое на срезе сопла имеют, по-видимому, много общих черт. В основном эти механизмы могут быть описаны в рамках невязкой модели Эйлера [1.13].
Б. Второй вид неустойчивости имеет место в диапазоне  и связан с коллективным взаимодействием кольцевых вихрей в начальном участке круглой струи, причем здесь преобладают низкочастотные
и связан с коллективным взаимодействием кольцевых вихрей в начальном участке круглой струи, причем здесь преобладают низкочастотные
пульсации, генерируемые наиболее крупными вихрями. В конце начального участка характерное число Струхаля, определенное по диаметру сопла, составляет  причем разброс значений
причем разброс значений  обусловлен влиянием начальных условий на срезе сопла.
обусловлен влиянием начальных условий на срезе сопла.
Хотя взаимодействие вихревых колец в пределах начального участка является чисто нелинейным процессом, их характерная частота была определена в рамках линейной теории устойчивости в приближении локальной параллельности [1.44], в которой учтено влияние конечной толщины слоя смешения ближе к концу начального участка или, точнее, влияние поперечной кривизны слоя смешения. Было получено, что в конце начального участка  что согласуется с данными эксперимента.
что согласуется с данными эксперимента.
Анализ линейной устойчивости слабо расходящегося течения [1.28] качественно согласуется с наблюдениями, выделяя моду с наибольшим коэффициентом усиления по амплитуде давления, которая соответствует числу Струхаля  Как указано в [1.18], в этих теориях содержится в неявном виде нелинейность, поскольку измеряемые в эксперименте профили средней скорости, использованные в расчетах, уже включают результат действия рейнольдсовых напряжений. Этим значениям чисел Струхаля соответствует так называемая предпочтительная мода. Как показано в экспериментах [1.38], при
Как указано в [1.18], в этих теориях содержится в неявном виде нелинейность, поскольку измеряемые в эксперименте профили средней скорости, использованные в расчетах, уже включают результат действия рейнольдсовых напряжений. Этим значениям чисел Струхаля соответствует так называемая предпочтительная мода. Как показано в экспериментах [1.38], при  число Струхаля предпочтительной моды остается постоянным и равным 0,44.
число Струхаля предпочтительной моды остается постоянным и равным 0,44.
Исходя из значений  для начального ламинарного пограничного слоя на срезе сопла и
для начального ламинарного пограничного слоя на срезе сопла и  в конце начального участка, можно оценить число попарных слияний вихрей [1.41]:
в конце начального участка, можно оценить число попарных слияний вихрей [1.41]:

Полагая здесь  получим
получим  т.е. в пределах начального участка струи может произойти 3-4 попарных слияний кольцевых вихрей. Если в начальном участке круглой струи с начальным ламинарным пограничным слоем реализуется 3-4 спаривания вихрей, то при начальном турбулентном пограничном слое - только 1-2 спаривания.
т.е. в пределах начального участка струи может произойти 3-4 попарных слияний кольцевых вихрей. Если в начальном участке круглой струи с начальным ламинарным пограничным слоем реализуется 3-4 спаривания вихрей, то при начальном турбулентном пограничном слое - только 1-2 спаривания.
Коллективное взаимодействие большого числа вихрей также может быть описано в рамках невязкой модели Эйлера [1.13]. Проведенные в рамках этой модели расчеты показали тенденцию к спариванию вихрей и к выделению длинноволновых спектральных составляющих.
Благодаря механизму неустойчивости Кельвина-Гельмгольца двумерные волны экспоненциально нарастают вниз по течению и происходит их свертывание в вихри. Согласно данным эксперимента процесс свертывания заканчивается в той точке вниз по потоку, где амплитуда основной компоненты с частотой  достигает максимума. При этом происходит возбуждение субгармоники
достигает максимума. При этом происходит возбуждение субгармоники  амплитуда которой на три порядка меньше основной. Рост субгармоники ниже по течению на нелинейной стадии развития неустойчивости приводит к спариванию соседних вихрей, причем
амплитуда которой на три порядка меньше основной. Рост субгармоники ниже по течению на нелинейной стадии развития неустойчивости приводит к спариванию соседних вихрей, причем
место спаривания приходится на то сечение вниз по течению, где субгармоника достигает максимума [1.36].
В. Третий тип неустойчивости связан с возникновением азимутальной неоднородности крупномасштабных вихрей, которая в конце начального участка приводит к распаду кольцевых вихрей на "клубки". Именно этот тип неустойчивости ответственен за образование "звездообразных" структур, описанных выше. Расчеты по линейной теории [1.44] для первой азимутальной моды  показывают, что максимальные значения коэффициентов пространственного усиления этой моды наблюдаются при тех же частотах, которые были получены для осесимметричных возмущений, т.е. для нулевой моды
показывают, что максимальные значения коэффициентов пространственного усиления этой моды наблюдаются при тех же частотах, которые были получены для осесимметричных возмущений, т.е. для нулевой моды 
О потере азимутальной однородности сформировавшихся кольцевых вихрей, что соответствует нелинейной стадии развития возмущений в слое смешения, можно с некоторым приближением судить по поведению изолированного вихревого кольца. В самом деле известно, что вихревое кольцо в идеальной жидкости неустойчиво, причем число образующихся азимутальных волн определяется размером ядра вихря. Другая причина возможной потери азимутальной однородности вступает в действие при взаимодействии двух соосных кольцевых вихрей. Анализ показал [1.24], что расширяющийся передний кольцевой вихрь в меньшей мере, а сжимающийся задний - в гораздо большей мере чувствителен к радиальным возмущениям, следствием чего является более ранняя потеря им азимутальной однородности (рис. 
Аналогичные виды неустойчивости наблюдаются и в начальном участке плоской турбулентной струи. В слое смешения вблизи сопла картина течения и механизм неустойчивости в плоских и круглых струях весьма близки. При  неустойчивость течения в начальном участке плоской струи связана с коллективным взаимодействием крупномасштабных вихрей. Наконец, нарушение двумерности этих прямолинейных вихрей вдоль размаха играет ту же роль, что и нарушение азимутальной однородности кольцевых вихрей в круглой струе
неустойчивость течения в начальном участке плоской струи связана с коллективным взаимодействием крупномасштабных вихрей. Наконец, нарушение двумерности этих прямолинейных вихрей вдоль размаха играет ту же роль, что и нарушение азимутальной однородности кольцевых вихрей в круглой струе 
Для суждения о нарушении осевой симметрии в круглой турбулентной струе (о модовом составе крупномасштабных когерентных структур) используются измерения пространственной азимутальной корреляции продольных пульсаций скорости, пульсаций температуры [1.48] в слое смешения, а также пульсаций давления вне струи в ее ближнем акустическом поле. Так, по данным измерений азимутальной корреляции пульсаций скорости  ортогонального Фурье-разложения
ортогонального Фурье-разложения

коэффициенты которого

определяется изменение  вдоль по потоку. Здесь
вдоль по потоку. Здесь  соответствует нулевой моде
соответствует нулевой моде  высшим модам
высшим модам 
Соответствующие эксперименты и расчеты показали, что при  модовый состав турбулентных пульсаций заметно изменяется: при
модовый состав турбулентных пульсаций заметно изменяется: при  преобладает нулевая мода, с увеличением
преобладает нулевая мода, с увеличением  относительная энергия продольных пульсаций скорости становится преобладающей для 1-й моды и возрастает для мод
относительная энергия продольных пульсаций скорости становится преобладающей для 1-й моды и возрастает для мод  Аналогичным образом изменяются при
Аналогичным образом изменяются при  и 6, вычисленные по данным измерений азимутальной корреляции пульсаций давления вне струи [1.46]. Эти результаты являются естественным отражением деформации крупномасштабных когерентных структур вдоль струи - от кольцевых вихрей в слое смешения вблизи среза сопла до звездообразных структур в конце начального участка.
и 6, вычисленные по данным измерений азимутальной корреляции пульсаций давления вне струи [1.46]. Эти результаты являются естественным отражением деформации крупномасштабных когерентных структур вдоль струи - от кольцевых вихрей в слое смешения вблизи среза сопла до звездообразных структур в конце начального участка.
На рис. 1.9 приведены изменения азимутальной корреляции пульсаций скорости и давления в окружном направлении для круглой струи при  и модовый состав этих пульсаций в круглой струе
и модовый состав этих пульсаций в круглой струе 
Рис. 1.9. (см. скан) Азимутальные корреляции пульсаций продольной скорости в круглой струе для  и 0,17 при
и 0,17 при  ; изменение мод при
; изменение мод при 

Рис. 1.10. Интерпретация первой - четвертой мод в разложении Фурье
Нулевая мода соответствует осесимметричному вихревому кольцу. Простая интерпретация первой, второй, третьей и четвертой мод в результате Фурье продемонстрирована на рис. 1.10.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ДОЗВУКОВЫЕ ТУРБУЛЕНТНЫЕ СТРУИ
- 1.1. Аэродинамические характеристики турбулентных струй. Когерентные структуры
- 1.2. Когерентные структуры и гидродинамическая неустойчивость
- 1.3. Акустические характеристики дозвуковых турбулентных струй
- 1.4. Начальные условия истечения турбулентных струй
- 1.5. Методы управления турбулентными струями
- ГЛАВА 2. УПРАВЛЕНИЕ АЭРОДИНАМИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ ДОЗВУКОВЫХ ТУРБУЛЕНТНЫХ СТРУЙ
- 2.1. Восприимчивость турбулентных струй к слабым гармоническим акустическим возмущениям. Влияние частоты возбуждения
- 2.2. Влияние уровня акустического возбуждения
- 2.3. Влияние режима течения в пограничном слое на срезе сопла
- 2.4. Влияние начальной турбулентности потока на эффективность акустического возбуждения струи
- 2.5. Деформация поперечного сечения струи при ее поперечном акустическом возбуждении
- 2.6. Акустическое возбуждение струи, истекающей из диафрагмы
- 2.7. Вибрационное возбуждение турбулентной струи
- 2.8. Акустическое возбуждение высокоскоростных струй
- 2.9. Изменение модового состава турбулентных пульсаций при акустическом возбуждении струи. Локализация мест спаривания и разрушения когерентных структур при акустическом возбуждении струи. Механизмы акустического возбуждения струи
- 2.10. Влияние спутного потока на интенсификацию турбулентного смешения в струе при низкочастотном акустическом возбуждении
- 2.11. Тональное акустическое возбуждение неизотермических газовых струй
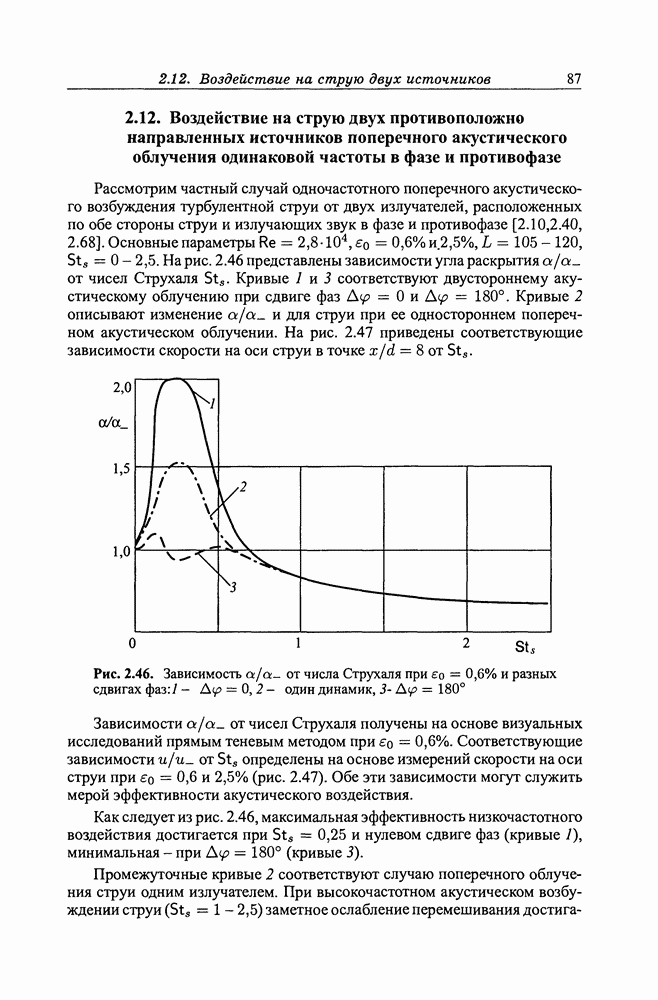
- 2.12. Воздействие на струю двух противоположно направленных источников поперечного акустического облучения одинаковой частоты в фазе и противофазе
- 2.13. Воздействие на струю акустических возмущений высших азимутальных мод
- 2.14. Многочастотное акустическое возбуждение струи. Субгармонический резонанс
- 2.15. Акустическое возбуждение турбулентной струи при нарушении гармоничности воздействующего сигнала
- 2.16. Акустическое возбуждение некруглых струй
- ГЛАВА 3. УПРАВЛЕНИЕ АКУСТИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ ДОЗВУКОВЫХ ТУРБУЛЕНТНЫХ СТРУЙ
- 3.1. Акустические характеристики ближнего и дальнего поля турбулентных струй при их акустическом возбуждении
- 3.2. Акустическое возбуждение неизотермических струй
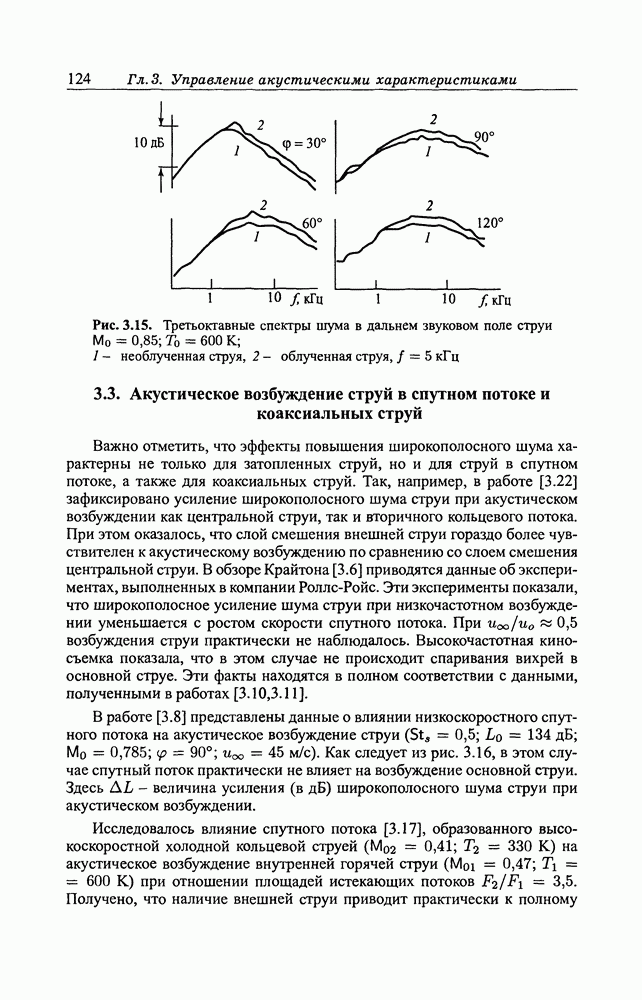
- 3.3. Акустическое возбуждение струй в спутном потоке и коаксиальных струй
- 3.4. О механизмах генерации шума дозвуковыми турбулентными струями
- ГЛАВА 4. ВОЗДЕЙСТВИЕ НА ДОЗВУКОВУЮ СТРУЮ ИНТЕНСИВНЫХ АКУСТИЧЕСКИХ ВОЗМУЩЕНИЙ
- 4.1. Высокоамплитудное низкочастотное периодическое возбуждение круглой струи и плоского слоя смешения
- 4.2. Визуализация течения в дозвуковой круглой струе при продольном и поперечном интенсивном акустическом возбуждении
- ГЛАВА 5. САМОВОЗБУЖДЕНИЕ ТУРБУЛЕНТНЫХ СТРУЙНЫХ ТЕЧЕНИЙ
- 5.1. Схемы самовозбуждения турбулентных струйных течений
- 5.2. Нормальное и косое натекание околозвуковой струи на экран
- 5.3. Автоколебания в аэродинамических трубах с открытой рабочей частью
- ГЛАВА 6. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ПЕРИОДИЧЕСКОГО ВОЗБУЖДЕНИЯ ДОЗВУКОВЫХ ТУРБУЛЕНТНЫХ СТРУЙ
- 6.2. Моделирование плоских и круглых турбулентных струй на основе метода дискретных вихрей при низкочастотном и высокочастотном гармоническом возбуждении
- 6.3. Численное моделирование турбулентного слоя смешения на основе нестационарных уравнений Рейнольдса, замкнутых с помощью дифференциальной модели турбулентости
- 6.4. Численное моделирование турбулентных струйных течений на основе обобщенных уравнений Рейнольдса (трехчленное разложение). Влияние низкочастотного и высокочастотного гармонического возбуждения
- 6.5. Об одной любопытной аналогии
- ГЛАВА 7. СВЕРХЗВУКОВЫЕ НЕИЗОБАРИЧЕСКИЕ ТУРБУЛЕНТНЫЕ СТРУИ. УПРАВЛЕНИЕ АЭРОДИНАМИЧЕСКИМИ И АКУСТИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ
- 7.1. Аэродинамические характеристики сверхзвуковых турбулентных струй
- 7.2. Механизм шумообразования. Широкополосный шум и дискретные составляющие
- 7.3. Акустическое возбуждение сверхзвуковых струй. Активное управление
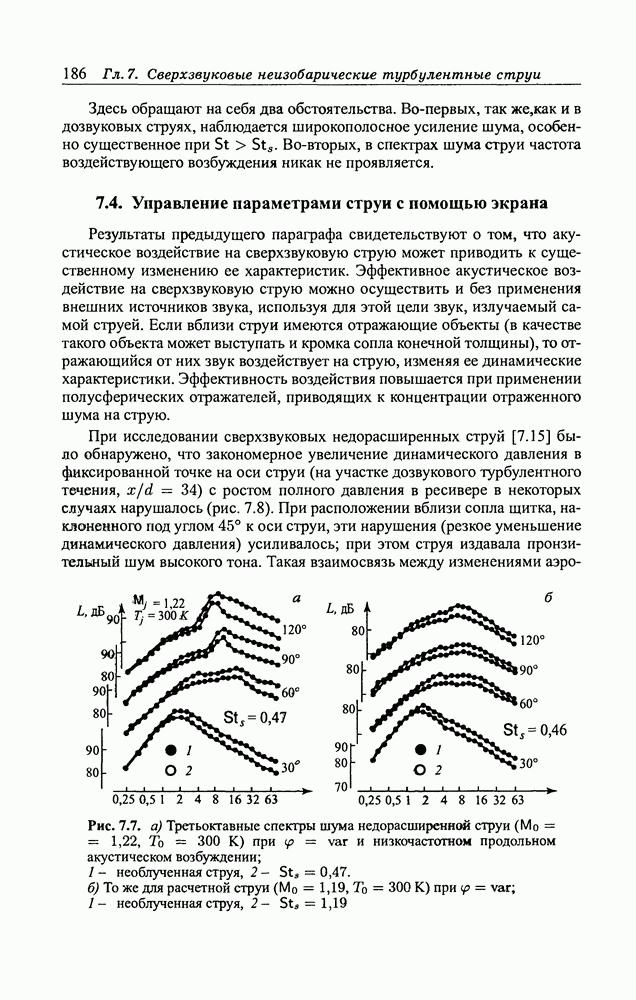
- 7.4. Управление параметрами струи с помощью экрана
- ГЛАВА 8. СНИЖЕНИЕ ШУМА РЕАКТИВНЫХ СТРУЙ ТРД
- 8.1. Акустический глушитель шума реактивной струи ТРД
- 8.2. Струйная система для снижения шума сверхзвуковых струй. Подавление дискретной составляющей
- 8.3. Снижение избыточного шума ТРД, обусловленного аэроакустическим взаимодействием
- ГЛАВА 9. АКУСТИЧЕСКИЕ МЕТОДЫ УПРАВЛЕНИЯ АВТОКОЛЕБАНИЯМИ В АЭРОДИНАМИЧЕСКИХ ТРУБАХ С ОТКРЫТОЙ РАБОЧЕЙ ЧАСТЬЮ
- 9.2. Подавление автоколебаний при высокочастотном акустическом возбуждении слоя смешения
- 9.3. Генерация автоколебаний и создание однородного пульсирующего потока в рабочей части трубы при низкочастотном возбуждении слоя смешения
- 9.4. Подавление автоколебаний при помощи антишума
- ГЛАВА 10. ВЗАИМОДЕЙСТВИЕ СЛОЯ СМЕШЕНИЯ С ПОЛОСТЬЮ
- 10.1. Отрывное обтекание полости
- 10.2. Пульсации пристеночного давления при обтекании полости и способы их уменьшения
- 10.3. Пульсации давления в околозвуковых аэродинамических трубах с закрытой рабочей частью и способы их уменьшения
- 10.4. Подавление автоколебаний в тупиковых отростках газопроводов
- 10.5. Акустическое управление течением в полости