| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.2. Моделирование плоских и круглых турбулентных струй на основе метода дискретных вихрей при низкочастотном и высокочастотном гармоническом возбуждении
6.2.1. При моделировании плоских и круглых турбулентных струй методом дискретных вихрей рассматривается случай идеальной несжимаемой жидкости. Применительно к плоским струям при этом могут быть использованы два подхода. В первом из них граничные условия непротекания на

Рис. 6.4. Утолщение вдоль по потоку слоя смешения в начальном участке круглой невозбужденной  и возбужденной (2) турбулентной струи.
и возбужденной (2) турбулентной струи. 

Рис. 6.5. Изменение продольных пульсаций скорости вдоль оси круглой невозбужденной  и возбужденной (2) турбулентной струи.
и возбужденной (2) турбулентной струи. 
твердых поверхностях сопла выполняются только в конечном числе контрольных точек, как и в случае круглых струй. Во втором - граничные условия непротекания выполняются точно во всех точках твердых поверхностей. В этом последнем случае используется конформное отображение плоскости течения на верхнюю полуплоскость. При достаточно тесном
расположении контрольных точек в первом случае оба подхода приводят к практически совпадающим результатам [6.1].
При моделировании плоских турбулентных струй предположение о наличии плоскости симметрии для мгновенного течения приводит к практически полному отсутствию перемешивания вихревых структур разного знака, которые формируются по обе стороны от плоскости симметрии. В качестве примера на рис. 6.6 представлены вихревые структуры плоской струи в фиксированный момент времени для симметричного и асимметричного случаев. Во втором из них, в полном соответствии с экспериментом, наблюдается интенсивное перемешивание сгустков завихренности разных знаков. Приведенные на рис. 6.7 распределения средней скорости вдоль оси струи, рассчитанные при симметричном и асимметричном расположении вихревых структур, показывают, что только во втором случае данные расчета согласуются с экспериментом как в начальном, так и в основном участках струи [6.2].
Моделирование периодического возбуждения плоской турбулентной струи с гармоническим законом изменения продольной скорости на срезе сопла

позволило исследовать влияние числа Струхаля  и амплитуды
и амплитуды  на изменение вдоль оси струи средней скорости
на изменение вдоль оси струи средней скорости  и ее продольных пульсаций
и ее продольных пульсаций  при
при  и 2,0 (см. рис.6.8).
и 2,0 (см. рис.6.8).

Рис. 6.6. Вихревые структуры плоской турбулентной струи при симметричном  и несимметричном (2) приближении в фиксированной момент времени
и несимметричном (2) приближении в фиксированной момент времени

Рис. 6.7. Распределение средней скорости вдоль оси плоской турбулентной струи; 1,2- эксперименты, 3 - при симметричном и 4- несимметричном приближении
При этом  Эти результаты заимствованы из
Эти результаты заимствованы из  При низкочастотном периодическом возбуждении
При низкочастотном периодическом возбуждении  наблюдается определенная тенденция к уменьшению длины начального участка (при
наблюдается определенная тенденция к уменьшению длины начального участка (при  При больших амплитудах
При больших амплитудах  и, соответственно,
и, соответственно,  ) обнаружено аномальное немонотонное изменение скорости вдоль оси струи, которое наблюдалось ранее в круглых пульсирующих струях (см. главу
) обнаружено аномальное немонотонное изменение скорости вдоль оси струи, которое наблюдалось ранее в круглых пульсирующих струях (см. главу  и 4.5). При высокочастотном возбуждении
и 4.5). При высокочастотном возбуждении  и очень высоком уровне возбуждения
и очень высоком уровне возбуждения  и, соответственно,
и, соответственно,  зафиксировано возрастание средней скорости на оси струи и соответствующее уменьшение ее продольных пульсаций. При меньших значениях
зафиксировано возрастание средней скорости на оси струи и соответствующее уменьшение ее продольных пульсаций. При меньших значениях  в этом последнем случае эффект высокочастотного возбуждения оказался менее отчетливым.
в этом последнем случае эффект высокочастотного возбуждения оказался менее отчетливым.
Рассмотрим моделирование высокочастотного периодического возбуждения плоского турбулентного сдвигового слоя [6.26] на основе разновидности метода дискретных вихрей (метод вихря в ячейке) с использованием двумерных уравнений Эйлера. Изучалось развитие слоя смешения во времени. Конечная толщина сдвигового слоя моделировалась четырьмя параллельными цепочками точечных вихрей, поперечное расстояние между которыми выбиралась из условия, чтобы осредненный по продольной координате профиль скорости в поперечном сечении

выражался в виде, близком к гиперболическому тангенсу. Именно такой профиль скорости имеет место в плоских турбулентных слоях смешения.
Исследовано влияние частоты  и амплитуды А периодического гармонического возбуждения на отношение
и амплитуды А периодического гармонического возбуждения на отношение  где
где  соответственно, среднеквадратичные значения пульсаций скорости при наличии и отсутствии периодического возбуждения (см. рис. 6.9). При этом отношение
соответственно, среднеквадратичные значения пульсаций скорости при наличии и отсутствии периодического возбуждения (см. рис. 6.9). При этом отношение  является функцией периода
является функцией периода  гармонических возмущений.
гармонических возмущений.

Рис. 6.8. Изменение средней скорости (а) и продольных пульсаций скорости (б) вдоль оси плоской турбулентной струи при отсутствии и наличии периодического возбуждения. 
Основные выводы этого исследования: 1) При малых амплитудах периодического возбуждения  подавление турбулентности не имеет места; 2) При амплитуде 0,05 максимальное подавление происходит на частоте, соответствующей максимальной нестабильности слоя смешения
подавление турбулентности не имеет места; 2) При амплитуде 0,05 максимальное подавление происходит на частоте, соответствующей максимальной нестабильности слоя смешения  При высоких амплитудах
При высоких амплитудах  теряется предпочтительность этого числа
теряется предпочтительность этого числа 
6.2.2. Аналогично при моделировании круглых струй в рамках метода дискретного вихрей с помощью набора вихревых колец, т.е. при постулировании жесткого условия осевой симметрии, результаты расчета приходят в противоречие с данными эксперимента, так как при этом не реализуются расширение струи и падение скорости вдоль по потоку.

Рис. 6.9. Влияние частоты (числа Струхаля  и амплитуды
и амплитуды  периодического возбуждения турбулентного слоя смешения на отношение
периодического возбуждения турбулентного слоя смешения на отношение 
При моделировании круглой турбулентной струи в трехмерной постановке сходящие с кромки сопла вихревые кольца аппроксимируются вихревыми многоугольниками [6.1,6.2], что позволяет описывать деформации этих колец как в их плоскостях, так и в продольном направлении, вдоль их движения. Это иллюстрируется  сравнением вихревой структуры круглой затопленной струи в двух случаях: когда решение получено при требовании осевой симметрии мгновенного течения (1) и при снятии указанного требования (2); во втором случае осевая симметрия сохраняется только в пределах 2,5 калибров
сравнением вихревой структуры круглой затопленной струи в двух случаях: когда решение получено при требовании осевой симметрии мгновенного течения (1) и при снятии указанного требования (2); во втором случае осевая симметрия сохраняется только в пределах 2,5 калибров  Далее наблюдается азимутальная и продольная деформация вихревых многоугольников, а при
Далее наблюдается азимутальная и продольная деформация вихревых многоугольников, а при  стохастизация течения. При решении задачи в трехмерной постановке получено совпадение расчетных и экспериментальных значений скорости и других параметров течения (профили средней скорости, трех компонент пульсаций скорости, рейнольдсова напряжения сдвига) как в начальном, так и в основном участках струи. На рис. 6.11 показаны изменения осевой скорости вдоль оси струи, полученные в осесимметричных и трехмерных расчетах, и их сравнение с данными эксперимента [6.8]. В цитированной работе также показано, что даже в пределах начального участка
стохастизация течения. При решении задачи в трехмерной постановке получено совпадение расчетных и экспериментальных значений скорости и других параметров течения (профили средней скорости, трех компонент пульсаций скорости, рейнольдсова напряжения сдвига) как в начальном, так и в основном участках струи. На рис. 6.11 показаны изменения осевой скорости вдоль оси струи, полученные в осесимметричных и трехмерных расчетах, и их сравнение с данными эксперимента [6.8]. В цитированной работе также показано, что даже в пределах начального участка  осесимметричное приближение дает завышенные значение пульсаций скорости.
осесимметричное приближение дает завышенные значение пульсаций скорости.
К сожалению, описанный подход пока не реализован для случая периодического возбуждения круглых турбулентных струй. Попытка соответствующего решения предпринята в работе [6.7] в предположении осевой симметрии мгновенного течения. При этом делается ряд дополнительных допущений: задаются радиусы ядер сносимых в поток кольцевых вихрей; вместо одной цепочки кольцевых вихрей задаются две такие цепочки, несколько разнесенные вдоль радиуса; циркуляция сходящих с кромки

(кликните для просмотра скана)
круглого цилиндрического сопла кольцевых вихрей и скорость их конвекции задаются в виде гармонических функций времени.

Такой способ моделирования для невозбужденных струй  в пределах начального участка
в пределах начального участка  качественно верно описывает процесс попарного слияния сгустков завихренности, профили средней скорости, эжекцию и другие статистические характеристики. Расчет характеристик периодически возбужденных струй при значениях амплитуды
качественно верно описывает процесс попарного слияния сгустков завихренности, профили средней скорости, эжекцию и другие статистические характеристики. Расчет характеристик периодически возбужденных струй при значениях амплитуды  и числа Струхаля
и числа Струхаля  показал, что в диапазоне
показал, что в диапазоне  возбуждение с достаточной амплитудой генерирует крупномасштабные вихри в струе. Если
возбуждение с достаточной амплитудой генерирует крупномасштабные вихри в струе. Если  эти вихри очень велики и образуются при
эти вихри очень велики и образуются при  при
при  большие вихри образуются уже при
большие вихри образуются уже при  и сохраняются на расстоянии в несколько калибров вдоль по потоку. При
и сохраняются на расстоянии в несколько калибров вдоль по потоку. При  вихри, которые образуются на частоте возбуждения, малы и быстро разрушаются в процессе взаимодействия с другими вихрями.
вихри, которые образуются на частоте возбуждения, малы и быстро разрушаются в процессе взаимодействия с другими вихрями.
Расчет эжекционных характеристик струи обнаруживает тенденцию: при низкочастотном возбуждении эжекция несколько возрастает, при высокочастотном уменьшается (рис. 6.12). К сожалению, сделанный вывод нельзя признать однозначным, что, по-видимому, объясняется принятыми допущениями.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ДОЗВУКОВЫЕ ТУРБУЛЕНТНЫЕ СТРУИ
- 1.1. Аэродинамические характеристики турбулентных струй. Когерентные структуры
- 1.2. Когерентные структуры и гидродинамическая неустойчивость
- 1.3. Акустические характеристики дозвуковых турбулентных струй
- 1.4. Начальные условия истечения турбулентных струй
- 1.5. Методы управления турбулентными струями
- ГЛАВА 2. УПРАВЛЕНИЕ АЭРОДИНАМИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ ДОЗВУКОВЫХ ТУРБУЛЕНТНЫХ СТРУЙ
- 2.1. Восприимчивость турбулентных струй к слабым гармоническим акустическим возмущениям. Влияние частоты возбуждения
- 2.2. Влияние уровня акустического возбуждения
- 2.3. Влияние режима течения в пограничном слое на срезе сопла
- 2.4. Влияние начальной турбулентности потока на эффективность акустического возбуждения струи
- 2.5. Деформация поперечного сечения струи при ее поперечном акустическом возбуждении
- 2.6. Акустическое возбуждение струи, истекающей из диафрагмы
- 2.7. Вибрационное возбуждение турбулентной струи
- 2.8. Акустическое возбуждение высокоскоростных струй
- 2.9. Изменение модового состава турбулентных пульсаций при акустическом возбуждении струи. Локализация мест спаривания и разрушения когерентных структур при акустическом возбуждении струи. Механизмы акустического возбуждения струи
- 2.10. Влияние спутного потока на интенсификацию турбулентного смешения в струе при низкочастотном акустическом возбуждении
- 2.11. Тональное акустическое возбуждение неизотермических газовых струй
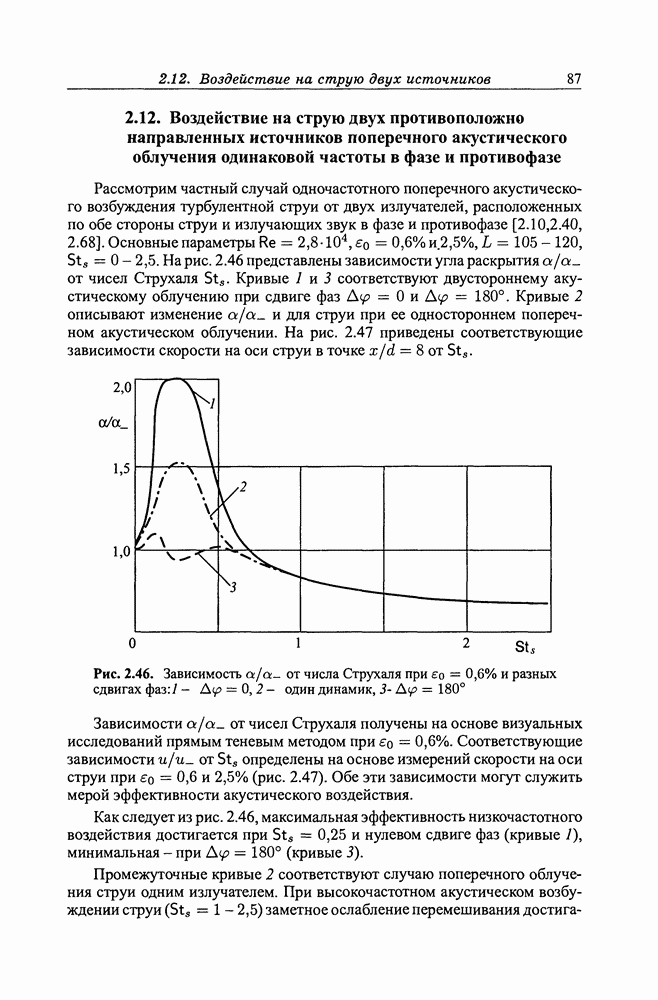
- 2.12. Воздействие на струю двух противоположно направленных источников поперечного акустического облучения одинаковой частоты в фазе и противофазе
- 2.13. Воздействие на струю акустических возмущений высших азимутальных мод
- 2.14. Многочастотное акустическое возбуждение струи. Субгармонический резонанс
- 2.15. Акустическое возбуждение турбулентной струи при нарушении гармоничности воздействующего сигнала
- 2.16. Акустическое возбуждение некруглых струй
- ГЛАВА 3. УПРАВЛЕНИЕ АКУСТИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ ДОЗВУКОВЫХ ТУРБУЛЕНТНЫХ СТРУЙ
- 3.1. Акустические характеристики ближнего и дальнего поля турбулентных струй при их акустическом возбуждении
- 3.2. Акустическое возбуждение неизотермических струй
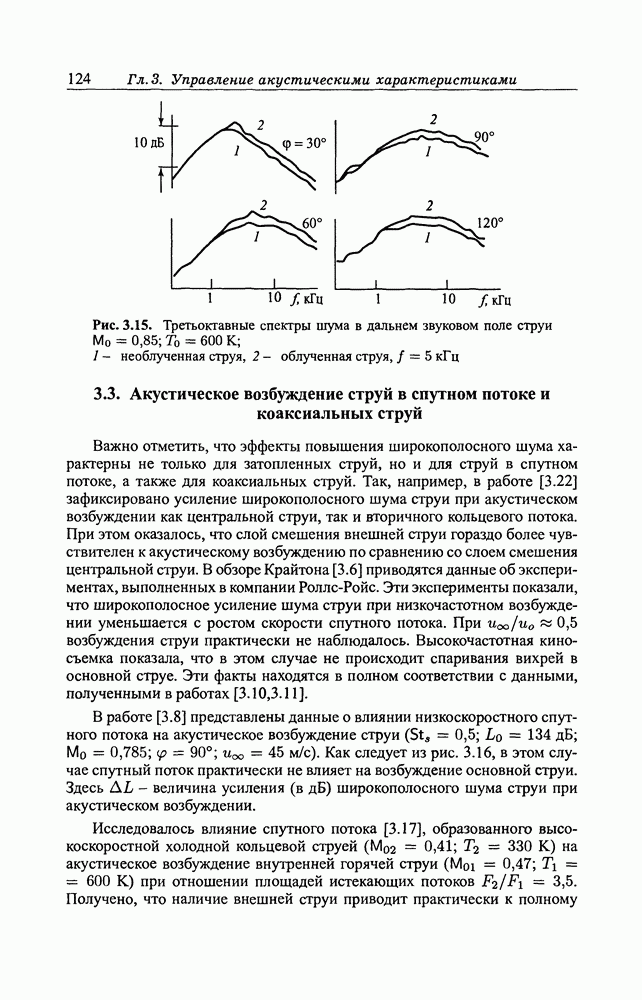
- 3.3. Акустическое возбуждение струй в спутном потоке и коаксиальных струй
- 3.4. О механизмах генерации шума дозвуковыми турбулентными струями
- ГЛАВА 4. ВОЗДЕЙСТВИЕ НА ДОЗВУКОВУЮ СТРУЮ ИНТЕНСИВНЫХ АКУСТИЧЕСКИХ ВОЗМУЩЕНИЙ
- 4.1. Высокоамплитудное низкочастотное периодическое возбуждение круглой струи и плоского слоя смешения
- 4.2. Визуализация течения в дозвуковой круглой струе при продольном и поперечном интенсивном акустическом возбуждении
- ГЛАВА 5. САМОВОЗБУЖДЕНИЕ ТУРБУЛЕНТНЫХ СТРУЙНЫХ ТЕЧЕНИЙ
- 5.1. Схемы самовозбуждения турбулентных струйных течений
- 5.2. Нормальное и косое натекание околозвуковой струи на экран
- 5.3. Автоколебания в аэродинамических трубах с открытой рабочей частью
- ГЛАВА 6. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ПЕРИОДИЧЕСКОГО ВОЗБУЖДЕНИЯ ДОЗВУКОВЫХ ТУРБУЛЕНТНЫХ СТРУЙ
- 6.2. Моделирование плоских и круглых турбулентных струй на основе метода дискретных вихрей при низкочастотном и высокочастотном гармоническом возбуждении
- 6.3. Численное моделирование турбулентного слоя смешения на основе нестационарных уравнений Рейнольдса, замкнутых с помощью дифференциальной модели турбулентости
- 6.4. Численное моделирование турбулентных струйных течений на основе обобщенных уравнений Рейнольдса (трехчленное разложение). Влияние низкочастотного и высокочастотного гармонического возбуждения
- 6.5. Об одной любопытной аналогии
- ГЛАВА 7. СВЕРХЗВУКОВЫЕ НЕИЗОБАРИЧЕСКИЕ ТУРБУЛЕНТНЫЕ СТРУИ. УПРАВЛЕНИЕ АЭРОДИНАМИЧЕСКИМИ И АКУСТИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ
- 7.1. Аэродинамические характеристики сверхзвуковых турбулентных струй
- 7.2. Механизм шумообразования. Широкополосный шум и дискретные составляющие
- 7.3. Акустическое возбуждение сверхзвуковых струй. Активное управление
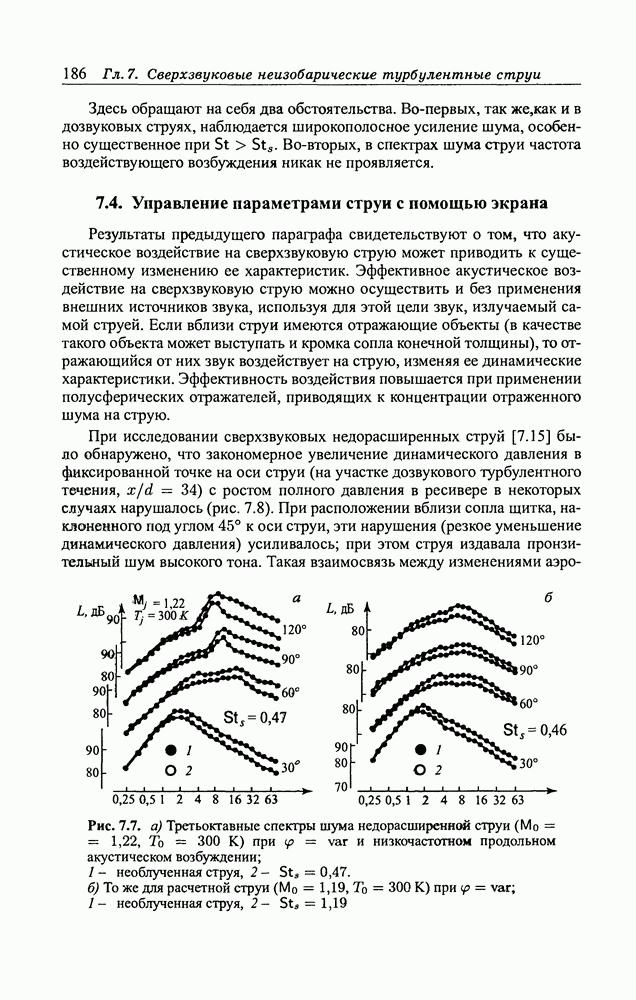
- 7.4. Управление параметрами струи с помощью экрана
- ГЛАВА 8. СНИЖЕНИЕ ШУМА РЕАКТИВНЫХ СТРУЙ ТРД
- 8.1. Акустический глушитель шума реактивной струи ТРД
- 8.2. Струйная система для снижения шума сверхзвуковых струй. Подавление дискретной составляющей
- 8.3. Снижение избыточного шума ТРД, обусловленного аэроакустическим взаимодействием
- ГЛАВА 9. АКУСТИЧЕСКИЕ МЕТОДЫ УПРАВЛЕНИЯ АВТОКОЛЕБАНИЯМИ В АЭРОДИНАМИЧЕСКИХ ТРУБАХ С ОТКРЫТОЙ РАБОЧЕЙ ЧАСТЬЮ
- 9.2. Подавление автоколебаний при высокочастотном акустическом возбуждении слоя смешения
- 9.3. Генерация автоколебаний и создание однородного пульсирующего потока в рабочей части трубы при низкочастотном возбуждении слоя смешения
- 9.4. Подавление автоколебаний при помощи антишума
- ГЛАВА 10. ВЗАИМОДЕЙСТВИЕ СЛОЯ СМЕШЕНИЯ С ПОЛОСТЬЮ
- 10.1. Отрывное обтекание полости
- 10.2. Пульсации пристеночного давления при обтекании полости и способы их уменьшения
- 10.3. Пульсации давления в околозвуковых аэродинамических трубах с закрытой рабочей частью и способы их уменьшения
- 10.4. Подавление автоколебаний в тупиковых отростках газопроводов
- 10.5. Акустическое управление течением в полости