| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.4. Численное моделирование турбулентных струйных течений на основе обобщенных уравнений Рейнольдса (трехчленное разложение). Влияние низкочастотного и высокочастотного гармонического возбуждения
Предполагается, что входящие в уравнения Навье-Стокса переменные (компоненты скорости и давления) могут быть представлены в виде тройного разложения [6.14]:

где  не зависящая от времени составляющая,
не зависящая от времени составляющая,  крупномасштабная когерентная и
крупномасштабная когерентная и  случайная, мелкомасштабная составляющие. При таком разложении предполагается, что когерентные и некогерентные пульсации не коррелированны. Система уравнений, описывающая поведение каждой из трех составляющих течения, получается из уравнения Навье-Стокса и уравнения неразрывности после представления входящих в них величин в виде (6.4) и применения соответствующих операторов осреднения: осреднения по времени и фазового осреднения, используемого для выделения периодической, когерентной составляющей. В итоге получается система дифференциальных уравнений для осредненного, периодического и случайного движений, в которую наряду с рейнольдсовыми напряжениями сдвига
случайная, мелкомасштабная составляющие. При таком разложении предполагается, что когерентные и некогерентные пульсации не коррелированны. Система уравнений, описывающая поведение каждой из трех составляющих течения, получается из уравнения Навье-Стокса и уравнения неразрывности после представления входящих в них величин в виде (6.4) и применения соответствующих операторов осреднения: осреднения по времени и фазового осреднения, используемого для выделения периодической, когерентной составляющей. В итоге получается система дифференциальных уравнений для осредненного, периодического и случайного движений, в которую наряду с рейнольдсовыми напряжениями сдвига  вызванными мелкомасштабным турбулентным движением, входят дополнительные напряжения
вызванными мелкомасштабным турбулентным движением, входят дополнительные напряжения  обусловленные периодическими, когерентными структурами. В этих уравнениях содержатся члены, учитывающие взаимодействие периодического и случайного движений, а также каждого из них с осредненным движением
обусловленные периодическими, когерентными структурами. В этих уравнениях содержатся члены, учитывающие взаимодействие периодического и случайного движений, а также каждого из них с осредненным движением  молекулярная вязкость полагается пренебрежимо малой по сравнению с турбулентной вязкостью.
молекулярная вязкость полагается пренебрежимо малой по сравнению с турбулентной вязкостью.
На основе такого подхода были рассчитаны турбулентные струи и следы в несжимаемой жидкости при наличии одночастотного и двухчастотного периодического возбуждения  При этом использовалось приближение пограничного слоя, струя полагалась
При этом использовалось приближение пограничного слоя, струя полагалась

(кликните для просмотра скана)
изобарической, жидкость - несжимаемой и невязкой. Известно несколько подходов к решению таких задач, обычно сводящихся к системе интегральных соотношений. Для определения параметров мелкомасштабной турбулентности используются различные полуэмпирические модели турбулентности (от алгебраических моделей с постоянной вихревой вязкостью поперек слоя смешения до дифференциальных моделей) или же эмпирические формулы.
Для нахождения периодических когерентных составляющих обычно используется линейная теория устойчивости в невязком приближении и в предположении локальной параллельности течения. При этом периодические компоненты скорости и давления представляются в виде

где  комплексная функция от
комплексная функция от  действительная часть ее соответствует волновому числу, а мнимая отрицательная часть - коэффициенту усиления возмущений,
действительная часть ее соответствует волновому числу, а мнимая отрицательная часть - коэффициенту усиления возмущений,  - круговая частота и
- круговая частота и  азимутальное волновое число. Предполагается, что входящие в (6.4) периодические возмущения могут быть представлены в виде (6.5). При решении задачи следует учесть наличие нелинейных волновых процессов. С этой целью используется энергетический интегральный метод, т.е. вместо дифференциальных уравнений переноса кинетической энергии среднего течения, периодического крупномасштабного и случайного мелкомасштабного течений рассматриваются интегральные соотношения, полученные интегрированием поперек слоя смешения исходных дифференциальных уравнений.
азимутальное волновое число. Предполагается, что входящие в (6.4) периодические возмущения могут быть представлены в виде (6.5). При решении задачи следует учесть наличие нелинейных волновых процессов. С этой целью используется энергетический интегральный метод, т.е. вместо дифференциальных уравнений переноса кинетической энергии среднего течения, периодического крупномасштабного и случайного мелкомасштабного течений рассматриваются интегральные соотношения, полученные интегрированием поперек слоя смешения исходных дифференциальных уравнений.
В качестве примера приведем такую систему интегральных соотношений для круглой струи [6.8]:

Здесь  соответственно кинетическая энергия турбулентного и периодического движений
соответственно кинетическая энергия турбулентного и периодического движений 
- соответственно скорость диссипации кинетической энергии турбулентности и периодического движения;

Рис. 6.14. Сравнение данных расчета  и экспериментов для пульсаций давления вдоль по потоку в середине слоя смешения
и экспериментов для пульсаций давления вдоль по потоку в середине слоя смешения  и поперечных профилей пульсаций давления
и поперечных профилей пульсаций давления  в круглой турбулентной струе при ее низкочастотном акустическом возбуждении
в круглой турбулентной струе при ее низкочастотном акустическом возбуждении  на нулевой
на нулевой  первой
первой  и второй
и второй  азимутальных модах.
азимутальных модах. 

Рис. 6.15. Сравнение расчета [6.22] и эксперимента [2.49] для изменения толщины потери импульса  вдоль слоя смешения круглой турбулентной струи при ее высокочастотном акустическом возбуждении
вдоль слоя смешения круглой турбулентной струи при ее высокочастотном акустическом возбуждении 
диссипативная функция определяет перенос энергии от периодических возмущений к мелкомасштабным, турбулентным возмущениям.
Для решения системы (6.6) требуется задать профили средней скорости в различных сечениях слоя смешения, выражения для рейнольдсовых напряжений  Для определения
Для определения  используется модель турбулентности; для определения
используется модель турбулентности; для определения  выражение (6.5), которое представляется в виде
выражение (6.5), которое представляется в виде  где
где  амплитудное значение соответствующего периодического возмущения. Таким образом, из линейной теории устойчивости заимствуются только относительные профили компонент скорости и давления, и система (6.6) описывает нелинейный процесс
амплитудное значение соответствующего периодического возмущения. Таким образом, из линейной теории устойчивости заимствуются только относительные профили компонент скорости и давления, и система (6.6) описывает нелинейный процесс
взаимодействия периодических и случайных компонент.
Система (6.6) позволяет определить три параметра - эффективную толщину слоя смешения, амплитудное или среднее значение кинетической энергии турбулентности и амплитудное значение периодических пульсаций. Для этого требуется задать начальные значения этих параметров и характерную частоту периодических пульсаций или число Струхаля  Таким образом, открывается возможность учитывать влияние на развитие струи таких параметров, как начальная турбулентность и начальный уровень периодического возбуждения, а также частота возбуждения и азимутальное волновое число
Таким образом, открывается возможность учитывать влияние на развитие струи таких параметров, как начальная турбулентность и начальный уровень периодического возбуждения, а также частота возбуждения и азимутальное волновое число 
В качестве примера на рис. 6.14 сравниваются расчетные и опытные значения пульсаций давления вдоль слоя смешения и поперечных профилей пульсаций давления турбулентной струи при ее акустическом возбуждении плоскими  и высшими азимутальными
и высшими азимутальными  и 2) модами [6.23]. В работе [6.22] приведен расчет нарастания толщины потери импульса вдоль слоя смешения круглой струи при ее высокочастотном возбуждении
и 2) модами [6.23]. В работе [6.22] приведен расчет нарастания толщины потери импульса вдоль слоя смешения круглой струи при ее высокочастотном возбуждении  Результаты расчета
Результаты расчета  хорошо описывают соответствующую экспериментальную зависимость, полученную ранее при акустическом возбуждении струи (см. рис. 2.36).
хорошо описывают соответствующую экспериментальную зависимость, полученную ранее при акустическом возбуждении струи (см. рис. 2.36).
Кривые  на рис. 6.16 иллюстрируют эффект насыщения низкочастотного акустического возбуждения струи
на рис. 6.16 иллюстрируют эффект насыщения низкочастотного акустического возбуждения струи  при увеличении интенсивности акустического возбуждения [6.27].
при увеличении интенсивности акустического возбуждения [6.27].
В работе [6.19] показано, что одновременное периодическое возбуждение струи на частотах, соответствующих числам Струхаля  и 0,4, приводит к интенсификации попарного слияния вихрей и, как следствие, к утолщению слоя смешения по сравнению с одночастотным возбуждением.
и 0,4, приводит к интенсификации попарного слияния вихрей и, как следствие, к утолщению слоя смешения по сравнению с одночастотным возбуждением.

Рис. 6.16. Эффект насыщения при низкочастотном  акустическом возбуждении турбулентной струи при увеличении интенсивности возбуждения в сечении
акустическом возбуждении турбулентной струи при увеличении интенсивности возбуждения в сечении  - расчет, 2 - эксперимент
- расчет, 2 - эксперимент
Наоборот, при высокочастотном возбуждении с частотами, соответствующими числам Струхаля  и 2,4, наблюдается уменьшение толщины слоя смешения по сравнению с одночастотным возбуждением (рис. 6.17). Эффективность такого двухчастотного возбуждения зависит от фазового соотношения сигналов основного тона и субгармоники.
и 2,4, наблюдается уменьшение толщины слоя смешения по сравнению с одночастотным возбуждением (рис. 6.17). Эффективность такого двухчастотного возбуждения зависит от фазового соотношения сигналов основного тона и субгармоники.

Рис. 6.17. Расчет изменения вдоль по потоку толщины потери импульса  в слое смешения круглой турбулентной струи при двухчастотном и одночастотном периодическом возбуждении с уровнем
в слое смешения круглой турбулентной струи при двухчастотном и одночастотном периодическом возбуждении с уровнем  а также при отсутствии возбуждения
а также при отсутствии возбуждения 
а) низкочастотное возбуждение:  - невозбужденная струя;
- невозбужденная струя;
б) высокочастотное возбуждение:  и
и  - невозбужденная струя
- невозбужденная струя
Сходные результаты получены при трехчастотном периодическом возбуждении струи  на нулевой моде
на нулевой моде  осесимметричные возмущения) при сдвиге фаз между первым и вторым
осесимметричные возмущения) при сдвиге фаз между первым и вторым  и между вторым и третьим -
и между вторым и третьим -  периодическими возмущениями [6.20]. Было исследовано влияние частоты периодических возмущений на их взаимодействие, рост энергии турбулентности и эффективной толщины слоя смешения на участке протяженностью 9 калибров. Показано, что при
периодическими возмущениями [6.20]. Было исследовано влияние частоты периодических возмущений на их взаимодействие, рост энергии турбулентности и эффективной толщины слоя смешения на участке протяженностью 9 калибров. Показано, что при  утолщение слоя смешения вдоль по потоку максимальное (рис. 6.18).
утолщение слоя смешения вдоль по потоку максимальное (рис. 6.18).
Усовершенствование этого метода [6.21] позволило описать ряд важных эффектов. При этом параметры течения полагались состоящими из четырех компонент: среднего течения, мелкомасштабной турбулентности, основной и субгармонических периодических компонент

После ряда упрощений уравнения количества движения для среднего течения  основной
основной  и субгармонических
и субгармонических  компонент движения, а также для мелкомасштабной турбулентности
компонент движения, а также для мелкомасштабной турбулентности  интегрируются поперек
интегрируются поперек

Рис. 6.18. Влияние начального сдвига фаз  на толщину потери импульса
на толщину потери импульса  в слое смешения круглой турбулентной струи при ее трехчастотном периодическом возбуждении
в слое смешения круглой турбулентной струи при ее трехчастотном периодическом возбуждении  без возбуждения,
без возбуждения, 
потока, что приводит к системе интегральных соотношений, в которых учитывается взаимодействие всех компонент течения. В итоге определяются изменения вдоль потока толщины потери импульса, амплитудных значений энергии мелкомасштабной турбулентности, периодических компонент основной и субгармонических частот, число попарных слияний вихрей при заданных начальных значениях этих величин, сдвиге фаз между колебаниями на основной и субгармонической частотах и числе Струхаля  определенном по частоте
определенном по частоте  периодического возбуждения.
периодического возбуждения.
В цитированной выше работе выполнены расчеты изменения толщины потери импульса вдоль по потоку при начальных уровнях периодического возбуждения  и числах Струхаля
и числах Струхаля  для фиксированного низкого начального значения уровня мелкомасштабной турбулентности
для фиксированного низкого начального значения уровня мелкомасштабной турбулентности  в круглой струе. Показано, что при
в круглой струе. Показано, что при  толщина в при
толщина в при  монотонно увеличивается с ростом уровня периодического возбуждения (рис. 6.19), начиная от
монотонно увеличивается с ростом уровня периодического возбуждения (рис. 6.19), начиная от  при этом не наблюдается попарного слияния вихрей, т.е. субгармоника несущественна. При
при этом не наблюдается попарного слияния вихрей, т.е. субгармоника несущественна. При  с ростом уровня возбуждения
с ростом уровня возбуждения  утолщение слоя смешения вдоль по потоку становится немонотонным и происходит одно спаривание вихрей.
утолщение слоя смешения вдоль по потоку становится немонотонным и происходит одно спаривание вихрей.
При  возбуждение с уровнем
возбуждение с уровнем  приводит к утончению слоя смешения; при этом формируются четыре спаривания вихрей. Важно отметить, что при больших числах Струхаля
приводит к утончению слоя смешения; при этом формируются четыре спаривания вихрей. Важно отметить, что при больших числах Струхаля  и очень больших уровнях периодического возбуждения
и очень больших уровнях периодического возбуждения  вместо утончения происходит утолщение слоя смешения, т.е. подтверждается обнаруженная в опытах смена знака воздействия.
вместо утончения происходит утолщение слоя смешения, т.е. подтверждается обнаруженная в опытах смена знака воздействия.
Рис. 6.19. (см. скан) Влияние частоты (числа Струхаля) и уровня  одночастотного периодического возбуждения на изменение толщины потери импульса слоя смешения круглой турбулентной струи.
одночастотного периодического возбуждения на изменение толщины потери импульса слоя смешения круглой турбулентной струи. 
Из представленных материалов можно заключить, что изложенный в п. 6.4 метод моделирования в наибольшей степени пригоден для анализа влияния периодического возбуждения турбулентных струй на их аэродинамические характеристики.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ДОЗВУКОВЫЕ ТУРБУЛЕНТНЫЕ СТРУИ
- 1.1. Аэродинамические характеристики турбулентных струй. Когерентные структуры
- 1.2. Когерентные структуры и гидродинамическая неустойчивость
- 1.3. Акустические характеристики дозвуковых турбулентных струй
- 1.4. Начальные условия истечения турбулентных струй
- 1.5. Методы управления турбулентными струями
- ГЛАВА 2. УПРАВЛЕНИЕ АЭРОДИНАМИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ ДОЗВУКОВЫХ ТУРБУЛЕНТНЫХ СТРУЙ
- 2.1. Восприимчивость турбулентных струй к слабым гармоническим акустическим возмущениям. Влияние частоты возбуждения
- 2.2. Влияние уровня акустического возбуждения
- 2.3. Влияние режима течения в пограничном слое на срезе сопла
- 2.4. Влияние начальной турбулентности потока на эффективность акустического возбуждения струи
- 2.5. Деформация поперечного сечения струи при ее поперечном акустическом возбуждении
- 2.6. Акустическое возбуждение струи, истекающей из диафрагмы
- 2.7. Вибрационное возбуждение турбулентной струи
- 2.8. Акустическое возбуждение высокоскоростных струй
- 2.9. Изменение модового состава турбулентных пульсаций при акустическом возбуждении струи. Локализация мест спаривания и разрушения когерентных структур при акустическом возбуждении струи. Механизмы акустического возбуждения струи
- 2.10. Влияние спутного потока на интенсификацию турбулентного смешения в струе при низкочастотном акустическом возбуждении
- 2.11. Тональное акустическое возбуждение неизотермических газовых струй
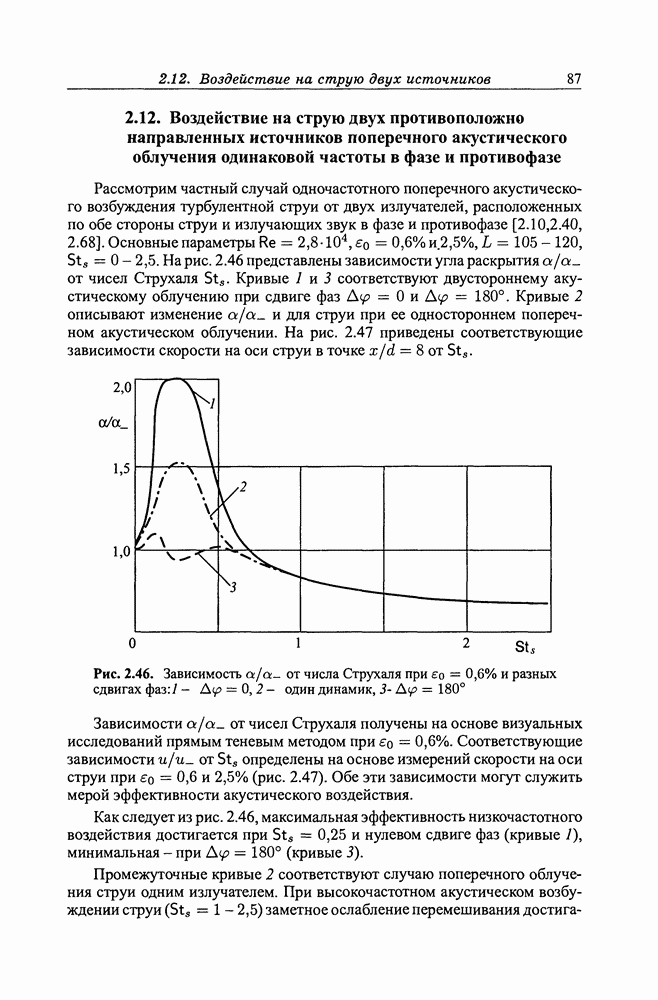
- 2.12. Воздействие на струю двух противоположно направленных источников поперечного акустического облучения одинаковой частоты в фазе и противофазе
- 2.13. Воздействие на струю акустических возмущений высших азимутальных мод
- 2.14. Многочастотное акустическое возбуждение струи. Субгармонический резонанс
- 2.15. Акустическое возбуждение турбулентной струи при нарушении гармоничности воздействующего сигнала
- 2.16. Акустическое возбуждение некруглых струй
- ГЛАВА 3. УПРАВЛЕНИЕ АКУСТИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ ДОЗВУКОВЫХ ТУРБУЛЕНТНЫХ СТРУЙ
- 3.1. Акустические характеристики ближнего и дальнего поля турбулентных струй при их акустическом возбуждении
- 3.2. Акустическое возбуждение неизотермических струй
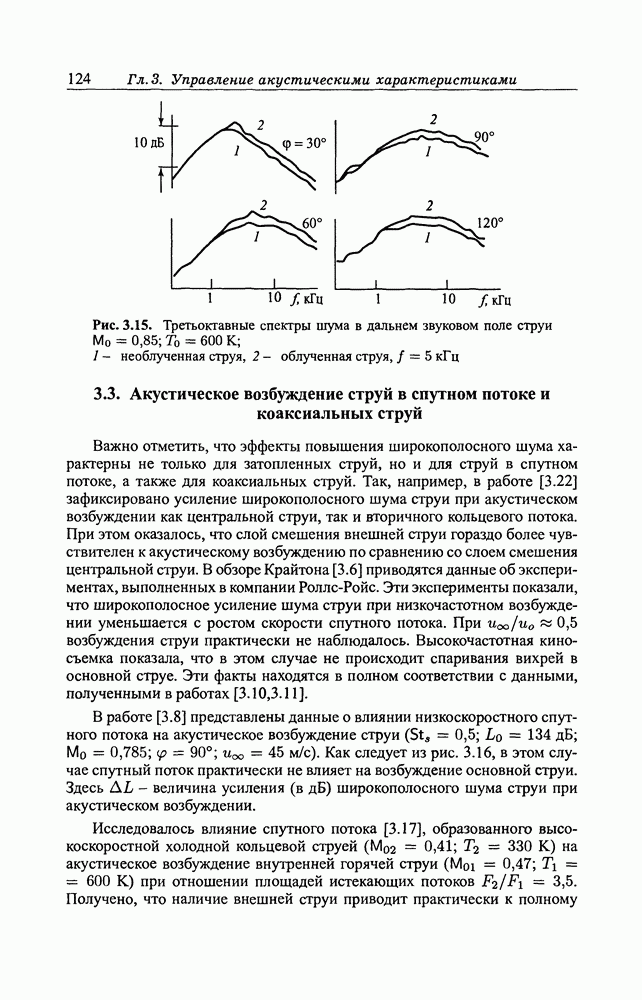
- 3.3. Акустическое возбуждение струй в спутном потоке и коаксиальных струй
- 3.4. О механизмах генерации шума дозвуковыми турбулентными струями
- ГЛАВА 4. ВОЗДЕЙСТВИЕ НА ДОЗВУКОВУЮ СТРУЮ ИНТЕНСИВНЫХ АКУСТИЧЕСКИХ ВОЗМУЩЕНИЙ
- 4.1. Высокоамплитудное низкочастотное периодическое возбуждение круглой струи и плоского слоя смешения
- 4.2. Визуализация течения в дозвуковой круглой струе при продольном и поперечном интенсивном акустическом возбуждении
- ГЛАВА 5. САМОВОЗБУЖДЕНИЕ ТУРБУЛЕНТНЫХ СТРУЙНЫХ ТЕЧЕНИЙ
- 5.1. Схемы самовозбуждения турбулентных струйных течений
- 5.2. Нормальное и косое натекание околозвуковой струи на экран
- 5.3. Автоколебания в аэродинамических трубах с открытой рабочей частью
- ГЛАВА 6. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ПЕРИОДИЧЕСКОГО ВОЗБУЖДЕНИЯ ДОЗВУКОВЫХ ТУРБУЛЕНТНЫХ СТРУЙ
- 6.2. Моделирование плоских и круглых турбулентных струй на основе метода дискретных вихрей при низкочастотном и высокочастотном гармоническом возбуждении
- 6.3. Численное моделирование турбулентного слоя смешения на основе нестационарных уравнений Рейнольдса, замкнутых с помощью дифференциальной модели турбулентости
- 6.4. Численное моделирование турбулентных струйных течений на основе обобщенных уравнений Рейнольдса (трехчленное разложение). Влияние низкочастотного и высокочастотного гармонического возбуждения
- 6.5. Об одной любопытной аналогии
- ГЛАВА 7. СВЕРХЗВУКОВЫЕ НЕИЗОБАРИЧЕСКИЕ ТУРБУЛЕНТНЫЕ СТРУИ. УПРАВЛЕНИЕ АЭРОДИНАМИЧЕСКИМИ И АКУСТИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ
- 7.1. Аэродинамические характеристики сверхзвуковых турбулентных струй
- 7.2. Механизм шумообразования. Широкополосный шум и дискретные составляющие
- 7.3. Акустическое возбуждение сверхзвуковых струй. Активное управление
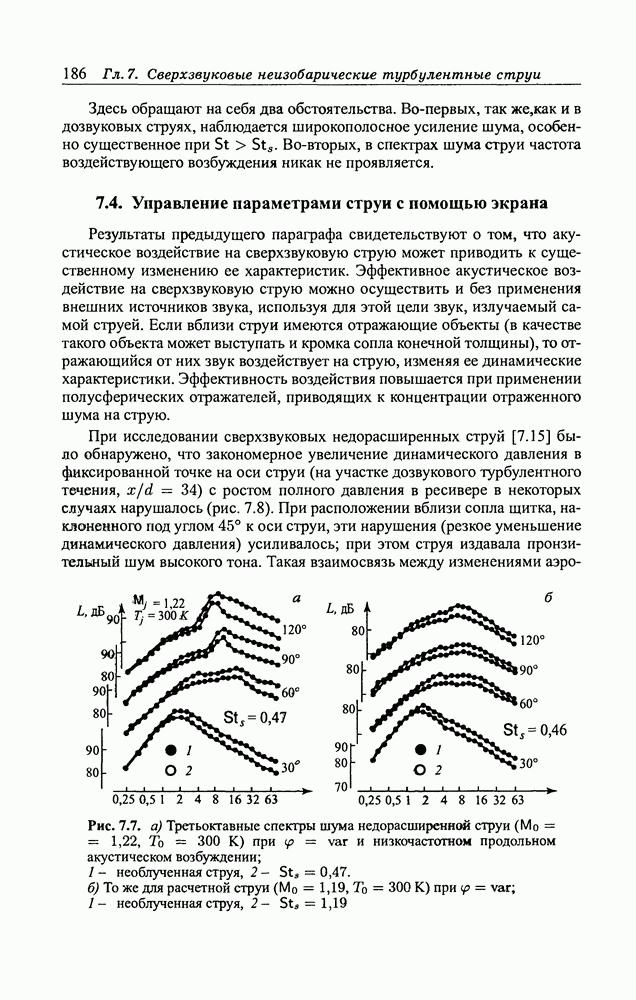
- 7.4. Управление параметрами струи с помощью экрана
- ГЛАВА 8. СНИЖЕНИЕ ШУМА РЕАКТИВНЫХ СТРУЙ ТРД
- 8.1. Акустический глушитель шума реактивной струи ТРД
- 8.2. Струйная система для снижения шума сверхзвуковых струй. Подавление дискретной составляющей
- 8.3. Снижение избыточного шума ТРД, обусловленного аэроакустическим взаимодействием
- ГЛАВА 9. АКУСТИЧЕСКИЕ МЕТОДЫ УПРАВЛЕНИЯ АВТОКОЛЕБАНИЯМИ В АЭРОДИНАМИЧЕСКИХ ТРУБАХ С ОТКРЫТОЙ РАБОЧЕЙ ЧАСТЬЮ
- 9.2. Подавление автоколебаний при высокочастотном акустическом возбуждении слоя смешения
- 9.3. Генерация автоколебаний и создание однородного пульсирующего потока в рабочей части трубы при низкочастотном возбуждении слоя смешения
- 9.4. Подавление автоколебаний при помощи антишума
- ГЛАВА 10. ВЗАИМОДЕЙСТВИЕ СЛОЯ СМЕШЕНИЯ С ПОЛОСТЬЮ
- 10.1. Отрывное обтекание полости
- 10.2. Пульсации пристеночного давления при обтекании полости и способы их уменьшения
- 10.3. Пульсации давления в околозвуковых аэродинамических трубах с закрытой рабочей частью и способы их уменьшения
- 10.4. Подавление автоколебаний в тупиковых отростках газопроводов
- 10.5. Акустическое управление течением в полости