| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9 КЛАСС
ГЛАВА 22. ОСНОВЫ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
Основа данного раздела — молекулярно-кинетическая теория строения вещества. Поэтому вначале решают задачи о свойствах атомов и молекул.
Подбор и методика решения задач по основам кинетической теории газов в большой мере зависят от последовательности и методики изучения материала. По новой программе изучение этого материала будет осуществляться в основном дедуктивным методом: центральное место отводится основному уравнению кинетической теории газов, из которого выводят уравнение состояния газов, а газовые законы рассматривают как его частные случаи.
В соответствии с этим при решении задач нужно прежде всего использовать основное уравнение кинетической теории газов и уравнение Клапейрона-Менделеева. Эти уравнения широко применяют при изучении всей молекулярной физики в IX классе, поэтому задачам по данной теме должно быть уделено особое внимание.
1. Основы молекулярно - кинетической теории
Для повторения и углубления имеющихся у учащихся сведений о молекулах и их свойствах вначале решают задачи, подобные рассмотренным в главе 4, с учетом знаний, полученных учащимися в VII—VIII классах. Далее основное внимание уделяют задачам, дающим понятие о методах изучения микромира и его закономерностях.
При решении задач можно познакомить учащихся с идеями и работами Авогадро, Гей-Люссака, Дальтона, Ломоносова, с использованием для изучения закономерностей микромира броуновского движения, с современными способами определения скоростей молекул (опыты Штерна), дать понятие о способах определения размеров и массы молекул и др.
Задачи с использованием молекулярно-кинетической теории ученики решают и на уроках химии. Поэтому здесь особенно необходима продуманная межпредметная связь физики с химией с тем, чтобы наилучшим образом использовать химические законы для формирования глубоких и прочных понятий о молекулярном строении вещества. В том числе на уроках физики полезно решить ряд «химических» задач (№ 515—519), а на уроках химии — несколько задач «с физическим» уклоном. Такая взаимосвязь позволяет ученикам посмотреть на одни и те же факты с разных точек зрения и, следовательно, лучше осознать их.
515. В 1811 г. Авогадро высказал гипотезу о том, что при одних и тех же условиях (температура и давление) в равных объемах любых газов содержится одинаковое число молекул. Используя эту гипотезу и формулу молекулы воды, определите, какой нужно взять объем водорода и кислорода, чтобы получить  водяных паров, имеющих такое же давление и температуру.
водяных паров, имеющих такое же давление и температуру.
Решение.  Из уравнения видно, что для получения двух молекул воды нужны две молекулы водорода и одна молекула кислорода. Из гипотезы Авогадро следует, что объемы газов при одинаковых условиях пропорциональны числу молекул. (В равных объемах находится одинаковое число молекул, а в объеме, например, вдвое большем находится и в два раза большее число молекул.) Следовательно, для получения
Из уравнения видно, что для получения двух молекул воды нужны две молекулы водорода и одна молекула кислорода. Из гипотезы Авогадро следует, что объемы газов при одинаковых условиях пропорциональны числу молекул. (В равных объемах находится одинаковое число молекул, а в объеме, например, вдвое большем находится и в два раза большее число молекул.) Следовательно, для получения  водяных паров нужно взять
водяных паров нужно взять  водорода и
водорода и  кислорода.
кислорода.
Учащимся нужно сказать, что последующие исследования подтвердили правильность гипотезы Авогадро.
516. В 1808 г. Гей-Люссак открыл, что отношения объемов газов, вступивших в химические реакции, выражаются простыми целыми числами. Какое предположение о строении молекул сложного вещества можно сделать из этого закона, используя гипотезу Авогадро? Ответ поясните примером.
Ответ. Поскольку по гипотезе Авогадро число молекул пропорционально объему газов, то можно предположить, что для образования молекулы сложного вещества нужно всегда определенное число молекул (атомов) простых веществ. Таким образом, мельчайшие частички (молекулы, атомы) одного вещества всегда соединяются определенным образом с молекулами (атомами) другого вещества (закон постоянства химического состава). Например, с  водорода
водорода  вступает в реакцию
вступает в реакцию  хлора
хлора  водорода вступает в реакцию, как это показано в предыдущей задаче,
водорода вступает в реакцию, как это показано в предыдущей задаче,  кислорода и т. д.
кислорода и т. д.
517. Дальтон установил закон кратных отношений, согласно которому если два элемента образуют несколько соединений, то с постоянной по величине массой одного элемента вступают в соединения такие количества другого элемента, которые относятся между собой как небольшие целые числа. Какое предположение о
молекулярном строении сложного вещества можно сделать из этого? Ответ поясните химическими формулами.
Ответ. Явление объясняют тем, что с одним и тем же количеством атомов одного элемента вступает в соединение целое число атомов другого элемента.
Примеры: 
518. Используя таблицу плотности газов, покажите, во сколько раз масса молекулы водорода  меньше массы молекулы кислорода
меньше массы молекулы кислорода 
Решение. Плотность водорода при нормальных условиях Рад  а кислорода —
а кислорода —  Так как в равных объемах газов содержится одинаковое число молекул, то
Так как в равных объемах газов содержится одинаковое число молекул, то

519. Вычислите в килограммах массу атома фтора, принимая за атомную единицу массы  массы атома углерода.
массы атома углерода.
Решение. Вычислим значение а.е.м. в килограммах.  где — масса килограмм-атома углерода,
где — масса килограмм-атома углерода,  число Авогадро. Так как в настоящее время принято, что
число Авогадро. Так как в настоящее время принято, что  то
то

Это значение а.е.м. ученики должны занести в свои таблицы. Для нахождения массы атома любого элемента это число нужно умножить на его атомную массу.

 Определите размер молекулы масла по масляному пятну на поверхности воды, предполагая, что молекулы располагаются в один слой.
Определите размер молекулы масла по масляному пятну на поверхности воды, предполагая, что молекулы располагаются в один слой.
Решение. Толщина слоя  где V — объем,
где V — объем,  масса и
масса и  плотность капли масла,
плотность капли масла,  соответственно площадь и диаметр пятна.
соответственно площадь и диаметр пятна.
Среднее значение массы капли следует поручить определить заранее группе учащихся с помощью весов, а диаметр пятна легко измерить на уроке. При этом нужно позаботиться о том, чтобы объем капли был не более  иначе поверхность пятна будет чрезмерно большой. Для обеспечения хорошей видимости пятна на поверхность воды в сосуде достаточных размеров (фотографическая кювета, аквариум, таз) насыпают ликоподий или мелкую пробковую пыль. С помощью пипетки, в отверстие которой вставлен кусочек лески диаметром
иначе поверхность пятна будет чрезмерно большой. Для обеспечения хорошей видимости пятна на поверхность воды в сосуде достаточных размеров (фотографическая кювета, аквариум, таз) насыпают ликоподий или мелкую пробковую пыль. С помощью пипетки, в отверстие которой вставлен кусочек лески диаметром  получают маленькую капельку масла, которую опускают на поверхность воды и наблюдают, как ликоподий резко раздвигается к краям сосуда, а в середине образуется масляное пятно почти правильной круглой формы. Замерив его диаметр, производят расчеты.
получают маленькую капельку масла, которую опускают на поверхность воды и наблюдают, как ликоподий резко раздвигается к краям сосуда, а в середине образуется масляное пятно почти правильной круглой формы. Замерив его диаметр, производят расчеты.
В результате одного из опытов были получены следующие данные: среднее значение массы капли  диаметр пятна
диаметр пятна  см; плотность масла
см; плотность масла 
Подставив данные в формулу, найдем  см.
см.
Значение  см еще не может быть с полной уверенностью принято за величину диаметра молекулы, поскольку мы точно не знаем, как располагаются молекулы в пленке. Однако можно утверждать, что диаметр молекулы не больше h.
см еще не может быть с полной уверенностью принято за величину диаметра молекулы, поскольку мы точно не знаем, как располагаются молекулы в пленке. Однако можно утверждать, что диаметр молекулы не больше h.
521. Определите линейные размеры молекулы воды.
Решение. Формула воды  Атомный вес водорода
Атомный вес водорода  а кислорода (изотопа
а кислорода (изотопа  Поэтому масса киломоля воды примерно равна
Поэтому масса киломоля воды примерно равна  а объем
а объем  Объем молекулы
Объем молекулы

Пренебрегая промежутками между молекулами, ввиду их плотной упаковки, найдем приближенно линейный размер молекулы:

т. е. линейные размеры молекулы воды того же порядка, что и молекулы масла (№ 520), что косвенно подтверждает правомерность расчетов, выполненных в экспериментальной задаче.
522. Вычислите примерные размеры атома (молекулы) золота.
Решение.  Объем килограмм-атома
Объем килограмм-атома  Объем атома
Объем атома


Таким образом, и молекула золота имеет линейные размеры того же порядка  , как и молекула воды (№ 520).
, как и молекула воды (№ 520).
523. Чем крупнее броуновские частицы, тем меньше скорость и! хаотического движения. Почему?
Ответ. По второму закону Ньютона ускорение, которое получает частица массой  от ударов молекул, равно
от ударов молекул, равно  где
где  результирующая сила удароввсех молекул. Чем крупнее частицы, тем в большей мере взаимно компенсируются силы ударов молекул, действующие на нее с разных сторон. Кроме того, увеличивается масса частиц, и они становятся менее «подвижными».
результирующая сила удароввсех молекул. Чем крупнее частицы, тем в большей мере взаимно компенсируются силы ударов молекул, действующие на нее с разных сторон. Кроме того, увеличивается масса частиц, и они становятся менее «подвижными».
524: В морской воде находится сравнительно большое  на
на  воды) количество золота. Почему частицы золота размером
воды) количество золота. Почему частицы золота размером  см не оседают на дно, хотя золото — один из самых тяжелых металлов?
см не оседают на дно, хотя золото — один из самых тяжелых металлов?
Ответ. Частицы золота размером  соизмеримы по величине с молекулами воды (№ 522). От ударов молекул воды они получают большие ускорения и скорости (№ 523) и движутся не в одном направлении — вниз, а хаотически в разных направлениях.
соизмеримы по величине с молекулами воды (№ 522). От ударов молекул воды они получают большие ускорения и скорости (№ 523) и движутся не в одном направлении — вниз, а хаотически в разных направлениях.
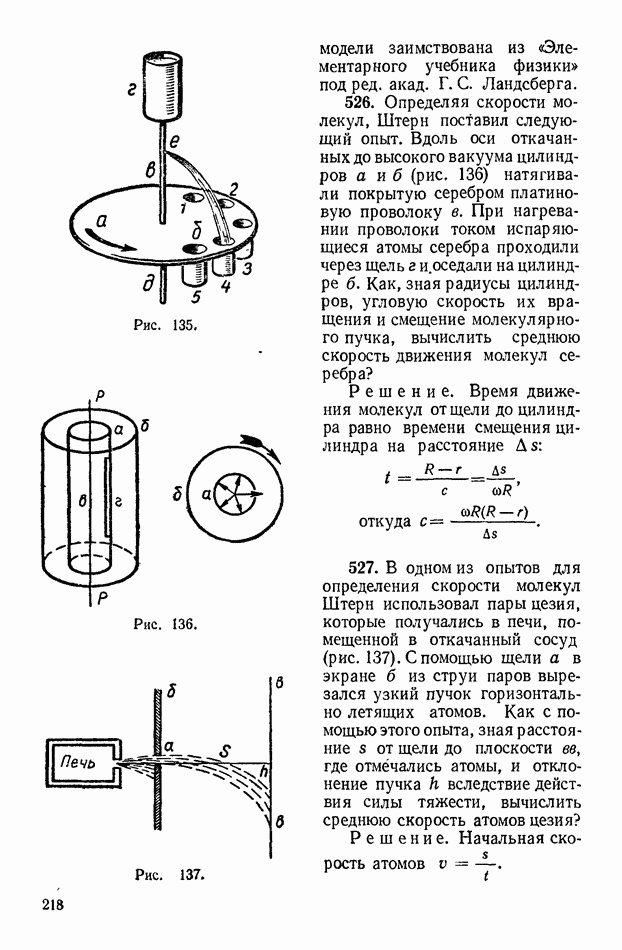
525(э). На рисунке 135 показан прибор, состоящий из диска а с укрепленными на нем стаканчиками  и трубки в, впаянной в дно сосуда
и трубки в, впаянной в дно сосуда  Прибор с помощью штока
Прибор с помощью штока  может крепиться на центробежной машине. Сосуд
может крепиться на центробежной машине. Сосуд  наполняют доверху водой, которая тонкой струей вытекает из отверстия
наполняют доверху водой, которая тонкой струей вытекает из отверстия  и попадает в средний стаканчик
и попадает в средний стаканчик  Приведя прибор во вращение, можно добиться, чтобы струя попадала, например, в стаканчик
Приведя прибор во вращение, можно добиться, чтобы струя попадала, например, в стаканчик  Как с помощью этого прибора определить скорость вытекания струи воды из отверстия
Как с помощью этого прибора определить скорость вытекания струи воды из отверстия 
Решение. Горизонтальную составляющую скорости струи можно определить, приравняв время движения струи по радиусу  и время
и время  перемещения стаканчика
перемещения стаканчика  на место стаканчика
на место стаканчика 

В одном из опытов были получены следующие данные. При  - вычисления дают
- вычисления дают  сек
сек
Проверка. См. задачу 504.
Задачу решают для того, чтобы подготовить учащихся к пониманию опыта Штерна по определению скорости молекул. Идея
модели заимствована из «Элементарного учебника физики» под ред. акад. Г. С. Ландсберга.
526. Определяя скорости молекул, Штерн поставил следующий опыт. Вдоль оси откачанных до высокого вакуума цилиндров  (рис. 136) натягивали покрытую серебром платиновую проволоку
(рис. 136) натягивали покрытую серебром платиновую проволоку  При нагревании проволоки током испаряющиеся атомы серебра проходили через щель г и оседали на цилиндре
При нагревании проволоки током испаряющиеся атомы серебра проходили через щель г и оседали на цилиндре  Как, зная радиусы цилиндров, угловую скорость их вращения и смещение молекулярного пучка, вычислить среднюю скорость движения молекул серебра?
Как, зная радиусы цилиндров, угловую скорость их вращения и смещение молекулярного пучка, вычислить среднюю скорость движения молекул серебра?
Решение. Время движения молекул от щели до цилиндра равно времени смещения цилиндра на расстояние 

527. В одном из опытов для определения скорости молекул Штерн использовал пары цезия, которые получались в печи, помещенной в откачанный сосуд (рис. 137). С помощью щели а в экране  из струи паров вырезался узкий пучок горизонтально летящих атомов. Как с помощью этого опыта, зная расстояние
из струи паров вырезался узкий пучок горизонтально летящих атомов. Как с помощью этого опыта, зная расстояние  от щели до плоскости
от щели до плоскости  где отмечались атомы, и отклонение пучка
где отмечались атомы, и отклонение пучка  вследствие действия силы тяжести, вычислить среднюю скорость атомов цезия?
вследствие действия силы тяжести, вычислить среднюю скорость атомов цезия?
Решение. Начальная скорость атомов 

Рис. 135.

Рис. 136.

Рис. 137.

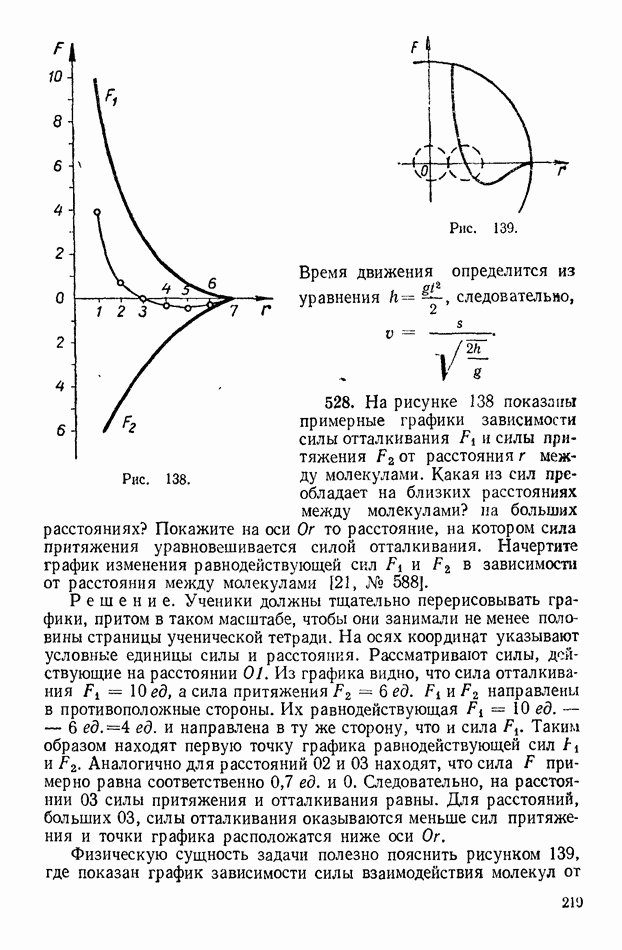
Рис. 138.

Рис. 139.
Время движения определится из уравнения  следовательно,
следовательно, 

528. На рисунке 138 показаны примерные графики зависимости силы отталкивания  и силы притяжения
и силы притяжения  от расстояния
от расстояния  между молекулами. Какая из сил преобладает на близких расстояниях между молекулами? на больших расстояниях? Покажите на оси
между молекулами. Какая из сил преобладает на близких расстояниях между молекулами? на больших расстояниях? Покажите на оси  то расстояние, на котором сила притяжения уравновешивается силой отталкивания. Начертите график изменения равнодействующей сил
то расстояние, на котором сила притяжения уравновешивается силой отталкивания. Начертите график изменения равнодействующей сил  в зависимости от расстояния между молекулами [21, № 588].
в зависимости от расстояния между молекулами [21, № 588].
Решение. Ученики должны тщательно перерисовывать графики, притом в таком масштабе, чтобы они занимали не менее половины страницы ученической тетради. На осях координат указывают условные единицы силы и расстояния. Рассматривают силы, действующие на расстоянии  Из графика видно, что сила отталкивания
Из графика видно, что сила отталкивания  а сила притяжения
а сила притяжения  направлены в противоположные стороны. Их равнодействующая
направлены в противоположные стороны. Их равнодействующая  и направлена в ту же сторону, что и сила
и направлена в ту же сторону, что и сила  Таким образом находят первую точку графика равнодействующей сил
Таким образом находят первую точку графика равнодействующей сил  Аналогично для расстояний
Аналогично для расстояний  находят, что сила
находят, что сила  примерно равна соответственно
примерно равна соответственно  и 0. Следовательно, на расстоянии
и 0. Следовательно, на расстоянии  силы притяжения и отталкивания равны. Для расстояний, больших
силы притяжения и отталкивания равны. Для расстояний, больших  силы отталкивания оказываются меньше сил притяжения и точки графика расположатся ниже оси
силы отталкивания оказываются меньше сил притяжения и точки графика расположатся ниже оси 
Физическую сущность задачи полезно пояснить рисунком 139, где показан график зависимости силы взаимодействия молекул от

Рис. 140.
расстояния. На расстоянии  (рис. 138) силы притяжения и отталкивания равны. Изобразим вокруг молекул сферы радиуса — (рис. 140, а). При сближении молекул на расстояние, меньшее
(рис. 138) силы притяжения и отталкивания равны. Изобразим вокруг молекул сферы радиуса — (рис. 140, а). При сближении молекул на расстояние, меньшее  проявляются силы отталкивания и молекулы ведут себя как упругие шары радиуса
проявляются силы отталкивания и молекулы ведут себя как упругие шары радиуса  (рис. 140, б). Поэтому в кинетической теории диаметр
(рис. 140, б). Поэтому в кинетической теории диаметр  обычно называют диаметром молекулы, хотя истинные ее размеры значительно меньше.
обычно называют диаметром молекулы, хотя истинные ее размеры значительно меньше.
При удалении молекул на расстояние, большее  проявляются силы притяжения (рис. 140, б), которые сначала возрастают, а потом на расстоянии
проявляются силы притяжения (рис. 140, б), которые сначала возрастают, а потом на расстоянии  уменьшаются до нуля и связь между молекулами утрачивается. Сферу радиуса
уменьшаются до нуля и связь между молекулами утрачивается. Сферу радиуса  называют сферой молекулярного действия.
называют сферой молекулярного действия.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВИДЫ ЗАДАЧ И ОБЩИЕ ВОПРОСЫ МЕТОДИКИ ИХ РЕШЕНИЯ
- 1. Задачи как средство обучения и воспитания учащихся на занятиях по физике
- 2. Классификация задач
- 3. Методика решения физической задачи
- ГЛАВА 2. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ РАЗНЫХ ТИПОВ
- 2. Экспериментальные задачи
- 3. Вычислительные задачи
- 4. Графические задачи
- ГЛАВА 3. МЕТОДИКА ПРОВЕДЕНИЯ ЗАНЯТИЙ ПО РЕШЕНИЮ ЗАДАЧ
- 2. Решение задач на уроках
- 3. Решение задач на внеклассных занятиях
- 4. О некоторых особенностях решения задач в различных классах
- 6 Класс
- 1. Существование молекул. Размеры молекул
- 2. Движение молекул
- 3. Молекулярные силы
- 4. Особенности строения газов, жидкостей и твердых тел
- ГЛАВА 5. ДВИЖЕНИЕ И СИЛЫ
- 1. Механическое движение. Скорость
- 2. Масса. Плотность вещества
- 3. Инерция
- 4. Сила тяжести. Вес тел
- 5. Графическое изображение и сложение сил
- 6. Сила давления. Давление
- 7. Сила трения. Силы взаимодействия молекул
- ГЛАВА 6. ДАВЛЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ (ГИДРО- И АЭРОСТАТИКА)
- 2. Весовое давление жидкости
- 3. Атмосферное давление
- 4. Архимедова сила
- ГЛАВА 7. РАБОТА И МОЩНОСТЬ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- 1. Механическая работа
- 2. Мощность
- 3. Рычаги. Блоки
- 4. Механическая энергия
- 7 КЛАСС
- ГЛАВА 8. ТЕПЛОПЕРЕДАЧА И РАБОТА
- 2. Способы передачи теплоты
- 3. Количество теплоты. Удельная теплоемкость
- 4. Теплота сгорания топлива. Тепловая отдача
- ГЛАВА 9. ИЗМЕНЕНИЕ АГРЕГАТНЫХ СОСТОЯНИЙ ВЕЩЕСТВА
- 1. Плавление и отвердевание
- 2. Испарение
- 3. Кипение и конденсация
- ГЛАВА 10. ТЕПЛОВЫЕ МАШИНЫ
- ГЛАВА 11. СТРОЕНИЕ АТОМА
- ГЛАВА 12. СИЛА ТОКА, НАПРЯЖЕНИЕ, СОПРОТИВЛЕНИЕ
- 1. Электрический ток. Электрическая цепь
- 2. Сила тока
- 3. Напряжение
- 4. Сопротивление проводников
- 5. Закон Ома для участка цепи
- 6. Соединения проводников
- ГЛАВА 13. РАБОТА И МОЩНОСТЬ ТОКА
- 1. Работа и мощность тока
- 2. Тепловое действие тока
- ГЛАВА 14. ЭЛЕКТРОМАГНИТНЫЕ ЯВЛЕНИЯ
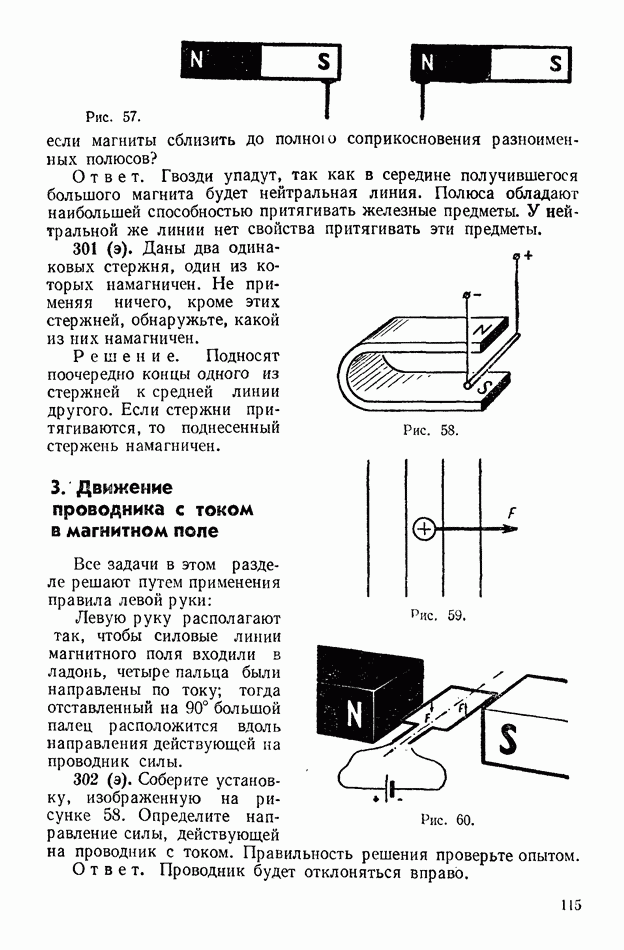
- 2. Постоянные магниты
- 3. Движение проводника с током в магнитном поле
- 8 КЛАСС
- 1. Система отсчета. Относительность механического движения. Сложение перемещений
- 2. Скорость. Сложение скоростей
- ГЛАВА 16. НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ
- 2. Ускорение
- 3: Скорость при равнопеременном движении
- 4. Перемещение и путь в равнопеременном движении
- 5. Движение по окружности
- ГЛАВА 17. ЗАКОНЫ ДВИЖЕНИЯ
- 1. Первый закон Ньютона (закон инерции)
- 2. Закон сохранения импульса (количества движения)
- 3. Второй закон Ньютона
- 4. Третий закон Ньютона
- ГЛАВА 18. СИЛЫ В ПРИРОДЕ
- 1. Гравитационные силы
- 2. Силы упругости
- 3. Силы трения
- ГЛАВА 19. РАВНОВЕСИЕ ТЕЛ (СТАТИКА)
- 1. Сложение и разложение сил
- 2. Момент силы. Равновесие тел, имеющих ось вращения
- 3. Центр тяжести. Виды равновесия. Устойчивость тел
- ГЛАВА 20. ПРИМЕНЕНИЕ ЗАКОНОВ ДВИЖЕНИЯ НЬЮТОНА
- 1. Прямолинейное движение под действием постоянной силы
- 2. Движение тела, брошенного горизонтально и под углом к горизонту
- 3. Движение по окружности
- 4. Движение планет и искусственных спутников
- ГЛАВА 21. РАБОТА И ЭНЕРГИЯ
- 1. Работа и мощность
- 2. Механическая энергия
- 3. Движение жидкостей и газов
- 9 КЛАСС
- 1. Основы молекулярно — кинетической теории
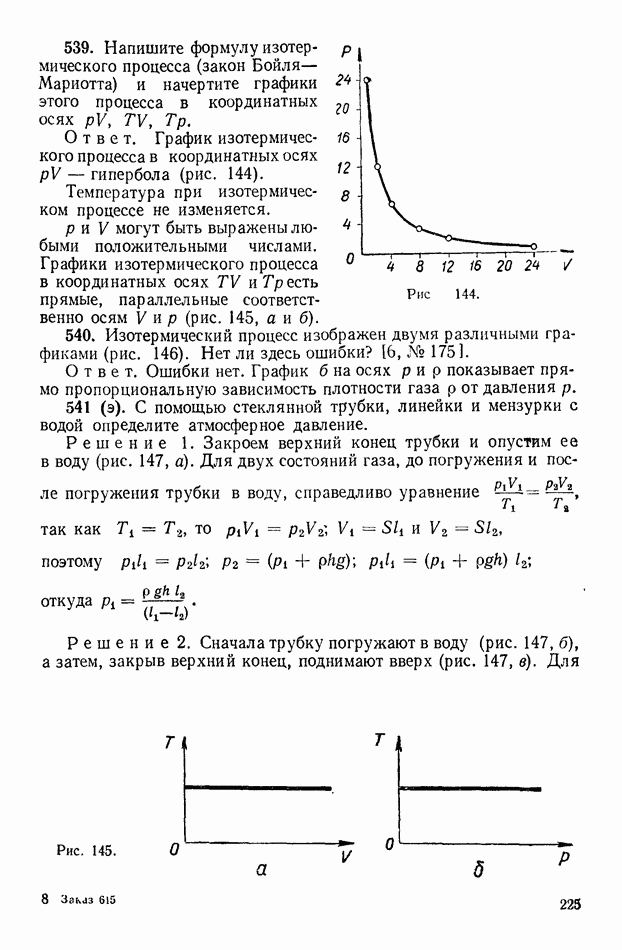
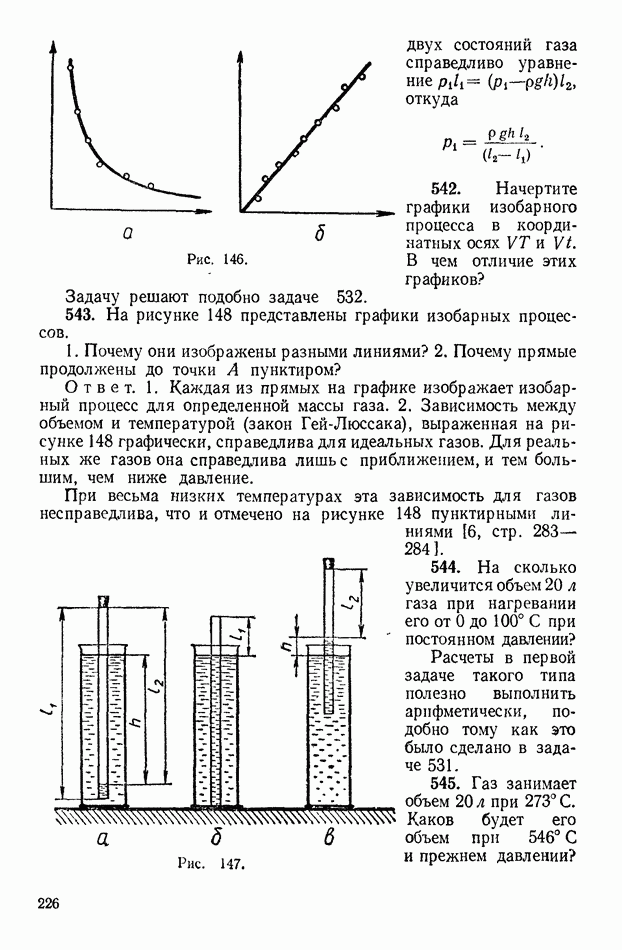
- 2. Свойства газов
- ГЛАВА 23. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
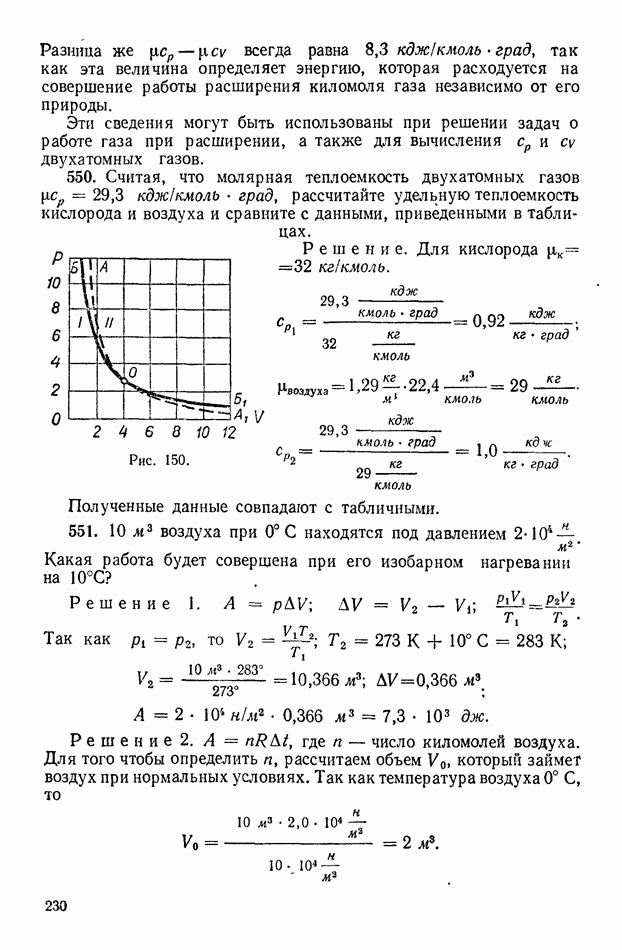
- 2. Работа при расширении газа
- ГЛАВА 24. СВОЙСТВА ПАРОВ
- 2. Кипение
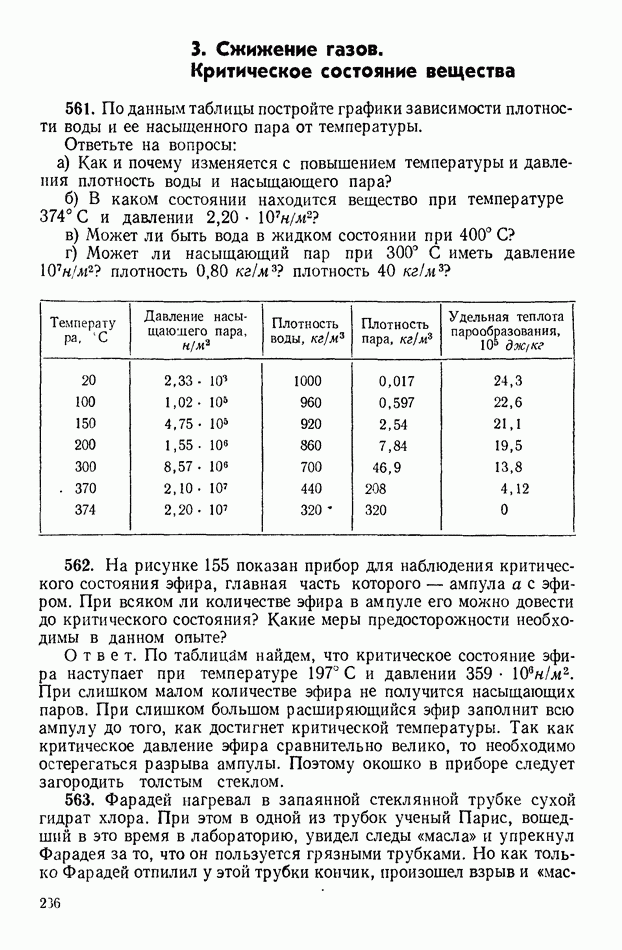
- 3. Сжижение газов. Критическое состояние вещества
- 4. Влажность
- ГЛАВА 25. СВОЙСТВА ЖИДКОСТЕЙ И ТВЕРДЫХ ТЕЛ
- 2. Смачивание и несмачивание. Давление под кривой поверхностью, капиллярные явления
- 3. Свойства твердых тел
- 4. Тепловое расширение жидкостей и твердых тел
- ГЛАВА 26. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 2. Напряженность электрического поля
- 3. Потенциал электрического поля
- 4. Электрическая емкость
- ГЛАВА 27. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОНЫ ПОСТОЯННОГО ТОКА
- 2. Соединения проводников
- 3. Закон Ома для полной цепи
- 4. Работа, мощность, тепловое действие тока
- 5. Термоток
- ГЛАВА 28. ЭЛЕКТРОМАГНЕТИЗМ
- 1. Магнитное поле тока
- 2. Электромагнитная индукция
- ГЛАВА 29. ОСНОВЫ ЭЛЕКТРОНИКИ
- 2. Электрический ток в электролитах
- 3. Электрический ток в газах
- 4. Электрические свойства полупроводников
- 10 КЛАСС
- ГЛАВА 30. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ. ЗВУК
- 2. Колебания математического маятника
- 3. Упругие колебания. Превращение энергии при колебательном движении
- 4. Сдвиг фаз. Сложение колебаний
- 5. Распространение колебаний в упругой среде. Волны
- 6. Интерференция и дифракция волн
- 7. Инфразвук и ультразвук
- ГЛАВА 31. ПЕРЕМЕННЫЙ ТОК
- ГЛАВА 32. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ГЛАВА 33. ВОЛНОВЫЕ СВОЙСТВА СВЕТА
- 1. Скорость света
- 2. Интерференция и дифракция света
- ГЛАВА 34. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- 2. Отражение света
- 3. Преломление света
- 4. Линзы
- 5. Оптические приборы
- ГЛАВА 35. ИЗЛУЧЕНИЕ И СПЕКТРЫ
- 1. Явление дисперсии и спектры
- 2. Фотометрия и законы освещенности
- ГЛАВА 36. ДЕЙСТВИЕ СВЕТА. КВАНТЫ СВЕТА
- 1. Кванты света
- 2. Фотоэффект
- ГЛАВА 37. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- ГЛАВА 38. ФИЗИКА АТОМНОГО ЯДРА