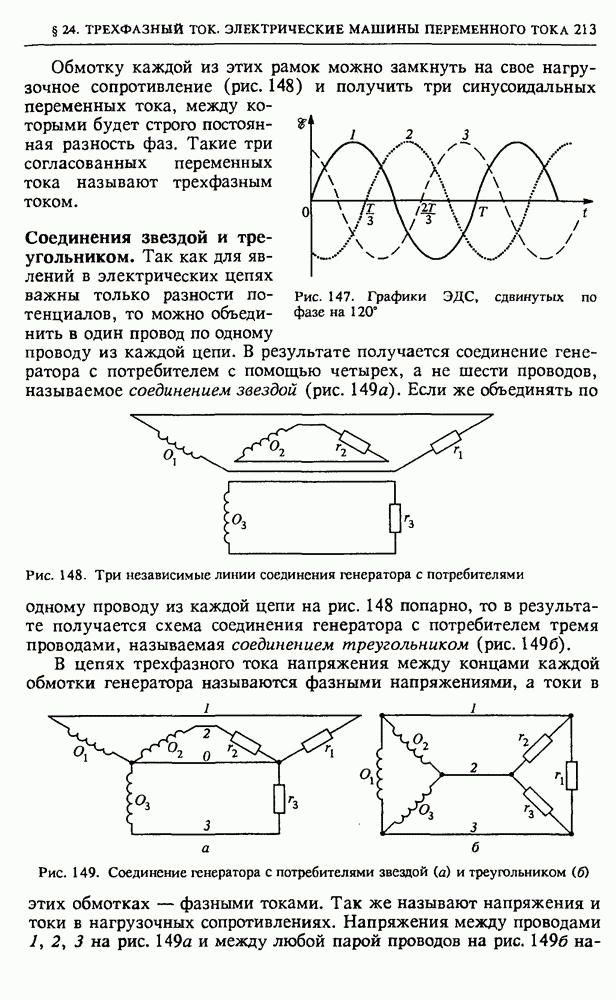
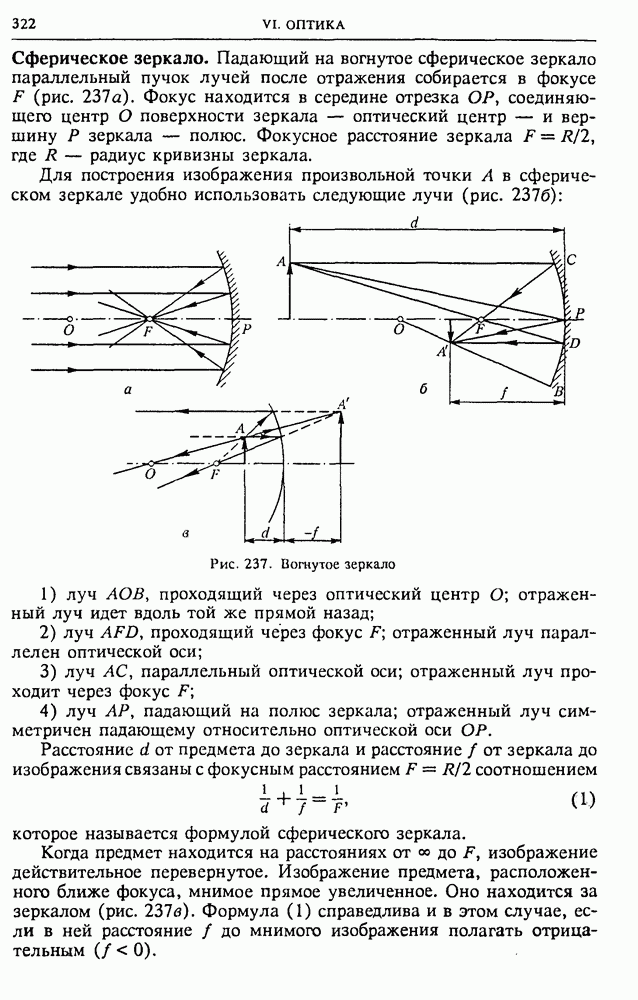
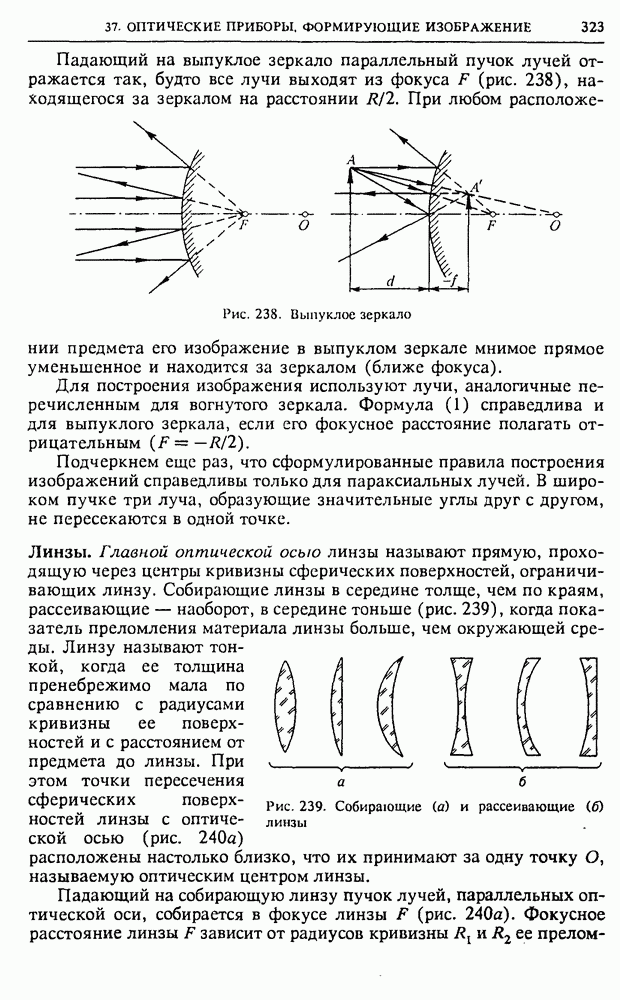
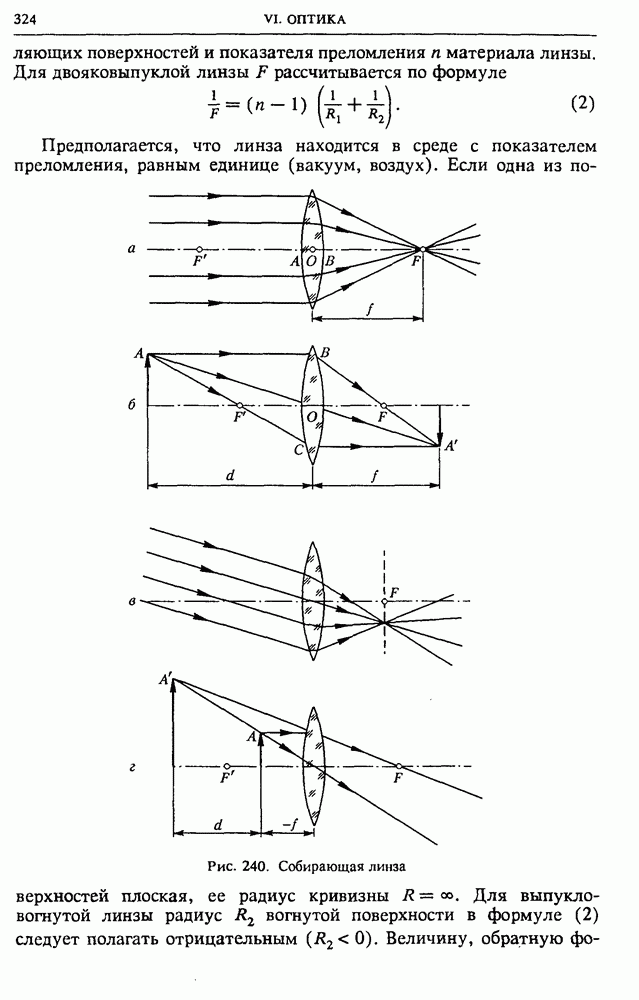
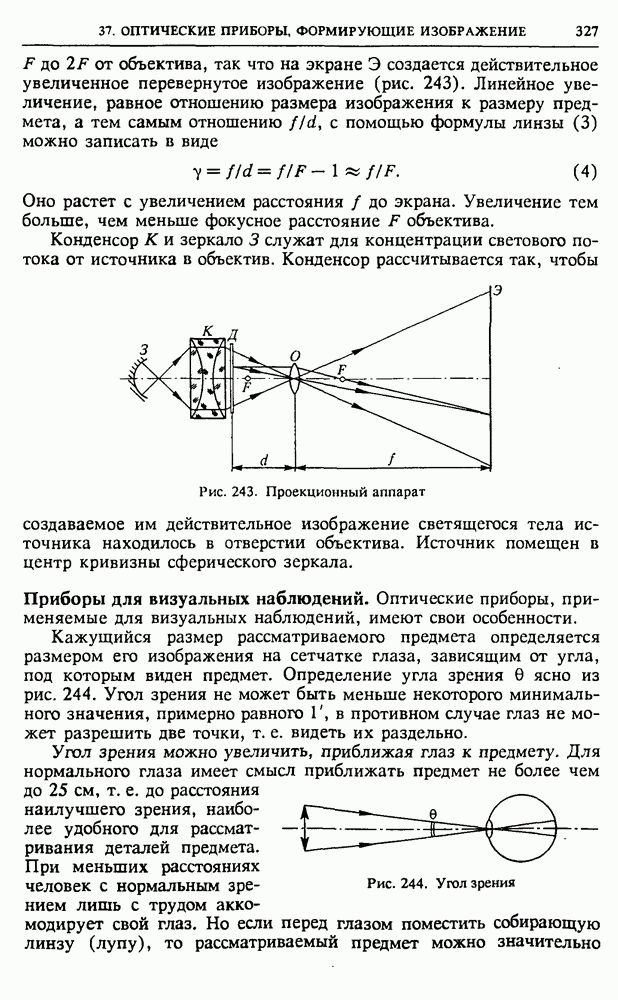
| << Предыдущий параграф | Следующий параграф >> |
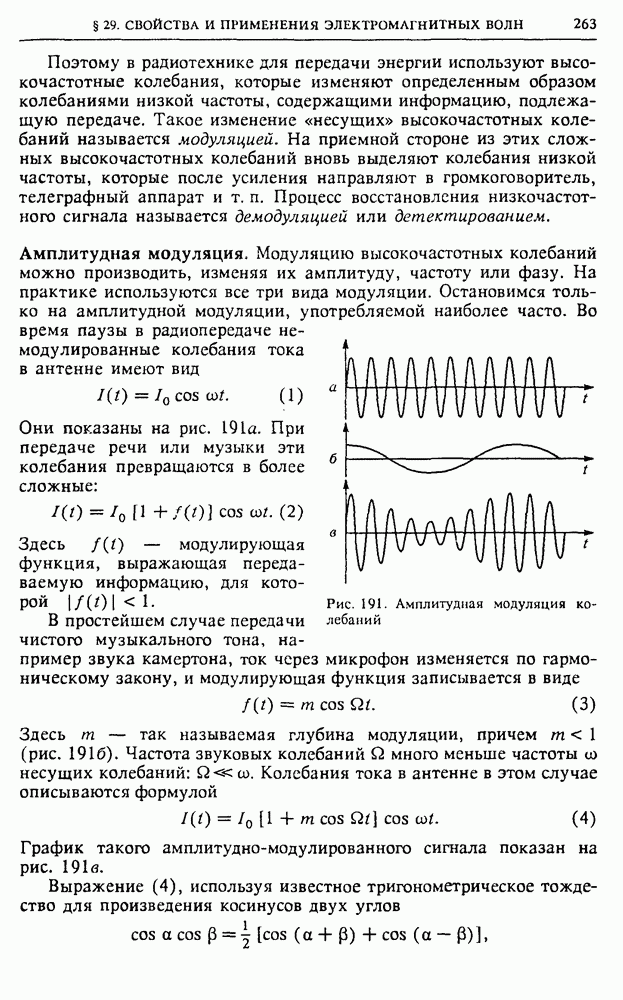
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
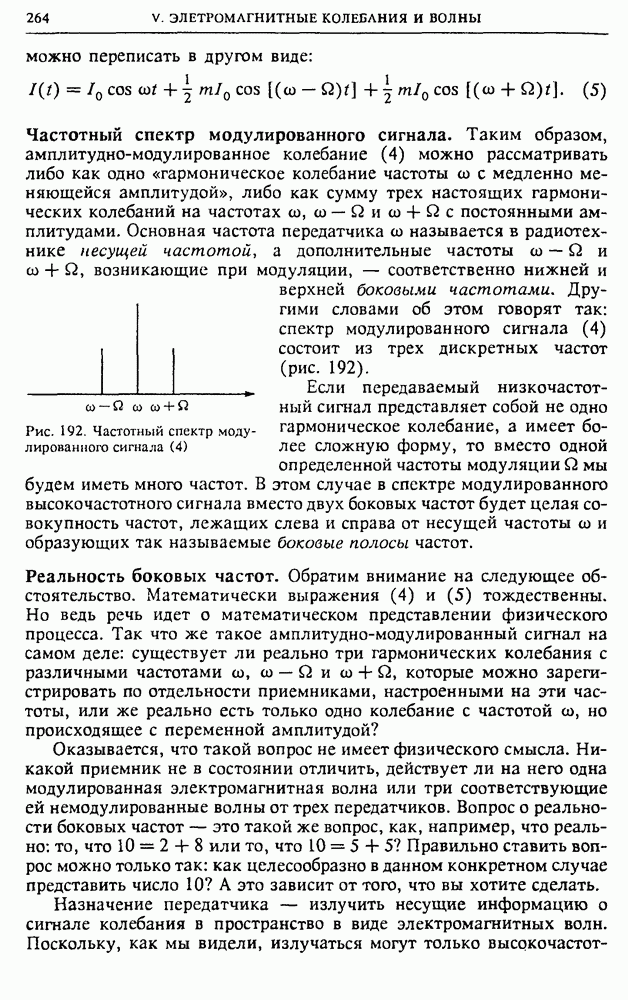
Широкое использование синусоидального переменного тока в технике и народном хозяйстве связано со многими его преимуществами, в частности с удобством его преобразования с помощью трансформаторов и с исключительной простотой повсеместно применяемых асинхронных двигателей.
Почему из всех возможных форм периодических переменных токов наибольшее распространение получили переменные токи именно синусоидальной формы? Дело в том, что синусоидальные токи по сравнению со всеми другими токами позволяют наиболее просто и экономично осуществлять передачу, распределение, преобразование и использование электрической энергии.
§ 22. Цепи переменного тока. Закон Ома
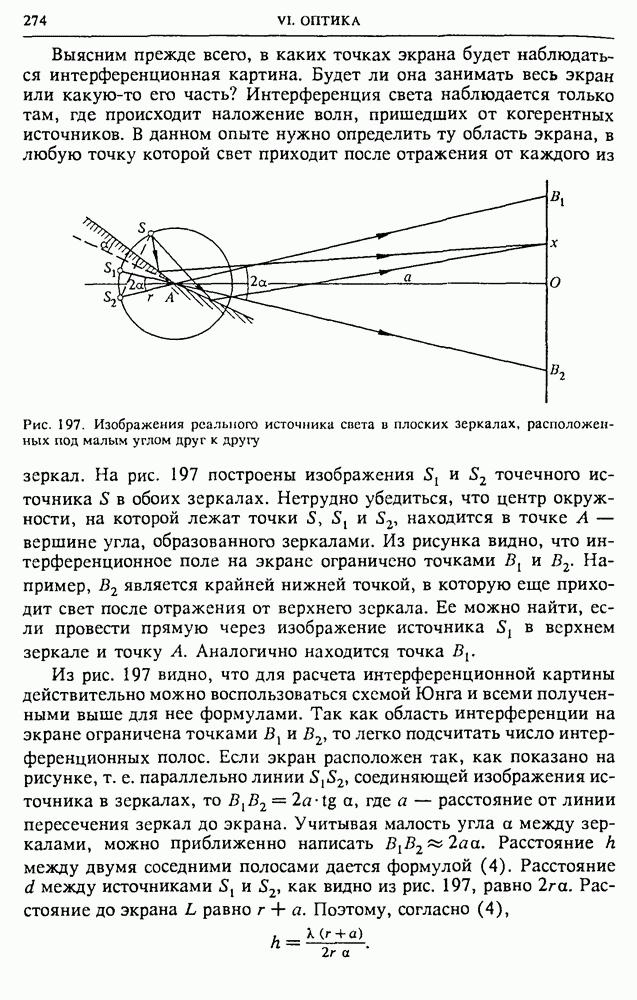
Только в случае синусоидальных токов сохраняются неизменными формы кривых зависимости от времени напряжения и токов на всех участках линейной электрической цепи, т. е. цепи, содержащей резисторы, конденсаторы, катушки индуктивности. В цепи, содержащей нелинейные элементы — диоды, транзисторы, электронные лампы и т. п. — форма этих кривых не сохраняется при любой, в том числе и синусоидальной, зависимости от времени подаваемого напряжения.
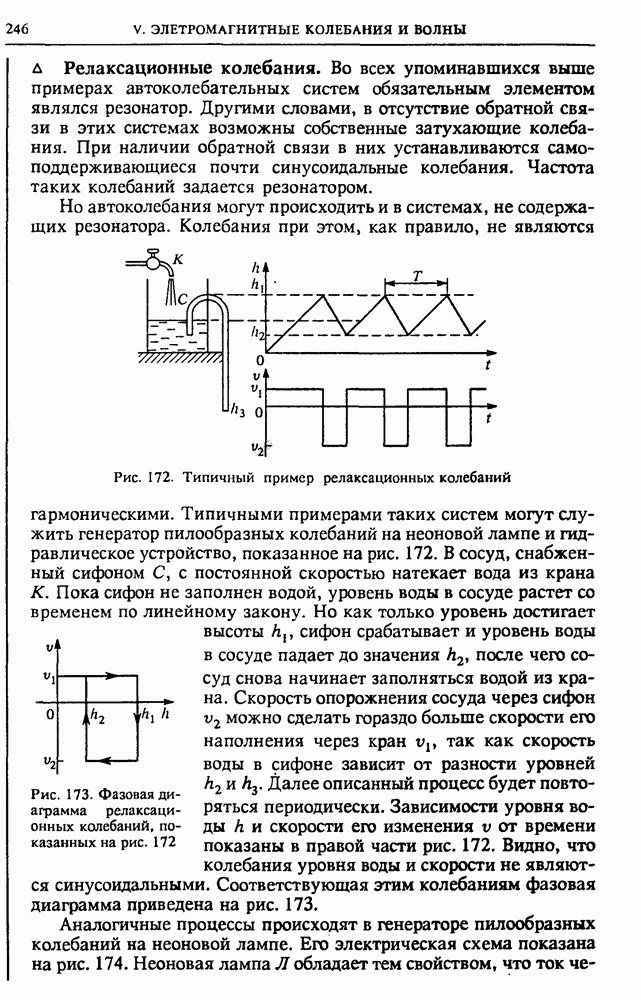
Прямоугольные импульсы в RС-цепочке. Рассмотрим следующую простую линейную цепь, состоящую из конденсатора С и резистора R (рис. 135). Посмотрим, что будет на выходе этой цепи, если на ее вход подавать напряжение в виде прямоугольных импульсов.

Рис. 135. RС-цепочка
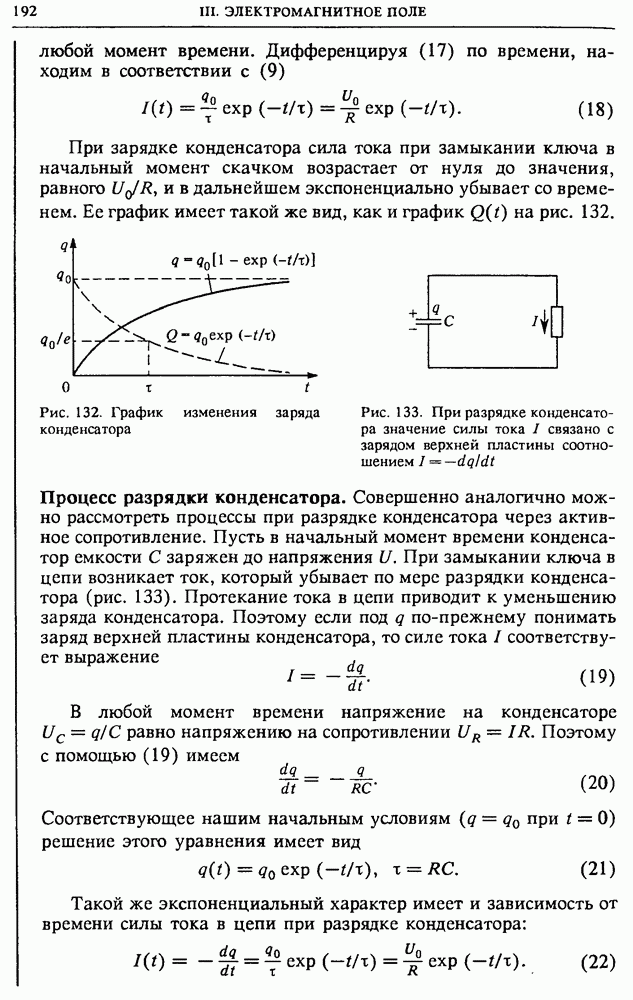
Начало каждого прямоугольного импульса соответствует подключению к цепи источника постоянного напряжения на время, равное длительности импульса. При этом в цепи скачком возникает ток, который постепенно уменьшается по мере того, как конденсатор заряжается.
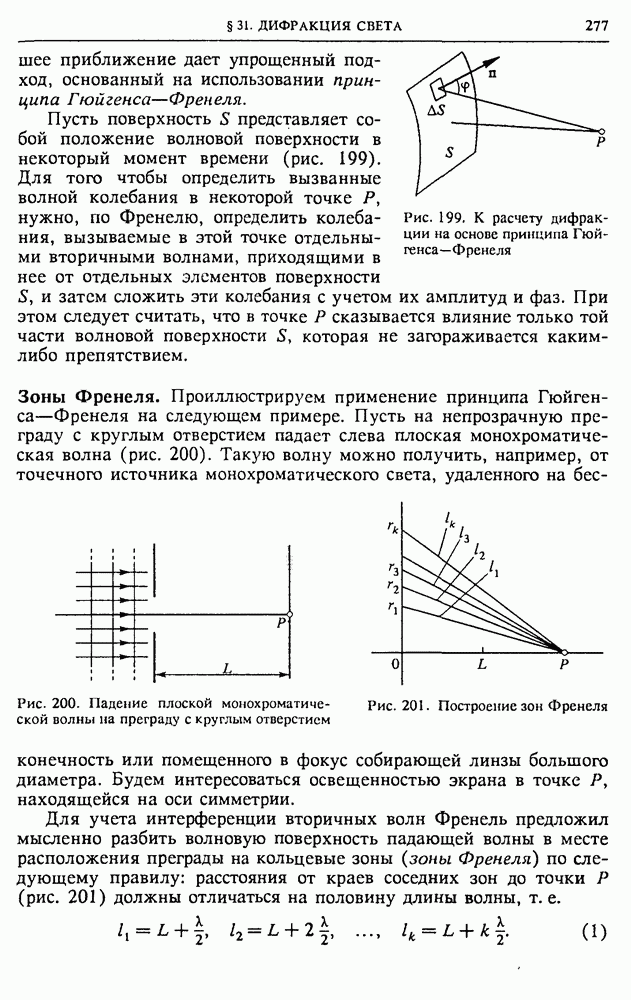
Время, в течение которого продолжается процесс зарядки конденсатора, определяется произведением  Если это время меньше длительности подаваемого на вход прямоугольного импульса, то ток
Если это время меньше длительности подаваемого на вход прямоугольного импульса, то ток

Рис. 136. Преобразование прямоугольных импульсов напряжения RC-цепочкой
зарядки прекратится раньше, чем закончится прямоугольный импульс. Именно этот случай изображен на рис. 136.
В момент прихода заднего фронта прямоугольного импульса подаваемое напряжение скачком обращается в нуль. Но этого можно добиться только путем короткого замыкания входных клемм схемы. Цепь, содержащая  и С, становится короткозамкнутой, и конденсатор С разряжается через сопротивление
и С, становится короткозамкнутой, и конденсатор С разряжается через сопротивление  Направление тока разрядки противоположно зарядному току, поэтому выходное напряжение на сопротивлении
Направление тока разрядки противоположно зарядному току, поэтому выходное напряжение на сопротивлении  имеет противоположную полярность (рис. 136).
имеет противоположную полярность (рис. 136).
Таким образом, форма выходного напряжения оказывается совершенно иной, чем форма входного напряжения.
Синусоидальное напряжение в RC-цепочке. Посмотрим теперь, что получится, если на вход той же  -цепочки подать синусоидальное напряжение
-цепочки подать синусоидальное напряжение

Будем считать, что это напряжение действует в течение достаточно большого по сравнению с  промежутка времени, так что все переходные процессы к рассматриваемому моменту уже закончились. Тогда ток в цепи будет изменяться по синусоидальному закону с той же частотой со, причем между приложенным напряжением и током будет некоторый сдвиг по фазе.
промежутка времени, так что все переходные процессы к рассматриваемому моменту уже закончились. Тогда ток в цепи будет изменяться по синусоидальному закону с той же частотой со, причем между приложенным напряжением и током будет некоторый сдвиг по фазе.

Рис. 137. Изменяющаяся по синусоидальному закону величина  может быть представлена как проекция вращающегося вектора длины
может быть представлена как проекция вращающегося вектора длины 
Чтобы найти амплитуду этого тока и сдвиг по фазе, воспользуемся тем обстоятельством, что мгновенное значение любой изменяющейся по синусоидальному закону величины  можно представить как проекцию вектора длиной
можно представить как проекцию вектора длиной  на некоторое заранее выбранное направление, причем сам вектор равномерно вращается в плоскости с угловой скоростью
на некоторое заранее выбранное направление, причем сам вектор равномерно вращается в плоскости с угловой скоростью  равной циклической частоте, а длина вектора равна амплитудному значению
равной циклической частоте, а длина вектора равна амплитудному значению  соответствующей величины (рис. 137). С помощью такого представления каждой исследуемой схеме можно сопоставить определенную векторную диаграмму.
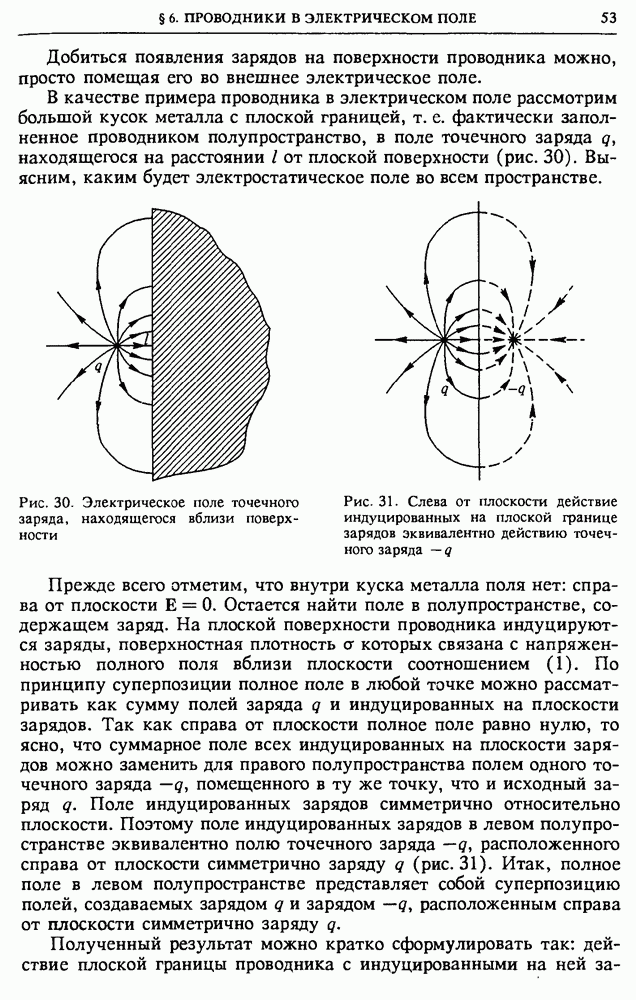
соответствующей величины (рис. 137). С помощью такого представления каждой исследуемой схеме можно сопоставить определенную векторную диаграмму.
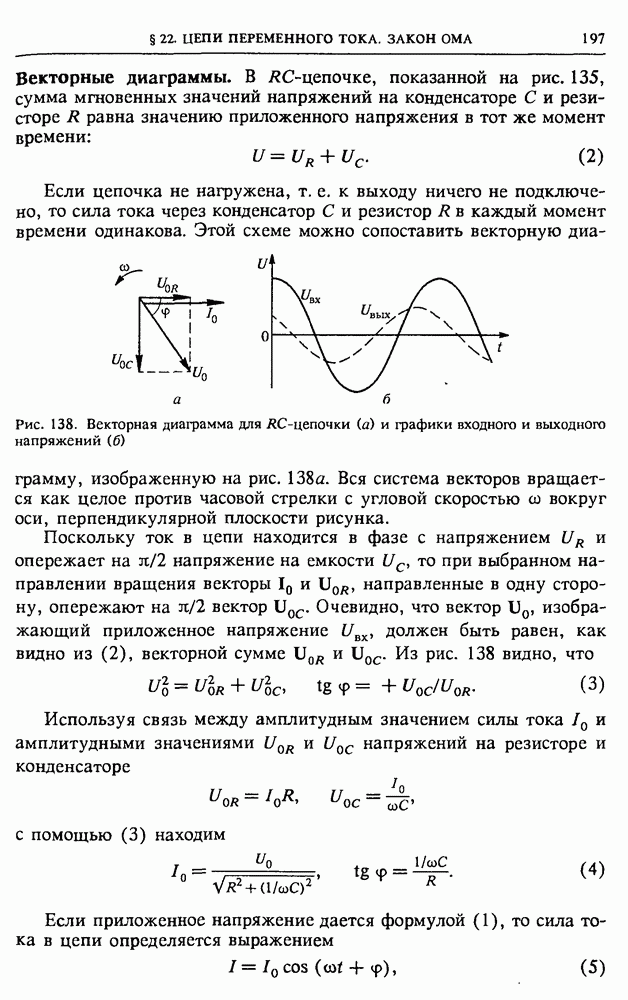
Векторные диаграммы. В  -цепочке, показанной на рис. 135, сумма мгновенных значений напряжений на конденсаторе С и резисторе
-цепочке, показанной на рис. 135, сумма мгновенных значений напряжений на конденсаторе С и резисторе  равна значению приложенного напряжения в тот же момент времени:
равна значению приложенного напряжения в тот же момент времени:

Если цепочка не нагружена, т. е. к выходу ничего не подключено, то сила тока через конденсатор С и резистор  в каждый момент времени одинакова. Этой схеме можно сопоставить векторную диаграмму, изображенную на рис. 138а.
в каждый момент времени одинакова. Этой схеме можно сопоставить векторную диаграмму, изображенную на рис. 138а.

Рис. 138. Векторная диаграмма для  -цепочки (а) и графики входного и выходного напряжений (б)
-цепочки (а) и графики входного и выходного напряжений (б)
Вся система векторов вращается как целое против часовой стрелки с угловой скоростью со вокруг оси, перпендикулярной плоскости рисунка.
Поскольку ток в цепи находится в фазе с напряжением  и опережает на
и опережает на  напряжение на емкости
напряжение на емкости  то при выбранном направлении вращения векторы
то при выбранном направлении вращения векторы  направленные в одну сторону, опережают на
направленные в одну сторону, опережают на  вектор
вектор  Очевидно, что вектор
Очевидно, что вектор  изображающий приложенное напряжение
изображающий приложенное напряжение  должен быть равен, как видно из (2), векторной сумме
должен быть равен, как видно из (2), векторной сумме  Из рис. 138 видно, что
Из рис. 138 видно, что

Используя связь между амплитудным значением силы тока  и амплитудными значениями
и амплитудными значениями  напряжений на резисторе и конденсаторе
напряжений на резисторе и конденсаторе

с помощью (3) находим

Если приложенное напряжение дается формулой (1), то сила тока в цепи определяется выражением

где  и определяются формулами (4). Это значит, что выходное напряжение
и определяются формулами (4). Это значит, что выходное напряжение  (рис. 135), совпадающее с напряжением на резисторе
(рис. 135), совпадающее с напряжением на резисторе  как и подаваемое напряжение
как и подаваемое напряжение  будет синусоидальным, но опережающим его по фазе на угол
будет синусоидальным, но опережающим его по фазе на угол  Из второй формулы (4) следует, что этот сдвиг по фазе зависит не только от соотношения между С и
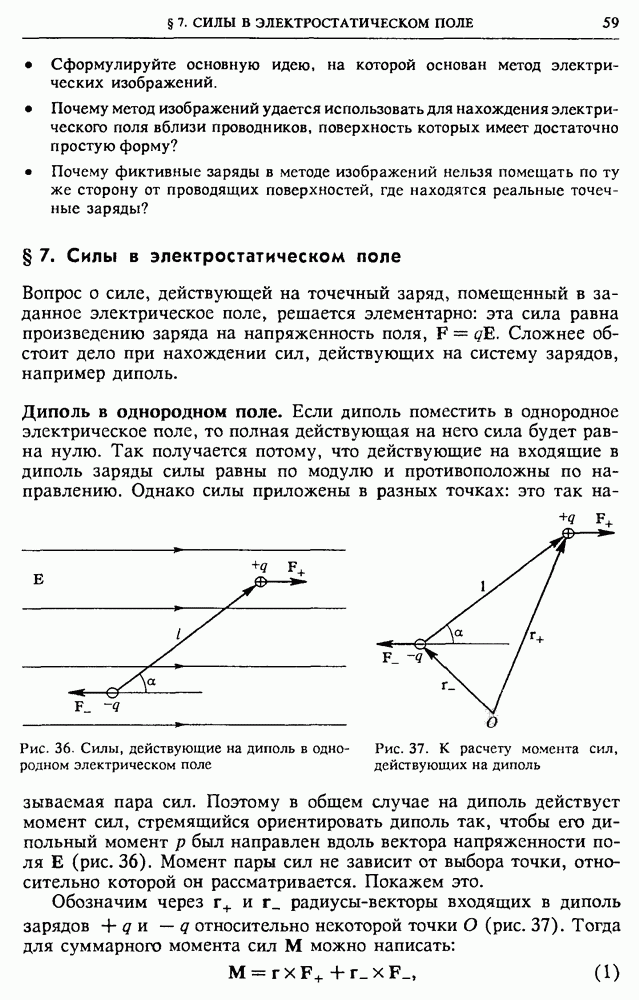
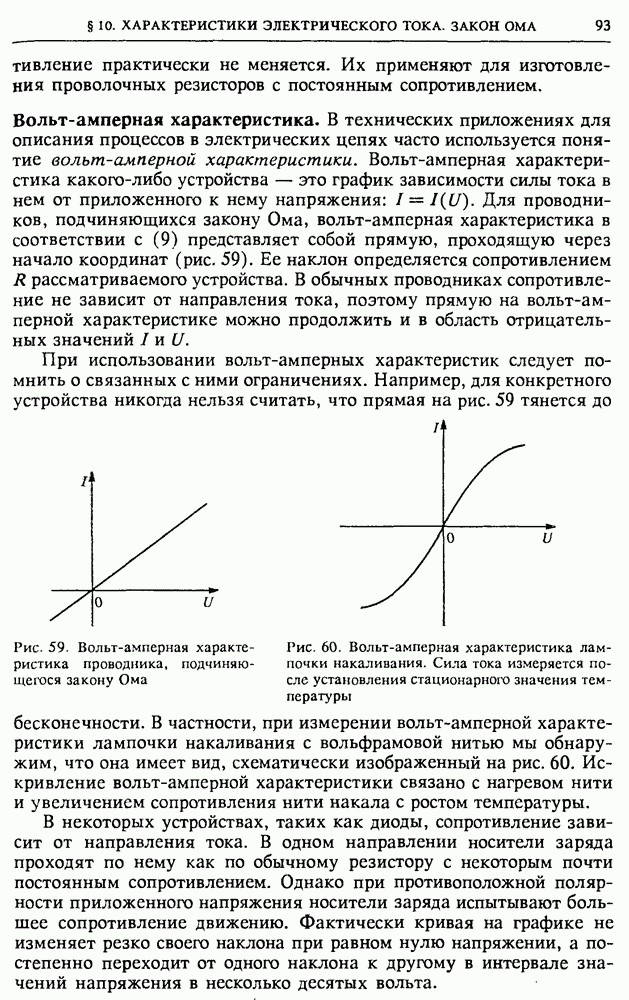
Из второй формулы (4) следует, что этот сдвиг по фазе зависит не только от соотношения между С и  но и от частоты
но и от частоты  входного напряжения.
входного напряжения.
Подчеркнем еще раз, что для сохранения формы передаваемого напряжения необходимо использовать именно синусоидальный переменный ток.
Проиллюстрированный на примере  -цепочки метод векторных диаграмм можно применять для исследования любых линейных цепей переменного тока.
-цепочки метод векторных диаграмм можно применять для исследования любых линейных цепей переменного тока.
Последовательная RLC-цепь. Рассмотрим произвольную последовательную цепь переменного тока, содержащую активное сопротивление  емкость С и индуктивность
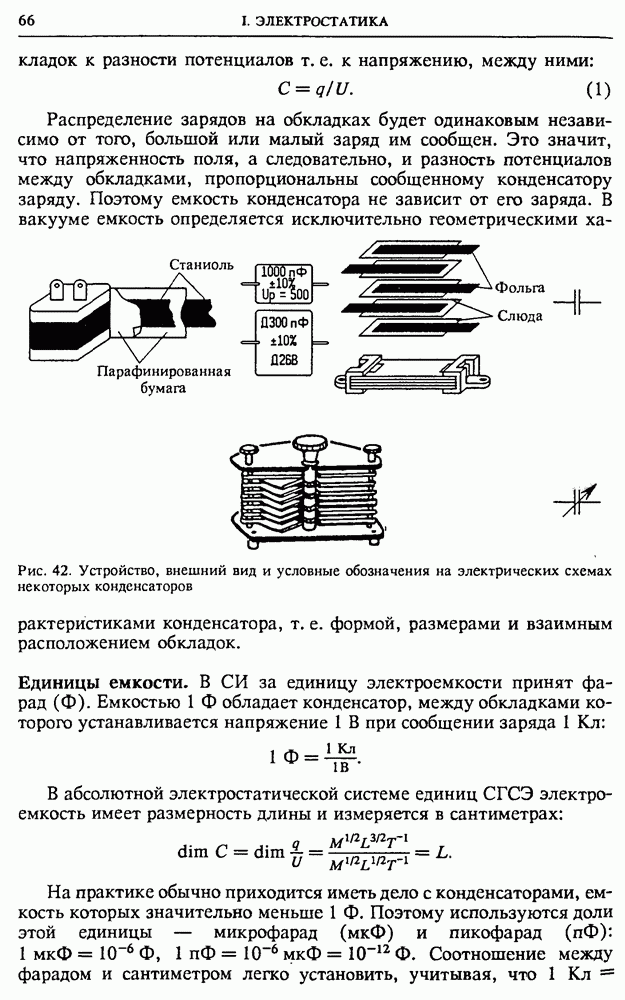
емкость С и индуктивность  (рис. 139). Будем считать, что на вход этой цепи подано синусоидальное напряжение, даваемое формулой (1). В последовательной цепи квазистационарного переменного тока сила тока I в каждый момент времени во всех участках цепи одинакова. Сумма мгновенных значений напряжений на сопротивлении
(рис. 139). Будем считать, что на вход этой цепи подано синусоидальное напряжение, даваемое формулой (1). В последовательной цепи квазистационарного переменного тока сила тока I в каждый момент времени во всех участках цепи одинакова. Сумма мгновенных значений напряжений на сопротивлении  емкости С и индуктивности
емкости С и индуктивности  равна значению приложенного напряжения
равна значению приложенного напряжения  в тот же момент времени:
в тот же момент времени:


Рис. 139. Последовательная RLC цепь
Этой схеме можно сопоставить векторную диаграмму, изображенную на рис. 140а. Каждой величине — току  напряжениям на сопротивлении
напряжениям на сопротивлении  емкости С и индуктивности
емкости С и индуктивности  — сопоставляются векторы, длина каждого из которых равна амплитудному значению соответствующей величины. Вся система векторов вращается как целое с угловой скоростью со. Мгновенные значения величин
— сопоставляются векторы, длина каждого из которых равна амплитудному значению соответствующей величины. Вся система векторов вращается как целое с угловой скоростью со. Мгновенные значения величин  получаются проецированием соответствующих векторов на заранее выбранное фиксированное направление
получаются проецированием соответствующих векторов на заранее выбранное фиксированное направление  Поскольку, как мы видели, ток в цепи изменяется в фазе с напряжением
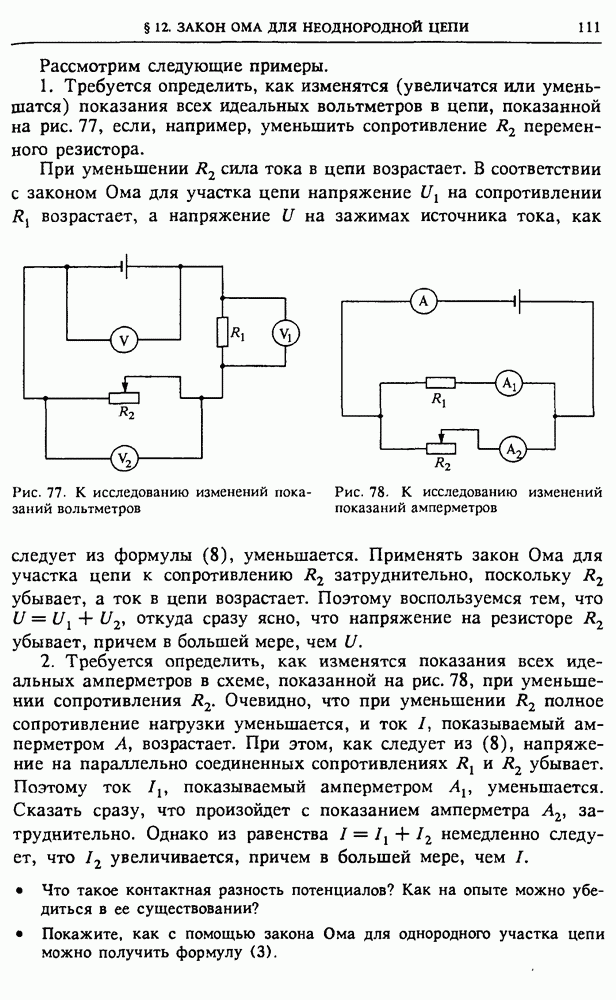
Поскольку, как мы видели, ток в цепи изменяется в фазе с напряжением  отстает на
отстает на  от напряжения на индуктивности
от напряжения на индуктивности  и опережает на
и опережает на  напряжение на емкости
напряжение на емкости  то при указанном направлении вращения вектор
то при указанном направлении вращения вектор  опережает векторы
опережает векторы  на
на  которые в свою очередь опережают на
которые в свою очередь опережают на  вектор
вектор 
Вектор, изображающий приложенное напряжение, равен сумме векторов  так как проекция результирующего вектора, которая определяет мгновенное значение приложенного напряжения
так как проекция результирующего вектора, которая определяет мгновенное значение приложенного напряжения  равна сумме проекций составляющих векторов, равных мгновенным значениям напряжений
равна сумме проекций составляющих векторов, равных мгновенным значениям напряжений  и
и  в полном соответствии с
в полном соответствии с
равенством (6) (рис. 1406). Из этого рисунка видно, что

Используя связь между амплитудным значением тока  и амплитудными значениями напряжений на отдельных элементах цепи:
и амплитудными значениями напряжений на отдельных элементах цепи:

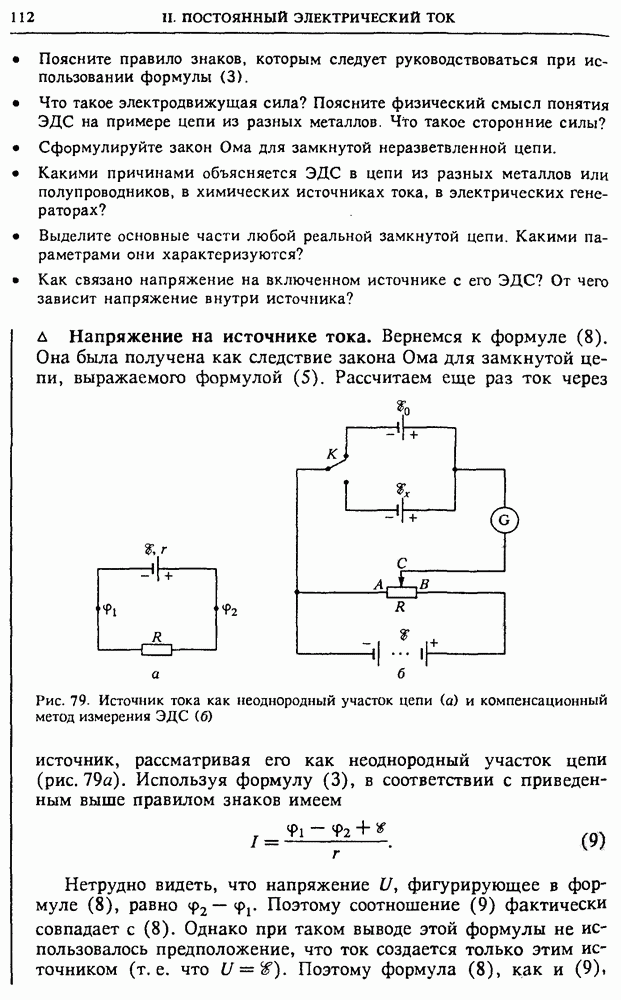
с помощью (7) получаем

Итак, если приложенное напряжение  то ток в цепи
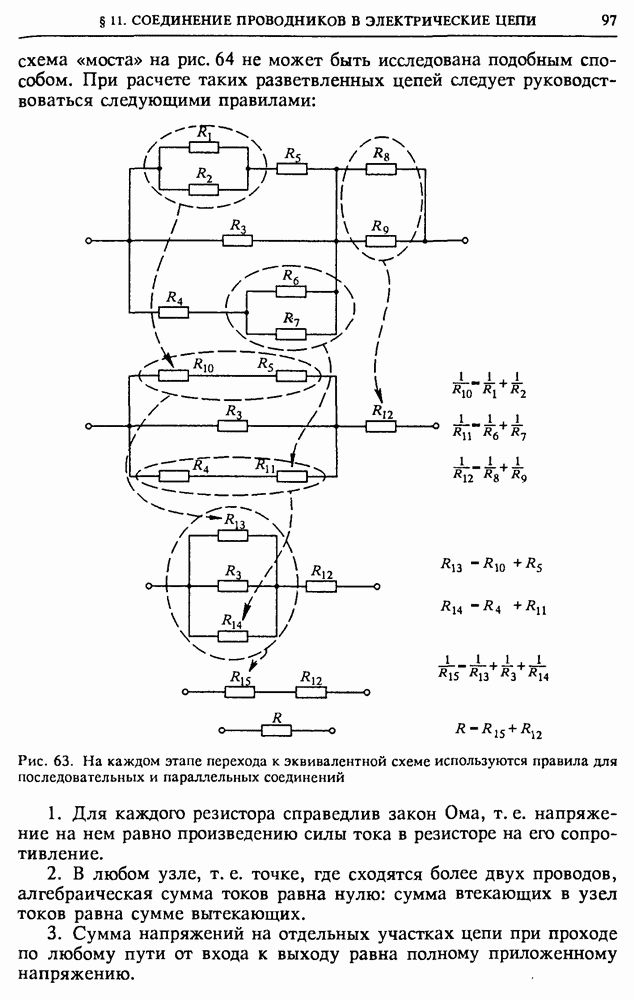
то ток в цепи  где
где  определяются формулами (8) и (9). Ток в цепи, как и напряжение, меняется по синусоидальному закону, но между током и напряжением существует сдвиг по фазе, равный
определяются формулами (8) и (9). Ток в цепи, как и напряжение, меняется по синусоидальному закону, но между током и напряжением существует сдвиг по фазе, равный 
С помощью векторной диаграммы на рис. 1406 теперь легко написать выражения для мгновенных напряжений на отдельных элементах схемы:

Выясним, что покажет вольтметр, если его подключить к какому-либо из элементов схемы.

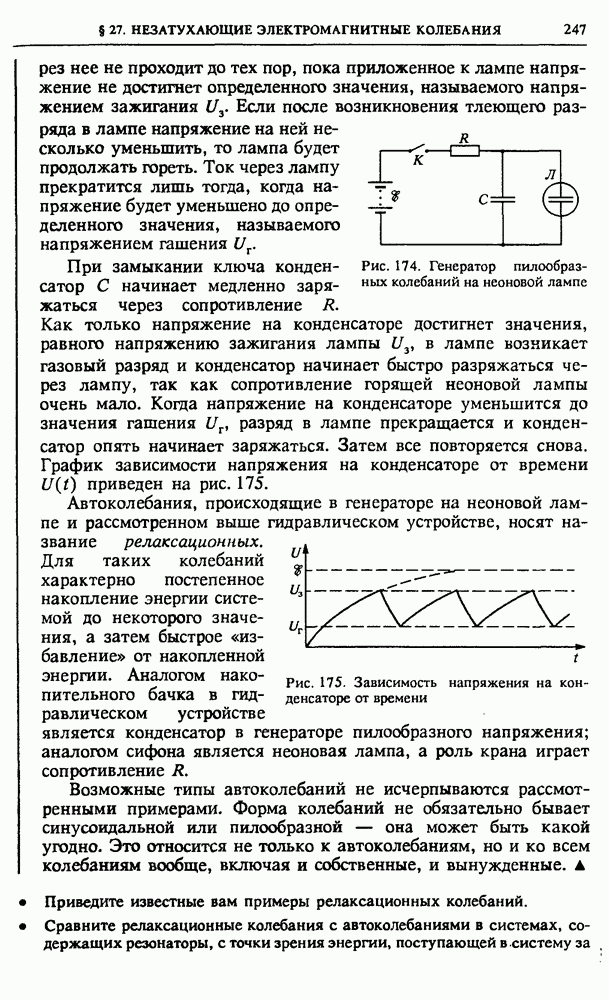
Рис. 140. Векторная диаграмма для последовательной RLC-цепи (а); к определению связи между приложенным напряжением и током в цепи (б)
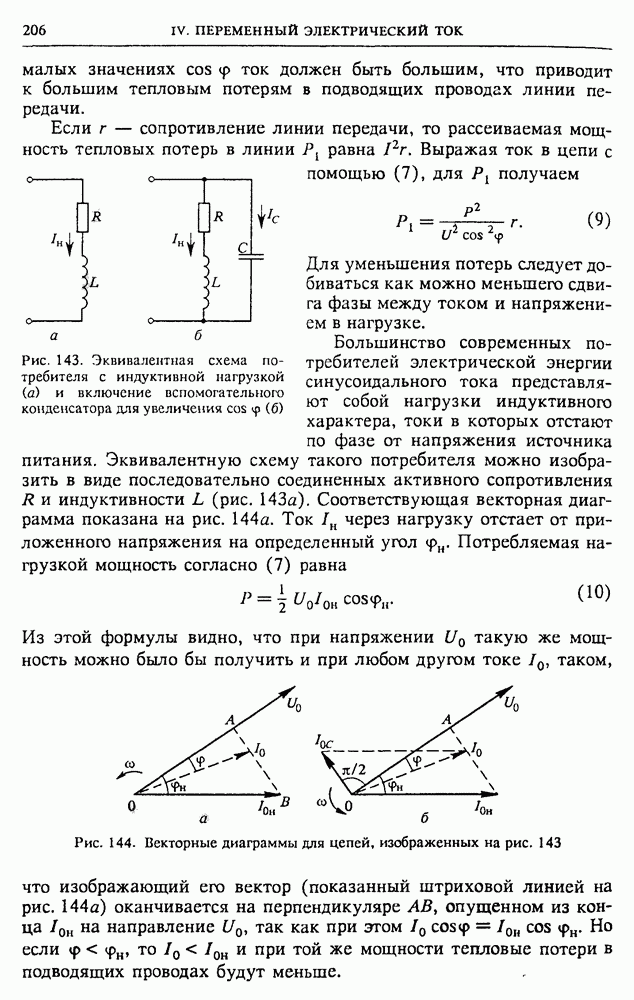
Произведя измерения напряжений на всех элементах схемы по отдельности, можно убедиться, что сумма этих напряжений всегда больше действующего значения подаваемого на схему напряжения. Более того, напряжение на любом из реактивных сопротивлений может быть гораздо больше подаваемого напряжения. Напряжение же на активном сопротивлении никогда не бывает больше подаваемого напряжения.
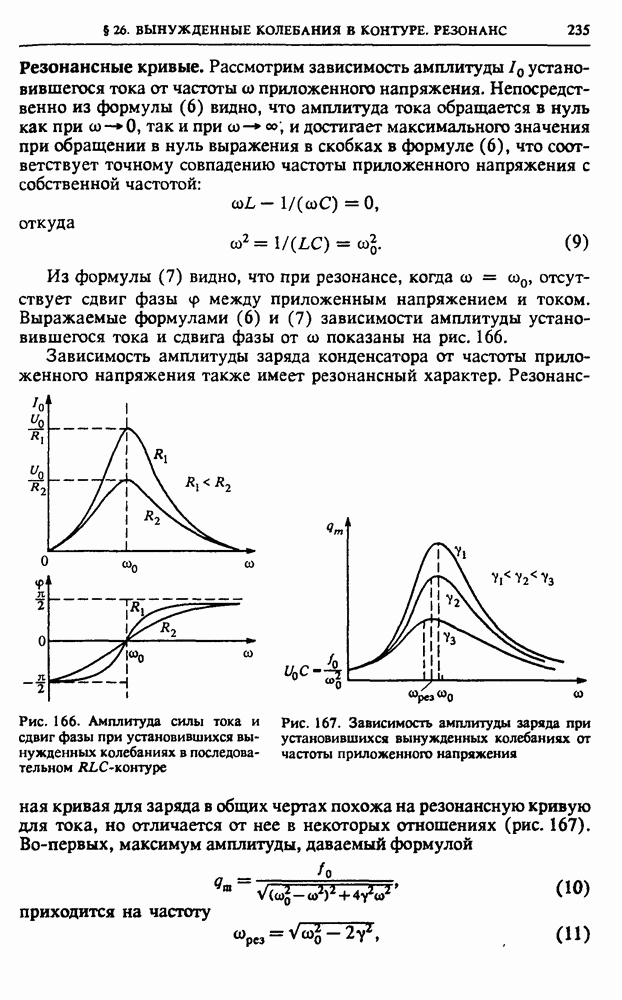
Резонанс напряжений. Если при измерении напряжений на реактивных элементах напряжения окажутся равными друг другу, то это значит, что равны реактивные сопротивления:  Такую ситуацию называют резонансом напряжений в цепи переменного тока. При этом напряжение на активном сопротивлении равно приложенному внешнему напряжению. Сопротивление всей последовательной цепи при резонансе напряжений становится чисто активным и равным R. Сдвиг фаз между приложенным напряжением и током в этом случае отсутствует.
Такую ситуацию называют резонансом напряжений в цепи переменного тока. При этом напряжение на активном сопротивлении равно приложенному внешнему напряжению. Сопротивление всей последовательной цепи при резонансе напряжений становится чисто активным и равным R. Сдвиг фаз между приложенным напряжением и током в этом случае отсутствует.

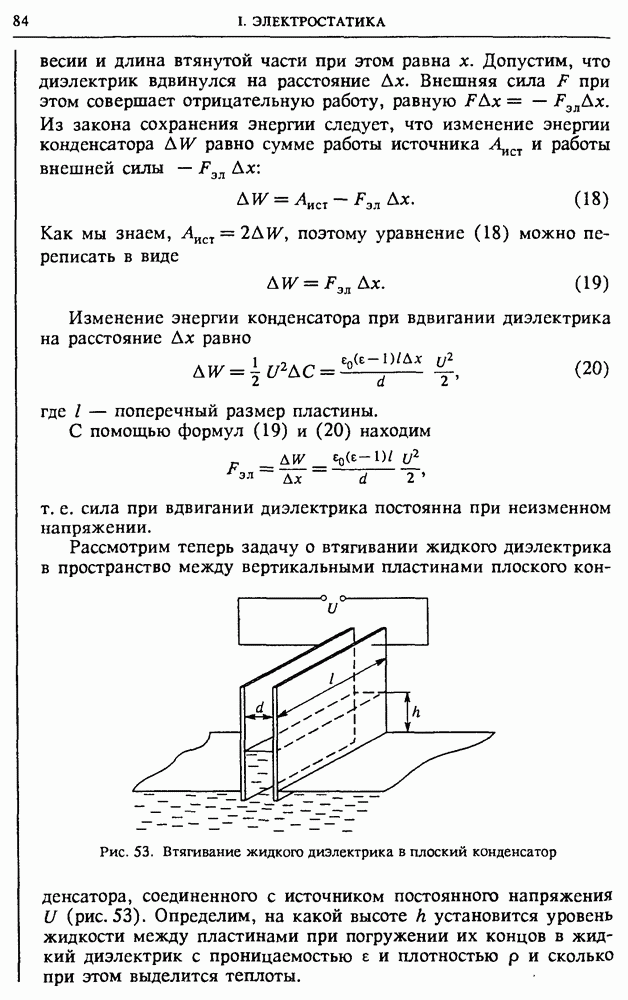
Рис. 141. Параллельное соединение  и С
и С
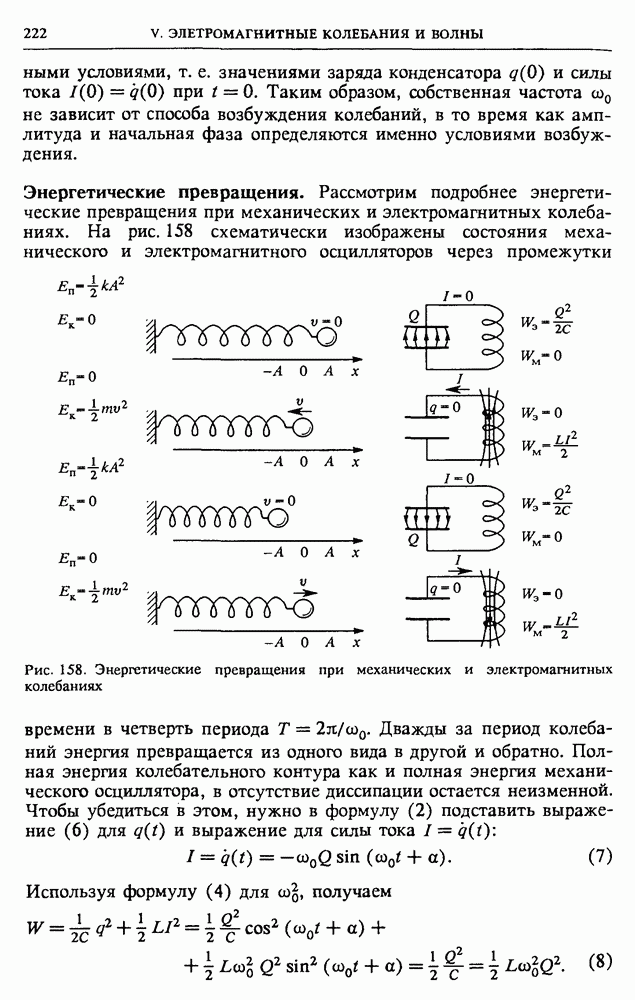
При резонансе напряжений дважды за период колебаний происходят взаимные превращения энергии электрического поля конденсатора в энергию магнитного поля катушки и обратно. Энергия, подводимая к контуру из внешней цепи, целиком идет на компенсацию джоулевых потерь в активном сопротивлении контура.
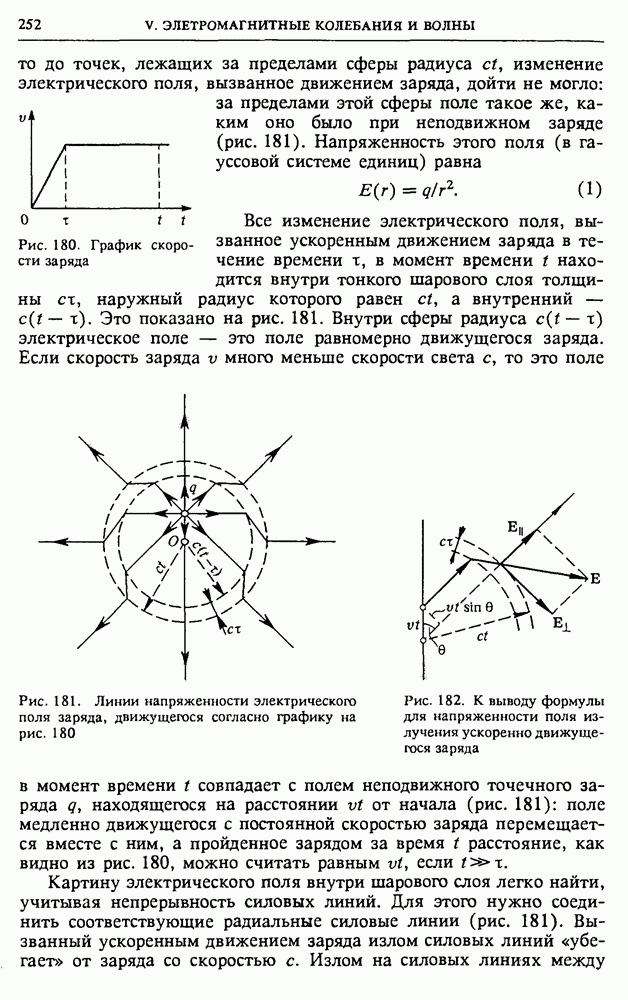
Параллельная RLC-цепь. Рассмотрим цепь переменного тока, содержащую параллельно соединенные активное сопротивление  индуктивность
индуктивность  и емкость С (рис. 141), на которую подается переменное синусоидальное напряжение
и емкость С (рис. 141), на которую подается переменное синусоидальное напряжение  Как и в случае последовательного соединения элементов, эту цепь удобно исследовать с помощью векторных диаграмм. Напряжение на всех параллельно соединенных элементах одинаково и равно приложенному напряжению
Как и в случае последовательного соединения элементов, эту цепь удобно исследовать с помощью векторных диаграмм. Напряжение на всех параллельно соединенных элементах одинаково и равно приложенному напряжению  Мгновенное значение квазистационарного тока в неразветвленной части цепи
Мгновенное значение квазистационарного тока в неразветвленной части цепи  равно алгебраической сумме токов в параллельных участках:
равно алгебраической сумме токов в параллельных участках:


Рис. 142. Векторная диаграмма для параллельной RLC-цепи
Поскольку ток через сопротивление  находится в фазе с приложенным напряжением, ток в ветви, содержащей емкость, опережает напряжение на
находится в фазе с приложенным напряжением, ток в ветви, содержащей емкость, опережает напряжение на  а ток через индуктивность отстает от напряжения на
а ток через индуктивность отстает от напряжения на  то векторная диаграмма, соответствующая этой цепи, имеет вид, изображенный на рис. 142. Учитывая связь между амплитудными значениями токов в различных элементах и амплитудным значением приложенного напряжения:
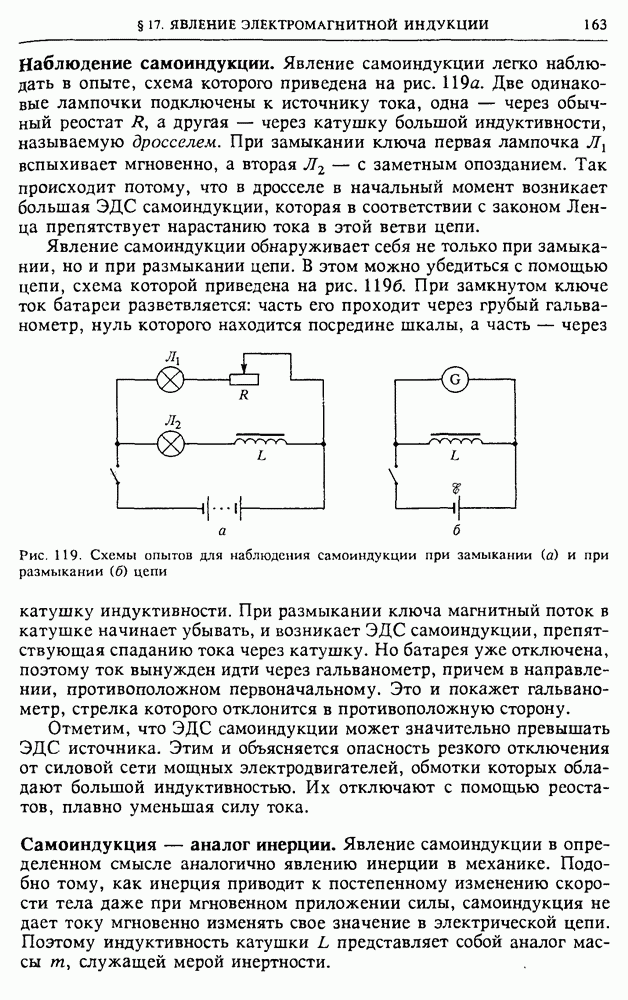
то векторная диаграмма, соответствующая этой цепи, имеет вид, изображенный на рис. 142. Учитывая связь между амплитудными значениями токов в различных элементах и амплитудным значением приложенного напряжения:

с помощью векторной диаграммы на рис. 142 получаем следующие выражения для амплитуды тока в неразветвленной части цепи и для
сдвига по фазе между приложенным напряжением и этим током:

Таким образом, ток в неразветвленной части цепи равен  где
где  определяются формулами (11) и (12). Векторная диаграмма дает также возможность написать выражение для мгновенных значений тока в отдельных ветвях цепи:
определяются формулами (11) и (12). Векторная диаграмма дает также возможность написать выражение для мгновенных значений тока в отдельных ветвях цепи:

Резонанс токов. При равенстве емкостного и индуктивного сопротивлений, т. е. при  сдвиг фаз между током в неразветвленной части цепи и напряжением обращается в нуль. Токи
сдвиг фаз между током в неразветвленной части цепи и напряжением обращается в нуль. Токи  и
и
11 при этом равны по величине, и так как они находятся в противофазе, то ток в неразветвленной части становится равным току  через активное сопротивление.
через активное сопротивление.
Заметим, что токи  и
и  в отдельных ветвях цепи могут значительно превосходить ток в проводящих проводах. Такая ситуация носит название резонанса токов. При этом, как и в последовательной .
в отдельных ветвях цепи могут значительно превосходить ток в проводящих проводах. Такая ситуация носит название резонанса токов. При этом, как и в последовательной . -цепи при резонансе напряжений, происходит обмен энергией между электрическим и магнитным полями, сосредоточенными в емкости и индуктивности, а источник питания только компенсирует потери энергии за счет выделения джоулевой теплоты на сопротивлении
-цепи при резонансе напряжений, происходит обмен энергией между электрическим и магнитным полями, сосредоточенными в емкости и индуктивности, а источник питания только компенсирует потери энергии за счет выделения джоулевой теплоты на сопротивлении  Если сопротивление
Если сопротивление  вообще убрать из цепи
вообще убрать из цепи  то энергетические потери в такой идеализированной схеме отсутствуют и ток в подводящих проводах равен нулю, хотя в контуре, состоящем из
то энергетические потери в такой идеализированной схеме отсутствуют и ток в подводящих проводах равен нулю, хотя в контуре, состоящем из  и С, ток может быть сколь угодно большим. В этом случае на резонансной частоте
и С, ток может быть сколь угодно большим. В этом случае на резонансной частоте  полное реактивное сопротивление контура неограниченно возрастает.
полное реактивное сопротивление контура неограниченно возрастает.
Резонанс токов, наряду с резонансом напряжений, широко используется в технике. В качестве примера можно указать на использование резонансных свойств RLC-цепи для выделения сигнала нужной частоты в антенне радиоприемника при настройке на определенную радиостанцию. Другим важным примером использования резонанса токов является индукционная печь, в которой нагревание и плавление металлов производятся вихревыми токами. Параллельно нагревающей катушке, в которую помещается разогреваемый металл, присоединяют конденсатор и подбирают его емкость так, чтобы получить на частоте питающего генератора резонанс токов. Тогда через подводящие провода и генератор пойдет сравнительно небольшой ток, который может быть во много раз меньше тока в  -контуре, образованном конденсатором и нагревающей катушкой.
-контуре, образованном конденсатором и нагревающей катушкой.
• В чем заключаются достоинства переменного тока синусоидальной формы?
• Как преобразуются прямоугольные импульсы  -цепочкой? Рассмотрите случай, когда длительность импульсов много больше
-цепочкой? Рассмотрите случай, когда длительность импульсов много больше  и когда она много меньше
и когда она много меньше  .
.
• Поясните идею метода векторных диаграмм для расчета цепей синусоидального переменного тока?
• Поясните, почему на векторной диаграмме на рис. 137 вектор, изображающий приложенное напряжение, равен сумме векторов, изображающих напряжения на сопротивлении  и емкости С.
и емкости С.
• Рассмотрите последовательную  -цепочку и постройте соответствующую ей векторную диаграмму. Найдите сдвиг фаз между приложенным напряжением и током в цепи. Будет ли ток отставать от напряжения или опережать его?
-цепочку и постройте соответствующую ей векторную диаграмму. Найдите сдвиг фаз между приложенным напряжением и током в цепи. Будет ли ток отставать от напряжения или опережать его?
• Если в общей формуле (9) для последовательной  -цепи положить
-цепи положить  , то для сдвига фаз получается выражение, отличающееся знаком от формулы (4) для RC-цепи. Как по-вашему, с чем связано это различие?
, то для сдвига фаз получается выражение, отличающееся знаком от формулы (4) для RC-цепи. Как по-вашему, с чем связано это различие?
• При каких соотношениях между параметрами последовательной RLC-цепи ток в ней опережает по фазе приложенное напряжение, а при каких — отстает от него?
• Поясните, почему на векторной диаграмме для параллельной RLC-цепи складываются токи, а не напряжения?
• Что такое резонанс напряжений и резонанс токов? Какие энергетические превращения при этом происходят в цепи?
• Можно ли применять векторные диаграммы для нахождения тока сразу после приложения переменного напряжения?
Закон Ома. Закон Ома — это утверждение о пропорциональности между током и напряжением в цепи.
Рассмотрим для простоты участок цепи, содержащий последовательно соединенные резистор  конденсатор С и катушку индуктивности
конденсатор С и катушку индуктивности  Такая цепь была подробно рассмотрена выше. Как было показано, вид закона Ома имеет только соотношение между амплитудными значениями тока и напряжения в цепи:
Такая цепь была подробно рассмотрена выше. Как было показано, вид закона Ома имеет только соотношение между амплитудными значениями тока и напряжения в цепи:

Наличие определенного сдвига по фазе  между током и напряжением приводит к тому, что мгновенные значения тока и напряжения не пропорциональны друг другу и мы не можем с помощью вещественных чисел представить ток в цепи как отношение приложенного напряжения к сопротивлению.
между током и напряжением приводит к тому, что мгновенные значения тока и напряжения не пропорциональны друг другу и мы не можем с помощью вещественных чисел представить ток в цепи как отношение приложенного напряжения к сопротивлению.
Однако это можно легко сделать, используя комплексные числа. Разумеется, ток, напряжение и сопротивление цепи, как и любые другие измеряемые на опыте физические величины, должны выражаться вещественными числами. Мгновенные значения
интересующих нас физических величин получаются в результате проецирования векторной диаграммы, изображенной на рис. 140. Но вектор на плоскости можно задать с помощью комплексного числа. Будем фиксировать мгновенное значение каждого из вращающихся векторов на рис. 140 заданием некоторого комплексного числа. В частности, вектору, изображающему ток, сопоставим комплексное число  вектору, изображающему напряжение, — комплексное число
вектору, изображающему напряжение, — комплексное число  Поскольку угол
Поскольку угол  между этими вращающимися векторами постоянен, комплексные числа
между этими вращающимися векторами постоянен, комплексные числа  сопоставляемые этим векторам, можно связать равенством
сопоставляемые этим векторам, можно связать равенством  где
где  — некоторое постоянное комплексное число.
— некоторое постоянное комплексное число.
Это соотношение формально имеет вид закона Ома для участка цепи, причем комплексное число  как-то характеризует сопротивление этого участка цепи переменному току. Найдем вид этого числа. Запишем выражения для
как-то характеризует сопротивление этого участка цепи переменному току. Найдем вид этого числа. Запишем выражения для  и
и  в тригонометрической форме:
в тригонометрической форме:

и учтем, что разность аргументов этих комплексных чисел равна постоянному сдвигу фаз  между напряжением и током. Используя равенства (14) и правило деления комплексных чисел, заданных в тригонометрической форме, получим
между напряжением и током. Используя равенства (14) и правило деления комплексных чисел, заданных в тригонометрической форме, получим

Таким образом, модуль  комплексного числа
комплексного числа  как видно из выражений (13) и (15), равен
как видно из выражений (13) и (15), равен

а его аргумент  представляет собой сдвиг фаз между напряжением и током и определяется формулой (9). Переходя от тригонометрической к алгебраической форме комплексного числа и учитывая, что
представляет собой сдвиг фаз между напряжением и током и определяется формулой (9). Переходя от тригонометрической к алгебраической форме комплексного числа и учитывая, что

получаем для  выражение
выражение

Комплексное число  полностью характеризует сопротивление рассматриваемого участка цепи синусоидальному переменному току с частотой со. Оно носит название комплексного сопротивления или импеданса цепи. Зная
полностью характеризует сопротивление рассматриваемого участка цепи синусоидальному переменному току с частотой со. Оно носит название комплексного сопротивления или импеданса цепи. Зная  легко найти амплитуду тока и сдвиг по фазе между напряжением и током.
легко найти амплитуду тока и сдвиг по фазе между напряжением и током.
Формула (16) показывает, что импеданс последовательной цепи можно получить, если элементам схемы  и С сопоставить комплексные сопротивления переменному току по следующему правилу:
и С сопоставить комплексные сопротивления переменному току по следующему правилу:

после чего сложить эти «сопротивления» по правилу сложения сопротивлений в последовательной цепи.
Полученный рецепт имеет совершенно общий характер и справедлив для любой разветвленной цепи: всем элементам сопоставляются комплексные сопротивления по правилу (17), которые затем складываются по правилам для цепей постоянного тока.
Отметим, что формулы (14) и (15) можно записать компактнее, если воспользоваться формулой Эйлера

При этом, очевидно,  и
и

• Сформулируйте основную идею использования комплексных чисел для анализа цепей синусоидального переменного тока.
• Сформулируйте правила расчета произвольной разветвленной цепи, содержащей RLC-элементы.
• Рассмотрите с помощью комплексных чисел параллельную RLC-цепь и получите формулы (11) и (12).
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- I. ЭЛЕКТРОСТАТИКА
- § 1. Электрический заряд. Закон Кулона
- § 2. Электрическое поле. Напряженность поля
- § 3. Теорема Гаусса
- § 4. Потенциал электростатического поля. Энергия системы зарядов
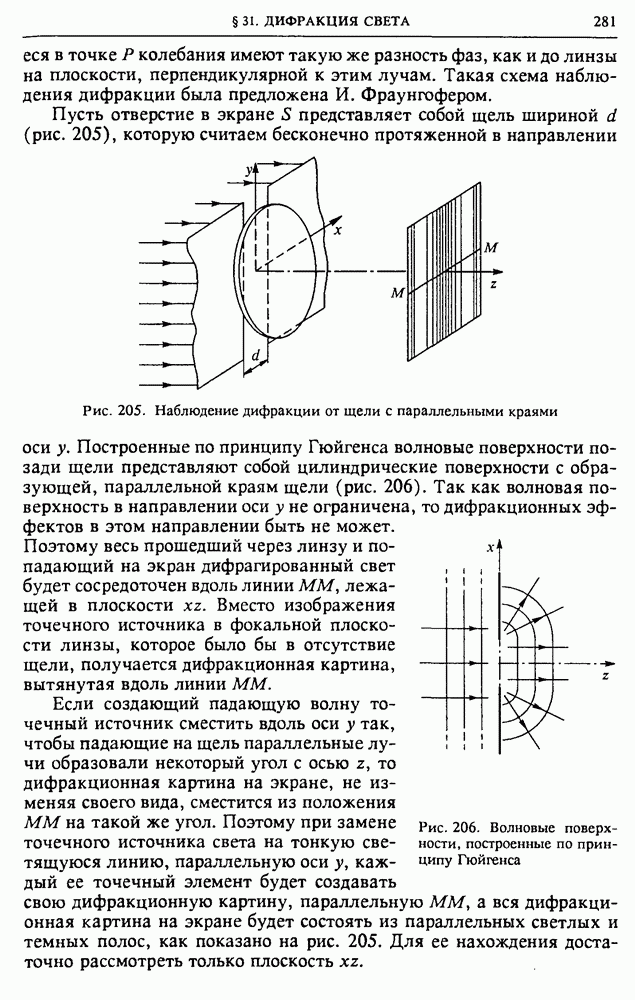
- § 5. Расчет электрических полей
- § 6. Проводники в электрическом поле
- § 7. Силы в электростатическом поле
- § 8. Конденсаторы. Электроемкость
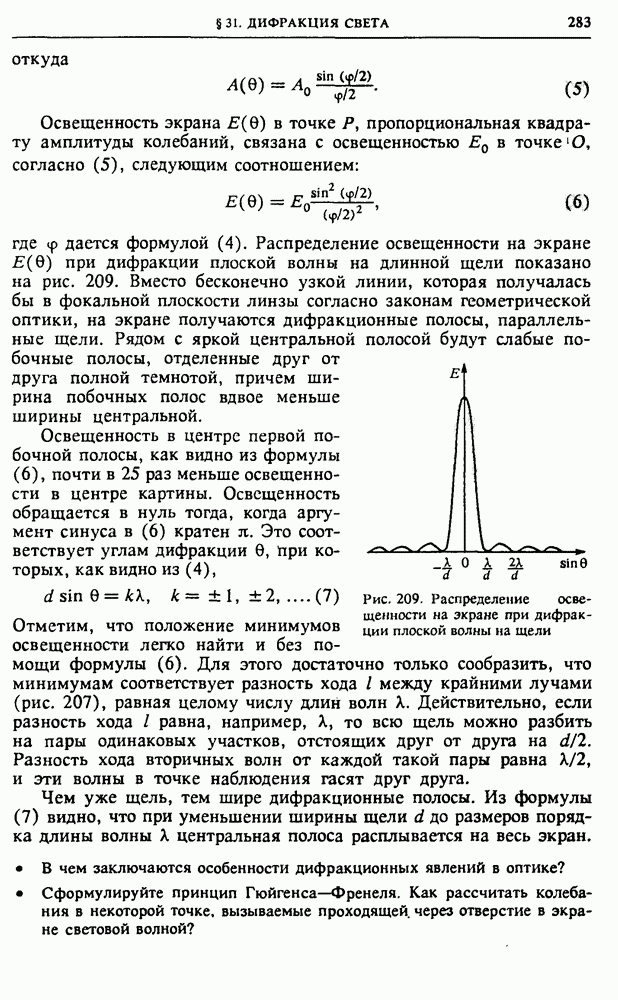
- § 9. Энергия электрического поля
- II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 10. Характеристики электрического тока. Закон Ома
- § 11. Соединение проводников в электрические цепи
- § 12. Закон Ома для неоднородной цепи
- § 13. Расчет цепей постоянного тока
- § 14. Работа и мощность постоянного тока
- § 15. Магнитное поле постоянного тока
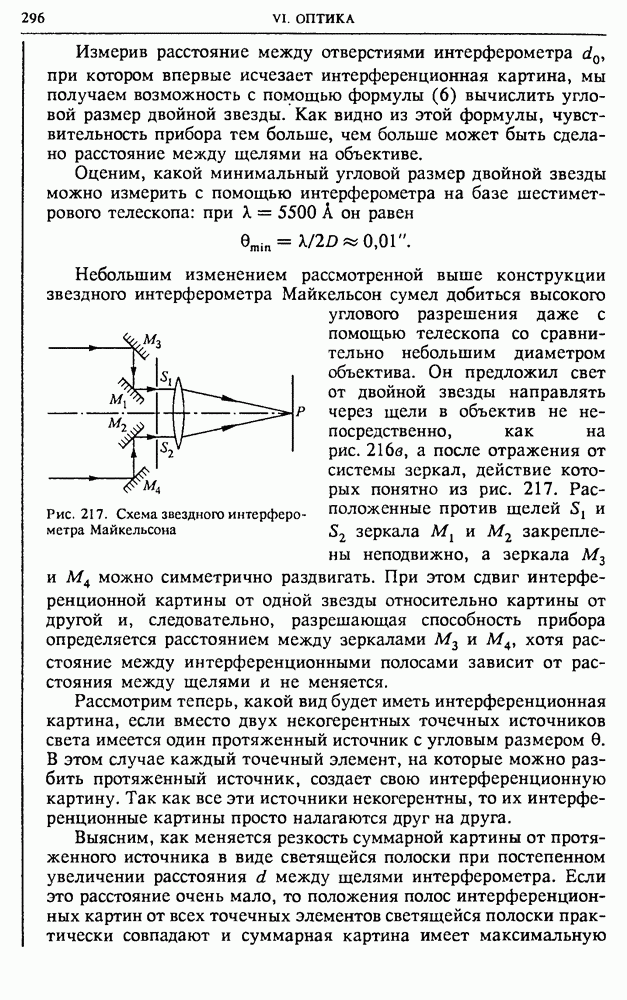
- § 16. Действие магнитного поля на движущиеся заряды
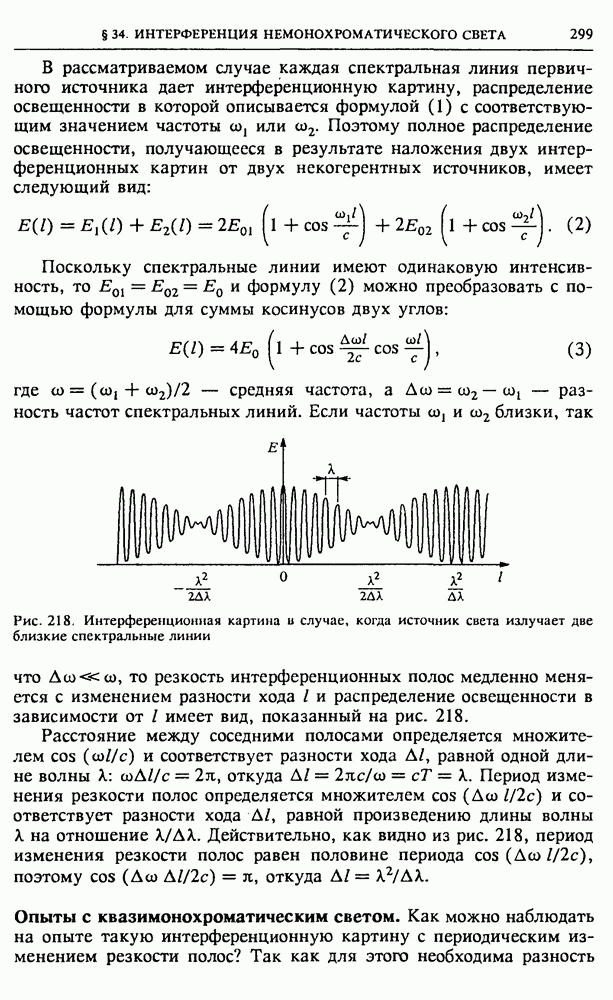
- III. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 17. Явление электромагнитной индукции
- § 18. Электрические машины постоянного тока
- § 19. Энергия магнитного поля
- § 20. Основы теории электромагнитного поля
- § 21. Квазистационарные явления в электрических цепях
- IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 22. Цепи переменного тока. Закон Ома
- § 23. Работа и мощность переменного тока. Передача электроэнергии
- § 24. Трехфазный ток. Электрические машины переменного тока
- V. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 25. Колебательный контур
- § 26. Вынужденные колебания в контуре. Резонанс
- § 27. Незатухающие электромагнитные колебания
- § 28. Электромагнитные волны
- § 29. Свойства и применения электромагнитных волн
- VI. ОПТИКА
- § 30. Свет как электромагнитные волны. Интерференция
- § 31. Дифракция света
- § 32. Спектральные приборы. Дифракционная решетка
- § 33. Протяженные источники света
- § 34. Интерференция немонохроматического света
- § 35. Физические принципы голографии
- § 36. Геометрическая оптика
- § 37. Оптические приборы, формирующие изображение