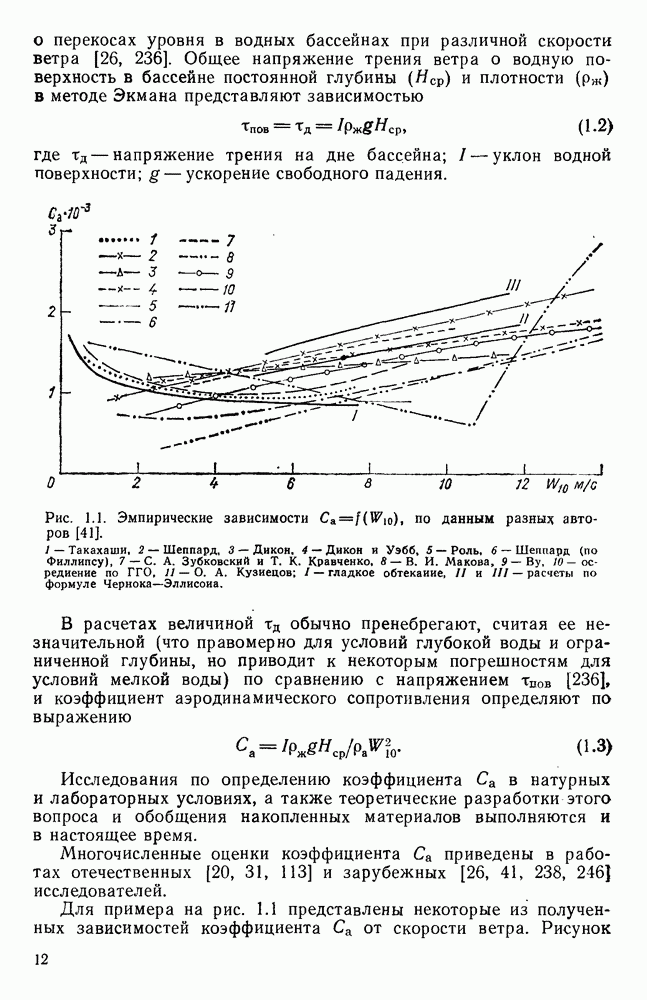
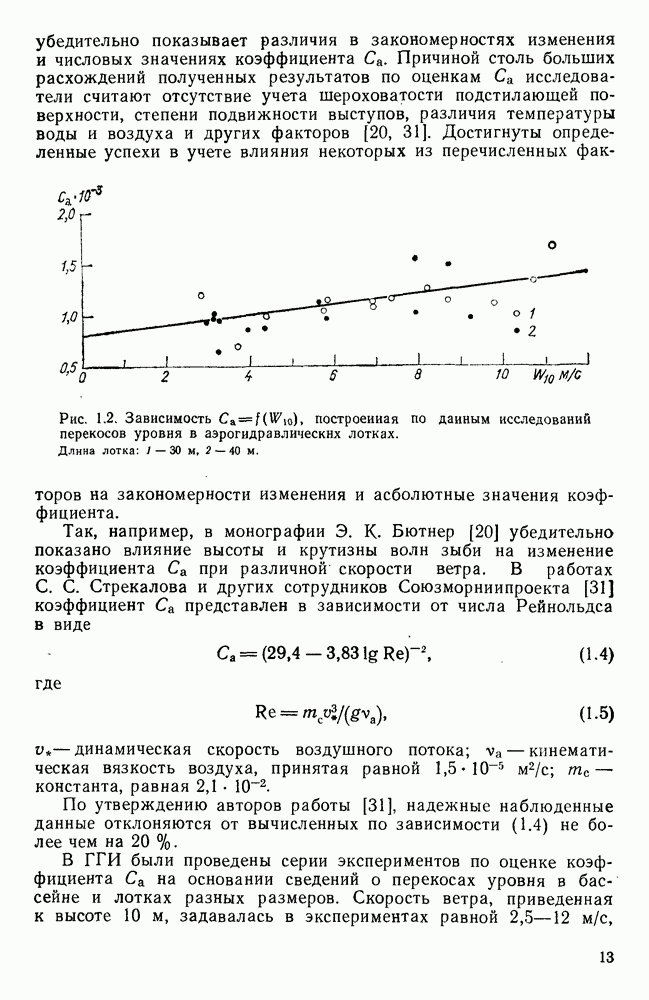
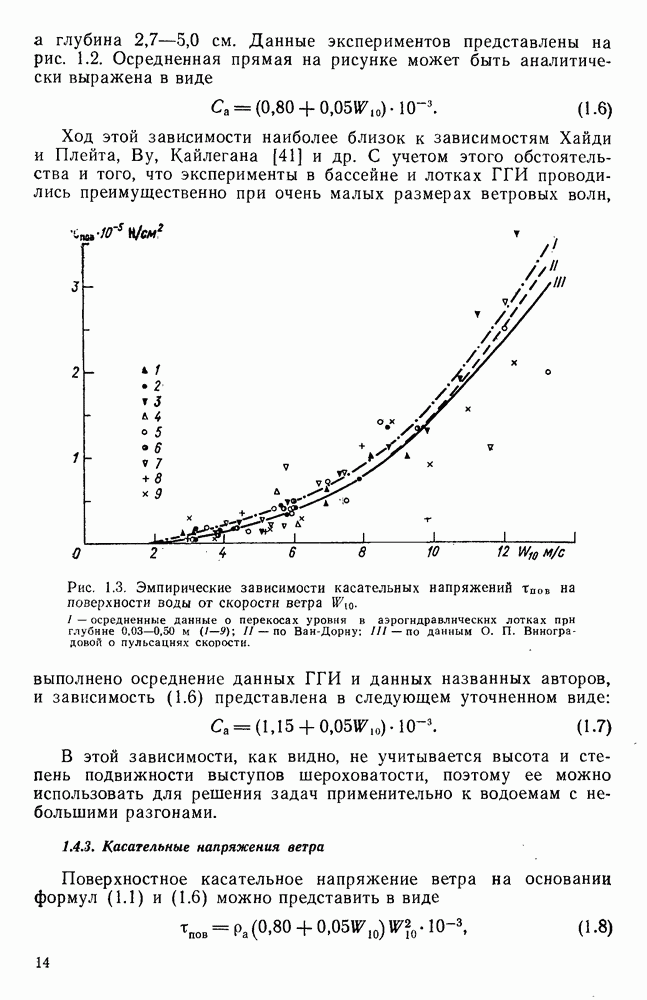
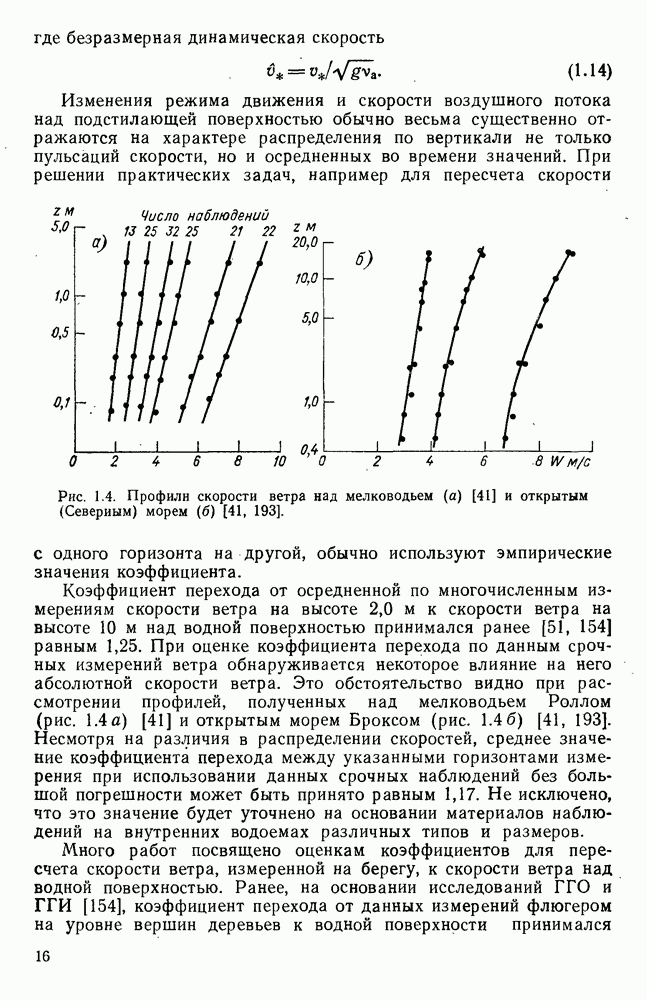
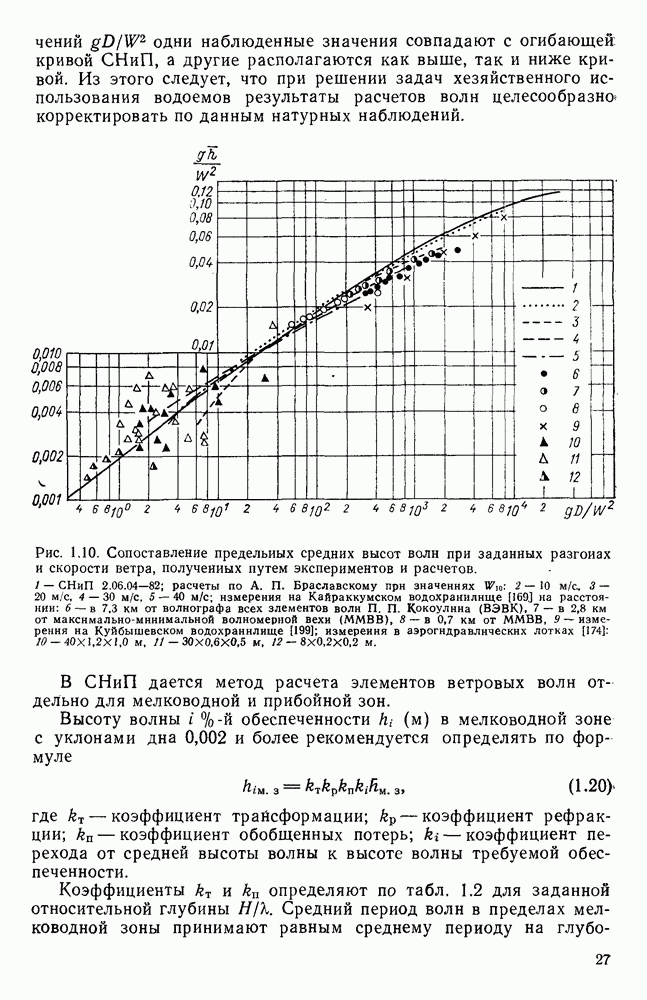
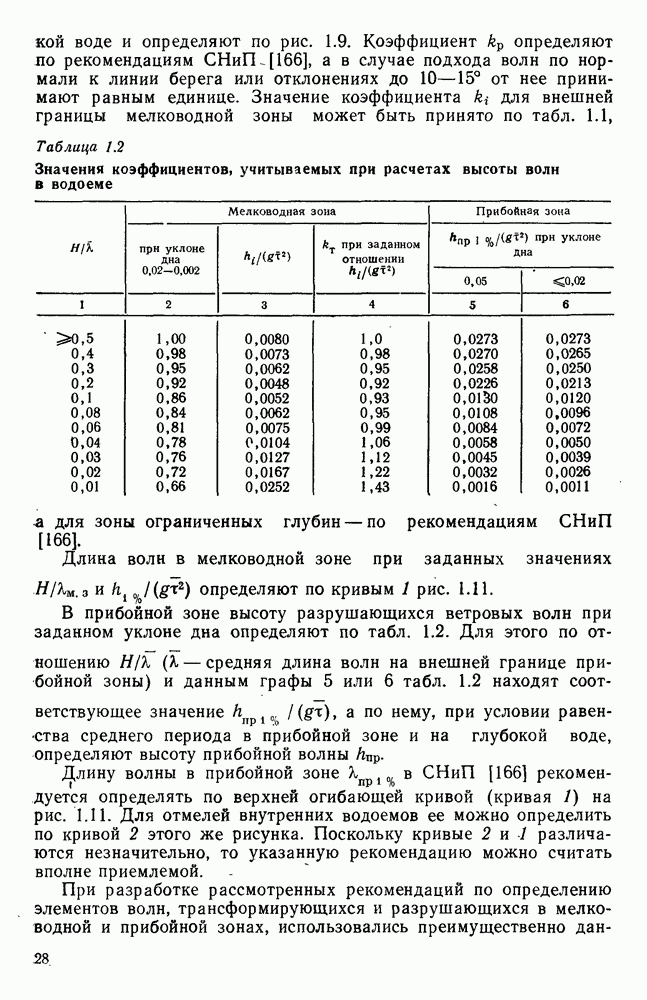
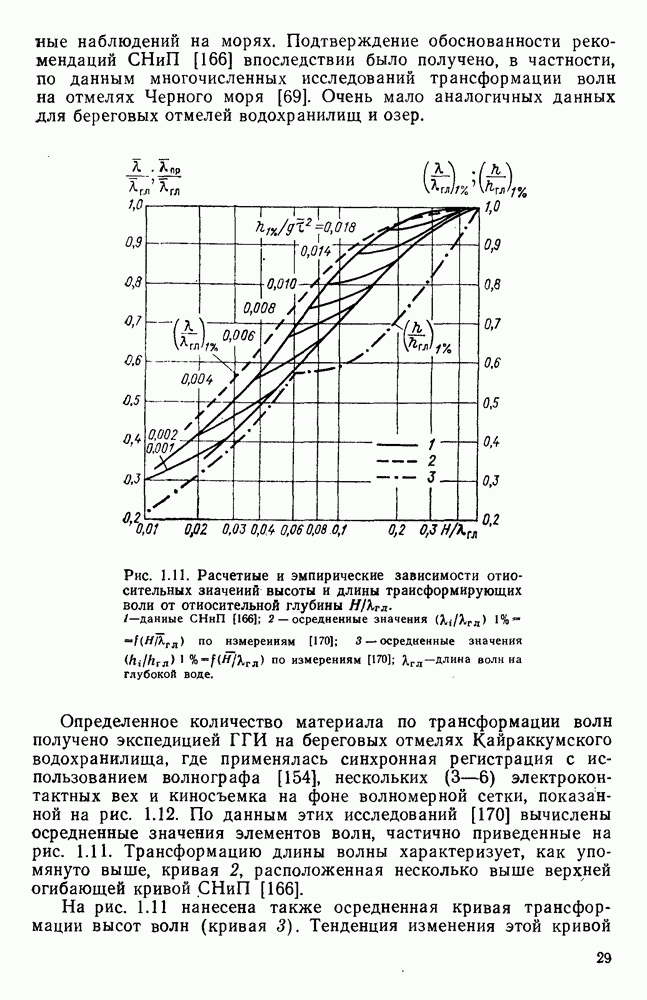
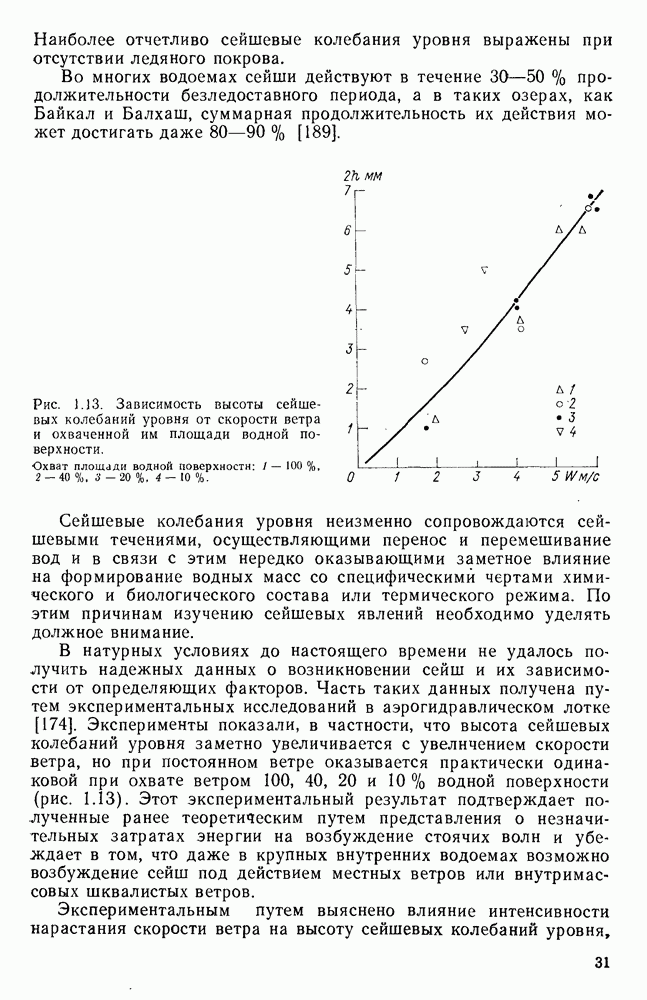
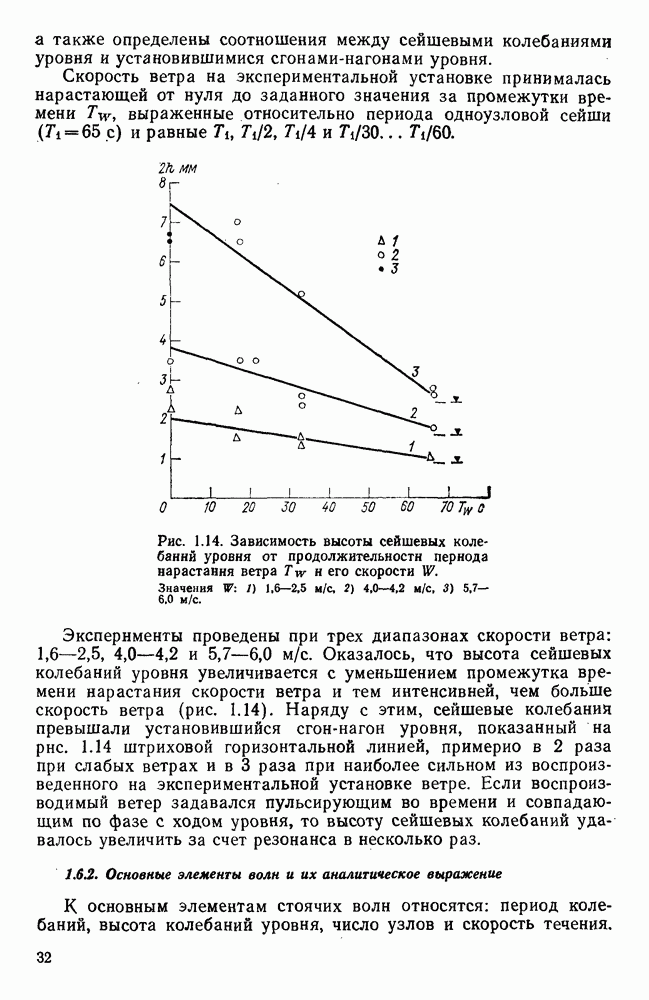
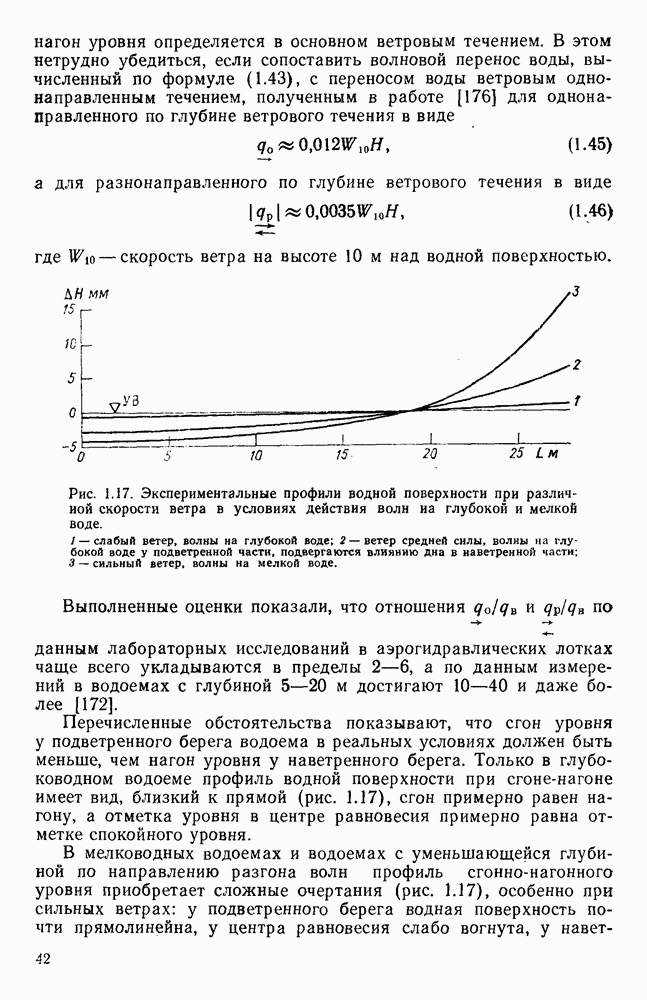
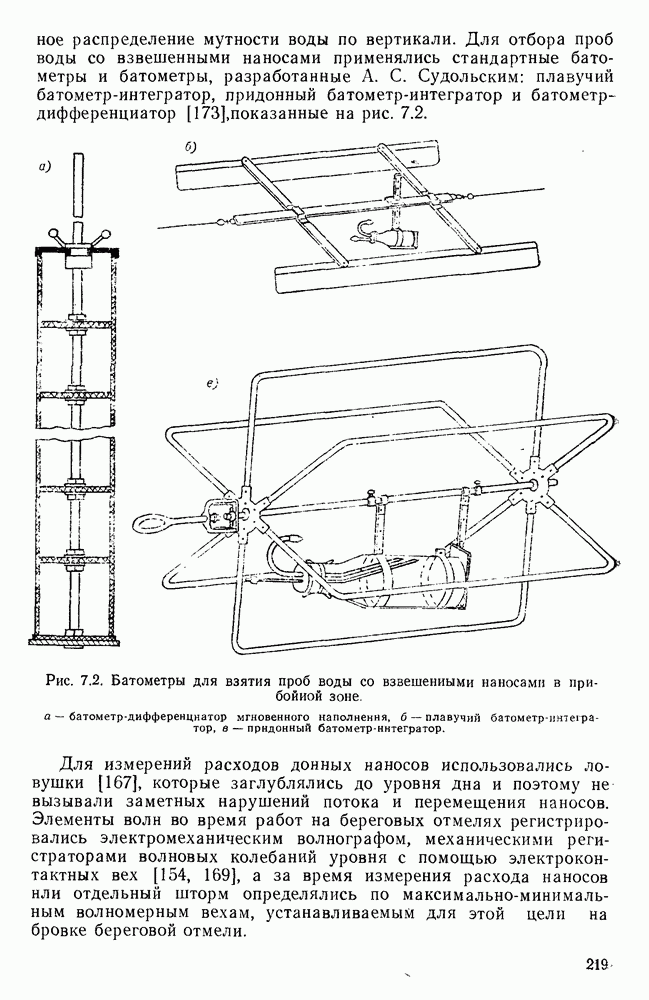
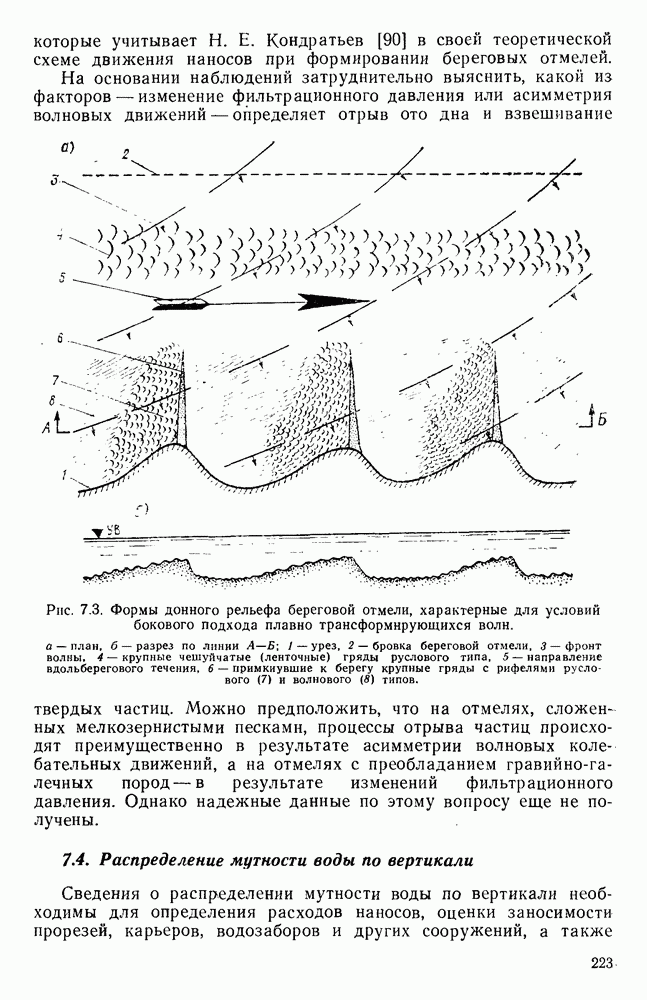
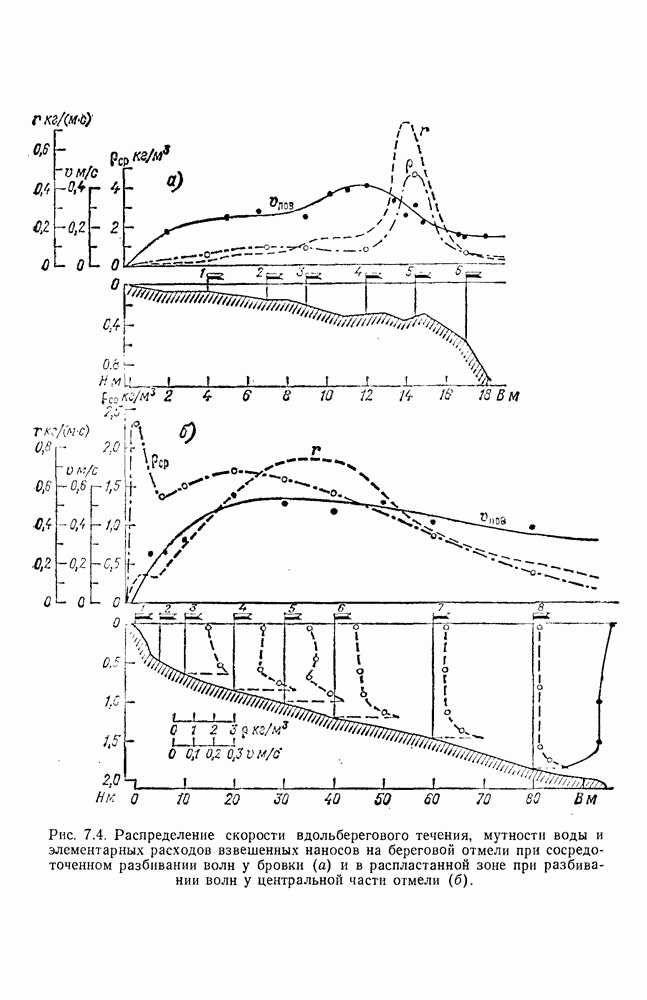
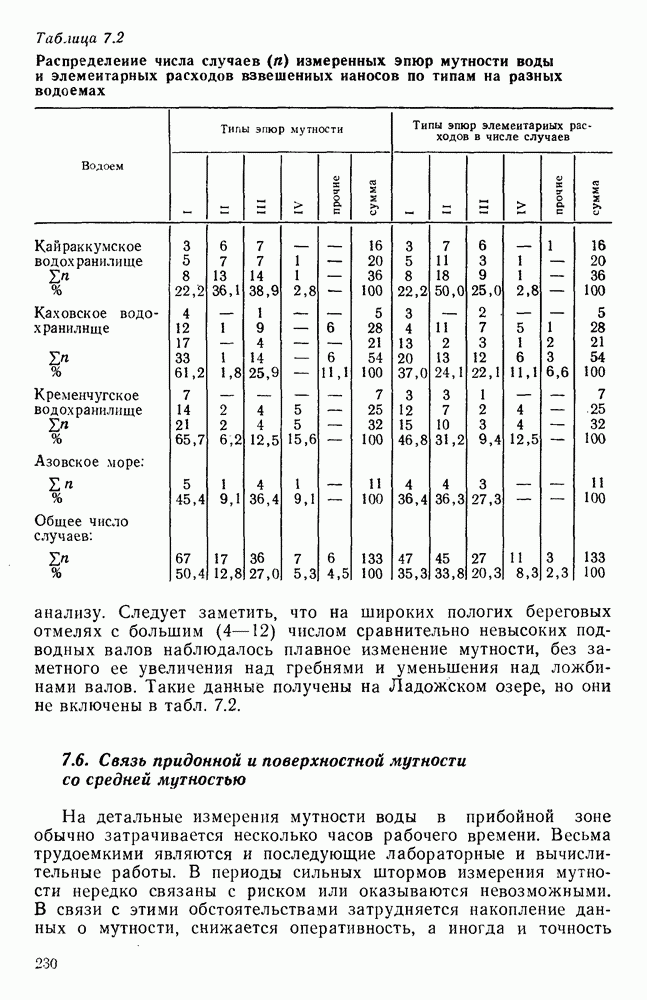
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
1.6.2. Основные элементы волн и их аналитическое выражение
К основным элементам стоячих волн относятся: период колебаний, высота колебаний уровня, число узлов и скорость течения.
При изучении динамики конкретных водоемов, наряду с перечисленными элементами, устанавливают местоположение узлов и пучностей, распределение высоты колебаний и скорости течения вдоль водоема или по его акватории.
Детальные представления о распределении стоячих волновых колебаний уровня вдоль оси водоема прямоугольной формы можно получить на основании рассмотрения уравнения профиля волны, которое в условиях глубокой воды  и ограниченной глубины
и ограниченной глубины  имеет вид [86, 95, 191]
имеет вид [86, 95, 191]

где  амплитуда, равная половине общей высоты колебания уровня.
амплитуда, равная половине общей высоты колебания уровня.

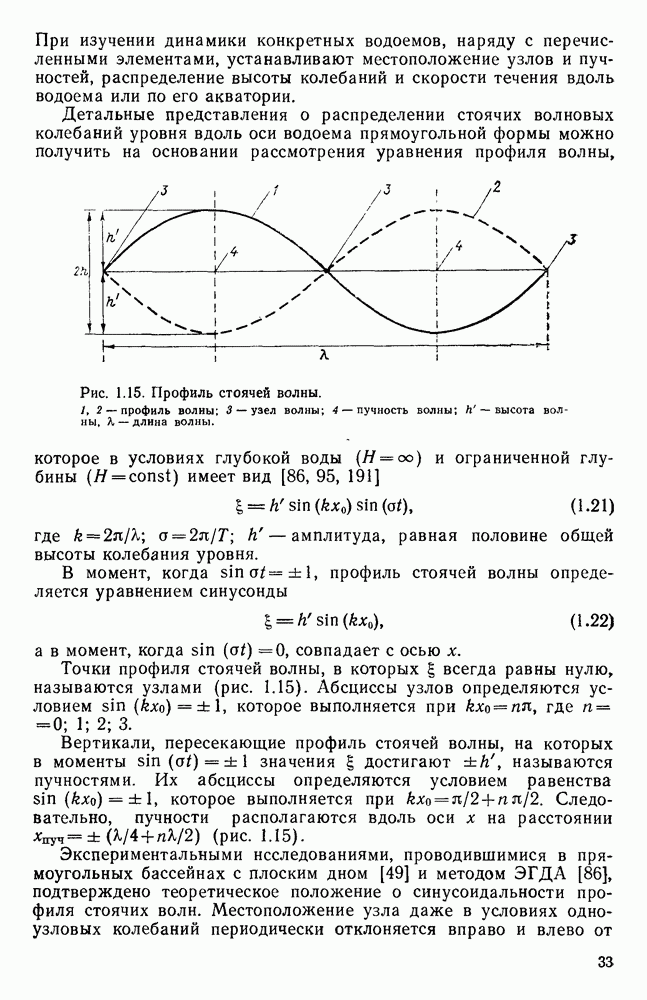
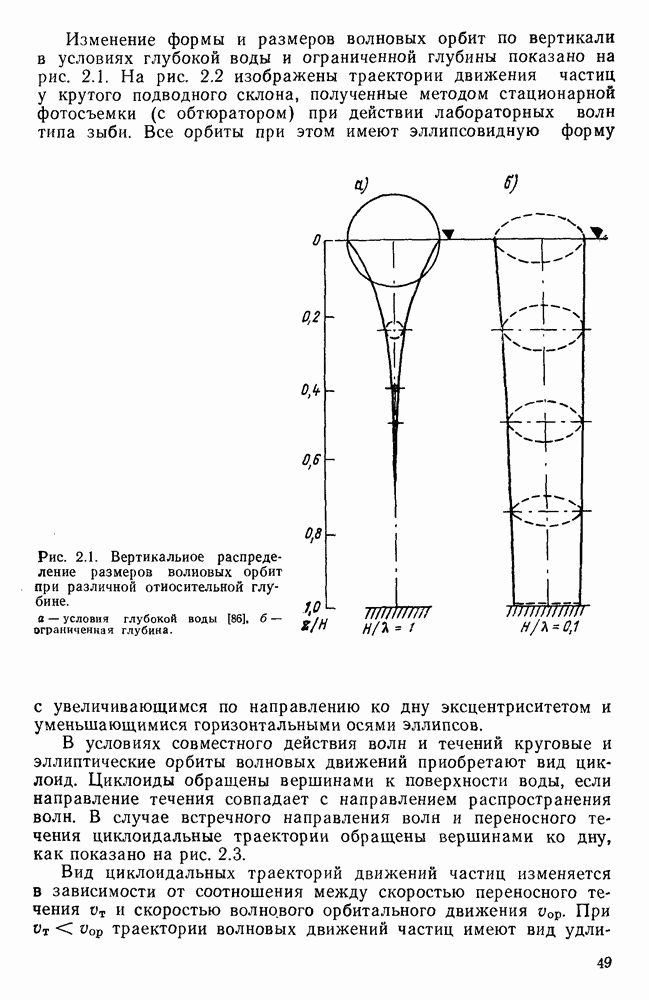
Рис. 1.15. Профиль стоячей волны. 1, 2 — профиль волны; 3 — узел волны; 4 — пучность волны;  высота волны, X — длина волны.
высота волны, X — длина волны.
В момент, когда  профиль стоячей волны определяется уравнением синусоиды
профиль стоячей волны определяется уравнением синусоиды

а в момент, когда  совпадает с осью
совпадает с осью 
Точки профиля стоячей волны, в которых  всегда равны нулю, называются узлами (рис. 1.15). Абсциссы узлов определяются условием
всегда равны нулю, называются узлами (рис. 1.15). Абсциссы узлов определяются условием  которое выполняется при
которое выполняется при  где
где  .
.
Вертикали, пересекающие профиль стоячей волны, на которых в моменты  значения
значения  достигают
достигают  называются пучностями. Их абсциссы определяются условием равенства
называются пучностями. Их абсциссы определяются условием равенства  которое выполняется при
которое выполняется при  Следовательно, пучности располагаются вдоль оси
Следовательно, пучности располагаются вдоль оси  на расстоянии Л-пуч
на расстоянии Л-пуч  (рис. 1.15).
(рис. 1.15).
Экспериментальными исследованиями, проводившимися в прямоугольных бассейнах с плоским дном [49] и методом  [86], подтверждено теоретическое положение о синусоидальности профиля стоячих волн. Местоположение узла даже в условиях одноузловых колебаний периодически отклоняется вправо и влево от
[86], подтверждено теоретическое положение о синусоидальности профиля стоячих волн. Местоположение узла даже в условиях одноузловых колебаний периодически отклоняется вправо и влево от
поперечной оси бассейна. Одновременно с этим отмечается несимметричность волнового профиля, причем в момент перехода через статистический уровень он не приобретает вида горизонтальной линии [49], а высота колебаний в пучностях так же, как и местоположение узла, подвергается периодическим изменениям.
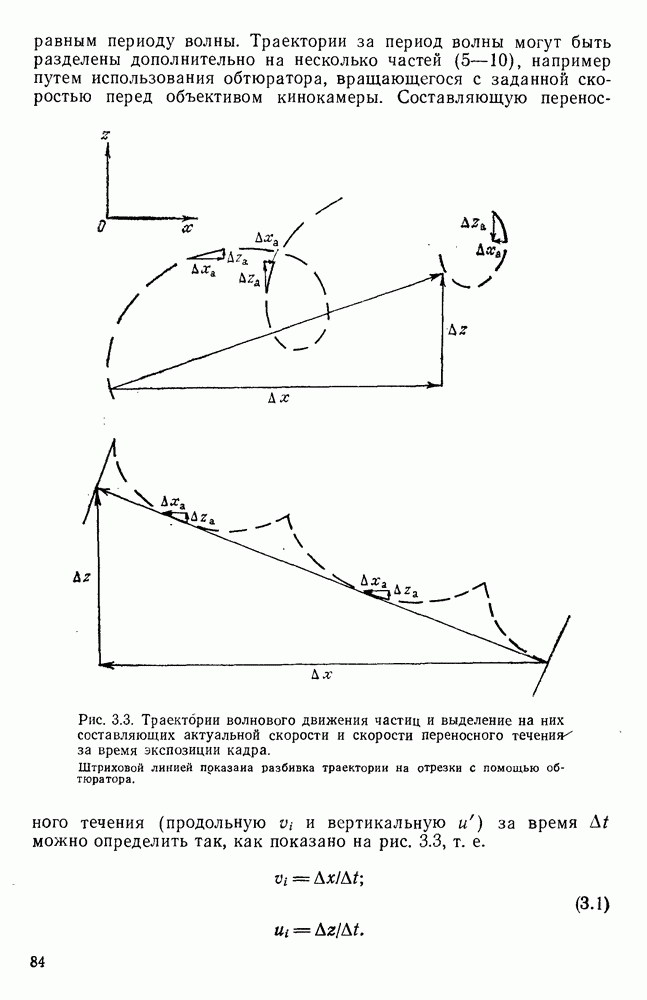
Для водоема типа канала, исходя из выражения потенциала скорости стоячей волны, получают выражения для составляющих скорости, уравнений движения и длин траекторий перемещения жидких частиц. Составляющие скорости движения жидких частиц при условии ограниченной глубины канала описываются в решениях первого приближения точности уравнениями:

Уравнения движения жидких частиц с начальными координатами  и
и  представляются в виде:
представляются в виде:

а длины траекторий перемещения частиц — в виде

Из формулы (1.27) видно, что длина траекторий, а следовательно и скорость движения частиц, убывает от узла к пучности волны и от поверхности воды ко дну.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ВОЗДЕЙСТВИЕ ВЕТРА И ВОЛНОВЫЕ ПРОЦЕССЫ
- 1.1. Методы изучения взаимодействующих сложных явлений и процессов
- 1.2. Масштабы динамических явлений
- 1.3. Причины динамических явлений
- 1.4. Ветер над водной поверхностью
- 1.4.2. Коэффициент аэродинамического сопротивления
- 1.4.3. Касательные напряжения ветра
- 1.4.4. Профили ветра и их трансформация над подстилающей поверхностью
- 1.4.5. Режимные статистические и расчетные характеристики ветра
- 1.5. Ветровые волны
- 1.5.2. Классификация волн и их элементов
- 1.5.3. Расчет элементов ветровых волн и учет их изменчивости
- 1.6. Стоячие волны
- 1.6.2. Основные элементы волн и их аналитическое выражение
- 1.6.3. Периоды сейшевых колебаний уровня
- 1.6.4. Затухание стоячих колебаний уровня во времени
- 1.7. Внутренние волны
- 1.8. Сгонно-нагонные явления
- Глава 2. ПРОСТРАНСТВЕННАЯ СТРУКТУРА ПЕРЕНОСА ВОД ТЕЧЕНИЯМИ
- 2.1. Многообразие видов движений и масштабов пространственных структур
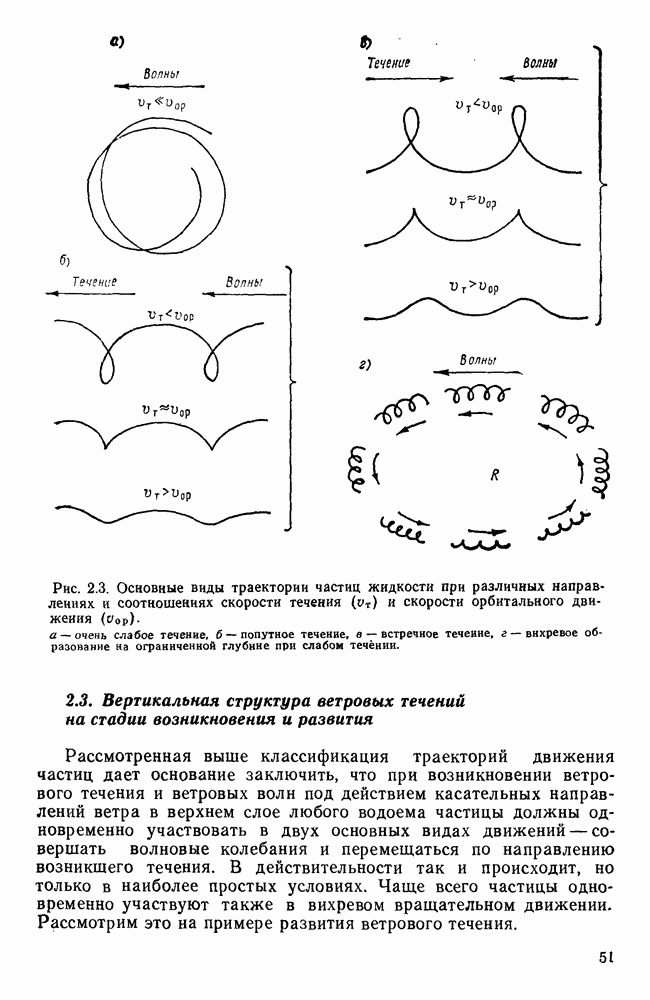
- 2.2. Траектории движений частиц жидкости при совместном действии волн и течений
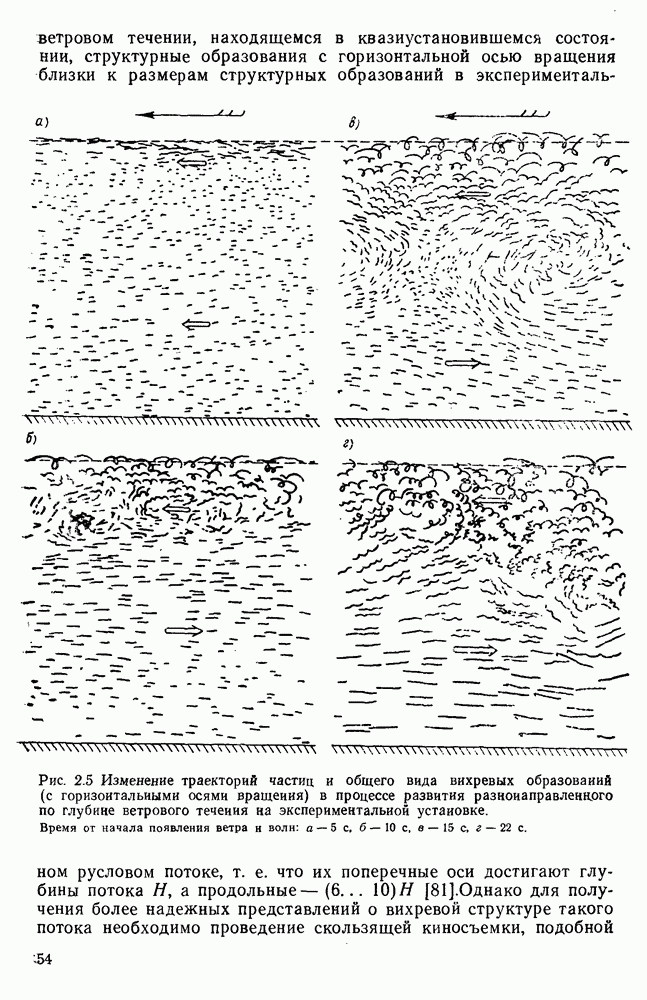
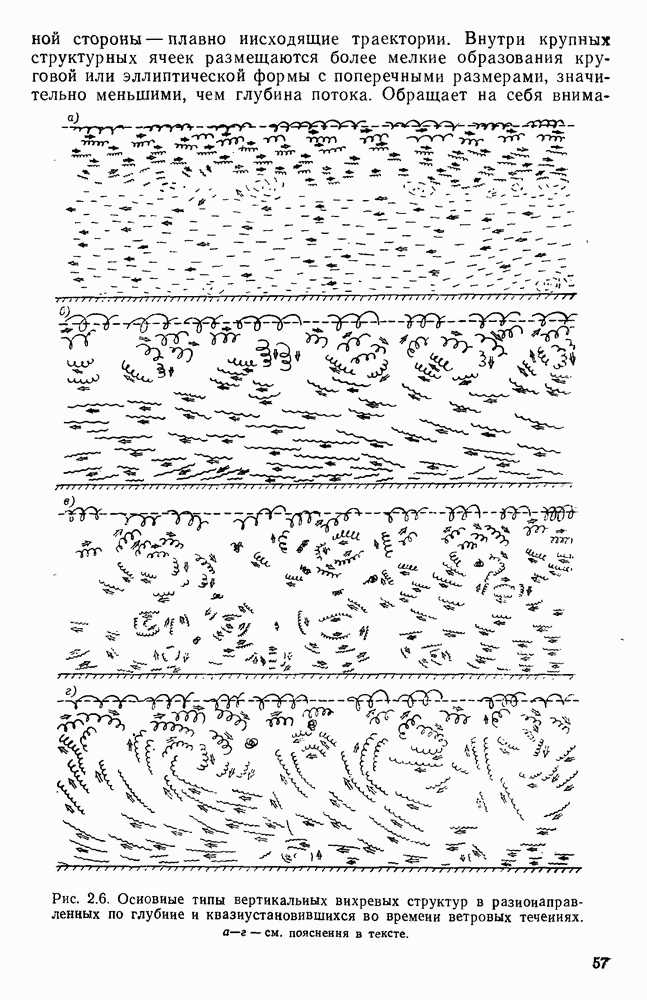
- 2.3. Вертикальная структура ветровых течений на стадии возникновения и развития
- 2.4. Вертикальная структура квазиустановившихся ветровых течений
- 2.5. Количественные характеристики вертикальных вихревых образований
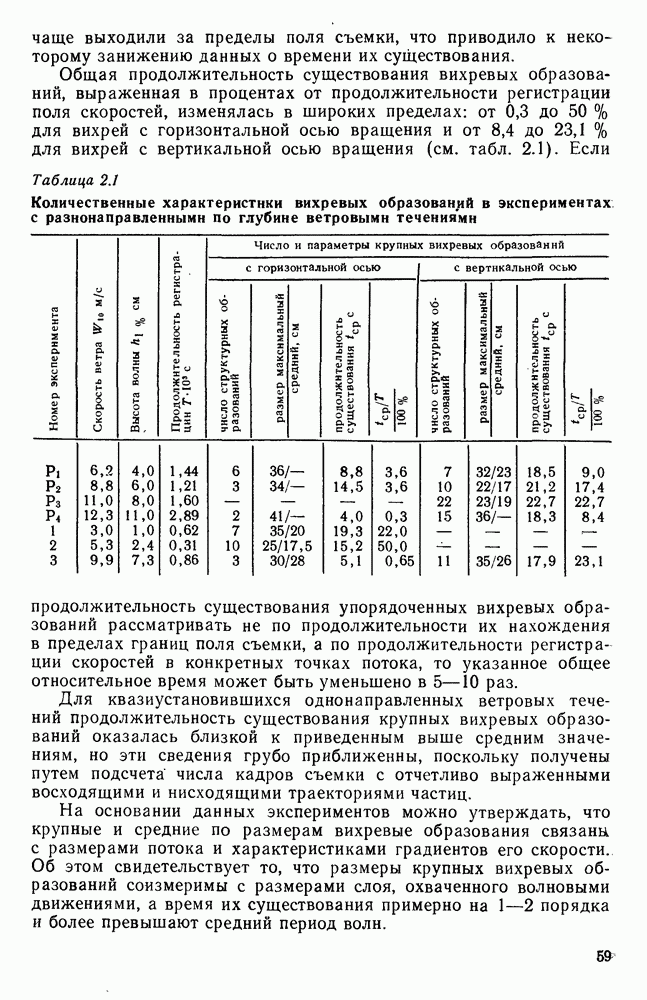
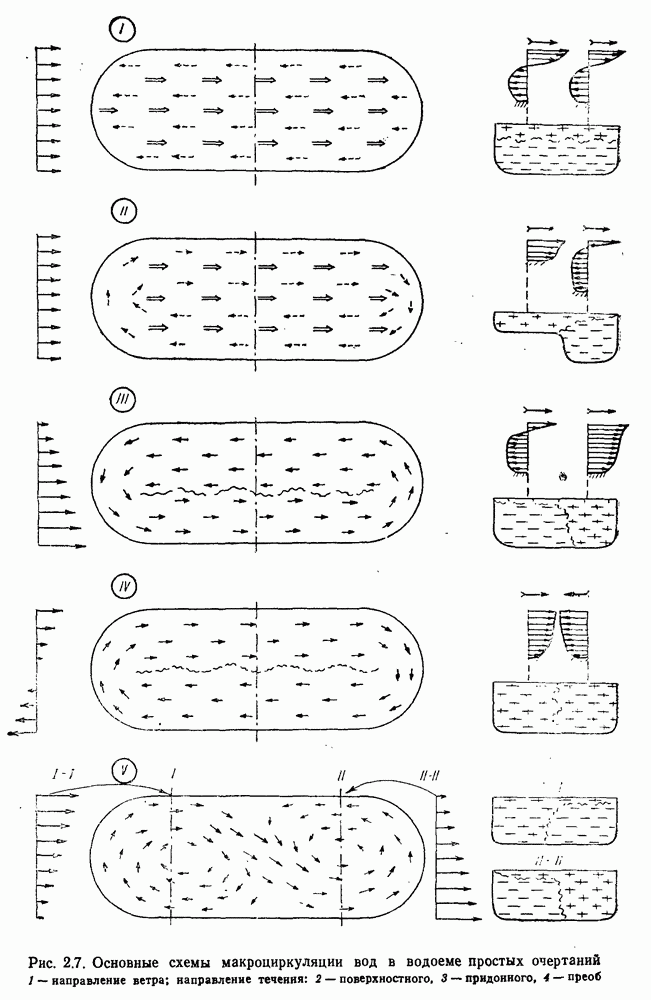
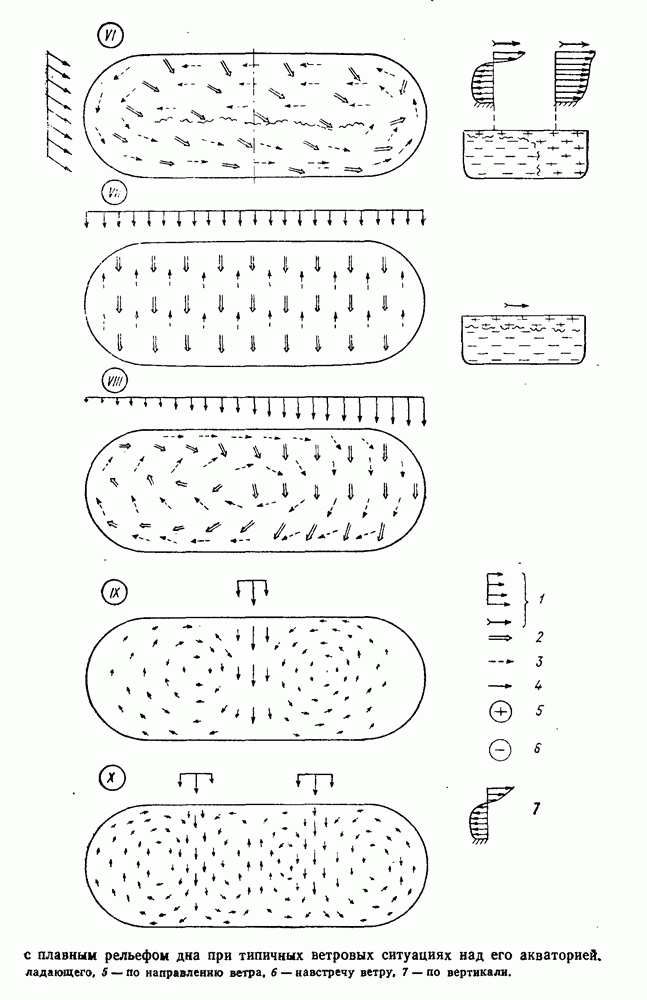
- 2.6. Макроциркуляция вод в водоеме при ветровых течениях
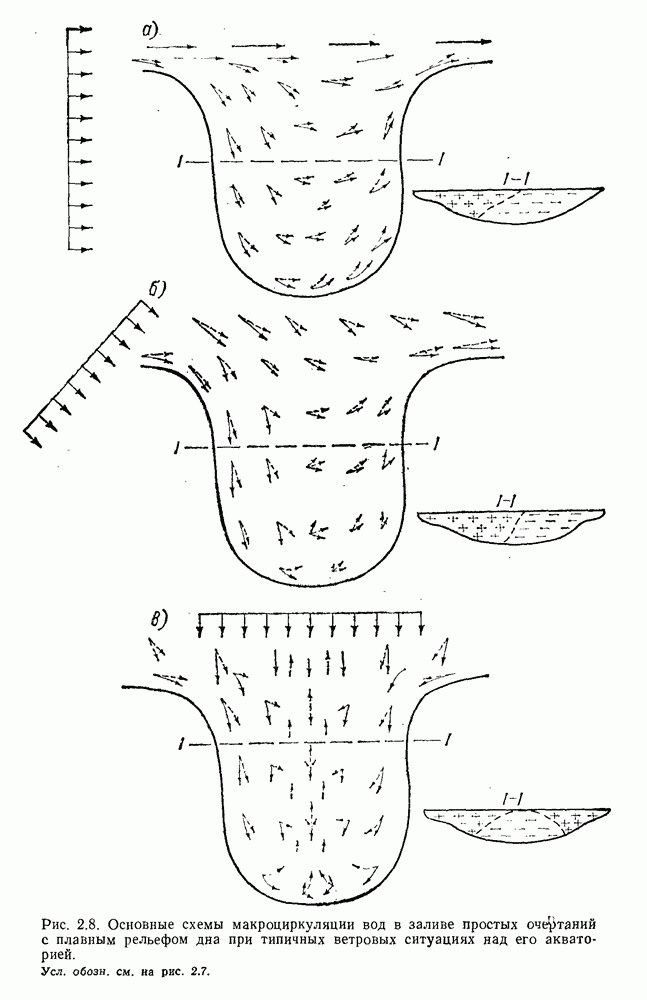
- 2.7. Макроциркуляция вод в заливе при ветровых течениях
- 2.8. Инерционные и синоптические вихри
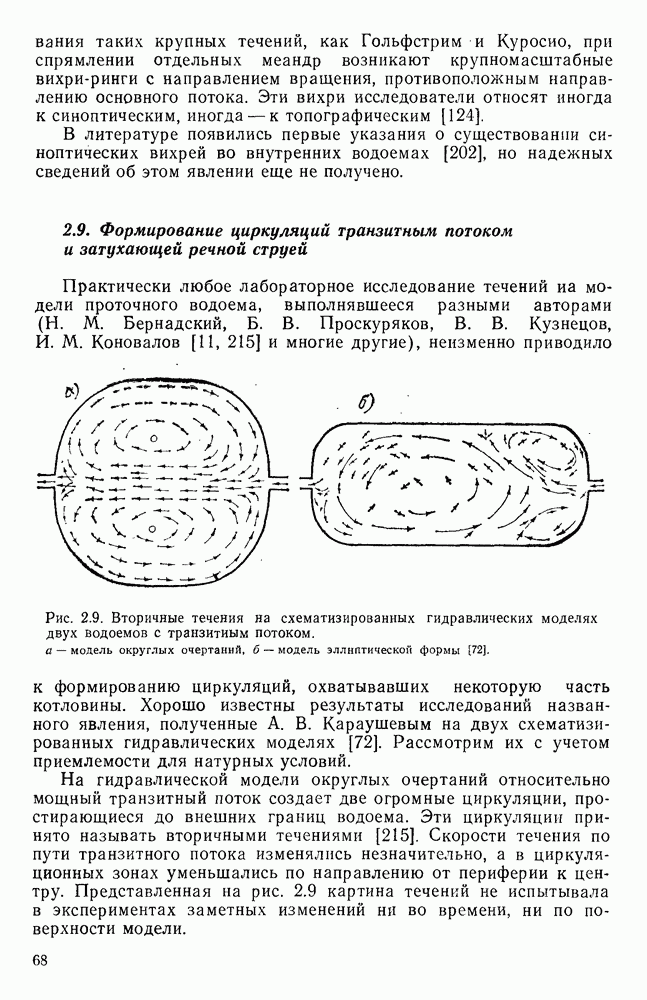
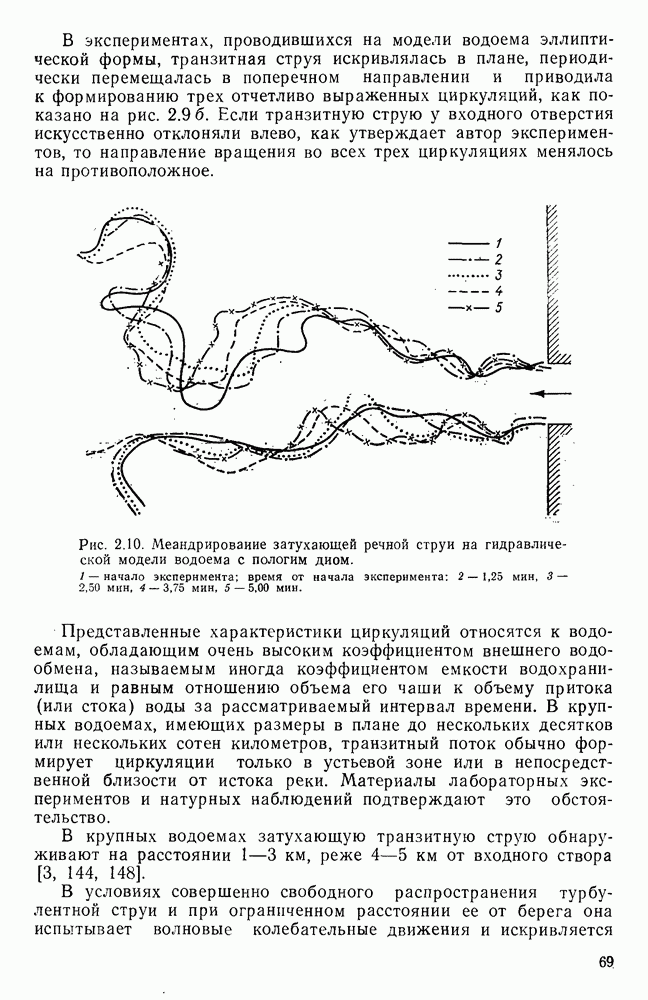
- 2.9. Формирование циркуляций транзитным потоком и затухающей речной струей
- 2.10. Структура сейшевых течений
- Глава 3. КИНЕМАТИКА ВЕТРОВЫХ И СУММАРНЫХ ТЕЧЕНИЙ
- 3.1. Совершенствование представлений о кинематике течений
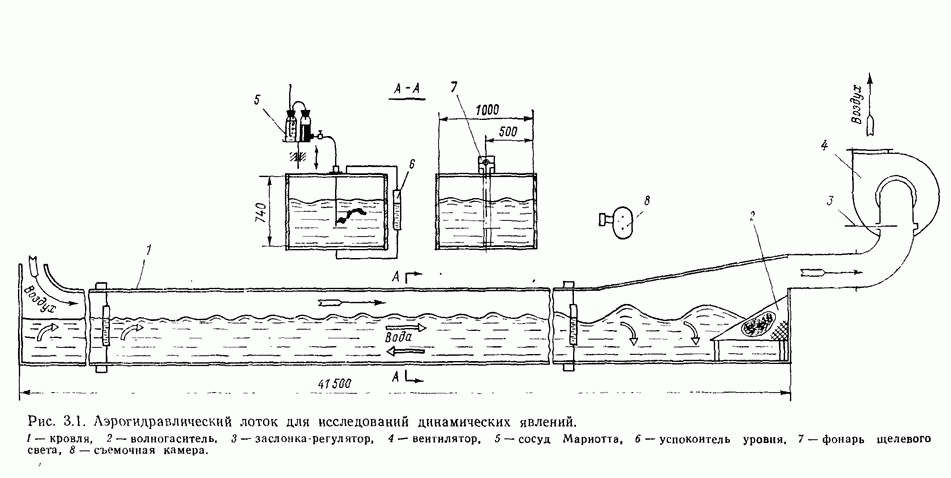
- 3.2. Методы исследований кинематики течений
- 3.3. Методика обработки записей течений
- 3.4. Оценка кинематических характеристик
- 3.5. Изменение мелкомасштабных пульсаций скорости во времени и по глубине
- 3.6. Изменение средних квадратических значений пульсационных составляющих скорости
- 3.7. Вертикальное распределение моментов корреляции в ветровых течениях
- 3.8. Энергетические характеристики ветровых течений по данным экспериментов
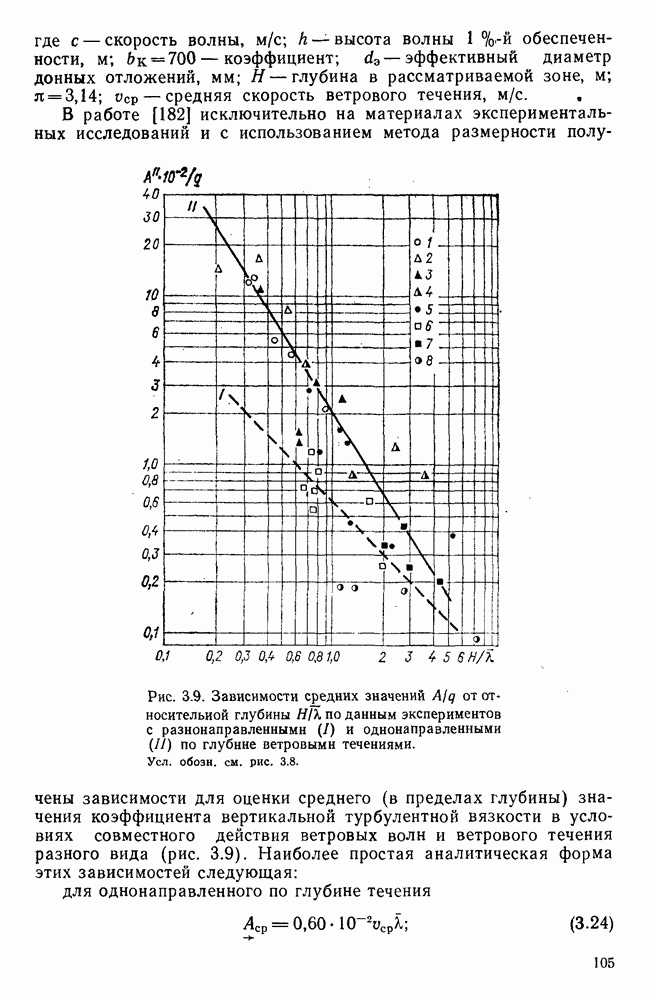
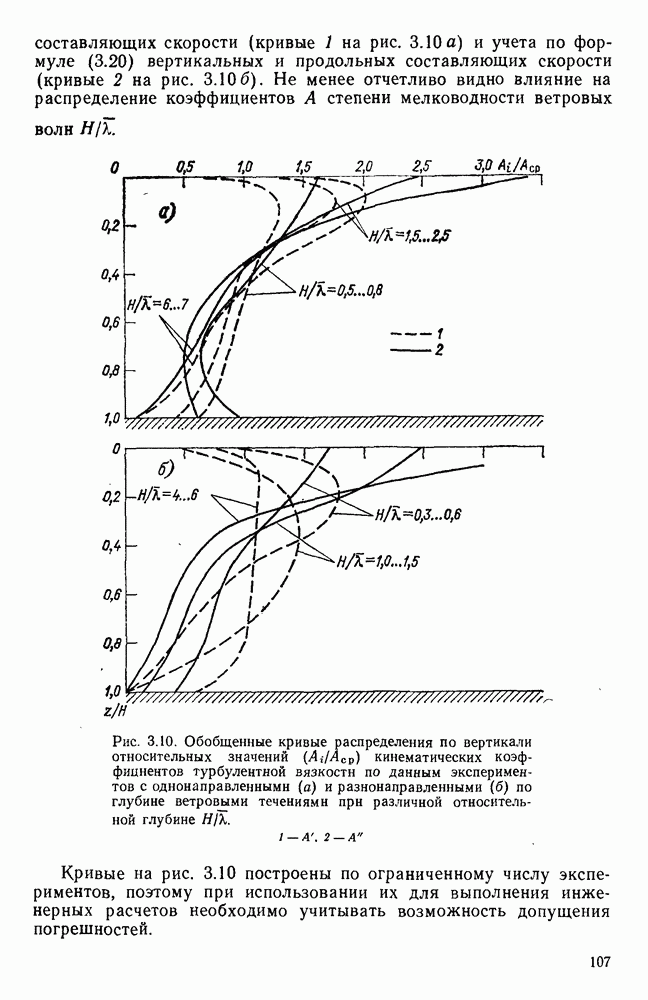
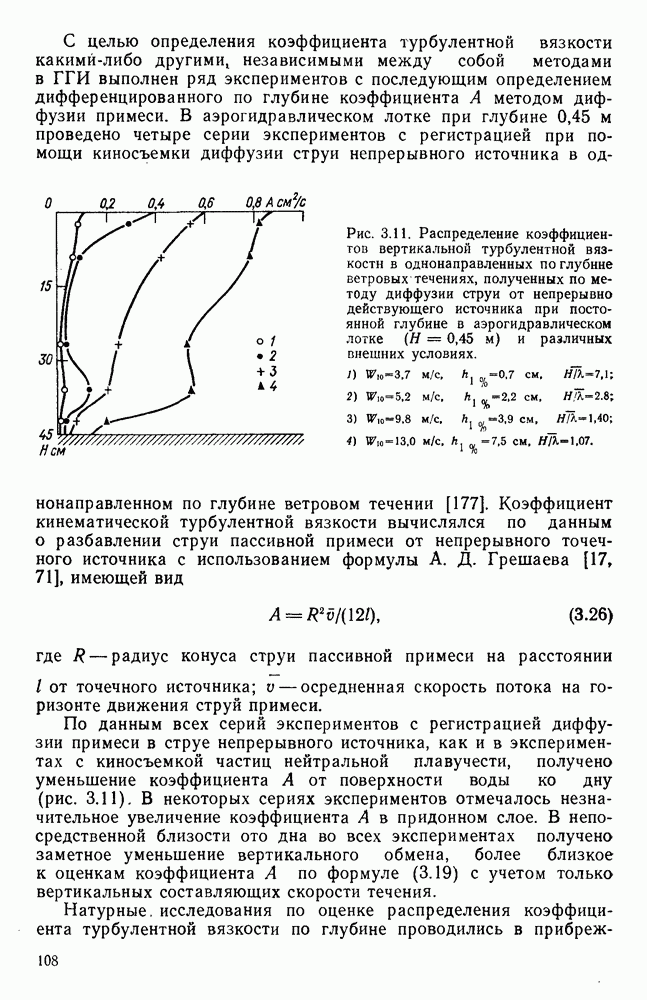
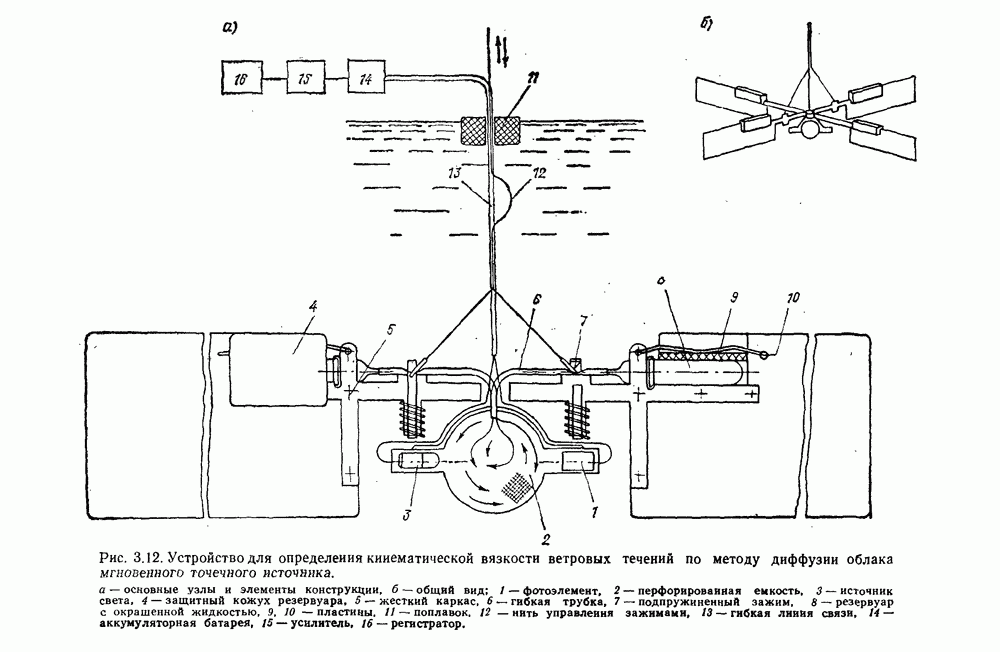
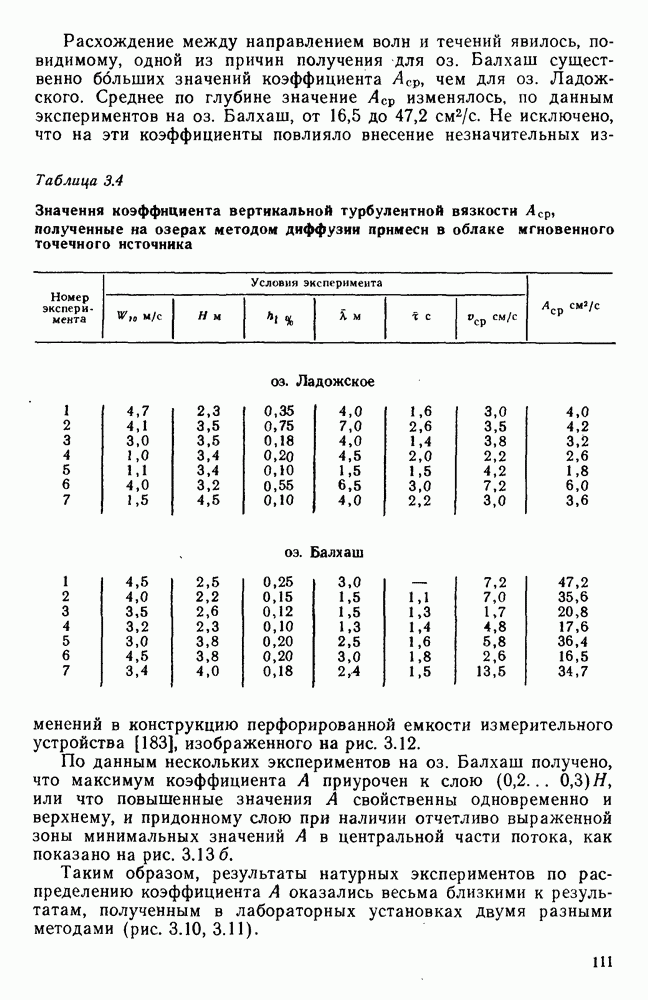
- 3.9. Коэффициенты вертикальной турбулентной вязкости и методы их оценки
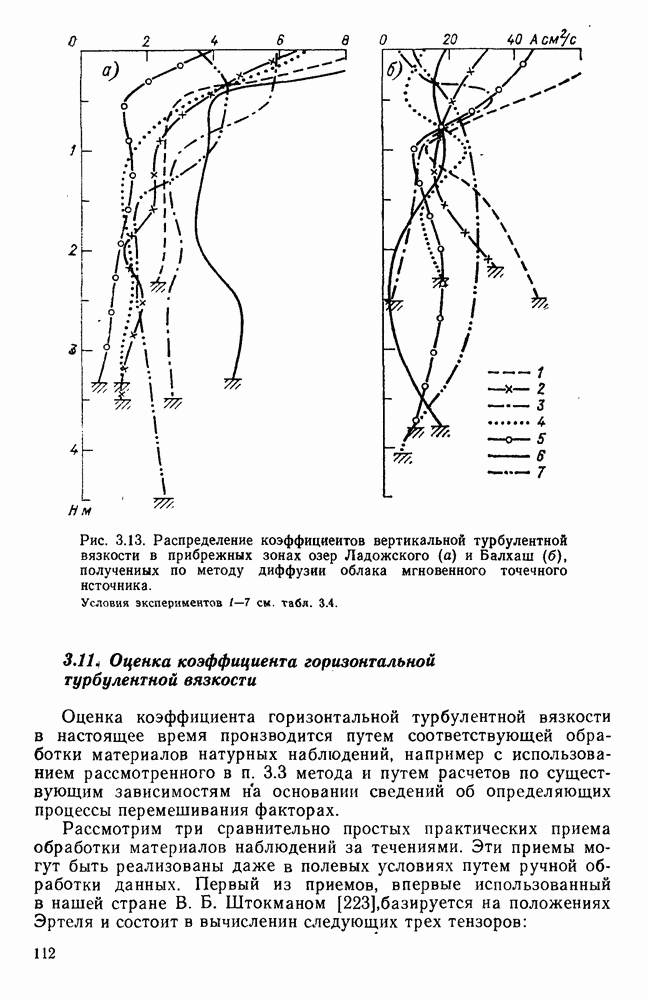
- 3.10. Распределение коэффициента вертикальной турбулентной вязкости
- 3.11. Оценка коэффициента горизонтальной турбулентной вязкости
- Глава 4. ВЕТРОВЫЕ ТЕЧЕНИЯ В УСЛОВИЯХ РАЗВИТИЯ И СТАБИЛИЗАЦИИ
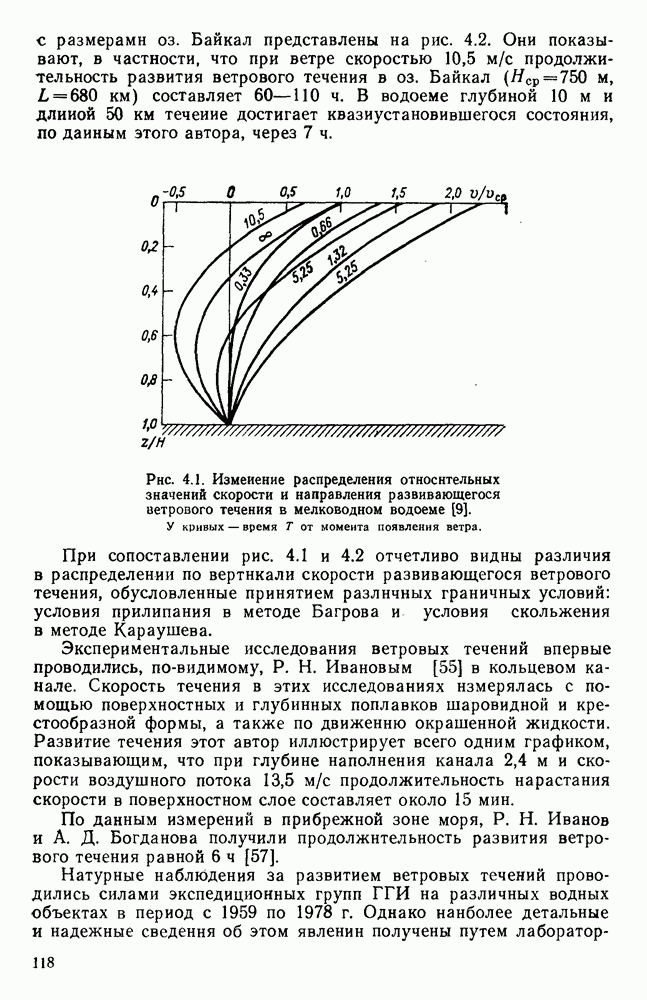
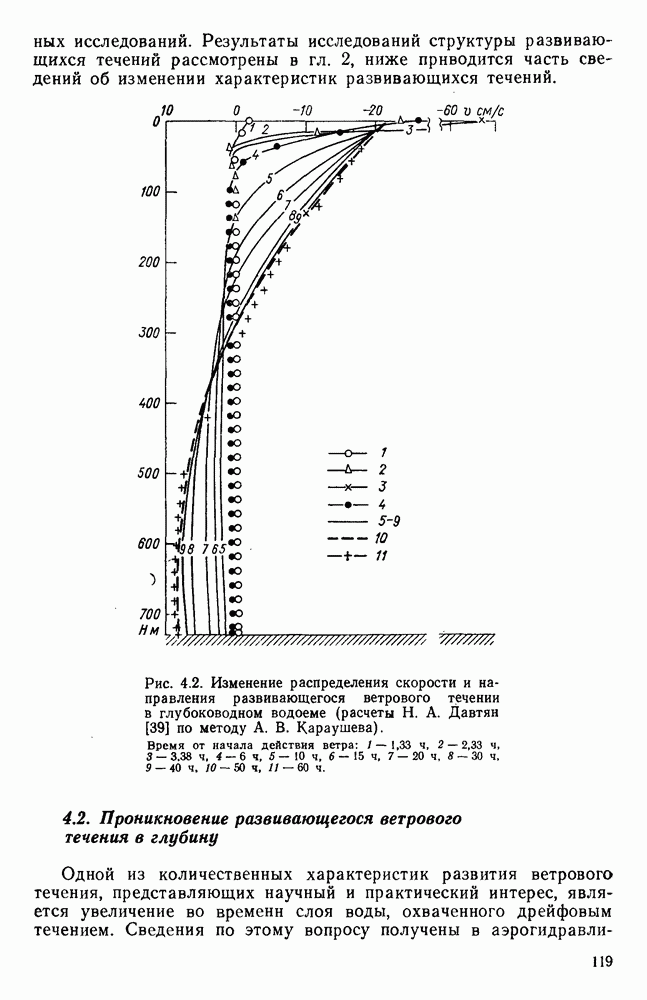
- 4.1. Совершенствование представлений о развитии ветровых течений
- 4.2. Проникновение развивающегося ветрового течения в глубину
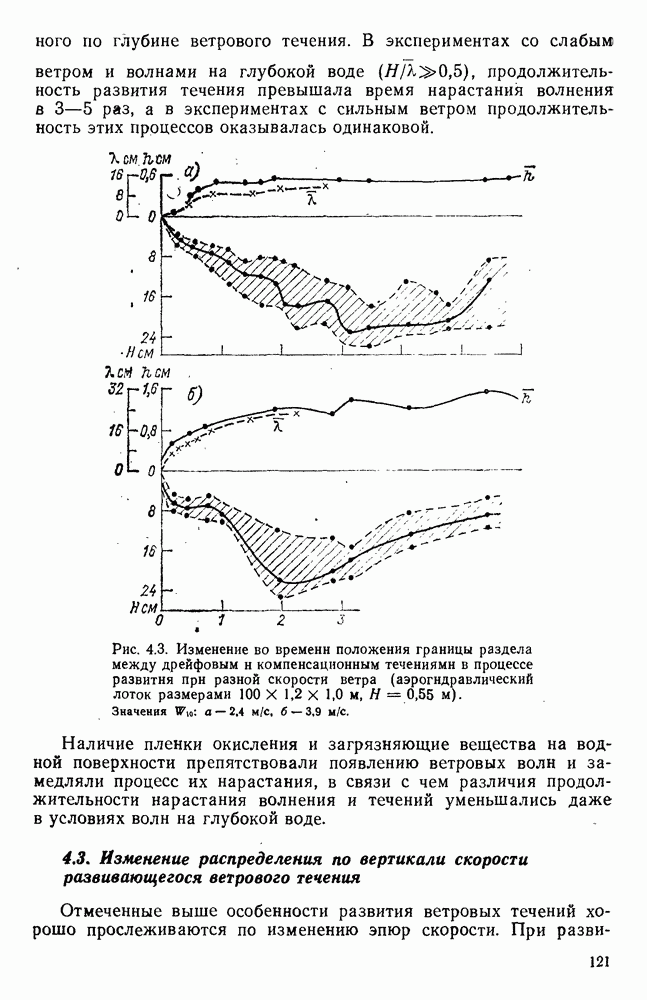
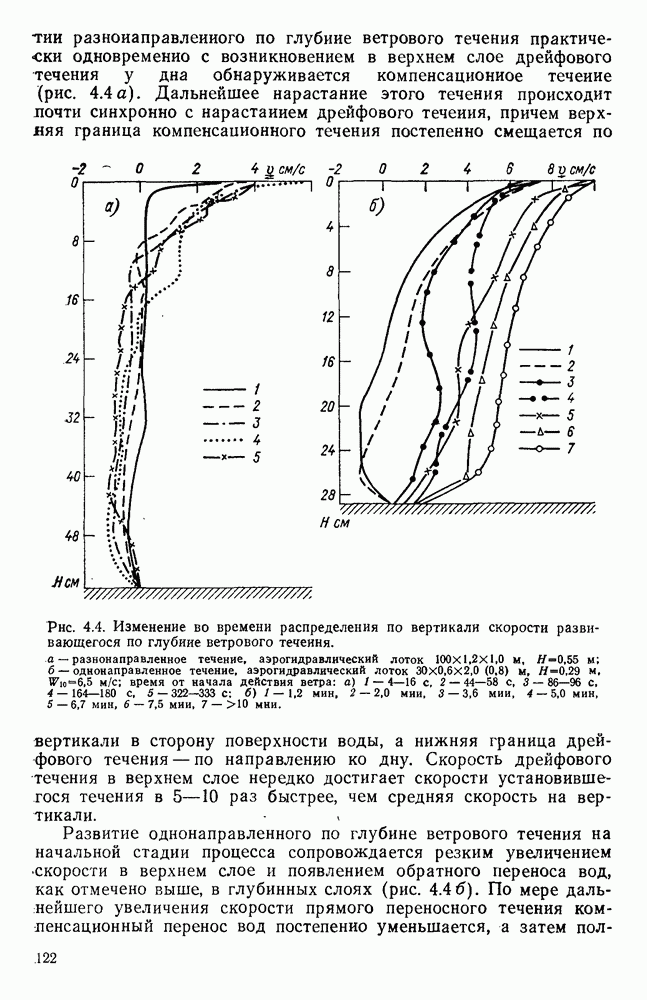
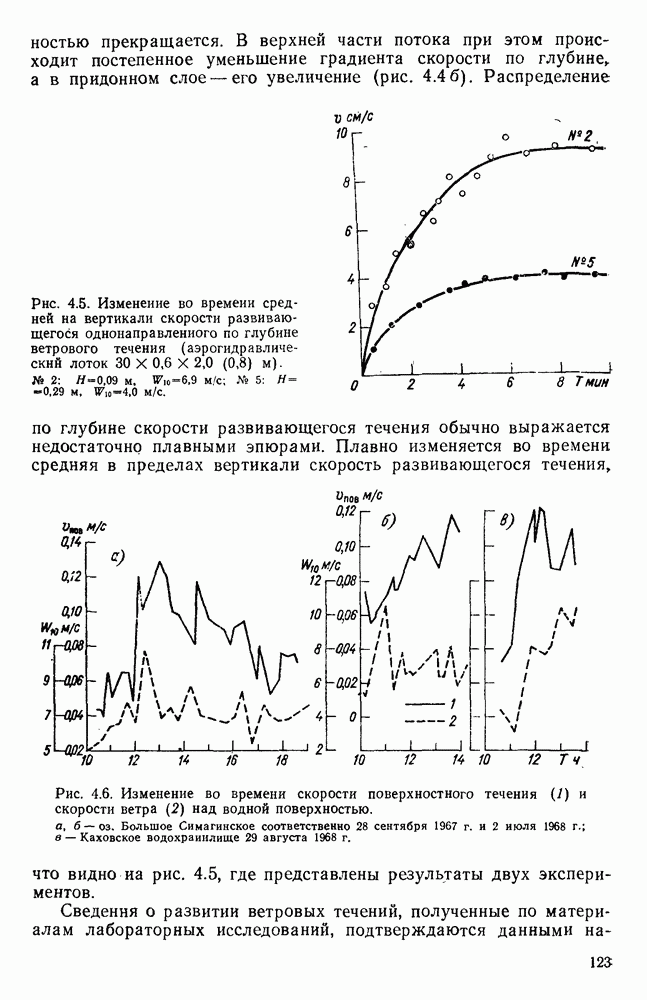
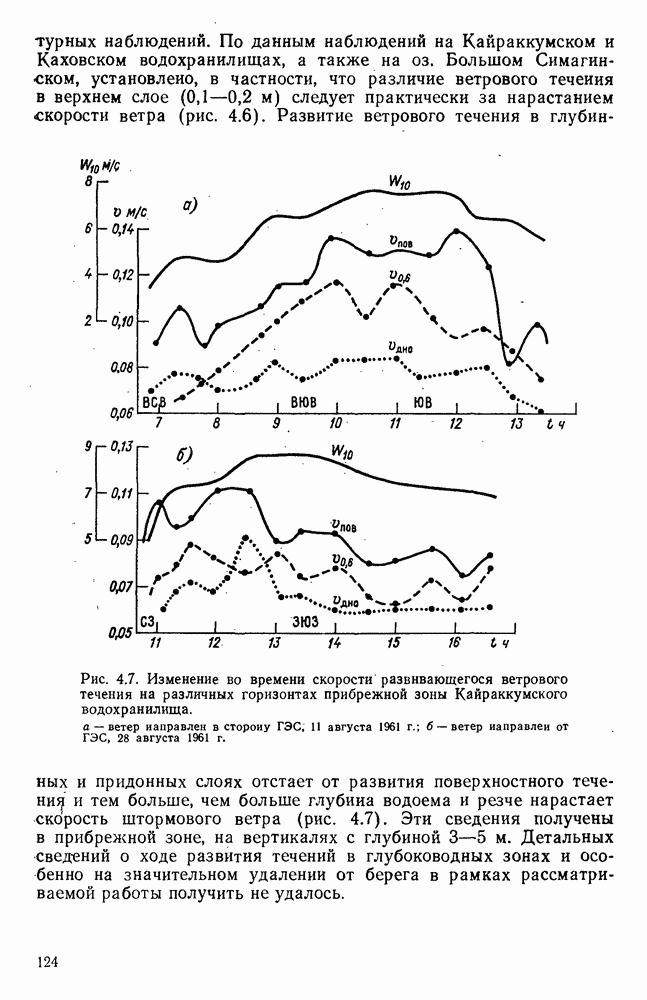
- 4.3. Изменение распределения по вертикали скорости развивающегося ветрового течения
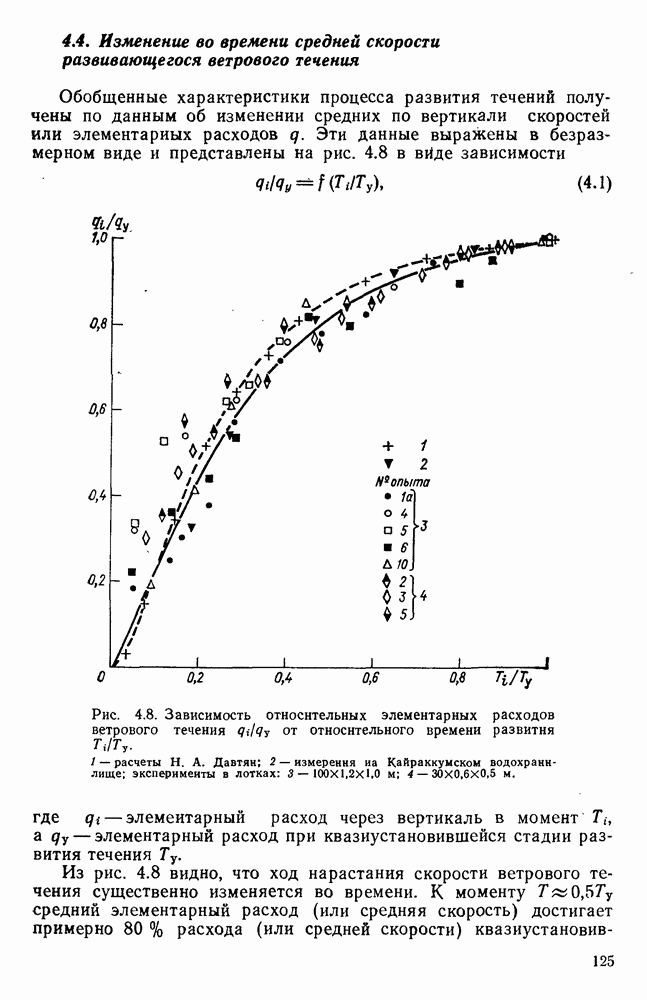
- 4.4. Изменение во времени средней скорости развивающегося ветрового течения
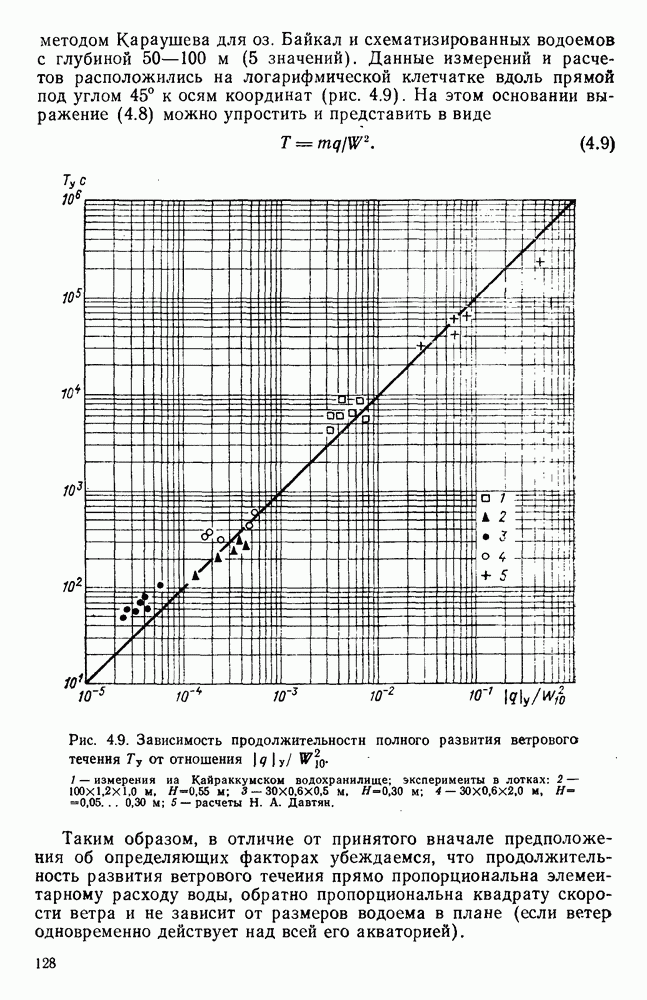
- 4.5. Продолжительность развития ветрового течения
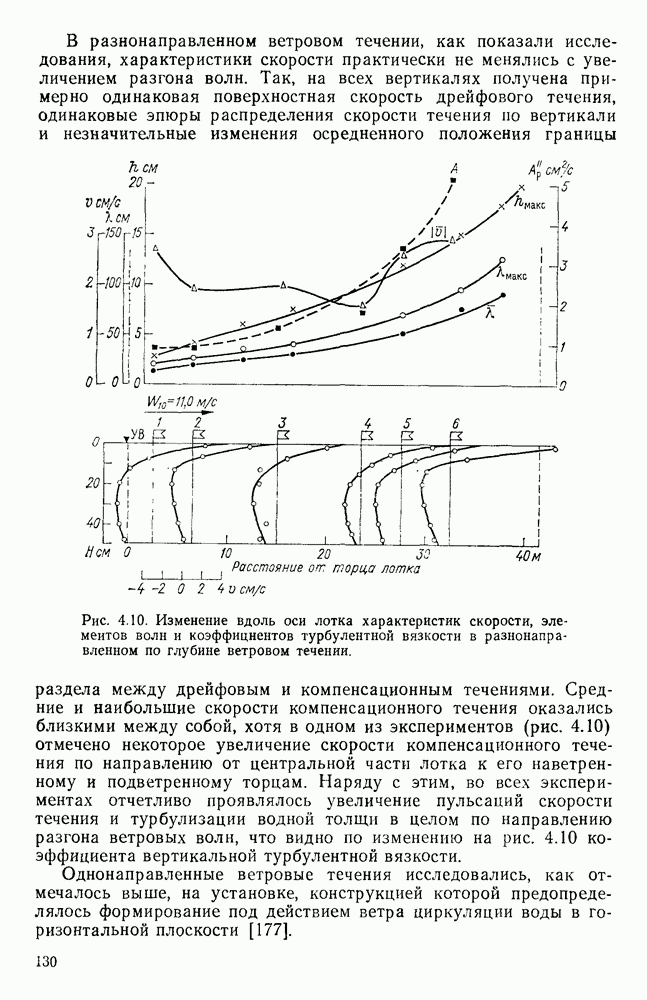
- 4.6. Изменение скорости ветрового течения по пути разгона волн
- 4.7. Соотношение между скоростями ветрового течения и ветра
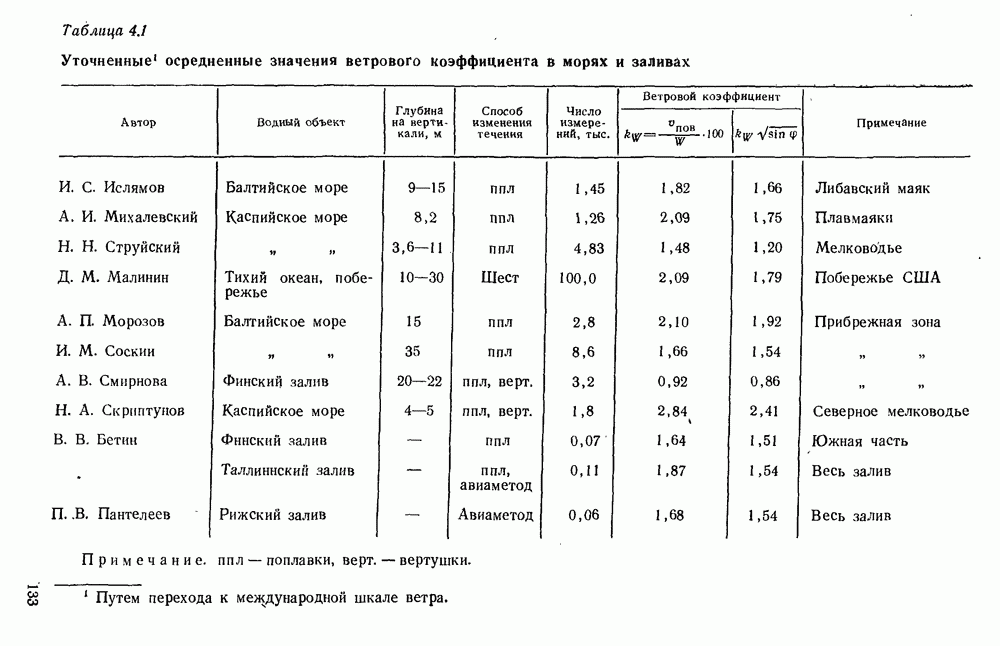
- 4.7.2. Ветровой коэффициент для прибрежных зон морей и океанов
- 4.7.3. Ветровой коэффициент для морских заливов
- 4.7.4. Ветровой коэффициент для внутренних водоемов
- 4.8. Оценка влияния на поверхностное ветровое течение глубины и шероховатости дна водоема
- 4.9. Предельное проникновение ветрового течения в глубину
- 4.10. Отклонения направлений ветровых течений от направления ветра
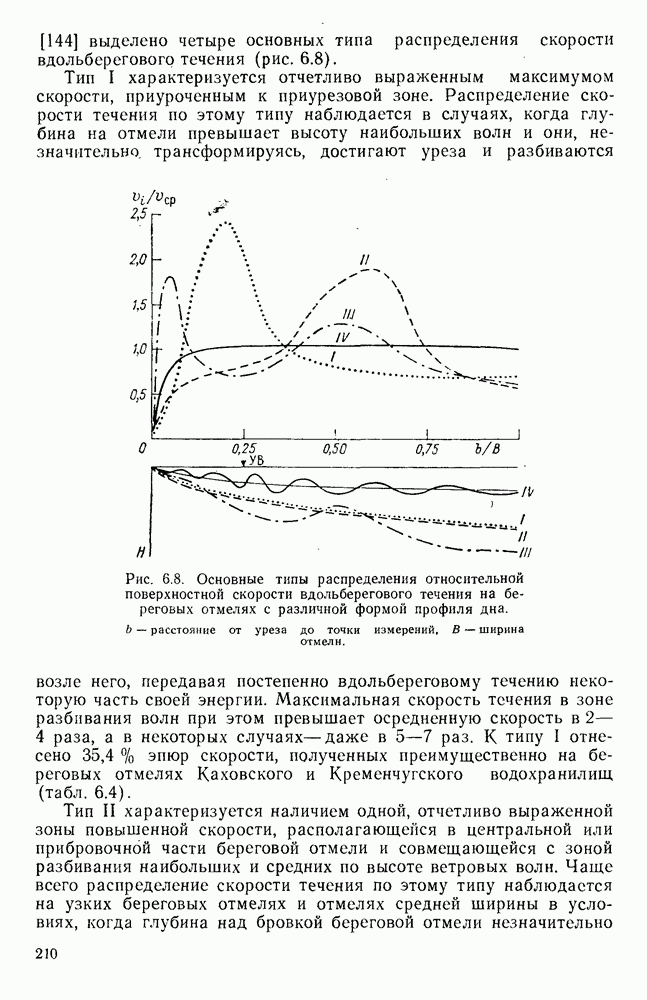
- 4.11. Теоретические решения задачи о вертикальном распределении скорости ветровых течений
- 4.12. Распределение скорости квазиустановившихся ветровых течений по данным экспериментов
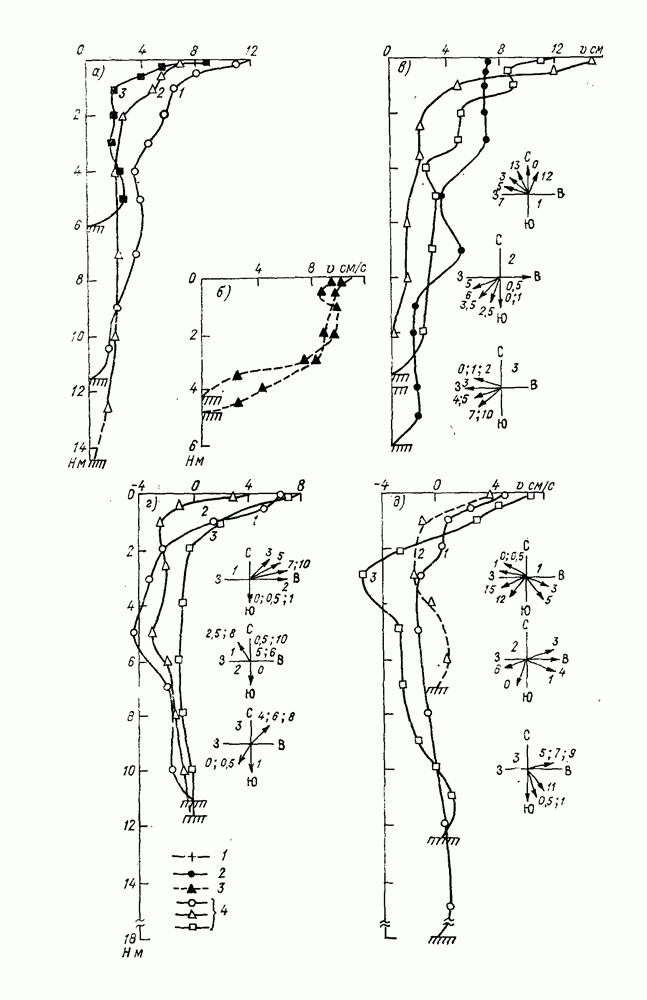
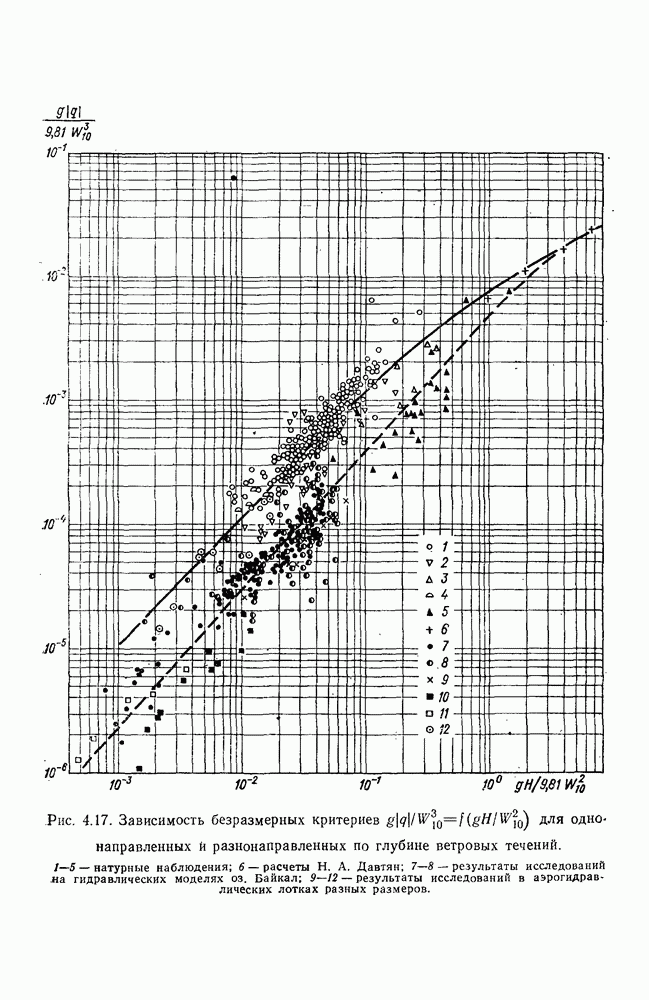
- 4.13. Перенос вод через вертикаль
- 4.14. Взаимодействие ветровых, стоковых и сейшевых течений
- 4.15. Соотношение переносов воды дрейфовым и волновым течениями
- 4.16. Установление режимных статистических характеристик течений
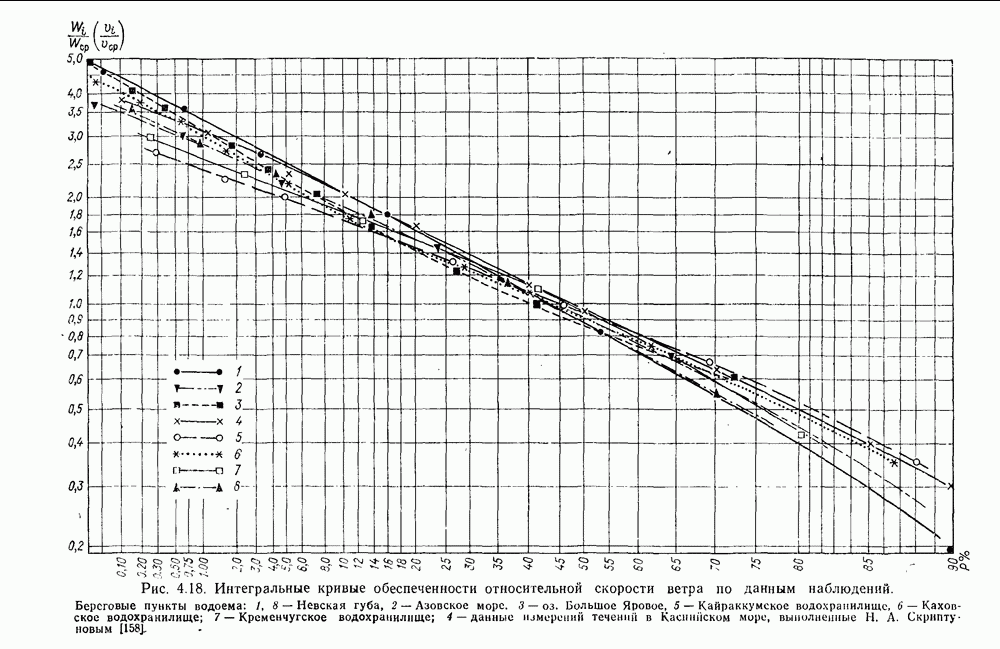
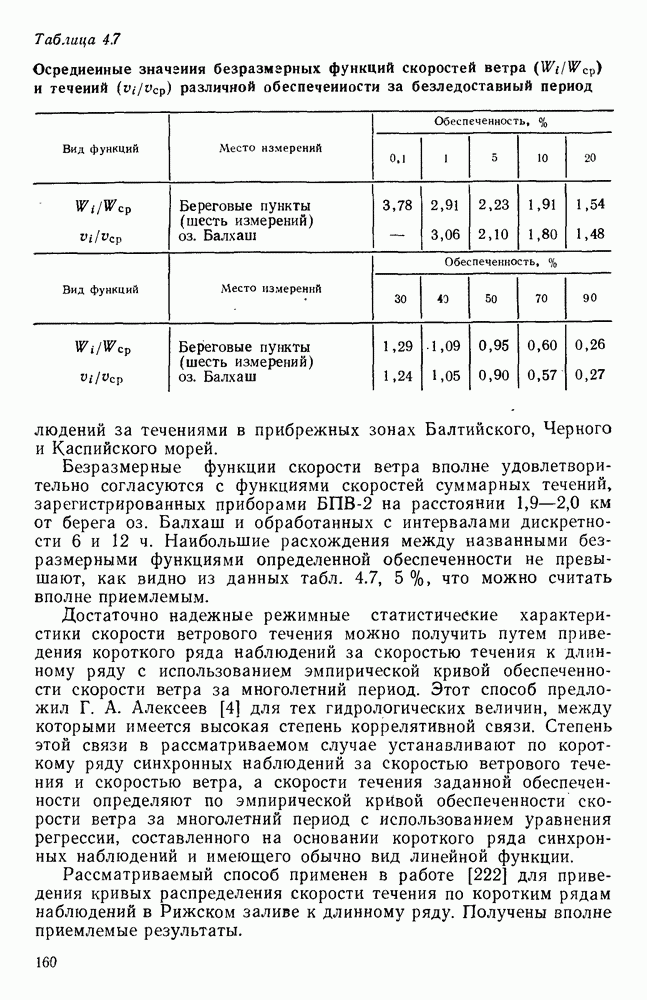
- 4.16.2. Выбор функций распределения скорости течения при ограниченных данных наблюдений
- 4.17. Внутренний водообмен при ветровых течениях
- 4.18. Моделирование ветровых течений
- 4.18.2. Математические модели течений и примеры их реализации
- 4.18.3. Физическое моделирование
- Глава 5. СЕЙШЕВЫЕ ТЕЧЕНИЯ
- 5.1. Основные черты и особенности сейшевых течений
- 5.2. Методы оценки скорости сейшевого течения
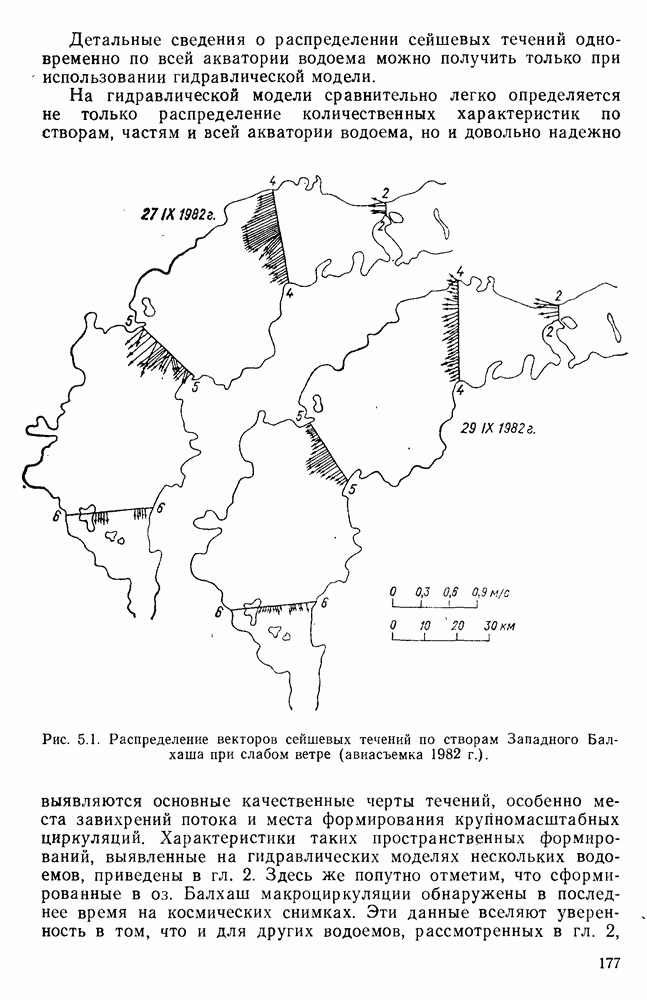
- 5.3. Распределение сейшевых течений по акватории водоема
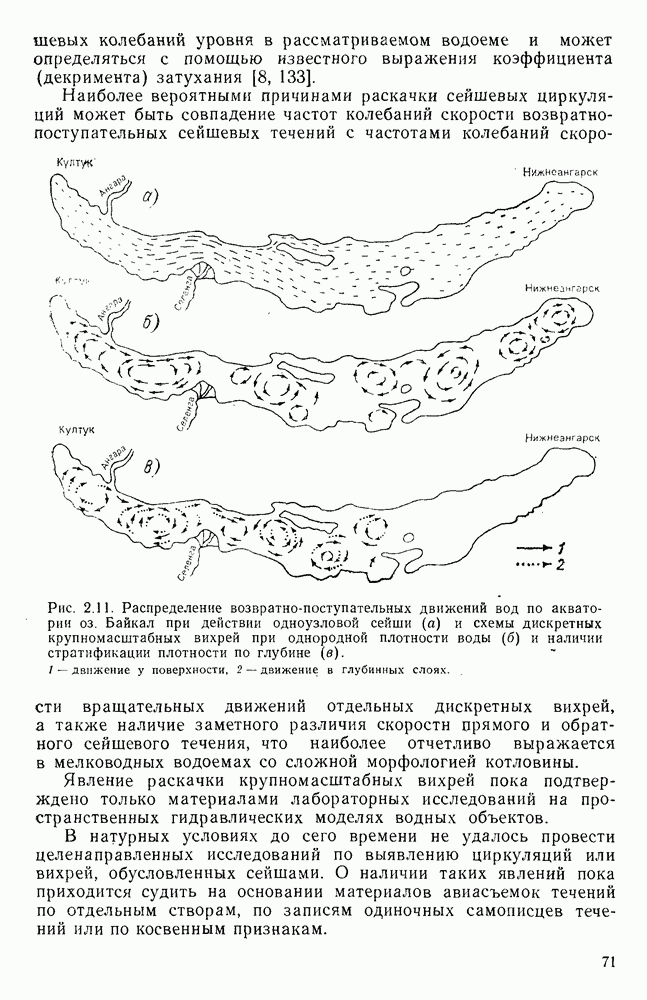
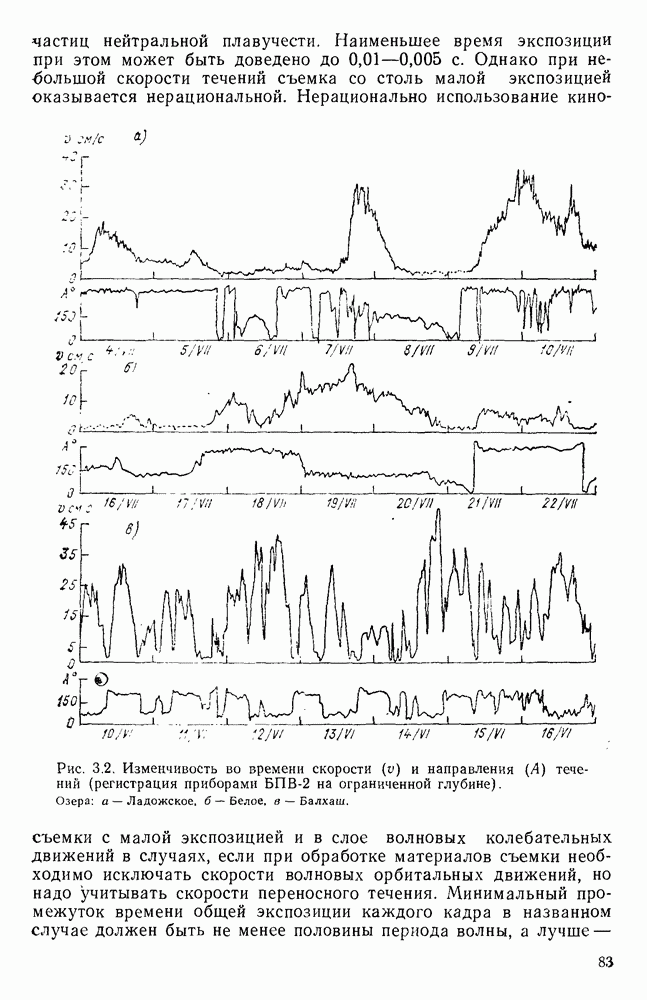
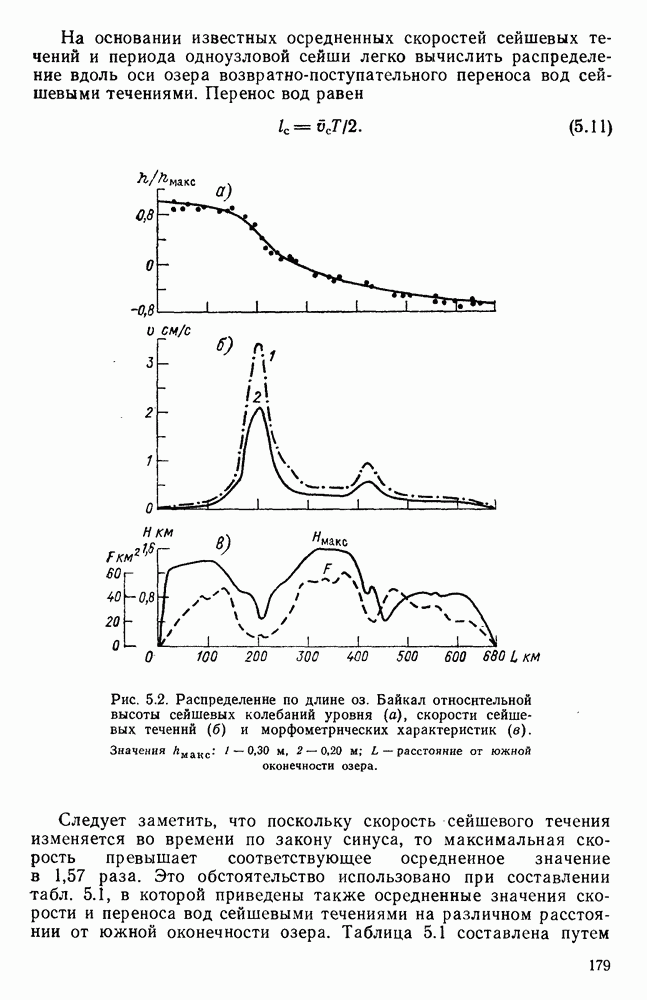
- 5.4. Сейшевые течения в оз. Байкал
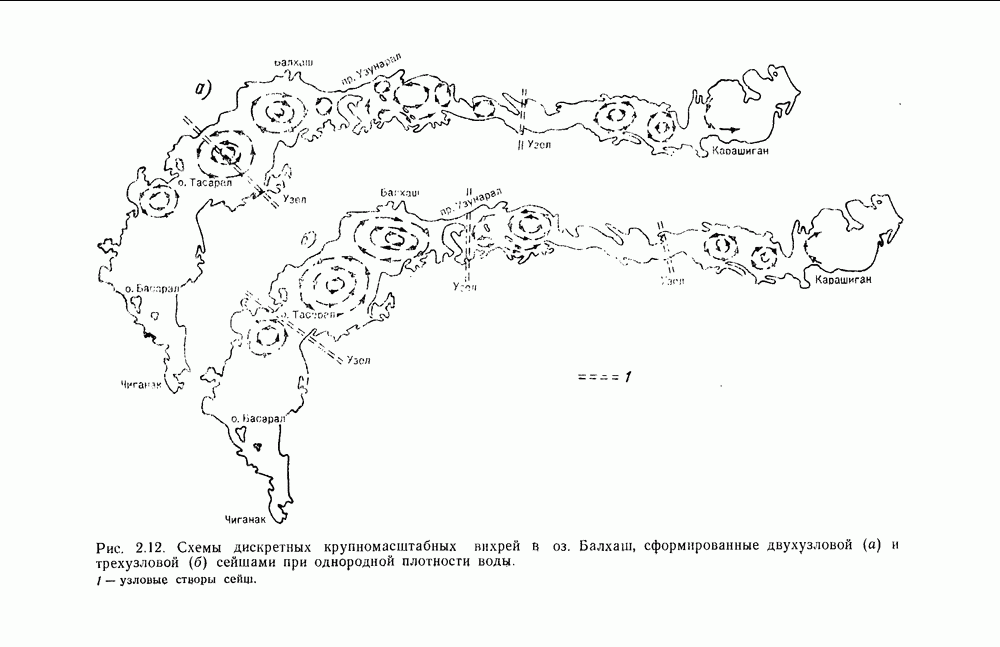
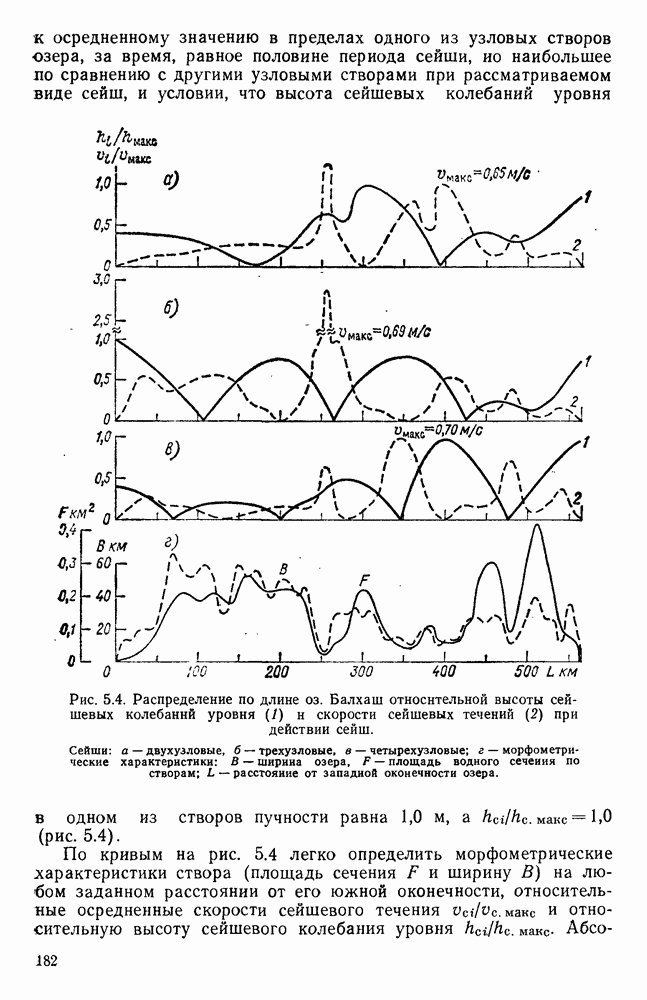
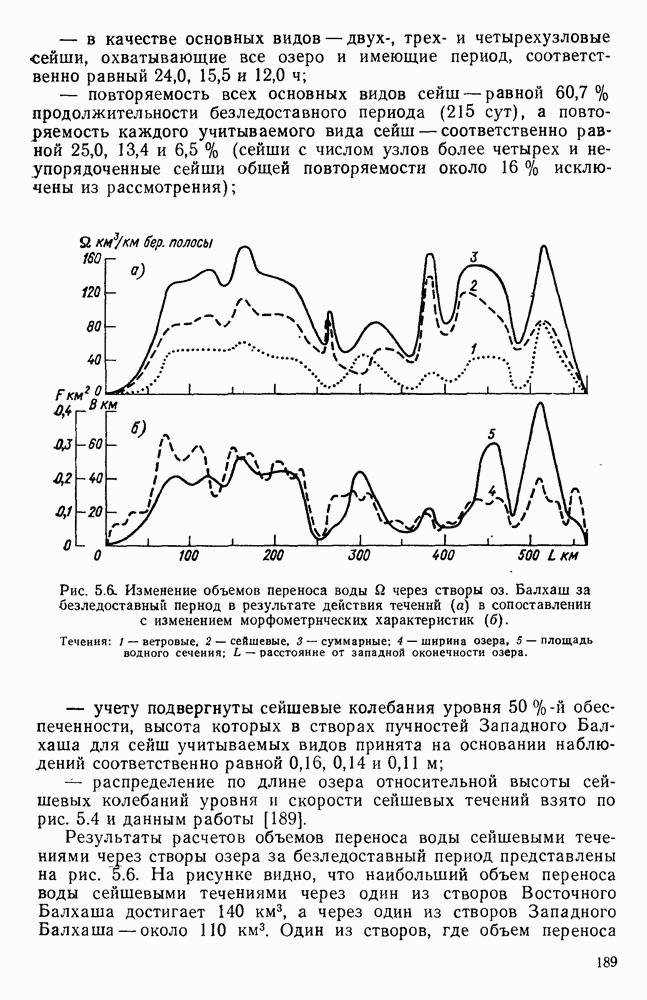
- 5.5. Сейшевые течения в оз. Балхаш
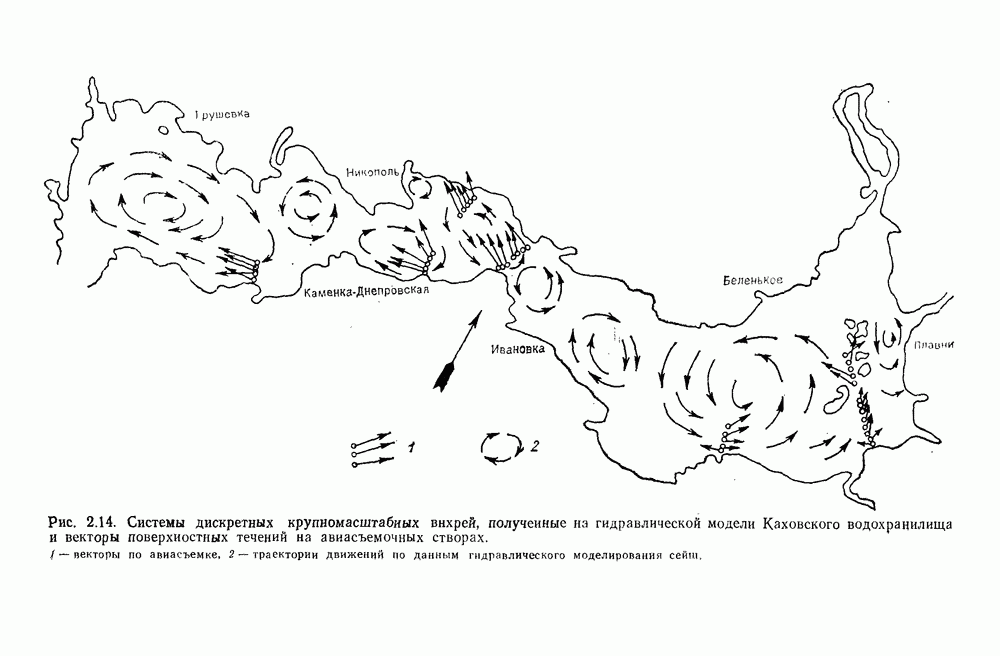
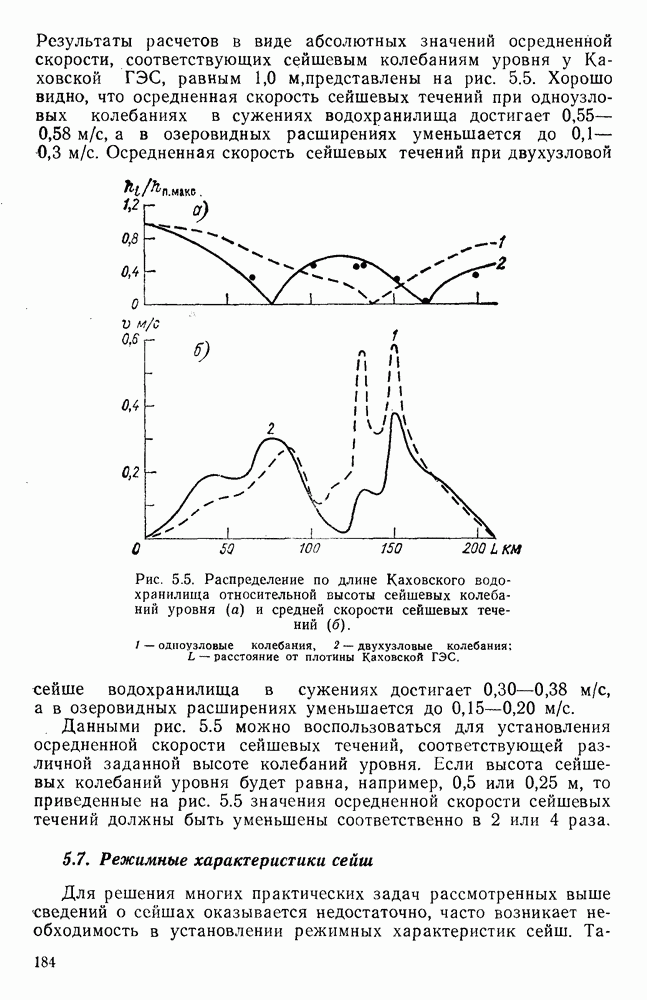
- 5.6. Сейшевые течения в Каховском водохранилище
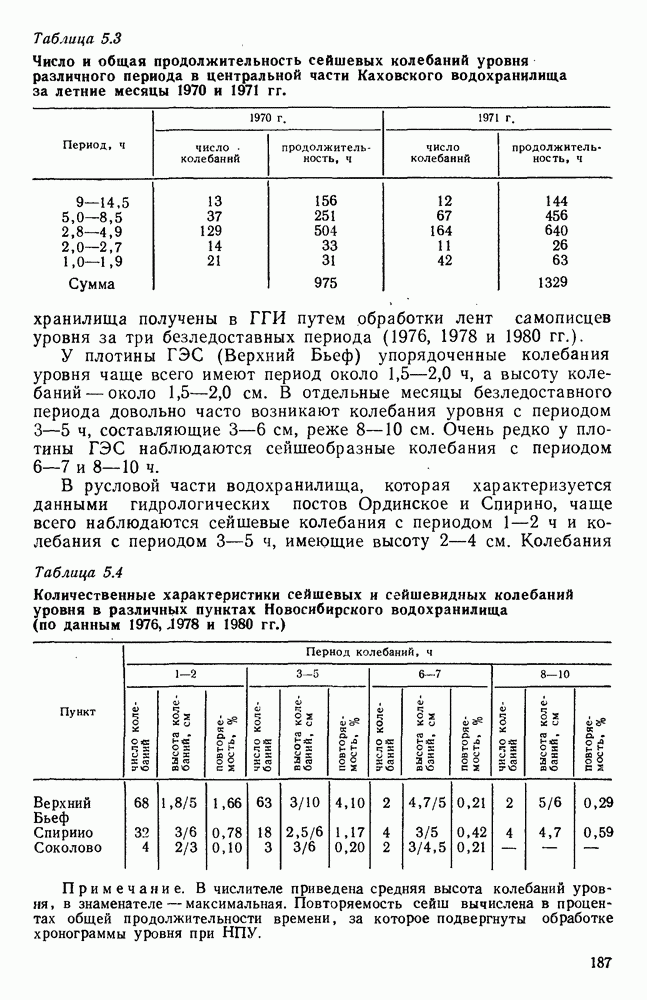
- 5.7. Режимные характеристики сейш
- 5.8. Объемы переноса вод сейшевыми течениями
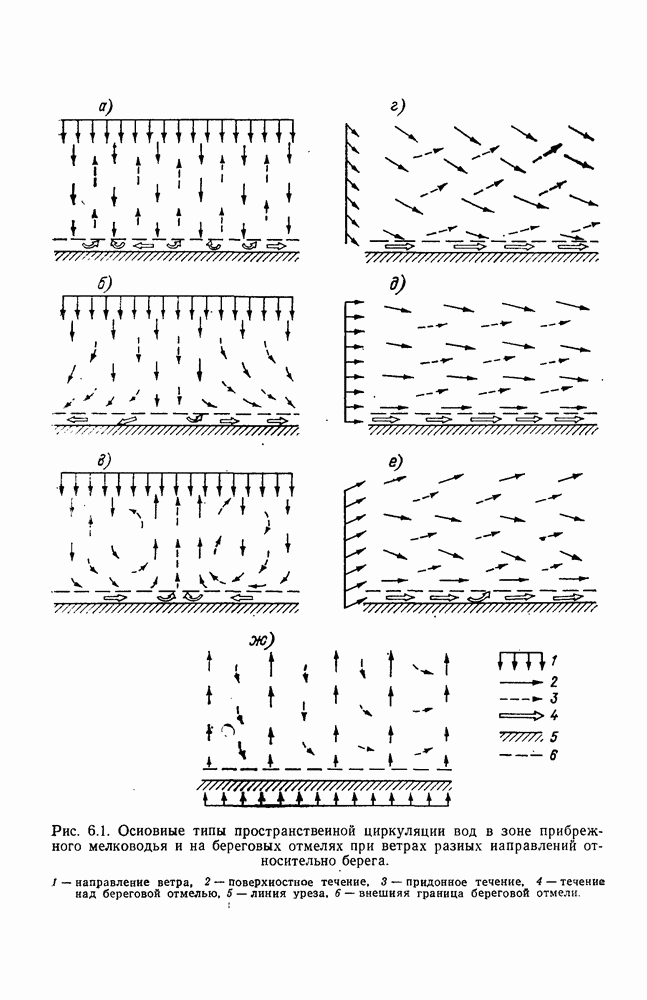
- Глава 6. ТЕЧЕНИЯ В ЗОНЕ ПРИБРЕЖНОГО МЕЛКОВОДЬЯ И НА БЕРЕГОВЫХ ОТМЕЛЯХ
- 6.2. Течения в зоне прибрежного мелководья
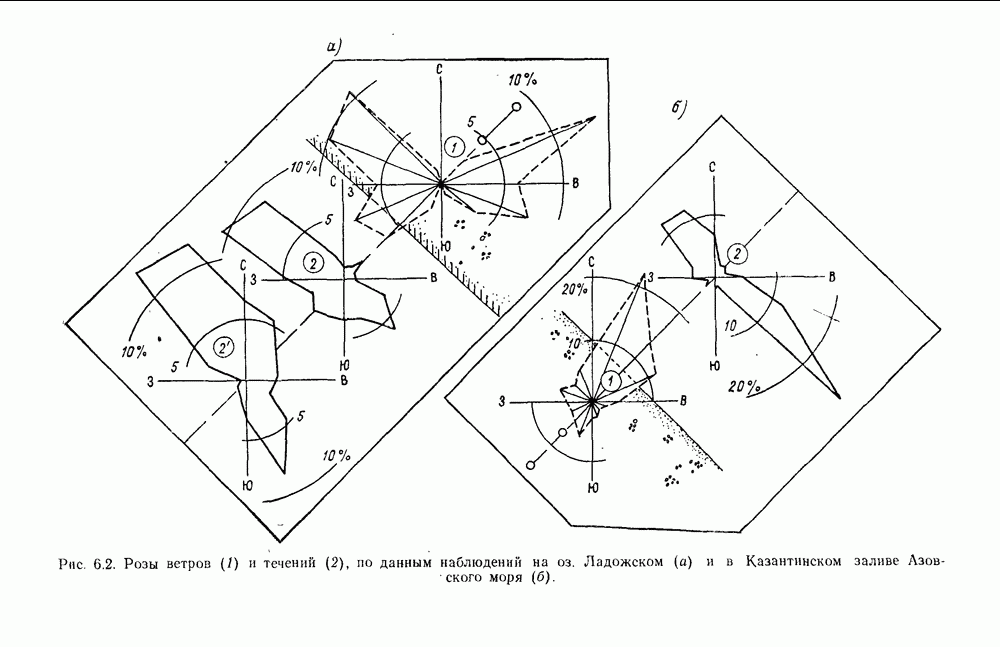
- 6.2.2. Повторяемость различных типов циркуляции вод
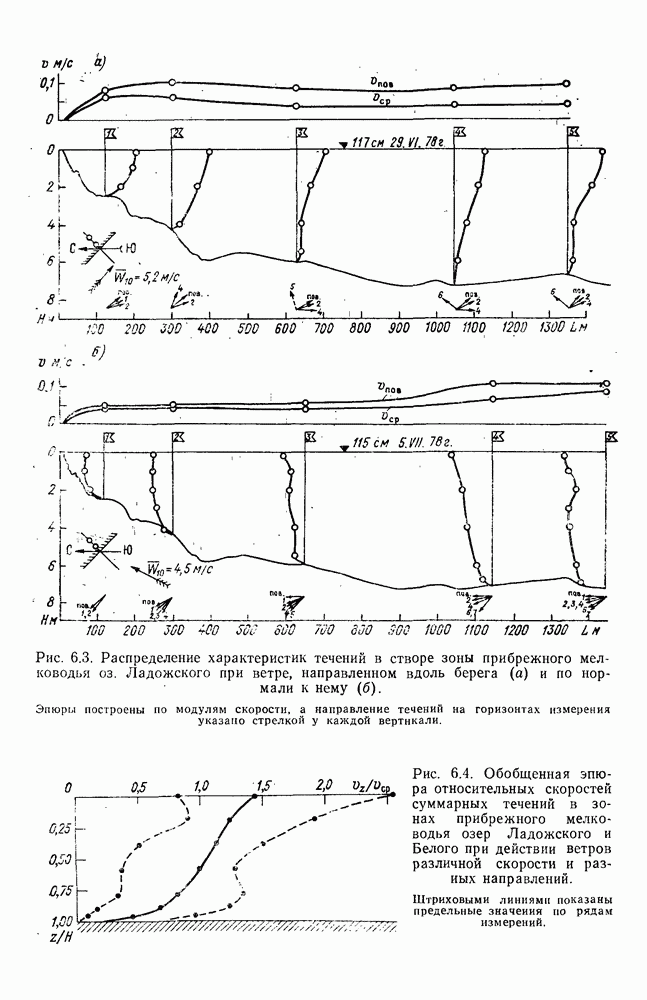
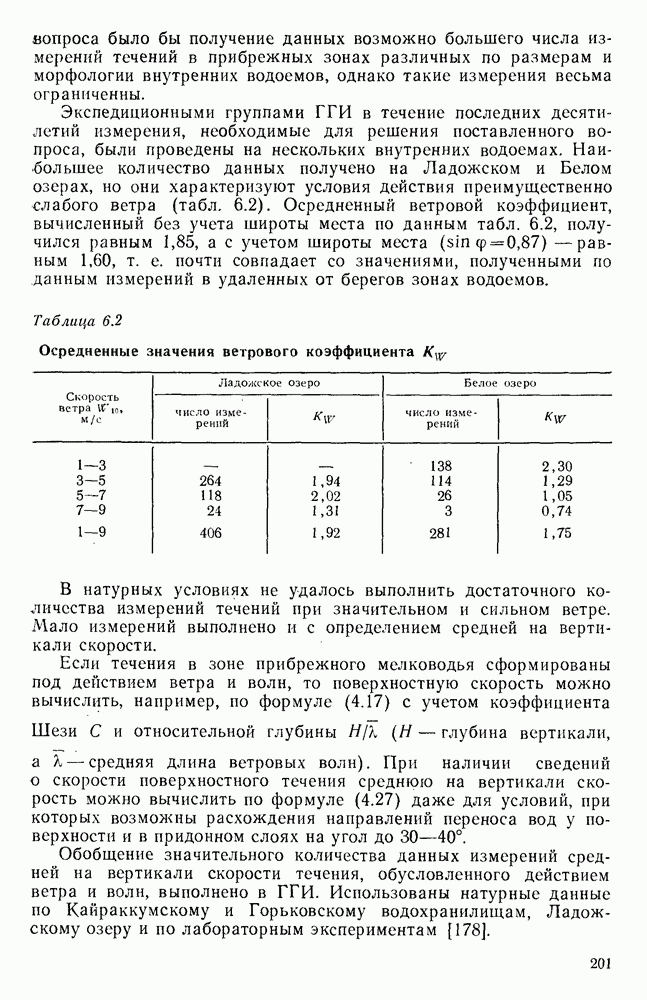
- 6.2.3. Распределение скорости течения по глубине
- 6.2.4. Изменение скорости течения по ширине зоны
- 6.2.5. Количественные характеристики скорости течения
- 6.2.6. Режимные статистические характеристики скорости течений
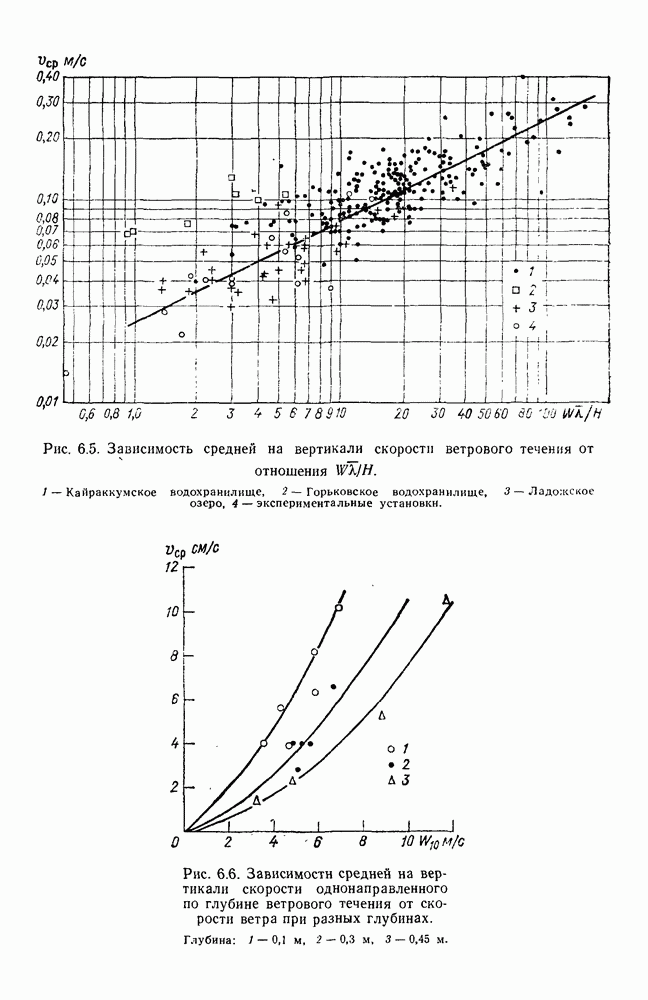
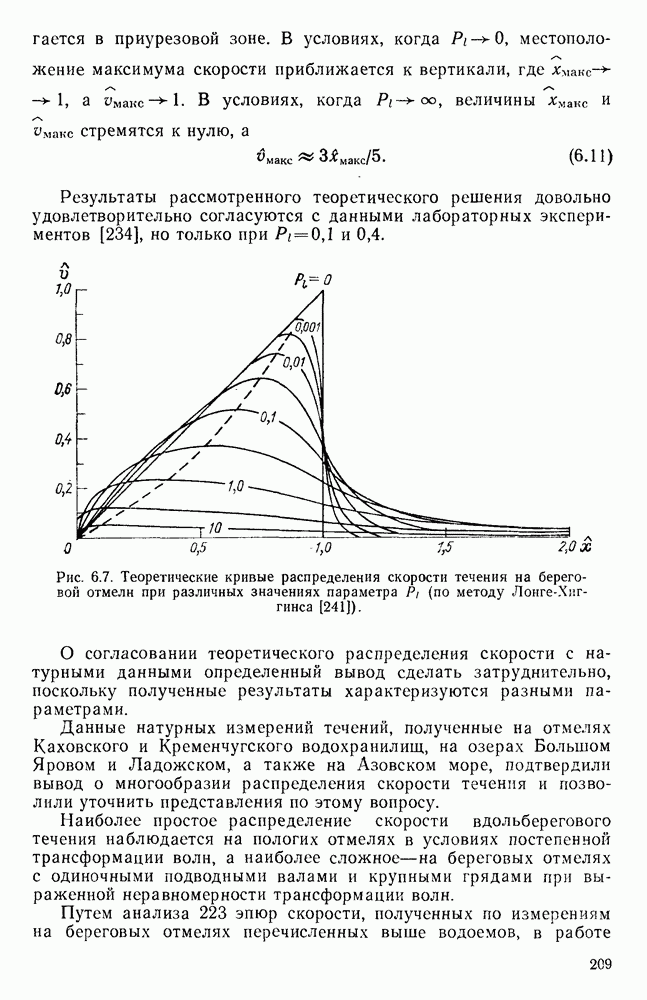
- 6.3. Течения на береговых отмелях
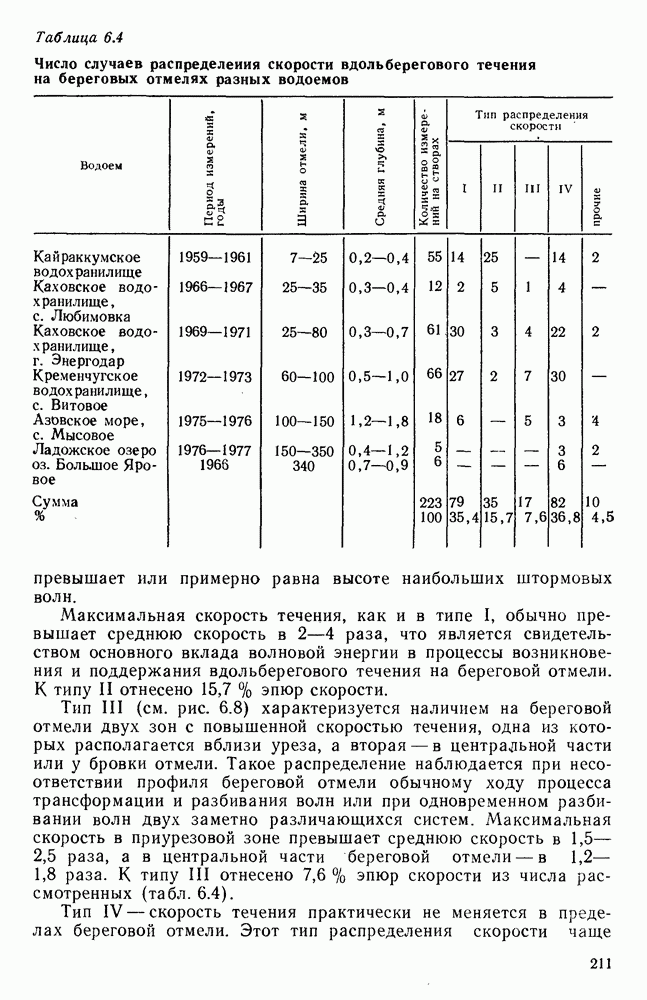
- 6.3.2. Распределение скорости вдольберегового течения
- 6.3.3. Расчет средней скорости вдольберегового течения
- Глава 7. ПЕРЕМЕЩЕНИЕ НАНОСОВ НА БЕРЕГОВЫХ ОТМЕЛЯХ
- 7.2. Методы изучения перемещения наносов
- 7.3. Основные черты механизма перемещения наносов
- 7.4. Распределение мутности воды по вертикали
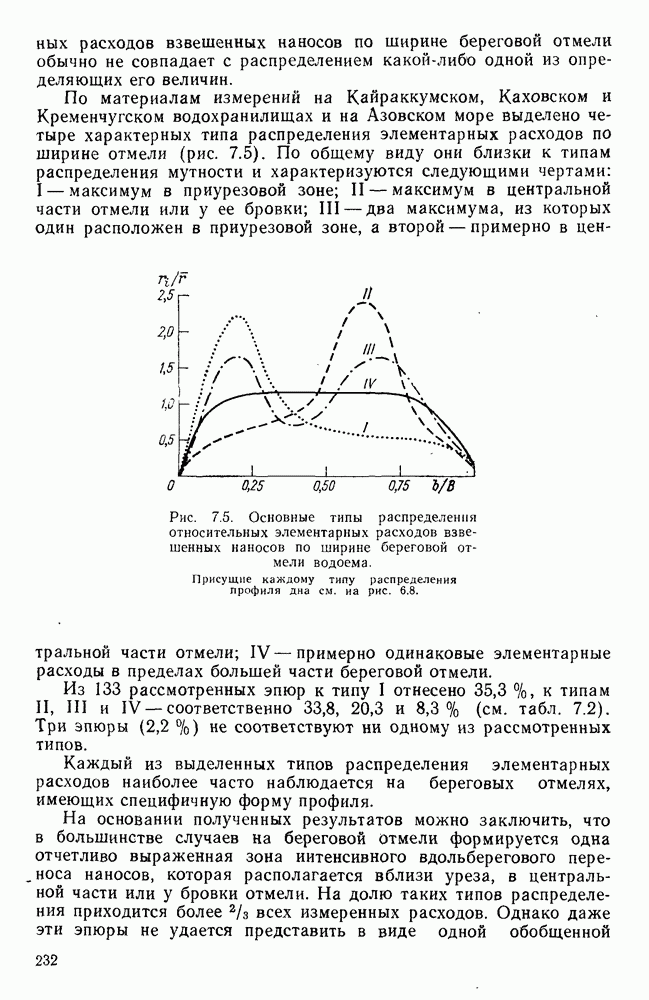
- 7.5. Распределение мутности воды по ширине береговой отмели
- 7.6. Связь придонной и поверхностной мутности со средней мутностью
- 7.7. Элементарные расходы взвешенных наносов
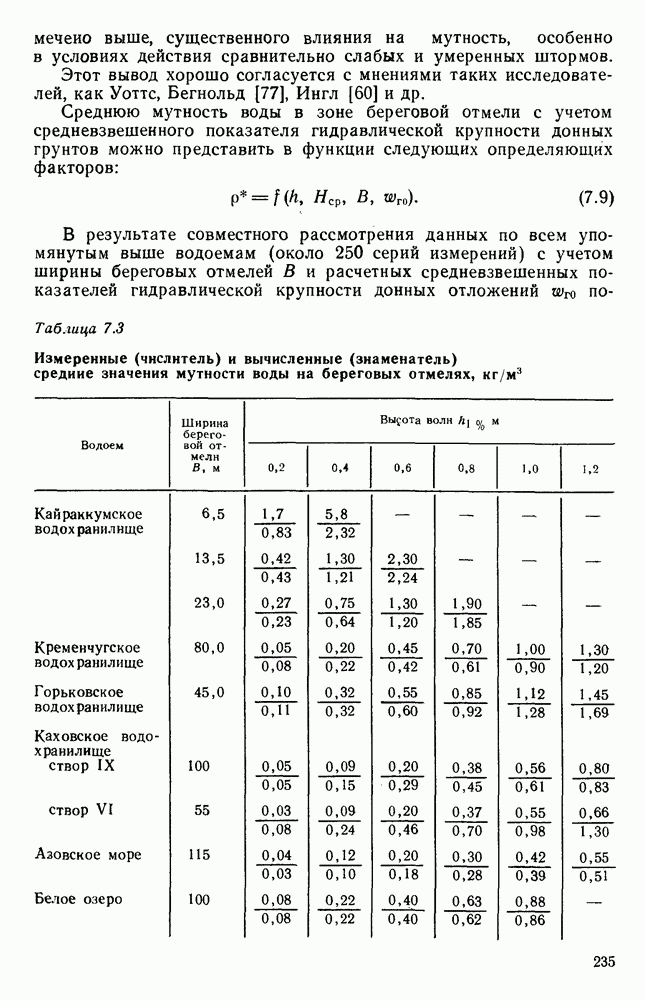
- 7.8. Зависимость средней мутности от определяющих факторов
- 7.9. Расходы донных наносов и их связь со взвешенными наносами
- 7.10. Расчет вдольберегового переноса твердого материала
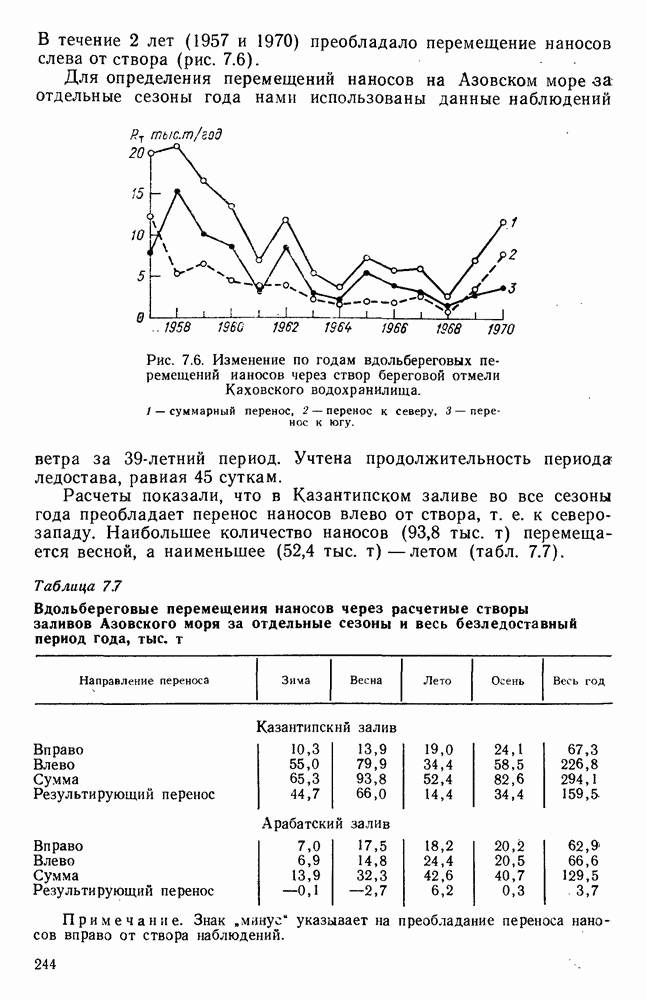
- 7.11. Сезонная и межгодовая изменчивость вдольбереговых перемещений наносов