| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.18.3. Физическое моделирование
Использования физических моделей для изучения циркуляции жидкости в результате действия различных факторов были начаты очень давно. Однако разнообразные целенаправленные исследования ветровых течений в бассейнах, каналах и на пространственных моделях водных объектов были развернуты в нашей стране лишь в послевоенные годы [38] и продолжаются до наших дней. Методика этих исследований непрерывно совершенствуется. В исследованиях ветровых течений, проводившихся Р. Н.
Ивановым [55] в круговом штормовом бассейне Морского гидрофизического института АН СССР, и в исследованиях Е. Г. Никифорова [131], проводившихся в остекленном лотке, скорость течения измерялась по движению глубинных и поверхностных поплавков, а в более поздних исследованиях экспериментаторами использовались, как отмечалось выше, более совершенные измерительные средства: гидрометрические вертушки, турбулиметры, термоанемометры и др.
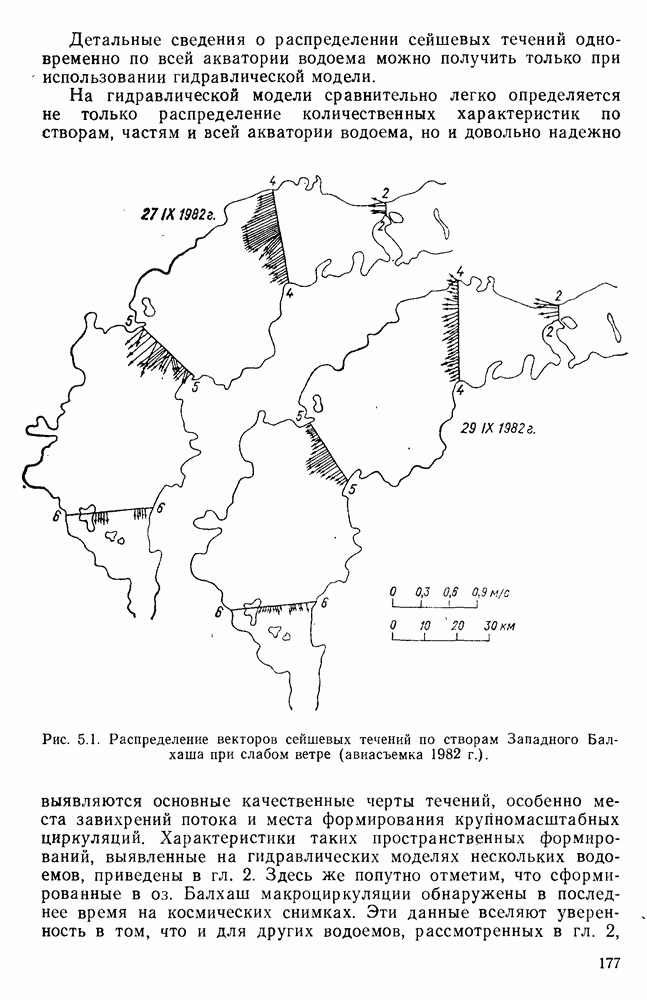
Очень важные сведения о ветровых и сейшевых течениях получены на пространственных физических моделях конкретных водоемов.
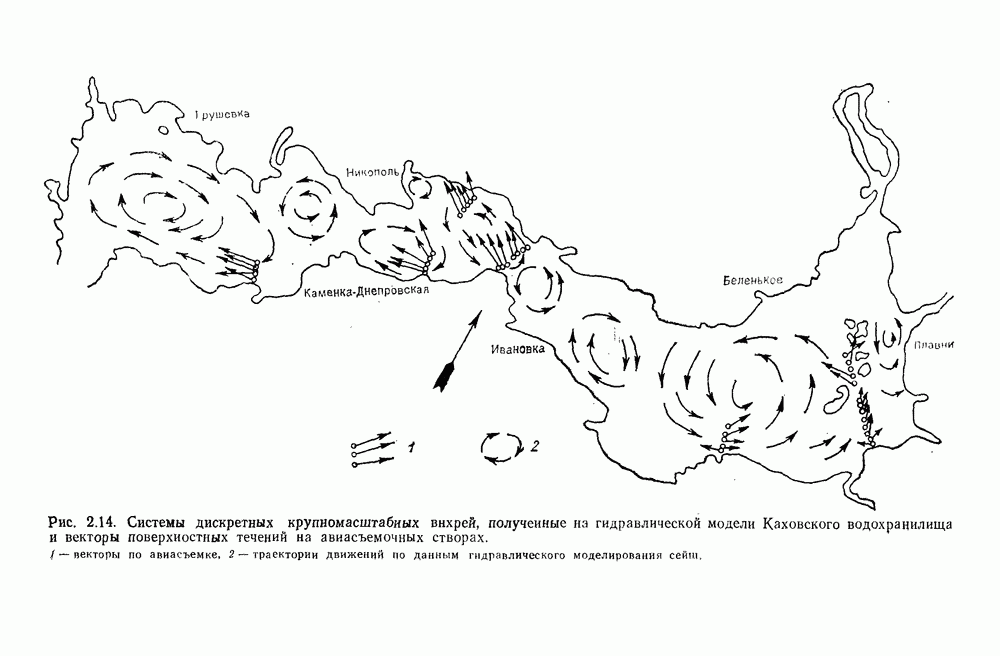
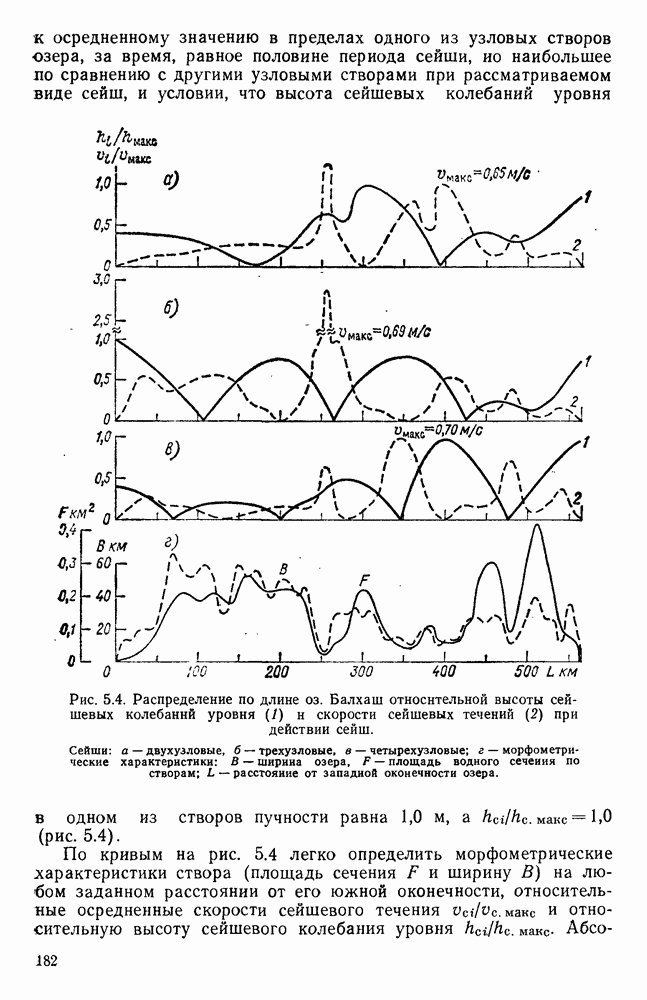
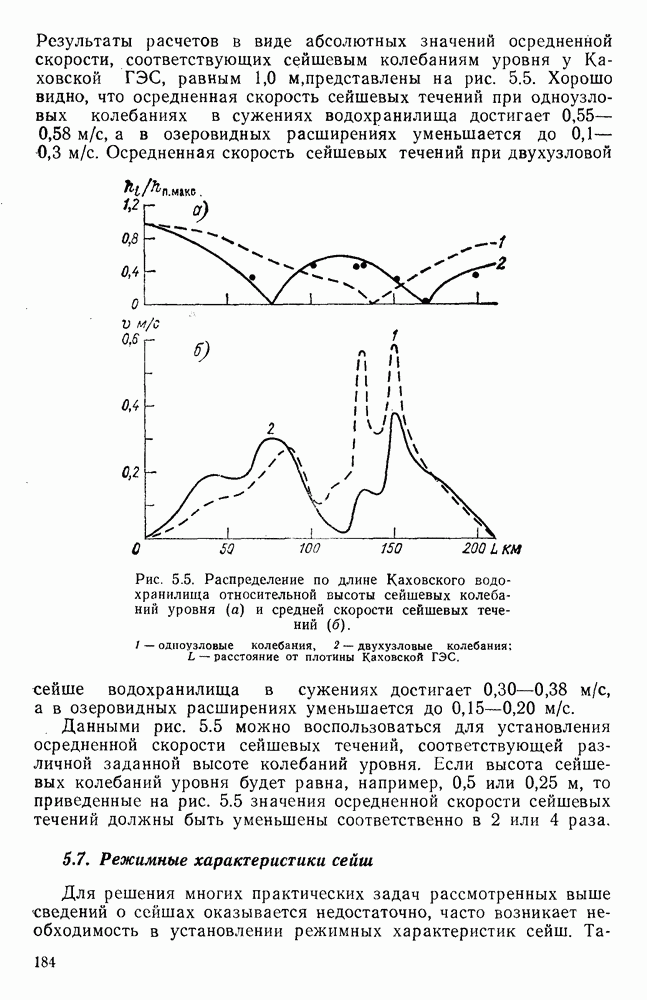
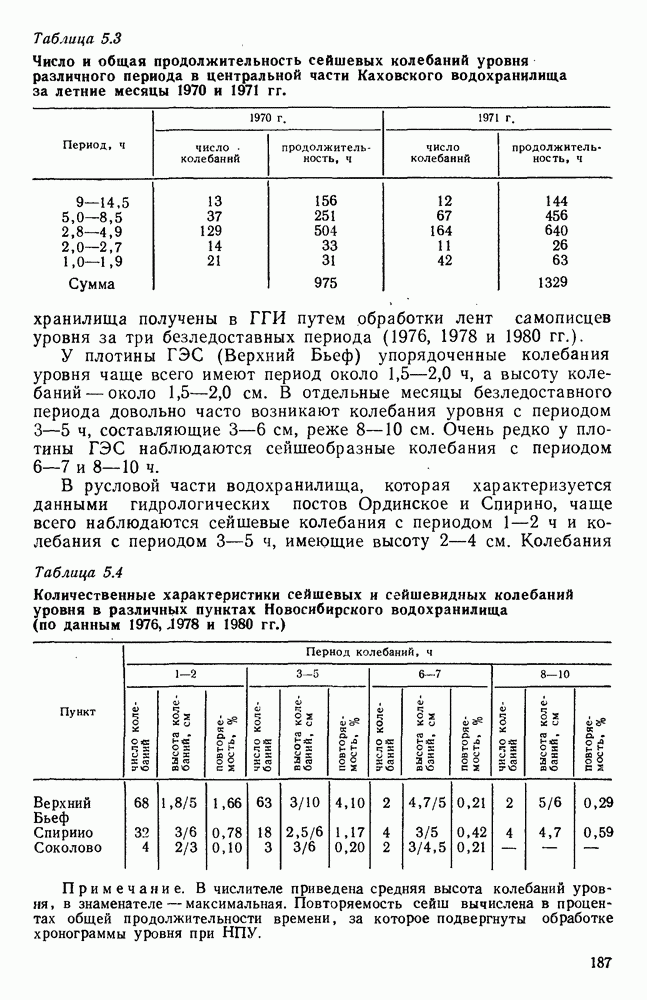
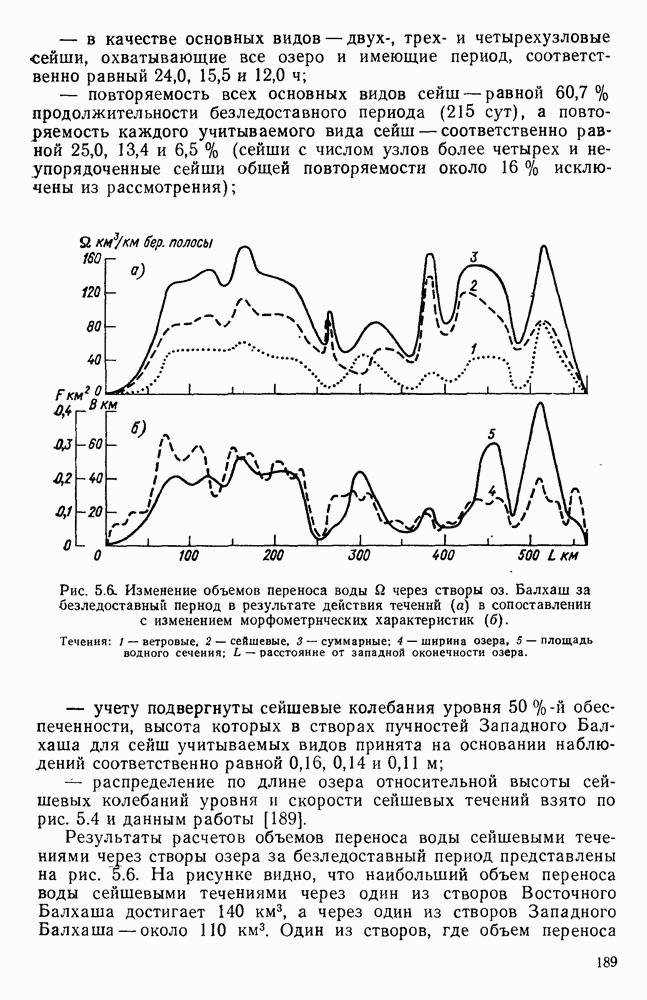
В ГГИ, в частности, такие исследования выполнялись на пространственных моделях озер Байкал [37, 171], Балхаш [181, 189], Лукомльского [54]; на моделях водохранилищ [184] и заливов (Финского и Рижского) [57] и других водных объектов. По материалам этих исследований получены такого рода сведения, которые не удавалось получить длительное время ни в натурных условиях, ни путем математического моделирования.
Для обеспечения физического моделирования ветровых течений необходимо располагать следующими сведениями: подводным рельефом котловины в виде плана или карты; схемой характерных полей ветра над водоемом в безледоставный период; таблицей по вторяемостей ветра различной скорости по направлениям; схемой ветровых течений и режимными характеристиками течений в отдельных частях водоема.
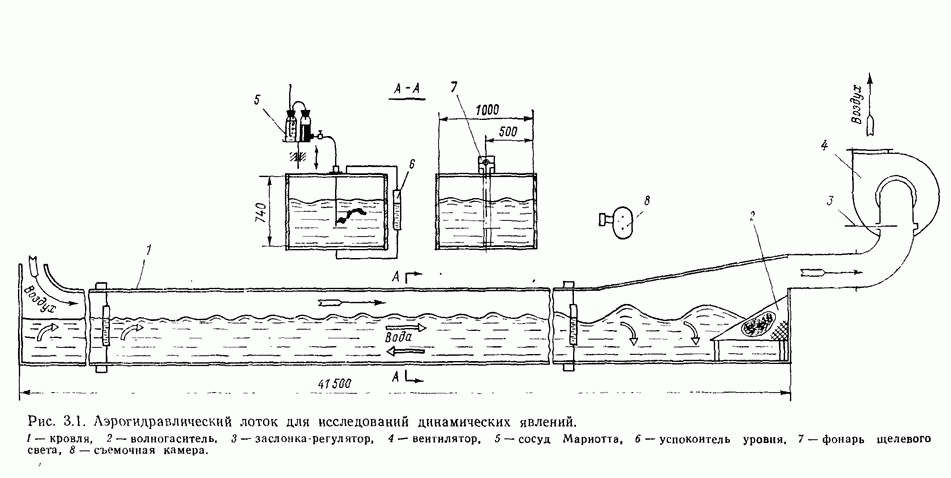
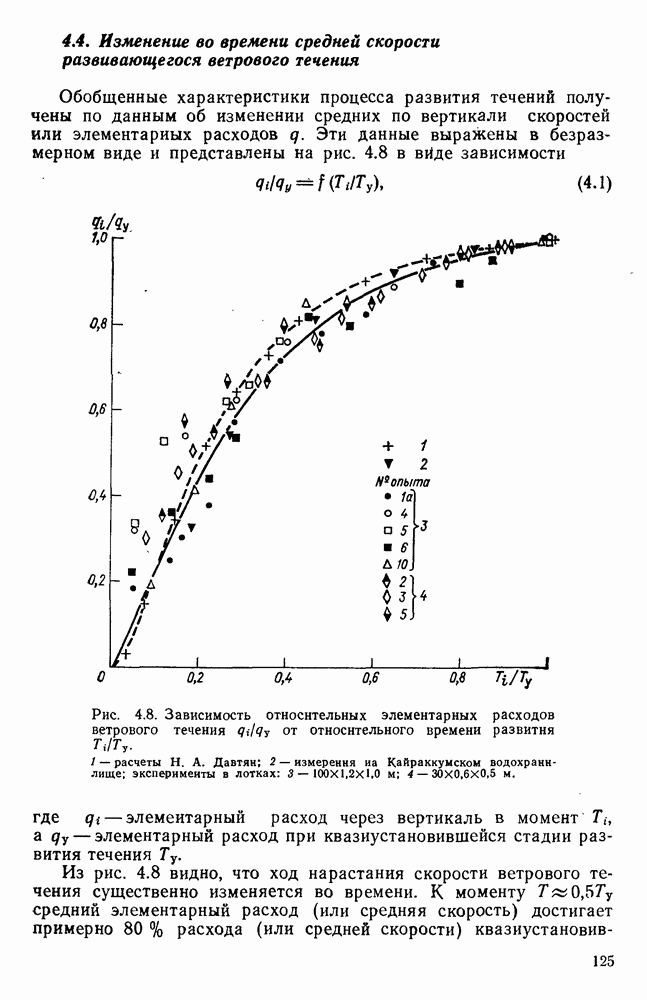
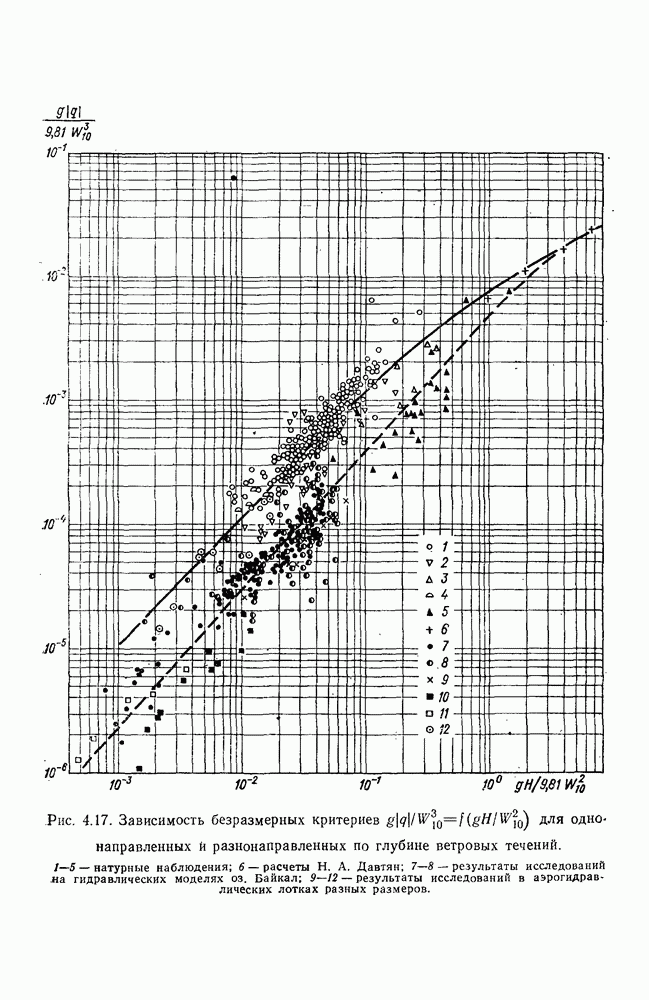
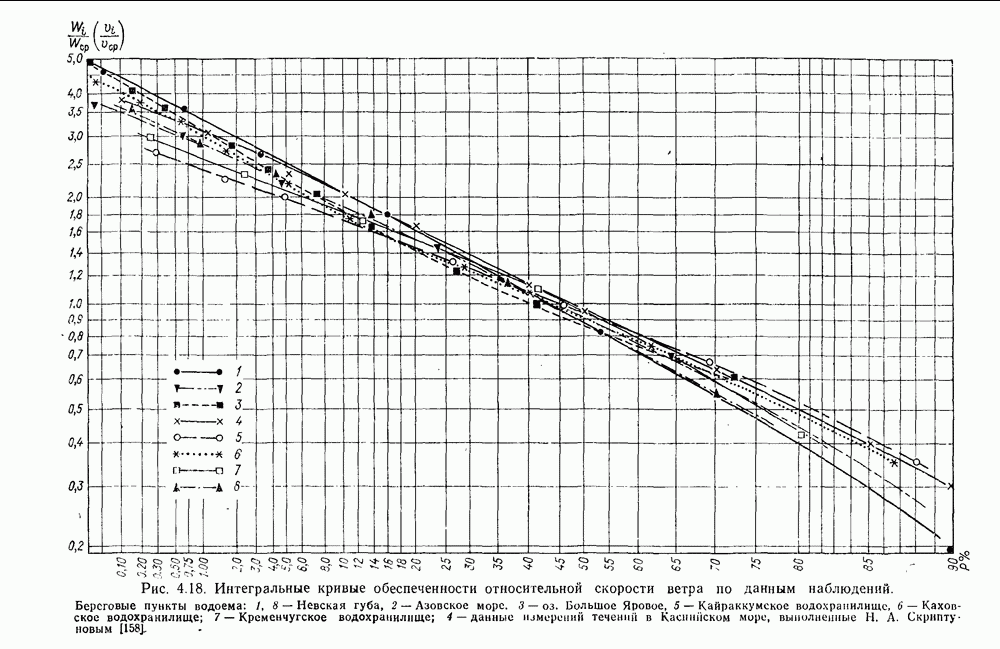
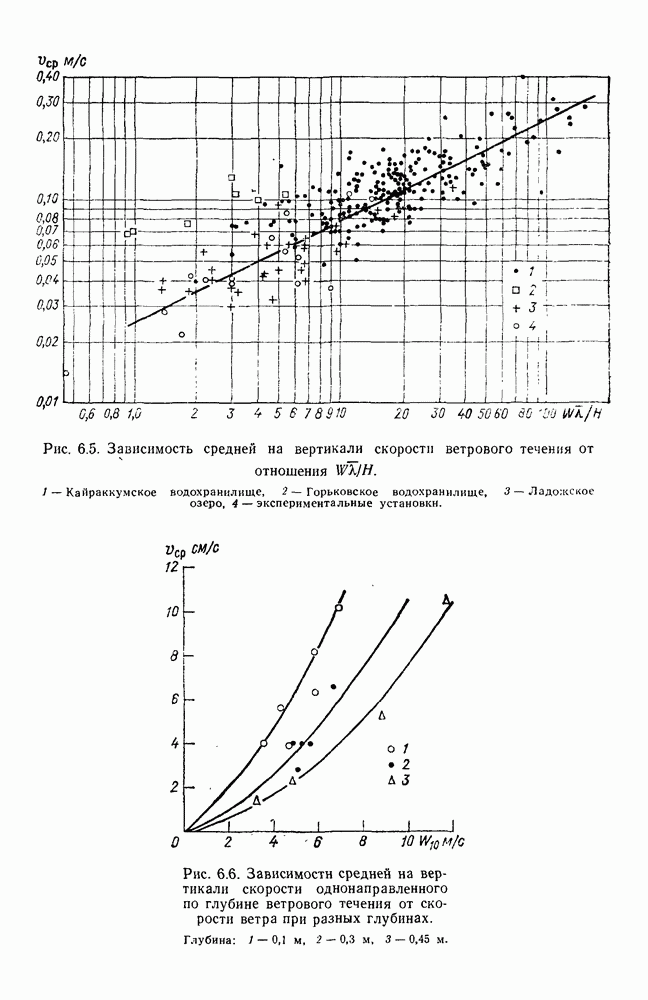
Для воспроизведения над водной поверхностью модели типичных ветровых ситуаций необходимо располагать набором вентиляторов различной мощности и устройствами для измерений характеристик ветра, скорости и направления течений, колебаний уровня и других динамических элементов. Для пересчета с модели на натуру скоростей ветровых течений используют разные методы. Наиболее простой метод предложен Н. Е. Кондратьевым и базируется на использовании обобщенного ветрового коэффициента или эмпирической кривой зависимости  построенной по данным измерений течений в натурных условиях [37, 38]. При этом поступают следующим образом. По ветровому коэффициенту или эмпирической кривой
построенной по данным измерений течений в натурных условиях [37, 38]. При этом поступают следующим образом. По ветровому коэффициенту или эмпирической кривой  вычисляют скорость течения, соответствующую воспроизведенному над пространственной моделью ветру. Эту скорость течения считают равной средней скорости течения на модели при воспроизведенном ветре, а скорость течения в различных местах модели определяют путем умножения средней скорости на отношение измеренного вектора скорости к вектору скорости, соответствующему осредненному значению вектора в рассматриваемом эксперименте. Наряду с наличием простого метода оценки скоростей ветровых течений по данным экспериментов на пространственной модели водного объекта, имеются критерии моделирования, разработанные на строгой теоретической основе. К числу таких разработок относится, например, метод А. В. Караушева [74] и Н. А. Давтян [38].
вычисляют скорость течения, соответствующую воспроизведенному над пространственной моделью ветру. Эту скорость течения считают равной средней скорости течения на модели при воспроизведенном ветре, а скорость течения в различных местах модели определяют путем умножения средней скорости на отношение измеренного вектора скорости к вектору скорости, соответствующему осредненному значению вектора в рассматриваемом эксперименте. Наряду с наличием простого метода оценки скоростей ветровых течений по данным экспериментов на пространственной модели водного объекта, имеются критерии моделирования, разработанные на строгой теоретической основе. К числу таких разработок относится, например, метод А. В. Караушева [74] и Н. А. Давтян [38].
А. В. Караушев [74] вывел критерии моделирования ветровых течений на основе совместного рассмотрения дифференциального уравнения турбулентного движения потока и выражения касательного напряжения ветра на водной поверхности. При этом он пришел к выводу, что динамическое подобие водного потока, сформированного на неискаженной гидравлической модели водоема под действием ветра, обеспечивается при выполнении следующих трех равенств:

где индексом «н» обозначены параметры натурного объекта, а индексом «м» - соответствующие параметры на пространственной гидравлической модели.
Характеристические критериальные величины при этом определяются выражениями:

где  соответственно средние значения глубины, скорости течения, скорости ветра, уклона водной поверхности и безразмерной высоты волны, равной отношению высоты волны на водном объекте к высоте волны
соответственно средние значения глубины, скорости течения, скорости ветра, уклона водной поверхности и безразмерной высоты волны, равной отношению высоты волны на водном объекте к высоте волны  — плотность воды;
— плотность воды;  коэффициент, равный
коэффициент, равный  — коэффициент турбулентной вязкости, учитывающий влияние волнового перемешивания:
— коэффициент турбулентной вязкости, учитывающий влияние волнового перемешивания:

 высота волны,
высота волны,  с — скорость волны,
с — скорость волны,  скорость ветрового течения,
скорость ветрового течения,  постоянный коэффициент, согласно оценкам [183], равный 100;
постоянный коэффициент, согласно оценкам [183], равный 100;  эффективный диаметр частиц донных отложений,
эффективный диаметр частиц донных отложений, 
Система критериальных уравнений масштабов для обеспечения физического моделирования ветровых течений на неискаженных гидравлических моделях представлена Караушевым в виде

где  .
.
А. В. Караушев отмечает, что одинаковые значения  не всегда обеспечиваются по каждому из трех выведенных им
не всегда обеспечиваются по каждому из трех выведенных им
критериев. Для принятия наиболее обоснованного значения скорости ветра над моделью необходимы натурные данные и дальнейшее совершенствование методики лабораторных экспериментов.
Критерии моделирования ветровых течений на искаженных по масштабам пространственных моделях разработаны Давтян [38], исходя из уравнений турбулентного движения и принятия следующих условий: плотность жидкости по глубине постоянна; вертикальный перенос отсутствует. Коэффициент турбулентной вязкости постоянен в пределах между поверхностью и дном водоема. Для натурного и модельного объектов принята тождественность следующих чисел: Струхаля  Россби
Россби  , Эйлера
, Эйлера  , Фруда
, Фруда  и параметров, характеризующих воздействия ветра на водную поверхность
и параметров, характеризующих воздействия ветра на водную поверхность  и турбулентность потока
и турбулентность потока  в виде:
в виде:

Исходя из (4.63), получены следующие зависимости:
для неискаженного моделирования

для искаженного моделирования

где  - масштабы соответственно вертикальных и горизонтальных размеров котловины водоема;
- масштабы соответственно вертикальных и горизонтальных размеров котловины водоема;  масштабы соответственно времени и скорости;
масштабы соответственно времени и скорости;  масштаб параметра Кориолиса; От — масштаб касательного напряжения;
масштаб параметра Кориолиса; От — масштаб касательного напряжения;  масштаб давления;
масштаб давления;  масштаб коэффициента турбулентной вязкости.
масштаб коэффициента турбулентной вязкости.
Критериальные соотношения (4.64) и (4.65) можно удовлетворить только на модели, масштаб которой относится к натуре, как  Во всех других случаях приходится ограничиваться какими-либо двумя или тремя критериями.
Во всех других случаях приходится ограничиваться какими-либо двумя или тремя критериями.
Для неискаженного и искаженного моделирования Давтян рекомендует обеспечивать удовлетворение двух условий:  а также добиваться на модели формирования гравитационных волн, сохранять глубоководность по условиям волнения и турбулентный режим потока по скоростям течения.
а также добиваться на модели формирования гравитационных волн, сохранять глубоководность по условиям волнения и турбулентный режим потока по скоростям течения.
Основные соотношения для неискаженного моделирования при этом сводятся к следующим:

а для искаженного моделирования

При моделировании ускорения Кориолиса угловую скорость вращения гидравлической модели определяют из условия подобия радиусов вращения  и широты места
и широты места  по выражению
по выражению

На основании рассмотрения предложенных методов установления критериальных соотношений видно, что физическое моделирование ветровых течений является весьма трудоемким делом в отношении как техники экспериментов, так и пересчета данных моделирования к натурным условиям. Однако выполненные ранее эксперименты [37, 185] показывают, что затраты труда и средств чаще всего окупаются большой ценностью получаемых материалов.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВОЗДЕЙСТВИЕ ВЕТРА И ВОЛНОВЫЕ ПРОЦЕССЫ
- 1.1. Методы изучения взаимодействующих сложных явлений и процессов
- 1.2. Масштабы динамических явлений
- 1.3. Причины динамических явлений
- 1.4. Ветер над водной поверхностью
- 1.4.2. Коэффициент аэродинамического сопротивления
- 1.4.3. Касательные напряжения ветра
- 1.4.4. Профили ветра и их трансформация над подстилающей поверхностью
- 1.4.5. Режимные статистические и расчетные характеристики ветра
- 1.5. Ветровые волны
- 1.5.2. Классификация волн и их элементов
- 1.5.3. Расчет элементов ветровых волн и учет их изменчивости
- 1.6. Стоячие волны
- 1.6.2. Основные элементы волн и их аналитическое выражение
- 1.6.3. Периоды сейшевых колебаний уровня
- 1.6.4. Затухание стоячих колебаний уровня во времени
- 1.7. Внутренние волны
- 1.8. Сгонно-нагонные явления
- Глава 2. ПРОСТРАНСТВЕННАЯ СТРУКТУРА ПЕРЕНОСА ВОД ТЕЧЕНИЯМИ
- 2.1. Многообразие видов движений и масштабов пространственных структур
- 2.2. Траектории движений частиц жидкости при совместном действии волн и течений
- 2.3. Вертикальная структура ветровых течений на стадии возникновения и развития
- 2.4. Вертикальная структура квазиустановившихся ветровых течений
- 2.5. Количественные характеристики вертикальных вихревых образований
- 2.6. Макроциркуляция вод в водоеме при ветровых течениях
- 2.7. Макроциркуляция вод в заливе при ветровых течениях
- 2.8. Инерционные и синоптические вихри
- 2.9. Формирование циркуляций транзитным потоком и затухающей речной струей
- 2.10. Структура сейшевых течений
- Глава 3. КИНЕМАТИКА ВЕТРОВЫХ И СУММАРНЫХ ТЕЧЕНИЙ
- 3.1. Совершенствование представлений о кинематике течений
- 3.2. Методы исследований кинематики течений
- 3.3. Методика обработки записей течений
- 3.4. Оценка кинематических характеристик
- 3.5. Изменение мелкомасштабных пульсаций скорости во времени и по глубине
- 3.6. Изменение средних квадратических значений пульсационных составляющих скорости
- 3.7. Вертикальное распределение моментов корреляции в ветровых течениях
- 3.8. Энергетические характеристики ветровых течений по данным экспериментов
- 3.9. Коэффициенты вертикальной турбулентной вязкости и методы их оценки
- 3.10. Распределение коэффициента вертикальной турбулентной вязкости
- 3.11. Оценка коэффициента горизонтальной турбулентной вязкости
- Глава 4. ВЕТРОВЫЕ ТЕЧЕНИЯ В УСЛОВИЯХ РАЗВИТИЯ И СТАБИЛИЗАЦИИ
- 4.1. Совершенствование представлений о развитии ветровых течений
- 4.2. Проникновение развивающегося ветрового течения в глубину
- 4.3. Изменение распределения по вертикали скорости развивающегося ветрового течения
- 4.4. Изменение во времени средней скорости развивающегося ветрового течения
- 4.5. Продолжительность развития ветрового течения
- 4.6. Изменение скорости ветрового течения по пути разгона волн
- 4.7. Соотношение между скоростями ветрового течения и ветра
- 4.7.2. Ветровой коэффициент для прибрежных зон морей и океанов
- 4.7.3. Ветровой коэффициент для морских заливов
- 4.7.4. Ветровой коэффициент для внутренних водоемов
- 4.8. Оценка влияния на поверхностное ветровое течение глубины и шероховатости дна водоема
- 4.9. Предельное проникновение ветрового течения в глубину
- 4.10. Отклонения направлений ветровых течений от направления ветра
- 4.11. Теоретические решения задачи о вертикальном распределении скорости ветровых течений
- 4.12. Распределение скорости квазиустановившихся ветровых течений по данным экспериментов
- 4.13. Перенос вод через вертикаль
- 4.14. Взаимодействие ветровых, стоковых и сейшевых течений
- 4.15. Соотношение переносов воды дрейфовым и волновым течениями
- 4.16. Установление режимных статистических характеристик течений
- 4.16.2. Выбор функций распределения скорости течения при ограниченных данных наблюдений
- 4.17. Внутренний водообмен при ветровых течениях
- 4.18. Моделирование ветровых течений
- 4.18.2. Математические модели течений и примеры их реализации
- 4.18.3. Физическое моделирование
- Глава 5. СЕЙШЕВЫЕ ТЕЧЕНИЯ
- 5.1. Основные черты и особенности сейшевых течений
- 5.2. Методы оценки скорости сейшевого течения
- 5.3. Распределение сейшевых течений по акватории водоема
- 5.4. Сейшевые течения в оз. Байкал
- 5.5. Сейшевые течения в оз. Балхаш
- 5.6. Сейшевые течения в Каховском водохранилище
- 5.7. Режимные характеристики сейш
- 5.8. Объемы переноса вод сейшевыми течениями
- Глава 6. ТЕЧЕНИЯ В ЗОНЕ ПРИБРЕЖНОГО МЕЛКОВОДЬЯ И НА БЕРЕГОВЫХ ОТМЕЛЯХ
- 6.2. Течения в зоне прибрежного мелководья
- 6.2.2. Повторяемость различных типов циркуляции вод
- 6.2.3. Распределение скорости течения по глубине
- 6.2.4. Изменение скорости течения по ширине зоны
- 6.2.5. Количественные характеристики скорости течения
- 6.2.6. Режимные статистические характеристики скорости течений
- 6.3. Течения на береговых отмелях
- 6.3.2. Распределение скорости вдольберегового течения
- 6.3.3. Расчет средней скорости вдольберегового течения
- Глава 7. ПЕРЕМЕЩЕНИЕ НАНОСОВ НА БЕРЕГОВЫХ ОТМЕЛЯХ
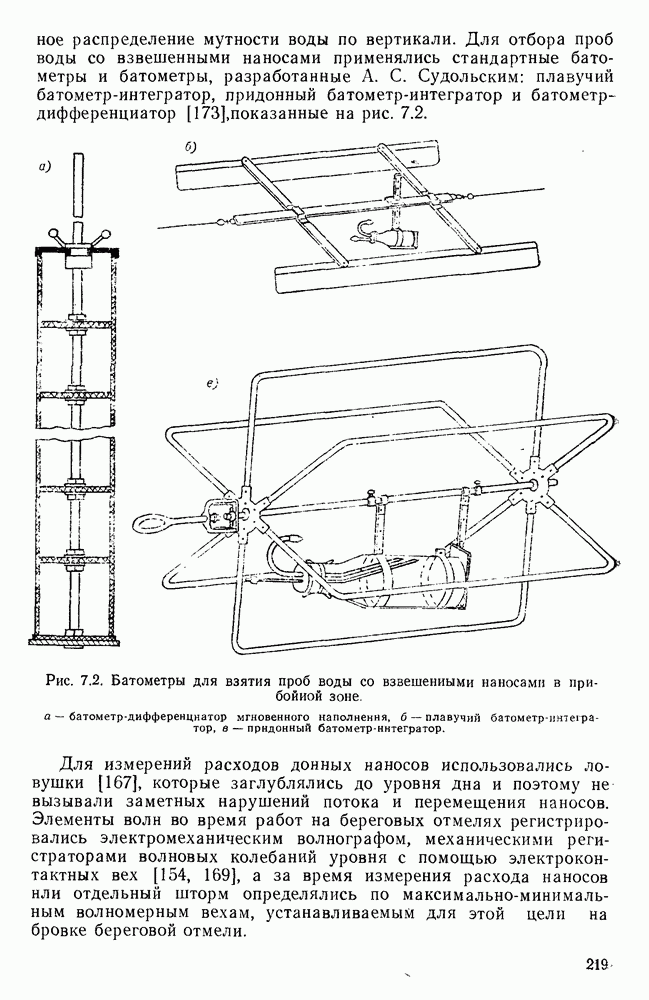
- 7.2. Методы изучения перемещения наносов
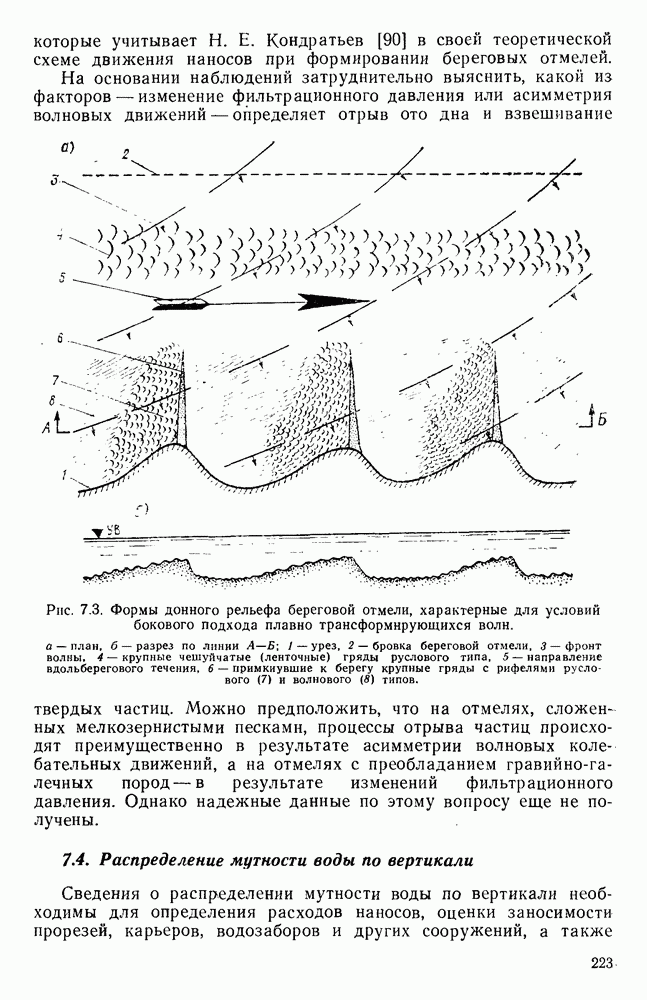
- 7.3. Основные черты механизма перемещения наносов
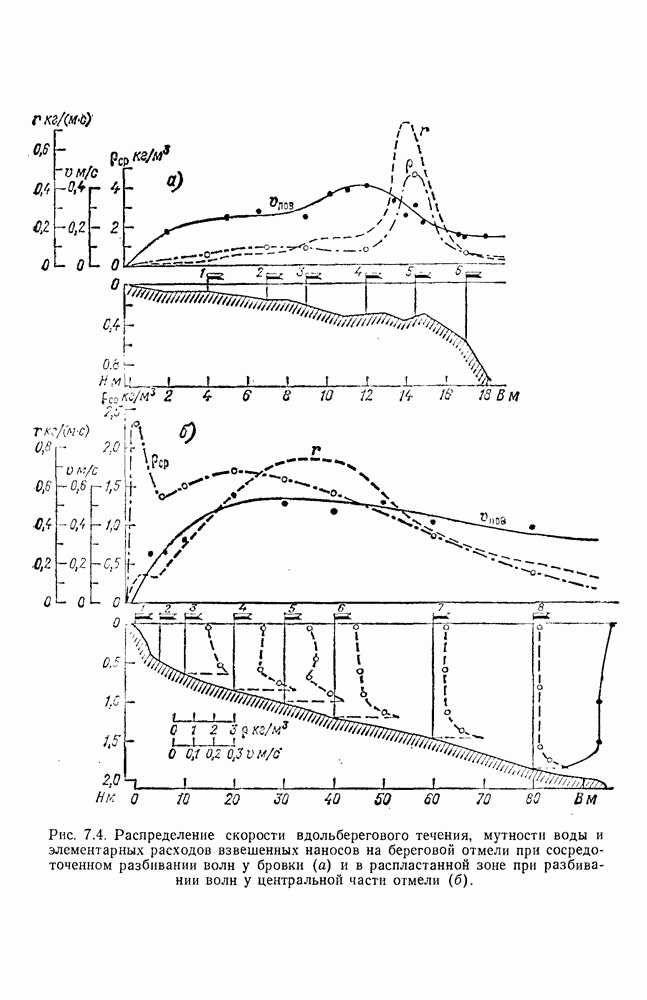
- 7.4. Распределение мутности воды по вертикали
- 7.5. Распределение мутности воды по ширине береговой отмели
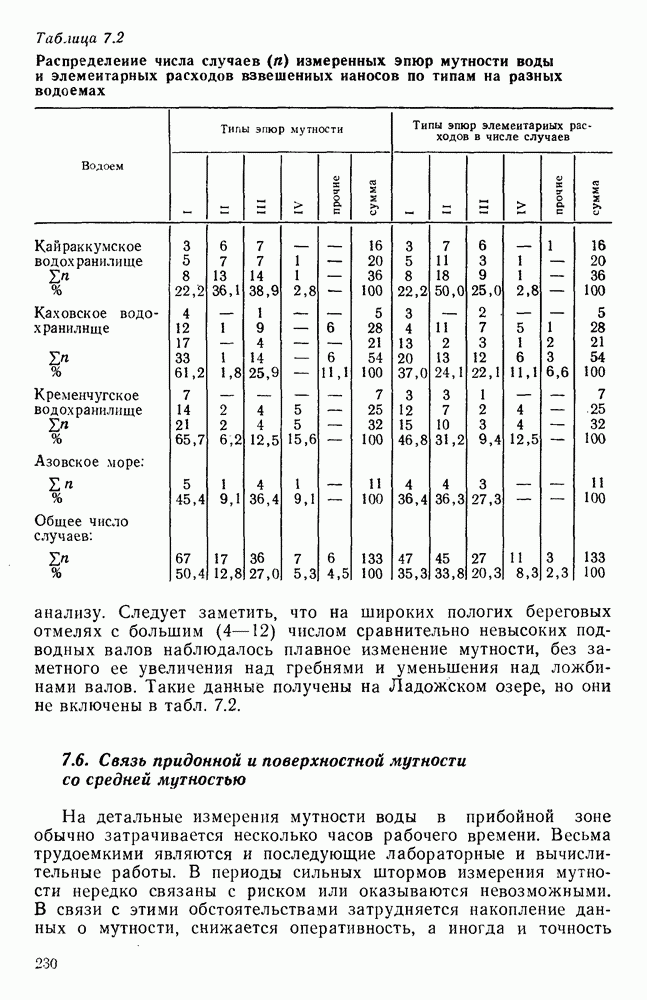
- 7.6. Связь придонной и поверхностной мутности со средней мутностью
- 7.7. Элементарные расходы взвешенных наносов
- 7.8. Зависимость средней мутности от определяющих факторов
- 7.9. Расходы донных наносов и их связь со взвешенными наносами
- 7.10. Расчет вдольберегового переноса твердого материала
- 7.11. Сезонная и межгодовая изменчивость вдольбереговых перемещений наносов