| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.2. Методы оценки скорости сейшевого течения
Имеющиеся в литературных источниках сведения о скорости сейшевых течений относятся преимущественно к проливам и прибрежным зонам. Утверждается, что скорость течения в узких проливах водоемов может достигать 2-3 м/с, а в широких обычно не превышает 1,0 м/с [8, 19, 208]. В прибрежных зонах крупных внутренних водоемов были измерены скорости сейшевых течений, равные 0,2-0,3 м/с.
Очень мало сведений о сейшевых течениях на открытых и удаленных от берегов пространствах водоемов. Оценку скорости для таких районов приходится производить с использованием расчетных формул.
Для расчета средней скорости сейшевого течения в прямоугольном бассейне постоянной глубины  и длины
и длины  при высоте колебания уровня
при высоте колебания уровня  рекомендуется формула [8, 80, 133]
рекомендуется формула [8, 80, 133]

которая получена путем решения дифференциального уравнения
движения и с учетом выражения периода сейши по Меридиану  приводится к виду
приводится к виду

Эту формулу впервые использовал для практических целей, по-видимому, Праудмен. Он установил, что в одном из озер Шотландии, имеющем длину 50 км и среднюю глубину 60 м, при высоте сейшевых колебаний уровня около 0,1 м средняя скорость сейшевого течения составляет около 4 см/с.
Близкие к реальным значения средней скорости сейшевых течений получены с использованием формулы (5.2) авторами монографии [8]. Ими были определены средние значения скорости сейшевых течений для нескольких внутренних водоемов: Аральское море - 15,4 см/с при  Байкал — 2,5 см/с при
Байкал — 2,5 см/с при  Балхаш — 6,1 см/с при
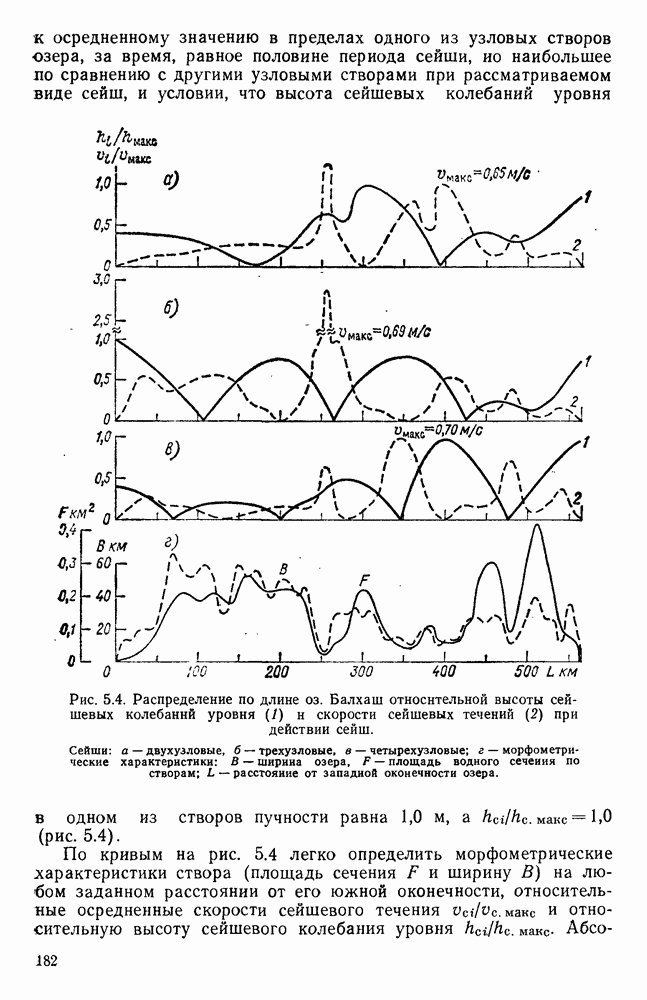
Балхаш — 6,1 см/с при  Так как по формуле (5.2) не удается учесть морфологию водоема и различия в распределении высоты сейшевых колебаний уровня, среднюю скорость сейшевого течения в работах [144, 171] предложено оценивать по переливающимся объемам жидкости с использованием выражения
Так как по формуле (5.2) не удается учесть морфологию водоема и различия в распределении высоты сейшевых колебаний уровня, среднюю скорость сейшевого течения в работах [144, 171] предложено оценивать по переливающимся объемам жидкости с использованием выражения

где  площадь поперечного сечения водоема по створу;
площадь поперечного сечения водоема по створу;  период сейшевых колебаний уровня;
период сейшевых колебаний уровня;  площадь поверхности водоема, заключенная между расчетным створом и створом ближайшей пучности; — среднее превышение сейшевого уровня над статическим уровнем в пределах рассматриваемого участка водоема;
площадь поверхности водоема, заключенная между расчетным створом и створом ближайшей пучности; — среднее превышение сейшевого уровня над статическим уровнем в пределах рассматриваемого участка водоема;  площадь осевой плоскости, заключенная между сейшевым и статическим уровнями в пределах между расчетным створом и створом ближайшей пучности.
площадь осевой плоскости, заключенная между сейшевым и статическим уровнями в пределах между расчетным створом и створом ближайшей пучности.
По выражению (5.3) можно вычислить среднюю скорость сейшевого течения в любом створе водоема при наличии сведений по морфологии и о распределении высоты сейшевых колебаний уровня вдоль оси водоема или по его акватории.
Можно не сомневаться, что вычисленные таким методом количественные характеристики течений более полны и надежны, чем результаты вычислений по формуле (5.2), использовавшейся впервые Праудменом. В ГГИ с помощью формулы (5.3) получены достаточно детальные сведения о средней скорости сейшевых течений для нескольких крупных водоемов. Они сопоставлялись также с данными исследований на пространственных гидравлических моделях и оказались вполне приемлемыми для практического использования, что показано ниже.
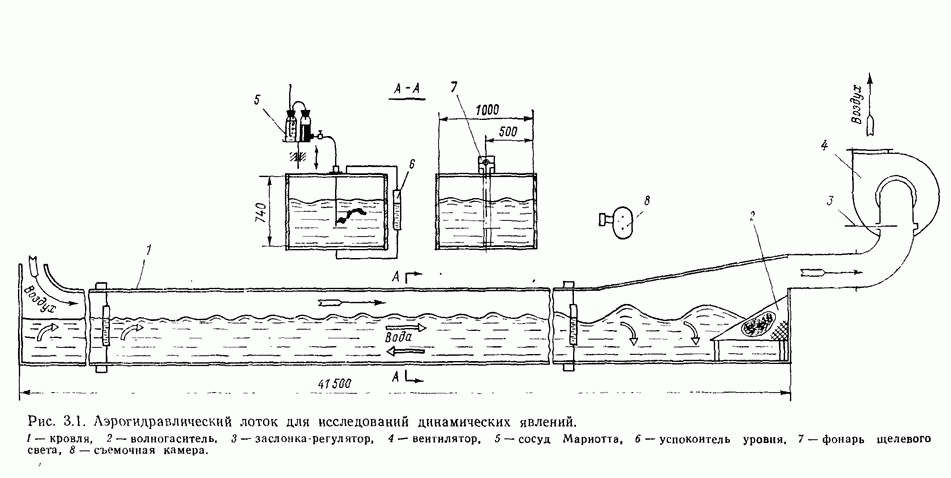
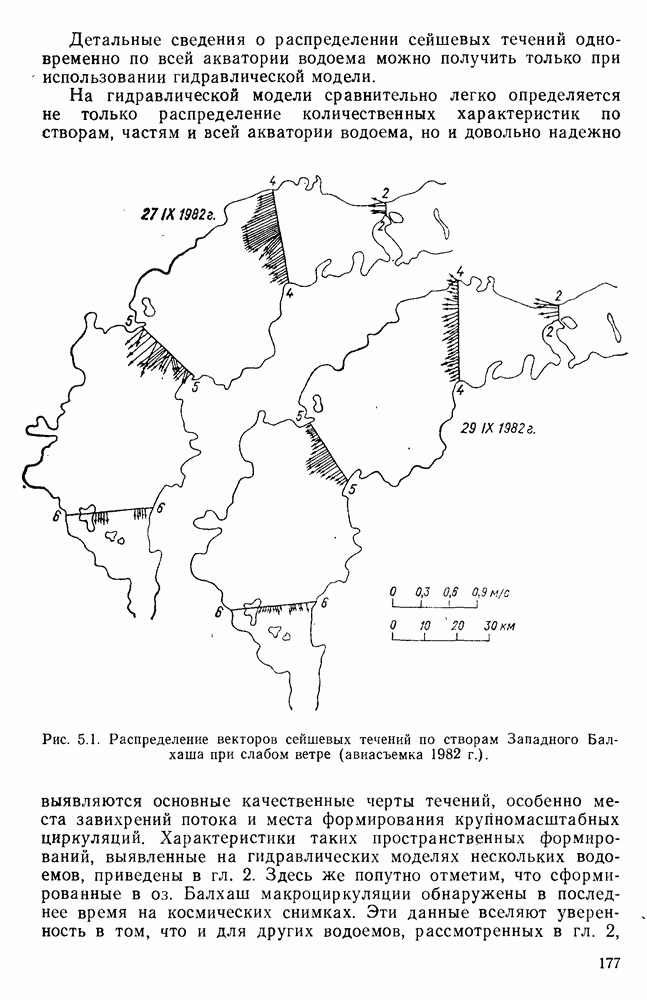
В случае необходимости получения детальных сведений о сейшевых течениях в водоеме или отдельной его части, достаточно обособленной от водоема, приходится обращаться к гидравлическому моделированию. Следует отметить, что первые исследования сейшевых явлений в нашей стране проводились на
гидравлической модели оз. Байкал [160, 161]. Авторами этих исследований была показана возможность использования для этого мелкомасштабных моделей, в частности в масштабе 
Поскольку при моделировании сейшевых явлений определяющими являются силы тяжести, то на модели («м») и в натуре («н») должно быть обеспечено равенство чисел Фруда, представляемых, например, в виде [217]

где  характерная скорость;
характерная скорость;  характерный линейный размер.
характерный линейный размер.
В случае воспроизведения рельефа котловины водного объекта без искажения геометрических размеров выражения для вычисления скорости, расхода воды и времени представляются соответственно в виде [217]:

В этих выражениях характерный горизонтальный размер модели  принимается равным единице,
принимается равным единице,  показывает кратность превышения размеров натурного объекта над размерами объектов на модели.
показывает кратность превышения размеров натурного объекта над размерами объектов на модели.
При строительстве гидравлических моделей мелководных водоемов обычно приходится допускать искажение геометрических размеров, чаще всего путем воспроизведения вертикальных размеров рельефа котловины в более крупном масштабе, чем горизонтальных. Размеры объектов, измеренные по горизонтали  при этом не соответствуют размерам, измеренным по вертикали
при этом не соответствуют размерам, измеренным по вертикали  Гидравлическая модель водного объекта характеризуется двумя масштабами: горизонтальным в виде отношения
Гидравлическая модель водного объекта характеризуется двумя масштабами: горизонтальным в виде отношения  и вертикальным в виде отношения
и вертикальным в виде отношения 
Для пересчета в натурные условия гидравлических характеристик исследуемого на искаженной модели явления используют следующие выражения для скорости течения, расхода воды и времени:

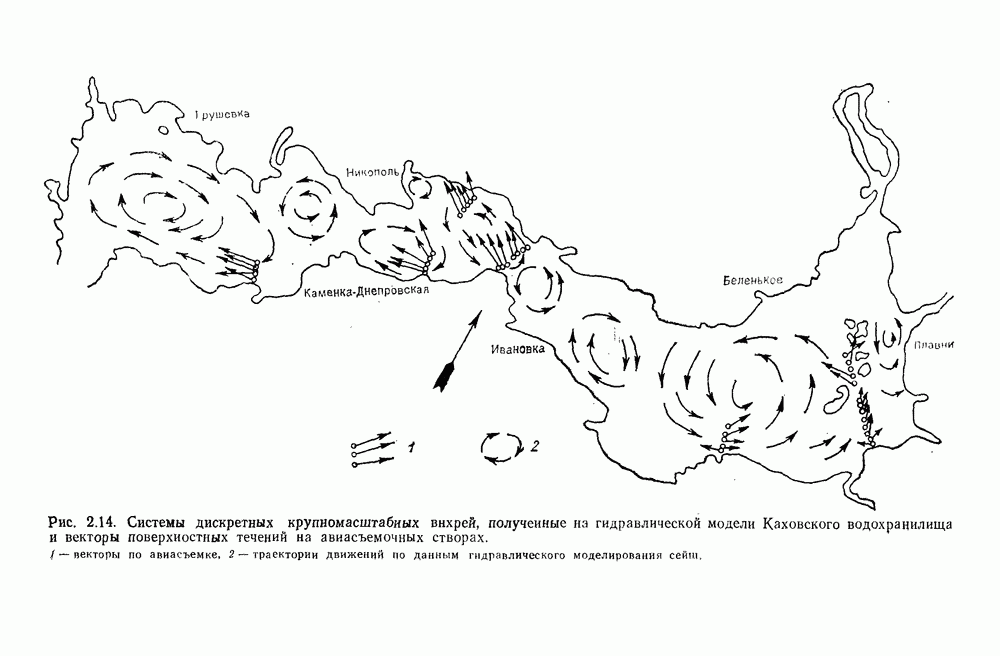
Выражения (5.8) — (5.10) обеспечивают получение достаточно надежных количественных характеристик сейш по данным моделирования. Пересчету на натурные условия могут быть подвергнуты не только осредненные, но и мгновенные характеристики. В результате может быть получено, например, распределение скорости сейшевого течения и его направления по акватории изучаемого водоема или участка.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВОЗДЕЙСТВИЕ ВЕТРА И ВОЛНОВЫЕ ПРОЦЕССЫ
- 1.1. Методы изучения взаимодействующих сложных явлений и процессов
- 1.2. Масштабы динамических явлений
- 1.3. Причины динамических явлений
- 1.4. Ветер над водной поверхностью
- 1.4.2. Коэффициент аэродинамического сопротивления
- 1.4.3. Касательные напряжения ветра
- 1.4.4. Профили ветра и их трансформация над подстилающей поверхностью
- 1.4.5. Режимные статистические и расчетные характеристики ветра
- 1.5. Ветровые волны
- 1.5.2. Классификация волн и их элементов
- 1.5.3. Расчет элементов ветровых волн и учет их изменчивости
- 1.6. Стоячие волны
- 1.6.2. Основные элементы волн и их аналитическое выражение
- 1.6.3. Периоды сейшевых колебаний уровня
- 1.6.4. Затухание стоячих колебаний уровня во времени
- 1.7. Внутренние волны
- 1.8. Сгонно-нагонные явления
- Глава 2. ПРОСТРАНСТВЕННАЯ СТРУКТУРА ПЕРЕНОСА ВОД ТЕЧЕНИЯМИ
- 2.1. Многообразие видов движений и масштабов пространственных структур
- 2.2. Траектории движений частиц жидкости при совместном действии волн и течений
- 2.3. Вертикальная структура ветровых течений на стадии возникновения и развития
- 2.4. Вертикальная структура квазиустановившихся ветровых течений
- 2.5. Количественные характеристики вертикальных вихревых образований
- 2.6. Макроциркуляция вод в водоеме при ветровых течениях
- 2.7. Макроциркуляция вод в заливе при ветровых течениях
- 2.8. Инерционные и синоптические вихри
- 2.9. Формирование циркуляций транзитным потоком и затухающей речной струей
- 2.10. Структура сейшевых течений
- Глава 3. КИНЕМАТИКА ВЕТРОВЫХ И СУММАРНЫХ ТЕЧЕНИЙ
- 3.1. Совершенствование представлений о кинематике течений
- 3.2. Методы исследований кинематики течений
- 3.3. Методика обработки записей течений
- 3.4. Оценка кинематических характеристик
- 3.5. Изменение мелкомасштабных пульсаций скорости во времени и по глубине
- 3.6. Изменение средних квадратических значений пульсационных составляющих скорости
- 3.7. Вертикальное распределение моментов корреляции в ветровых течениях
- 3.8. Энергетические характеристики ветровых течений по данным экспериментов
- 3.9. Коэффициенты вертикальной турбулентной вязкости и методы их оценки
- 3.10. Распределение коэффициента вертикальной турбулентной вязкости
- 3.11. Оценка коэффициента горизонтальной турбулентной вязкости
- Глава 4. ВЕТРОВЫЕ ТЕЧЕНИЯ В УСЛОВИЯХ РАЗВИТИЯ И СТАБИЛИЗАЦИИ
- 4.1. Совершенствование представлений о развитии ветровых течений
- 4.2. Проникновение развивающегося ветрового течения в глубину
- 4.3. Изменение распределения по вертикали скорости развивающегося ветрового течения
- 4.4. Изменение во времени средней скорости развивающегося ветрового течения
- 4.5. Продолжительность развития ветрового течения
- 4.6. Изменение скорости ветрового течения по пути разгона волн
- 4.7. Соотношение между скоростями ветрового течения и ветра
- 4.7.2. Ветровой коэффициент для прибрежных зон морей и океанов
- 4.7.3. Ветровой коэффициент для морских заливов
- 4.7.4. Ветровой коэффициент для внутренних водоемов
- 4.8. Оценка влияния на поверхностное ветровое течение глубины и шероховатости дна водоема
- 4.9. Предельное проникновение ветрового течения в глубину
- 4.10. Отклонения направлений ветровых течений от направления ветра
- 4.11. Теоретические решения задачи о вертикальном распределении скорости ветровых течений
- 4.12. Распределение скорости квазиустановившихся ветровых течений по данным экспериментов
- 4.13. Перенос вод через вертикаль
- 4.14. Взаимодействие ветровых, стоковых и сейшевых течений
- 4.15. Соотношение переносов воды дрейфовым и волновым течениями
- 4.16. Установление режимных статистических характеристик течений
- 4.16.2. Выбор функций распределения скорости течения при ограниченных данных наблюдений
- 4.17. Внутренний водообмен при ветровых течениях
- 4.18. Моделирование ветровых течений
- 4.18.2. Математические модели течений и примеры их реализации
- 4.18.3. Физическое моделирование
- Глава 5. СЕЙШЕВЫЕ ТЕЧЕНИЯ
- 5.1. Основные черты и особенности сейшевых течений
- 5.2. Методы оценки скорости сейшевого течения
- 5.3. Распределение сейшевых течений по акватории водоема
- 5.4. Сейшевые течения в оз. Байкал
- 5.5. Сейшевые течения в оз. Балхаш
- 5.6. Сейшевые течения в Каховском водохранилище
- 5.7. Режимные характеристики сейш
- 5.8. Объемы переноса вод сейшевыми течениями
- Глава 6. ТЕЧЕНИЯ В ЗОНЕ ПРИБРЕЖНОГО МЕЛКОВОДЬЯ И НА БЕРЕГОВЫХ ОТМЕЛЯХ
- 6.2. Течения в зоне прибрежного мелководья
- 6.2.2. Повторяемость различных типов циркуляции вод
- 6.2.3. Распределение скорости течения по глубине
- 6.2.4. Изменение скорости течения по ширине зоны
- 6.2.5. Количественные характеристики скорости течения
- 6.2.6. Режимные статистические характеристики скорости течений
- 6.3. Течения на береговых отмелях
- 6.3.2. Распределение скорости вдольберегового течения
- 6.3.3. Расчет средней скорости вдольберегового течения
- Глава 7. ПЕРЕМЕЩЕНИЕ НАНОСОВ НА БЕРЕГОВЫХ ОТМЕЛЯХ
- 7.2. Методы изучения перемещения наносов
- 7.3. Основные черты механизма перемещения наносов
- 7.4. Распределение мутности воды по вертикали
- 7.5. Распределение мутности воды по ширине береговой отмели
- 7.6. Связь придонной и поверхностной мутности со средней мутностью
- 7.7. Элементарные расходы взвешенных наносов
- 7.8. Зависимость средней мутности от определяющих факторов
- 7.9. Расходы донных наносов и их связь со взвешенными наносами
- 7.10. Расчет вдольберегового переноса твердого материала
- 7.11. Сезонная и межгодовая изменчивость вдольбереговых перемещений наносов