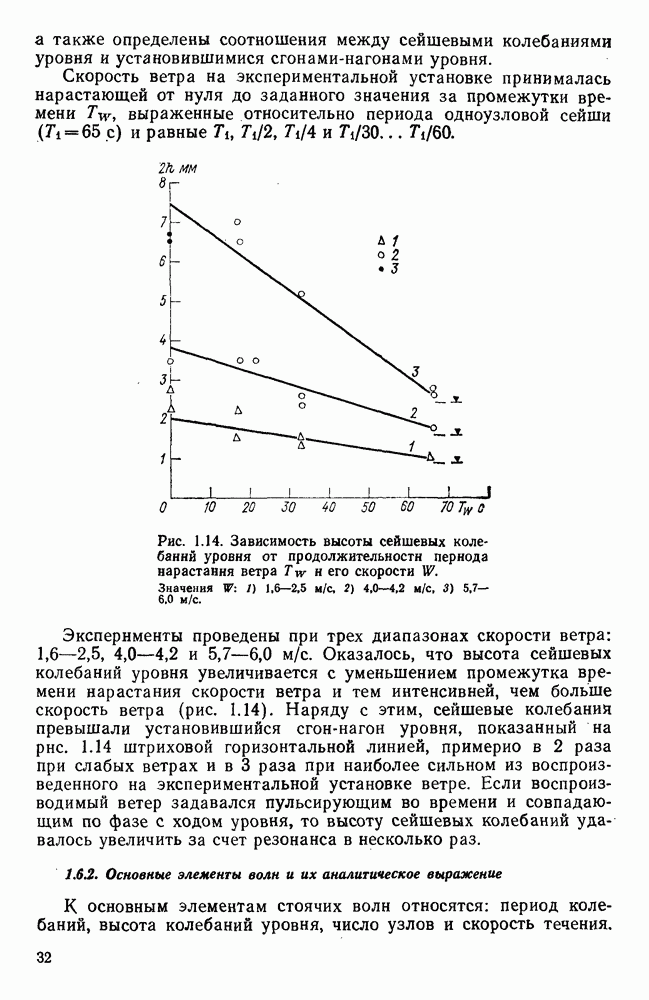
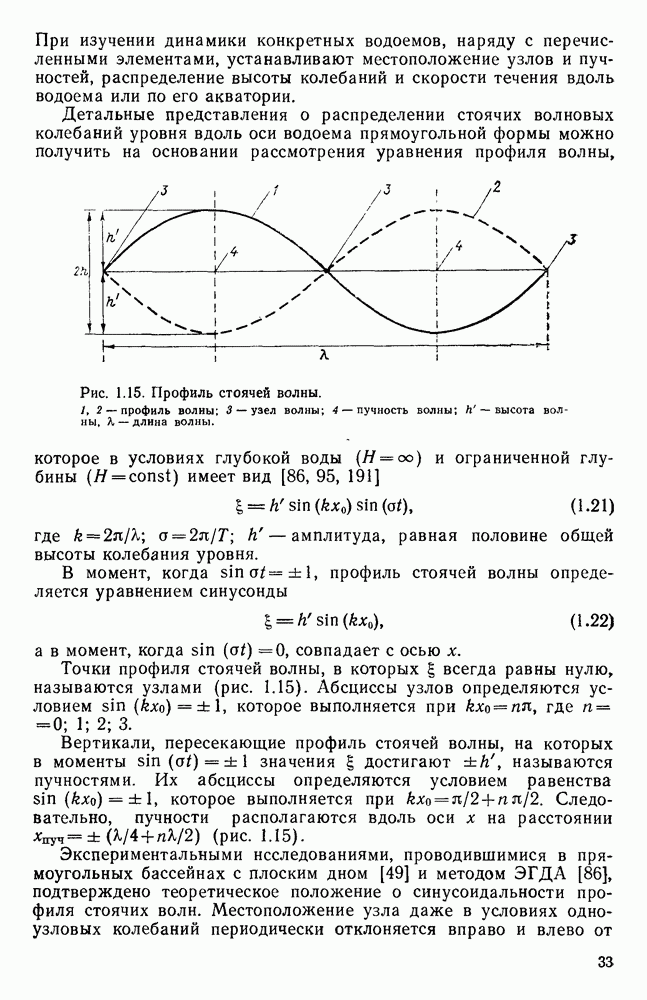
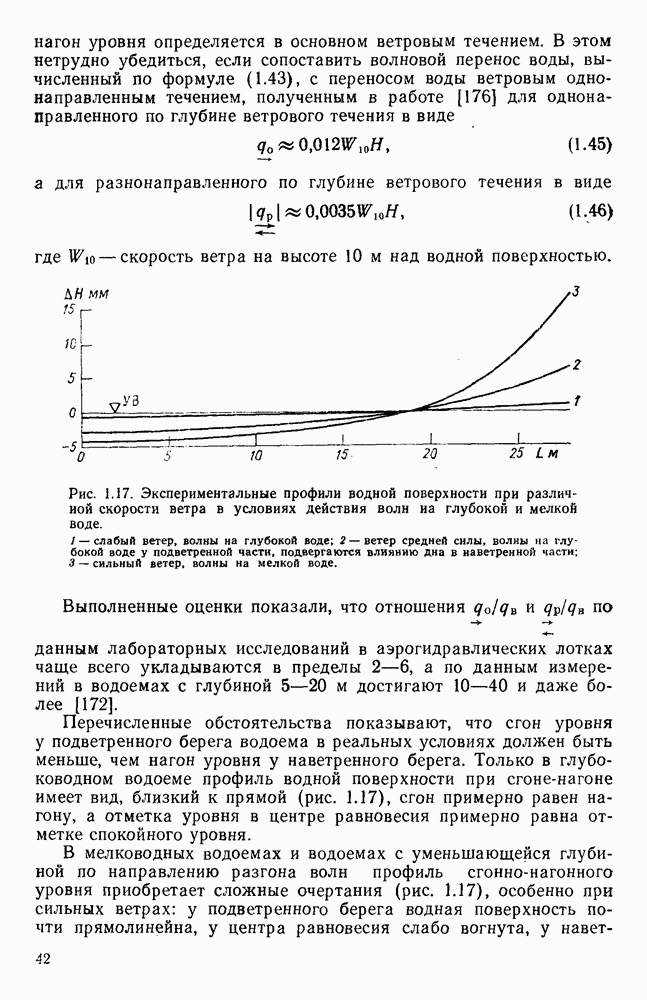
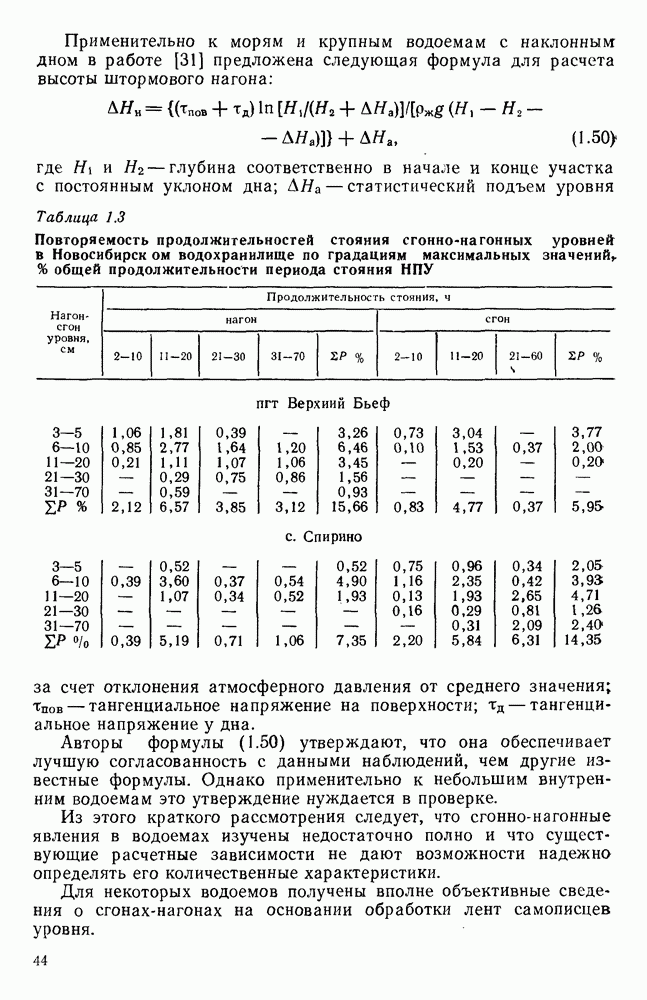
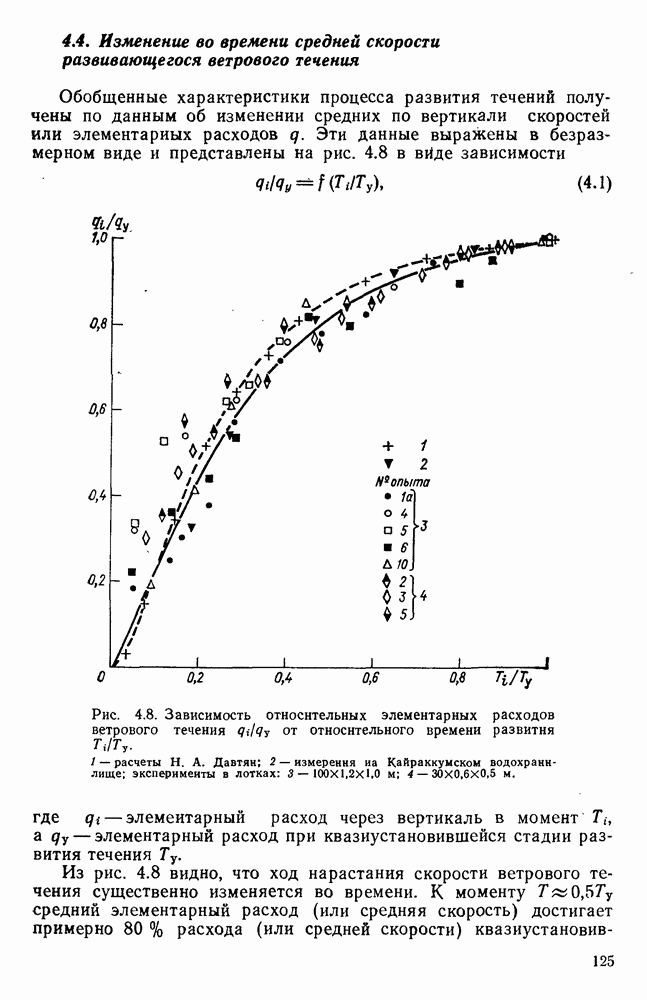
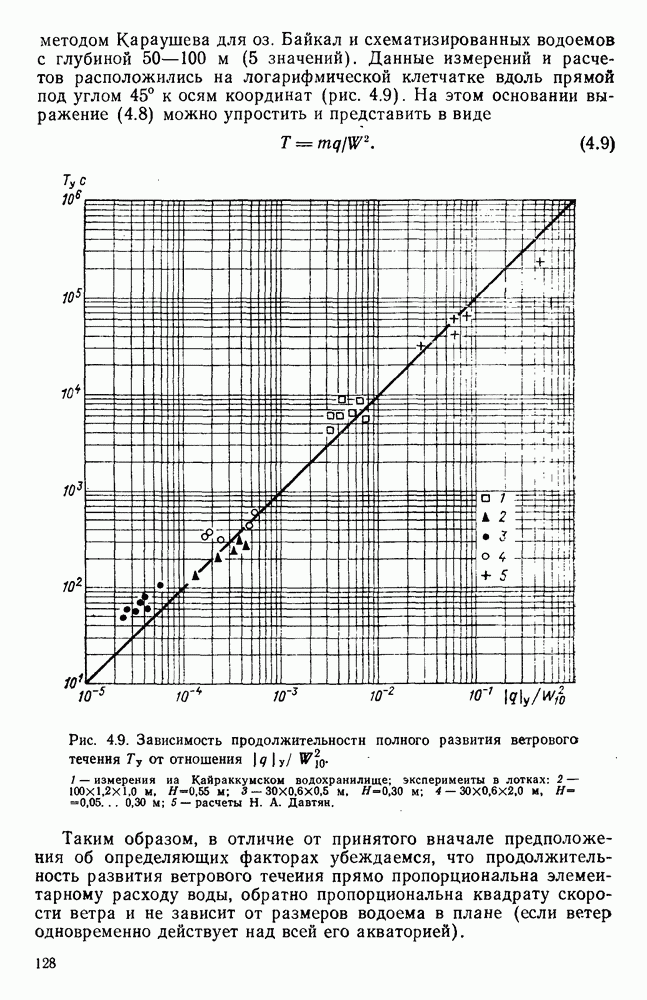
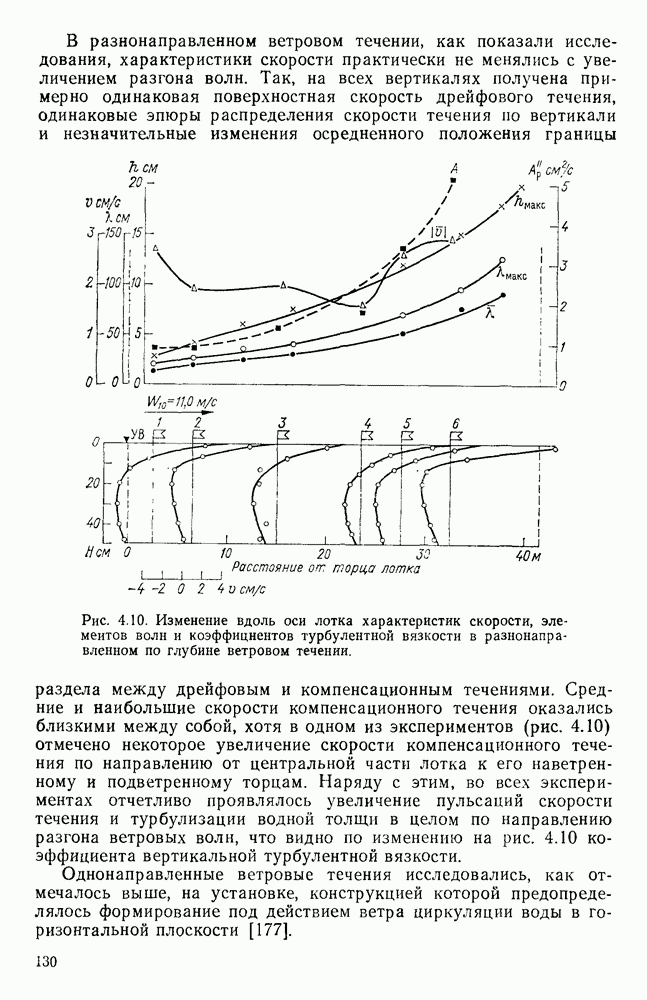
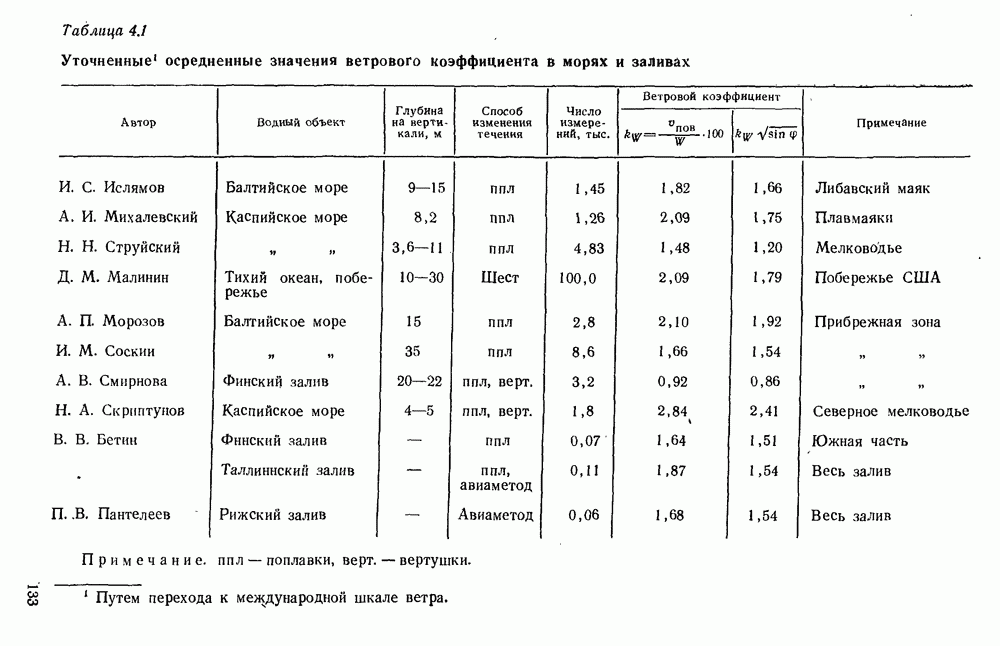
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
1.4.2. Коэффициент аэродинамического сопротивления
Коэффициент аэродинамического сопротивления водной поверхности  обычно определяют по зависимости [20, 26, 41, 140, 245]
обычно определяют по зависимости [20, 26, 41, 140, 245]

где  плотность воздуха;
плотность воздуха;  касательное напряжение воздушного потока на водной поверхности;
касательное напряжение воздушного потока на водной поверхности;  скорость ветра на высоте
скорость ветра на высоте  над водной поверхностью;
над водной поверхностью;  скорость трения, или динамическая скорость.
скорость трения, или динамическая скорость.
Параметры, входящие в зависимость (1.1), чаще всего определяют по данным о распределении скорости ветра по высоте или характеристиках его пульсации. Методика измерения этих величин приводится в работах [20, 31, 247].
Вполне надежные оценки коэффициента  можно также получить методом Экмана, основанным на использовании сведений
можно также получить методом Экмана, основанным на использовании сведений
о перекосах уровня в водных бассейнах при различной скорости ветра [26, 236]. Общее напряжение трения ветра о водную поверхность в бассейне постоянной глубины  и плотности
и плотности  в методе Экмана представляют зависимостью
в методе Экмана представляют зависимостью

где  напряжение трения на дне бассейна;
напряжение трения на дне бассейна;  уклон водной поверхности;
уклон водной поверхности;  ускорение свободного падения.
ускорение свободного падения.

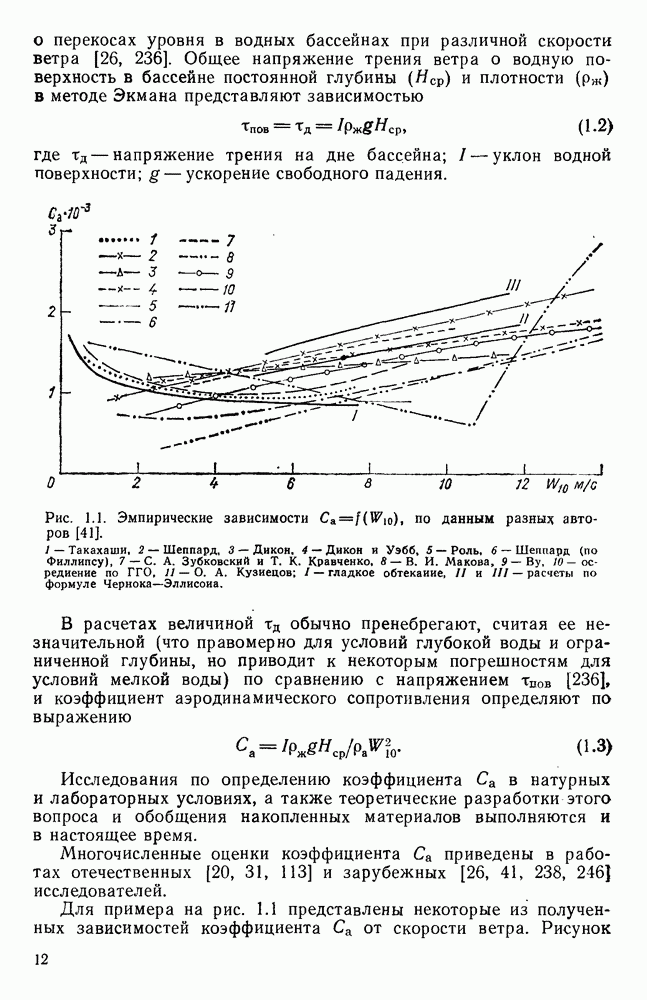
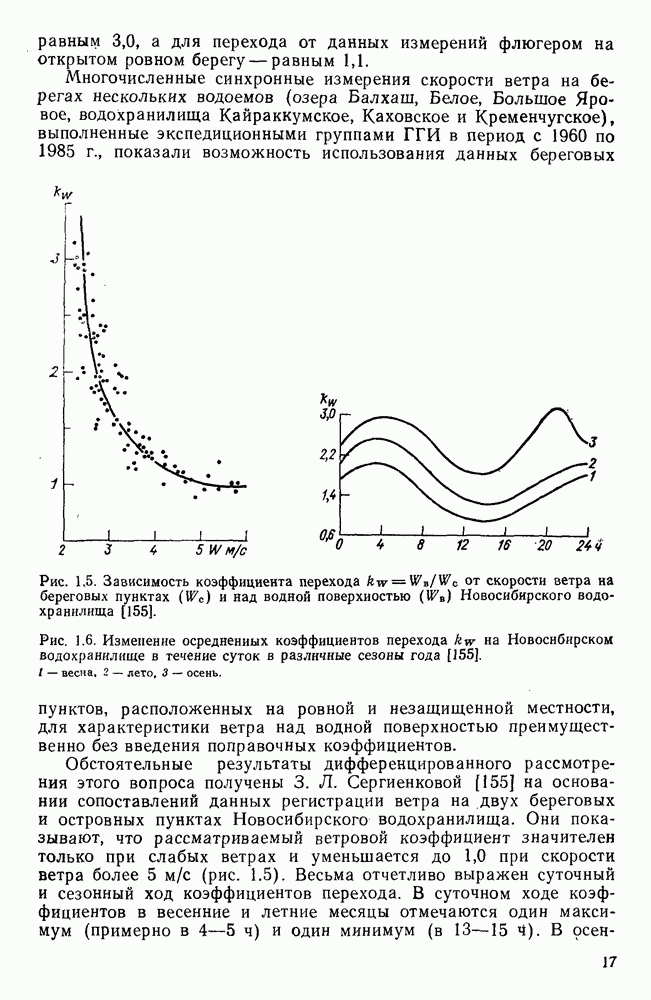
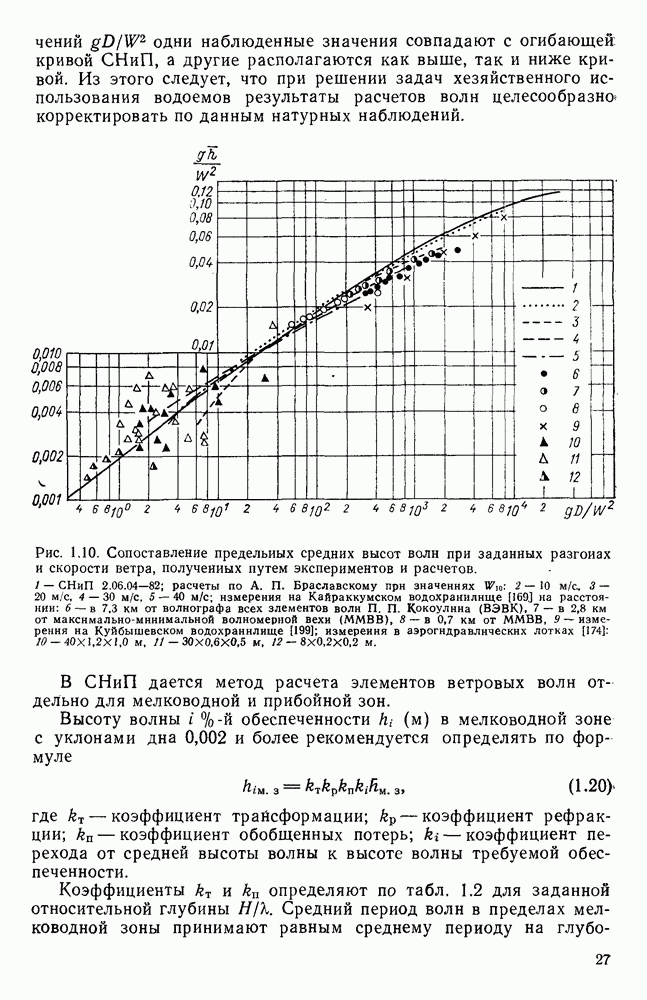
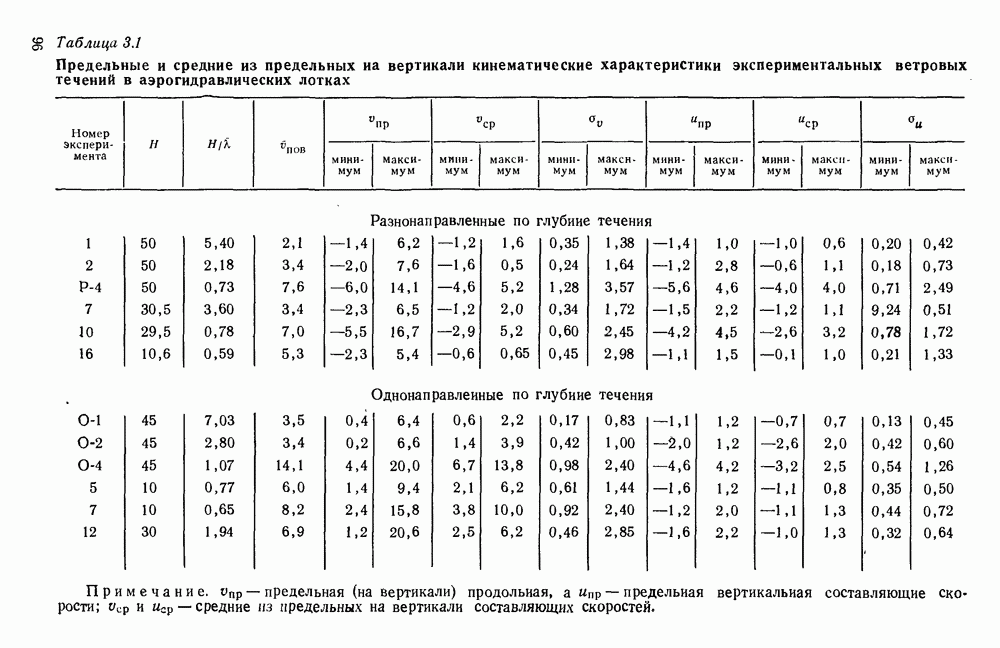
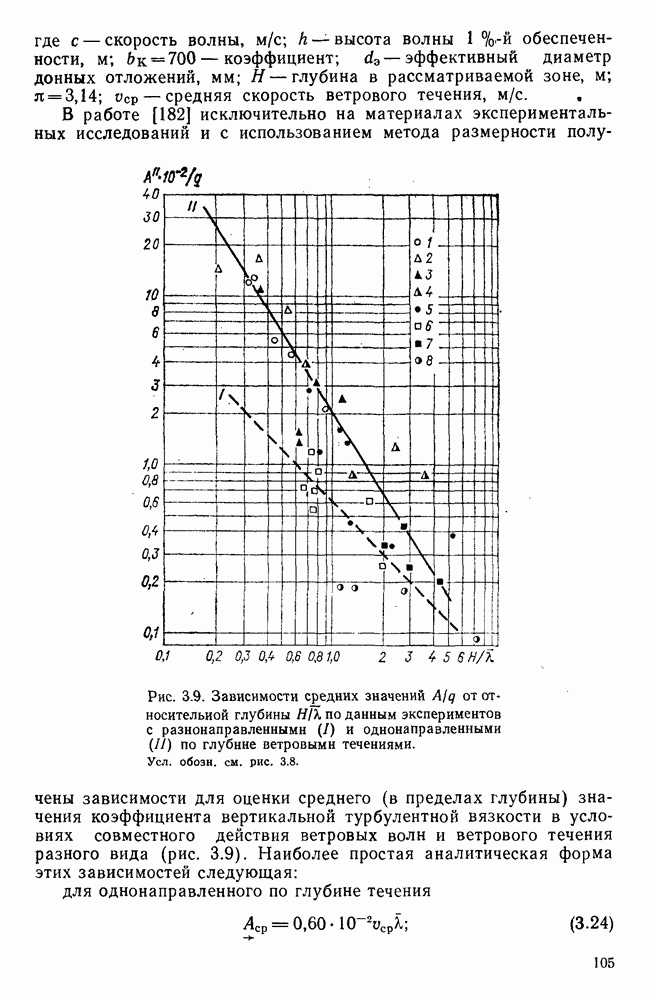
Рис. 1.1. Эмпирические зависимости  по данным разных авторов [41]. 1 — Такахаши, 2 — Шеппард, 3 — Дикон, 4 — Дикон и Уэбб, 5 — Роль, 6 — Шеппард (по Филлипсу), 7 — С. А. Зубковский и Т. К. Кравченко, 8 — В. И. Макова,
по данным разных авторов [41]. 1 — Такахаши, 2 — Шеппард, 3 — Дикон, 4 — Дикон и Уэбб, 5 — Роль, 6 — Шеппард (по Филлипсу), 7 — С. А. Зубковский и Т. К. Кравченко, 8 — В. И. Макова,  осреднение по ГГО, 11 - О. А. Кузнецов; I - гладкое обтекание, II и III — расчеты по формуле Чернока-Эллисоиа.
осреднение по ГГО, 11 - О. А. Кузнецов; I - гладкое обтекание, II и III — расчеты по формуле Чернока-Эллисоиа.
В расчетах величиной  обычно пренебрегают, считая ее незначительной (что правомерно для условий глубокой воды и ограниченной глубины, но приводит к некоторым погрешностям для условий мелкой воды) по сравнению с напряжением тпов [236], и коэффициент аэродинамического сопротивления определяют по выражению
обычно пренебрегают, считая ее незначительной (что правомерно для условий глубокой воды и ограниченной глубины, но приводит к некоторым погрешностям для условий мелкой воды) по сравнению с напряжением тпов [236], и коэффициент аэродинамического сопротивления определяют по выражению

Исследования по определению коэффициента в натурных и лабораторных условиях, а также теоретические разработки этого вопроса и обобщения накопленных материалов выполняются и в настоящее время.
Многочисленные оценки коэффициента  приведены в работах отечественных [20, 31, 113] и зарубежных [26, 41, 238, 246] исследователей.
приведены в работах отечественных [20, 31, 113] и зарубежных [26, 41, 238, 246] исследователей.
Для примера на рис. 1.1 представлены некоторые из полученных зависимостей коэффициента  от скорости ветра. Рисунок
от скорости ветра. Рисунок
убедительно показывает различия в закономерностях изменения и числовых значениях коэффициента  Причиной столь больших расхождений полученных результатов по оценкам
Причиной столь больших расхождений полученных результатов по оценкам  исследователи считают отсутствие учета шероховатости подстилающей поверхности, степени подвижности выступов, различия температуры воды и воздуха и других факторов [20, 31]. Достигнуты определенные успехи в учете влияния некоторых из перечисленных факторов на закономерности изменения и асболютные значения коэффициента.
исследователи считают отсутствие учета шероховатости подстилающей поверхности, степени подвижности выступов, различия температуры воды и воздуха и других факторов [20, 31]. Достигнуты определенные успехи в учете влияния некоторых из перечисленных факторов на закономерности изменения и асболютные значения коэффициента.

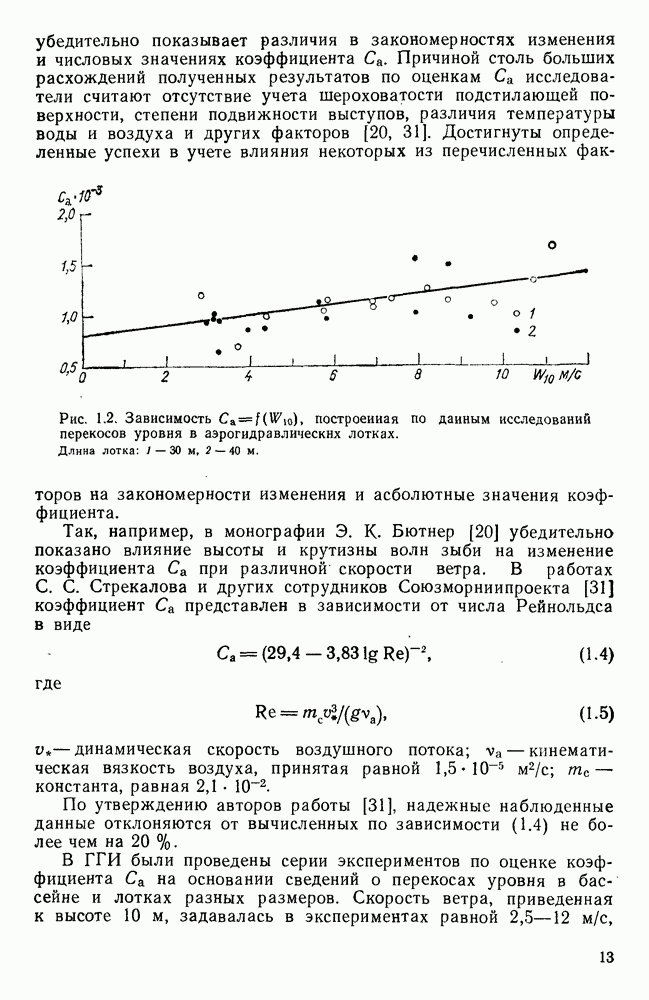
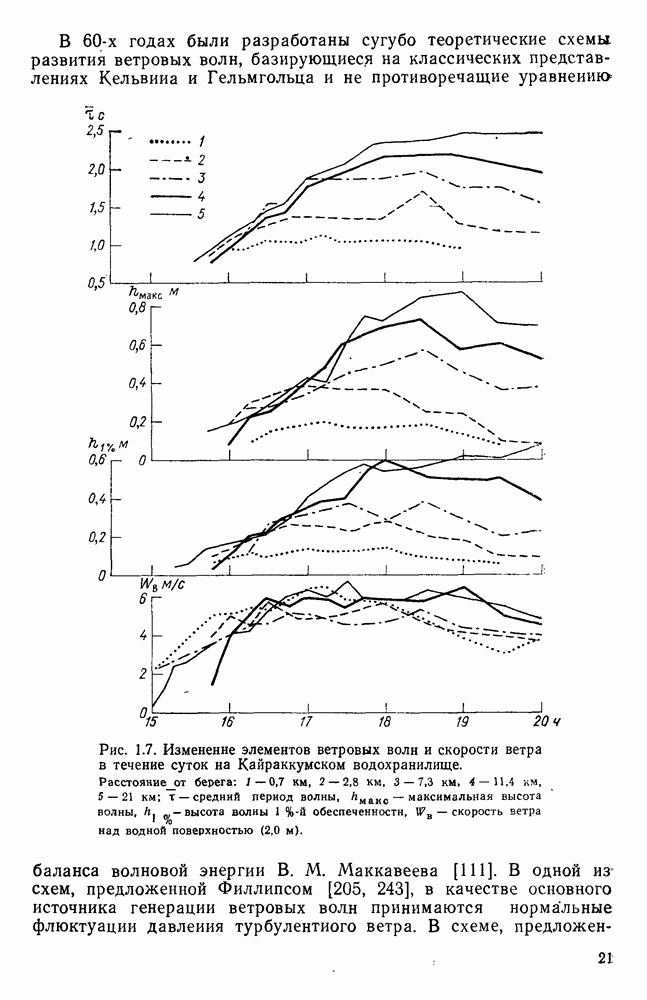
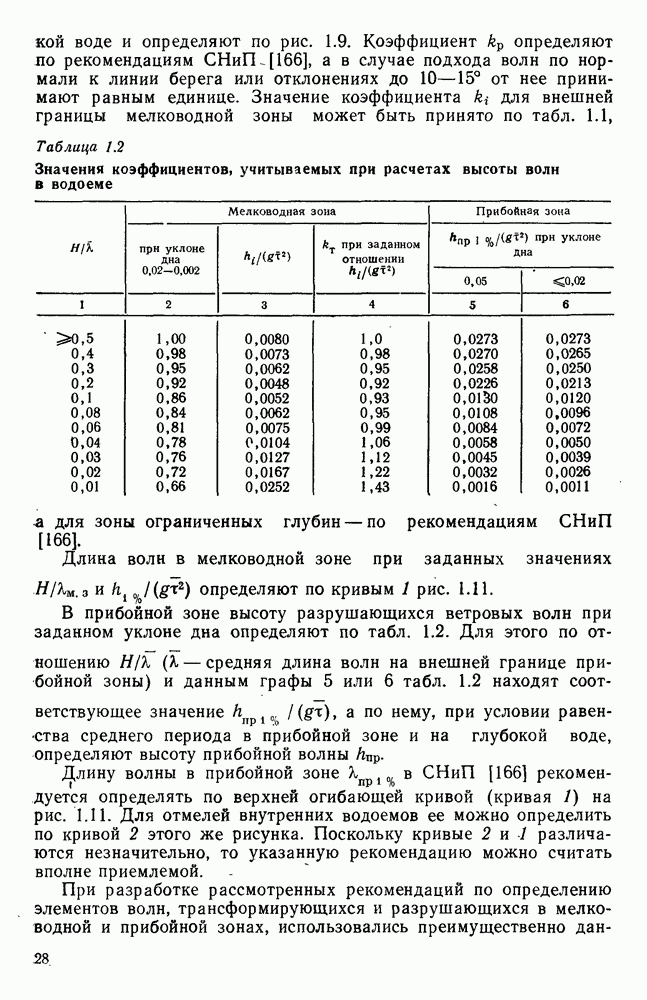
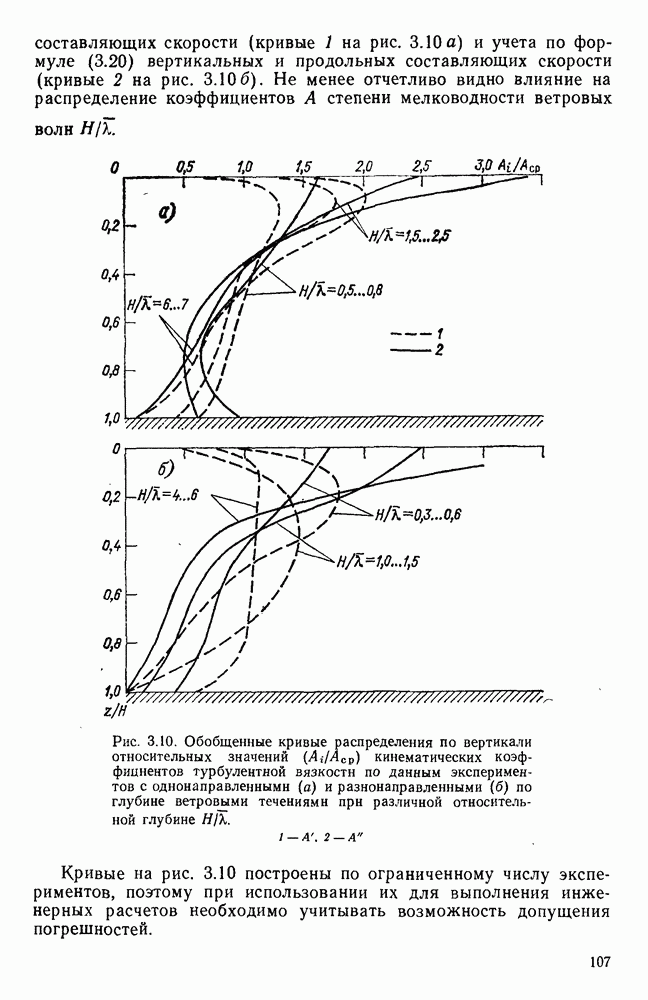
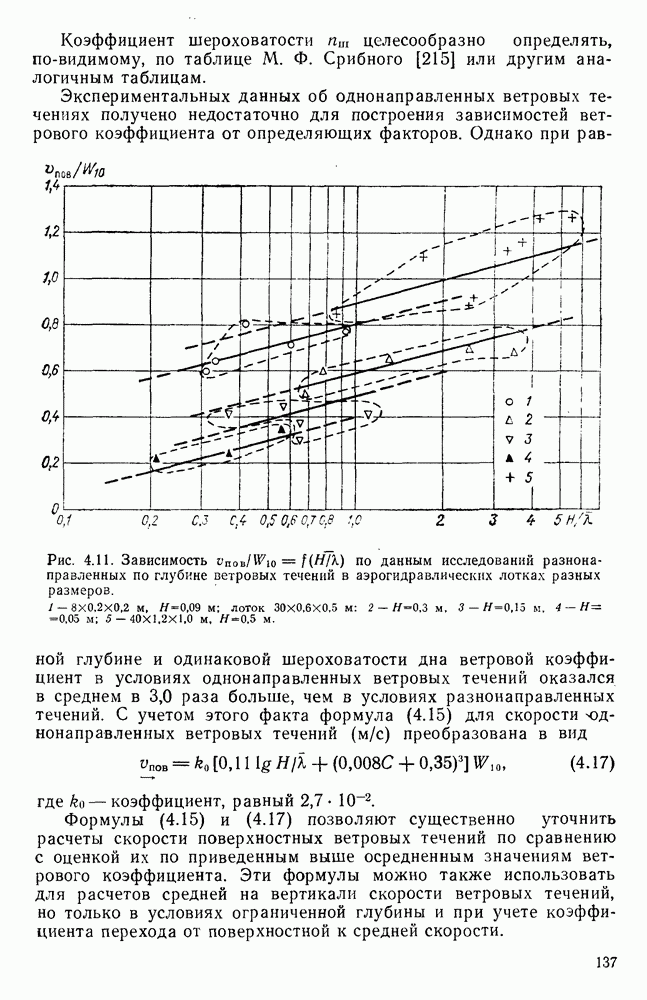
Рис. 1.2. Зависимость  построенная по данным исследований перекосов уровня в аэрогидравлическнх лотках. Длина лотка:
построенная по данным исследований перекосов уровня в аэрогидравлическнх лотках. Длина лотка: 
Так, например, в монографии Э. К. Бютнер [20] убедительно показано влияние высоты и крутизны волн зыби на изменение коэффициента  при различной скорости ветра. В работах С. С. Стрекалова и других сотрудников Союзморниипроекта [31] коэффициент
при различной скорости ветра. В работах С. С. Стрекалова и других сотрудников Союзморниипроекта [31] коэффициент  представлен в зависимости от числа Рейнольдса в виде
представлен в зависимости от числа Рейнольдса в виде

где

 динамическая скорость воздушного потока;
динамическая скорость воздушного потока;  кинематическая вязкость воздуха, принятая равной
кинематическая вязкость воздуха, принятая равной  константа, равная
константа, равная 
По утверждению авторов работы [31], надежные наблюденные данные отклоняются от вычисленных по зависимости (1.4) не более чем на 
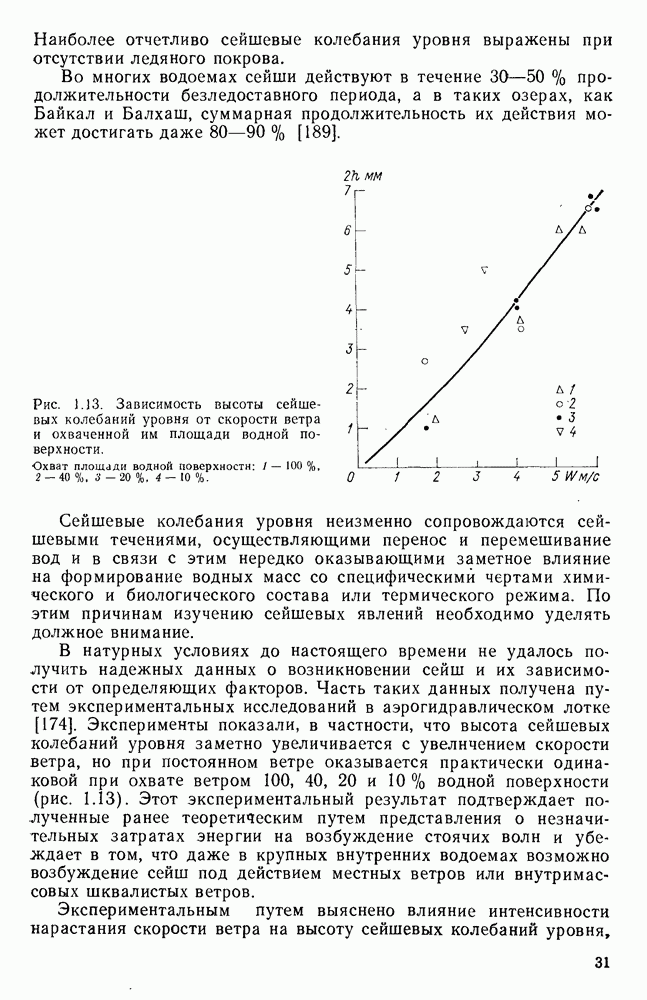
В ГГИ были проведены серии экспериментов по оценке коэффициента  на основании сведений о перекосах уровня в бассейне и лотках разных размеров. Скорость ветра, приведенная к высоте
на основании сведений о перекосах уровня в бассейне и лотках разных размеров. Скорость ветра, приведенная к высоте  задавалась в экспериментах равной
задавалась в экспериментах равной 
а глубина  Данные экспериментов представлены на рис. 1.2. Осредненная прямая на рисунке может быть аналитически выражена в виде
Данные экспериментов представлены на рис. 1.2. Осредненная прямая на рисунке может быть аналитически выражена в виде

Ход этой зависимости наиболее близок к зависимостям Хайди и Плейта, By, Кайлегана [41] и др. С учетом этого обстоятельства и того, что эксперименты в бассейне и лотках ГГИ проводились преимущественно при очень малых размерах ветровых волн, выполнено осреднение данных ГГИ и данных названных авторов, и зависимость (1.6) представлена в следующем уточненном виде:


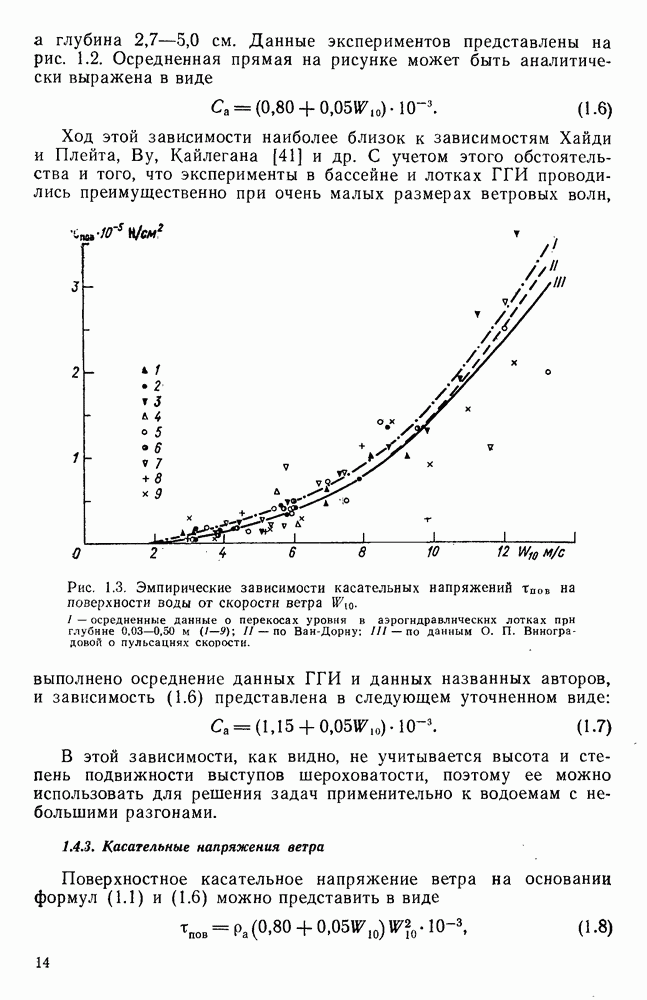
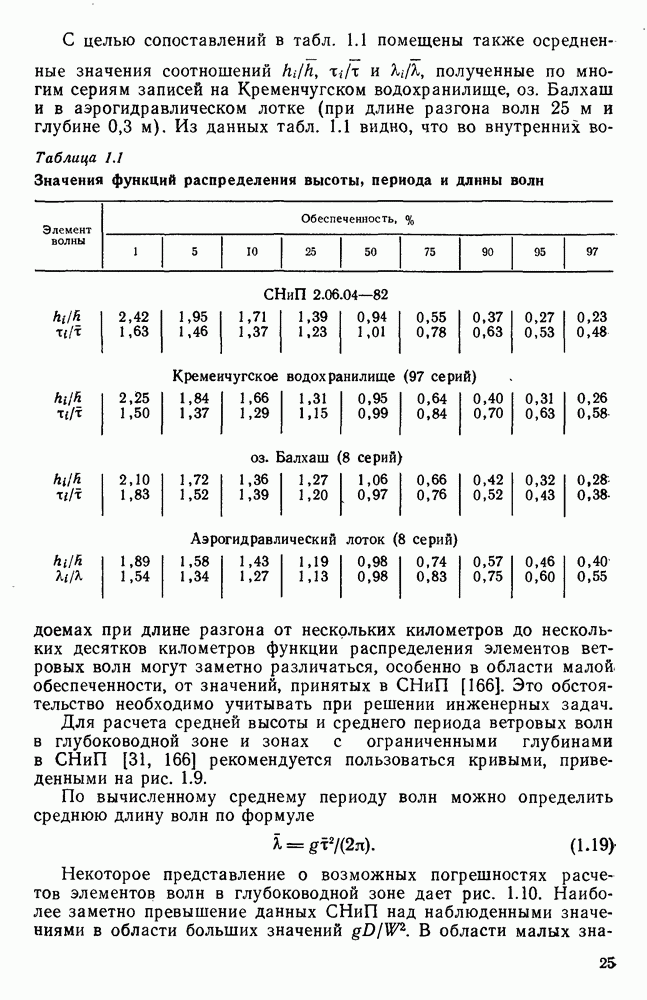
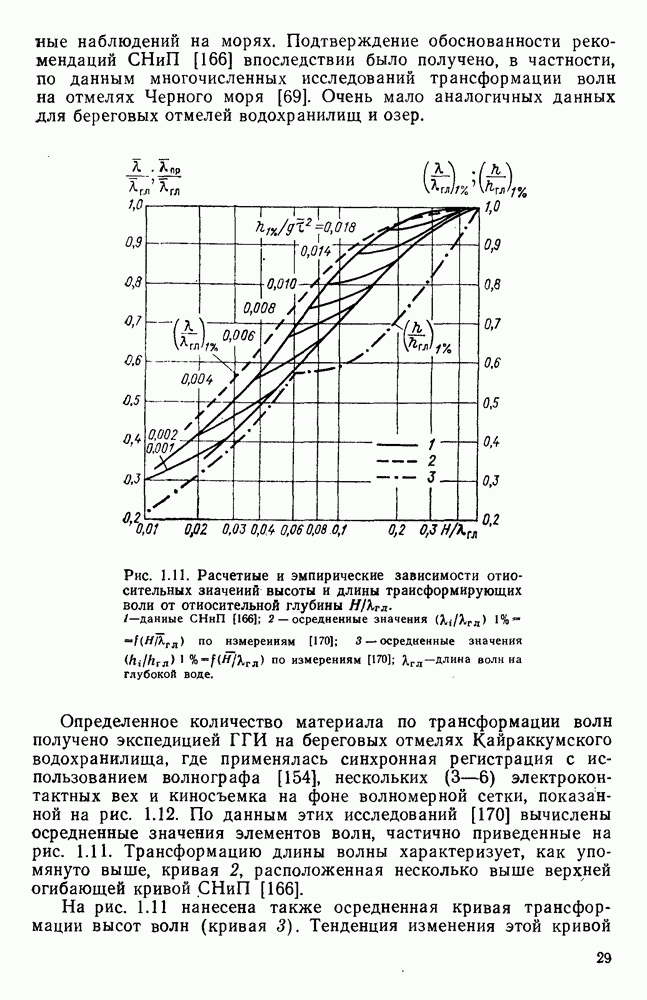
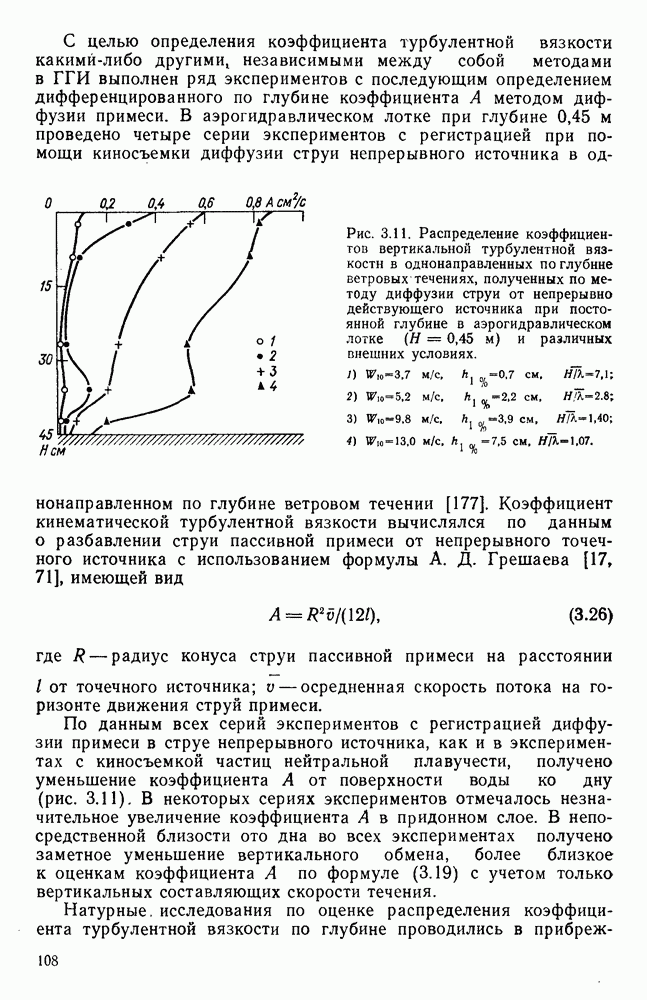
Рис. 1.3. Эмпирические зависимости касательных напряжений  на поверхности воды от скорости ветра
на поверхности воды от скорости ветра  осредненные данные о перекосах уровня в аэрогндравлнческнх лотках при глубине 0,03-0,50 м (1-9); II - по Ван-Дорну; III - по данным О. П. Виноградовой о пульсациях скорости.
осредненные данные о перекосах уровня в аэрогндравлнческнх лотках при глубине 0,03-0,50 м (1-9); II - по Ван-Дорну; III - по данным О. П. Виноградовой о пульсациях скорости.
В этой зависимости, как видно, не учитывается высота и степень подвижности выступов шероховатости, поэтому ее можно использовать для решения задач применительно к водоемам с небольшими разгонами.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ВОЗДЕЙСТВИЕ ВЕТРА И ВОЛНОВЫЕ ПРОЦЕССЫ
- 1.1. Методы изучения взаимодействующих сложных явлений и процессов
- 1.2. Масштабы динамических явлений
- 1.3. Причины динамических явлений
- 1.4. Ветер над водной поверхностью
- 1.4.2. Коэффициент аэродинамического сопротивления
- 1.4.3. Касательные напряжения ветра
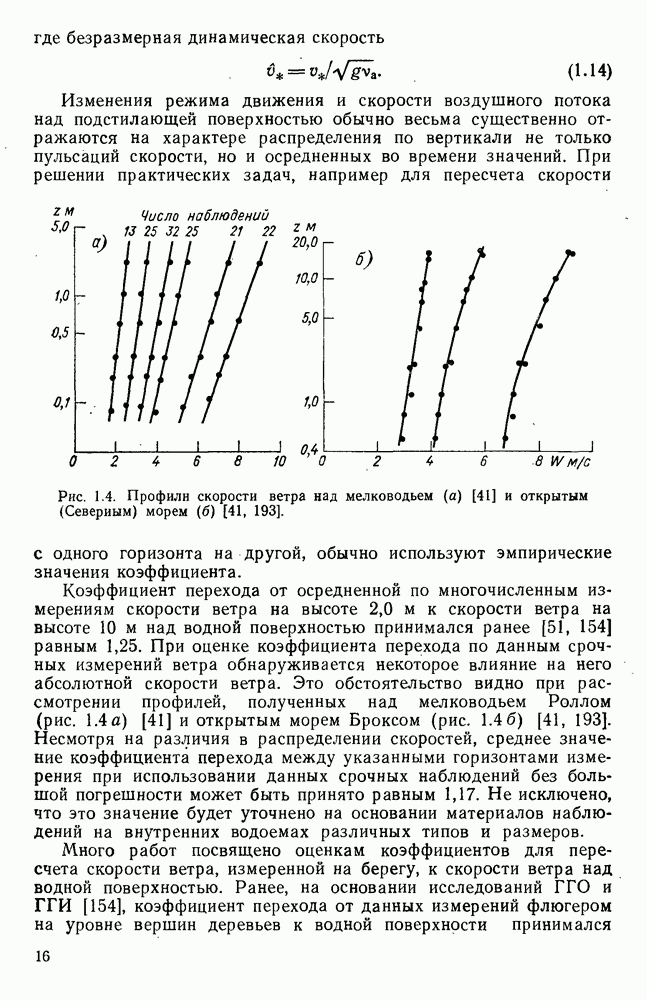
- 1.4.4. Профили ветра и их трансформация над подстилающей поверхностью
- 1.4.5. Режимные статистические и расчетные характеристики ветра
- 1.5. Ветровые волны
- 1.5.2. Классификация волн и их элементов
- 1.5.3. Расчет элементов ветровых волн и учет их изменчивости
- 1.6. Стоячие волны
- 1.6.2. Основные элементы волн и их аналитическое выражение
- 1.6.3. Периоды сейшевых колебаний уровня
- 1.6.4. Затухание стоячих колебаний уровня во времени
- 1.7. Внутренние волны
- 1.8. Сгонно-нагонные явления
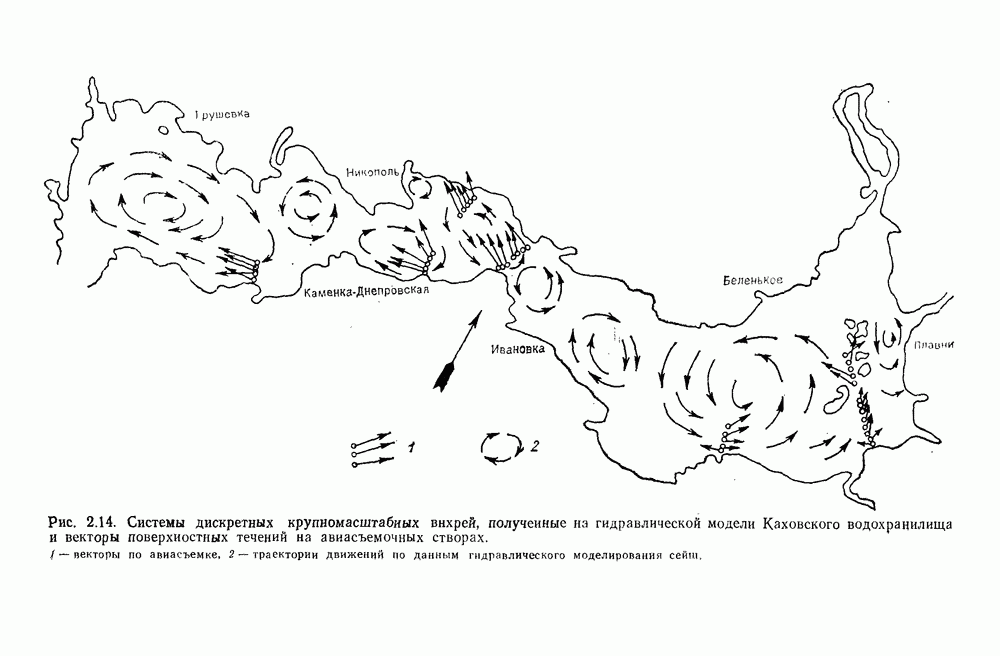
- Глава 2. ПРОСТРАНСТВЕННАЯ СТРУКТУРА ПЕРЕНОСА ВОД ТЕЧЕНИЯМИ
- 2.1. Многообразие видов движений и масштабов пространственных структур
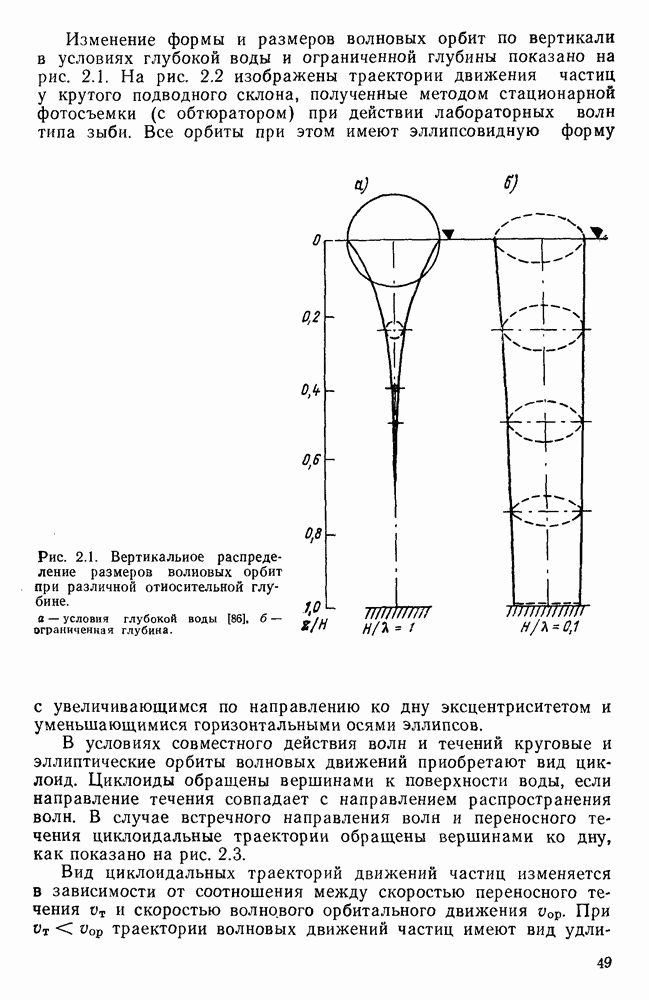
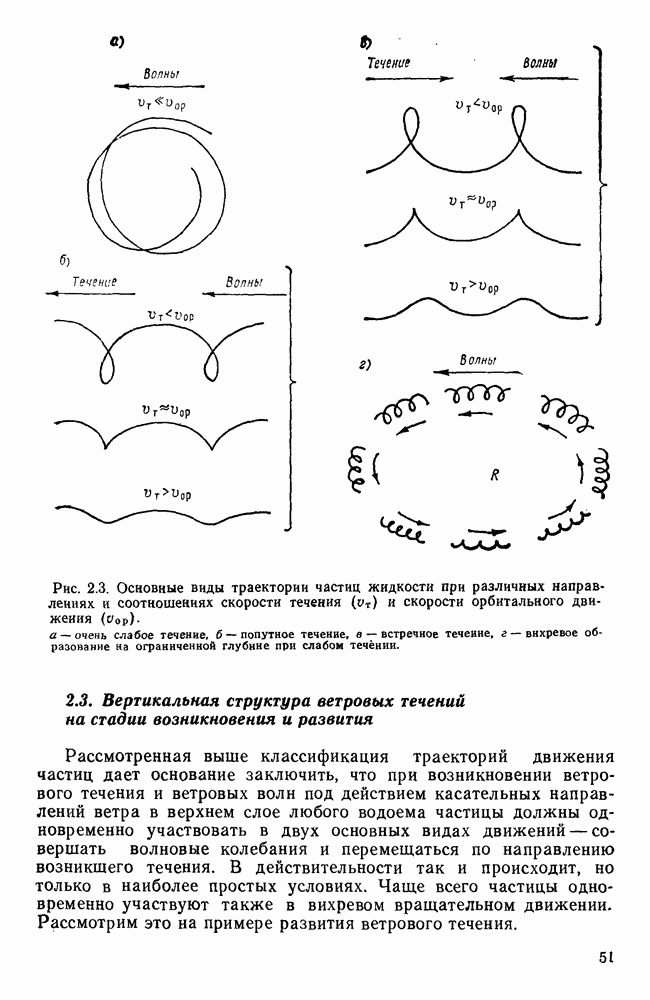
- 2.2. Траектории движений частиц жидкости при совместном действии волн и течений
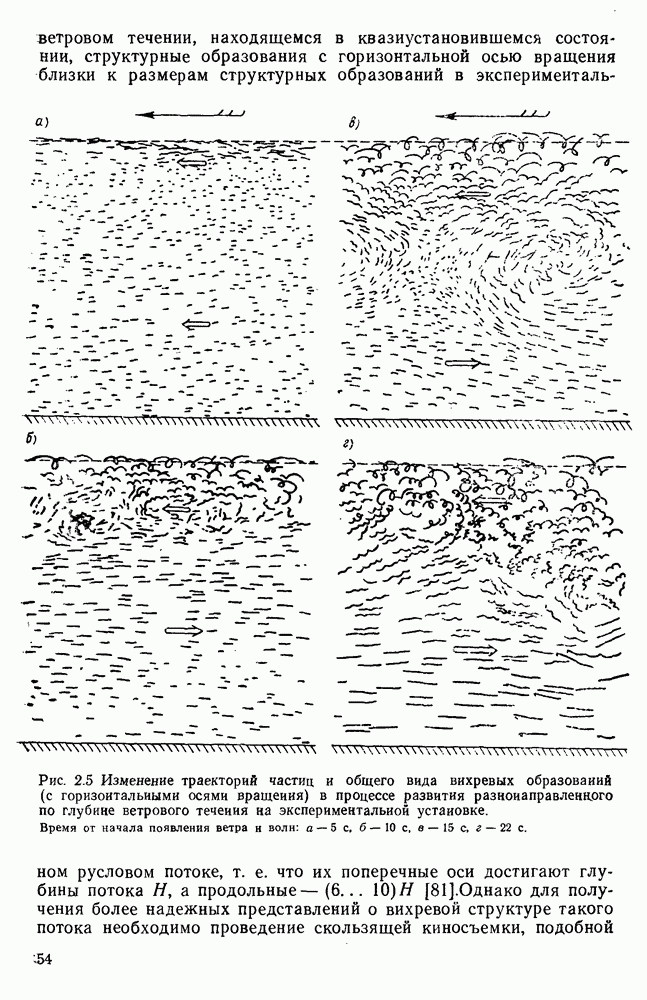
- 2.3. Вертикальная структура ветровых течений на стадии возникновения и развития
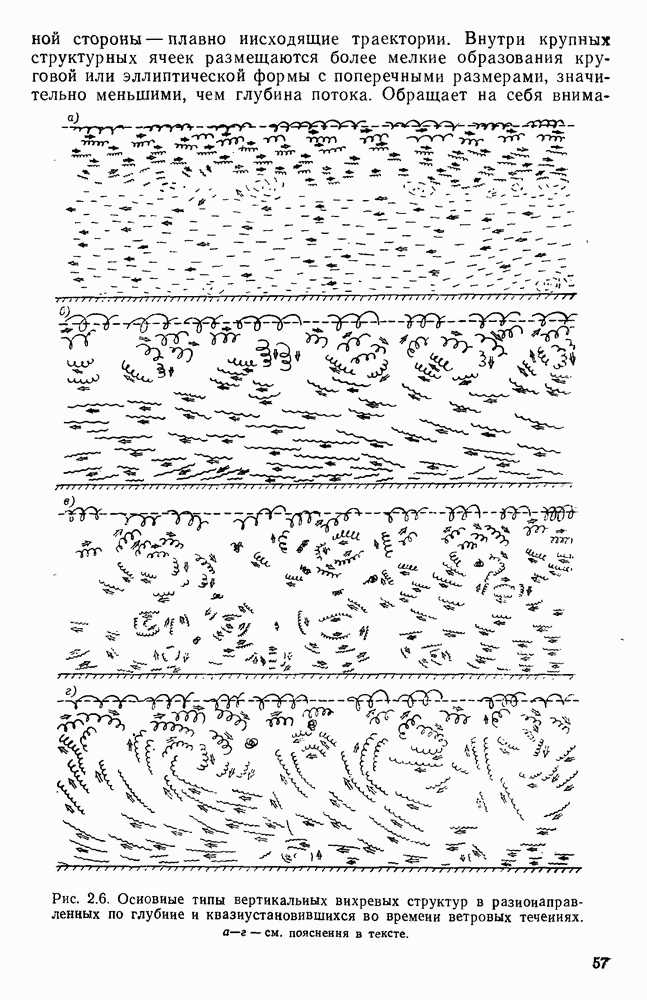
- 2.4. Вертикальная структура квазиустановившихся ветровых течений
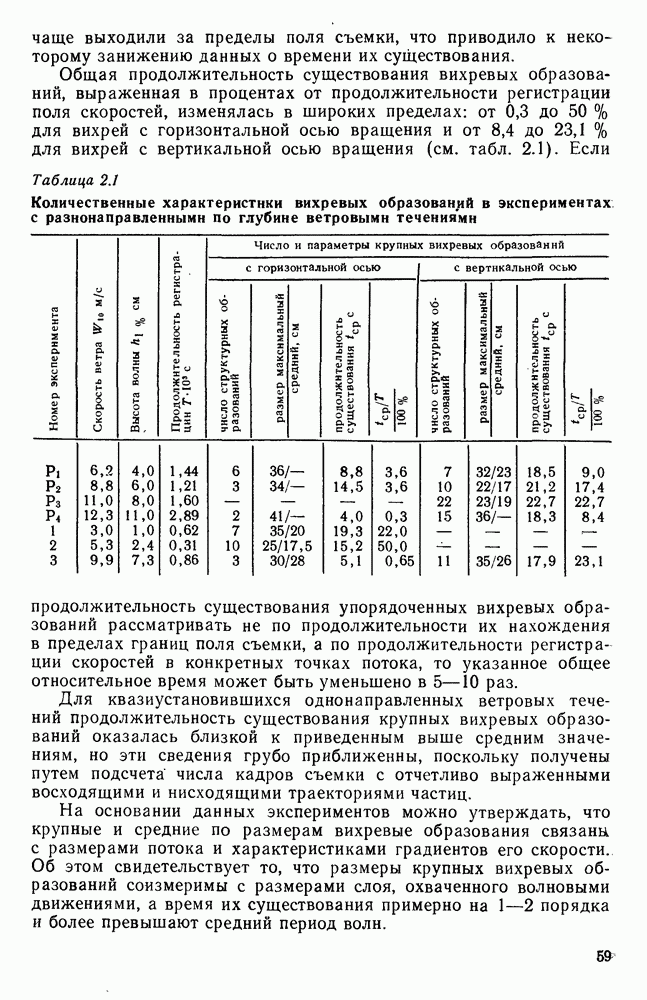
- 2.5. Количественные характеристики вертикальных вихревых образований
- 2.6. Макроциркуляция вод в водоеме при ветровых течениях
- 2.7. Макроциркуляция вод в заливе при ветровых течениях
- 2.8. Инерционные и синоптические вихри
- 2.9. Формирование циркуляций транзитным потоком и затухающей речной струей
- 2.10. Структура сейшевых течений
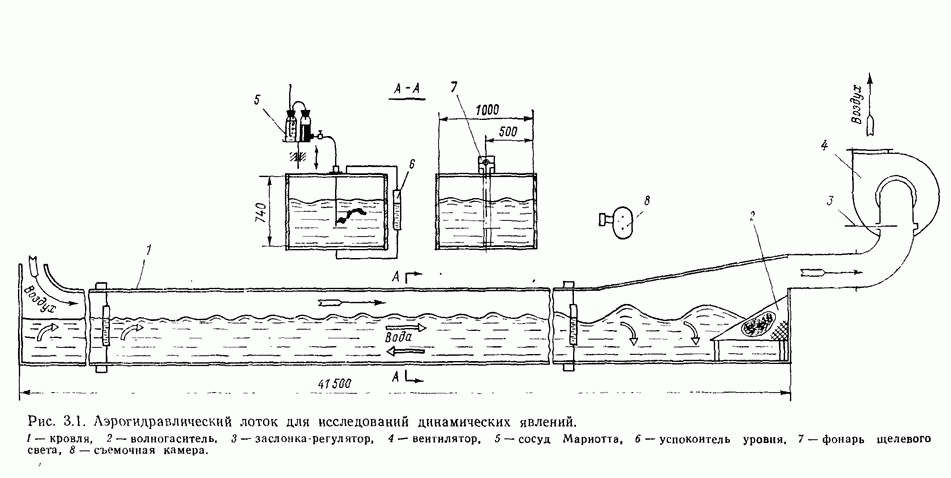
- Глава 3. КИНЕМАТИКА ВЕТРОВЫХ И СУММАРНЫХ ТЕЧЕНИЙ
- 3.1. Совершенствование представлений о кинематике течений
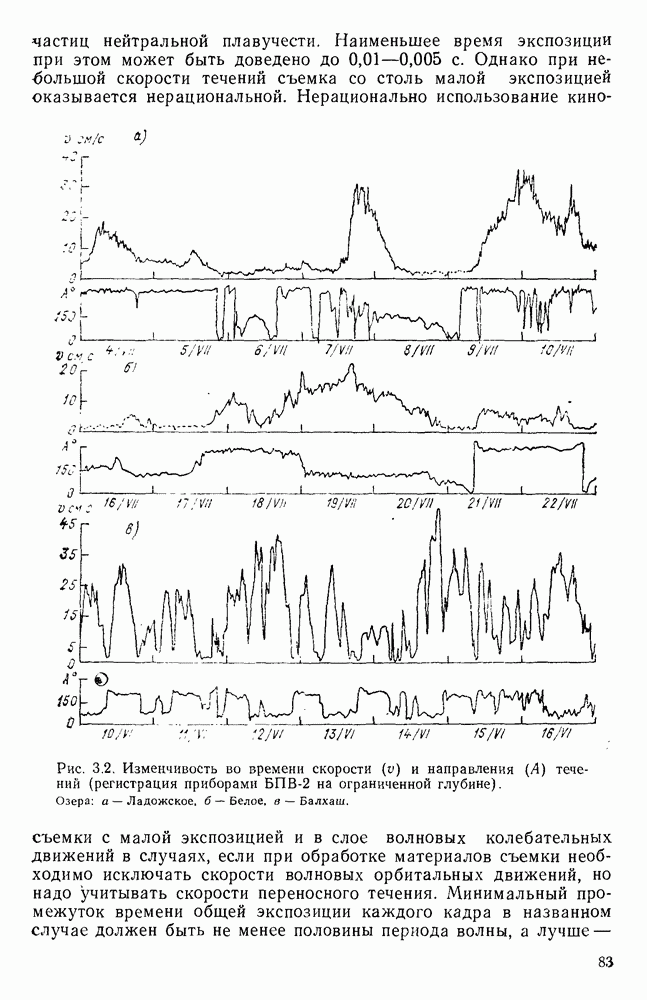
- 3.2. Методы исследований кинематики течений
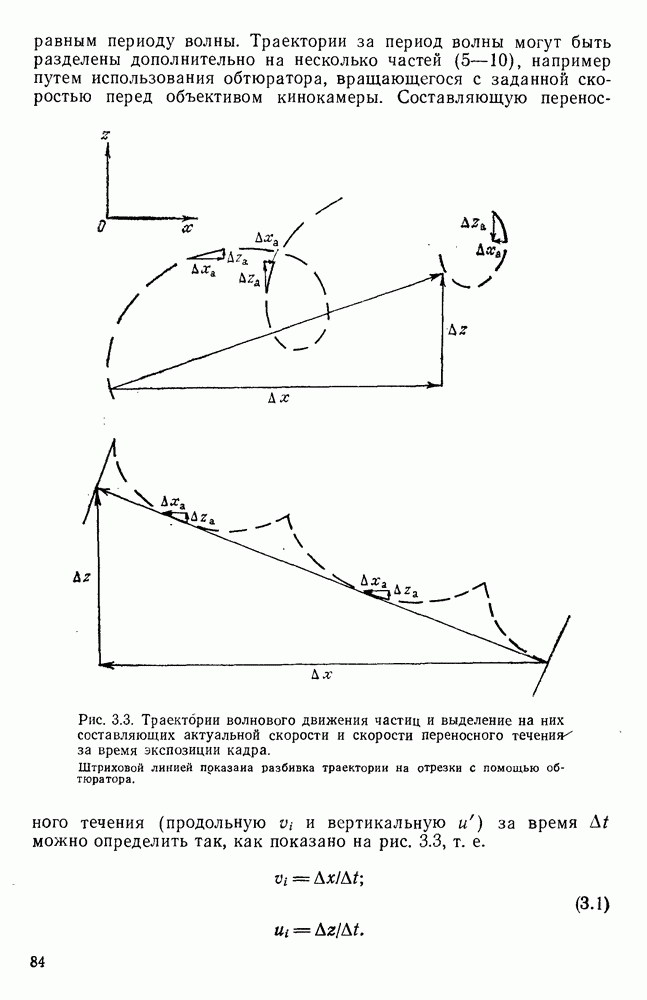
- 3.3. Методика обработки записей течений
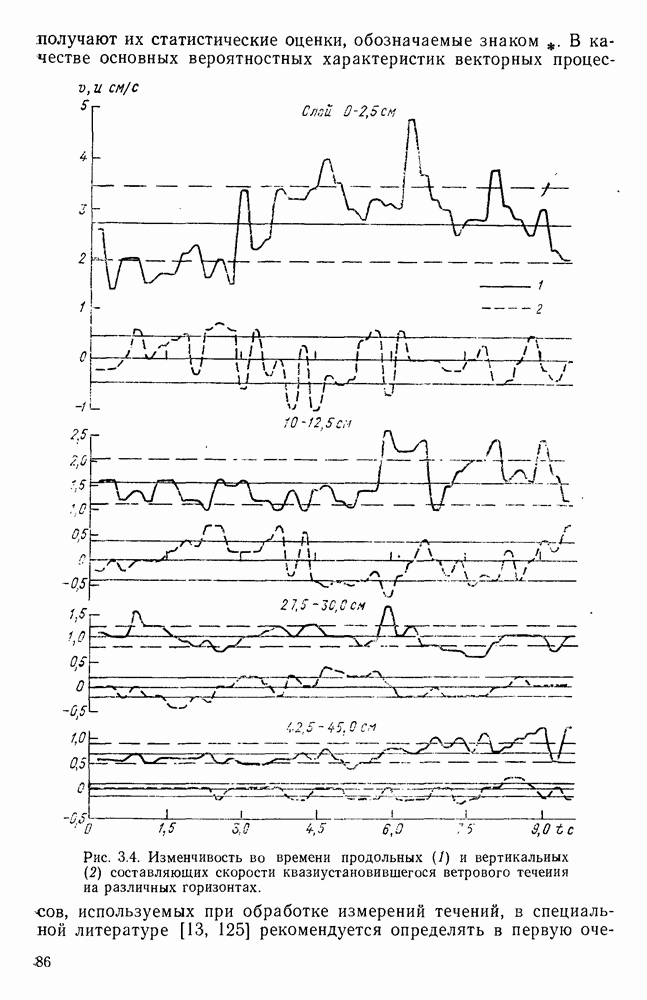
- 3.4. Оценка кинематических характеристик
- 3.5. Изменение мелкомасштабных пульсаций скорости во времени и по глубине
- 3.6. Изменение средних квадратических значений пульсационных составляющих скорости
- 3.7. Вертикальное распределение моментов корреляции в ветровых течениях
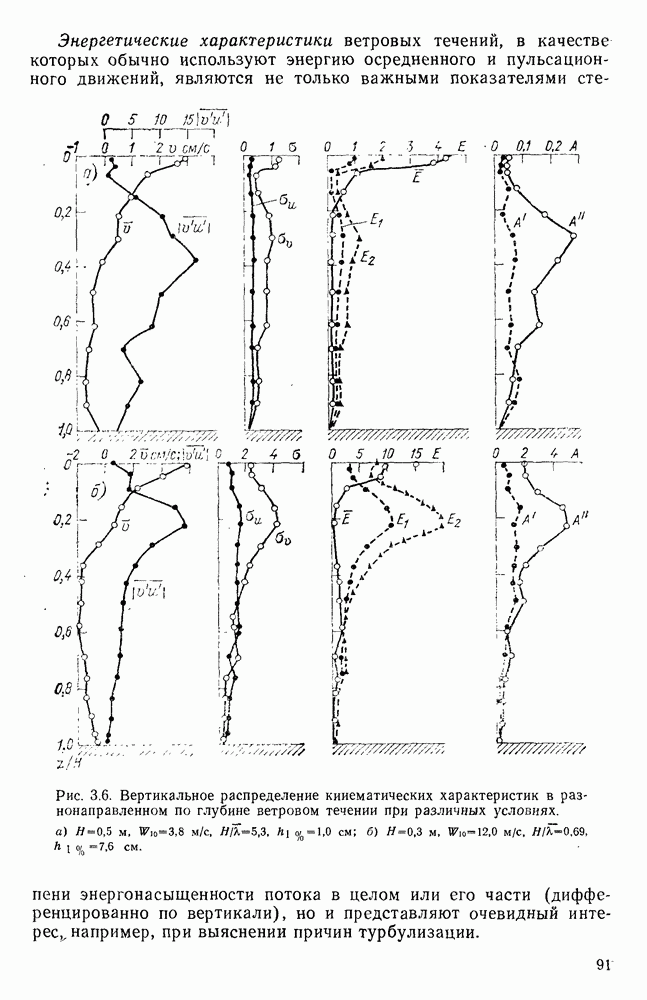
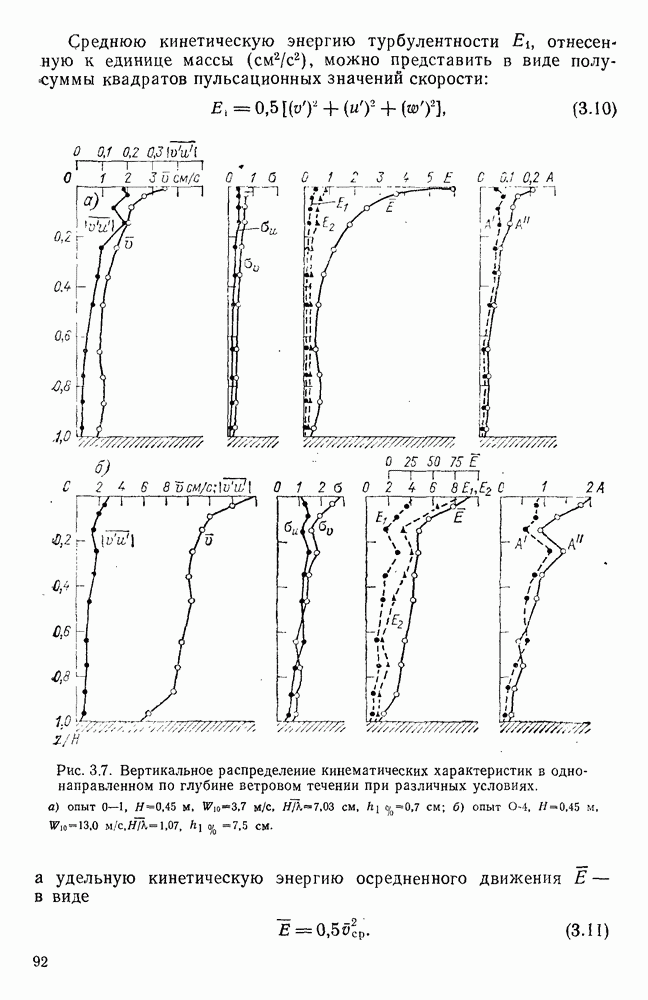
- 3.8. Энергетические характеристики ветровых течений по данным экспериментов
- 3.9. Коэффициенты вертикальной турбулентной вязкости и методы их оценки
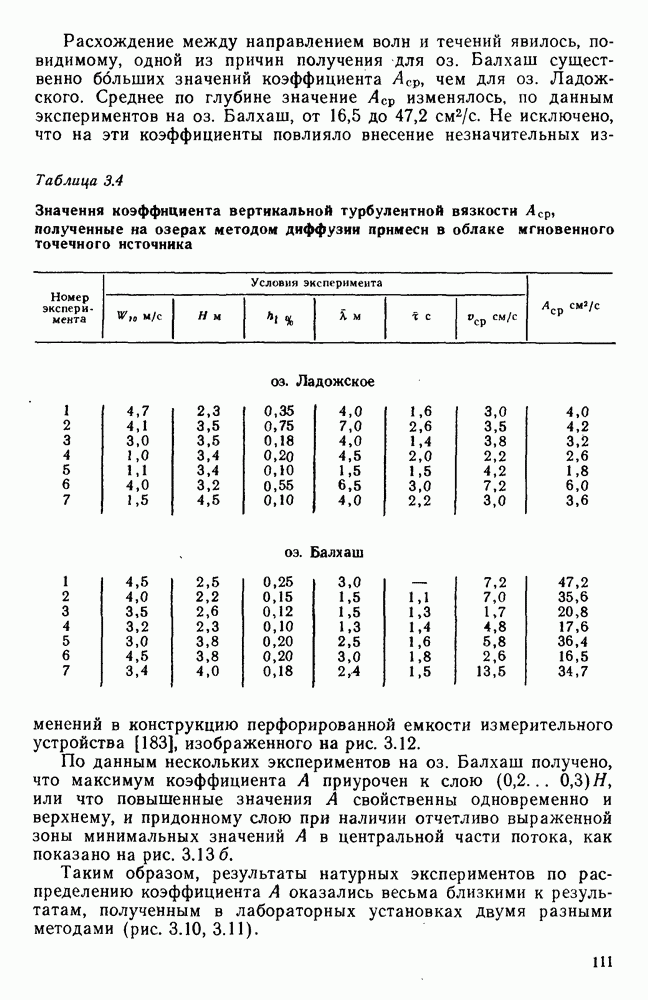
- 3.10. Распределение коэффициента вертикальной турбулентной вязкости
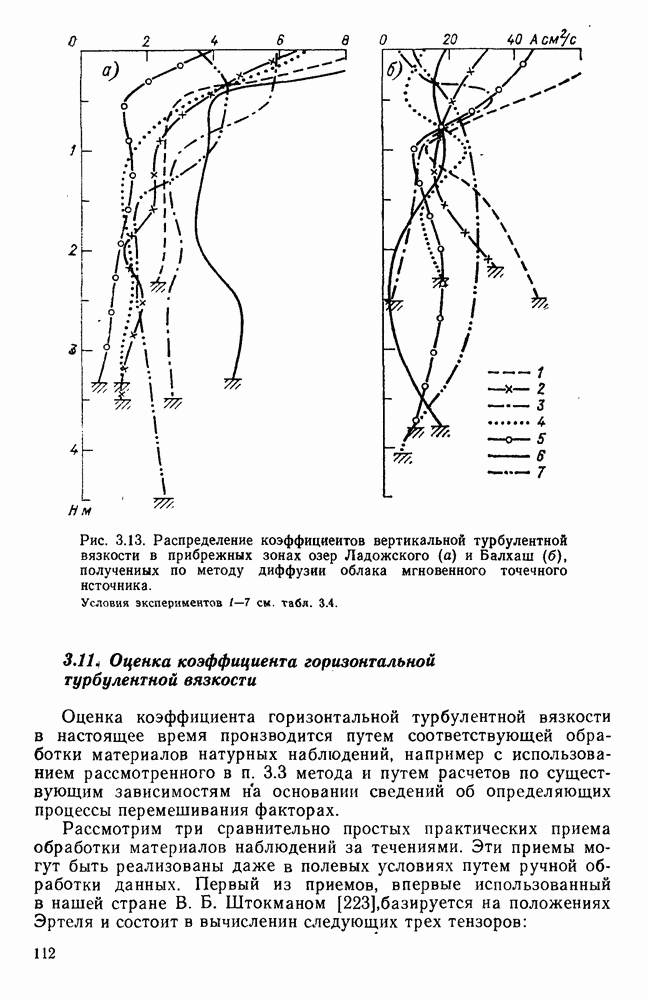
- 3.11. Оценка коэффициента горизонтальной турбулентной вязкости
- Глава 4. ВЕТРОВЫЕ ТЕЧЕНИЯ В УСЛОВИЯХ РАЗВИТИЯ И СТАБИЛИЗАЦИИ
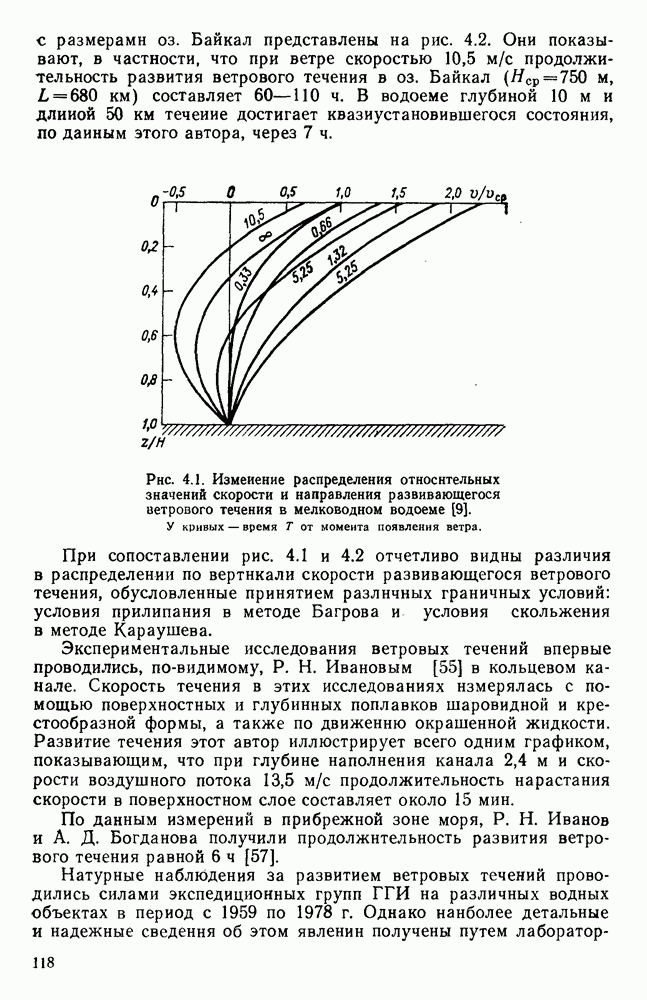
- 4.1. Совершенствование представлений о развитии ветровых течений
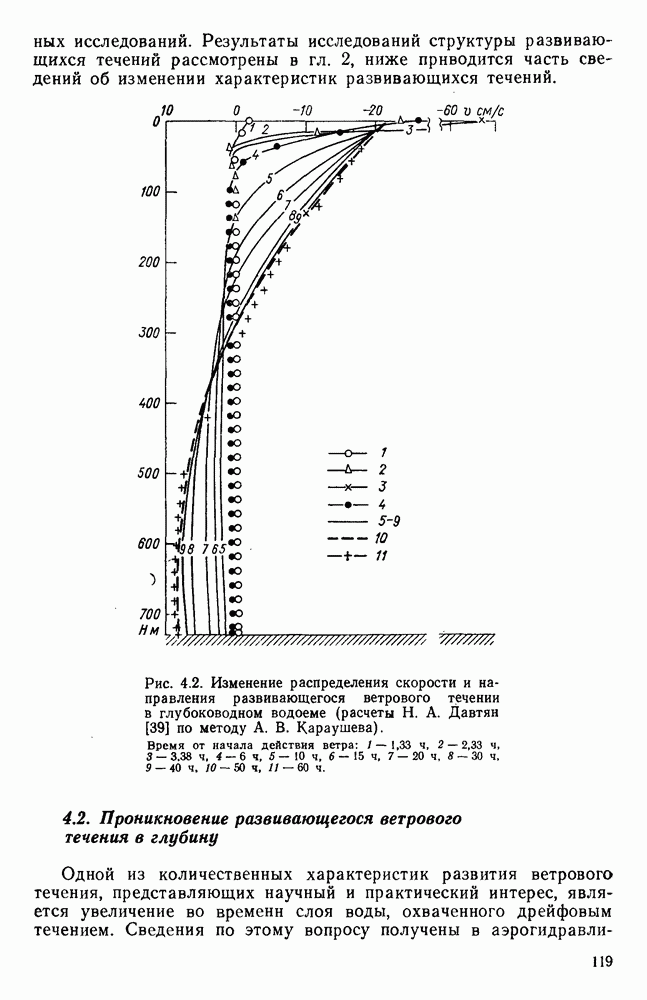
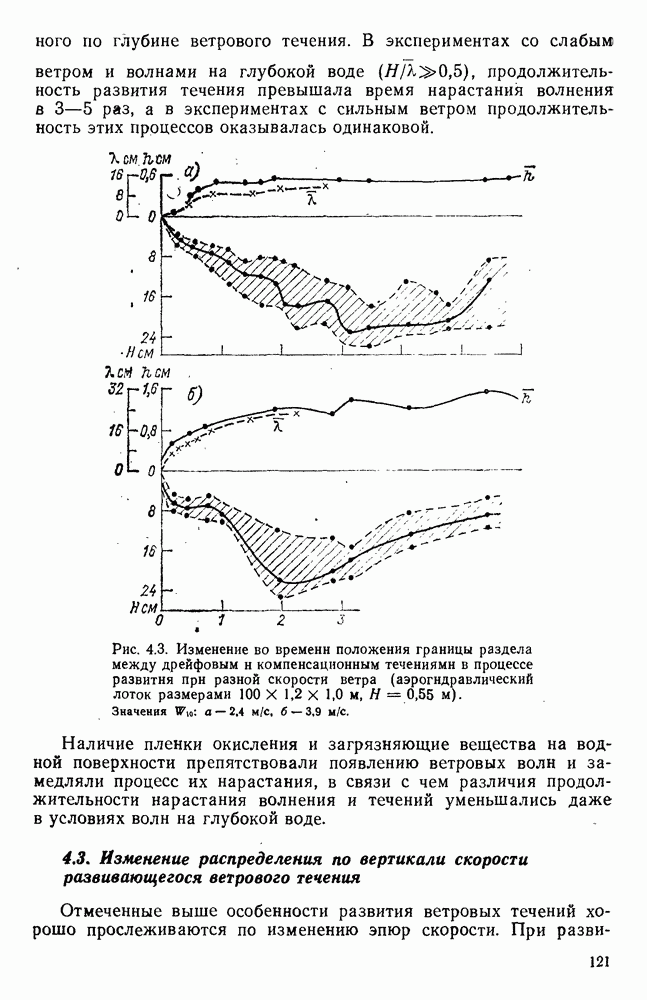
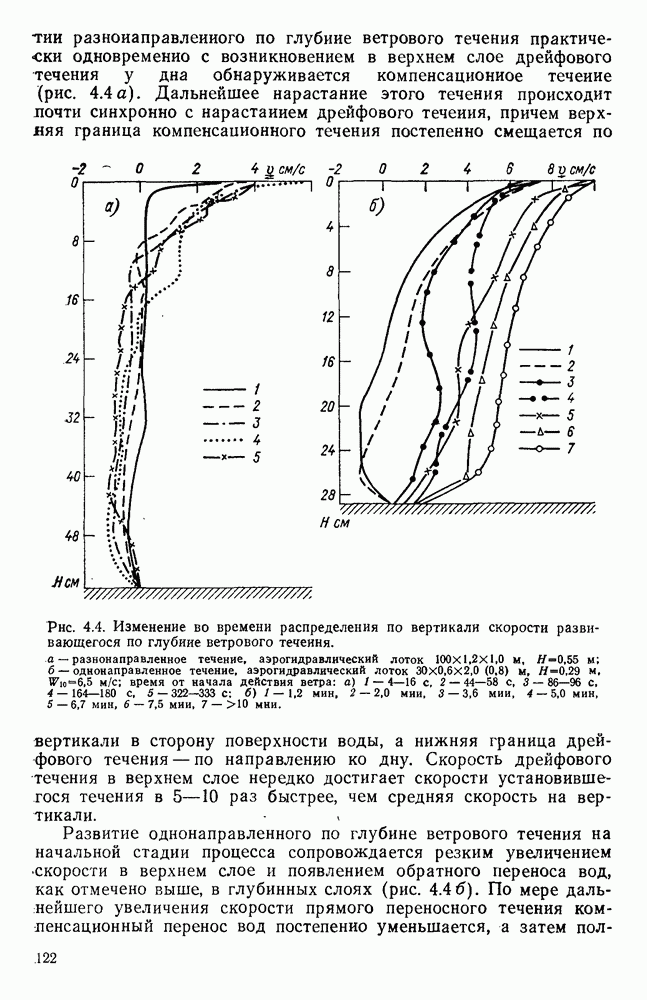
- 4.2. Проникновение развивающегося ветрового течения в глубину
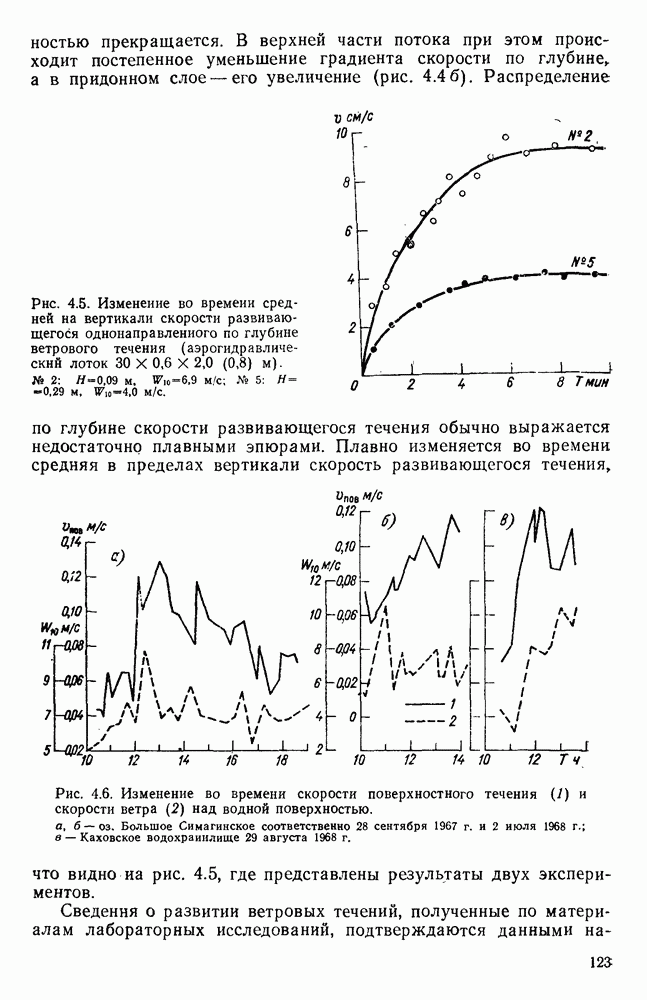
- 4.3. Изменение распределения по вертикали скорости развивающегося ветрового течения
- 4.4. Изменение во времени средней скорости развивающегося ветрового течения
- 4.5. Продолжительность развития ветрового течения
- 4.6. Изменение скорости ветрового течения по пути разгона волн
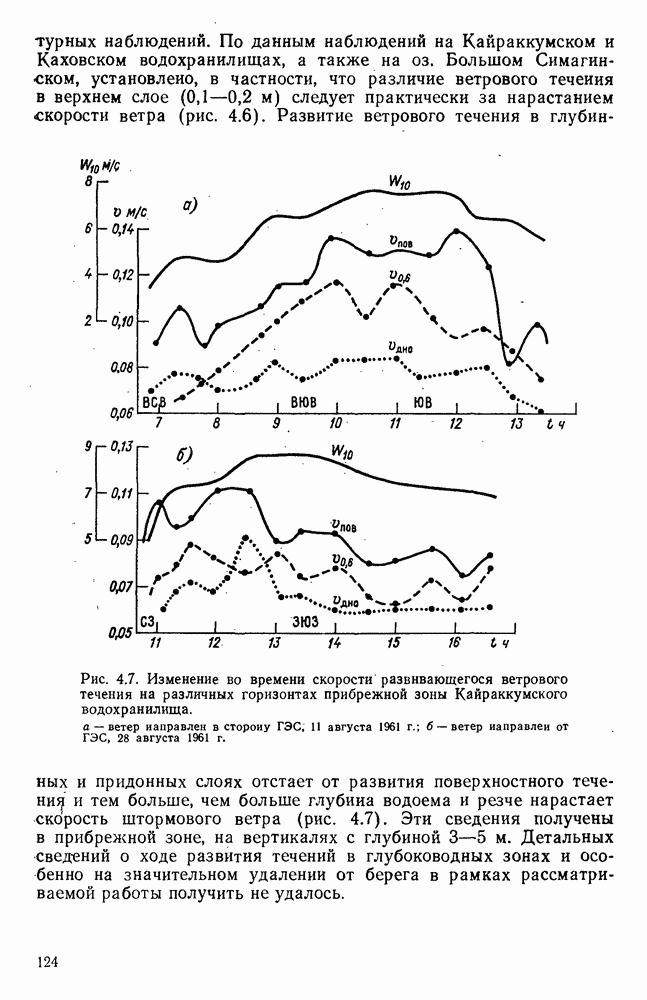
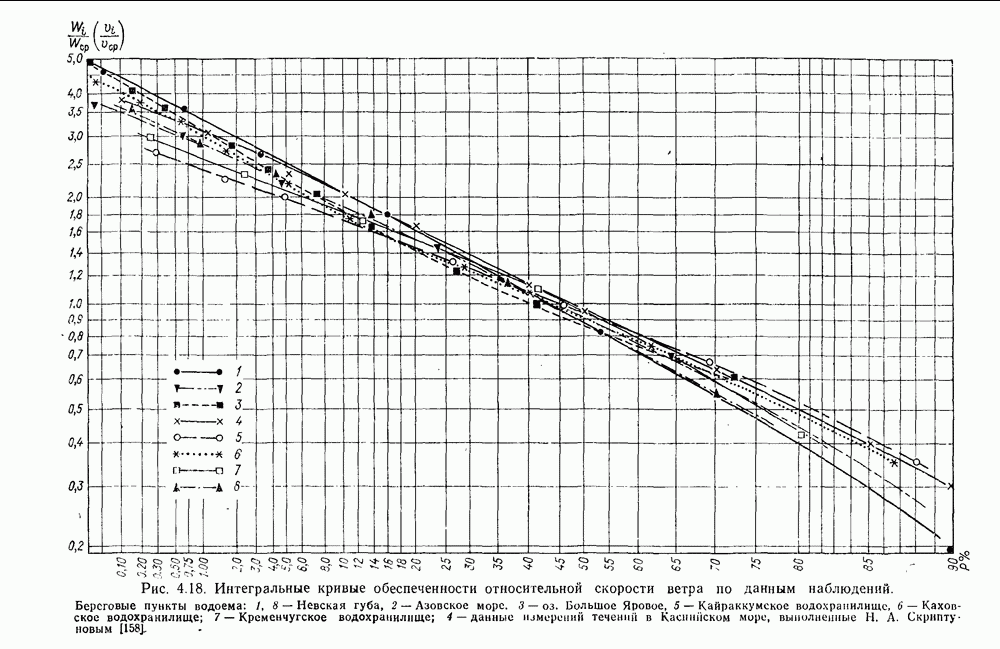
- 4.7. Соотношение между скоростями ветрового течения и ветра
- 4.7.2. Ветровой коэффициент для прибрежных зон морей и океанов
- 4.7.3. Ветровой коэффициент для морских заливов
- 4.7.4. Ветровой коэффициент для внутренних водоемов
- 4.8. Оценка влияния на поверхностное ветровое течение глубины и шероховатости дна водоема
- 4.9. Предельное проникновение ветрового течения в глубину
- 4.10. Отклонения направлений ветровых течений от направления ветра
- 4.11. Теоретические решения задачи о вертикальном распределении скорости ветровых течений
- 4.12. Распределение скорости квазиустановившихся ветровых течений по данным экспериментов
- 4.13. Перенос вод через вертикаль
- 4.14. Взаимодействие ветровых, стоковых и сейшевых течений
- 4.15. Соотношение переносов воды дрейфовым и волновым течениями
- 4.16. Установление режимных статистических характеристик течений
- 4.16.2. Выбор функций распределения скорости течения при ограниченных данных наблюдений
- 4.17. Внутренний водообмен при ветровых течениях
- 4.18. Моделирование ветровых течений
- 4.18.2. Математические модели течений и примеры их реализации
- 4.18.3. Физическое моделирование
- Глава 5. СЕЙШЕВЫЕ ТЕЧЕНИЯ
- 5.1. Основные черты и особенности сейшевых течений
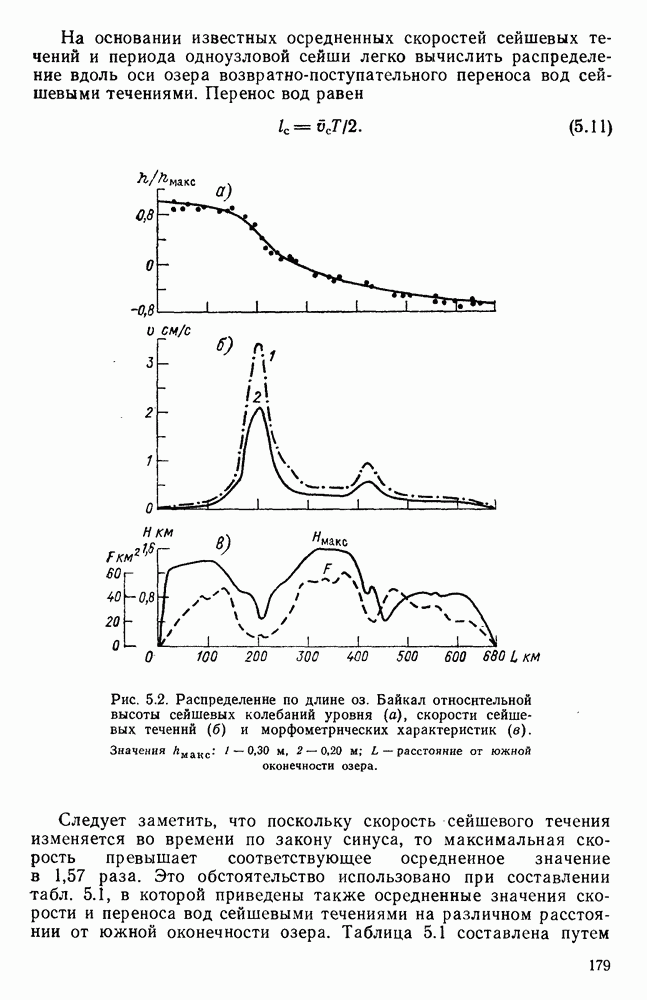
- 5.2. Методы оценки скорости сейшевого течения
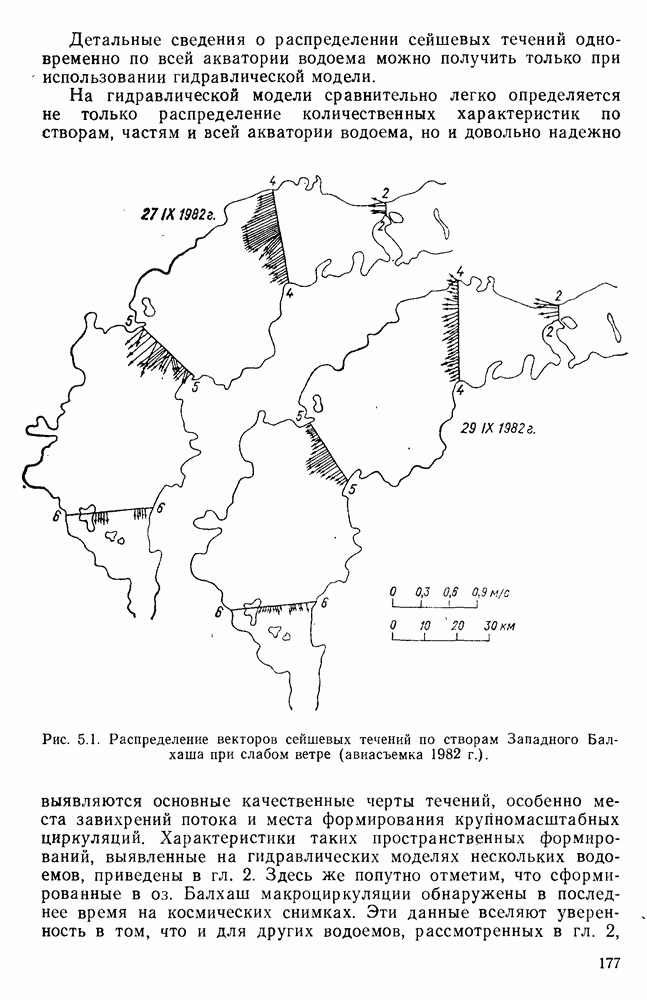
- 5.3. Распределение сейшевых течений по акватории водоема
- 5.4. Сейшевые течения в оз. Байкал
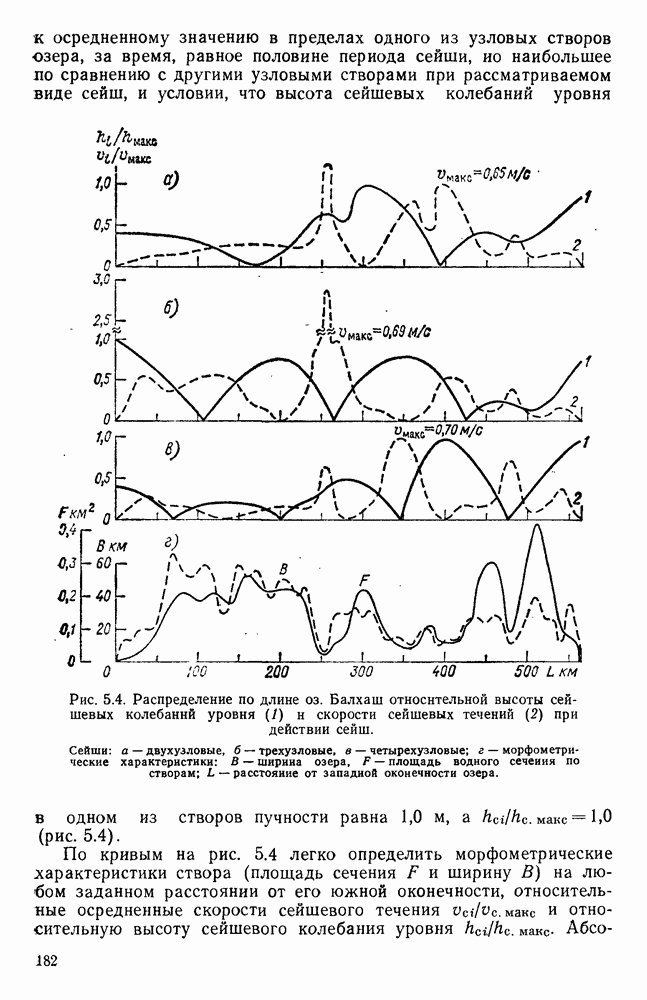
- 5.5. Сейшевые течения в оз. Балхаш
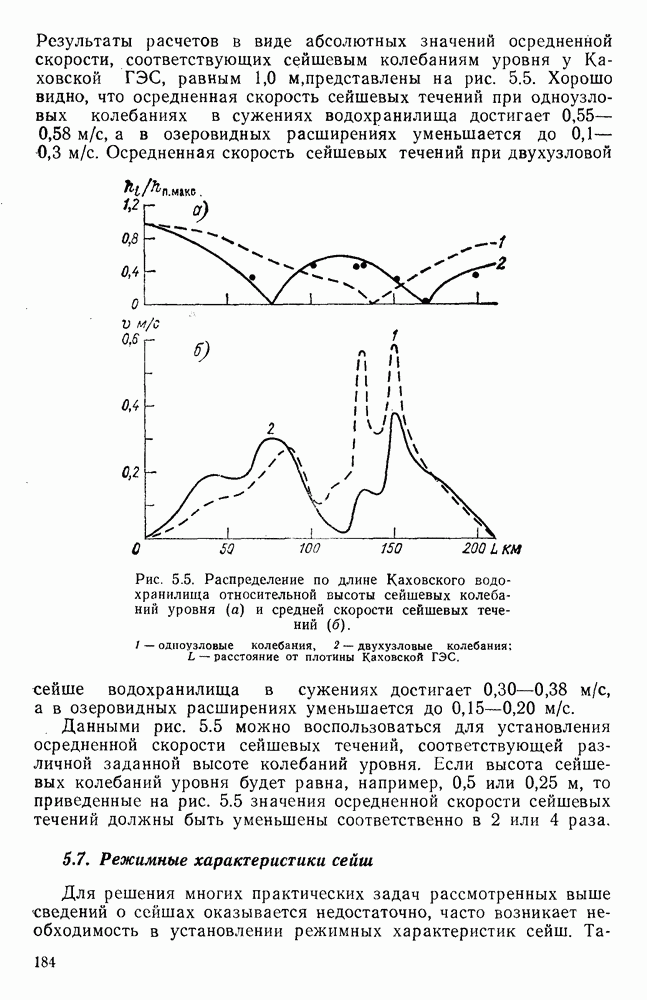
- 5.6. Сейшевые течения в Каховском водохранилище
- 5.7. Режимные характеристики сейш
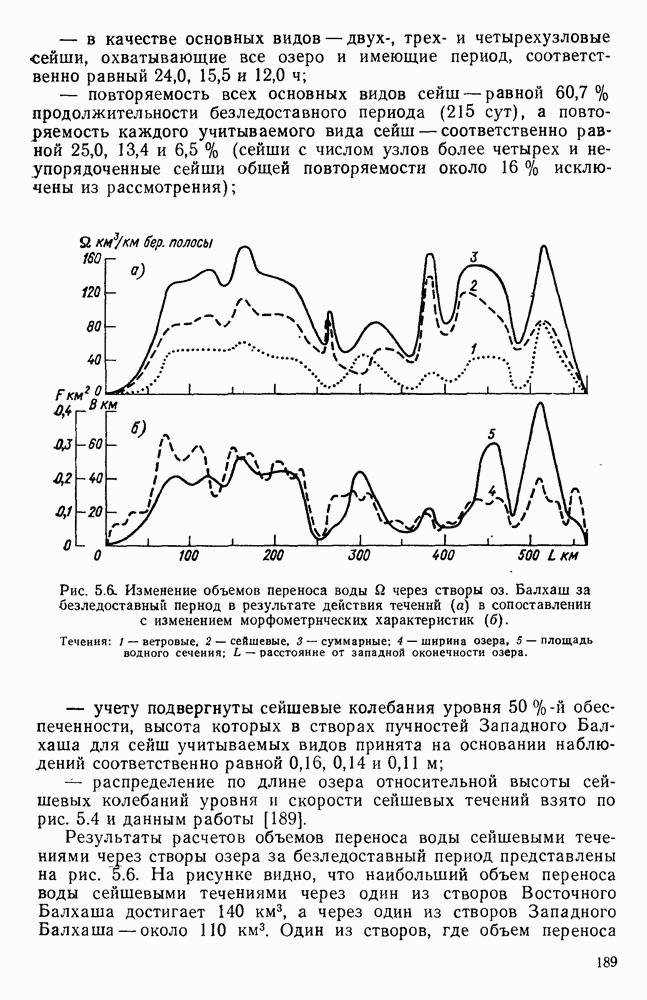
- 5.8. Объемы переноса вод сейшевыми течениями
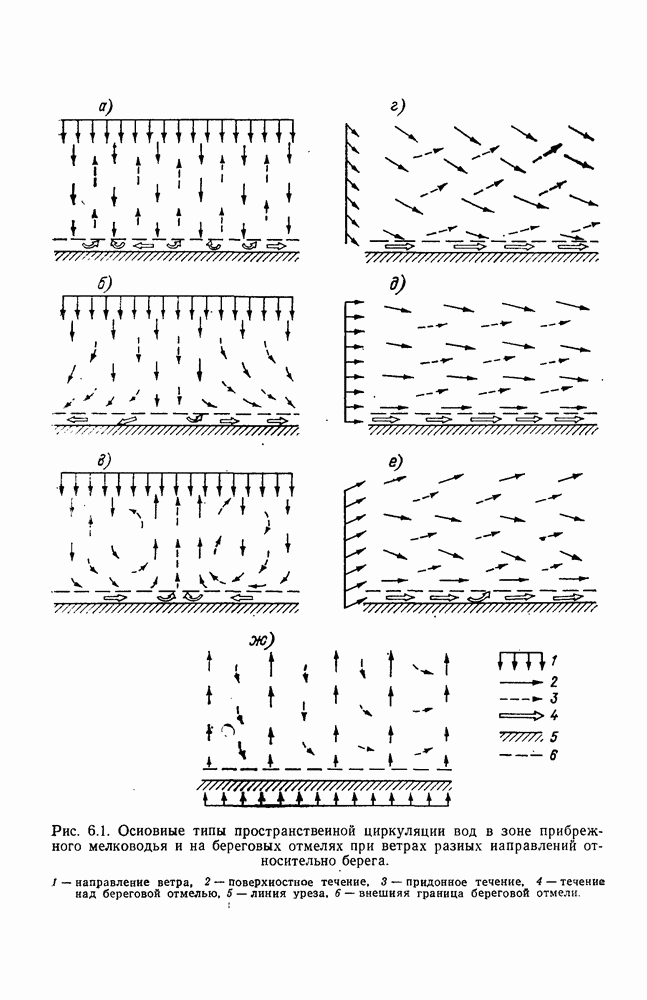
- Глава 6. ТЕЧЕНИЯ В ЗОНЕ ПРИБРЕЖНОГО МЕЛКОВОДЬЯ И НА БЕРЕГОВЫХ ОТМЕЛЯХ
- 6.2. Течения в зоне прибрежного мелководья
- 6.2.2. Повторяемость различных типов циркуляции вод
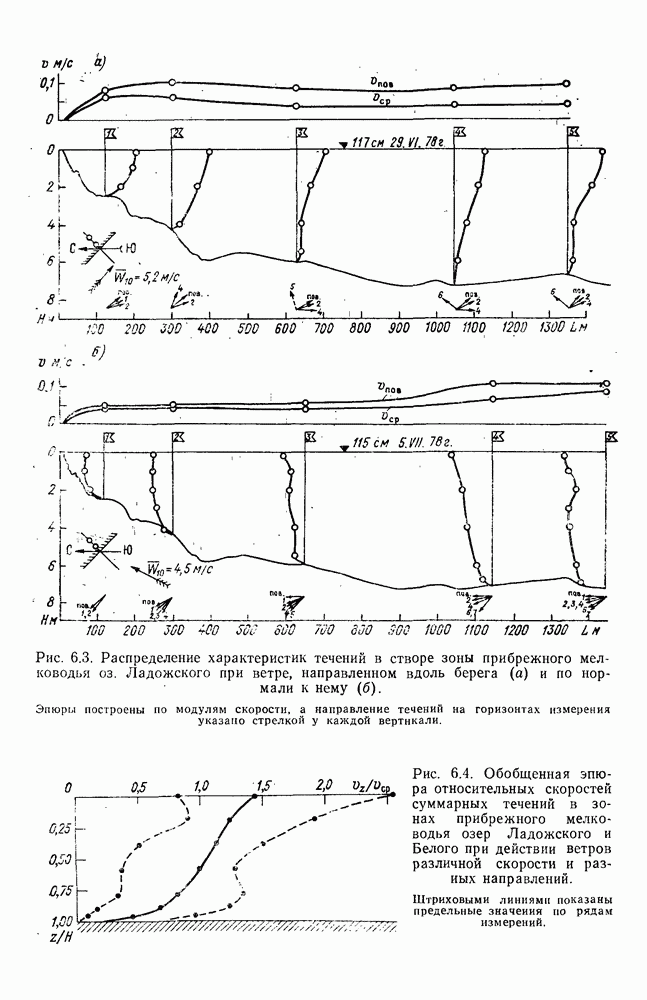
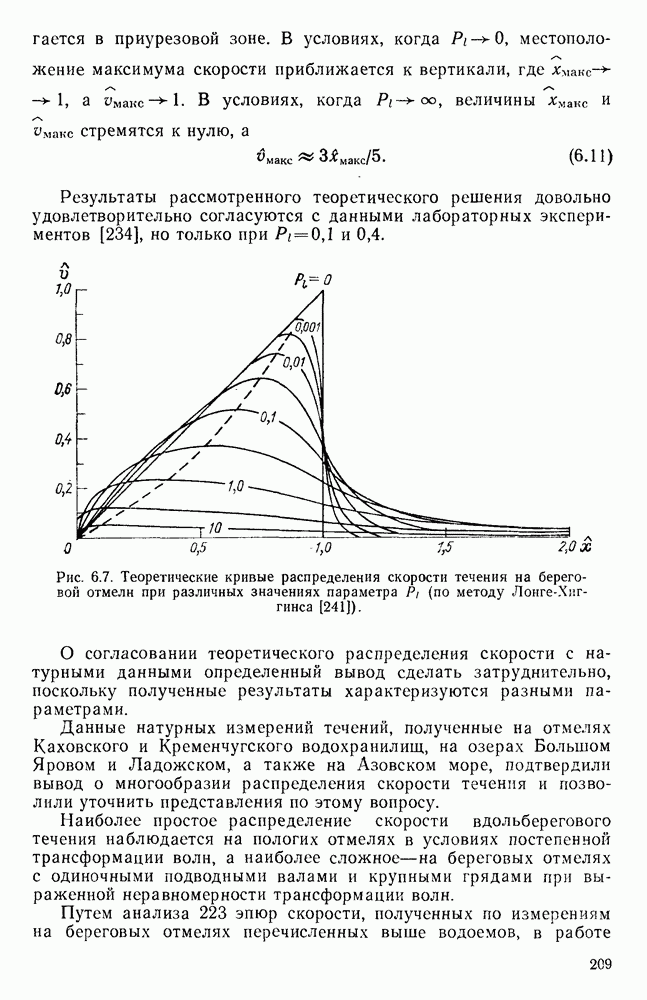
- 6.2.3. Распределение скорости течения по глубине
- 6.2.4. Изменение скорости течения по ширине зоны
- 6.2.5. Количественные характеристики скорости течения
- 6.2.6. Режимные статистические характеристики скорости течений
- 6.3. Течения на береговых отмелях
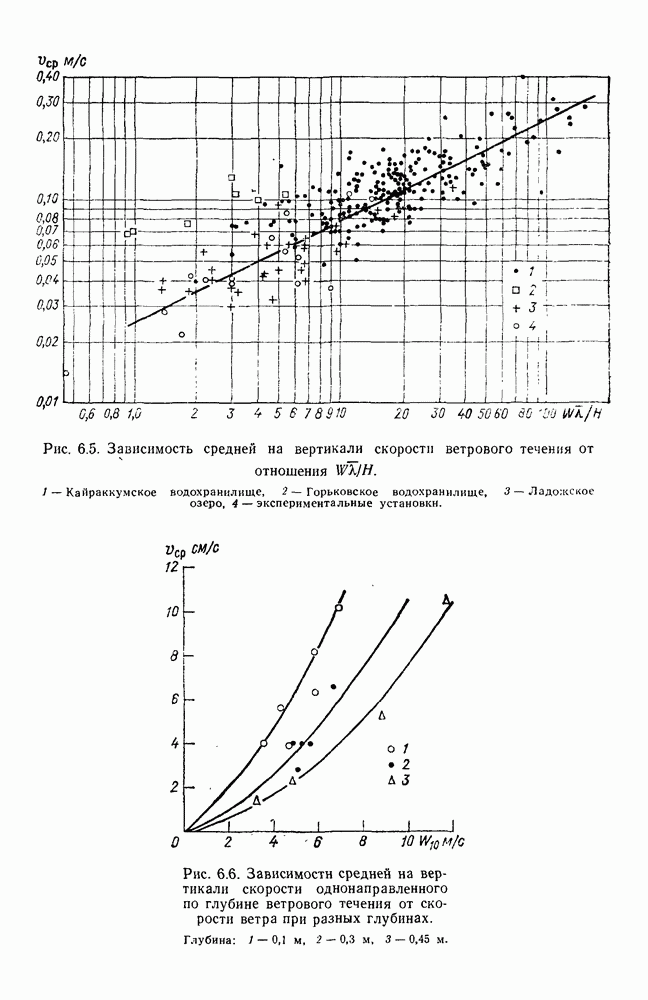
- 6.3.2. Распределение скорости вдольберегового течения
- 6.3.3. Расчет средней скорости вдольберегового течения
- Глава 7. ПЕРЕМЕЩЕНИЕ НАНОСОВ НА БЕРЕГОВЫХ ОТМЕЛЯХ
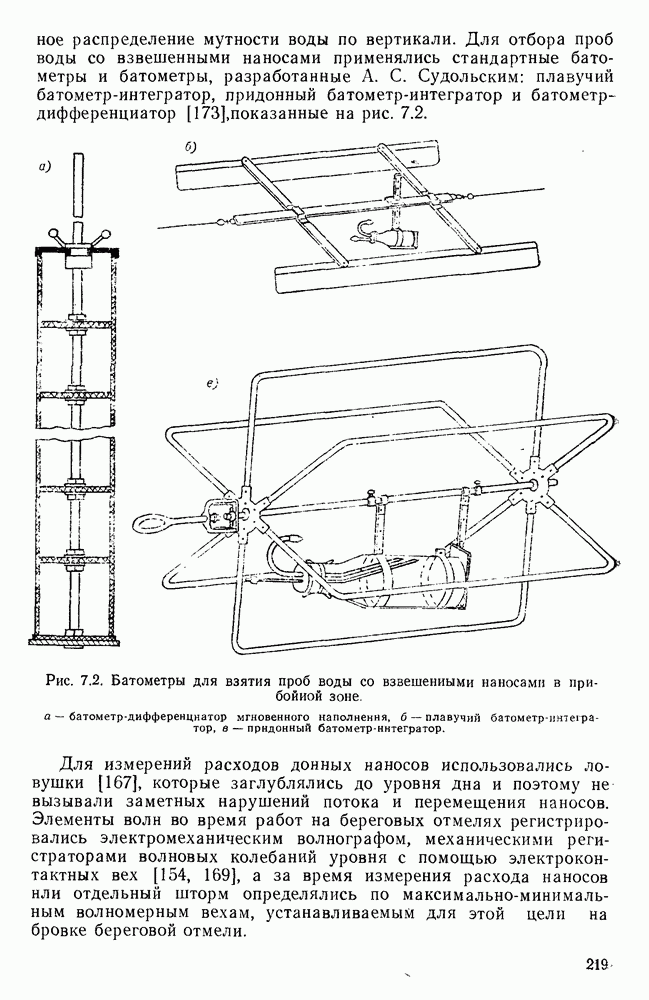
- 7.2. Методы изучения перемещения наносов
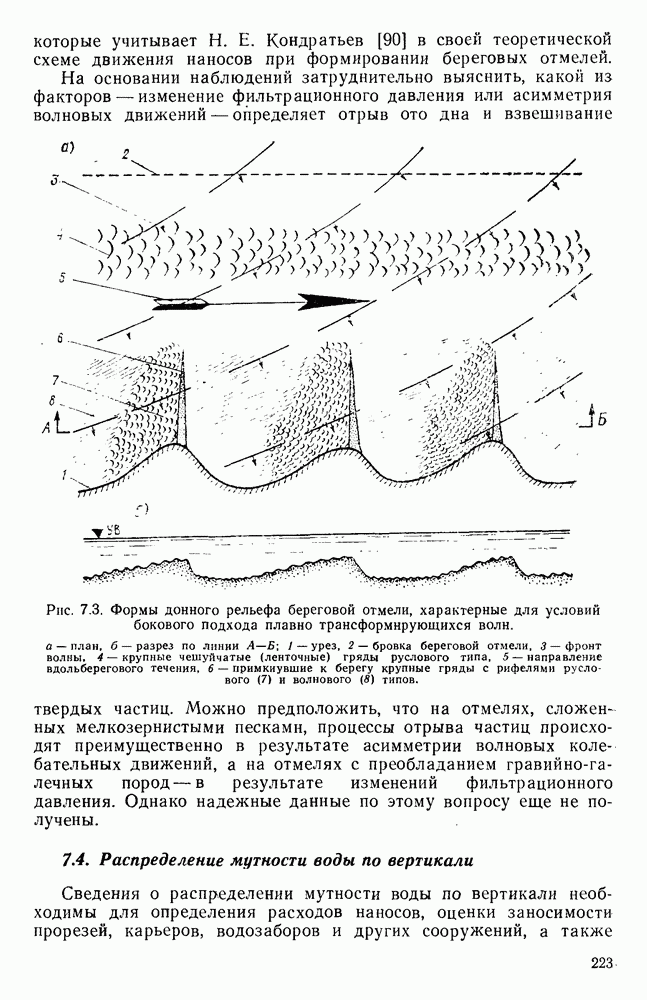
- 7.3. Основные черты механизма перемещения наносов
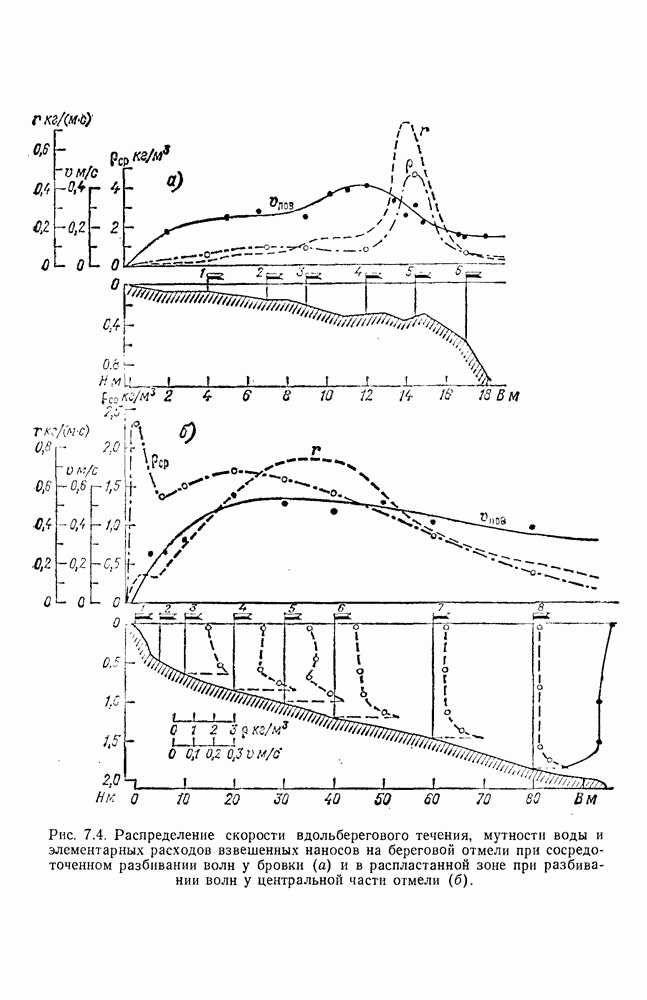
- 7.4. Распределение мутности воды по вертикали
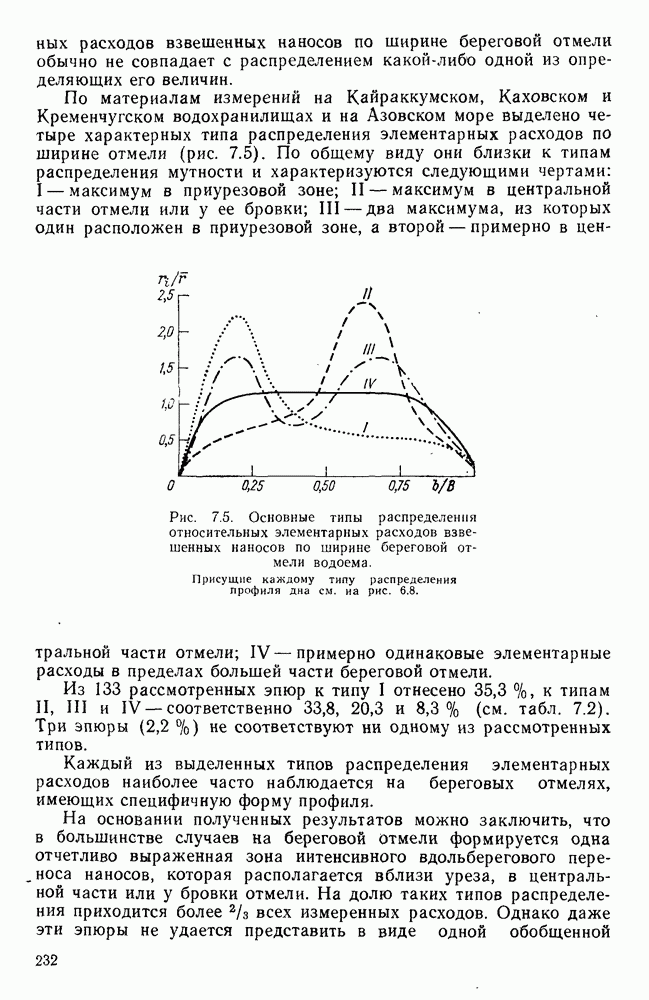
- 7.5. Распределение мутности воды по ширине береговой отмели
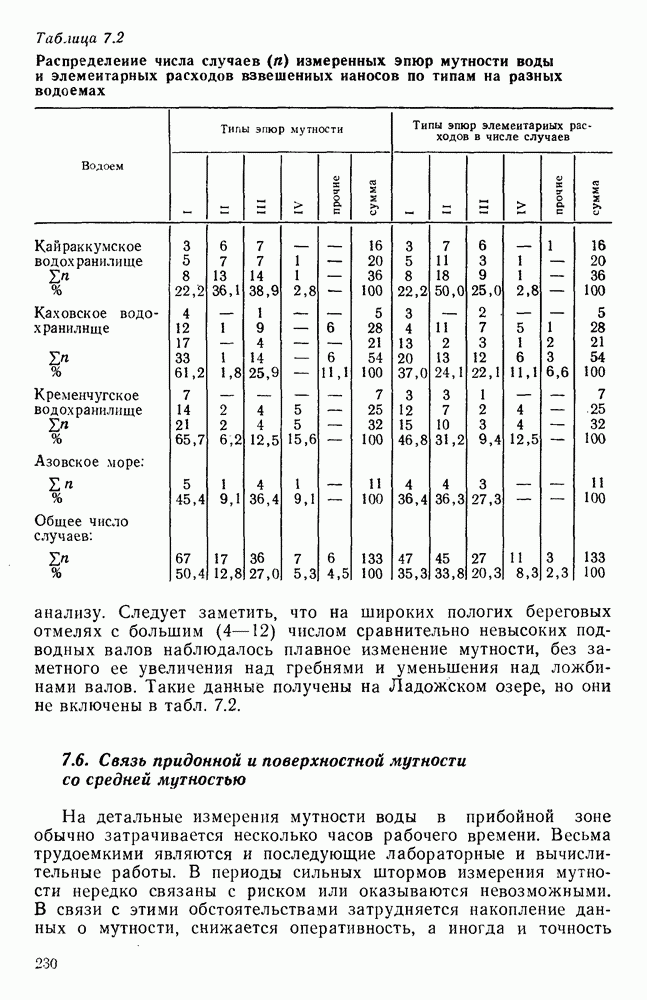
- 7.6. Связь придонной и поверхностной мутности со средней мутностью
- 7.7. Элементарные расходы взвешенных наносов
- 7.8. Зависимость средней мутности от определяющих факторов
- 7.9. Расходы донных наносов и их связь со взвешенными наносами
- 7.10. Расчет вдольберегового переноса твердого материала
- 7.11. Сезонная и межгодовая изменчивость вдольбереговых перемещений наносов