| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
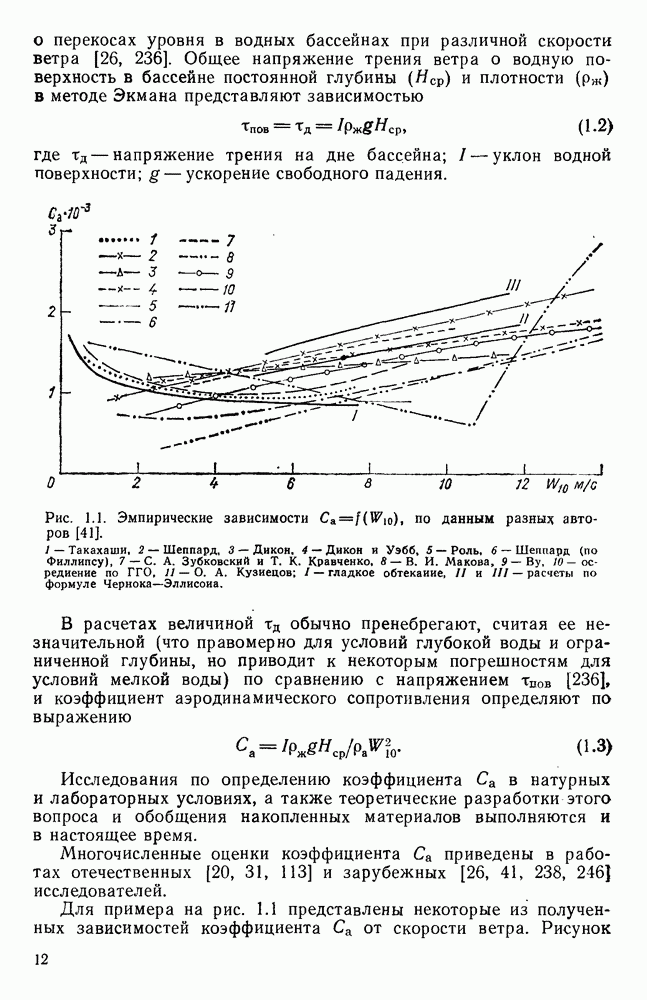
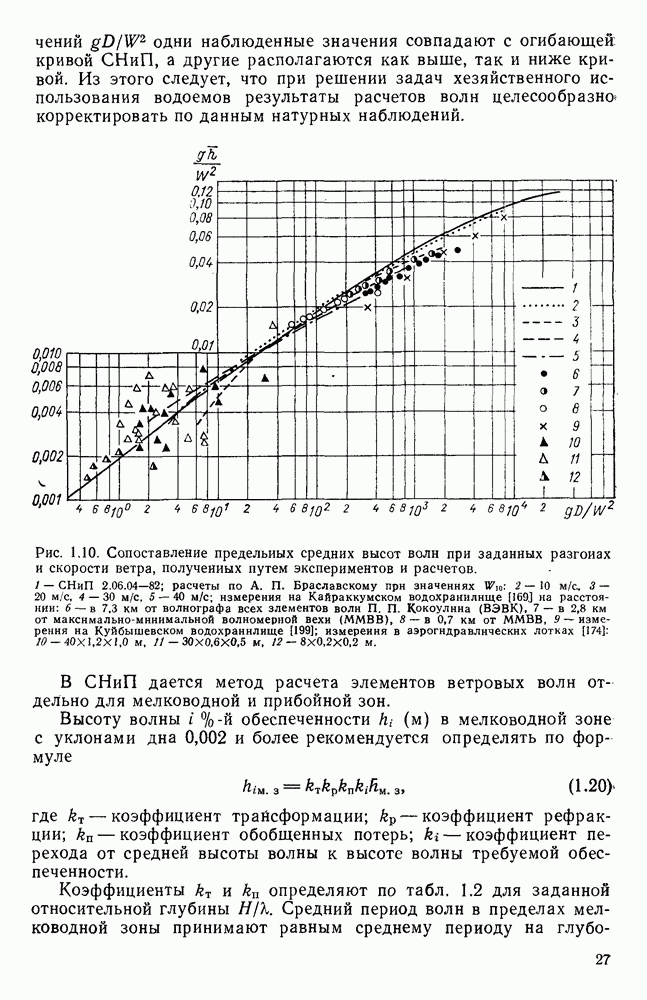
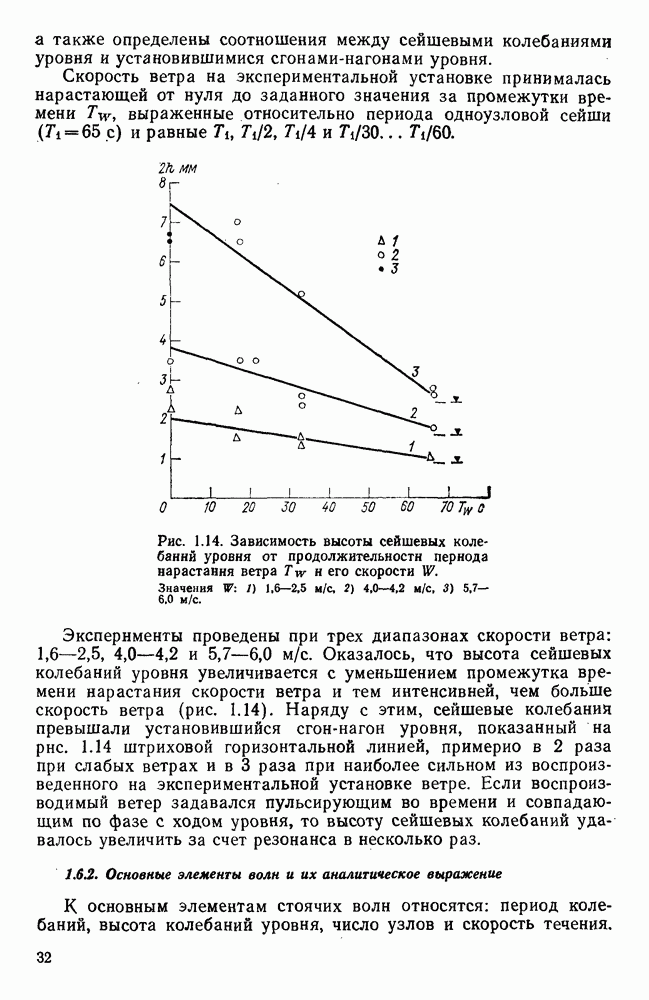
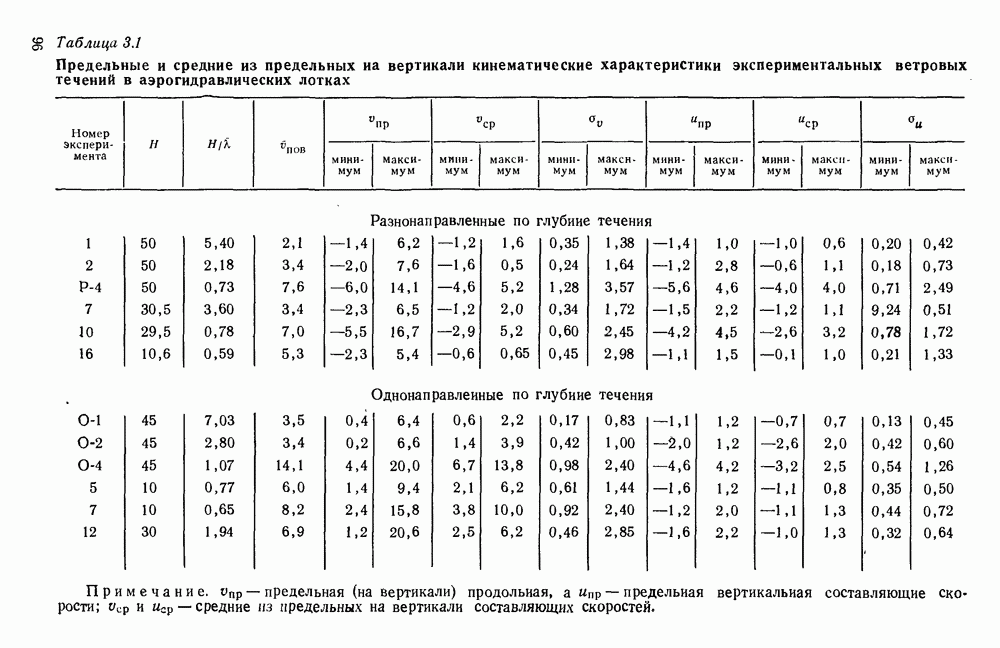
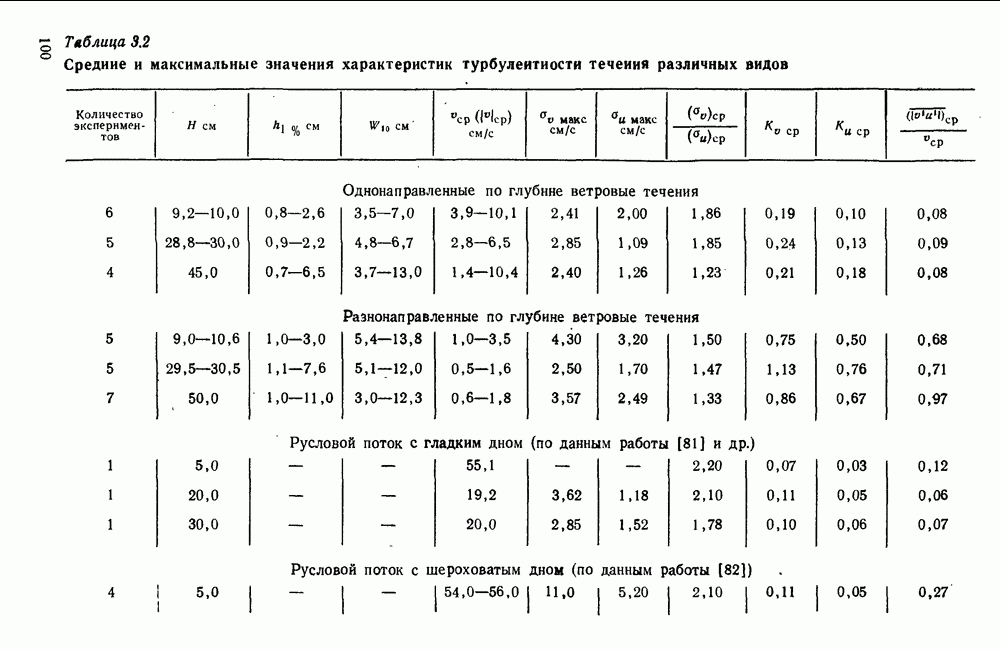
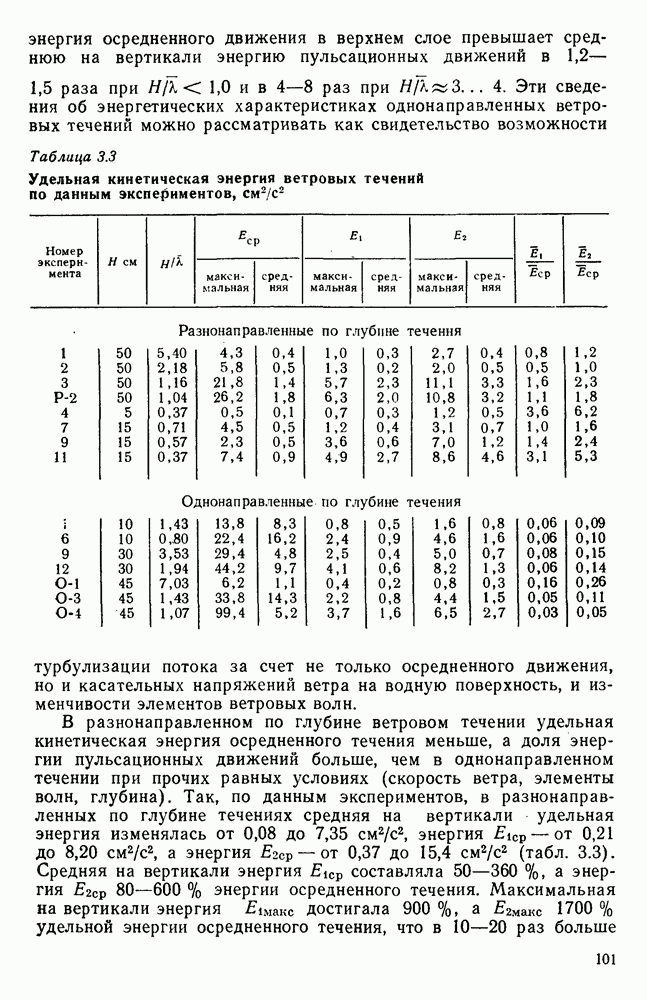
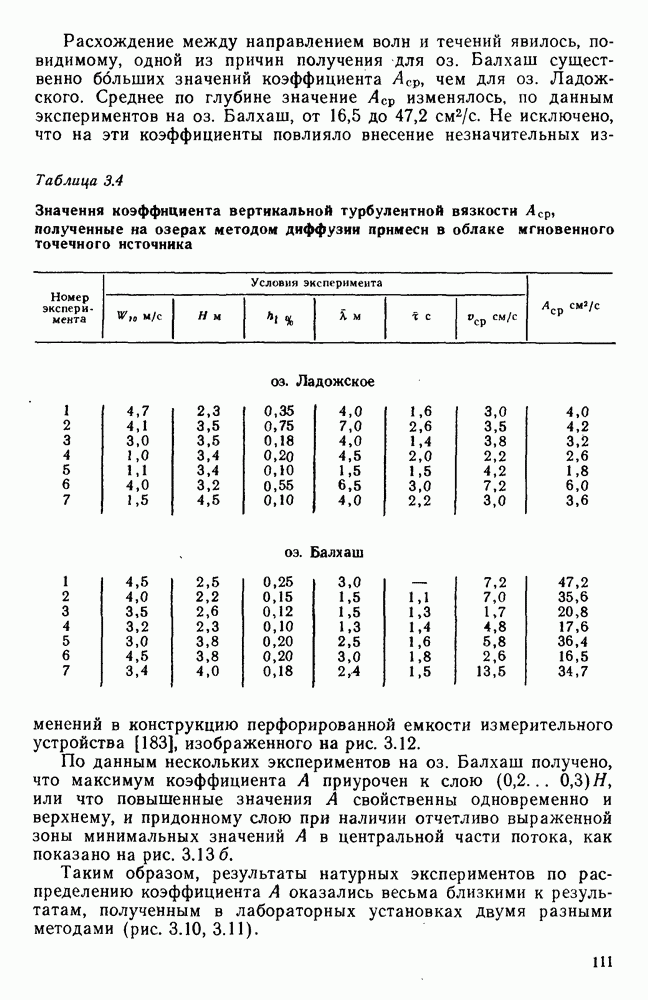
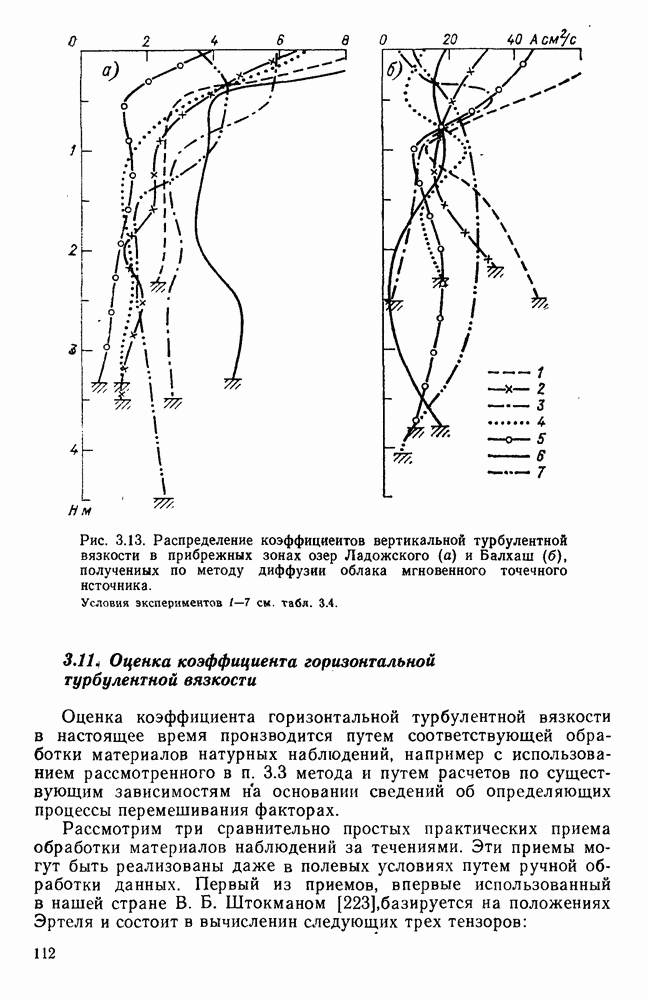
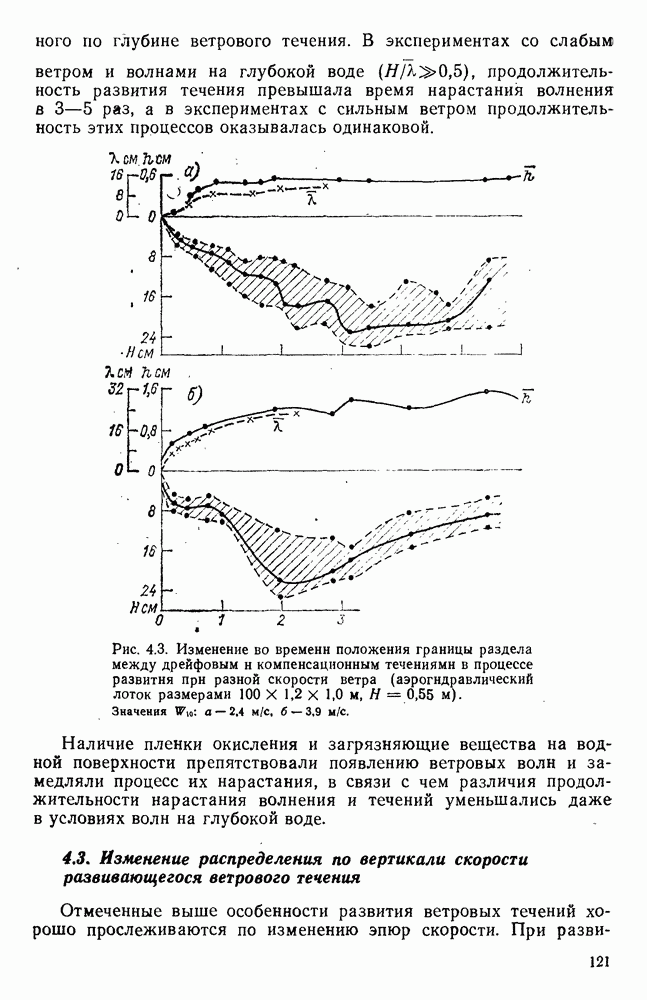
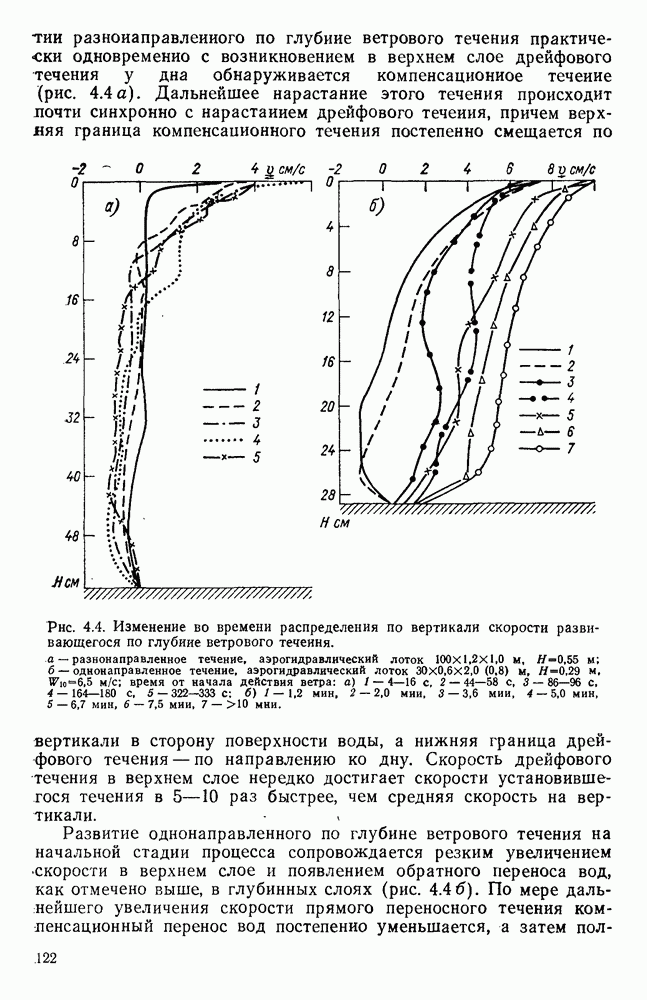
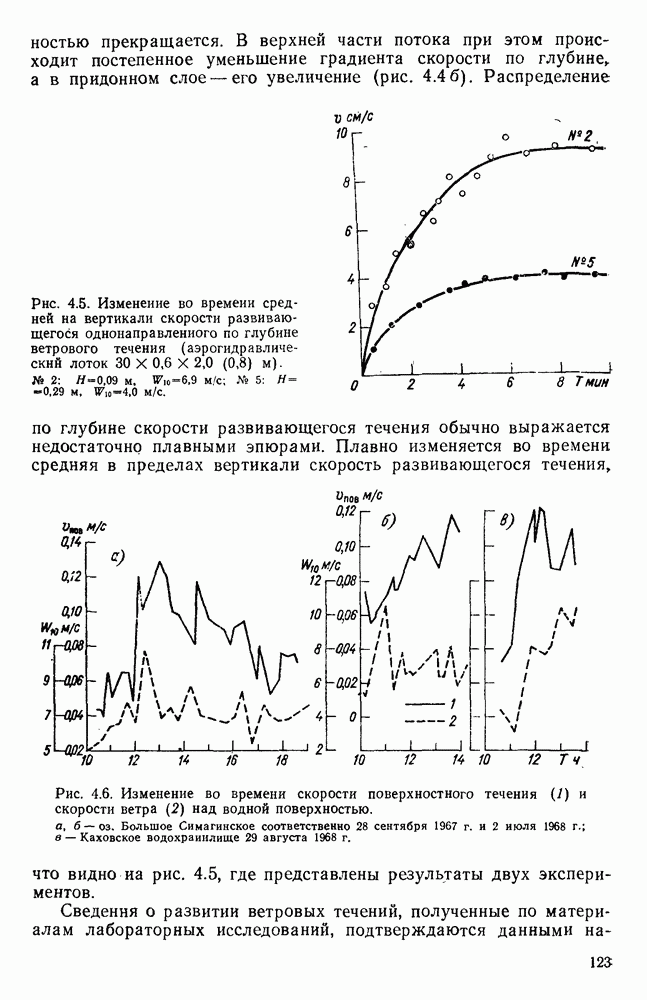
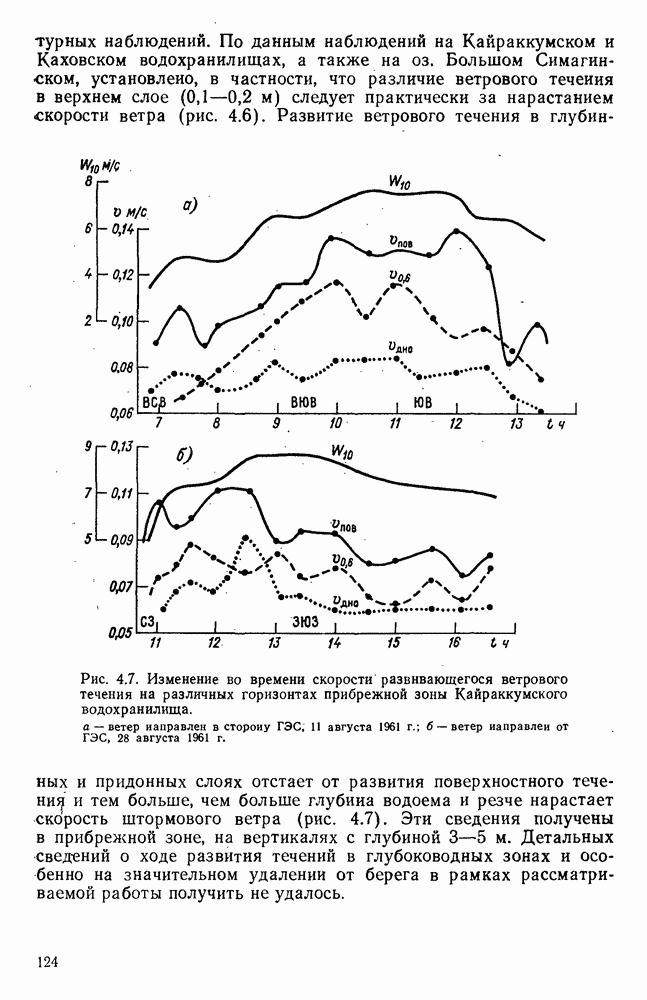
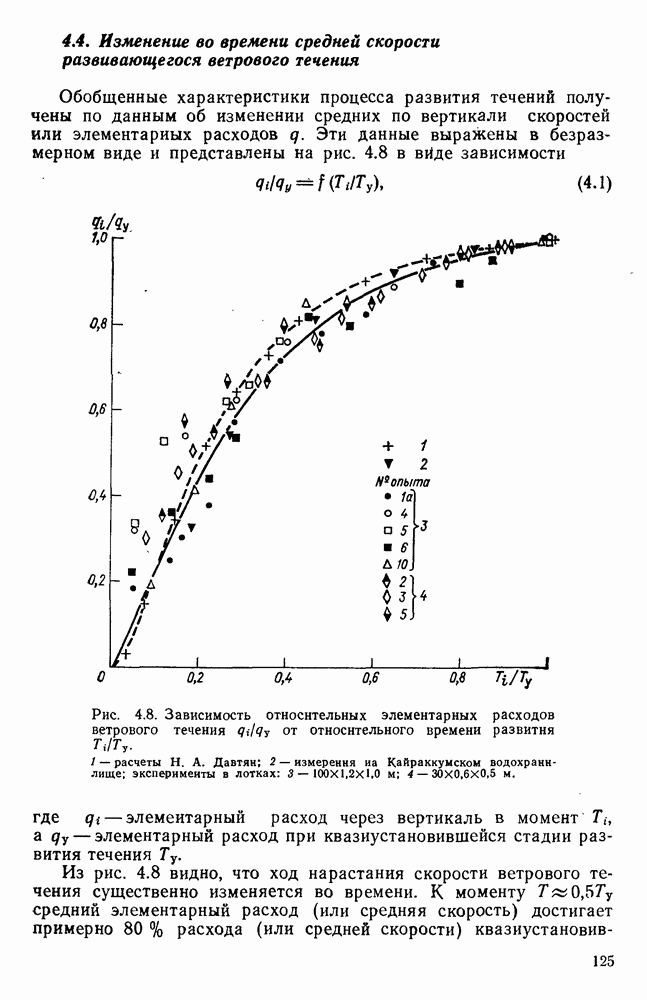
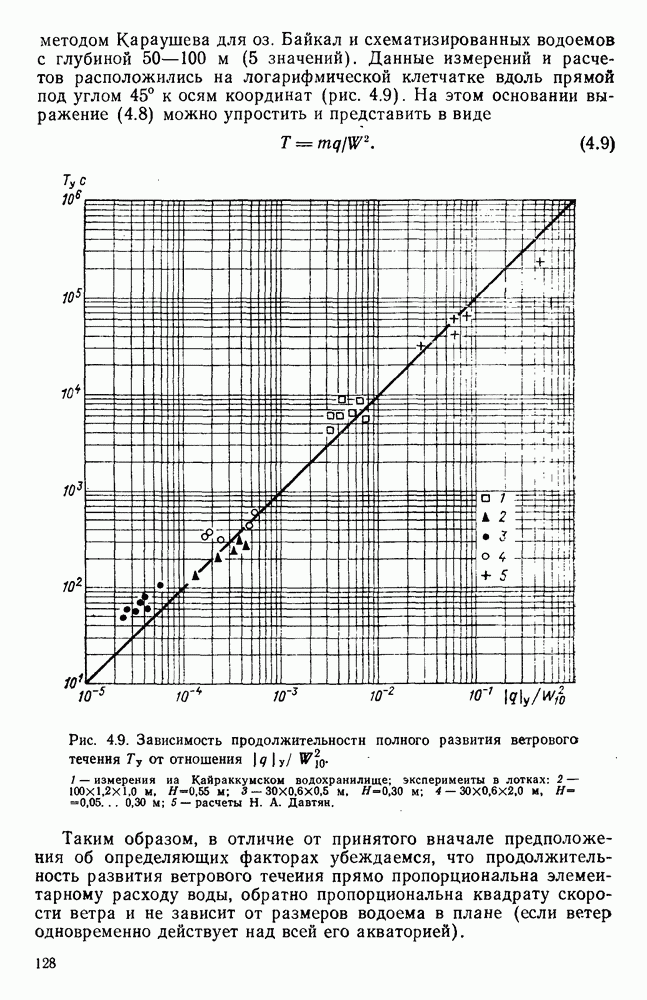
4.8. Оценка влияния на поверхностное ветровое течение глубины и шероховатости дна водоема
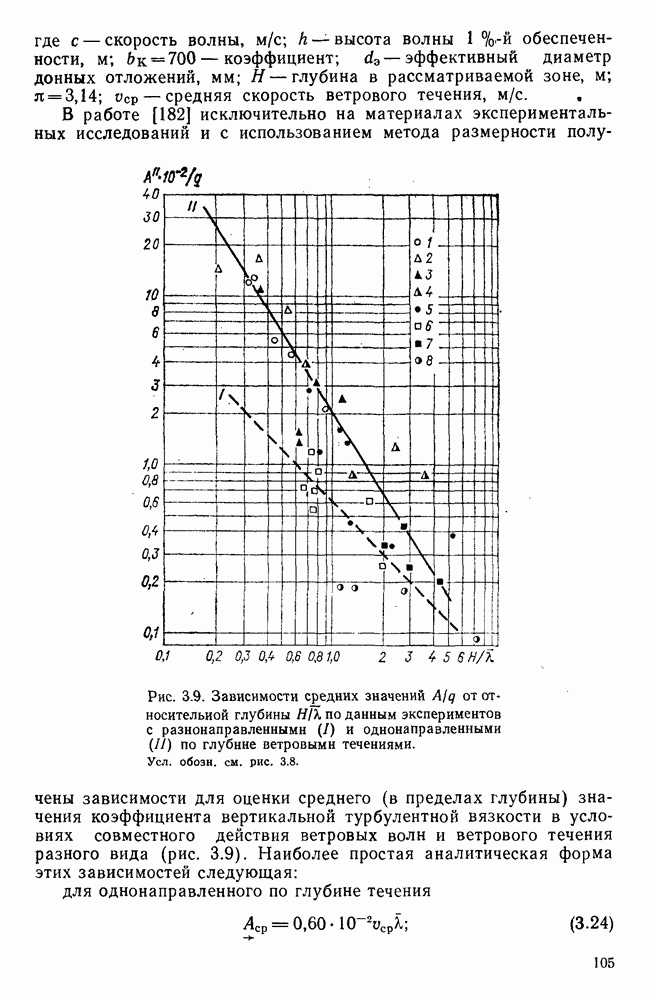
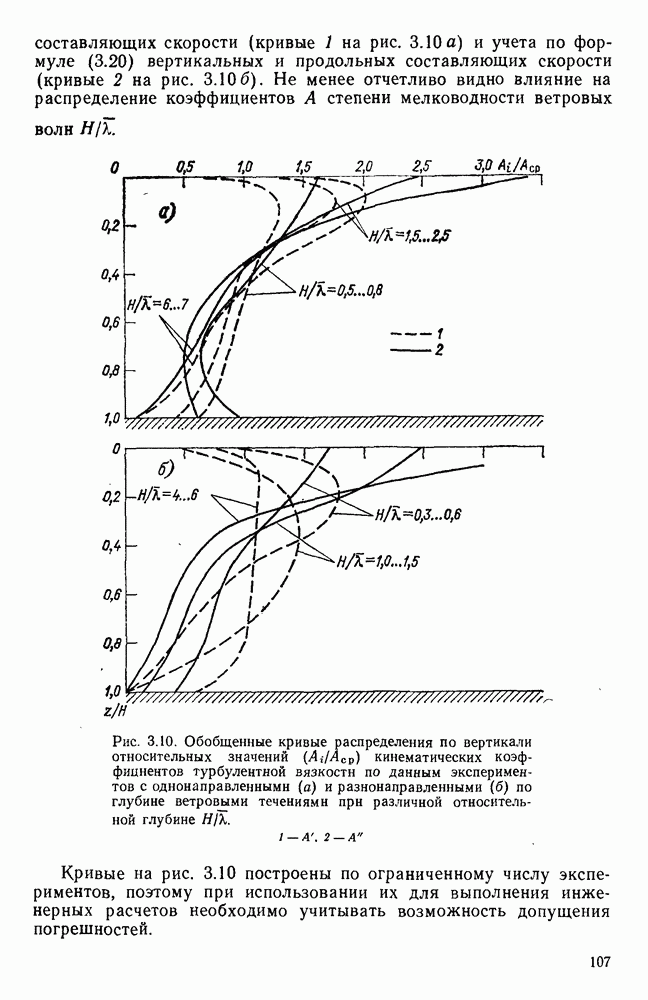
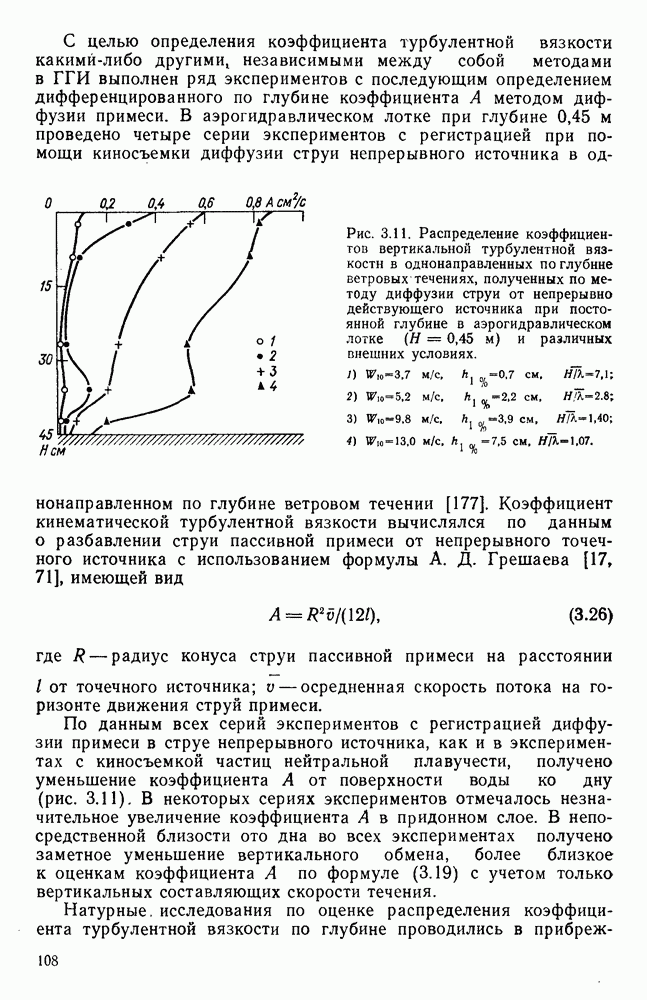
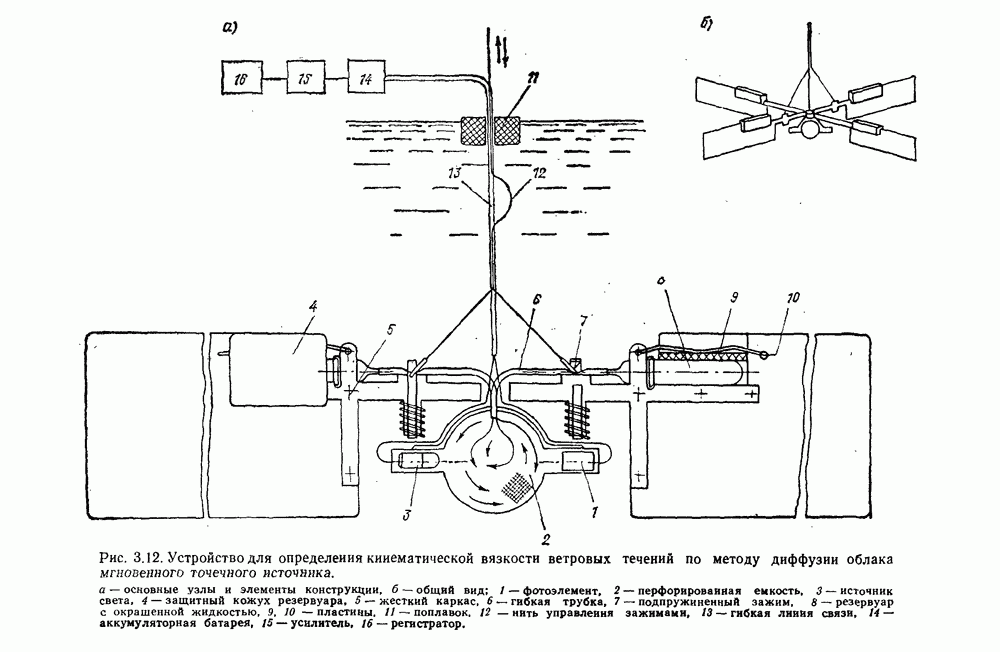
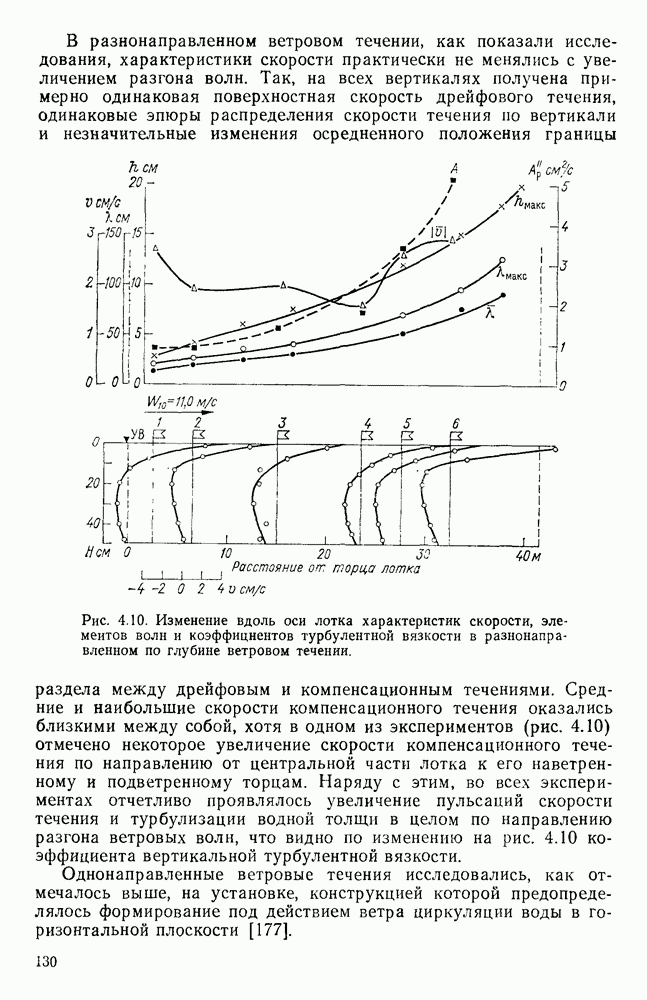
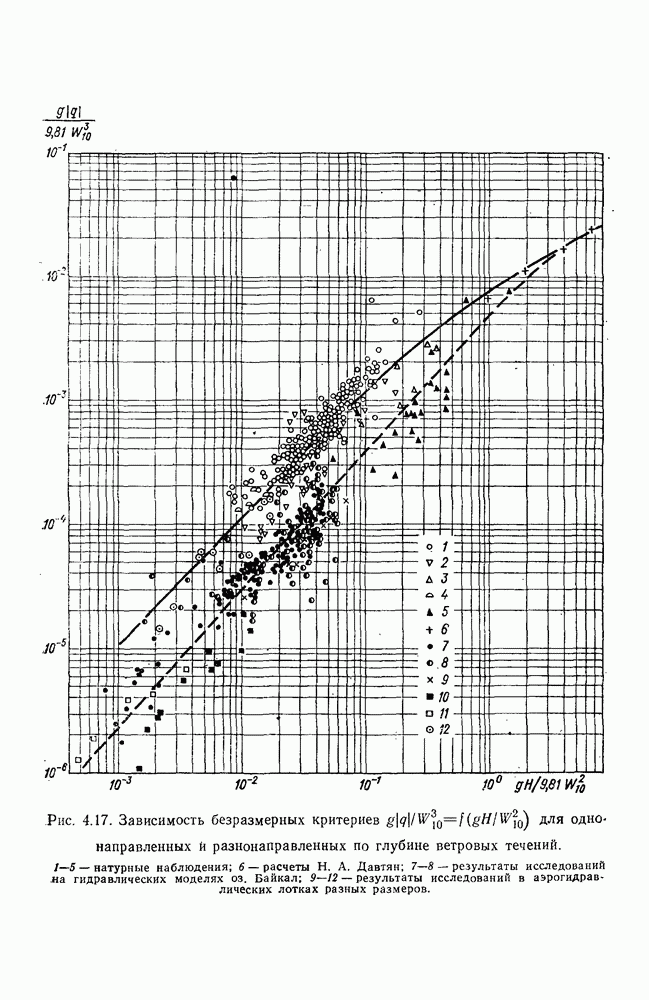
Для выяснения влияния глубины места измерения на скорость поверхностного ветрового течения в работе [178] использованы материалы экспериментальных исследований разнонаправленных ветровых течений, полученные в аэрогидравлических лотках различных размеров с бетонным и стеклянным дном. Они показали, что результаты каждой серии экспериментов, проведенных при определенной глубине и шероховатости дна, располагаются на полулогарифмическом графике зависимости

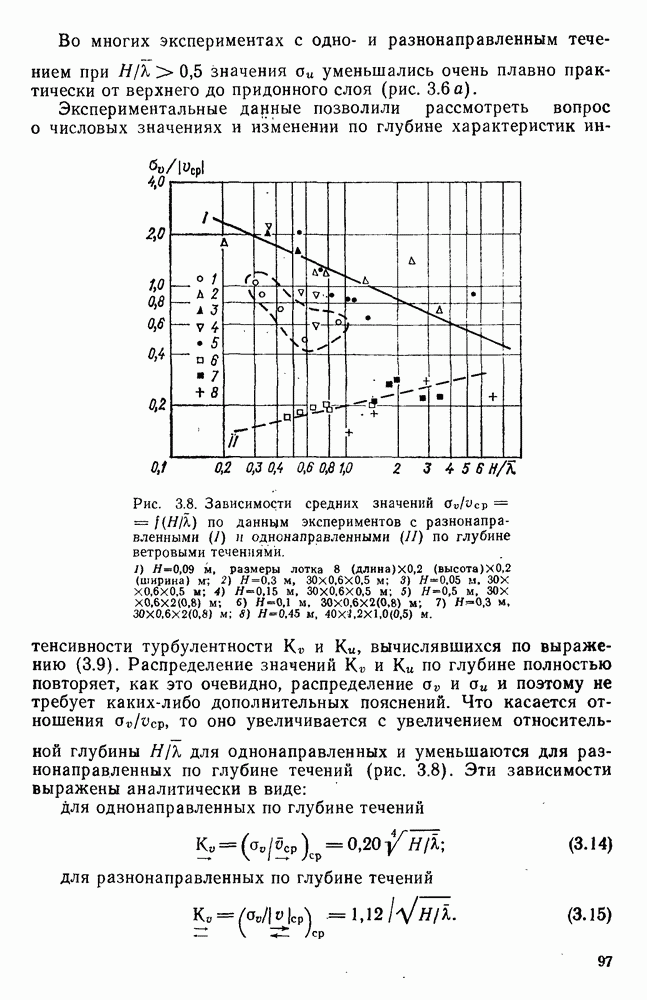
в виде групп точек, по каждой из которых можно провести прямую, как показано на рис. 4.11.
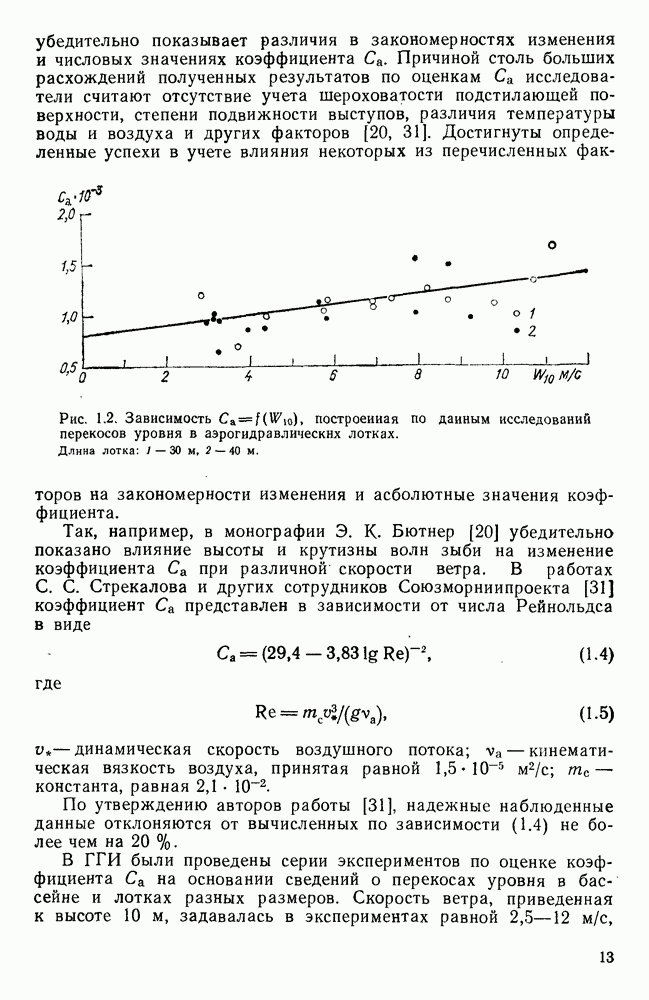
Эти прямые примерно параллельны между собой, что позволяет аппроксимировать их одной аналитической зависимостью

где  коэффициент, равный
коэффициент, равный  если
если  выражены в метрах в
выражены в метрах в  в метрах; С — коэффициент Шези.
в метрах; С — коэффициент Шези.
Для определения коэффициента Шези С можно воспользоваться, например, формулой Маннинга в виде [73, 215]

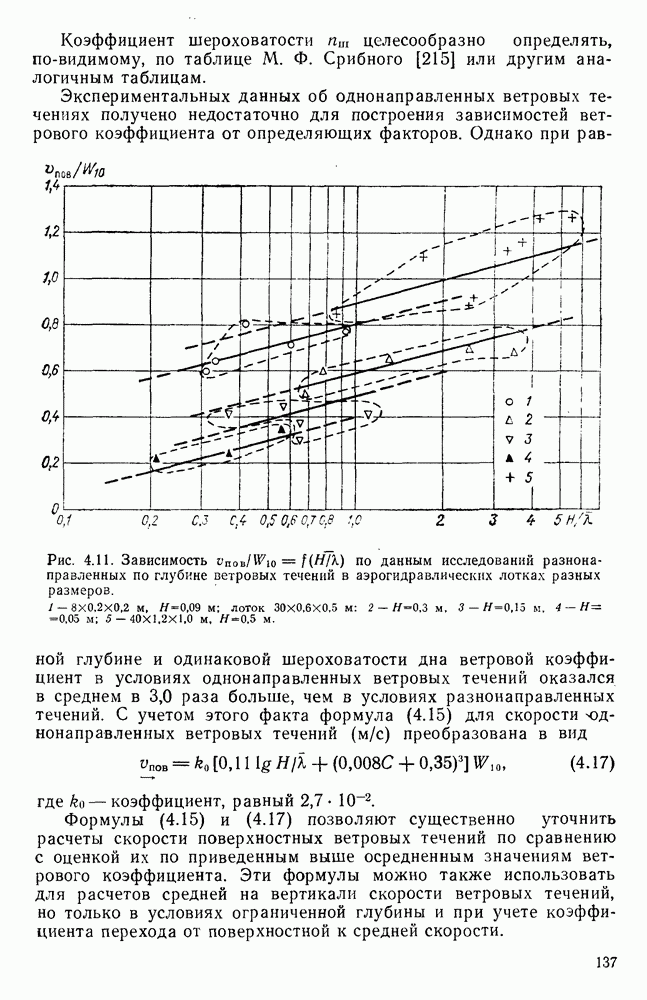
Коэффициент шероховатости  целесообразно определять, по-видимому, по таблице М. Ф. Срибного [215] или другим аналогичным таблицам.
целесообразно определять, по-видимому, по таблице М. Ф. Срибного [215] или другим аналогичным таблицам.
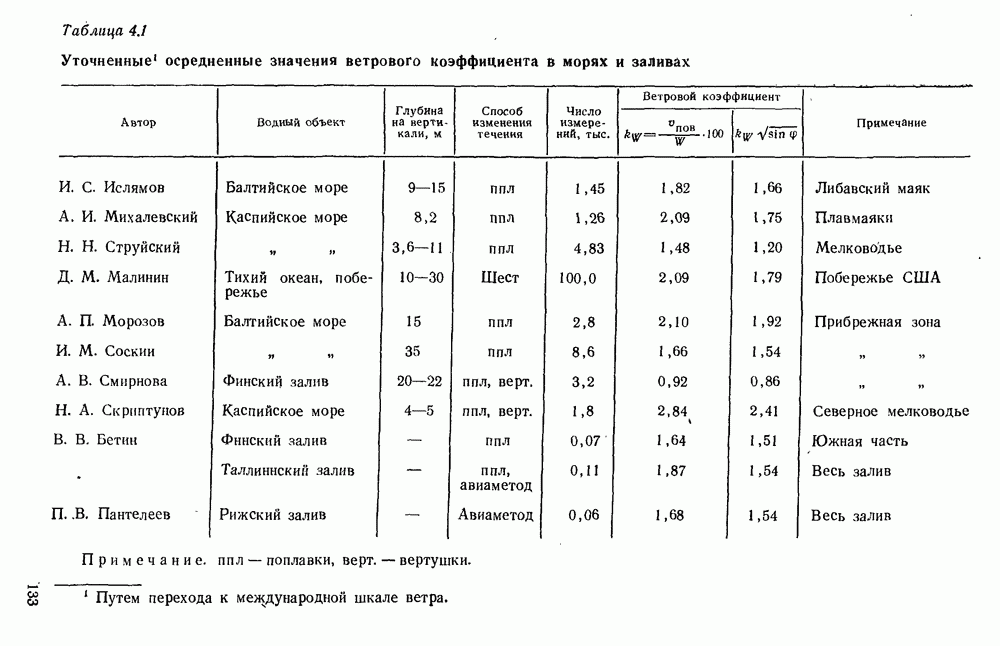
Экспериментальных данных об однонаправленных ветровых течениях получено недостаточно для построения зависимостей ветрового коэффициента от определяющих факторов.

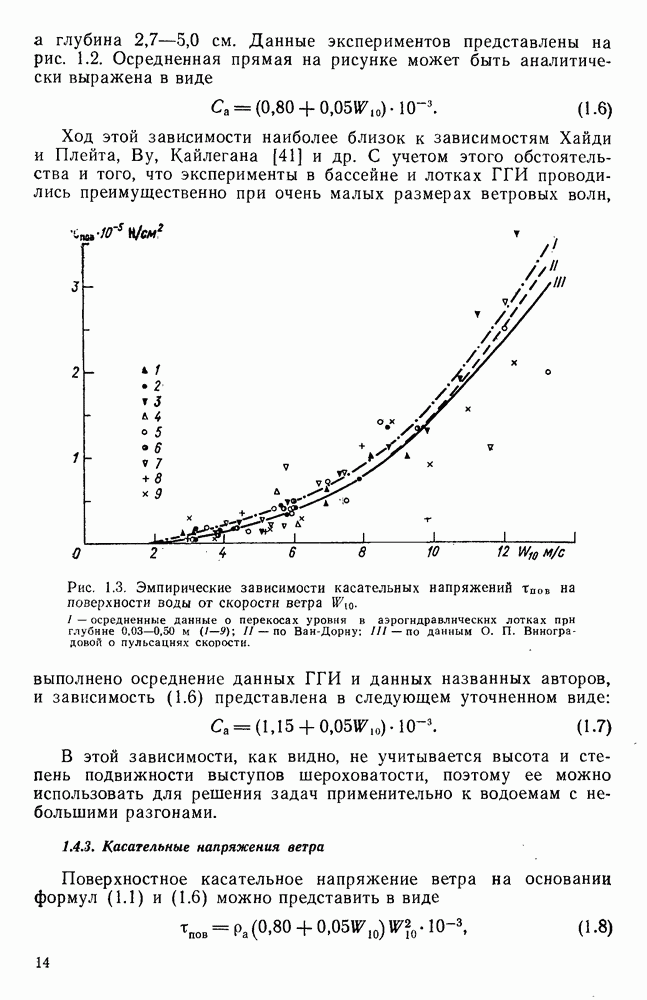
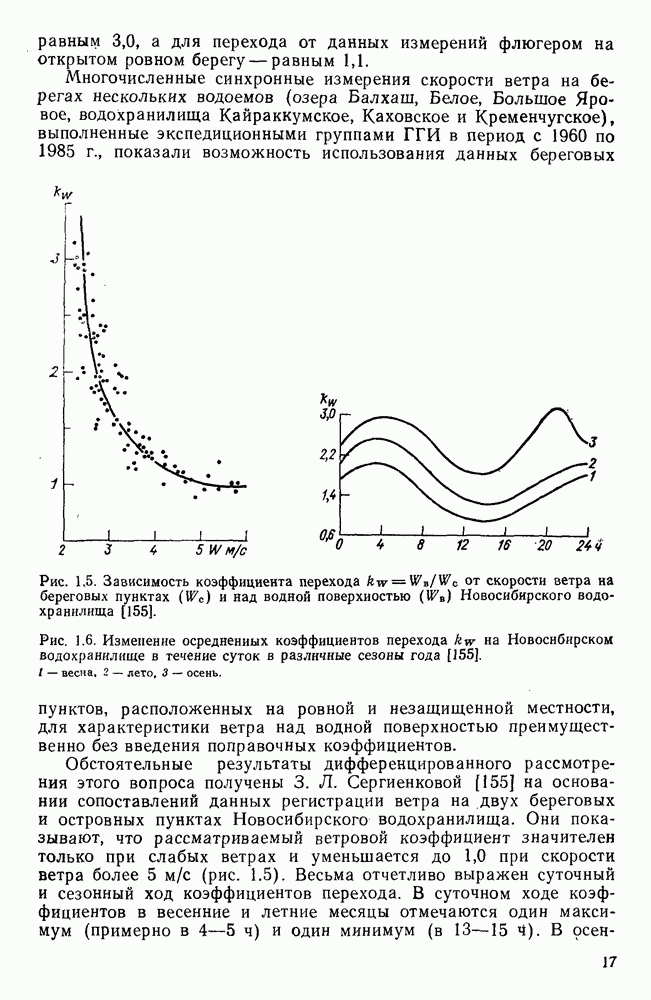
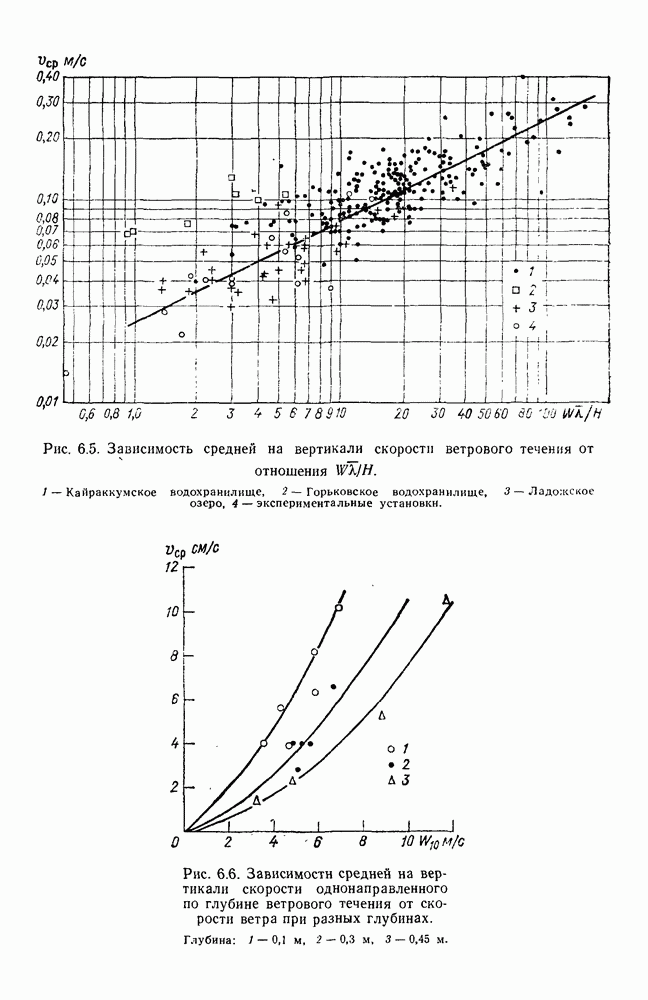
Рис. 4.11. Зависимость  по данным исследований разнонаправленных по глубине ветровых течений в аэрогидравлических лотках разных размеров.
по данным исследований разнонаправленных по глубине ветровых течений в аэрогидравлических лотках разных размеров.  лоток
лоток 
Однако при равной глубине и одинаковой шероховатости дна ветровой коэффициент в условиях однонаправленных ветровых течений оказался в среднем в 3,0 раза больше, чем в условиях разнонаправленных течений. С учетом этого факта формула (4.15) для скорости однонаправленных ветровых течений  преобразована в вид
преобразована в вид

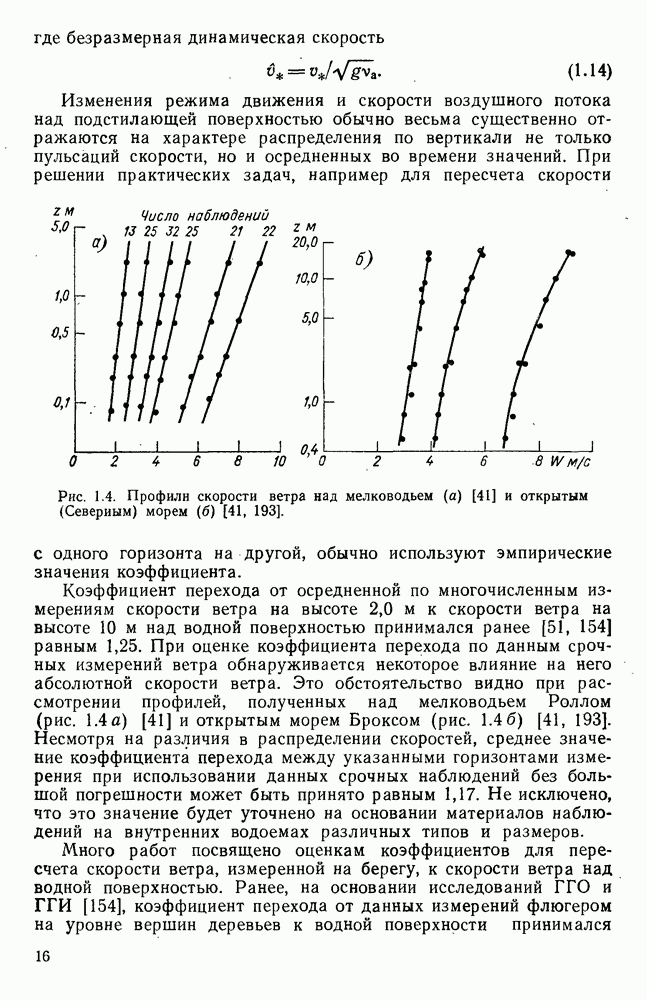
где  коэффициент, равный
коэффициент, равный 
Формулы (4.15) и (4.17) позволяют существенно уточнить расчеты скорости поверхностных ветровых течений по сравнению с оценкой их по приведенным выше осредненным значениям ветрового коэффициента. Эти формулы можно также использовать для расчетов средней на вертикали скорости ветровых течений, но только в условиях ограниченной глубины и при учете коэффициента перехода от поверхностной к средней скорости.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ВОЗДЕЙСТВИЕ ВЕТРА И ВОЛНОВЫЕ ПРОЦЕССЫ
- 1.1. Методы изучения взаимодействующих сложных явлений и процессов
- 1.2. Масштабы динамических явлений
- 1.3. Причины динамических явлений
- 1.4. Ветер над водной поверхностью
- 1.4.2. Коэффициент аэродинамического сопротивления
- 1.4.3. Касательные напряжения ветра
- 1.4.4. Профили ветра и их трансформация над подстилающей поверхностью
- 1.4.5. Режимные статистические и расчетные характеристики ветра
- 1.5. Ветровые волны
- 1.5.2. Классификация волн и их элементов
- 1.5.3. Расчет элементов ветровых волн и учет их изменчивости
- 1.6. Стоячие волны
- 1.6.2. Основные элементы волн и их аналитическое выражение
- 1.6.3. Периоды сейшевых колебаний уровня
- 1.6.4. Затухание стоячих колебаний уровня во времени
- 1.7. Внутренние волны
- 1.8. Сгонно-нагонные явления
- Глава 2. ПРОСТРАНСТВЕННАЯ СТРУКТУРА ПЕРЕНОСА ВОД ТЕЧЕНИЯМИ
- 2.1. Многообразие видов движений и масштабов пространственных структур
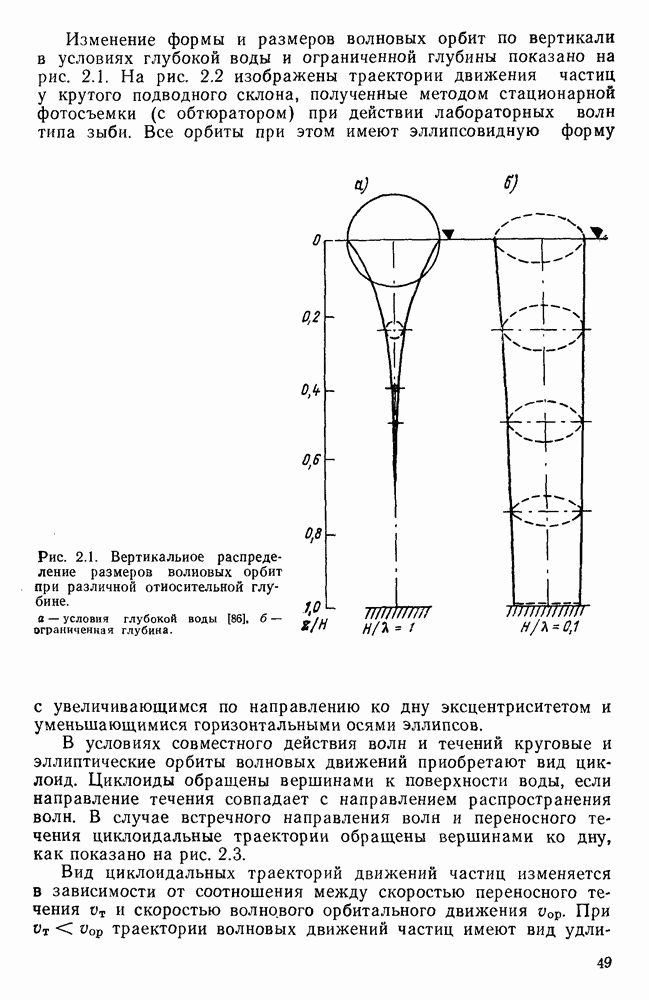
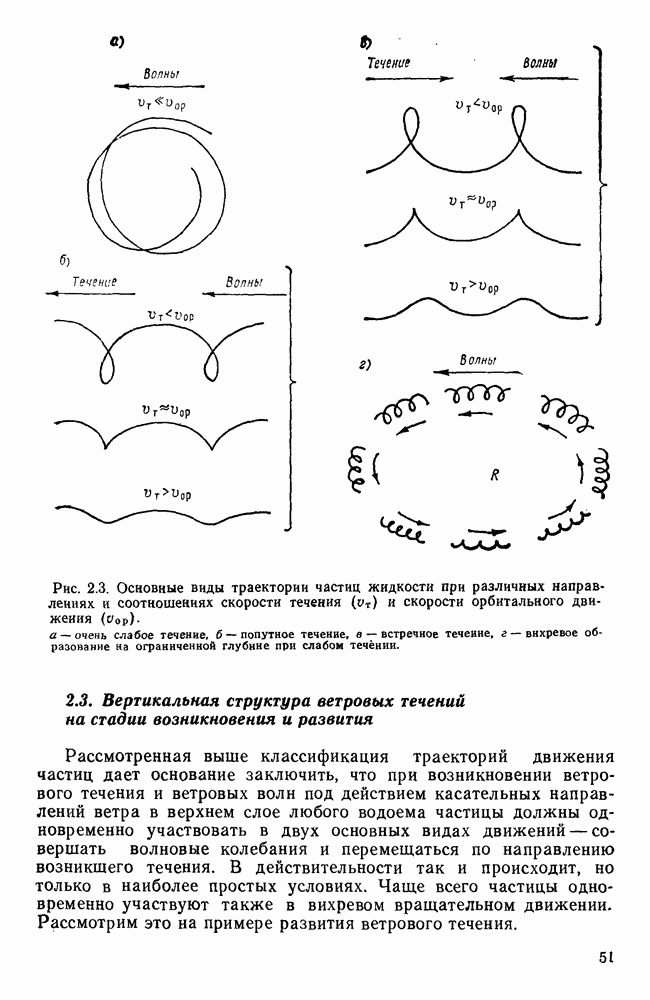
- 2.2. Траектории движений частиц жидкости при совместном действии волн и течений
- 2.3. Вертикальная структура ветровых течений на стадии возникновения и развития
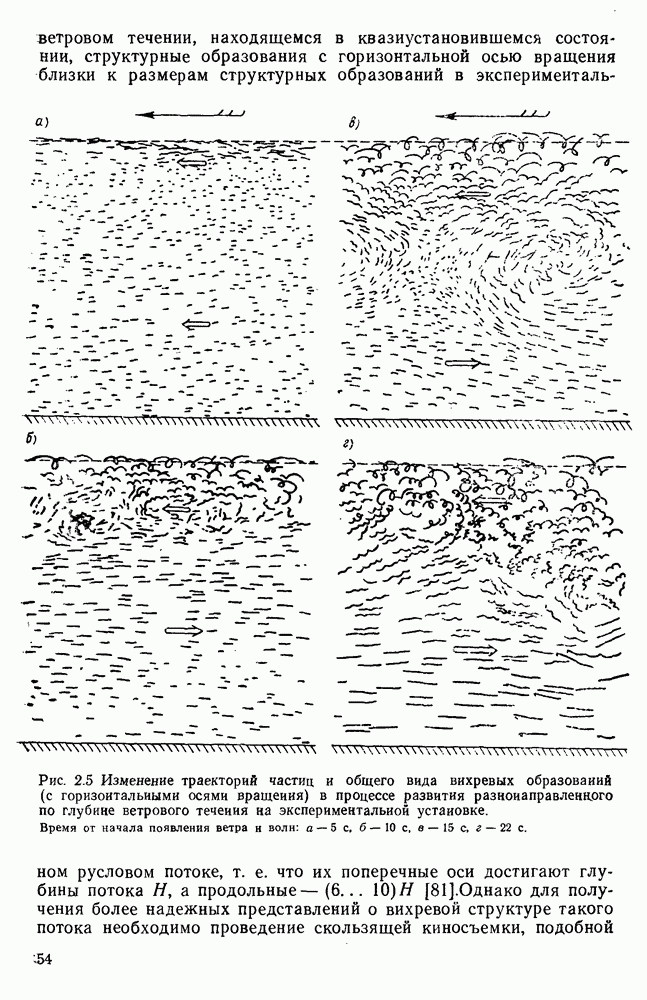
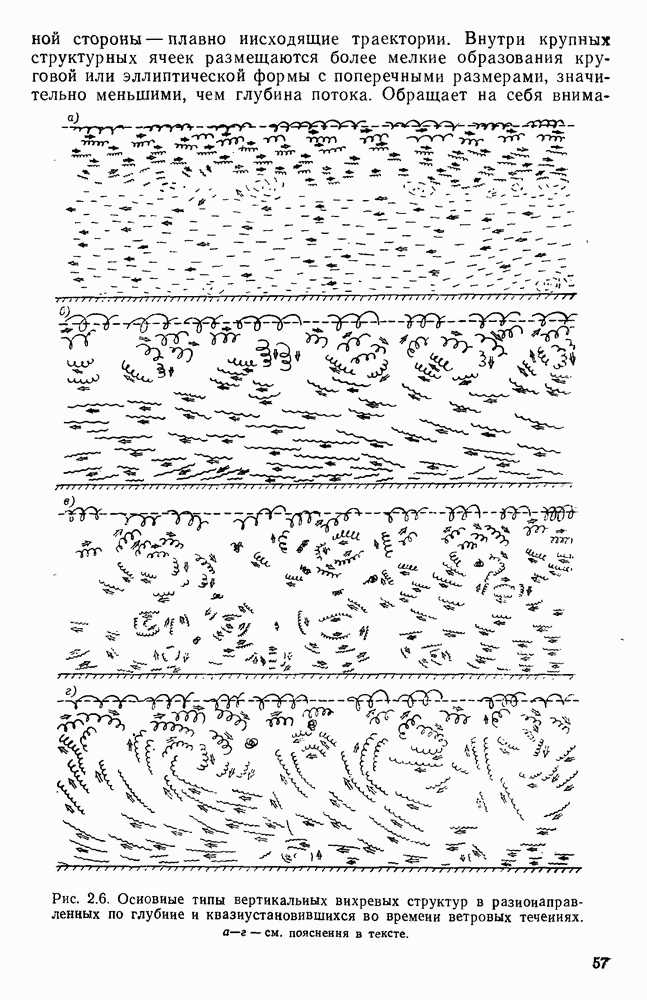
- 2.4. Вертикальная структура квазиустановившихся ветровых течений
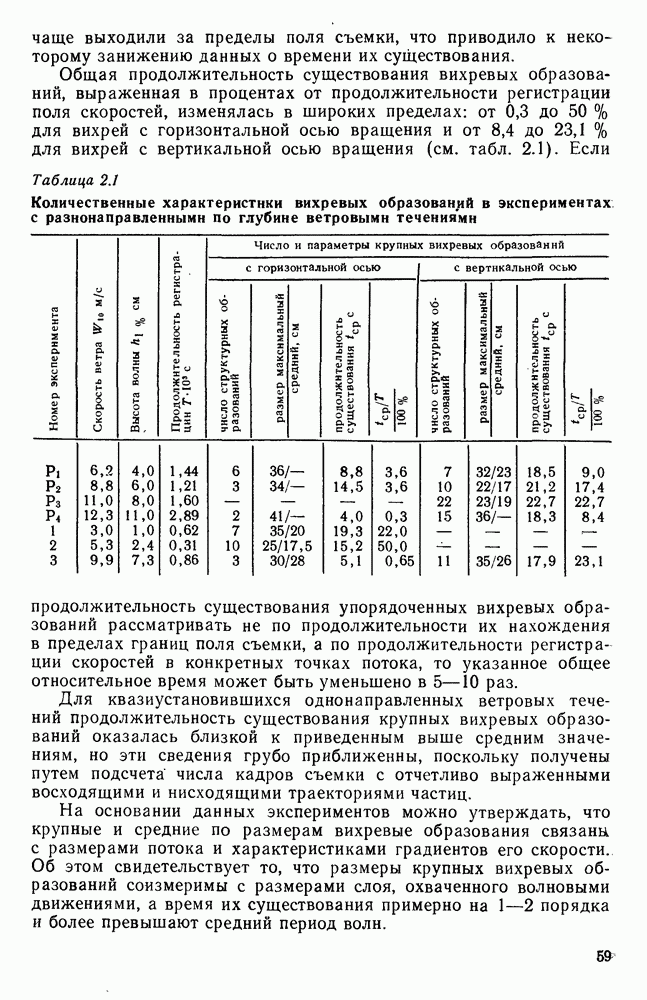
- 2.5. Количественные характеристики вертикальных вихревых образований
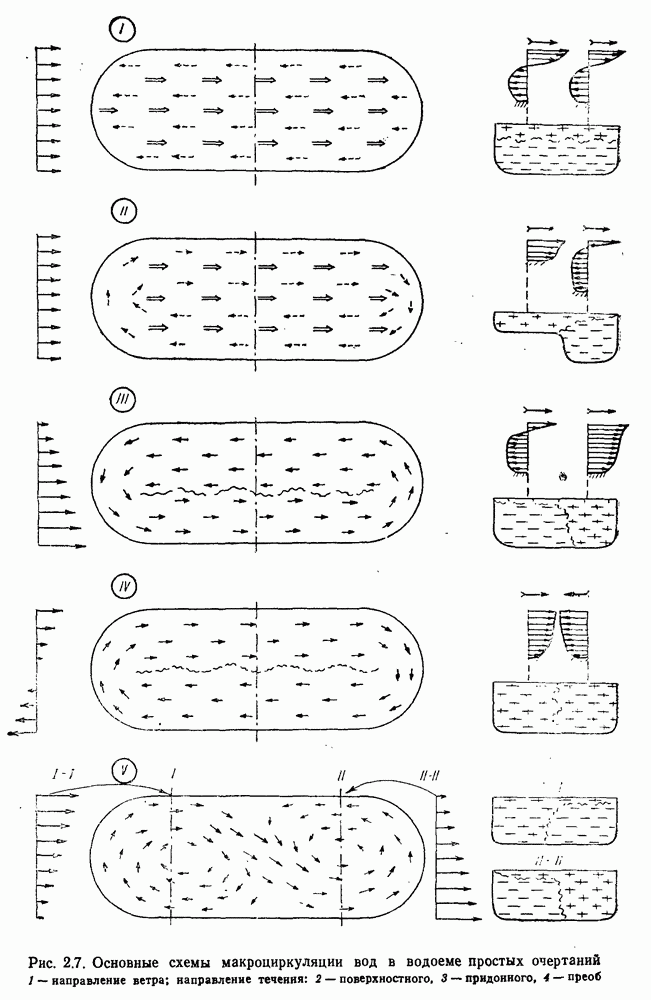
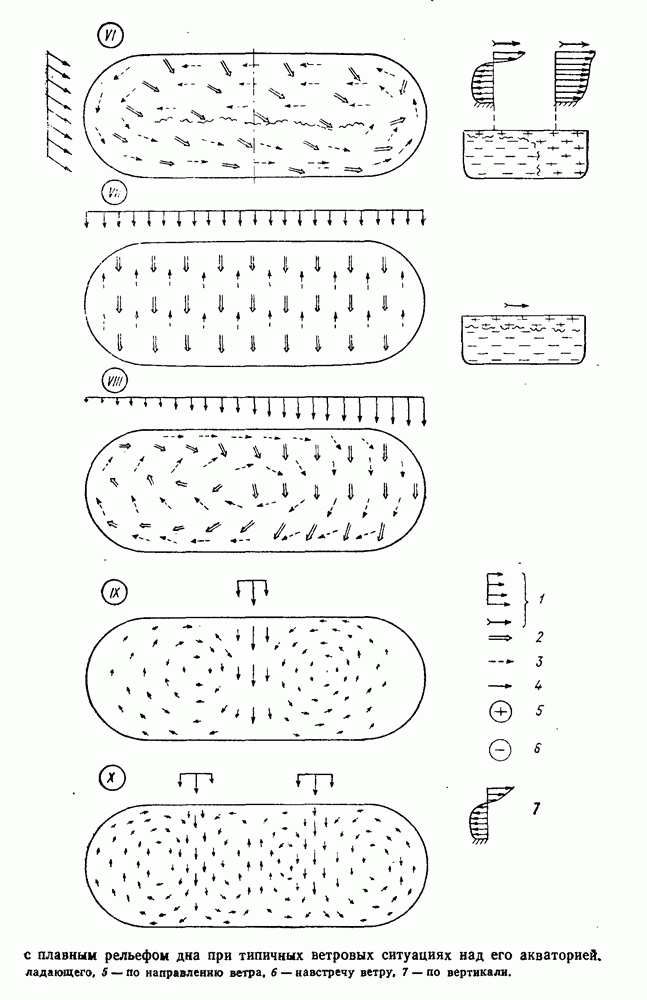
- 2.6. Макроциркуляция вод в водоеме при ветровых течениях
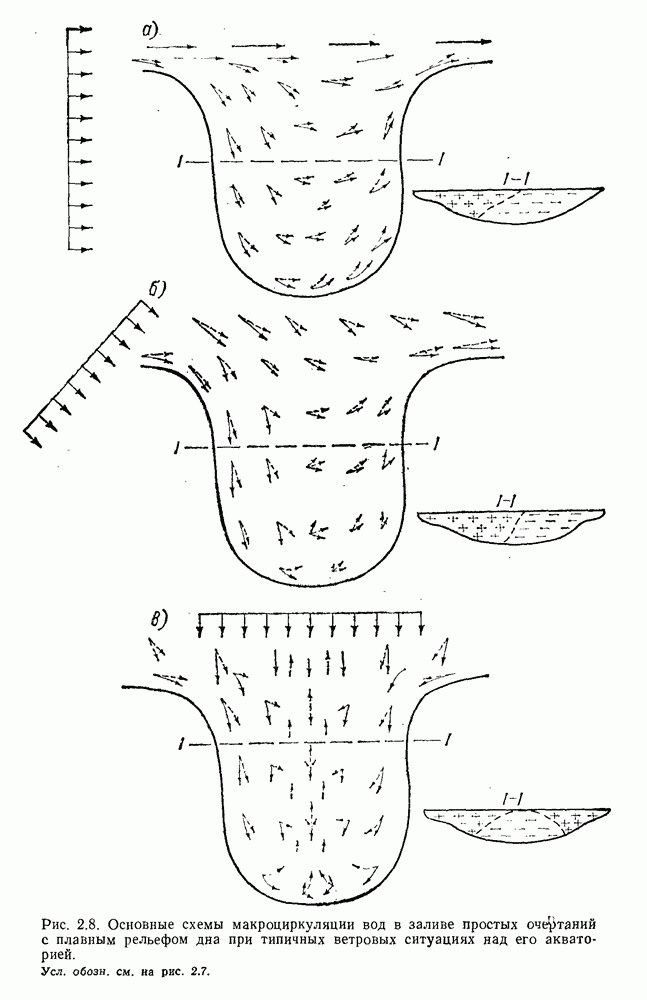
- 2.7. Макроциркуляция вод в заливе при ветровых течениях
- 2.8. Инерционные и синоптические вихри
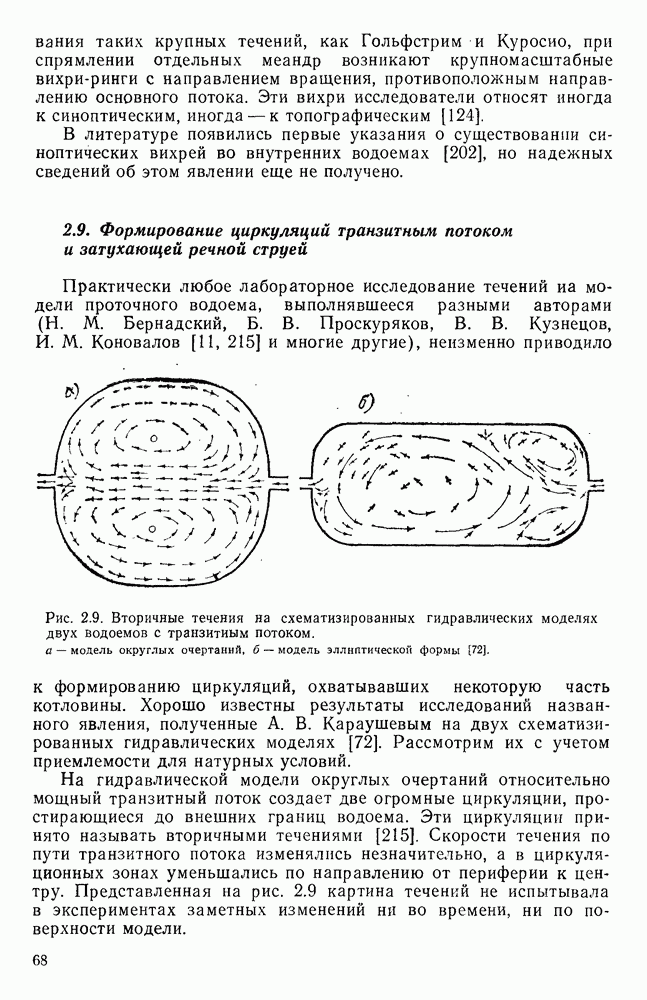
- 2.9. Формирование циркуляций транзитным потоком и затухающей речной струей
- 2.10. Структура сейшевых течений
- Глава 3. КИНЕМАТИКА ВЕТРОВЫХ И СУММАРНЫХ ТЕЧЕНИЙ
- 3.1. Совершенствование представлений о кинематике течений
- 3.2. Методы исследований кинематики течений
- 3.3. Методика обработки записей течений
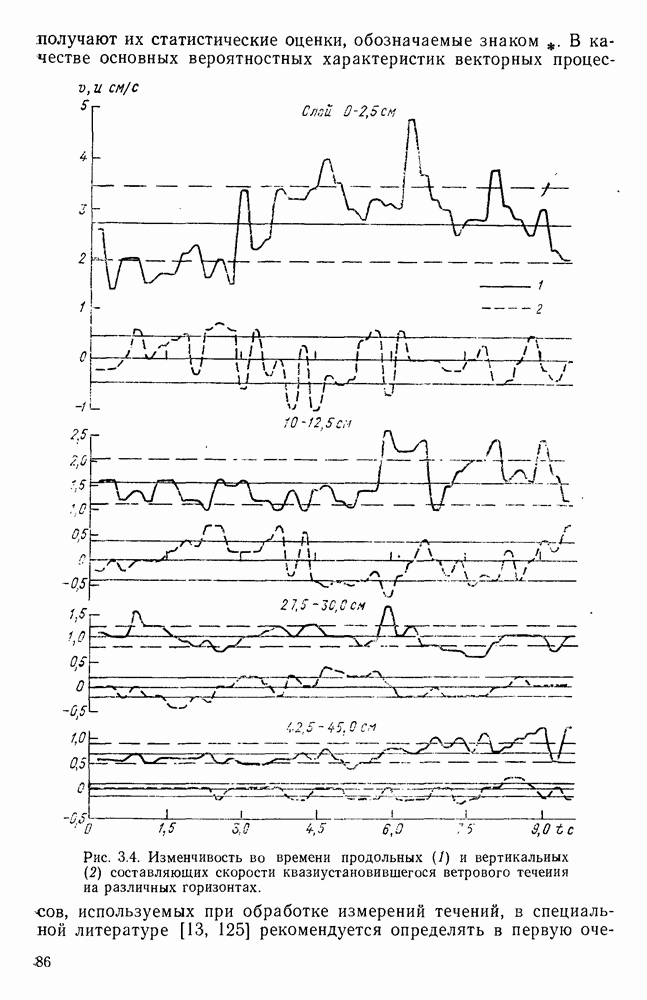
- 3.4. Оценка кинематических характеристик
- 3.5. Изменение мелкомасштабных пульсаций скорости во времени и по глубине
- 3.6. Изменение средних квадратических значений пульсационных составляющих скорости
- 3.7. Вертикальное распределение моментов корреляции в ветровых течениях
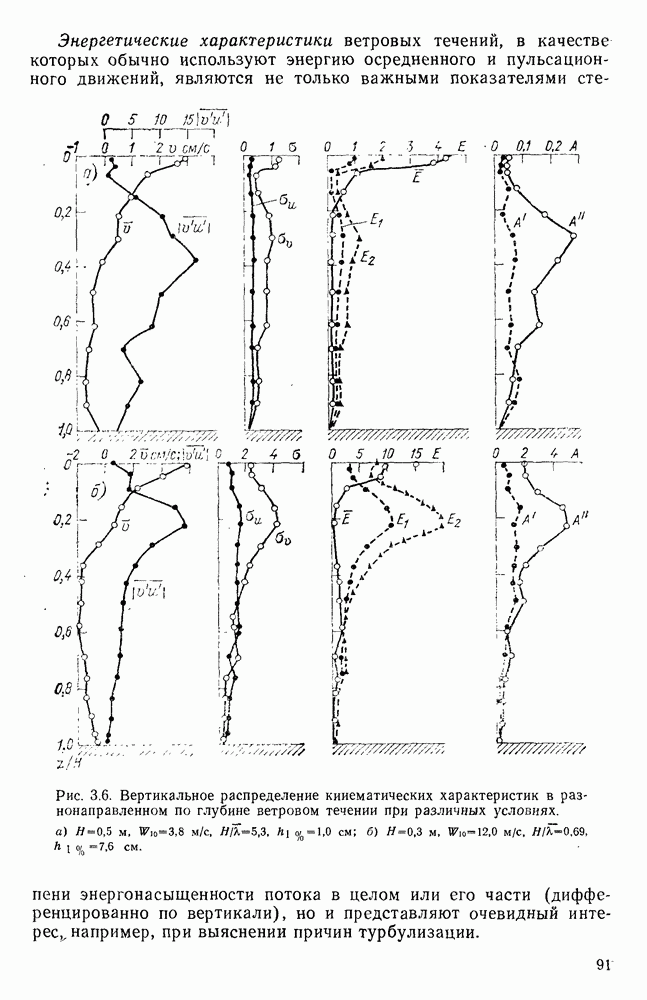
- 3.8. Энергетические характеристики ветровых течений по данным экспериментов
- 3.9. Коэффициенты вертикальной турбулентной вязкости и методы их оценки
- 3.10. Распределение коэффициента вертикальной турбулентной вязкости
- 3.11. Оценка коэффициента горизонтальной турбулентной вязкости
- Глава 4. ВЕТРОВЫЕ ТЕЧЕНИЯ В УСЛОВИЯХ РАЗВИТИЯ И СТАБИЛИЗАЦИИ
- 4.1. Совершенствование представлений о развитии ветровых течений
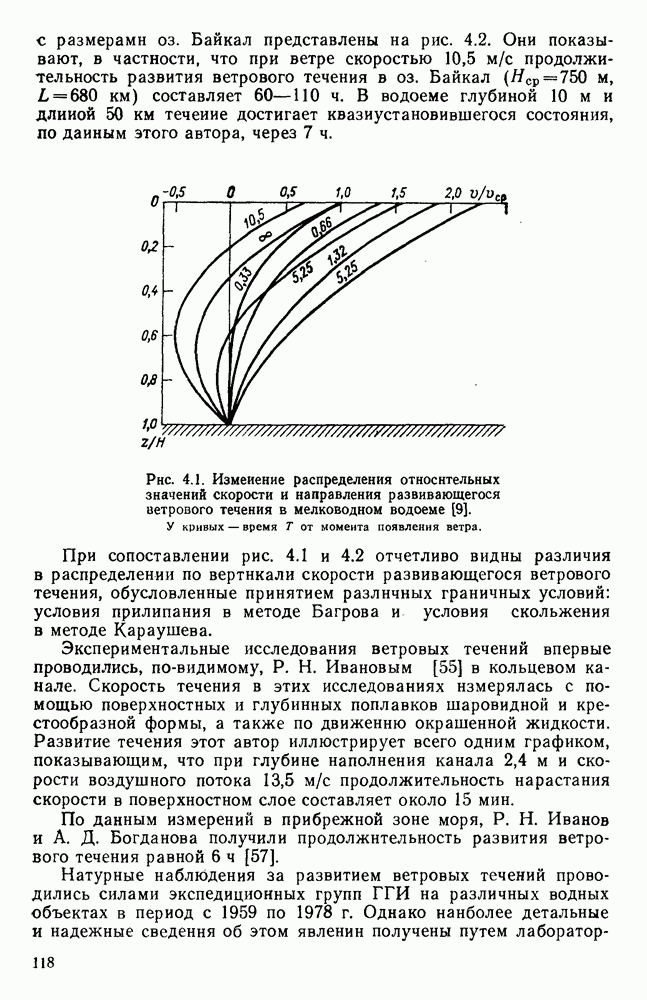
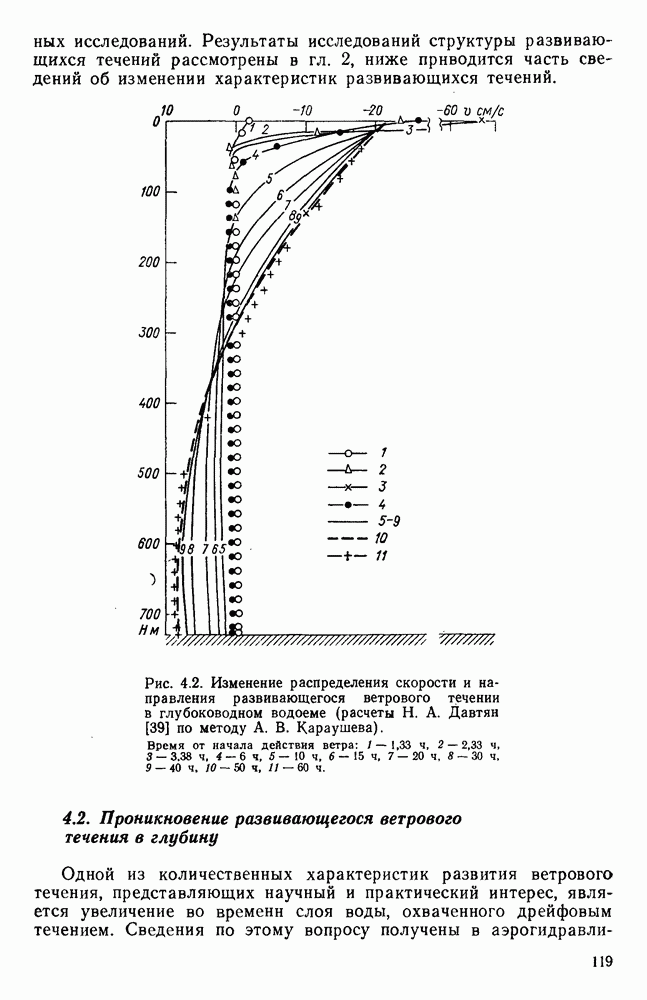
- 4.2. Проникновение развивающегося ветрового течения в глубину
- 4.3. Изменение распределения по вертикали скорости развивающегося ветрового течения
- 4.4. Изменение во времени средней скорости развивающегося ветрового течения
- 4.5. Продолжительность развития ветрового течения
- 4.6. Изменение скорости ветрового течения по пути разгона волн
- 4.7. Соотношение между скоростями ветрового течения и ветра
- 4.7.2. Ветровой коэффициент для прибрежных зон морей и океанов
- 4.7.3. Ветровой коэффициент для морских заливов
- 4.7.4. Ветровой коэффициент для внутренних водоемов
- 4.8. Оценка влияния на поверхностное ветровое течение глубины и шероховатости дна водоема
- 4.9. Предельное проникновение ветрового течения в глубину
- 4.10. Отклонения направлений ветровых течений от направления ветра
- 4.11. Теоретические решения задачи о вертикальном распределении скорости ветровых течений
- 4.12. Распределение скорости квазиустановившихся ветровых течений по данным экспериментов
- 4.13. Перенос вод через вертикаль
- 4.14. Взаимодействие ветровых, стоковых и сейшевых течений
- 4.15. Соотношение переносов воды дрейфовым и волновым течениями
- 4.16. Установление режимных статистических характеристик течений
- 4.16.2. Выбор функций распределения скорости течения при ограниченных данных наблюдений
- 4.17. Внутренний водообмен при ветровых течениях
- 4.18. Моделирование ветровых течений
- 4.18.2. Математические модели течений и примеры их реализации
- 4.18.3. Физическое моделирование
- Глава 5. СЕЙШЕВЫЕ ТЕЧЕНИЯ
- 5.1. Основные черты и особенности сейшевых течений
- 5.2. Методы оценки скорости сейшевого течения
- 5.3. Распределение сейшевых течений по акватории водоема
- 5.4. Сейшевые течения в оз. Байкал
- 5.5. Сейшевые течения в оз. Балхаш
- 5.6. Сейшевые течения в Каховском водохранилище
- 5.7. Режимные характеристики сейш
- 5.8. Объемы переноса вод сейшевыми течениями
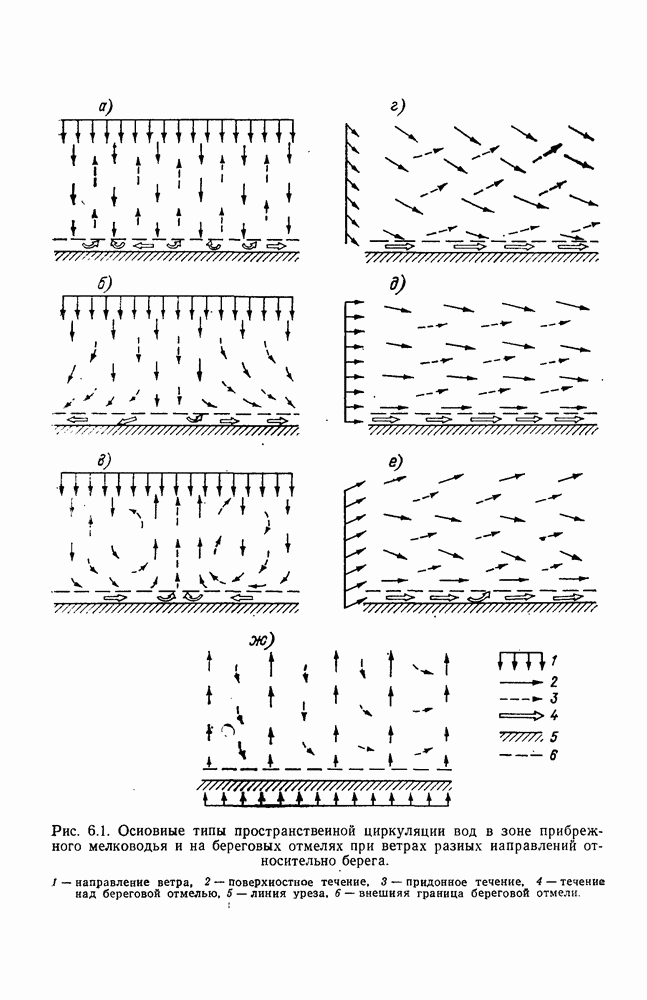
- Глава 6. ТЕЧЕНИЯ В ЗОНЕ ПРИБРЕЖНОГО МЕЛКОВОДЬЯ И НА БЕРЕГОВЫХ ОТМЕЛЯХ
- 6.2. Течения в зоне прибрежного мелководья
- 6.2.2. Повторяемость различных типов циркуляции вод
- 6.2.3. Распределение скорости течения по глубине
- 6.2.4. Изменение скорости течения по ширине зоны
- 6.2.5. Количественные характеристики скорости течения
- 6.2.6. Режимные статистические характеристики скорости течений
- 6.3. Течения на береговых отмелях
- 6.3.2. Распределение скорости вдольберегового течения
- 6.3.3. Расчет средней скорости вдольберегового течения
- Глава 7. ПЕРЕМЕЩЕНИЕ НАНОСОВ НА БЕРЕГОВЫХ ОТМЕЛЯХ
- 7.2. Методы изучения перемещения наносов
- 7.3. Основные черты механизма перемещения наносов
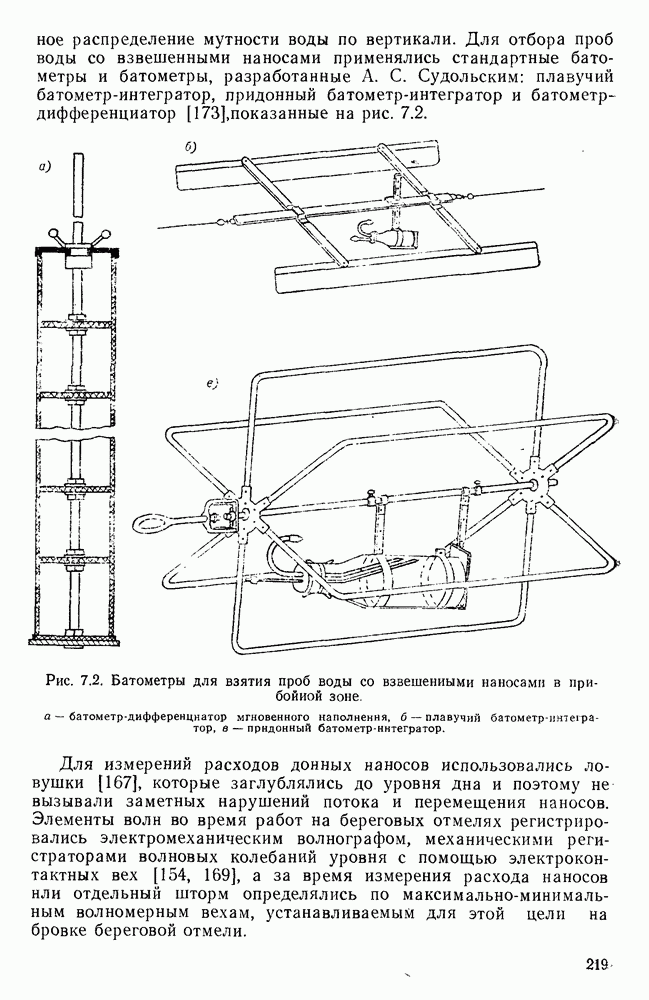
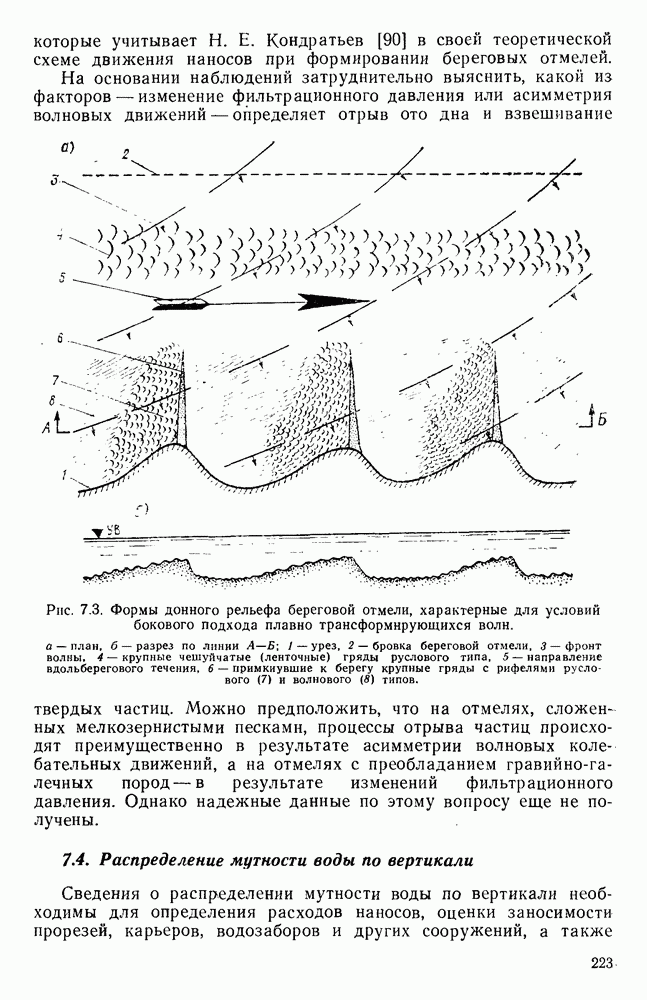
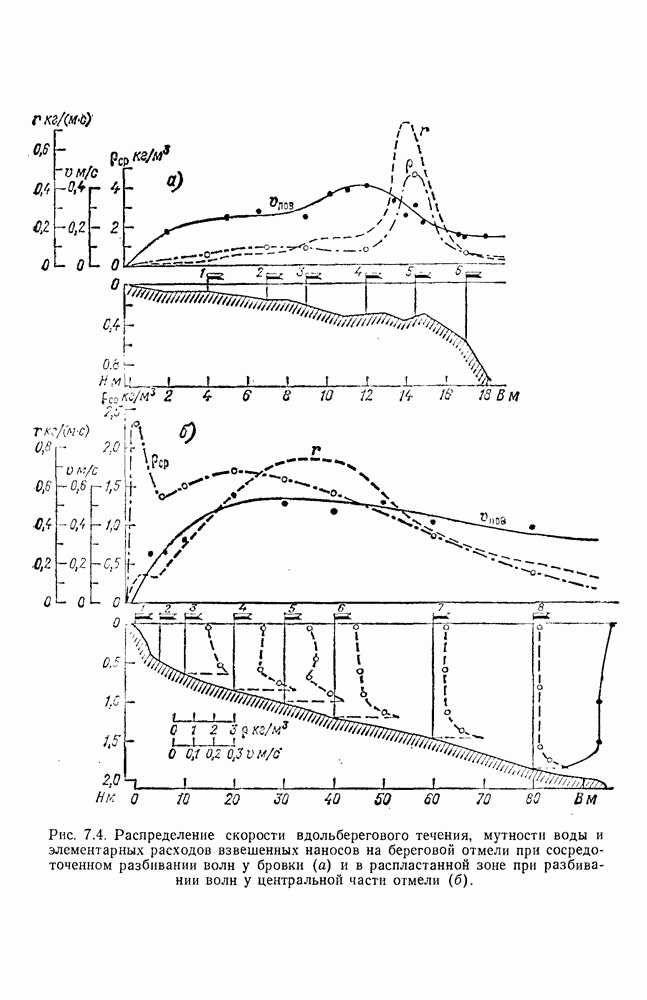
- 7.4. Распределение мутности воды по вертикали
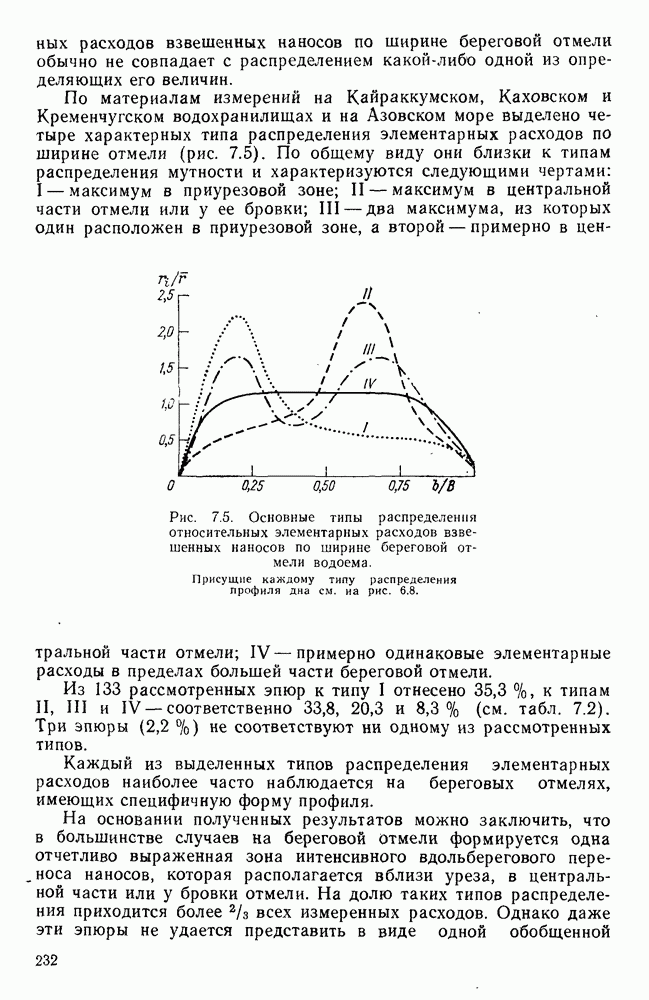
- 7.5. Распределение мутности воды по ширине береговой отмели
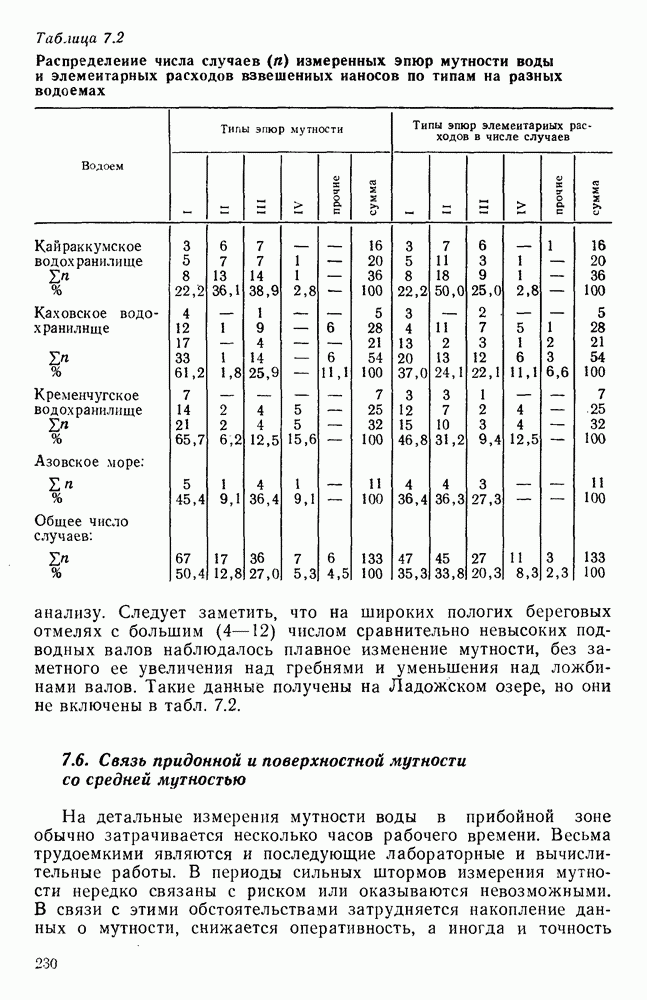
- 7.6. Связь придонной и поверхностной мутности со средней мутностью
- 7.7. Элементарные расходы взвешенных наносов
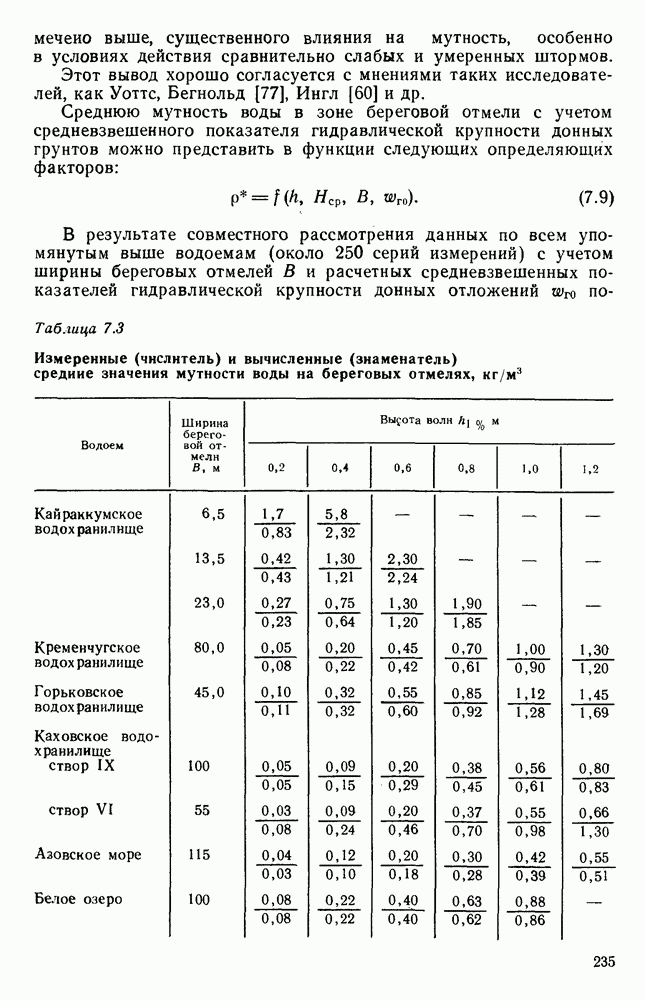
- 7.8. Зависимость средней мутности от определяющих факторов
- 7.9. Расходы донных наносов и их связь со взвешенными наносами
- 7.10. Расчет вдольберегового переноса твердого материала
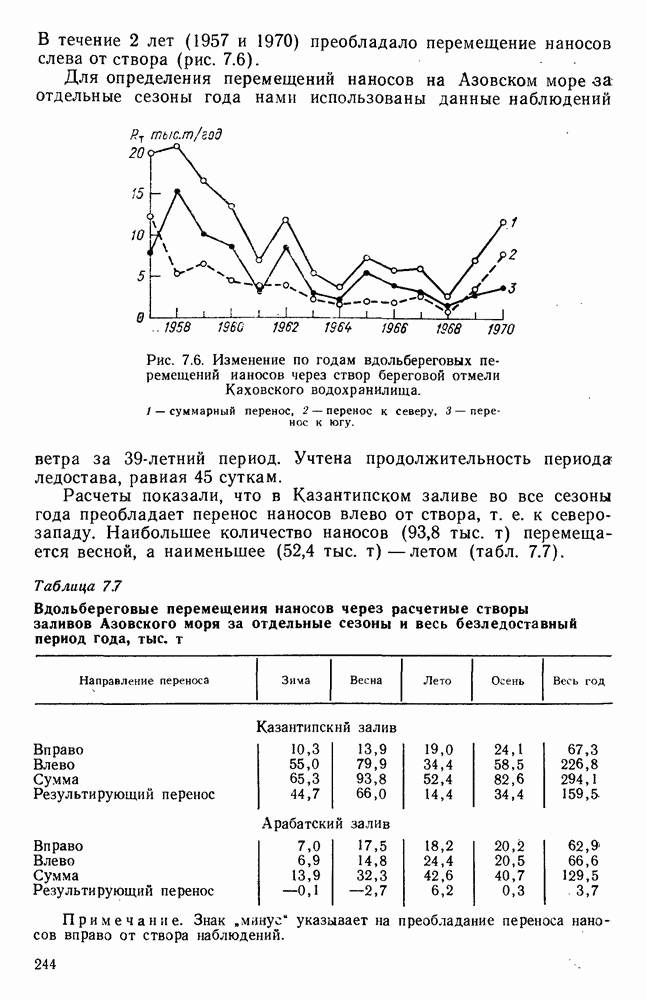
- 7.11. Сезонная и межгодовая изменчивость вдольбереговых перемещений наносов