| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. АППРОКСИМАЦИЯ ФУНКЦИЙ РАБОЧЕГО ЗАТУХАНИЯ
Для построения фильтра необходимо знать математическое описание его АЧХ, например, функцией  После этого следует попытаться теоретически получить эту функцию, соединяя между собой определенным образом элементы фильтра (отрезки линий, емкости, индуктивности, сопротивления). Функцию
После этого следует попытаться теоретически получить эту функцию, соединяя между собой определенным образом элементы фильтра (отрезки линий, емкости, индуктивности, сопротивления). Функцию  можно вычислить, зная структуру фильтра.
можно вычислить, зная структуру фильтра.
Теоретически возможен машинный синтез фильтра путем многократного анализа с корректировкой параметров элементов после каждого счета. При этом можно АЧХ не задавать непрерывной функцией  а задать в виде дискретных величин (таблично). Однако этот метод слишком громоздок и его можно применять лишб в исключительных случаях. Практически во всех случаях расчета (синтеза) фильтров следует задаваться аппроксимацией функции его коэффициента рабочего затухания
а задать в виде дискретных величин (таблично). Однако этот метод слишком громоздок и его можно применять лишб в исключительных случаях. Практически во всех случаях расчета (синтеза) фильтров следует задаваться аппроксимацией функции его коэффициента рабочего затухания  При этом следует учесть, что не все функции пригодны для этого, а только удовлетворяющие условиям физической реализуемости, т. е. для получения которых можно создать реальный фильтр.
При этом следует учесть, что не все функции пригодны для этого, а только удовлетворяющие условиям физической реализуемости, т. е. для получения которых можно создать реальный фильтр.
Известны несколько функций, аппроксимирующих АЧХ фильтров НЧ без учета диссипативных потерь. При аппроксимации максимально плоской характеристикой (характеристика Баттерворса) затухание монотонно растет при отклонении частоты от средней [72]:

где  — параметр, который равен числу реактивных элементов в фильтре-прототипе
— параметр, который равен числу реактивных элементов в фильтре-прототипе 
Чебышевская характеристика затухания описывается следующими математическими выражениями:

где  — коэффициент пульсаций.
— коэффициент пульсаций.
Сравним различные аппроксимации [43]. Характеристика по Баттерворсу — максимально плоская в районе средней частоты и везде монотонна; характеристика по Чебышеву — равноволновая в полосе пропускания. Характеристика по Баттерворсу определяется одним параметром  по Чебышеву — двумя
по Чебышеву — двумя  На скатах фильтра затухание в характеристике по Чебышеву растет
На скатах фильтра затухание в характеристике по Чебышеву растет  большинстве случаев быстрее на
большинстве случаев быстрее на  дБ по сравнению с характеристикой по Баттерворсу. Поэтому чебышевский фильтр имеет меньшее число
дБ по сравнению с характеристикой по Баттерворсу. Поэтому чебышевский фильтр имеет меньшее число
элементов при одинаковых полосах пропускания и крутизне. ФЧХ чебышевского фильтра менее линейна, чем максимально плоского. Для аппроксимации применяют полиномы Чебышева первого и второго родов, а также ультрасферические полиномы (Гегенбауэра), полиномы Лежандра, Лагерра, Эрмита. Возможна также аппроксимация эллиптическими функциями с помощью отрезков прямых линий, потенциальной аналогии и др.
До сих пор рассматривали АЧХ фильтра нижних частот (ФНЧ). Чтобы перейти к характеристикам других фильтров, следует применить преобразование независимой частотной переменной, т. е. требуется перейти от частотной переменной ФНЧ  , к частотной переменной других фильтров
, к частотной переменной других фильтров  , где
, где  Для фильтра верхних частот
Для фильтра верхних частот  Для ППФ
Для ППФ

Для ПЭФ

Аппроксимация АЧХ фильтров с учетом диссипативных потерь рассмотрена в работе [25].
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Главв 1. РАСЧЕТ ЭЛЕМЕНТОВ ГИБРИДНЫХ ИНТЕГРАЛЬНЫХ СХЕМ
- 1. ПОНЯТИЕ ГИБРИДНОЙ ИНТЕГРАЛЬНОЙ СХЕМЫ СВЧ
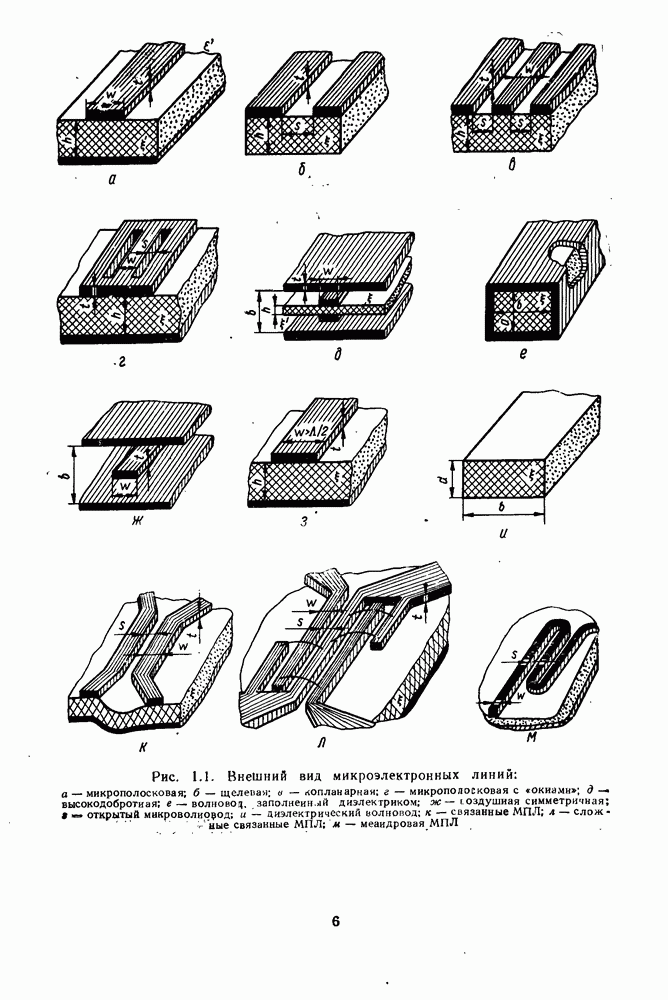
- 2. ОСНОВНЫЕ ЛИНИИ ПЕРЕДАЧ ГИС СВЧ
- 3. РАСЧЕТ ПАРАМЕТРОВ ЛИНИЙ
- Главв 2. УСТРОЙСТВА ДЕЛЕНИЯ (СУММИРОВАНИЯ) МОЩНОСТИ СВЧ
- 1. ПРИМЕНЕНИЕ ДЕЛИТЕЛЕЙ (СУММАТОРОВ) МОЩНОСТИ
- 2. ЭЛЕМЕНТЫ МНОГОКАНАЛЬНЫХ ДЕЛИТЕЛЕЙ
- 3. МНОГОКАНАЛЬНЫЕ ДЕЛИТЕЛИ. АЛГОРИТМЫ РАСЧЕТА МНОГОКАНАЛЬНЫХ ДЕЛИТЕЛЕЙ
- 4. ЧЕТЫРЕХКАНАЛЬНЫЕ ДЕЛИТЕЛИ МОЩНОСТИ
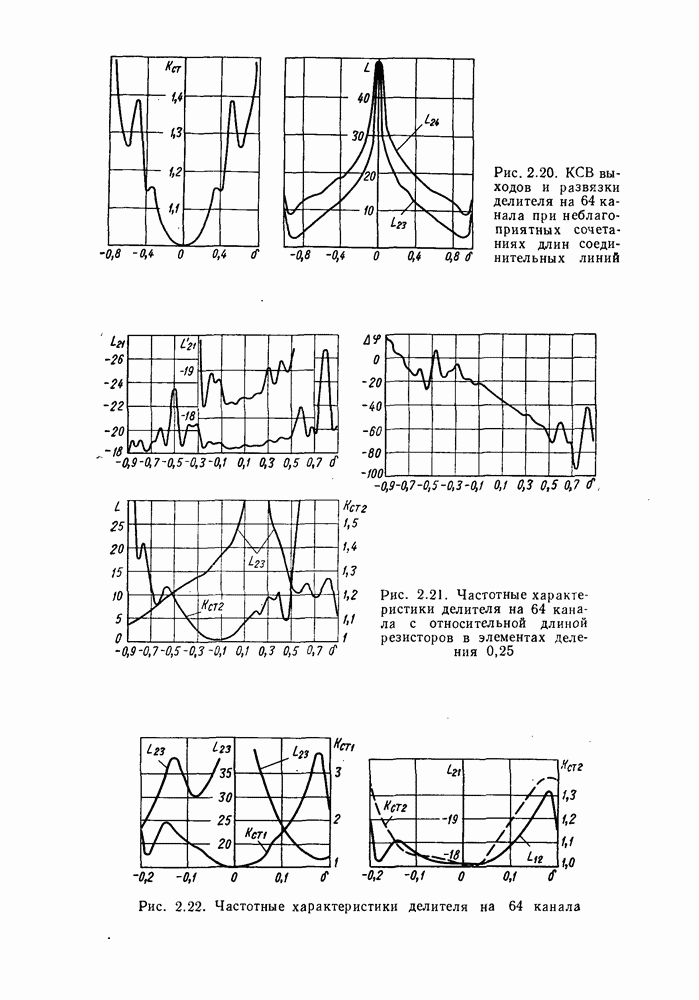
- 5. ДЕЛИТЕЛИ МОЩНОСТИ НА 64 КАНАЛА
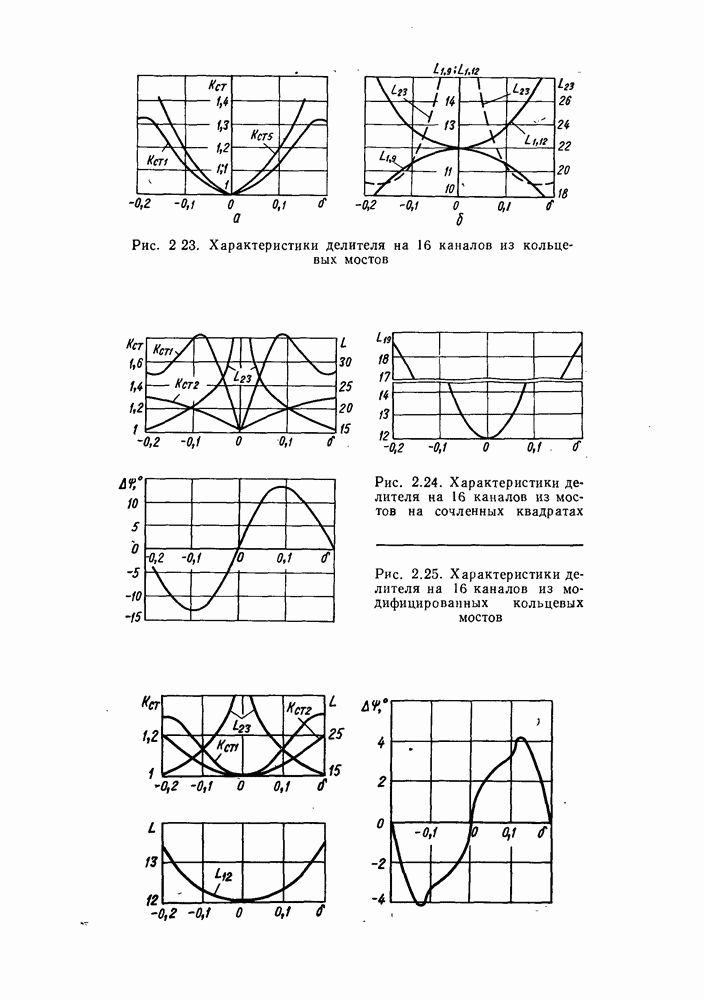
- 6. ХАРАКТЕРИСТИКИ ДЕЛИТЕЛЕЙ, ВЫПОЛНЕННЫХ ИЗ МОСТОВЫХ УСТРОЙСТВ
- 7. РЕКОМЕНДАЦИИ ДЛЯ ПРОЕКТИРОВАНИЯ ДЕЛИТЕЛЕЙ (СУММАТОРОВ) МОЩНОСТИ
- Глава 3. ИЗБИРАТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ОСНОВНЫЕ ТРЕБОВАНИЯ К ИЗБИРАТЕЛЬНЫМ УСТРОЙСТВАМ И ИХ ПАРАМЕТРЫ
- 2. АППРОКСИМАЦИЯ ФУНКЦИЙ РАБОЧЕГО ЗАТУХАНИЯ
- 3. РАСЧЕТ ТОПОЛОГИЙ ФИЛЬТРОВ
- 4. АНАЛИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- Глава 4. СМЕСИТЕЛИ
- 1. ПАРАМЕТРЫ СМЕСИТЕЛЕЙ И ОСНОВНЫЕ ТРЕБОВАНИЯ К НИМ
- 2. ВЫБОР АКТИВНЫХ ЭЛЕМЕНТОВ
- 3. СХЕМЫ СМЕСИТЕЛЕЙ
- 4. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СМЕСИТЕЛЕЙ
- 5. СМЕСИТЕЛИ НА КОМБИНАЦИЯХ ЛИНИЙ ПЕРЕДАЧ
- 6. РЕЗУЛЬТАТЫ РАСЧЕТОВ И ЭКСПЕРИМЕНТОВ
- Глава 5. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ТРЕБОВАНИЯ К МАЛОШУМЯЩИМ УСИЛИТЕЛЯМ СВЧ И ИХ ПАРАМЕТРЫ
- 2. УСИЛИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 3. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ТРАНЗИСТОРА
- 4. РАСЧЕТ УСИЛИТЕЛЕЙ
- 5. ИСПОЛЬЗОВАНИЕ ЭВМ ПРИ ПРОЕКТИРОВАНИИ УСИЛИТЕЛЕЙ
- 6. ТОПОЛОГИЧЕСКИЕ СХЕМЫ МИКРОЭЛЕКТРОННЫХ СВЧ УСИЛИТЕЛЕЙ
- 7. МНОГОКАСКАДНЫЕ УСИЛИТЕЛИ
- 8. ВЛИЯНИЕ ВНЕШНИХ ФАКТОРОВ НА РАБОТУ УСИЛИТЕЛЕЙ С ПТ
- Глава 6. УСТРОЙСТВА, УПРАВЛЯЮЩИЕ МОЩНОСТЬЮ
- 2. УПРАВЛЯЮЩИЕ ЭЛЕМЕНТЫ
- 3. МАТЕМАТИЧЕСКИЙ АППАРАТ ДЛЯ РАСЧЕТА УСТРОЙСТВ НА СОСРЕДОТОЧЕННЫХ ЭЛЕМЕНТАХ
- 4. УСТРОЙСТВА НА СОСРЕДОТОЧЕННЫХ УПРАВЛЯЮЩИХ ЭЛЕМЕНТАХ
- 5. УСТРОЙСТВА НА ЭЛЕМЕНТАХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- Глава 7. ФАЗОВРАЩАТЕЛИ
- 1. ПАРАМЕТРЫ ПОЛУПРОВОДНИКОВЫХ ФАЗОВРАЩАТЕЛЕЙ
- 2. СХЕМЫ ФАЗОВРАЩАТЕЛЕЙ И АНАЛИЗ ХАРАКТЕРИСТИК ФАЗОВРАЩАТЕЛЯ С НАПРАВЛЕННЫМ ОТВЕТВИТЕЛЕМ
- Глава 8. ОГРАНИЧИТЕЛИ МОЩНОСТИ
- 1. ПАРАМЕТРЫ ОГРАНИЧИТЕЛЕЙ МОЩНОСТИ
- 2. ОГРАНИЧИТЕЛЬНЫЕ ДИОДЫ
- 3. СХЕМЫ ОГРАНИЧИТЕЛЕЙ МОЩНОСТИ И ИХ РАСЧЕТ
- СПИСОК ЛИТЕРАТУРЫ