| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
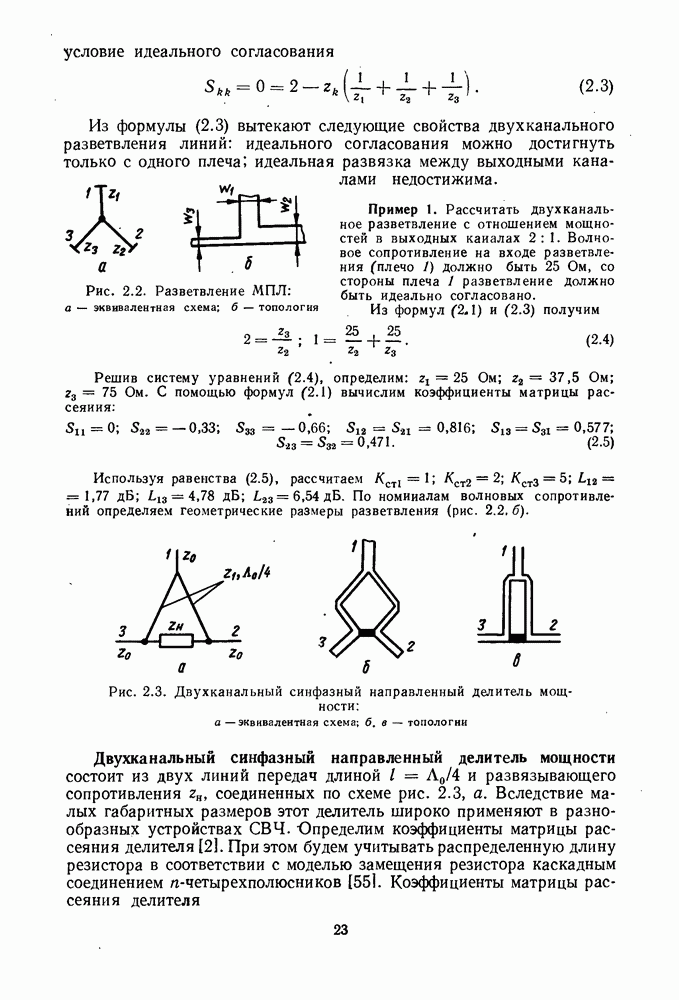
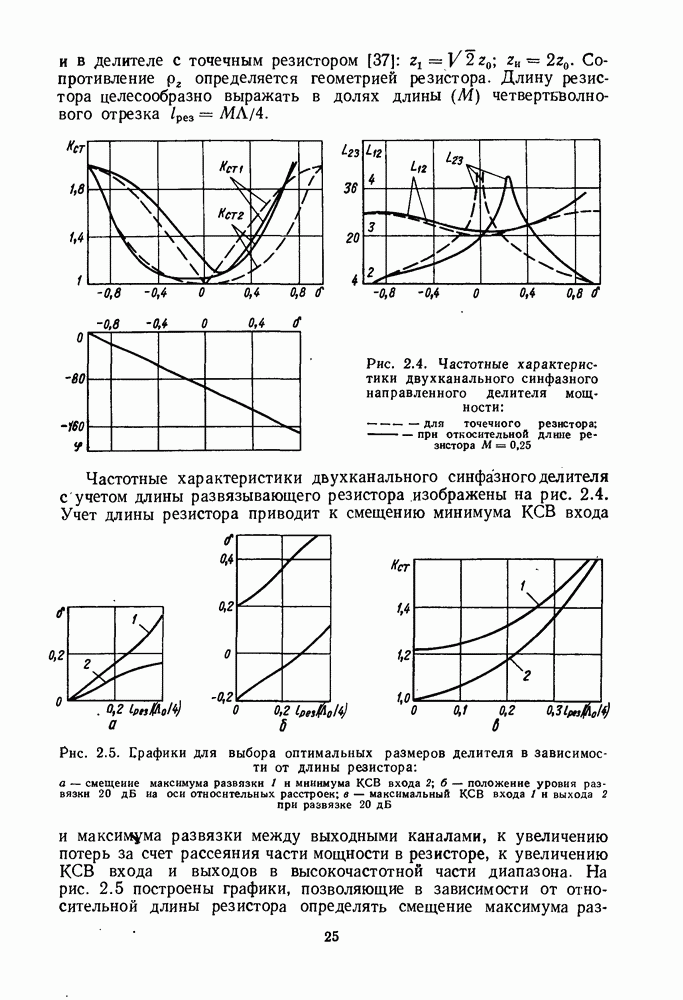
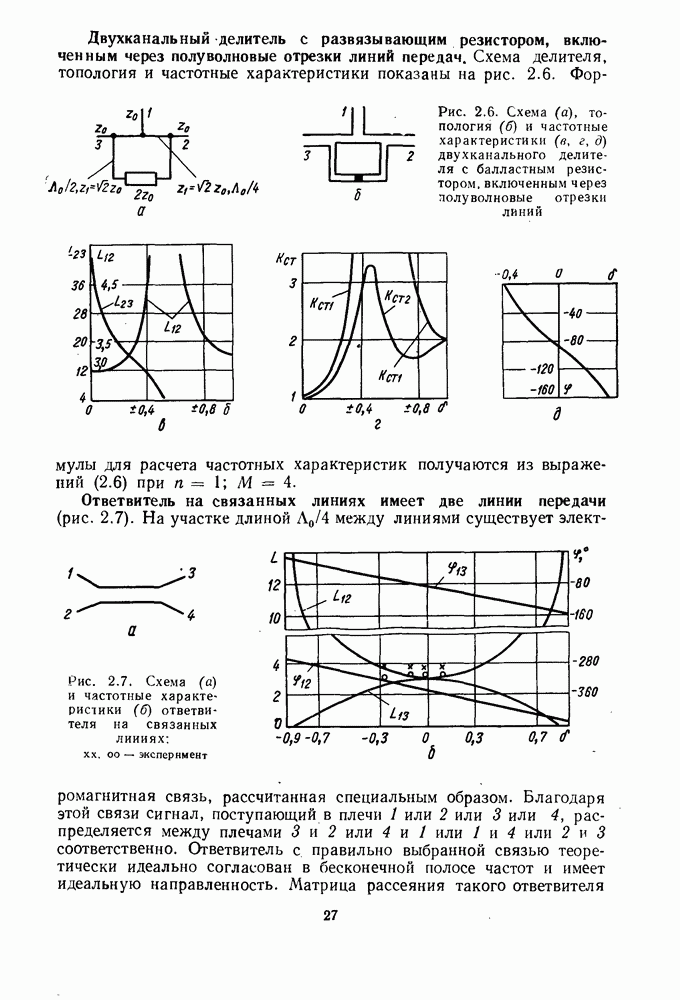
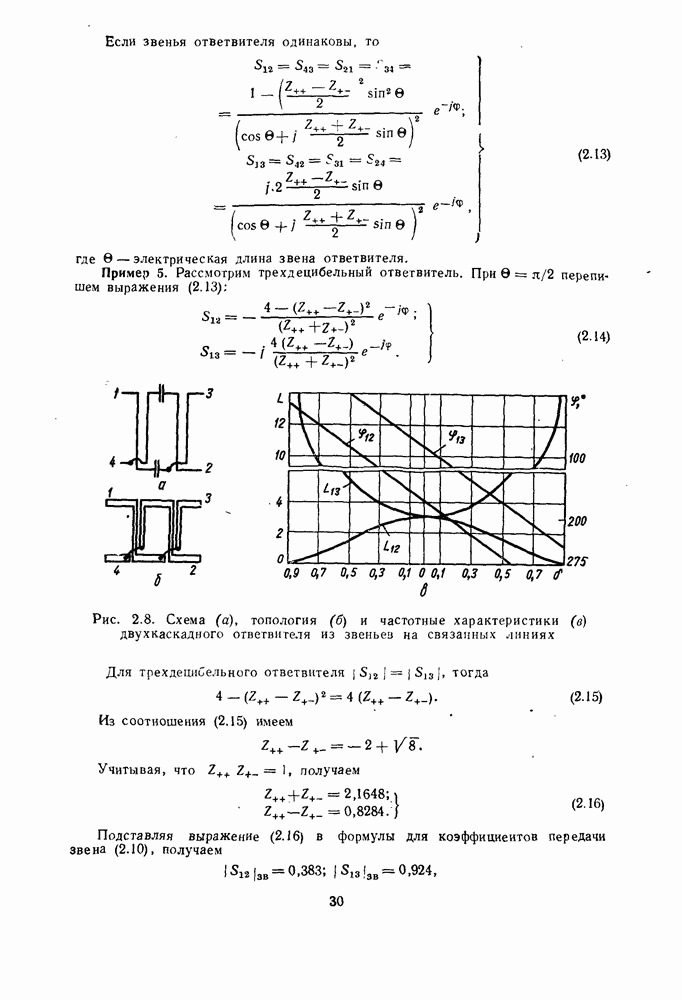
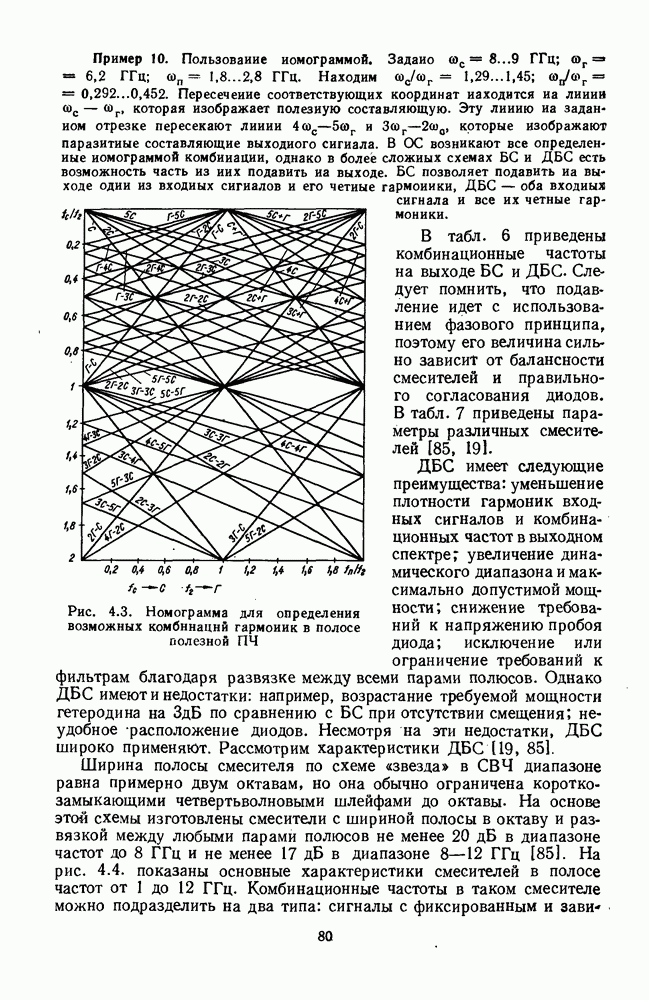
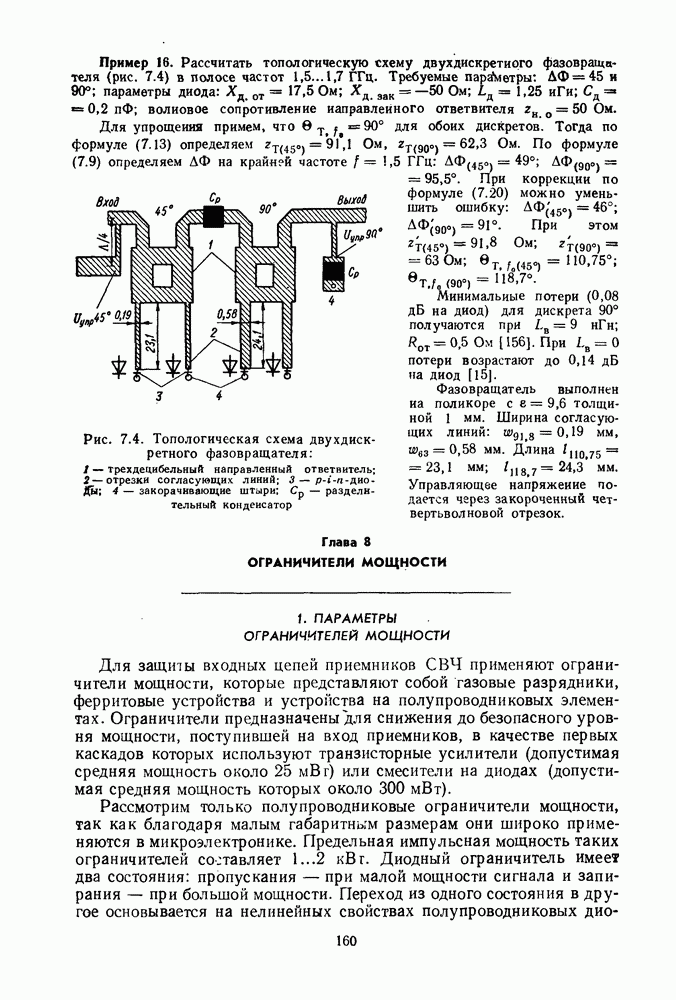
4. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СМЕСИТЕЛЕЙ
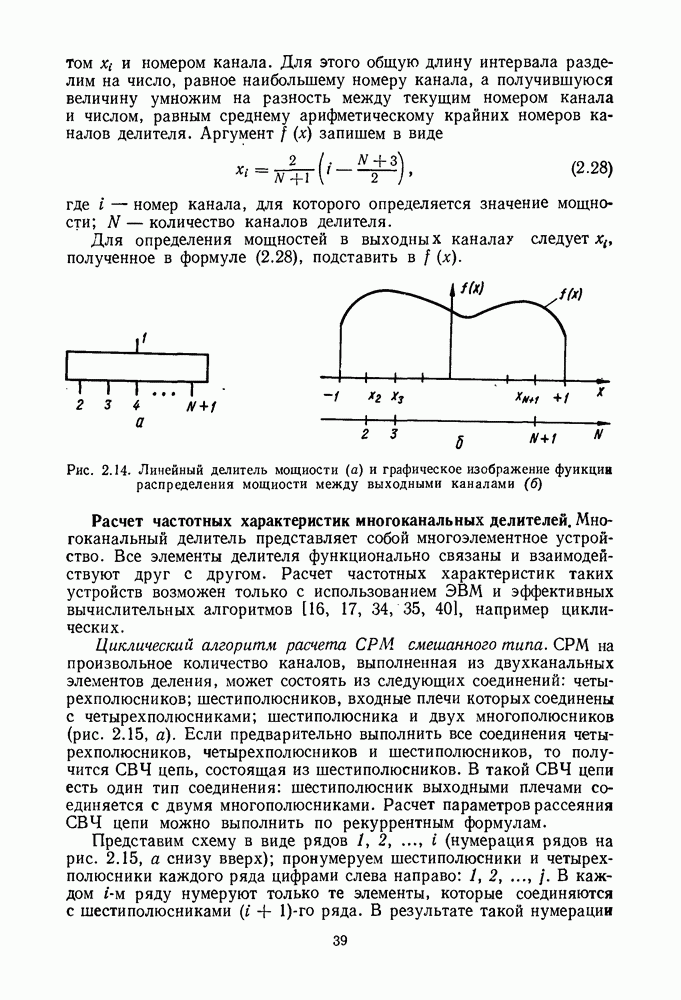
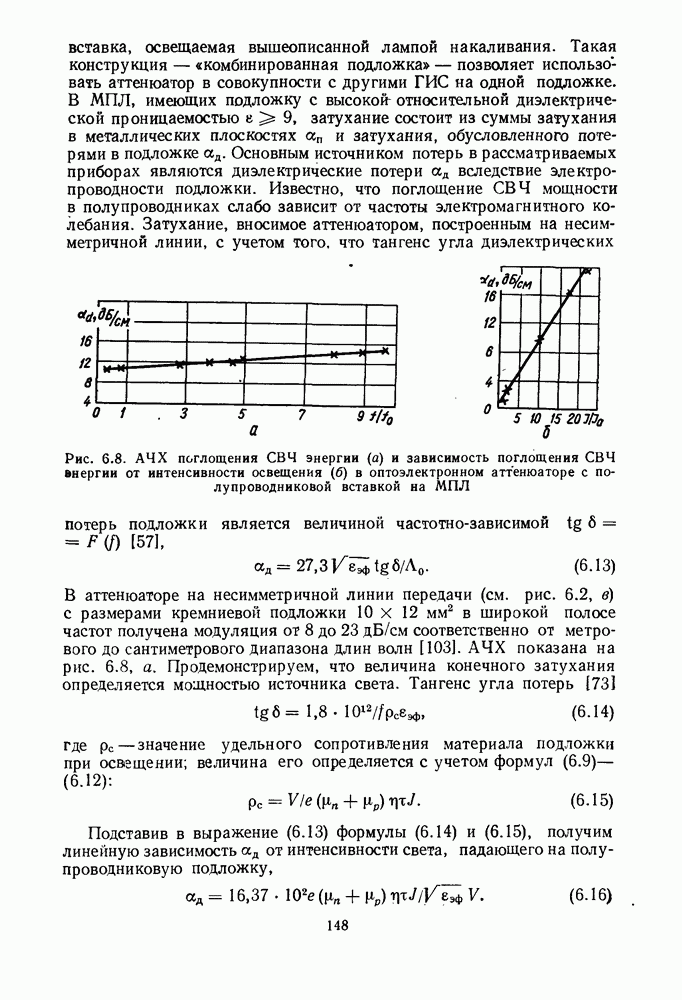
Математическая модель смесительного диода. Для анализа работы смесителей обычно применяют модель смесительного диода в виде матрицы параметров проводимости или параметров рассеяния. Такую
модель получают, измеряя вольт-амперную характеристику диода и его реактивности. Принимают, что ток и напряжение на диоде состоят из слагаемых, частоты которых равны  где
где  - круговая частота гетеродина;
- круговая частота гетеродина;  круговая промежуточная частота. Ток через диод является функцией напряжения и производной от напряжения по времени:
круговая промежуточная частота. Ток через диод является функцией напряжения и производной от напряжения по времени:  Предполагают также, что составляющие частоты сигнала, зеркальной частоты и боковых частот настолько малы, что их можно рассматривать как вариации
Предполагают также, что составляющие частоты сигнала, зеркальной частоты и боковых частот настолько малы, что их можно рассматривать как вариации  и
и  Запишем уравнение вариаций [58]
Запишем уравнение вариаций [58]

где 
Учитывая только частоты сигнальную, промежуточную и зеркальную, получаем комплексную Матрицу проводимости диода

Где
Матрица всего диода с учетом индуктивности выводов  и сопротивления
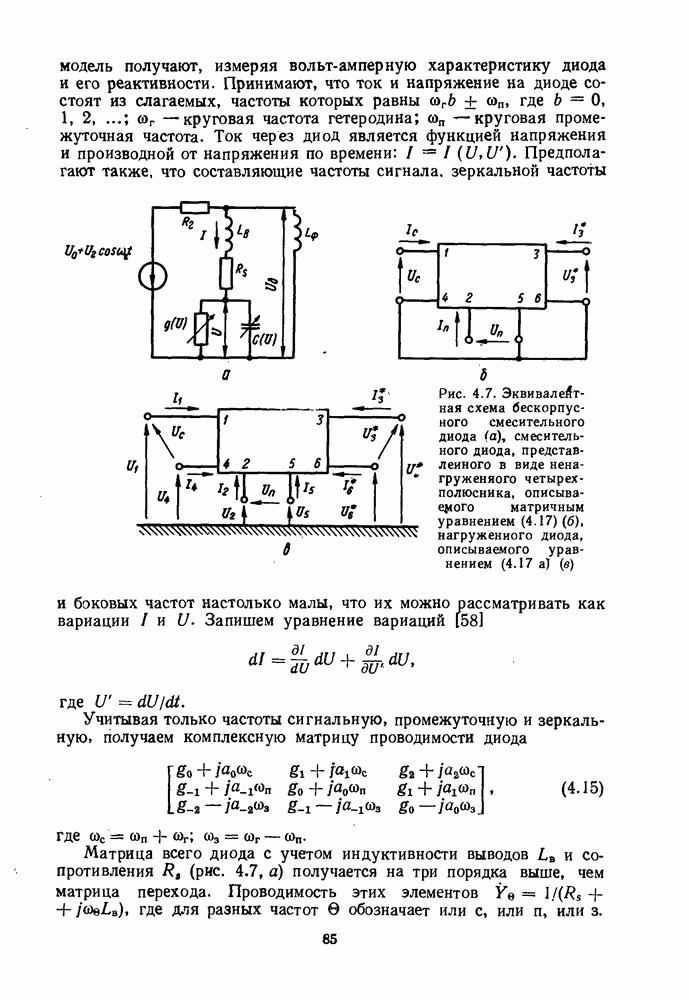
и сопротивления  (рис. 4.7, а) получается на три порядка выше, чем матрица перехода. Проводимость этих элементов
(рис. 4.7, а) получается на три порядка выше, чем матрица перехода. Проводимость этих элементов  где для разных частот 0 обозначает или с, или
где для разных частот 0 обозначает или с, или  или
или  .
.

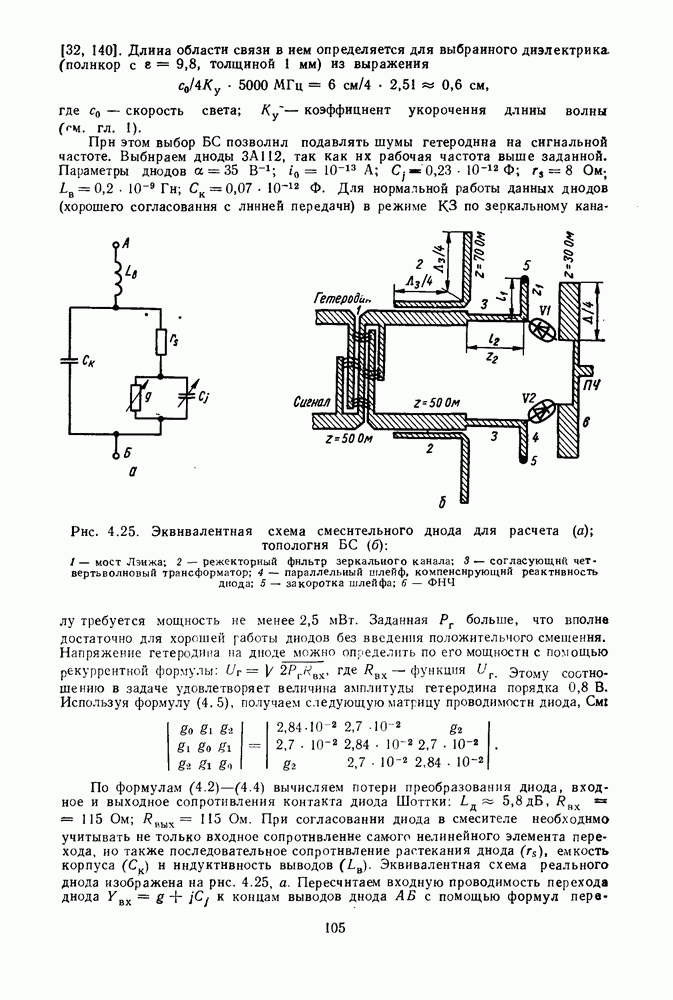
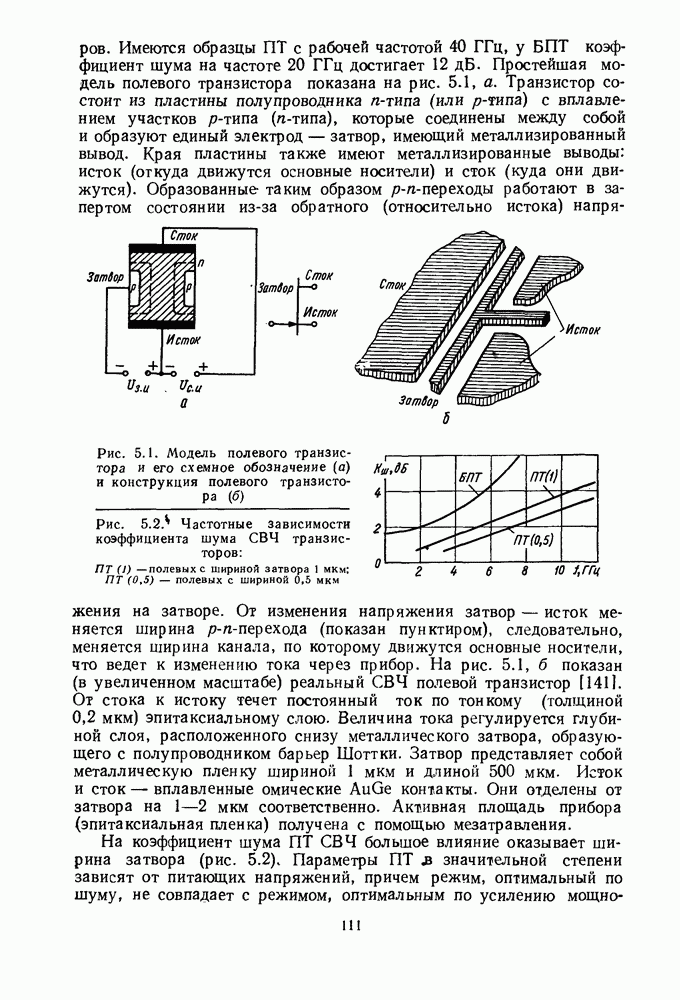
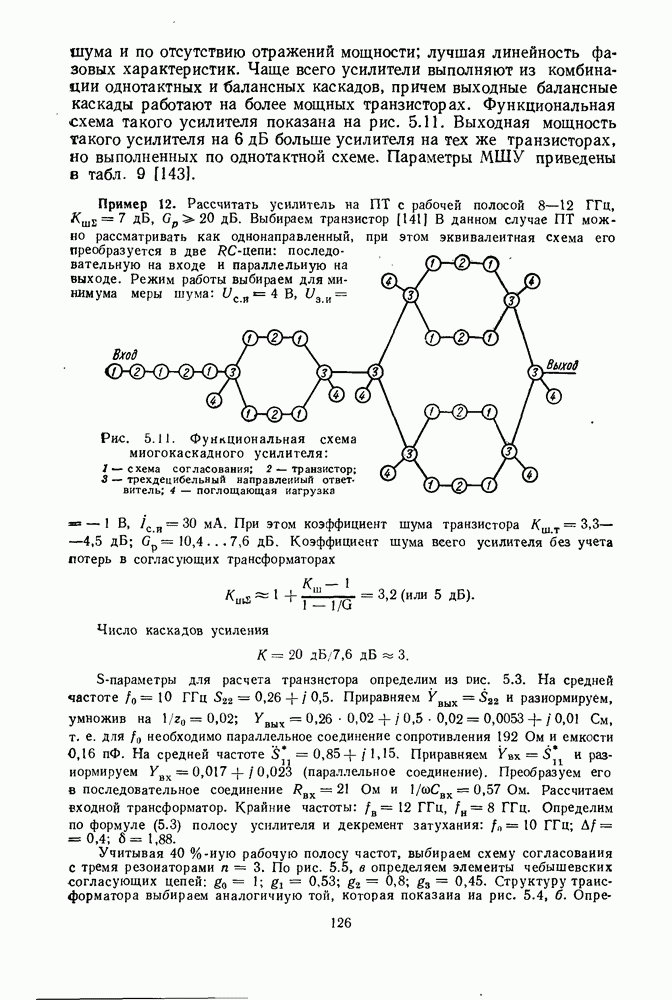
Рис. 4.7. Эквивалентная схема бескорпусного смесительного диода  смесительного диода, представленного в виде ненагруженяого четырехполюсника, описываемого матричным уравнением
смесительного диода, представленного в виде ненагруженяого четырехполюсника, описываемого матричным уравнением  нагруженного диода, описываемого уравнением (4.17 а) (в)
нагруженного диода, описываемого уравнением (4.17 а) (в)
Если обозначить элементы матрицы (4.15)  то матрица проводимости смесительного диода принимает вид
то матрица проводимости смесительного диода принимает вид

Определим элементы матрицы (4.16). Смесительный диод представим эквивалентной схемой (рис. 4.7, а), для которой составляется система дифференциальных нелинейных уравнений, из решения которой находят величины  как функции времени. Затем эти функции раскладывают в ряд Фурье по частоте гетеродина. Система дифференциальных уравнений решается на ЭВМ методом Рунге-Кута и имеет вид
как функции времени. Затем эти функции раскладывают в ряд Фурье по частоте гетеродина. Система дифференциальных уравнений решается на ЭВМ методом Рунге-Кута и имеет вид

где  — коэффициент, характеризующий наклон вольт-амперной характеристики диода;
— коэффициент, характеризующий наклон вольт-амперной характеристики диода;  — обменный ток диода;
— обменный ток диода;  — емкость перехода диода при нулевом смещении;
— емкость перехода диода при нулевом смещении;  — потенциальный барьер (являются параметрами диода);
— потенциальный барьер (являются параметрами диода);  постоянное смещение на диоде;
постоянное смещение на диоде;  — амплитуда напряжения гетеродина.
— амплитуда напряжения гетеродина.
Функции, раскладываемые в ряд Фурье, имеют вид

Элементы матрицы (4.15) определяют численным методом по формулам

где 
Если исключить внутренние узлы схемы по методу работы [98], то матричное уравнение смесительного диода (4.16) в терминах параметров проводимости

Такой матрице соответствует эквивалентная схема на рис. 4.7, б, где каждая пара полюсов работает лишь на одной частоте. В реальных схемах очень часто приходится соединять все полюса с землей

(кликните для просмотра скана)
через какую-либо нагрузку (например, фильтр), поэтому необходимо преобразовать эквивалентную схему диода так, как показано на рис. 4.7, в. Такой схеме соответствует неопределенная матрица проводимости шестого порядка, для которой справедливы равенства [98]

Полученная модель смесительного диода позволяет исследовать математические модели смесителей при любом включении диода.
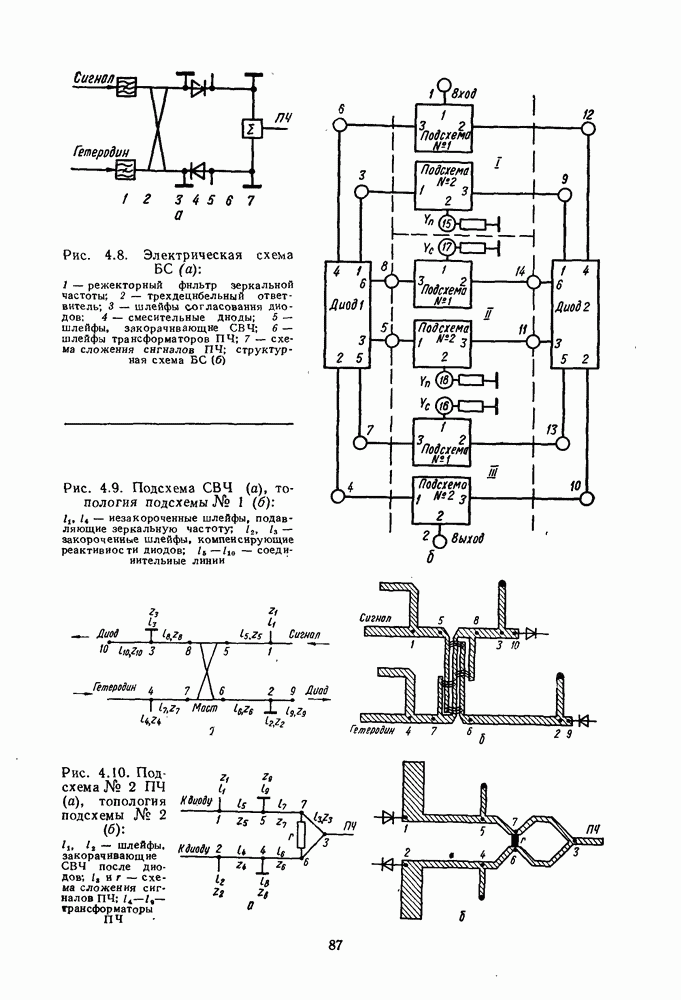
Математическая модель микрополоскового балансного смесителя включает математические модели его составных частей: смесительного диода, направленного ответвителя, шлейфов схем согласования и соединительных линий. Если представить математическую модель диода выражением (4.17 а), то расчет БС целесообразно проводить в терминах параметров проводимости. Электрическая схема БС показана на рис. 4.8, а, структурная схема его модели — на рис. 4.8, б. В этой модели все элементы выражены через  -параметры (рассчитанные на частотах:
-параметры (рассчитанные на частотах:  — сигнала, II — зеркальной, III — промежуточной), поэтому для расчета всего смесителя можно применить метод многополюсных подсхем [98]. Математическую модель БС строят следующим образом: выражают в
— сигнала, II — зеркальной, III — промежуточной), поэтому для расчета всего смесителя можно применить метод многополюсных подсхем [98]. Математическую модель БС строят следующим образом: выражают в  -матрицах все элементы схемы рис.
-матрицах все элементы схемы рис.  сокращают внутренние узлы в подсхемах на рис. 4.9 и 4.10; связывают У-матрицы всех элементов. В результате получают модель
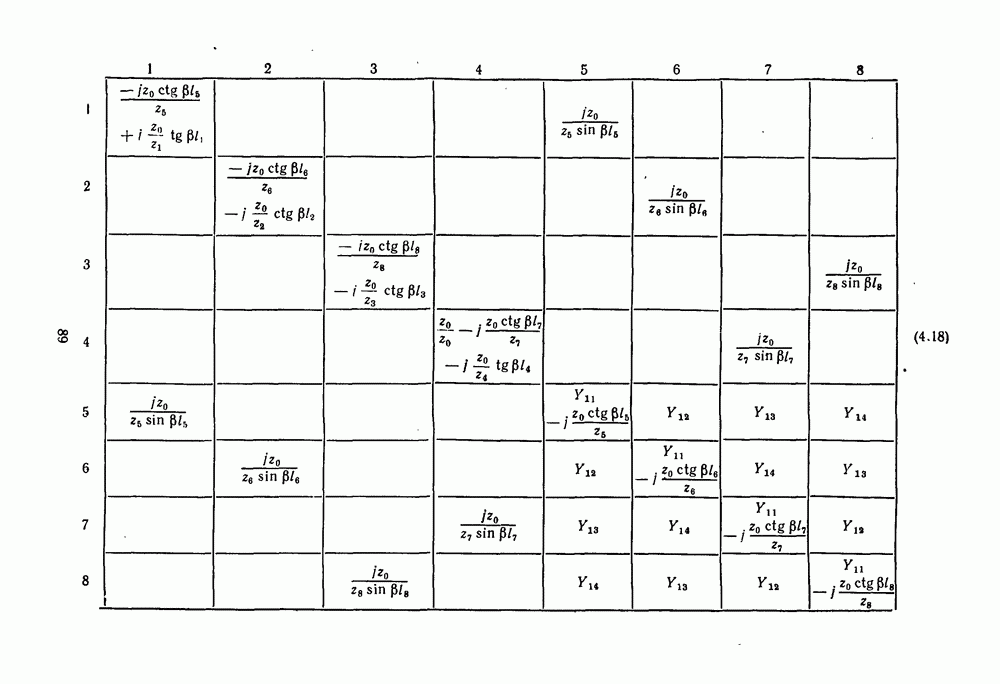
сокращают внутренние узлы в подсхемах на рис. 4.9 и 4.10; связывают У-матрицы всех элементов. В результате получают модель  которая выражается матрицей проводимости 18-го порядка. Определим элементы этой матрицы. Электрическая схема СВЧ (подсхема № 1) показана на рис. 4.9, а, ее матрица проводимости имеет вид (см. стр. 89).
которая выражается матрицей проводимости 18-го порядка. Определим элементы этой матрицы. Электрическая схема СВЧ (подсхема № 1) показана на рис. 4.9, а, ее матрица проводимости имеет вид (см. стр. 89).
Эта матрица составляется по правилам, указанным в работе [98] (подразумевается, что  Элементы матрицы проводимости трехдецибельного ответвителя проводимости шлейфов и соединительных линий приведены в работе [68], где
Элементы матрицы проводимости трехдецибельного ответвителя проводимости шлейфов и соединительных линий приведены в работе [68], где  — волновое сопротивление линии.
— волновое сопротивление линии.
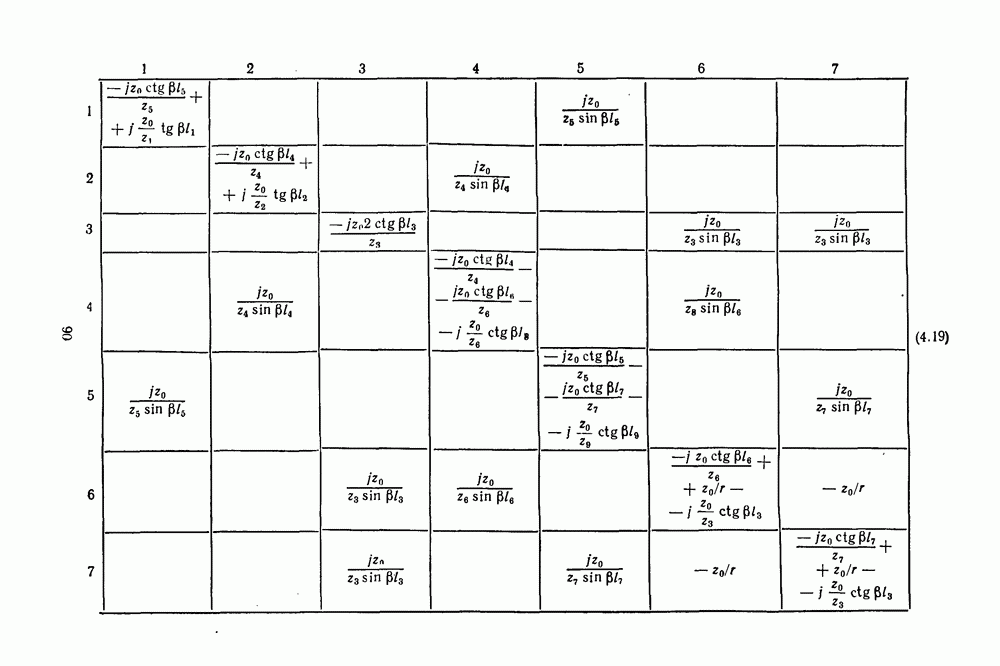
Подсхема №  показана на рис. 4.10, а, ее матрица проводимости имеет вид (см. стр. 90).
показана на рис. 4.10, а, ее матрица проводимости имеет вид (см. стр. 90).
Эта матрица составляется по тем же правилам, что и матрица (4.18). Такую схему суммирования ПЧ с помощью развязанных сумматоров мощности целесообразно применять при ПЧ больше 600 МГц. При отсутствии сумматоров матрица значительно упрощается. Для сокращения порядка матриц подсхем СВЧ и ПЧ до  порядка пользуются формулами работы [98].
порядка пользуются формулами работы [98].

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)
В матрице проводимости всего БС (4.20) [приняты следующие  обозначения: С, — элементы сокращенной до 3-го порядка матрицы подсхемы СВЧ;
обозначения: С, — элементы сокращенной до 3-го порядка матрицы подсхемы СВЧ;  - матрицы подсхемы ПЧ;
- матрицы подсхемы ПЧ;  - элементы матрицы 6-го порядка смесительного диода. В зависимости от частоты, на которой рассчитывалась проводимость элемента матрицы подсхемы, над символами и
- элементы матрицы 6-го порядка смесительного диода. В зависимости от частоты, на которой рассчитывалась проводимость элемента матрицы подсхемы, над символами и  ставятся следующие индексы:
ставятся следующие индексы:  для промежуточной частоты;
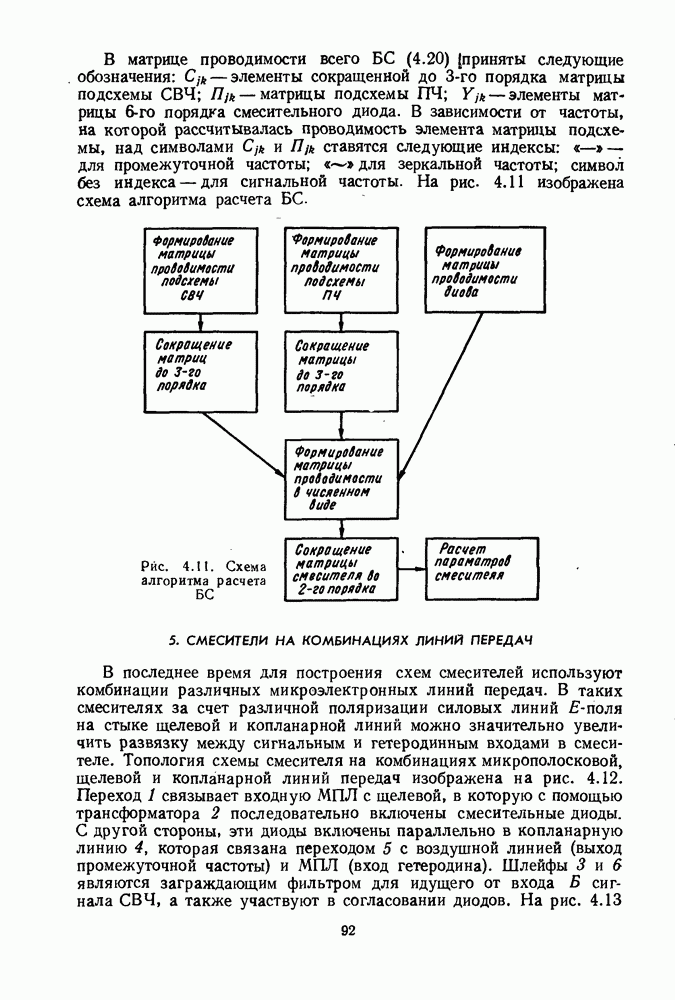
для промежуточной частоты;  для зеркальной частоты; символ без индекса — для сигнальной частоты. На рис. 4.11 изображена схема алгоритма расчета БС.
для зеркальной частоты; символ без индекса — для сигнальной частоты. На рис. 4.11 изображена схема алгоритма расчета БС.

Рис. 4.11. Схема алгоритма расчета БС
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Главв 1. РАСЧЕТ ЭЛЕМЕНТОВ ГИБРИДНЫХ ИНТЕГРАЛЬНЫХ СХЕМ
- 1. ПОНЯТИЕ ГИБРИДНОЙ ИНТЕГРАЛЬНОЙ СХЕМЫ СВЧ
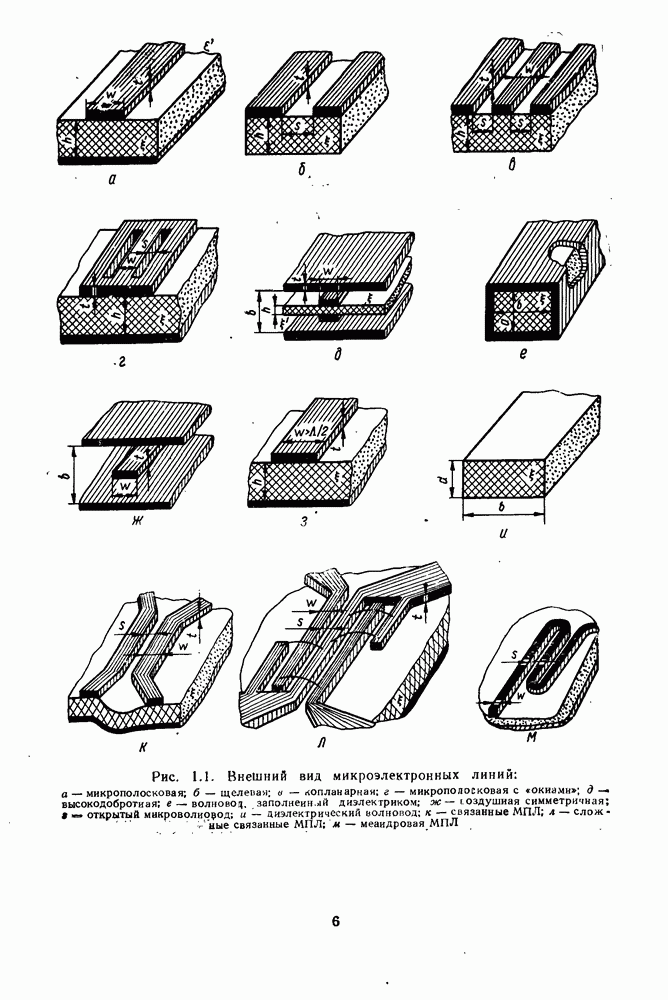
- 2. ОСНОВНЫЕ ЛИНИИ ПЕРЕДАЧ ГИС СВЧ
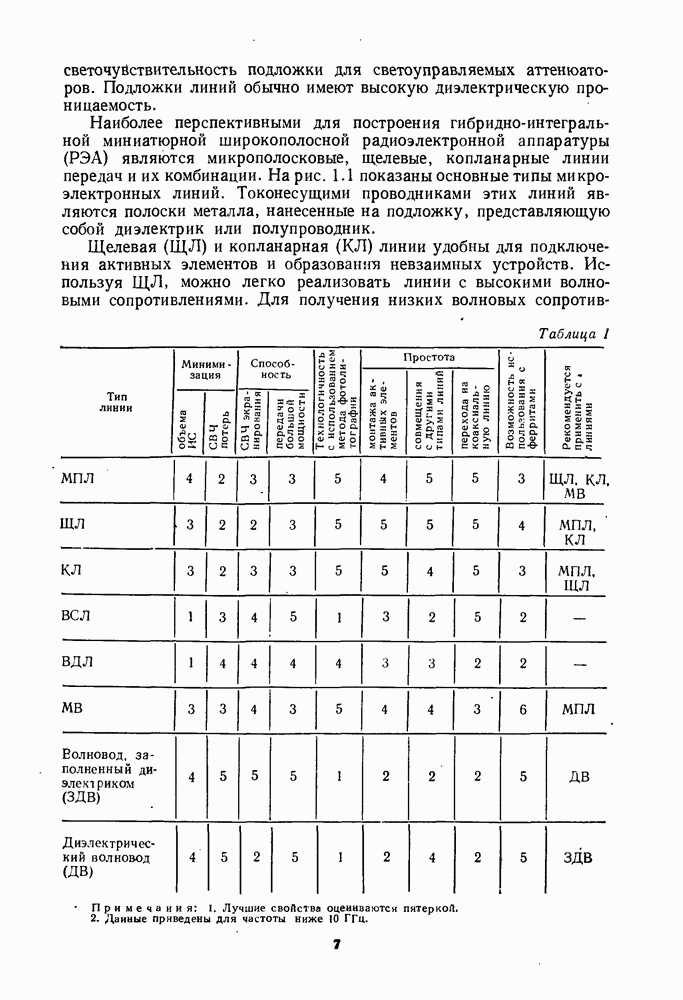
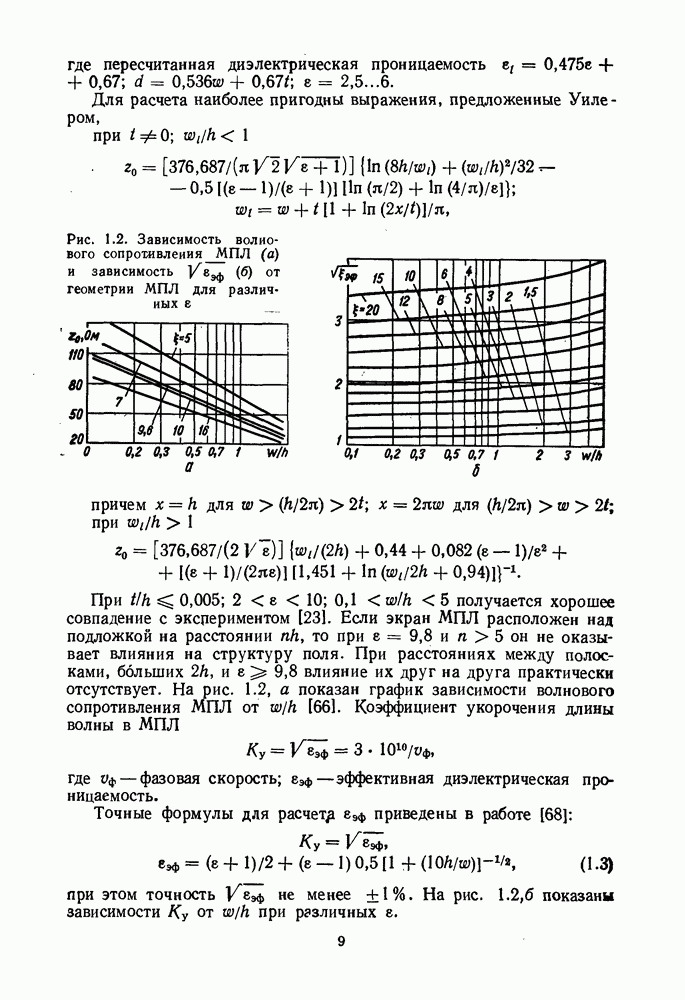
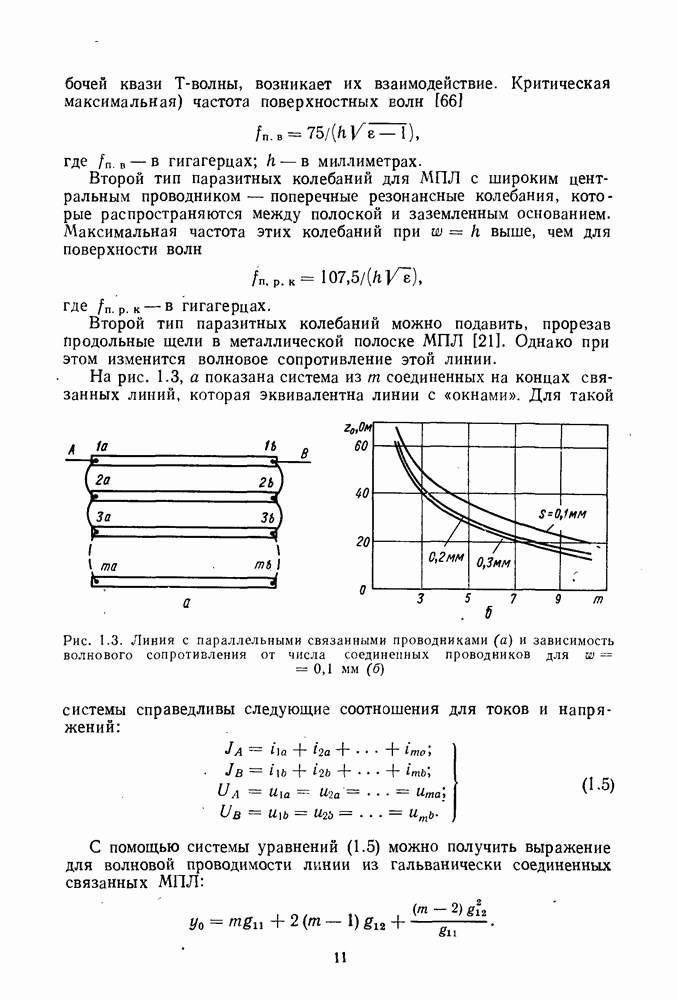
- 3. РАСЧЕТ ПАРАМЕТРОВ ЛИНИЙ
- Главв 2. УСТРОЙСТВА ДЕЛЕНИЯ (СУММИРОВАНИЯ) МОЩНОСТИ СВЧ
- 1. ПРИМЕНЕНИЕ ДЕЛИТЕЛЕЙ (СУММАТОРОВ) МОЩНОСТИ
- 2. ЭЛЕМЕНТЫ МНОГОКАНАЛЬНЫХ ДЕЛИТЕЛЕЙ
- 3. МНОГОКАНАЛЬНЫЕ ДЕЛИТЕЛИ. АЛГОРИТМЫ РАСЧЕТА МНОГОКАНАЛЬНЫХ ДЕЛИТЕЛЕЙ
- 4. ЧЕТЫРЕХКАНАЛЬНЫЕ ДЕЛИТЕЛИ МОЩНОСТИ
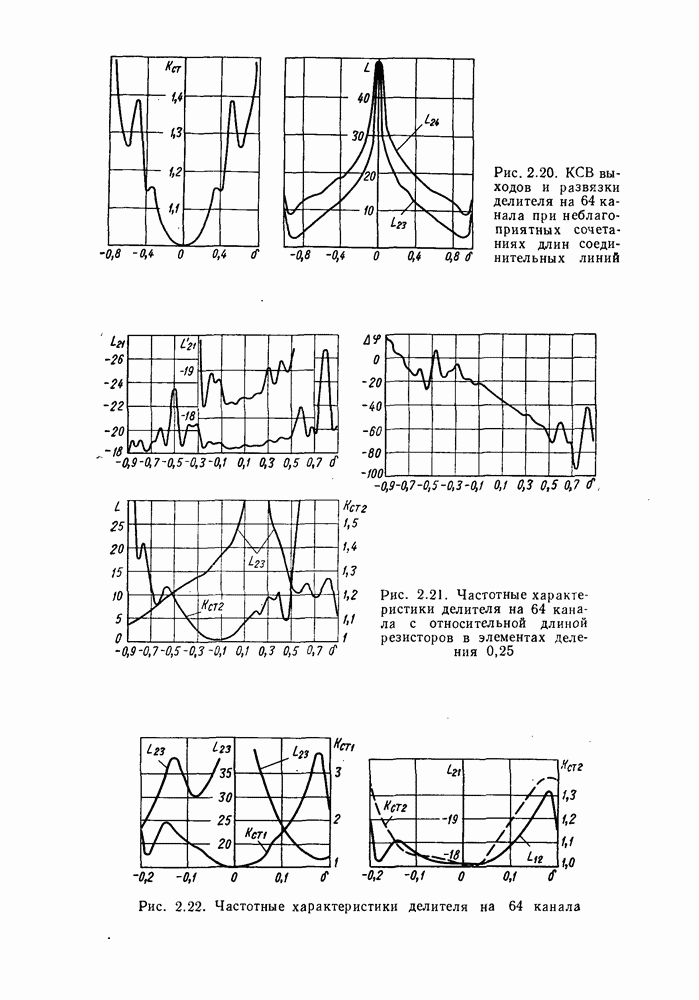
- 5. ДЕЛИТЕЛИ МОЩНОСТИ НА 64 КАНАЛА
- 6. ХАРАКТЕРИСТИКИ ДЕЛИТЕЛЕЙ, ВЫПОЛНЕННЫХ ИЗ МОСТОВЫХ УСТРОЙСТВ
- 7. РЕКОМЕНДАЦИИ ДЛЯ ПРОЕКТИРОВАНИЯ ДЕЛИТЕЛЕЙ (СУММАТОРОВ) МОЩНОСТИ
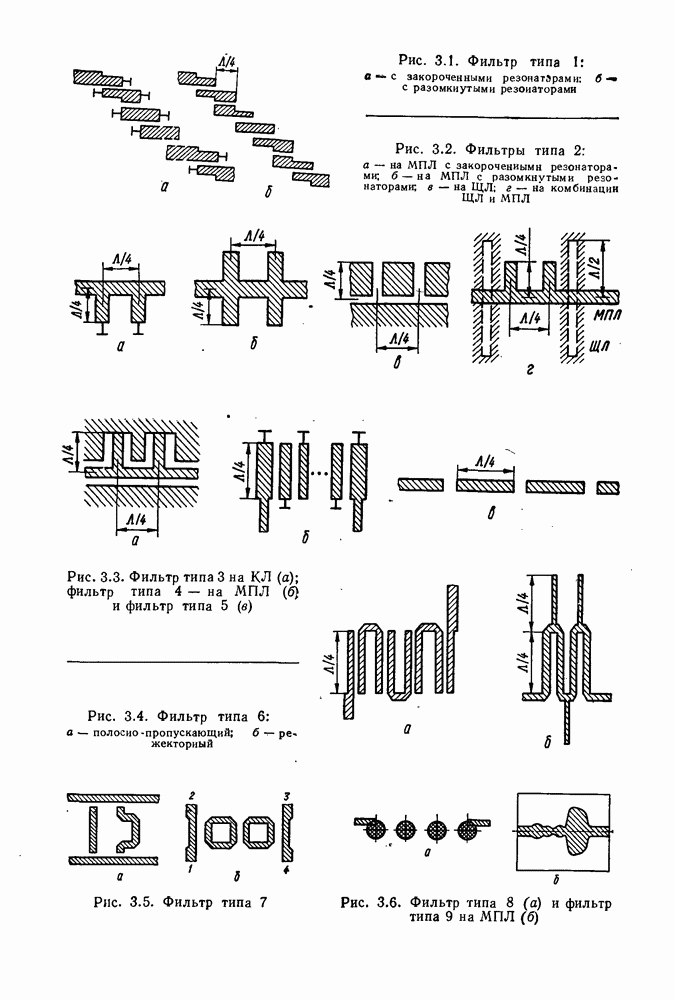
- Глава 3. ИЗБИРАТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ОСНОВНЫЕ ТРЕБОВАНИЯ К ИЗБИРАТЕЛЬНЫМ УСТРОЙСТВАМ И ИХ ПАРАМЕТРЫ
- 2. АППРОКСИМАЦИЯ ФУНКЦИЙ РАБОЧЕГО ЗАТУХАНИЯ
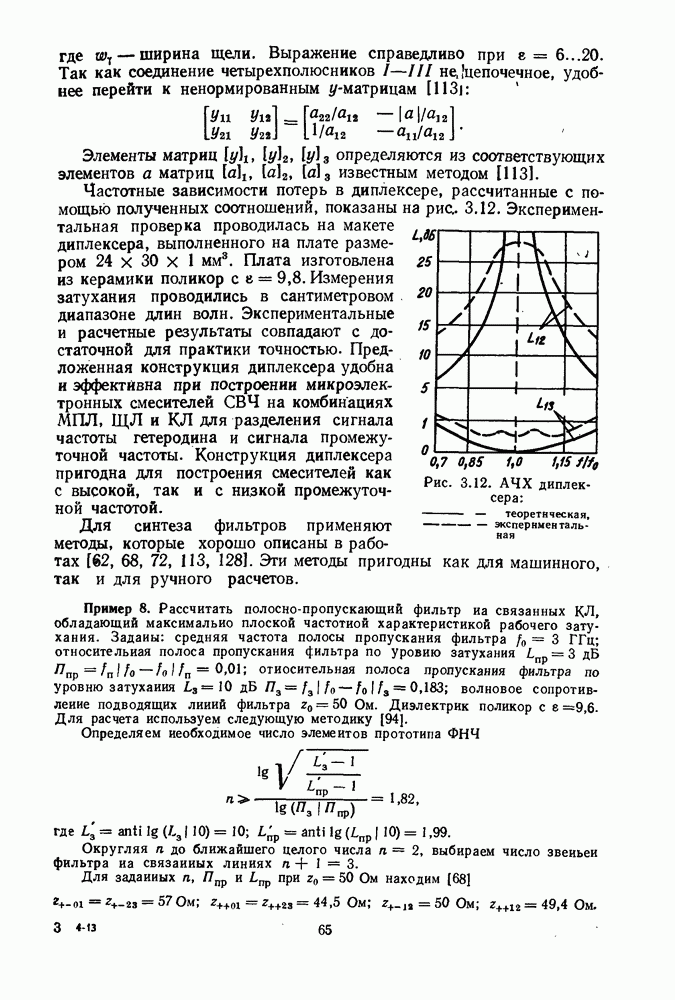
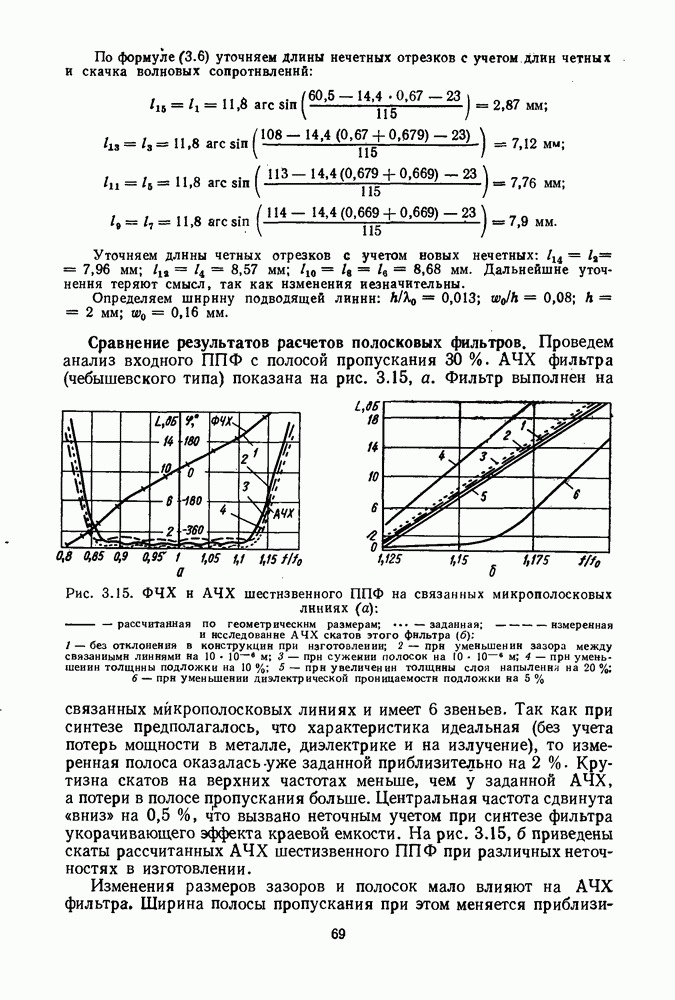
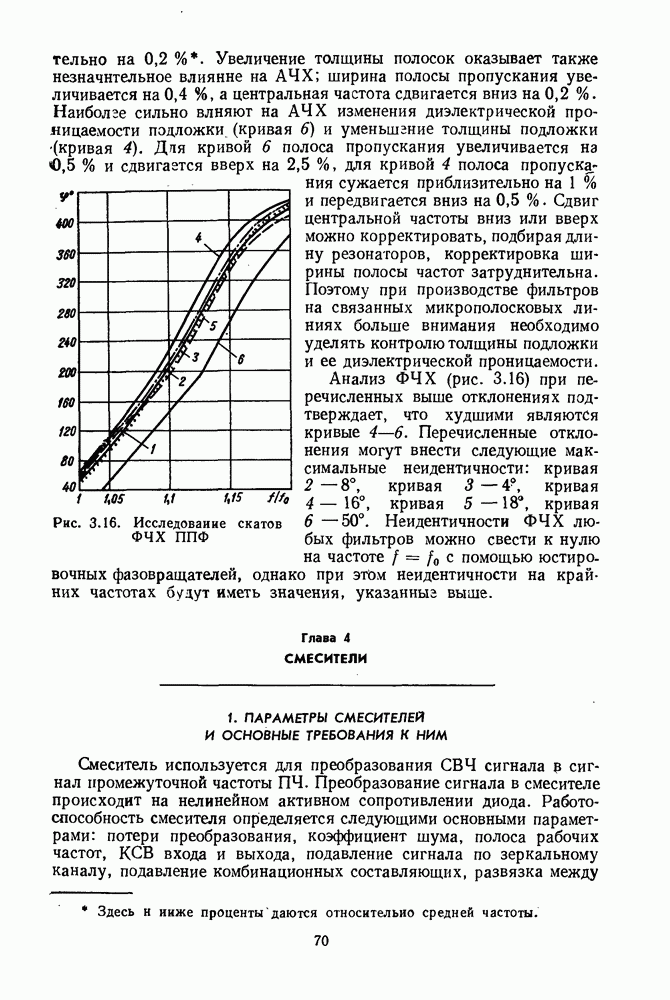
- 3. РАСЧЕТ ТОПОЛОГИЙ ФИЛЬТРОВ
- 4. АНАЛИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- Глава 4. СМЕСИТЕЛИ
- 1. ПАРАМЕТРЫ СМЕСИТЕЛЕЙ И ОСНОВНЫЕ ТРЕБОВАНИЯ К НИМ
- 2. ВЫБОР АКТИВНЫХ ЭЛЕМЕНТОВ
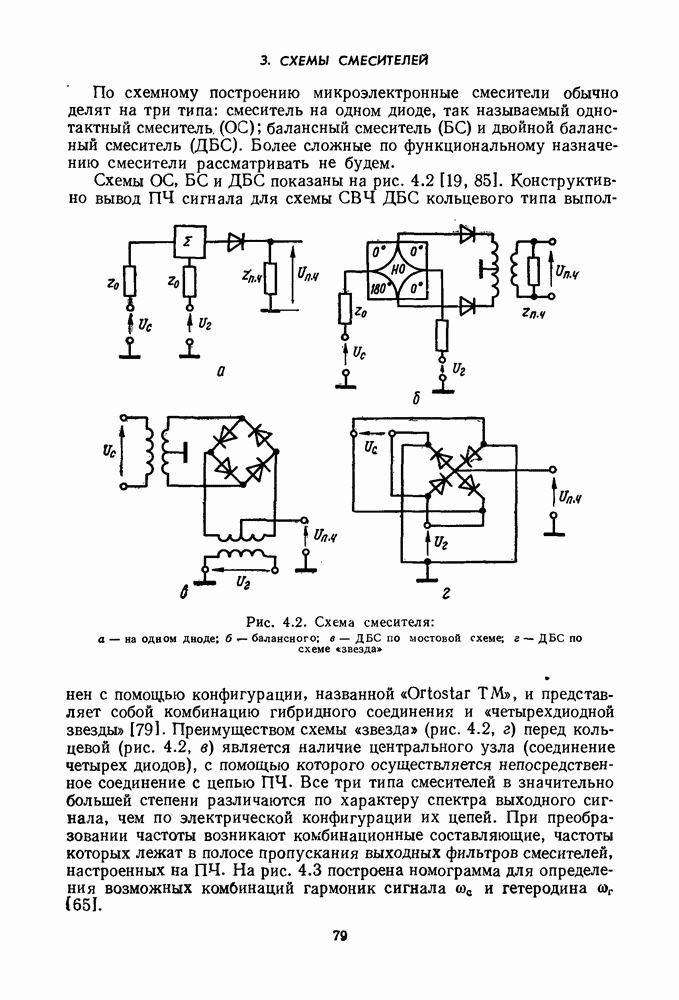
- 3. СХЕМЫ СМЕСИТЕЛЕЙ
- 4. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СМЕСИТЕЛЕЙ
- 5. СМЕСИТЕЛИ НА КОМБИНАЦИЯХ ЛИНИЙ ПЕРЕДАЧ
- 6. РЕЗУЛЬТАТЫ РАСЧЕТОВ И ЭКСПЕРИМЕНТОВ
- Глава 5. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ТРЕБОВАНИЯ К МАЛОШУМЯЩИМ УСИЛИТЕЛЯМ СВЧ И ИХ ПАРАМЕТРЫ
- 2. УСИЛИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 3. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ТРАНЗИСТОРА
- 4. РАСЧЕТ УСИЛИТЕЛЕЙ
- 5. ИСПОЛЬЗОВАНИЕ ЭВМ ПРИ ПРОЕКТИРОВАНИИ УСИЛИТЕЛЕЙ
- 6. ТОПОЛОГИЧЕСКИЕ СХЕМЫ МИКРОЭЛЕКТРОННЫХ СВЧ УСИЛИТЕЛЕЙ
- 7. МНОГОКАСКАДНЫЕ УСИЛИТЕЛИ
- 8. ВЛИЯНИЕ ВНЕШНИХ ФАКТОРОВ НА РАБОТУ УСИЛИТЕЛЕЙ С ПТ
- Глава 6. УСТРОЙСТВА, УПРАВЛЯЮЩИЕ МОЩНОСТЬЮ
- 2. УПРАВЛЯЮЩИЕ ЭЛЕМЕНТЫ
- 3. МАТЕМАТИЧЕСКИЙ АППАРАТ ДЛЯ РАСЧЕТА УСТРОЙСТВ НА СОСРЕДОТОЧЕННЫХ ЭЛЕМЕНТАХ
- 4. УСТРОЙСТВА НА СОСРЕДОТОЧЕННЫХ УПРАВЛЯЮЩИХ ЭЛЕМЕНТАХ
- 5. УСТРОЙСТВА НА ЭЛЕМЕНТАХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- Глава 7. ФАЗОВРАЩАТЕЛИ
- 1. ПАРАМЕТРЫ ПОЛУПРОВОДНИКОВЫХ ФАЗОВРАЩАТЕЛЕЙ
- 2. СХЕМЫ ФАЗОВРАЩАТЕЛЕЙ И АНАЛИЗ ХАРАКТЕРИСТИК ФАЗОВРАЩАТЕЛЯ С НАПРАВЛЕННЫМ ОТВЕТВИТЕЛЕМ
- Глава 8. ОГРАНИЧИТЕЛИ МОЩНОСТИ
- 1. ПАРАМЕТРЫ ОГРАНИЧИТЕЛЕЙ МОЩНОСТИ
- 2. ОГРАНИЧИТЕЛЬНЫЕ ДИОДЫ
- 3. СХЕМЫ ОГРАНИЧИТЕЛЕЙ МОЩНОСТИ И ИХ РАСЧЕТ
- СПИСОК ЛИТЕРАТУРЫ