| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. АНАЛИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
АЧХ и ФЧХ микроэлектронного фильтра можно вычислить следующим образом.
1. Разбить условно фильтр на несколько звеньев, математические модели которых в виде матриц четырехполюсников известны.
2. Выразить математическую модель матрицей передачи  или
или 
3. Перемножить цепочку матриц (эта и последующие операции обычно выполняются на ЭВМ). Если звено выражено ненормированной матрицей передачи  то «скачки» волнового сопротивления линий между звеньями не учитываются. Если звенья выражены нормированной волновой матрицей передачи, то следует между матрицами звеньев вставлять матрицу «скачка» [68].
то «скачки» волнового сопротивления линий между звеньями не учитываются. Если звенья выражены нормированной волновой матрицей передачи, то следует между матрицами звеньев вставлять матрицу «скачка» [68].
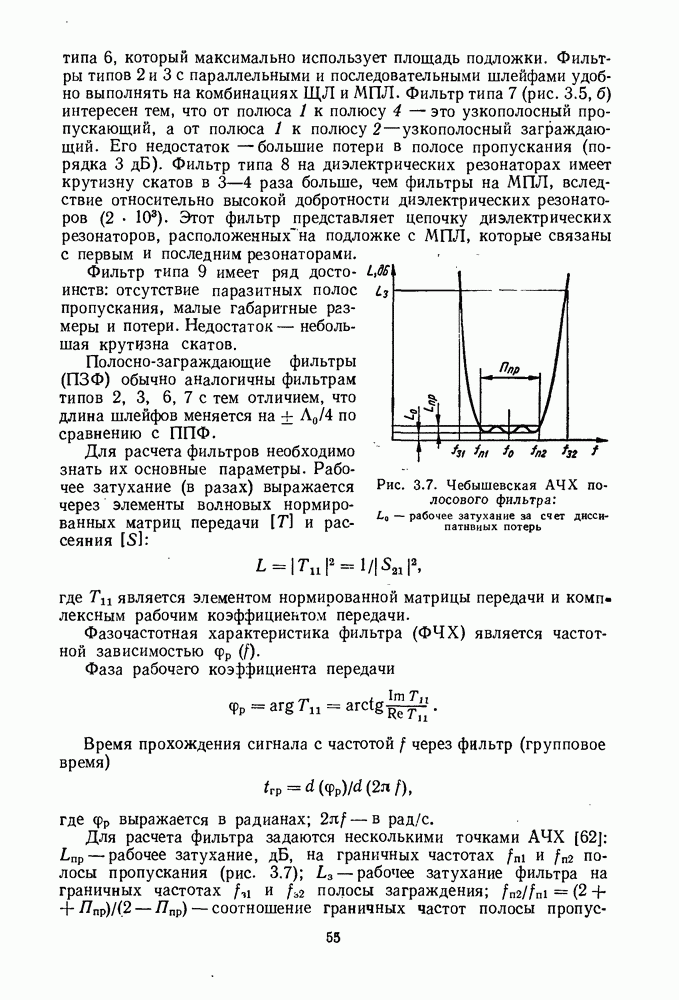
4. Вычислить коэффициент передачи получившегося эквивалентного четырехполюсника (рабочее затухание) [113]:

где  — сопротивления генератора и нагрузки соответственно.
— сопротивления генератора и нагрузки соответственно.
Ненормированная матрица звена фильтра  одинаковых связанных линиях имеет вид [150]
одинаковых связанных линиях имеет вид [150]

где  — геометрическая длина участка связи;
— геометрическая длина участка связи;  — рабочая длина волны в применяемой линии; а — диссипативные потери, в дБ, на единицу длины волны в применяемом типе линии;
— рабочая длина волны в применяемой линии; а — диссипативные потери, в дБ, на единицу длины волны в применяемом типе линии;  ненормированные волновые сопротивления связанных полосковых линий для четного и нечетного типов колебаний, которые определяются приближенными выражениями [118]:
ненормированные волновые сопротивления связанных полосковых линий для четного и нечетного типов колебаний, которые определяются приближенными выражениями [118]:

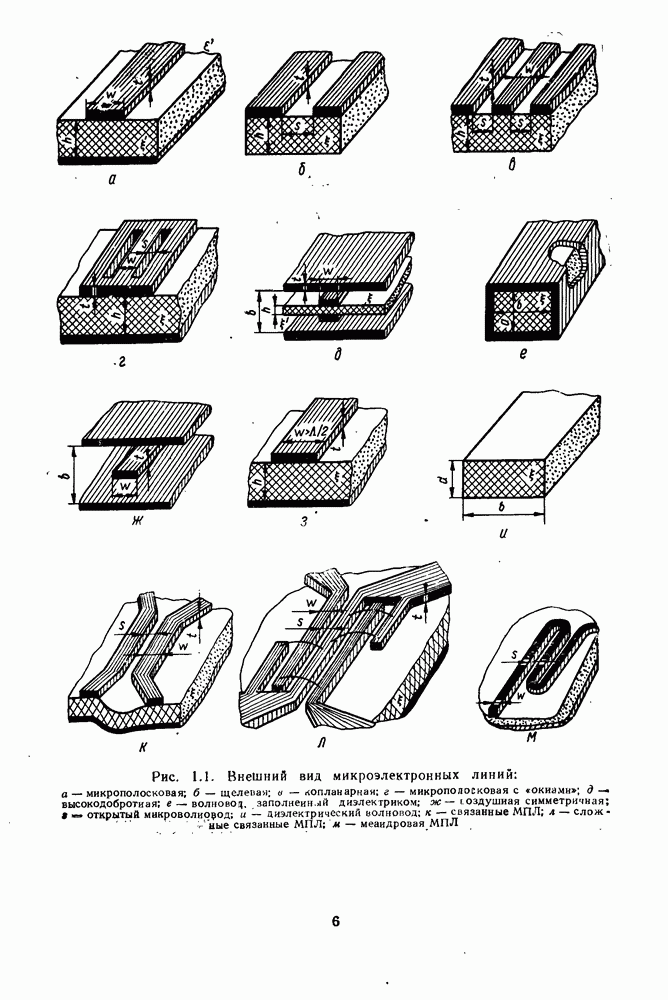
где  геометрические размеры связанных МПЛ (рис. 1.1, к);
геометрические размеры связанных МПЛ (рис. 1.1, к);  - относительная диэлектрическая проницаемость подложки (для поликора
- относительная диэлектрическая проницаемость подложки (для поликора 
Более точные электродинамические методы определения  связанных МПЛ и КЛ подробно рассмотрены в работе [23].
связанных МПЛ и КЛ подробно рассмотрены в работе [23].
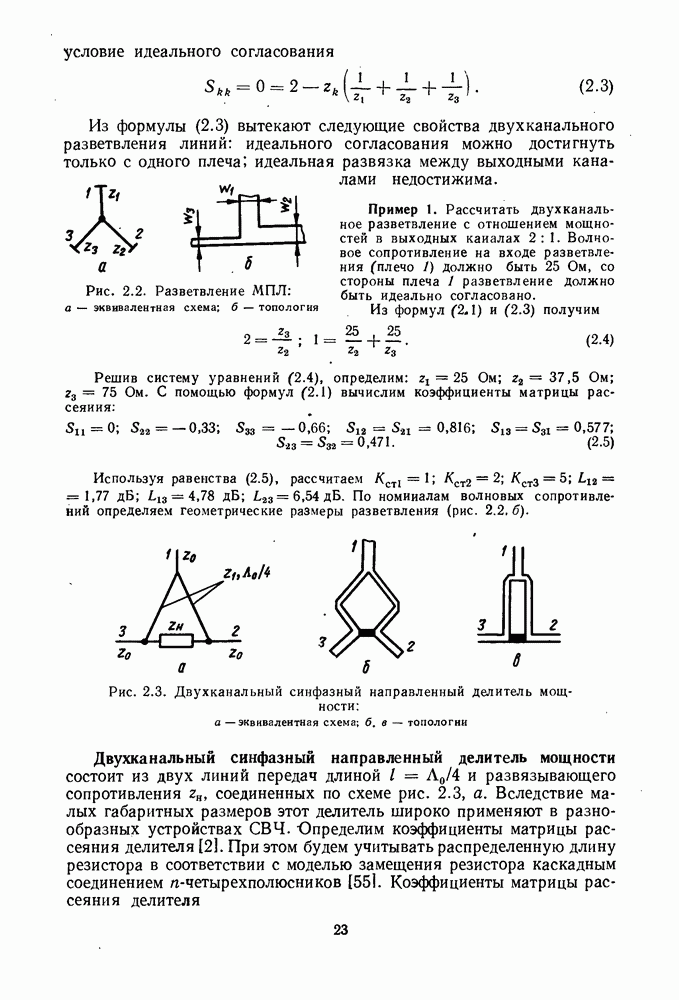
Одно звено фильтра с параллельными шлейфами (короткозамкнутого или незакороченного), которые расположены на различном расстоянии друг от друга, показано на рис. 3.9, а. Такие фильтры имеют АЧХ, аналогичные АЧХ ППФ, ФНЧ, ФВЧ, ПЗФ.
Ненормированная  матрица звена имеет вид
матрица звена имеет вид

где  — коэффициент распространения на единицу длины;
— коэффициент распространения на единицу длины;  — рабочая длина волны в передающей линии.
— рабочая длина волны в передающей линии.

Рис. 3.10. Топологические схемы диплексера (а) и мультиплексера (б)

Рис. 3.11. Эквивалентная схема диплексера (а) и структурная схема для его расчета (б)
Проводимость  соответствует входной ненормированной проводимости незакороченного или короткозамкнутого шлейфа
соответствует входной ненормированной проводимости незакороченного или короткозамкнутого шлейфа

где  — волновое сопротивление шлейфа;
— волновое сопротивление шлейфа;  — длина шлейфа.
— длина шлейфа.
Для анализа фильтров на комбинациях линий применяют те же алгоритмы, что и для микрополосковых фильтров.
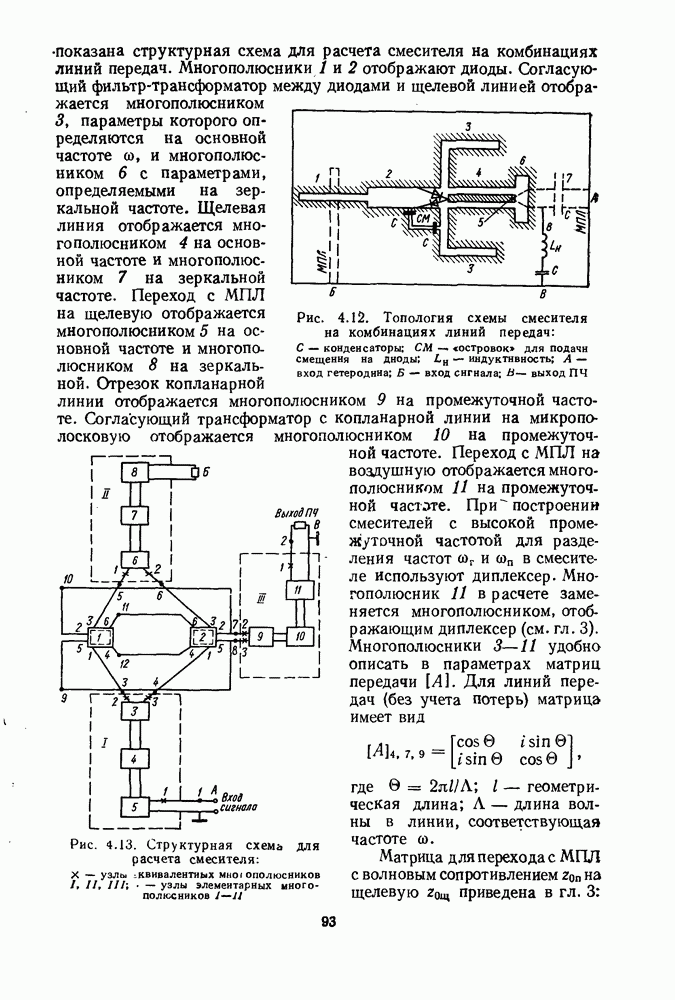
В качестве примера фильтров на комбинациях линий рассмотрим диплексер (рис. 3.10, а). Переход, связывающий МПЛ и ЩЛ для передачи СВЧ энергии от входа 1 ко входу 3, и наоборот, образован закороченным щелевым шлейфом длиной  и МПЛ длиной
и МПЛ длиной  нагруженной щелевыми шлейфами длиной
нагруженной щелевыми шлейфами длиной  . Шлейф
. Шлейф  и линия 12 образуют полосно-пропускающий фильтр для идущего от входа
и линия 12 образуют полосно-пропускающий фильтр для идущего от входа  сигнала СВЧ. Передача энергии СВЧ в направлении 1—3 осуществляется в рабочей полосе микрополоскового щелевого перехода, а в направлении 1—2 определяется частотным диапазоном пропускания щелевого фильтра. В этой конструкции эффективно используется площадь
сигнала СВЧ. Передача энергии СВЧ в направлении 1—3 осуществляется в рабочей полосе микрополоскового щелевого перехода, а в направлении 1—2 определяется частотным диапазоном пропускания щелевого фильтра. В этой конструкции эффективно используется площадь
подложки, так как СВЧ элементы схемы формируются на обеих плоскостях диэлектрической подложки. Это повышает коэффициент интеграции благодаря увеличению плотности заполнения схемы. Такое построение позволяет достаточно просто реализовать многоканальные частотно-разделительные устройства путем каскадного соединения схем, каждая из которых рассчитана на требуемую частоту пропускания (рис. 3.10, б). Эквивалентная схема диплексера показана на рис. 3.11, а, где  волновые сопротивления МПЛ и ЩЛ;
волновые сопротивления МПЛ и ЩЛ;  - геометрические длины двух щелевых и микрополоскового шлейфов:
- геометрические длины двух щелевых и микрополоскового шлейфов:  индуктивности закороченных щелевых шлейфов перехода и фильтра;
индуктивности закороченных щелевых шлейфов перехода и фильтра;  коэффициенты трансформации, определяющие связь микрополосковой линии с щелевой [120]. На рис. 3.11,б изображена структурная схема расчета диплексера. Переход с микрополосковой линии на щелевую отображается многополюсником
коэффициенты трансформации, определяющие связь микрополосковой линии с щелевой [120]. На рис. 3.11,б изображена структурная схема расчета диплексера. Переход с микрополосковой линии на щелевую отображается многополюсником  отрезок микрополосковой линии длиной
отрезок микрополосковой линии длиной  отображается многополюсником II, а многополюсником
отображается многополюсником II, а многополюсником  отображается фильтр, образованный микрополосковой линией и щелевыми шлейфами длиной
отображается фильтр, образованный микрополосковой линией и щелевыми шлейфами длиной  Матрицы рассмотренных многополюсников [29, 120]
Матрицы рассмотренных многополюсников [29, 120]

где

 — длина волны в
— длина волны в  -длина волны в свободном пространстве;
-длина волны в свободном пространстве;  длина волны в
длина волны в  — входная проводимость щелевых шлейфов длиной
— входная проводимость щелевых шлейфов длиной  с учетом индуктивностей
с учетом индуктивностей  закороченных концов [137];
закороченных концов [137];  — толщина подложки.
— толщина подложки.
Выражение для определения нормированного реактивного сопротивления  получено аппроксимацией численных результатов:
получено аппроксимацией численных результатов:

где  ширина щели. Выражение справедливо при
ширина щели. Выражение справедливо при  Так как соединение четырехполюсников
Так как соединение четырехполюсников  не, цепочечное, удобнее перейти к ненормированным матрицам
не, цепочечное, удобнее перейти к ненормированным матрицам 

Элементы матриц  определяются из соответствующих элементов а матриц
определяются из соответствующих элементов а матриц  известным методом [113].
известным методом [113].
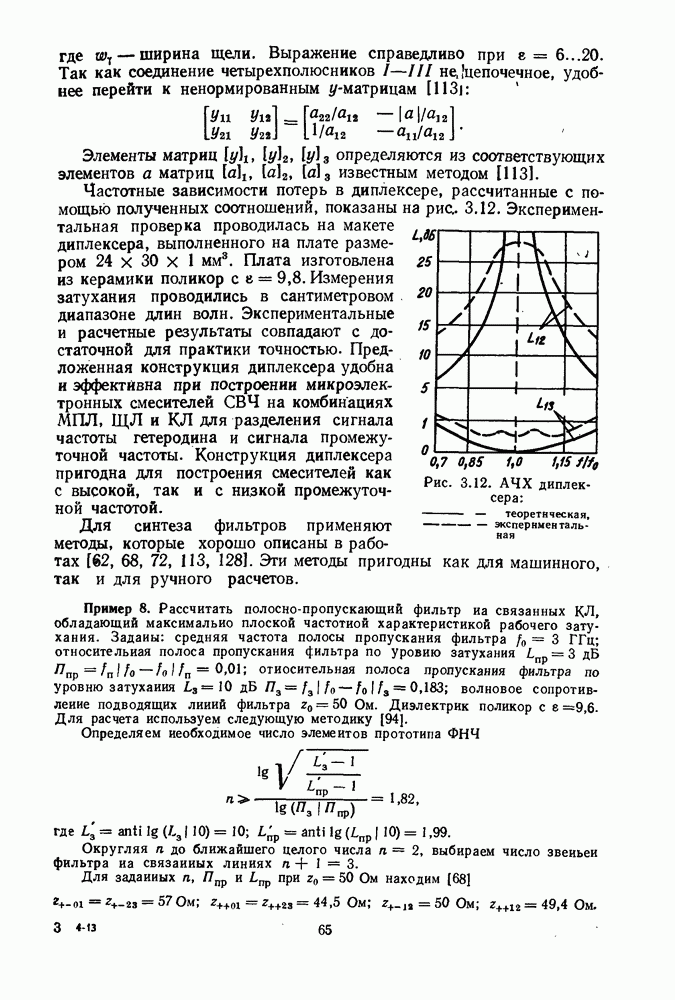
Частотные зависимости потерь в диплексере, рассчитанные с помощью полученных соотношений, показаны на рис. 3.12. Экспериментальная проверка проводилась на макете диплексера, выполненного на плате размером  Плата изготовлена из керамики поликор с
Плата изготовлена из керамики поликор с  Измерения затухания проводились в сантиметровом диапазоне длин волн. Экспериментальные и расчетные результаты совпадают с достаточной для практики точностью. Предложенная конструкция диплексера удобна и эффективна при построении микроэлектронных смесителей СВЧ на комбинациях
Измерения затухания проводились в сантиметровом диапазоне длин волн. Экспериментальные и расчетные результаты совпадают с достаточной для практики точностью. Предложенная конструкция диплексера удобна и эффективна при построении микроэлектронных смесителей СВЧ на комбинациях  и КЛ для разделения сигнала частоты гетеродина и сигнала промежуточной частоты. Конструкция диплексера пригодна для построения смесителей как с высокой, так и с низкой промежуточной частотой.
и КЛ для разделения сигнала частоты гетеродина и сигнала промежуточной частоты. Конструкция диплексера пригодна для построения смесителей как с высокой, так и с низкой промежуточной частотой.

Рис.  диплексера:
диплексера:  теоретическая,
теоретическая,  экспериментальная
экспериментальная
Для синтеза фильтров применяют методы, которые хорошо описаны в работах [62, 68, 72, 113, 128]. Эти методы пригодны как для машинного, так и для ручного расчетов.
Пример 8. Рассчитать полосно-пропускающий фильтр на связанных  обладающий максимально плоской частотной характеристикой рабочего затухания. Заданы: средняя частота полосы пропускания фильтра
обладающий максимально плоской частотной характеристикой рабочего затухания. Заданы: средняя частота полосы пропускания фильтра  относительная полоса пропускания фильтра по уровню затухания
относительная полоса пропускания фильтра по уровню затухания  дБ
дБ  относительная полоса пропускания фильтра по уровню затухания
относительная полоса пропускания фильтра по уровню затухания  волновое сопротивление подводящих линий фильтра
волновое сопротивление подводящих линий фильтра  Ом. Диэлектрик поликор с
Ом. Диэлектрик поликор с  Для расчета используем следующую методику [94].
Для расчета используем следующую методику [94].
Определяем необходимое число элементов прототипа ФНЧ

где  .
.
Округляя  до ближайшего целого числа
до ближайшего целого числа  выбираем число звеньев фильтра на связанных линиях
выбираем число звеньев фильтра на связанных линиях 
Для заданных  при
при  Ом находим [68]
Ом находим [68]

Определяем вспомогательные коэффициенты  выражений [66]
выражений [66]

 — волновое сопротивление подводимых линий;
— волновое сопротивление подводимых линий;  — размеры, показанные на рис. 3. 13, а,
— размеры, показанные на рис. 3. 13, а,

Значении  можно найтн из графиков работы [66]:
можно найтн из графиков работы [66]:

Задаемся  тогда из (3.2) получаем
тогда из (3.2) получаем  Например, при
Например, при  При
При  Подставляем в выражение
Подставляем в выражение  получаем
получаем  Повторяем процесс для нового
Повторяем процесс для нового  Проверяем, подставляя
Проверяем, подставляя  в формулу (3.4). Получаем
в формулу (3.4). Получаем  Остановимся на этих значениях. Следует заметить, что точность графиков (3.3) и (3.4) невелика и это вляяет на точность расчета.
Остановимся на этих значениях. Следует заметить, что точность графиков (3.3) и (3.4) невелика и это вляяет на точность расчета.
Рис. 3.13. (см. скан)Поперечный разрез связанных копланарных линий (а) и топология полосно-пропускающего фильтра на связанных копланарных линиях (б)
Зададимся  тогда
тогда  Определим
Определим  Проверяем, подставляя в формулу (3.4)
Проверяем, подставляя в формулу (3.4)  .
.
Повторяем цикл расчета:  Определяем
Определяем 
Проверяем  Останавливаемся на этих значениях. Итак:
Останавливаемся на этих значениях. Итак: 
Чтобы в копланарной линии сконцентрировать все поле в подложке, достаточно толщину диэлектрика взять в 2 раза больше ширины щели  , т. е.
, т. е.  , где
, где  — ширина центрального проводника;
— ширина центрального проводника;  расстояние между двумя заземленными пластинами, причем
расстояние между двумя заземленными пластинами, причем 
Длина области связи  где
где  длина волны в свободном пространстве, соответствующая центральной частоте
длина волны в свободном пространстве, соответствующая центральной частоте  фильтра.
фильтра.
Для  Ом определяем размеры
Ом определяем размеры  подводящей
подводящей  где
где  . Выбираем
. Выбираем  мм, тогда
мм, тогда  мм. Проверяем неравенства
мм. Проверяем неравенства  и выбираем
и выбираем  мм. Провернем неравенство
мм. Провернем неравенство  Для
Для  см неравенство выполняется. Определяем длину резонаторов:
см неравенство выполняется. Определяем длину резонаторов: 
Топология ППФ показана на рис. 3. 13, б. Недостатком подобных фильтров является то, что, еслн не соблюдаются неравенства  при
при  «земляной» проводник звена фильтра упирается в центральный проводник предыдущего звена, поэтому «земляной» проводник выполняют не на всю длину центрального проводника. Этот недостаток влияет на точность расчетов, так как не учитывается емкость торцов резонаторов.
«земляной» проводник звена фильтра упирается в центральный проводник предыдущего звена, поэтому «земляной» проводник выполняют не на всю длину центрального проводника. Этот недостаток влияет на точность расчетов, так как не учитывается емкость торцов резонаторов.

Рис. 3.14. Топология ФНЧ на щелевой линии
Пример 9. Рассчитать ФНЧ на щелевой линии. Расчет веден для фильтра с чебышевской частотной характеристикой рабочего затухания. Заданы: частота по уровню  дБ
дБ  ; частота по уровню
; частота по уровню  ; волновое сопротивление подводящих линий
; волновое сопротивление подводящих линий  Ом; волновые сопротивления отрезков лнннй передачи
Ом; волновые сопротивления отрезков лнннй передачи  Ом,
Ом,  Ом. Диэлектриком служит поликор с
Ом. Диэлектриком служит поликор с  Число элементов прототнпного
Число элементов прототнпного 

где 
Округляем  . С помощью таблицы [114] для заданных
. С помощью таблицы [114] для заданных  записываем:
записываем: 
Топология ФНЧ изображена на рис. 3.14. Реактивные сопротивления индуктивностей и реактивные проводимости емкостей определим с помощью выражений 

Для щелевой лннни  находим
находим  .
.
 . Для ЩЛ расширение щели эквивалентно индуктивности, а сужение — емкости, т. е. обратно по сравнению с микрополосковой линией. Определяем по графику [155], что длина волны в линни Л меньше рабочей длины: для
. Для ЩЛ расширение щели эквивалентно индуктивности, а сужение — емкости, т. е. обратно по сравнению с микрополосковой линией. Определяем по графику [155], что длина волны в линни Л меньше рабочей длины: для  Ом;
Ом; 
Для схемы рис. 3. 14 дляны нечетных отрезков определяем по формуле 
Вычисляем длины отрезков лнннй передач, используя нижеприведенные выражения:

 причем для щелевой линии
причем для щелевой линии 

Для рассматриваемого случая

Рассчитываем сопротивление краевой индуктивности пои переходе от ЩЛ с большим волновым сопротивлением 115 Ом к линии с малым волновым сопротивлением 30 Ом (3. 1 г).
Для рассматриваемого случая  ;
;

Вычисляем длины четных отрезков по формуле (3. 5):

По формуле (3.6) уточняем длины нечетных отрезков с учетом длин четных и скачка волновых сопротивлений:

Уточняем длины четных отрезков с учетом новых нечетных:  мм. Дальнейшие уточнения теряют смысл, так как изменения незначительны.
мм. Дальнейшие уточнения теряют смысл, так как изменения незначительны.
Определяем ширину подводящей линии:  .
.

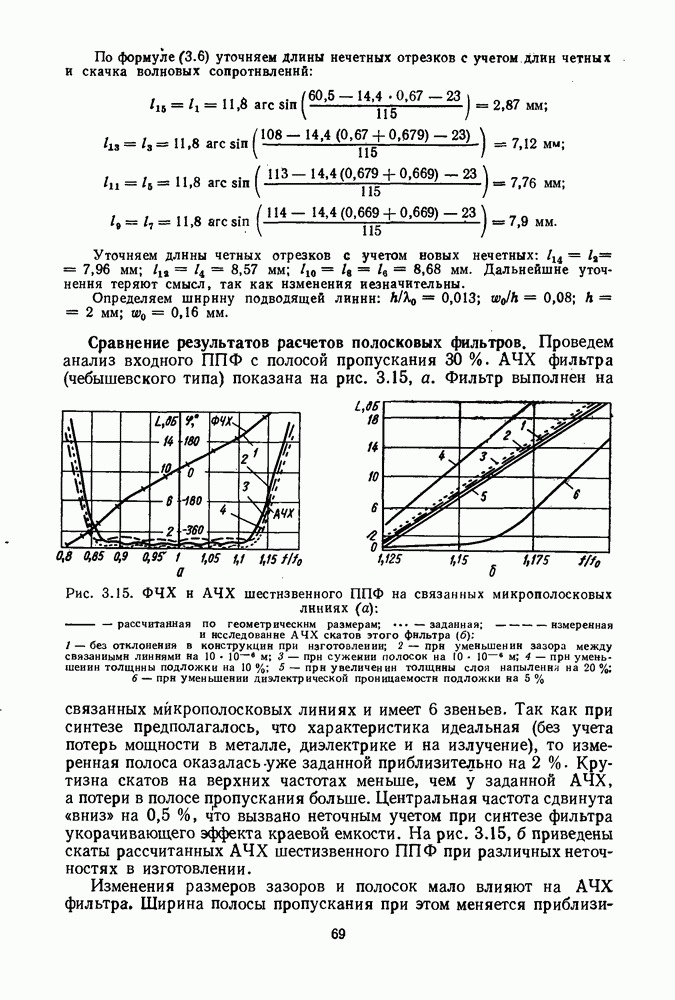
Рис. 3.15. ФЧХ и АЧХ шестнзвенного ППФ на связанных микрополосковых линиях (а):  — рассчитанная по геометрическим размерам;
— рассчитанная по геометрическим размерам;  — заданная;
— заданная;  измеренная и исследование АЧХ скатов этого фильтра
измеренная и исследование АЧХ скатов этого фильтра  — без отклонения в конструкции при изготовлении; 2 — при уменьшении зазора между связанными линиями на
— без отклонения в конструкции при изготовлении; 2 — при уменьшении зазора между связанными линиями на  — при сужении полосок на
— при сужении полосок на  — при уменьшении толщины подложки на
— при уменьшении толщины подложки на  — при увеличении толщины слоя напылении на
— при увеличении толщины слоя напылении на  — при уменьшении диэлектрической проницаемости подложки на
— при уменьшении диэлектрической проницаемости подложки на 
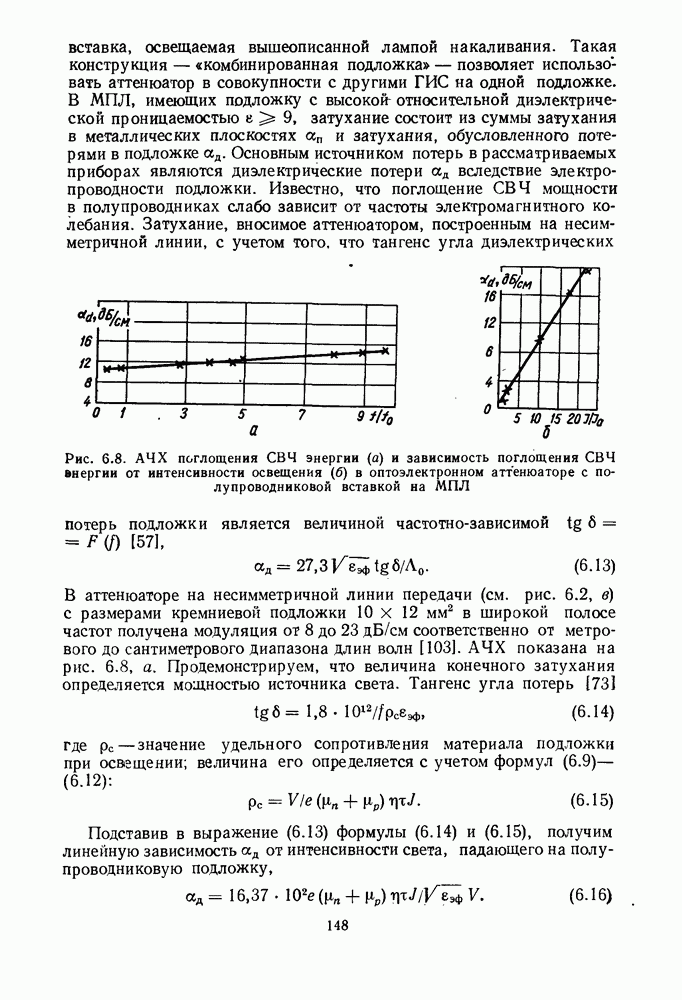
Сравнение результатов расчетов полосковых фильтров. Проведем анализ входного ППФ с полосой пропускания 30 %. АЧХ фильтра (чебышевского типа) показана на рис. 3.15, а. Фильтр выполнен на связанных микрополосковых линиях и имеет 6 звеньев. Так как при синтезе предполагалось, что характеристика идеальная (без учета потерь мощности в металле, диэлектрике и на излучение), то измеренная полоса оказалась уже заданной приблизительно на  Крутизна скатов на верхних частотах меньше, чем у заданной АЧХ, а потери в полосе пропускания больше. Центральная частота сдвинута «вниз» на
Крутизна скатов на верхних частотах меньше, чем у заданной АЧХ, а потери в полосе пропускания больше. Центральная частота сдвинута «вниз» на  что вызвано неточным учетом при синтезе фильтра укорачивающего эффекта краевой емкости. На рис.
что вызвано неточным учетом при синтезе фильтра укорачивающего эффекта краевой емкости. На рис.  приведены скаты рассчитанных АЧХ шестизвенного ППФ при различных неточностях в изготовлении.
приведены скаты рассчитанных АЧХ шестизвенного ППФ при различных неточностях в изготовлении.
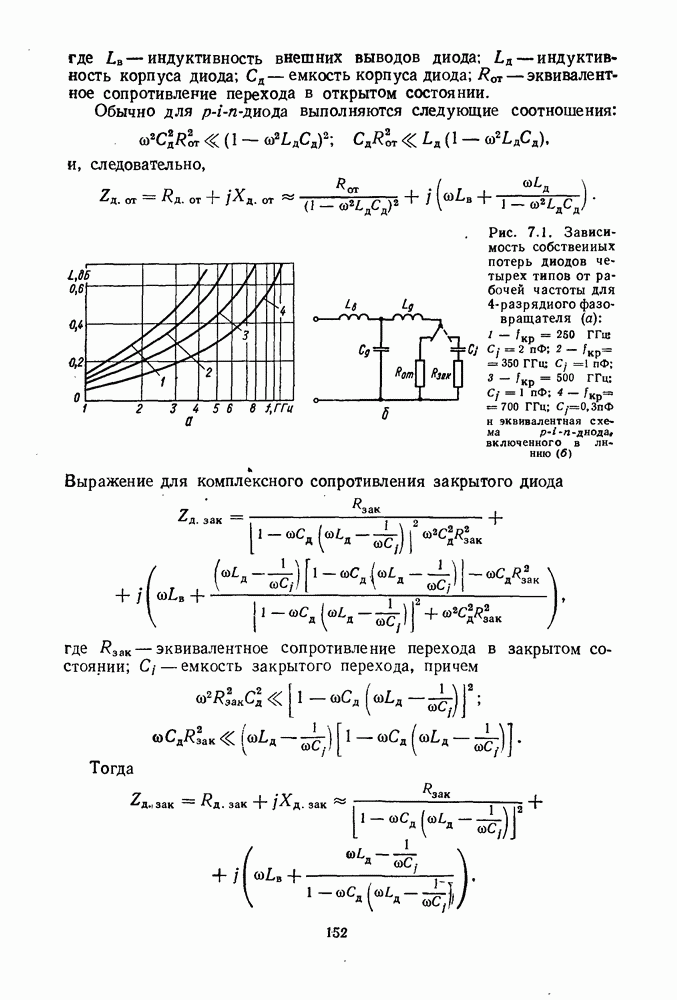
Изменения размеров зазоров и полосок мало влияют на АЧХ фильтра. Ширина полосы пропускания при этом меняется
приблизительно на 0,2 %. Увеличение толщины полосок оказывает также незначительное влияние на АЧХ; ширина полосы пропускания увеличивается на 0,4 %, а центральная частота сдвигается вниз на 0,2 %. Наиболге сильно влияют на АЧХ изменения диэлектрической проницаемости подложки (кривая 6) и уменьшгние толщины подложки (кривая 4). Для кривой 6 полоса пропускания увеличивается на  и сдвигается вверх на 2,5 %, для кривой 4 полоса пропускания сужается приблизительно на 1 % и передвигается вниз на 0,5 %. Сдвиг центральной частоты вниз или вверх можно корректировать, подбирая длину резонаторов, корректировка ширины полосы частот затруднительна. Поэтому при производстве фильтров на связанных микрополосковых линиях больше внимания необходимо уделять контролю толщины подложки и ее диэлектрической проницаемости.
и сдвигается вверх на 2,5 %, для кривой 4 полоса пропускания сужается приблизительно на 1 % и передвигается вниз на 0,5 %. Сдвиг центральной частоты вниз или вверх можно корректировать, подбирая длину резонаторов, корректировка ширины полосы частот затруднительна. Поэтому при производстве фильтров на связанных микрополосковых линиях больше внимания необходимо уделять контролю толщины подложки и ее диэлектрической проницаемости.

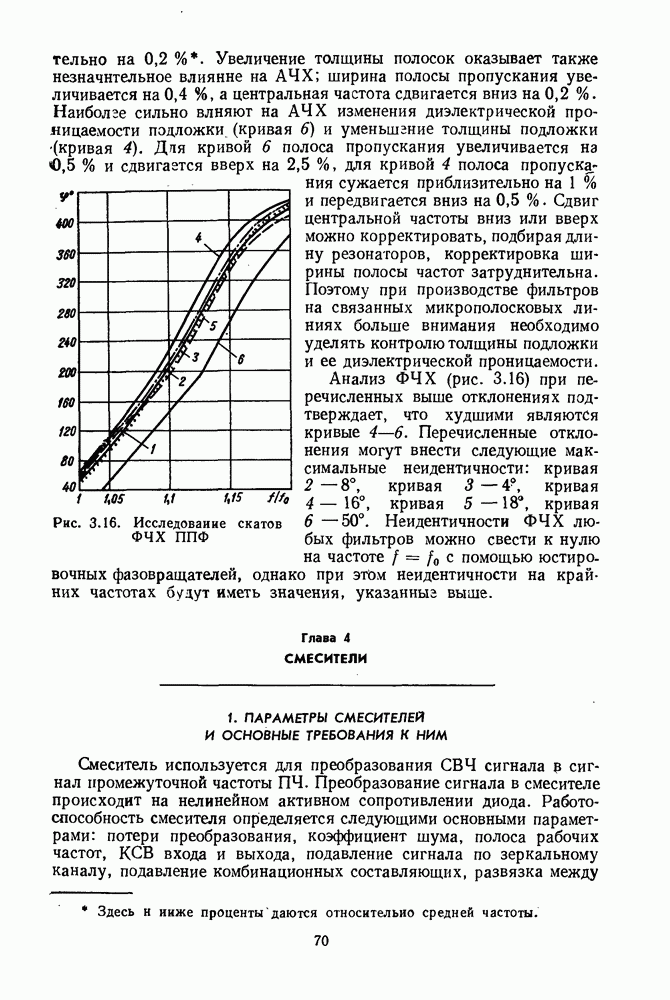
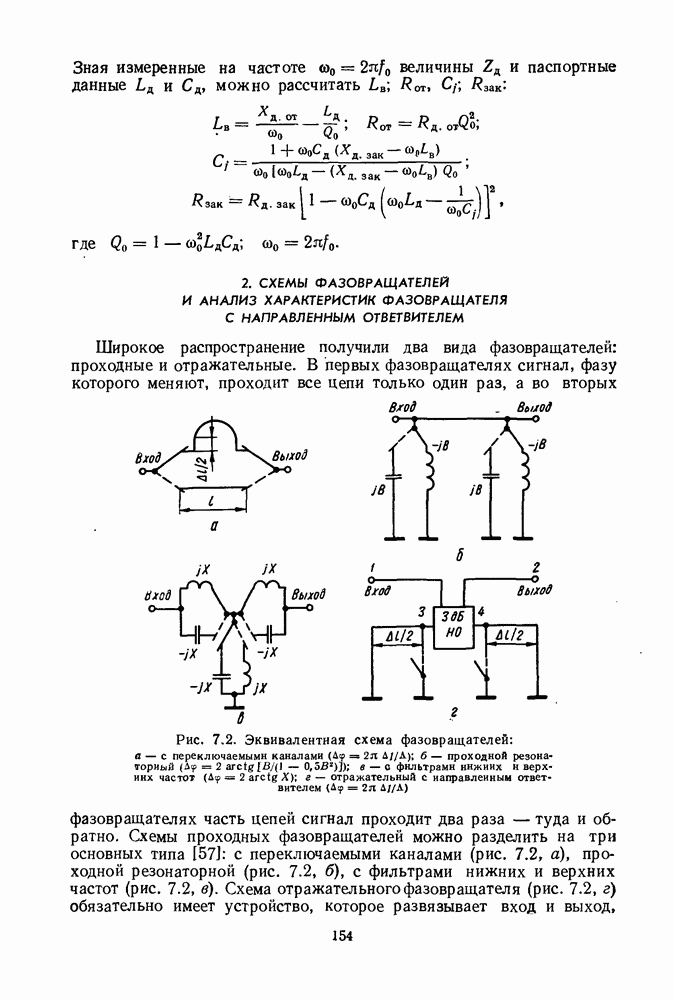
Рис. 3.16. Исследование скатов ФЧХ ППФ
Анализ ФЧХ (рис. 3.16) при перечисленных выше отклонениях подтверждает, что худшими являются кривые 4—6. Перечисленные отклонения могут внести следующие максимальные неидентичности: кривая 2—8°, кривая  кривая
кривая  кривая 5 — 18°, кривая 6 — 50°. Неидентичности ФЧХ любых фильтров можно свести к нулю на частоте
кривая 5 — 18°, кривая 6 — 50°. Неидентичности ФЧХ любых фильтров можно свести к нулю на частоте  с помощью котировочных фазовращателей, однако при этом неидентичности на крайних частотах будут иметь значения, указанные выше.
с помощью котировочных фазовращателей, однако при этом неидентичности на крайних частотах будут иметь значения, указанные выше.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Главв 1. РАСЧЕТ ЭЛЕМЕНТОВ ГИБРИДНЫХ ИНТЕГРАЛЬНЫХ СХЕМ
- 1. ПОНЯТИЕ ГИБРИДНОЙ ИНТЕГРАЛЬНОЙ СХЕМЫ СВЧ
- 2. ОСНОВНЫЕ ЛИНИИ ПЕРЕДАЧ ГИС СВЧ
- 3. РАСЧЕТ ПАРАМЕТРОВ ЛИНИЙ
- Главв 2. УСТРОЙСТВА ДЕЛЕНИЯ (СУММИРОВАНИЯ) МОЩНОСТИ СВЧ
- 1. ПРИМЕНЕНИЕ ДЕЛИТЕЛЕЙ (СУММАТОРОВ) МОЩНОСТИ
- 2. ЭЛЕМЕНТЫ МНОГОКАНАЛЬНЫХ ДЕЛИТЕЛЕЙ
- 3. МНОГОКАНАЛЬНЫЕ ДЕЛИТЕЛИ. АЛГОРИТМЫ РАСЧЕТА МНОГОКАНАЛЬНЫХ ДЕЛИТЕЛЕЙ
- 4. ЧЕТЫРЕХКАНАЛЬНЫЕ ДЕЛИТЕЛИ МОЩНОСТИ
- 5. ДЕЛИТЕЛИ МОЩНОСТИ НА 64 КАНАЛА
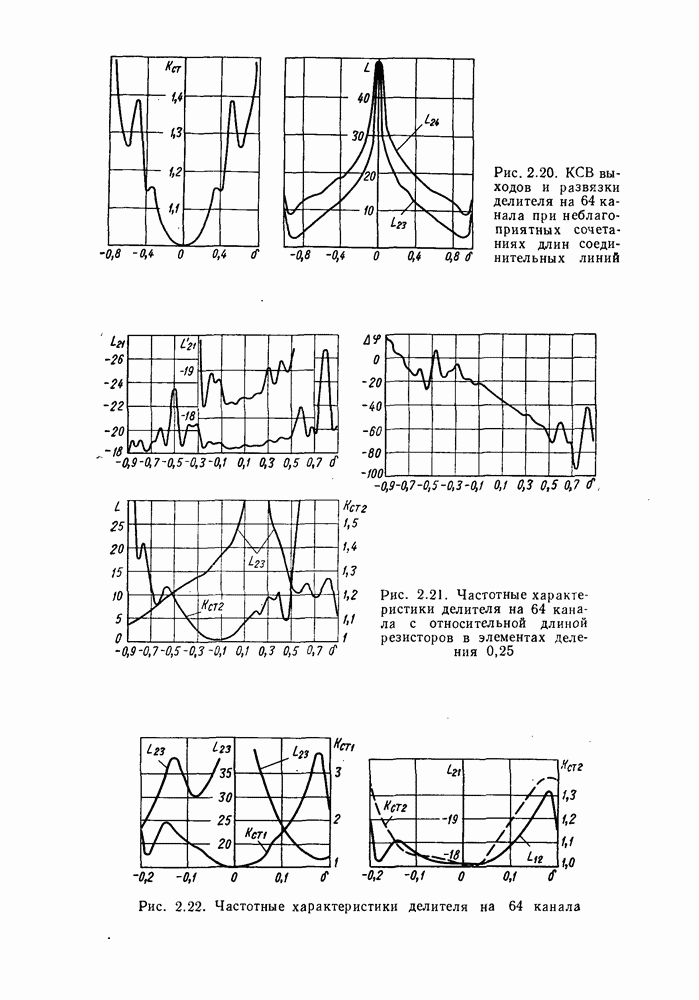
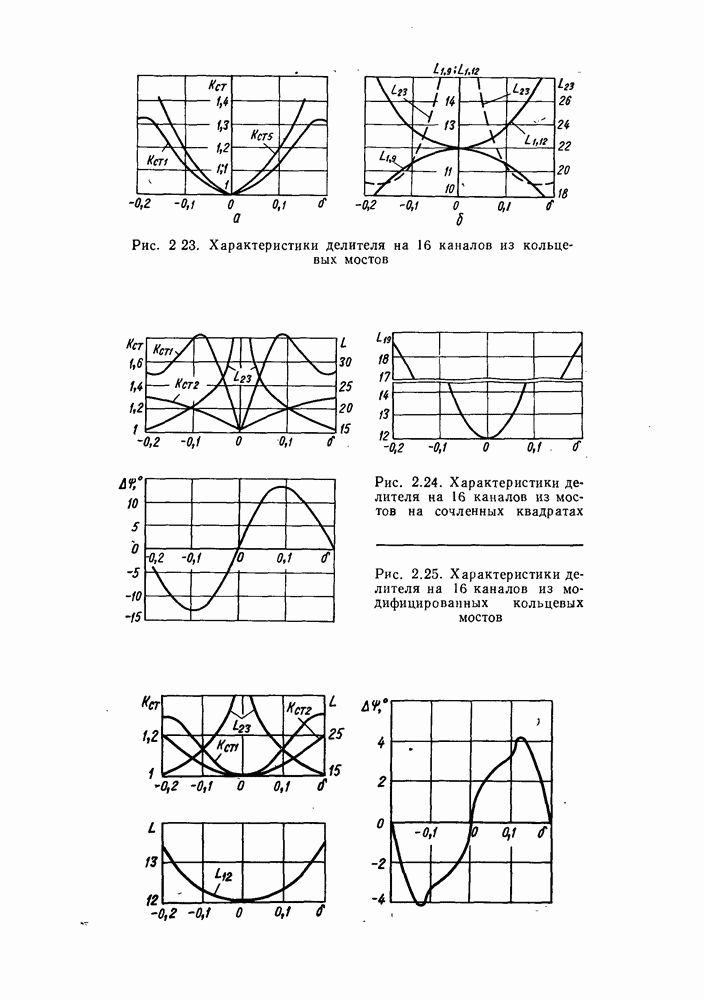
- 6. ХАРАКТЕРИСТИКИ ДЕЛИТЕЛЕЙ, ВЫПОЛНЕННЫХ ИЗ МОСТОВЫХ УСТРОЙСТВ
- 7. РЕКОМЕНДАЦИИ ДЛЯ ПРОЕКТИРОВАНИЯ ДЕЛИТЕЛЕЙ (СУММАТОРОВ) МОЩНОСТИ
- Глава 3. ИЗБИРАТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ОСНОВНЫЕ ТРЕБОВАНИЯ К ИЗБИРАТЕЛЬНЫМ УСТРОЙСТВАМ И ИХ ПАРАМЕТРЫ
- 2. АППРОКСИМАЦИЯ ФУНКЦИЙ РАБОЧЕГО ЗАТУХАНИЯ
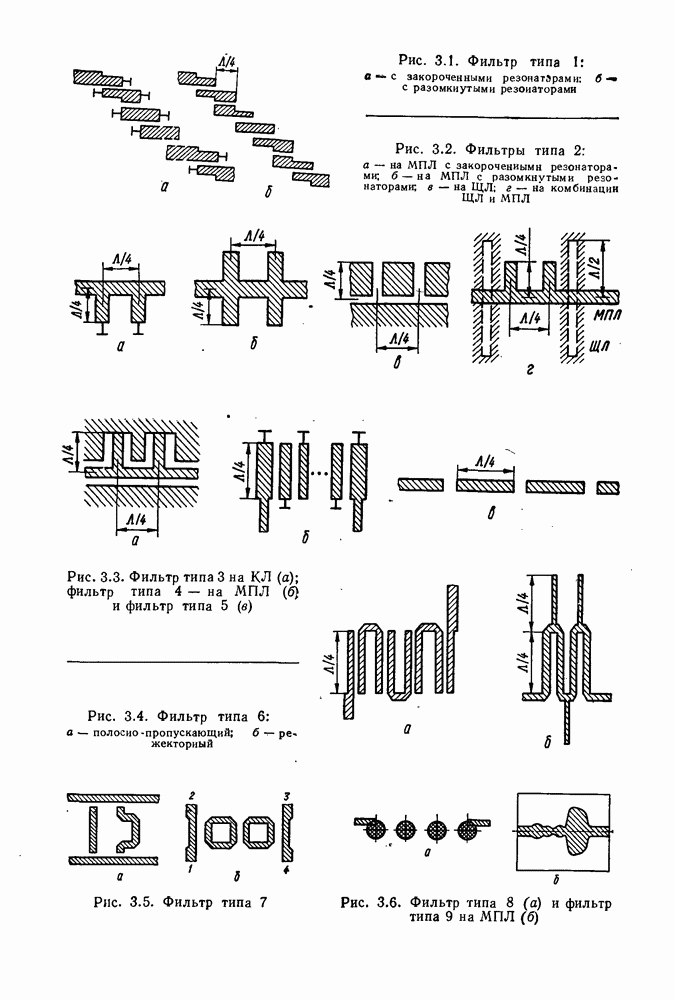
- 3. РАСЧЕТ ТОПОЛОГИЙ ФИЛЬТРОВ
- 4. АНАЛИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- Глава 4. СМЕСИТЕЛИ
- 1. ПАРАМЕТРЫ СМЕСИТЕЛЕЙ И ОСНОВНЫЕ ТРЕБОВАНИЯ К НИМ
- 2. ВЫБОР АКТИВНЫХ ЭЛЕМЕНТОВ
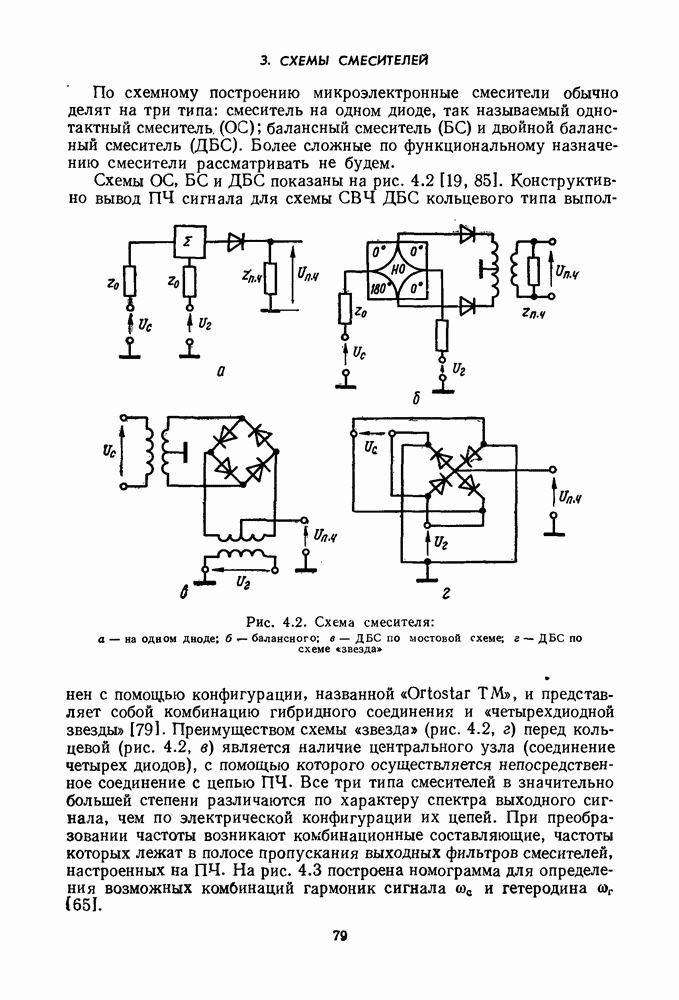
- 3. СХЕМЫ СМЕСИТЕЛЕЙ
- 4. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СМЕСИТЕЛЕЙ
- 5. СМЕСИТЕЛИ НА КОМБИНАЦИЯХ ЛИНИЙ ПЕРЕДАЧ
- 6. РЕЗУЛЬТАТЫ РАСЧЕТОВ И ЭКСПЕРИМЕНТОВ
- Глава 5. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ТРЕБОВАНИЯ К МАЛОШУМЯЩИМ УСИЛИТЕЛЯМ СВЧ И ИХ ПАРАМЕТРЫ
- 2. УСИЛИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 3. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ТРАНЗИСТОРА
- 4. РАСЧЕТ УСИЛИТЕЛЕЙ
- 5. ИСПОЛЬЗОВАНИЕ ЭВМ ПРИ ПРОЕКТИРОВАНИИ УСИЛИТЕЛЕЙ
- 6. ТОПОЛОГИЧЕСКИЕ СХЕМЫ МИКРОЭЛЕКТРОННЫХ СВЧ УСИЛИТЕЛЕЙ
- 7. МНОГОКАСКАДНЫЕ УСИЛИТЕЛИ
- 8. ВЛИЯНИЕ ВНЕШНИХ ФАКТОРОВ НА РАБОТУ УСИЛИТЕЛЕЙ С ПТ
- Глава 6. УСТРОЙСТВА, УПРАВЛЯЮЩИЕ МОЩНОСТЬЮ
- 2. УПРАВЛЯЮЩИЕ ЭЛЕМЕНТЫ
- 3. МАТЕМАТИЧЕСКИЙ АППАРАТ ДЛЯ РАСЧЕТА УСТРОЙСТВ НА СОСРЕДОТОЧЕННЫХ ЭЛЕМЕНТАХ
- 4. УСТРОЙСТВА НА СОСРЕДОТОЧЕННЫХ УПРАВЛЯЮЩИХ ЭЛЕМЕНТАХ
- 5. УСТРОЙСТВА НА ЭЛЕМЕНТАХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- Глава 7. ФАЗОВРАЩАТЕЛИ
- 1. ПАРАМЕТРЫ ПОЛУПРОВОДНИКОВЫХ ФАЗОВРАЩАТЕЛЕЙ
- 2. СХЕМЫ ФАЗОВРАЩАТЕЛЕЙ И АНАЛИЗ ХАРАКТЕРИСТИК ФАЗОВРАЩАТЕЛЯ С НАПРАВЛЕННЫМ ОТВЕТВИТЕЛЕМ
- Глава 8. ОГРАНИЧИТЕЛИ МОЩНОСТИ
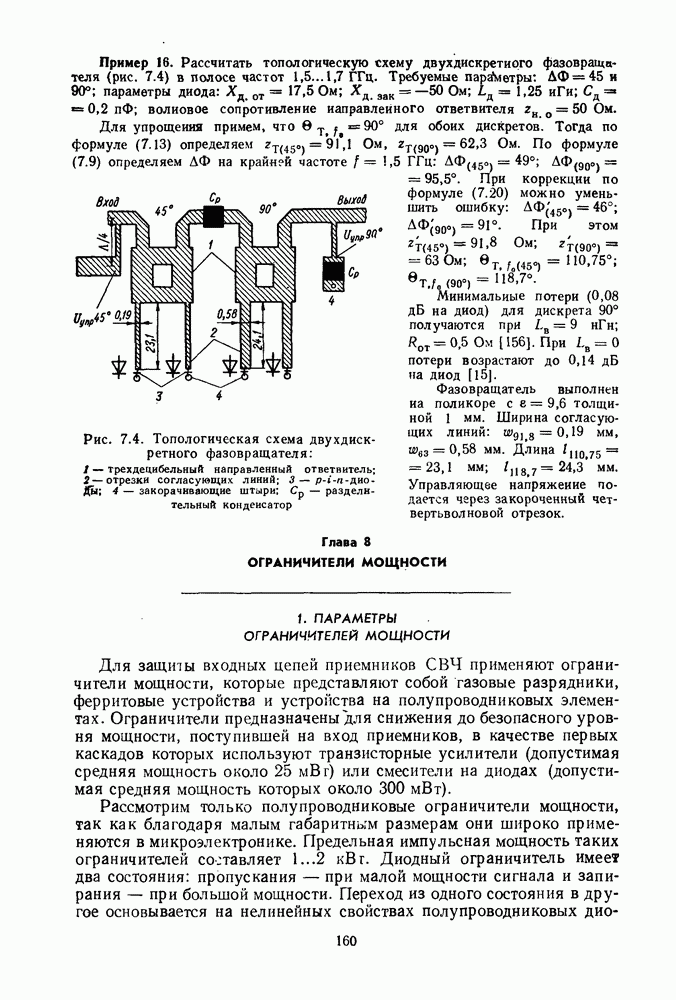
- 1. ПАРАМЕТРЫ ОГРАНИЧИТЕЛЕЙ МОЩНОСТИ
- 2. ОГРАНИЧИТЕЛЬНЫЕ ДИОДЫ
- 3. СХЕМЫ ОГРАНИЧИТЕЛЕЙ МОЩНОСТИ И ИХ РАСЧЕТ
- СПИСОК ЛИТЕРАТУРЫ