| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. ЭЛЕМЕНТЫ МНОГОКАНАЛЬНЫХ ДЕЛИТЕЛЕЙ
Параллельное разветвление линий передач. Простейшим двухканальным делителем является разветвление МПЛ (рис. 2.2). Разветвление содержит три линии. Коэффициенты матрицы рассеяния разветвления, полученные методом свертывания [38],

где  — количество линий передач в разветвлении;
— количество линий передач в разветвлении;  — волновое сопротивление
— волновое сопротивление  линии;
линии;  — геометрическая длина
— геометрическая длина  линии;
линии;  — постоянная распространения
— постоянная распространения  линии..
линии..
Из соотношений (2.1) для двухканального разветвления (рис. 2.2) запишем коэффициенты деления

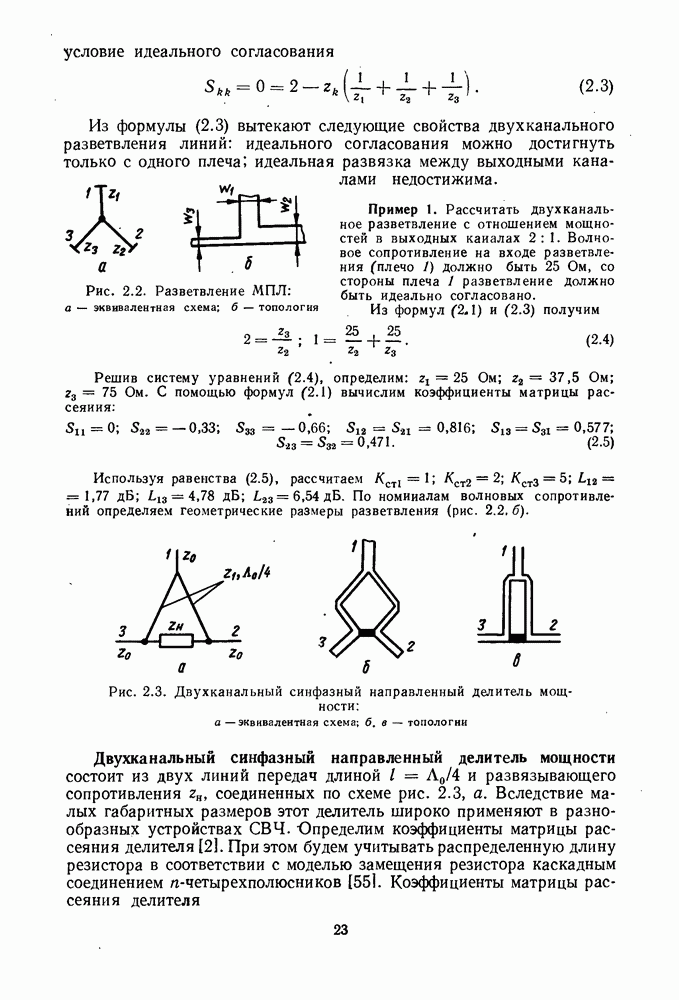
условие идеального согласования

Из формулы (2.3) вытекают следующие свойства двухканального разветвления линий: идеального согласования можно достигнуть только с одного плеча; идеальная развязка между выходными каналами недостижима.
Пример 1. Рассчитать двухканальное разветвление с отношением мощностей в выходных каналах  Волновое сопротивление на входе разветвления (плечо
Волновое сопротивление на входе разветвления (плечо  должно быть 25 Ом, со стороны плеча
должно быть 25 Ом, со стороны плеча  разветвление должно быть идеально согласовано.
разветвление должно быть идеально согласовано.
Из формул (2.1) и  получим
получим

Решив систему уравнений (2.4), определим:  Ом;
Ом;  . С помощью формул (2.1) вычислим коэффициенты матрицы рассеяния:
. С помощью формул (2.1) вычислим коэффициенты матрицы рассеяния:

Используя равенства (2.5), рассчитаем  . По номиналам волновых сопротивлений определяем геометрические размеры разветвления (рис. 2.2, б).
. По номиналам волновых сопротивлений определяем геометрические размеры разветвления (рис. 2.2, б).

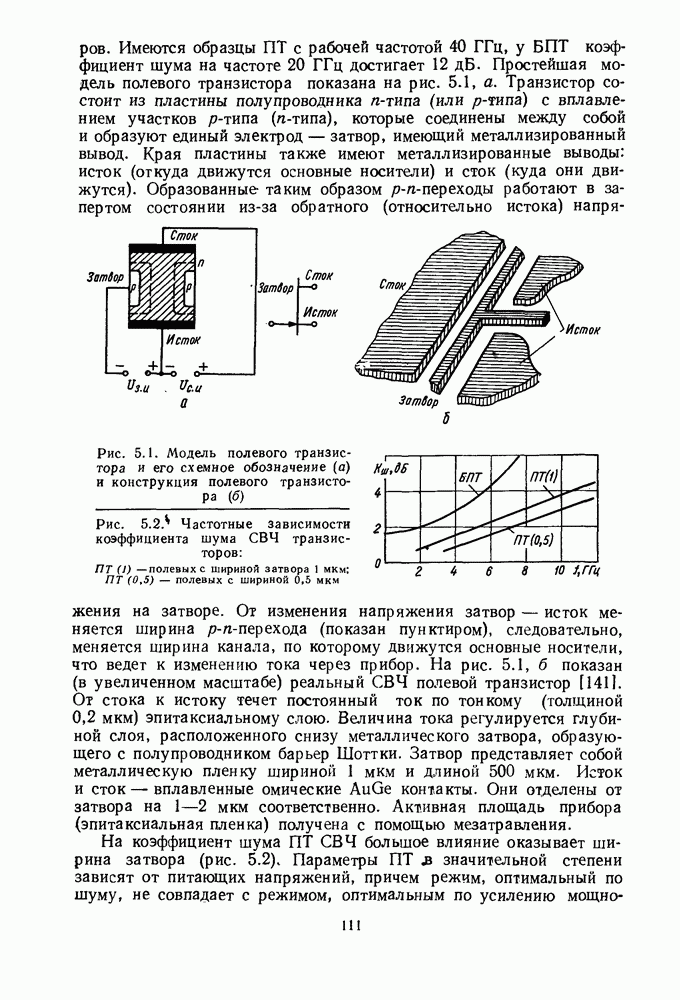
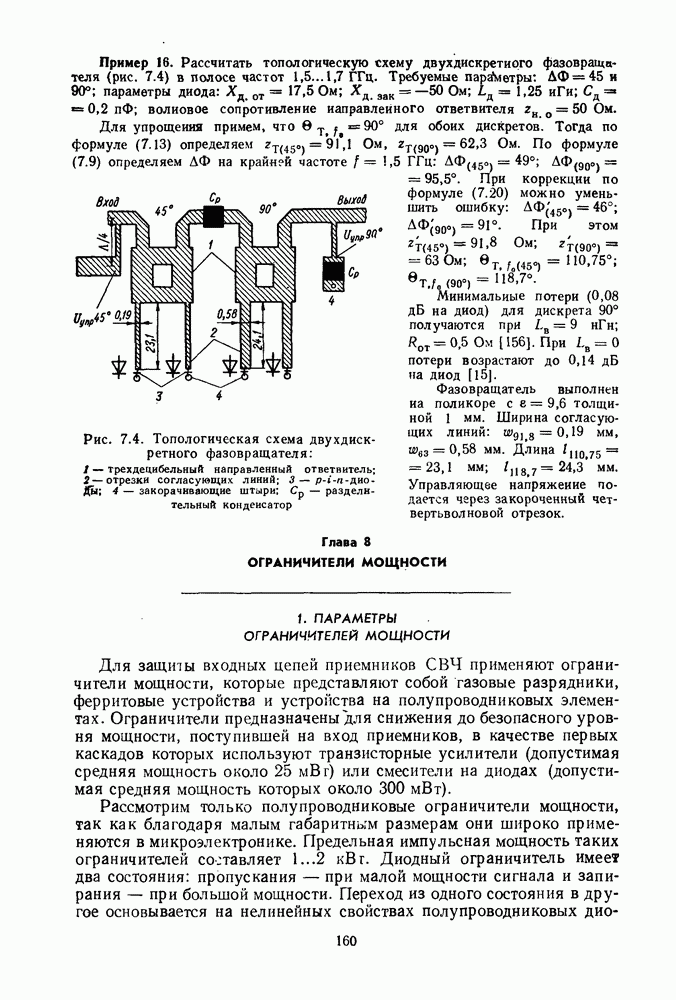
Рис. 2.2. Разветвление МПЛ: а — эквивалентная схема; б — топология

Рис. 2.3. Двухканальный синфазный направленный делитель мощности: а — эквивалентная схема; б, в — топологии
Двухканальный синфазный направленный делитель мощности состоит из двух линий передач длиной  и развязывающего сопротивления
и развязывающего сопротивления  соединенных по схеме рис. 2.3, а. Вследствие малых габаритных размеров этот делитель широко применяют в разнообразных устройствах СВЧ. Определим коэффициенты матрицы рассеяния делителя [2]. При этом будем учитывать распределенную длину резистора в соответствии с моделью замещения резистора каскадным соединением
соединенных по схеме рис. 2.3, а. Вследствие малых габаритных размеров этот делитель широко применяют в разнообразных устройствах СВЧ. Определим коэффициенты матрицы рассеяния делителя [2]. При этом будем учитывать распределенную длину резистора в соответствии с моделью замещения резистора каскадным соединением  -четырехполюсников [55]. Коэффициенты матрицы рассеяния делителя
-четырехполюсников [55]. Коэффициенты матрицы рассеяния делителя
(см. скан)
где  — полиномы Чебышева 1-го и 2-го рода соответственно;
— полиномы Чебышева 1-го и 2-го рода соответственно;  — геометрическая длина резистора; я — число разбиений резистора;
— геометрическая длина резистора; я — число разбиений резистора;  — электрическая длина
— электрическая длина  части резистора;
части резистора;  — волновое сопротивление линии передачи с внутренним проводником такого сечения, геометрические размеры которого совпадают с размерами поперечного сечения резистора;
— волновое сопротивление линии передачи с внутренним проводником такого сечения, геометрические размеры которого совпадают с размерами поперечного сечения резистора;  — электрическая длина четвертьволнового трансформатора;
— электрическая длина четвертьволнового трансформатора;  — относительная частотная расстройка.
— относительная частотная расстройка.
Выражения (2.6) позволяют вычислить коэффициенты матрицы рассеяния делителя с конечной длиной развязывающего резистора. Исходными данными для расчета являются волновые сопротивления  сопротивление развязывающего резистора
сопротивление развязывающего резистора  число звеньев, на которые разбивается резистор
число звеньев, на которые разбивается резистор  длина резистора
длина резистора  диапазон изменения частотной расстройки
диапазон изменения частотной расстройки  . Для расчетов по формулам
. Для расчетов по формулам  целесообразно принимать такими же, как
целесообразно принимать такими же, как
и в делителе с точечным резистором  Сопротивление
Сопротивление  определяется геометрией резистора. Длину резистора целесообразно выражать в долях длины
определяется геометрией резистора. Длину резистора целесообразно выражать в долях длины  четвертьволнового отрезка
четвертьволнового отрезка 

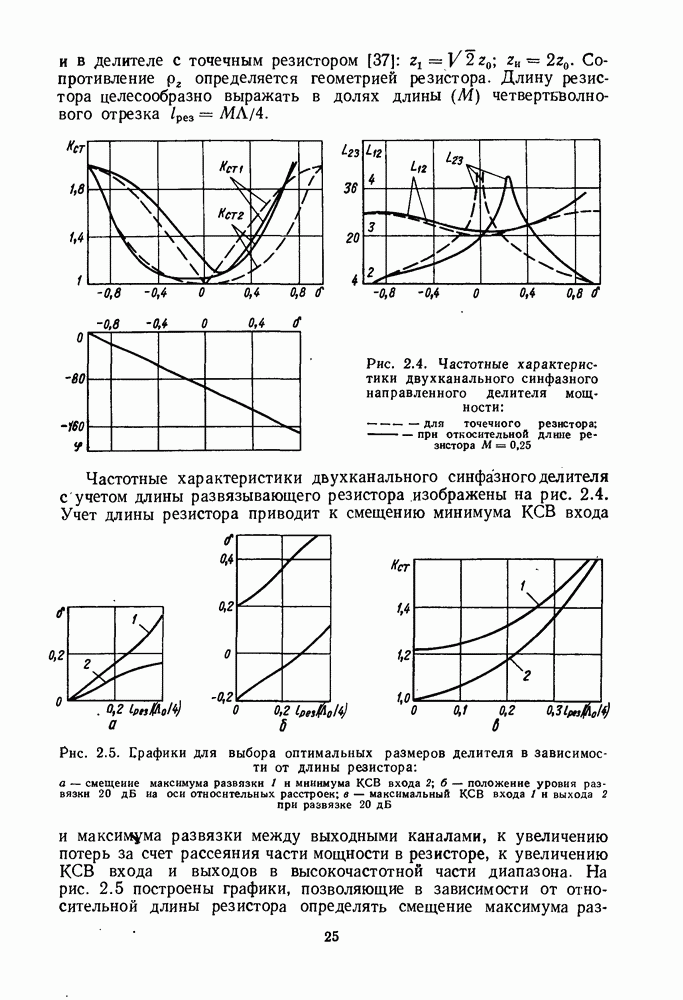
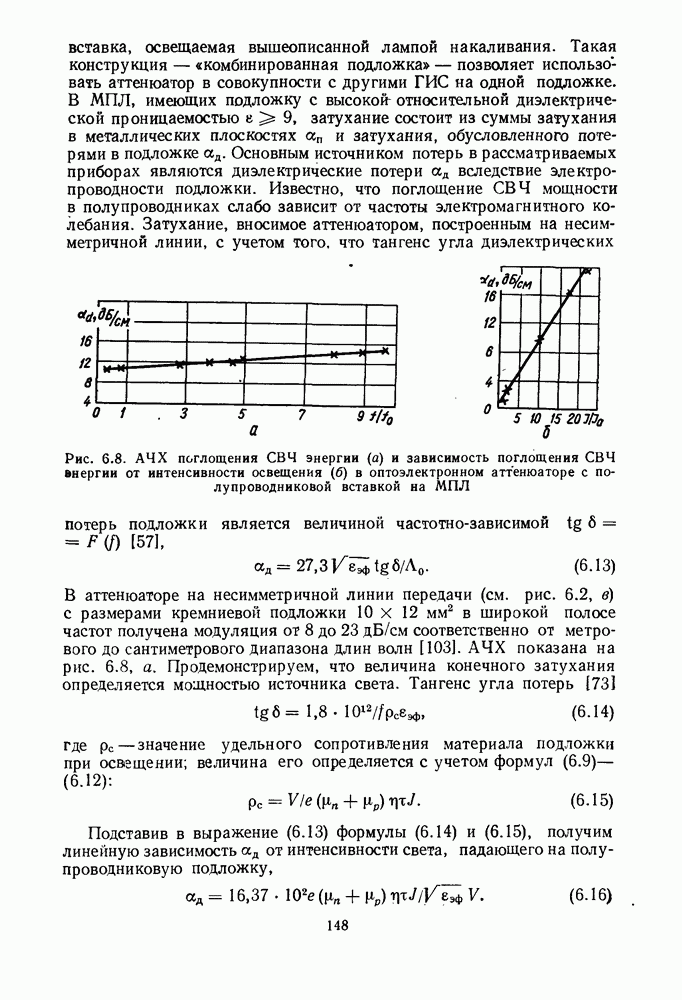
Рис. 2.4. Частотные характеристики двухканального синфазного направленного делителя мощности:  - для точечного резистора;
- для точечного резистора;  — при относительной длине резистора
— при относительной длине резистора 
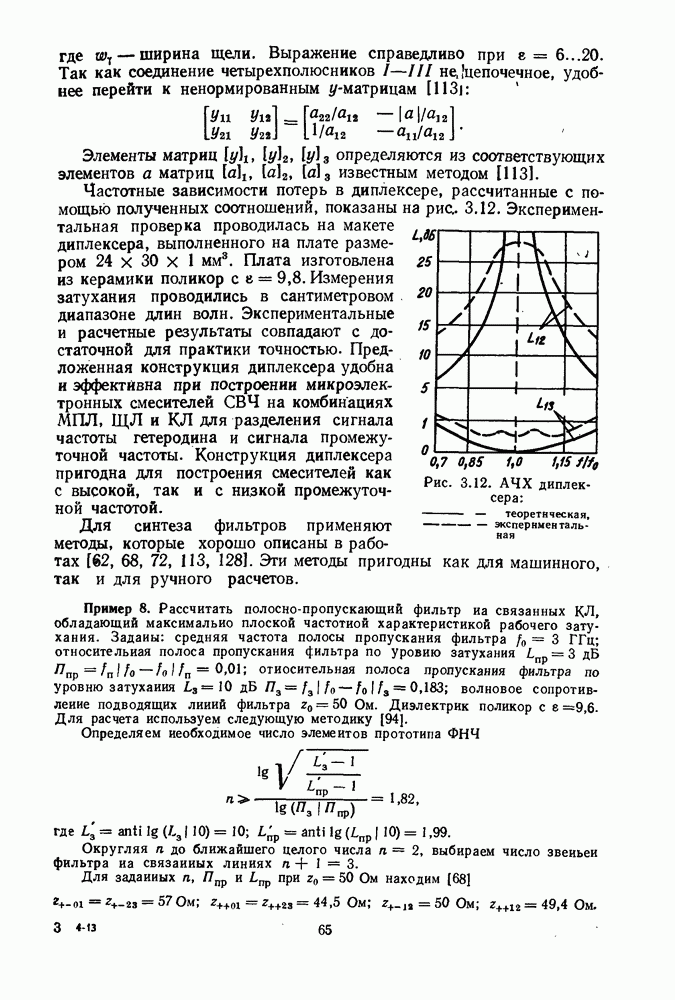
Частотные характеристики дьухканального синфазного делителя с учетом длины развязывающего резистора изображены на рис. 2.4.

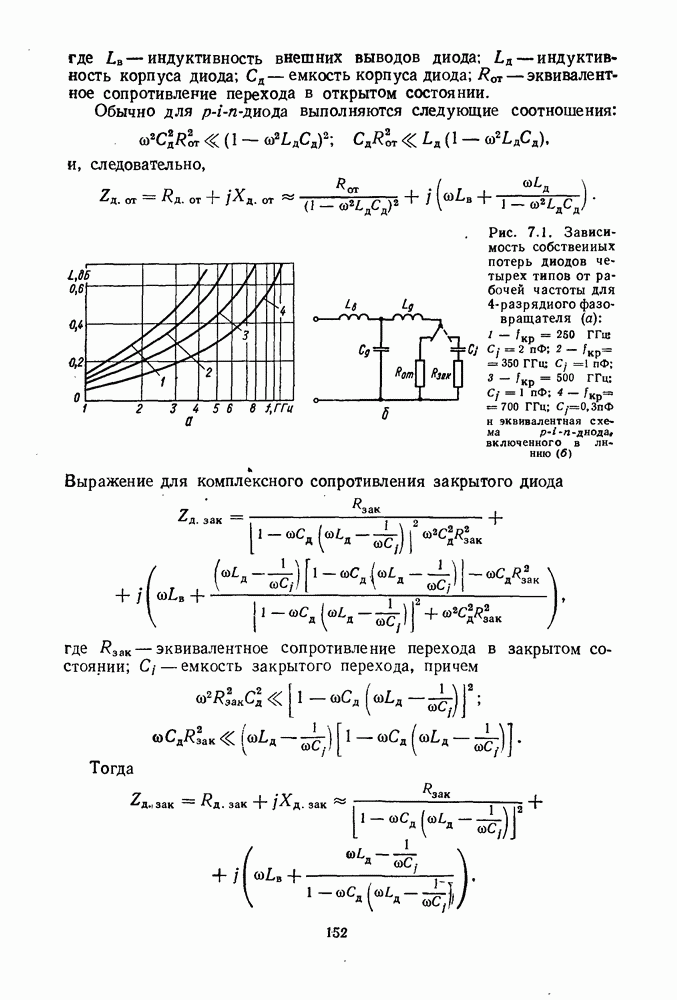
Рис. 2.5. Графики для выбора оптимальных размеров делителя в зависимости от длины резистора: а — смещение максимума развязки  и минимума КСВ входа 2; б — положение уровня развязки 20 дБ на оси относительных расстроек; в — максимальный КСВ входа 1 и выхода 2 при развязке 20 дБ
и минимума КСВ входа 2; б — положение уровня развязки 20 дБ на оси относительных расстроек; в — максимальный КСВ входа 1 и выхода 2 при развязке 20 дБ
Учет длины резистора приводит к смещению минимума КСВ входа и максимума развязки между выходными каналами, к увеличению потерь за счет рассеяния части мощности в резисторе, к увеличению КСВ входа и выходов в высокочастотной части диапазона. На рис. 2.5 построены графики, позволяющие в зависимости от относительной длины резистора определять смещение максимума развязки
между выходными каналами, положение минимума КСВ входа, относительную расстройку  для уровня развязки 20 дБ, максимальное значение КСВ входа и выхода в полосе частот, обеспечивающей уровень развязки между выходными каналами 20 дБ. Графики позволяют выбирать оптимальные геометрические размеры делителя с учетом длины развязывающего резистора и определять предельные параметры делителя по уровню развязки 20 дБ.
для уровня развязки 20 дБ, максимальное значение КСВ входа и выхода в полосе частот, обеспечивающей уровень развязки между выходными каналами 20 дБ. Графики позволяют выбирать оптимальные геометрические размеры делителя с учетом длины развязывающего резистора и определять предельные параметры делителя по уровню развязки 20 дБ.
Пример 2. Рассчитать делитель на 2 канала на МПЛ по следующим данным: максимальная развязка на частоте  диэлектрическая проницаемость подложки
диэлектрическая проницаемость подложки  толщина подложки 1 мм; сопротивление материала резистора 50 Ом/квадрат; мощность рассеяния материала резистора
толщина подложки 1 мм; сопротивление материала резистора 50 Ом/квадрат; мощность рассеяния материала резистора  максимальная мощность рассеяния на резисторе делителя
максимальная мощность рассеяния на резисторе делителя  входы и выходы делителя должны оканчиваться линиями с волновым сопротивлением 50 Ом.
входы и выходы делителя должны оканчиваться линиями с волновым сопротивлением 50 Ом. 
Сопротивление трансформатора  Ом и сопротивление балластного резистора
Ом и сопротивление балластного резистора  Ом.
Ом.
Определяем геометрические размеры резистора. Поскольку материал резистора имеет сопротивление 50 Ом/квадрат,  для получения сопротивления 100 Ом резистор должен представлять собой прямоугольник с отношением сторон
для получения сопротивления 100 Ом резистор должен представлять собой прямоугольник с отношением сторон  Для того чтобы резистор мог рассеивать мощность
Для того чтобы резистор мог рассеивать мощность  его площадь
его площадь  Выбираем резистор с размерами
Выбираем резистор с размерами  Таким образом, резистор представляет собой линию шириной 2,5 мм и длиной 5 мм.
Таким образом, резистор представляет собой линию шириной 2,5 мм и длиной 5 мм.
Коэффициент укорочения длины волны (см. гл. 
Составляем уравнение  где
где  — частота, на которой должен быть максимум развязки;
— частота, на которой должен быть максимум развязки;  — частота, на которой делитель идеально согласован и имеет максимум развязки в предположении, что резистор точечный;
— частота, на которой делитель идеально согласован и имеет максимум развязки в предположении, что резистор точечный;  — относительная частотная расстройка.
— относительная частотная расстройка.
Преобразуем уравнение

Подставляем в уравнение (2.7) величины, заданные в условии, и по рис. 2.5, а определяем  и отношение
и отношение  :
:

Длина четвертьволнового трансформатора  . Для точечного резистора делитель был бы идеально согласован и имел бы максимальную развязку на частоте
. Для точечного резистора делитель был бы идеально согласован и имел бы максимальную развязку на частоте 
Определяем предельные характеристики делителя: максимум развязки на частоте  минимум КСВ входа на частоте
минимум КСВ входа на частоте  , уровень развязки 20 дБ в диапазоне частот
, уровень развязки 20 дБ в диапазоне частот  , максимальный КСВ входа и выхода 1,36 и 1,22 соответственно в диапазоне частот
, максимальный КСВ входа и выхода 1,36 и 1,22 соответственно в диапазоне частот  (рис. 2.5, в).
(рис. 2.5, в).
Зная сопротивления трансформатора и балластного резистора, можно определить ширину проводников. Таким образом, определены все геометрические размеры и параметры делителя.
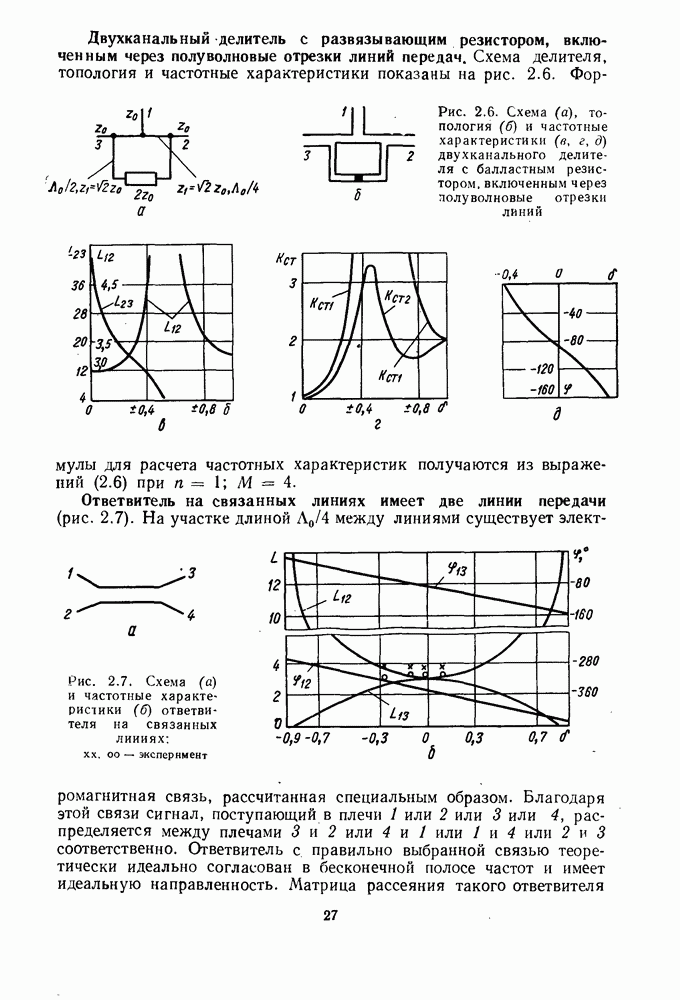
Двухканальный делитель с развязывающим резистором, включенным через полуволновые отрезки линий передач. Схема делителя, топология и частотные характеристики показаны на рис. 2.6.

Рис. 2.6. Схема (а), топология  и частотные характеристики
и частотные характеристики  двухканального делителя с балластным резистором. включенным через лолуволновые отрезки линий
двухканального делителя с балластным резистором. включенным через лолуволновые отрезки линий
Формулы для расчета частотных характеристик получаются из выражений (2.6) при 
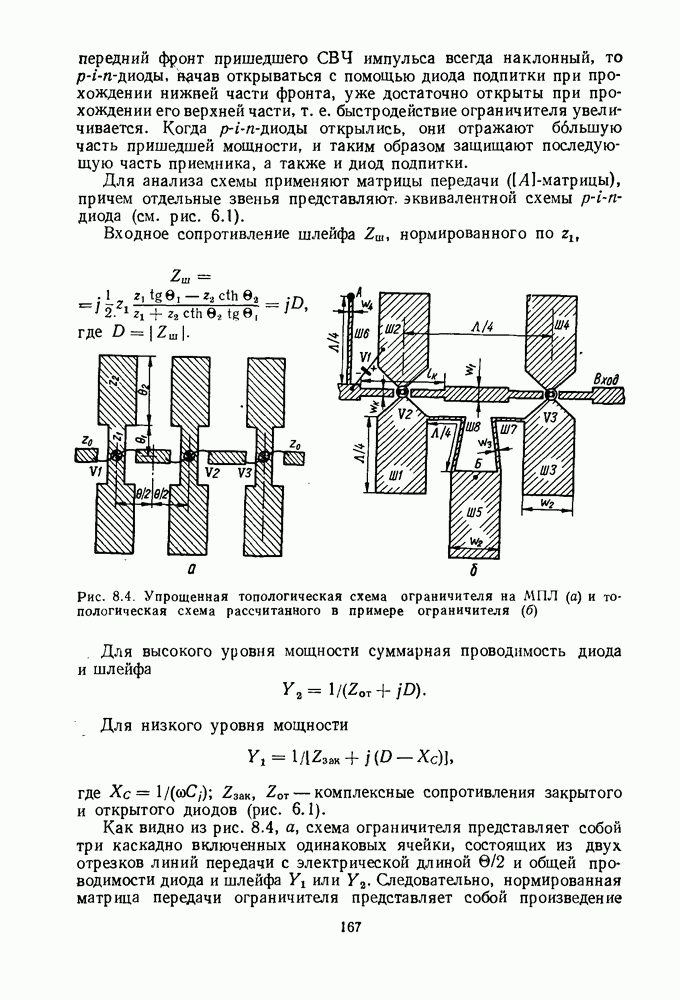
Ответвитель на связанных линиях имеет две линии передачи (рис. 2.7). На участке длиной  между линиями существует электромагнитная связь, рассчитанная специальным образом.
между линиями существует электромагнитная связь, рассчитанная специальным образом.

Рис. 2.7. Схема (а) и частотные характеристики (б) ответвителя на связанных линиях:  — эксперимент
— эксперимент
Благодаря этой связи сигнал, поступающий в плечи 1 или 2 или 3 или 4, распределяется между плечами 3 и 2 или 4 и 1 или  или 2 и 3 соответственно. Ответвитель с правильно выбранной связью теоретически идеально согласован в бесконечной полосе частот и имеет идеальную направленность. Матрица рассеяния такого ответвителя
или 2 и 3 соответственно. Ответвитель с правильно выбранной связью теоретически идеально согласован в бесконечной полосе частот и имеет идеальную направленность. Матрица рассеяния такого ответвителя

 — электрическая длина области связи;
— электрическая длина области связи;  — геометрическая длина области связи;
— геометрическая длина области связи;  — текущая длина волны;
— текущая длина волны;  — относительная частотная расстройка;
— относительная частотная расстройка;  — центральная частота;
— центральная частота;  — абсолютная частотная расстройка;
— абсолютная частотная расстройка;  — нормированное сопротивление четного и нечетного типа колебаний соответственно:
— нормированное сопротивление четного и нечетного типа колебаний соответственно:  — ненормированные сопротивления четного и нечетного типов колебаний соответственно;
— ненормированные сопротивления четного и нечетного типов колебаний соответственно;  — волновое сопротивление подводящих линий.
— волновое сопротивление подводящих линий.
При  коэффициенты матрицы (2.8) принимают вид
коэффициенты матрицы (2.8) принимают вид

Условие идеального согласования и направленности ответвителя

для ненормированных сопротивлений

Нормированная матрица проводимости ответвителя для втекающих токов

Пример 3. Рассчитать ответвитель на связанных линиях. Задано: коэффициент передачи из плеча 1 в плечо  Из формулы
Из формулы  определяем
определяем  Используя формулы (2.9) и (2.10), вычисляем нормированные и ненормированные сопротивления четного и нечетного типов колебаний:
Используя формулы (2.9) и (2.10), вычисляем нормированные и ненормированные сопротивления четного и нечетного типов колебаний:

Находим геометрические размеры сечения связанных полосковых линий. Пример 4. Рассчитать трехдецибельный ответвитель на четырех связанных линиях (мост Ленжа). Определяем  вычисляем
вычисляем

По формулам (2. 12) находим сопротивления четного и нечетного типов колебаний при условии, что волновое сопротивление подводящих линий  .
.
Рассчитываем геометрические размеры моста. При этом задаемся следующими параметрами:  . В результате получим
. В результате получим  На рис. 2. 7 изображены топология рассчитанного ответвителя и частотные характеристики.
На рис. 2. 7 изображены топология рассчитанного ответвителя и частотные характеристики.
Двухкаскадиый ответвитель из звеньев на связанных линиях (рис. 2.8, а). Матрица рассеяния ответвителя

где 

 — электрическая длина соединительных линий;
— электрическая длина соединительных линий;  и
и  — коэффициенты рассеяния первого и второго звеньев ответвителя соответственно.
— коэффициенты рассеяния первого и второго звеньев ответвителя соответственно.
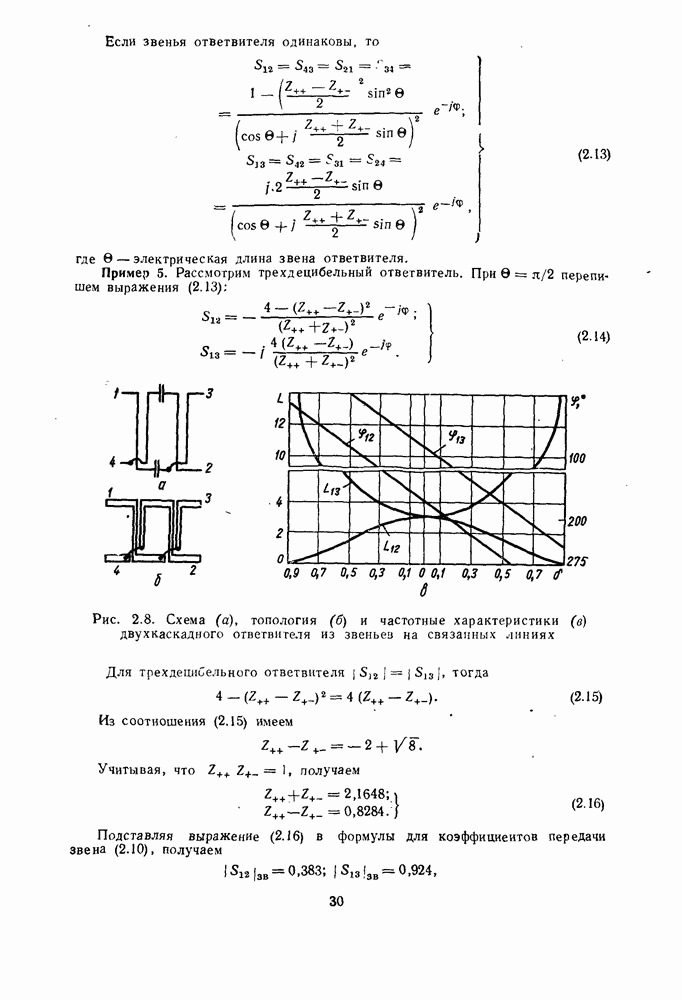
Если звенья ответвителя одинаковы, то

где  — электрическая длина звена ответвителя.
— электрическая длина звена ответвителя.
Пример 5. Рассмотрим трехдецибельный ответвитель. При  перепишем выражения (2.13):
перепишем выражения (2.13):


Рис. 2.8. Схема (а), топология (б) и частотные характеристики (в) двухкаскадного ответвителя из звеньев на связанных линиях
Для трехдецибельного ответвителя  тогда
тогда

Из соотношения (2.15) имеем

Учитывая, что  получаем
получаем

Подставляя выражение (2.16) в формулы для коэффициентов передачи звена (2.10), получаем

или в децибелах

Как видно, два звена со связью - 8,3 дБ обеспечивают выполнение ответвителя со связью — 3 дБ.
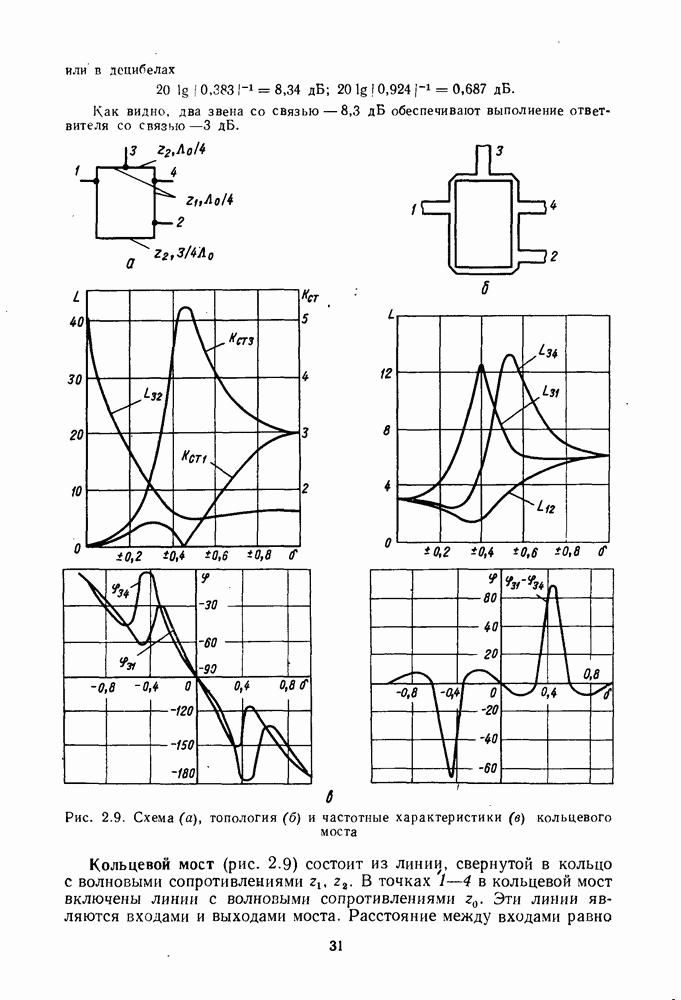
Рис. 2.9. (см. скан) Схема (а), топология (б) и частотные характеристики (в) кольцевого моста
Кольцевой мост (рис. 2.9) состоит из линии, свернутой в кольцо с волновыми сопротивлениями  . В точках 1—4 в кольцевой мост включены линии с волновыми сопротивлениями
. В точках 1—4 в кольцевой мост включены линии с волновыми сопротивлениями  Эти линии являются входами и выходами моста. Расстояние между входами равно
Эти линии являются входами и выходами моста. Расстояние между входами равно
 (
( - длина волны в кольцевой линии на центральной частоте). Кольцевой мост работает следующим образом. При возбуждении моста с любого из плеч по кольцевой линии распространяются две электромагнитные волны навстречу друг другу. Сечения, где электромагнитные волны синфазны или противофазны, соответствуют местам подключения входных (выходных) линий. Таким образом, при возбуждении моста с плеча
- длина волны в кольцевой линии на центральной частоте). Кольцевой мост работает следующим образом. При возбуждении моста с любого из плеч по кольцевой линии распространяются две электромагнитные волны навстречу друг другу. Сечения, где электромагнитные волны синфазны или противофазны, соответствуют местам подключения входных (выходных) линий. Таким образом, при возбуждении моста с плеча  сигналы поступают в плечи
сигналы поступают в плечи
2 и 3 и сдвинуты друг относительно друга на 180°, в плечо 4 сигнал не поступает. При возбуждении моста с плеча 2 сигналы поступают в плечи 1 и 4 и сдвинуты относительно друг друга на 180°, в плечо 3 сигнал не поступает. При возбуждении моста с плеча 3 в плечи 1 и 4 поступают синфазные сигналы, в плечо 2 сигнал не поступает. При возбуждении моста с плеча 4 в плечи 2 и 3 поступают синфазные сигналы, в плечо  сигнал не поступает. Естественно, что такое распространение возбуждающего сигнала возможно при соответствующем выборе волновых сопротивлений кольцевой цепи и только для центральной частоты. Параметры рассеяния моста, полученные методом четного и нечетного возбуждений, имеют вид:
сигнал не поступает. Естественно, что такое распространение возбуждающего сигнала возможно при соответствующем выборе волновых сопротивлений кольцевой цепи и только для центральной частоты. Параметры рассеяния моста, полученные методом четного и нечетного возбуждений, имеют вид:
(см. скан)
 — относительная частотная расстройка;
— относительная частотная расстройка;  -центральная частота.
-центральная частота.
При  (соответствует центральной частоте)
(соответствует центральной частоте)

Условие идеального согласования всех плеч для центральной частоты

При выполнении условия (2.19) получаем

Используя формулы (2.18) — (2.20), запишек

Пример 6. Рассчитать кольцевой мост. Задан коэффициент передачи  плеча 1 в плечо
плеча 1 в плечо  Из формулы
Из формулы  определяем
определяем  Вычисляем
Вычисляем  и находим
и находим

Задаемся сопротивлением  и вычисляем
и вычисляем

и геометрические размеры отрезков линий передачи.
Частотные характеристики кольцевого моста построены на рис. 2. 9, в.
Двухшлейфный ответвитель (рис. 2.10) отличается от кольцевого моста тем, что между плечами 1—2 включен отрезок линии длиной  При возбуждении ответвителя с плеча 1 (3) сигнал распределяется между плечами 3 и 4 (1 и 2), а в плечо 2 (4) сигнал не поступает. При возбуждении ответвителя с плеча 2 (4) сигнал распределяется между плечами 3 и 4 (1 и 2), в плечо 1 (3) сигнал не поступает. Сигналы, поступающие в плечи 3 и 4, 1 и 2 при возбуждении ответвителя с плеч
При возбуждении ответвителя с плеча 1 (3) сигнал распределяется между плечами 3 и 4 (1 и 2), а в плечо 2 (4) сигнал не поступает. При возбуждении ответвителя с плеча 2 (4) сигнал распределяется между плечами 3 и 4 (1 и 2), в плечо 1 (3) сигнал не поступает. Сигналы, поступающие в плечи 3 и 4, 1 и 2 при возбуждении ответвителя с плеч  сдвинуты друг относительно друга на 90°. Параметры рассеяния двухшлейфного ответвителя определяются из соотношений (2.17) при замене в них
сдвинуты друг относительно друга на 90°. Параметры рассеяния двухшлейфного ответвителя определяются из соотношений (2.17) при замене в них  Сделав такую замену, получим
Сделав такую замену, получим

На центральной частоте  получаем
получаем 
Идеальное согласование со всех плеч двухшлейфного ответвителя достигается при выполнении условий

Для условия (2.22)

Для условия (2.23)

Коэффициент деления ответвителя

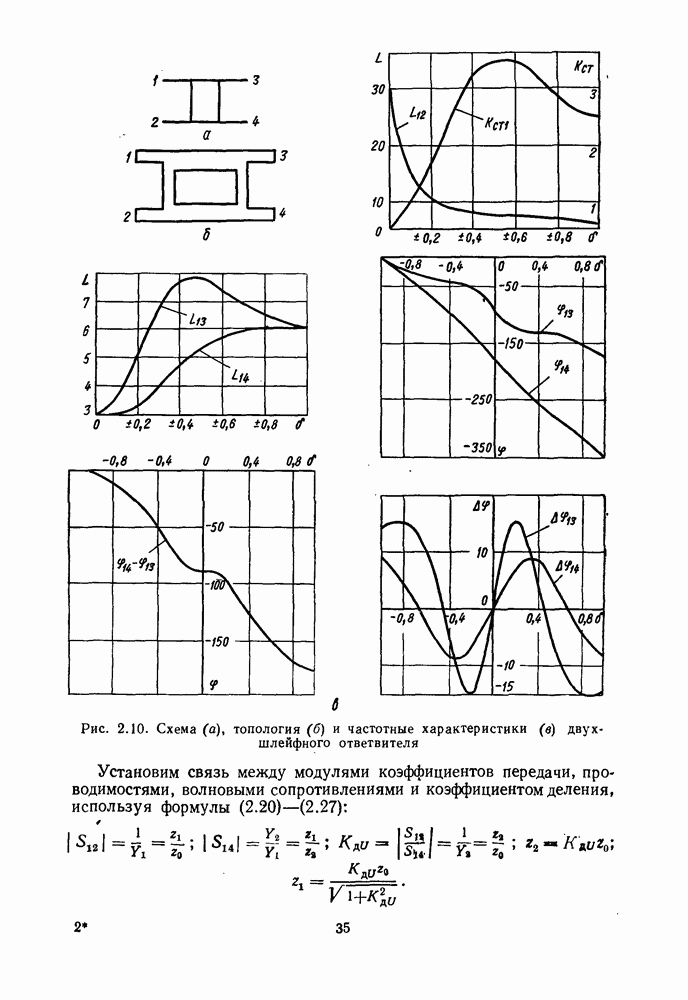
Рис. 2.10. (см. скан) Схема (а), топология (б) и частотные характеристики (в) двухшлейфного ответвителя
Установим связь между модулями коэффициентов передачи, проводимостями, волновыми сопротивлениями и коэффициентом деления, используя формулы (2.20)-(2.27):


(кликните для просмотра скана)
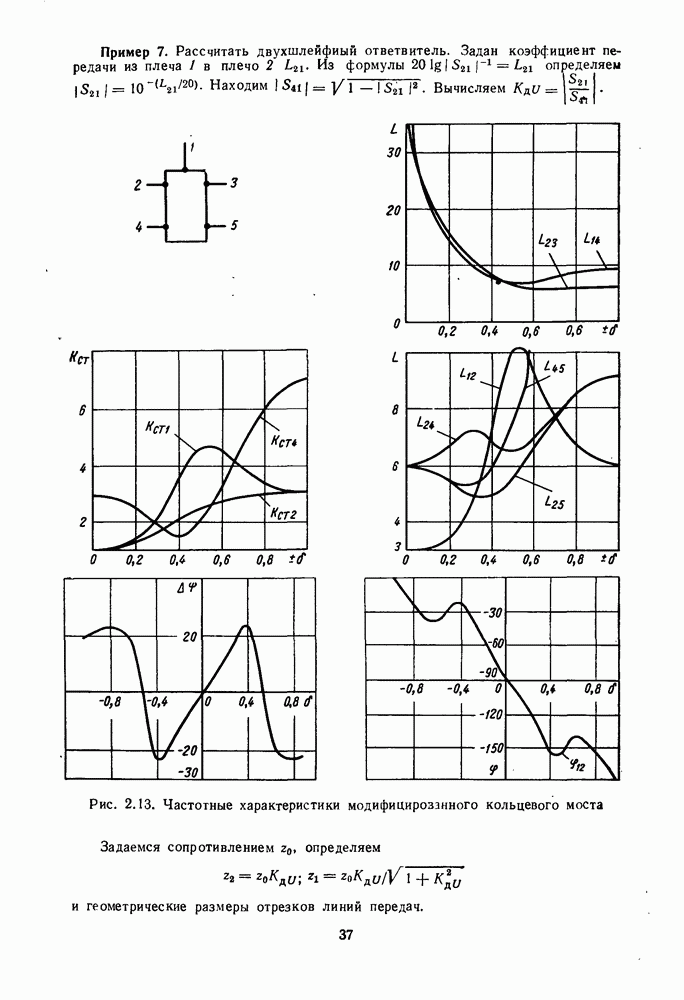
Пример 7. Рассчитать двухшлейфиый ответвитель. Задан коэффициент передачи из плеча  в плечо
в плечо  Из формулы
Из формулы  определяем
определяем  Находим
Находим  Вычисляем
Вычисляем 
Рис. 2.13. (см. скан) Частотные характеристики модифицированного кольцевого моста
Задаемся сопротивлением  определяем
определяем

и геометрические размеры отрезков линий передач.
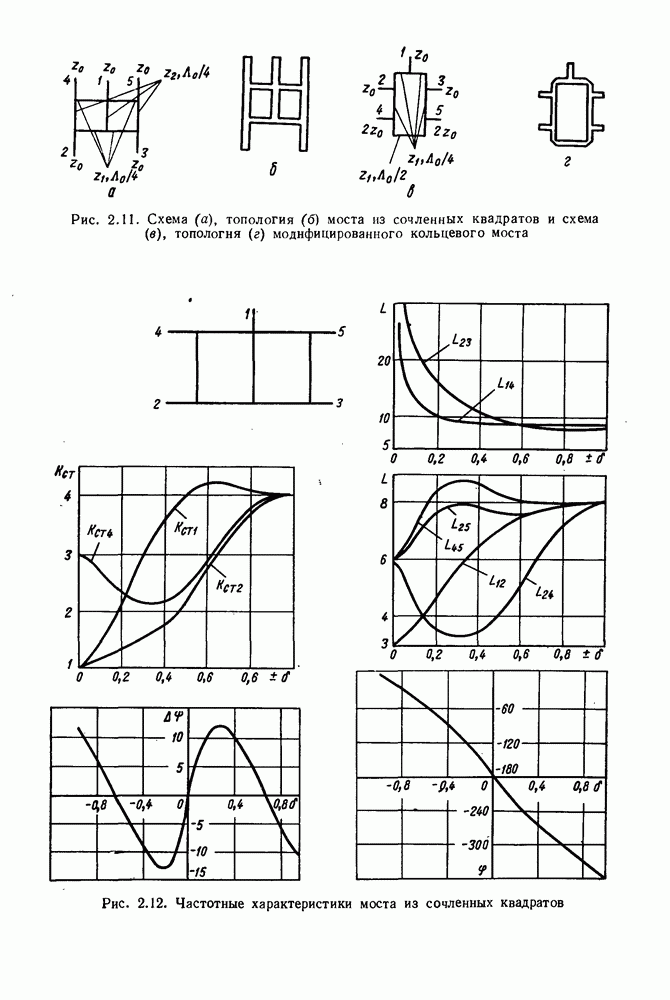
Мост из сочлененных квадратов (модифицированный кольцевой мост). Мосты конструктивно отличаются друг от друга расположением выходных каналов (2, 3) относительно входа (1) и балластных нагрузок (4, 5) (рис. 2.11). Условия идеального согласования плеч на центральной частоте для моста из сочленных квадратов  Для модифицированного кольцевого места:
Для модифицированного кольцевого места: 
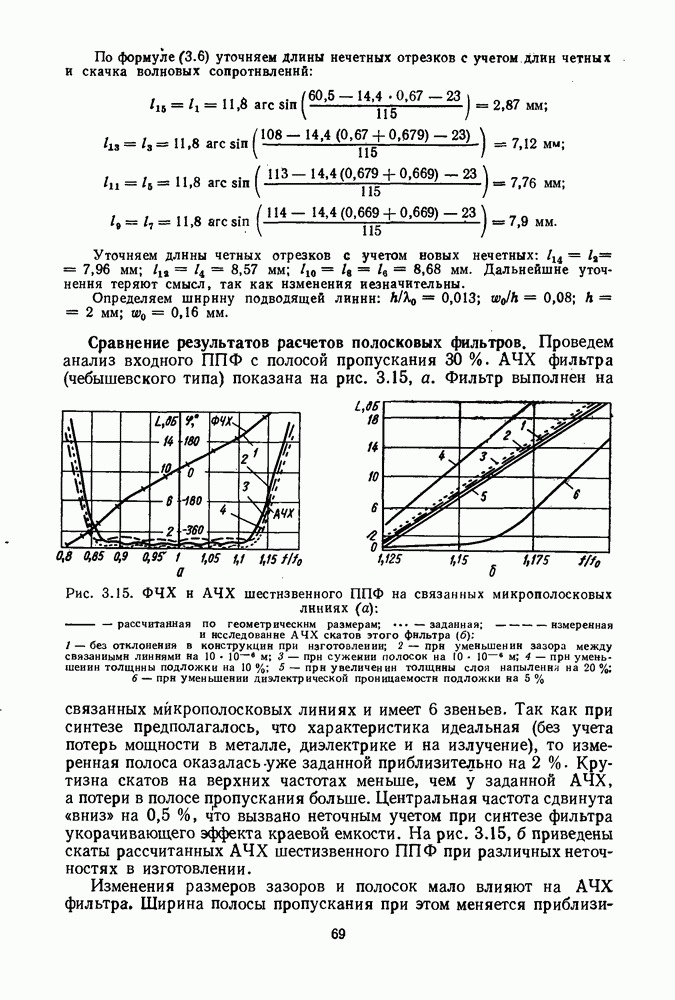
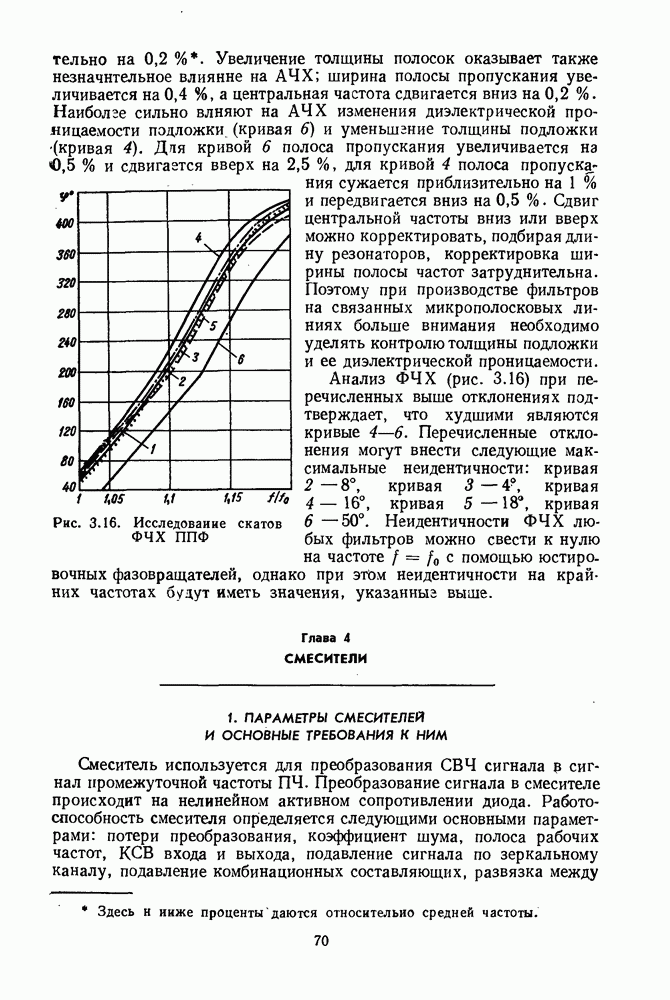
Получить формулы для расчета частотных характеристик таких устройств в аналитическом виде сложно, поэтому устройства представляют в виде соединения более простых элементов: мост из сочленных квадратов из одного разветвления на 4, пяти разветвлений на 3, двух балластных нагрузок и семи четвертьволновых соединительных линий. Модифицированный кольцевой мост представляют как соединений пяти разветвлений на 3, четырех четвертьволновых линий, одной полуволновой линии и двух балластных нагрузок. Частотные характеристики мостов, рассчитанные через матрицы рассеяния элементов, изображены на рис. 2.12 и 2.13.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Главв 1. РАСЧЕТ ЭЛЕМЕНТОВ ГИБРИДНЫХ ИНТЕГРАЛЬНЫХ СХЕМ
- 1. ПОНЯТИЕ ГИБРИДНОЙ ИНТЕГРАЛЬНОЙ СХЕМЫ СВЧ
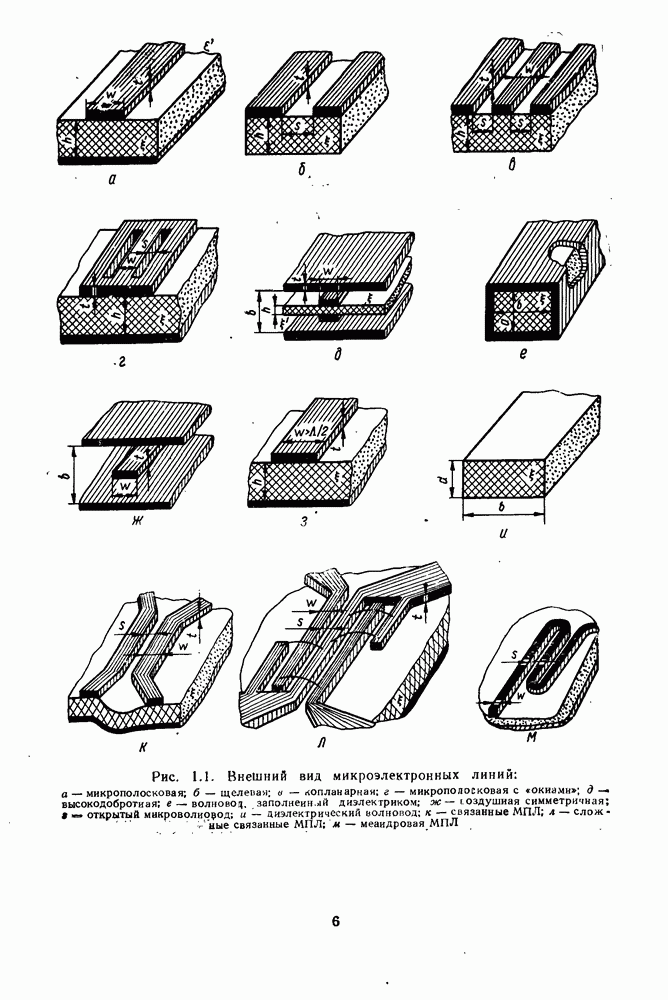
- 2. ОСНОВНЫЕ ЛИНИИ ПЕРЕДАЧ ГИС СВЧ
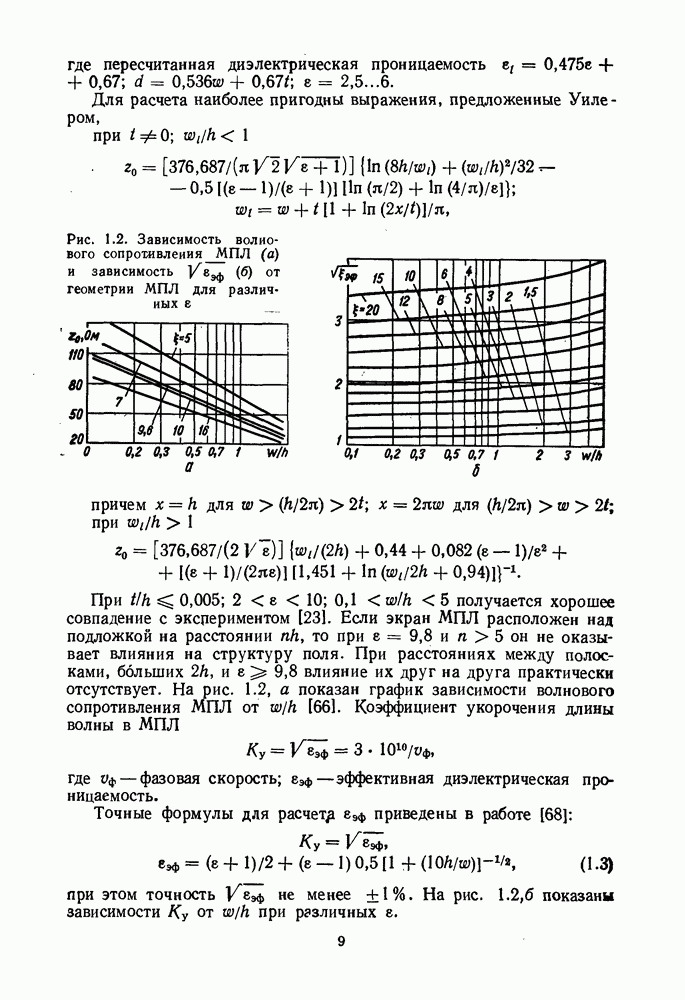
- 3. РАСЧЕТ ПАРАМЕТРОВ ЛИНИЙ
- Главв 2. УСТРОЙСТВА ДЕЛЕНИЯ (СУММИРОВАНИЯ) МОЩНОСТИ СВЧ
- 1. ПРИМЕНЕНИЕ ДЕЛИТЕЛЕЙ (СУММАТОРОВ) МОЩНОСТИ
- 2. ЭЛЕМЕНТЫ МНОГОКАНАЛЬНЫХ ДЕЛИТЕЛЕЙ
- 3. МНОГОКАНАЛЬНЫЕ ДЕЛИТЕЛИ. АЛГОРИТМЫ РАСЧЕТА МНОГОКАНАЛЬНЫХ ДЕЛИТЕЛЕЙ
- 4. ЧЕТЫРЕХКАНАЛЬНЫЕ ДЕЛИТЕЛИ МОЩНОСТИ
- 5. ДЕЛИТЕЛИ МОЩНОСТИ НА 64 КАНАЛА
- 6. ХАРАКТЕРИСТИКИ ДЕЛИТЕЛЕЙ, ВЫПОЛНЕННЫХ ИЗ МОСТОВЫХ УСТРОЙСТВ
- 7. РЕКОМЕНДАЦИИ ДЛЯ ПРОЕКТИРОВАНИЯ ДЕЛИТЕЛЕЙ (СУММАТОРОВ) МОЩНОСТИ
- Глава 3. ИЗБИРАТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ОСНОВНЫЕ ТРЕБОВАНИЯ К ИЗБИРАТЕЛЬНЫМ УСТРОЙСТВАМ И ИХ ПАРАМЕТРЫ
- 2. АППРОКСИМАЦИЯ ФУНКЦИЙ РАБОЧЕГО ЗАТУХАНИЯ
- 3. РАСЧЕТ ТОПОЛОГИЙ ФИЛЬТРОВ
- 4. АНАЛИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- Глава 4. СМЕСИТЕЛИ
- 1. ПАРАМЕТРЫ СМЕСИТЕЛЕЙ И ОСНОВНЫЕ ТРЕБОВАНИЯ К НИМ
- 2. ВЫБОР АКТИВНЫХ ЭЛЕМЕНТОВ
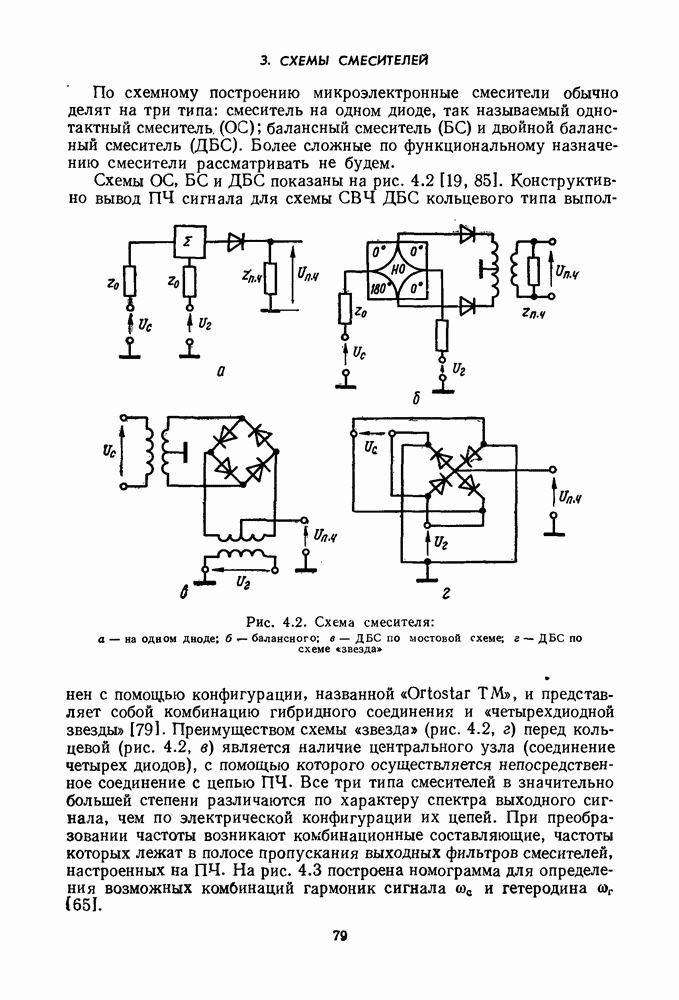
- 3. СХЕМЫ СМЕСИТЕЛЕЙ
- 4. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СМЕСИТЕЛЕЙ
- 5. СМЕСИТЕЛИ НА КОМБИНАЦИЯХ ЛИНИЙ ПЕРЕДАЧ
- 6. РЕЗУЛЬТАТЫ РАСЧЕТОВ И ЭКСПЕРИМЕНТОВ
- Глава 5. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ТРЕБОВАНИЯ К МАЛОШУМЯЩИМ УСИЛИТЕЛЯМ СВЧ И ИХ ПАРАМЕТРЫ
- 2. УСИЛИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 3. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ТРАНЗИСТОРА
- 4. РАСЧЕТ УСИЛИТЕЛЕЙ
- 5. ИСПОЛЬЗОВАНИЕ ЭВМ ПРИ ПРОЕКТИРОВАНИИ УСИЛИТЕЛЕЙ
- 6. ТОПОЛОГИЧЕСКИЕ СХЕМЫ МИКРОЭЛЕКТРОННЫХ СВЧ УСИЛИТЕЛЕЙ
- 7. МНОГОКАСКАДНЫЕ УСИЛИТЕЛИ
- 8. ВЛИЯНИЕ ВНЕШНИХ ФАКТОРОВ НА РАБОТУ УСИЛИТЕЛЕЙ С ПТ
- Глава 6. УСТРОЙСТВА, УПРАВЛЯЮЩИЕ МОЩНОСТЬЮ
- 2. УПРАВЛЯЮЩИЕ ЭЛЕМЕНТЫ
- 3. МАТЕМАТИЧЕСКИЙ АППАРАТ ДЛЯ РАСЧЕТА УСТРОЙСТВ НА СОСРЕДОТОЧЕННЫХ ЭЛЕМЕНТАХ
- 4. УСТРОЙСТВА НА СОСРЕДОТОЧЕННЫХ УПРАВЛЯЮЩИХ ЭЛЕМЕНТАХ
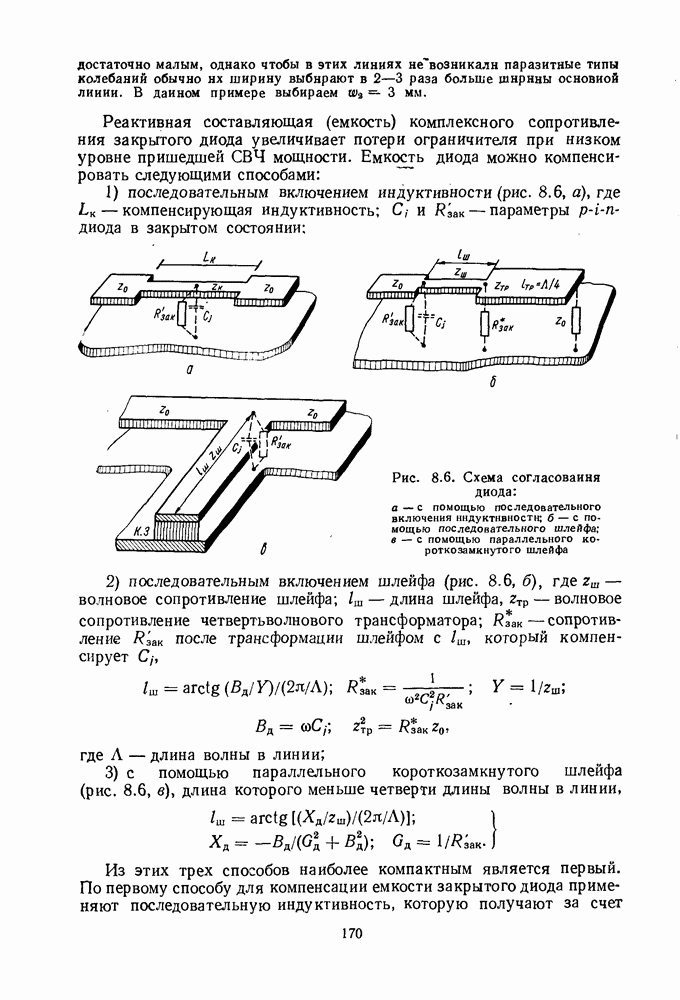
- 5. УСТРОЙСТВА НА ЭЛЕМЕНТАХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
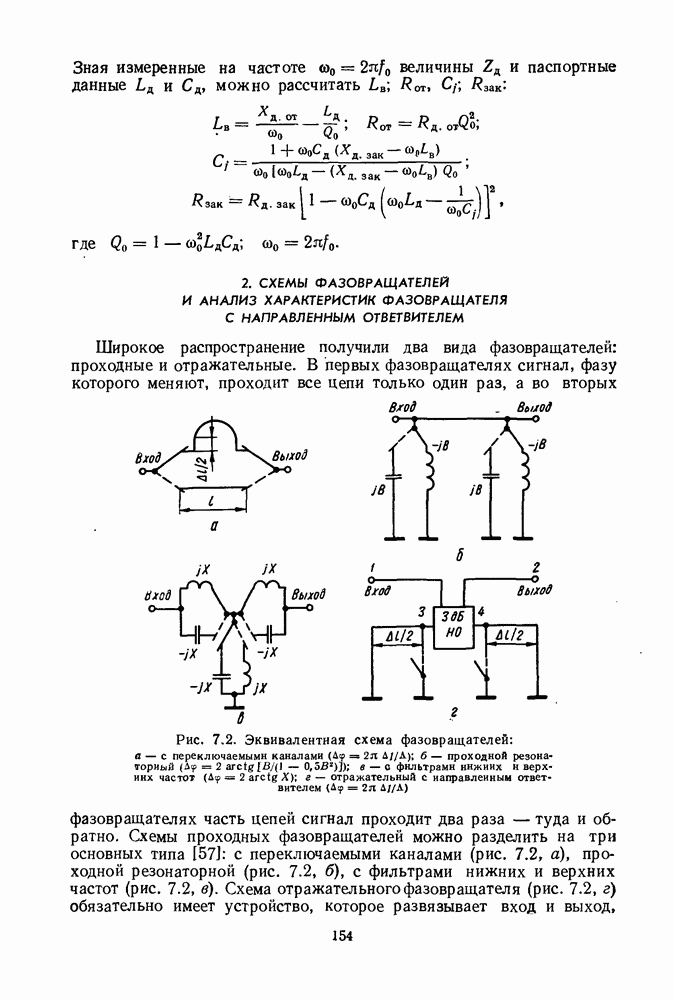
- Глава 7. ФАЗОВРАЩАТЕЛИ
- 1. ПАРАМЕТРЫ ПОЛУПРОВОДНИКОВЫХ ФАЗОВРАЩАТЕЛЕЙ
- 2. СХЕМЫ ФАЗОВРАЩАТЕЛЕЙ И АНАЛИЗ ХАРАКТЕРИСТИК ФАЗОВРАЩАТЕЛЯ С НАПРАВЛЕННЫМ ОТВЕТВИТЕЛЕМ
- Глава 8. ОГРАНИЧИТЕЛИ МОЩНОСТИ
- 1. ПАРАМЕТРЫ ОГРАНИЧИТЕЛЕЙ МОЩНОСТИ
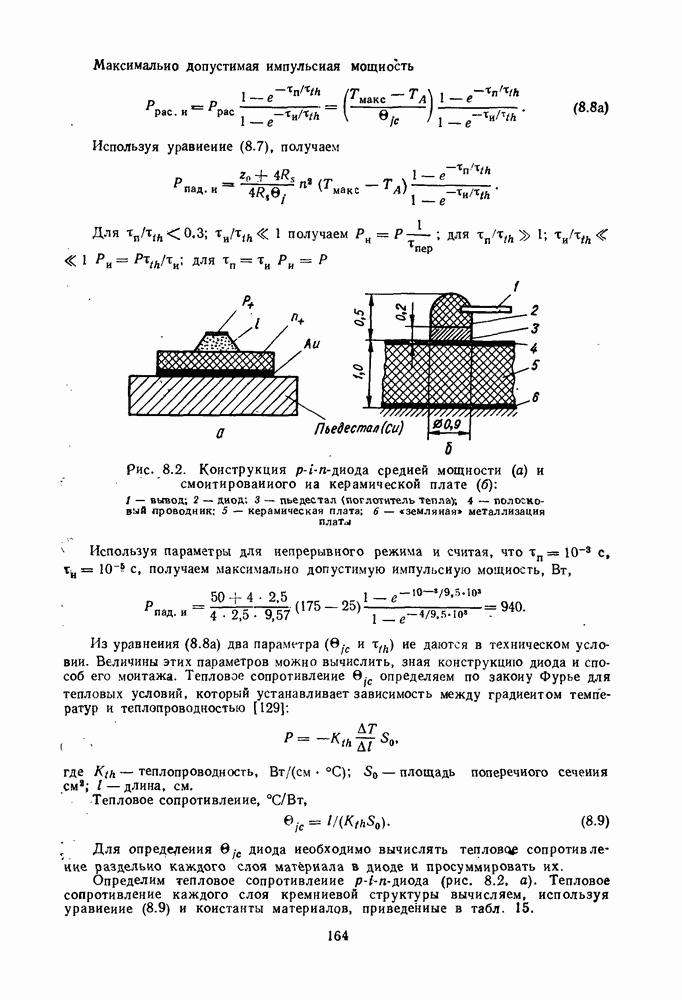
- 2. ОГРАНИЧИТЕЛЬНЫЕ ДИОДЫ
- 3. СХЕМЫ ОГРАНИЧИТЕЛЕЙ МОЩНОСТИ И ИХ РАСЧЕТ
- СПИСОК ЛИТЕРАТУРЫ