| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. РАСЧЕТ ПАРАМЕТРОВ ЛИНИЙ
МПЛ представляет собой несимметричную полосковую линию, токонесущий проводник которой нанесен на диэлектрик с большой относительной диэлектрической проницаемостью. Структура поля МПЛ близка к структуре поля поперечной электромагнитной Т-волны. Однако наличие диэлектриков с разными диэлектрическими проницаемостями усложняет структуру поля. Скорость распространения волны в МПЛ зависит от частоты. Ранее рассматривали эту линию, как будто заполненную однородным диэлектриком с эффективной диэлектрической постоянной. Выражение для волнового сопротивления  МПЛ с однородным заполнением и полоской нулевой толщины [23]
МПЛ с однородным заполнением и полоской нулевой толщины [23]
при 

при 

где  — ширина полоски;
— ширина полоски;  — толщина подложки;
— толщина подложки;  — диэлектрическая постоянная среды, если МПЛ расположена в воздухе, т. е.
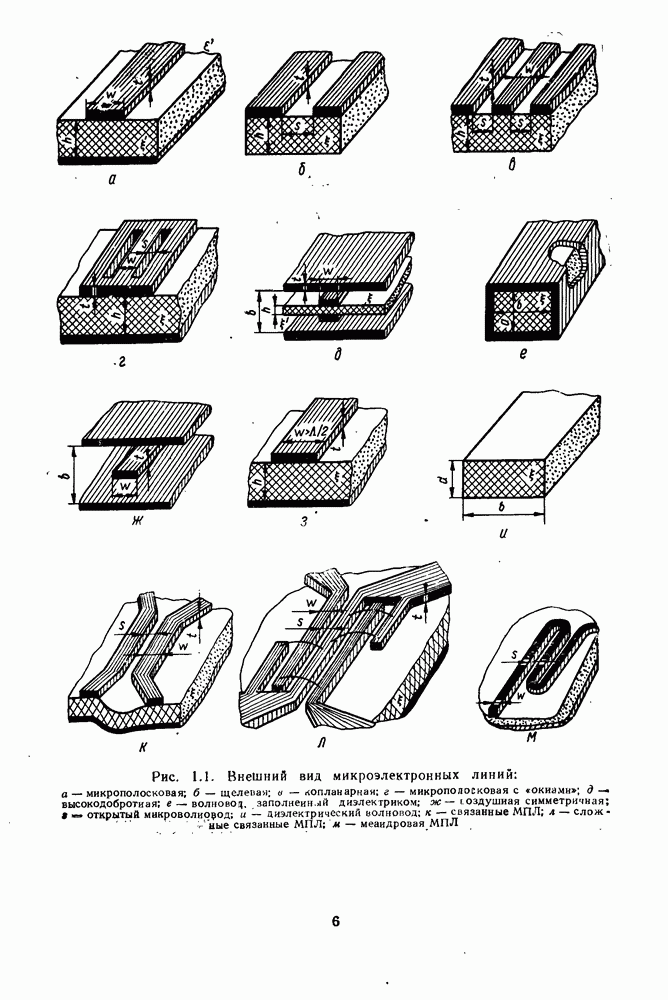
— диэлектрическая постоянная среды, если МПЛ расположена в воздухе, т. е.  (рис. 1.1, а).
(рис. 1.1, а).
Такие линии применяют редко, поэтому интерес представляет случай, когда  и толщина полоски
и толщина полоски  Тогда волновое сопротивление МПЛ с точностью
Тогда волновое сопротивление МПЛ с точностью  и
и  определяют по следующей формуле [4]:
определяют по следующей формуле [4]:

где пересчитанная диэлектрическая проницаемость 
Для расчета наиболее пригодны выражения, предложенные Уилером,
при 

причем  для
для  для
для  при
при 

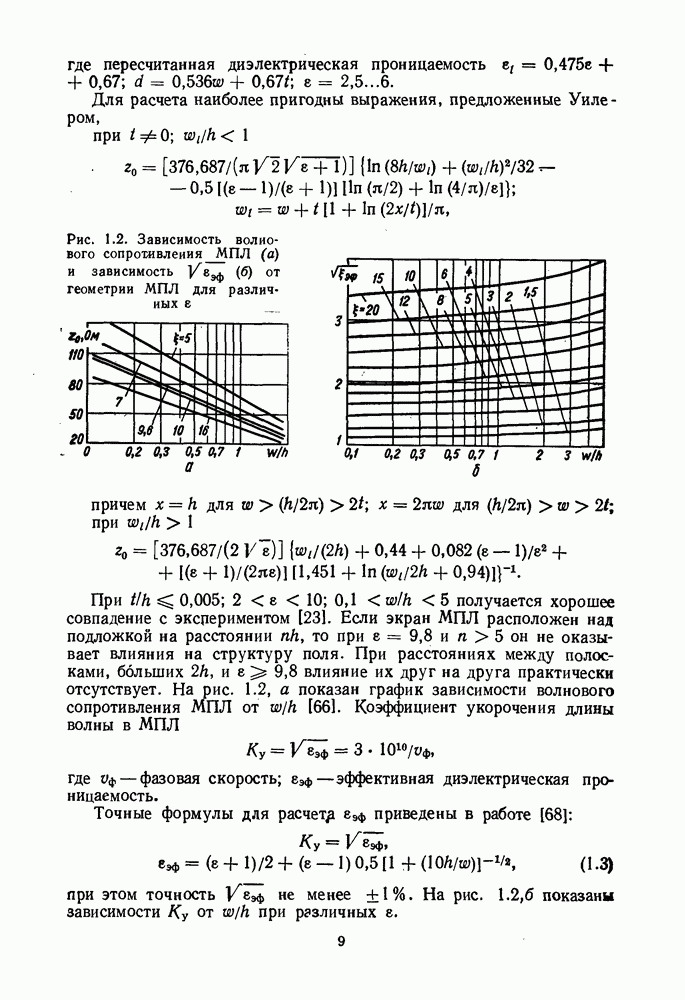
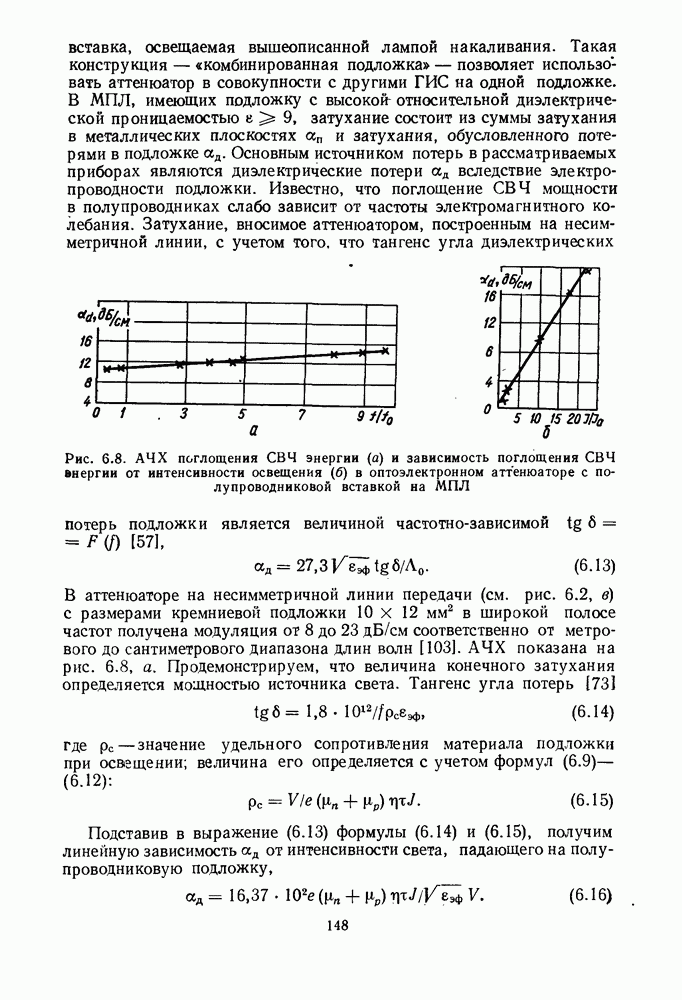
Рис. 1.2. (см. скан) Зависимость волнового сопротивления МПЛ (а) и зависимость  от геометрии МПЛ для различных
от геометрии МПЛ для различных 
При  получается хорошее совпадение с экспериментом [23]. Если экран МПЛ расположен над подложкой на расстоянии
получается хорошее совпадение с экспериментом [23]. Если экран МПЛ расположен над подложкой на расстоянии  то при
то при  он не оказывает влияния на структуру поля. При расстояниях между полосками, больших
он не оказывает влияния на структуру поля. При расстояниях между полосками, больших  и
и  влияние их друг на друга практически отсутствует. На рис. 1.2, а показан график зависимости волнового сопротивления МПЛ от
влияние их друг на друга практически отсутствует. На рис. 1.2, а показан график зависимости волнового сопротивления МПЛ от  Коэффициент укорочения длины волны в МПЛ
Коэффициент укорочения длины волны в МПЛ

где  — фазовая скорость;
— фазовая скорость;  -эффективная диэлектрическая проницаемость.
-эффективная диэлектрическая проницаемость.
Точные формулы для расчету  приведены в работе [68]:
приведены в работе [68]:

при этом точность  не менее ±1%. На рис. 1.2,б показаны зависимости
не менее ±1%. На рис. 1.2,б показаны зависимости  от
от  при различных
при различных  .
.
Потери в МПЛ состоят из потерь в диэлектрике  в проводнике
в проводнике  и на излучение
и на излучение  Потери на излучение уменьшаются с ростом
Потери на излучение уменьшаются с ростом  и при 10 ими можно пренебречь по сравнению с потерями в проводнике и диэлектрике. Для МПЛ на диэлектрической подложке с
и при 10 ими можно пренебречь по сравнению с потерями в проводнике и диэлектрике. Для МПЛ на диэлектрической подложке с  потерями в диэлектрике можно пренебречь по сравнению с потерями в проводнике. Толщина напыления проводника должна быть не менее 3 скин-слоев (для меди
потерями в диэлектрике можно пренебречь по сравнению с потерями в проводнике. Толщина напыления проводника должна быть не менее 3 скин-слоев (для меди  мкм на частоте 10 ГГц и 6 мкм на частоте 1 ГГц) [66]. При
мкм на частоте 10 ГГц и 6 мкм на частоте 1 ГГц) [66]. При  -слоя потери в проводнике в
-слоя потери в проводнике в  можно определить из выражений [66]: при
можно определить из выражений [66]: при 

при

где для меди на частоте  поверхностное сопротивление
поверхностное сопротивление  Ом [66];
Ом [66];  — удельная линейная проводимость;
— удельная линейная проводимость;  мкм — толщина. скин-слоя на частоте
мкм — толщина. скин-слоя на частоте  При этом
При этом  для
для  Ом. Добротность МПЛ целесообразно определять через добротность резонатора. Добротность МПЛ четвертьволнового резонатора, определяемая потерями в проводнике [66],
Ом. Добротность МПЛ целесообразно определять через добротность резонатора. Добротность МПЛ четвертьволнового резонатора, определяемая потерями в проводнике [66],

Добротность, определяемая потерями в диэлектрике,

Результирующая добротность четвертьволнового резонатора

Она колеблется в пределах 20—400 [66], например, при  мм;
мм;  Ом;
Ом;  и медном проводнике
и медном проводнике  .
.
Рабочая частота МПЛ должна быть ниже определенной критической частоты, при которой возникают паразитные колебания двух типов. Первый тип паразитных колебаний поверхностные волны, которые распространяются на поверхности диэлектрической подложки на ее границе с заземленной плоскостью вдоль последней. Если фазовая скорость поверхностной волны равна фазовой скорости 
бочей квази Т-волны, возникает их взаимодействие. Критическая максимальная) частота поверхностных волн [66]

где  — в гигагерцах;
— в гигагерцах;  — в миллиметрах.
— в миллиметрах.
Второй тип паразитных колебаний для МПЛ с широким центральным проводником — поперечные резонансные колебания, которые распространяются между полоской и заземленным основанием. Максимальная частота этих колебаний при  выше, чем для поверхности волн
выше, чем для поверхности волн

где  — в гигагерцах.
— в гигагерцах.
Второй тип паразитных колебаний можно подавить, прорезав продольные щели в металлической полоске  Однако при этом изменится волновое сопротивление этой линии.
Однако при этом изменится волновое сопротивление этой линии.
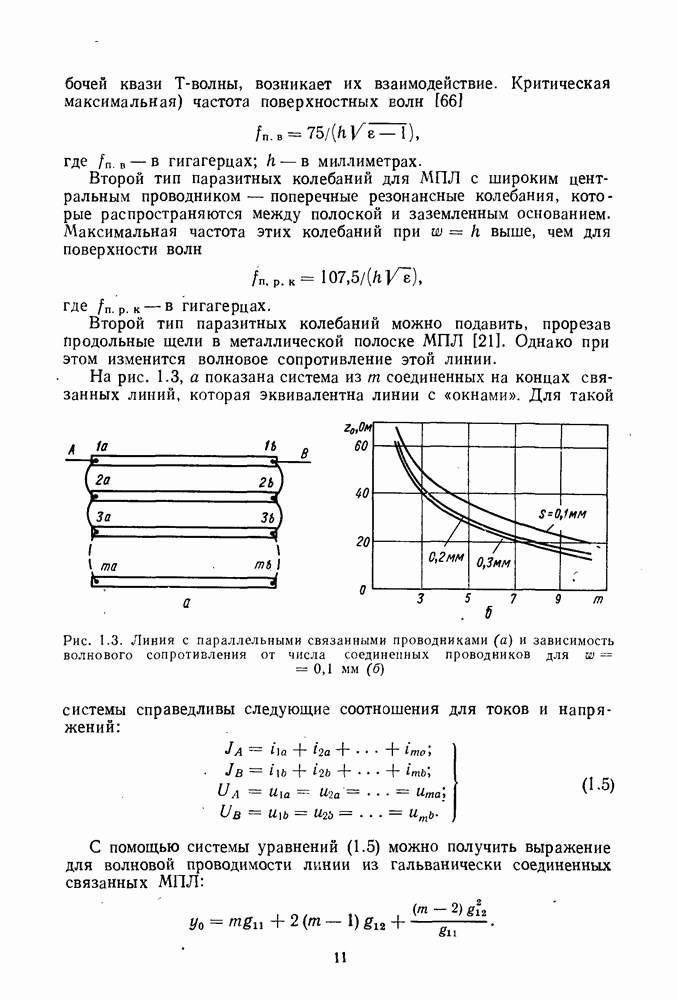
На рис. 1.3, а показана система из  соединенных на концах связанных линий, которая эквивалентна линии с «окнами».
соединенных на концах связанных линий, которая эквивалентна линии с «окнами».

Рис. 1.3. Линия с параллельными связанными проводниками (а) и зависимость волнового сопротивления от числа соединенных проводников для 
Для такой системы справедливы следующие соотношения для токов и напряжений:

С помощью системы уравнений (1.5) можно получить выражение для волновой проводимости линии из гальванически соединенных связанных МПЛ:

Проводимости  определяют из работы [32]
определяют из работы [32]

где  — волновые проводимости четного и нечетного типов колебаний пары связанных линий. Эти проводимости можно вычислить, зная конструкцию линии [118].
— волновые проводимости четного и нечетного типов колебаний пары связанных линий. Эти проводимости можно вычислить, зная конструкцию линии [118].
Зависимость волнового сопротивления от числа соединенных линий показана на рис.  при следующих параметрах МПЛ:
при следующих параметрах МПЛ:  ; расстояние между соседними полосками
; расстояние между соседними полосками  ; ширина полоски
; ширина полоски  мм; толщина диэлектрика
мм; толщина диэлектрика  мм;
мм;  толщина напыленного слоя металла
толщина напыленного слоя металла  мм.
мм.
Коэффициент укорочения длины волны в такой линии

где 

Рис. 1.4. Четыре связанные линии (а) и меандровая линия передачи (б)
Выражение, получено для пары связанных линий, однако справедливо и для большего их числа, если учитывать связи только между соседними проводниками. Потери в проводнике для такой линии определяются аналогично потерям в проводнике одиночной МПЛ. При этом в формулы подставляется значение волнового сопротивленияне всей линии, а только одного из параллельных связанных проводников. Две связанные МПЛ описываются характеристическими сопротивлениями четного и нечетного колебаний [118]. При этом каждая из этих связанных линий расщеплена на  частей, причем части линий как бы «переплетены» между собой (рис. 1.4, а, где
частей, причем части линий как бы «переплетены» между собой (рис. 1.4, а, где  Такое «переплетение» использовано Лэнжем [140] для построения трехдецибельного ответвителя (см. рис.
Такое «переплетение» использовано Лэнжем [140] для построения трехдецибельного ответвителя (см. рис.  Характеристические сопротивления для четного и нечетного типов колебаний:
Характеристические сопротивления для четного и нечетного типов колебаний:

где  — число частей, на которые делят каждую из двух полосковых линий.
— число частей, на которые делят каждую из двух полосковых линий.
Формулы получены из выражений для параллельного соединения погонных емкостей [118] и введения эмпирического поправочного коэффициента. Микрополосковые меандровые линии широко применяют в ИС для получения заданного набега фазы сигнала [1].
На рис. 1.4, б показана линия передачи, свернутая в меандр. Между параллельными линиями имеется электромагнитная связь. Для такой линии справедливы следующие соотношения токов и напряжений:

где  — число связанных линий;
— число связанных линий;  — параллельная проводимость соединительного поворота;
— параллельная проводимость соединительного поворота;

Если длина соединительного поворота между смежными линиями в несколько раз меньше длины волны в системе, линия описывается следующей системой уравнений [311:

где  — признак мнимого числа;
— признак мнимого числа;  — длина области связи; — собственная проводимость при
— длина области связи; — собственная проводимость при  и проводимость связи двух соседних линий при
и проводимость связи двух соседних линий при 
Электромагнитная связь через линии при расчете не учитывается, а влияние соединений между параллельными линиями определяется как  где
где  — параллельная емкость поворота. Если линии имеют равные между собой волновые сопротивления и расположены на равных расстояниях друг от друга, то можно получить матрицу проводимости линии, представленной в виде четырехполюсника,
— параллельная емкость поворота. Если линии имеют равные между собой волновые сопротивления и расположены на равных расстояниях друг от друга, то можно получить матрицу проводимости линии, представленной в виде четырехполюсника,

где 
Элементы матрицы  системы меандровой линии для
системы меандровой линии для  определяются по следующим формулам:
определяются по следующим формулам:

где  порядок матрицы коэффициентов;
порядок матрицы коэффициентов;  — определитель и алгебраическое дополнение матрицы коэффициентов.
— определитель и алгебраическое дополнение матрицы коэффициентов.
Матрица коэффициентов в общем виде является диагонально-ленточной и имеет следующие особенности: 1) главная диагональ состоит из коэффициентов  кроме клеток 11 и
кроме клеток 11 и  которые состоят из коэффициентов
которые состоят из коэффициентов  каждая строка матрицы состоит из последовательности коэффициентов
каждая строка матрицы состоит из последовательности коэффициентов  и для 1-й и
и для 1-й и  строк
строк 

причем коэффициенты матрицы: 
Проводимости  определяются из работы [31]:
определяются из работы [31]:  где
где  — характеристические проводимости четного и нечетного типов колебаний одинаковых связанных линий.
— характеристические проводимости четного и нечетного типов колебаний одинаковых связанных линий.
Щелевая линия. Структура поля в ЩЛ имеет эллиптически поляризованные области, характерные для волны  Допущение квазипоперечной Т-волны в ней дает гораздо большие ошибки, чем для МПЛ. В результате дисперсия в
Допущение квазипоперечной Т-волны в ней дает гораздо большие ошибки, чем для МПЛ. В результате дисперсия в  выражена сильнее, чем в МПЛ, и ее волновое сопротивление зависит от частоты, особенно при больших значениях
выражена сильнее, чем в МПЛ, и ее волновое сопротивление зависит от частоты, особенно при больших значениях  Например, волновое сопротивление
Например, волновое сопротивление  -омной линии в диапазоне частот
-омной линии в диапазоне частот  увеличивается примерно на
увеличивается примерно на  Однако для расчета волнового сопротивления можно применять известную для квази Т-волны формулу
Однако для расчета волнового сопротивления можно применять известную для квази Т-волны формулу  где С — электростатическая емкость линии
где С — электростатическая емкость линии

 — скорость распространения волны в линии [22]
— скорость распространения волны в линии [22]

Тогда

где  — относительная диэлектрическая проницаемость подложки;
— относительная диэлектрическая проницаемость подложки;  — полные эллиптические интегралы 1-го и 2-го рода;
— полные эллиптические интегралы 1-го и 2-го рода;  — диэлектрическая проницаемость свободного пространства;
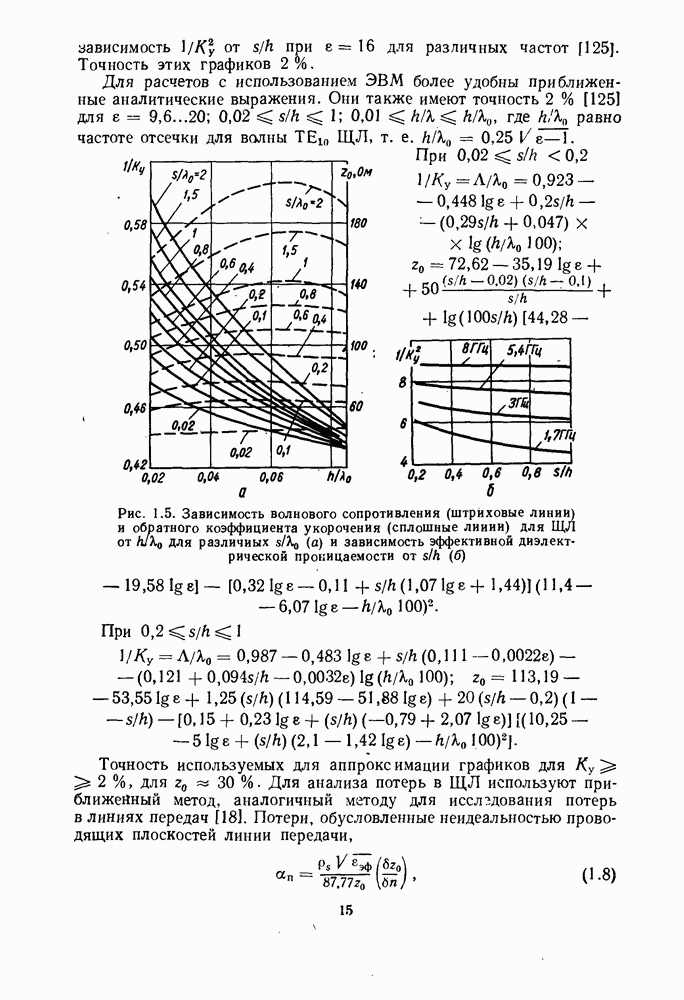
— диэлектрическая проницаемость свободного пространства;  — длина распространяющейся в линии волны. Точность этих формул около 30% [23]. На рис. 1.5, а показан график зависимости волнового сопротивления
— длина распространяющейся в линии волны. Точность этих формул около 30% [23]. На рис. 1.5, а показан график зависимости волнового сопротивления  и обратного коэффициента укорочения
и обратного коэффициента укорочения  от
от  при
при  и при различном
и при различном  а на рис. 1.5, б
а на рис. 1.5, б
зависимость  от
от  при
при  для различных частот [125]. Точность этих графиков 2%.
для различных частот [125]. Точность этих графиков 2%.
Для расчетов с использованием ЭВМ более удобны приближенные аналитические выражения. Они также имеют точность  для
для  где
где  равно частоте отсечки для волны
равно частоте отсечки для волны  т. е.
т. е. 
При 

Рис. 1.5. (см. скан) Зависимость волнового сопротивления (штриховые линии) и обратного коэффициента укорочения (сплошные линии) для  для различных
для различных  и зависимость эффективной диэлектрической проницаемости от
и зависимость эффективной диэлектрической проницаемости от 

При 

Точность используемых для аппроксимации графиков для  для
для  Для анализа потерь в ЩЛ используют приближенный метод, аналогичный методу для исследования потерь в линиях передач [18]. Потери, обусловленные неидеальностью проводящих плоскостей линии передачи,
Для анализа потерь в ЩЛ используют приближенный метод, аналогичный методу для исследования потерь в линиях передач [18]. Потери, обусловленные неидеальностью проводящих плоскостей линии передачи,

где  поверхностное сопротивление проводников;
поверхностное сопротивление проводников;  бесконечно малое приращение волнового сопротивления, обусловленное бесконечно малым равномерным уменьшением размера
бесконечно малое приращение волнового сопротивления, обусловленное бесконечно малым равномерным уменьшением размера  всех проводников в направлении, перпендикулярном к их поверхностям;
всех проводников в направлении, перпендикулярном к их поверхностям;  эффективная диэлектрическая проницаемость.
эффективная диэлектрическая проницаемость.
Учитывая приращение волнового сопротивления  и используя выражение (1.8), получаем
и используя выражение (1.8), получаем

где  и
и  — ширина щели и толщина диэлектрической подложки
— ширина щели и толщина диэлектрической подложки  .
.
С помощью соотношений (1.8) и (1.9) запишем аналитические выражения для вычисления потерь в проводниках ЩЛ:
при 

при 

При расчете потерь поверхностное сопротивление для меди  где
где  мм;
мм;  Зависимость потерь в проводниках от толщины диэлектрической подложки показана на рис. 1.6, а. Наибольшее влияние на потери оказывает ширина щели: при уменьшении ширины щели потери возрастают; величина потерь в проводниках
Зависимость потерь в проводниках от толщины диэлектрической подложки показана на рис. 1.6, а. Наибольшее влияние на потери оказывает ширина щели: при уменьшении ширины щели потери возрастают; величина потерь в проводниках  слабо зависит от толщины подложки.
слабо зависит от толщины подложки.
Для определения диэлектрических потерь в  используют понятие эффективной диэлектрической проницаемости [66, 125]. Это характерно для исследования квази Т-волны в микроэлектронных линиях с неоднородным заполнением:
используют понятие эффективной диэлектрической проницаемости [66, 125]. Это характерно для исследования квази Т-волны в микроэлектронных линиях с неоднородным заполнением:  где
где  — скорость света;
— скорость света;  — фазовая скорость волны в данной линнн. Тангенс эффективных диэлектрических потерь
— фазовая скорость волны в данной линнн. Тангенс эффективных диэлектрических потерь

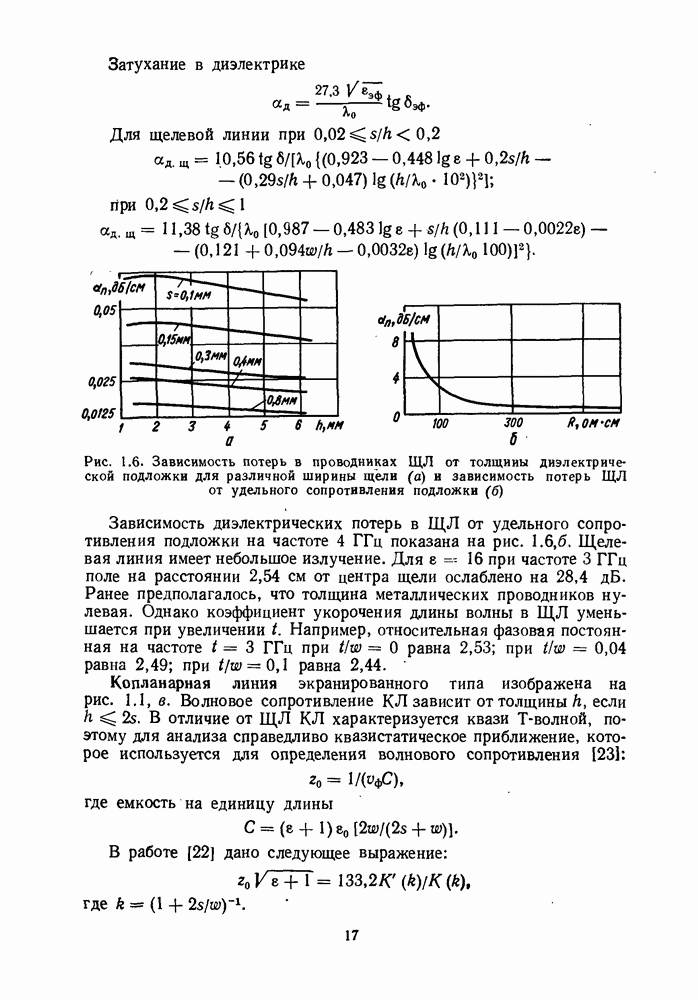
Затухание в диэлектрике

Для щелевой линии при 

при 


Рис. 1.6. Зависимость потерь в проводниках ЩЛ от толщины диэлектрической подложки для различной ширины щели (а) и зависимость потерь ЩЛ от удельного сопротивления подложки (б)
Зависимость диэлектрических потерь в ЩЛ от удельного сопротивления подложки на частоте  показана на рис. 1.6, б. Щелевая линия имеет небольшое излучение. Для
показана на рис. 1.6, б. Щелевая линия имеет небольшое излучение. Для  при частоте
при частоте  поле на расстоянии 2,54 см от центра щели ослаблено на 28,4 дБ. Ранее предполагалось, что толщина металлических проводников нулевая. Однако коэффициент укорочения длины волны в ЩЛ уменьшается при увеличении
поле на расстоянии 2,54 см от центра щели ослаблено на 28,4 дБ. Ранее предполагалось, что толщина металлических проводников нулевая. Однако коэффициент укорочения длины волны в ЩЛ уменьшается при увеличении  Например, относительная фазовая постоянная на частоте
Например, относительная фазовая постоянная на частоте  при
при  равна 2,53; при
равна 2,53; при  равна 2,49; при
равна 2,49; при  равна 2,44.
равна 2,44.
Копланарная линия экранированного типа изображена на рис. 1.1, в. Волновое сопротивление КЛ зависит от толщины  если
если  . В отличие от ЩЛ КЛ характеризуется квази Т-волной, поэтому для анализа справедливо квазистатическое приближение, которое используется для определения волнового сопротивления [231:
. В отличие от ЩЛ КЛ характеризуется квази Т-волной, поэтому для анализа справедливо квазистатическое приближение, которое используется для определения волнового сопротивления [231:

где емкость на единицу длины

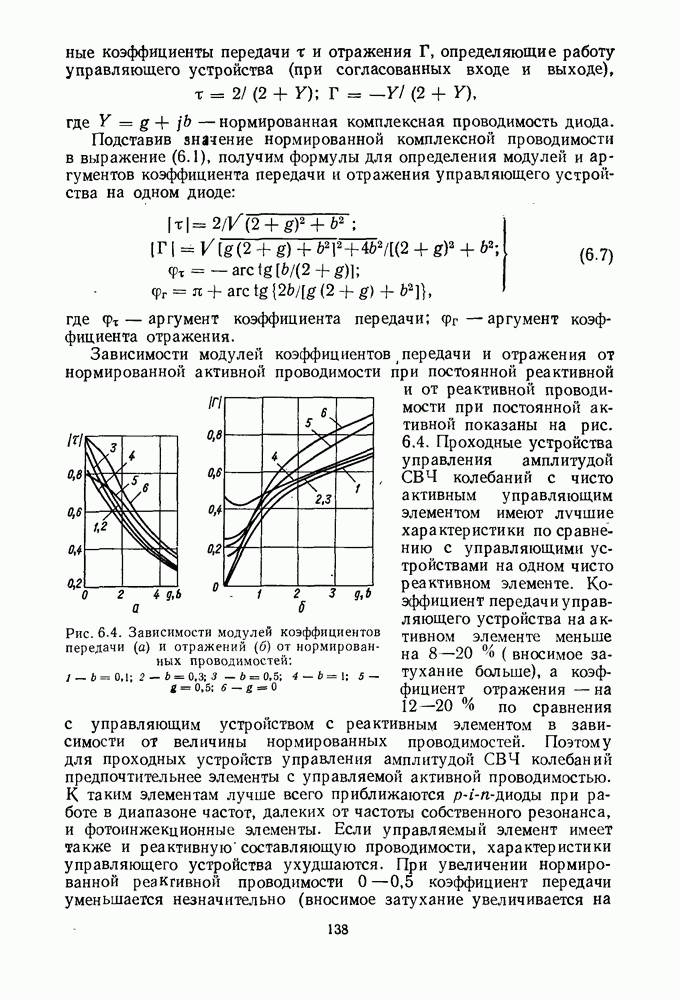
В работе [22] дано следующее выражение:

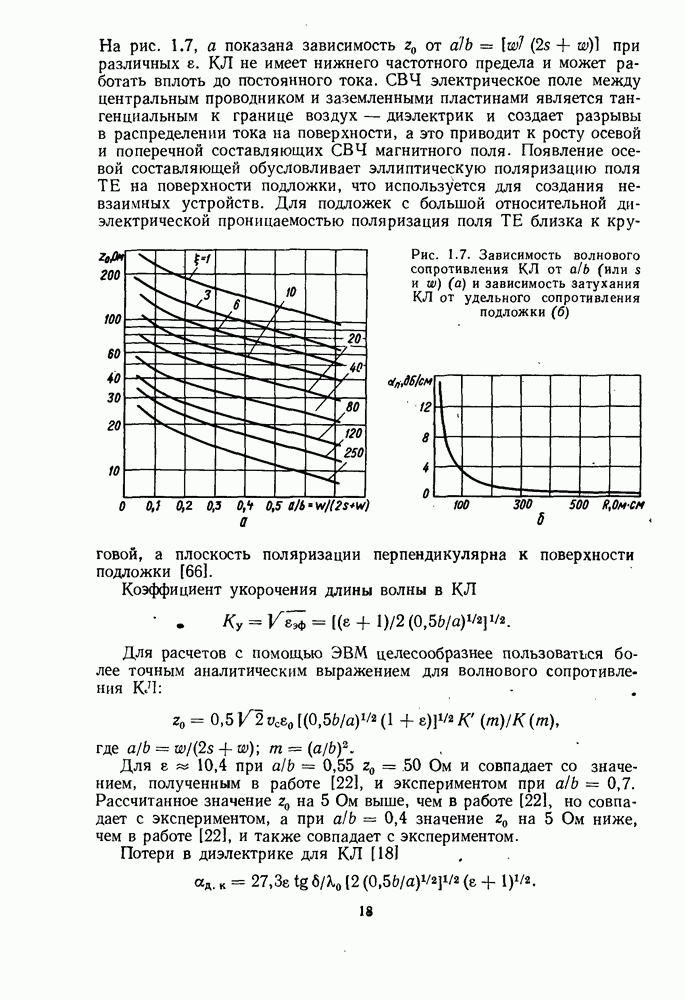
На рис. 1.7, а показана зависимость  от
от  при различных е.
при различных е.  не имеет нижнего частотного предела и может работать вплоть до постоянного тока. СВЧ электрическое поле между центральным проводником и заземленными пластинами является тангенциальным к границе воздух — диэлектрик и создает разрывы в распределении тока на поверхности, а это приводит к росту осевой и поперечной составляющих СВЧ магнитного поля. Появление осевой составляющей обусловливает эллиптическую поляризацию поля ТЕ на поверхности подложки, что используется для создания невзаимных устройств. Для подложек с большой относительной диэлектрической проницаемостью поляризация поля ТЕ близка к круговой, а плоскость поляризации перпендикулярна к поверхности подложки [66].
не имеет нижнего частотного предела и может работать вплоть до постоянного тока. СВЧ электрическое поле между центральным проводником и заземленными пластинами является тангенциальным к границе воздух — диэлектрик и создает разрывы в распределении тока на поверхности, а это приводит к росту осевой и поперечной составляющих СВЧ магнитного поля. Появление осевой составляющей обусловливает эллиптическую поляризацию поля ТЕ на поверхности подложки, что используется для создания невзаимных устройств. Для подложек с большой относительной диэлектрической проницаемостью поляризация поля ТЕ близка к круговой, а плоскость поляризации перпендикулярна к поверхности подложки [66].

Рис. 1.7. Зависимость волнового сопротивления КЛ от  (или s и w) (а) и зависимость затухания КЛ от удельного сопротивления подложки (б)
(или s и w) (а) и зависимость затухания КЛ от удельного сопротивления подложки (б)
Коэффициент укорочения длины волны в КЛ

Для расчетов с помощью ЭВМ целесообразнее пользоваться более точным аналитическим выражением для волнового сопротивления 

где 
Для  при
при  Ом и совпадает со значением, полученным в работе [22], и экспериментом при
Ом и совпадает со значением, полученным в работе [22], и экспериментом при  Рассчитанное значение
Рассчитанное значение  на 5 Ом выше, чем в работе [223, но совпадает с экспериментом, а при
на 5 Ом выше, чем в работе [223, но совпадает с экспериментом, а при  значение
значение  на 5 Ом ниже, чем в работе [22], и также совпадает с экспериментом.
на 5 Ом ниже, чем в работе [22], и также совпадает с экспериментом.
Потери в диэлектрике для КЛ [18]

Зависимость диэлектрических потерь в КЛ от удельного сопротивления подложки показана на рис. 
Высокодобротная линия (ВДЛ). Можно с достаточной для инженерной практики точностью считать, что в ВДЛ распространяется квазипоперечная Т-волна. Потери в ВДЛ (см. рис. 1.1, д) больше, чем в воздушной симметричной линии (ВСЛ) (см. рис. 1.1, ж) вследствие того, что примыкающая к полоскам область диэлектрика имеет высокую напряженность поля. Волновое сопротивление ВДЛ [23]

где  — скорость распространения волны в линии. Это выражение справедливо при ограничениях
— скорость распространения волны в линии. Это выражение справедливо при ограничениях  Коэффициент укорочения длины волны
Коэффициент укорочения длины волны  уменьшается с увеличением отношения
уменьшается с увеличением отношения  и почти не зависит от величины относительной диэлектрической проницаемости подложки
и почти не зависит от величины относительной диэлектрической проницаемости подложки 

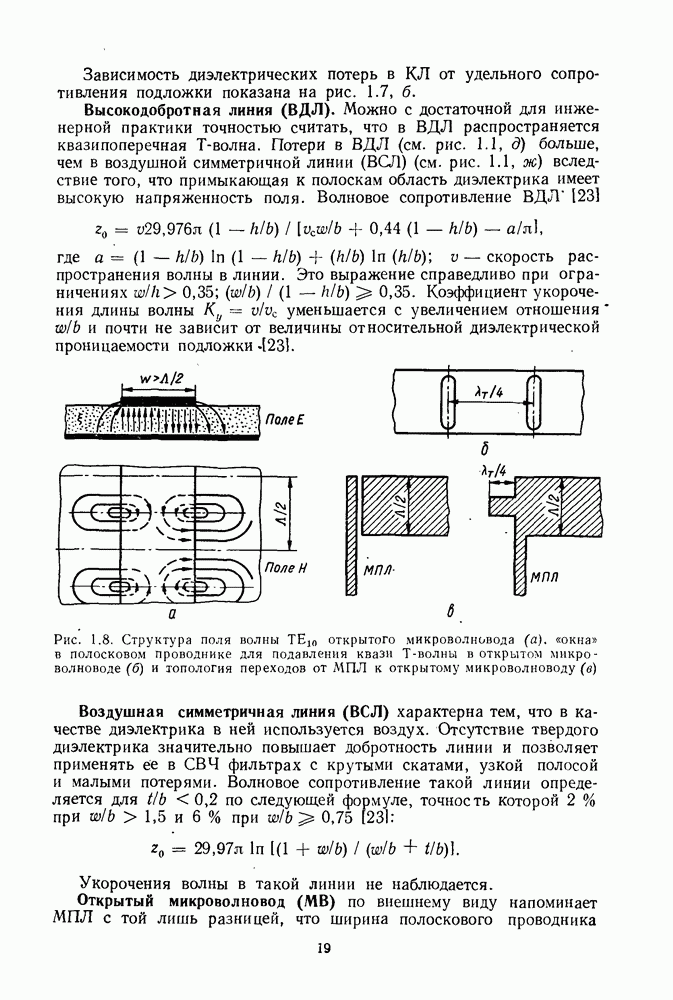
Рис. 1.8. Структура поля волны  открытого микроволновода (а), «окна» в полосковом проводнике для подавления квази Т-волны в открытом микроволноводе (б) и топология переходов от МПЛ к открытому микроволноводу (в)
открытого микроволновода (а), «окна» в полосковом проводнике для подавления квази Т-волны в открытом микроволноводе (б) и топология переходов от МПЛ к открытому микроволноводу (в)
Воздушная симметричная линия (ВСЛ) характерна тем, что в качестве диэлектрика в ней используется воздух. Отсутствие твердого диэлектрика значительно повышает добротность линии и позволяет применять ее в СВЧ фильтрах с крутыми скатами, узкой полосой и малыми потерями. Волновое сопротивление такой линии определяется для  по следующей формуле, точность которой
по следующей формуле, точность которой  при
при  при
при  [23]:
[23]:

Укорочения волны в такой линии не наблюдается.
Открытый микроволновод  по внешнему виду напоминает МПЛ с той лишь разницей, что ширина полоскового проводника
по внешнему виду напоминает МПЛ с той лишь разницей, что ширина полоскового проводника
у него должна быть больше, чем половина рабочей длины волны.  Структура поля основной волны
Структура поля основной волны  открытого микроволновода показана на рис. 1.8, а. Электрическое поле является асимметричным по отношению к продольной оси волновода, а магнитное поле — симметричным [127]. Основное поле сосредоточено в области, лежащей под полосковым проводником. Квази Т-волна также может распространяться в этой системе и для ее подавления применяют специальные конструкции, например, в виде поперечных щелей в полоске (рис. 1.8, б). Коэффициент укорочения волны в открытом микроволноводе на частоте 6 ГГц равен 2,57, а ненагруженная добротность 605. Для MB на диэлектрике с относительной диэлектрической проницаемостью в
открытого микроволновода показана на рис. 1.8, а. Электрическое поле является асимметричным по отношению к продольной оси волновода, а магнитное поле — симметричным [127]. Основное поле сосредоточено в области, лежащей под полосковым проводником. Квази Т-волна также может распространяться в этой системе и для ее подавления применяют специальные конструкции, например, в виде поперечных щелей в полоске (рис. 1.8, б). Коэффициент укорочения волны в открытом микроволноводе на частоте 6 ГГц равен 2,57, а ненагруженная добротность 605. Для MB на диэлектрике с относительной диэлектрической проницаемостью в  толщиной 1,59 мм, с шириной полоскового проводника
толщиной 1,59 мм, с шириной полоскового проводника  мм частота отсечки равна
мм частота отсечки равна  при этом длина резонаторов 38,1 мм. Вследствие больших габаритных размеров полосковых проводников MB не применяют в СВЧ диапазоне, а только в миллиметровом. На рис. 1.8, в показаны два вида переходов с микрополоски на MB, основанных на ортогональности волн
при этом длина резонаторов 38,1 мм. Вследствие больших габаритных размеров полосковых проводников MB не применяют в СВЧ диапазоне, а только в миллиметровом. На рис. 1.8, в показаны два вида переходов с микрополоски на MB, основанных на ортогональности волн  и Т.
и Т.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Главв 1. РАСЧЕТ ЭЛЕМЕНТОВ ГИБРИДНЫХ ИНТЕГРАЛЬНЫХ СХЕМ
- 1. ПОНЯТИЕ ГИБРИДНОЙ ИНТЕГРАЛЬНОЙ СХЕМЫ СВЧ
- 2. ОСНОВНЫЕ ЛИНИИ ПЕРЕДАЧ ГИС СВЧ
- 3. РАСЧЕТ ПАРАМЕТРОВ ЛИНИЙ
- Главв 2. УСТРОЙСТВА ДЕЛЕНИЯ (СУММИРОВАНИЯ) МОЩНОСТИ СВЧ
- 1. ПРИМЕНЕНИЕ ДЕЛИТЕЛЕЙ (СУММАТОРОВ) МОЩНОСТИ
- 2. ЭЛЕМЕНТЫ МНОГОКАНАЛЬНЫХ ДЕЛИТЕЛЕЙ
- 3. МНОГОКАНАЛЬНЫЕ ДЕЛИТЕЛИ. АЛГОРИТМЫ РАСЧЕТА МНОГОКАНАЛЬНЫХ ДЕЛИТЕЛЕЙ
- 4. ЧЕТЫРЕХКАНАЛЬНЫЕ ДЕЛИТЕЛИ МОЩНОСТИ
- 5. ДЕЛИТЕЛИ МОЩНОСТИ НА 64 КАНАЛА
- 6. ХАРАКТЕРИСТИКИ ДЕЛИТЕЛЕЙ, ВЫПОЛНЕННЫХ ИЗ МОСТОВЫХ УСТРОЙСТВ
- 7. РЕКОМЕНДАЦИИ ДЛЯ ПРОЕКТИРОВАНИЯ ДЕЛИТЕЛЕЙ (СУММАТОРОВ) МОЩНОСТИ
- Глава 3. ИЗБИРАТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ОСНОВНЫЕ ТРЕБОВАНИЯ К ИЗБИРАТЕЛЬНЫМ УСТРОЙСТВАМ И ИХ ПАРАМЕТРЫ
- 2. АППРОКСИМАЦИЯ ФУНКЦИЙ РАБОЧЕГО ЗАТУХАНИЯ
- 3. РАСЧЕТ ТОПОЛОГИЙ ФИЛЬТРОВ
- 4. АНАЛИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
- Глава 4. СМЕСИТЕЛИ
- 1. ПАРАМЕТРЫ СМЕСИТЕЛЕЙ И ОСНОВНЫЕ ТРЕБОВАНИЯ К НИМ
- 2. ВЫБОР АКТИВНЫХ ЭЛЕМЕНТОВ
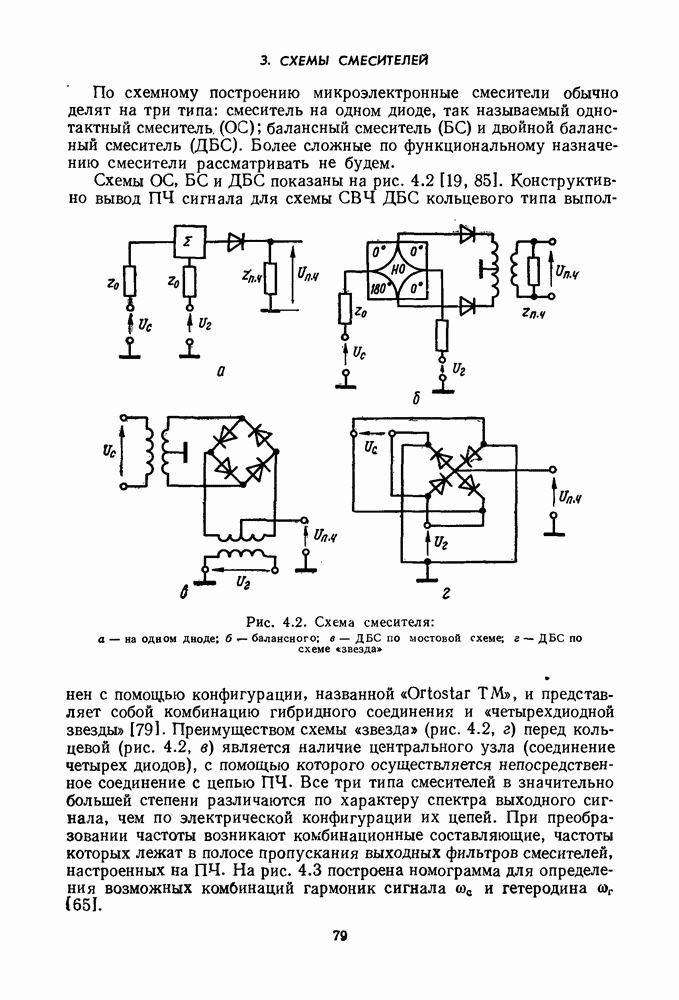
- 3. СХЕМЫ СМЕСИТЕЛЕЙ
- 4. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СМЕСИТЕЛЕЙ
- 5. СМЕСИТЕЛИ НА КОМБИНАЦИЯХ ЛИНИЙ ПЕРЕДАЧ
- 6. РЕЗУЛЬТАТЫ РАСЧЕТОВ И ЭКСПЕРИМЕНТОВ
- Глава 5. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ТРЕБОВАНИЯ К МАЛОШУМЯЩИМ УСИЛИТЕЛЯМ СВЧ И ИХ ПАРАМЕТРЫ
- 2. УСИЛИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 3. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ТРАНЗИСТОРА
- 4. РАСЧЕТ УСИЛИТЕЛЕЙ
- 5. ИСПОЛЬЗОВАНИЕ ЭВМ ПРИ ПРОЕКТИРОВАНИИ УСИЛИТЕЛЕЙ
- 6. ТОПОЛОГИЧЕСКИЕ СХЕМЫ МИКРОЭЛЕКТРОННЫХ СВЧ УСИЛИТЕЛЕЙ
- 7. МНОГОКАСКАДНЫЕ УСИЛИТЕЛИ
- 8. ВЛИЯНИЕ ВНЕШНИХ ФАКТОРОВ НА РАБОТУ УСИЛИТЕЛЕЙ С ПТ
- Глава 6. УСТРОЙСТВА, УПРАВЛЯЮЩИЕ МОЩНОСТЬЮ
- 2. УПРАВЛЯЮЩИЕ ЭЛЕМЕНТЫ
- 3. МАТЕМАТИЧЕСКИЙ АППАРАТ ДЛЯ РАСЧЕТА УСТРОЙСТВ НА СОСРЕДОТОЧЕННЫХ ЭЛЕМЕНТАХ
- 4. УСТРОЙСТВА НА СОСРЕДОТОЧЕННЫХ УПРАВЛЯЮЩИХ ЭЛЕМЕНТАХ
- 5. УСТРОЙСТВА НА ЭЛЕМЕНТАХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- Глава 7. ФАЗОВРАЩАТЕЛИ
- 1. ПАРАМЕТРЫ ПОЛУПРОВОДНИКОВЫХ ФАЗОВРАЩАТЕЛЕЙ
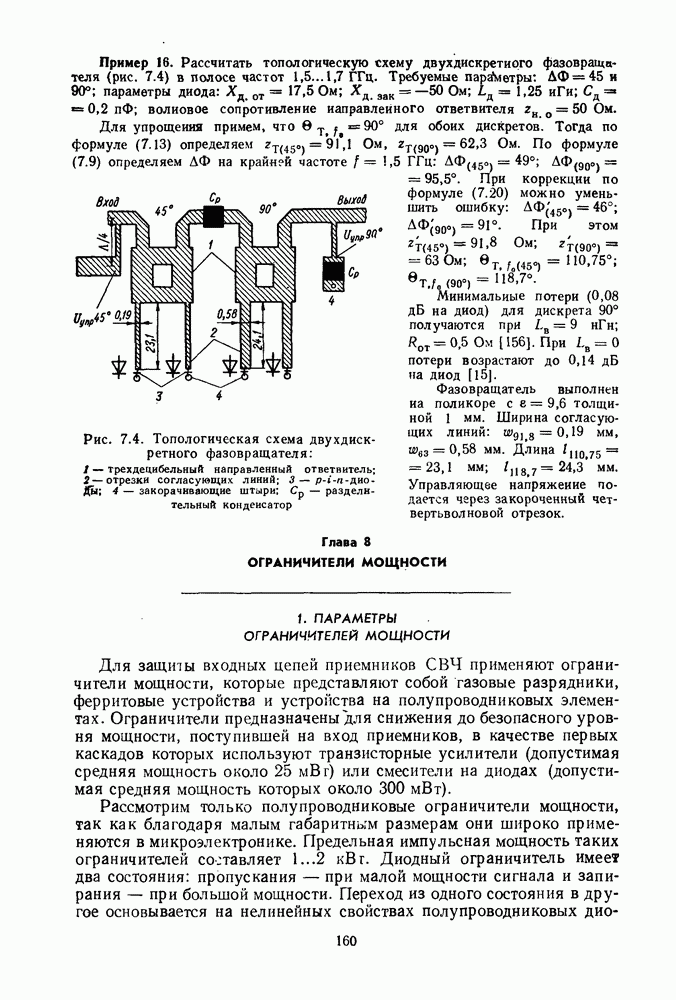
- 2. СХЕМЫ ФАЗОВРАЩАТЕЛЕЙ И АНАЛИЗ ХАРАКТЕРИСТИК ФАЗОВРАЩАТЕЛЯ С НАПРАВЛЕННЫМ ОТВЕТВИТЕЛЕМ
- Глава 8. ОГРАНИЧИТЕЛИ МОЩНОСТИ
- 1. ПАРАМЕТРЫ ОГРАНИЧИТЕЛЕЙ МОЩНОСТИ
- 2. ОГРАНИЧИТЕЛЬНЫЕ ДИОДЫ
- 3. СХЕМЫ ОГРАНИЧИТЕЛЕЙ МОЩНОСТИ И ИХ РАСЧЕТ
- СПИСОК ЛИТЕРАТУРЫ