| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 6.4. Формула Ньютона – Лейбница
Эта формула имеет вид
 (1)
(1)
Здесь ![]() - непрерывная на отрезке
- непрерывная на отрезке ![]() функция, а
функция, а ![]() - какая-либо ее
первообразная на этом отрезке.
- какая-либо ее
первообразная на этом отрезке.
Формула Ньютона – Лейбница была
уже доказана в § 6.1. Там предполагалось известным, что непрерывная на ![]() функция
функция ![]() интегрируема и
имеет первообразную на
интегрируема и
имеет первообразную на ![]() .
.
Теперь мы уже знаем из § 6.3, что
интегрируемость непрерывной на ![]() функции влечет за собой существование
у нее первообразной на
функции влечет за собой существование
у нее первообразной на ![]() .
.
Приведем другое доказательство формулы Ньютона – Лейбница. Вернемся к функции
 .
(2)
.
(2)
Заметим, что
 . (3)
. (3)
Кроме того, мы знаем, что ![]() есть первообразная
для
есть первообразная
для ![]() на
на ![]() . Поэтому, если
. Поэтому, если ![]() есть какая-либо,
вообще другая, первообразная, то существует константа
есть какая-либо,
вообще другая, первообразная, то существует константа ![]() такая, что
такая, что
![]() . (4)
. (4)
Из (2), (3), (4) получим
 ,
,
и мы доказали формулу (1).
П р и м е р 1. 
 .
.
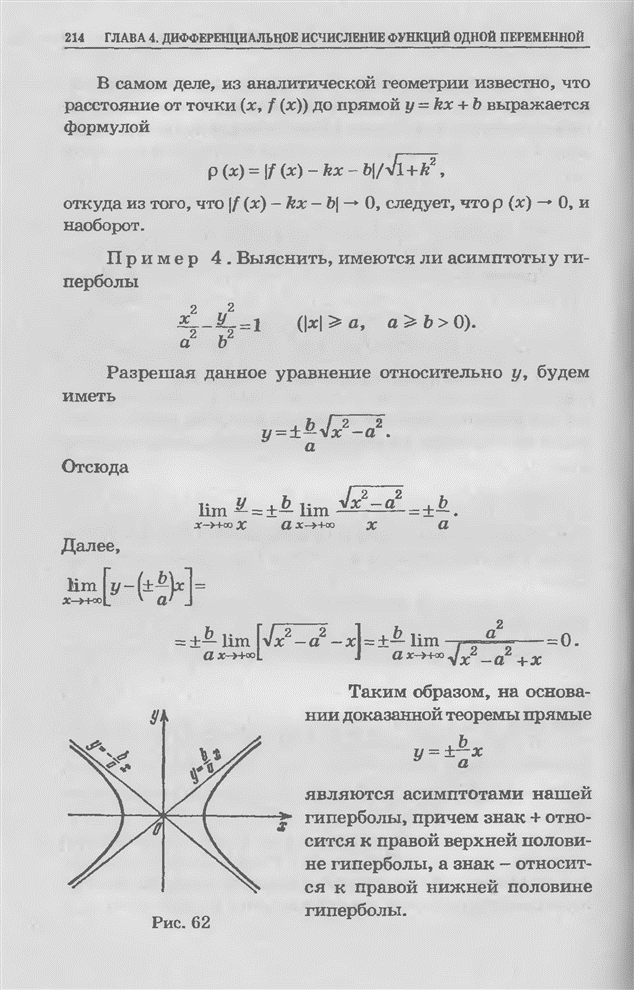
Это показывает, что площадь
(рис. 78) заштрихованной фигуры, лежащей под параболой ![]() , равна
, равна ![]() .
.
П р и м е р 2.
 .
.
Таким образом, площадь фигуры
(рис. 79), ограниченной сверху синусоидой ![]() и снизу – осью
и снизу – осью ![]() , равна 2.
, равна 2.

Рис. 78 Рис. 79
П р и м е р 3. Функция

непрерывна на отрезке ![]() , за исключением
точки
, за исключением
точки ![]() .
Отрезок
.
Отрезок ![]() можно
разрезать на два отрезка
можно
разрезать на два отрезка ![]() ,
, ![]() , где она монотонна, следовательно,
интегрируема. Поэтому
, где она монотонна, следовательно,
интегрируема. Поэтому ![]() интегрируема на
интегрируема на ![]() . Справедлива формула
. Справедлива формула
 . (5)
. (5)
В самом деле, на полуинтервале ![]() функция
функция ![]() непрерывна:
непрерывна: ![]() . Ее первообразная
на этом полуинтервале равна
. Ее первообразная
на этом полуинтервале равна ![]() . Поэтому, применяя формулу Ньютона –
Лейбница, получим
. Поэтому, применяя формулу Ньютона –
Лейбница, получим
 . (6)
. (6)
В силу теоремы 1 ![]() непрерывна, в частности, в точке
непрерывна, в частности, в точке ![]() , поэтому
, поэтому
![]() .
(7)
.
(7)
Для ![]()
 . (8)
. (8)
Из (6), (7), (8) следует (5).
Более элегантная формула получится, если интегрировать от
точки ![]() :
:
 . (9)
. (9)
Под интегралом в (9) стоит
разрывная в точке ![]() ограниченная
функция, интеграл как функция верхнего предела
ограниченная
функция, интеграл как функция верхнего предела ![]() , есть непрерывная функция, в том числе
и в точке
, есть непрерывная функция, в том числе
и в точке ![]() ,
что согласуется с теоремой 1 § 6.3. Однако производная
,
что согласуется с теоремой 1 § 6.3. Однако производная ![]() не существует, и это не
противоречит теореме 2 § 6.3, которая гарантирует существование производной
не существует, и это не
противоречит теореме 2 § 6.3, которая гарантирует существование производной ![]() , только если
, только если ![]() непрерывна в точке
непрерывна в точке ![]() .
.
Т е о р е м а 1 (о замене переменной). Имеет место равенство
 , (10)
, (10)
где функция ![]() непрерывно
дифференцируема на
непрерывно
дифференцируема на ![]() ,
, ![]() и
и ![]() непрерывна на
непрерывна на ![]() - образе отрезка
- образе отрезка ![]() при помощи функции
при помощи функции ![]() .
.
Д о к а з а т е л ь с т в о.
Пусть ![]() и
и ![]() - первообразные
функции соответственно
- первообразные
функции соответственно ![]() и
и ![]() . Тогда (см. § 5.2, (1) и ниже)
справедливо тождество
. Тогда (см. § 5.2, (1) и ниже)
справедливо тождество ![]() ,
, ![]() , где
, где ![]() - некоторая постоянная. Поэтому
- некоторая постоянная. Поэтому
![]() (11)
(11)
Но на основании формулы Ньютона – Лейбница левая часть (11) равна левой части (10), а правая часть (11) – правой части (10), а это доказывает формулу (10).
П р и м е р 4.

 .
.
З а м е ч а н и е. Верхний предел
интегрирования по ![]() можно
взять равным
можно
взять равным ![]() ,
а результат будет тот же, и это согласуется с теоремой 1.
,
а результат будет тот же, и это согласуется с теоремой 1.
П р и м е р 5.
 ,
,
потому что в полученном интеграле нижний предел равен верхнему.
П р и м е р 6. Если ![]() - четная функция
- четная функция ![]() , то
, то
 ,
,
потому, что
 .
.
П р и м е р 7. Если ![]() - нечетная функция
- нечетная функция ![]() , то
, то
 .
.
П р и м е р 8. Если ![]() - периодическая функция периода
- периодическая функция периода ![]() , то
, то

потому, что
 ,
,
и, следовательно,
 .
.
П р и м е р 9.

 .
.
П р и м е р 10. Решим пример 5, используя примеры 8, 7:
 ,
,
так как функция ![]() нечетная.
нечетная.
Т е о р е м а 2. Справедлива формула интегрирования по частям для определенного интеграла:
 ,
(12)
,
(12)
где ![]() и
и ![]() - непрерывно
дифференцируемые на
- непрерывно
дифференцируемые на ![]() функции.
функции.
Д о к а з а т е л ь с т в о.
Произведение ![]() имеет
на
имеет
на ![]() непрерывную
производную
непрерывную
производную
![]() .
.
Поэтому по теореме Ньютона – Лейбница

 ,
,
откуда следует (12).
П р и м е р (11).


Т е о р е м а 3 (о среднем для
определенного интеграла). Для непрерывной на отрезке ![]() функции
функции ![]() существует точка
существует точка ![]() такая, что
такая, что
 .
(13)
.
(13)
Д о к а з а т е л ь с т в о. Так
как ![]() непрерывна,
то для нее существует первообразная
непрерывна,
то для нее существует первообразная ![]() , поэтому
, поэтому
 . (14)
. (14)
Первое равенство в (14) есть
формула Ньютона-Лейбница для непрерывной на ![]() функции
функции ![]() . Второе равенство есть формула
Лагранжа для
. Второе равенство есть формула
Лагранжа для ![]() .
Наконец третье следует из того, что
.
Наконец третье следует из того, что ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- § 1.1. Предмет математики. Переменные и постоянные величины, множества
- § 1.2. Операции над множествами
- § 1.3. Символика математической логики
- § 1.4. Действительные числа
- § 1.5. Определение равенства и неравенства
- § 1.6. Определение арифметических действий
- 1.6.1. Общие соображения
- 1.6.2. Стабилизирующиеся последовательности
- 1.6.3. Определение арифметических действий
- § 1.7. Основные свойства действительных чисел
- § 1.8. Аксиоматический подход к понятию действительного числа
- § 1.9. Неравенства для абсолютных величин
- § 1.10. Отрезок, интервал, ограниченное множество
- § 1.11. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел
- Глава 2. Предел последовательности
- § 2.1. Понятие предела последовательности
- § 2.2. Арифметические действия с переменными, имеющими предел
- § 2.3. Бесконечно малая и бесконечно большая величины
- § 2.4. Неопределенные выражения
- § 2.5. Монотонные последовательности
- § 2.6. Число e
- § 2.7. Принцип вложенных отрезков
- § 2.8. Точные верхняя и нижняя грани множества
- § 2.9. Теорема Больцано-Вейерштрасса
- § 2.10. Верхний и нижний пределы
- § 2.11. Условие Коши сходимости последовательности
- § 2.12. Полнота и непрерывность множества действительных чисел
- Глава 3. Функция. Предел функции
- § 3.1. Функция
- 3.1.1. Функция от одной переменной.
- 3.1.2. Функции многих переменных.
- 3.1.3. Полярная система координат
- § 3.2. Предел функции
- § 3.3. Непрерывность функции
- § 3.4. Разрывы первого и второго рода
- § 3.5. Функции, непрерывные на отрезке
- § 3.6. Обратная непрерывная функция
- § 3.7. Равномерная непрерывность функции
- § 3.8. Элементарные функции
- § 3.9. Замечательные пределы
- § 3.10. Порядок переменной. Эквивалентность
- Глава 4. Дифференциальное исчисление функций одной переменной
- § 4.1. Производная
- § 4.2. Геометрический смысл производной
- § 4.3. Производные элементарных функций
- § 4.4. Производная сложной функции
- § 4.5. Производная обратной функции
- § 4.6. Производные элементарных функций (продолжение)
- § 4.7. Дифференциал функции
- 4.7.1. Дифференцируемые функции
- 4.7.2. Дифференциал функции
- 4.7.3. Приближенное выражение приращения функции
- § 4.8. Другое определение касательной
- § 4.9. Производная высшего порядка
- § 4.10. Дифференциал высшего порядка. Инвариантное свойство дифференциала первого порядка
- § 4.11 Дифференцирование параметрически заданных функций
- § 4.12. Теоремы о среднем значении
- § 4.13. Раскрытие неопределенностей
- § 4.14. Формула Тейлора
- § 4.15. Ряд Тейлора
- § 4.16. Формулы и ряды Тейлора элементарных функций
- § 4.17. Локальный экстремум функции
- § 4.18. Экстремальные значения функции на отрезке
- § 4.19. Выпуклость кривой. Точка перегиба
- § 4.20. Асимптота графика функции
- § 4.21. Непрерывная и гладкая кривая
- § 4.22. Схема построения графика функции
- § 4.23. Вектор-функция. Векторы касательной и нормали
- Глава 5. неопределенные интегралы
- § 5.1. Неопределенный интеграл. Таблица интегралов
- § 5.2. Методы интегрирования
- § 5.3. Комплексные числа
- § 5.4. Теория многочлена n-й степени
- § 5.5. Действительный многочлен n-й степени
- § 5.6. Интегрирование рациональных выражений
- § 5.7. Интегрирование иррациональных функций
- Глава 6. Определенный Интеграл
- § 6.1. Задачи, приводящие к понятию определенного интеграла, и его определение
- § 6.2. Свойства определенных интегралов
- § 6.3. Интеграл как функция верхнего предела
- § 6.4. Формула Ньютона – Лейбница
- § 6.5. Остаток формулы Тейлора в интегральной форме
- § 6.6. Суммы Дарбу. Условия существования интеграла
- § 6.7. Интегрируемость непрерывных и монотонных функций
- § 6.8. Несобственные интегралы
- § 6.9. Несобственные интегралы от неотрицательных функций
- § 6.10. Интегрирование по частям несобственных интегралов
- § 6.11. Несобственный интеграл с особенностями в нескольких точках
- Глава 7. Приложения интегралов. Приближенные методы
- § 7.1. Площадь в полярных координатах
- § 7.2. Объем тела вращения
- § 7.3. Гладкая кривая в пространстве. Длина дуги
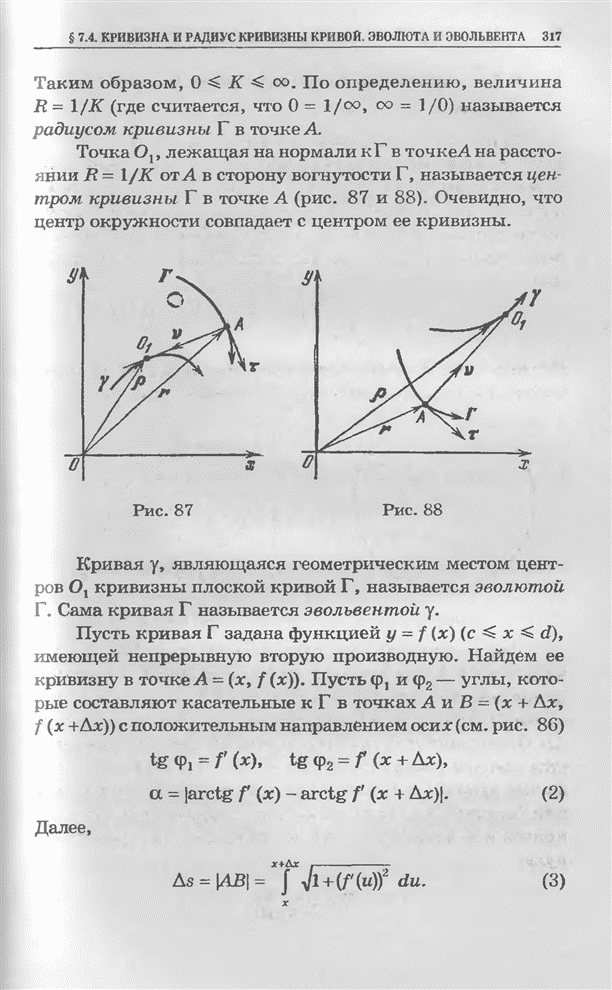
- § 7.4. Кривизна и радиус кривизны кривой. Эволюта и эвольвента
- § 7.5. Площадь поверхности вращения
- § 7.6. Интерполяционная формула Лагранжа
- § 7.7. Квадратурные формулы прямоугольников и трапеций
- § 7.8. Формула Симпсона
- Глава 8. Дифференциальное исчисление функций многих переменных
- § 8.1. Предварительные сведения
- § 8.2. Предел функции
- § 8.3. Непрерывная функция
- § 8.4. Частные производные и производная по направлению
- § 8.5. Дифференцируемые функции
- § 8.6. Применение дифференциала в приближенных вычислениях
- § 8.7. Касательная плоскость. Геометрический смысл дифференциала
- § 8.8. Производная сложной функции. Производная по направлению. Градиент
- 8.8.1. Производная сложной функции
- 8.8.2. Производная по направлению
- 8.8.3. Градиент функции
- 8.8.4. Однородные функции
- § 8.9. Дифференциал функции. Дифференциал высшего порядка
- § 8.10. Формула Тейлора
- § 8.11. Замкнутое множество
- § 8.12. Непрерывная функция на замкнутом ограниченном множестве
- § 8.13. Экстремумы
- § 8.14. Нахождение наибольших и наименьших значений функции
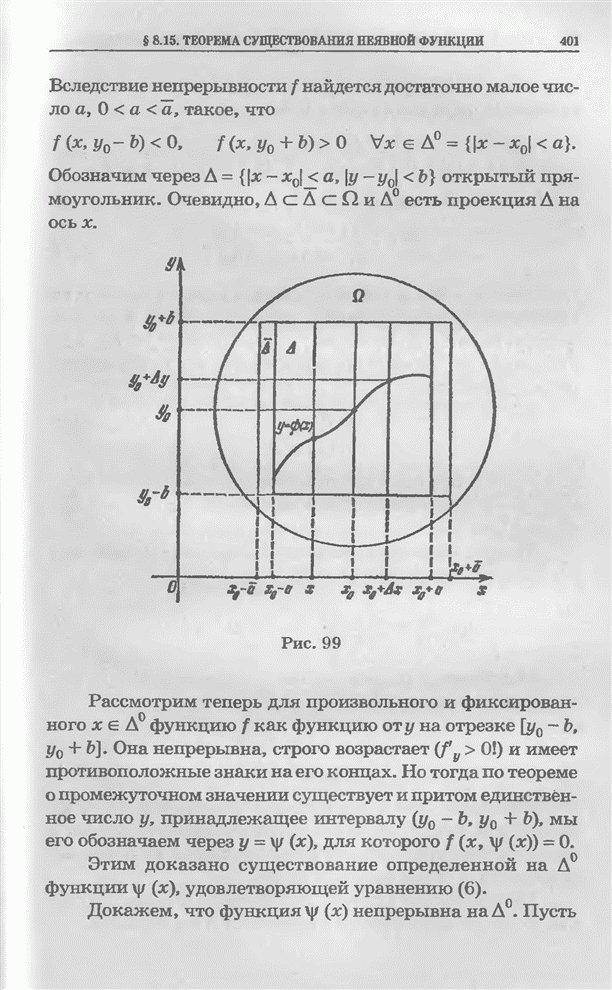
- § 8.15. Теорема существования неявной функции
- § 8.16. Касательная плоскость и нормаль
- § 8.17. Системы функций, заданных неявно
- § 8.18. Отображения
- § 8.19. Условный (относительный) экстремум
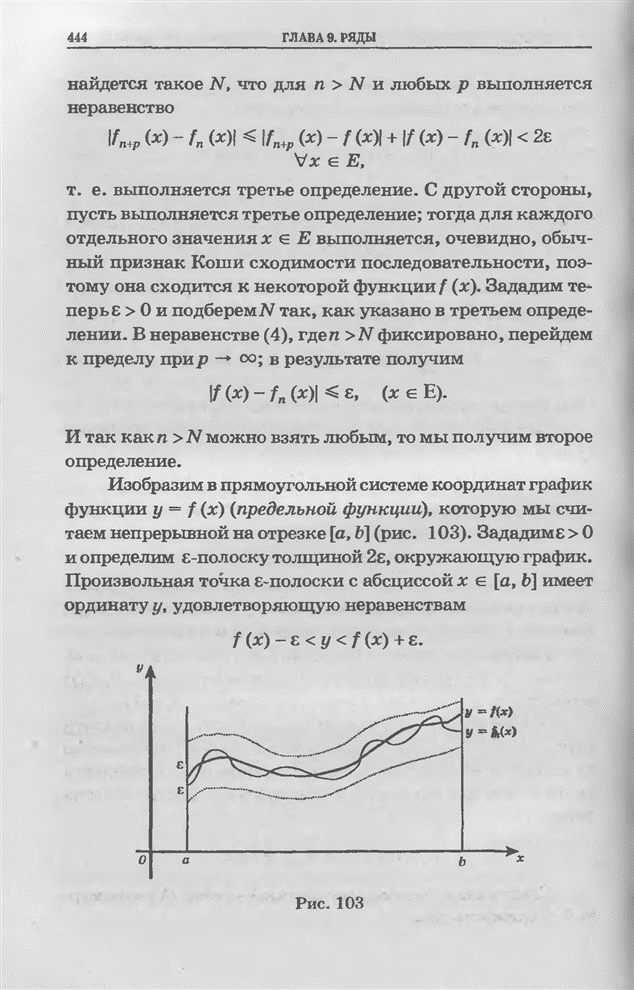
- Глава 9. Ряды
- § 9.1. Понятие ряда
- § 9.2. Несобственный интеграл и ряд
- § 9.3. Действия с рядами
- § 9.4. Ряды с неотрицательными членами
- § 9.5. Ряд Лейбница
- § 9.6. Абсолютно сходящиеся ряды
- § 9.7. Условно сходящиеся ряды с действительными членами
- § 9.8. Последовательности и ряды функций. Равномерная сходимость
- § 9.9. Интегрирование и дифференцирование равномерно сходящихся рядов
- § 9.10. Перемножение абсолютно сходящихся рядов
- § 9.11. Степенные ряды
- § 9.12. Дифференцирование и интегрирование степенных рядов
- § 9.13. Функции exp(z), sinz, cosz от комплексного переменного
- § 9.14. Ряды в приближенных вычислениях
- § 9.15. Понятие кратного ряда
- § 9.16. Суммирование рядов и последовательностей