| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
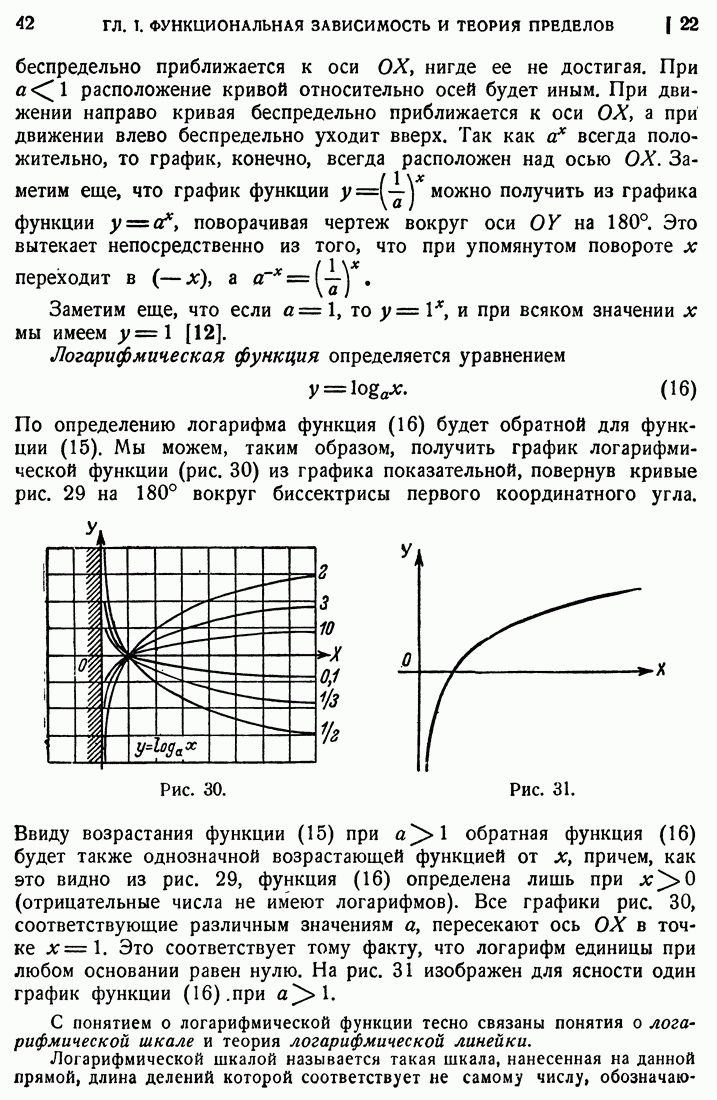
107. Определение центров тяжести. Теоремы Гульдина.
Если дана система  материальных точек
материальных точек

массы которых равны, соответственно,

то центром тяжести системы Q называется точка, координаты которой  удовлетворяют условиям
удовлетворяют условиям

где М означает полную массу системы

При определении центра тяжести можно каким угодно образом группировать точки системы, разбивая их на частные системы с тем, чтобы при вычислении координат центра тяжести Q всей системы заменять всю группу точек, вошедших в какую угодно частную систему, одной точкой, а именно ее центром тяжести, приписав ей массу, равную сумме масс вошедших в нее точек.
Мы не будем останавливаться на доказательстве этого общего принципа, которое не представляет труда и легко может быть проверено на простейших частных случаях системы с тремя, четырьмя и т. д. точками.

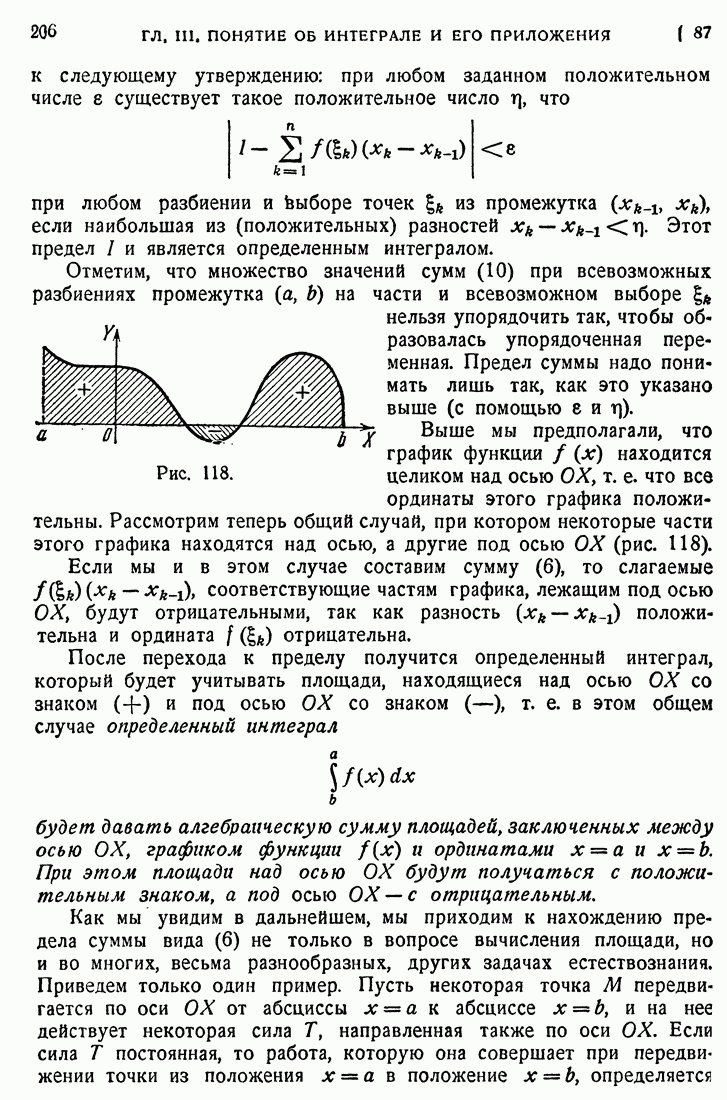
Рис. 142.
В дальнейшем мы будем иметь дело не с системами точек, а с тем случаем, когда масса заполняет сплошь некоторую плоскую фигуру (область) или линию.
Для простоты ограничимся рассмотрением лишь однородных тел, плотность которых примем за единицу, так что масса такой фигуры будет равняться ее длине, если она имеет вид линии, и площади, если она имеет вид плоской области.
Пусть сперва нужно определить центр тяжести дуги кривой АВ (рис. 142), длина которой s. Следуя предыдущему общему принципу, разобьем дугу АВ на  малых элементов
малых элементов  . Центр тяжести всей системы можно вычислить, заменив каждый из этих элементов одной точкой, центром тяжести рассматриваемого элемента, сосредоточив в ней всю массу элемента
. Центр тяжести всей системы можно вычислить, заменив каждый из этих элементов одной точкой, центром тяжести рассматриваемого элемента, сосредоточив в ней всю массу элемента 
Рассмотрим один из таких элементов  и обозначим координаты его концов через
и обозначим координаты его концов через  координаты же его центра тяжести обозначим через (х, у). При достаточном уменьшении элемента
координаты же его центра тяжести обозначим через (х, у). При достаточном уменьшении элемента  можем считать, что точка
можем считать, что точка  сколь угодно мало отстоит от точки
сколь угодно мало отстоит от точки 
По формулам (31) имеем, как и в [104],

откуда, вычислив s по формуле

и определим координаты центра тяжести О.
Из формул (32) и (33) вытекает важная теорема:
Теорема 1 Гульдина. Площадь поверхности, полученной при вращении дуги данной плоской кривой вокруг некоторой оси, лежащей в ее плоскости и не пересекающей ее, равняется произведению длины вращающейся дуги на длину пути, описанного при этом вращении центром тяжести дуги.

Рис. 143.
В самом деле, приняв ось вращения за ось ОХ, для поверхности F тела, описанного при вращении дуги АВ, имеем (27) [106]

[в силу (33)], что и требовалось доказать.
Рассмотрим теперь некоторую плоскую область S (площадь которой обозначим также через S). Допустим для простоты, что эта область (рис. 143) ограничена двумя кривыми, ординаты которых обозначим через

Следуя общему принципу, указанному в начале этого номера, разобьем фигуру на  вертикальных полосок
вертикальных полосок  прямыми, параллельными оси OY. При вычислении координат центра тяжести О фигуры мы можем заменить каждую такую полоску ее центром тяжести, сосредоточив в нем массу полосок
прямыми, параллельными оси OY. При вычислении координат центра тяжести О фигуры мы можем заменить каждую такую полоску ее центром тяжести, сосредоточив в нем массу полосок  Рассмотрим одну из таких полосок; обозначим через
Рассмотрим одну из таких полосок; обозначим через  абсциссы ограничивающих ее прямых и
абсциссы ограничивающих ее прямых и  через х, у — координаты центра тяжести.
через х, у — координаты центра тяжести.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- ГЛАВА I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
- 1. Величина и ее измерение.
- 2. Число.
- 3. Величины постоянные и переменные.
- 4. Промежуток.
- 5. Понятие о функции.
- 6. Аналитический способ задания функциональной зависимости.
- 7. Неявные функции.
- 8. Табличный способ.
- 9. Графический способ изображения чисел.
- 10. Координаты.
- 11. График и уравнение кривой.
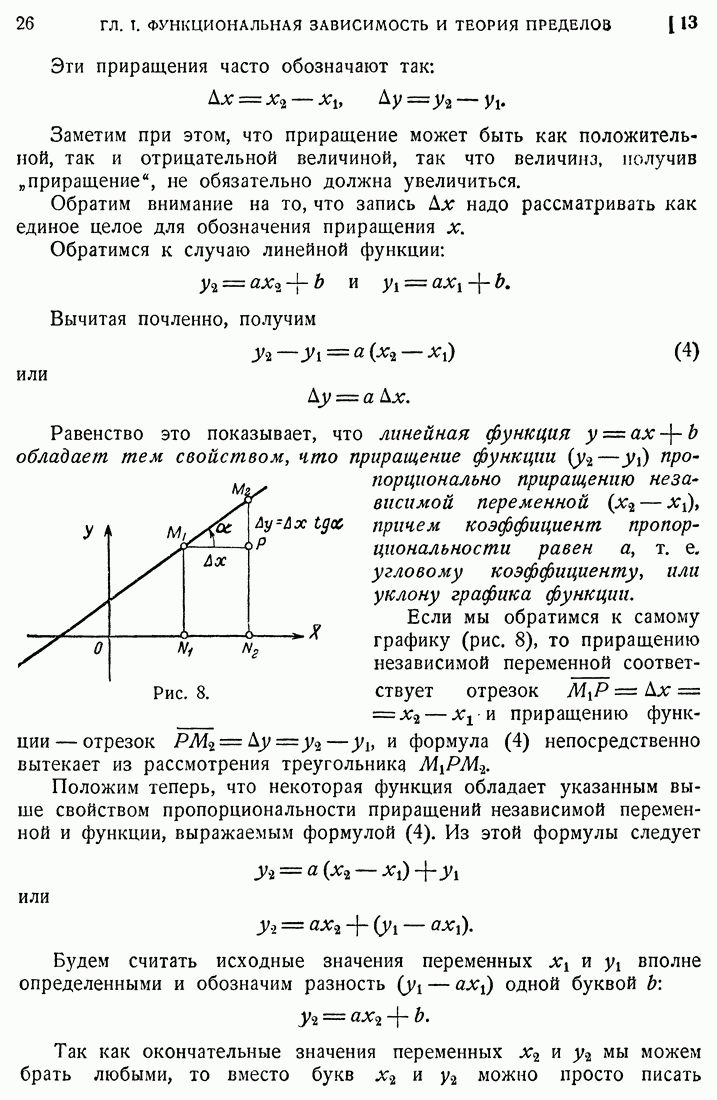
- 12. Линейная функция.
- 13. Приращение. Основное свойство линейной функции.
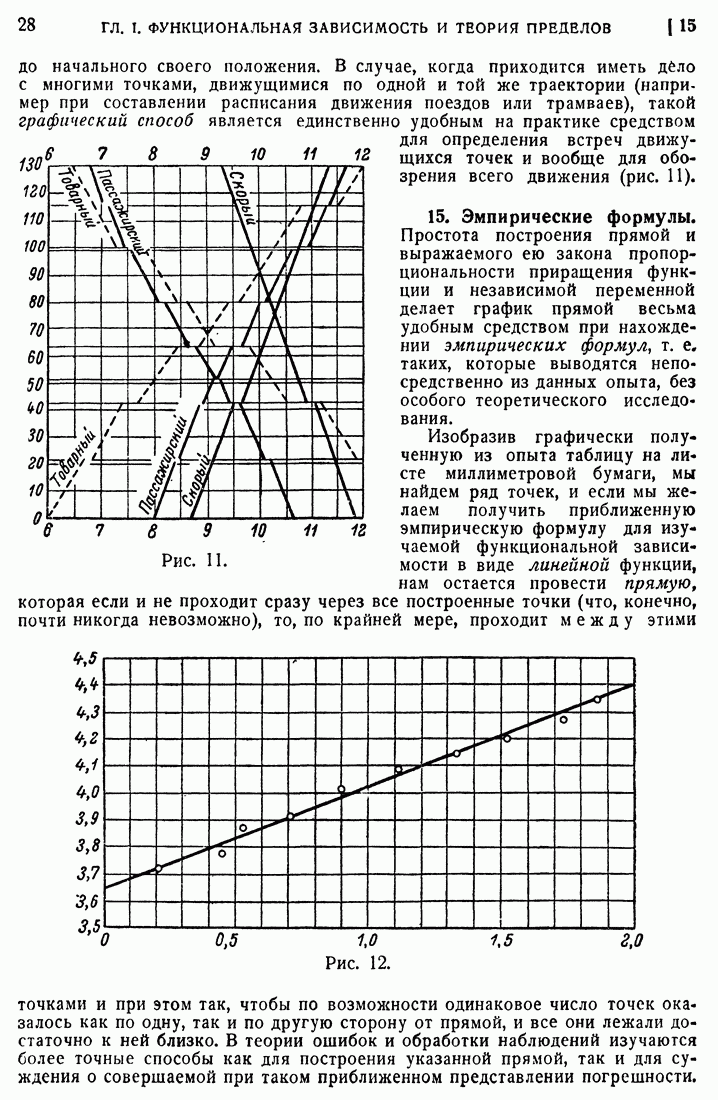
- 14. График равномерного движения.
- 15. Эмпирические формулы.
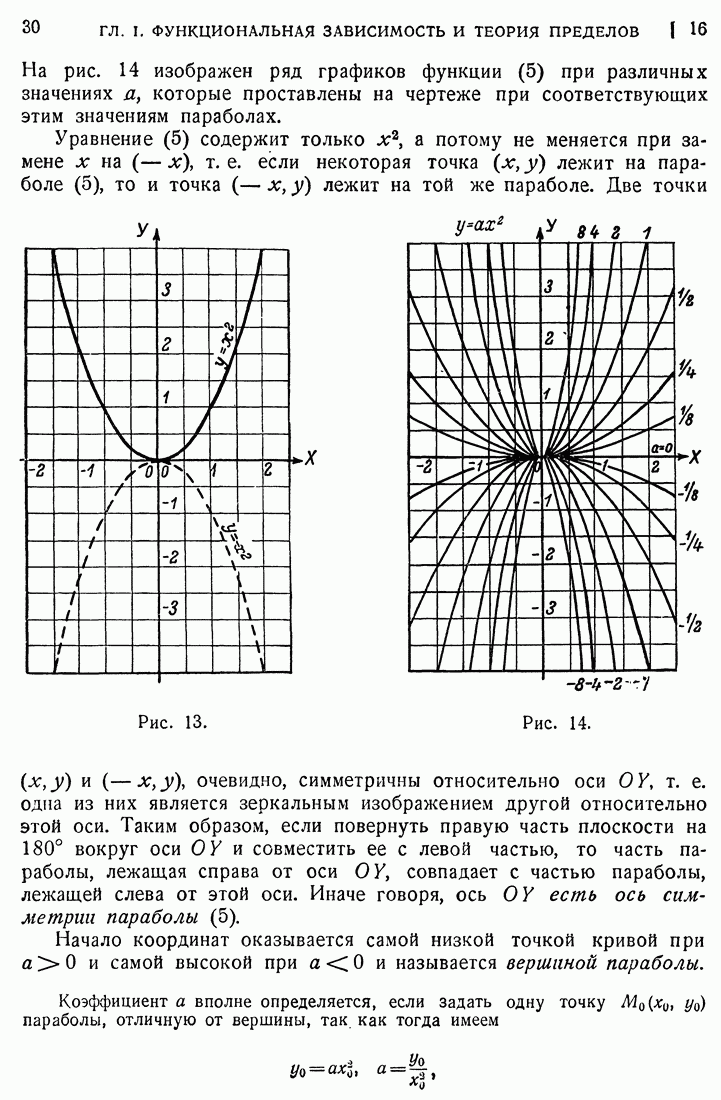
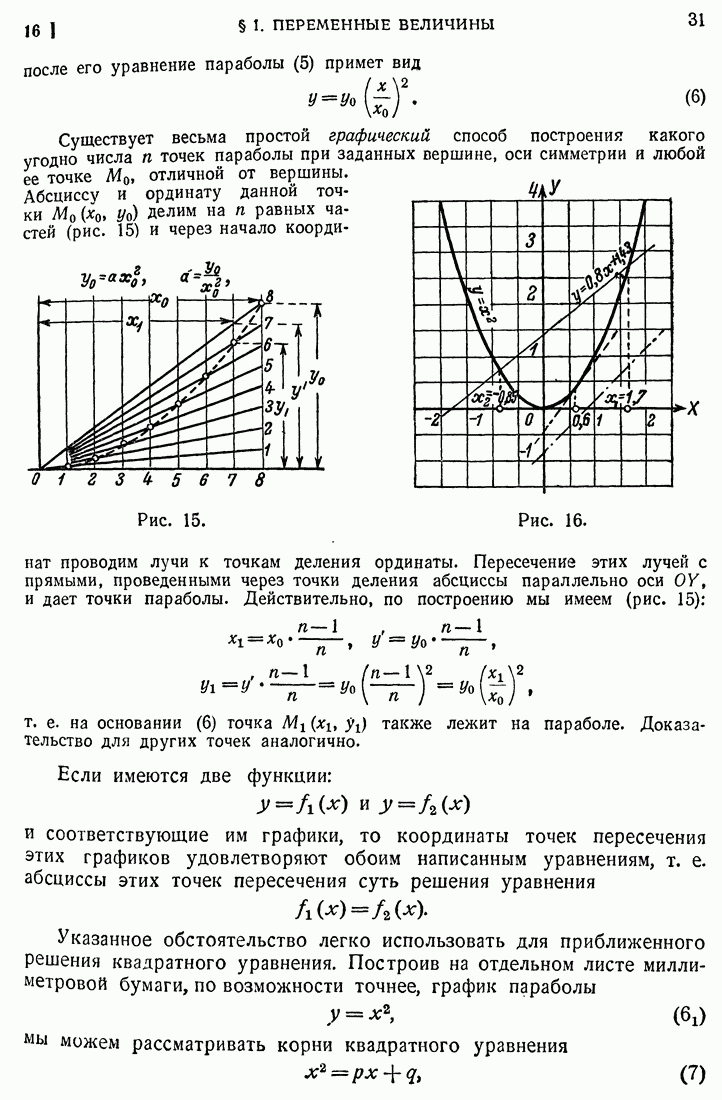
- 16. Парабола второй степени.
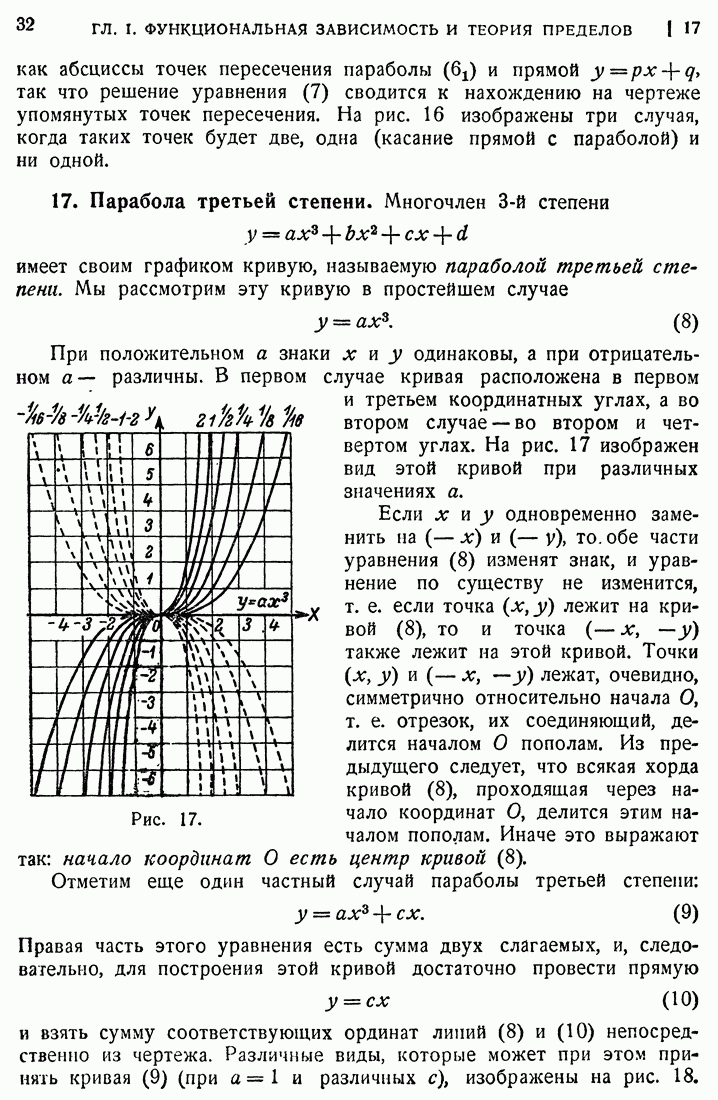
- 17. Парабола третьей степени.
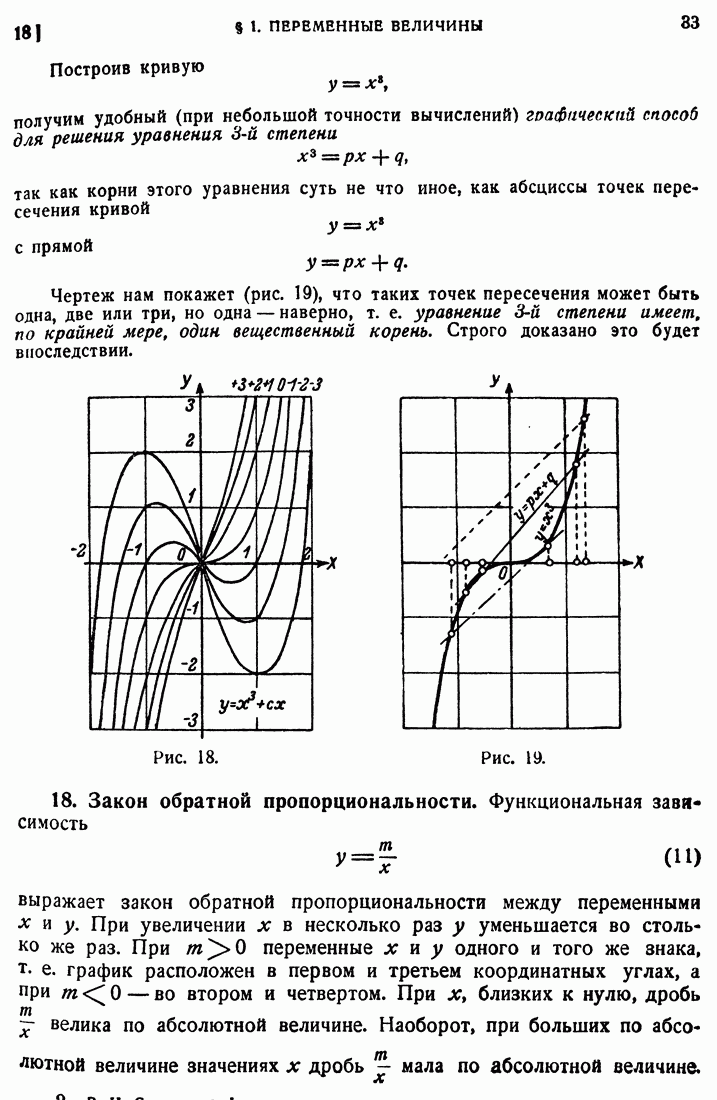
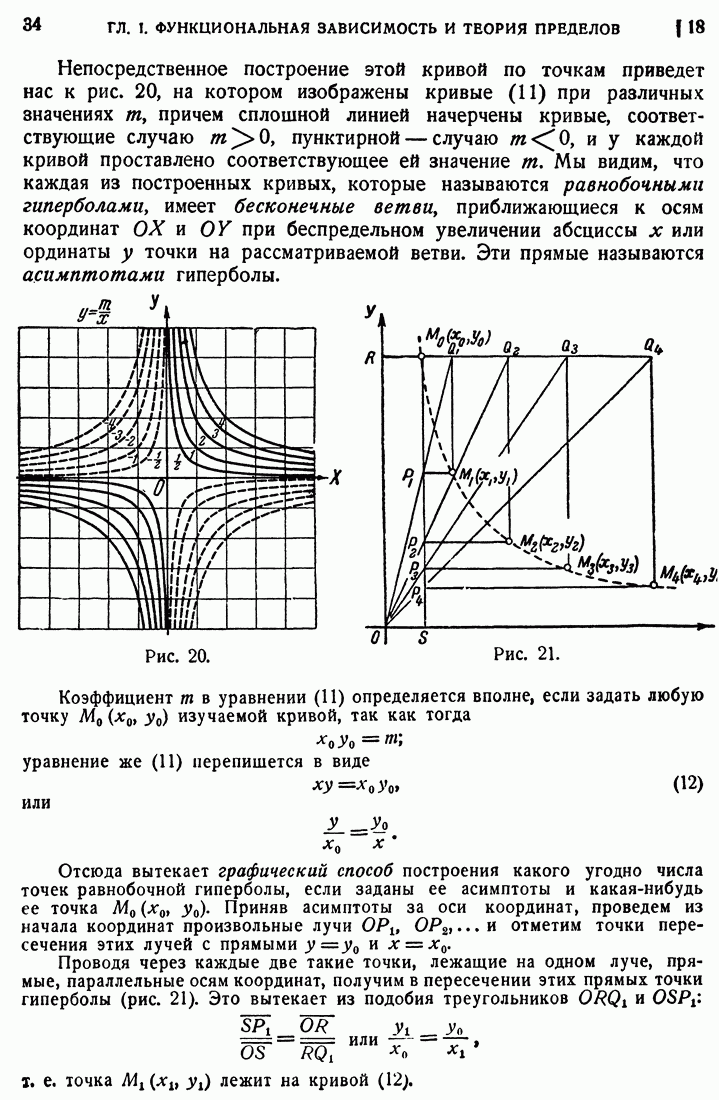
- 18. Закон обратной пропорциональности.
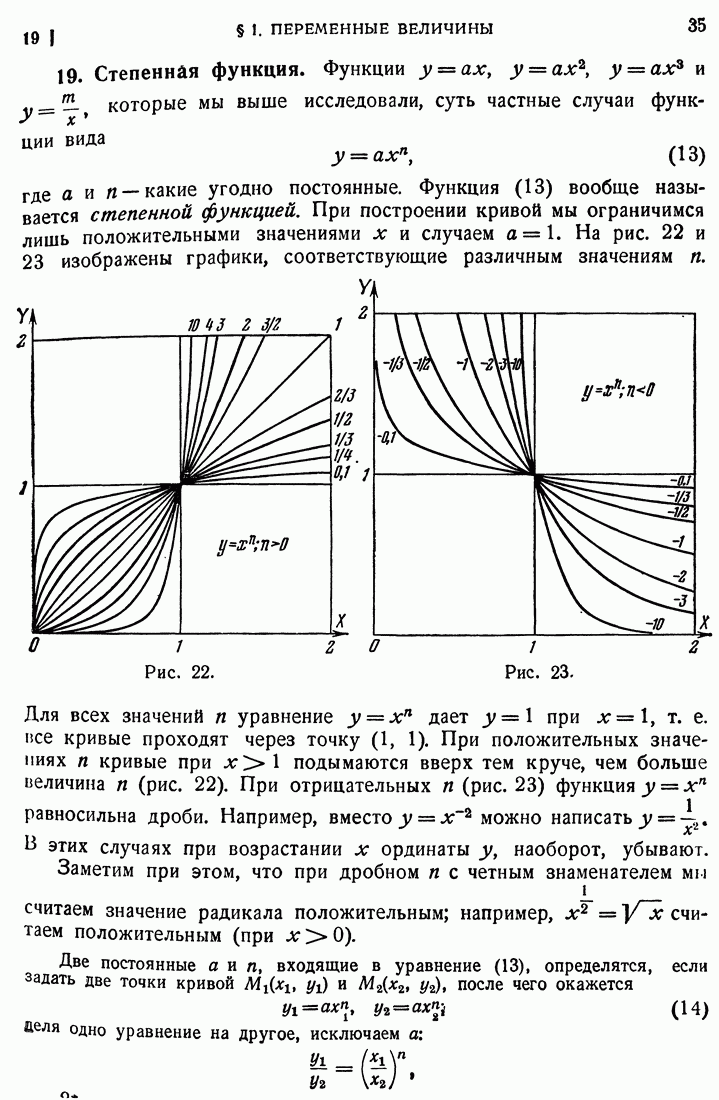
- 19. Степенная функция.
- 20. Обратные функции.
- 21. Многозначность функции.
- 22. Показательная и логарифмическая функции.
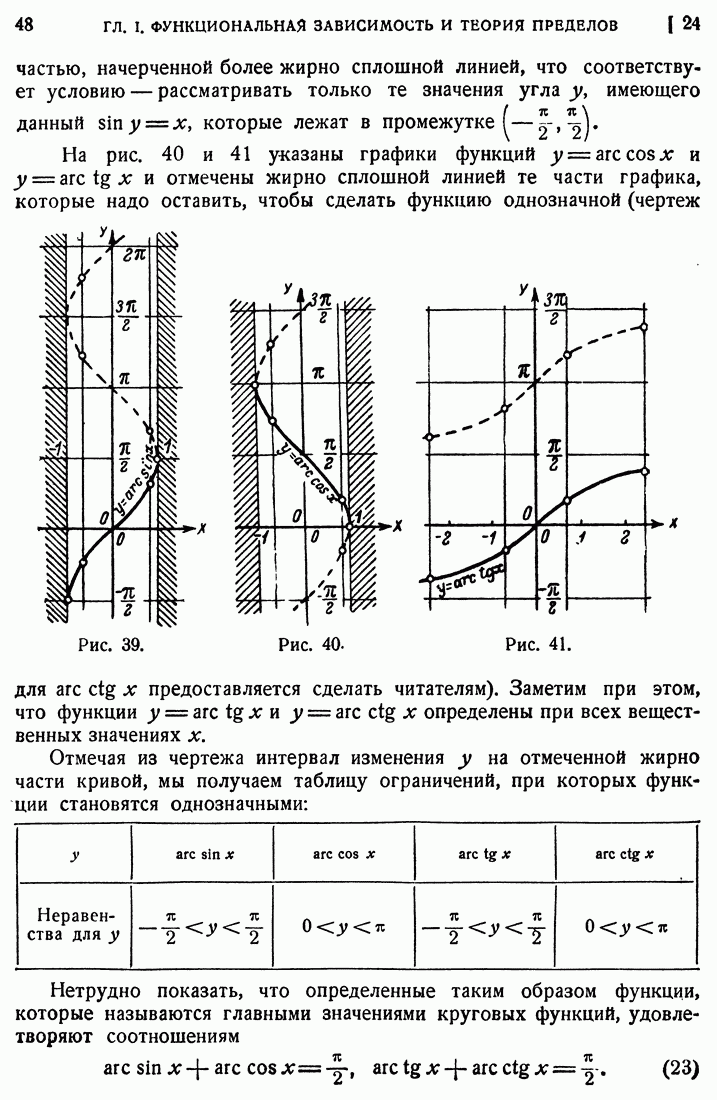
- 23. Тригонометрические функции.
- 24. Обратные тригонометрические, или круговые, функции.
- § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ
- 25. Упорядоченное переменное.
- 26. Величины бесконечно малые.
- 27. Предел переменной величины.
- 28. Основные теоремы.
- 29. Величины бесконечно большие.
- 30. Монотонные переменные.
- 31. Признак Коши существования предела.
- 32. Одновременное изменение двух переменных величин, связанных функциональной зависимостью.
- 33. Примеры.
- 34. Непрерывность функции.
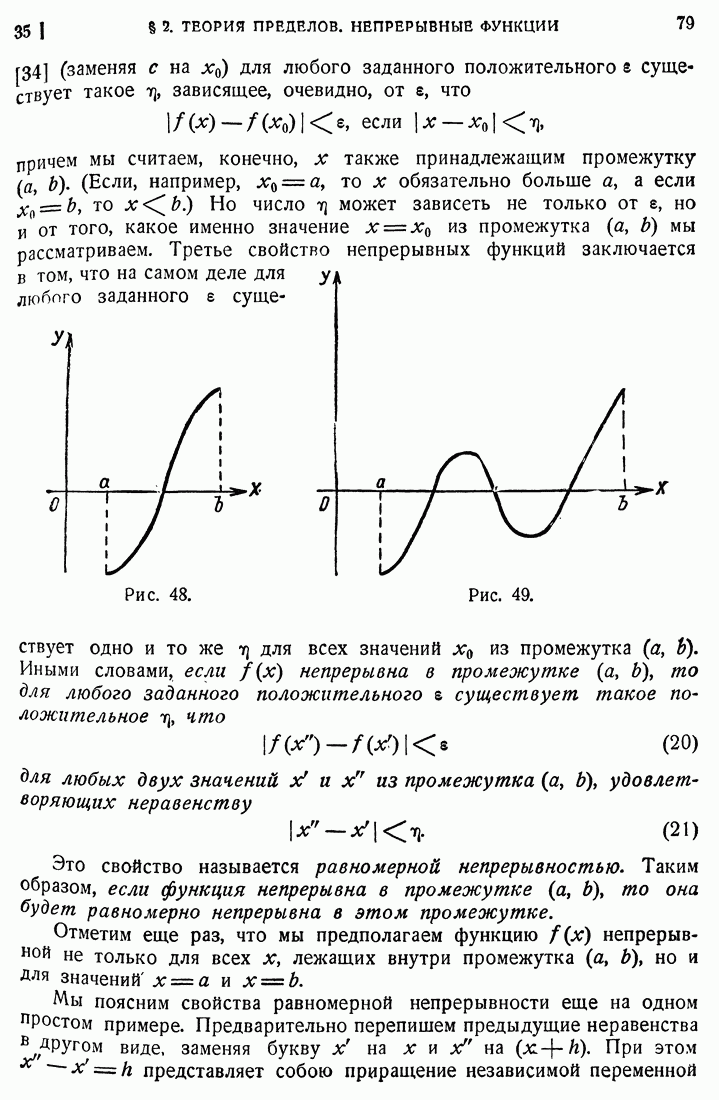
- 35. Свойства непрерывных функций.
- 36. Сравнение бесконечно малых и бесконечно больших величин.
- 37. Примеры.
- 38. Число е.
- 39. Недоказанные предложения.
- 40. Вещественные числа.
- 41. Действия над вещественными числами.
- 42. Точные границы числовых множеств. Признаки существования предела.
- 43. Свойства непрерывных функций.
- 44. Непрерывность элементарных функций.
- ГЛАВА II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
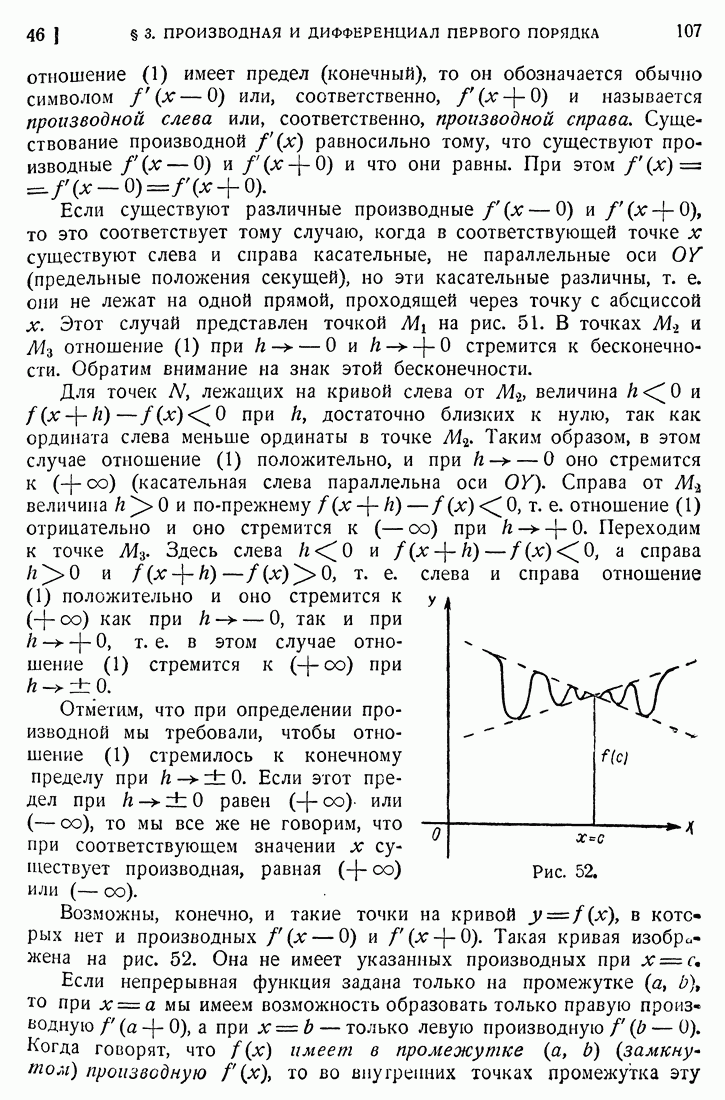
- 45. Понятие о производной.
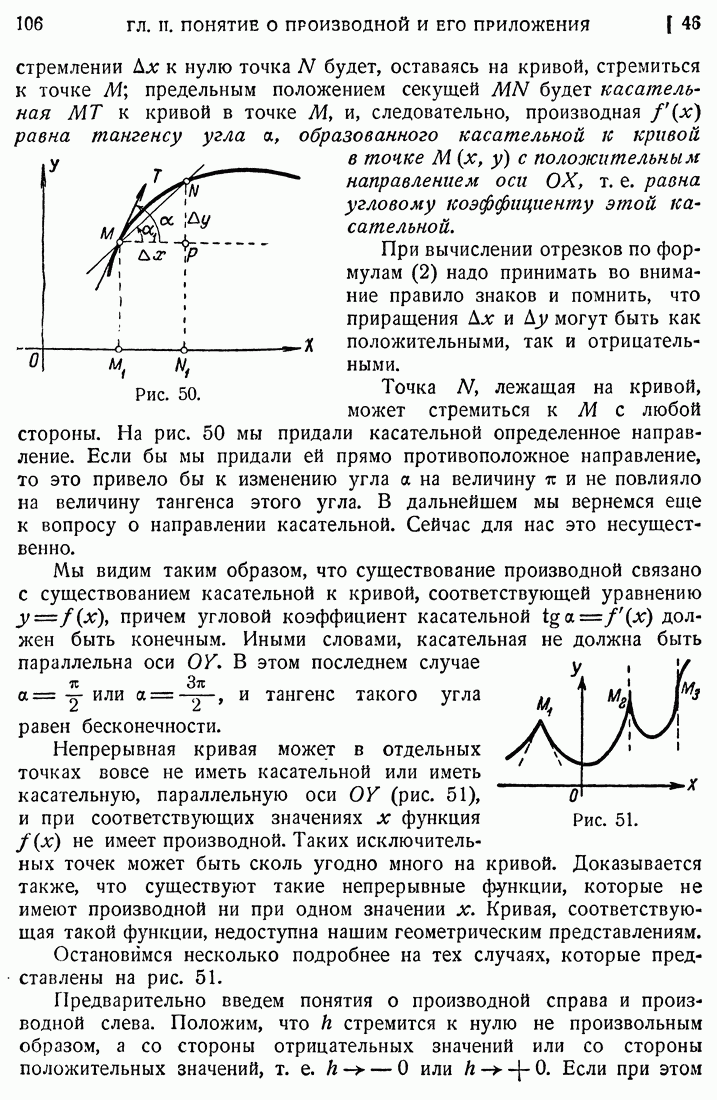
- 46. Геометрическое значение производной.
- 47. Производные простейших функций.
- 48. Производные сложных и обратных функций.
- 49. Таблица производных и примеры.
- 50. Понятие о дифференциале.
- 51. Некоторые дифференциальные уравнения.
- 52. Оценка погрешностей.
- § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- 53. Производные высших порядков.
- 54. Механическое значение второй производной.
- 55. Дифференциалы высших порядков.
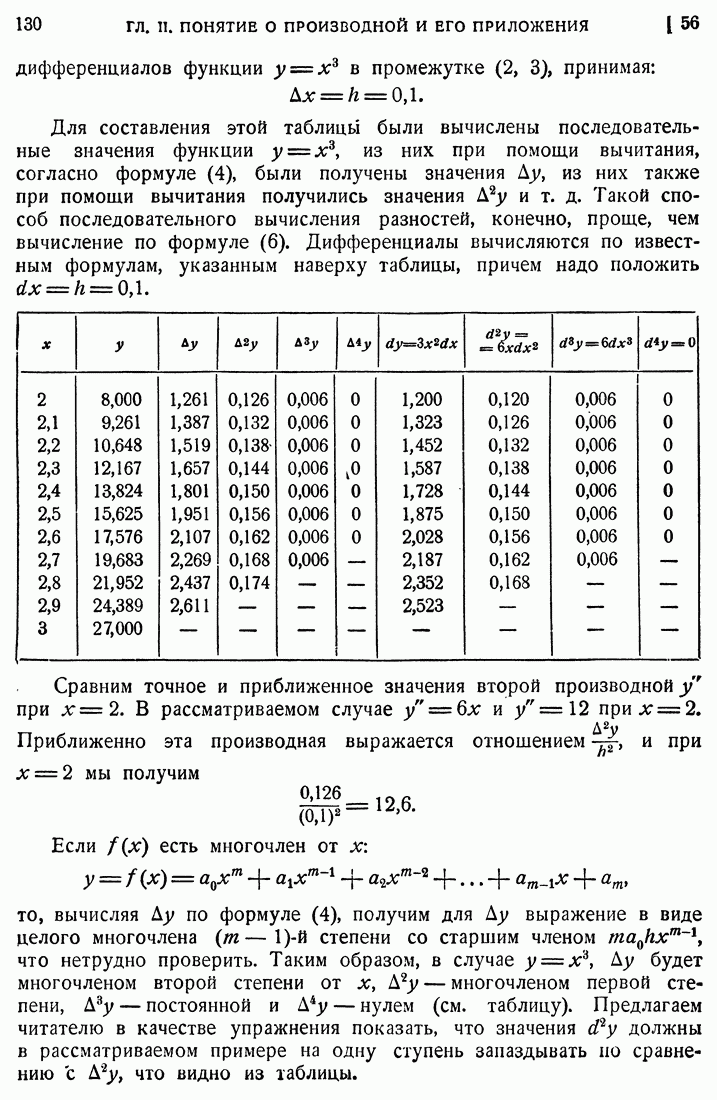
- 56. Разности функций.
- § 5. ПРИЛОЖЕНИЕ ПОНЯТИЯ О ПРОИЗВОДНОЙ К ИЗУЧЕНИЮ ФУНКЦИЙ
- 57. Признаки возрастания и убывания функций.
- 58. Максимумы и минимумы функций.
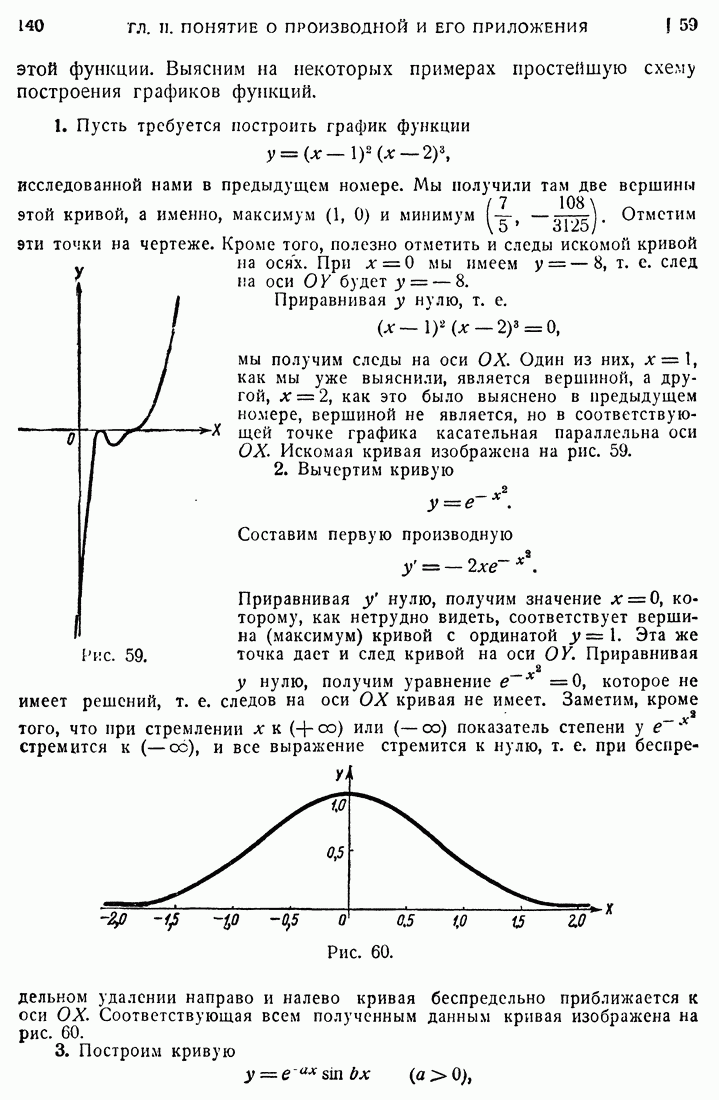
- 59. Построение графиков.
- 60. Наибольшее и наименьшее значения функций.
- 61. Теорема Ферма.
- 62. Теорема Ролля.
- 63. Формула Лагранжа.
- 64. Формула Коши.
- 65. Раскрытие неопределенностей.
- 66. Различные виды неопределенностей.
- § 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
- 68. Частные производные и полный дифференциал функции двух независимых переменных.
- 69. Производные сложных и неявных функций.
- § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОНЯТИЯ О ПРОИЗВОДНЫХ
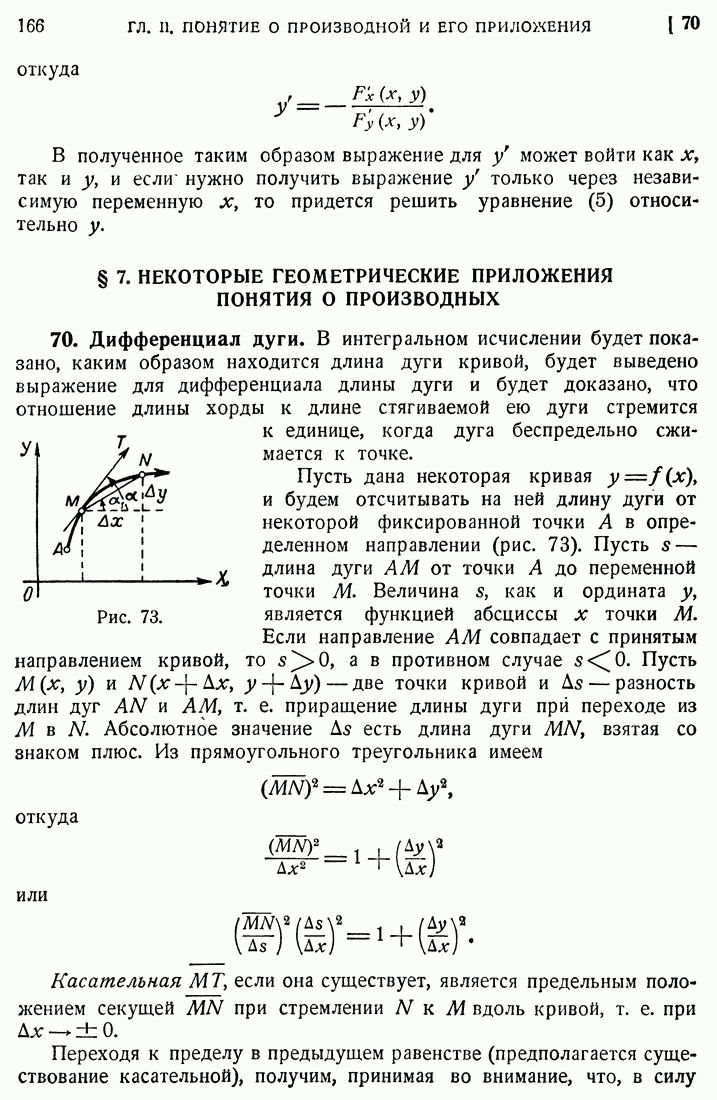
- 70. Дифференциал дуги.
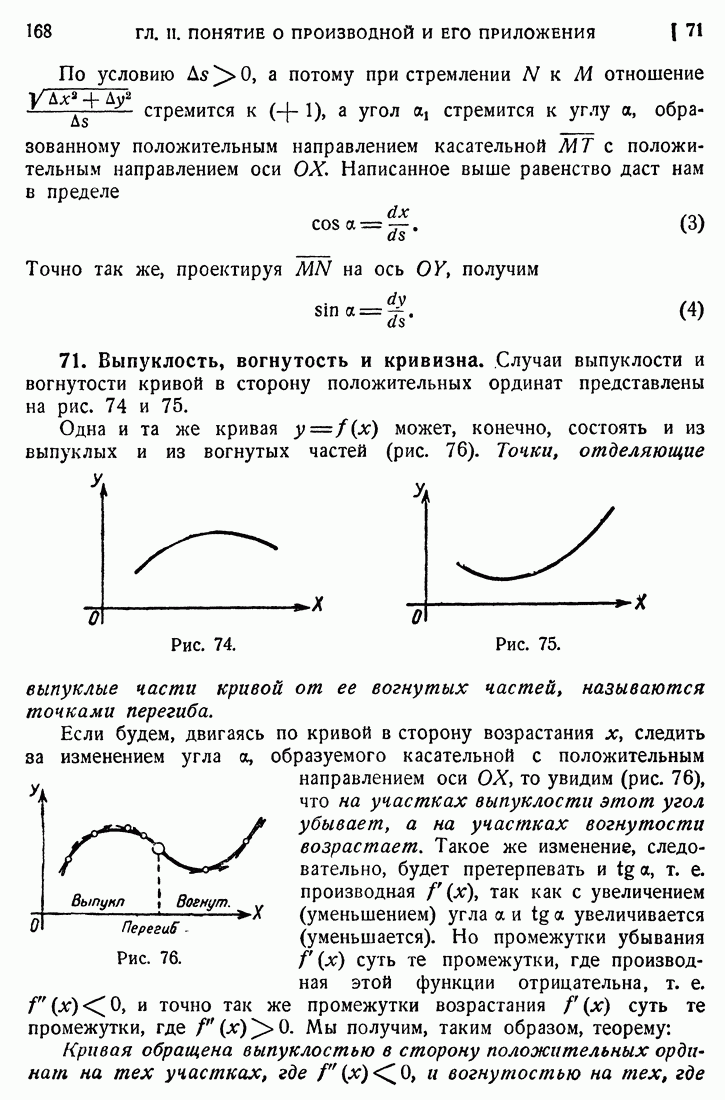
- 71. Выпуклость, вогнутость и кривизна.
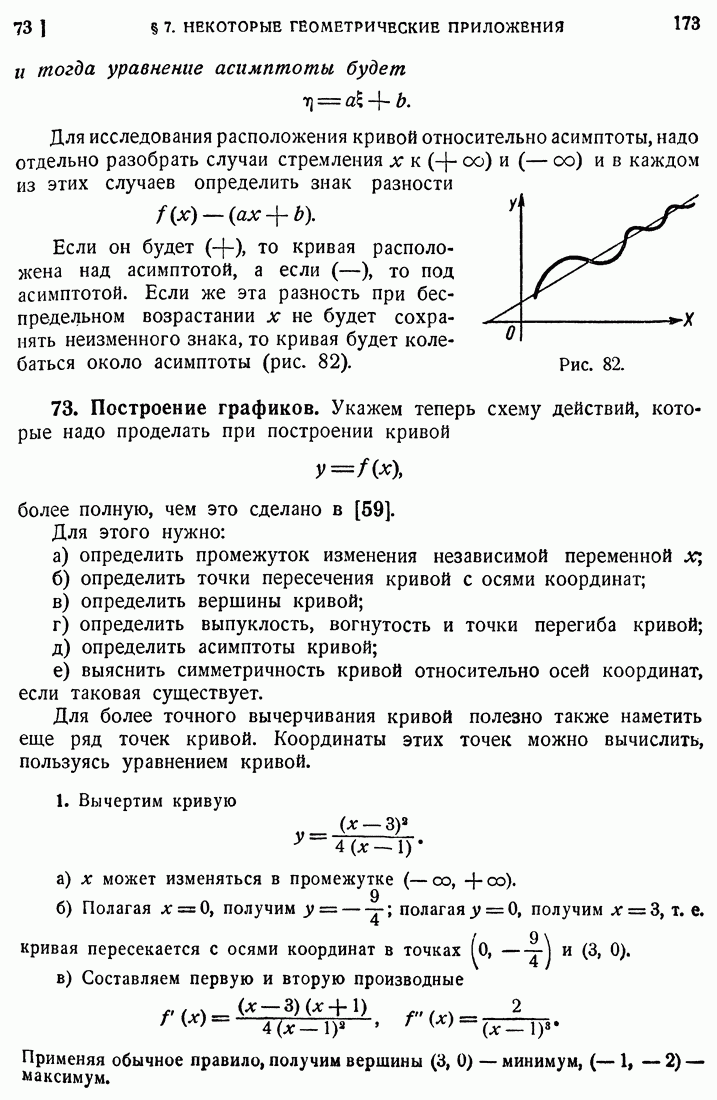
- 72. Асимптоты.
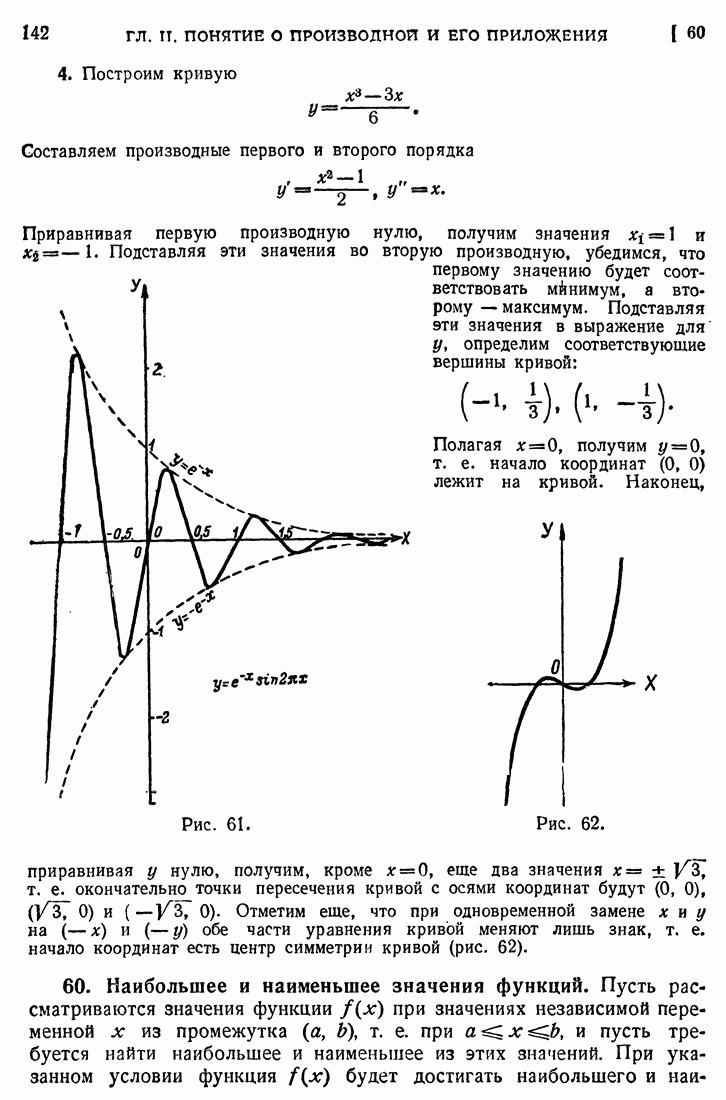
- 73. Построение графиков.
- 74. Параметрическое задание кривой.
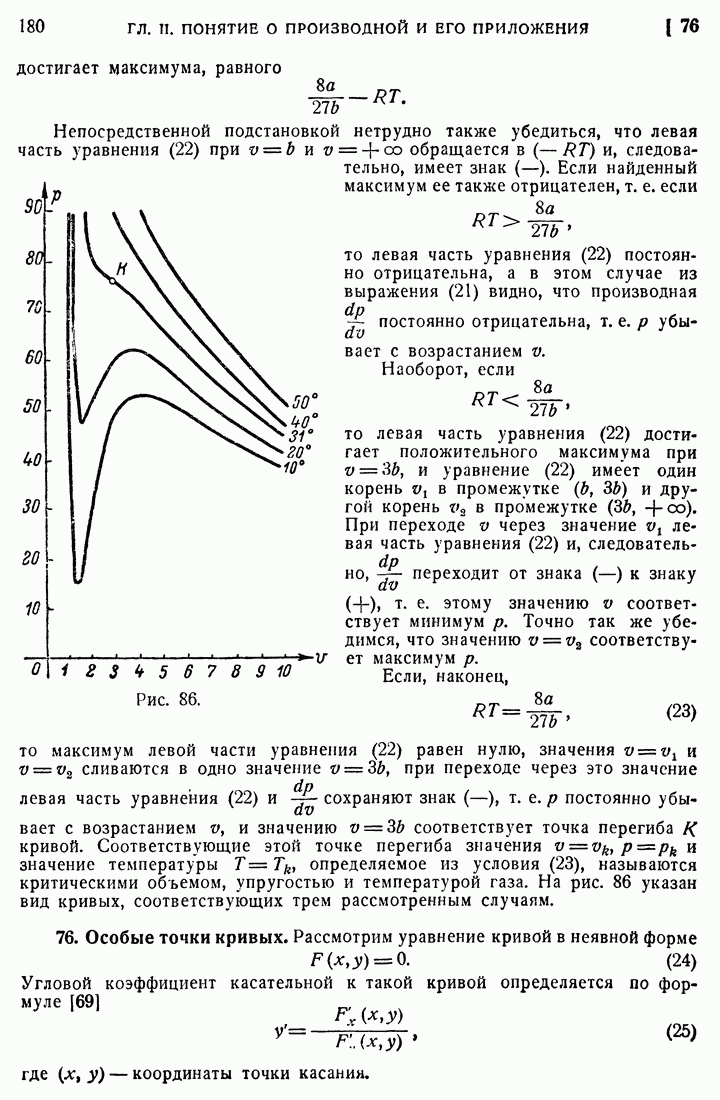
- 75. Уравнение Ван-дер-Ваальса.
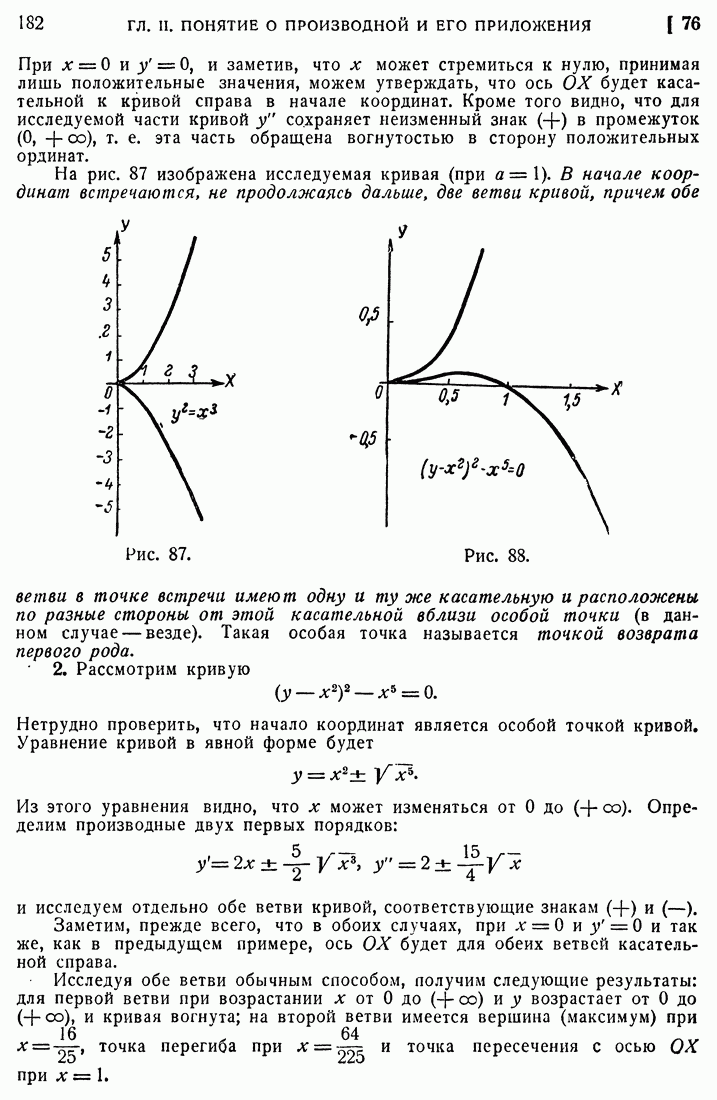
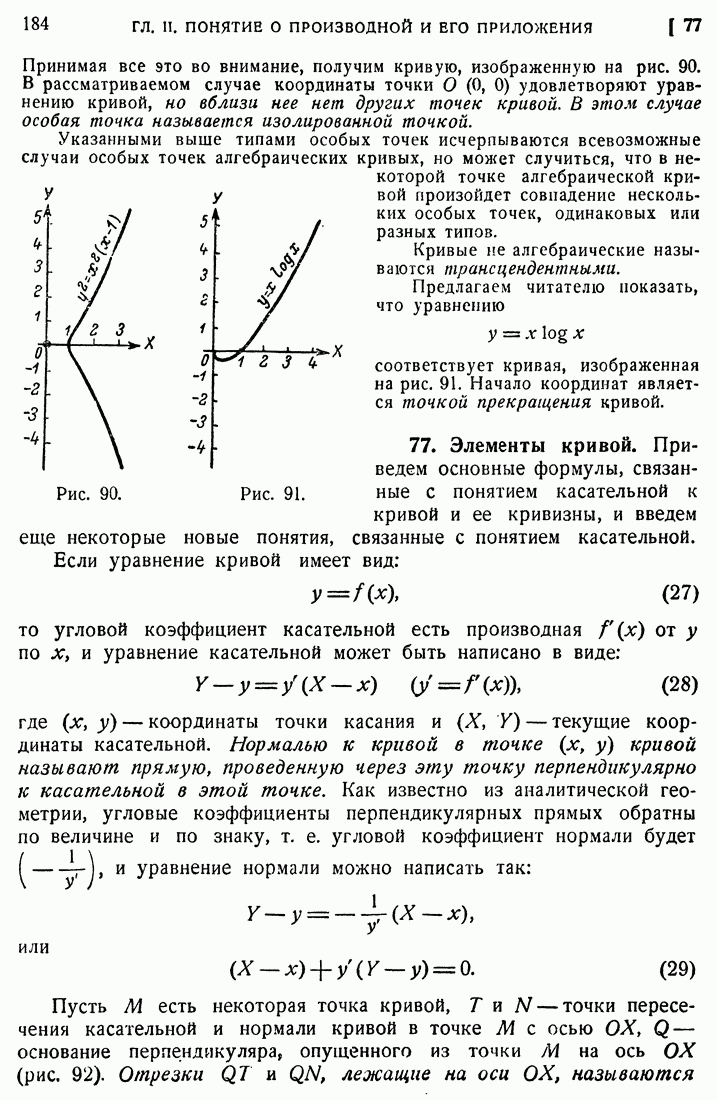
- 76. Особые точки кривых.
- 77. Элементы кривой.
- 78. Цепная линия.
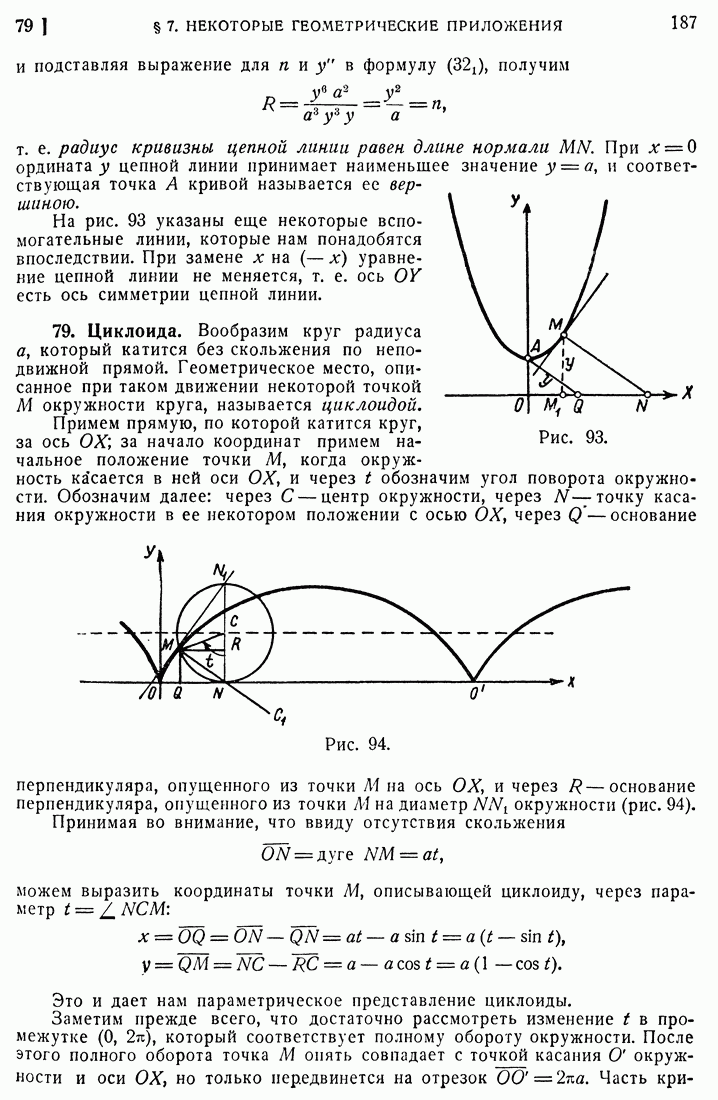
- 79. Циклоида.
- 80. Эпициклоиды и гипоциклоиды.
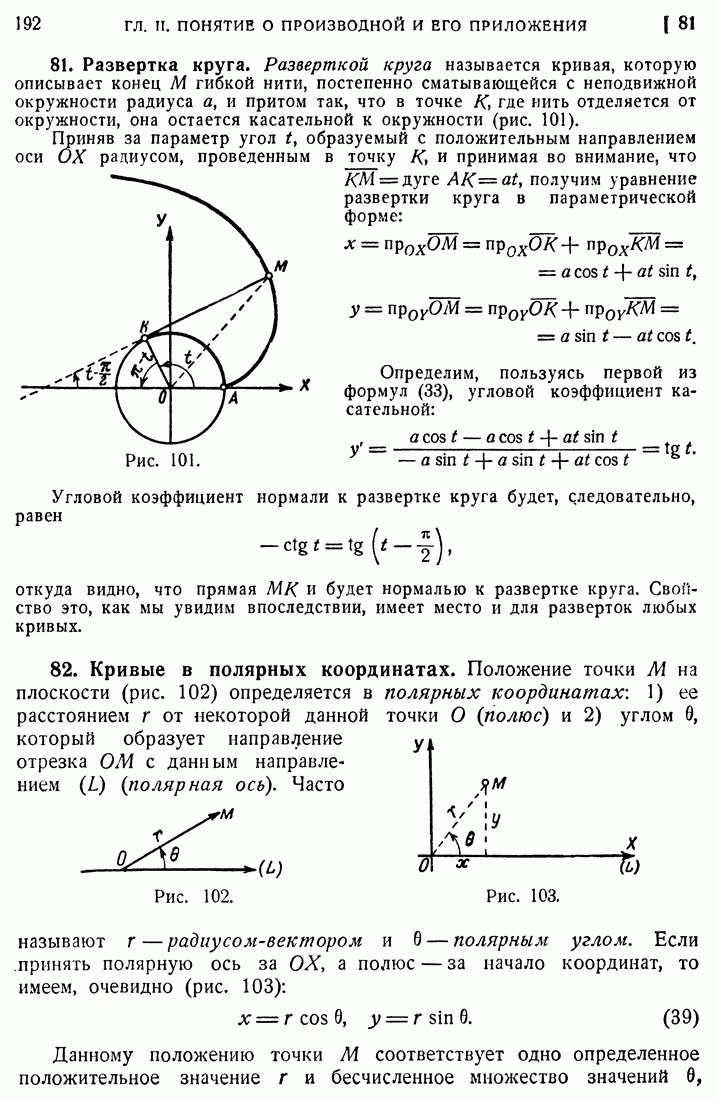
- 81. Развертка круга.
- 82. Кривые в полярных координатах.
- 83. Спирали.
- 85. Овалы Кассини и лемниската.
- ГЛАВА III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
- 86. Понятие о неопределенном интеграле.
- 87. Определенный интеграл как предел суммы.
- 88. Связь определенного и неопределенного интегралов.
- 89. Свойства неопределенного интеграла.
- 90. Таблица простейших интегралов.
- 91. Правило интегрирования по частям.
- 92. Правило замены переменных. Примеры.
- 93. Примеры дифференциальных уравнений первого порядка.
- § 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 94. Основные свойства определенного интеграла.
- 95. Теорема о среднем.
- 96. Существование первообразной функции.
- 97. Разрыв подынтегральной функции.
- 98. Бесконечные пределы.
- 99. Замена переменной под знаком определенного интеграла.
- 100. Интегрирование по частям.
- § 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
- 101. Вычисление площадей.
- 102. Площадь сектора.
- 103. Длина дуги.
- 104. Вычисление объемов тел по их поперечным сечениям.
- 105. Объем тела вращения.
- 106. Поверхность тела вращения.
- 107. Определение центров тяжести. Теоремы Гульдина.
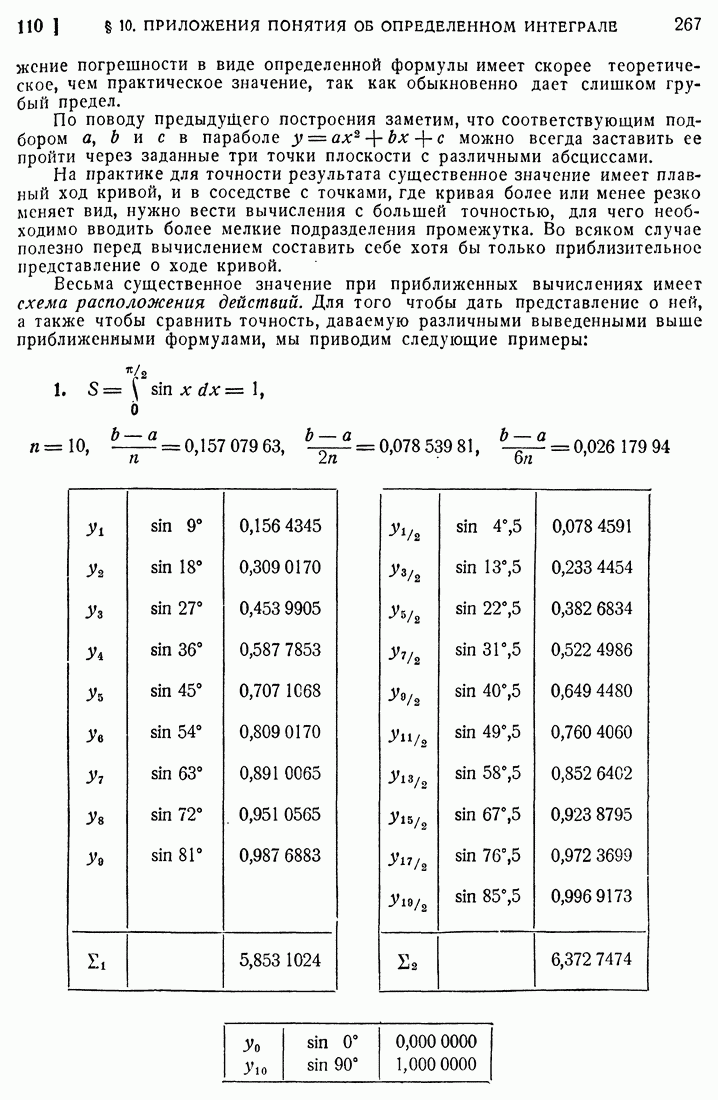
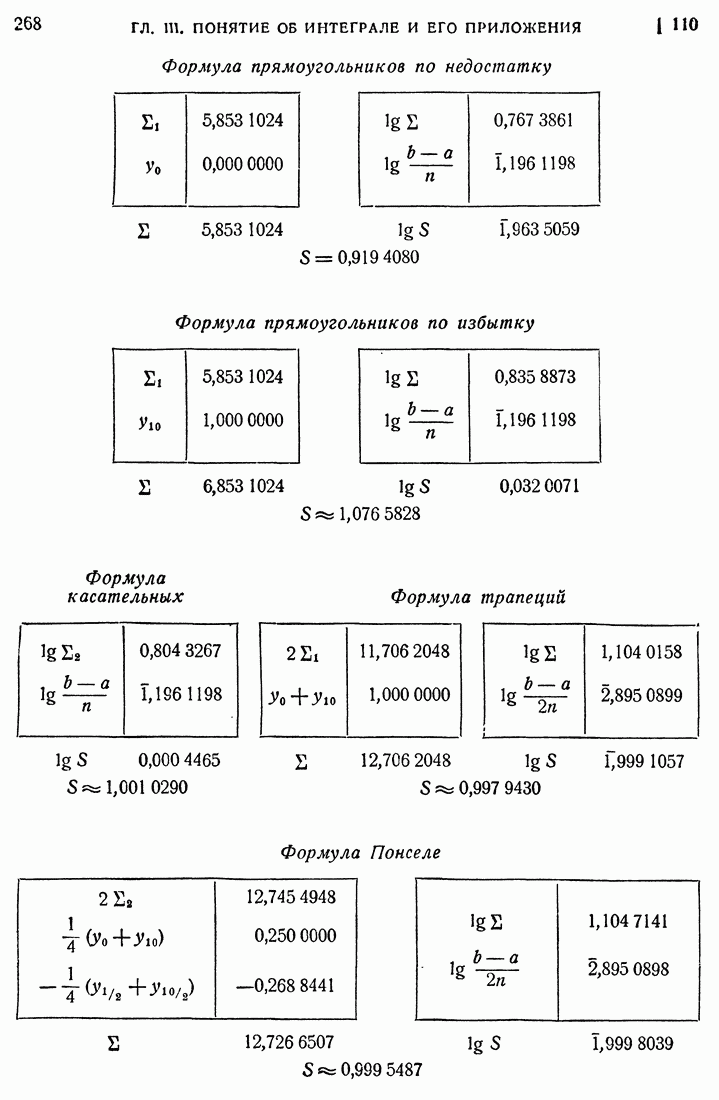
- 108. Приближенное вычисление определенных интегралов; формулы прямоугольников и трапеций.
- 109. Формула касательных и формула Понселе.
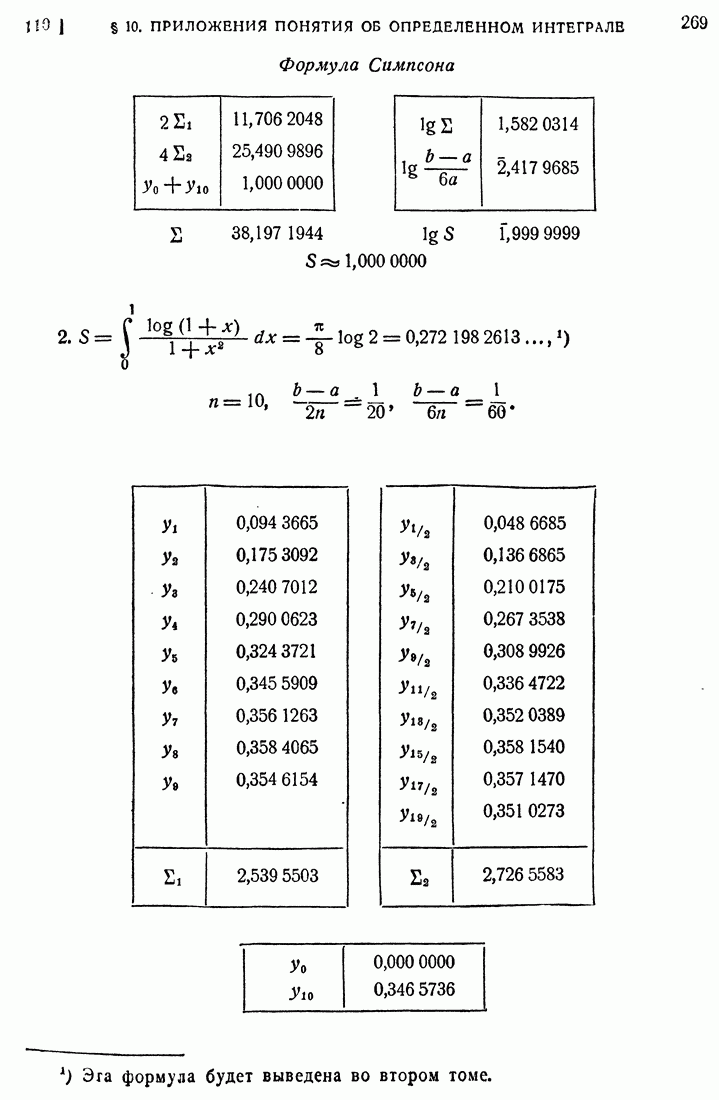
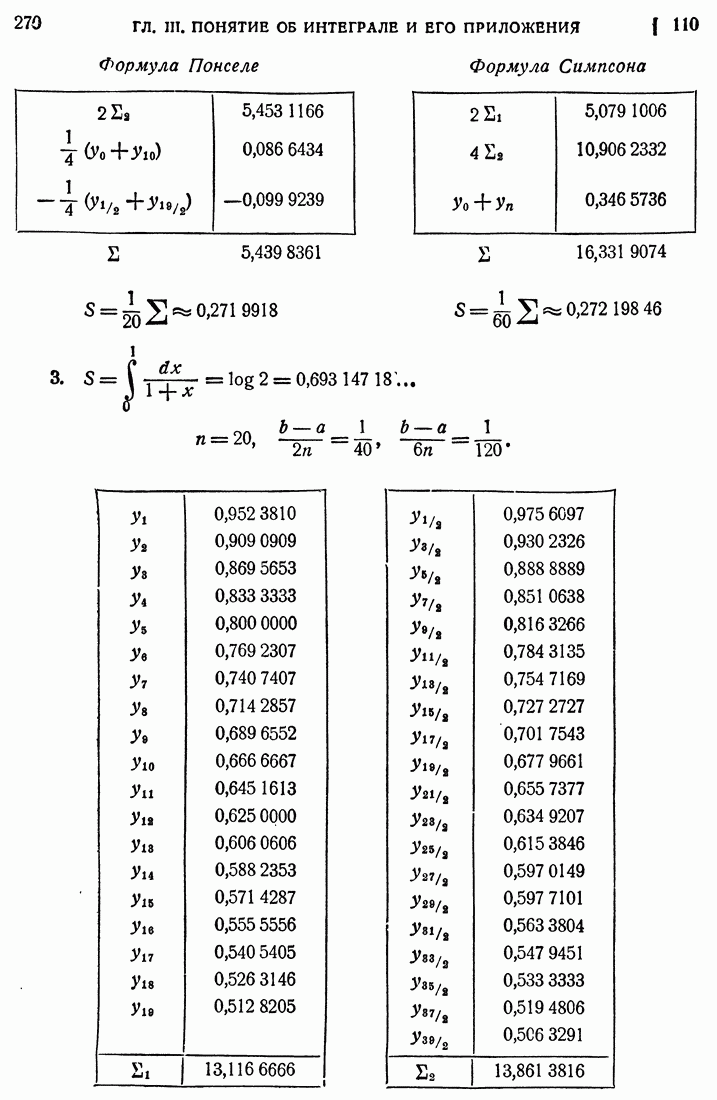
- 110. Формула Симпсона.
- 111. Вычисление определенного интеграла с переменным верхним пределом.
- 112. Графические способы.
- 113. Площади быстро колеблющихся кривых.
- § 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
- 115. Разбиение промежутка на части и образование различных сумм.
- 116. Интегрируемые функции.
- 117. Свойства интегрируемых функций.
- ГЛАВА IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
- 118. Понятие о бесконечном ряде.
- 119. Основные свойства бесконечных рядов.
- 120. Ряды с положительными членами. Признаки сходимости.
- 121. Признаки Коши и Даламбера.
- 122. Интегральный признак сходимости Коши.
- 123. Знакопеременные ряды.
- 124. Абсолютно сходящиеся ряды.
- 125. Общий признак сходимости.
- § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ
- 126. Формула Тейлора.
- 127. Различные виды формулы Тейлора.
- 128. Ряды Тейлора и Маклорена.
- 129. Разложение exp(x).
- 130. Разложение sin x и cos x.
- 131. Бином Ньютона.
- 132. Разложение log(1+x).
- 133. Разложение arctg x.
- 134. Приближенные формулы.
- 135. Максимумы, минимумы и точки перегиба.
- 136. Раскрытие неопределенностей.
- § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ
- 137. Свойства абсолютно сходящихся рядов.
- 138. Умножение абсолютно сходящихся рядов.
- 139. Признак Куммера.
- 140. Признак Гаусса.
- 141. Гипергеометрический ряд.
- 142. Двойные ряды.
- 143. Ряды с переменными членами. Равномерно сходящиеся ряды.
- 144. Равномерно сходящиеся последовательности функций.
- 145. Свойства равномерно сходящихся последовательностей.
- 146. Свойства равномерно сходящихся рядов.
- 147. Признаки равномерной сходимости.
- 148. Степенные ряды. Радиус сходимости.
- 149. Вторая теорема Абеля.
- 150. Дифференцирование и интегрирование степенного ряда.
- ГЛАВА V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ
- 152. О предельном переходе.
- 153. Частные производные и полный дифференциал первого порядка.
- 154. Однородные функции.
- 155. Частные производные высших порядков.
- 156. Дифференциалы высших порядков.
- 157. Неявные функции.
- 158. Пример.
- 159. Существование неявных функций.
- 160. Кривые в пространстве и поверхности.
- § 16. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 161. Распространение формулы Тейлора на случай функции от нескольких независимых переменных.
- 162. Необходимые условия максимума и минимума функции.
- 163. Исследование максимума и минимума функции двух независимых переменных.
- 164. Примеры.
- 165. Дополнительные замечания о нахождении максимумов и минимумов функции.
- 166. Наибольшее и наименьшее значения функции.
- 167. Относительные максимумы и минимумы.
- 168. Дополнительные замечания.
- 169. Примеры.
- ГЛАВА VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
- 170. Комплексные числа.
- 171. Сложение и вычитание комплексных чисел.
- 172. Умножение комплексных чисел.
- 173. Деление комплексных чисел.
- 174. Возвышение в степень.
- 175. Извлечение корня.
- 176. Показательная функция.
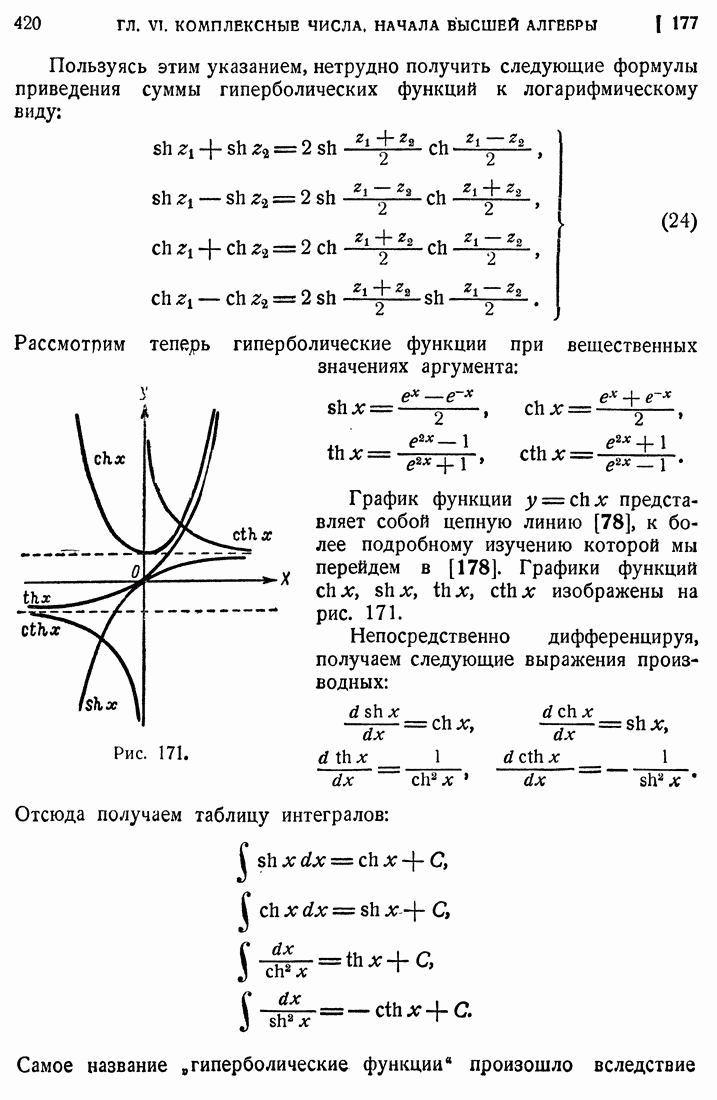
- 177. Тригонометрические и гиперболические функции.
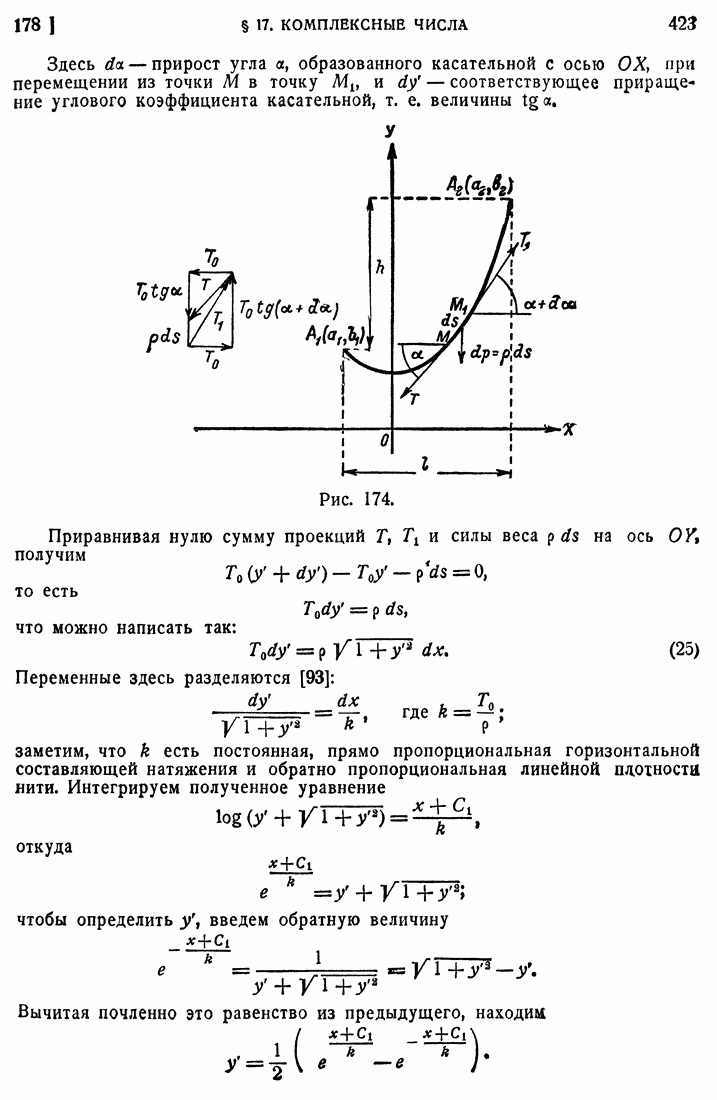
- 178. Цепная линия.
- 179. Логарифмирование.
- 180. Синусоидальные величины и векторные диаграммы.
- 181. Примеры.
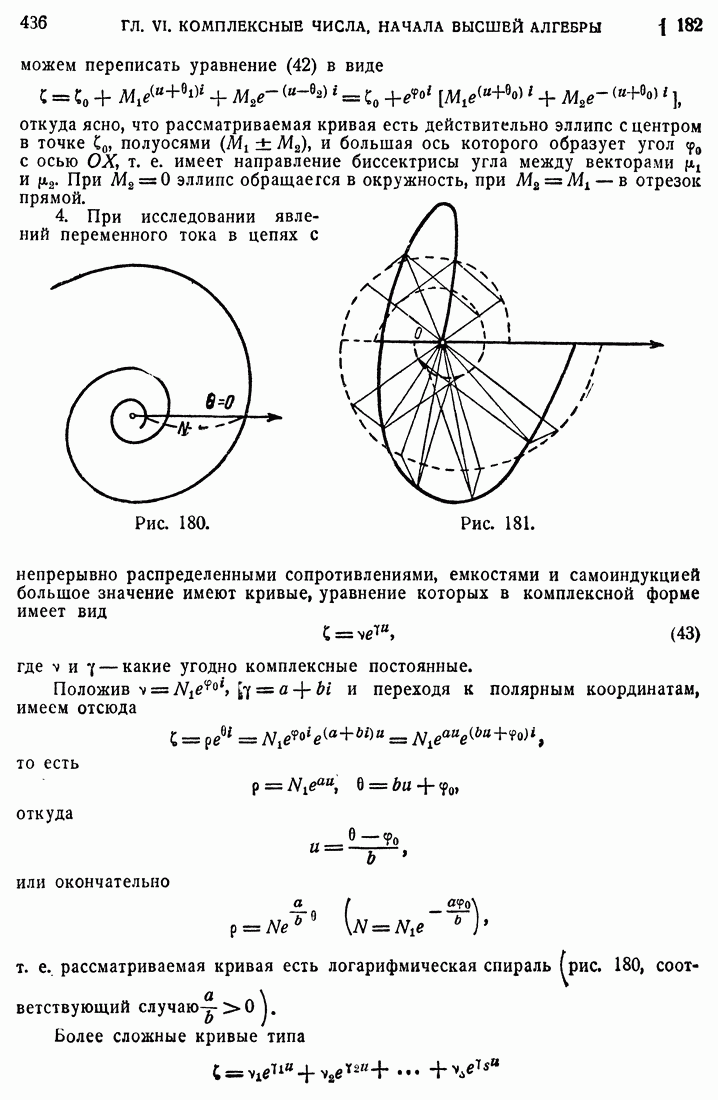
- 182. Кривые в комплексной форме.
- 183. Представление гармонического колебания в комплексной форме.
- § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ И ВЫЧИСЛЕНИЕ ИХ КОРНЕЙ
- 185. Разложение многочлена на множители.
- 186. Кратные корни.
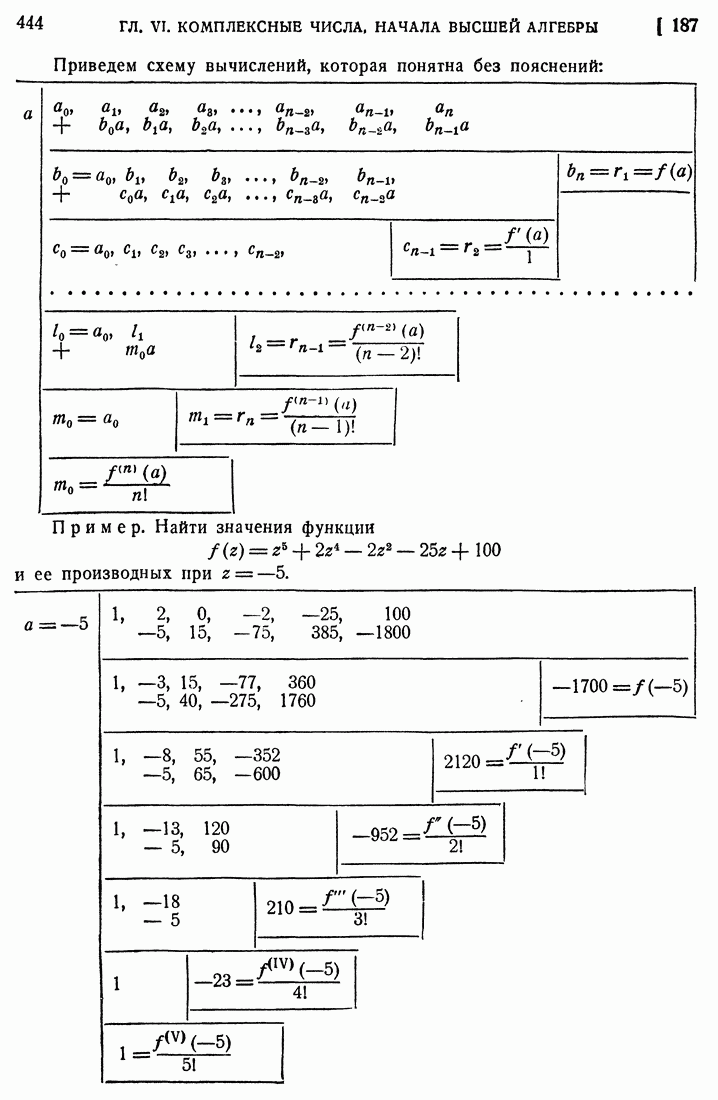
- 187. Правило Горнера.
- 188. Общий наибольший делитель.
- 189. Вещественные многочлены.
- 190. Зависимость между корнями уравнения и его коэффициентами.
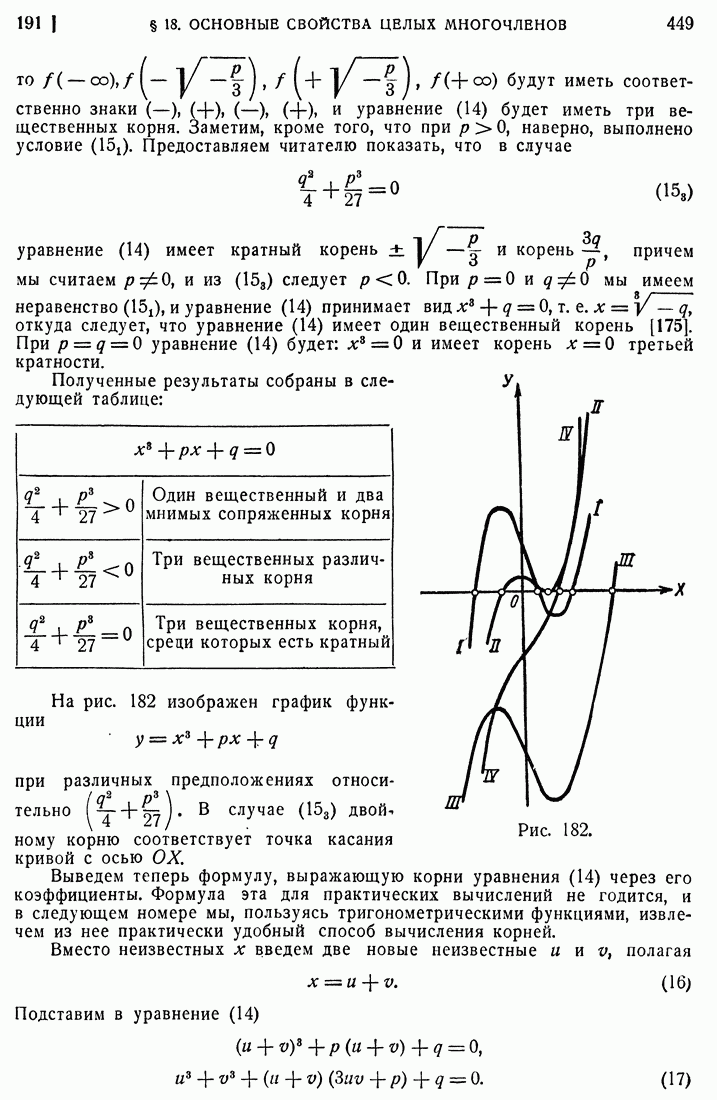
- 191. Уравнение третьей степени.
- 192. Решение кубического уравнения в тригонометрической форме.
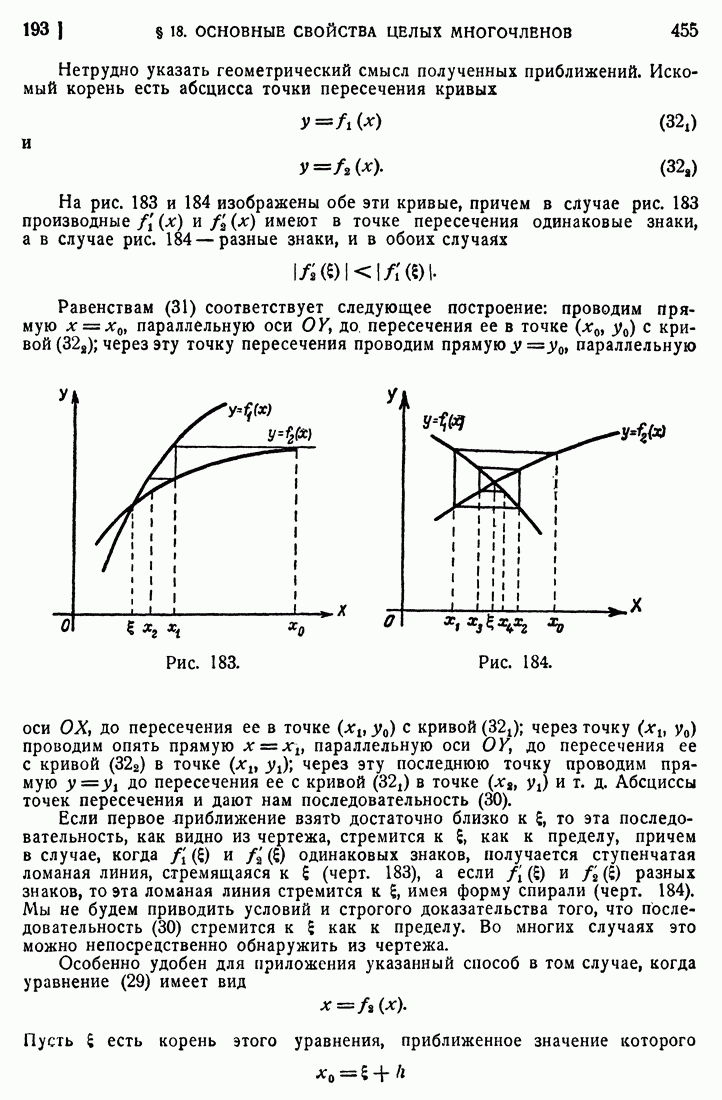
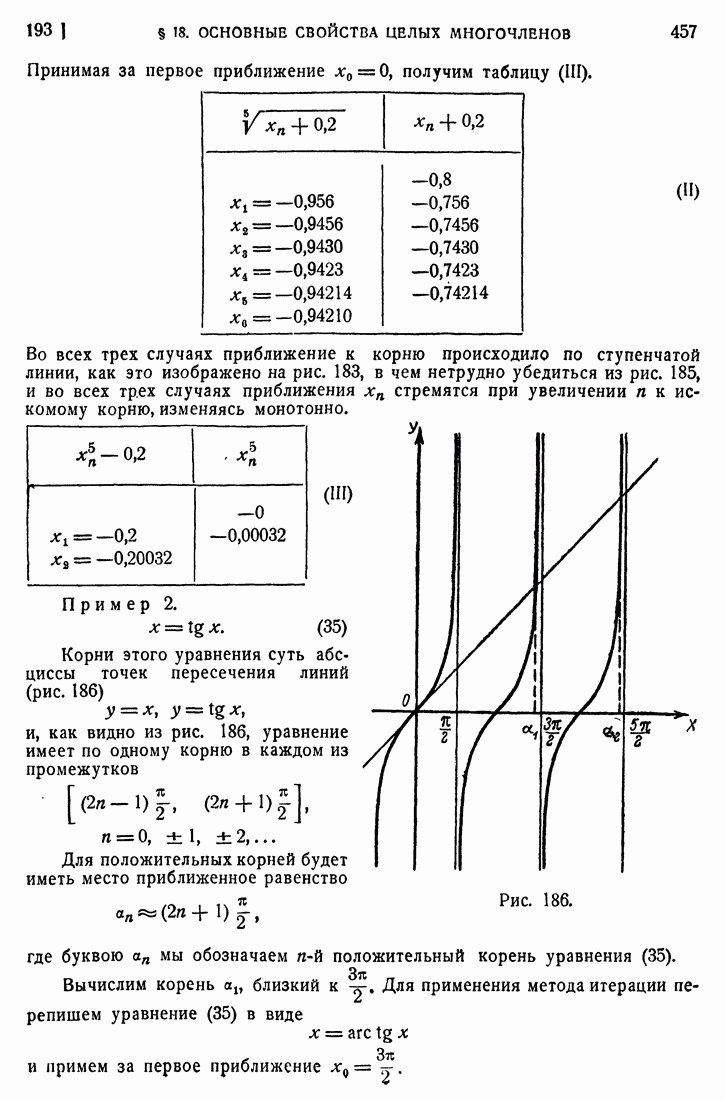
- 193. Способ итерации.
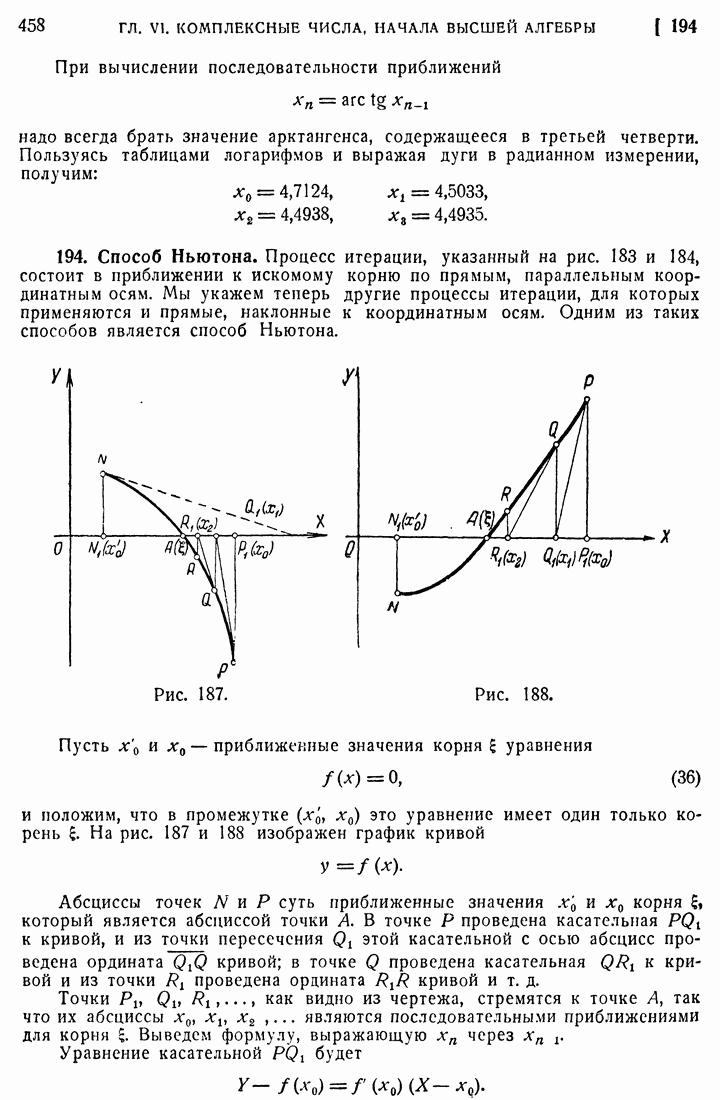
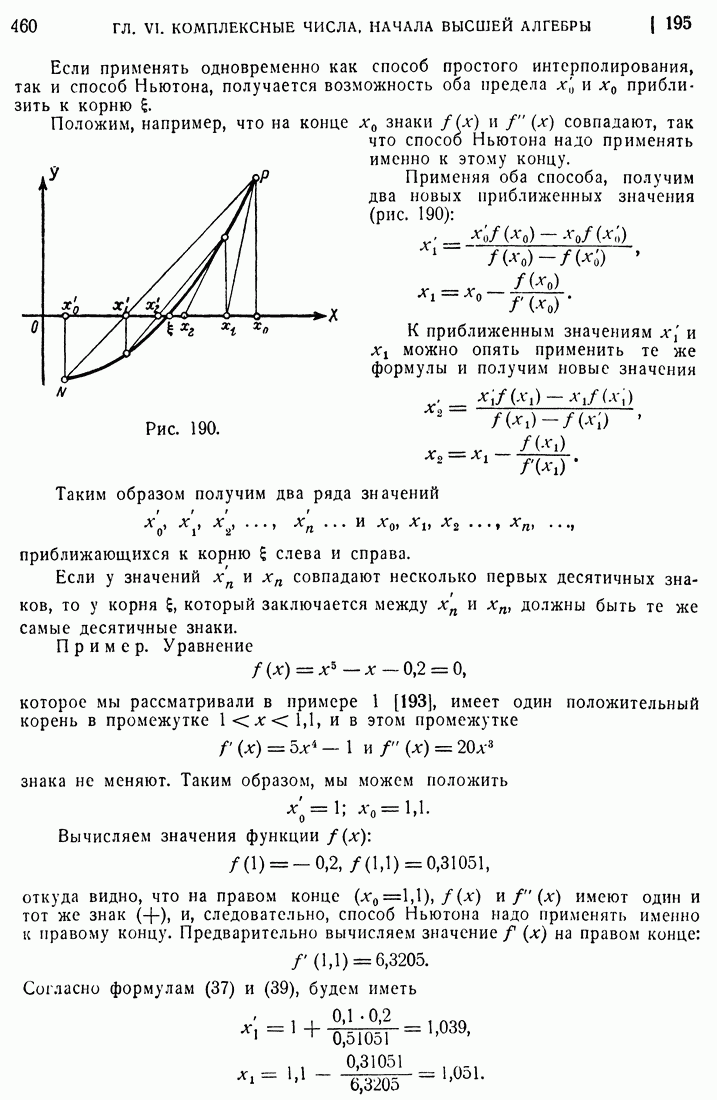
- 194. Способ Ньютона.
- 195. Способ простого интерполирования.
- § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИИ
- 196. Разложение рациональной дроби на простейшие.
- 197. Интегрирование рациональной дроби.
- 198. Интеграл от выражений, содержащих радикалы.
- 199. Интегралы вида…
- 200. Интегралы вида…
- 201. Интегралы вида…