| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
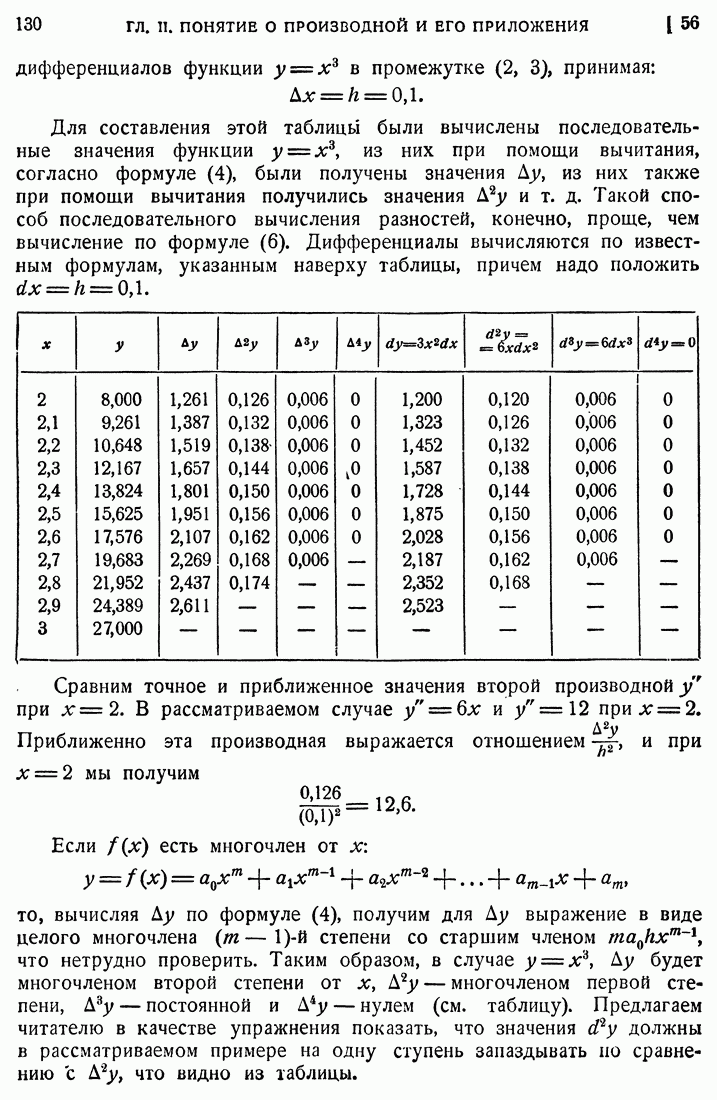
166. Наибольшее и наименьшее значения функции.
Положим, что  буется найти наибольшее значение некоторой функции
буется найти наибольшее значение некоторой функции  заданной в определенной области. Указанный в [163] прием позволяет нам найти все максимумы функции внутри этой области, т. е. те точки внутри области, в которых значения функции не меньше, чем в соседних с ними точках. Для нахождения наибольшего значения функции надо принять во внимание значения функции на границе (контуре) данной области и сравнить ее максимумы внутри области со значениями на контуре. Наибольшее из всех этих значений и будет наибольшим значением функции в данной области. Аналогично находится и наименьшее значение функции в данной области. Для разъяснения сказанного рассмотрим пример.
заданной в определенной области. Указанный в [163] прием позволяет нам найти все максимумы функции внутри этой области, т. е. те точки внутри области, в которых значения функции не меньше, чем в соседних с ними точках. Для нахождения наибольшего значения функции надо принять во внимание значения функции на границе (контуре) данной области и сравнить ее максимумы внутри области со значениями на контуре. Наибольшее из всех этих значений и будет наибольшим значением функции в данной области. Аналогично находится и наименьшее значение функции в данной области. Для разъяснения сказанного рассмотрим пример.
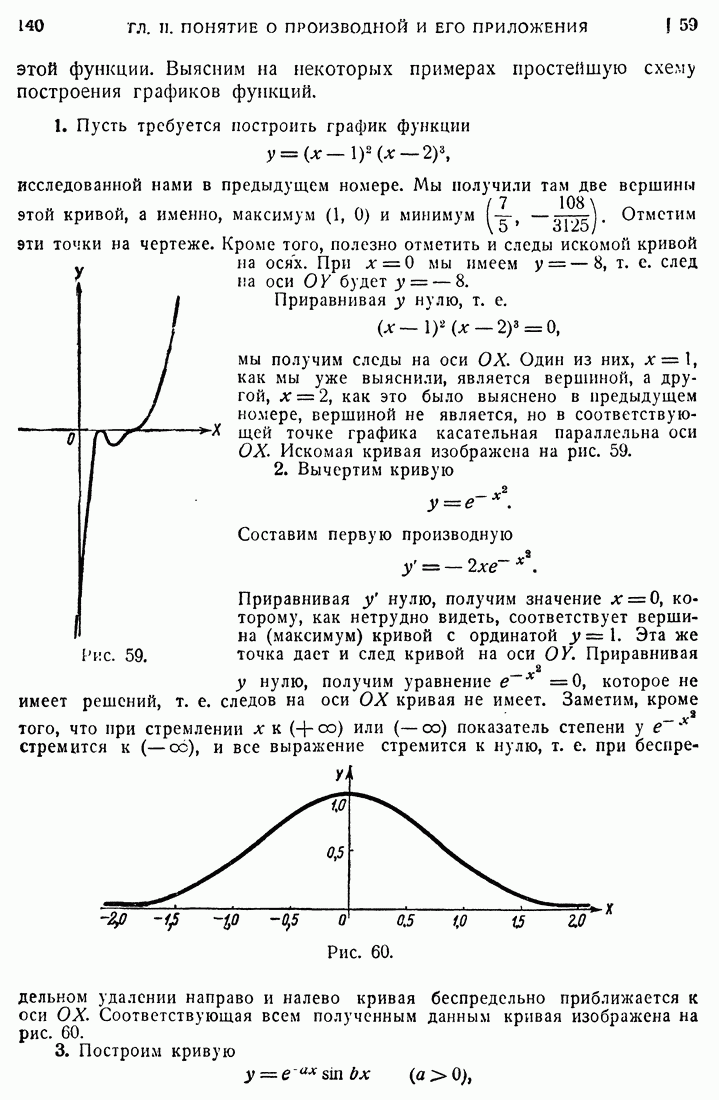
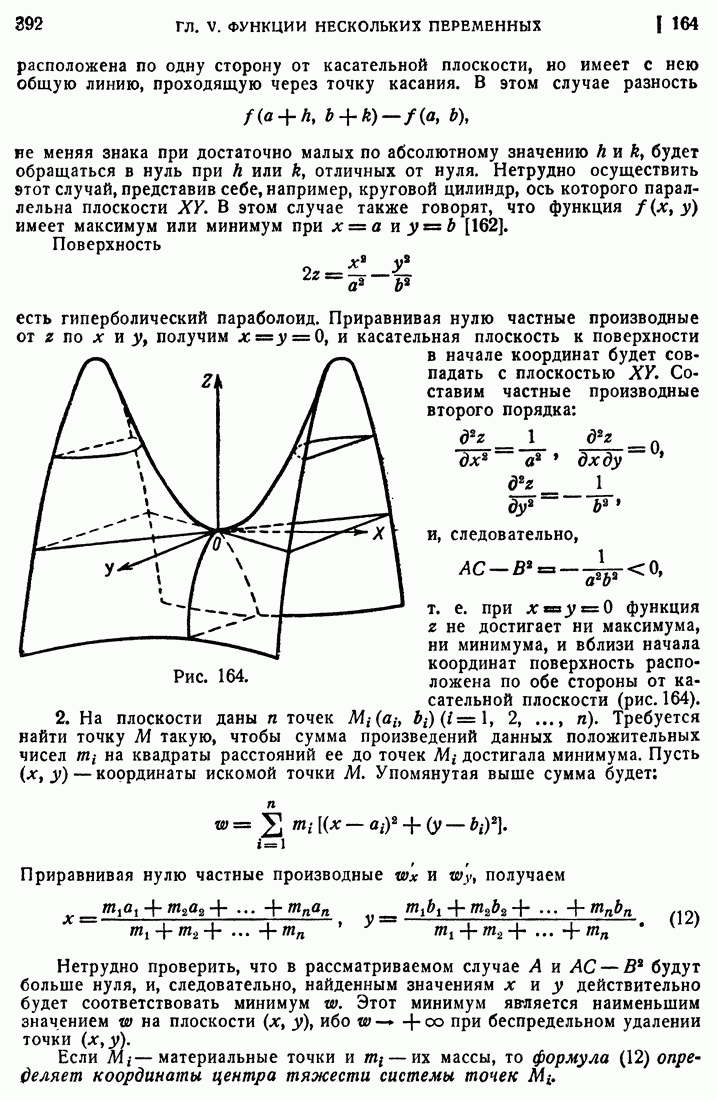
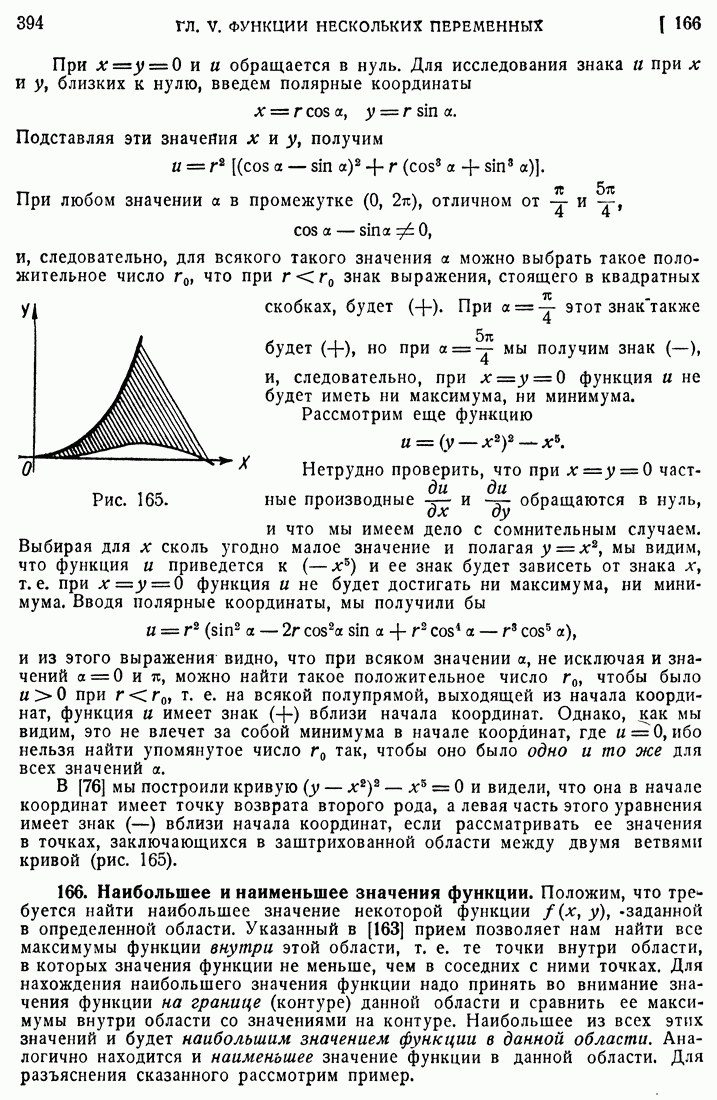
На плоскости дан треугольник ОАВ (рис. 166), образованный осями ОХ и OY и прямой

Требуется найти такую точку этого треугольника, для которой сумма квадратов ее расстояний до вершин треугольника была бы наименьшей.
Принимая во внимание, что вершины А и В имеют координаты (1, 0) и (0, 1), мы можем написать выражение для вышеупомянутой суммы квадратов расстояний переменной точки  до
до  треугольника:
треугольника:


Рис. 166.
Приравнивая нулю частные производные первого порядка, получим  и нетрудно показать, что этим значениям соответствует минимум
и нетрудно показать, что этим значениям соответствует минимум  Исследуем теперь значения z на контуре треугольника. Для исследования z на стороне ОА надо в выражении для
Исследуем теперь значения z на контуре треугольника. Для исследования z на стороне ОА надо в выражении для  положить
положить 

причем  может меняться в промежутке (0, 1),
может меняться в промежутке (0, 1),
Поступая согласно [60], убедимся, что z на стороне ОА принимает наименьшее значение  в точке С, для которой
в точке С, для которой  Точно так же и на стороне ОВ наименьшее значение z будет равно
Точно так же и на стороне ОВ наименьшее значение z будет равно  и будет достигаться в точке D, для которой
и будет достигаться в точке D, для которой  . Для исследования значений z на стороне АВ надо, согласно уравнению (16), в выражении z положить
. Для исследования значений z на стороне АВ надо, согласно уравнению (16), в выражении z положить 

причем  может меняться в. промежутке (0, 1). В данном случае наименьшее значение z будет
может меняться в. промежутке (0, 1). В данном случае наименьшее значение z будет  и будет достигаться в точке Е, для которой
и будет достигаться в точке Е, для которой  Мы получаем, таким образом, следующую таблицу возможных наименьших значений функции:
Мы получаем, таким образом, следующую таблицу возможных наименьших значений функции:

Из этой таблицы мы видим, что наименьшее значение  будет достигаться в точке (
будет достигаться в точке ( ). Рассматриваемая задача может быть также решена и для любого треугольника, и искомая точка является центром тяжести треугольника.
). Рассматриваемая задача может быть также решена и для любого треугольника, и искомая точка является центром тяжести треугольника.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- ГЛАВА I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
- 1. Величина и ее измерение.
- 2. Число.
- 3. Величины постоянные и переменные.
- 4. Промежуток.
- 5. Понятие о функции.
- 6. Аналитический способ задания функциональной зависимости.
- 7. Неявные функции.
- 8. Табличный способ.
- 9. Графический способ изображения чисел.
- 10. Координаты.
- 11. График и уравнение кривой.
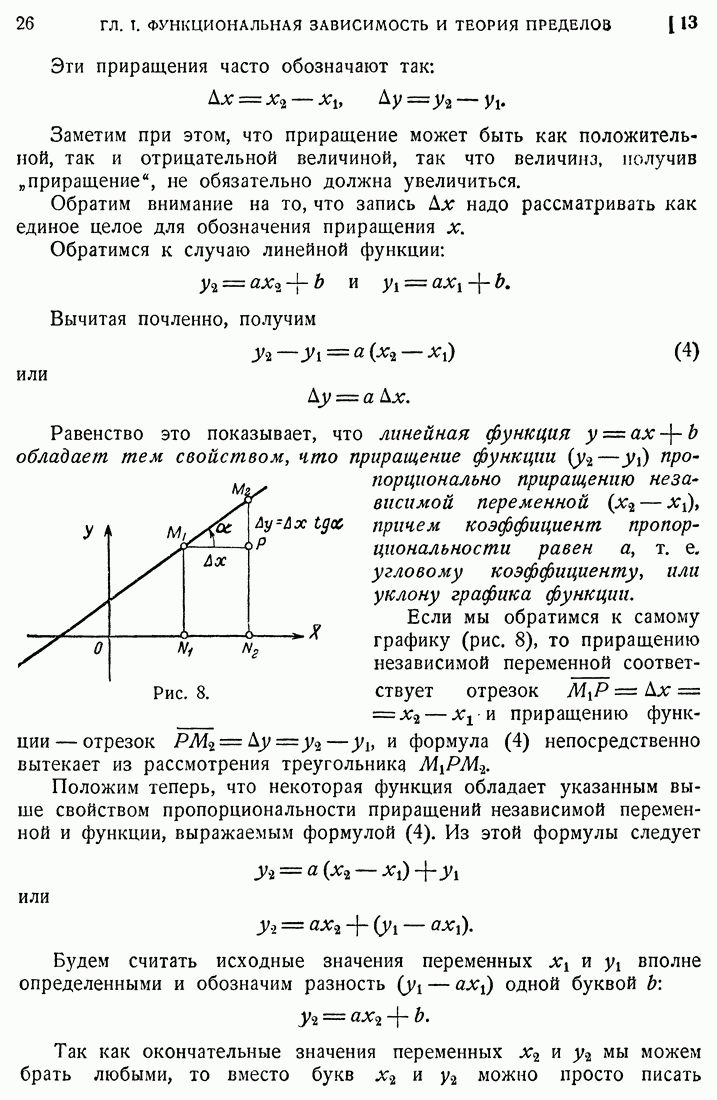
- 12. Линейная функция.
- 13. Приращение. Основное свойство линейной функции.
- 14. График равномерного движения.
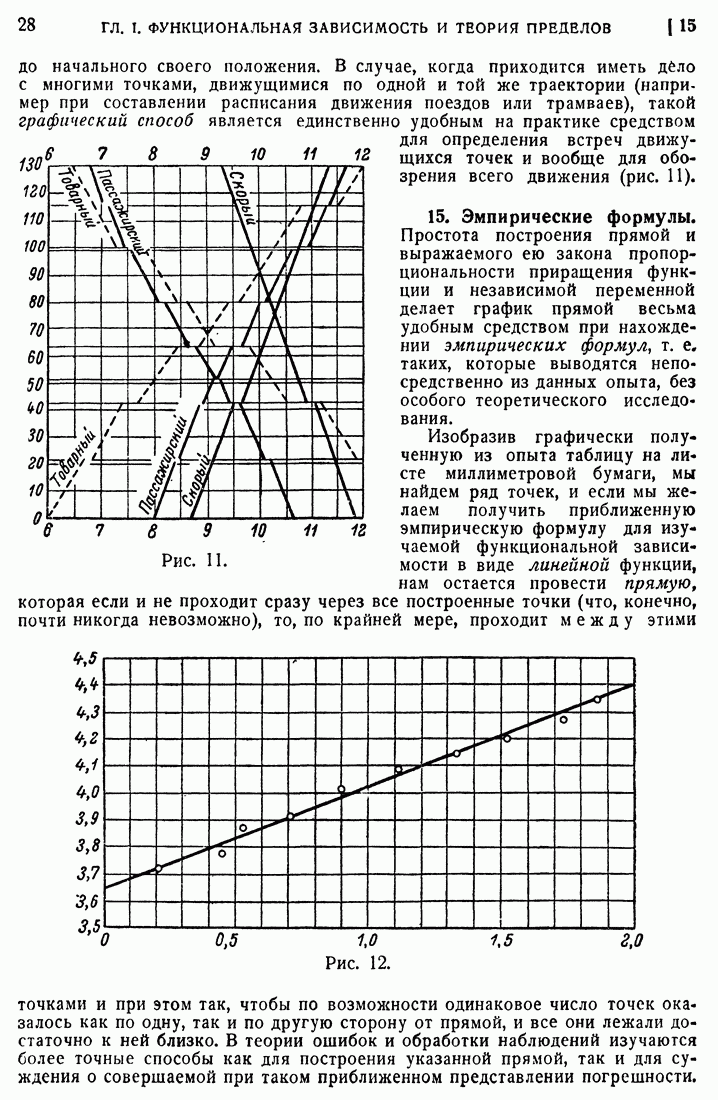
- 15. Эмпирические формулы.
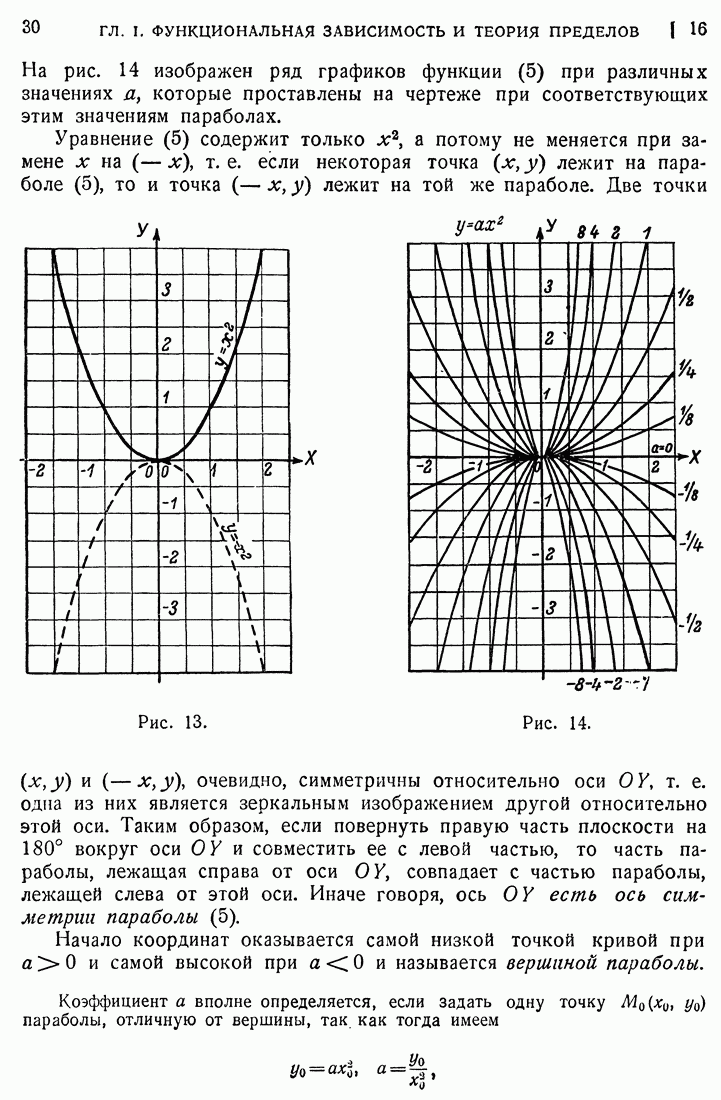
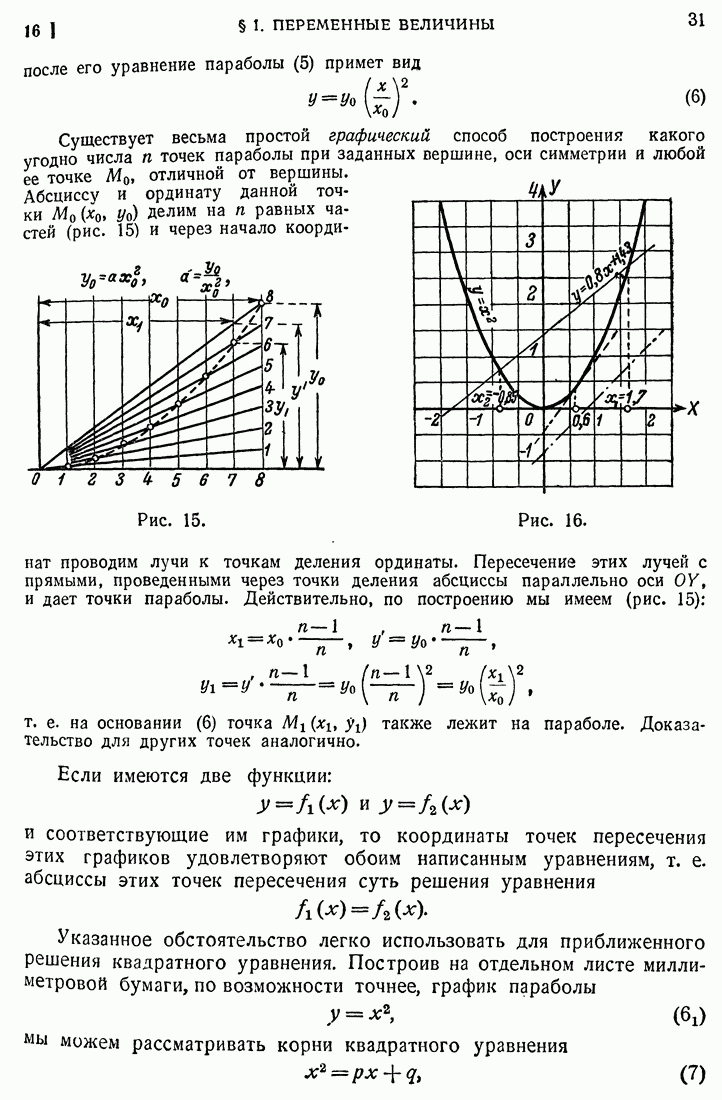
- 16. Парабола второй степени.
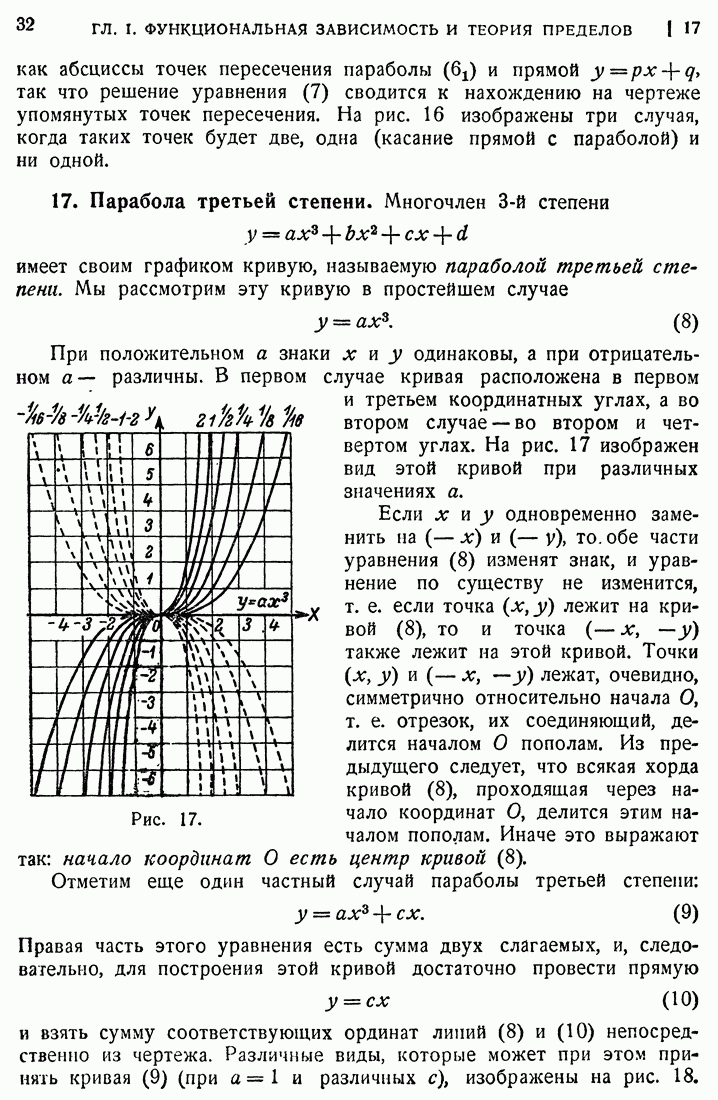
- 17. Парабола третьей степени.
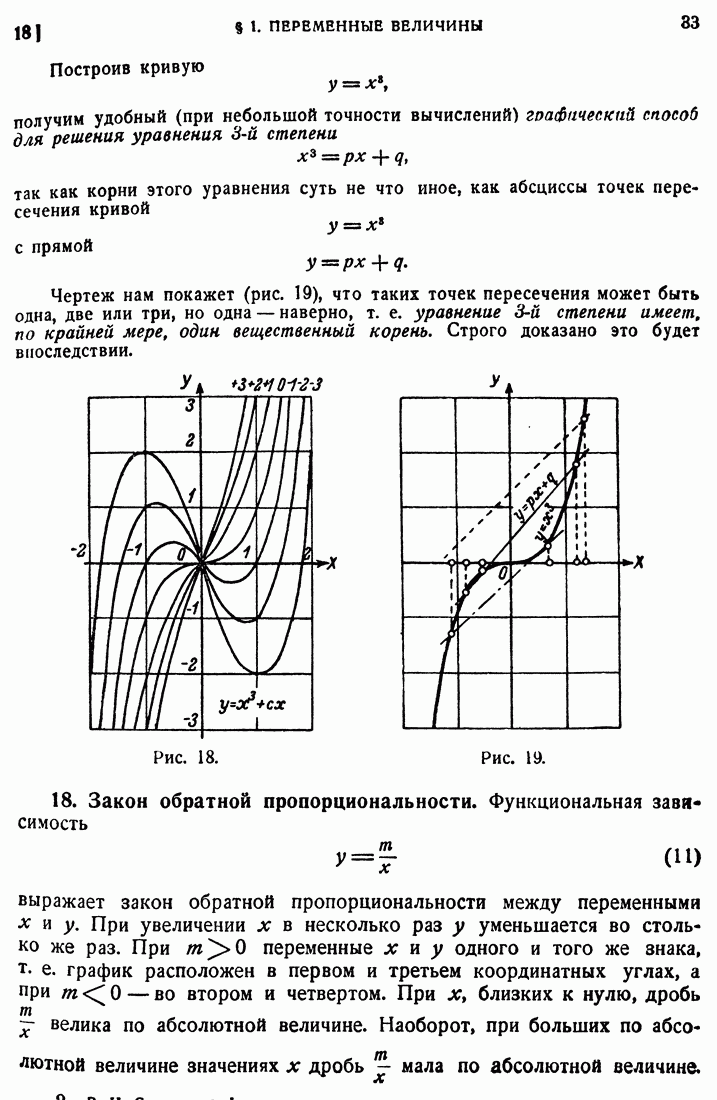
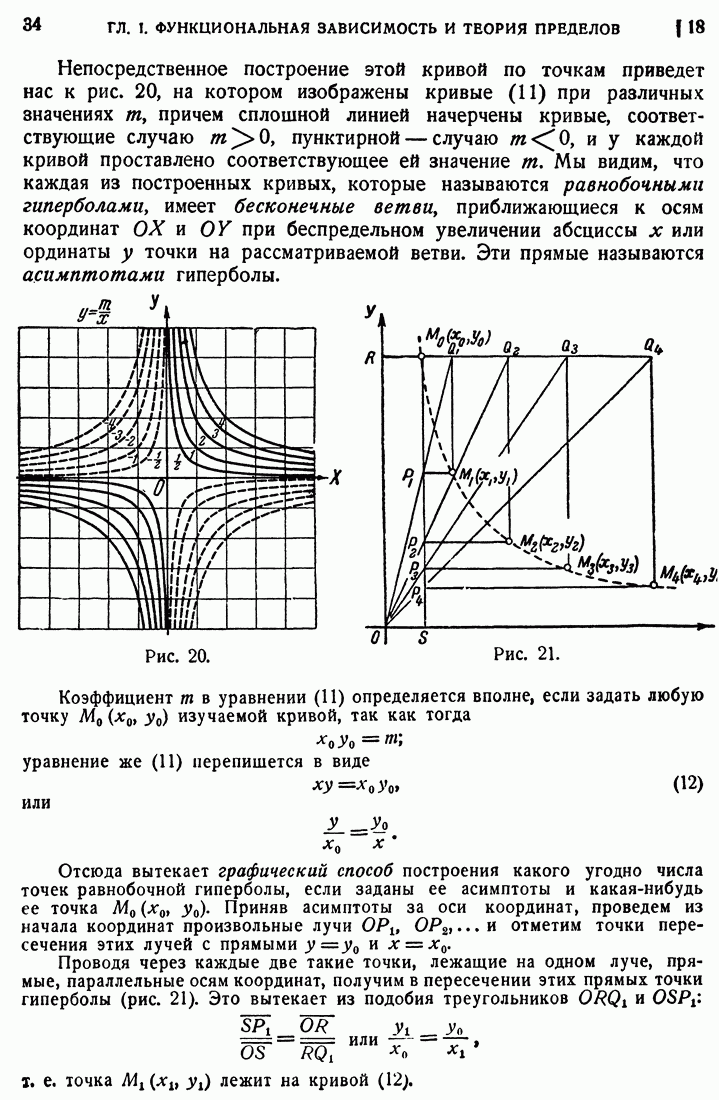
- 18. Закон обратной пропорциональности.
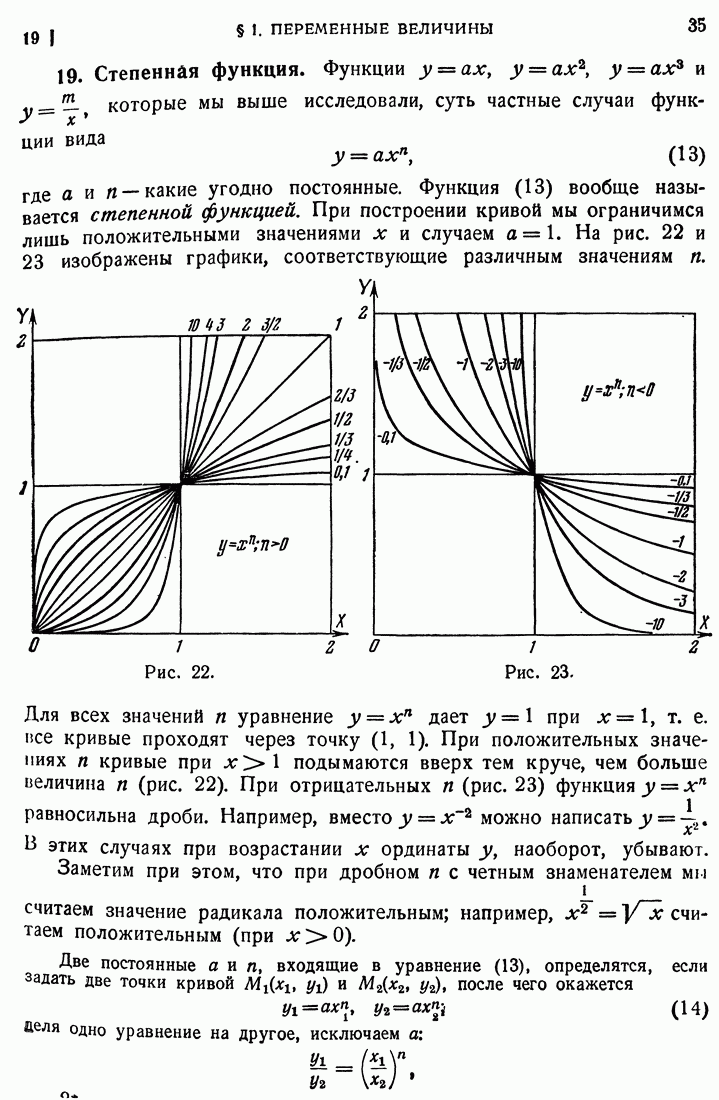
- 19. Степенная функция.
- 20. Обратные функции.
- 21. Многозначность функции.
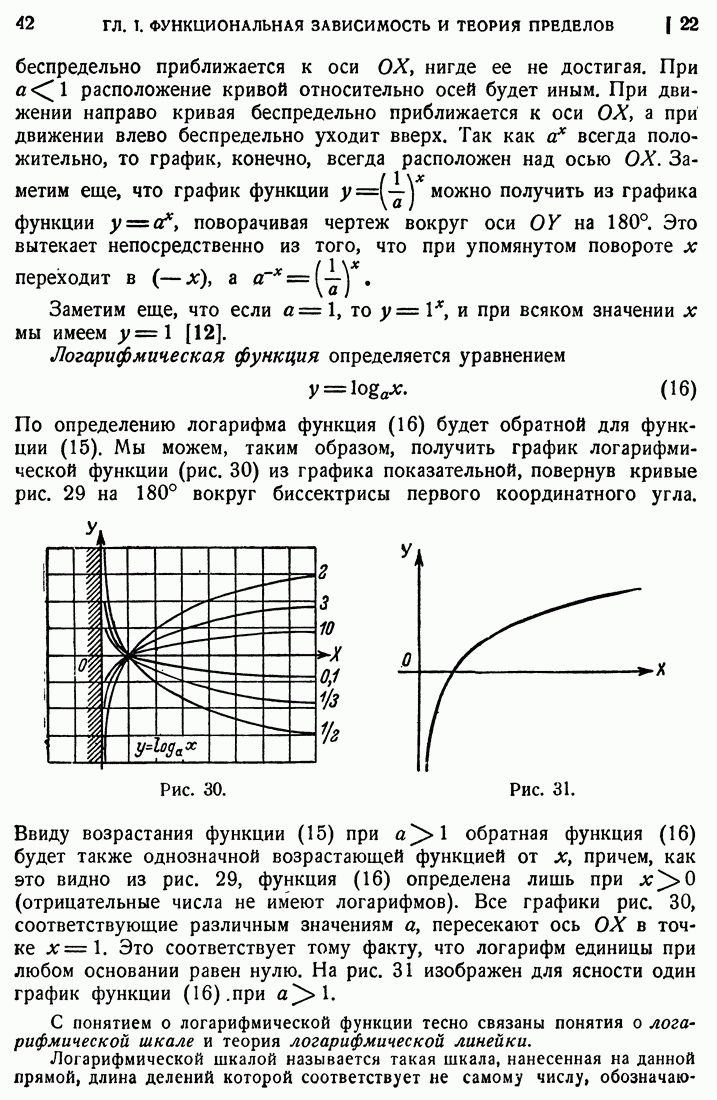
- 22. Показательная и логарифмическая функции.
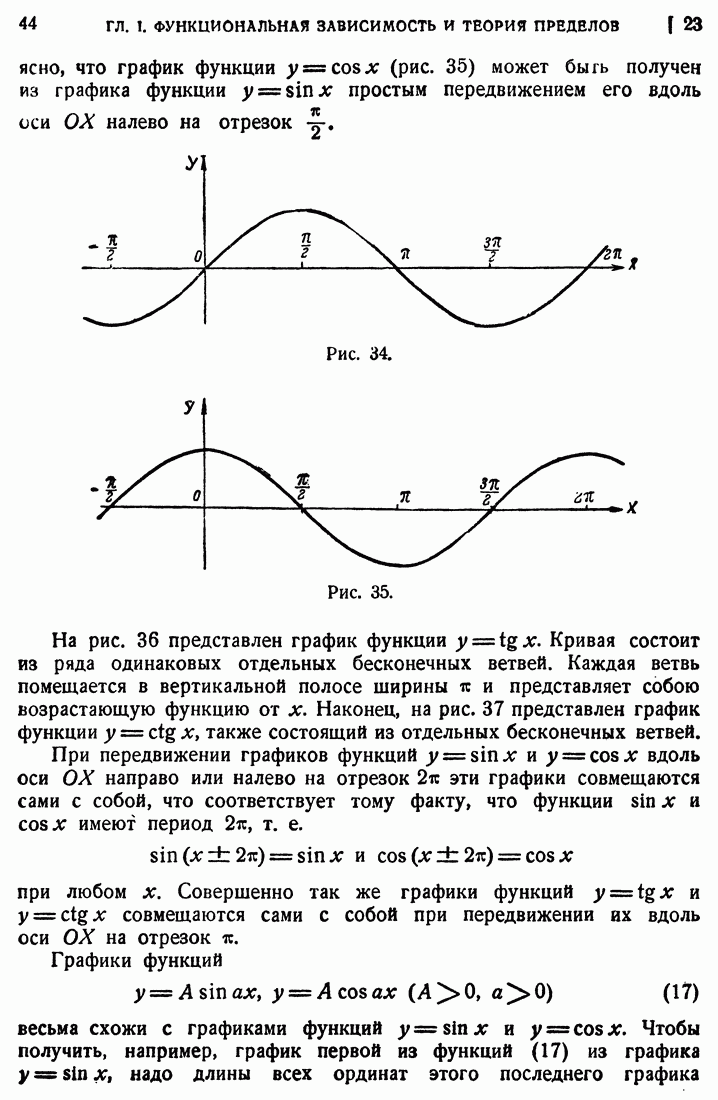
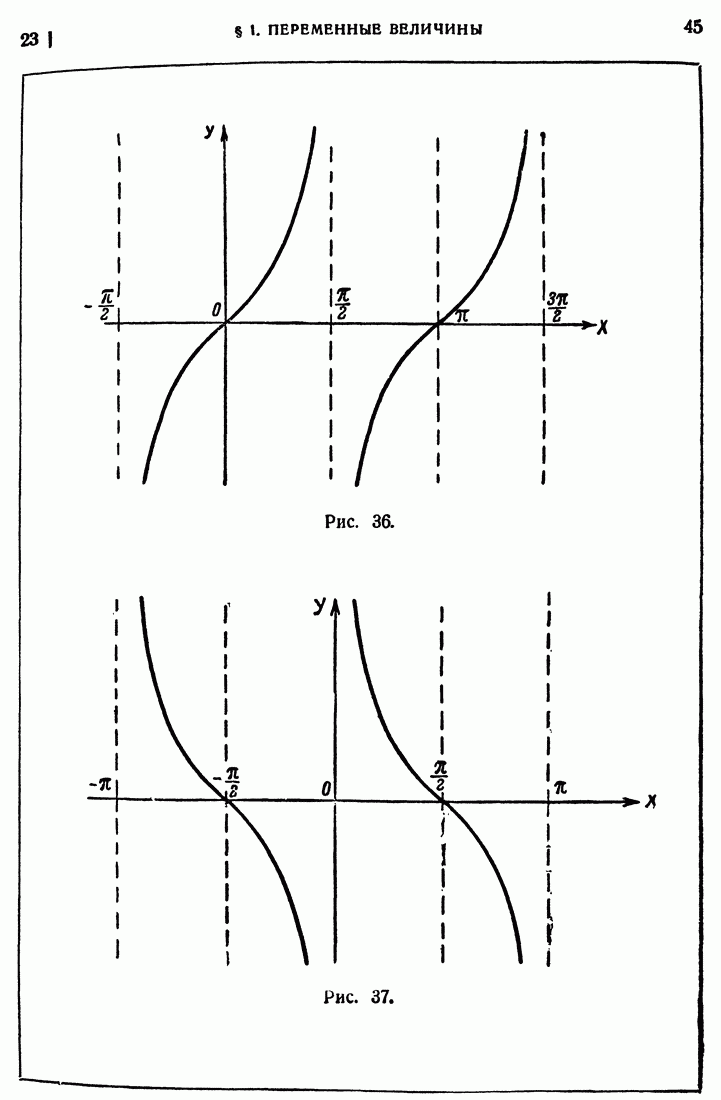
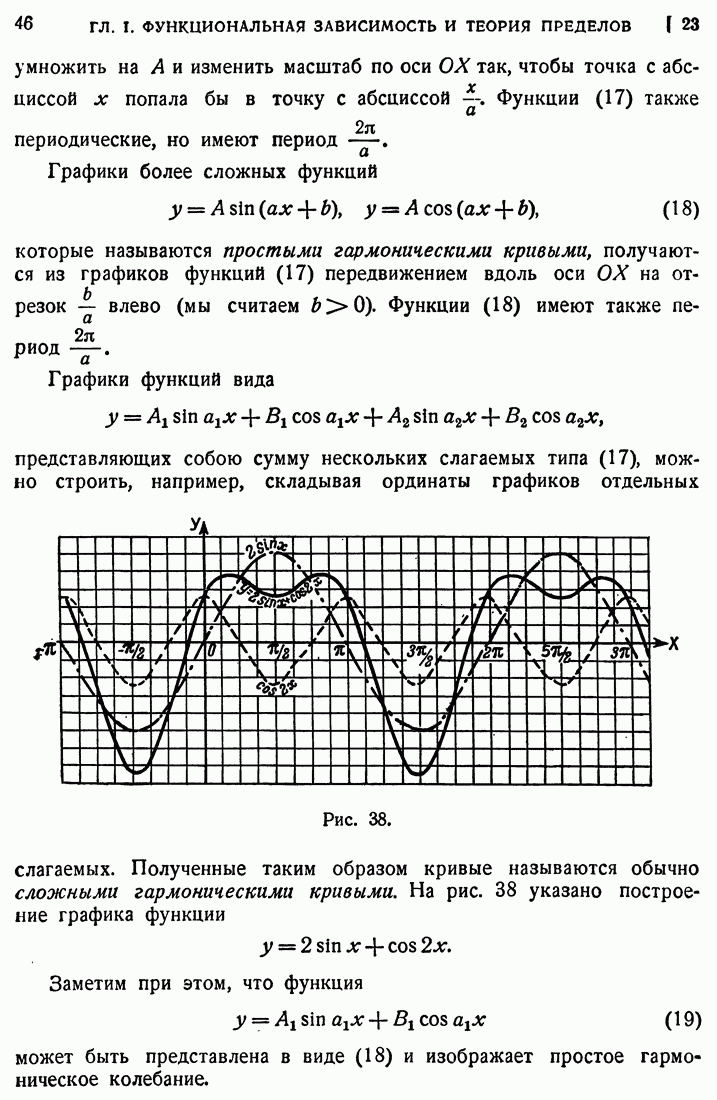
- 23. Тригонометрические функции.
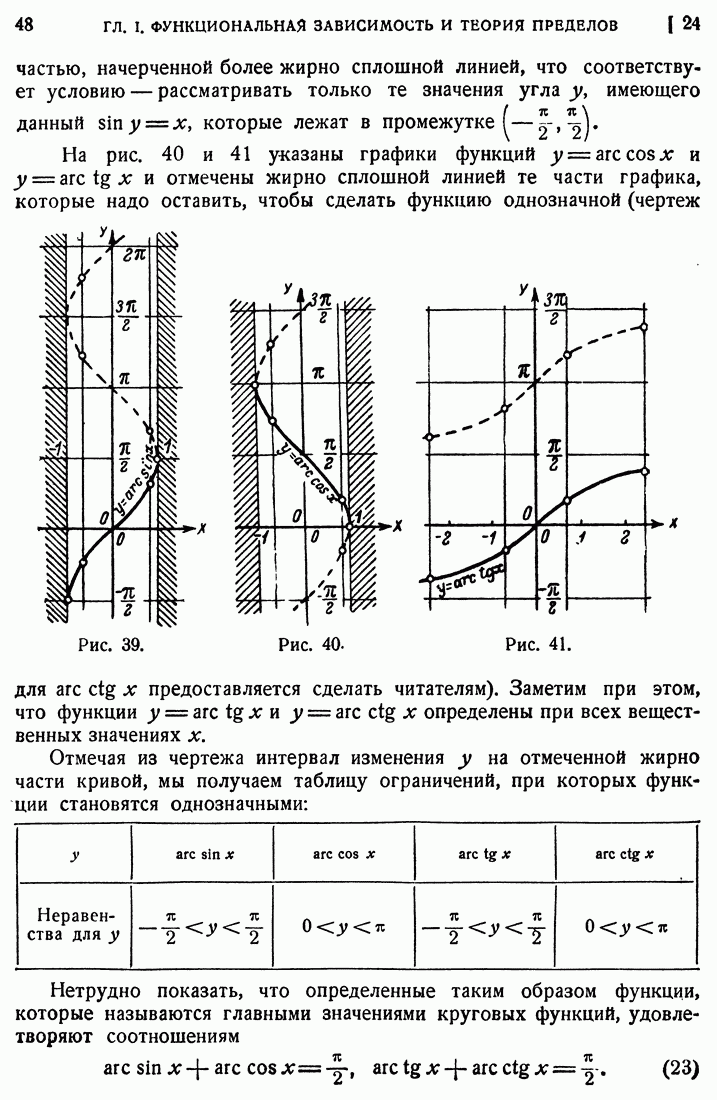
- 24. Обратные тригонометрические, или круговые, функции.
- § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ
- 25. Упорядоченное переменное.
- 26. Величины бесконечно малые.
- 27. Предел переменной величины.
- 28. Основные теоремы.
- 29. Величины бесконечно большие.
- 30. Монотонные переменные.
- 31. Признак Коши существования предела.
- 32. Одновременное изменение двух переменных величин, связанных функциональной зависимостью.
- 33. Примеры.
- 34. Непрерывность функции.
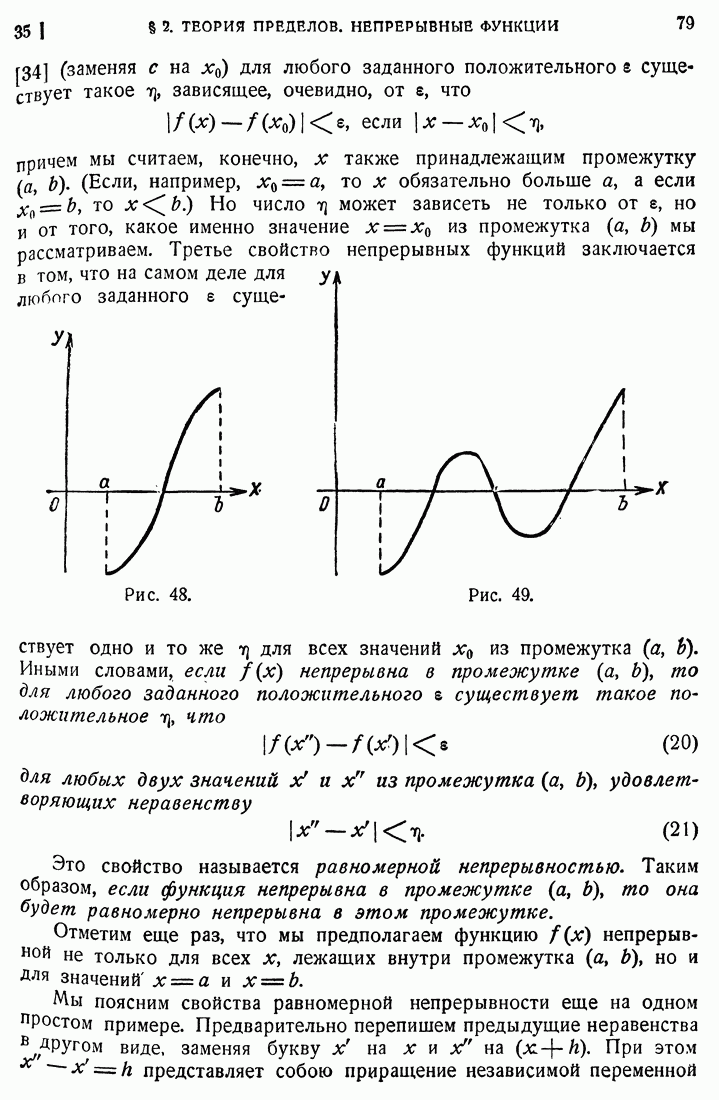
- 35. Свойства непрерывных функций.
- 36. Сравнение бесконечно малых и бесконечно больших величин.
- 37. Примеры.
- 38. Число е.
- 39. Недоказанные предложения.
- 40. Вещественные числа.
- 41. Действия над вещественными числами.
- 42. Точные границы числовых множеств. Признаки существования предела.
- 43. Свойства непрерывных функций.
- 44. Непрерывность элементарных функций.
- ГЛАВА II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
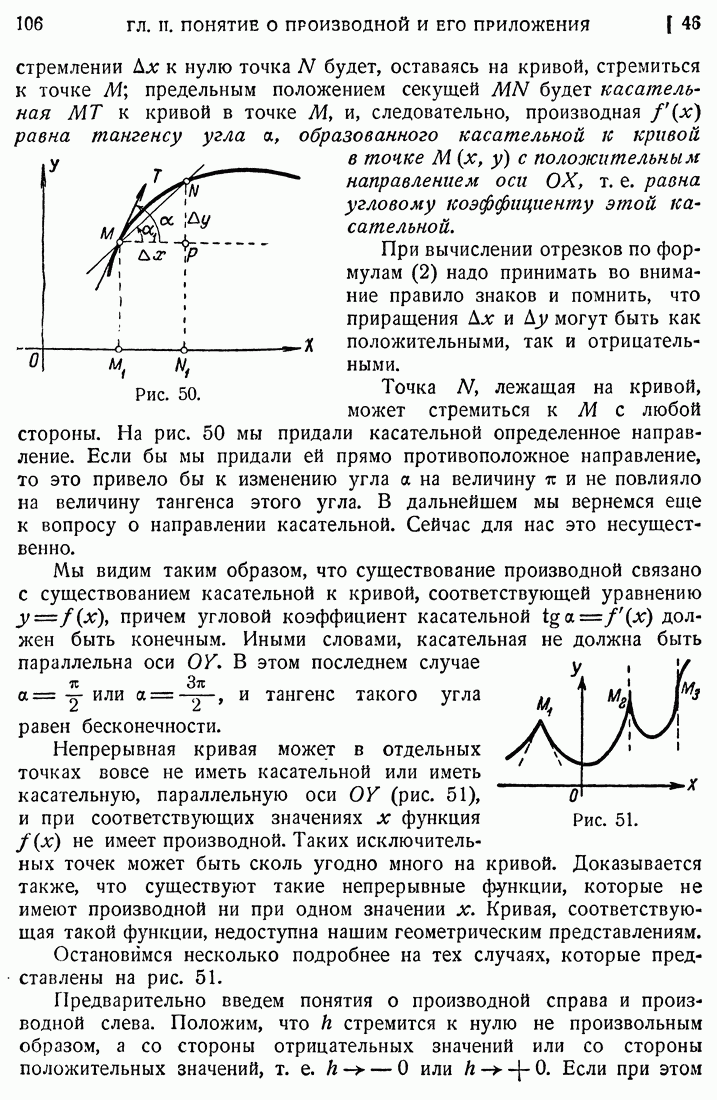
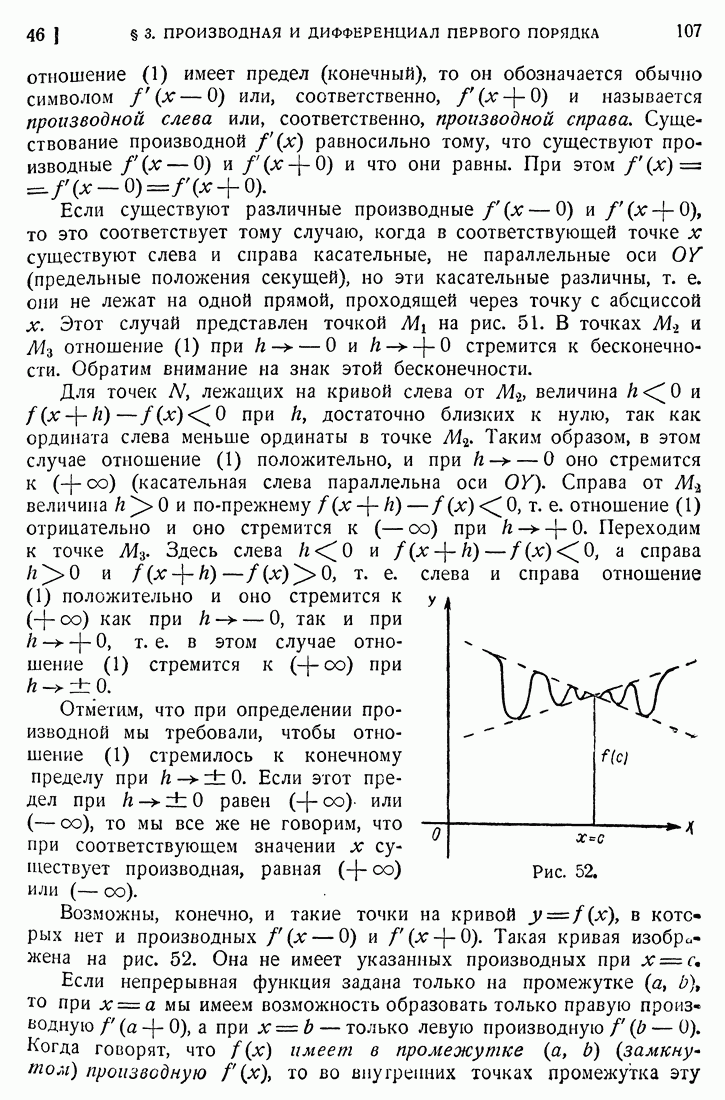
- 45. Понятие о производной.
- 46. Геометрическое значение производной.
- 47. Производные простейших функций.
- 48. Производные сложных и обратных функций.
- 49. Таблица производных и примеры.
- 50. Понятие о дифференциале.
- 51. Некоторые дифференциальные уравнения.
- 52. Оценка погрешностей.
- § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- 53. Производные высших порядков.
- 54. Механическое значение второй производной.
- 55. Дифференциалы высших порядков.
- 56. Разности функций.
- § 5. ПРИЛОЖЕНИЕ ПОНЯТИЯ О ПРОИЗВОДНОЙ К ИЗУЧЕНИЮ ФУНКЦИЙ
- 57. Признаки возрастания и убывания функций.
- 58. Максимумы и минимумы функций.
- 59. Построение графиков.
- 60. Наибольшее и наименьшее значения функций.
- 61. Теорема Ферма.
- 62. Теорема Ролля.
- 63. Формула Лагранжа.
- 64. Формула Коши.
- 65. Раскрытие неопределенностей.
- 66. Различные виды неопределенностей.
- § 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
- 68. Частные производные и полный дифференциал функции двух независимых переменных.
- 69. Производные сложных и неявных функций.
- § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОНЯТИЯ О ПРОИЗВОДНЫХ
- 70. Дифференциал дуги.
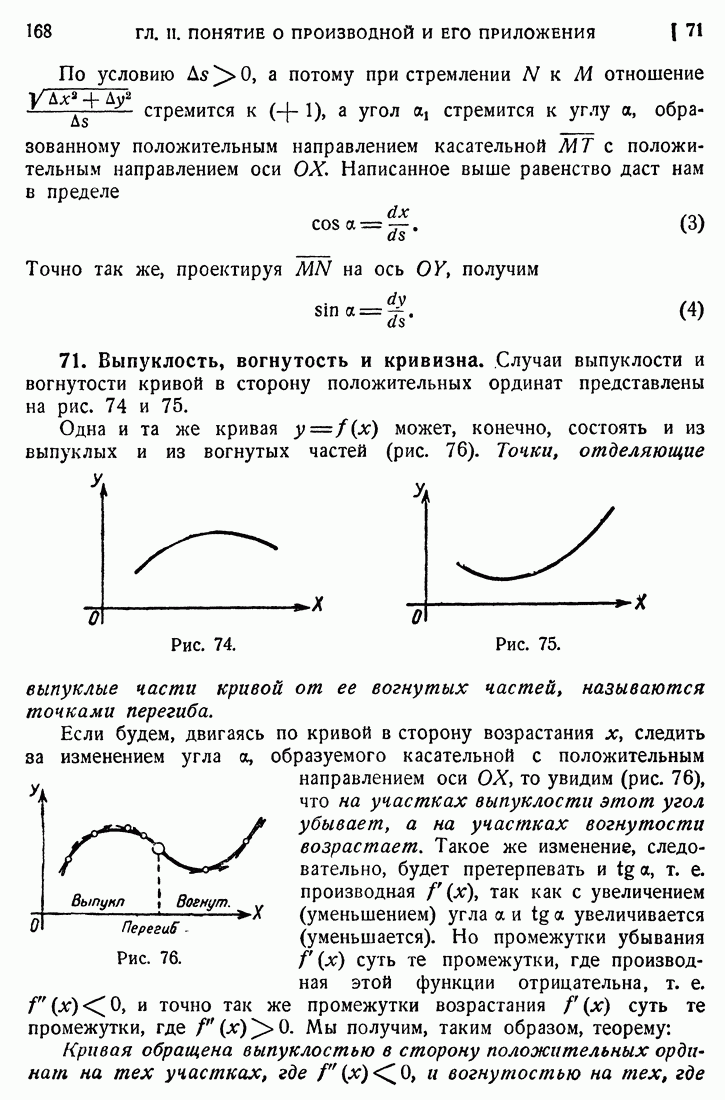
- 71. Выпуклость, вогнутость и кривизна.
- 72. Асимптоты.
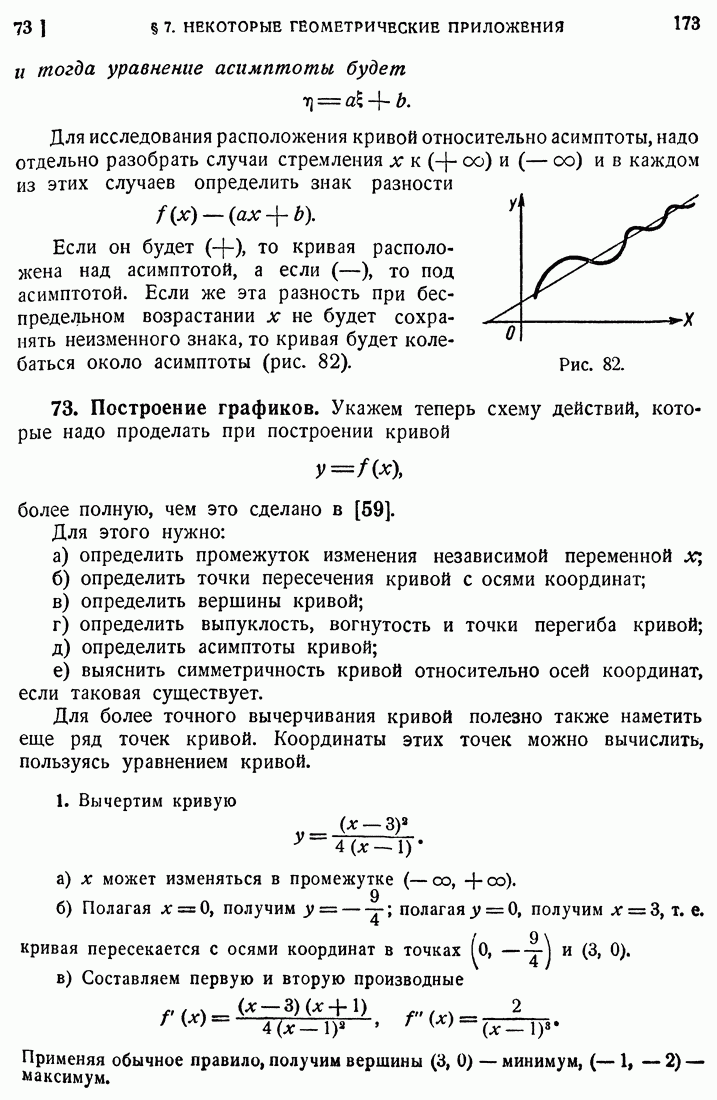
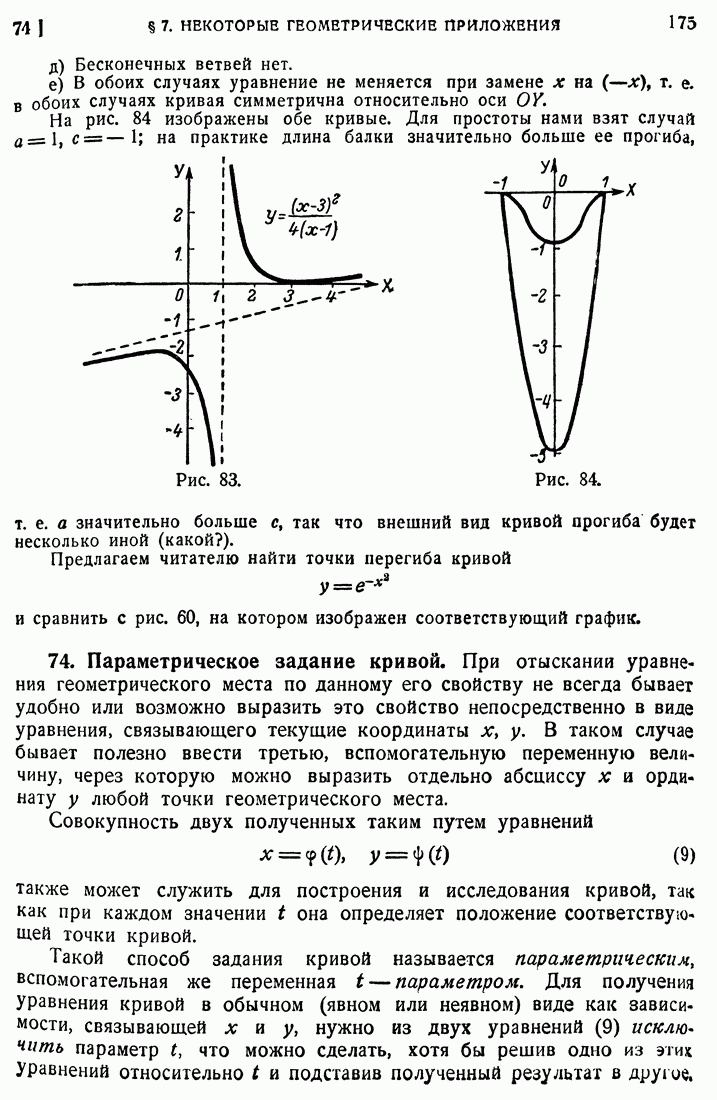
- 73. Построение графиков.
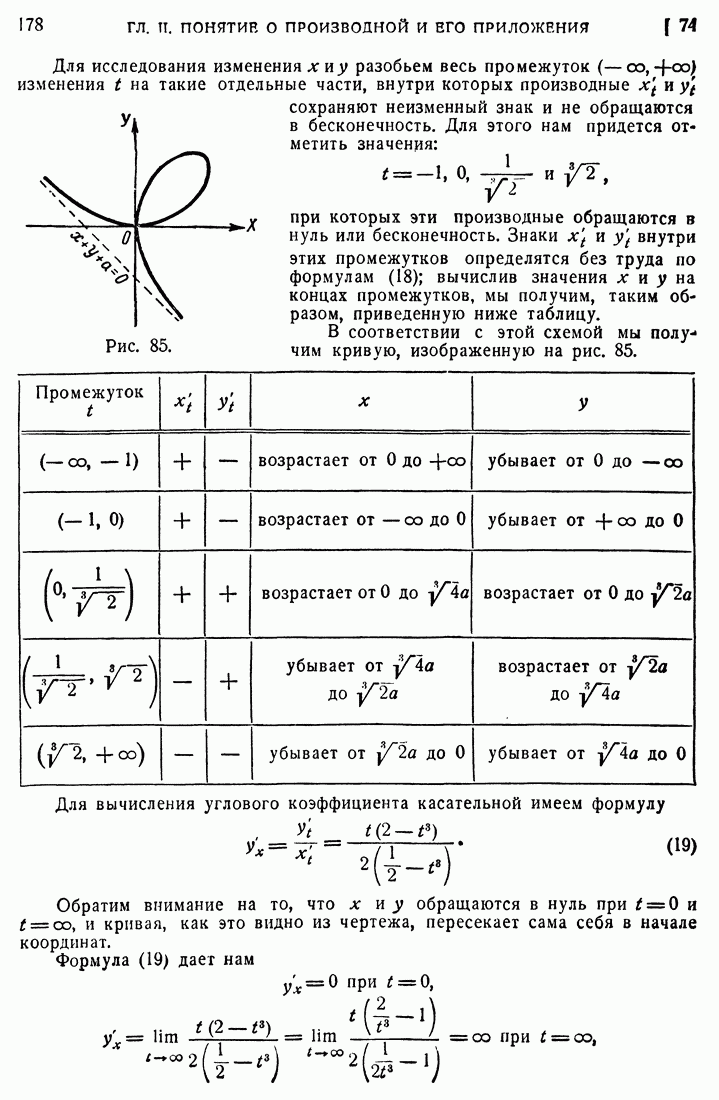
- 74. Параметрическое задание кривой.
- 75. Уравнение Ван-дер-Ваальса.
- 76. Особые точки кривых.
- 77. Элементы кривой.
- 78. Цепная линия.
- 79. Циклоида.
- 80. Эпициклоиды и гипоциклоиды.
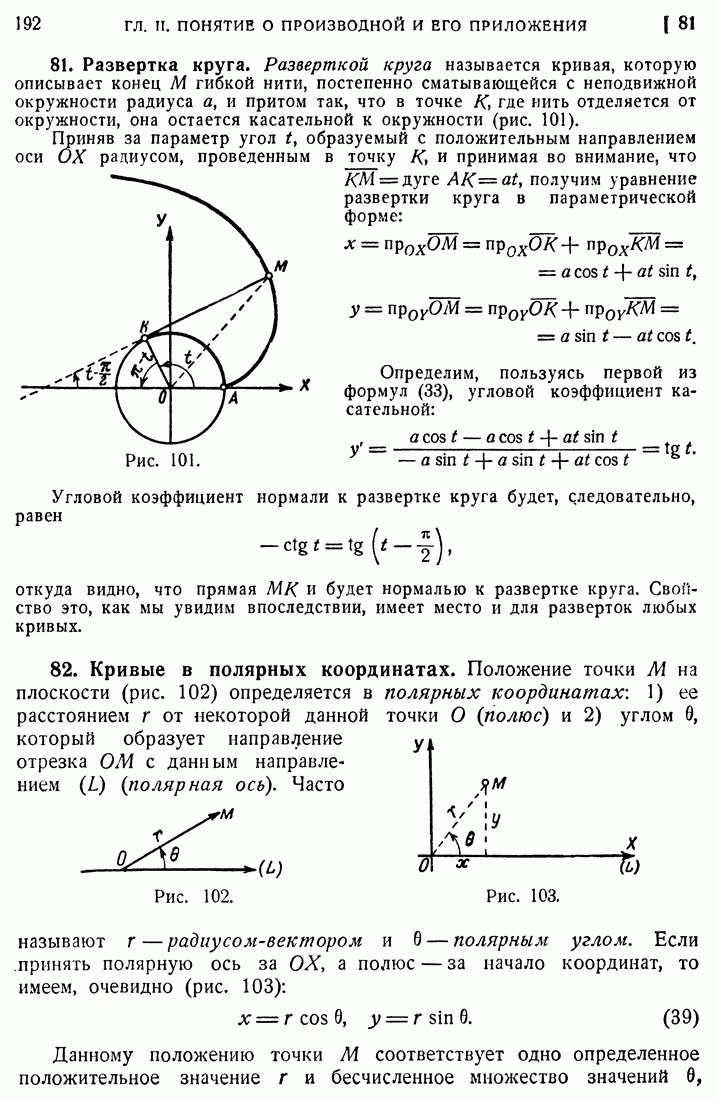
- 81. Развертка круга.
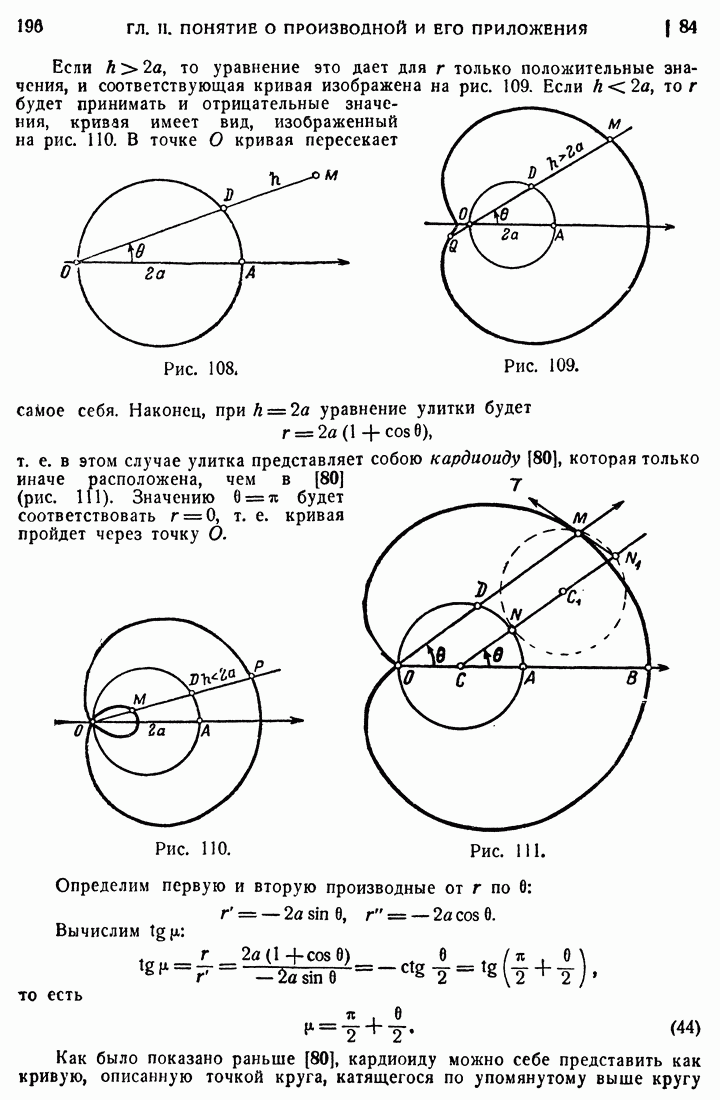
- 82. Кривые в полярных координатах.
- 83. Спирали.
- 85. Овалы Кассини и лемниската.
- ГЛАВА III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
- 86. Понятие о неопределенном интеграле.
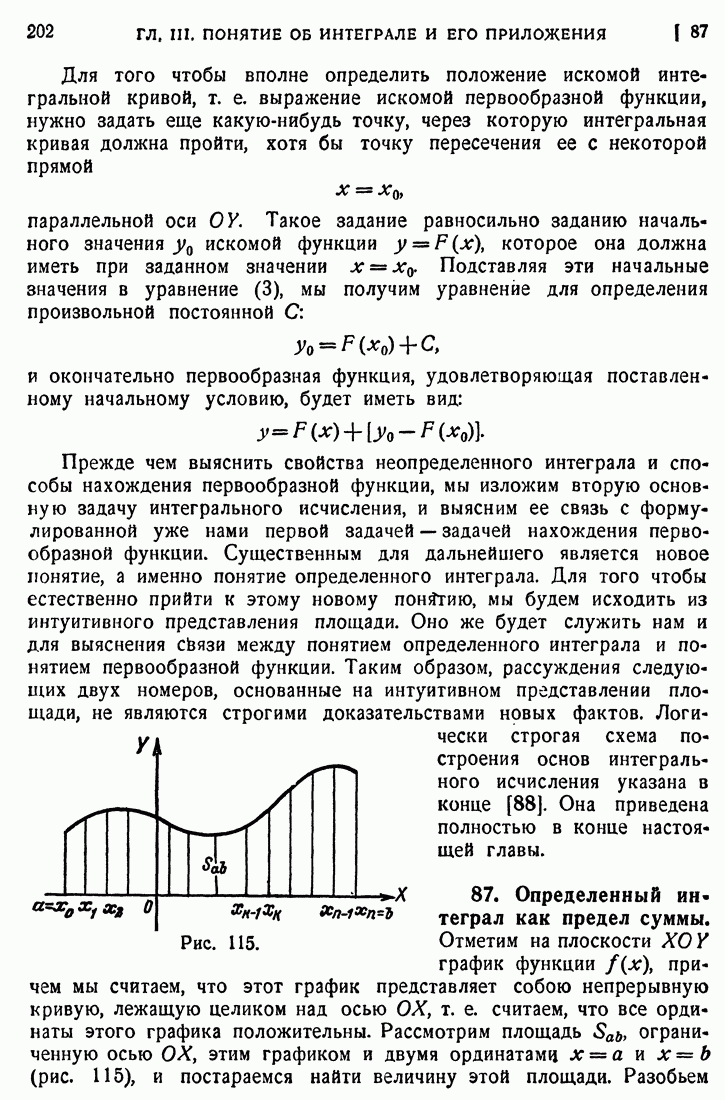
- 87. Определенный интеграл как предел суммы.
- 88. Связь определенного и неопределенного интегралов.
- 89. Свойства неопределенного интеграла.
- 90. Таблица простейших интегралов.
- 91. Правило интегрирования по частям.
- 92. Правило замены переменных. Примеры.
- 93. Примеры дифференциальных уравнений первого порядка.
- § 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 94. Основные свойства определенного интеграла.
- 95. Теорема о среднем.
- 96. Существование первообразной функции.
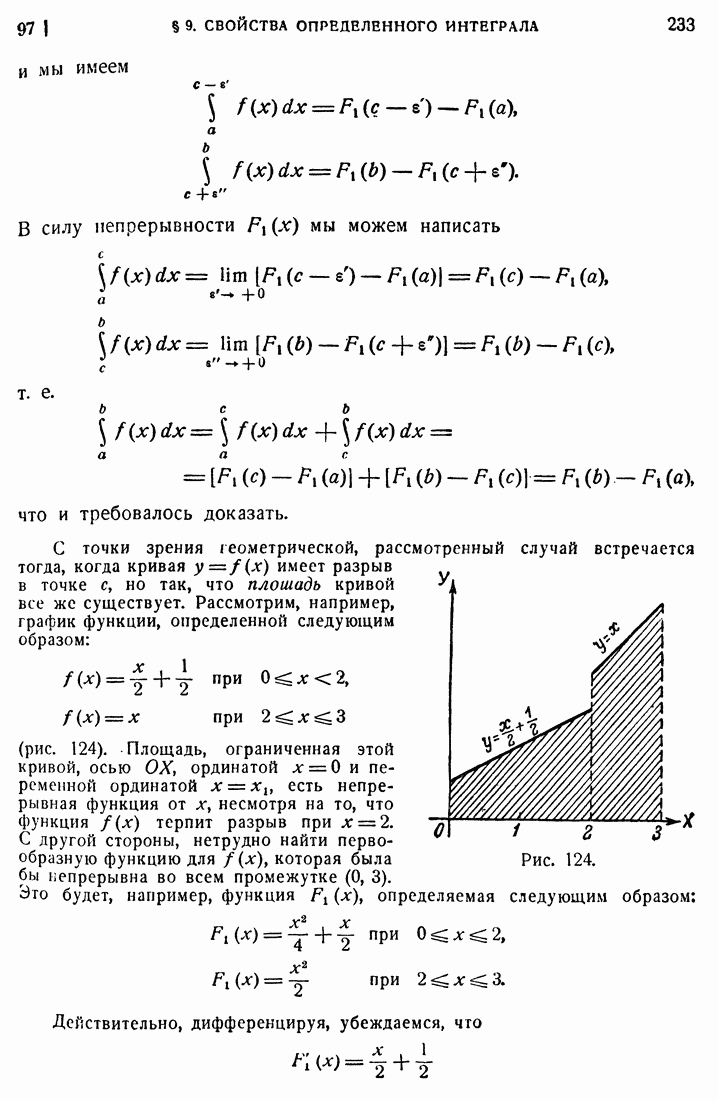
- 97. Разрыв подынтегральной функции.
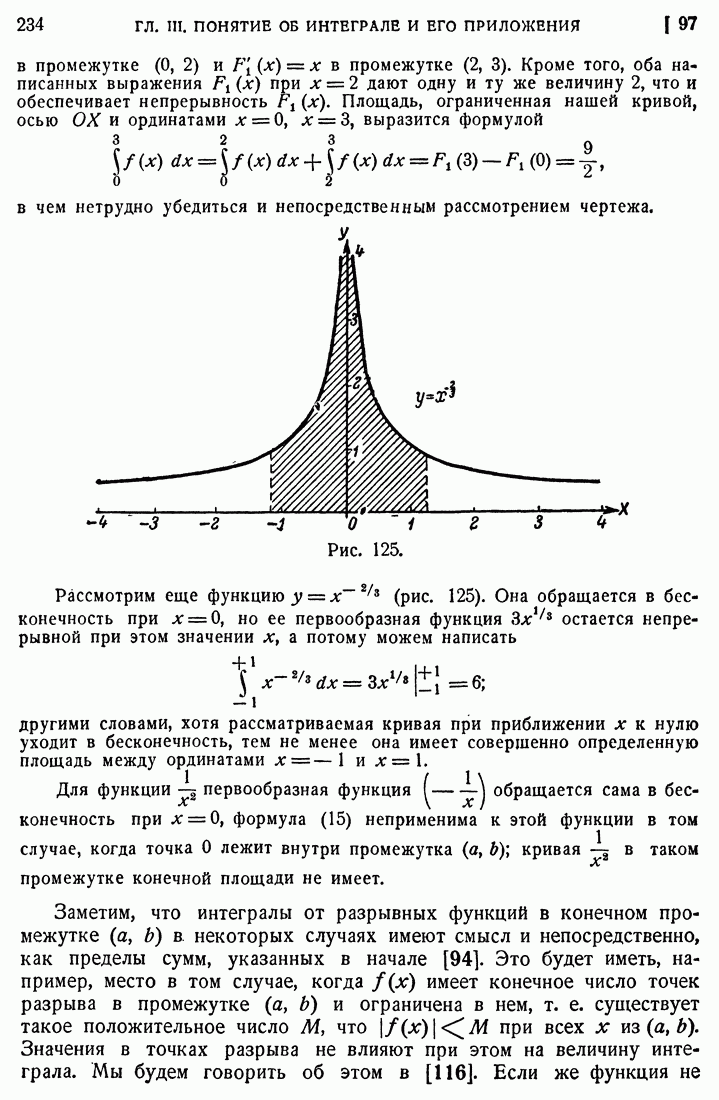
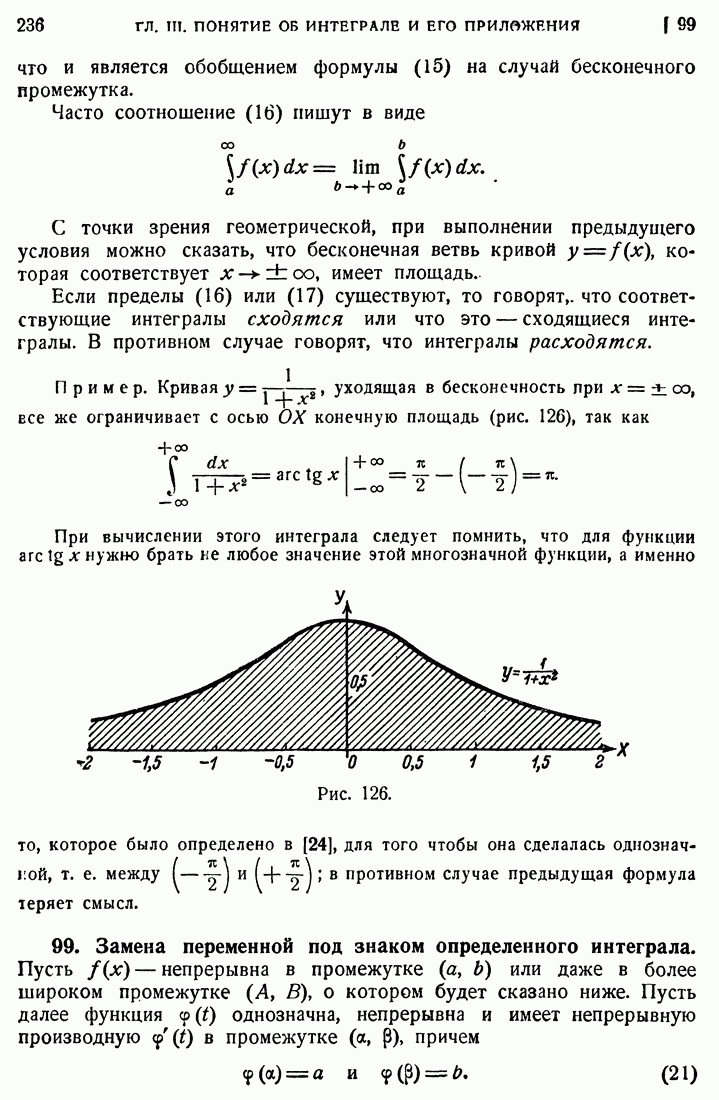
- 98. Бесконечные пределы.
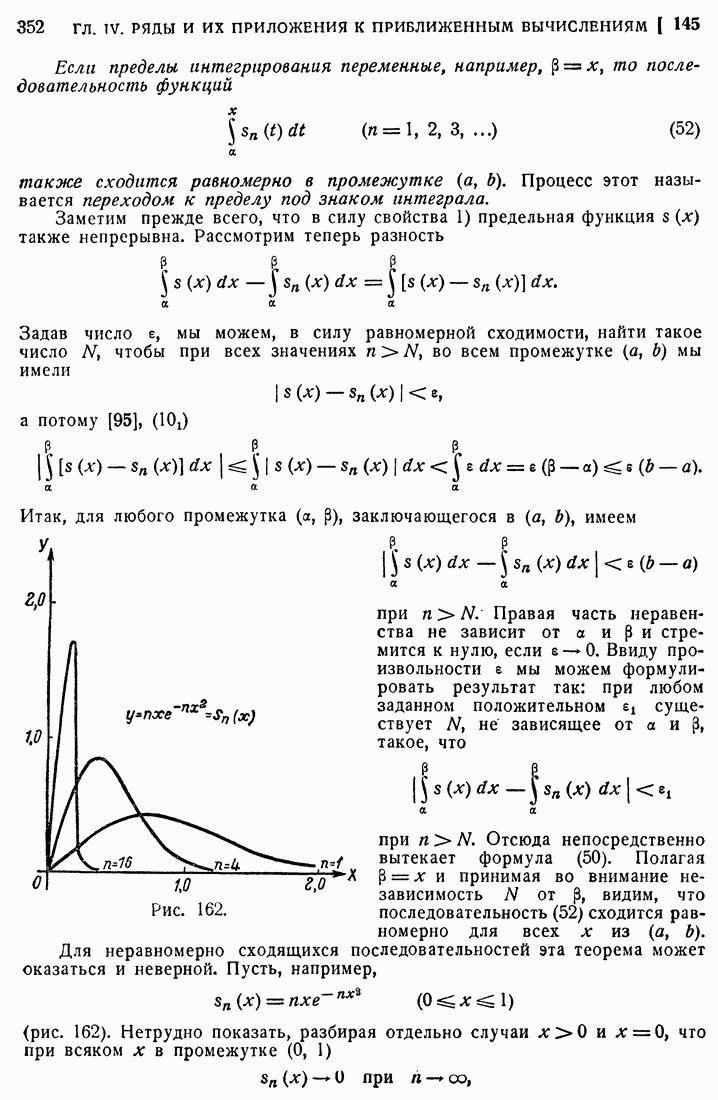
- 99. Замена переменной под знаком определенного интеграла.
- 100. Интегрирование по частям.
- § 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
- 101. Вычисление площадей.
- 102. Площадь сектора.
- 103. Длина дуги.
- 104. Вычисление объемов тел по их поперечным сечениям.
- 105. Объем тела вращения.
- 106. Поверхность тела вращения.
- 107. Определение центров тяжести. Теоремы Гульдина.
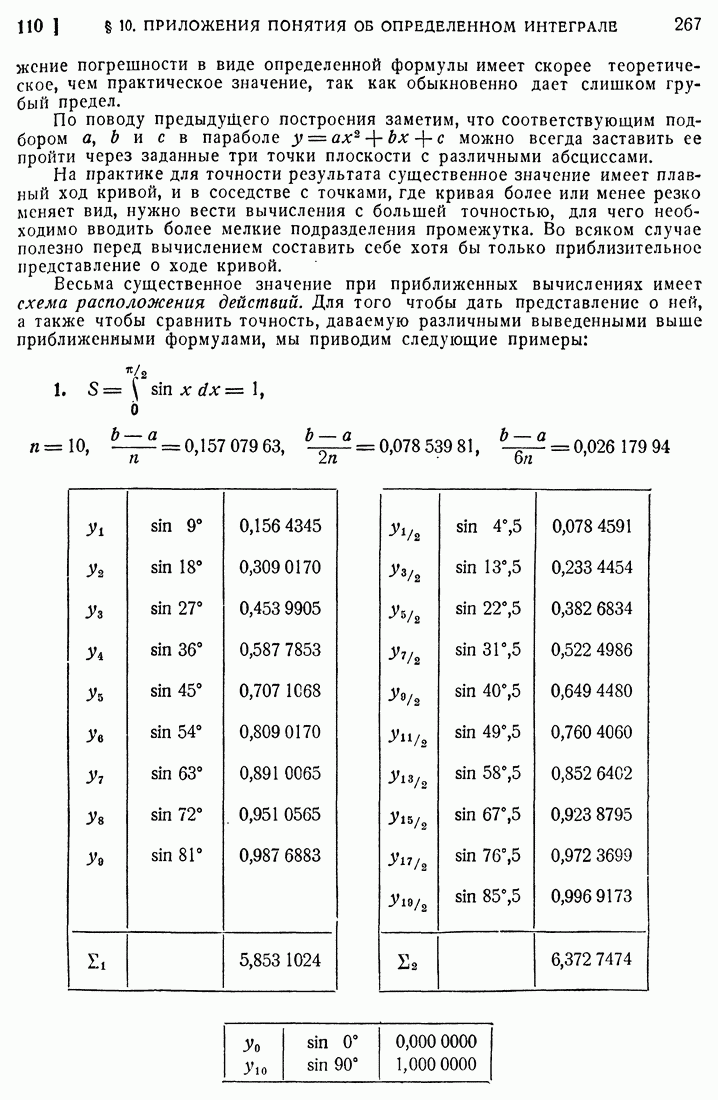
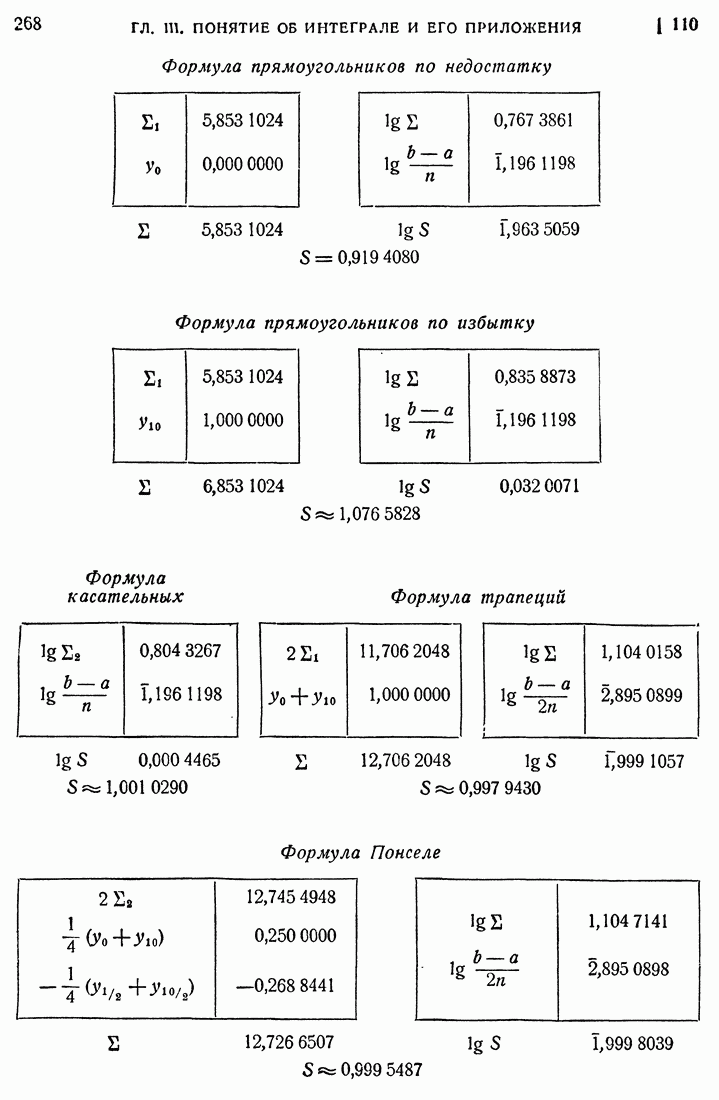
- 108. Приближенное вычисление определенных интегралов; формулы прямоугольников и трапеций.
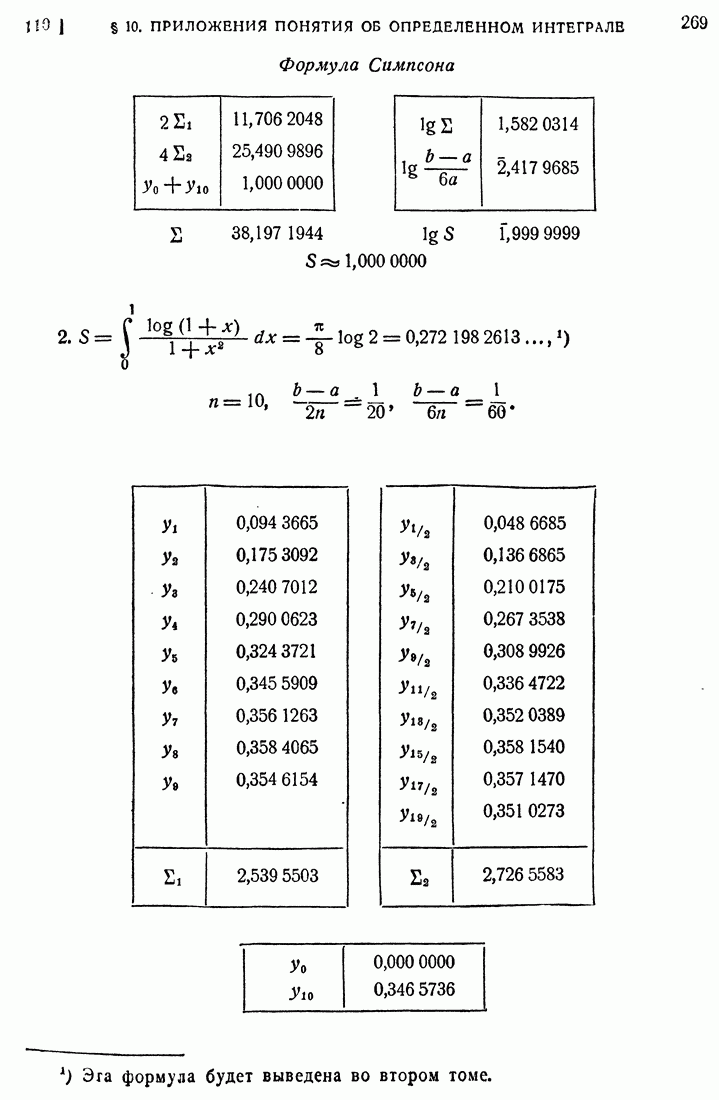
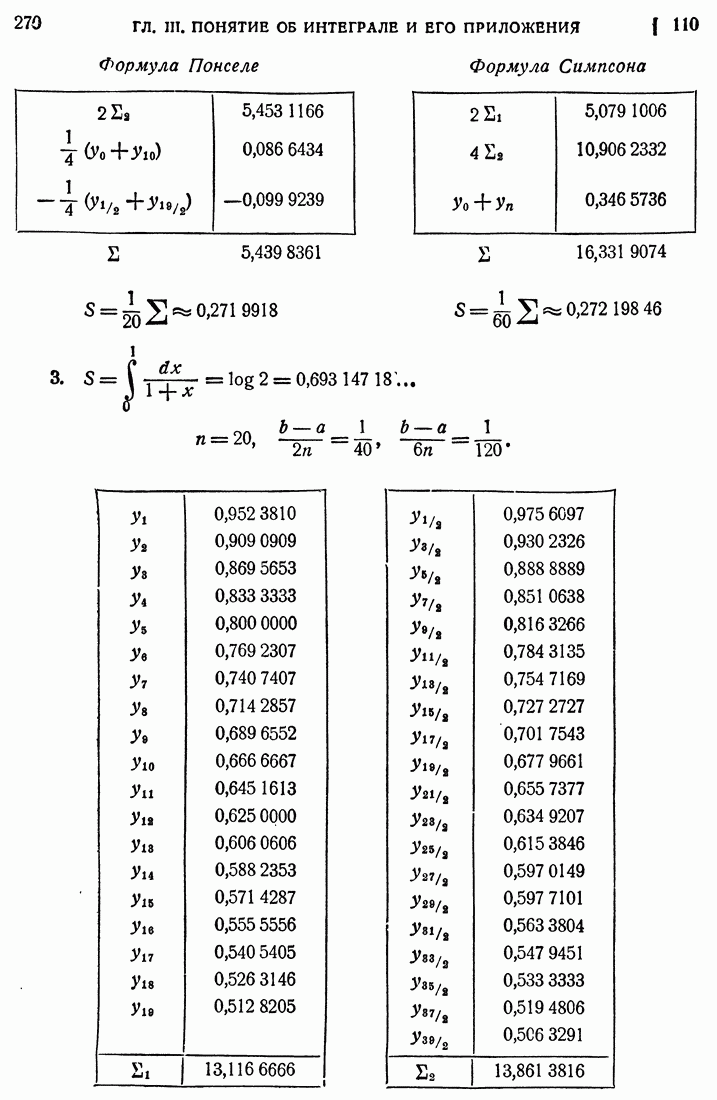
- 109. Формула касательных и формула Понселе.
- 110. Формула Симпсона.
- 111. Вычисление определенного интеграла с переменным верхним пределом.
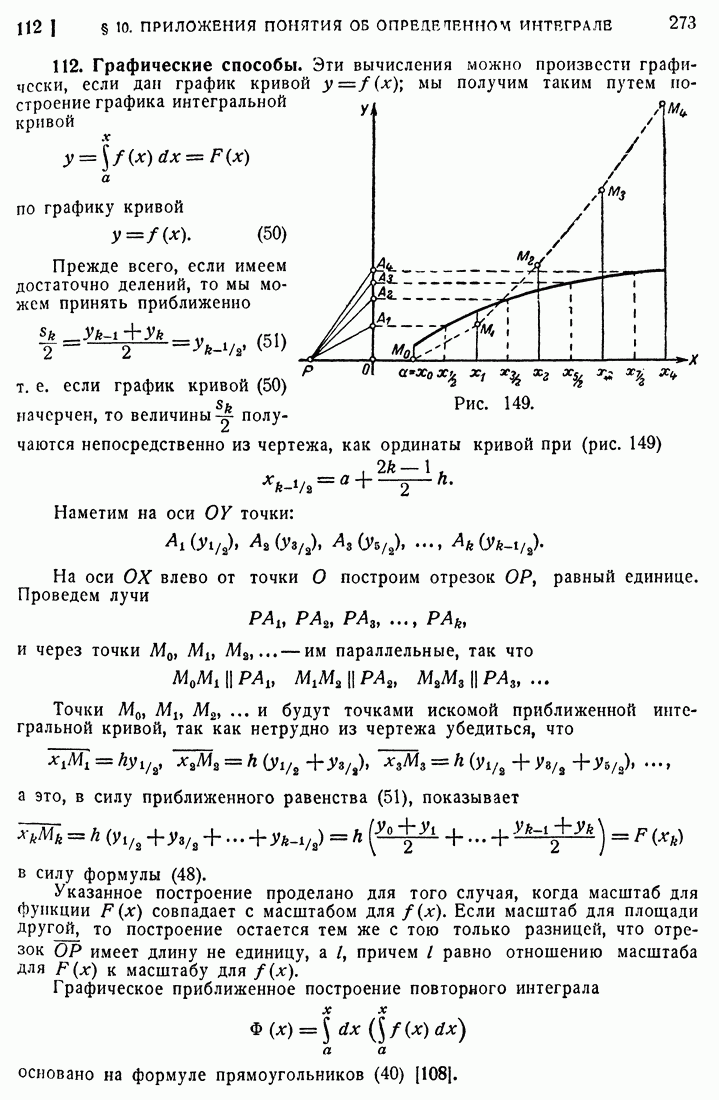
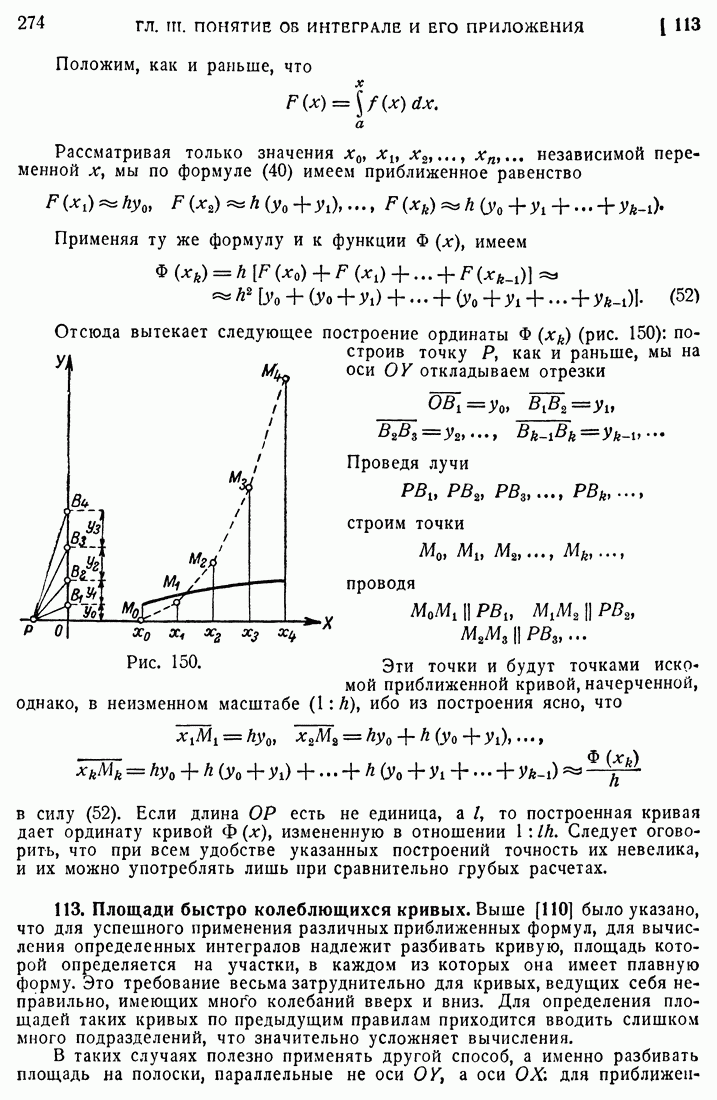
- 112. Графические способы.
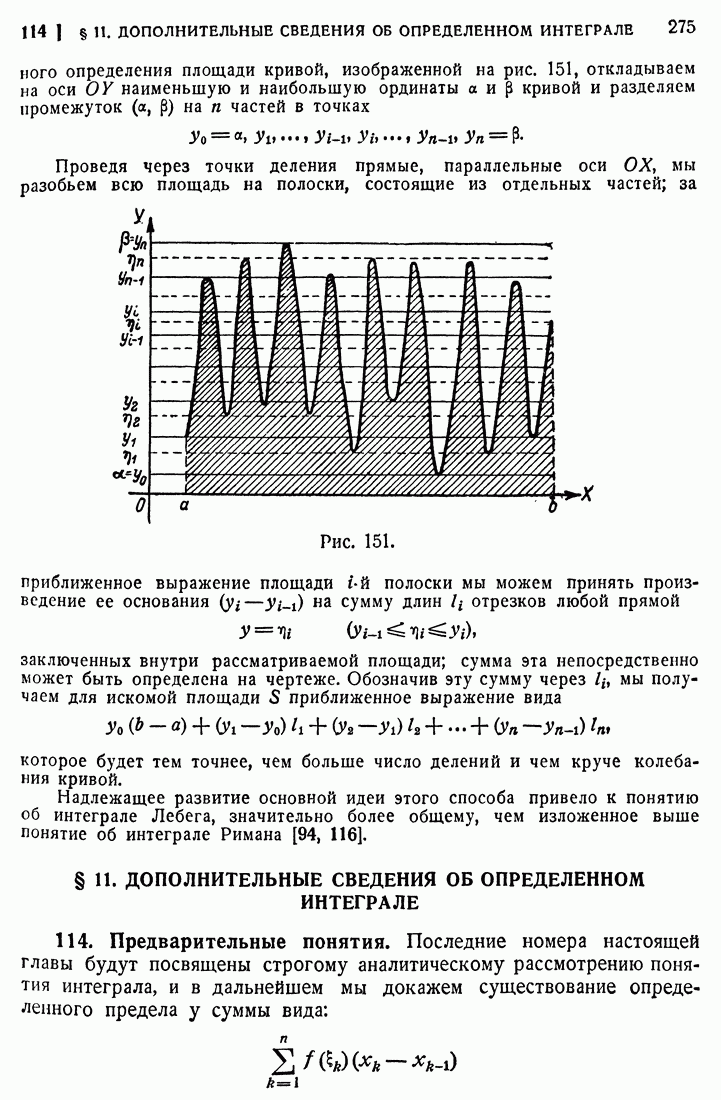
- 113. Площади быстро колеблющихся кривых.
- § 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
- 115. Разбиение промежутка на части и образование различных сумм.
- 116. Интегрируемые функции.
- 117. Свойства интегрируемых функций.
- ГЛАВА IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
- 118. Понятие о бесконечном ряде.
- 119. Основные свойства бесконечных рядов.
- 120. Ряды с положительными членами. Признаки сходимости.
- 121. Признаки Коши и Даламбера.
- 122. Интегральный признак сходимости Коши.
- 123. Знакопеременные ряды.
- 124. Абсолютно сходящиеся ряды.
- 125. Общий признак сходимости.
- § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ
- 126. Формула Тейлора.
- 127. Различные виды формулы Тейлора.
- 128. Ряды Тейлора и Маклорена.
- 129. Разложение exp(x).
- 130. Разложение sin x и cos x.
- 131. Бином Ньютона.
- 132. Разложение log(1+x).
- 133. Разложение arctg x.
- 134. Приближенные формулы.
- 135. Максимумы, минимумы и точки перегиба.
- 136. Раскрытие неопределенностей.
- § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ
- 137. Свойства абсолютно сходящихся рядов.
- 138. Умножение абсолютно сходящихся рядов.
- 139. Признак Куммера.
- 140. Признак Гаусса.
- 141. Гипергеометрический ряд.
- 142. Двойные ряды.
- 143. Ряды с переменными членами. Равномерно сходящиеся ряды.
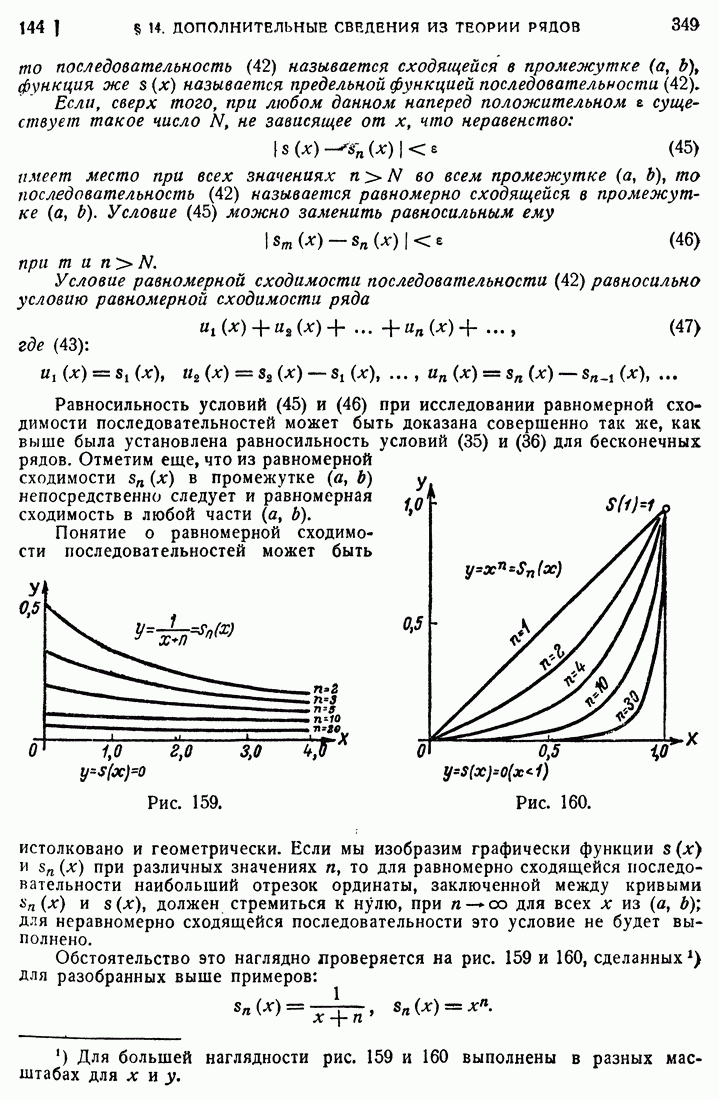
- 144. Равномерно сходящиеся последовательности функций.
- 145. Свойства равномерно сходящихся последовательностей.
- 146. Свойства равномерно сходящихся рядов.
- 147. Признаки равномерной сходимости.
- 148. Степенные ряды. Радиус сходимости.
- 149. Вторая теорема Абеля.
- 150. Дифференцирование и интегрирование степенного ряда.
- ГЛАВА V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ
- 152. О предельном переходе.
- 153. Частные производные и полный дифференциал первого порядка.
- 154. Однородные функции.
- 155. Частные производные высших порядков.
- 156. Дифференциалы высших порядков.
- 157. Неявные функции.
- 158. Пример.
- 159. Существование неявных функций.
- 160. Кривые в пространстве и поверхности.
- § 16. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 161. Распространение формулы Тейлора на случай функции от нескольких независимых переменных.
- 162. Необходимые условия максимума и минимума функции.
- 163. Исследование максимума и минимума функции двух независимых переменных.
- 164. Примеры.
- 165. Дополнительные замечания о нахождении максимумов и минимумов функции.
- 166. Наибольшее и наименьшее значения функции.
- 167. Относительные максимумы и минимумы.
- 168. Дополнительные замечания.
- 169. Примеры.
- ГЛАВА VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
- 170. Комплексные числа.
- 171. Сложение и вычитание комплексных чисел.
- 172. Умножение комплексных чисел.
- 173. Деление комплексных чисел.
- 174. Возвышение в степень.
- 175. Извлечение корня.
- 176. Показательная функция.
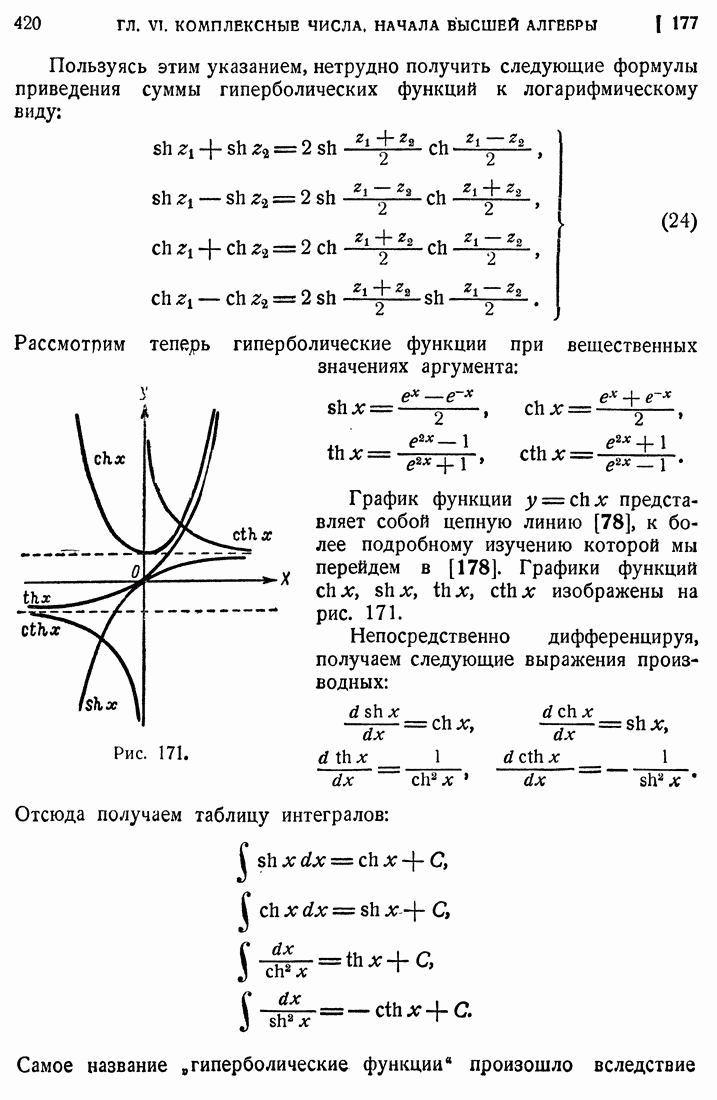
- 177. Тригонометрические и гиперболические функции.
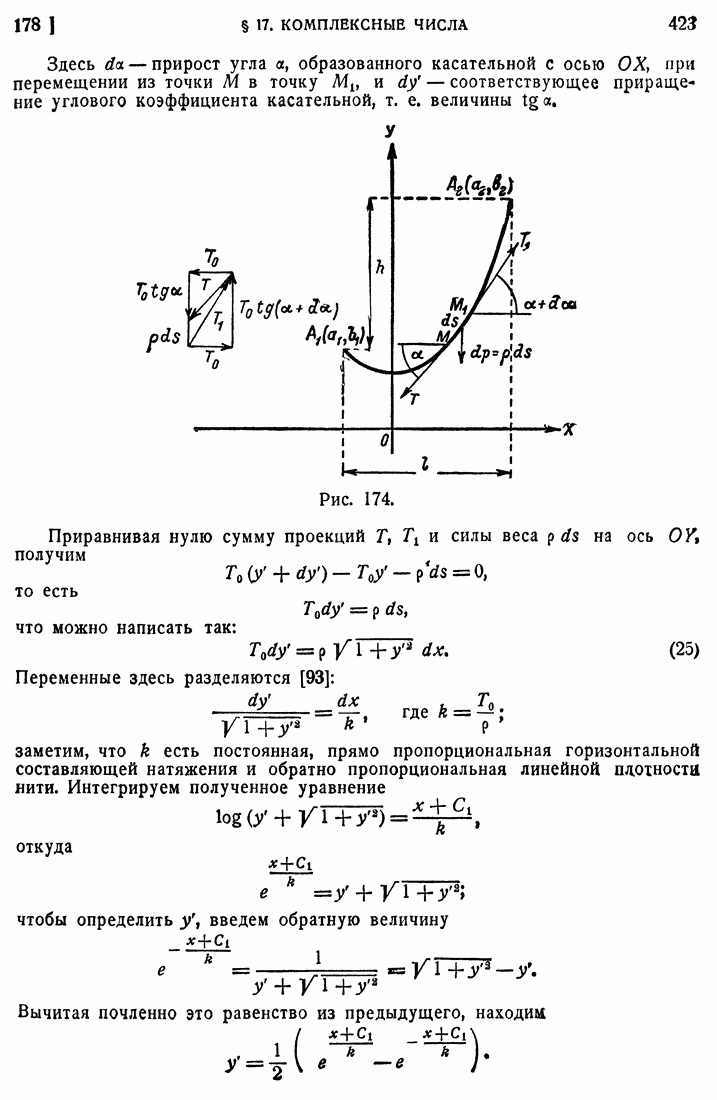
- 178. Цепная линия.
- 179. Логарифмирование.
- 180. Синусоидальные величины и векторные диаграммы.
- 181. Примеры.
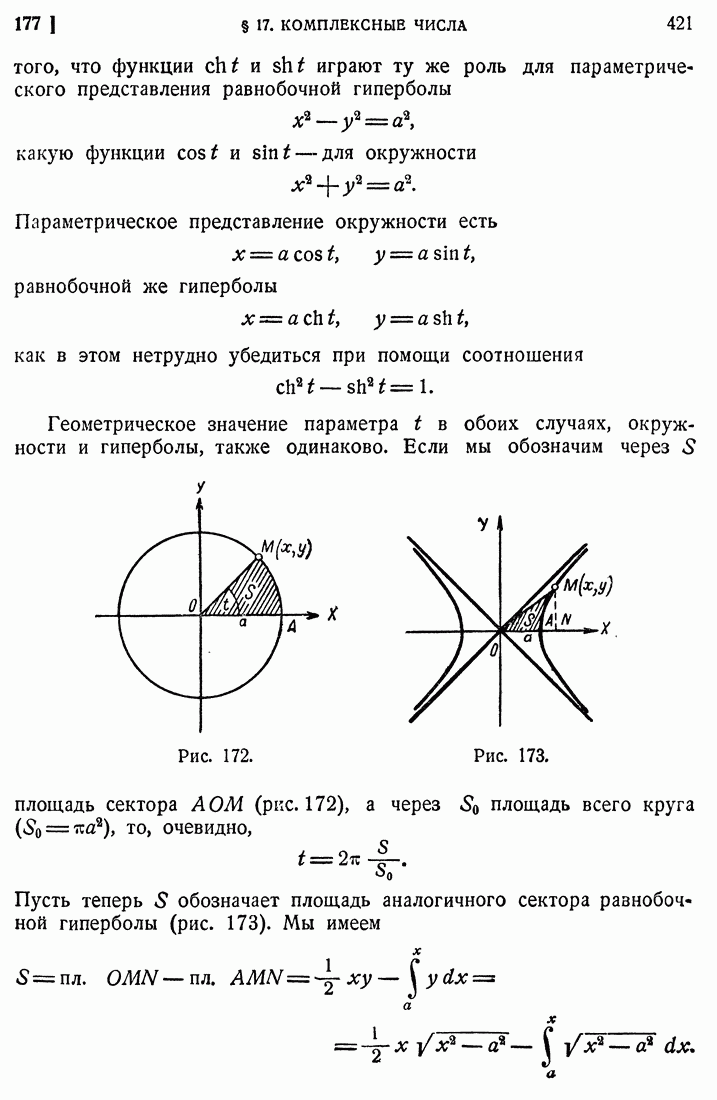
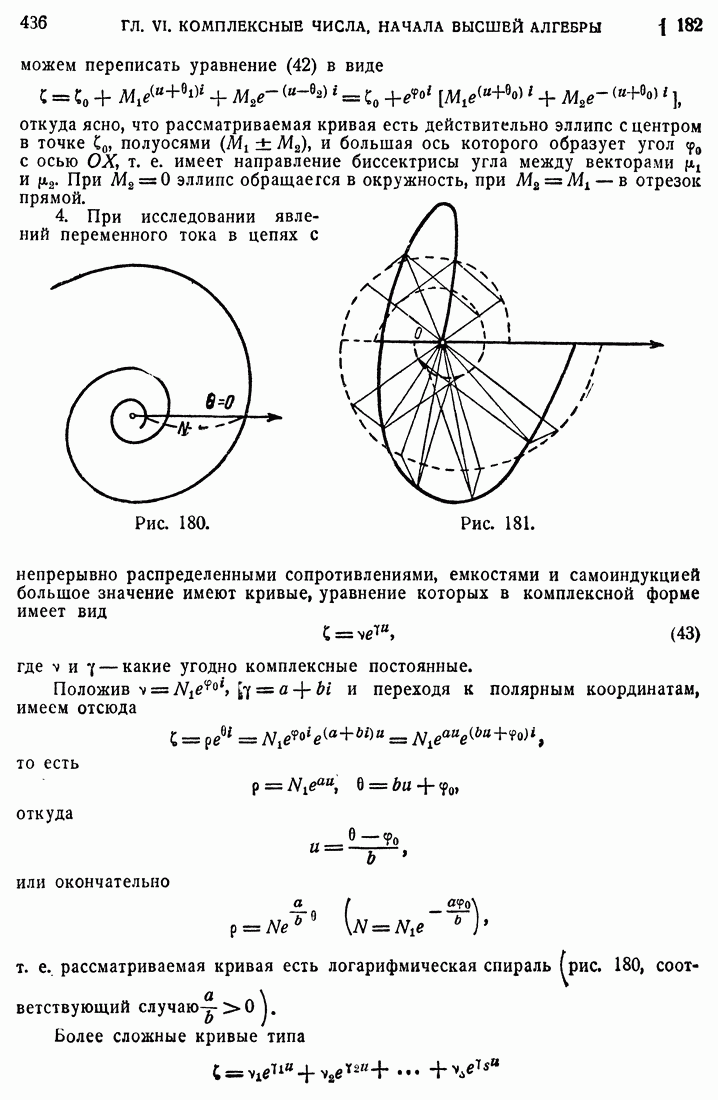
- 182. Кривые в комплексной форме.
- 183. Представление гармонического колебания в комплексной форме.
- § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ И ВЫЧИСЛЕНИЕ ИХ КОРНЕЙ
- 185. Разложение многочлена на множители.
- 186. Кратные корни.
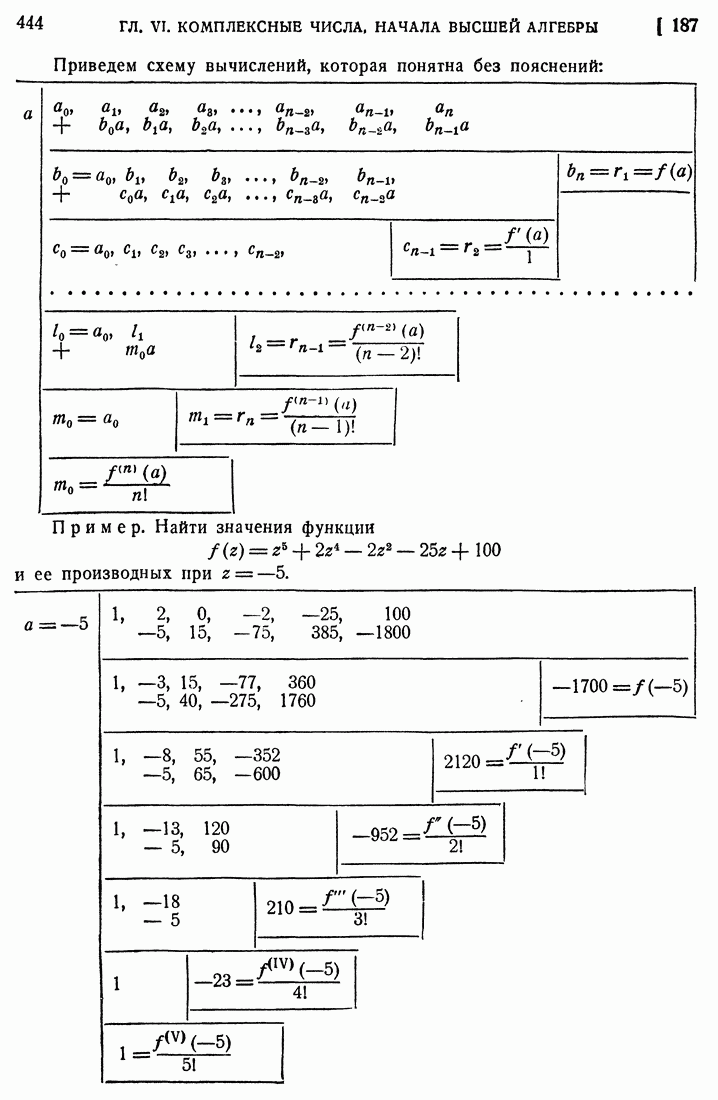
- 187. Правило Горнера.
- 188. Общий наибольший делитель.
- 189. Вещественные многочлены.
- 190. Зависимость между корнями уравнения и его коэффициентами.
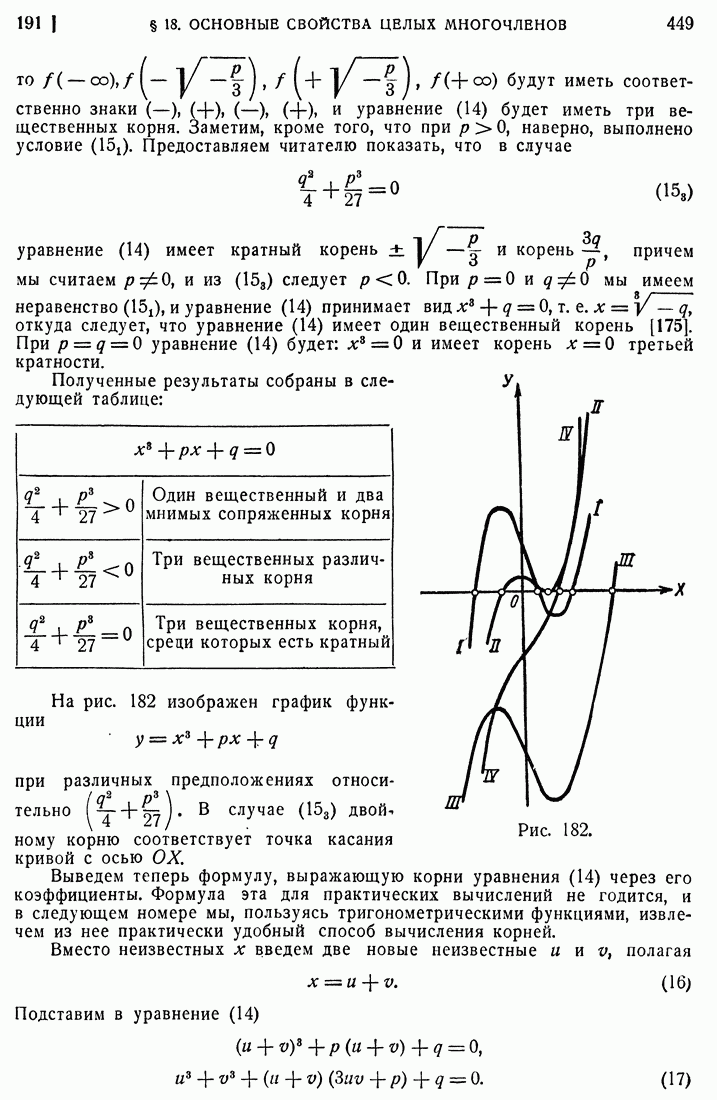
- 191. Уравнение третьей степени.
- 192. Решение кубического уравнения в тригонометрической форме.
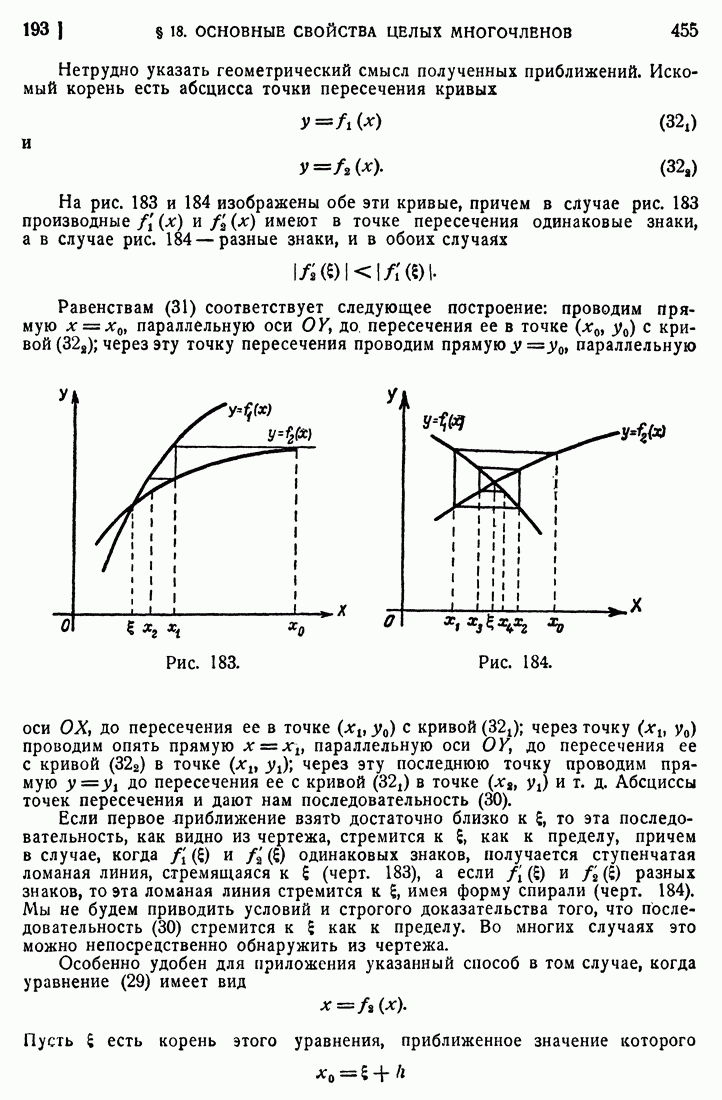
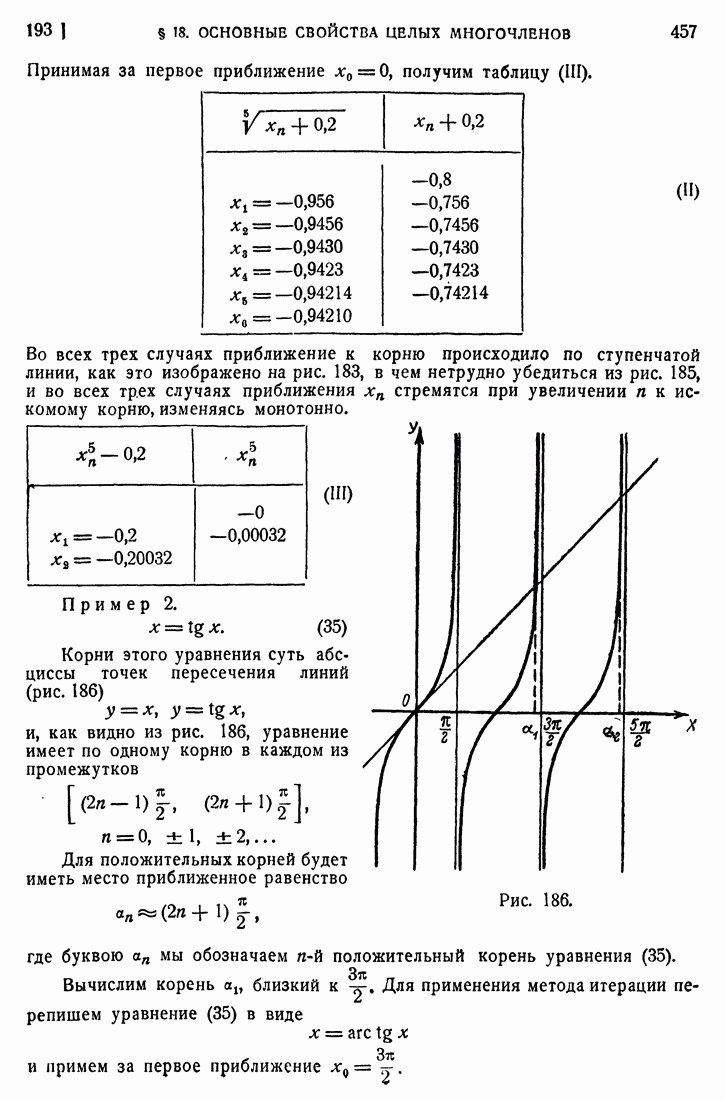
- 193. Способ итерации.
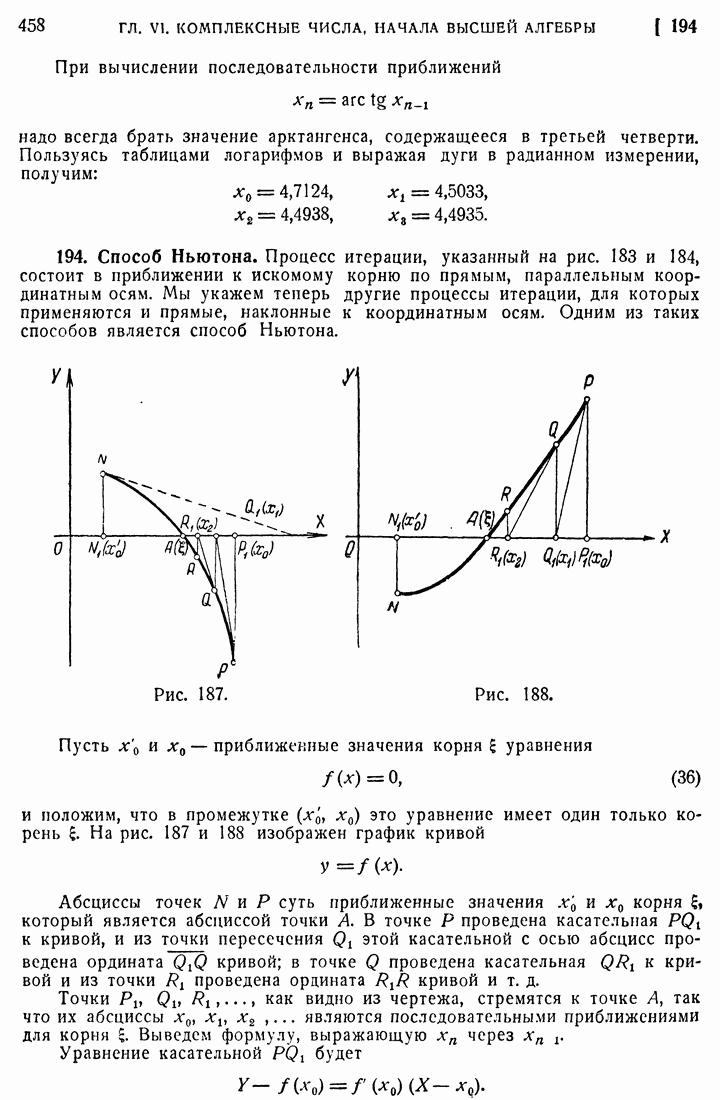
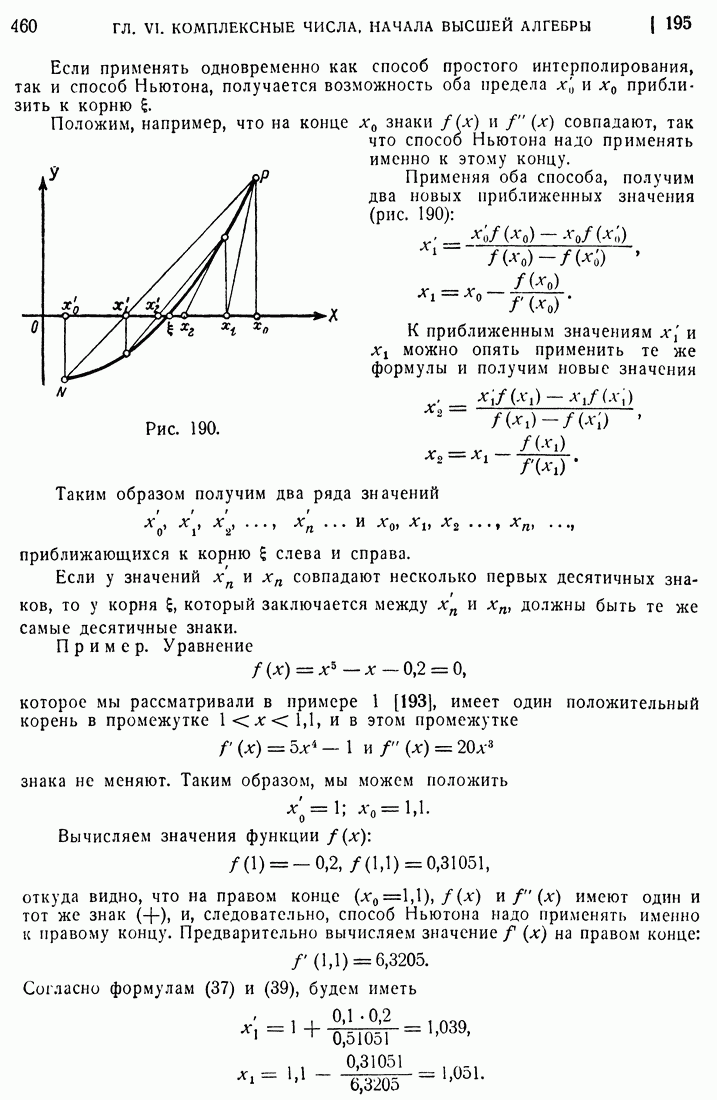
- 194. Способ Ньютона.
- 195. Способ простого интерполирования.
- § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИИ
- 196. Разложение рациональной дроби на простейшие.
- 197. Интегрирование рациональной дроби.
- 198. Интеграл от выражений, содержащих радикалы.
- 199. Интегралы вида…
- 200. Интегралы вида…
- 201. Интегралы вида…