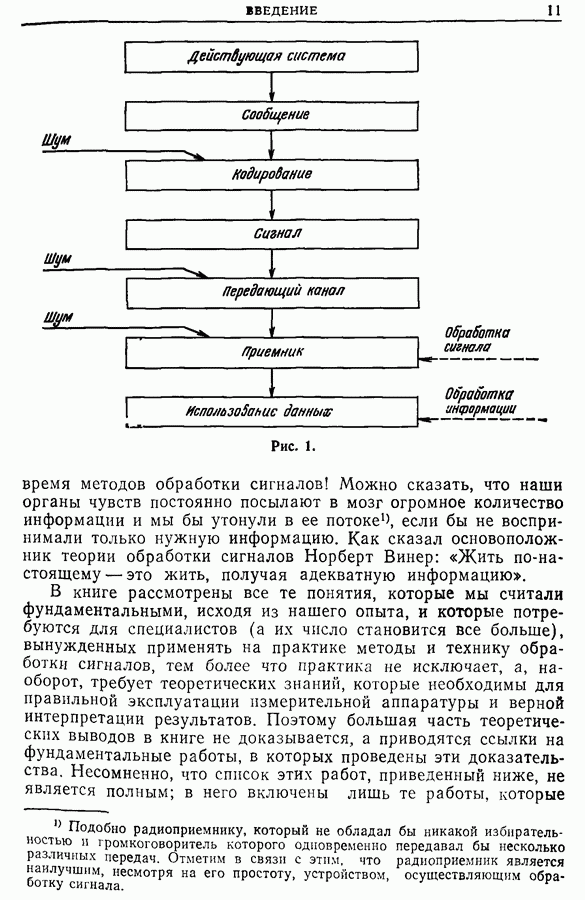
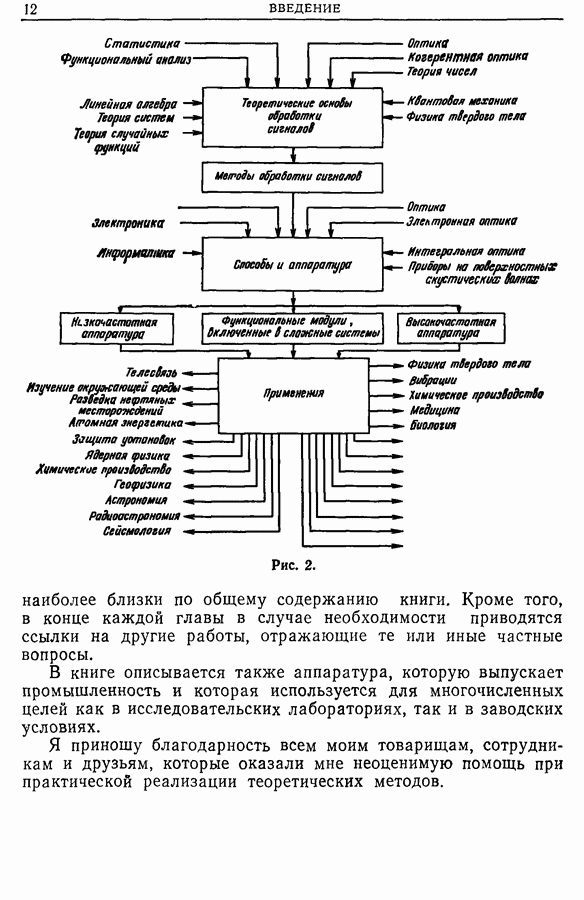
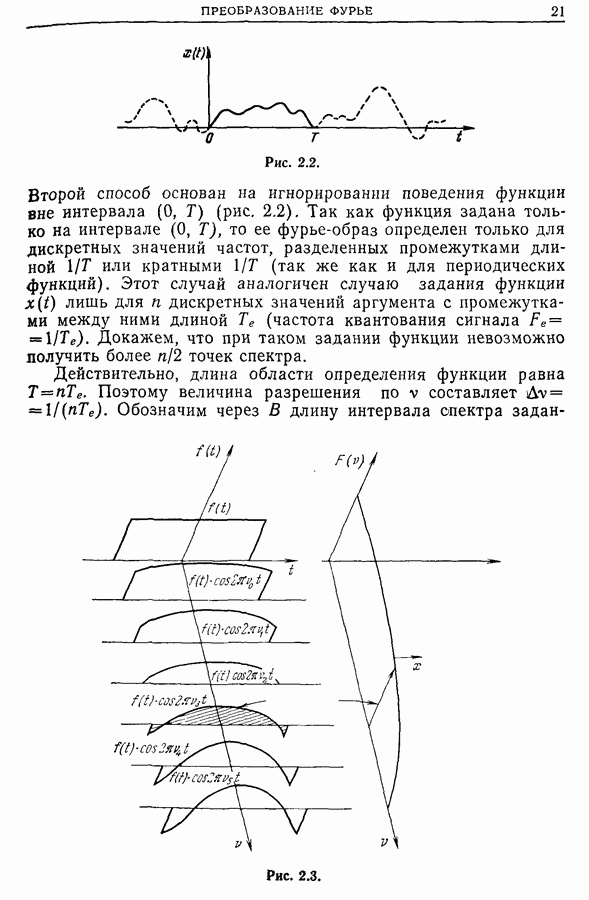
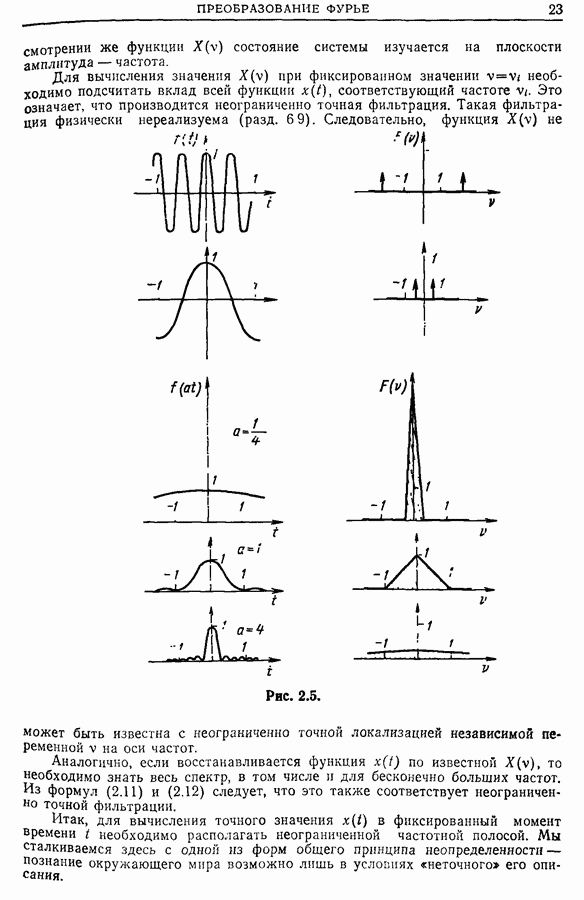
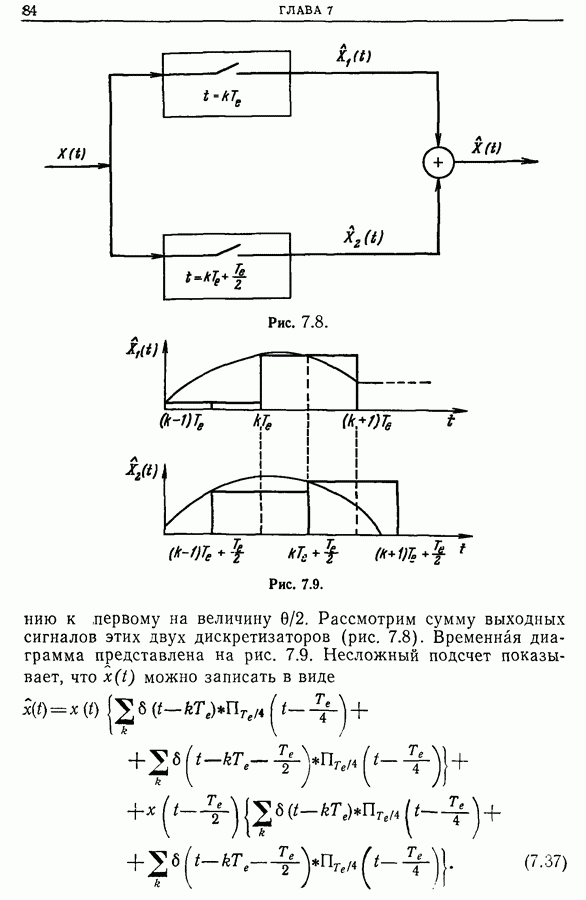
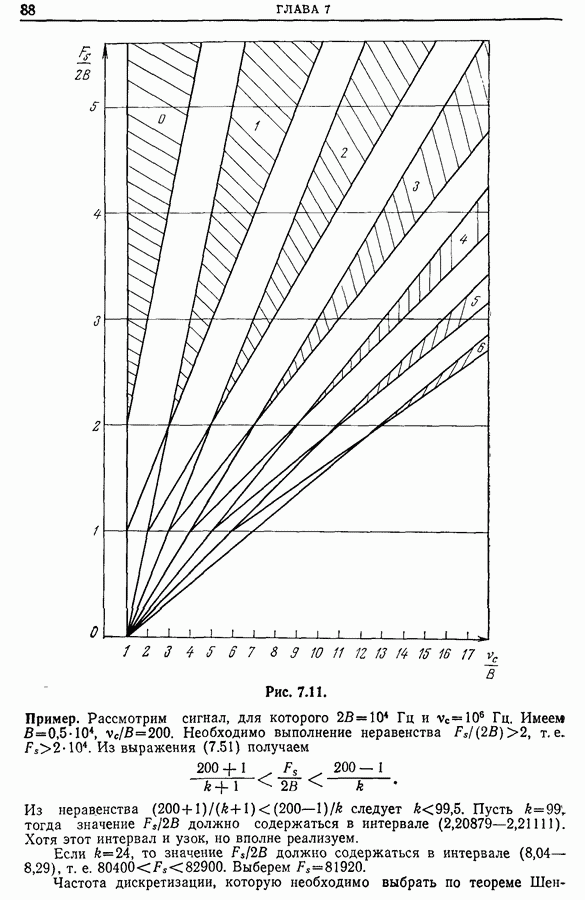
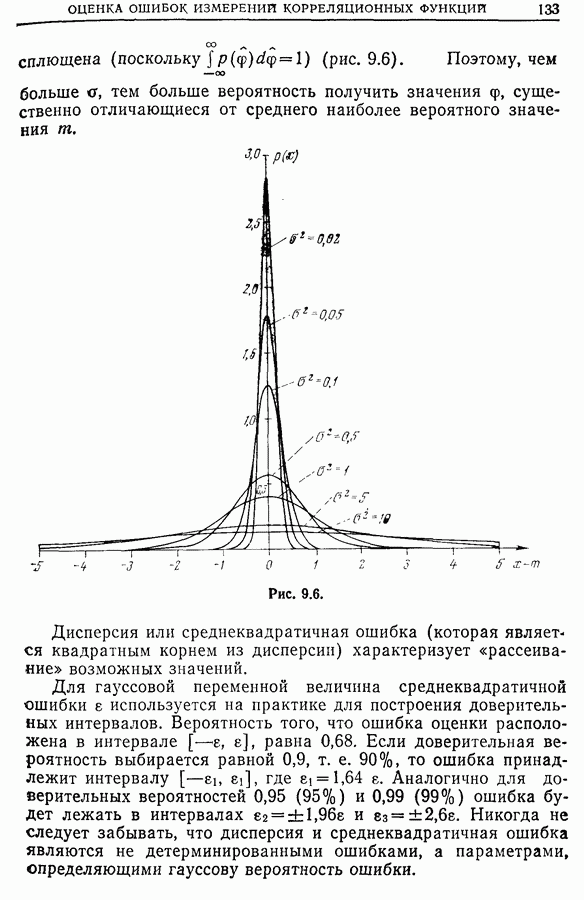
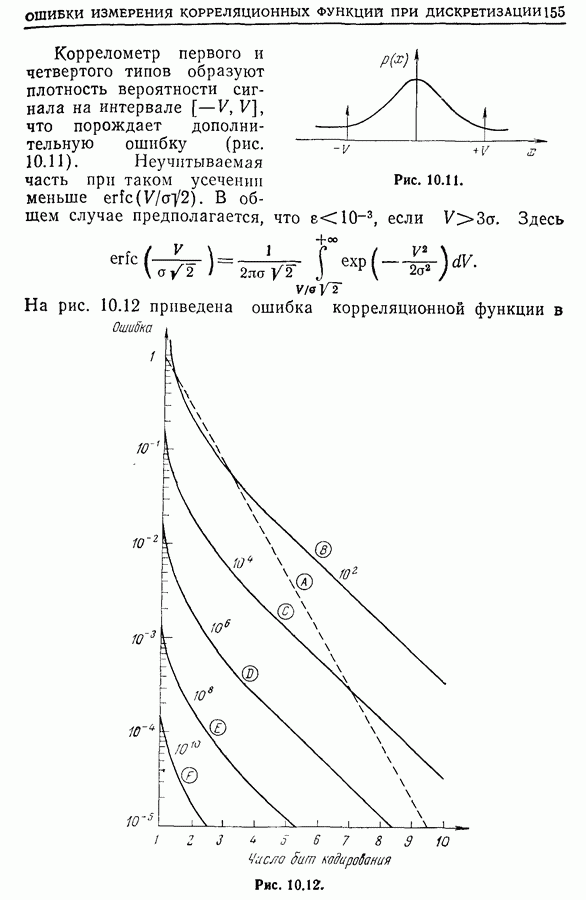
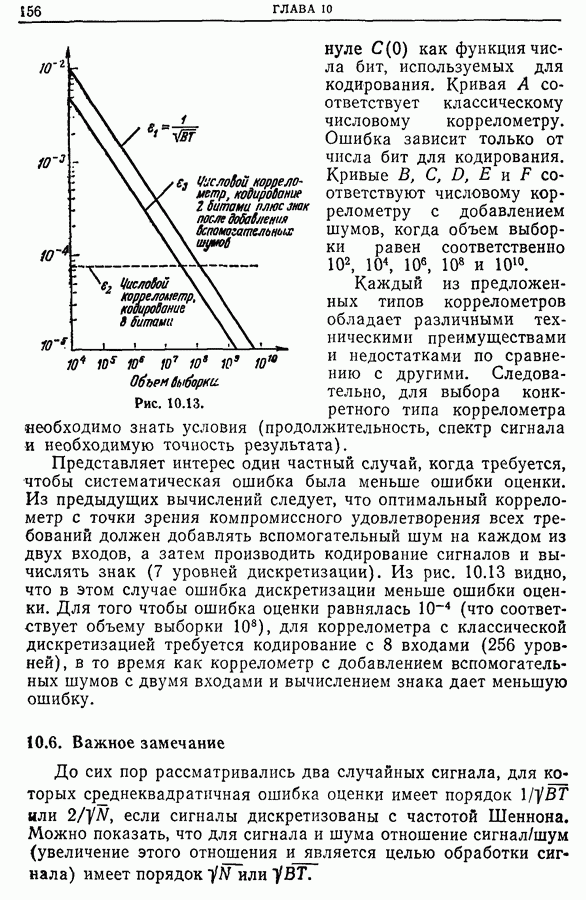
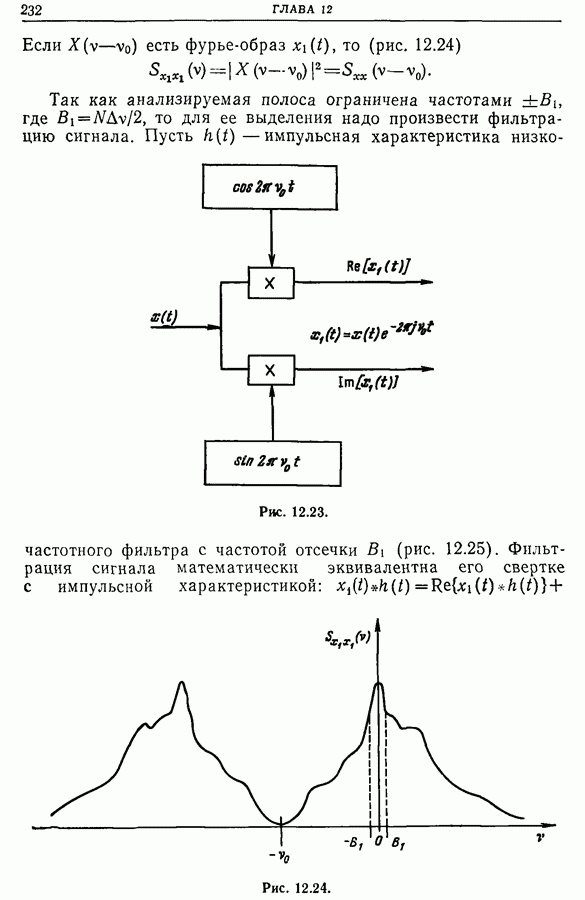
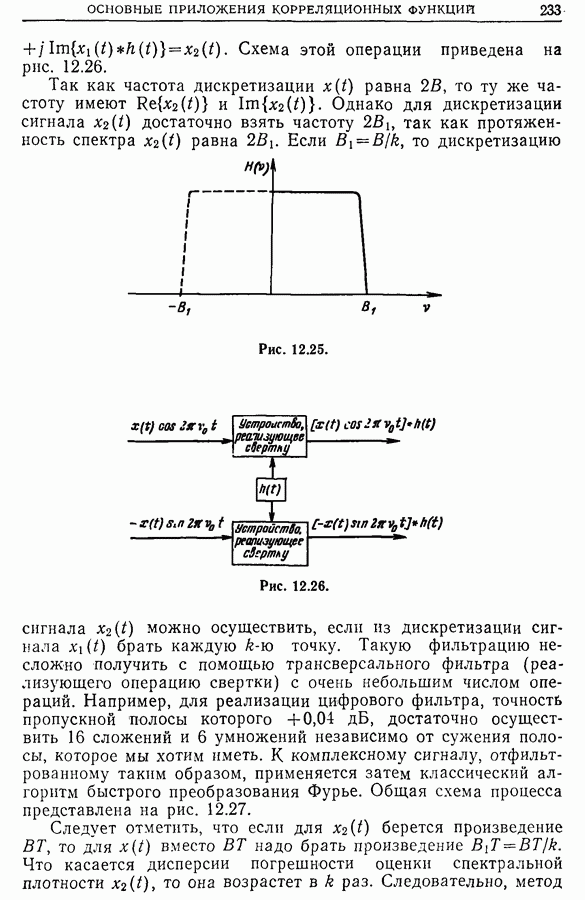
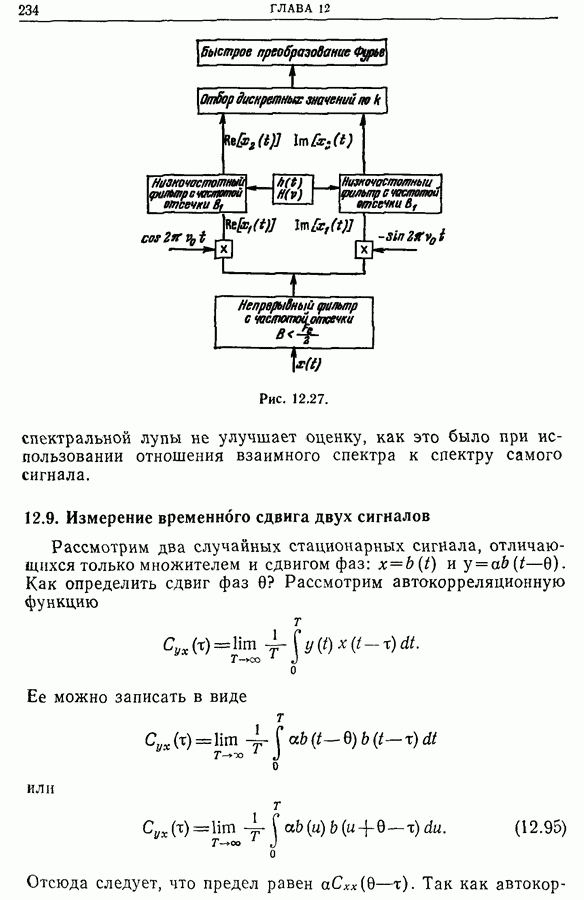
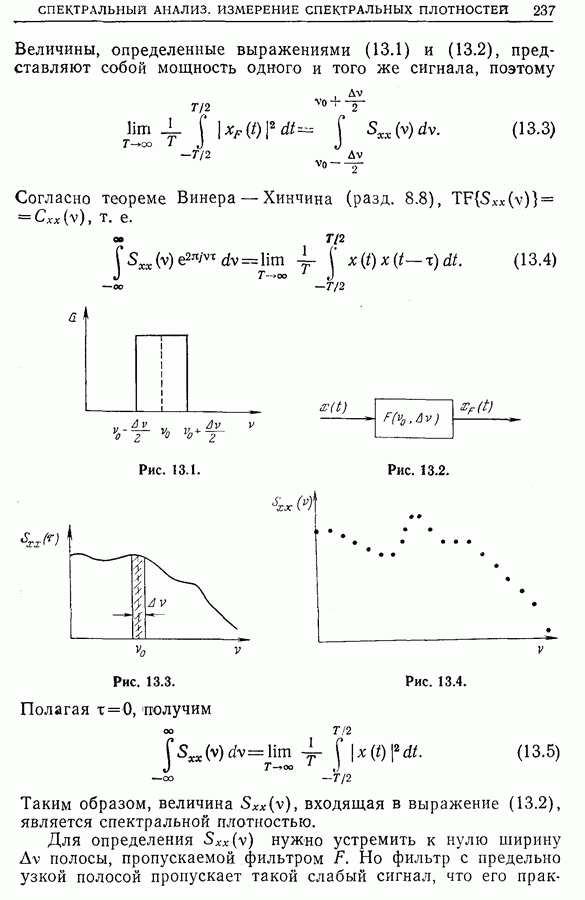
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 11. ОСНОВНЫЕ СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
Теория, мой друг, суха,
Но зеленеет жизни древо.
Гете
Введение
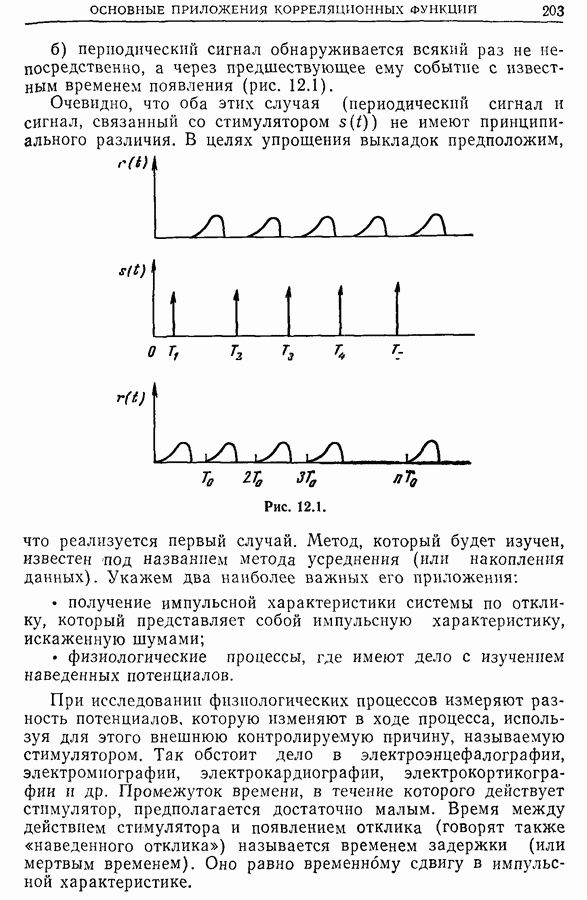
Мы разбили множество функций на три класса: 1) случайные стационарные функции (имеется в виду стационарность 2-го порядка, которые не содержат периодичностей и моменты 1-го и 2-го порядка которых не зависят от начала отсчета времени;
2) периодические функции; 3) переходные функции, которые не содержат периодичностей и для которых выбор начала отсчета времени имеет существенное значение.
11.1. Центрированные случайные стационарные функции, обладающие свойством эргодичности
Определение.
Автокорреляционной функцией называется функция

Ниже мы будем рассматривать центрированные сигналы, т. е. сигналы с нулевым средним значением. Напомним (разд. 8.11), что в случае центрированных сигналов к корреляционной функции центрированного сигнала следует добавить произведение  средних значений, а к спектральной плотности
средних значений, а к спектральной плотности  — произведение
— произведение  где
где  — импульсная функция Дирака.
— импульсная функция Дирака.
Были определены также спектральная плотность (мощности)

взаимная корреляционная функция

и взаимная спектральная плотность (мощности)

Ниже, если не оговорено противное, будут рассматриваться вещественные временные функции, т. е. такие, которым соответствуют вещественные корреляционные функции.
Свойства автокорреляционной функции.
Автокорреляционные функции обладают рядом свойств, которые мы приведем без доказательства.
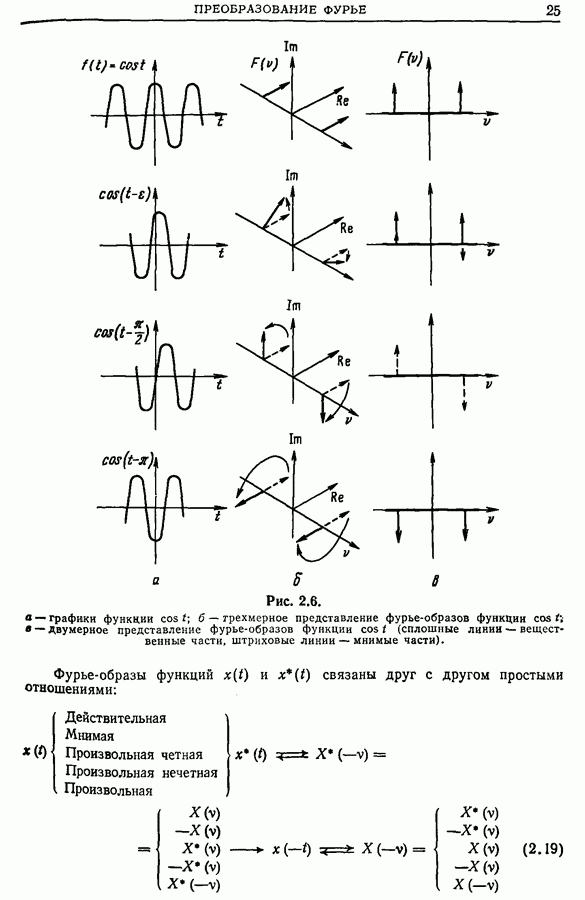
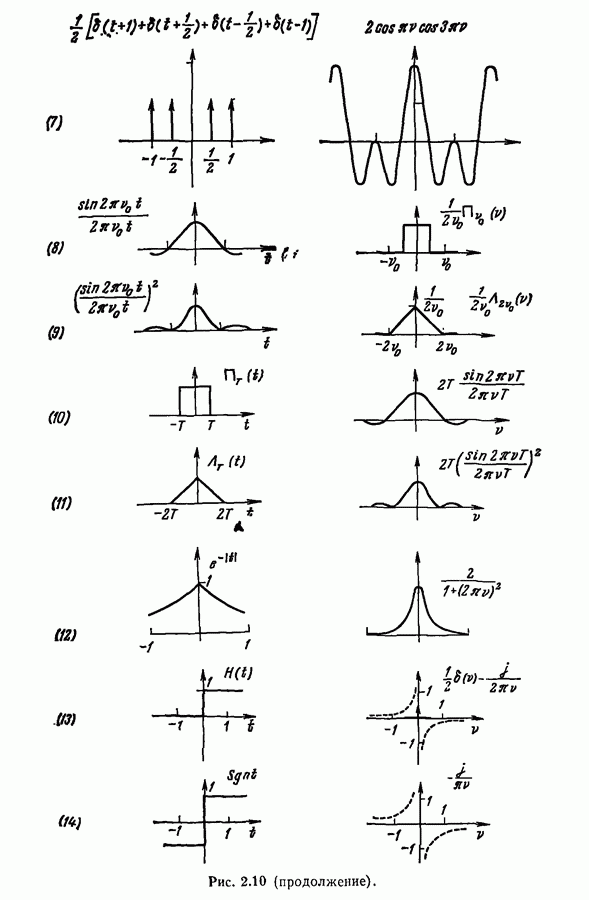
1. Четность:

Из этого свойства следует, что достаточно определить автокорреляционную функцию только для положительных (или отрицательных) значений  а затем можно продолжить эту функцию четным образом на отрицательные (положительные) значения
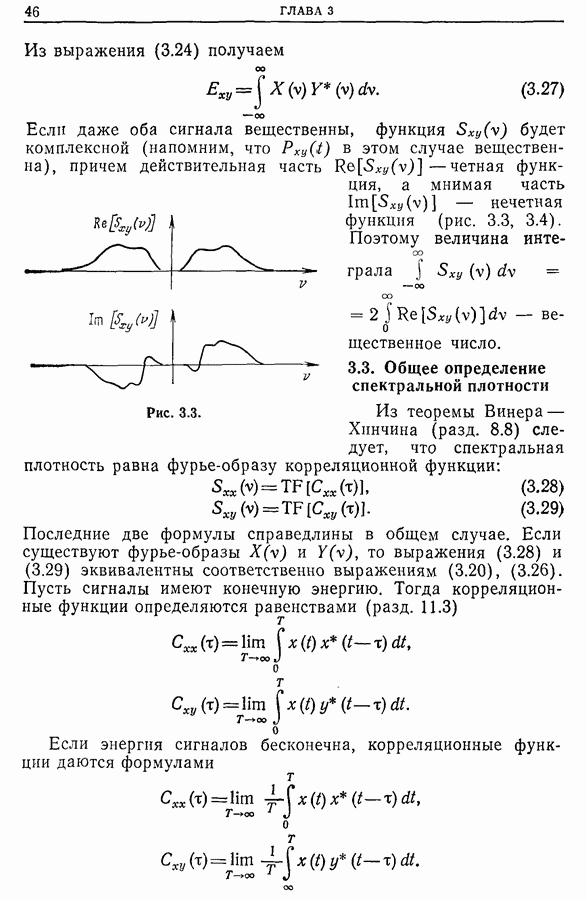
а затем можно продолжить эту функцию четным образом на отрицательные (положительные) значения  . Из четности автокорреляционной функции вытекает, что ее фурье-образ содержит только косинусоидальные члены преобразования:
. Из четности автокорреляционной функции вытекает, что ее фурье-образ содержит только косинусоидальные члены преобразования:

2. Автокорреляционная функция имеет максимум при  Если
Если  то
то

Отметим, что величина

представляет собой среднее значение квадрата, или дисперсию, или квадрат эффективного значения, или среднюю мощность функции 
3. При неограниченном росте  автокорреляционная функция случайного центрированного сигнала стремится к нулю
автокорреляционная функция случайного центрированного сигнала стремится к нулю

Следовательно, для любого положительного  существует такое положительное
существует такое положительное  что при условии
что при условии  выполняется неравенство
выполняется неравенство 
Свойства спектральной плотности.
Поскольку  — вещественная четная функция, то спектральная плотность
— вещественная четная функция, то спектральная плотность  также является вещественной четной функцией. Поэтому
также является вещественной четной функцией. Поэтому

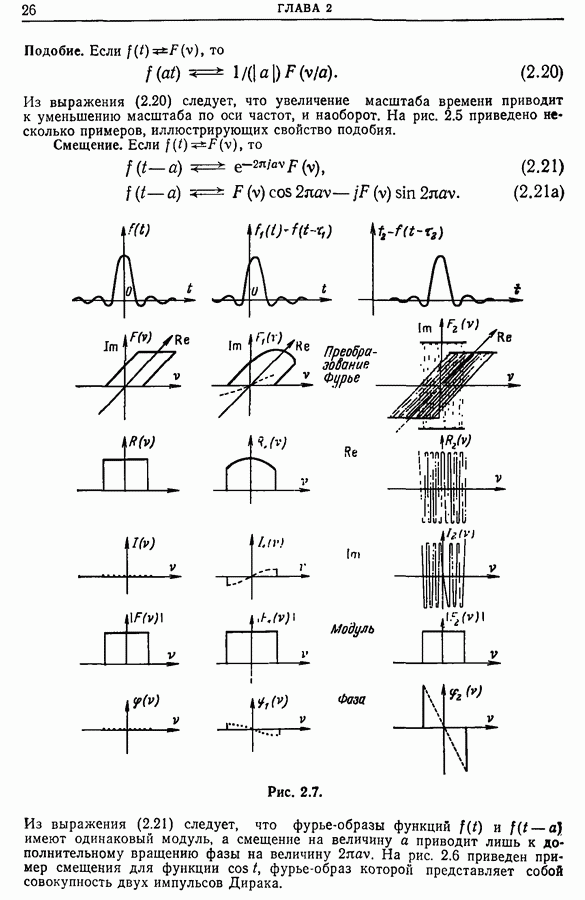
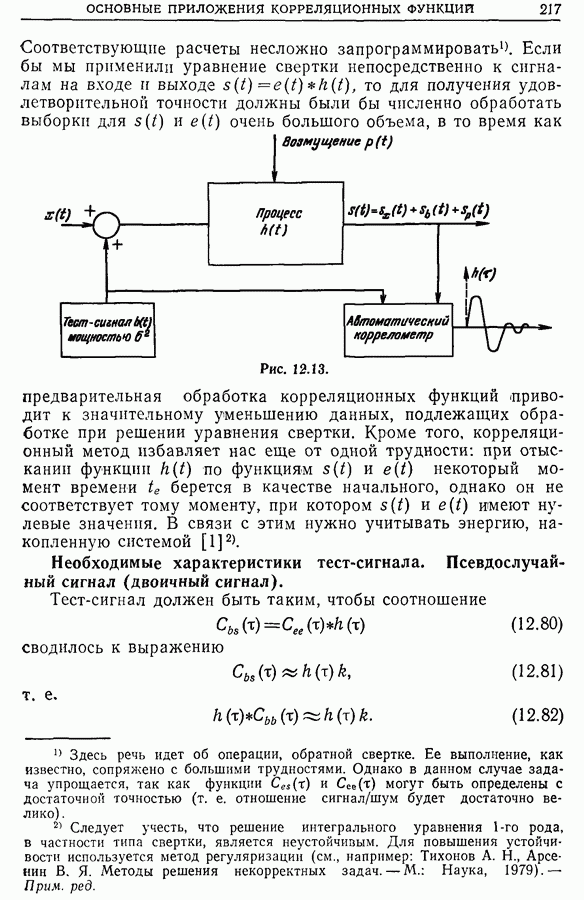
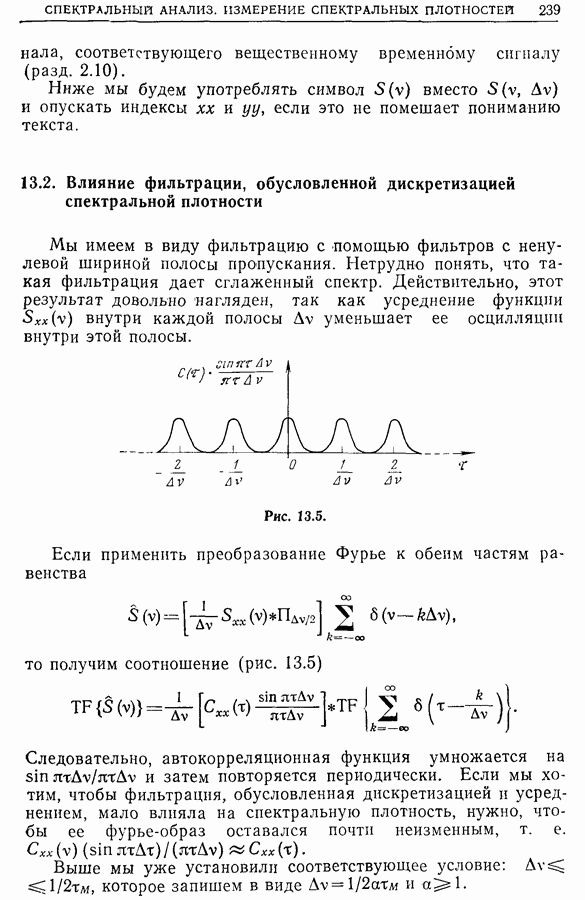
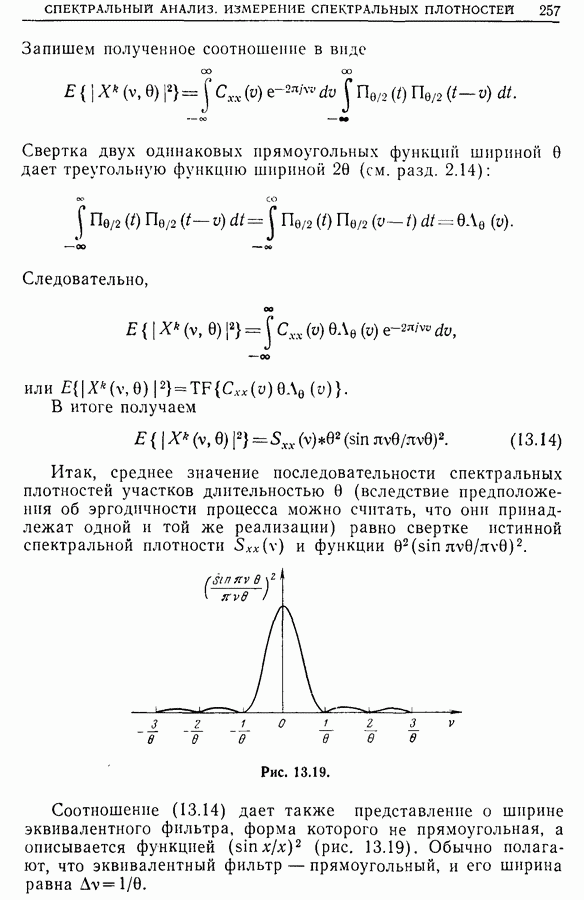
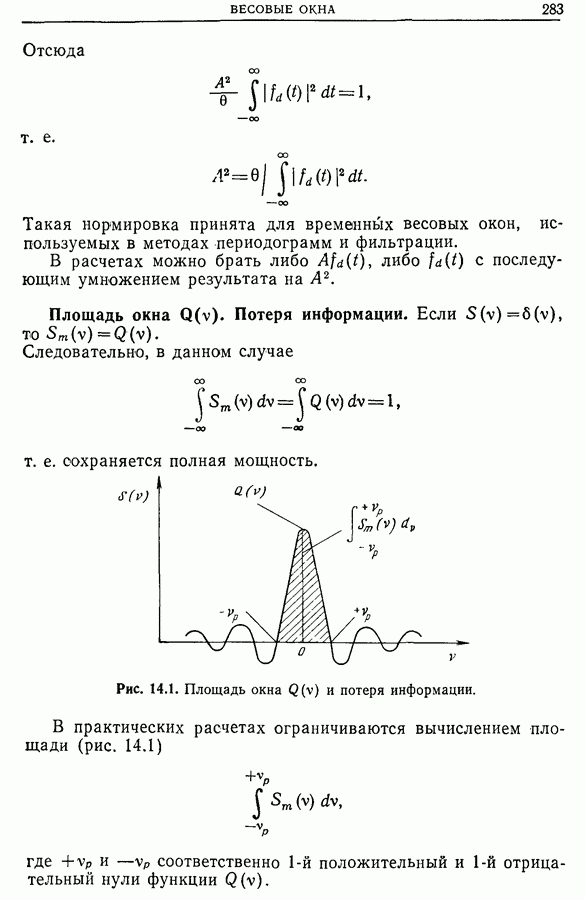
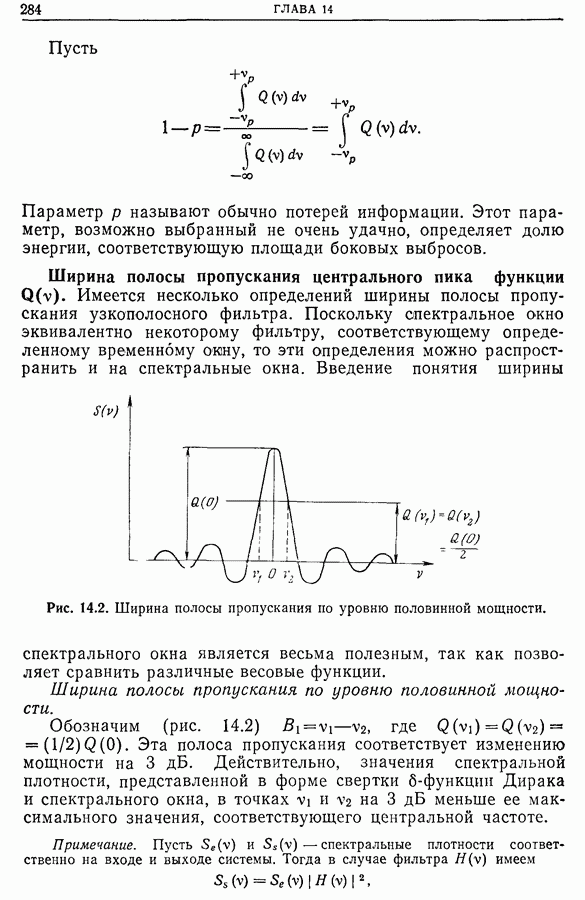
Это фундаментальное соотношение позволяет переходить от спектральной плотности мощности к автокорреляционной функции и наоборот. Важное приложение соотношения (11.8) рассмотрено в гл. 13, в которой мы покажем, что целесообразнее всего определять спектральную плотность по автокорреляционной функции.
Если сигнал не содержит постоянной компоненты, т. е.  то из выражения (11.8) следует,что
то из выражения (11.8) следует,что  . Наиболее часто центрирование сигнала достигается высокочастотной фильтрацией. В этом случае, как показано в разд. 8.11, отсекается постоянная составляющая, и, следовательно, алгебраическая площадь, ограниченная графиком автокорреляционной функции центрированного сигнала, равна нулю. Этот результат имеет важное практическое значение.
. Наиболее часто центрирование сигнала достигается высокочастотной фильтрацией. В этом случае, как показано в разд. 8.11, отсекается постоянная составляющая, и, следовательно, алгебраическая площадь, ограниченная графиком автокорреляционной функции центрированного сигнала, равна нулю. Этот результат имеет важное практическое значение.
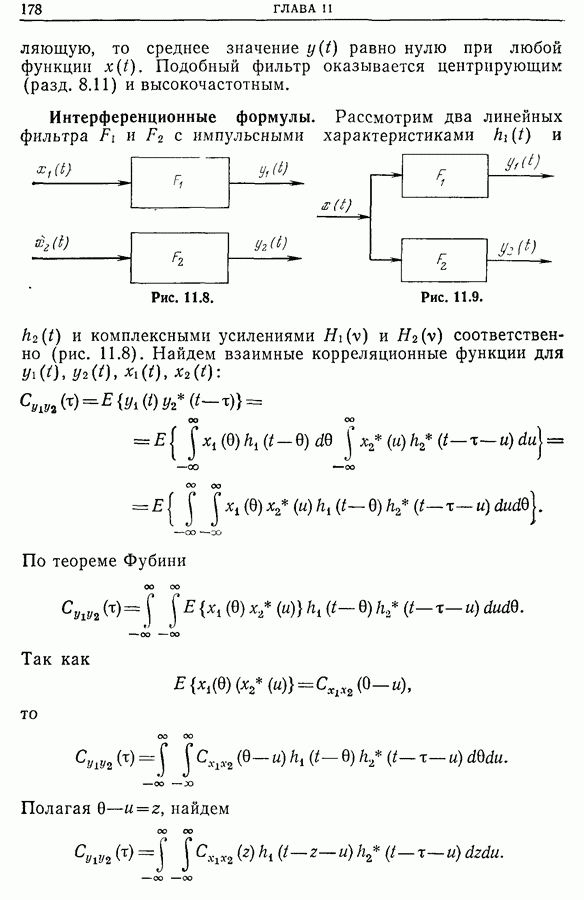
Взаимная корреляция двух случайных функций.
Применяя корреляционный оператор к двум различным случайным функциям, получим взаимную корреляционную функцию

Очевидно, что паре функций  соответствуют две корреляционные функции. Вторая взаимная корреляционная функция определяется аналогично:
соответствуют две корреляционные функции. Вторая взаимная корреляционная функция определяется аналогично:

Приведем без доказательства некоторые свойства взаимных корреляционных функций.
Если заменить  на
на  то
то

В общем случае взаимные корреляционные функции не обладают свойством четности или нечетности и не имеют максимума
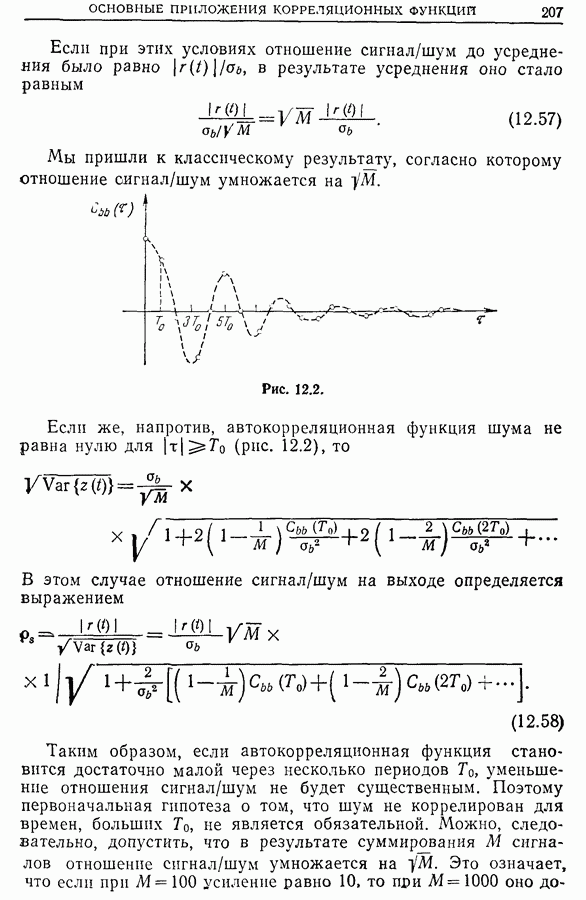
при  Взаимные корреляционные функции двух случайных центрированных функций стремятся к нулю при
Взаимные корреляционные функции двух случайных центрированных функций стремятся к нулю при 

Кроме того, для любых значений  справедливо неравенство
справедливо неравенство

Если две случайные функции независимы, то при любом времени корреляции соответствующие взаимные корреляционные функции тождественно равны нулю. Обратное утверждение неверно.
Взаимный спектр. Взаимная спектральная плотность.
По аналогии со спектральной плотностью мощности фурье-образ взаимной корреляционной функции называют взаимной спектральной плотностью мощности, или взаимным спектром:

В общем случае  — комплексная функция, так что
— комплексная функция, так что

Произведение  определяет мощность взаимодействия в полосе частот
определяет мощность взаимодействия в полосе частот  , как мы видели, тесно связано с обменной информацией между случайными величинами
, как мы видели, тесно связано с обменной информацией между случайными величинами  в этой полосе. Очевидно, что если
в этой полосе. Очевидно, что если  -вещественная функция, то
-вещественная функция, то  обладает эрмитовой симметрией.
обладает эрмитовой симметрией.
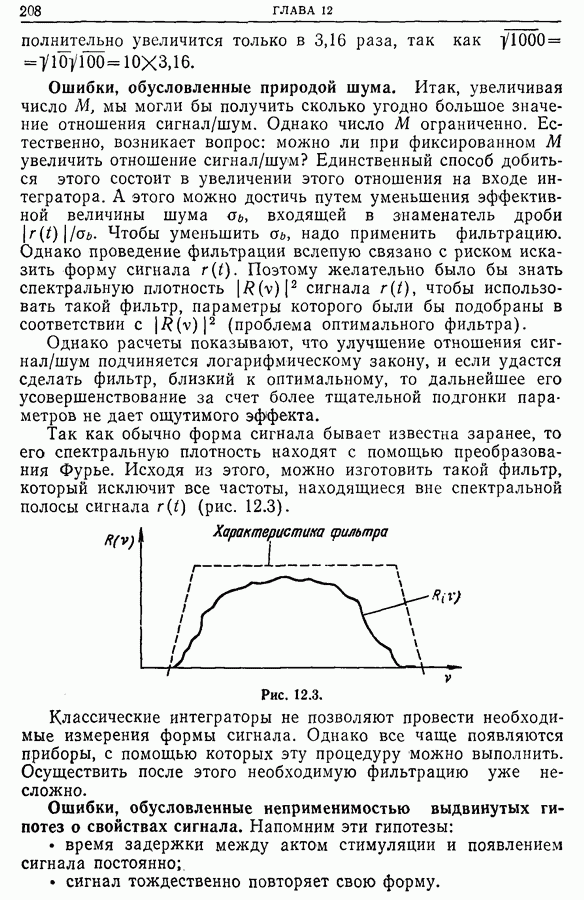
Белый шум.
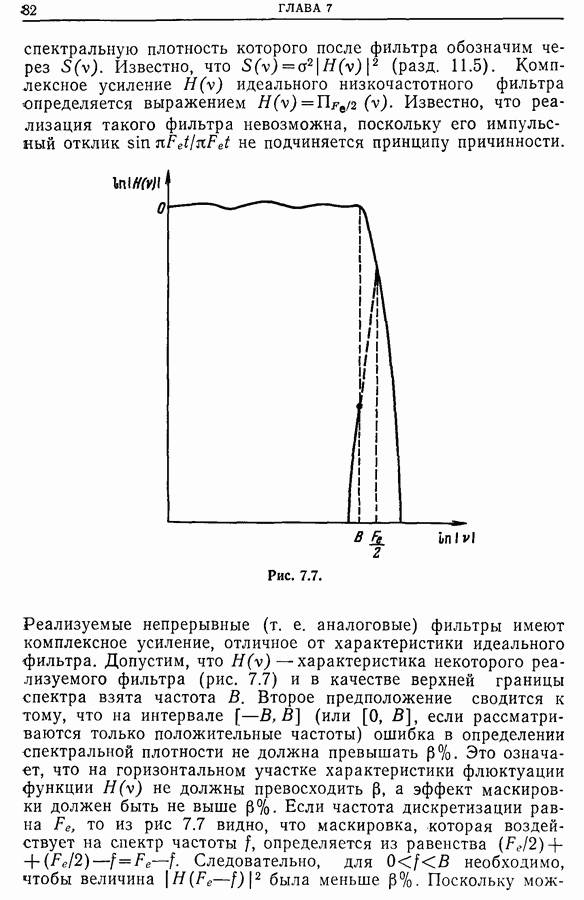
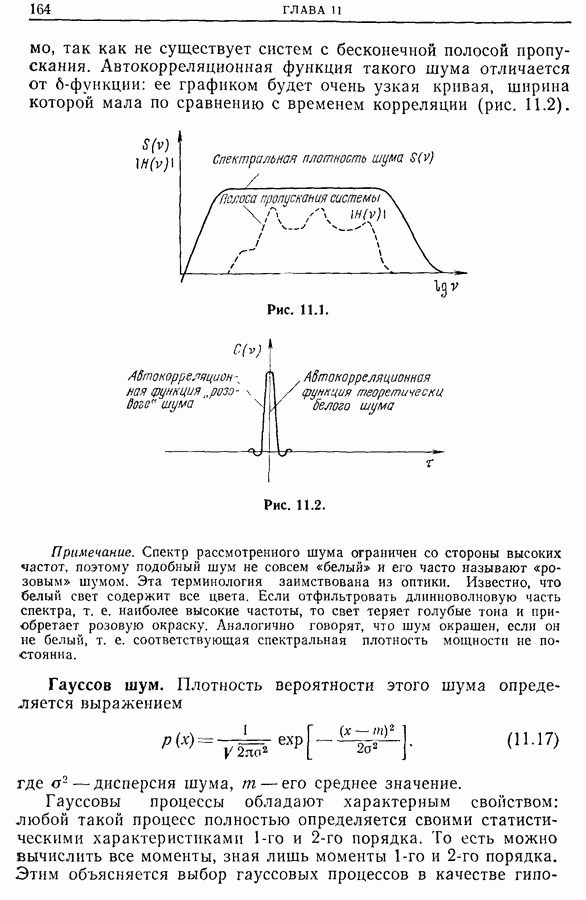
На практике широкое применение находит случайный процесс, называемый белым шумом, спектральная плотность мощности которого постоянна по всему диапазону частот. Мощность белого шума не зависит от частоты, и его автокорреляционной функцией будет  -функция Дирака. Реально белый шум не существует; но если спектральная плотность шума постоянна внутри полосы, пропускаемой системой, то такой шум можно считать белым (рис. 11.1). Это условие всегда
-функция Дирака. Реально белый шум не существует; но если спектральная плотность шума постоянна внутри полосы, пропускаемой системой, то такой шум можно считать белым (рис. 11.1). Это условие всегда
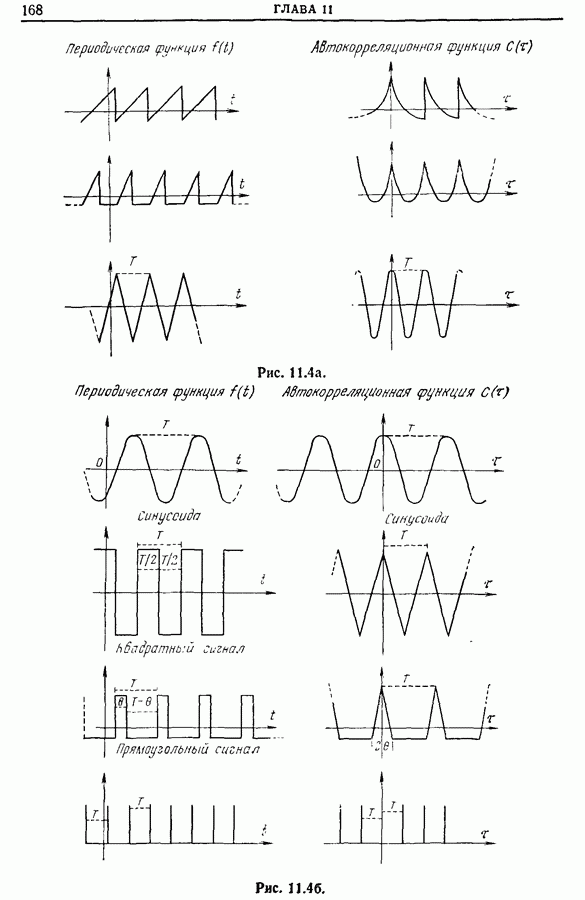
выполнимо, так как не существует систем с бесконечной полосой пропускания. Автокорреляционная функция такого шума отличается от  -функции: ее графиком будет очень узкая кривая, ширина которой мала по сравнению с временем корреляции (рис. 11.2).
-функции: ее графиком будет очень узкая кривая, ширина которой мала по сравнению с временем корреляции (рис. 11.2).

Рис. 11.1.

Рис. 11.2.
Примечание. Спектр рассмотренного шума ограничен со стороны высоких частот, поэтому подобный шум не совсем «белый» и его часто называют «розовым» шумом. Эта терминология заимствована из оптики. Известно, что белый свет содержит все цвета. Если отфильтровать длинноволновую часть спектра, т. е. наиболее высокие частоты, то свет теряет голубые тона и приобретает розовую окраску. Аналогично говорят, что шум окрашен, если он не белый, т. е. соответствующая спектральная плотность мощности не постоянна.
Гауссов шум.
Плотность вероятности этого шума определяется выражением

где  — дисперсия шума,
— дисперсия шума,  — его среднее значение.
— его среднее значение.
Гауссовы процессы обладают характерным свойством: любой такой процесс полностью определяется своими статистическими характеристиками 1-го и 2-го порядка. То есть можно вычислить все моменты, зная лишь моменты 1-го и 2-го порядка. Этим объясняется выбор гауссовых процессов в качестве
гипотезы при расчетах, содержащих погрешности оценок и требующих вычисления моментов более высоких порядков (разд. 8.10). Кроме того, согласно центральной предельной теореме, сумма произвольных случайных процессов стремится к гауссову процессу при возрастании числа слагаемых. Сходимость оказывается настолько быстрой, что если число слагаемых больше 5 или 6, то результирующий процесс очень близок к гауссову.

Рис. 11.3.
Пуассоновский шум.
В ядерной физике часто встречается шум другого типа, порожденный импульсами, распределенными по закону Пуассона. Вероятность появления  импульсов в интервале
импульсов в интервале  равна
равна

где  — параметр закона Пуассона, или средняя частота.
— параметр закона Пуассона, или средняя частота.
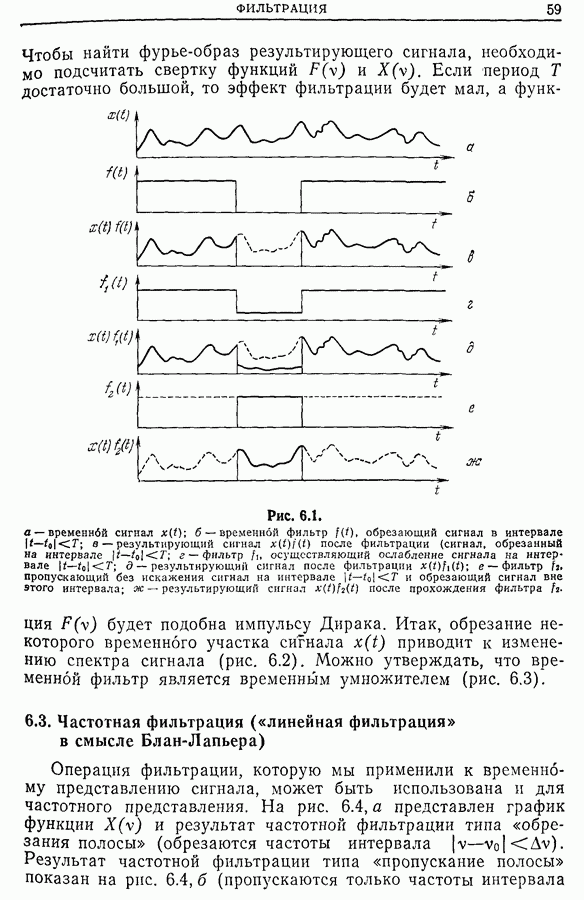
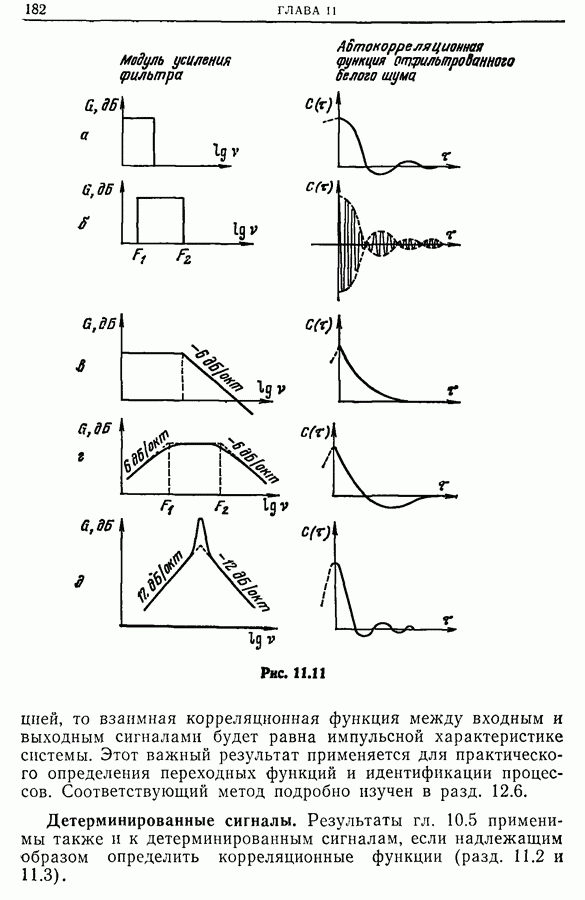
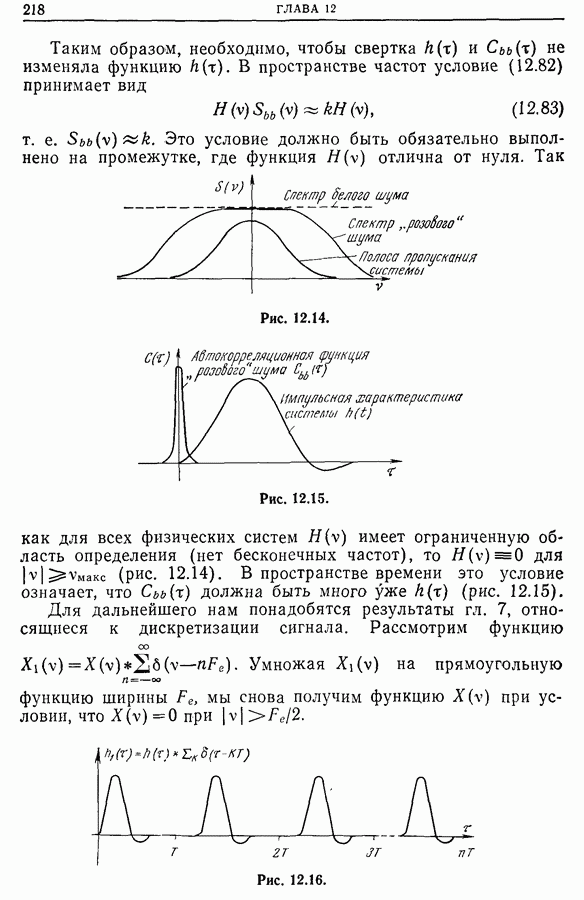
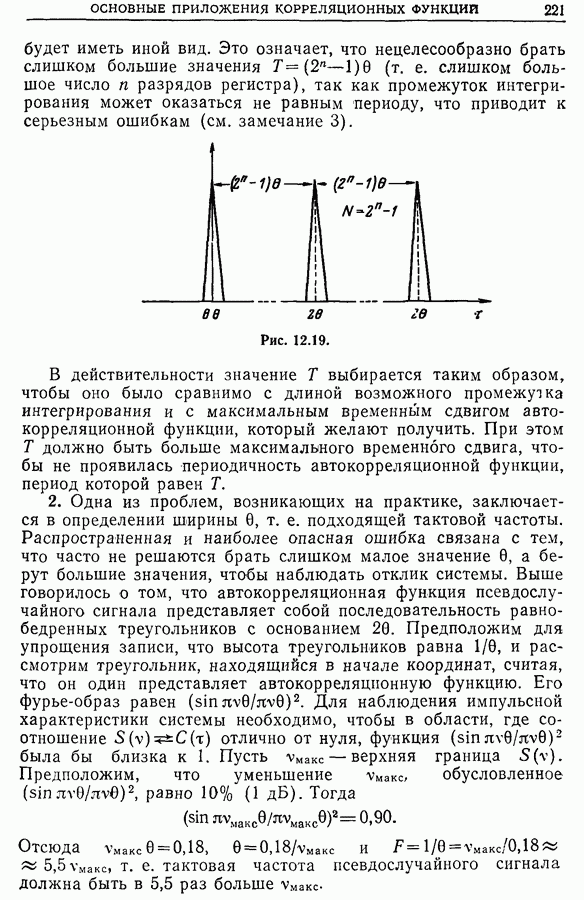
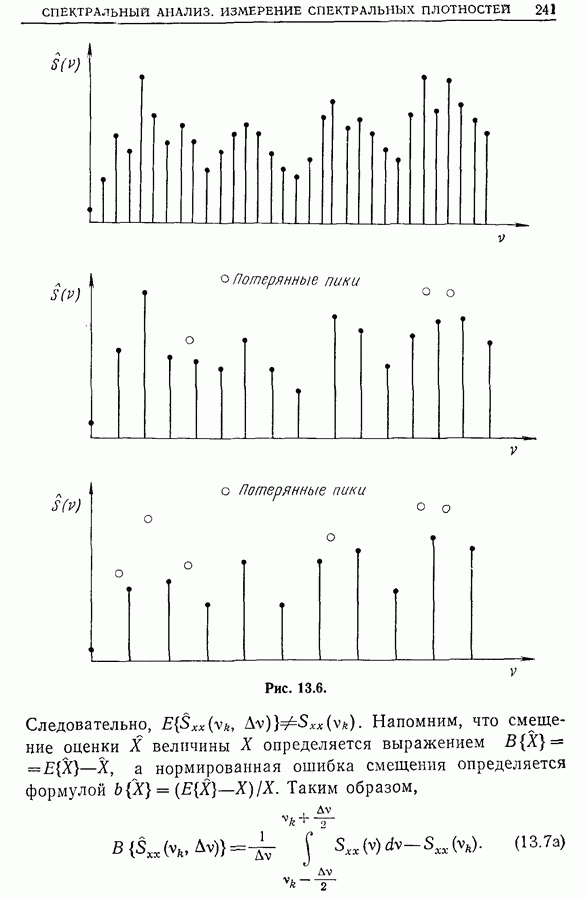
Из рис. 11.31 видно, что автокорреляционные функции последовательностей импульсов, распределенных по закону Пуассона и имеющих либо постоянный знак (положительный или отрицательный), либо случайный знак, по существу не
отличаются одна от другой; если же знак импульсов чередуется, то вид корреляционной функции существенно иной. Наличие распределения импульсов с чередующимся знаком увеличивает «память» вероятностного процесса, так как знак последующего импульса определяется знаком предыдущего; именно это приводит к «уширению» графика автокорреляционной функции.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- Глава 1. ФИЗИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ШУМАХ КАК О СЛУЧАЙНЫХ ПРОЦЕССАХ
- Глава 2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 2.2. Преобразование Фурье непериодических функций
- 2.3. Преобразование Фурье физических функций
- 2.4. Физический смысл преобразования Фурье
- 2.5. Условия существования преобразования Фурье
- 2.6. Некоторые свойства преобразования Фурье
- 2.7. Несколько функций и их фурье-образы
- 2.8. Частный случай вещественных сигналов
- 2.9. Отрицательные частоты
- 2.10. Аналитический сигнал
- 2.11. Почему выбрано преобразование Фурье?
- 2.12 Физическая реализация фурье-образа. Преобразование Фурье в оптике
- 2.13. Свойства функции sin х/х
- 2.14. Лямбда-функция
- Глава 3. МОЩНОСТЬ И ЭНЕРГИЯ СИГНАЛОВ
- 3.2. Частотная мощность. Спектральная плотность мощности. Спектр мощности
- 3.3. Общее определение спектральной плотности
- 3.4. Теорема Парсеваля
- 3.5. Понятие скалярного произведения и нормы
- Глава 4. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- 4.2. Связь между фурье-образом и изображением Лапласа
- Глава 5. СВЕРТКА
- 5.2. Уравнение свертки
- 5.3. Несколько замечаний относительно свертки
- 5.4. Физическая интерпретация свертки
- 5.5. Прямая и обратная задачи, связанные с операцией свертки
- 5.6. Свертка и преобразование Фурье. Теорема Планшереля
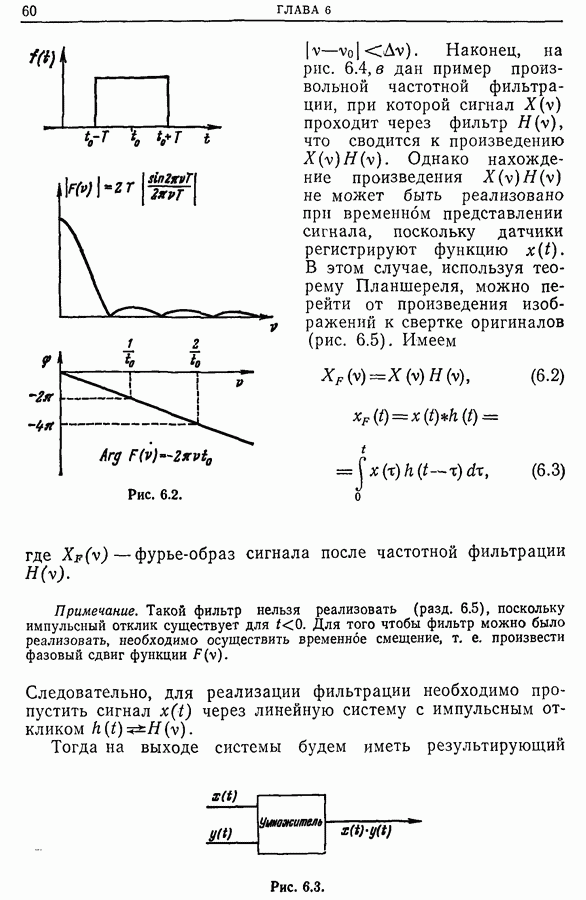
- Глава 6. ФИЛЬТРАЦИЯ
- 6.2. Временная фильтрация
- 6.3. Частотная фильтрация («линейная фильтрация» в смысле Блан-Лапьера)
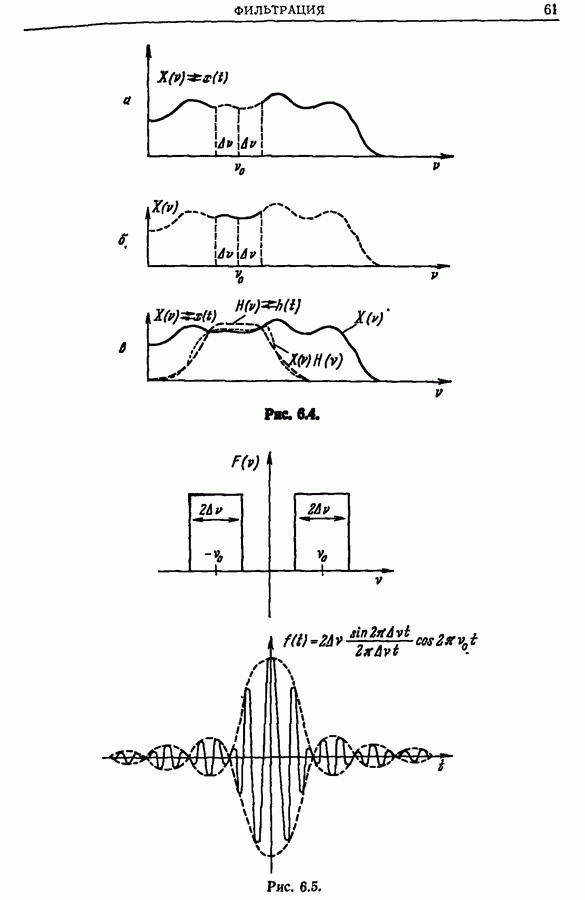
- 6.4. Связь между фильтрацией и сверткой
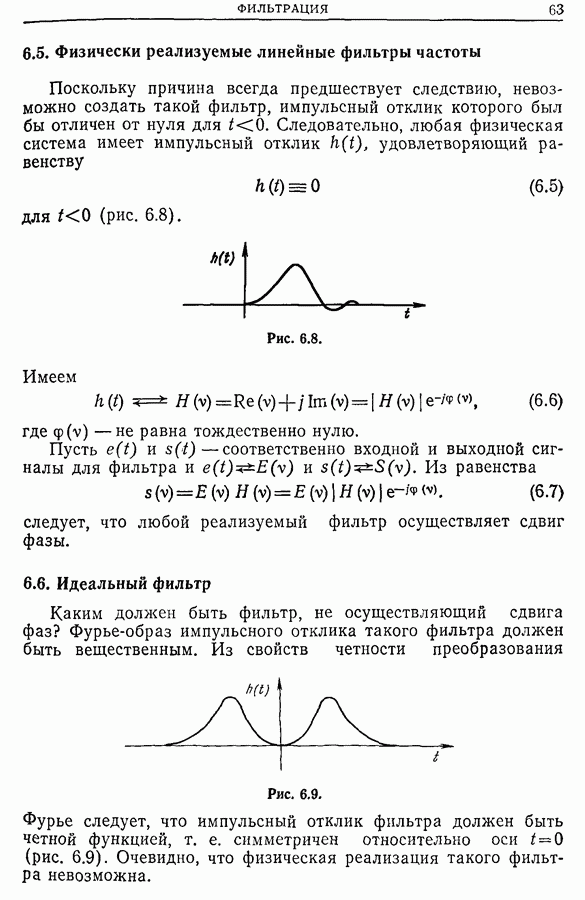
- 6.5. Физически реализуемые линейные фильтры частоты
- 6.6. Идеальный фильтр
- 6.7. Реализуемые непрерывные аналоговые фильтры [3]
- 6.8. Фильтры с линейным сдвигом фаз
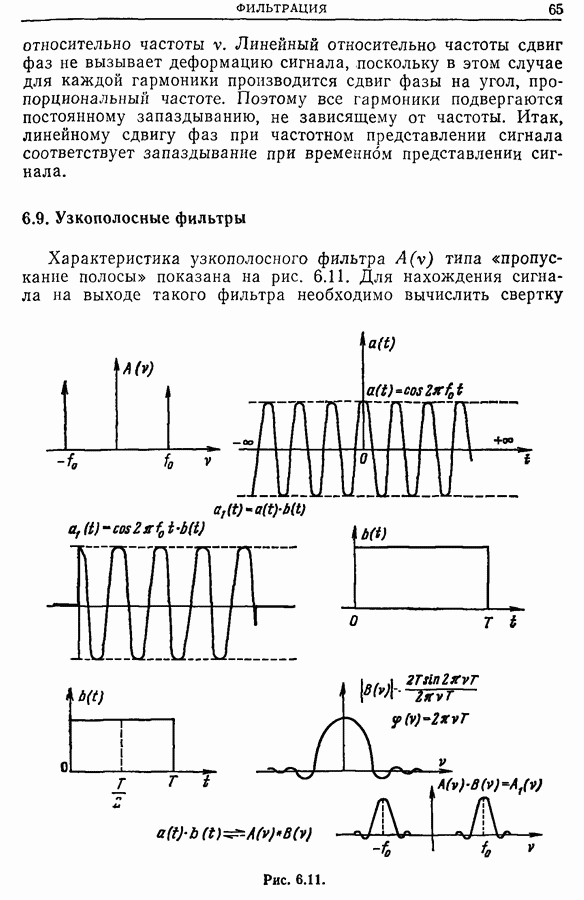
- 6.9. Узкополосные фильтры
- 6.10. Обобщение понятия фильтрации
- Глава 7. ДИСКРЕТИЗАЦИЯ
- 7.2. Теоремы дискретизации
- 7.3. Дискретизация сигналов конечной длительности
- 7.4. Дискретизация фурье-образов
- 7.5. Выбор частоты дискретизации на практике
- 7.6. Противомаскировочный фильтр
- 7.7. Физическая дискретизация. Комбинированная дискретизация
- 7.8. Субдискретизация. Обобщение теоремы Шеннона [9]
- 7.9. Заключение
- Глава 8. КОРРЕЛЯЦИЯ И НЕКОТОРЫЕ ДРУГИЕ ПОНЯТИЯ СТАТИСТИКИ
- 8.2. Величина, характеризующая «связь» между двумя физическими процессами. Случай, когда известна одна реализация физического процесса, наблюдаемая в течение большого интервала времени
- 8.3. Эргодичность
- 8.4. Коэффициент корреляции и теория информации
- 8.5. Практические замечания
- 8.6. Характеристические функции
- 8.7. Спектральная плотность случайного сигнала
- 8.8. Связь между временными представлениями сигналов и спектральными плотностями. Теорема Винера — Хинчина
- 8.9. Функция связи
- 8.10. Распределение Гаусса, или нормальное распределение
- 8.11. Спектральная плотность и центрирование сигналов
- Глава 9. ОЦЕНКА ОШИБОК ИЗМЕРЕНИЙ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 9.2. Оценка корреляционных функций
- 9.3. Оценка спектральных плотностей
- 9.4. Оценка одномерной плотности вероятности
- 9.5. Последовательное вычисление среднего значения и дисперсии
- 9.6. Физическая интерпретация дисперсии
- 9.7. Идеальный интегратор и низкочастотный фильтр
- 9.8. Дискретные сигналы
- Глава 10. ОШИБКИ ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ПРИ ДИСКРЕТИЗАЦИИ СИГНАЛОВ
- 10.2. Коррелометры с вспомогательными шумами
- 10.3. Условия на вспомогательные шумы, при которых отсутствует смещение оценки корреляционной функции
- 10.4. Вычисление дисперсии. Состоятельность оценки
- 10.5. Практические приложения
- 10.6. Важное замечание
- 10.7. Замечание относительно генераторов вспомогательных шумов
- Глава 11. ОСНОВНЫЕ СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 11.2. Периодические функции
- 11.3. Переходные функции
- 11.4. Дистрибутивность операций вычисления корреляции и спектральной плотности
- 11.5. Связь между входным и выходным сигналами линейной однородной во времени системы при условии, что входной сигнал является случайным и стационарным 2-го порядка
- Глава 12. ОСНОВНЫЕ ПРИЛОЖЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 12.2. Обнаружение периодического сигнала с известным периодом на фоне шума
- 12.3. Выделение сигнала на фоне шума. Усреднение
- 12.4. Обнаружение скрытых периодичностей
- 12.5. Получение спектральных плотностей по корреляционным функциям
- 12.6. Измерение динамических характеристик (переходных функций, импульсных характеристик) линейных систем. Идентификация процессов
- 12.7. Измерение когерентности
- 12.8. Применение когерентности к измерению передаточных функций линейных и однородных во времени систем. Спектральная лупа
- 12.9. Измерение временного сдвига двух сигналов
- Глава 13. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ИЗМЕРЕНИЕ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 13.2. Влияние фильтрации, обусловленной дискретизацией спектральной плотности
- 13.3. Дискретизация спектральной плотности, реализуемая на практике
- 13.4. Систематическая ошибка при измерении спектральной плотности
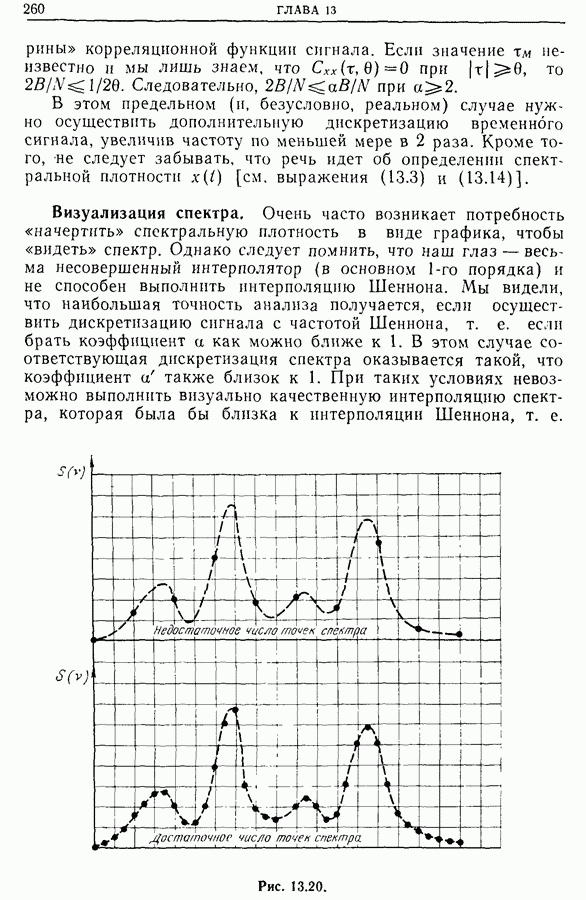
- 13.5. Измерение спектральной плотности
- 13.6. Спектральный анализ методом фильтрации
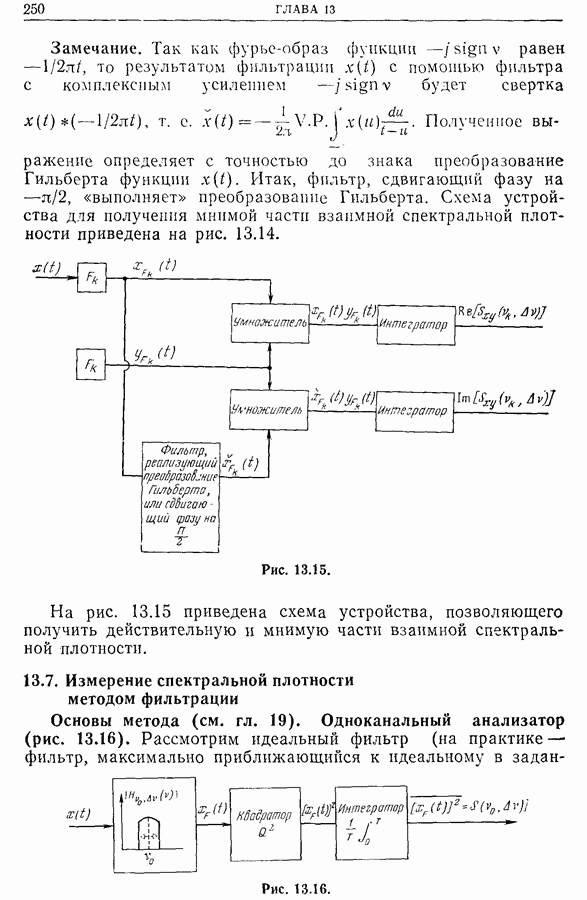
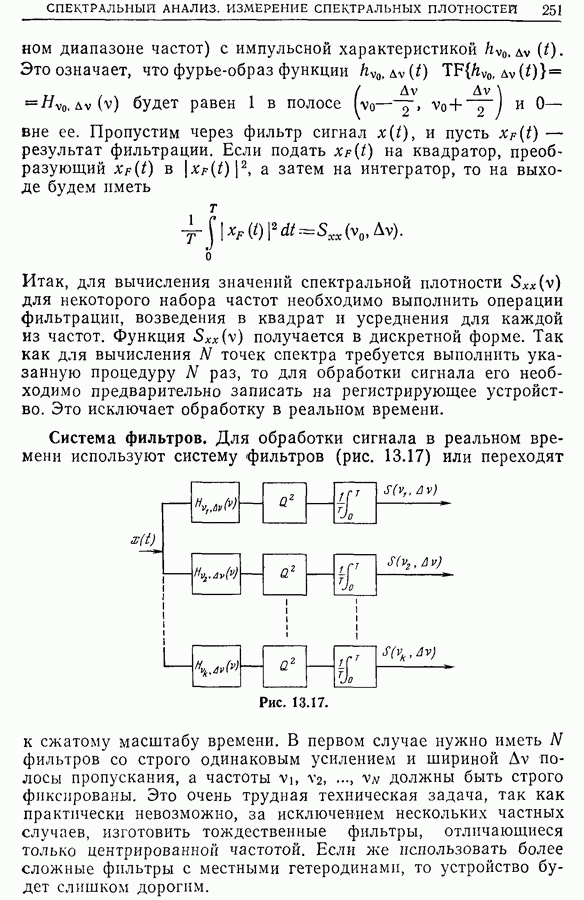
- 13.7. Измерение спектральной плотности методом фильтрации
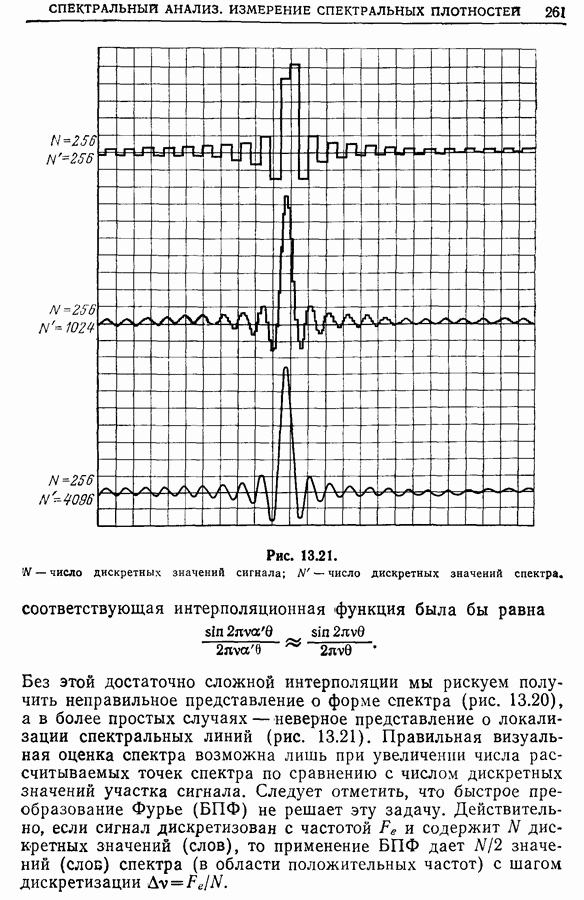
- 13.8. Дискретное преобразование Фурье и измерение спектральных плотностей [2, 6, 7]
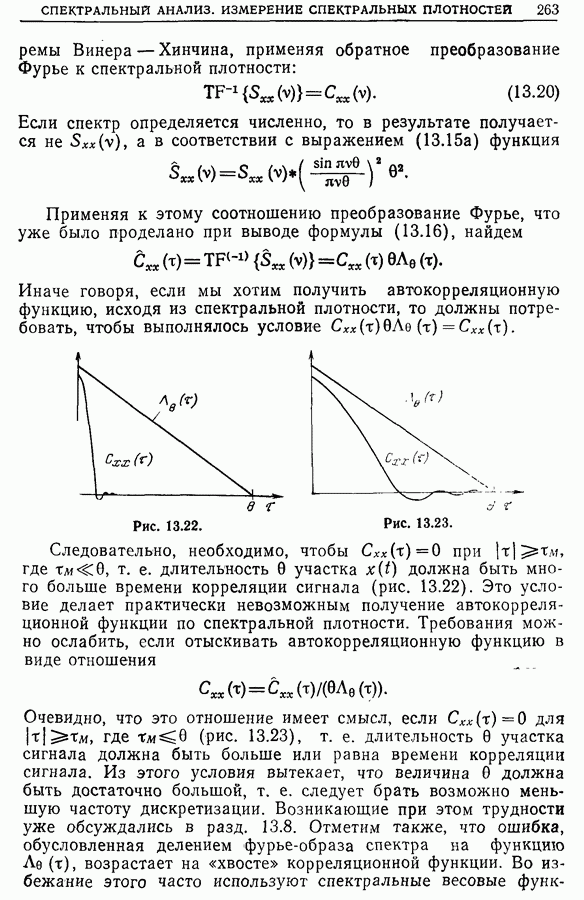
- 13.9. Вычисление автокорреляционных функций и взаимных корреляционных функций по спектральной плотности
- 13.10. Явление Гиббса
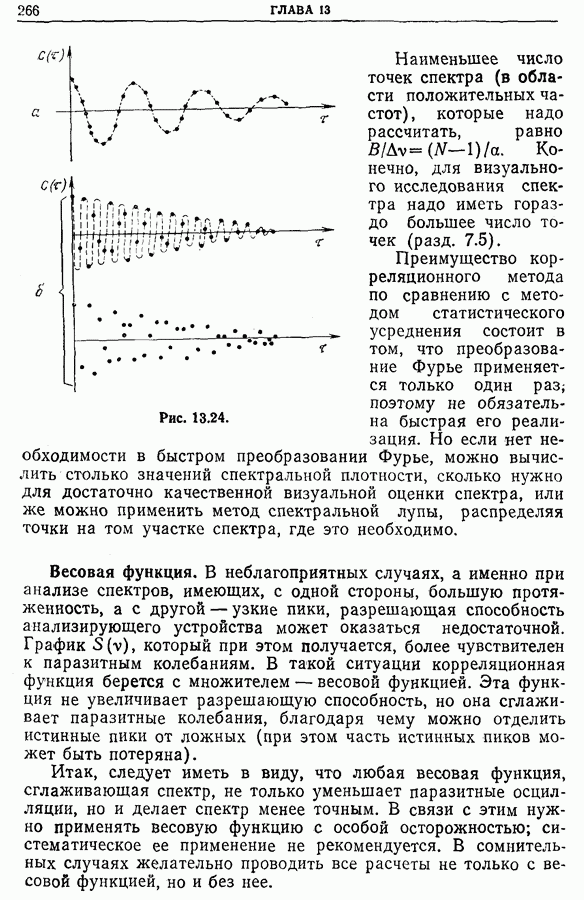
- 13.11. Корреляционный метод спектрального анализа
- 13.12. Корреляционный анализатор спектра
- 13.13. Точность определения спектральной плотности, полученной преобразованием Фурье корреляционной функции [1]
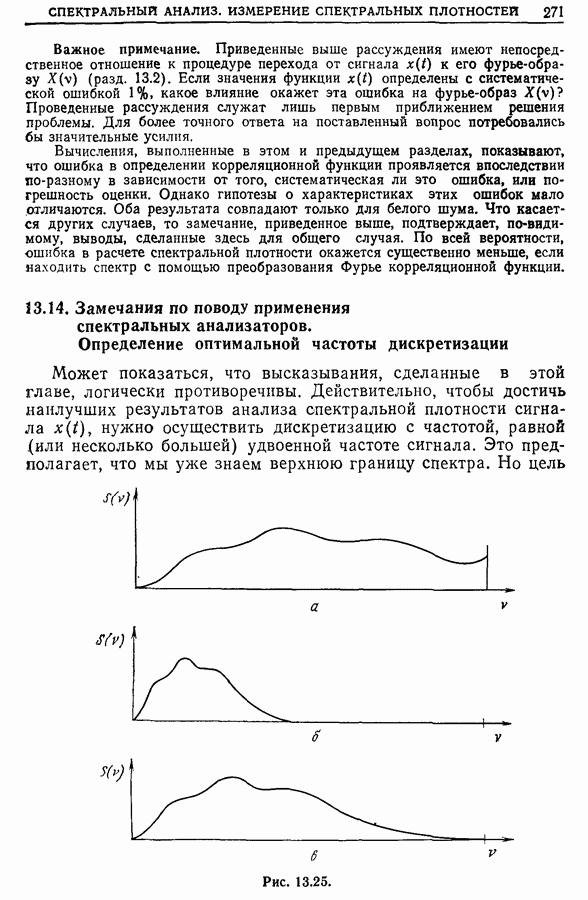
- 13.14. Замечания по поводу применения спектральных анализаторов. Определение оптимальной частоты дискретизации
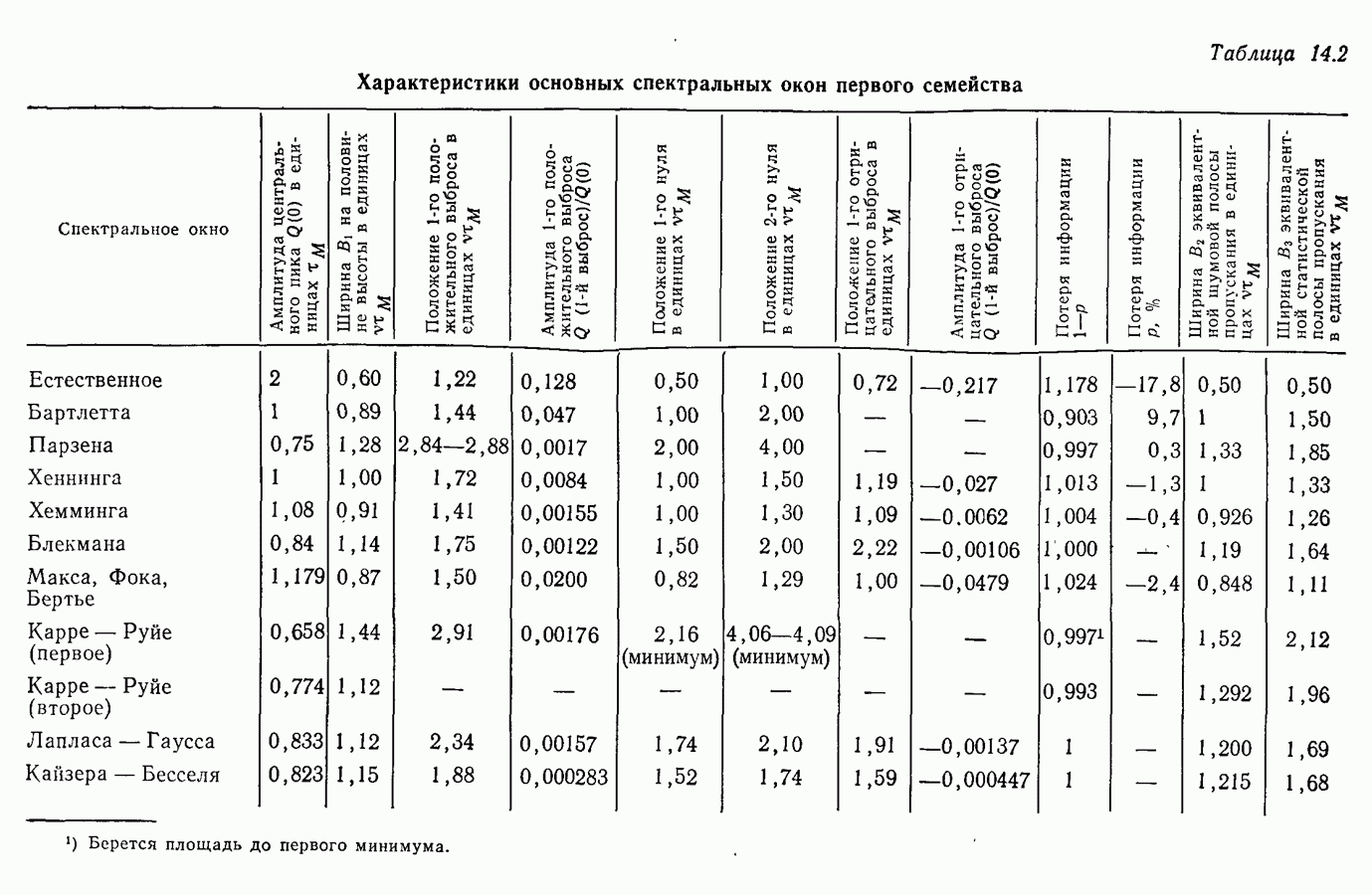
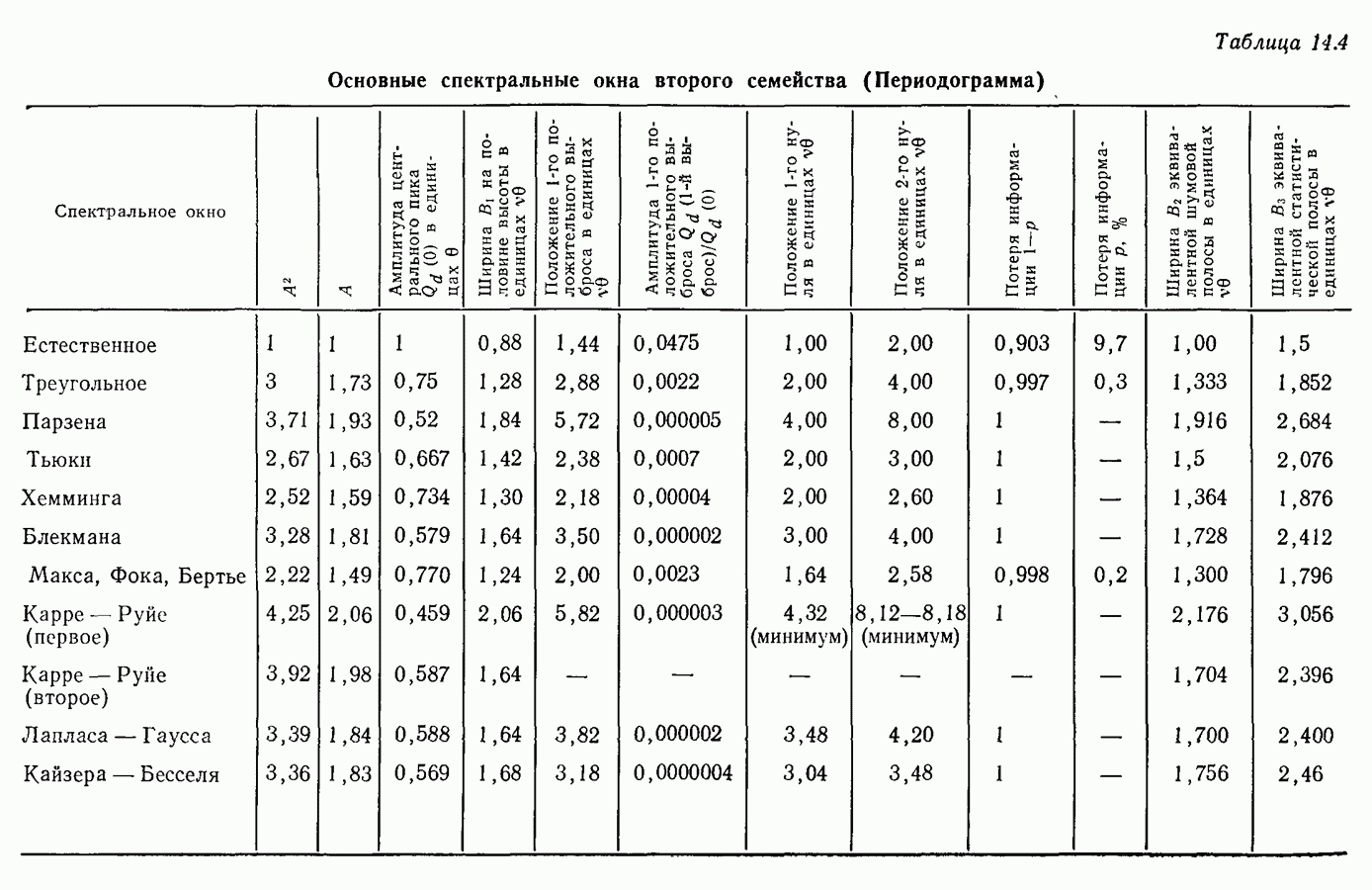
- Глава 14. ВЕСОВЫЕ ОКНА
- 14.2. Окна, связанные с преобразованием Фурье
- 14.3. Окна, используемые в методе коррелограмм
- 14.4. Окна, применяемые в методе периодограмм
- 14.5. Окна, применяемые в методе фильтрации с возведением в квадрат и усреднением
- 14.6. Основные характеристики временных и спектральных окон
- 14.7. Первое семейство временных весовых окон
- 14.8. Второе семейство временных весовых окон (Метод периодограмм)
- 14.9. Исследование спектра в простом случае
- 14.10. Выбор весовой функции