| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
12.2. Обнаружение периодического сигнала с известным периодом на фоне шума
Основы метода.
Итак, предположим, что основной период  сигнала известен. Рассмотрим взаимную корреляцию сигнала
сигнала известен. Рассмотрим взаимную корреляцию сигнала  с вспомогательным сигналом
с вспомогательным сигналом  основной период которого также равен
основной период которого также равен  :
:

или

Так как функции  независимы, то функция
независимы, то функция  равна нулю (с точностью до погрешности оценки), следовательно,
равна нулю (с точностью до погрешности оценки), следовательно,

Взаимная корреляционная функция  двух периодических сигналов с одинаковым основным периодом
двух периодических сигналов с одинаковым основным периодом  будет также периодической с тем же основным периодом. Отметим, что функция
будет также периодической с тем же основным периодом. Отметим, что функция  центрирована и имеет период
центрирована и имеет период  (никакие другие условия на нее не налагаются). Таким образом, имеется большая свобода выбора
(никакие другие условия на нее не налагаются). Таким образом, имеется большая свобода выбора  для ее построения можно исходить, например, из автокорреляционной функции для
для ее построения можно исходить, например, из автокорреляционной функции для 
Метод обнаружения сигнала с помощью взаимной корреляции имеет ряд достоинств. Например, соотношение (12.3) содержит функцию  стремящуюся к нулю с возрастанием
стремящуюся к нулю с возрастанием  но отличную от нуля в начальный момент времени. Функция
но отличную от нуля в начальный момент времени. Функция  не входит в соотношение (12.30), благодаря чему можно проводить измерения при малых значениях т. В выражении (12.3) содержатся три слагаемых, порождающих ошибку:
не входит в соотношение (12.30), благодаря чему можно проводить измерения при малых значениях т. В выражении (12.3) содержатся три слагаемых, порождающих ошибку:  тогда как в выражении (12.30) имеется только одно слагаемое
тогда как в выражении (12.30) имеется только одно слагаемое  Можно ожидать, что этот метод даст большое увеличение отношения сигнал/шум по
Можно ожидать, что этот метод даст большое увеличение отношения сигнал/шум по
сравнению с автокорреляционным методом. К сожалению, довольно часто мы не знаем достаточно точно значение периода функции 
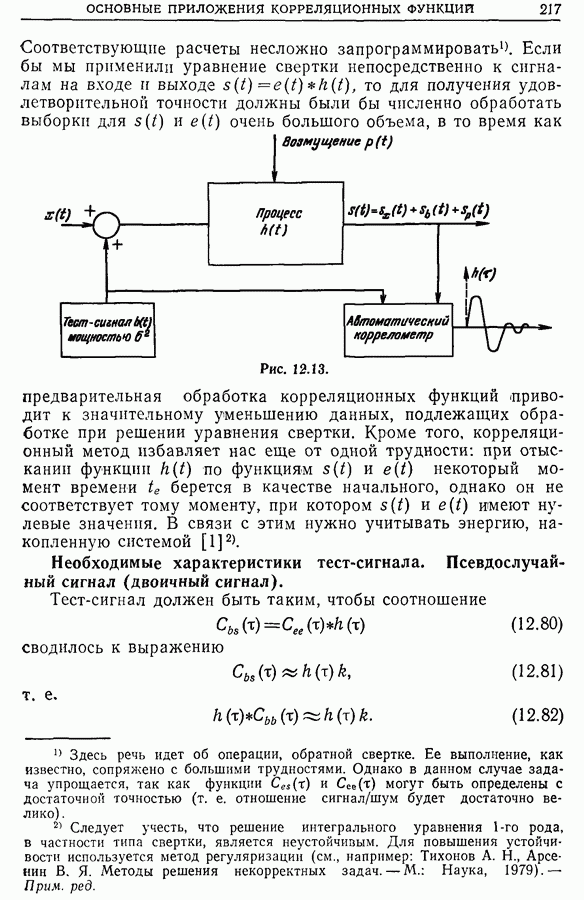
Увеличение отношения сигнал/шум при обнаружении периодического сигнала на фоне шума методом измерения его взаимной корреляции с периодическим сигналом той же частоты.
Для упрощения выкладок допустим, что оба периодических сигнала являются монохроматическими. Пусть

где по предположению b(t) - стационарный процесс 2-го порядка со спектральной плотностью  . Рассмотрим взаимную корреляцию
. Рассмотрим взаимную корреляцию  с периодическим сигналом
с периодическим сигналом  имеющим период
имеющим период  . Одна из взаимных корреляционных функций определяется соотношением
. Одна из взаимных корреляционных функций определяется соотношением 

Аналогично определяется другая функция:

Свойство  не обязательно выполняется для оценок:
не обязательно выполняется для оценок:

или в более подробной записи: 

Положим

где  — взаимные корреляционные функции двух периодических сигналов. Отметим, что в выражении для
— взаимные корреляционные функции двух периодических сигналов. Отметим, что в выражении для  сигнал частоты
сигнал частоты  запаздывает по отношению к сигналу частоты
запаздывает по отношению к сигналу частоты  , а в выражении для
, а в выражении для  запаздывающим является сигнал частоты
запаздывающим является сигнал частоты  . Величины
. Величины  представляют собой взаимные корреляционные функции шума
представляют собой взаимные корреляционные функции шума  и периодического сигнала.
и периодического сигнала.
Рассмотрим сначала взаимные корреляционные функции  Вычислим интеграл
Вычислим интеграл 

После простых, но громоздких тригонометрических преобразований находим

Это выражение можно записать в виде

где

Аналогичным образом находим  где
где  находятся из и
находятся из и  перестановкой
перестановкой 
Очевидно, что и  обращаются в нуль при условии
обращаются в нуль при условии  Таким образом,
Таким образом,  - периодические функции с частотами
- периодические функции с частотами  соответственно.
соответственно.
Если то амплитуды  стремятся
стремятся  нулю при стремлении Т к бесконечности. Если же
нулю при стремлении Т к бесконечности. Если же  , то
, то

и при  . Этот результат получается также при
. Этот результат получается также при 
Найдем теперь взаимную корреляционную функцию 
Имеем

Если функция  не равна тождественно нулю, то она периодична (с частотой
не равна тождественно нулю, то она периодична (с частотой  ), где
), где  . Это следует из тождества
. Это следует из тождества

которое становится очевидным, если учесть, что 
Необходимо отметить, что нами доказана периодичность оценки взаимной корреляционной функции шума и периодического сигнала частоты  а также периодичность взаимной корреляционной функции двух периодических сигналов на любом временном промежутке (кроме промежутка, длина которого кратна обоим периодам). Подобный результат не мог быть предсказан заранее.
а также периодичность взаимной корреляционной функции двух периодических сигналов на любом временном промежутке (кроме промежутка, длина которого кратна обоим периодам). Подобный результат не мог быть предсказан заранее.
Найдем 

где 
Полученное выражение является периодической функцией периода  оно обращается в нуль, если
оно обращается в нуль, если  . Само собой разумеется, что
. Само собой разумеется, что  если
если  . Найдем
. Найдем 

Выкладки, аналогичные проделанным в предыдущем разделе, приводят к следующему результату: 

В предположении, что  — центрированный сигнал, а Т велико по сравнению с
— центрированный сигнал, а Т велико по сравнению с  получим
получим

или

Делая те же допущения, что и в предыдущем разделе, найдем

Отношения сигнал/шум до вычисления корреляции и после вычисления равны соответственно  и
и

Усиление отношения сигнал/шум по мощности равно

а усиление по амплитуде 
Напомним, что увеличение отношения сигнал/шум является случайной величиной. Вероятность того, что эти величины примут значения, определенные полученными формулами, равна 
Заключение.
Из приведенного исследования взаимной корреляционной функции, полученной интегрированием по промежутку конечной длины, нельзя сделать никаких выводов о существовании периодического сигнала. В самом деле, корреляционная функция (на конечном промежутке интегрирования) периодична (выражения (12.37) и (12.38)), но это, однако, не означает присутствия периодического сигнала. Чтобы извлечь подобную информацию, необходимо знать временную эволюцию взаимной корреляционной функции. Если амплитуда ее периодической компоненты уменьшается с ростом Т, то можно считать, что сигнал не содержит периодической составляющей. В противном случае можно предполагать наличие такой составляющей. Кроме того, в любом случае представляет интерес измерение дисперсии и исследование ее эволюции во времени. Нельзя ограничиваться только нахождением корреляционной функции. Нужно обязательно определять зависимость оценки корреляционной функции от времени и одновременно с этим вычислять ее дисперсию.
Замечание 1.
При нахождении достаточно простых формул для погрешностей оценок делают ряд упрощающих допущений. Однако не следует переоценивать полученные при этом выражения: к ним надо относиться как  оценкам порядка соответствующих величин. Более предпочтительно проводить непосредственные оценки дисперсий, что современная вычислительная техника позволяет делать сравнительно легко.
оценкам порядка соответствующих величин. Более предпочтительно проводить непосредственные оценки дисперсий, что современная вычислительная техника позволяет делать сравнительно легко.
Замечание 2.
Как показано в разд. 9.8, для оценки усиления целесообразно использовать произведение ВТ, а не объем N выборки при дискретизации.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- Глава 1. ФИЗИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ШУМАХ КАК О СЛУЧАЙНЫХ ПРОЦЕССАХ
- Глава 2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 2.2. Преобразование Фурье непериодических функций
- 2.3. Преобразование Фурье физических функций
- 2.4. Физический смысл преобразования Фурье
- 2.5. Условия существования преобразования Фурье
- 2.6. Некоторые свойства преобразования Фурье
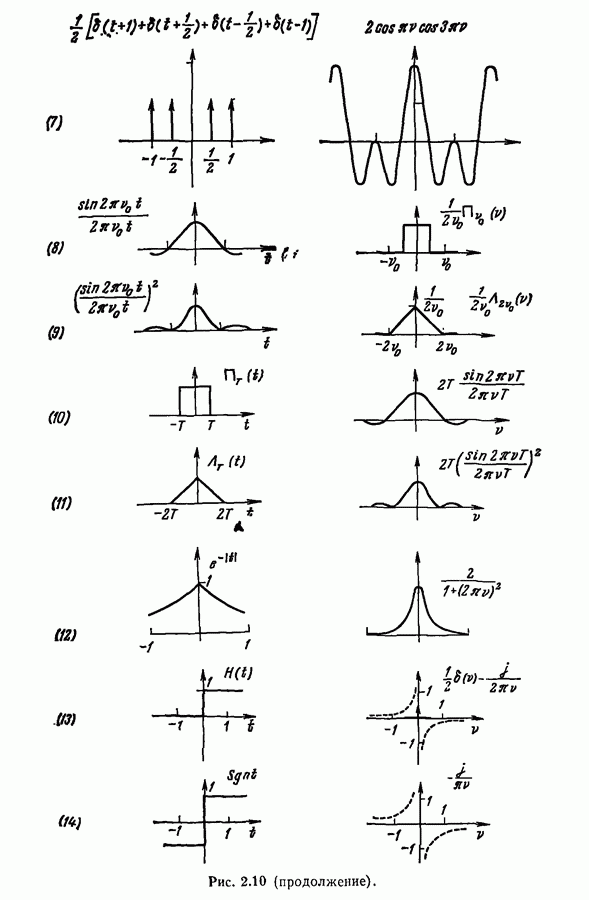
- 2.7. Несколько функций и их фурье-образы
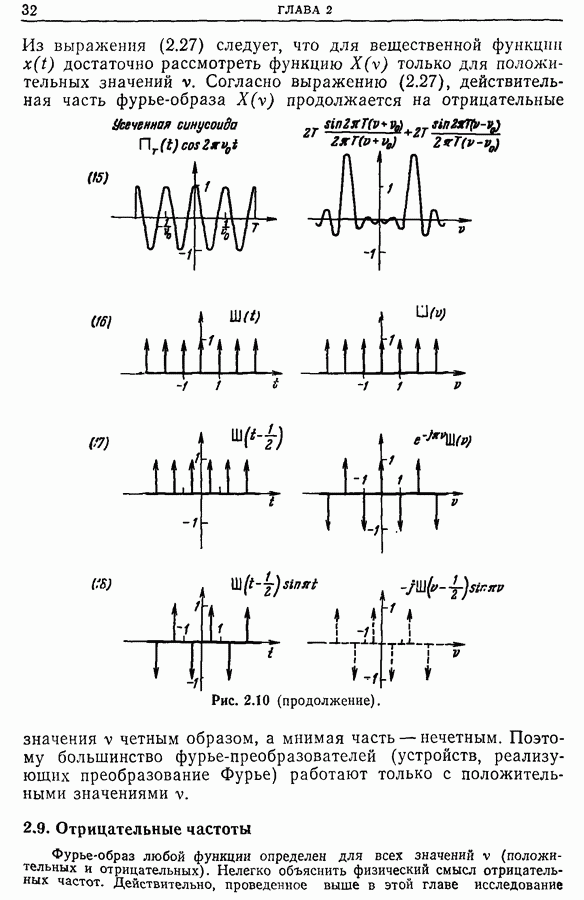
- 2.8. Частный случай вещественных сигналов
- 2.9. Отрицательные частоты
- 2.10. Аналитический сигнал
- 2.11. Почему выбрано преобразование Фурье?
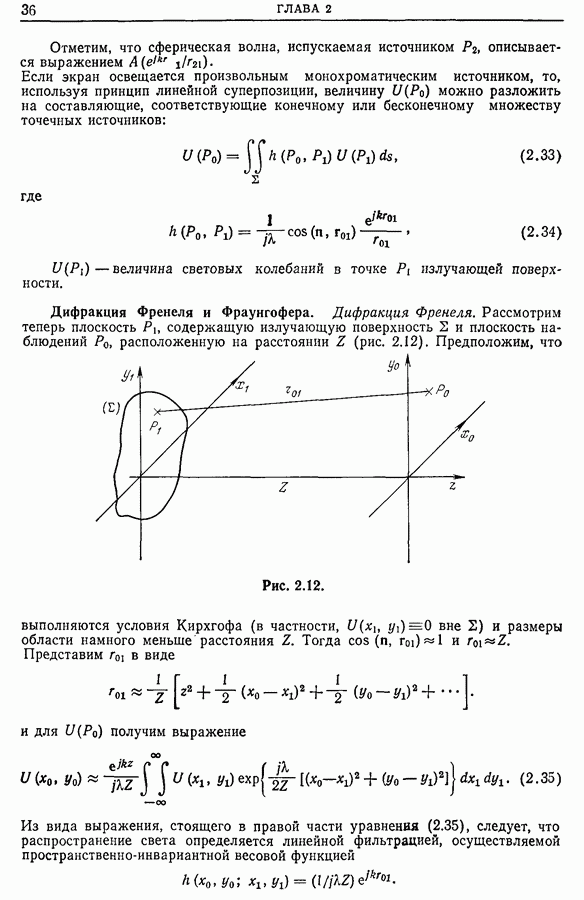
- 2.12 Физическая реализация фурье-образа. Преобразование Фурье в оптике
- 2.13. Свойства функции sin х/х
- 2.14. Лямбда-функция
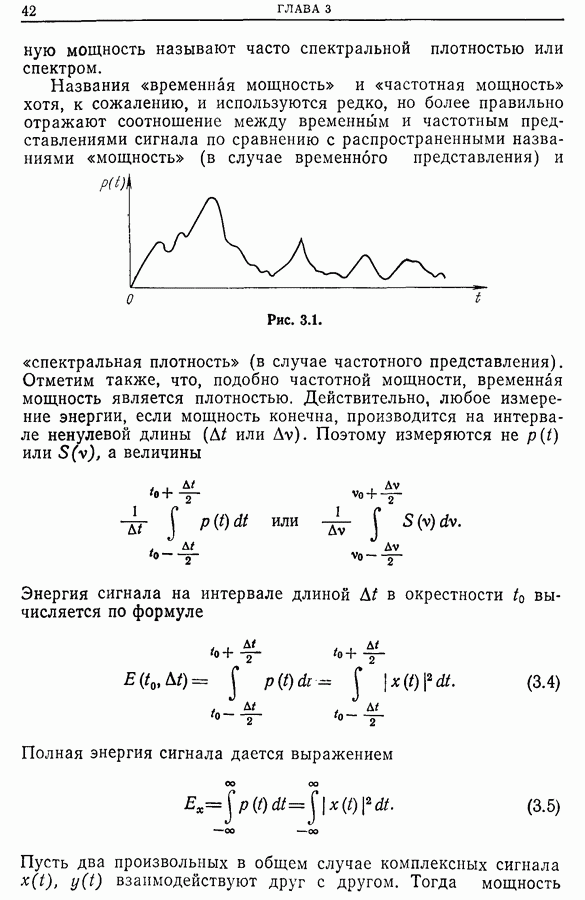
- Глава 3. МОЩНОСТЬ И ЭНЕРГИЯ СИГНАЛОВ
- 3.2. Частотная мощность. Спектральная плотность мощности. Спектр мощности
- 3.3. Общее определение спектральной плотности
- 3.4. Теорема Парсеваля
- 3.5. Понятие скалярного произведения и нормы
- Глава 4. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- 4.2. Связь между фурье-образом и изображением Лапласа
- Глава 5. СВЕРТКА
- 5.2. Уравнение свертки
- 5.3. Несколько замечаний относительно свертки
- 5.4. Физическая интерпретация свертки
- 5.5. Прямая и обратная задачи, связанные с операцией свертки
- 5.6. Свертка и преобразование Фурье. Теорема Планшереля
- Глава 6. ФИЛЬТРАЦИЯ
- 6.2. Временная фильтрация
- 6.3. Частотная фильтрация («линейная фильтрация» в смысле Блан-Лапьера)
- 6.4. Связь между фильтрацией и сверткой
- 6.5. Физически реализуемые линейные фильтры частоты
- 6.6. Идеальный фильтр
- 6.7. Реализуемые непрерывные аналоговые фильтры [3]
- 6.8. Фильтры с линейным сдвигом фаз
- 6.9. Узкополосные фильтры
- 6.10. Обобщение понятия фильтрации
- Глава 7. ДИСКРЕТИЗАЦИЯ
- 7.2. Теоремы дискретизации
- 7.3. Дискретизация сигналов конечной длительности
- 7.4. Дискретизация фурье-образов
- 7.5. Выбор частоты дискретизации на практике
- 7.6. Противомаскировочный фильтр
- 7.7. Физическая дискретизация. Комбинированная дискретизация
- 7.8. Субдискретизация. Обобщение теоремы Шеннона [9]
- 7.9. Заключение
- Глава 8. КОРРЕЛЯЦИЯ И НЕКОТОРЫЕ ДРУГИЕ ПОНЯТИЯ СТАТИСТИКИ
- 8.2. Величина, характеризующая «связь» между двумя физическими процессами. Случай, когда известна одна реализация физического процесса, наблюдаемая в течение большого интервала времени
- 8.3. Эргодичность
- 8.4. Коэффициент корреляции и теория информации
- 8.5. Практические замечания
- 8.6. Характеристические функции
- 8.7. Спектральная плотность случайного сигнала
- 8.8. Связь между временными представлениями сигналов и спектральными плотностями. Теорема Винера — Хинчина
- 8.9. Функция связи
- 8.10. Распределение Гаусса, или нормальное распределение
- 8.11. Спектральная плотность и центрирование сигналов
- Глава 9. ОЦЕНКА ОШИБОК ИЗМЕРЕНИЙ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 9.2. Оценка корреляционных функций
- 9.3. Оценка спектральных плотностей
- 9.4. Оценка одномерной плотности вероятности
- 9.5. Последовательное вычисление среднего значения и дисперсии
- 9.6. Физическая интерпретация дисперсии
- 9.7. Идеальный интегратор и низкочастотный фильтр
- 9.8. Дискретные сигналы
- Глава 10. ОШИБКИ ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ПРИ ДИСКРЕТИЗАЦИИ СИГНАЛОВ
- 10.2. Коррелометры с вспомогательными шумами
- 10.3. Условия на вспомогательные шумы, при которых отсутствует смещение оценки корреляционной функции
- 10.4. Вычисление дисперсии. Состоятельность оценки
- 10.5. Практические приложения
- 10.6. Важное замечание
- 10.7. Замечание относительно генераторов вспомогательных шумов
- Глава 11. ОСНОВНЫЕ СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 11.2. Периодические функции
- 11.3. Переходные функции
- 11.4. Дистрибутивность операций вычисления корреляции и спектральной плотности
- 11.5. Связь между входным и выходным сигналами линейной однородной во времени системы при условии, что входной сигнал является случайным и стационарным 2-го порядка
- Глава 12. ОСНОВНЫЕ ПРИЛОЖЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 12.2. Обнаружение периодического сигнала с известным периодом на фоне шума
- 12.3. Выделение сигнала на фоне шума. Усреднение
- 12.4. Обнаружение скрытых периодичностей
- 12.5. Получение спектральных плотностей по корреляционным функциям
- 12.6. Измерение динамических характеристик (переходных функций, импульсных характеристик) линейных систем. Идентификация процессов
- 12.7. Измерение когерентности
- 12.8. Применение когерентности к измерению передаточных функций линейных и однородных во времени систем. Спектральная лупа
- 12.9. Измерение временного сдвига двух сигналов
- Глава 13. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ИЗМЕРЕНИЕ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 13.2. Влияние фильтрации, обусловленной дискретизацией спектральной плотности
- 13.3. Дискретизация спектральной плотности, реализуемая на практике
- 13.4. Систематическая ошибка при измерении спектральной плотности
- 13.5. Измерение спектральной плотности
- 13.6. Спектральный анализ методом фильтрации
- 13.7. Измерение спектральной плотности методом фильтрации
- 13.8. Дискретное преобразование Фурье и измерение спектральных плотностей [2, 6, 7]
- 13.9. Вычисление автокорреляционных функций и взаимных корреляционных функций по спектральной плотности
- 13.10. Явление Гиббса
- 13.11. Корреляционный метод спектрального анализа
- 13.12. Корреляционный анализатор спектра
- 13.13. Точность определения спектральной плотности, полученной преобразованием Фурье корреляционной функции [1]
- 13.14. Замечания по поводу применения спектральных анализаторов. Определение оптимальной частоты дискретизации
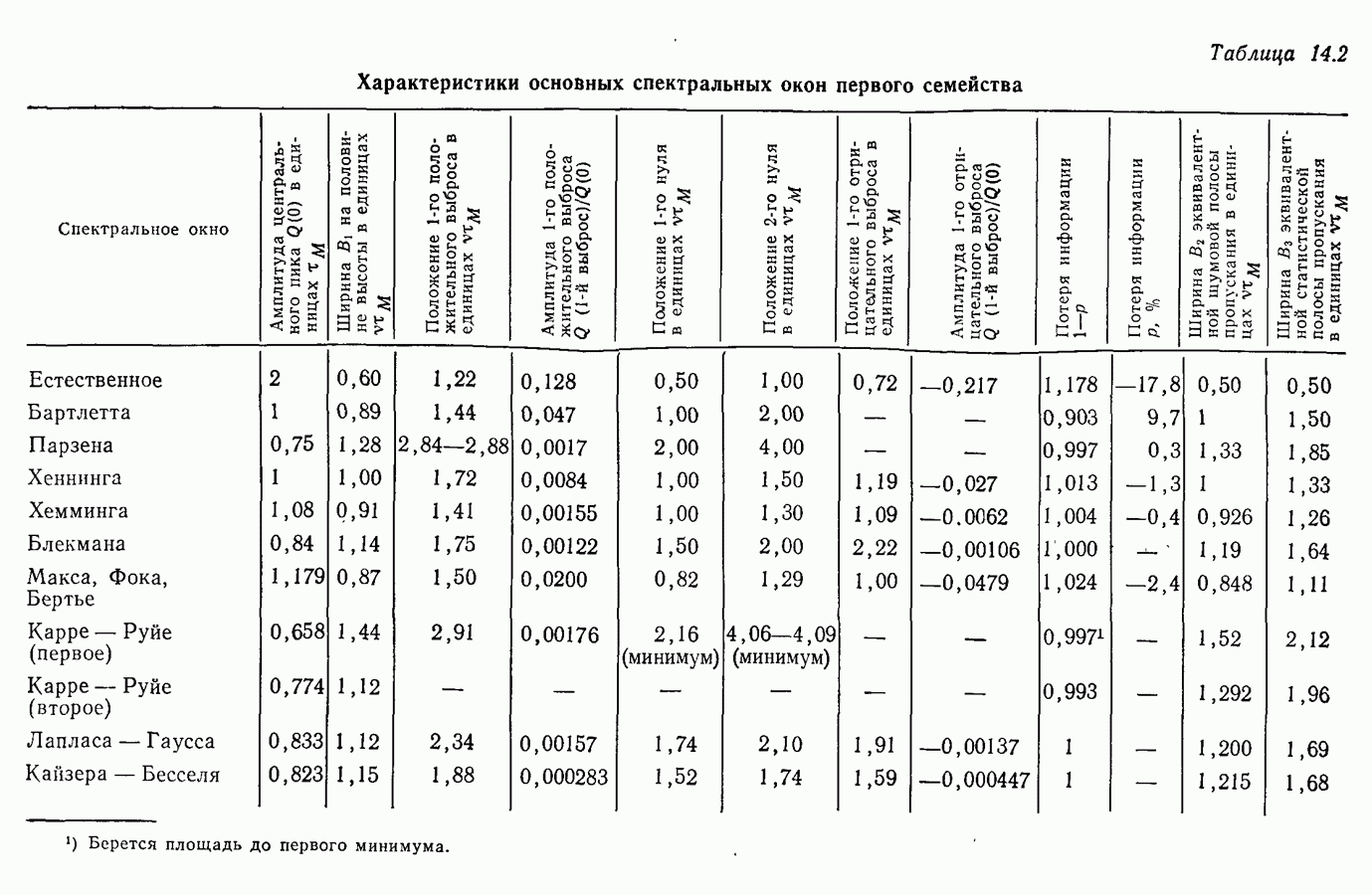
- Глава 14. ВЕСОВЫЕ ОКНА
- 14.2. Окна, связанные с преобразованием Фурье
- 14.3. Окна, используемые в методе коррелограмм
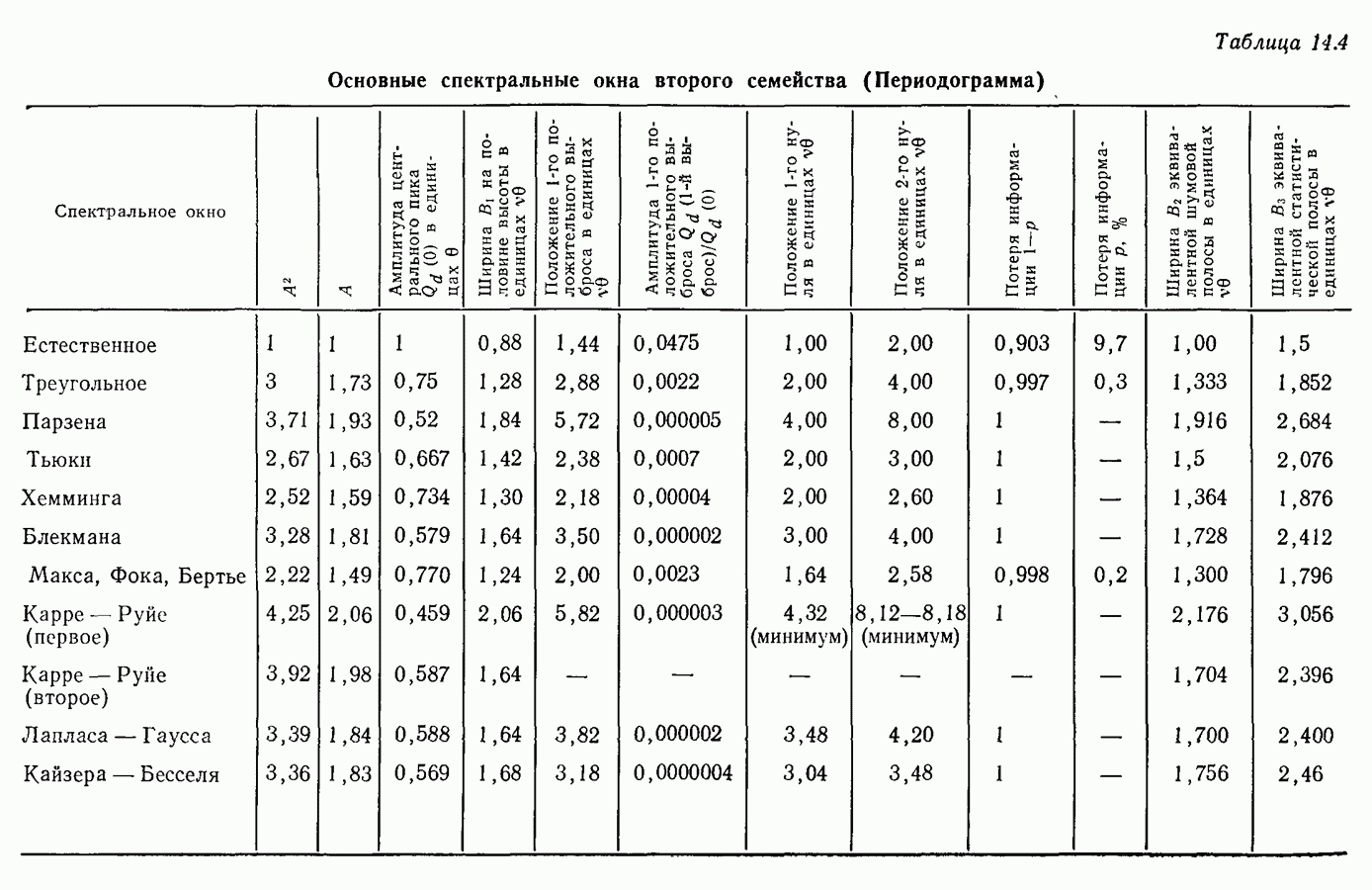
- 14.4. Окна, применяемые в методе периодограмм
- 14.5. Окна, применяемые в методе фильтрации с возведением в квадрат и усреднением
- 14.6. Основные характеристики временных и спектральных окон
- 14.7. Первое семейство временных весовых окон
- 14.8. Второе семейство временных весовых окон (Метод периодограмм)
- 14.9. Исследование спектра в простом случае
- 14.10. Выбор весовой функции