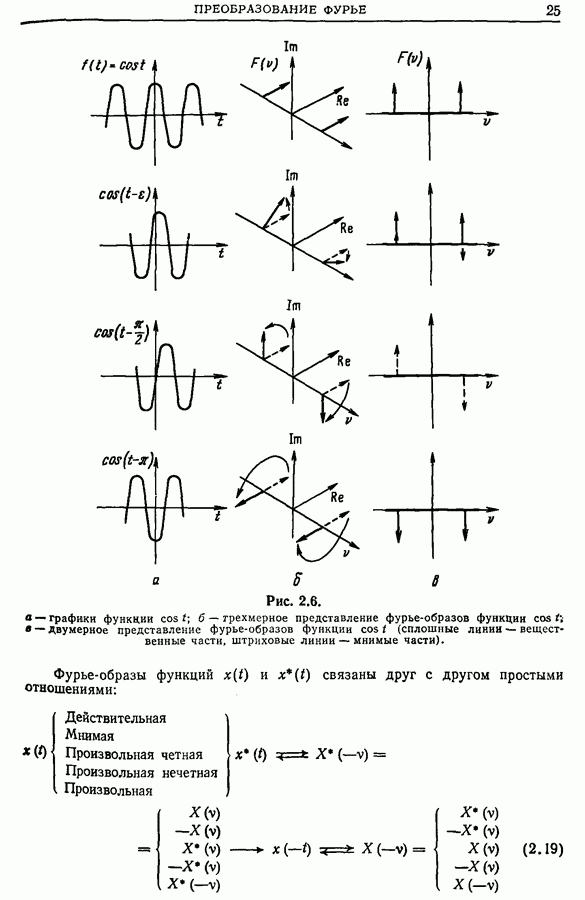
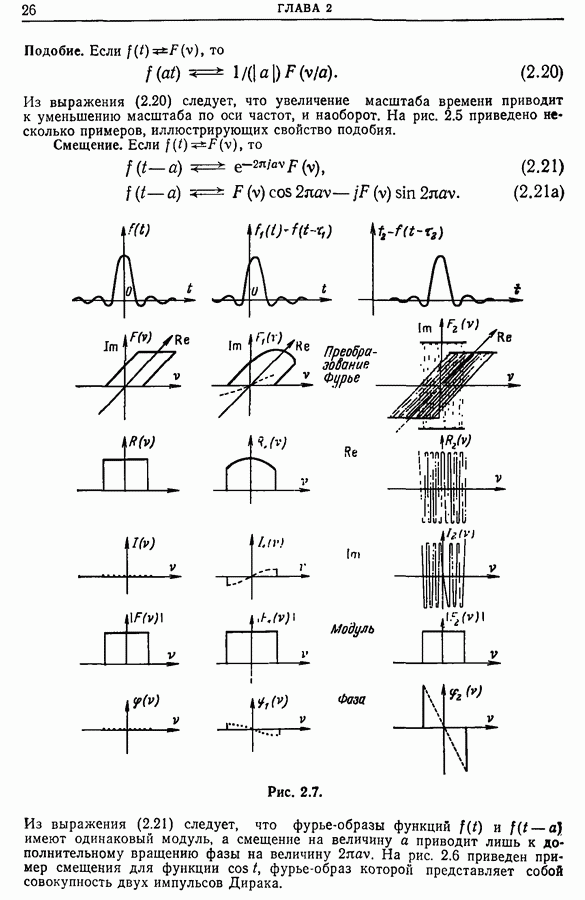
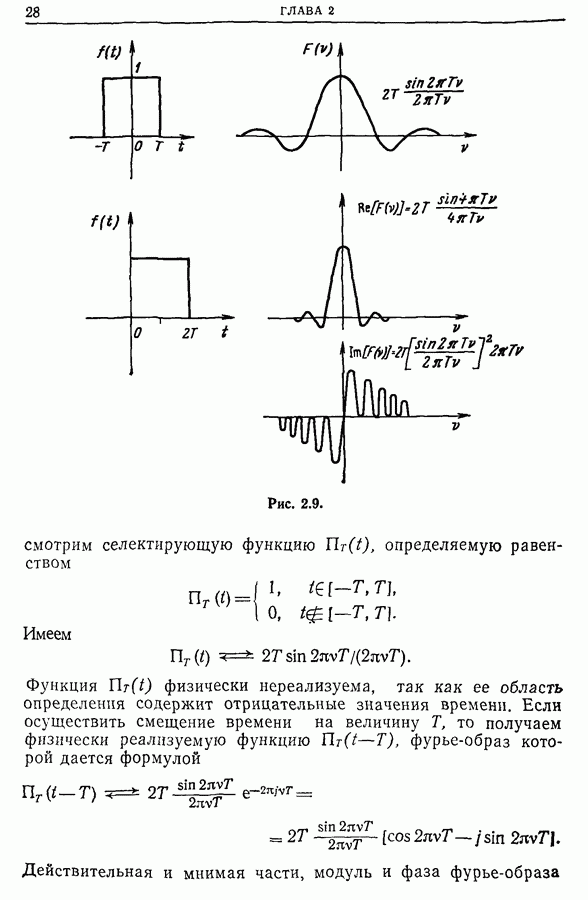
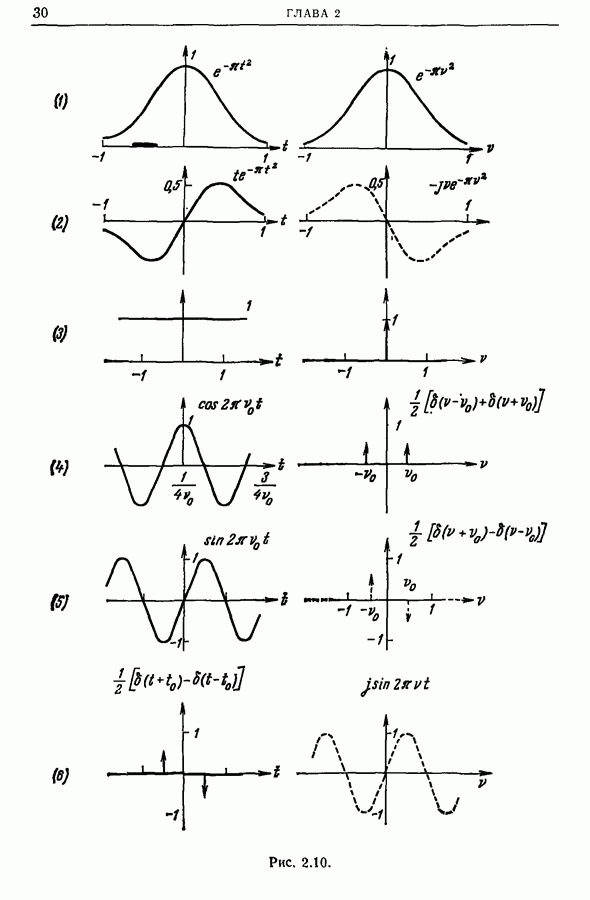
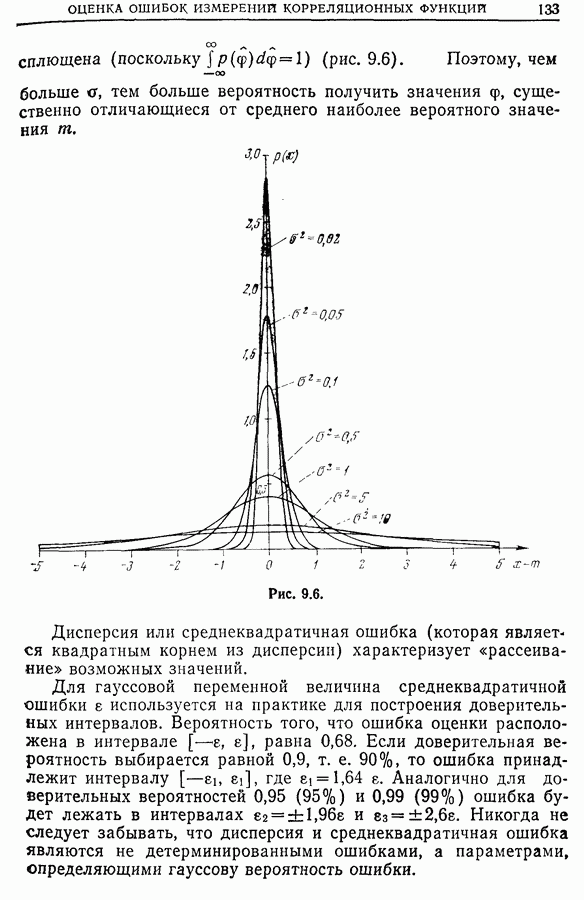
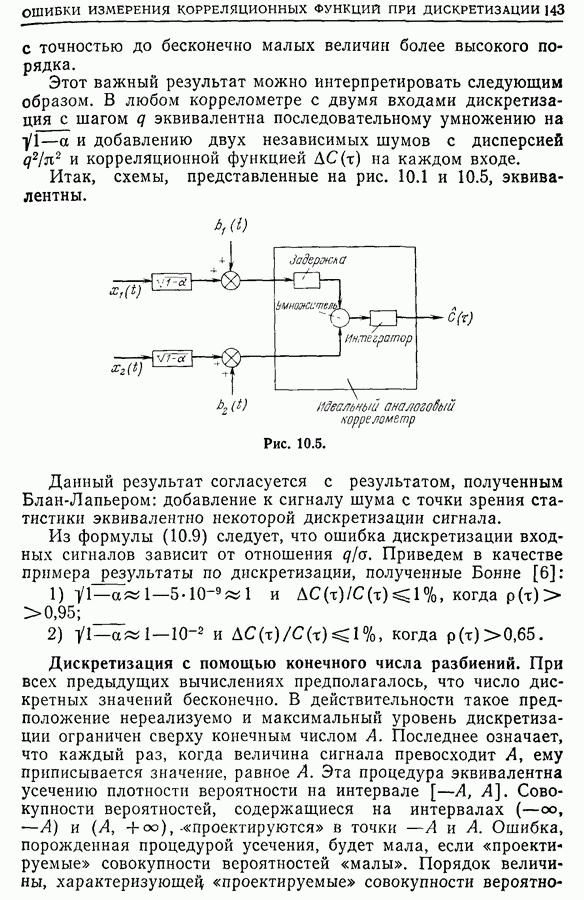
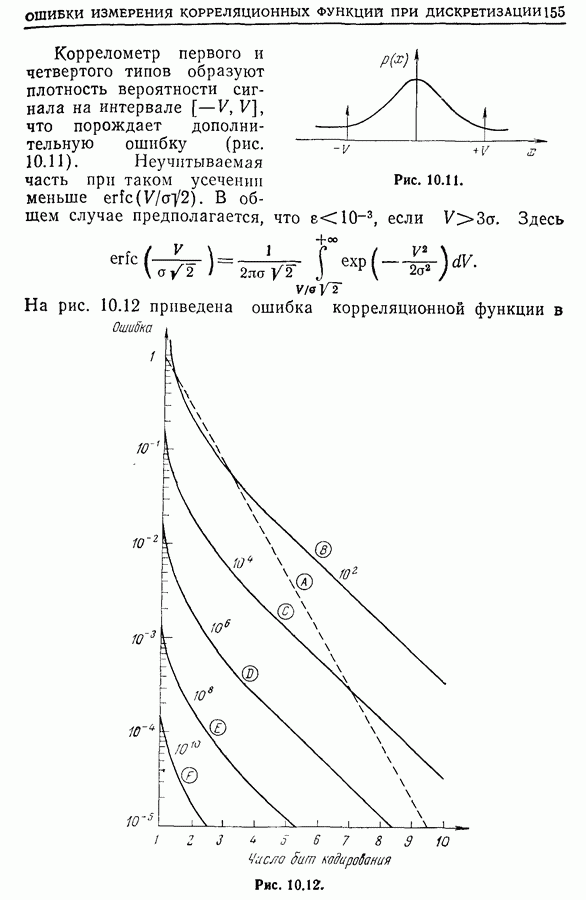
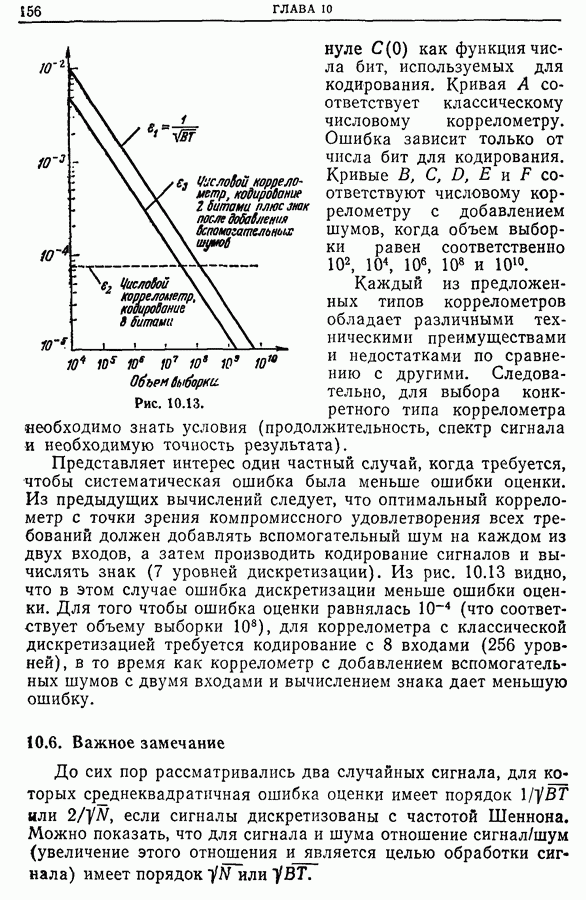
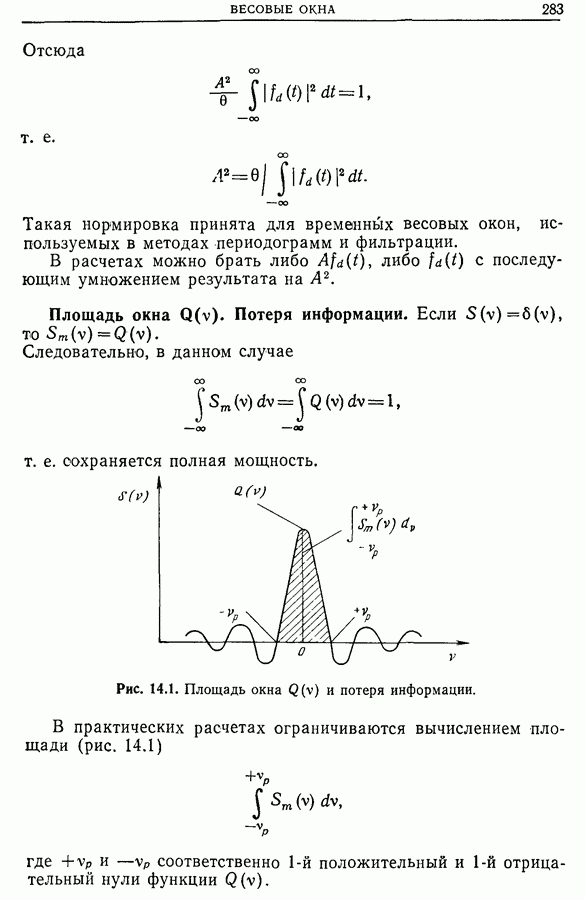
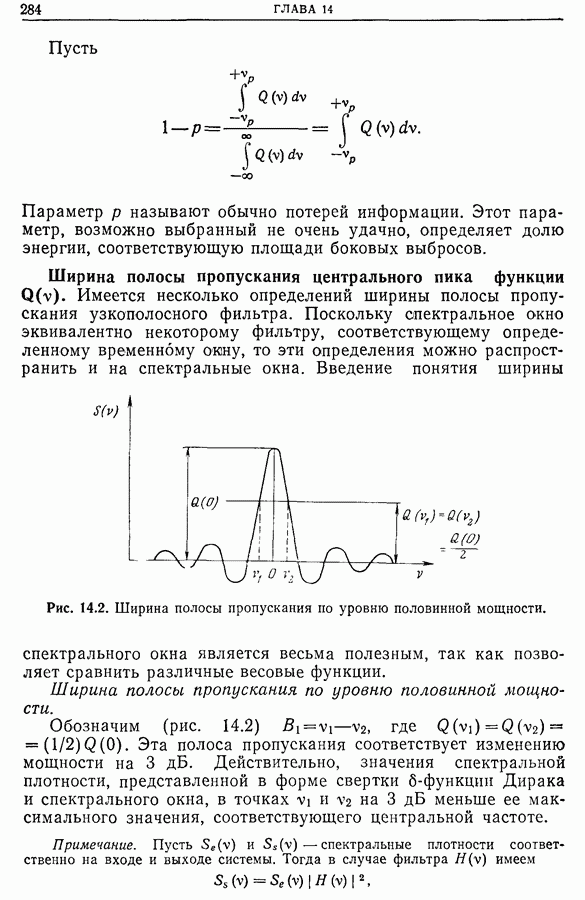
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
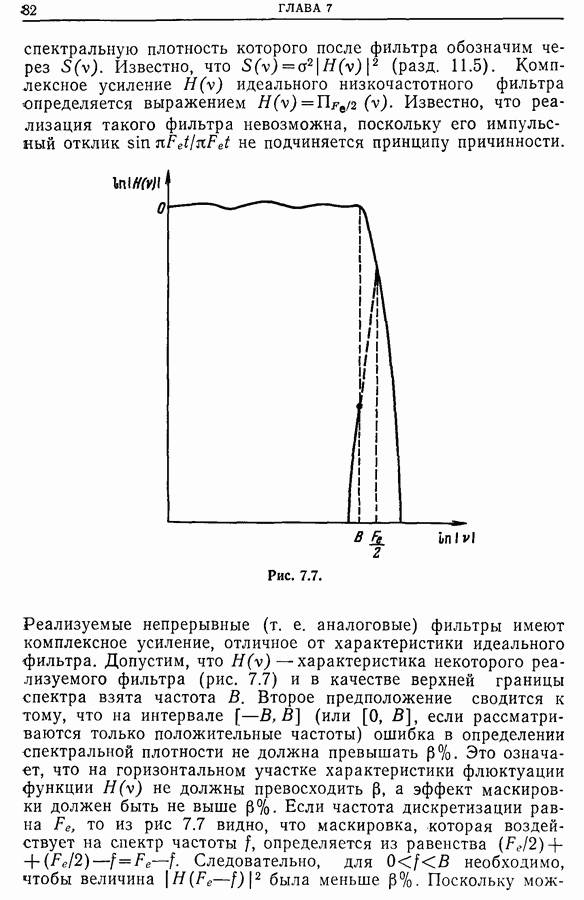
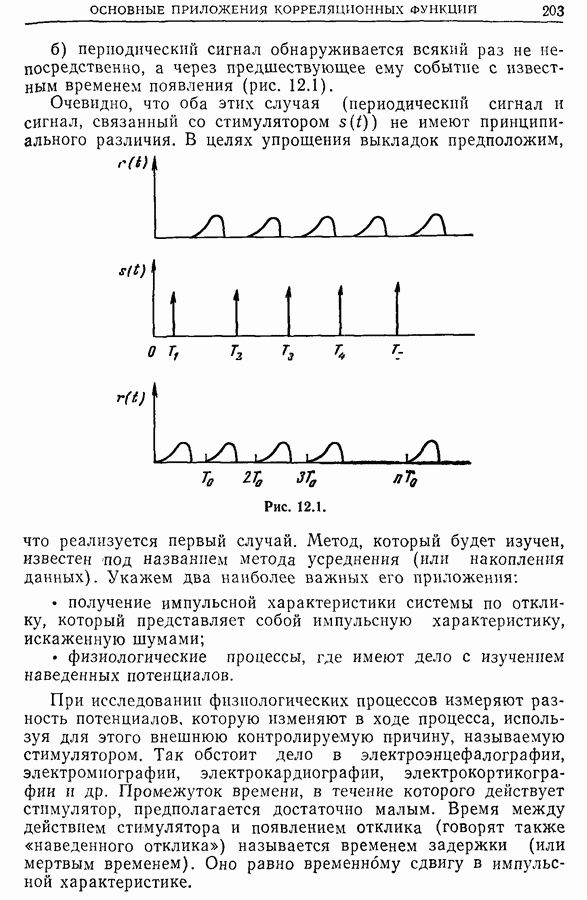
12.8. Применение когерентности к измерению передаточных функций линейных и однородных во времени систем. Спектральная лупа
Смещение спектра.
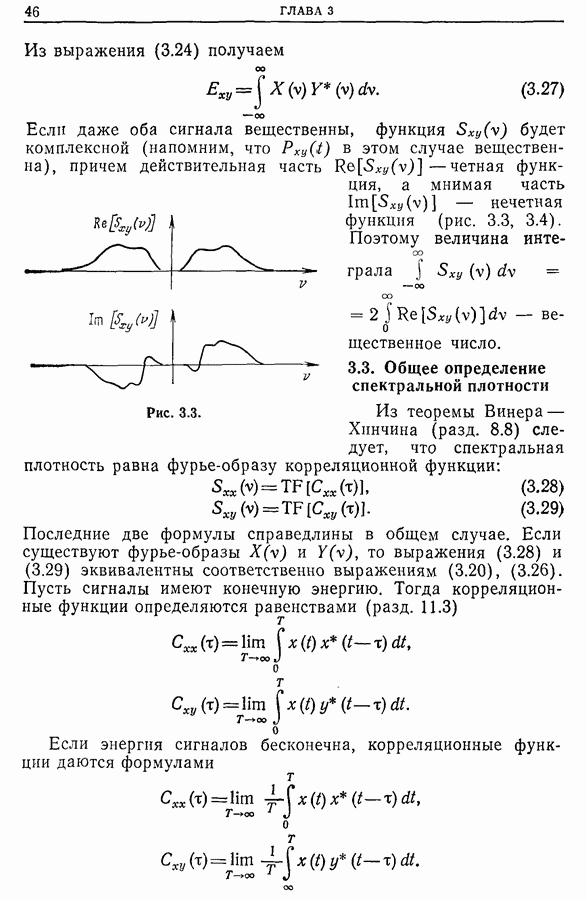
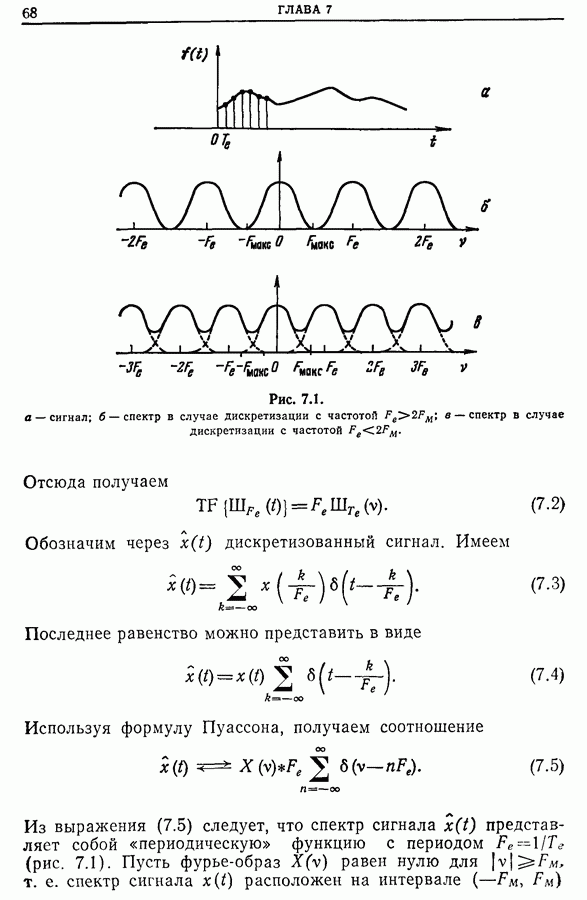
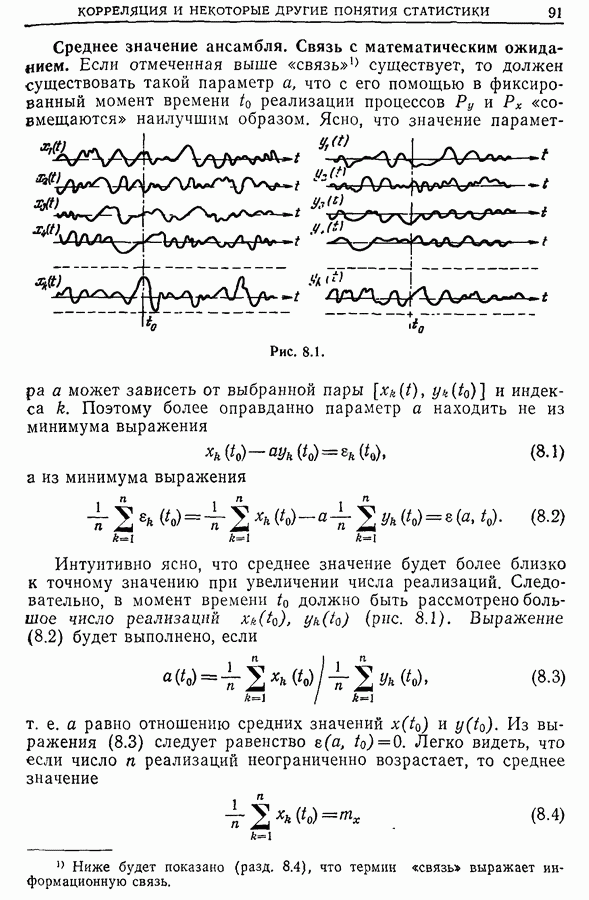
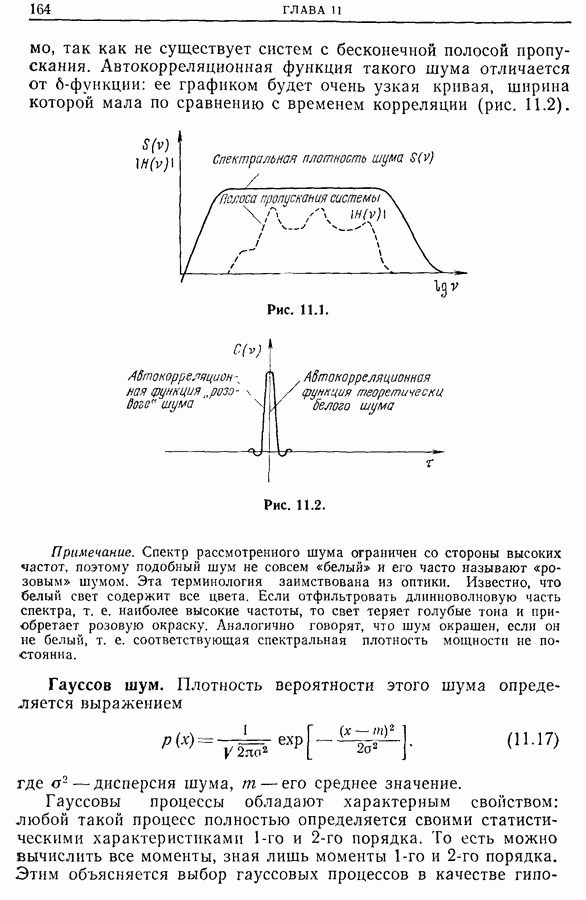
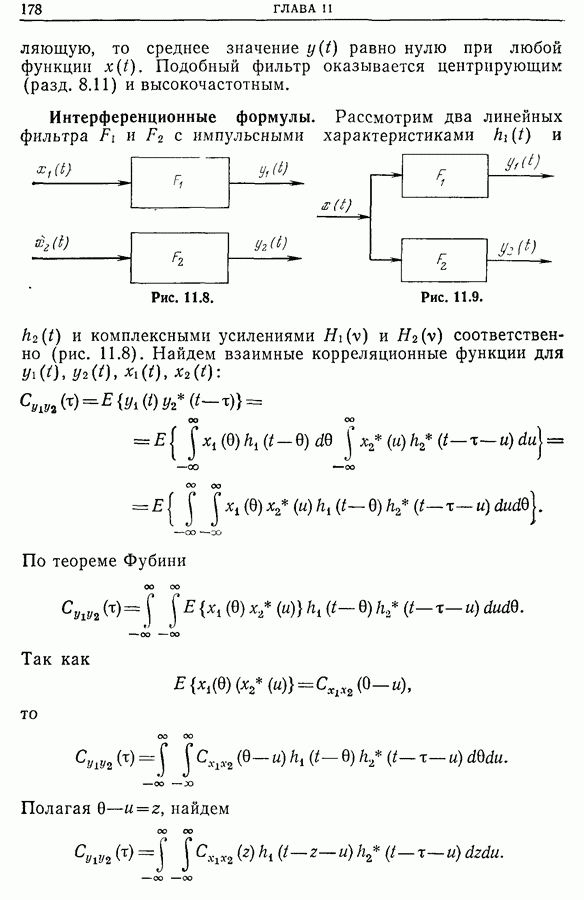
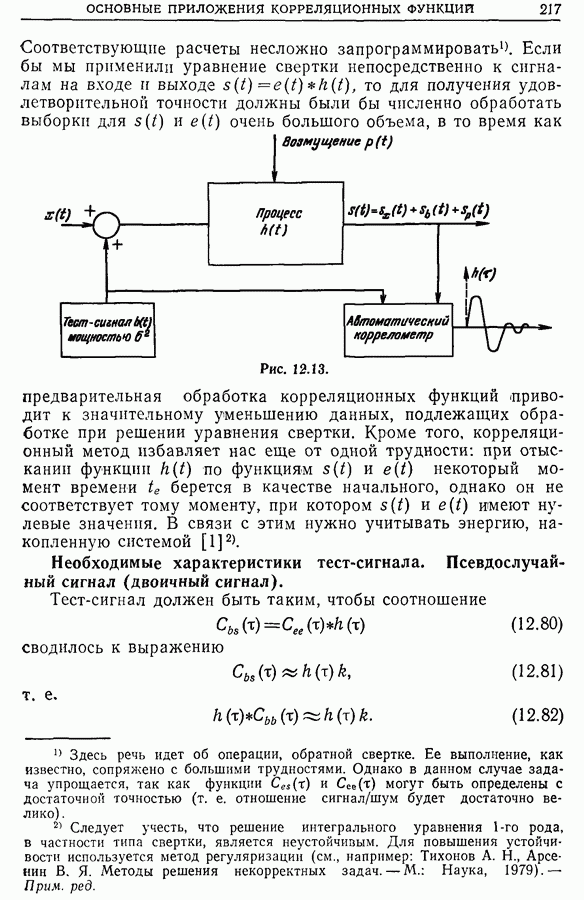
В предыдущем разделе показано, как получить импульсную характеристику или передаточную функцию (комплексное усиление), возбуждая систему сигналом, близким к белому шуму. В этом случае измерение импульсной характеристики сводится к измерению взаимной корреляционной функции  между входным и выходным сигналами, а измерение комплексного усиления — к измерению взаимного спектра
между входным и выходным сигналами, а измерение комплексного усиления — к измерению взаимного спектра  Однако эти измерения обладают двумя ошибками: погрешностью оценки (см. гл. 9) и ошибкой, обусловленной тем, что спектр
Однако эти измерения обладают двумя ошибками: погрешностью оценки (см. гл. 9) и ошибкой, обусловленной тем, что спектр  входного сигнала, строго говоря, не является постоянной величиной в рассматриваемой области частот (разд. 12.6).
входного сигнала, строго говоря, не является постоянной величиной в рассматриваемой области частот (разд. 12.6).
По-видимому, ошибку второго типа можно было бы скомпенсировать (хотя бы частично), если учесть истинные значения  Что касается погрешности оценки, она будет тем больше, чем меньше
Что касается погрешности оценки, она будет тем больше, чем меньше  (ширина эквивалентного фильтра) (разд. 13.8),
(ширина эквивалентного фильтра) (разд. 13.8),
что следует из равенства (разд. 9.3)

Таким образом, чтобы получить приемлемую дисперсию, нужно ограничить  снизу некоторой минимальной величиной. Мы будем, следовательно, иметь не
снизу некоторой минимальной величиной. Мы будем, следовательно, иметь не  а
а

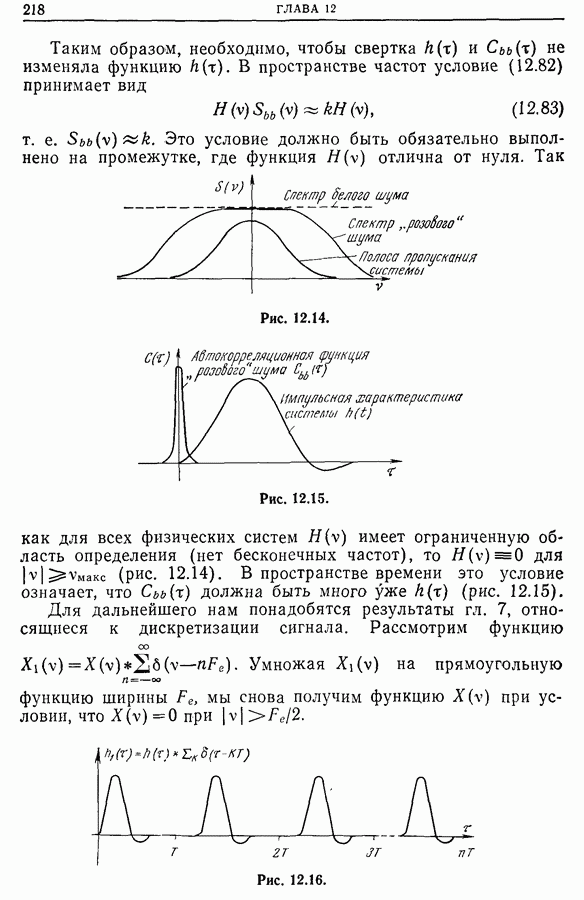
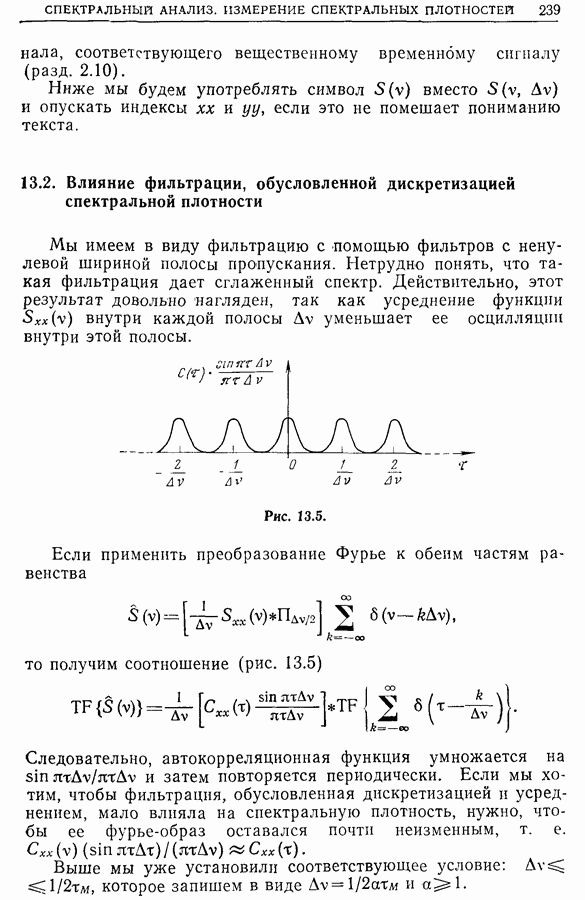
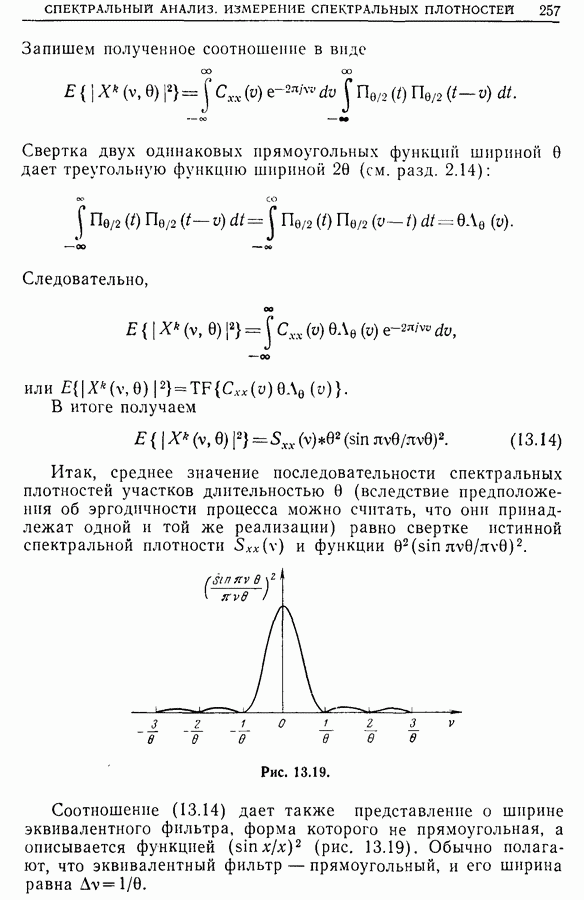
что порождает систематическую ошибку для спектральной плотности. В разд. 13.4 будет показано, что смещение, определенное выражением

оказывается равным 

Отсюда вытекает, что смещение будет больше в той части спектра, где имеется «узкая линия» (резонансная система с малым затуханием). Для уменьшения смещения надо уменьшить  , т. е. увеличить точность анализа. На первый взгляд это кажется невозможным, так как все
, т. е. увеличить точность анализа. На первый взгляд это кажется невозможным, так как все  точек спектра распределены по спектральной полосе, которую нужно анализировать. Однако существует метод «спектральной лупы» (см. ниже), который состоит в замене соответствующей частоты и в сосредоточении
точек спектра распределены по спектральной полосе, которую нужно анализировать. Однако существует метод «спектральной лупы» (см. ниже), который состоит в замене соответствующей частоты и в сосредоточении  исследуемых точек в полосе шириной
исследуемых точек в полосе шириной  с границами
с границами  где
где  . В результате степень точности анализа определяется отношением
. В результате степень точности анализа определяется отношением  Хотя при этом систематическая ошибка уменьшается, но возрастает погрешность оценки и уменьшается отношение сигнал/шум. Ниже мы убедимся, что можно уменьшить и систематическую ошибку, и погрешность оценки, вычисляя передаточную функцию как отношение взаимного спектра входного и выходного сигналов и спектра входного сигнала.
Хотя при этом систематическая ошибка уменьшается, но возрастает погрешность оценки и уменьшается отношение сигнал/шум. Ниже мы убедимся, что можно уменьшить и систематическую ошибку, и погрешность оценки, вычисляя передаточную функцию как отношение взаимного спектра входного и выходного сигналов и спектра входного сигнала.
Применение функции когерентности.
В гл. 11 выведено фундаментальное соотношение

имеющее в пространстве частот следующий вид:

Отсюда следует, что

Так как  — вещественная функция, то
— вещественная функция, то 
Рассмотрим снова функцию  Величины
Величины  определяются с некоторыми ошибками, но эти ошибки не независимы. Ниже мы исследуем погрешность оценки
определяются с некоторыми ошибками, но эти ошибки не независимы. Ниже мы исследуем погрешность оценки

Погрешность оценки функции когерентности.
Доказано [5], что

Из этого соотношения вытекает, что погрешность оценки  тем меньше, чем ближе к 1 функция когерентности. Из табл. 12.2 видно, как уменьшается величина
тем меньше, чем ближе к 1 функция когерентности. Из табл. 12.2 видно, как уменьшается величина  по сравнению
по сравнению  приближением
приближением  . Из табл. 12.2 видно, что погрешность оценки функции когерентности, когда эта функция близка к 1, много меньше погрешности оценки спектральной плотности. Даже при значениях
. Из табл. 12.2 видно, что погрешность оценки функции когерентности, когда эта функция близка к 1, много меньше погрешности оценки спектральной плотности. Даже при значениях  равных нескольким единицам, оценка когерентности оказывается довольно точной.
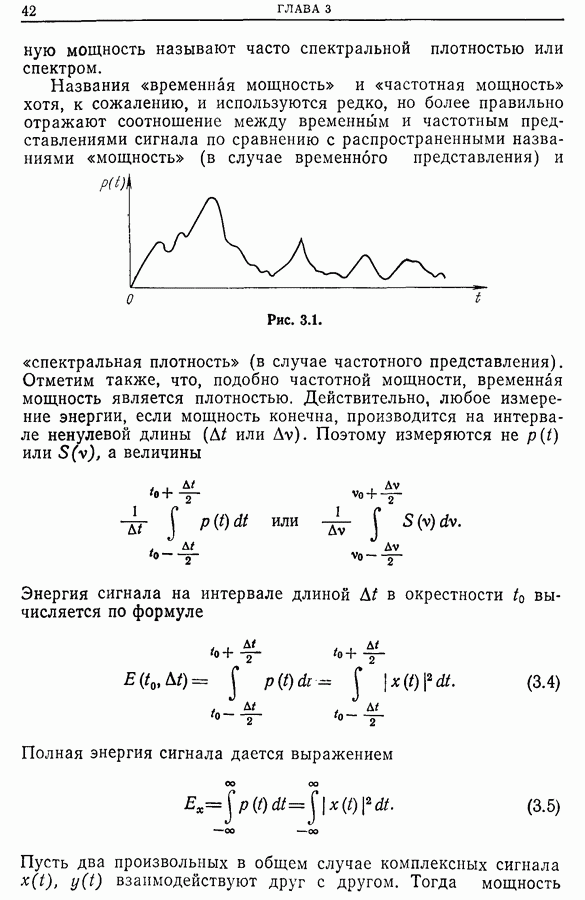
равных нескольким единицам, оценка когерентности оказывается довольно точной.
Таблица 12.2 (см. скан)
Погрешность оценки H(v).
Доказано [5], что погрешность оценки  определяется формулой
определяется формулой

где  определяет точность анализа,
определяет точность анализа,  — оценка функции когерентности. Из формулы следует, что погрешность для
— оценка функции когерентности. Из формулы следует, что погрешность для  тем меньше, чем ближе к 1 оценка
тем меньше, чем ближе к 1 оценка 
Общая ошибка для  состоит из двух ошибок: погрешности оценки и систематической ошибки. Мы исследуем систематическую ошибку, так как именно она может оказаться более существенной, поскольку она не уменьшается с увеличением промежутка интегрирования.
состоит из двух ошибок: погрешности оценки и систематической ошибки. Мы исследуем систематическую ошибку, так как именно она может оказаться более существенной, поскольку она не уменьшается с увеличением промежутка интегрирования.
Пусть  — систематические ошибки соответственно для
— систематические ошибки соответственно для  . Так как по определению смещения
. Так как по определению смещения

то

Аналогично

Следовательно,

или

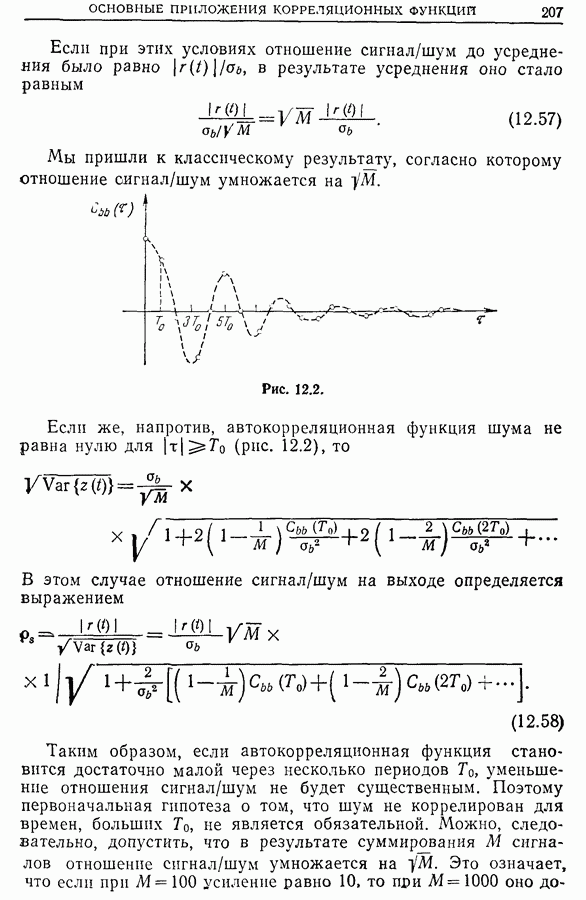
Если спектральная плотность сигнала постоянна в интересующей нас полосе, можно считать, что систематическая ошибка  равна нулю. С другой стороны, при этих условиях
равна нулю. С другой стороны, при этих условиях  отличается от
отличается от  постоянным множителем, поэтому
постоянным множителем, поэтому  и мы имеем
и мы имеем  Таким образом,
Таким образом,

или

Если  , а величина
, а величина  мала по сравнению с 1, то
мала по сравнению с 1, то

Выше мы уже говорили, что  . Следовательно,
. Следовательно,

Мы получили совершенно неожиданный результат: дисперсия абсолютной величины функции  тем меньше, чем меньше ширина
тем меньше, чем меньше ширина  анализируемой полосы. Поэтому для измерения передаточной функции нужно иметь эквивалентный фильтр с предельно узкой полосой пропускания».
анализируемой полосы. Поэтому для измерения передаточной функции нужно иметь эквивалентный фильтр с предельно узкой полосой пропускания».
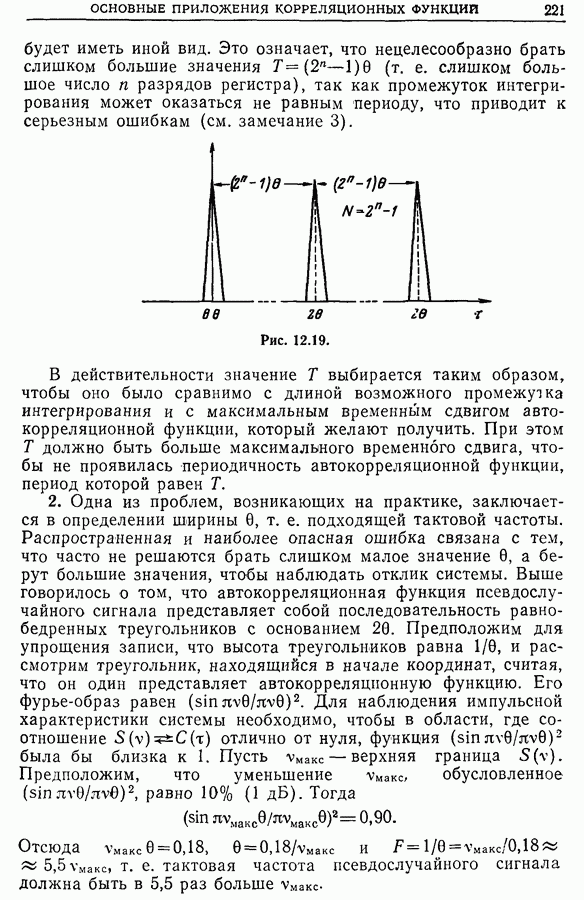
Из рассмотренного выше вытекает следующая методика быстрого и эффективного получения передаточных функций. Надо:
1) возбудить систему таким сигналом, спектральная плотность которого была бы возможно ближе к постоянной в той области, где по предположению передаточная функция не равна нулю;
2) измерить  исходя из отношения взаимного спектра
исходя из отношения взаимного спектра  и спектра
и спектра 
3) измерить когерентность 
4) выбрать результаты измерений, соответствующие тем частотам, при которых когерентность близка к 1.
Если выбрать частоты, при которых когерентность больше 0,9, то погрешность оценки окажется в 50 раз меньше погрешности, полученной классическим методом; при одинаковых погрешностях время интегрирования будет в 50 раз меньше того времени, которое необходимо по классической методике.
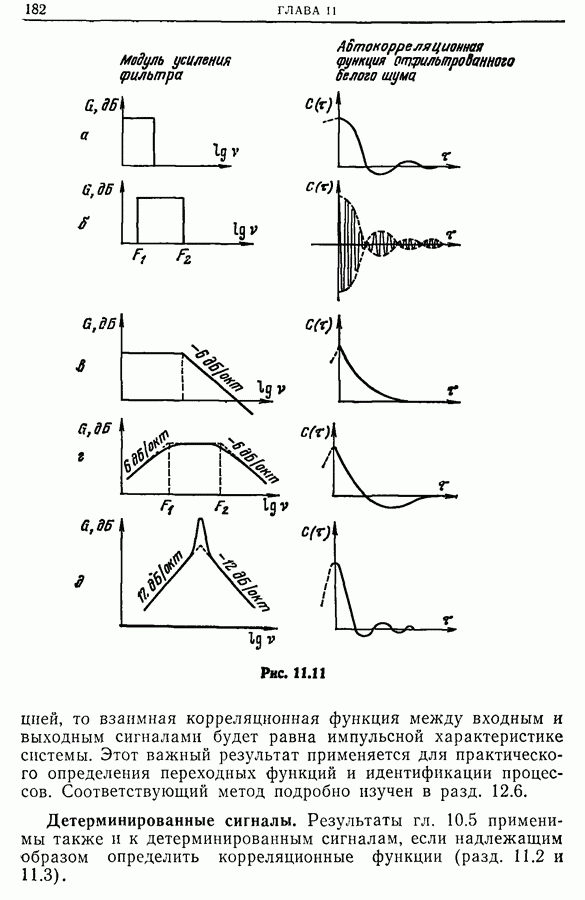
Системы, с близко расположенными резонансными линиями.
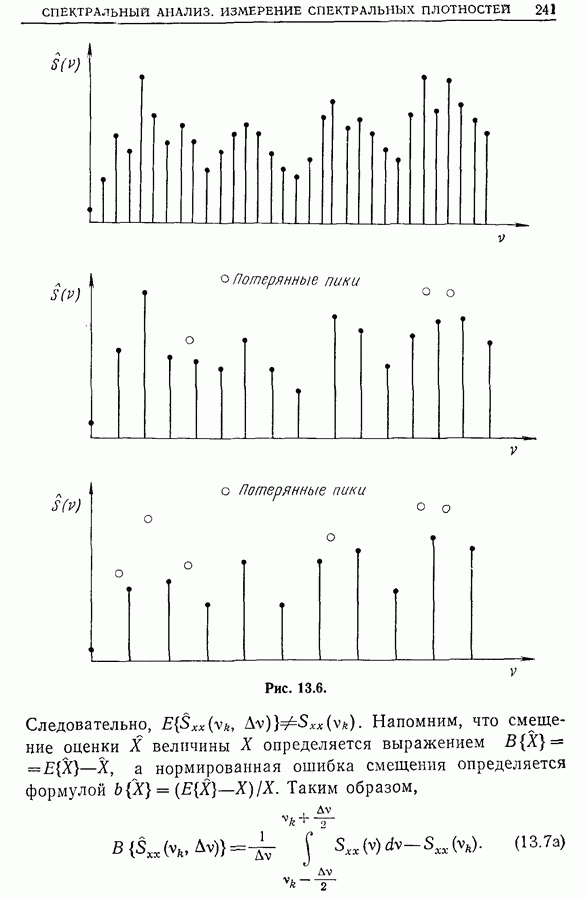
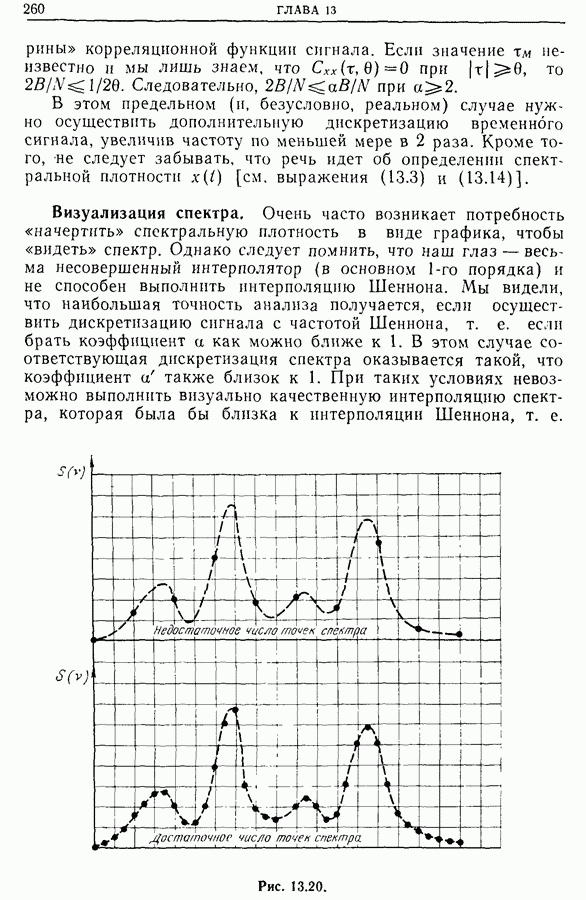
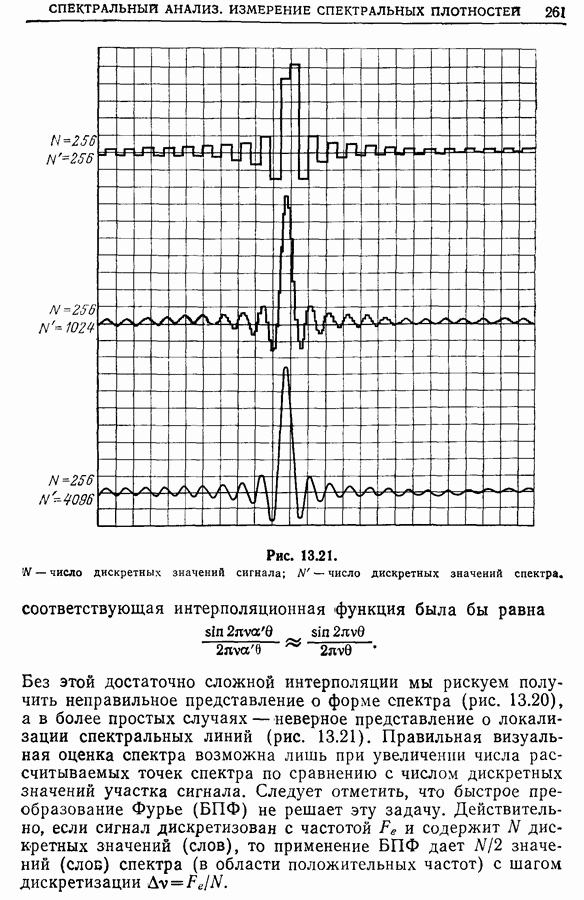
Комплексное усиление таких систем содержит узкие зоны, в которых спектральная плотность принимает большие значения (для простоты мы называем эти зоны «линиями»). Задача спектрального анализа состоит в том, чтобы эти линии не были пропущены при расчете спектра. Ведь не исключено, что расчетные точки спектра будут расположены достаточно далеко от линий. Конечно, этого можно избежать, если соответствующим образом осуществить дискретизацию спектральной плотности. Но это не всегда удается.
Кроме того, надо помнить о систематической ошибке, возникающей при расчете спектра. Как было показано, эту
ошибку можно уменьшить, уменьшая  но тогда возрастает погрешность оценки (разд. 9.9), т. е. мы сталкиваемся с двумя противоречивыми условиями.
но тогда возрастает погрешность оценки (разд. 9.9), т. е. мы сталкиваемся с двумя противоречивыми условиями.
Если применить метод, описанный в предыдущем разделе, и исходить из отношения  то величину
то величину  можно выбрать настолько малой, чтобы разделить две соседние линии. Но если вместо
можно выбрать настолько малой, чтобы разделить две соседние линии. Но если вместо  мы захотим взять меньшее значение
мы захотим взять меньшее значение  то должны будем рассчитать
то должны будем рассчитать  точек спектра, что существенно снижает ценность метода.
точек спектра, что существенно снижает ценность метода.
На практике предпочитают сгруппировать  точек в полосе шириной
точек в полосе шириной  около некоторой частоты
около некоторой частоты  Это достигается простым приемом: в пространстве частот производится трансляция путем умножения цифрового сигнала на
Это достигается простым приемом: в пространстве частот производится трансляция путем умножения цифрового сигнала на  Этот способ называется методом спектральной лупы.
Этот способ называется методом спектральной лупы.
Метод спектральной лупы.
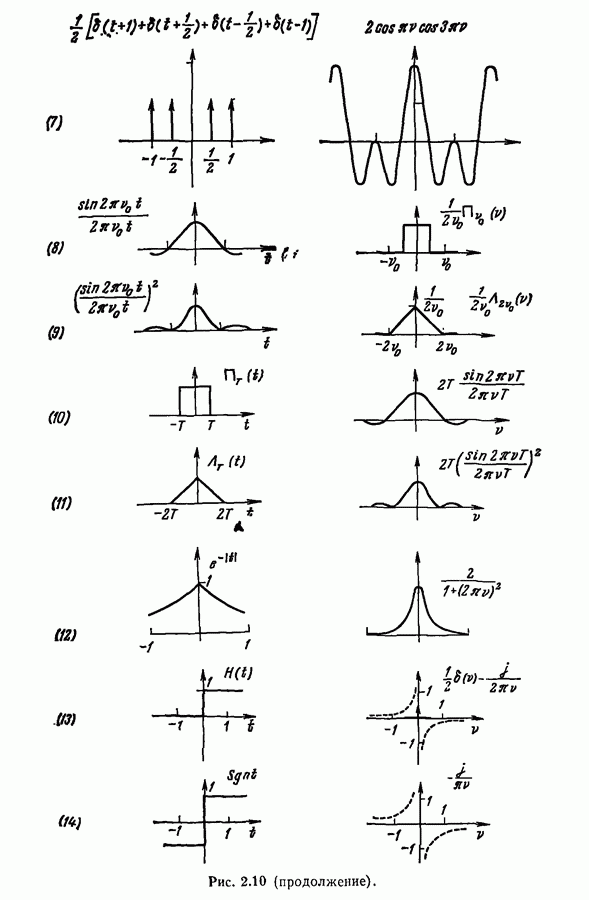
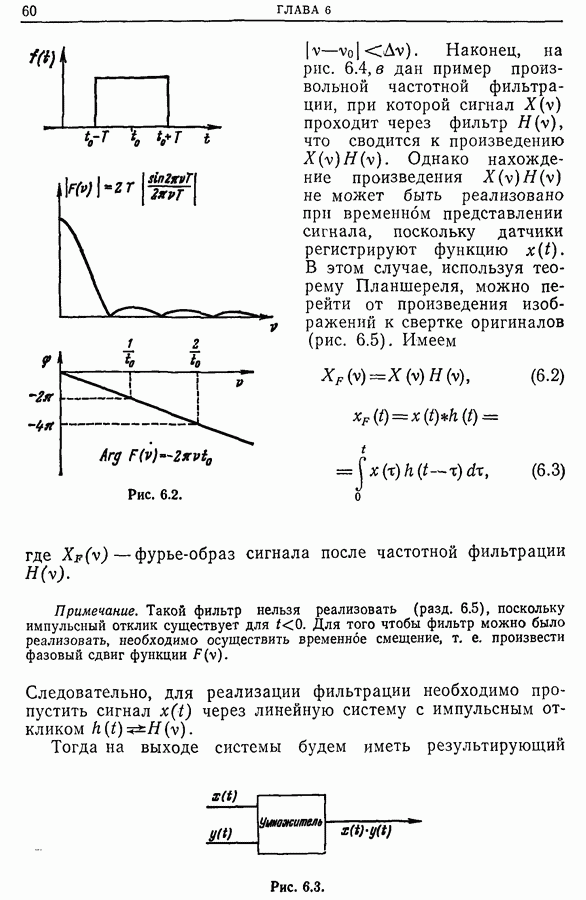
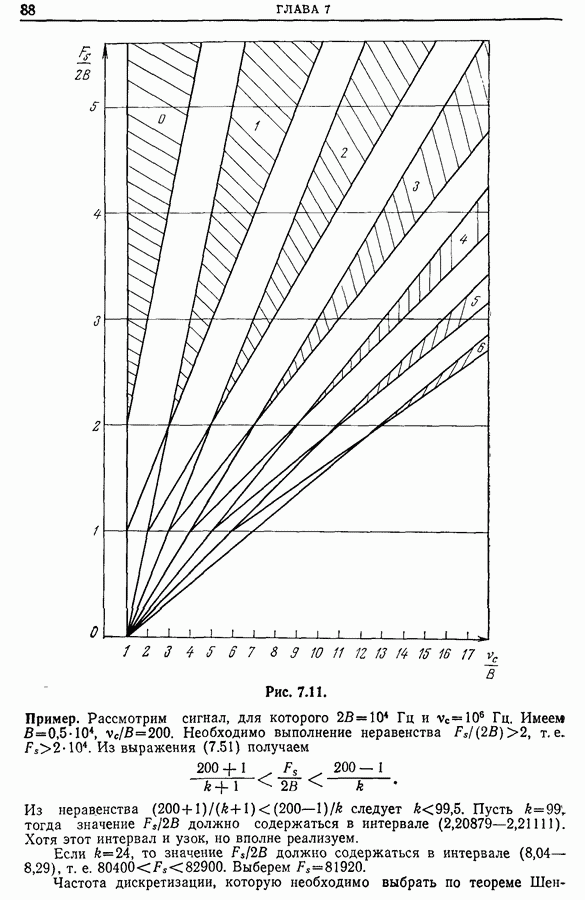
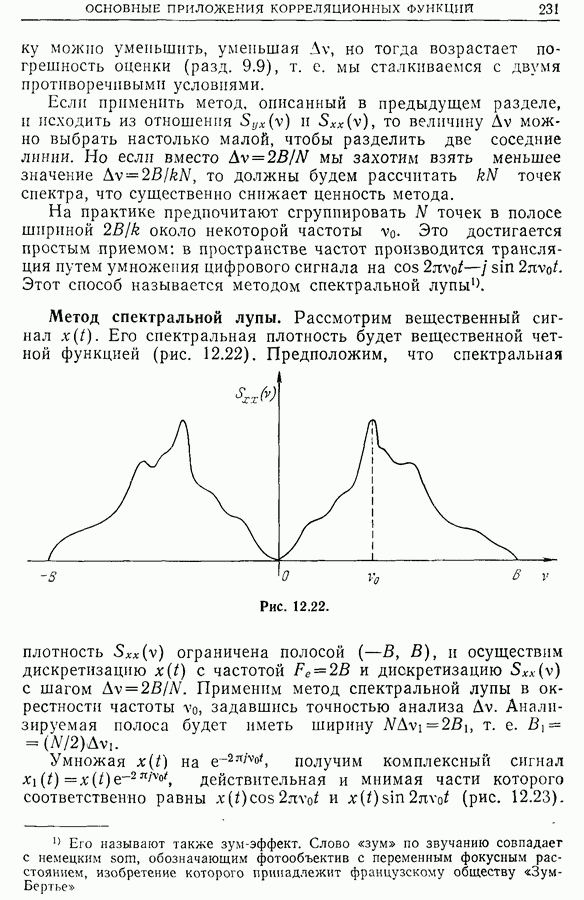
Рассмотрим вещественный сигнал  Его спектральная плотность будет вещественной четной функцией (рис. 12.22).
Его спектральная плотность будет вещественной четной функцией (рис. 12.22).

Рис. 12.22.
Предположим, что спектральная плотность  ограничена полосой
ограничена полосой  , и осуществим дискретизацию
, и осуществим дискретизацию  с частотой
с частотой  и дискретизацию
и дискретизацию  с шагом
с шагом  Применим метод спектральной лупы в окрестности частоты
Применим метод спектральной лупы в окрестности частоты  задавшись точностью анализа
задавшись точностью анализа  . Анализируемая полоса будет иметь ширину
. Анализируемая полоса будет иметь ширину 
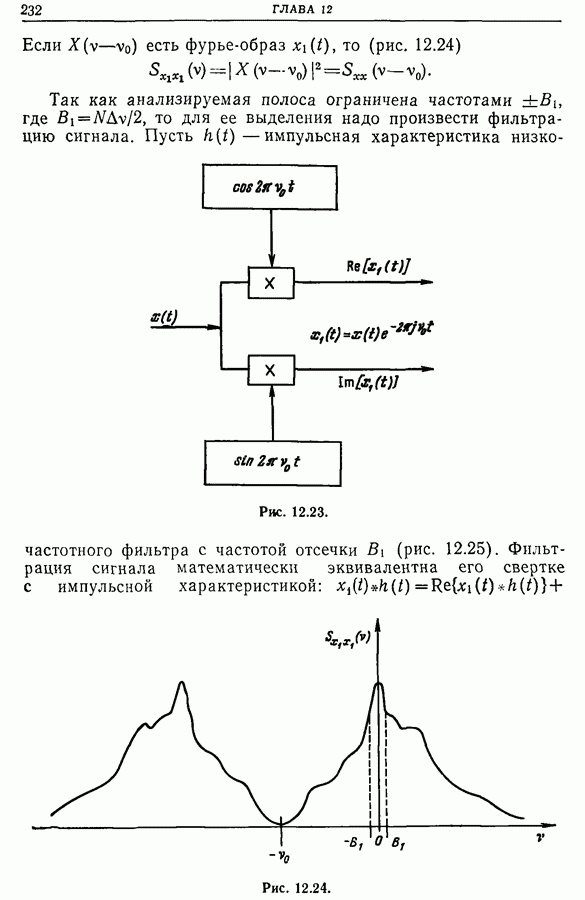
Умножая  на
на  получим комплексный сигнал
получим комплексный сигнал  действительная и мнимая части которого соответственно равны
действительная и мнимая части которого соответственно равны  (рис. 12.23).
(рис. 12.23).
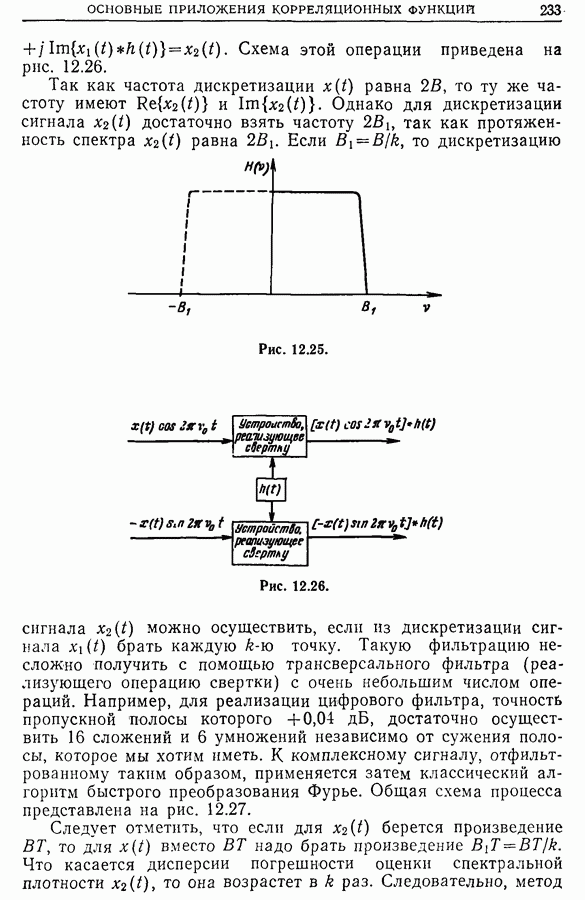
Если  есть фурье-образ
есть фурье-образ  то (рис. 12.24)
то (рис. 12.24)

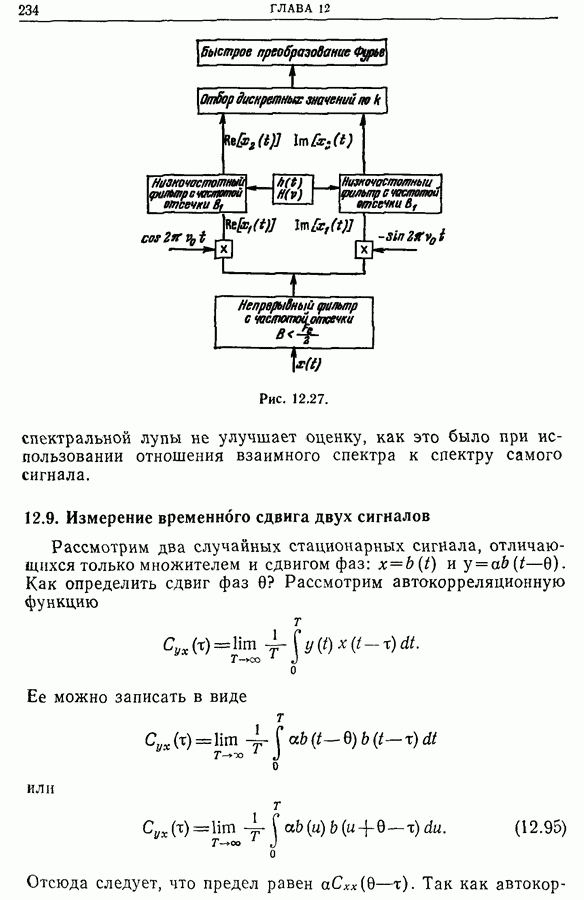
Так как анализируемая полоса ограничена частотами  где
где  то для ее выделения надо произвести фильтрацию сигнала. Пусть
то для ее выделения надо произвести фильтрацию сигнала. Пусть  — импульсная характеристика низкочастотного фильтра с частотой отсечки
— импульсная характеристика низкочастотного фильтра с частотой отсечки  (рис. 12.25).
(рис. 12.25).
Рис. 12.23. (см. скан)
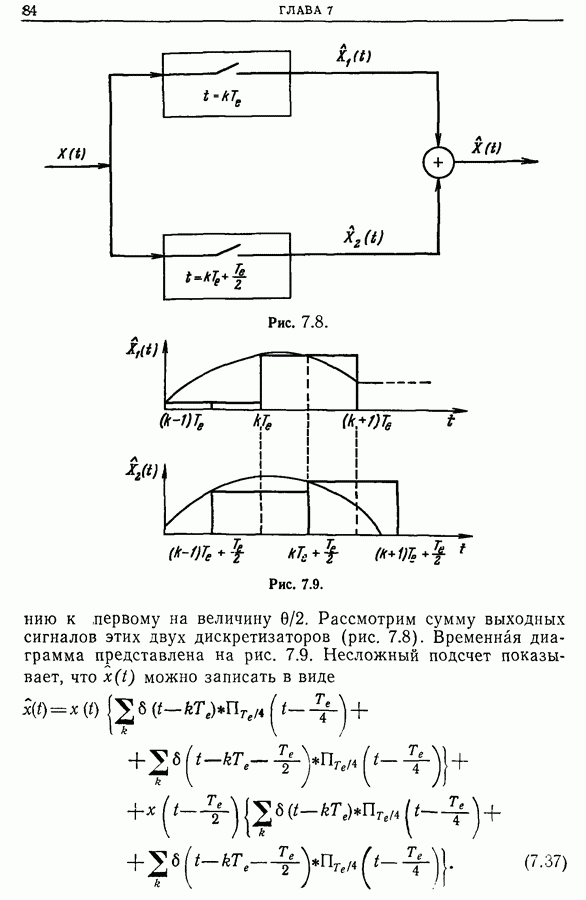
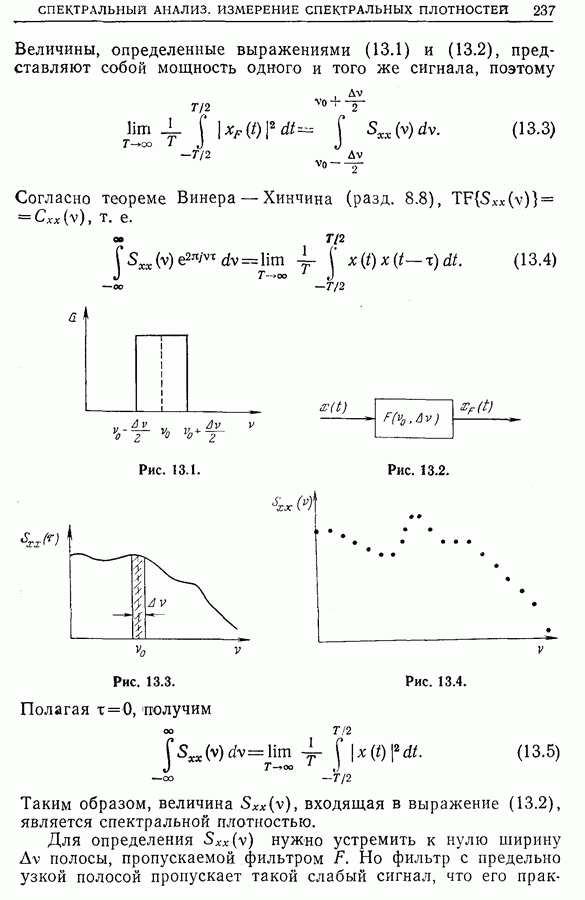
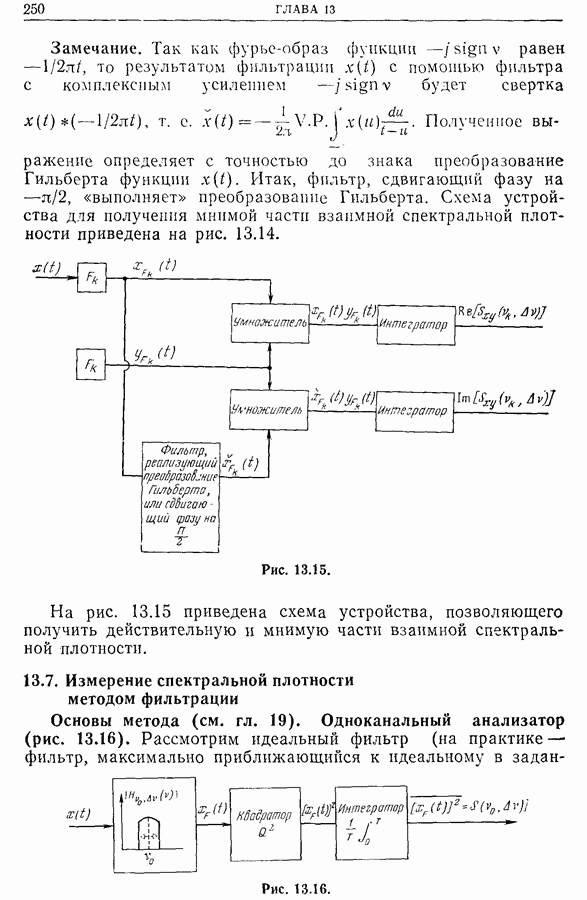
Фильтрация сигнала математически эквивалентна его свертке с импульсной характеристикой: 
Рис. 12.24. (см. скан)
 Схема этой операции приведена на рис. 12.26.
Схема этой операции приведена на рис. 12.26.
Так как частота дискретизации  равна
равна  то ту же частоту имеют
то ту же частоту имеют  Однако для дискретизации сигнала
Однако для дискретизации сигнала  достаточно взять частоту
достаточно взять частоту  так как протяженность спектра
так как протяженность спектра  равна
равна 

Рис. 12.25.

Рис. 12.26.
Если  то дискретизацию сигнала
то дискретизацию сигнала  можно осуществить, если из дискретизации сигнала
можно осуществить, если из дискретизации сигнала  брать каждую
брать каждую  точку. Такую фильтрацию несложно получить с помощью трансверсального фильтра (реализующего операцию свертки) с очень небольшим числом операций. Например, для реализации цифрового фильтра, точность пропускной полосы которого
точку. Такую фильтрацию несложно получить с помощью трансверсального фильтра (реализующего операцию свертки) с очень небольшим числом операций. Например, для реализации цифрового фильтра, точность пропускной полосы которого  дБ, достаточно осуществить 16 сложений и 6 умножений независимо от сужения полосы, которое мы хотим иметь. К комплексному сигналу, отфильтрованному таким образом, применяется затем классический алгоритм быстрого преобразования Фурье. Общая схема процесса представлена на рис. 12.27.
дБ, достаточно осуществить 16 сложений и 6 умножений независимо от сужения полосы, которое мы хотим иметь. К комплексному сигналу, отфильтрованному таким образом, применяется затем классический алгоритм быстрого преобразования Фурье. Общая схема процесса представлена на рис. 12.27.
Следует отметить, что если для  берется произведение ВТ, то для
берется произведение ВТ, то для  вместо
вместо  надо брать произведение
надо брать произведение  . Что касается дисперсии погрешности оценки спектральной плотности
. Что касается дисперсии погрешности оценки спектральной плотности  то она возрастет в
то она возрастет в  раз. Следовательно, метод
раз. Следовательно, метод
Рис. 12.27. (см. скан)
спектральной лупы не улучшает оценку, как это было при использовании отношения взаимного спектра к спектру самого сигнала.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
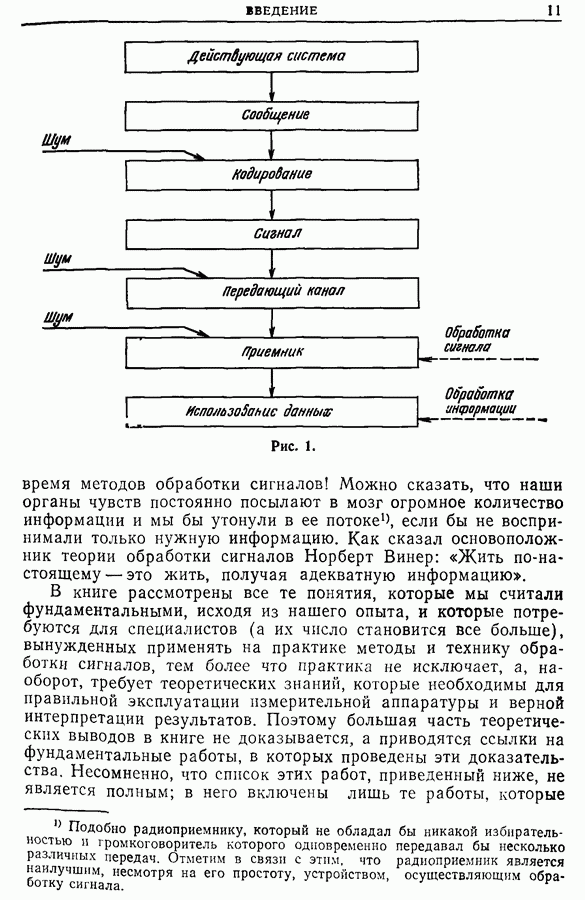
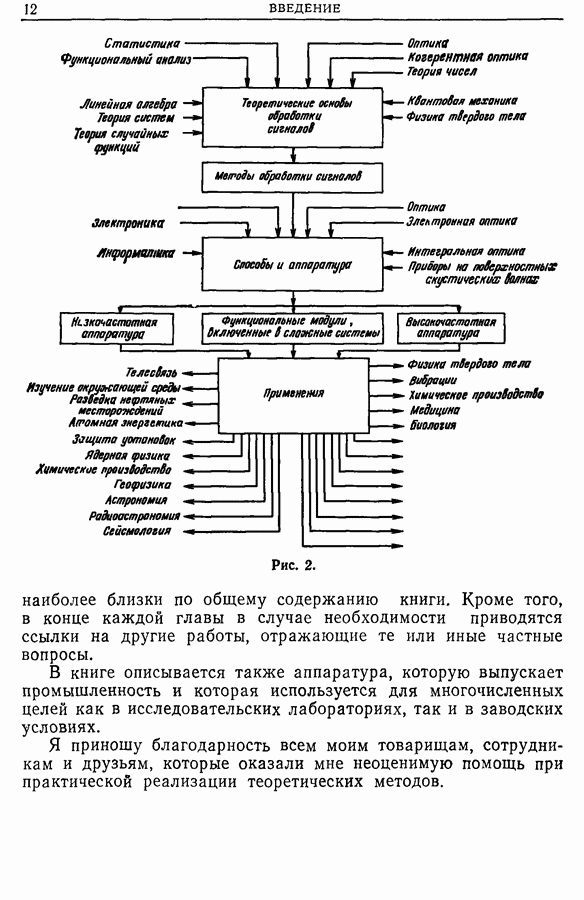
- ВВЕДЕНИЕ
- Глава 1. ФИЗИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ШУМАХ КАК О СЛУЧАЙНЫХ ПРОЦЕССАХ
- Глава 2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
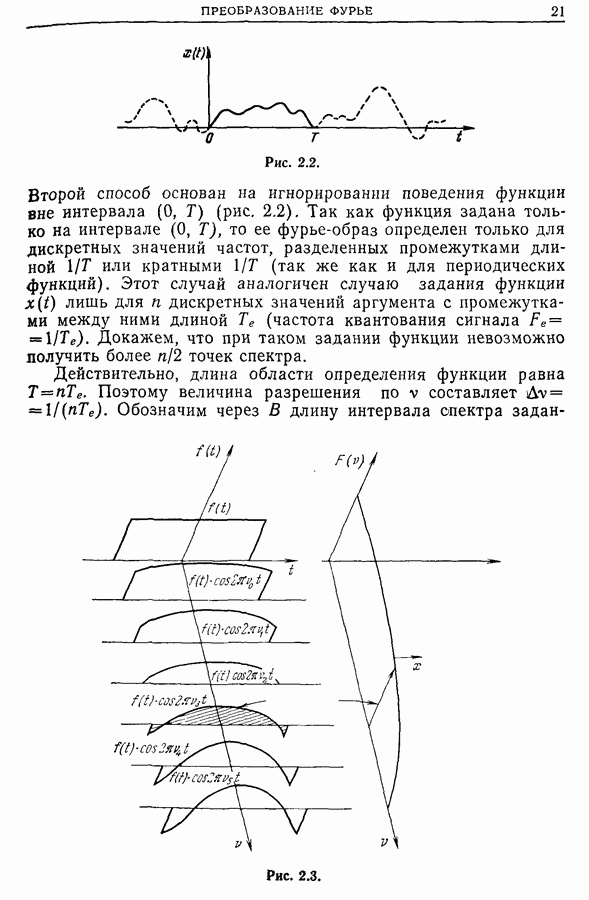
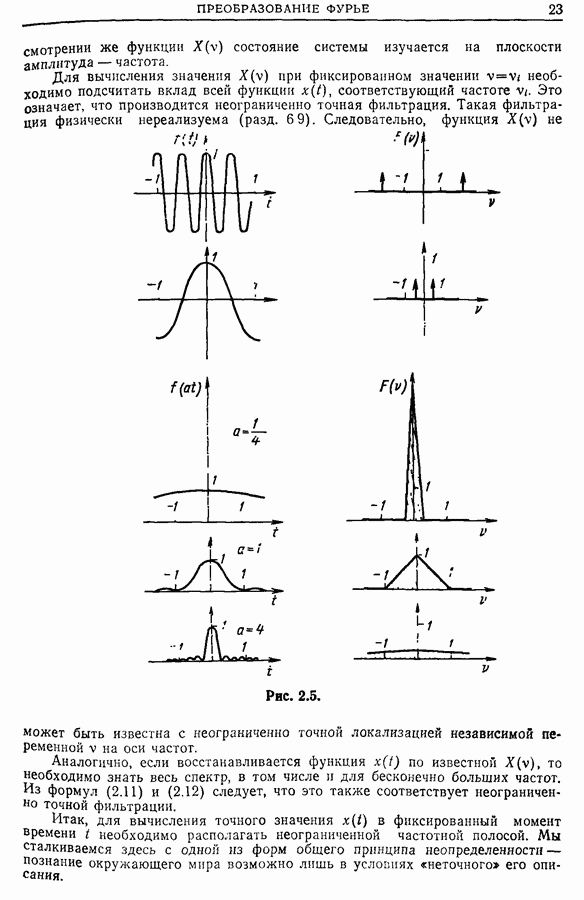
- 2.2. Преобразование Фурье непериодических функций
- 2.3. Преобразование Фурье физических функций
- 2.4. Физический смысл преобразования Фурье
- 2.5. Условия существования преобразования Фурье
- 2.6. Некоторые свойства преобразования Фурье
- 2.7. Несколько функций и их фурье-образы
- 2.8. Частный случай вещественных сигналов
- 2.9. Отрицательные частоты
- 2.10. Аналитический сигнал
- 2.11. Почему выбрано преобразование Фурье?
- 2.12 Физическая реализация фурье-образа. Преобразование Фурье в оптике
- 2.13. Свойства функции sin х/х
- 2.14. Лямбда-функция
- Глава 3. МОЩНОСТЬ И ЭНЕРГИЯ СИГНАЛОВ
- 3.2. Частотная мощность. Спектральная плотность мощности. Спектр мощности
- 3.3. Общее определение спектральной плотности
- 3.4. Теорема Парсеваля
- 3.5. Понятие скалярного произведения и нормы
- Глава 4. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
- 4.2. Связь между фурье-образом и изображением Лапласа
- Глава 5. СВЕРТКА
- 5.2. Уравнение свертки
- 5.3. Несколько замечаний относительно свертки
- 5.4. Физическая интерпретация свертки
- 5.5. Прямая и обратная задачи, связанные с операцией свертки
- 5.6. Свертка и преобразование Фурье. Теорема Планшереля
- Глава 6. ФИЛЬТРАЦИЯ
- 6.2. Временная фильтрация
- 6.3. Частотная фильтрация («линейная фильтрация» в смысле Блан-Лапьера)
- 6.4. Связь между фильтрацией и сверткой
- 6.5. Физически реализуемые линейные фильтры частоты
- 6.6. Идеальный фильтр
- 6.7. Реализуемые непрерывные аналоговые фильтры [3]
- 6.8. Фильтры с линейным сдвигом фаз
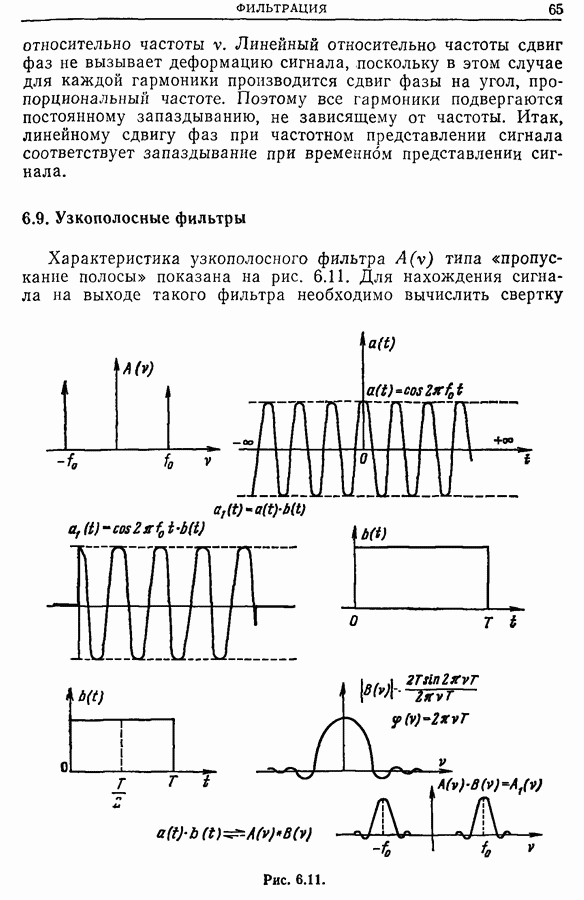
- 6.9. Узкополосные фильтры
- 6.10. Обобщение понятия фильтрации
- Глава 7. ДИСКРЕТИЗАЦИЯ
- 7.2. Теоремы дискретизации
- 7.3. Дискретизация сигналов конечной длительности
- 7.4. Дискретизация фурье-образов
- 7.5. Выбор частоты дискретизации на практике
- 7.6. Противомаскировочный фильтр
- 7.7. Физическая дискретизация. Комбинированная дискретизация
- 7.8. Субдискретизация. Обобщение теоремы Шеннона [9]
- 7.9. Заключение
- Глава 8. КОРРЕЛЯЦИЯ И НЕКОТОРЫЕ ДРУГИЕ ПОНЯТИЯ СТАТИСТИКИ
- 8.2. Величина, характеризующая «связь» между двумя физическими процессами. Случай, когда известна одна реализация физического процесса, наблюдаемая в течение большого интервала времени
- 8.3. Эргодичность
- 8.4. Коэффициент корреляции и теория информации
- 8.5. Практические замечания
- 8.6. Характеристические функции
- 8.7. Спектральная плотность случайного сигнала
- 8.8. Связь между временными представлениями сигналов и спектральными плотностями. Теорема Винера — Хинчина
- 8.9. Функция связи
- 8.10. Распределение Гаусса, или нормальное распределение
- 8.11. Спектральная плотность и центрирование сигналов
- Глава 9. ОЦЕНКА ОШИБОК ИЗМЕРЕНИЙ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 9.2. Оценка корреляционных функций
- 9.3. Оценка спектральных плотностей
- 9.4. Оценка одномерной плотности вероятности
- 9.5. Последовательное вычисление среднего значения и дисперсии
- 9.6. Физическая интерпретация дисперсии
- 9.7. Идеальный интегратор и низкочастотный фильтр
- 9.8. Дискретные сигналы
- Глава 10. ОШИБКИ ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ПРИ ДИСКРЕТИЗАЦИИ СИГНАЛОВ
- 10.2. Коррелометры с вспомогательными шумами
- 10.3. Условия на вспомогательные шумы, при которых отсутствует смещение оценки корреляционной функции
- 10.4. Вычисление дисперсии. Состоятельность оценки
- 10.5. Практические приложения
- 10.6. Важное замечание
- 10.7. Замечание относительно генераторов вспомогательных шумов
- Глава 11. ОСНОВНЫЕ СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
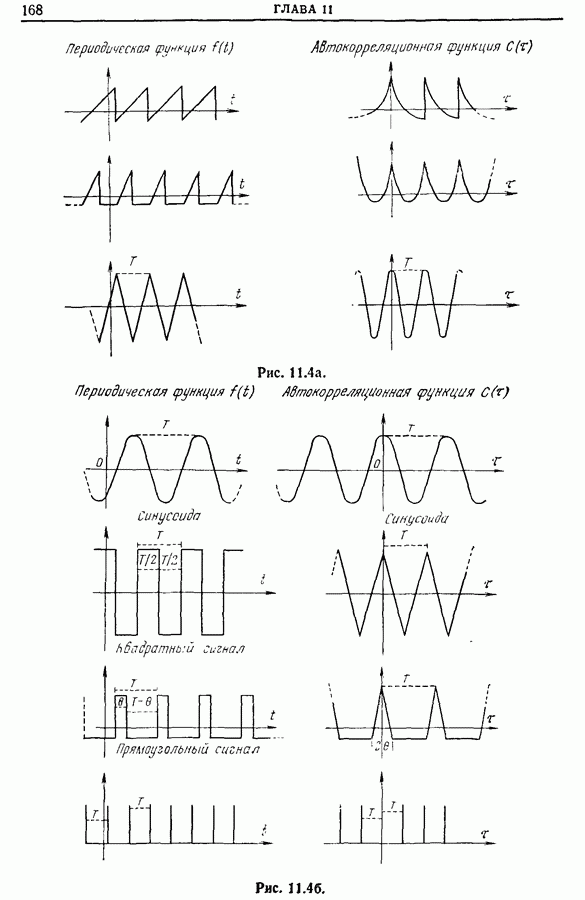
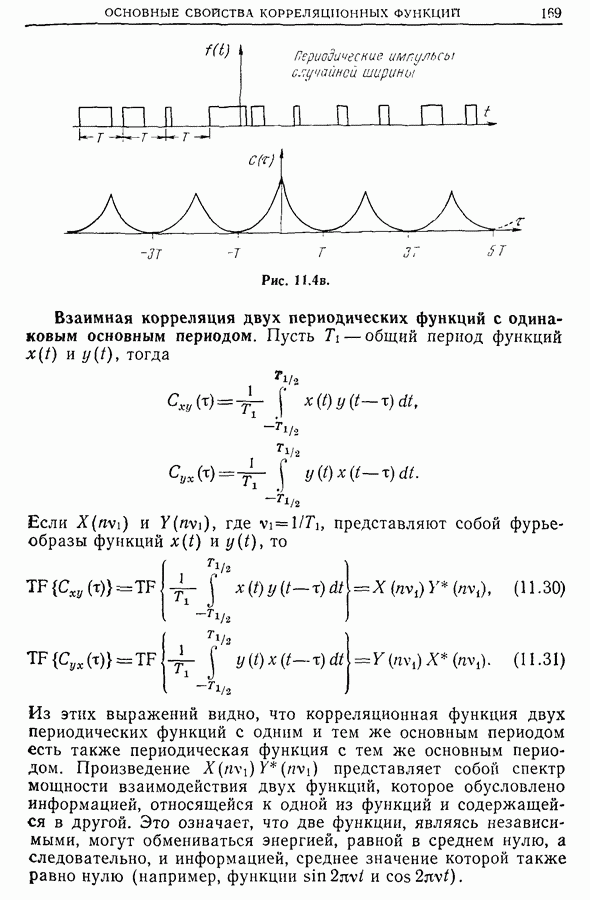
- 11.2. Периодические функции
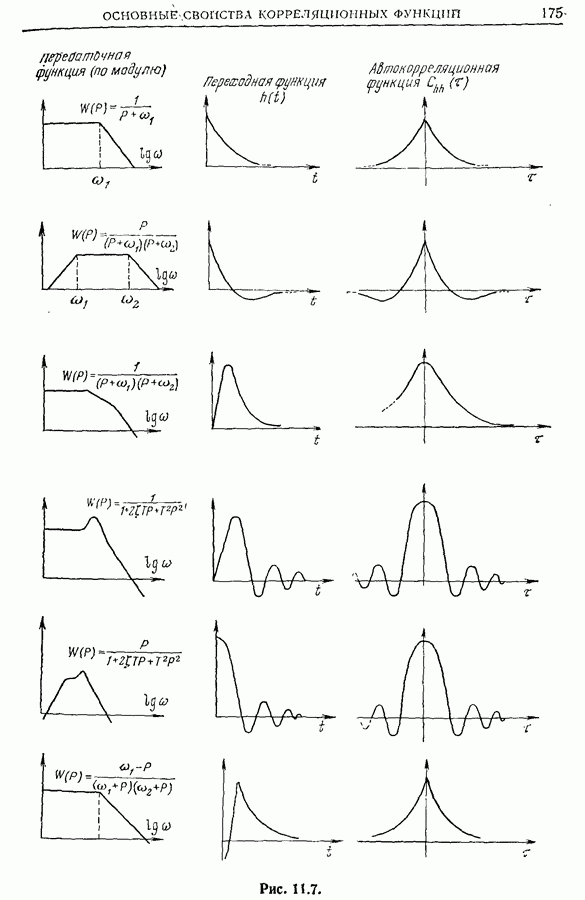
- 11.3. Переходные функции
- 11.4. Дистрибутивность операций вычисления корреляции и спектральной плотности
- 11.5. Связь между входным и выходным сигналами линейной однородной во времени системы при условии, что входной сигнал является случайным и стационарным 2-го порядка
- Глава 12. ОСНОВНЫЕ ПРИЛОЖЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 12.2. Обнаружение периодического сигнала с известным периодом на фоне шума
- 12.3. Выделение сигнала на фоне шума. Усреднение
- 12.4. Обнаружение скрытых периодичностей
- 12.5. Получение спектральных плотностей по корреляционным функциям
- 12.6. Измерение динамических характеристик (переходных функций, импульсных характеристик) линейных систем. Идентификация процессов
- 12.7. Измерение когерентности
- 12.8. Применение когерентности к измерению передаточных функций линейных и однородных во времени систем. Спектральная лупа
- 12.9. Измерение временного сдвига двух сигналов
- Глава 13. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ИЗМЕРЕНИЕ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
- 13.2. Влияние фильтрации, обусловленной дискретизацией спектральной плотности
- 13.3. Дискретизация спектральной плотности, реализуемая на практике
- 13.4. Систематическая ошибка при измерении спектральной плотности
- 13.5. Измерение спектральной плотности
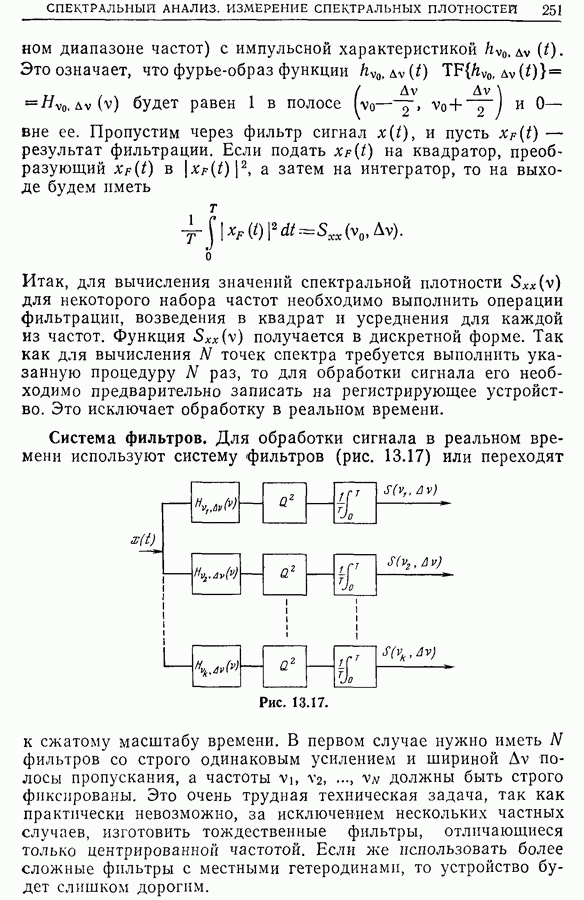
- 13.6. Спектральный анализ методом фильтрации
- 13.7. Измерение спектральной плотности методом фильтрации
- 13.8. Дискретное преобразование Фурье и измерение спектральных плотностей [2, 6, 7]
- 13.9. Вычисление автокорреляционных функций и взаимных корреляционных функций по спектральной плотности
- 13.10. Явление Гиббса
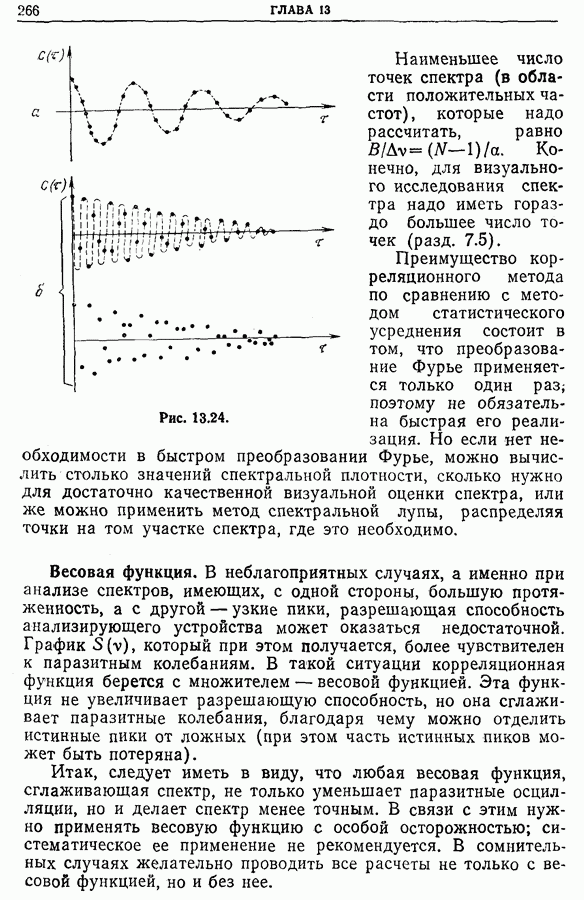
- 13.11. Корреляционный метод спектрального анализа
- 13.12. Корреляционный анализатор спектра
- 13.13. Точность определения спектральной плотности, полученной преобразованием Фурье корреляционной функции [1]
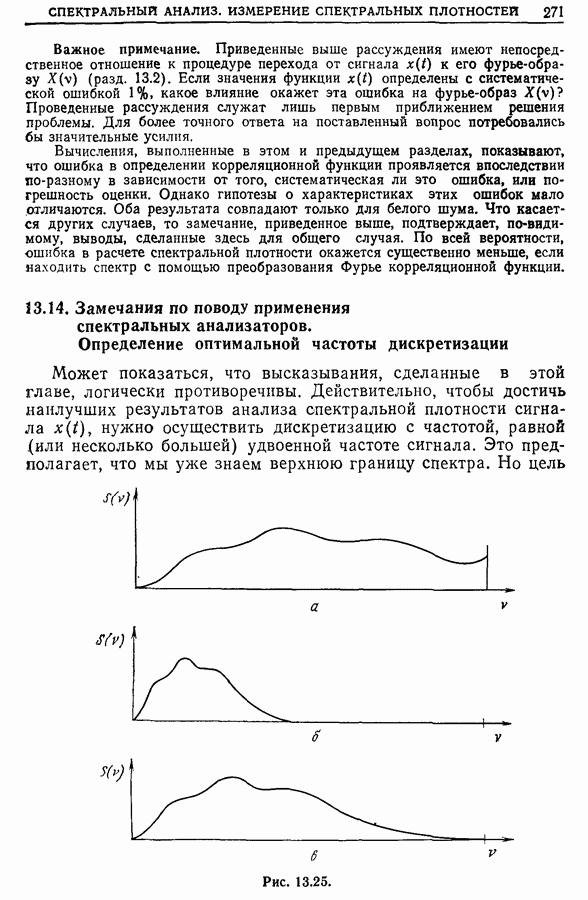
- 13.14. Замечания по поводу применения спектральных анализаторов. Определение оптимальной частоты дискретизации
- Глава 14. ВЕСОВЫЕ ОКНА
- 14.2. Окна, связанные с преобразованием Фурье
- 14.3. Окна, используемые в методе коррелограмм
- 14.4. Окна, применяемые в методе периодограмм
- 14.5. Окна, применяемые в методе фильтрации с возведением в квадрат и усреднением
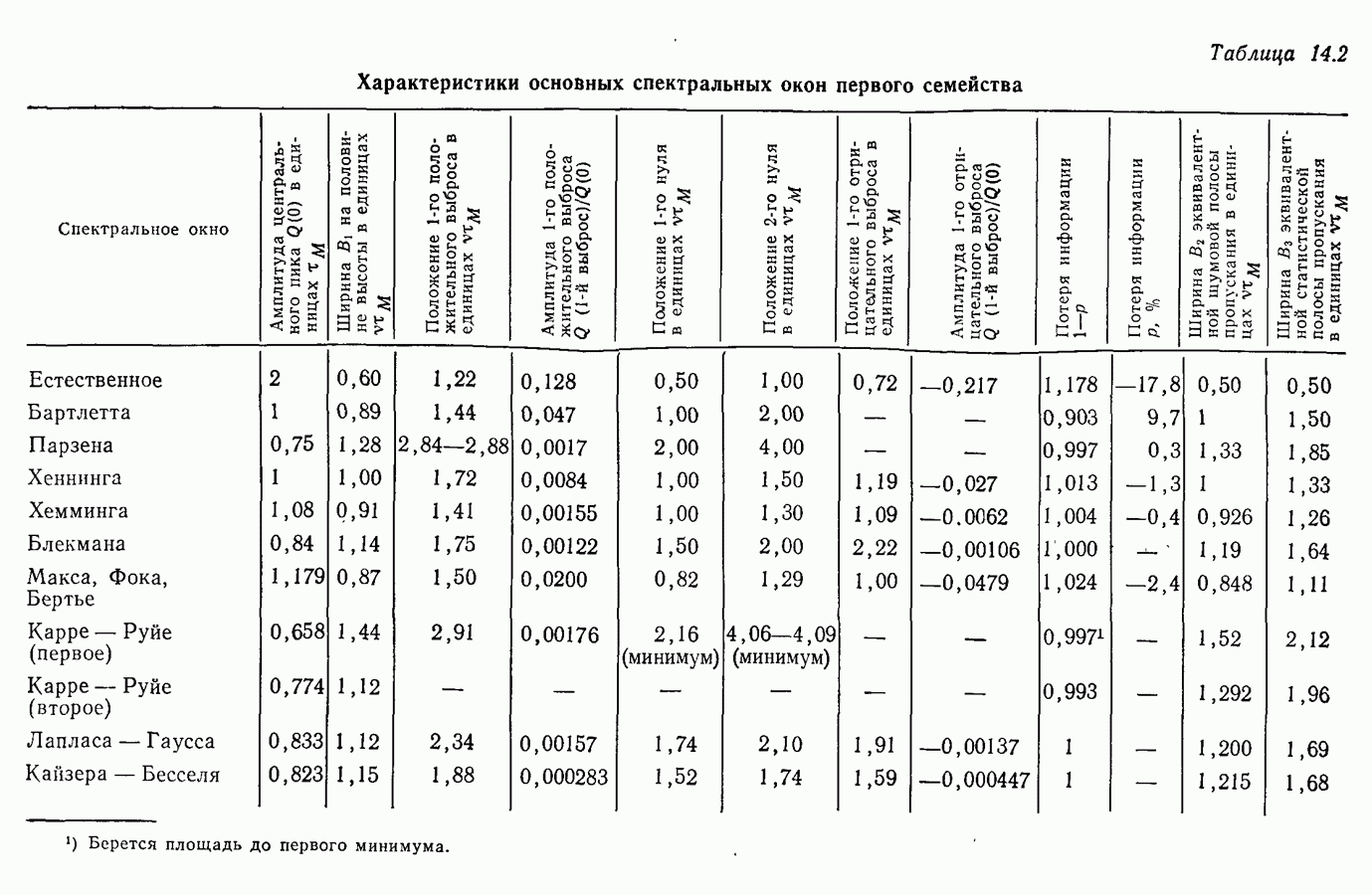
- 14.6. Основные характеристики временных и спектральных окон
- 14.7. Первое семейство временных весовых окон
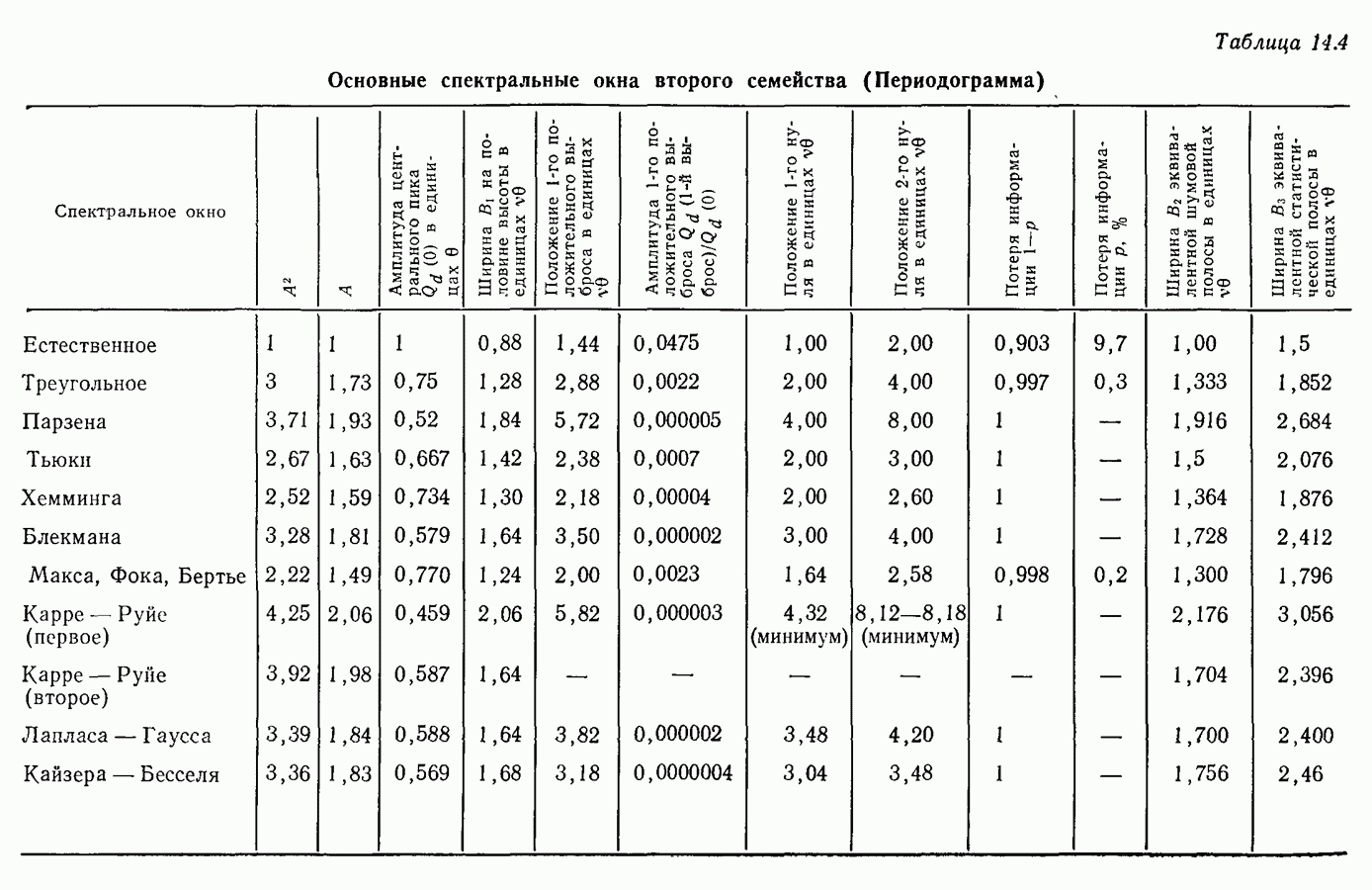
- 14.8. Второе семейство временных весовых окон (Метод периодограмм)
- 14.9. Исследование спектра в простом случае
- 14.10. Выбор весовой функции