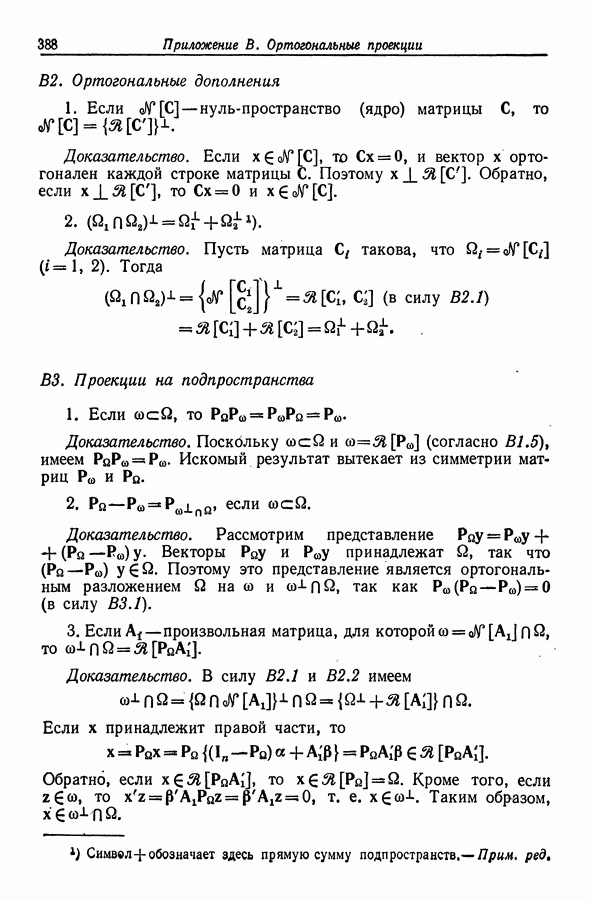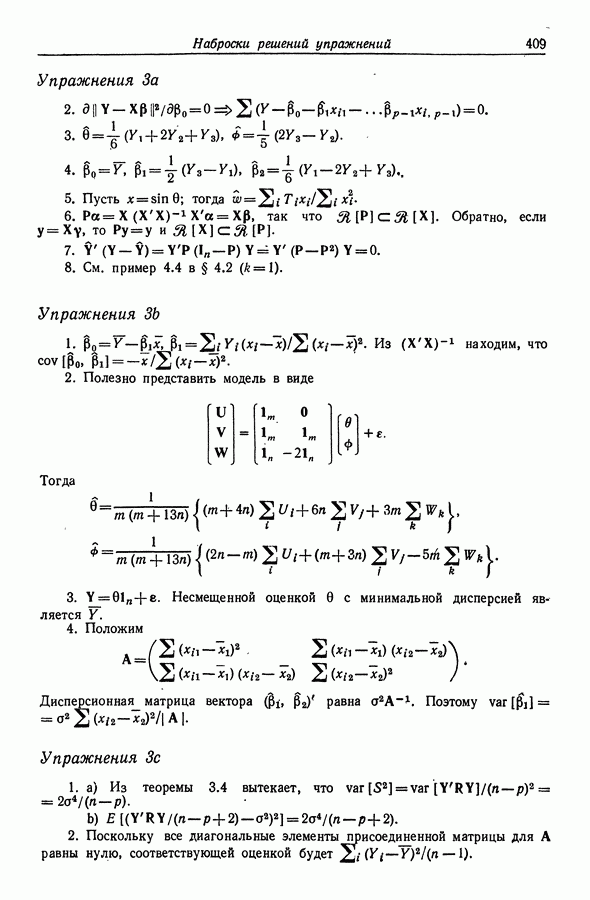| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.7. Введение дополнительных регрессоров
3.7.7. Общая теория
Предположим, что уже после того, как подобрана модель регрессии

мы хотим включить в нее дополнительные регрессоры  чтобы модель с введением этих регрессоров приняла вид
чтобы модель с введением этих регрессоров приняла вид

(здесь мы обозначили  и
и  где
где  - матрица размера
- матрица размера  ранга
ранга  -матрица размера
-матрица размера  ранга
ранга  и столбцы матрицы
и столбцы матрицы  линейно не зависят от столбцов матрицы X, т. е. матрица
линейно не зависят от столбцов матрицы X, т. е. матрица  размера
размера  имеет ранг
имеет ранг  Тогда имеются две возможности отыскания оценки наименьших квадратов
Тогда имеются две возможности отыскания оценки наименьших квадратов  вектора
вектора  . Во-первых, можно найти оценку
. Во-первых, можно найти оценку  и ее дисперсионную матрицу непосредственно из соотношений
и ее дисперсионную матрицу непосредственно из соотношений

Во-вторых, можно уменьшить количество необходимых выкладок, используя те вычисления, которые были проведены в процессе подбора модели. Соответствующие результаты приведены в теореме 3.7. Геометрическое доказательство этой теоремы, допускающее неполноту ранга матрицы X, приведено в разд. 3.8.3.
Лемма. Если  то матрица
то матрица  не вырождена.
не вырождена.
Доказательство. Пусть  Тогда по теореме 3.1 (i)
Тогда по теореме 3.1 (i)

т. е.  Поэтому
Поэтому  имеет вид
имеет вид  откуда при сделанном предположении о линейной независимости столбцов матрицы
откуда при сделанном предположении о линейной независимости столбцов матрицы  от столбцов матрицы X имеем
от столбцов матрицы X имеем  Следовательно, столбцы матрицы
Следовательно, столбцы матрицы  линейно независимы, и эта матрица является невырожденной.
линейно независимы, и эта матрица является невырожденной.
Теорема 3.7. Пусть  и
и

Тогда

Доказательство, (i) Пусть  Тогда
Тогда

поскольку  и т. д. Чтобы найти
и т. д. Чтобы найти  разобьем систему нормальных уравнений
разобьем систему нормальных уравнений  на две части и решим отдельно уравнения
на две части и решим отдельно уравнения  Используя
Используя  получаем следующие уравнения:
получаем следующие уравнения:

Из (3.29) вытекает, что

(ii) Подставляя (3.31) в (3.30), получаем

так что


Отсюда 
Имеем

так что

в силу симметричности и идемпотентности матрицы  (теорема 3-1 (0).
(теорема 3-1 (0).
(iv) Из (iii) имеем

(в последнем равенстве мы использовали 
Прежде всего

Далее, в силу теоремы 1.4

поскольку  (теорема 3.1 (iii)). Поэтому, используя n.(i), в соответствии с теоремами 1.5 и 1.4 имеем
(теорема 3.1 (iii)). Поэтому, используя n.(i), в соответствии с теоремами 1.5 и 1.4 имеем

(последнее - в силу  и
и

(здесь мы опять использовали 
Из доказанной теоремы вытекает, что, обратив однажды (при подборе первоначальной модели) матрицу  можно найти оценку
можно найти оценку  (в расширенной модели) и ее дисперсионную матрицу, обращая только матрицу
(в расширенной модели) и ее дисперсионную матрицу, обращая только матрицу  размера
размера  При таком подходе уже
При таком подходе уже
не требуется обращать матрицу  размера
размера  Ниже рассматривается случай
Ниже рассматривается случай 
3.7.2. Одна дополнительная переменная
Обозначим столбцы матрицы X символами  так что
так что

Предположим теперь, что мы намерены включить в подобранную модель еще один регрессор, скажем  так что в результате получится (в указанных выше обозначениях) модель с
так что в результате получится (в указанных выше обозначениях) модель с  . В соответствии с теоремой 3.7 оценки наименьших квадратов для этой расширенной модели вычисляются без затруднений, поскольку на сей раз матрица
. В соответствии с теоремой 3.7 оценки наименьших квадратов для этой расширенной модели вычисляются без затруднений, поскольку на сей раз матрица  равная
равная  состоит всего лишь из одного элемента, т. е. является скалярной величиной. Поэтому
состоит всего лишь из одного элемента, т. е. является скалярной величиной. Поэтому

и матрица легко находится с использованием матрицы  Простота, с которой производится "коррекция" оценок при переходе к модели с одной дополнительной переменной, наводит на мысль, что при необходимости включения в модель большего числа дополнительных переменных следует включать их в модель поочередно. Мы обратимся к такой ступенчатой процедуре в гл. 12.
Простота, с которой производится "коррекция" оценок при переходе к модели с одной дополнительной переменной, наводит на мысль, что при необходимости включения в модель большего числа дополнительных переменных следует включать их в модель поочередно. Мы обратимся к такой ступенчатой процедуре в гл. 12.
Указанный метод включения одной дополнительной переменной впервые подробно рассмотрел Cochran (1938); на случай нескольких переменных его обобщил Quenouille (1950).
3.7.3. Двухшаговый метод наименьших квадратов
Утверждения, содержащиеся в теореме 3.7, предполагают следующую последовательность шагов при намерении "расширить" матрицу плана:
(1) Вычисляем 
(2) Для получения  вектор
вектор  заменяем в квадратичной форме
заменяем в квадратичной форме  на
на  и минимизируем соответствующую форму по отношению к у. После выполнения указанной подстановки приходим к квадратичной форме
и минимизируем соответствующую форму по отношению к у. После выполнения указанной подстановки приходим к квадратичной форме

Приравнивая производную  нулю, получаем
нулю, получаем

откуда находим искомую оценку наименьших квадратов для у:

(3) Остаточную сумму квадратов  для расширенной модели находим как минимальное значение квадратичной формы
для расширенной модели находим как минимальное значение квадратичной формы  по теореме
по теореме  равное
равное 
(4) Для получения  заменяем
заменяем  на
на  в выражении для
в выражении для  т. е.
т. е.

(5) Коэффициент при  в уравнении
в уравнении  (соотношение (3.36)), равный
(соотношение (3.36)), равный  дает возможность легко вычислить дисперсионную матрицу
дает возможность легко вычислить дисперсионную матрицу 
Мы называем приведенную процедуру двухшаговым методом наименьших квадратов. Этод метод широко используется в гл. 10 при рассмотрении моделей дисперсионного анализа.
Интересно отметить, что указанный двухшаговый метод наименьших квадратов для подбора расширенной модели эквивалентен подбору "ортогонализованной" модели  имеющей ортогональную структуру, описанную в § 3.5 (поскольку
имеющей ортогональную структуру, описанную в § 3.5 (поскольку  Чтобы убедиться в этом, используем теорему
Чтобы убедиться в этом, используем теорему  и получим
и получим

или (обозначив 

Здесь  - решение уравнения
- решение уравнения  т. е. уравнения
т. е. уравнения  (матрица R симметрична и идемпотентна), так что
(матрица R симметрична и идемпотентна), так что  является оценкой наименьших квадратов для
является оценкой наименьших квадратов для  Эта идея снова появляется в разд. 3.8.3 (формула (3.53)).
Эта идея снова появляется в разд. 3.8.3 (формула (3.53)).
3.7.4. Остатки в двухшаговой процедуре
Остатки для расширенной модели имеют (с учетом (3.37)) вид

где 
Проведенные только что преобразования лежат в основе рекуррентного алгоритма для подбора моделей дисперсионного анализа
регрессиоными методами. Этот алгоритм разработал Wilkinson G. N. (1970) (см. также James, Wilkinson (1971), Rogers, Wilkinson (1974); Pearce и др. (1974)). Основные этапы алгоритма таковы:
(1) Вычисление остатков 
(2) Использование оператора  который Уилкинсон называет "выметающим" (не смешивать с методом "выметания" в разд. 12.2.2), для получения вектора "кажущихся остатков"
который Уилкинсон называет "выметающим" (не смешивать с методом "выметания" в разд. 12.2.2), для получения вектора "кажущихся остатков" 
(3) Повторное применение оператора  с целью получения значений истинных остатков
с целью получения значений истинных остатков 
Если столбцы матрицы  ортогональны столбцам матрицы X, то тогда
ортогональны столбцам матрицы X, то тогда  (в силу (3.39)), и этап (3) оказывается ненужным. В дальнейшем мы увидим (разд. 3.8.3), что рассмотренную процедуру можно использовать и в том случае, когда матрица X имеет неполный ранг.
(в силу (3.39)), и этап (3) оказывается ненужным. В дальнейшем мы увидим (разд. 3.8.3), что рассмотренную процедуру можно использовать и в том случае, когда матрица X имеет неполный ранг.
Полагая, что матрица X образована первыми  столбцами некоторой исходной матрицы X, а матрица
столбцами некоторой исходной матрицы X, а матрица  столбцом исходной матрицы
столбцом исходной матрицы  , указанный алгоритм можно использовать для такого подбора регрессии, при котором подбор производится поочередно для каждого столбца исходной матрицы. Такая ступенчатая процедура вполне уместна при планировании эксперимента, поскольку в этом случае столбцы исходной матрицы X соответствуют различным компонентам модели, таким, как общее среднее значение, главные эффекты, блочные эффекты, взаимодействия, причем обычно некоторые из ее столбцов бывают ортогональными. Кроме того, элементы матрицы плана равны 0 или 1, так что для многих стандартных планов выметающий оператор
, указанный алгоритм можно использовать для такого подбора регрессии, при котором подбор производится поочередно для каждого столбца исходной матрицы. Такая ступенчатая процедура вполне уместна при планировании эксперимента, поскольку в этом случае столбцы исходной матрицы X соответствуют различным компонентам модели, таким, как общее среднее значение, главные эффекты, блочные эффекты, взаимодействия, причем обычно некоторые из ее столбцов бывают ортогональными. Кроме того, элементы матрицы плана равны 0 или 1, так что для многих стандартных планов выметающий оператор  сводится к простой операции вычитания средних или некоторого кратного средних из остатков.
сводится к простой операции вычитания средних или некоторого кратного средних из остатков.
Упражнения 3g
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Глава I. СЛУЧАЙНЫЕ ВЕКТОРЫ
- 1.2. Линейные модели регрессии
- 1.3. Оператор взятия математического ожидания и ковариационный оператор
- 1.4. Средние и дисперсии квадратичных форм
- 1.5. Независимость случайных величин
- 1.6. Распределение хи-квадрат
- Глава 2. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- 2.2. Производящая функция моментов
- 2.3. Независимость нормальных случайных величин
- 2.4. Квадратичные формы от нормальных случайных величин
- Глава 3. ЛИНЕЙНАЯ РЕГРЕССИЯ: ОЦЕНИВАНИЕ И РАСПРЕДЕЛЕНИЯ
- 3.1. Оценивание по методу наименьших квадратов
- 3.2. Свойства оценок наименьших квадратов
- 3.3. Оценивание дисперсии
- 3.4. Теория распределений
- 3.5. Ортогональная структура матрицы плана
- 3.6. Обобщенный метод наименьших квадратов
- 3.7. Введение дополнительных регрессоров
- 3.8. Случай, когда матрица плана имеет неполный ранг
- 3.8.2. Оцениваемые функции (функции, допускающие оценку)
- 3.8.3. Введение дополнительных регрессоров
- 3.9. Оценивание при наличии линейных ограничений
- 3.9.1. Метод множителей Лагранжа
- 3.9.2. Метод ортогональных проекций
- 3.10. Другие методы оценивания
- 3.10.1. Смещенное оценивание
- 3.10.2. Неотрицательные оценки
- 3.10.3. Цензурированные данные
- 3.10.4. Устойчивое оценивание
- 3.11. Оптимальное планирование
- Глава 4. ЛИНЕЙНАЯ РЕГРЕССИЯ: ПРОВЕРКА ГИПОТЕЗ
- 4.1.2. Основания для использования F-критерия
- 4.1.3. Некоторые примеры
- 4.1.4. Линейная одномерная регрессия
- 4.1.5. Случай отклонения F-критерием гипотезы H
- 4.2. Множественный коэффициент корреляции
- 4.3. Каноническая форма модели при гипотезе H
- 4.4. Критерий согласия
- 4.5. Случай, когда матрица плана имеет неполный ранг
- 4.5.2. Гипотезы, допускающие проверку
- 4.6. Проверка гипотез при дополнительных ограничениях
- Глава 5. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ОБЛАСТИ
- 5.1. Совместное интервальное оценивание
- 5.1.3. Проверка гипотез и доверительные интервалы
- 5.1.4. Доверительные области
- 5.2. Доверительные полосы для поверхности регрессии
- 5.3. Доверительные интервалы для отклика
- 5.4. Расширение регрессионной матрицы
- Глава 6. НАРУШЕНИЯ ОСНОВНЫХ ПРЕДПОЛОЖЕНИЙ
- 6.1. Смещение
- 6.1.1. Смещение, вызванное неполнотой модели
- 6.1.2. Смещение, вызванное избыточностью модели
- 6.1.3. Смещение и случайные регрессоры
- 6.2. Неправильные предположения о дисперсионной матрице
- 6.2.2. Диагональная дисперсионная матрица
- 6.3. Устойчивость F-критерия к отклонениям от нормальности
- 6.3.2. Квадратично сбалансированные F-критерии
- 6.4. Значения регрессоров, измеренные с ошибкой
- 6.4.2. Ошибки округления
- 6.4.3. Некоторые рабочие приемы
- 6.5. Модели со случайными регрессорами
- 6.6. Анализ остатков
- 6.6.3. Статистические критерии, основанные на остатках
- 6.6.4. Графики частичных остатков
- 6.6.5. Преобразованные остатки
- 6.7. Преобразование данных
- Глава 7. ЛИНЕЙНАЯ ОДНОМЕРНАЯ РЕГРЕССИЯ
- 7.2. Доверительные интервалы и полосы
- 7.2.4. Доверительные интервалы для отклика
- 7.2.5. Оптимальное расположение наблюдений
- 7.2.6. Предсказание для обратной задачи (дискриминация)
- 7.3. Прямая, проходящая через начало координат
- 7.4. Взвешенный метод наименьших квадратов
- 7.4.2. Неизвестные веса
- 7.5. Сравнение прямых
- 7.5.2. Критерий параллельности
- 7.5.3. Критерий совпадения
- 7.5.4. Критерий пересечения прямых в одной точке
- 7.5.5. Использование фиктивных категоризованных регрессоров
- 7.5.6. Проверка гипотезы о равенстве дисперсий
- 7.6. Двухфазная линейная регрессия
- 7.7. Случайные регрессоры
- Глава 8. ПОЛИНОМИАЛЬНАЯ РЕГРЕССИЯ
- 8.1.2. Выбор порядка модели
- 8.2. Ортогональные полиномы
- 8.2.2. Получение ортогональных полиномов
- 8.2.3. Взвешенный метод наименьших квадратов
- 8.2.4. Использование ограничений
- 8.2.5. Равноотстоящие значения х
- 8.3, Кусочно-полиномиальная аппроксимация
- 8.3.2. Использование сплайн-функций
- 8.3.3. Многофазная полиномиальная регрессия
- 8.4. Оптимальное расположение точек
- 8.5. Многомерная полиномиальная регрессия
- Глава 9. ДИСПЕРСИОННЫЙ АНАЛИЗ
- 9.2. Классификация по двум признакам
- 9.2.2. Статистики критериев
- 9.2.3. Таблицы дисперсионного анализа
- 9.2.4. Доверительные интервалы
- 9.2.5. Неравные числа наблюдений для разных средних
- 9.3. Классификация по нескольким признакам при равных числах наблюдений для каждого среднего
- 9.4. Классификация с одним наблюдением на каждое среднее
- 9.5. Планы, имеющие структуру простых блоков
- Глава 10. КОВАРИАЦИОННЫЙ АНАЛИЗ И ПРОПУЩЕННЫЕ НАБЛЮДЕНИЯ
- 10.1. Ковариационный анализ
- 10.2. Пропущенные наблюдения
- 10.2.3. Метод ковариационного анализа
- 10.2.4. Пропущенные наблюдения в моделях ковариационного анализа
- Глава II. МЕТОДЫ ВЫЧИСЛЕНИЙ, ИСПОЛЬЗУЕМЫЕ В РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.2. Случай полного ранга
- 11.2.1. Метод исключения Гаусса
- 11.2.2. Метод разложения Холецкого (метод квадратного корня)
- 11.2.3. Разложение в произведение треугольных матриц
- 11.2.4. Ортогонально-треугольное разложение
- 11.3. Взвешенный метод наименьших квадратов
- 11.4. Сравнение методов
- 11.5.1. Метод Холецкого для обобщенной обратной матрицы для Х’Х
- 11.5.2. Сокращенный метод Дулитла
- 11.5.3. Построение обобщенной обратной матрицы для матрицы X с использованием преобразований Хаусхольдера
- 11.5.4. Ортогональное разложение с идентифицирующими ограничениями
- 11.5.5. Разложение по сингулярным значениям
- 11.6. Уточнение решения методом итераций
- 11.7. Центрирование и шкалирование данных
- 11.8. Обновление регрессии
- 11.9. Добавление или удаление определенного регрессора
- 11.10. Проверка гипотез
- 11.11. Проверка программ
- Глава 12. ВЫБОР «НАИЛУЧШЕЙ» РЕГРЕССИИ
- 12.2. Построение всех возможных регрессий
- 12.3. Построение только наилучших регрессий
- 12.3.2. t-упорядоченный поиск
- 12.4. Пошаговая регрессия
- 12.5. Другие методы
- 12.6. Общие замечания
- Приложение А. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ИЗ АЛГЕБРЫ МАТРИЦ
- А3. Положительно полуопределенные матрицы
- А4. Положительно определенные матрицы
- А5. Идемпотентные матрицы
- А6. Дифференцирование векторов
- А7. Разбиение матриц на блоки
- А8. Решение линейных уравнений
- А9. Два соотношения
- А10. Разложение по сингулярным значениям
- Приложение В. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
- В1. Ортогональное разложение векторов
- В2. Ортогональные дополнения
- В3. Проекции на подпространства
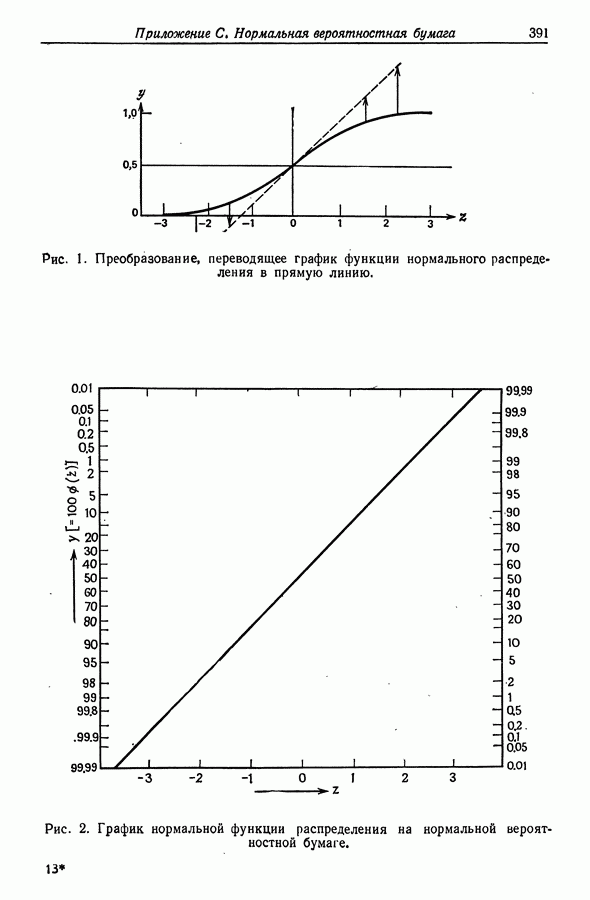
- Приложение С. НОРМАЛЬНАЯ ВЕРОЯТНОСТНАЯ БУМАГА
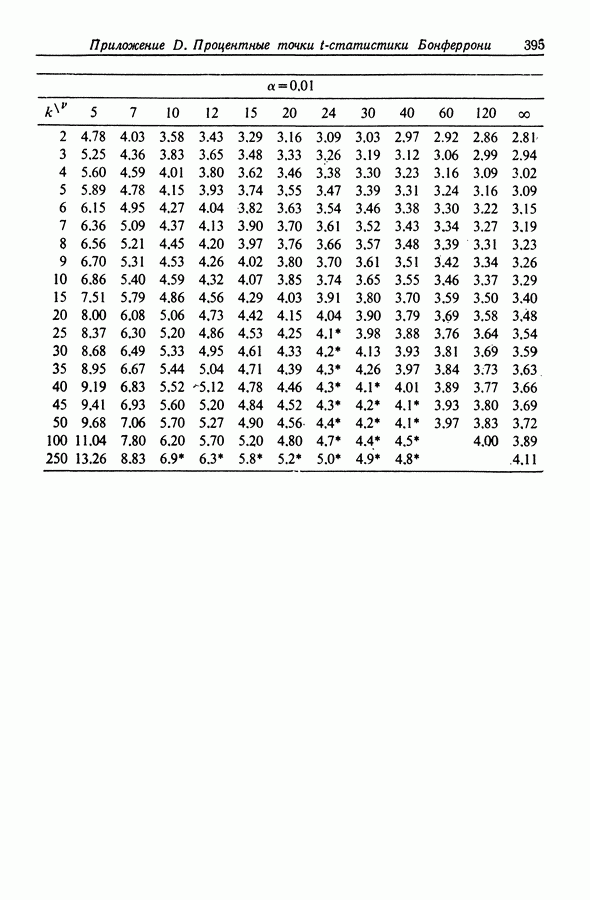
- Приложение D. ПРОЦЕНТНЫЕ ТОЧКИ t-СТАТИСТИКИ БОНФЕРРОНИ
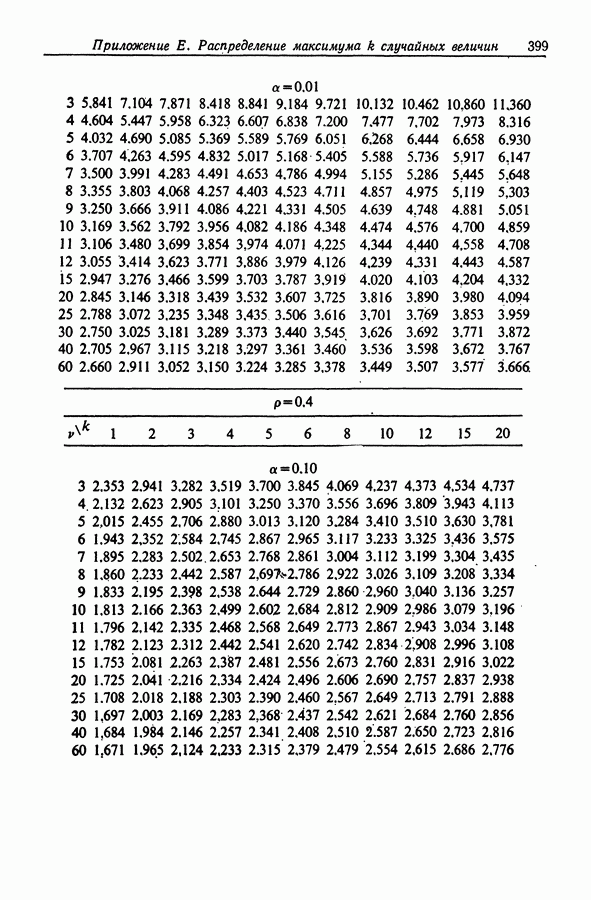
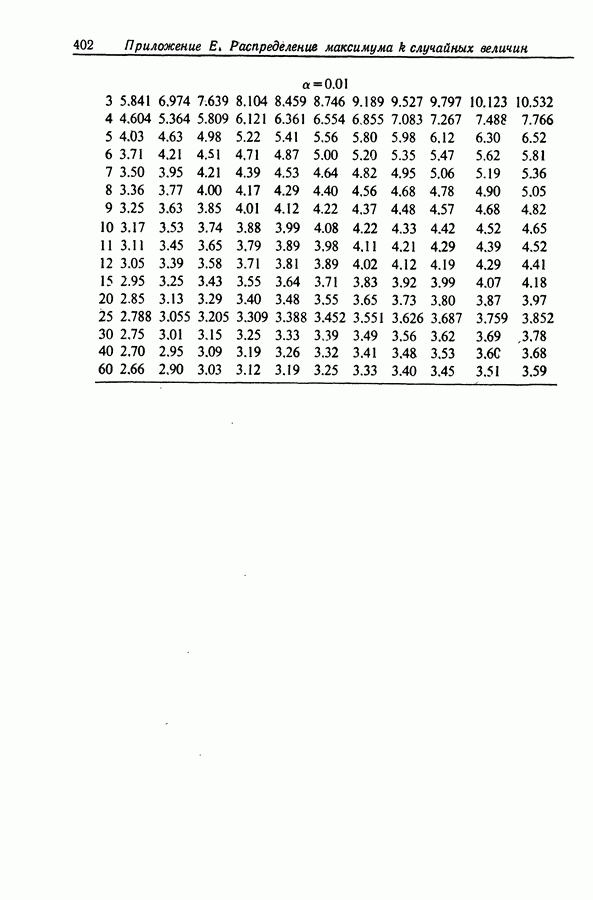
- Приложение Е. РАСПРЕДЕЛЕНИЕ МАКСИМУМА АБСОЛЮТНЫХ ВЕЛИЧИН К СЛУЧАЙНЫХ ВЕЛИЧИН, ИМЕЮЩИХ t-РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
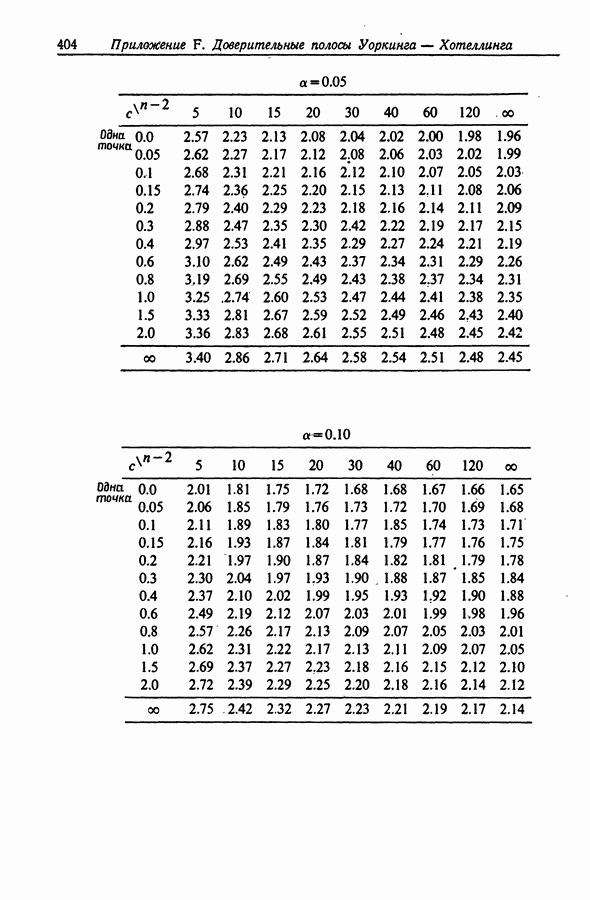
- Приложение F. ДОВЕРИТЕЛЬНЫЕ ПОЛОСЫ УОРКИНГА-ХОТЕЛЛИНГА ДЛЯ КОНЕЧНЫХ ИНТЕРВАЛОВ
- НАБРОСКИ РЕШЕНИЙ УПРАЖНЕНИЙ
- СПИСОК ЛИТЕРАТУРЫ