| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Введение. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ СОДЕРЖАНИЕ, ЗАДАЧИ, ОБЛАСТИ ПРИМЕНЕНИЯ
В.1. Предварительное обсуждение задач
Любой закон природы или общественного развития может быть выражен в конечном счете в виде описания характера или структуры взаимосвязей (зависимостей), существующих между изучаемыми явлениями или показателями (переменными величинами или просто переменными). Если эти зависимости: а) сто-хаотичны по своей природе, т. е. позволяют устанавливать лишь вероятностные логические соотношения между изучаемыми событиями А и 5, а именно соотношения типа «из факта осуществления события А следует, что событие В должно произойти, но не обязательно, а лишь с некоторой (как правило, близкой к единице) вероятностью Р»; б) выявляются на основании статистического наблюдения за анализируемыми событиями или переменными, осуществляемого по выборке из интересующей нас генеральной совокупности [14, п. 5.4.2], то мы оказываемся в рамках проблемы статистического исследования зависимостей. Соответствующий математический аппарат, будучи таким образом нацеленным в первую очередь на решение основной проблемы естествознания: как по отдельным, частным наблюдениям выявить и описать интересующую нас общую закономерность? — занимает, бесспорно, центральное место во всем прикладном математическом анализе.
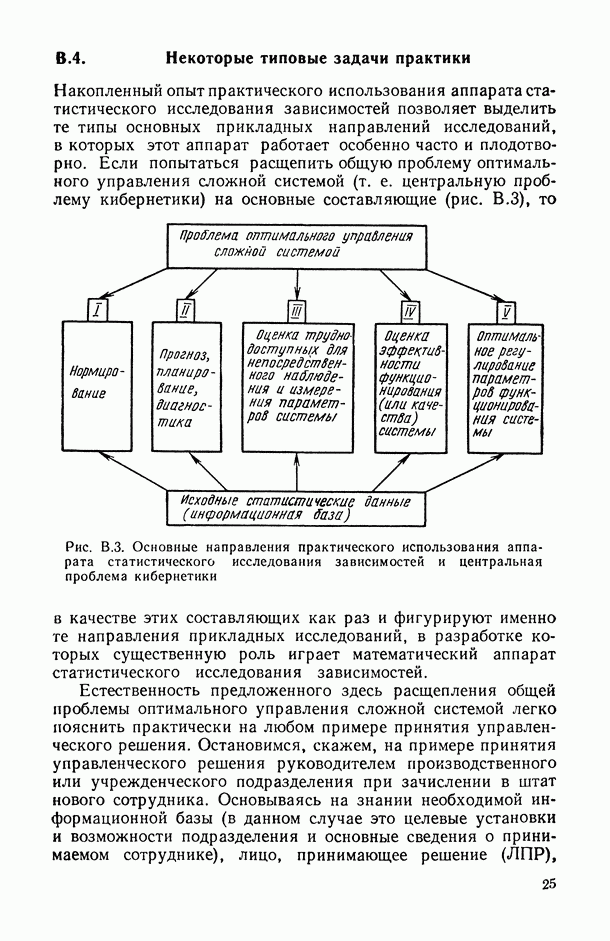
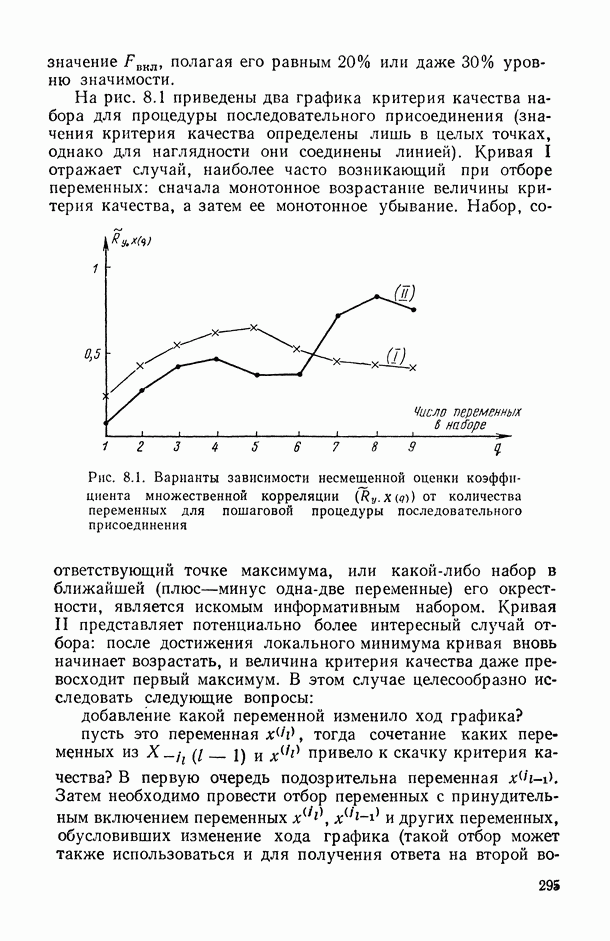
Перед тем как перейти к формулировке общей и частных задач статистического исследования зависимостей, условимся описывать функционирование изучаемого реального объекта (системы, процесса, явления) набором переменных (рис. В.1), среди которых:
 — так называемые «входные» переменные, описывающие условия функционирования (часть из них, как правило, поддается регулированию или частичному управлению); в соответствующих математических моделях их называют независимыми, факторами-аргументами, экзогенными, предикторными (или просто предикторами, т. е. предсказателями), объясняющими (в книге мы будем использовать в основном два последних термина);
— так называемые «входные» переменные, описывающие условия функционирования (часть из них, как правило, поддается регулированию или частичному управлению); в соответствующих математических моделях их называют независимыми, факторами-аргументами, экзогенными, предикторными (или просто предикторами, т. е. предсказателями), объясняющими (в книге мы будем использовать в основном два последних термина);
 — выходные переменные, характеризующие поведение или результат (эффективность) функционирования; в математических моделях их называют зависимыми, откликами, эндогенными, результирующими или объясняемыми (в книге используются в основном два последних термина);
— выходные переменные, характеризующие поведение или результат (эффективность) функционирования; в математических моделях их называют зависимыми, откликами, эндогенными, результирующими или объясняемыми (в книге используются в основном два последних термина);
 — латентные (т. е. скрытые, не поддающиеся непосредственному измерению) случайные «остаточные» компоненты, отражающие влияние (соответственно на
— латентные (т. е. скрытые, не поддающиеся непосредственному измерению) случайные «остаточные» компоненты, отражающие влияние (соответственно на  неучтенных «на входе» факторов, а также случайные ошибки в измерении анализируемых показателей (в математических моделях мы их, как правило, будем именовать просто «остатками»).
неучтенных «на входе» факторов, а также случайные ошибки в измерении анализируемых показателей (в математических моделях мы их, как правило, будем именовать просто «остатками»).

Рис. В.1. Общая схема взаимодействия переменных при статистическом исследовании зависимостей
Тогда общая задача статистического исследования зависимостей (в терминах изучаемых показателей) может быть сформулирована следующим образом: по результатам  измерений
измерений

исследуемых переменных на объектах (системах, процессах) анализируемой совокупности построить такую (векторнозначную) функцию

которая позволила бы наилучшим (в определенном смысле) образом восстанавливать значения результирующих (прогнозируемых) переменных  по заданным значениям объясняющих (предикторных) переменных
по заданным значениям объясняющих (предикторных) переменных 

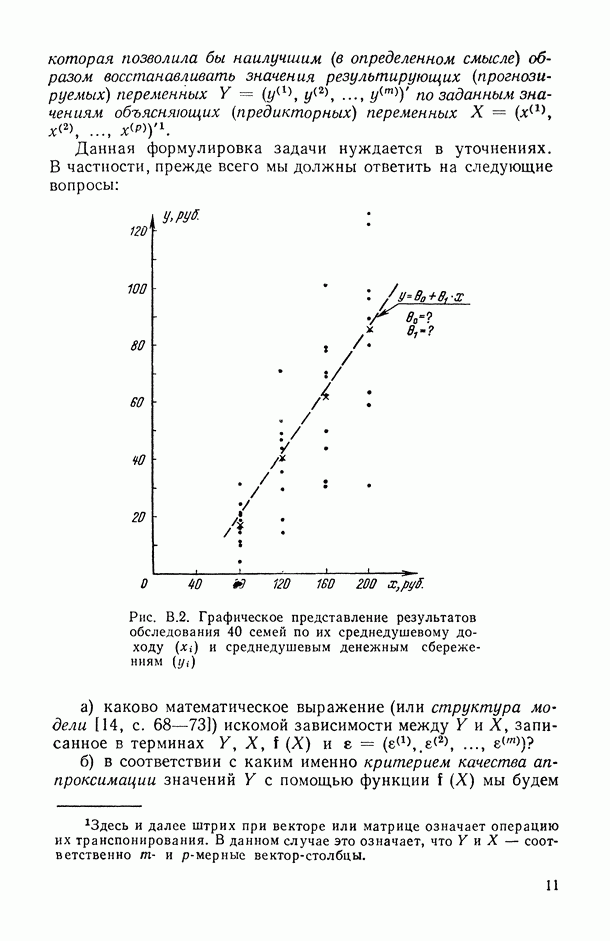
Рис. В.2. Графическое представление результатов обследования 40 семей по их среднедушевому доходу  и среднедушевым денежным сбережениям
и среднедушевым денежным сбережениям 
Данная формулировка задачи нуждается в уточнениях. В частности, прежде всего мы должны ответить на следующие вопросы:
а) каково математическое выражение (или структура модели [14, с. 68—73]) искомой зависимости между Y и X, записанное в терминах Y, X,  и
и 
б) в соответствии с каким именно критерием качества аппроксимации значений У с помощью функции  мы будем определять наилучший способ восстановления значений результирующих показателей по заданным значениям объясняющих переменных?
мы будем определять наилучший способ восстановления значений результирующих показателей по заданным значениям объясняющих переменных?
в) с какой именно прикладной целью мы проводим все наше исследование, т. е. для решения каких конкретных задач мы собираемся использовать построенную в результате исследования функцию  ?
?
Прежде чем обсуждать эти вопросы, рассмотрим пример.
Пример В.1. Анализируется «поведение» двумерной случайной величины  где
где  — среднедушевой доход и
— среднедушевой доход и  — среднедушевые денежные сбережения в семье, случайно извлеченной из рассматриваемой совокупности семей, однородной по своему потребительскому поведению (см., например, [1281). В табл. В.1 и на рис. В.2 представлены исходные статистические данные вида (В.1), характеризующие среднедушевые величины дохода
— среднедушевые денежные сбережения в семье, случайно извлеченной из рассматриваемой совокупности семей, однородной по своему потребительскому поведению (см., например, [1281). В табл. В.1 и на рис. В.2 представлены исходные статистические данные вида (В.1), характеризующие среднедушевые величины дохода  и денежных сбережений
и денежных сбережений  за определенный отрезок времени, а именно за месяц, в каждой
за определенный отрезок времени, а именно за месяц, в каждой  обследованной семье рассматриваемой совокупности семей (в данном условном примере объем
обследованной семье рассматриваемой совокупности семей (в данном условном примере объем  статистически обследованной совокупности семей равнялся 40). В этом примере имелась возможность при отборе исходных данных (выборки) контролировать значения предикторной переменной Н (условия активного эксперимента [14, с. 1211), что позволило, в частности, разбить статистически обследованные семьи на четыре равные по объему группы по доходам.
статистически обследованной совокупности семей равнялся 40). В этом примере имелась возможность при отборе исходных данных (выборки) контролировать значения предикторной переменной Н (условия активного эксперимента [14, с. 1211), что позволило, в частности, разбить статистически обследованные семьи на четыре равные по объему группы по доходам.
Мы видим, что даже в пределах каждой из этих групп величины среднедушевых сбережений семей подвержены некоторому неконтролируемому разбросу, обусловленному влиянием множества не поддающихся строгому учету и контролю факторов (т. е. налицо упомянутый выше стохастический характер зависимости между х и у). Однако это еще не значит, что расположение точек  являющихся геометрическим изображением результатов обследования семей по доходу и сбережениям, должно быть совершенно хаотичным и не должно обнаруживать некоторой вполне определенной тенденции, характеризующей зависимость денежных сбережений в семье
являющихся геометрическим изображением результатов обследования семей по доходу и сбережениям, должно быть совершенно хаотичным и не должно обнаруживать некоторой вполне определенной тенденции, характеризующей зависимость денежных сбережений в семье  от ее среднедушевого дохода
от ее среднедушевого дохода  При исследовании подобных зависимостей встают следующие основные вопросы (в скобках после вопроса указываются главы, параграфы или пункты настоящей книги, ему посвященные).
При исследовании подобных зависимостей встают следующие основные вопросы (в скобках после вопроса указываются главы, параграфы или пункты настоящей книги, ему посвященные).
1. Как исходя из конкретных прикладных целей исследования определить смысл, в котором понимается исследуемая зависимость? (В.2, § 5.3.)
2. Имеется ли вообще какая-либо связь между исследуемыми переменными (а в случае многих переменных — какова структура этих связей?) и как измерить тесноту этой связи? (Гл. 1-4.)
3. Каков общий математический вид искомой связи между  и
и  , т. е. как определяется общая структура соответствующей математической модели? (Гл. 6.)
, т. е. как определяется общая структура соответствующей математической модели? (Гл. 6.)
4. Как, отправляясь от принятой общей структуры модели, провести необходимую вычислительную обработку исходных данных (В.1) с целью получения конкретного вида зависимости  от
от  , что позволит в данном случае производить количественную оценку неизвестных денежных сбережений семьи по заданной величине ее среднедушевого дохода? (Гл. 7—10, 13, 14.)
, что позволит в данном случае производить количественную оценку неизвестных денежных сбережений семьи по заданной величине ее среднедушевого дохода? (Гл. 7—10, 13, 14.)
5. Поскольку наши выводы основаны на обработке ограниченного ряда наблюдений, то их количественные характеристики, естественно, подвержены (при повторениях соответствующих выборочных обследований) некоторому случайному разбросу. Как оценить степень точности наших выводов? (Гл. 11.)
6. Как решать все вопросы в ситуациях, когда среди объясняющих (предикторных) переменных могут быть и неколичественные? (Гл. 13.)
7. И наконец, если при сборе исходной статистической информации мы находимся в условиях активного эксперимента [14, с. 121, то как, при заданных затратах на наблюдения, оптимально выбрать матрицу плана [14, с. 26, 68], т. е. как определить те значения объясняющих (предикторных) переменных и то распределение заданного общего числа наблюдений между этими значениями, которые являются в некотором смысле наиболее выгодными с точки зрения достижения наивысшей точности наших статистических выводов?
Вернемся к нашему примеру и попробуем ответить на некоторые из поставленных здесь вопросов, в том числе на принципиальные вопросы а), б) и в), ответы на которые позволяют уточнить общую формулировку задачи статистического исследования зависимостей, данную выше.
Начнем «с конца», т. е. с уточнения конечных прикладных целей исследования (см. вопросы 1, а также а) и в)). Известно, что из двух анализируемых характеристик материальной сосостоятельности семьи характеристика денежных сбережений  относится к категории статистически труднодоступных: содержащиеся в ежегодных и единовременных выборочных семейных бюджетных обследованиях ЦСУ [85] сведения о сбережениях, как правило, непредставительны.
относится к категории статистически труднодоступных: содержащиеся в ежегодных и единовременных выборочных семейных бюджетных обследованиях ЦСУ [85] сведения о сбережениях, как правило, непредставительны.
Таблица В.1

Поэтому главной конечной целью нашего исследования (опирающегося, как мы будем всегда предполагать, на достоверную и репрезентативную выборку исходных данных) является возможность восстановления (прогноза):
удельной (т. е. в расчете на одного члена семьи за определенный отрезок времени) величины денежных сбережений в конкретной семье (у(x)) по заданному значению ее среднедушевого дохода 
удельной величины средних денежных сбережений  в семьях данной группы х по доходам.
в семьях данной группы х по доходам.
Таблица B.l

Этой цели мы сможем достигнуть, если сумеем математически описать закономерность изменения условных теоретических средних значений  в зависимости от
в зависимости от  а также изучить характер случайного разброса денежных сбережений
а также изучить характер случайного разброса денежных сбережений  отдельных семей данной группы
отдельных семей данной группы  по доходам относительно своего среднего значения
по доходам относительно своего среднего значения  (при любом интересующем нас значении среднедушевого дохода
(при любом интересующем нас значении среднедушевого дохода  ).
).
Это естественным образом приводит нас к необходимости рассмотрения математической модели вида

в которой остаточная компонента  отражает случайное отклонение денежных сбережений наугад выбранной отдельной семьи с доходом
отражает случайное отклонение денежных сбережений наугад выбранной отдельной семьи с доходом  от среднего значения
от среднего значения  этих сбережений, подсчитанного по всем семьям данной группы по доходам, а функция
этих сбережений, подсчитанного по всем семьям данной группы по доходам, а функция  описывает характер изменения условного среднего
описывает характер изменения условного среднего  (при
(при  ) в зависимости от изменения
) в зависимости от изменения  если дополнительно прийти к соглашению, что характер случайного разброса величин
если дополнительно прийти к соглашению, что характер случайного разброса величин  относительно своих средних
относительно своих средних  таков, что
таков, что  при всех
при всех 
Таким образом, из (В.3) мы непосредственно получаем

Чтобы покончить с вопросами 1, а) и в), остается уточнить общую структуру модели, т. е. определить, в каком классе F функций  мы будем производить аппроксимацию искомой зависимости
мы будем производить аппроксимацию искомой зависимости 
В нашем случае, учитывая однородный (по характеру потребительского поведения) состав исследуемой совокупности семей, естественно исходить из гипотезы об одинаковой (в среднем) склонности семей к сбережениям, выражающейся, в частности, в том, что все семьи начиная с некоторого «порогового» уровня дохода, склонны отделять в сбережения в среднем одинаковую долю дохода. Математически, как легко понять, это выразится в виде

где  и
и  — некоторые константы (неизвестные параметры модели). Так что
— некоторые константы (неизвестные параметры модели). Так что

где под  понимается семейство всех тех функций
понимается семейство всех тех функций  , которые могут быть получены при подстановке вместо
, которые могут быть получены при подстановке вместо  ее различных конкретных значений (
ее различных конкретных значений ( — векторный параметр).
— векторный параметр).
Такой выбор «класса допустимых решений»  подтверждается и характером расположения совокупности точек, являющихся геометрическим изображением исходных данных в нашлем примере (см. на рис. В.2 расположение «крестиков», ординаты которых определяются экспериментально подсчитанными, т. е. вычисленными на основании имеющихся выборочных данных, условными средними
подтверждается и характером расположения совокупности точек, являющихся геометрическим изображением исходных данных в нашлем примере (см. на рис. В.2 расположение «крестиков», ординаты которых определяются экспериментально подсчитанными, т. е. вычисленными на основании имеющихся выборочных данных, условными средними 
И наконец, следует уточнить, в соответствии с каким именно критерием качества аппроксимации неизвестных величин среднедушевых семейных денежных сбережений у  с помощью функции
с помощью функции  мы будем определять наилучший способ прогноза
мы будем определять наилучший способ прогноза  по х. Наиболее обоснованное и точное решение этого вопроса опирается на знание вероятностной природы (а именно типа закона распределения вероятностей) остатков
по х. Наиболее обоснованное и точное решение этого вопроса опирается на знание вероятностной природы (а именно типа закона распределения вероятностей) остатков  в модели (В.3). Так, например, известно [14, с. 281], что если предположить, что при любых значениях х распределение вероятностей остатков
в модели (В.3). Так, например, известно [14, с. 281], что если предположить, что при любых значениях х распределение вероятностей остатков  описывается
описывается  - нормальным законом (т. е. нормальным законом со средним значением, равным нулю, и с некоторой, вообще говоря, неизвестной, но постоянной, т. е. не зависящей от х дисперсией
- нормальным законом (т. е. нормальным законом со средним значением, равным нулю, и с некоторой, вообще говоря, неизвестной, но постоянной, т. е. не зависящей от х дисперсией  ) и что остатки
) и что остатки  , характеризующие различные наблюдения, статистически независимы, то наименьшая ошибка прогноза
, характеризующие различные наблюдения, статистически независимы, то наименьшая ошибка прогноза  с помощью модели
с помощью модели  (т. е. функция
(т. е. функция  подбирается из класса F) обеспечивается требованием метода наименьших квадратов
подбирается из класса F) обеспечивается требованием метода наименьших квадратов

В нашем примере явно нарушено условие постоянства дисперсии остатков (см. табл. В.1), т. е. условная дисперсия  существенно зависит от значения
существенно зависит от значения  Можно устранить это нарушение, поделив все анализируемые величины, откладываемые по оси
Можно устранить это нарушение, поделив все анализируемые величины, откладываемые по оси  , а следовательно, и остатки
, а следовательно, и остатки  на значения
на значения  (являющиеся статистическими оценками для
(являющиеся статистическими оценками для  ), т. е. перейдя к анализу остатков
), т. е. перейдя к анализу остатков 
Тогда можно показать (с помощью методов, описанных, например, в [14, § 11.1]), что гипотеза о  - нормальном характере распределения остатков (х не противоречит имею щимся в нашем распоряжении данным (представленным в табл. В.1) и, следовательно, требование (В.7) приводит к необходимости решения экстремальной задачи вида
- нормальном характере распределения остатков (х не противоречит имею щимся в нашем распоряжении данным (представленным в табл. В.1) и, следовательно, требование (В.7) приводит к необходимости решения экстремальной задачи вида

т. е. к системе из двух линейных уравнений с двумя неизвестными 

Решение системы (В.7") дает нам в качестве оценок  для неизвестных параметров соответственно
для неизвестных параметров соответственно  выражения:
выражения:

Расчет по этим формулам с использованием данных табл. В.1 дает нам решение задачи 4:

так что статистическая оценка искомой зависимости средней величины среднедушевых семейных сбережений  от значения среднедушевого дохода семей данной доходной группы
от значения среднедушевого дохода семей данной доходной группы  имеет в этом случае вид
имеет в этом случае вид

При другой статистической природе остатков 8 или при отсутствии достаточной информации о типе их вероятностного распределения возможен иной, чем по  выбор критерия качества аппроксимации
выбор критерия качества аппроксимации  (см. гл. 7). Отметим, однако, что наиболее широкое распространение в статистической практике именно критерия наименьших квадратов
(см. гл. 7). Отметим, однако, что наиболее широкое распространение в статистической практике именно критерия наименьших квадратов  подкреплено рядом исследований [15, 196]. В них обосновываются хорошие прогностические свойства моделей, полученных в соответствии с
подкреплено рядом исследований [15, 196]. В них обосновываются хорошие прогностические свойства моделей, полученных в соответствии с  и в ситуациях, характеризующихся различными отклонениями от нормальности и взаимной независимости остатков в
и в ситуациях, характеризующихся различными отклонениями от нормальности и взаимной независимости остатков в  .
.
Заканчивая обсуждение примера  и возвращаясь к общему описанию задач статистического исследования зависимостей, отметим, что функции
и возвращаясь к общему описанию задач статистического исследования зависимостей, отметим, что функции  описывающие поведение условных средних результирующего показателя
описывающие поведение условных средних результирующего показателя  (вычисленных при значениях предикторных переменных зафиксированных на уровне
(вычисленных при значениях предикторных переменных зафиксированных на уровне  в зависимости от изменения X, принято называть функциями регрессии (подробнее о различных определениях функции регрессии см. в гл. 5).
в зависимости от изменения X, принято называть функциями регрессии (подробнее о различных определениях функции регрессии см. в гл. 5).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Введение. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАВИСИМОСТЕЙ СОДЕРЖАНИЕ, ЗАДАЧИ, ОБЛАСТИ ПРИМЕНЕНИЯ
- В.2. Какова конечная прикладная цель статистического исследования зависимостей?
- В.3. Математический инструментарий
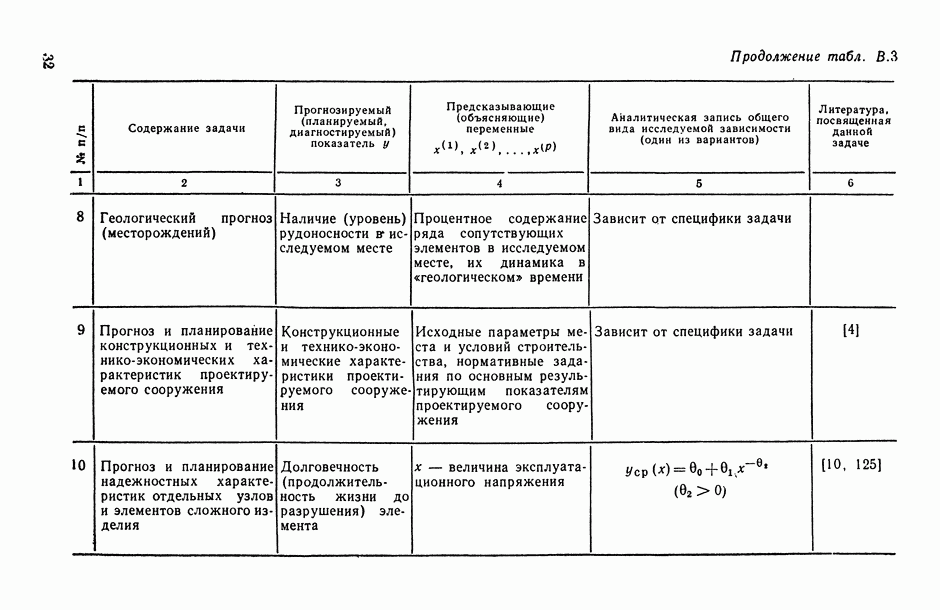
- В.4. Некоторые типовые задачи практики
- В.5. Основные типы зависимостей между количественными переменными
- В.6. Основные этапы статистического исследования зависимостей
- ВЫВОДЫ
- Раздел I. АНАЛИЗ СТРУКТУРЫ И ТЕСНОТЫ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ИССЛЕДУЕМЫМИ ПЕРЕМЕННЫМИ (корреляционный анализ)
- 1.1.1. Понятие индекса корреляции.
- 1.1.2. Коэффициент корреляции как измеритель степени тесноты связи в двумерных нормальных схемах.
- 1.1.3. Распределение выборочного коэффициента корреляции и проверка гипотезы о статистической значимости линейной связи.
- 1.1.4. Влияние ошибок измерения на величину коэффициента корреляции.
- 1.1.5. Измерение степени тесноты связи при нелинейной зависимости.
- 1.2. Анализ частных («очищенных») связей
- 1.2.2. Частные коэффициенты корреляции и их выборочные значения.
- 1.2.3. Статистические свойства выборочных частных коэффициентов корреляции (проверка на статистическую значимость их отличия от нуля, доверительные интервалы).
- 1.3. Анализ множественных связей
- 1.3.2. Множественный коэффициент корреляции и его свойства (общий случай).
- 1.3.3. Вычисление и свойства множественного коэффициента корреляции в рамках линейных нормальных моделей.
- 1.3.4. Примеры.
- ВЫВОДЫ
- Глава 2. АНАЛИЗ СТАТИСТИЧЕСКОЙ СВЯЗИ МЕЖДУ ПОРЯДКОВЫМИ (ОРДИНАЛЬНЫМИ) ПЕРЕМЕННЫМИ
- 2.1. Ранговая корреляция
- 2.1.2. Понятие ранговой корреляции.
- 2.1.3. Основные задачи статистического анализа связей между ранжировками.
- 2.1.4. Вероятностные пространства ранжировок, генерируемые порядковыми переменными [14, гл. 4, 5].
- 2.2. Анализ и измерение парных ранговых статистических связей
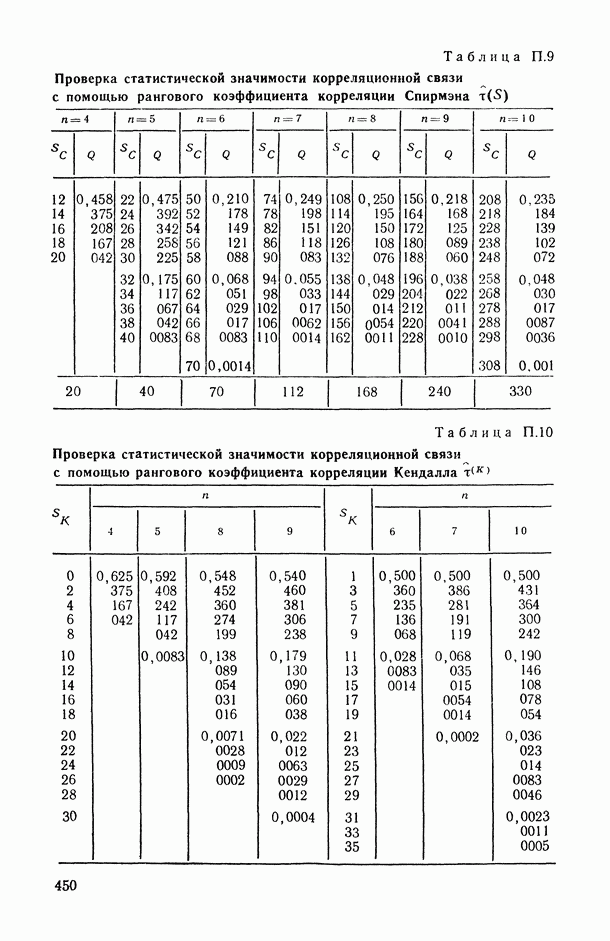
- 2.2.1. Ранговый коэффициент корреляции Спирмэна.
- 2.2.2. Ранговый коэффициент корреляции Кендалла.
- 2.2.3. Обобщенная формула для парного коэффициента корреляции и связь между коэффициентами Спирмэна и Кендалла.
- 2.2.4. Статистические свойства выборочных характеристик парной ранговой связи.
- 2.3. Анализ множественных ранговых связей
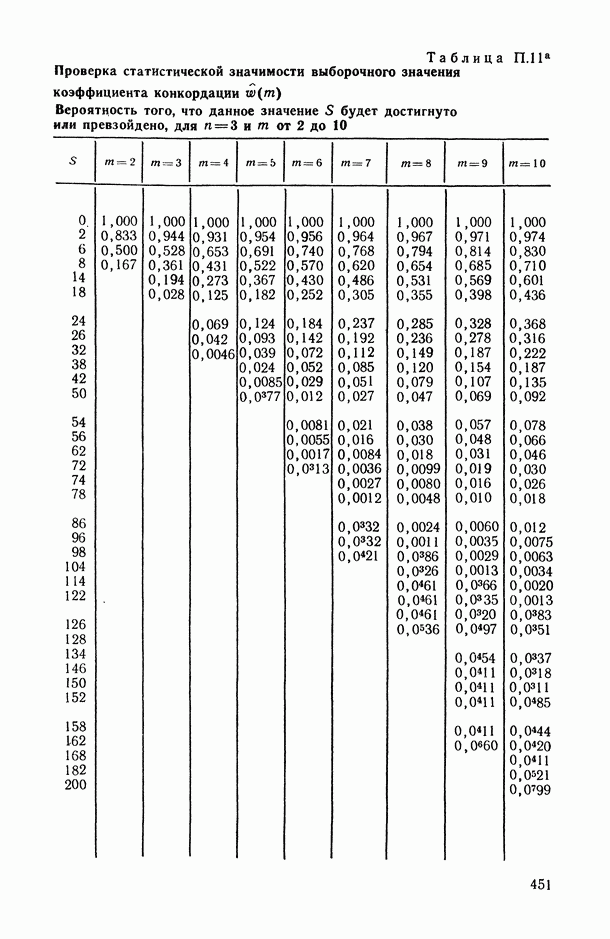
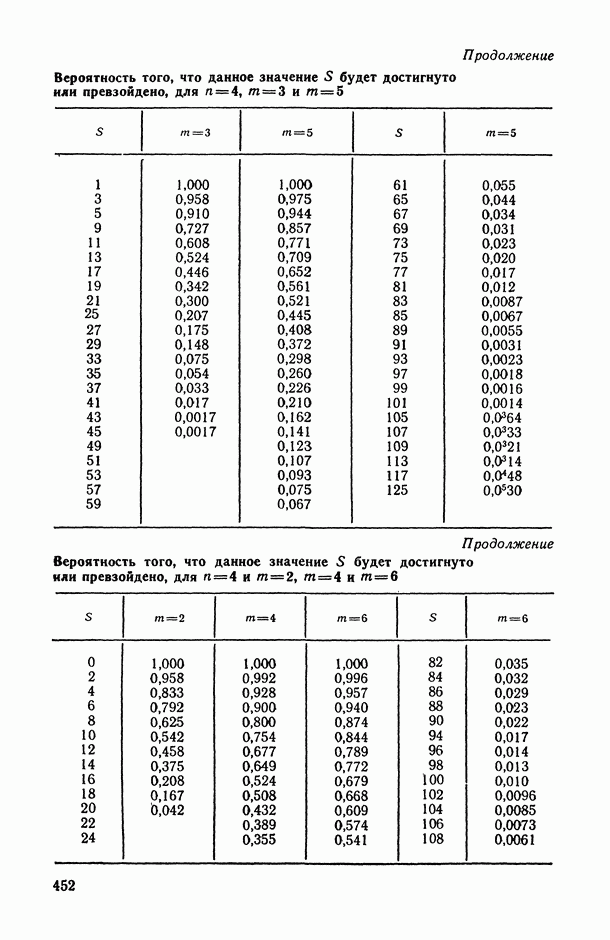
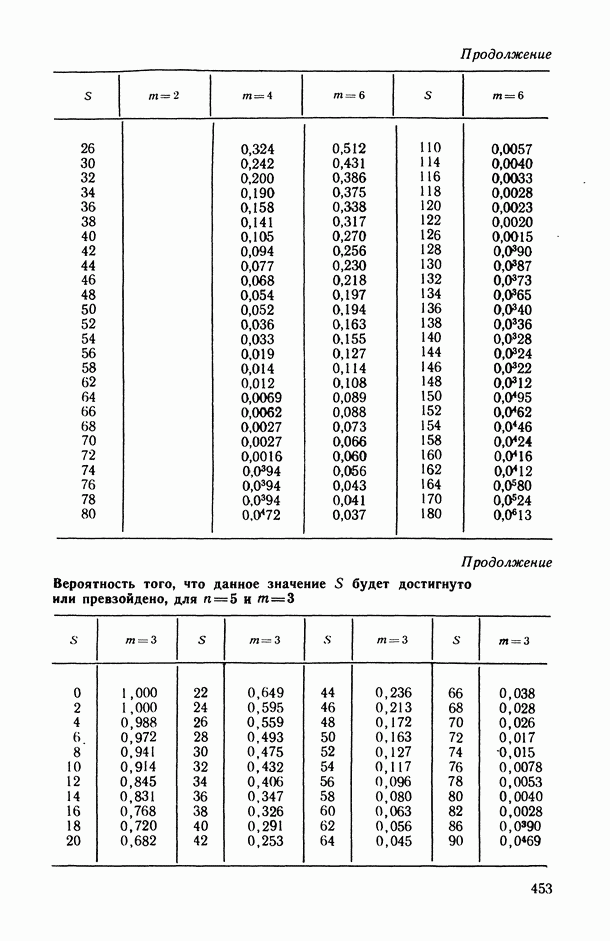
- 2.3.2. Проверка статистической значимости выборочного значения коэффициента конкордации.
- 2.3.3. Использование коэффициента конкордации в решении основных задач статистического анализа ранговых связей.
- 2.3.4. Примеры.
- ВЫВОДЫ
- Глава 3. АНАЛИЗ СВЯЗЕЙ МЕЖДУ КЛАССИФИКАЦИОННЫМИ (НОМИНАЛЬНЫМИ) ПЕРЕМЕННЫМИ
- 3.1. Таблицы сопряженности
- 3.1.2. Логарифмически-линейная. параметризация таблиц сопряженности.
- 3.1.3. Проверка гипотез.
- 3.1.4. Меры связи между строками и столбцами таблицы.
- 3.2. Приписывание численных значений качественным переменным (дуальное шкалирование)
- 3.2.1. Методическое место дуального шкалирования.
- 3.2.2. Максимизация F-отношения суммы квадратов отклонений между объектами к полной сумме квадратов отклонений.
- 3.2.3. Двойственность в определении V и W.
- 3.2.4. Максимизация коэффициента корреляции.
- 3.2.5. Изучение оптимального решения.
- 3.2.6. Таблицы «объект—многомерный отклик».
- ВЫВОДЫ
- Глава 4. АНАЛИЗ СТРУКТУРЫ СВЯЗЕЙ МЕЖДУ КОМПОНЕНТАМИ МНОГОМЕРНОГО ВЕКТОРА
- 4.1.1. Цепи Маркова.
- 4.1.3. Математические задачи, связанные с изучением распределений с ДСЗ.
- 4.2. Распределение с древообразной структурой зависимостей
- 4.2.1. Предварительные сведения из теории графов.
- 4.2.2. Распределения с древообразной структурой зависимостей (ДСЗ).
- 4.3. Оценка графа структуры зависимостей компонент нормального вектора
- 4.3.2. Построение графа структуры зависимостей по корреляционной матрице.
- 4.3.3. Асимптотика Колмогорова — Деева.
- 4.4. R(k)-распределения
- 4.4.1. Основные определения. Начнем с обобщения понятия распределения с ДСЗ.
- 4.4.2. Нормальное R(k)-распределение.
- 4.4.3. Восстановление графа структуры зависимостей.
- 4.5. Структура связей нормального вектора (общий случай)
- 4.5.1. Марковская тройка. Структура многомерного вектора.
- 4.5.2. Информационная интерпретация структуры связей.
- 4.5.3. Использование структуры для представления распределения в виде композиции более простых распределений.
- ВЫВОДЫ
- Раздел II. ИССЛЕДОВАНИЕ ВИДА ЗАВИСИМОСТИ МЕЖДУ КОЛИЧЕСТВЕННЫМИ ПЕРЕМЕННЫМИ (регрессионный анализ)
- 5.1. Функция регрессии как условное среднее и ее интерпретация в рамках многомерной нормальной модели
- 5.2. Функция «дельта»-регрессии как решение оптимизационной задачи
- 5.3. Взаимоотношения различных регрессий
- ВЫВОДЫ
- Глава 6. ВЫБОР ОБЩЕГО ВИДА ФУНКЦИИ РЕГРЕССИИ
- 6.1. Использование априорной информации о содержательной сущности анализируемой зависимости
- 6.2. Предварительный анализ геометрической структуры исходных данных
- 6.2.1. Содержание геометрического анализа парных корреляционных полей.
- 6.2.2. Учет и формализация «гладких» свойств искомой функции регрессии.
- 6.2.3. Некоторые вспомогательные преобразования, линеаризующие исследуемую парную зависимость.
- 6.3. Математико-статистические методы в задаче параметризации модели регрессии
- 6.3.1. Компромисс между сложностью регрессионной модели и точностью ее оценивания.
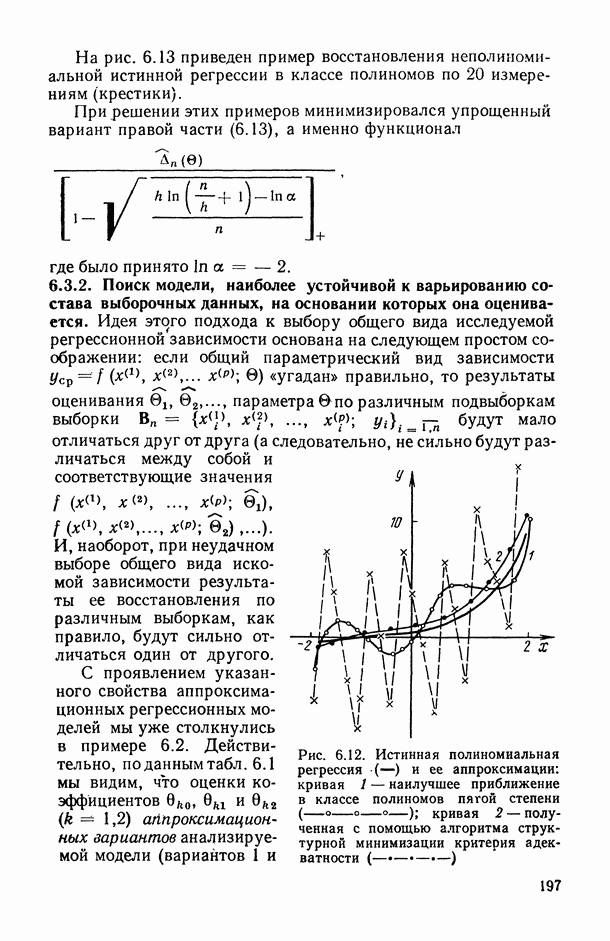
- 6.3.2. Поиск модели, наиболее устойчивой к варьированию состава выборочных данных, на основании которых она оценивается.
- 6.3.3. Статистические критерии проверки гипотез об общем виде функции регрессии.
- ВЫВОДЫ
- Глава 7. ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ, ЛИНЕЙНО ВХОДЯЩИХ В УРАВНЕНИЕ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ
- 7.1. Метод наименьших квадратов
- 7.1.2. Свойства мнк-оценок.
- 7.1.3. Ортогональная матрица плана.
- 7.1.4. Параболическая регрессия и система ортогональных полиномов Чебышева.
- 7.1.5. Обобщенный мнк.
- 7.2. Функции потерь, отличные от квадратичной
- 7.2.1. Функция потерь.
- 7.2.3. Функции потерь, имеющие горизонтальную асимптоту.
- 7.2.4. Эв-регрессия («лямбда»-регрессия).
- 7.2.5. Минимизация систематической ошибки.
- 7.3. Байесовское оценивание
- 7.3.1. Введение априорной плотности распределения параметров.
- 7.3.2. Апостериорное распределение параметров.
- 7.3.3. Повторная выборка из той же совокупности.
- 7.4. Многомерная регрессия
- 7.4.1. Случай известной ковариационной матрицы ошибок.
- 7.4.3. Эв-оценки.
- 7.4.4. Использование многомерной регрессии для параметризации многомерных распределений.
- 7.5. Оценивание параметров при наличии погрешностей в предикторных переменных (конфлюэнтный анализ)
- 7.5.1. Основные типы задач конфлюэнтного анализа.
- 7.5.2. Модифицированный мнк для схемы активного эксперимента.
- 7.5.3. Пассивные наблюдения.
- 7.5.4. Некоторые принципиальные отличия регрессионных задач (7.83) и (7.84).
- 7.5.5. Неявное задание отклика.
- 7.6. Оценивание в регрессионных моделях со случайными параметрами (регрессионные задачи второго рода)
- 7.6.2. Случай, когда средние значения и ковариационная матрица оцениваемых параметров известны (требуется оценить параметры).
- 7.6.3. Случай, когда известна только ковариационная матрица (требуется оценить параметры).
- 7.6.4. Случай неизвестных.
- ВЫВОДЫ
- Глава 8. ОЦЕНИВАНИЕ ПАРАМЕТРОВ РЕГРЕССИИ В УСЛОВИЯХ МУЛЬТИКОЛЛИНЕАРНОСТИ И ОТБОР СУЩЕСТВЕННЫХ ПРЕДИКТОРОВ
- 8.1. Явление мультиколлинеарности и его влияние на мнк-оценки
- 8.2. Регрессия на главные компоненты
- 8.3. Смещенное оценивание коэффициентов регрессии
- 8.4. Редуцированные оценки для стандартной модели линейной регрессии
- 8.4.2. Редуцированная оценка Мейера — Уилке.
- 8.5. Оценки, связанные с ортогональным разложением
- 8.5.1. Оптимальное взвешивание вклада главных компонент.
- 8.5.2. Оценка оптимальных вкладов главных компонент.
- 8.6. Вопросы точности вычислительной реализации процедур линейного оценивания
- 8.6.1. Два метода получения мнк-оценок.
- 8.6.2. Оценки величин возмущений для решений центрированной и соответствующей ей нормальной системы уравнений.
- 8.6.3. Центрирование и нормирование матрицы данных.
- 8.6.4. Вычисление элементов ковариационной матрицы.
- 8.7. Отбор существенных переменных в задачах линейной регрессии
- 8.7.1. Влияние отбора переменных на оценку уравнения регрессии.
- 8.7.2. Критерии качества уравнения регрессии.
- 8.7.3. Схемы генерации наборов переменных.
- 8.7.4. Пошаговые процедуры генерации наборов.
- 8.7.5. Оператор симметричного выметания.
- 8.7.6. Методические аспекты использования процедур отбора существенных предикторных переменных.
- ВЫВОДЫ
- Глава 9. ВЫЧИСЛИТЕЛЬНЫЕ АСПЕКТЫ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ
- 9.1. Итерационные методы поиска оценок метода наименьших квадратов (мнк-оценок)
- 9.1.2. Алгоритмы квазиградиентного типа.
- 9.2. Градиентный спуск
- 9.3. Метод Ньютона
- 9.4 Метод Ньютона-Гаусса и его модификации
- 9.4.2. Обсуждение скорости сходимости процедуры.
- 9.4.3. Рекомендации по правилу остановки итерационной процедуры.
- 9.5. Методы, не использующие вычисления производных
- 9.6. Способы нахождения начального приближения
- 9.7. Вопросы существования и единственности мнк-оценки
- ВЫВОДЫ
- Глава 10. НЕПАРАМЕТРИЧЕСКАЯ, ЛОКАЛЬНО-ПАРАМЕТРИЧЕСКАЯ И КУСОЧНАЯ АППРОКСИМАЦИЯ РЕГРЕССИОННЫХ ЗАВИСИМОСТЕЙ
- 10.1. Непараметрическое оценивание регрессии
- 10.2. Локальная параметрическая аппроксимация регрессии в одномерном случае
- 10.3. Кусочно-параметрическая (сплайновая) техника аппроксимации регрессионных зависимостей
- 10.3.1. Определение одномерных сплайнов.
- 10.3.2. Выбор порядка сплайна, числа и положения узлов.
- 10.3.3. Оценка параметров и проверка гипотез.
- 10.3.4. Билинейные сплайны.
- ВЫВОДЫ
- Глава II. ИССЛЕДОВАНИЕ точности СТАТИСТИЧЕСКИХ ВЫВОДОВ в РЕГРЕССИОННОМ АНАЛИЗЕ
- 11.1 Линейный (относительно оцениваемых параметров) нормальный вариант идеализированной схемы регрессионной зависимости
- 11.1.2. Решение основных задач по оценке точности регрессионной модели.
- 11.1.3. Случаи линейной (по предикторным переменным) и полиномиальной регрессии.
- 11.2. Нелинейный нормальный вариант идеализированной схемы регрессионной зависимости
- 11.2.2. Решение основных задач по оценке точности нелинейной регрессионной модели.
- 11.3. Исследование точности регрессионной модели в реалистической ситуации
- ВЫВОДЫ
- Глава 12. СТАТИСТИЧЕСКИЙ АНАЛИЗ АВТОРЕГРЕССИОННЫХ ДИНАМИЧЕСКИХ ЗАВИСИМОСТЕЙ
- 12.1. Дискретные динамические модели
- 12.2. Авторегрессия первого порядка
- 12.3. Авторегрессия произвольного порядка
- ВЫВОДЫ
- Раздел III. ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ КОЛИЧЕСТВЕННОГО РЕЗУЛЬТИРУЮЩЕГО ПОКАЗАТЕЛЯ ОТ ОБЪЯСНЯЮЩИХ ПЕРЕМЕННЫХ СМЕШАННОЙ ПРИРОДЫ
- Глава 13. ДИСПЕРСИОННЫЙ И КОВАРИАЦИОННЫЙ АНАЛИЗ
- 13.1. Классификация моделей дисперсионного анализа по способу организации исходных данных
- 13.2. Однофакторный дисперсионный анализ
- 13.3. Полный двухфакторный дисперсионный анализ
- 13.4. Модели дисперсионного анализа со случайными факторами
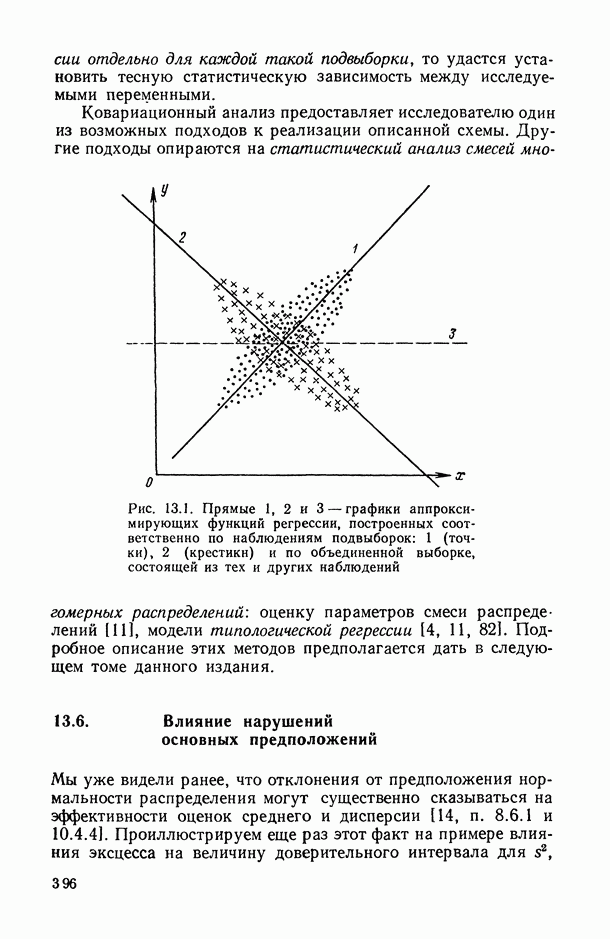
- 13.5. Ковариационный анализ (КА) и проблема статистического исследования смесей многомерных распределений
- 13.6. Влияние нарушений основных предположений
- ВЫВОДЫ
- Раздел IV. СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ АППАРАТА СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
- 14.1. Системы одновременных уравнений
- 14.2. Спецификация модели и проблема идентифицируемости
- 14.3. Рекурсивные системы
- 14.4. Двух- и трехшаговый методы наименьших квадратов
- 14.5. Метод неподвижной точки
- 14.6. Сравнение методов
- ВЫВОДЫ
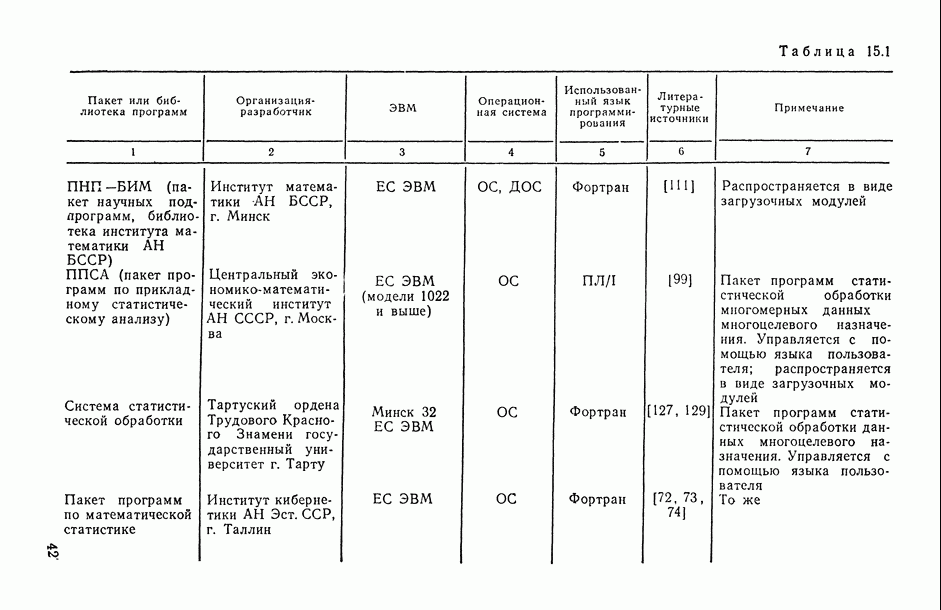
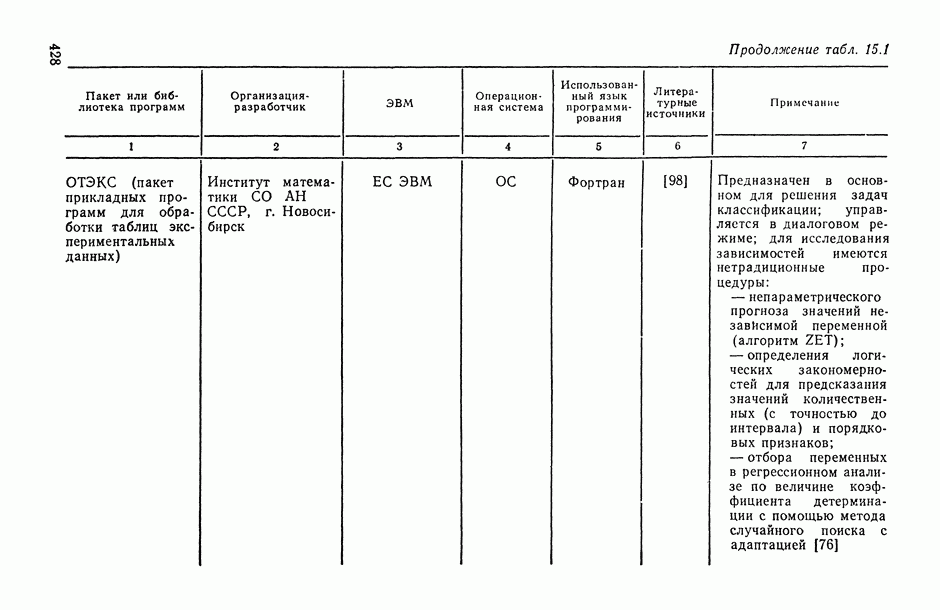
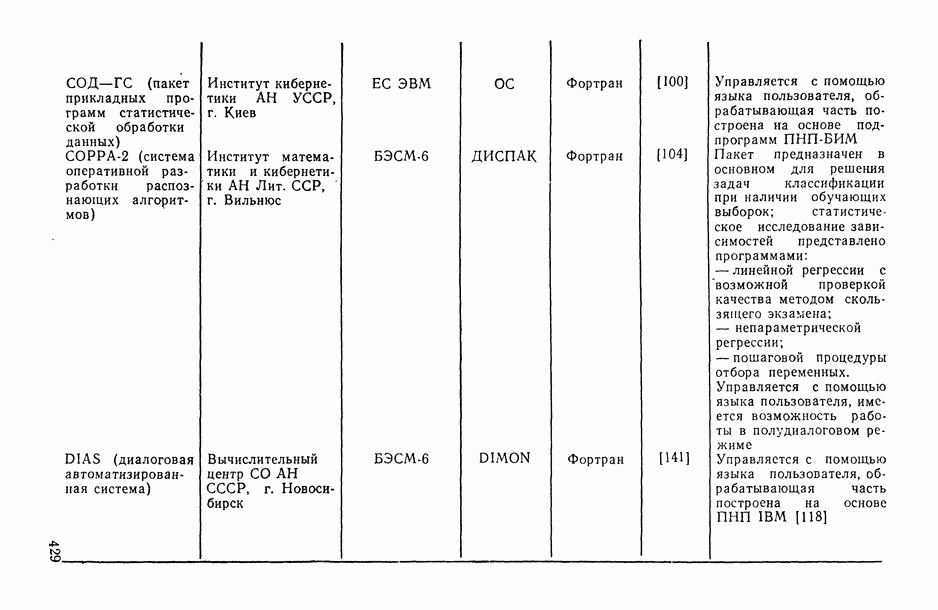
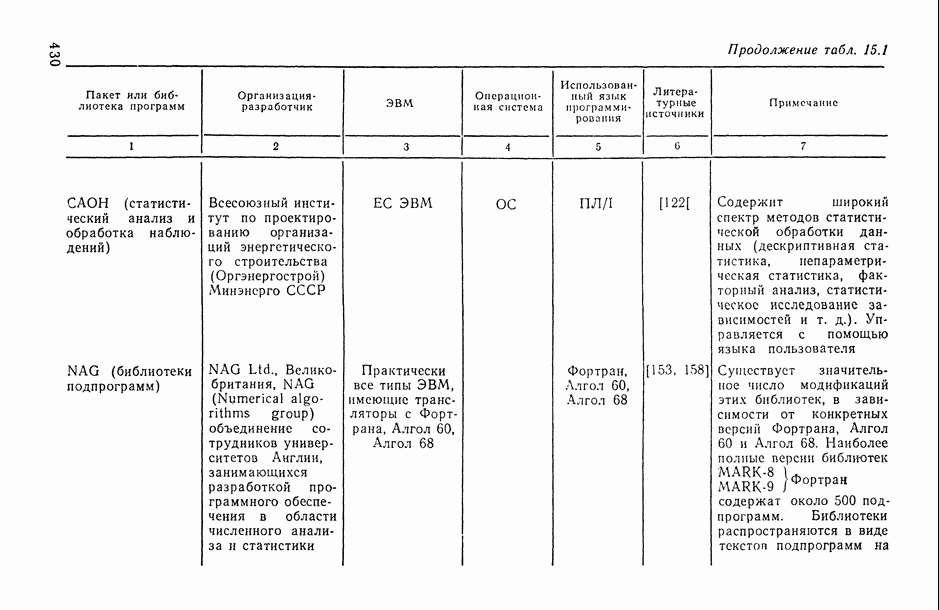
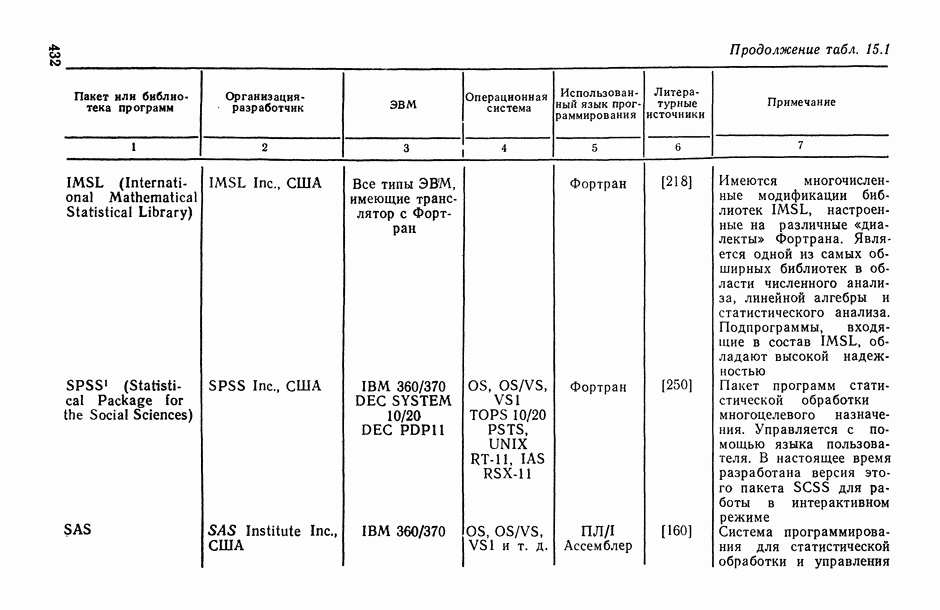
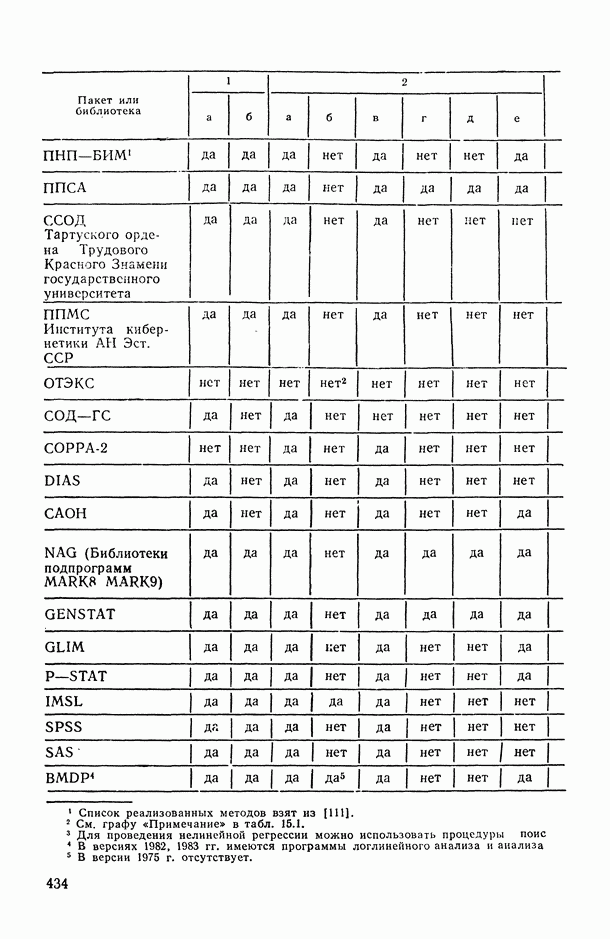
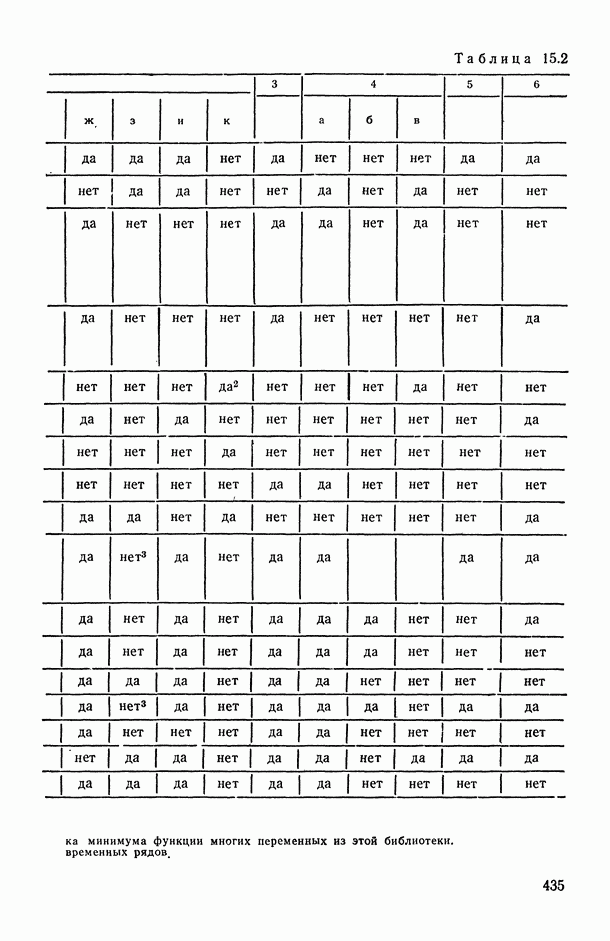
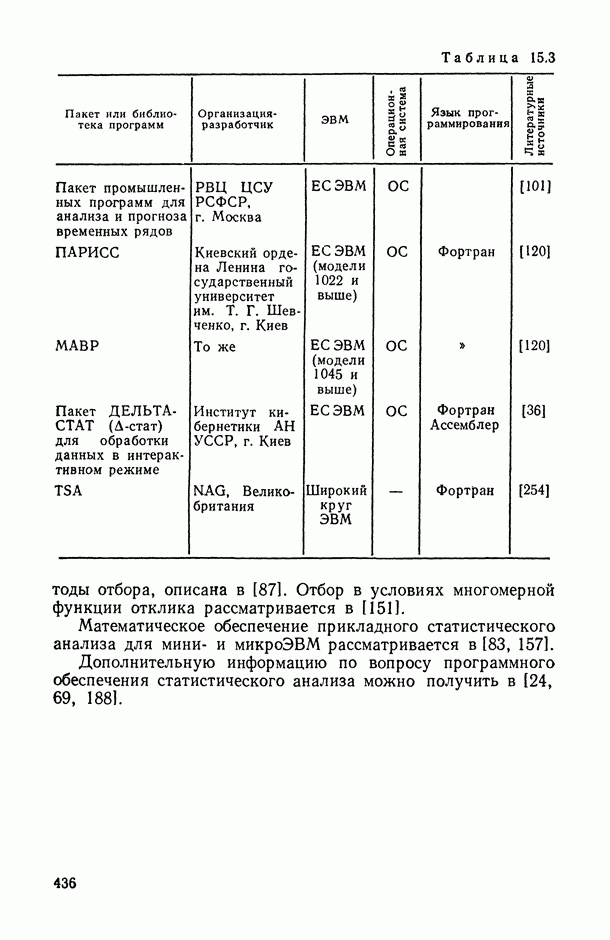
- Глава 15. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ СТАТИСТИЧЕСКОГО ИССЛЕДОВАНИЯ ЗАВИСИМОСТЕЙ
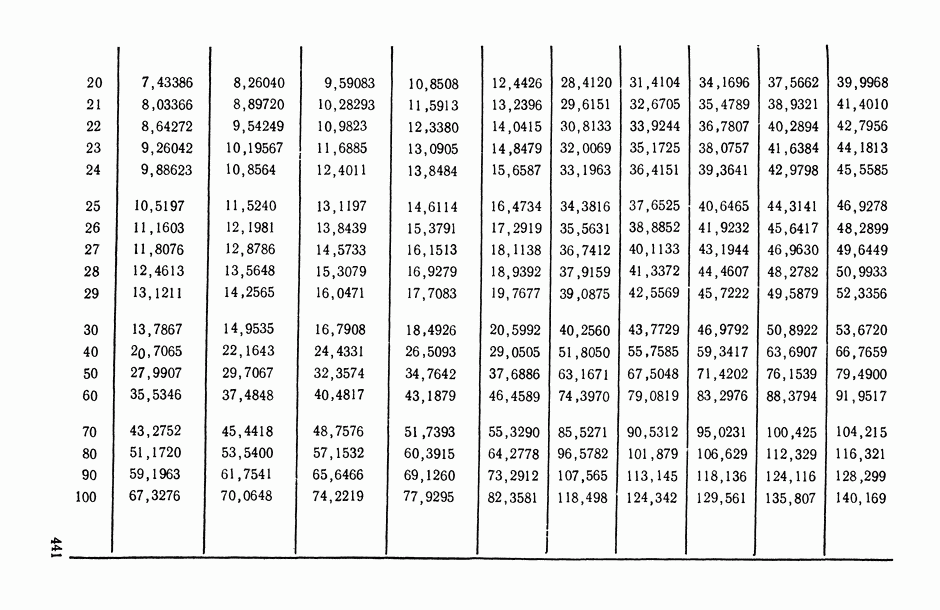
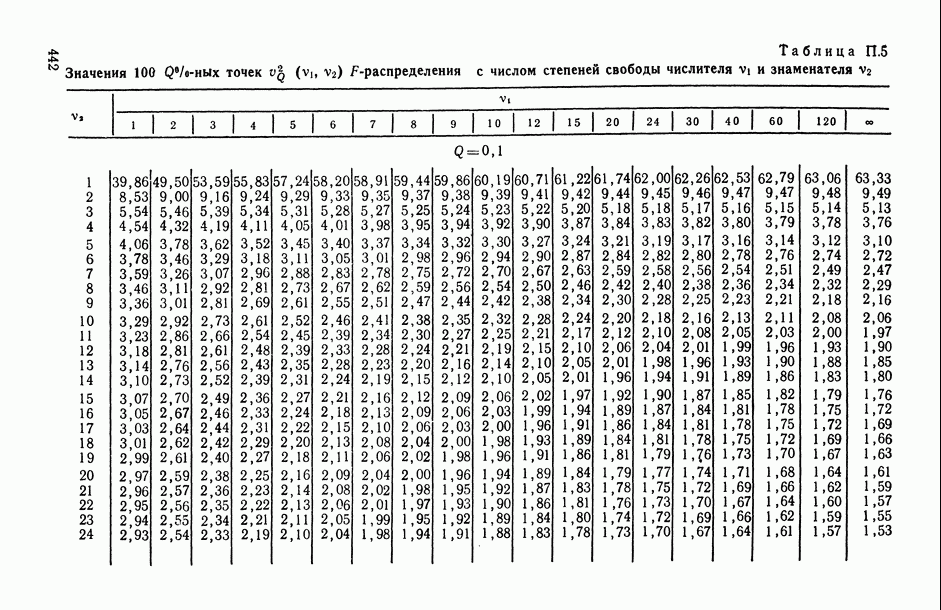
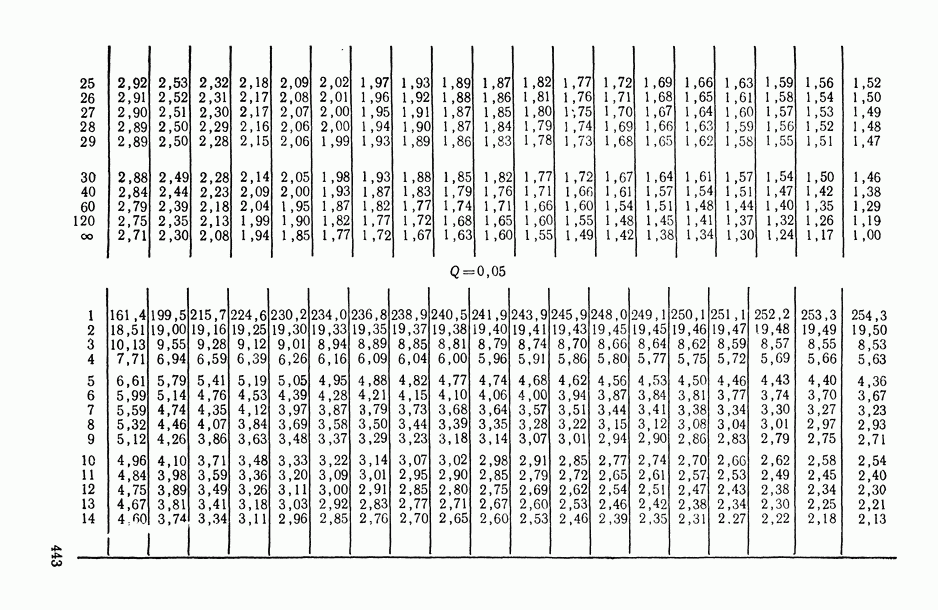
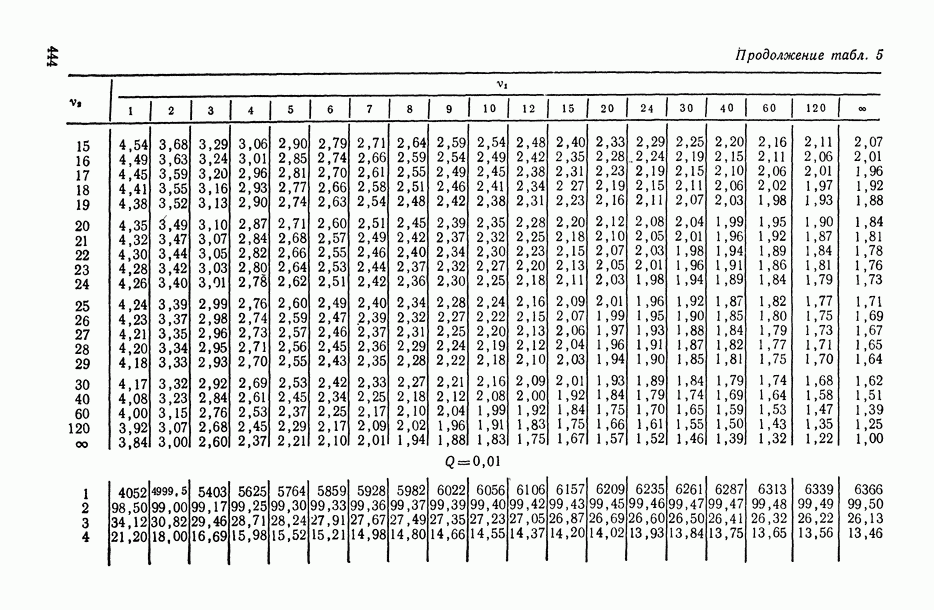
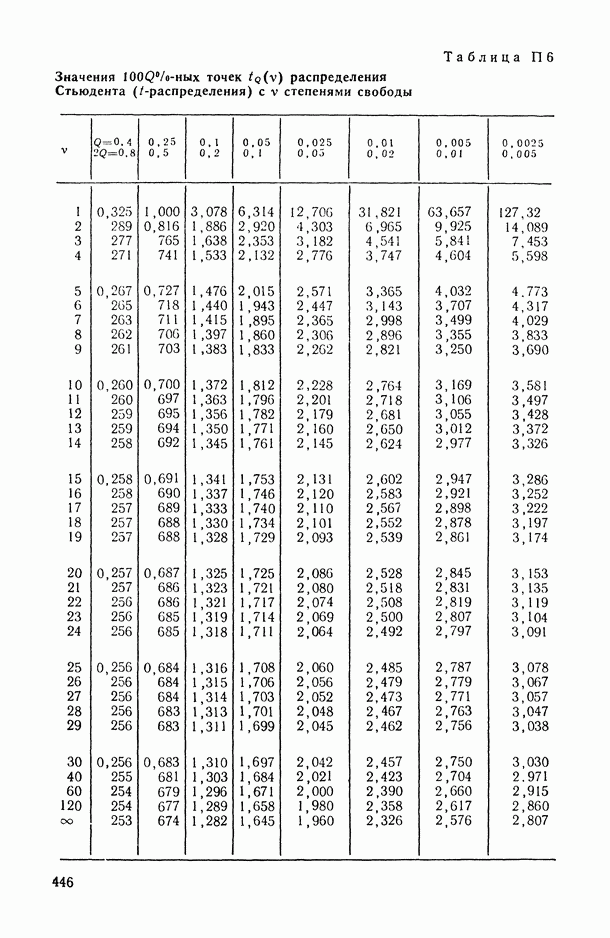
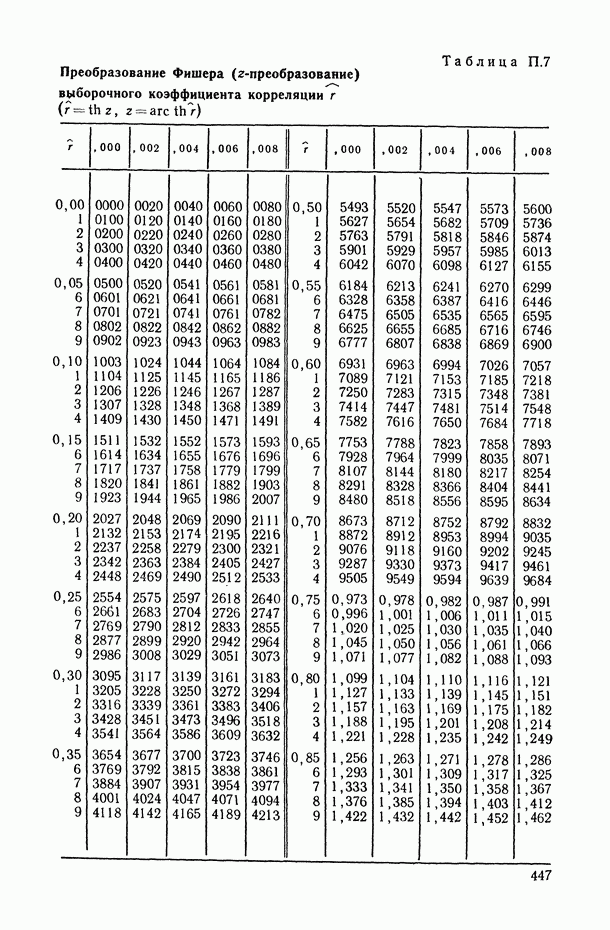
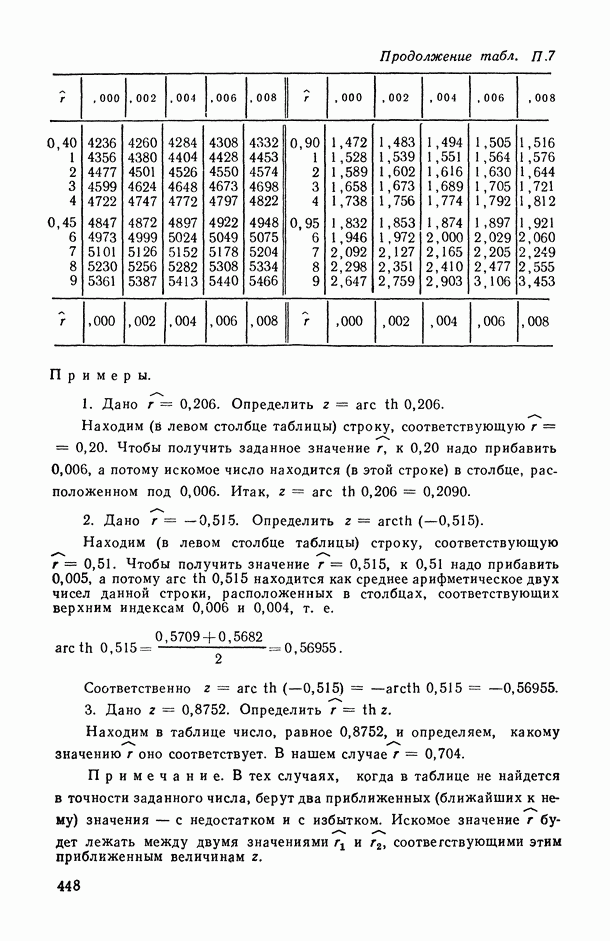
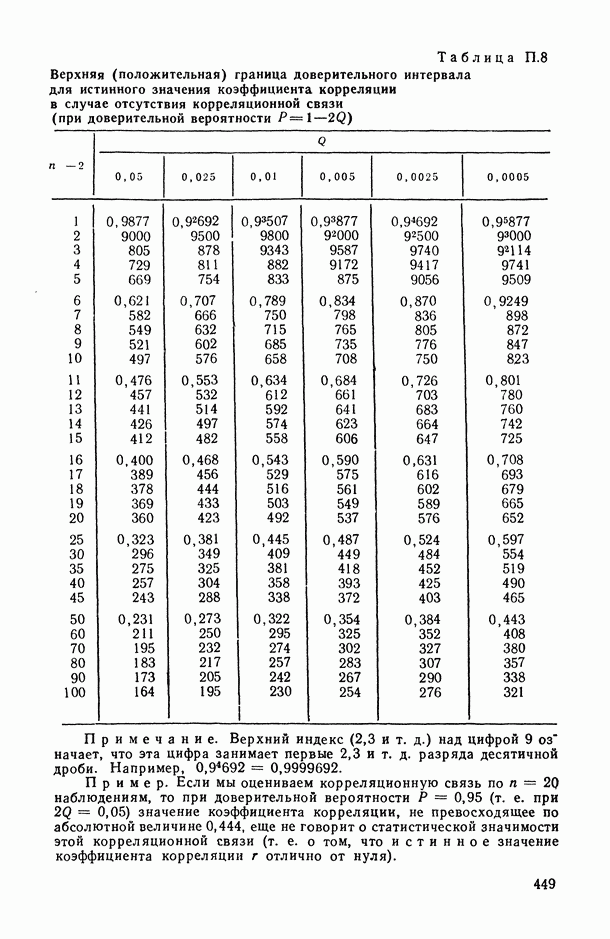
- ПРИЛОЖЕНИЯ. МАТЕМАТИКО-СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
- Таблица П.1. Значения функции плотности стандартного нормального закона распределения
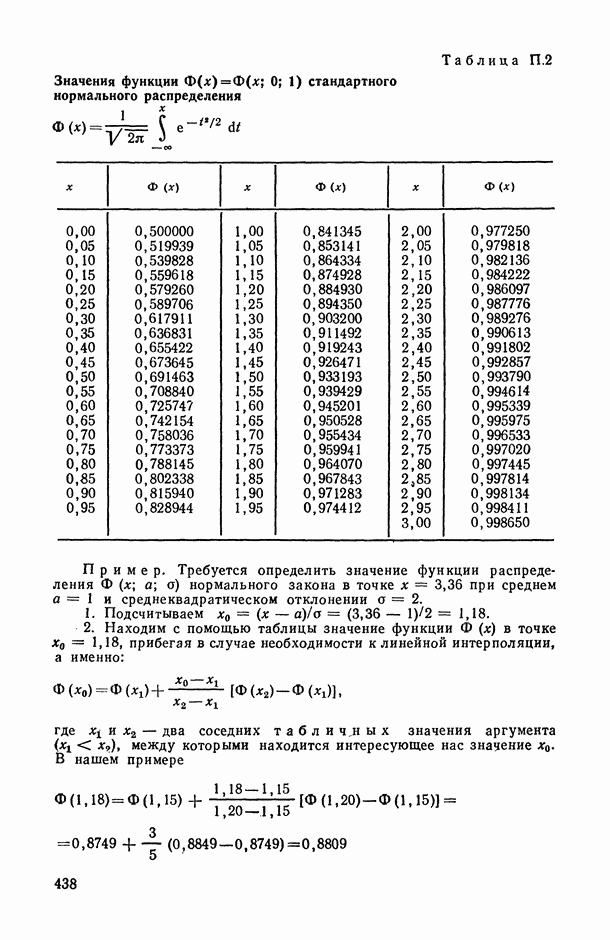
- Таблица П.2. Значения функции стандартного нормального распределения
- ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ