| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
27. Энергетическое состояние электрона в атоме.
Для электрона, находящегося под действием сил притяжения к ядру, уравнение Шредингера имеет решения не при любых, а только при определенных значениях энергии. Таким образом, квантованность энергетических состояний электрона в атоме (т. е. первый постулат Бора) оказывается следствием присущих электрону волновых свойств и не требует введения особых постулатов.Для лучшего понимания последнего утверждения рассмотрим упрощенную модель атома, «одномерный атом», в котором электрон может совершать лишь колебательные движения между крайними точками.
Будем считать также, что границы атома непроницаемы для электрона, так что он может находиться только внутри атома. Мы уже знаем, что состояние электрона в атоме характеризуется некоторой волной («волна де Бройля»). Но было бы неправильно представлять себе распространение этой волны как нечто подобное движению волны, образовавшейся на поверхности воды от брошенного камня: водяная волна неограниченно удаляется от места своего образования и постепенно расплывается, она не обладает устойчивостью во времени, тогда как электрон в атоме устойчив. Поэтому более правильной будет аналогия между состоянием электрона в атоме и состоянием звучащей струны, на которой образуются так называемые стоячие волны.
На рис. 6 схематически изображены стоячие волны, возникающие на колеблющейся струне, крайние точки которой закреплены. В точках, обозначенных буквой n, возникают пучности — здесь амплитуда колебания максимальна, в точках у струна не колеблется — это узлы, в которых амплитуда колебания равна нулю; в точках, расположенных между узлами и пучностями, амплитуда колебания имеет промежуточные значения. Поскольку конечные точки струны закреплены, здесь обязательно возникают узлы. В отличие от обычной «бегущей» волны, стоячая волна не перемещается в пространстве и не переносит энергии, которая лишь передается от одних точек струны к другим. Нетрудно видеть (рис. 6), что на струне с закрепленными концами длина стоячей волны может быть не любой, а только такой, чтобы на всей струне укладывалось целое число полуволн: одна (рис. 6, а), две (рис. 6,б), три (рис. 6, в) и т. д.
В рассматриваемой одномерной модели атома волна де Бройля тоже должна быть стоячей: это следует из того, что выйти за границы атома электрон не может и, следовательно, на границах атома волновая функция  (т. е. амплитуда волны) должна обращаться в нуль. Поэтому рис. 6 может рассматриваться как модель одномерного атома со стоячими волнами де Бройля, которые могут в этом атоме образоваться.
(т. е. амплитуда волны) должна обращаться в нуль. Поэтому рис. 6 может рассматриваться как модель одномерного атома со стоячими волнами де Бройля, которые могут в этом атоме образоваться.
Если длина одномерного атома равна l, то для случаев а, б и в на рис. 6 длина волны де Бройля будет выражаться следующим образом:

Следовательно, стоячая волна может образоваться только при условии

где  , т. е. целое число.
, т. е. целое число.

Рис. 6. Стоячие волны на струне.
С другой стороны, согласно уравнению де Бройля

Приравнивая правые части двух последних уравнений, получим для скорости электрона  выражение:
выражение:

Теперь, зная скорость электрона  , можно найти его кинетическую энергию Е:
, можно найти его кинетическую энергию Е:

Поскольку n — целое число, то последнее выражение показывает, что энергия электрона в одномерном атоме не может иметь произвольные значения: при n=1 она равна величине дроби  , при n=2 она в 4 раза больше, при n=3 — в 9 раз больше и т. д. Таким образом, в случае одномерного атома волновые свойства электрона, выражаемые уравнением де Бройля, действительно имеют следствием квантованность энергетических состояний электрона. При этом допустимые уровни энергии электрона определяются значением целого числа n, получившего название квантового числа.
, при n=2 она в 4 раза больше, при n=3 — в 9 раз больше и т. д. Таким образом, в случае одномерного атома волновые свойства электрона, выражаемые уравнением де Бройля, действительно имеют следствием квантованность энергетических состояний электрона. При этом допустимые уровни энергии электрона определяются значением целого числа n, получившего название квантового числа.
Разумеется, найденное выражение для энергии электрона относится к упрощенной модели атома. Но и для реального атома решение уравнения Шредингера также приводит к выводу о квантованности энергетических состояний электрона в атоме.
Модель одномерного атома позволяет понять, почему электрон, находящийся в атоме в стационарном состоянии, не излучает электромагнитной энергии (второй постулат теории Бора). Согласно модели Бора-Резерфорда, электрон в атоме совершал непрерывное движение с ускорением, т. е. все время менял свое состояние; в соответствии с требованиями электродинамики, он должен при этом излучать энергию. В одномерной модели атома стационарное состояние характеризуется образованием стоячей волны де Бройля; пока длина этой волны сохраняется постоянной, остается неизменным и состояние электрона, так что никакого излучения происходить не должно.
Становится ясным и вопрос о состоянии электрона при переходе из одного стационарного состояния в другое (в терминологии Бора — с одной стационарной орбиты на другую). Если, например, электрон из состояния, отвечающего рис. 6, а, переходит в состояние, соответствующее рис. 6,б, то во время этого перехода длина волны де Бройля будет иметь переменное значение, не отвечающее условию образования стоячей волны. Именно поэтому состояние электрона в этот промежуток времени будет неустойчивым; оно будет меняться до тех пор, пока длина волны де Бройля не будет вновь соответствовать условию образования стоячей волны, т. е. пока электрон не окажется в новом стационарном состоянии.
В упрощенной одномерной модели атома положение электрона относительно ядра определяется одной координатой, а его состояние— значением одного квантового числа. В двумерной (плоской) модели атома положение электрона определяется двумя координатами; в соответствии с этим, его состояние характеризуется значениями двух квантовых чисел. Аналогично в трехмерной (объемной) модели атома состояние электрона определяется значениями трех квантовых чисел. Наконец, изучение свойств электронов, входящих в состав реальных атомов, показало, что электрон обладает еще одной квантованной физической характеристикой (так называемый спин, см. § 30), не связанной с пространственным положением электрона. Таким образом, для полного описания состояния электрона в реальном атоме необходимо указать значения четырех квантовых чисел.
28. Главное квантовое число. Итак, в одномерной модели атома энергия электрона может принимать только определенные значения, иначе говоря — она квантована. Энергия электрона в реальном атоме также величина квантованная. Возможные энергетические состояния электрона в атоме определяются величиной главного квантового числа n, которое может принимать положительные целочисленные значения: 1, 2,... и т. д. Наименьшей энергией электрон обладает при n=1 с увеличением n энергия электрона возрастает. Поэтому состояние электрона, характеризующееся определенным значением главного квантового числа, принято называть энергетическим уровнем электрона в атоме: при n=1 электрон находится на первом энергетическом уровне, при n=2 — на втором и т. д.
Главное квантовое число определяет и размеры электронного облака. Для того чтобы увеличить размеры электронного облака, нужно часть его удалить на большее расстояние от ядра. Этому препятствуют силы электростатического притяжения электрона к ядру, преодоление которых требует затраты энергии. Поэтому большим размерам электронного облака соответствует более высокая энергия электрона в атоме и, следовательно, большее значение главного квантового числа n. Электроны же, характеризующиеся одним и тем же значением главного квантового числа, образуют в атоме электронные облака приблизительно одинаковых размеров; поэтому можно говорить о существовании в атоме электронных слоев или электронных оболочек, отвечающих определенным значениям главного квантового числа.
Для энергетических уровней электрона в атоме (т. е. для электронных слоев, или оболочек), соответствующих различным значениям n, приняты следующие буквенные обозначения:

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Глава I. АТОМНО-МОЛЕКУЛЯРНОЕ УЧЕНИЕ
- 4. Закон сохранения массы.
- 5. Основное содержание атомно-молекулярного учения.
- 6. Простое вещество и химический элемент.
- 7. Закон постоянства состава.
- 8. Закон объемных отношений.
- 9. Атомные и молекулярные массы. Моль.
- 10. Определение молекулярных масс веществ, находящихся в газообразном состоянии.
- 11. Парциальное давление газа.
- 12. Эквивалент. Закон эквивалентов.
- 13. Определение атомных масс. Валентность.
- 14. Химическая символика.
- 15. Важнейшие классы и номенклатура неорганических веществ.
- 16. Химические расчеты.
- Глава II ПЕРИОДИЧЕСКИЙ ЗАКОН Д. И. МЕНДЕЛЕЕВА
- 17. Периодический закон Д. И. Менделеева.
- 18. Периодическая система элементов.
- 19. Значение периодической системы.
- Глава III СТРОЕНИЕ АТОМА. РАЗВИТИЕ ПЕРИОДИЧЕСКОГО ЗАКОНА
- 20. Радиоктивность.
- 21. Ядерная модель атома.
- 22. Атомные спектры.
- 23. Квантовая теория света.
- 24. Строение электронной оболочки атома по Бору.
- 25. Исходные представления квантовой механики.
- 26. Волновая функция.
- 27. Энергетическое состояние электрона в атоме.
- 29. Орбитальное квантовое число. Формы электронных облаков.
- 30. Магнитное и спиновое квантовые числа.
- 31. Многоэлектронные атомы.
- 32. Принцип Паули. Электронная структура атомов и периодическая система элементов.
- 33. Размеры атомов и ионов.
- 34. Энергия ионизации и сродство к электрону.
- 35. Строение атомных ядер. Изотопы.
- 36. Радиоактивные элементы и их распад.
- 37. Искусственная радиоктивность. Ядерные реакции.
- Глава IV. ХИМИЧЕСКАЯ СВЯЗЬ И СТРОЕНИЕ МОЛЕКУЛ
- 38. Теория химического строения.
- 39. Ковалентная связь. Метод валентных связей.
- 40. Неполярная и полярная ковалентная связь.
- 41. Способы образования ковалентной связи.
- 42. Направленность ковалентной связи.
- 43. Гибридизация атомных электронных орбиталей.
- 44. Многоцентровые связи.
- 45. Метод молекулярных орбиталей.
- 46. Ионная связь.
- 47. Водородная связь.
- Глава V. СТРОЕНИЕ ТВЕРДОГО ТЕЛА И ЖИДКОСТИ
- 48. Межмолекулярное взаимодействие.
- 49. Кристаллическое состояние вещества.
- 50. Внутреннее строение кристаллов.
- 51. Реальные кристаллы.
- 52. Аморфное состояние вещества.
- 53. Жидкости.
- Глава VI. ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ ПРОТЕКАНИЯ ХИМИЧЕСКИХ РЕАКЦИЙ
- 54. Превращения энергии при химических реакциях.
- 55. Термохимия.
- 56. Термохимические расчеты.
- 57. Скорость химической реакции.
- 59. Зависимость скорости реакции от температуры и от природы реагирующих веществ.
- 60. Катализ.
- 61. Скорость реакции в гетерогенных системах.
- 62. Цепные реакции.
- 63. Необратимые и обратимые реакции. Химическое равновесие.
- 64. Смещение химического равновесия. Принцип Ле Шателье.
- 65. Факторы, определяющие направление протекания химических реакций.
- 66. Термодинамические величины. Внутренняя энергия и энтальпия.
- 67. Термодинамические величины. Энтропия и энергия Гиббса.
- 68. Стандартные термодинамические величины. Химико-термодинамические расчеты.
- Глава VII. ВОДА, РАСТВОРЫ
- 69. Вода в природе.
- 70. Физические свойства воды.
- 71. Диаграмма состояния воды.
- 72. Химические свойства воды.
- 73. Характеристика растворов. Процесс растворения.
- 74. Способы выражения состава растворов.
- 75. Гидраты и кристаллогидраты.
- 76. Растворимость.
- 77. Пересыщенные растворы.
- 78. Осмос.
- 79. Давление пара растворов.
- 80. Замерзание и кипение растворов.
- Глава VIII. РАСТВОРЫ ЭЛЕКТРОЛИТОВ
- 81. Особенности растворов солей, кислот и оснований.
- 82. Теория электролитической диссоциации.
- 83. Процесс диссоциации.
- 84. Степень диссоциации. Сила электролитов.
- 85. Константа диссоциации.
- 86. Сильные электролиты.
- 87. Свойства кислот, оснований и солей с точки зрения теории электролитической диссоциации.
- 88. Ионно-молекулярные уравнения.
- 89. Произведение растворимости.
- 90. Диссоциация воды. Водородный показатель.
- 91. Смещение ионных равновесий.
- 92. Гидролиз солей.
- Глава IX. ОКИСЛИТЕЛЬНО-ВОССТАНОВИТЕЛЬНЫЕ РЕАКЦИИ. ОСНОВЫ ЭЛЕКТРОХИМИИ
- 93. Окисленность элементов.
- 94. Окислительно-восстановительные реакции.
- 95. Составление уравнений окислительно-восстановительных реакций.
- 96. Важнейшие окислители и восстановители.
- 97. Окислительно-восстановительная двойственность.
- 98. Химические источники электрической энергии.
- 99. Электродные потенциалы.
- 100. Ряд напряжений металлов.
- 101. Электролиз.
- 102. Законы электролиза.
- 103. Электролиз в промышленности.
- 104. Электрохимическая поляризация.
- Глава X. ДИСПЕРСНЫЕ СИСТЕМЫ. КОЛЛОИДЫ
- 105. Дисперсное состояние вещества.
- 106. Состояние вещества на границе раздела фаз.
- 107. Коллоиды и коллоидные растворы.
- 108. Дисперсионный анализ.
- 109. Сорбция и сорбционные процессы.
- 110. Ионообменная адсорбция.
- 111. Хроматография.
- 112. Электрокинетические явления.
- 113. Устойчивость и коагуляция дисперсных систем.
- 114. Структурообразование в дисперсных системах.
- Глава XI. ВОДОРОД
- 115. Водород в природе. Получение водорода.
- 116. Свойства и применение водорода.
- 117. Пероксид водорода
- Глава XII. ГАЛОГЕНЫ
- 118. Галогены в природе. Физические свойства галогенов.
- 119. Химические свойства галогенов.
- 120. Получение и применение галогенов.
- 121. Соединения галогенов с водородом.
- 122. Кислородсодержащие соединения галогенов.
- Глава XIII. ГЛАВНАЯ ПОДГРУППА ШЕСТОЙ ГРУППЫ
- 123. Кислород в природе. Воздух.
- 124. Получение и свойства кислорода.
- 125. Озон.
- 126. Сера в природе. Получение серы.
- 127. Свойства и применение серы.
- 128. Сероводород. Сульфиды.
- 129. Диоксид серы. Сернистая кислота.
- 130. Триоксид серы. Серная кислота.
- 131. Получение и применение серной кислоты.
- 132. Пероксодвусерная кислота.
- 133. Тиосерная кислота.
- 134. Соединения серы с галогенами.
- 135. Селен (Selenium). Теллур (Tellurium).
- Глава XIV. ГЛАВНАЯ ПОДГРУППА ПЯТОЙ ГРУППЫ
- 136. Азот в природе. Получение и свойства азота.
- 137. Аммиак. Соли аммония.
- 138. Фиксация атмосферного азота. Получение аммиака.
- 139. Гидразин. Гидроксиламин. Азидоводород.
- 140. Оксиды азота.
- 141. Азотистая кислота.
- 142. Азотная кислота.
- 143. Промышленное получение азотной кислоты.
- 144. Круговорот азота в природе.
- 145. Фосфор в природе. Получение и свойства фосфора.
- 146. Соединения фосфора с водородом и галогенами.
- 147. Оксиды и кислоты фосфора.
- 148. Минеральные удобрения.
- 149. Мышьяк (Arsenicum).
- 150. Сурьма (Stibium).
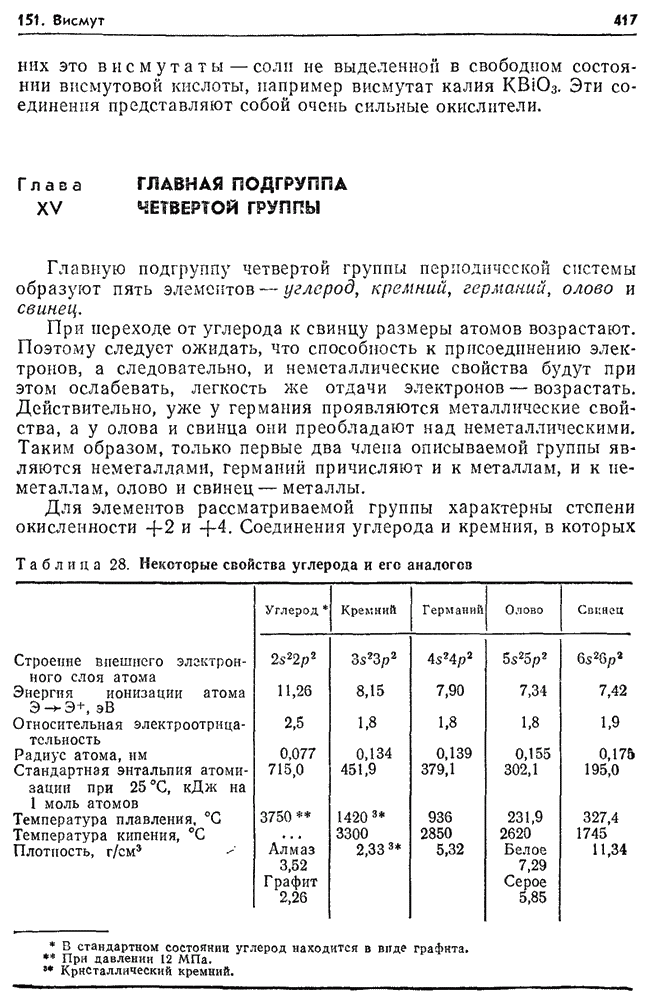
- 151. Висмут (Bismuthum).
- Глава XV. ГЛАВНАЯ ПОДГРУППА ЧЕТВЕРТОЙ ГРУППЫ
- 152. Углерод в природе.
- 153. Аллотропия углерода.
- 154. Химические свойства углерода. Карбиды.
- 155. Диоксид углерода. Угольная кислота.
- 156. Оксид углерода (II).
- 157. Соединения углерода с серой и азотом.
- 158. Топливо и его виды.
- 159. Газообразное топливо.
- 160. Общая характеристика органических соединений.
- 161. Отличительные особенности органических соединений.
- 162. Теория химического строения органических соединений.
- 163. Классификация органических соединений.
- 164. Предельные (насыщенные) углеводороды.
- 165. Непредельные (ненасыщенные) углеводороды.
- 166. Предельные циклические углеводороды.
- 167. Ароматические углеводороды.
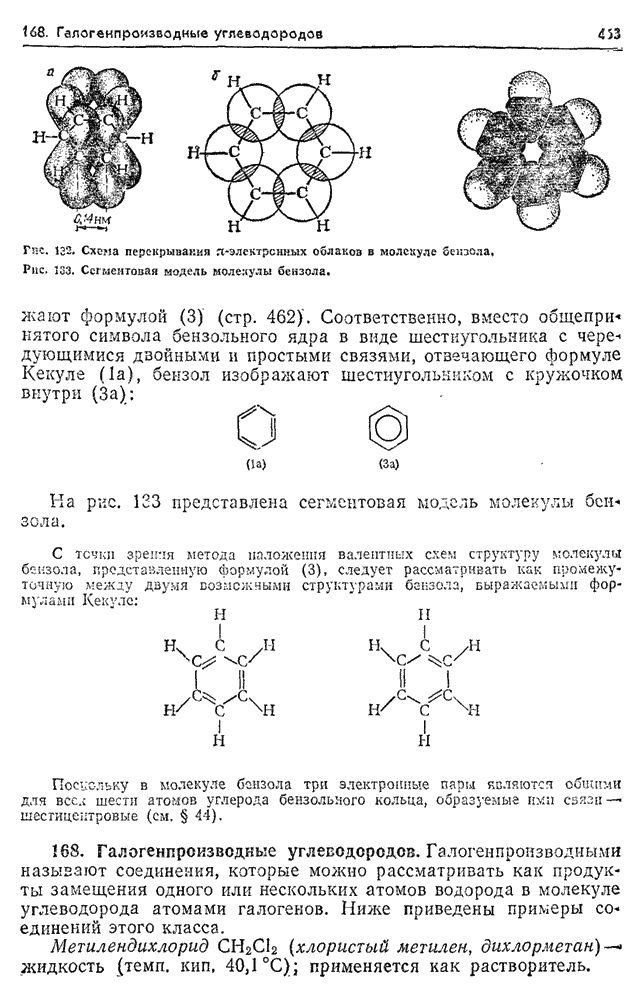
- 168. Галогенпроизводные углеводородов.
- 169. Спирты и фенолы.
- 170. Простые эфиры.
- 171. Альдегиды и кетоны.
- 172. Карбоновые кислоты.
- 173. Сложные эфиры карбоновых кислот. Жиры.
- 174. Углеводы.
- 175. Амины.
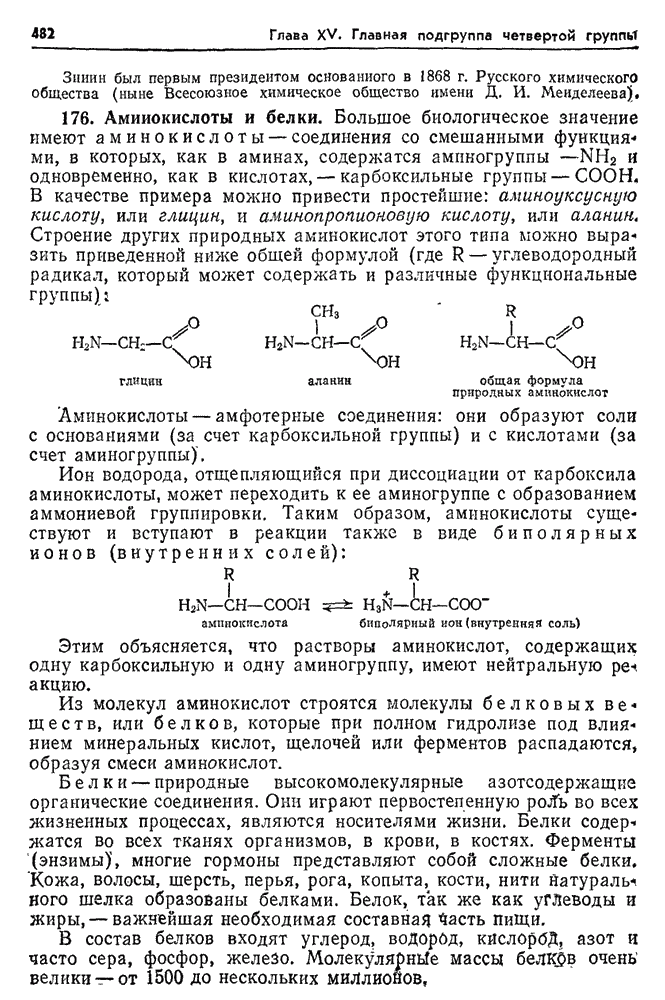
- 176. Аминокислоты и белки.
- 177. Природные и синтетические высокомолекулярные соединения (полимеры).
- 178. Кремний в природе. Получение и свойства кремния.
- 179. Соединения кремния с водородом и галогенами.
- 180. Диоксид кремния.
- 181. Кремниевые кислоты и их соли.
- 182. Стекло.
- 183. Керамика.
- 184. Цемент.
- 185. Кремнийорганические соединения.
- 186. Германий (Germanium).
- 187. Олово (Stannuin).
- 188. Свинец (Plumbum).
- 189. Свинцовый аккумулятор.
- Глава XVI. ОБЩИЕ СВОЙСТВА МЕТАЛЛОВ. СПЛАВЫ
- 190. Физические и химические свойства металлов. Электронное строение металлов, изоляторов и полупроводников.
- 191. Кристаллическое строение металлов.
- 192. Добывание металлов из руд.
- 193. Получение металлов высокой чистоты.
- 194. Сплавы.
- 195. Диаграммы состояния металлических систем.
- 196. Коррозия металлов.
- Глава XVII. ПЕРВАЯ ГРУППА ПЕРИОДИЧЕСКОЙ СИСТЕМЫ
- 197. Щелочные металлы в природе.
- 198. Натрий (Natrium).
- 199. Калий (Kalium).
- ПОДГРУППА МЕДИ
- 200. Медь. (Cuprum).
- 201. Серебро (Argentum).
- 202. Золото (Aurum).
- Глава XVIII. КОМПЛЕКСНЫЕ СОЕДИНЕНИЯ
- 203. Основные положения координационной теории.
- 204. Основные типы и номенклатура комплексных соединений.
- 205. Пространственное строение и изомерия комплексных соединений.
- 206. Природа химической связи в комплексных соединениях.
- 207. Диссоциация комплексных соединений в растворах.
- 208. Влияние координации на свойства лигандов и центрального атома.
- Глава XIX. ВТОРАЯ ГРУППА ПЕРИОДИЧЕСКОЙ СИСТЕМЫ
- 209. Бериллий (Beryllium).
- 210. Магний (Magnesium).
- 211. Кальций (Calcium).
- 212. Жесткость природных вод и ее устранение.
- 213. Стронций (Strontium). Барий (Barium).
- 214. Цинк (Zincum).
- 215. Кадмий (Cadmium).
- 216. Ртуть (Hydrargyrum).
- Глава XX. ТРЕТЬЯ ГРУППА ПЕРИОДИЧЕСКОЙ СИСТЕМЫ
- 217. Бор (Borum).
- 218. Алюминий (Aluminium).
- 219. Галлий (Gallium). Иидий (Indium). Таллий (Thallium).
- ПОБОЧНАЯ ПОДГРУППА ТРЕТЬЕЙ ГРУППЫ. ЛАНТАНОИДЫ. АКТИНОИДЫ
- 220. Подгруппа скандия.
- 221. Лантаноиды.
- 222. Актиноиды.
- Глава XXI. ПОБОЧНЫЕ ПОДГРУППЫ ЧЕТВЕРТОЙ, ПЯТОЙ, ШЕСТОЙ И СЕДЬМОЙ ГРУПП
- ПОДГРУППА ТИТАНА
- 224. Титан (Titanium).
- 225. Цирконий (Zirconium). Гафний (Hafnium).
- ПОДГРУППА ВАНАДИЯ
- 226. Ванадий (Vanadium).
- 227. Ниобий (Niobium). Тантал (Tantalum).
- ПОДГРУППА ХРОМА
- 228. Хром (Chromium).
- 229. Молибден (Mollbdenium).
- 230. Вольфрам (Wolfram).
- ПОДГРУППА МАРГАНЦА
- 231. Марганец (Manganum).
- 232. Рений (Rhenium).
- Глава XXII. ВОСЬМАЯ ГРУППА ПЕРИОДИЧЕСКОЙ СИСТЕМЫ
- 233. Общая характеристика благородных газов.
- 234. Гелий (Helium).
- 235. Неон. Аргон.
- ПОБОЧНАЯ ПОДГРУППА ВОСЬМОЙ ГРУППЫ
- 236. Железо (Ferrum).
- 237. Значение железа и его сплавов в технике. Развитие металлургии в СССР.
- 238. Физические свойства железа. Диаграмма состояния системы железо — углерод.
- 239. Производство чугуна и стали.
- 240. Термическая обработка стали.
- 241. Сплавы железа.
- 242. Химические свойства железа. Соединения железа.
- 243. Кобальт (Cobaltum).
- 244. Никель (Niccolum).
- 245. Общая характеристика платиновых металлов.
- 246. Платина (Platinum).
- 247. Палладий (Palladium). Иридий (Iridium).
- ПРИЛОЖЕНИЕ
- Некоторые единицы СИ
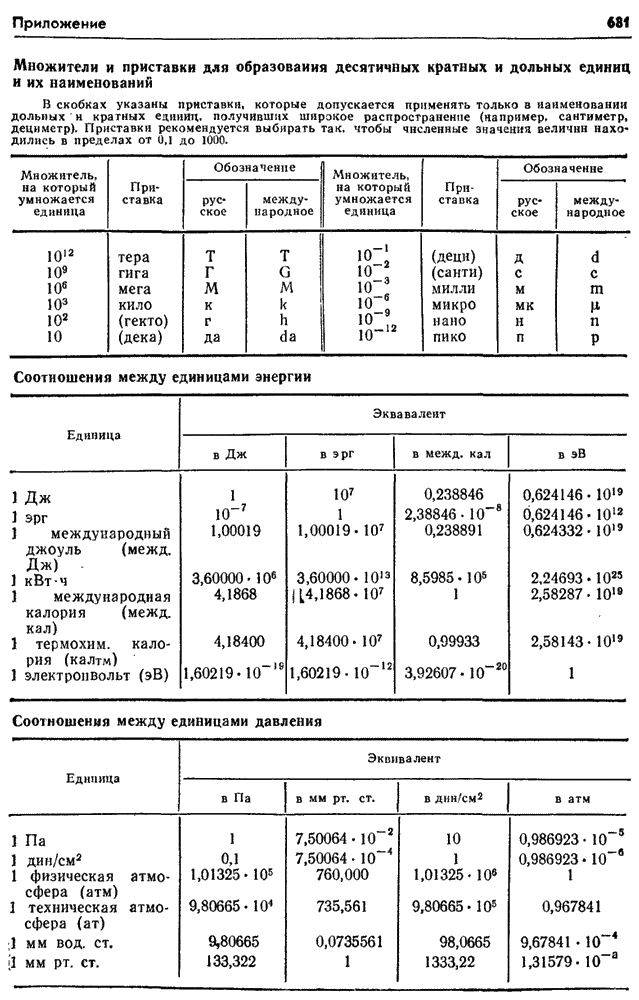
- Множители и приставки для образования десятичных кратных и дольных единиц и их наименований
- Соотношения между некоторыми внесистемными единицами и единицами СИ
- Литература для углубленного изучения общей и неорганической химии