| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
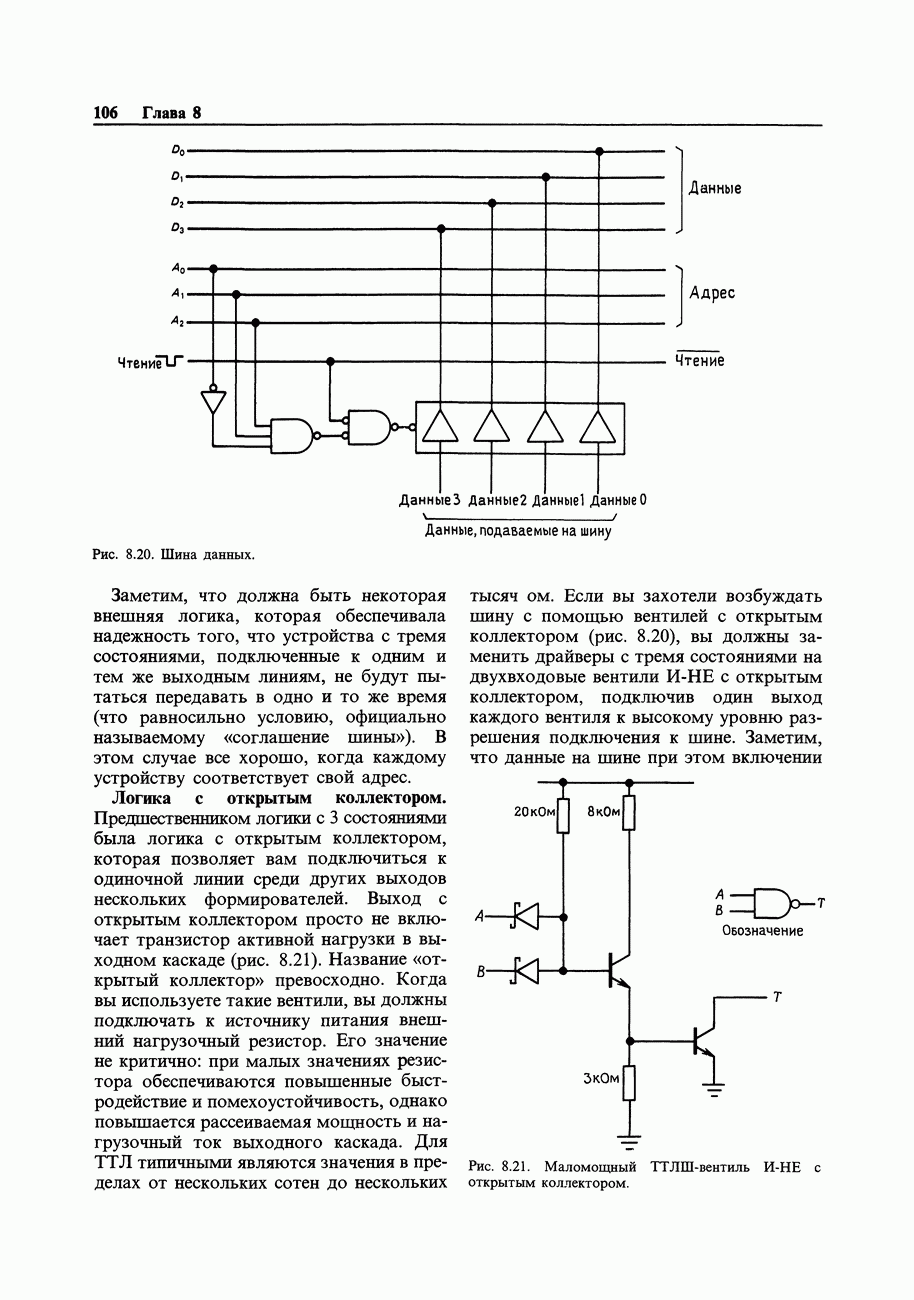
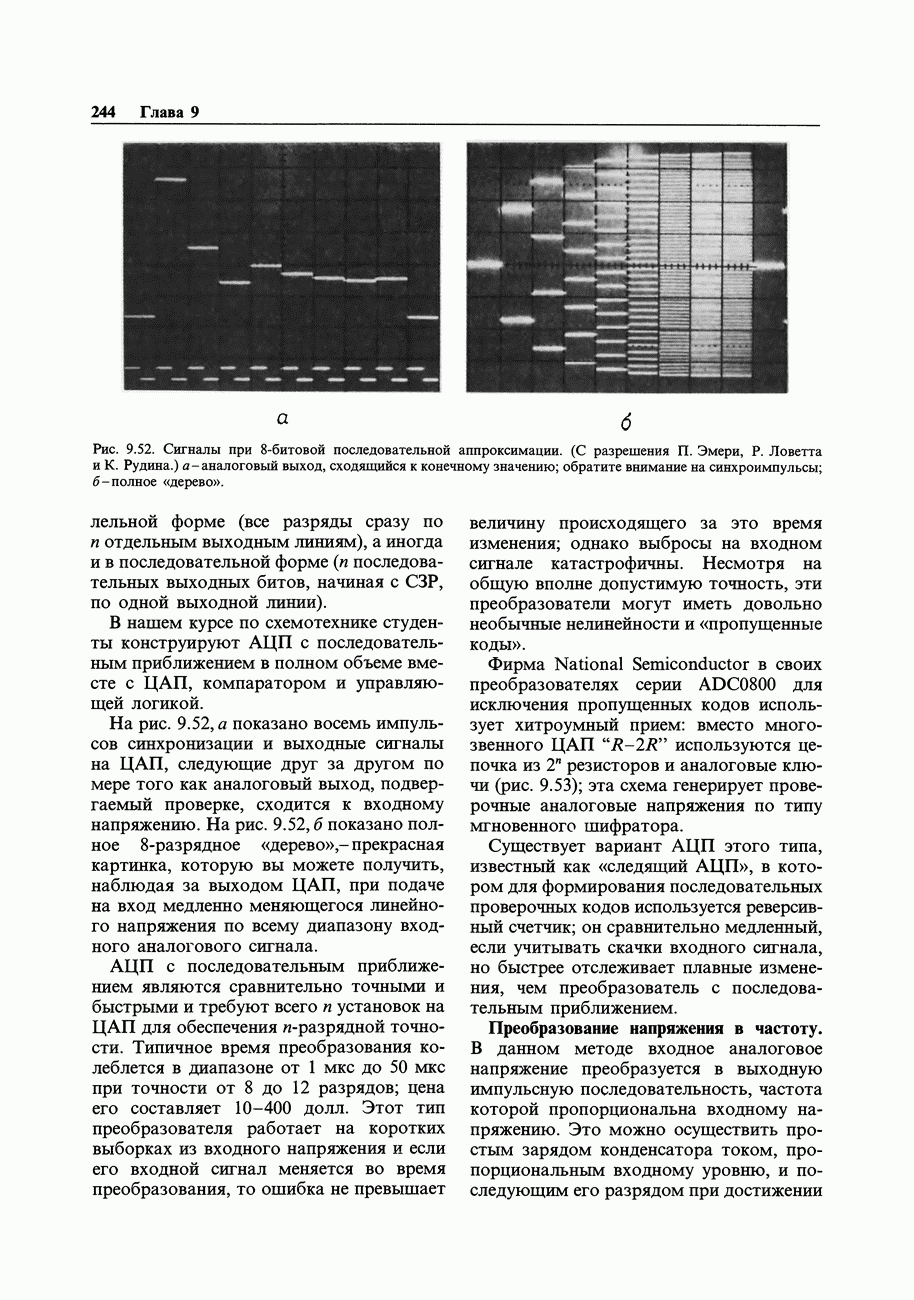
9.35. Энергетический спектр последовательности, сформированной при помощи регистра сдвига
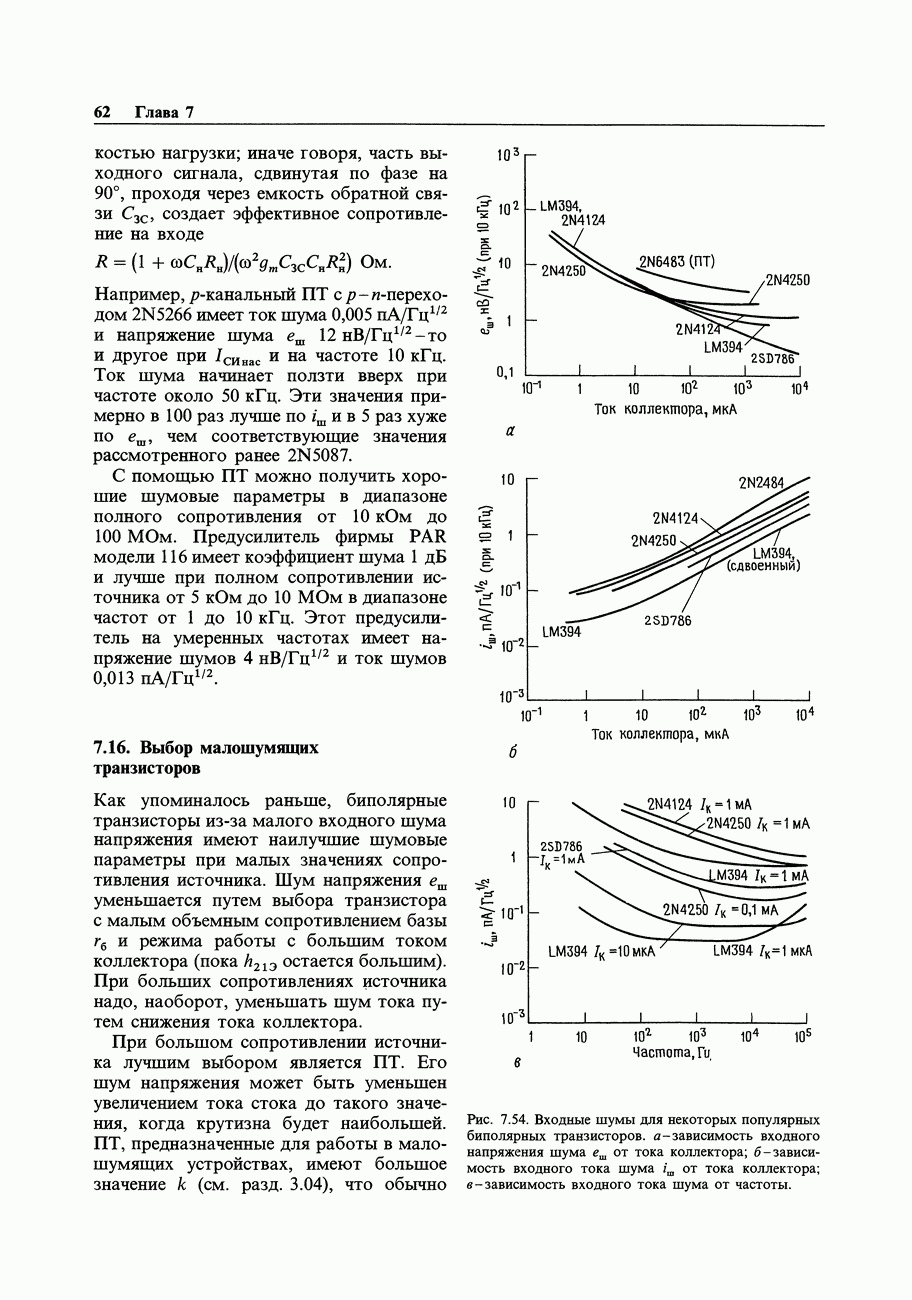
Спектр выходного сигнала, генерируемого регистром сдвига максимальной длины, составляют колебания шума от частоты повторения всей последовательности  до тактовой частоты и выше. До частоты 12% от тактовой спектр имеет плоскую часть с неравномерностью
до тактовой частоты и выше. До частоты 12% от тактовой спектр имеет плоскую часть с неравномерностью  дБ, затем наблюдается быстрое падение до уровня —0,3 дБ на частоте
дБ, затем наблюдается быстрое падение до уровня —0,3 дБ на частоте  . Таким образом, фильтр нижних частот с частотой среза в верхней области 5-10% от тактовой частоты будет преобразовывать выходной сигнал регистра сдвига в аналоговое напряжение шума с ограниченной полосой. Для этой цели достаточен даже простой RС-фильтр, хотя, если возникает необходимость в точной полосе шума, то желательно использовать активные фильтры с крутой характеристикой на частоте среза (см. гл. 5).
. Таким образом, фильтр нижних частот с частотой среза в верхней области 5-10% от тактовой частоты будет преобразовывать выходной сигнал регистра сдвига в аналоговое напряжение шума с ограниченной полосой. Для этой цели достаточен даже простой RС-фильтр, хотя, если возникает необходимость в точной полосе шума, то желательно использовать активные фильтры с крутой характеристикой на частоте среза (см. гл. 5).
Для того чтобы эти утверждения звучали более убедительно, обратимся к выходному сигналу регистра сдвига и его спектру. Обычно желательно исключить постоянную составляющую в цифровом сигнале, формируя выходной сигнал, в котором «1» соответствует напряжение  , а «0» — и В (рис. 9.84). Это можно легко сделать с помощью двухтактного транзисторного каскада, показанного на рис. 9.85. Можно также использовать МОП-транзисторы, схемы стабилизации напряжения с фиксирующими диодами, быстродействующий операционный усилитель с регулировкой тока постоянной составляющей в точке суммирования или КМОП-ключ
, а «0» — и В (рис. 9.84). Это можно легко сделать с помощью двухтактного транзисторного каскада, показанного на рис. 9.85. Можно также использовать МОП-транзисторы, схемы стабилизации напряжения с фиксирующими диодами, быстродействующий операционный усилитель с регулировкой тока постоянной составляющей в точке суммирования или КМОП-ключ  , работающий от
, работающий от  , с двумя входами, подключенными к источникам питания.
, с двумя входами, подключенными к источникам питания.

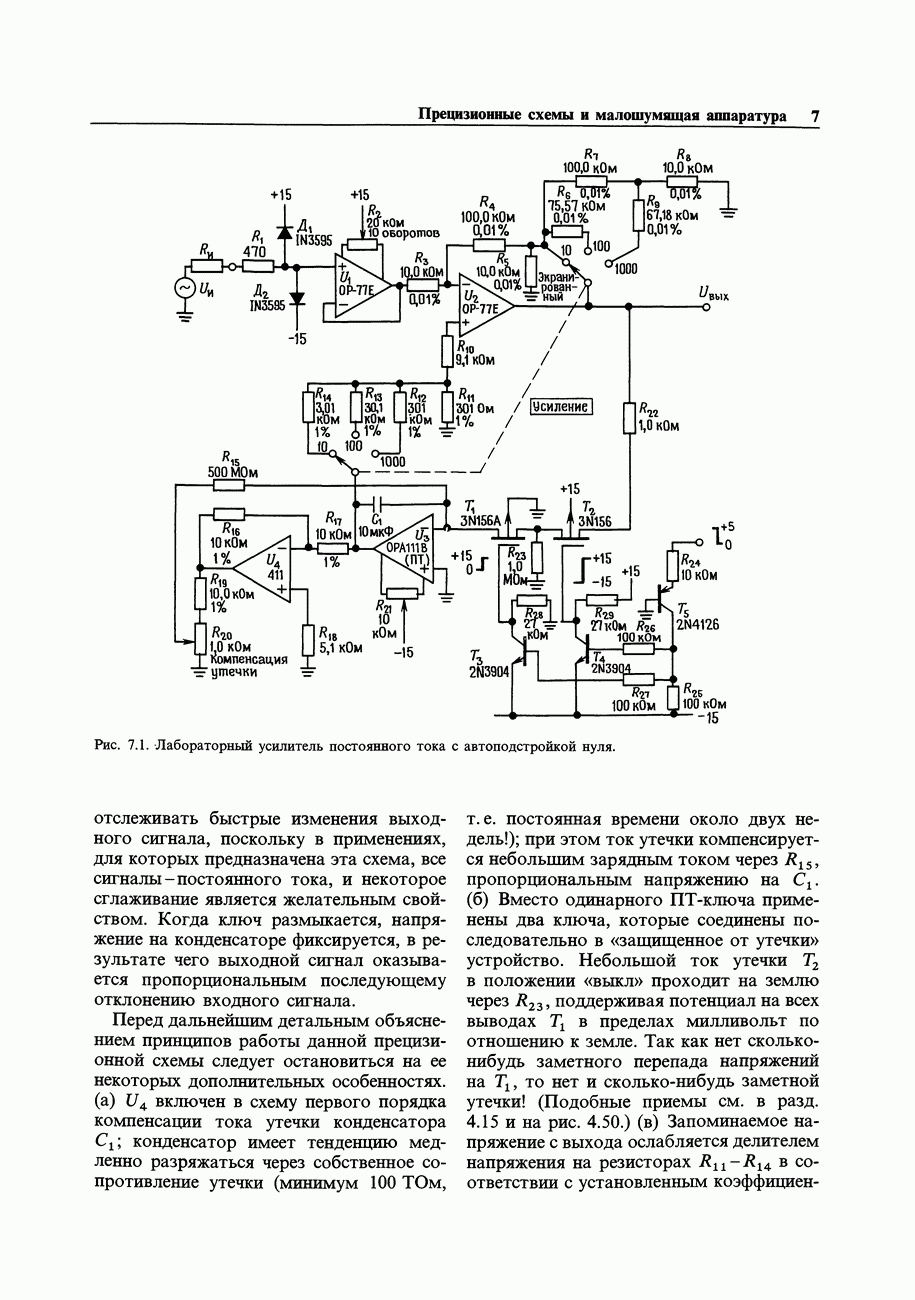
Рис. 9.85. Прецизионная биполярная выходная ступень с низким  .
.
Как мы отмечали выше, автокорреляционная функция последовательности символов на выходе содержит один пик. Если состояния на выходе представить числами  то цифровая автокорреляционная функция будет иметь вид, показанный на рис. 9.86; (цифровая автокорреляция - это сумма произведений соответствующих разрядов при сравнении последовательности двоичных символов с ее сдвинутой копией).
то цифровая автокорреляционная функция будет иметь вид, показанный на рис. 9.86; (цифровая автокорреляция - это сумма произведений соответствующих разрядов при сравнении последовательности двоичных символов с ее сдвинутой копией).

Рис. 9.86. Дискретная автокорреляционная функция для полного цикла максимальной последовательности.

Рис. 9.87. Непрерывная автокорреляционная функция для полного цикла максимальной последовательности.
Не путайте ее с непрерывной автокорреляционной функцией, которую рассмотрим несколько позже. Функция на этом графике определена только для сдвигов, соответствующих целому числу тактов. Для всех ненулевых сдвигов и сдвигов, не кратных общему периоду К, автокорреляционная функция постоянна и имеет значение — 1 (поскольку в последовательности есть дополнительная 1); по сравнению со значением функции при нулевом сдвиге (К) величина — 1 пренебрежимо мала. Если же неотфильтрованный выход регистра сдвига рассматривать как аналоговый сигнал (принимающий только два значения  и
и  , то нормализованная автокорреляционная функция будет, как показано на рис. 9.87, непрерывной. Другими словами, при сдвигах более чем на один такт вправо и влево корреляция между значениями сигнала полностью отсутствует.
, то нормализованная автокорреляционная функция будет, как показано на рис. 9.87, непрерывной. Другими словами, при сдвигах более чем на один такт вправо и влево корреляция между значениями сигнала полностью отсутствует.
Энергетический спектр неотфильтрованного сигнала на выходе регистра сдвига можно получить по автокорреляционной функции, используя стандартные математические средства.

Рис. 9.88. Энергетический спектр неотфильтрованного сигнала на выходе регистра сдвига.
В результате получаются равноудаленные серии пичков (дельта-функций), начинающихся с частоты повторения всей последовательности  и затем идущих через равные интервалы
и затем идущих через равные интервалы  . То, что спектр состоит из совокупности дискретных спектральных линий, отражает тот факт, что последовательность время от времени (периодически) повторяется. Пусть вас не удивляет странный вид спектра; он будет выглядеть непрерывным при любых изменениях и приложениях, которые занимают время, меньшее чем время цикла регистра. Огибающая спектра неотфильтрованного сигнала на выходе регистра показана на рис. 9.88. Она пропорциональна квадрату функции
. То, что спектр состоит из совокупности дискретных спектральных линий, отражает тот факт, что последовательность время от времени (периодически) повторяется. Пусть вас не удивляет странный вид спектра; он будет выглядеть непрерывным при любых изменениях и приложениях, которые занимают время, меньшее чем время цикла регистра. Огибающая спектра неотфильтрованного сигнала на выходе регистра показана на рис. 9.88. Она пропорциональна квадрату функции  . Обратите внимание на одно необычное свойство - на тактовой частоте и ее гармониках энергия шума равна нулю.
. Обратите внимание на одно необычное свойство - на тактовой частоте и ее гармониках энергия шума равна нулю.
Напряжение шума.
При генерации аналогового шума используется, разумеется, только часть низкочастотной области спектра. Оказывается, что удельную мощность шума на герц несложно выразить через половинную амплитуду а и тактовую частоту/такт. Мощность, выраженная через среднеквадратичное напряжение шума, будет иметь вид
Это относится к нижней части спектра, т. е. к той части, которая обычно используется (для того чтобы определить плотность мощности в любой части спектра, можно использовать огибающую).
Предположим, например, что регистр сдвига максимальной длины работает на частоте 1,0 МГц и организован таким образом, что выходное напряжение изменяется от  до —10,0 В. Выходной сигнал пропускается через
до —10,0 В. Выходной сигнал пропускается через  -фильтр нижних частот с затуханием 3 дБ на частоте
-фильтр нижних частот с затуханием 3 дБ на частоте  (рис. 9.89). Можно точно вычислить среднеквадратичное напряжение шума на выходе.
(рис. 9.89). Можно точно вычислить среднеквадратичное напряжение шума на выходе.

Рис. 9.89. Простой источник псевдослучайного шума.
Из предыдущего выражения мы знаем, что среднеквадратичное напряжение на выходе преобразователя уровней равно  . Из разд. 7.21 мы знаем также, что полоса шума НЧ-фильтра составляет
. Из разд. 7.21 мы знаем также, что полоса шума НЧ-фильтра составляет  или
или  . Поэтому выходное напряжение шума будет равно
. Поэтому выходное напряжение шума будет равно  , а его спектр будет соответствовать низкочастотному RC-фильтру.
, а его спектр будет соответствовать низкочастотному RC-фильтру.
| << Предыдущий параграф | Следующий параграф >> |
- ГЛАВА 7. ПРЕЦИЗИОННЫЕ СХЕМЫ И МАЛОШУМЯЩАЯ АППАРАТУРА
- 7.01. Соотношение точности и динамического диапазона
- 7.02. Бюджет погрешностей схемы
- 7.03. Пример схемы: прецизионный усилитель с автоматическим выбором нуля
- 7.04. «Бюджет погрешностей» при проектировании прецизионной схемы
- 7.05. Погрешности внешних цепей
- 7.06. Входные погрешности усилителя
- 7.07. Выходные погрешности усилителя
- 7.08. Усилители с автоподстройкой нуля (стабилизированные прерыванием)
- Кое-что еще о схемах с прерыванием
- ДИФФЕРЕНЦИАЛЬНЫЕ И ИЗМЕРИТЕЛЬНЫЕ УСИЛИТЕЛИ
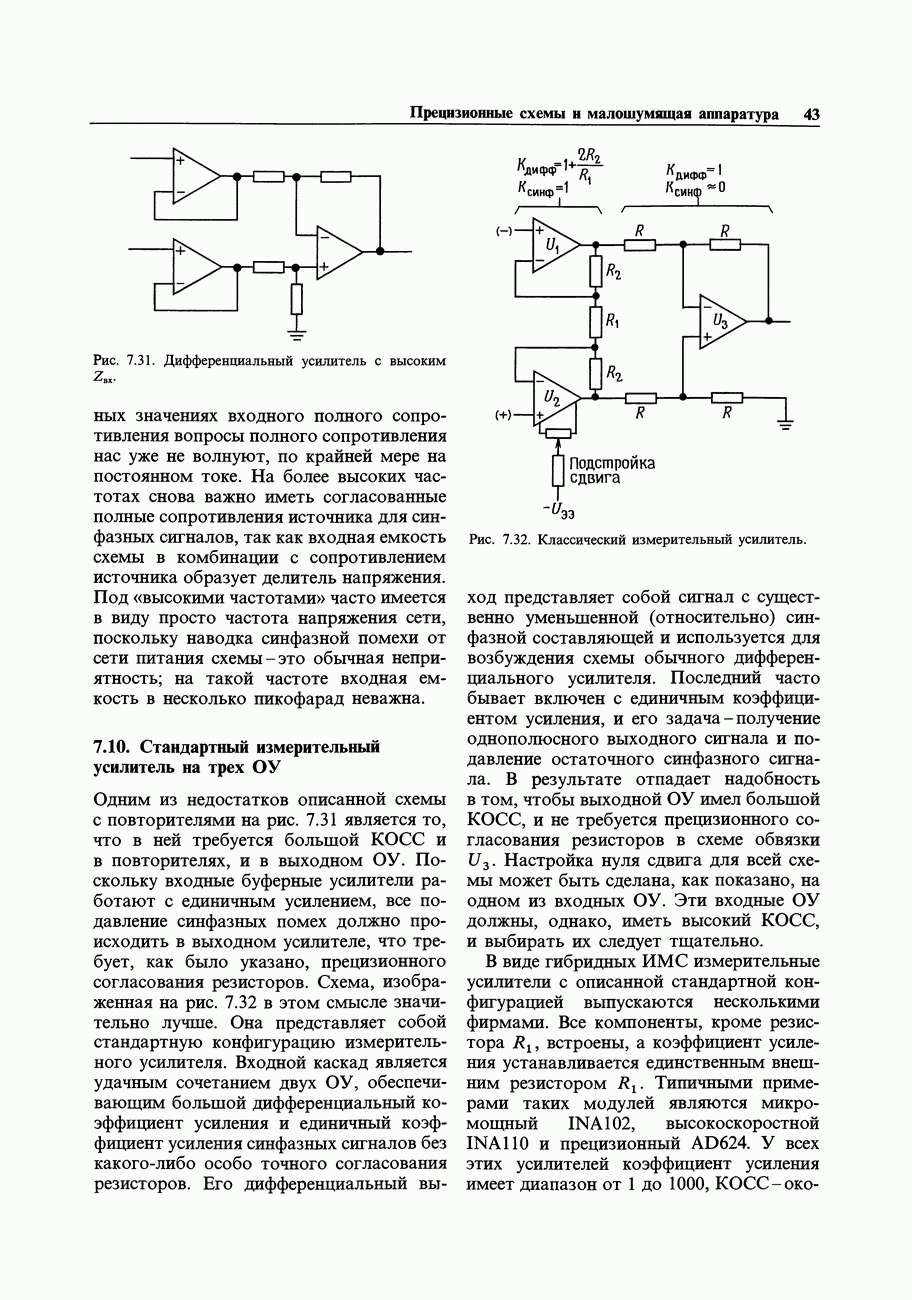
- 7.09. Простой разностный усилитель
- 7.10. Стандартный измерительный усилитель на трех ОУ
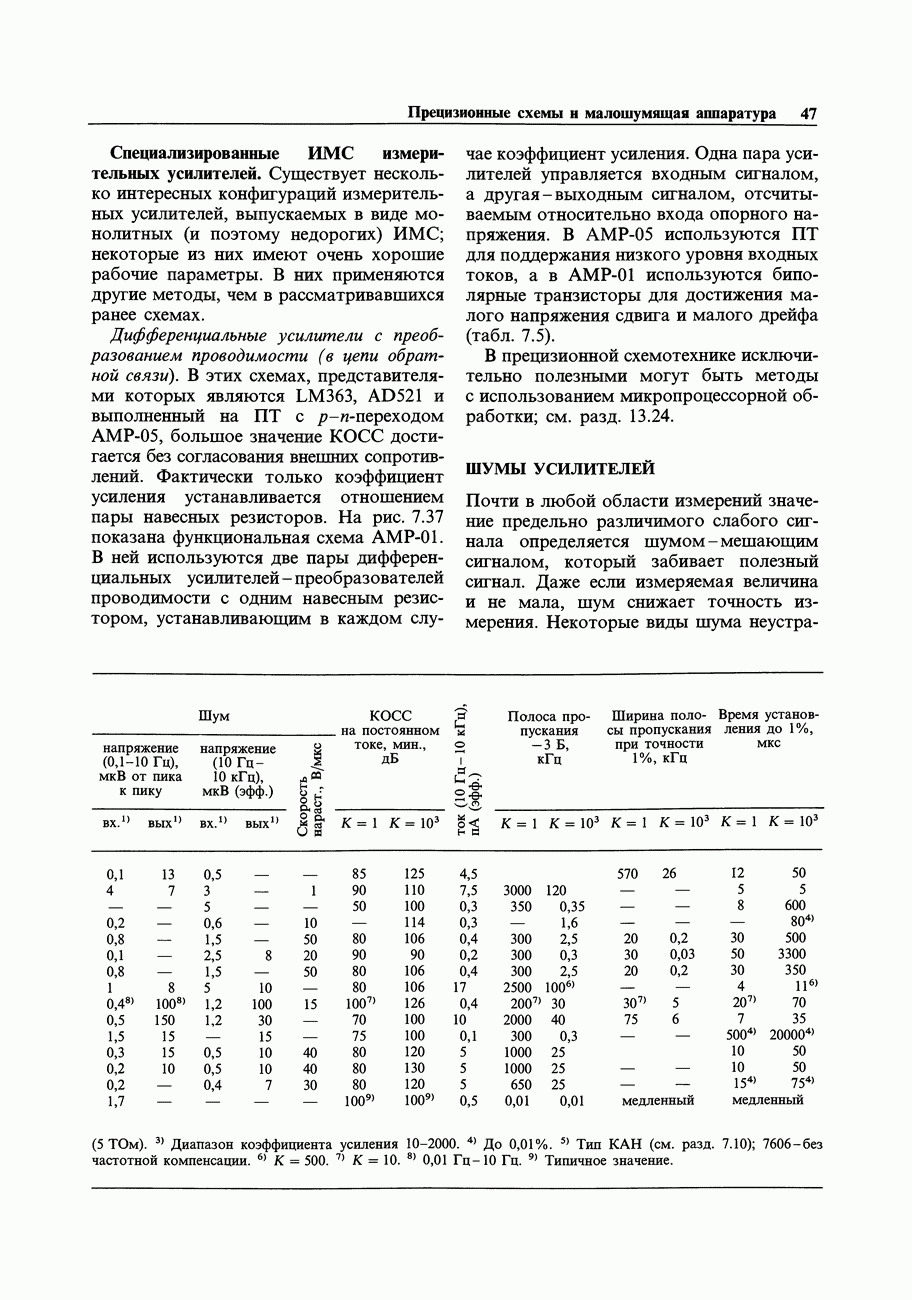
- ШУМЫ УСИЛИТЕЛЕЙ
- 7.11. Происхождение и виды шумов
- 7.12. Отношение сигнал/шум и коэффициент шума
- 7.13. Шум тока и напряжения транзисторного усилителя
- 7.14. Проектирование малошумящих схем на биполярных транзисторах
- 7.15. Шум ПТ
- 7.16. Выбор малошумящих транзисторов
- 7.17. Шум дифференциальных усилителей и усилителей с обратной связью
- ИЗМЕРЕНИЕ ШУМА И ИСТОЧНИКИ ШУМА
- 7.18. Измерение без источника шума
- 7.19. Измерение с источником шума
- 7.20. Генераторы шумов и сигналов
- 7.21. Ограничение полосы частот и измерение среднеквадратичного (эффективного) напряжения
- 7.22. Попурри на тему шумов
- ПОМЕХИ: ЭКРАНИРОВАНИЕ И ЗАЗЕМЛЕНИЕ
- 7.23. Помехи
- 7.24. Сигнальное заземление
- 7.25. Межприборное заземление
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 8. ЦИФРОВЫЕ СХЕМЫ
- 8.01. Цифровые и аналоговые сигналы
- 8.02. Логические состояния
- ЛОГИЧЕСКИЕ УРОВНИ
- 8.03. Числовые коды
- 8.04. Вентили и таблицы истинности
- 8.05. Схемы вентилей на дискретных элементах
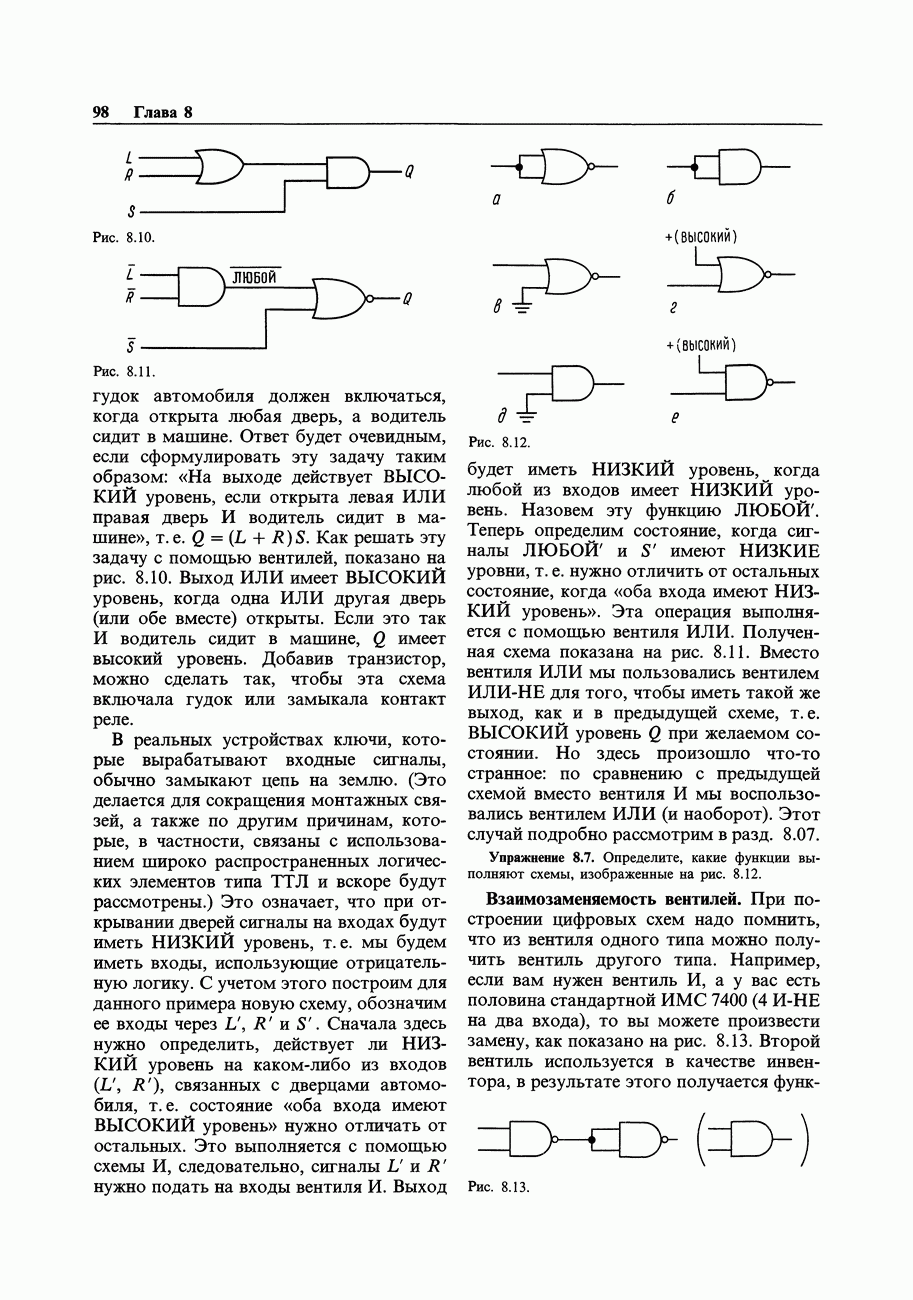
- 8.06. Пример схемы с вентилями
- 8.07. Логические обозначения при заданных уровнях
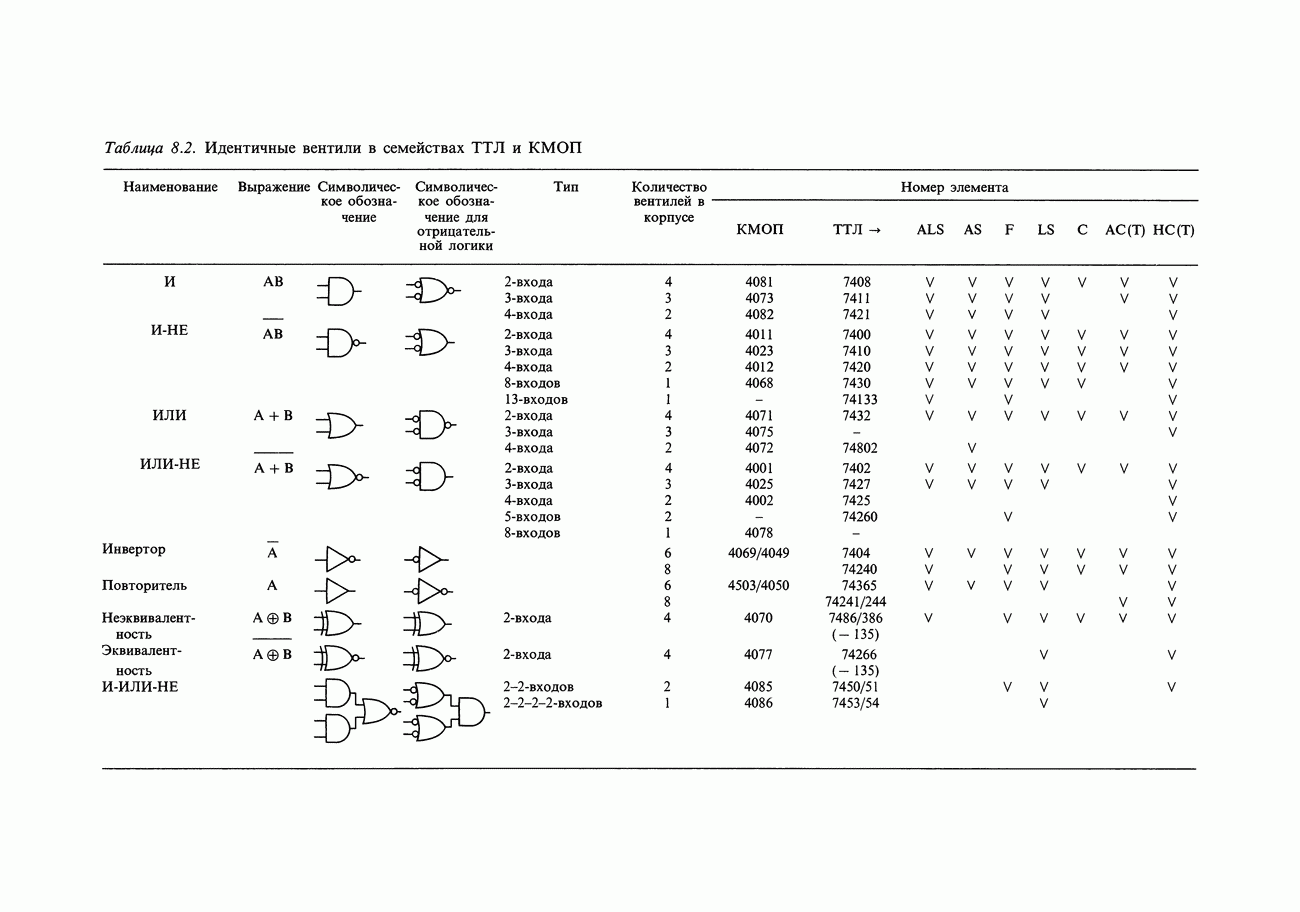
- 8.08. Каталог идентичных вентилей
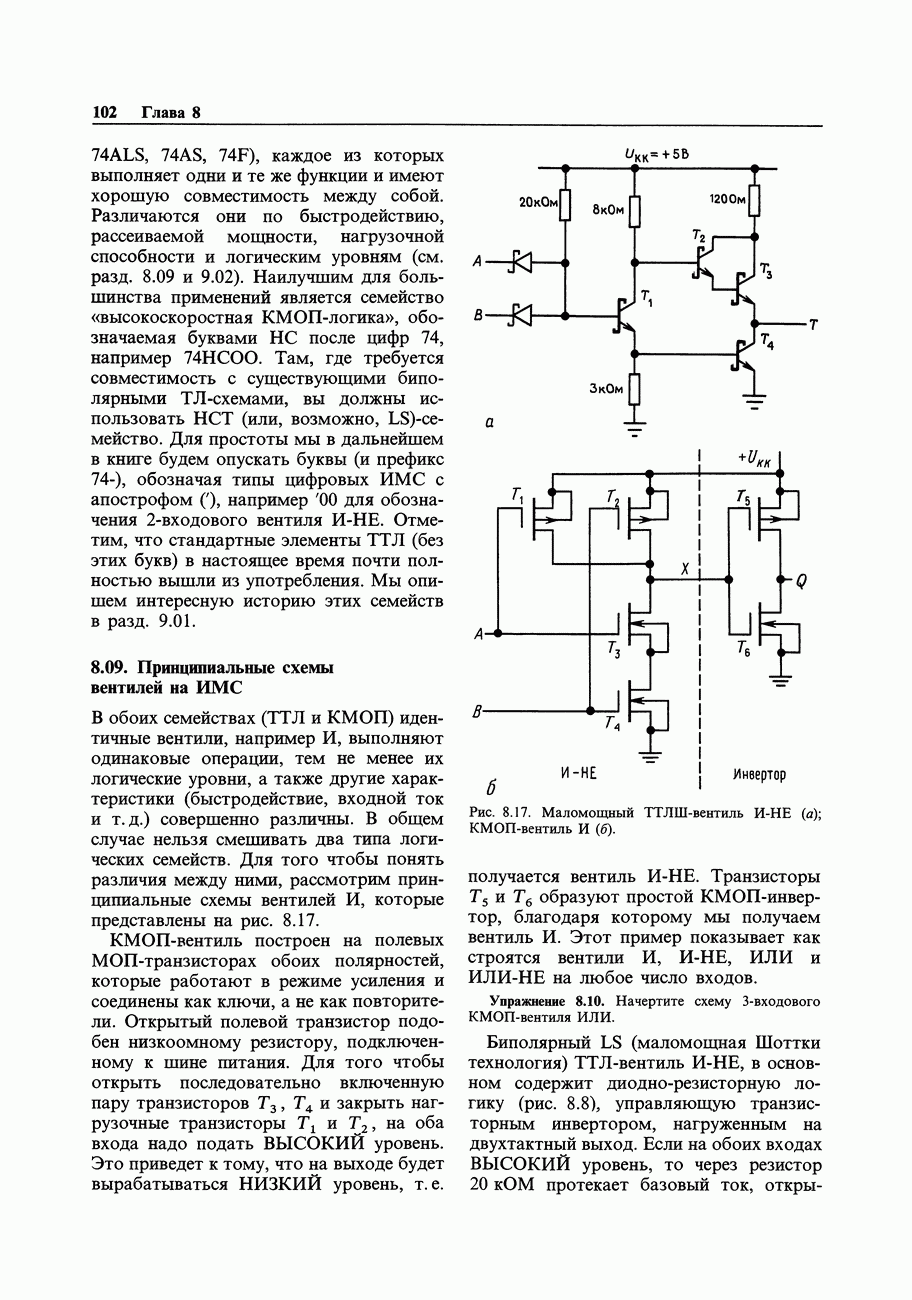
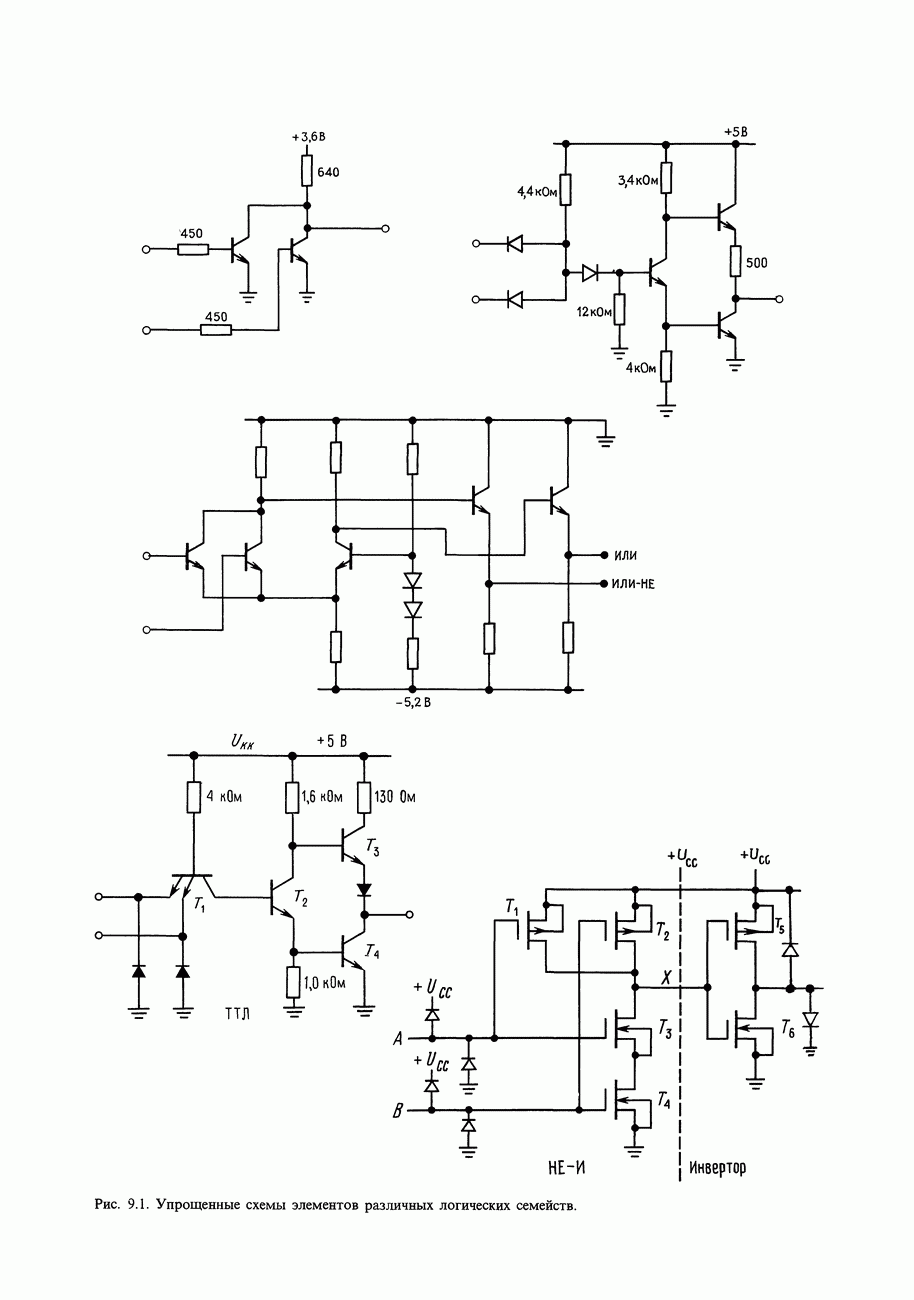
- 8.09. Принципиальные схемы вентилей на ИМС
- 8.10. Характеристики ТТЛ и КМОП
- 8.11. Элементы с тремя состояниями и с открытым коллектором
- КОМБИНАЦИОННАЯ ЛОГИКА
- 8.12. Логические тождества
- 8.13. Минимизация и карты Карно
- 8.14. Комбинационные функциональные схемы, реализованные на стандартных ИМС
- 8.15. Реализация произвольных таблиц истины
- ПОСЛЕДОВАТЕЛЬНОСТНАЯ ЛОГИКА
- 8.16. Устройства с памятью: триггеры
- 8.17. Тактируемые триггеры
- 8.18. Последовательностная логика-объединение памяти и вентилей
- 8.19. Синхронизатор
- МОНОСТАБИЛЬНЫЕ МУЛЬТИВИБРАТОРЫ
- 8.20. Характеристики одновибраторов
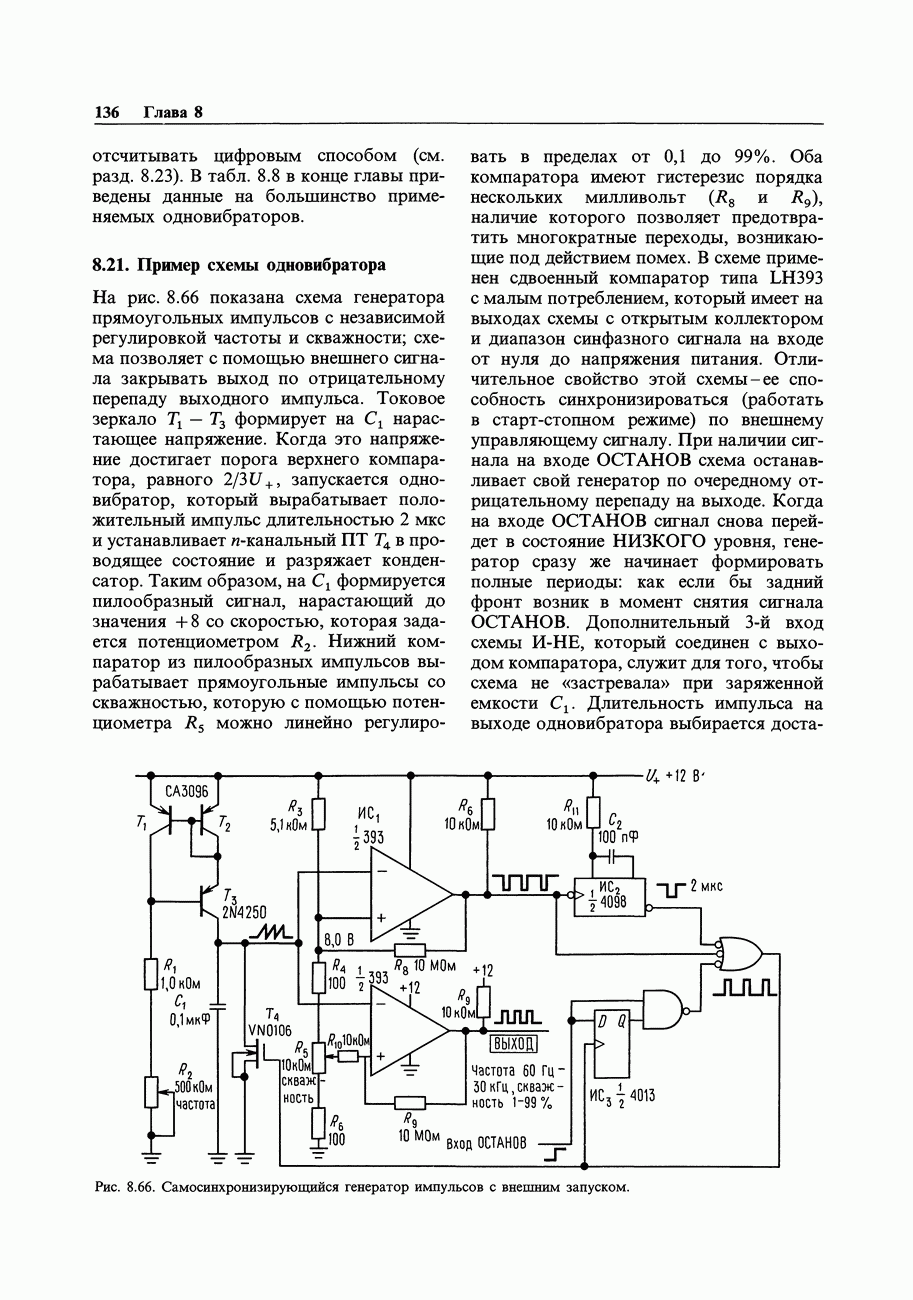
- 8.21. Пример схемы одновибратора
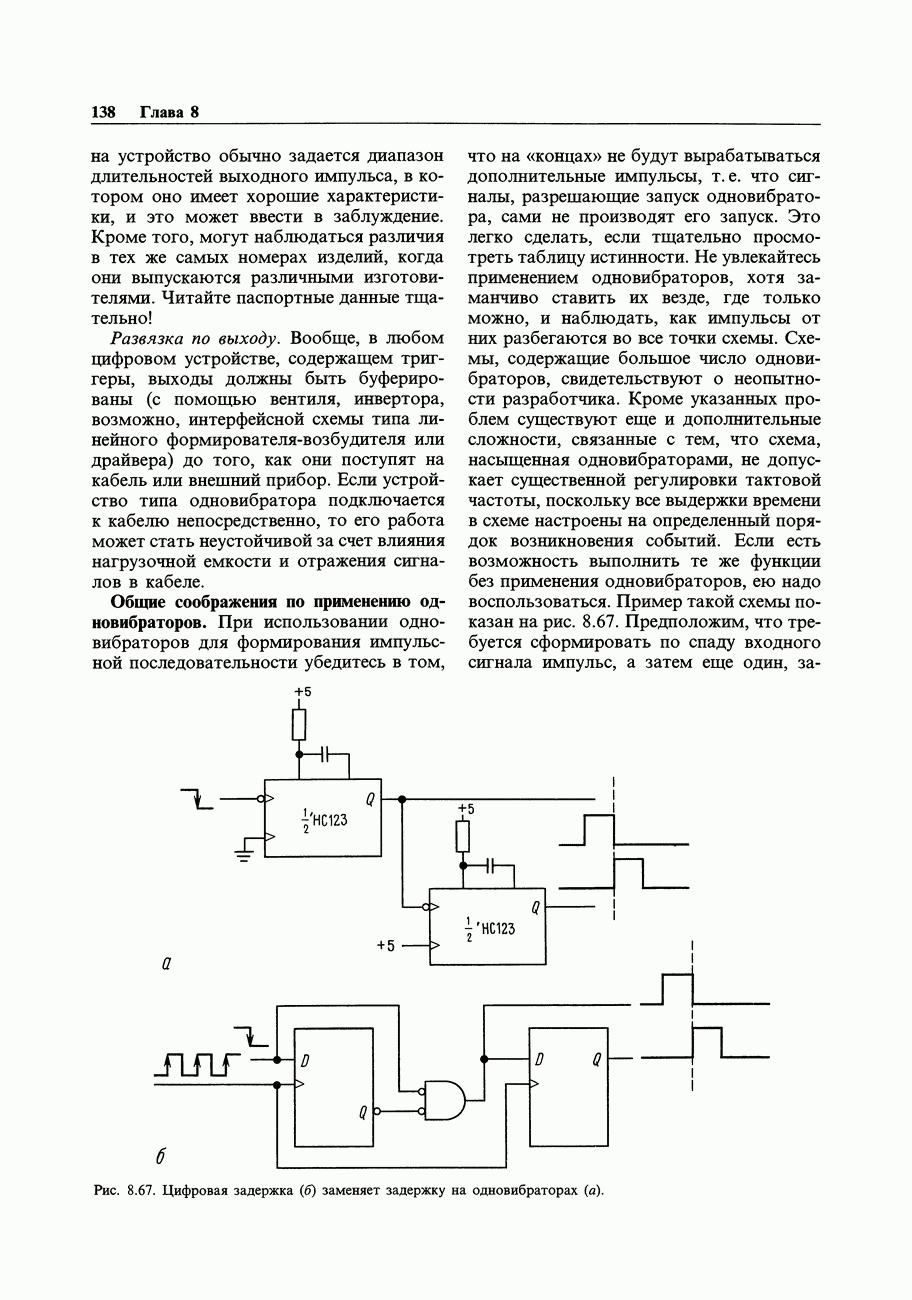
- 8.22. Предостережения относительно одновибраторов
- 8.23. Получение выдержки времени с помощью счетчиков
- ПОСЛЕДОВАТЕЛЬНОСТНЫЕ ФУНКЦИИ, РЕАЛИЗУЕМЫЕ НА СТАНДАРТНЫХ ИМС
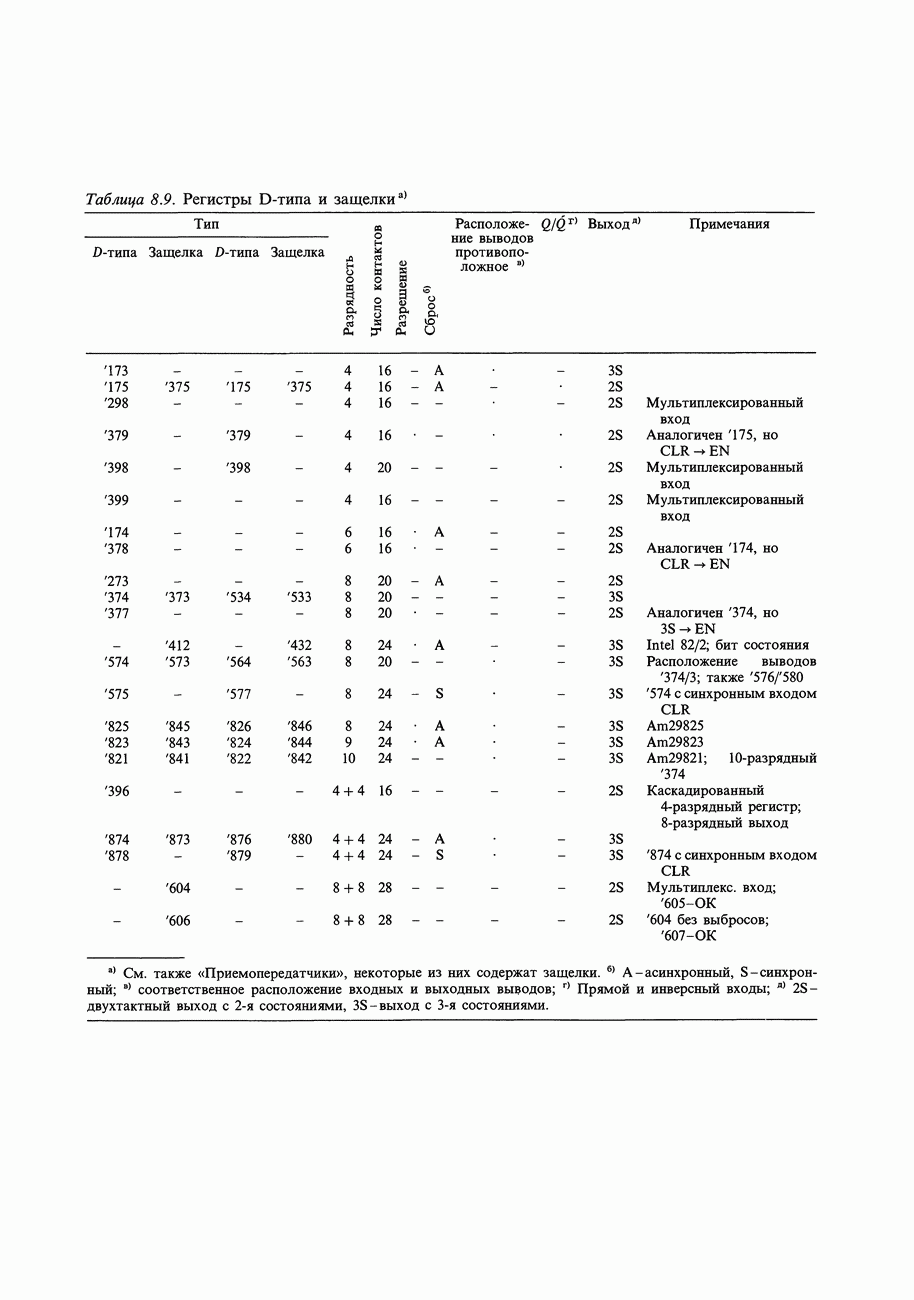
- 8.24. Фиксирующие схемы-защелки и регистры
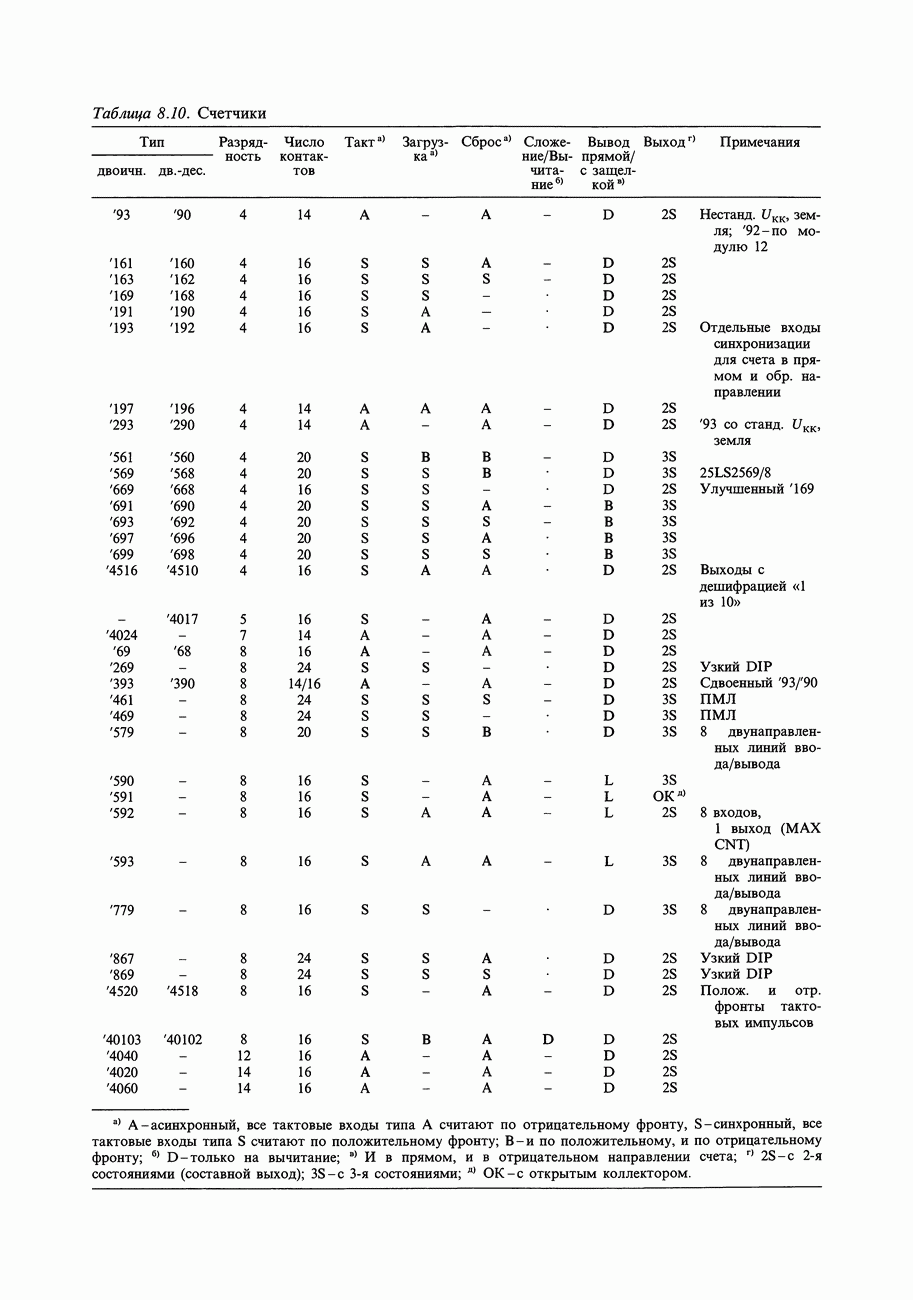
- 8.25. Счетчики
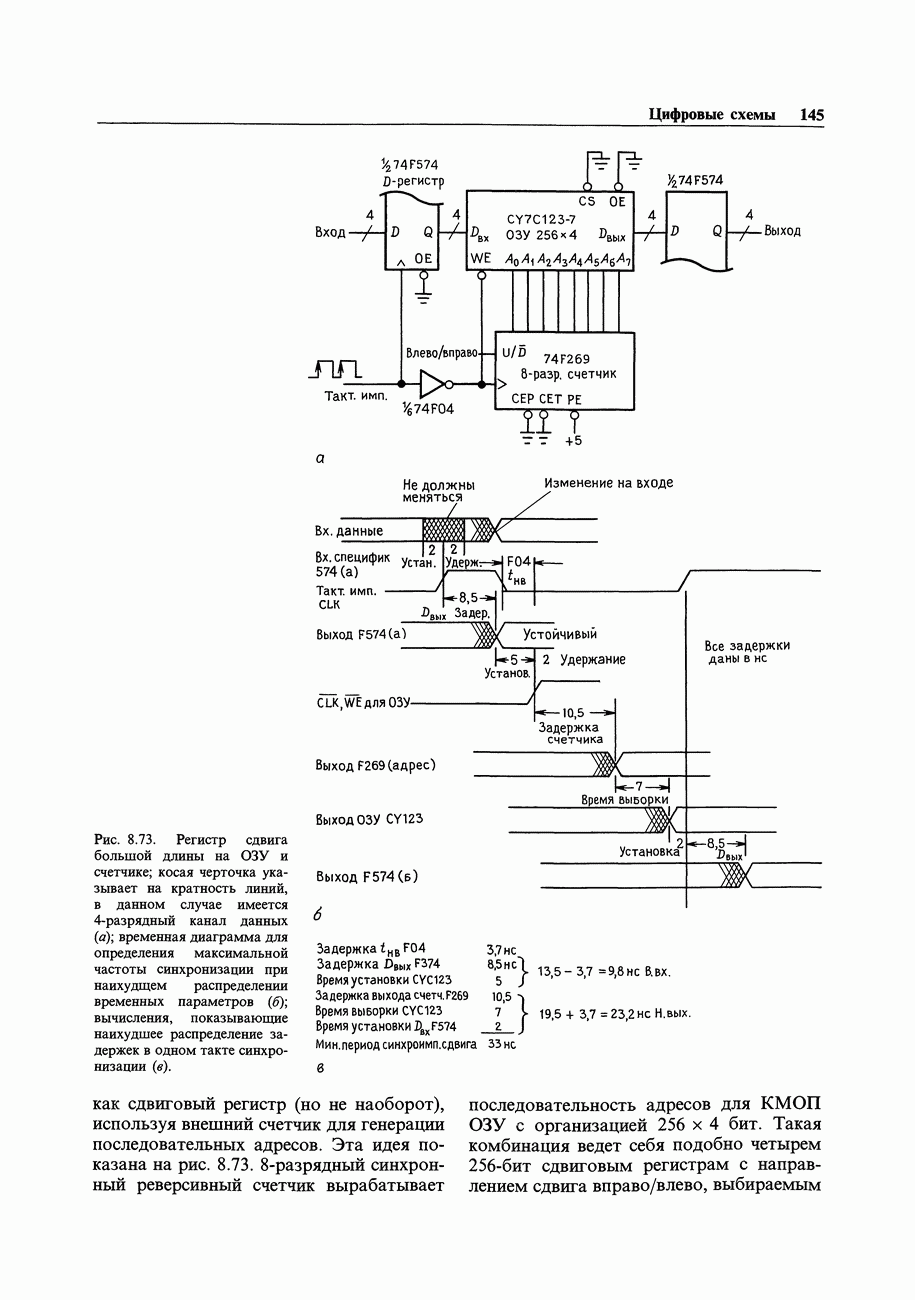
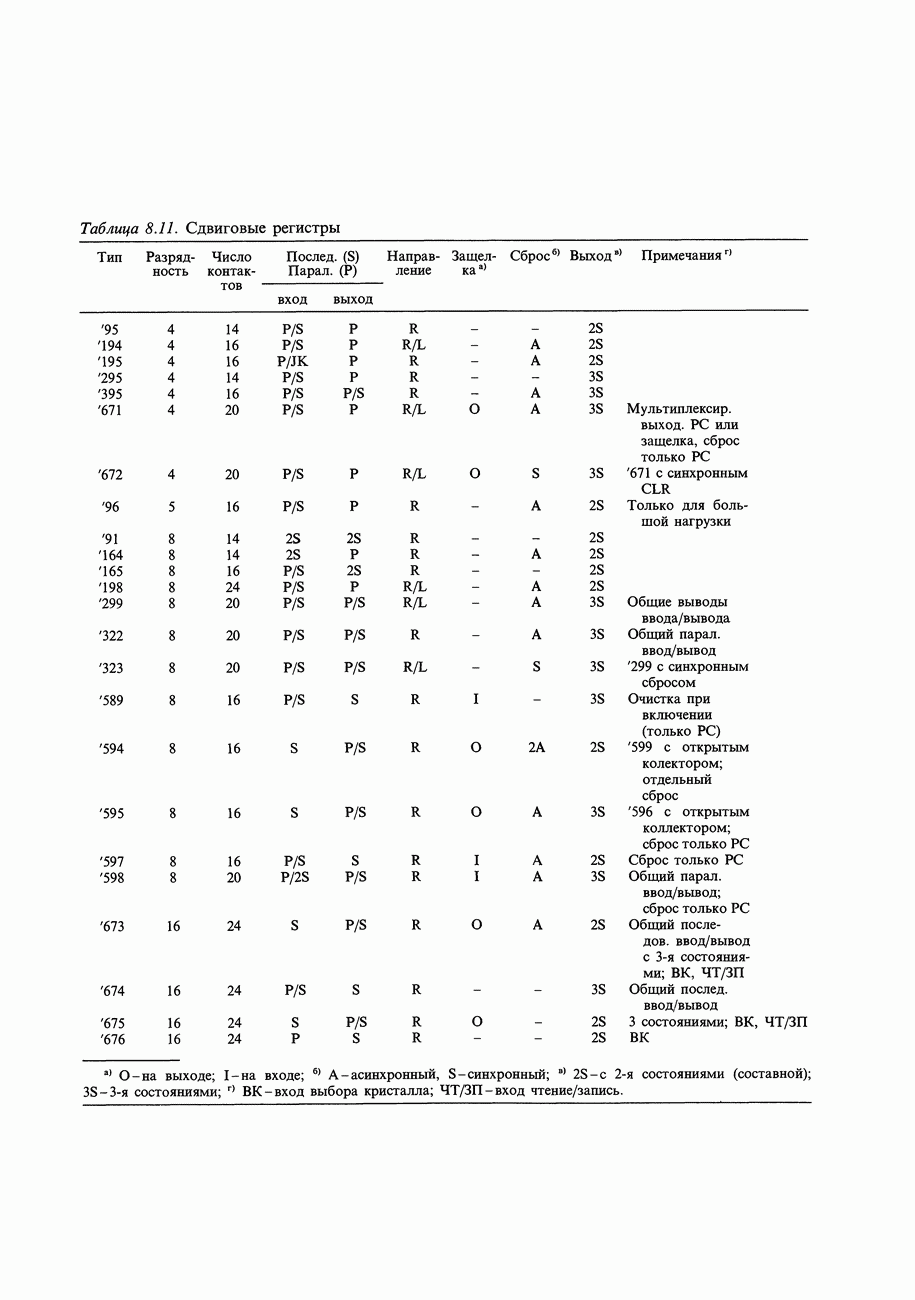
- 8.26. Регистры сдвига
- 8.27. Последовательностные ПМЛ
- Возможные применения программируемых логических интегральных схем (ПЛИС)
- 8.28. Разнообразные последовательностные схемы
- НЕКОТОРЫЕ ТИПОВЫЕ ЦИФРОВЫЕ СХЕМЫ
- 8.29. Счетчик по модулю n
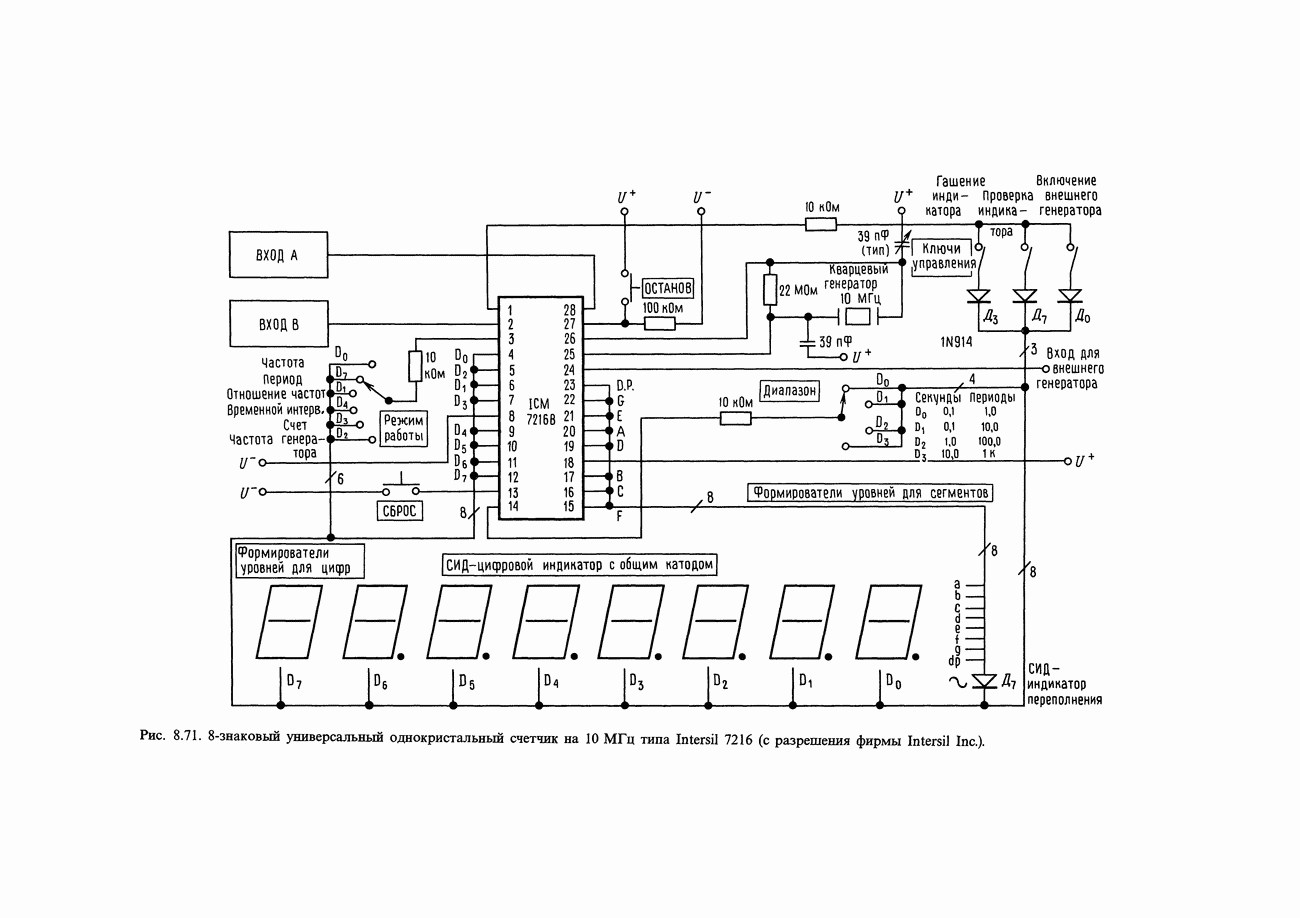
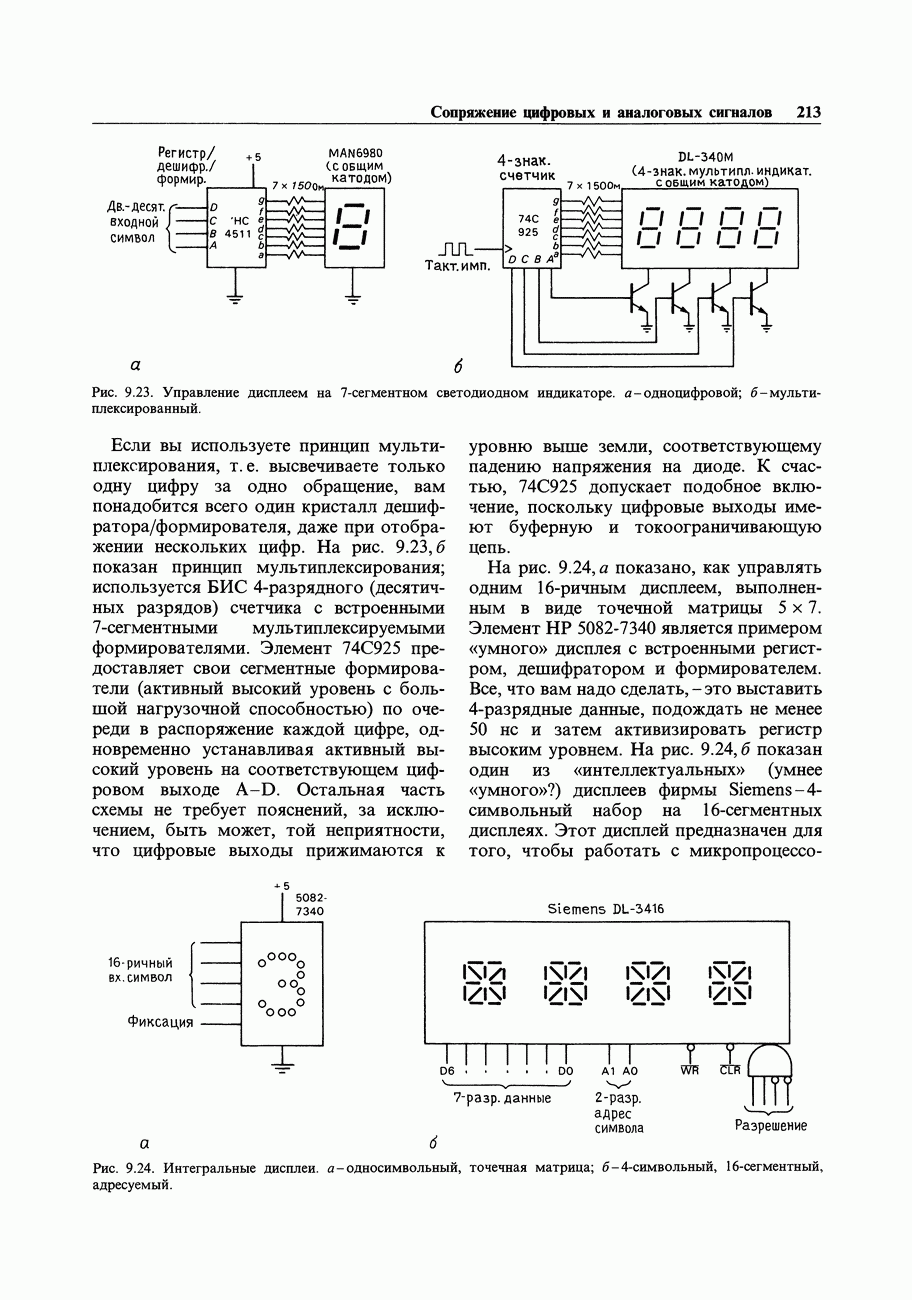
- 8.30. Мультиплексируемый цифровой индикатор на светодиодах
- 8.31. Привод звездного телескопа
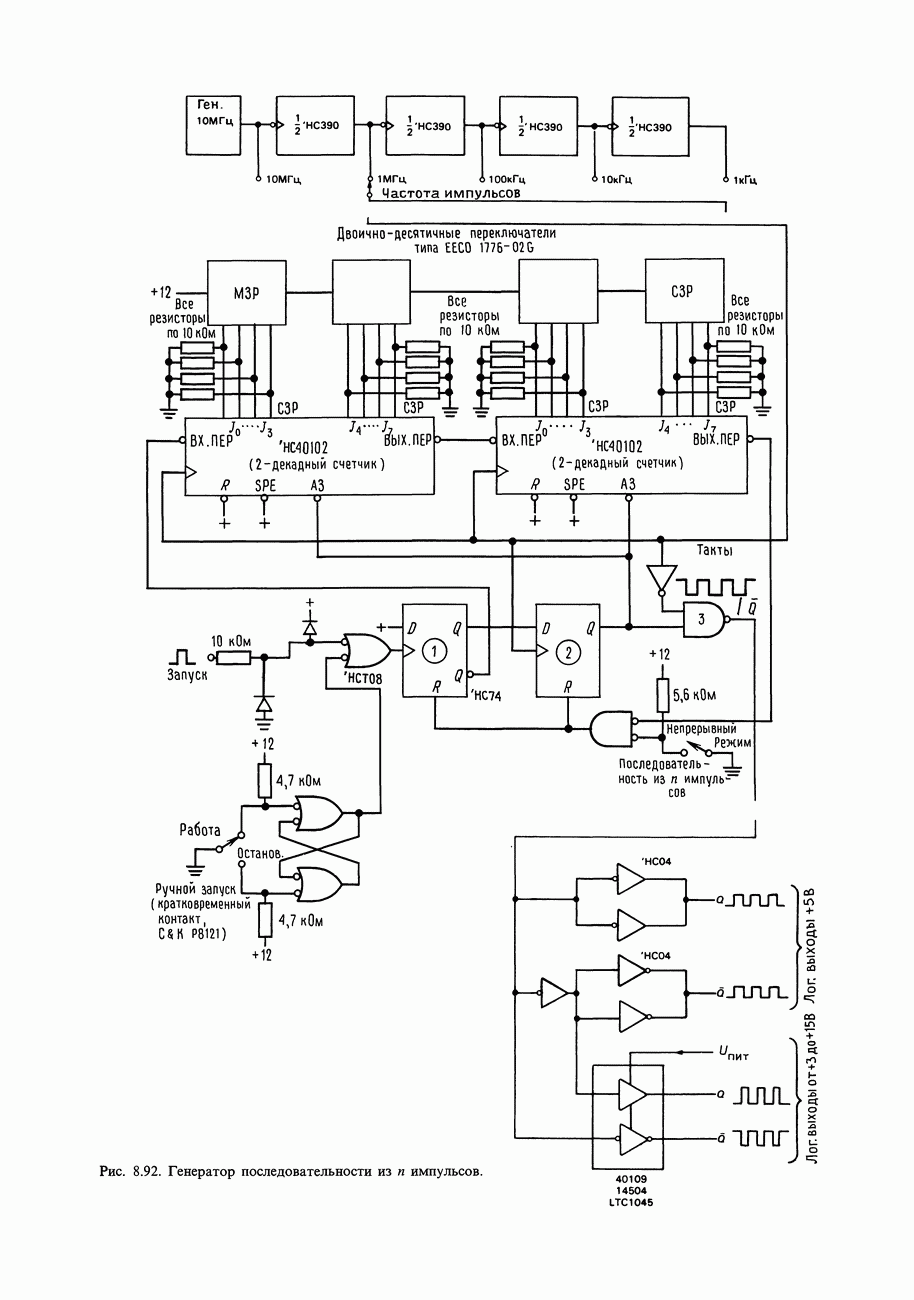
- 8.32. Генератор последовательности из n импульсов
- ПАТОЛОГИЯ В ЛОГИЧЕСКИХ СХЕМАХ
- 8.33. Проблемы статических режимов
- 8.34. Проблемы при переключениях
- 8.35. Прирожденные недостатки ТТЛ и КМОП
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 9. СОПРЯЖЕНИЕ ЦИФРОВЫХ И АНАЛОГОВЫХ СИГНАЛОВ
- 9.01. Хронология логических семейств
- 9.02. Входные и выходные характеристики
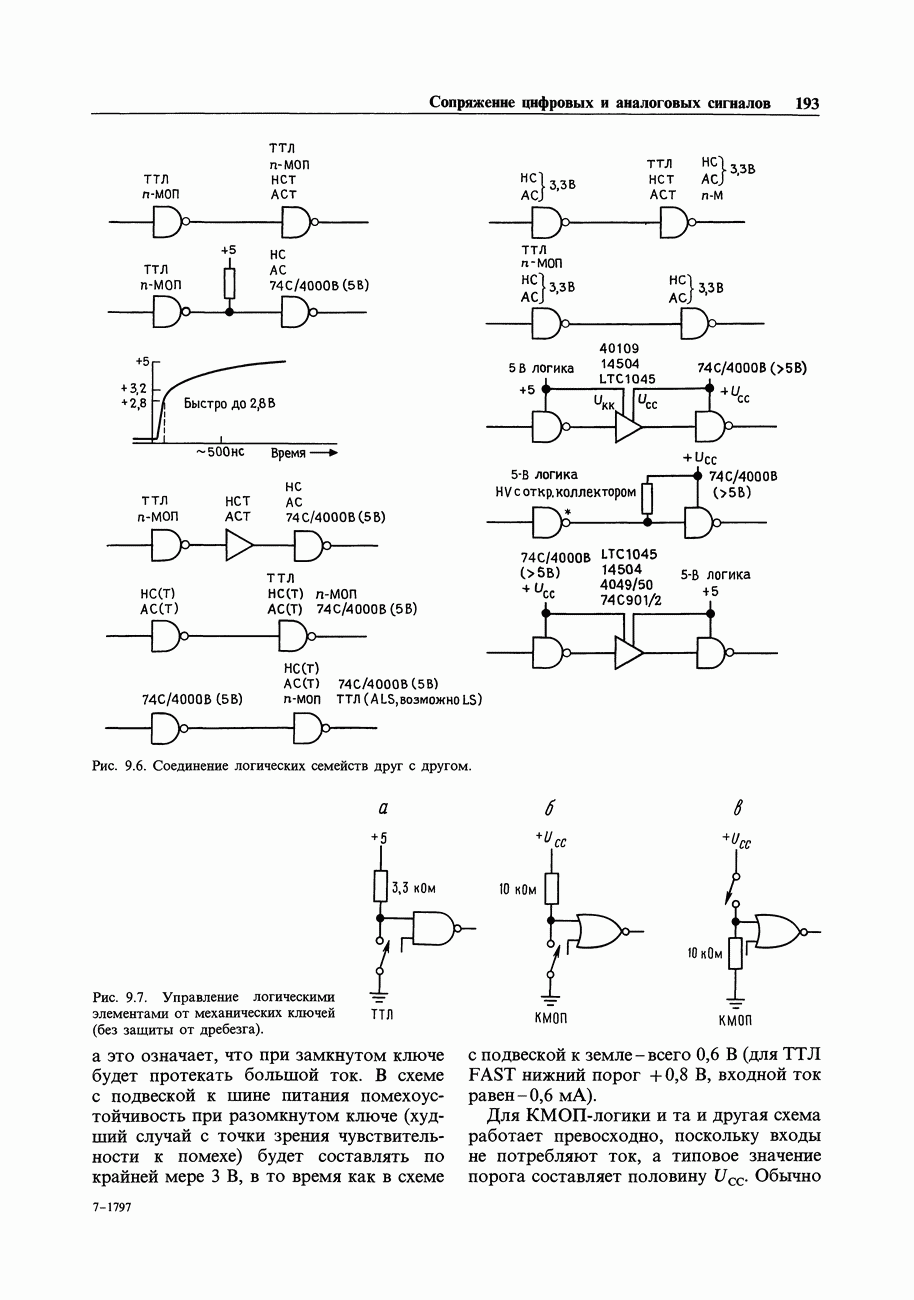
- 9.03. Сопряжение логических семейств
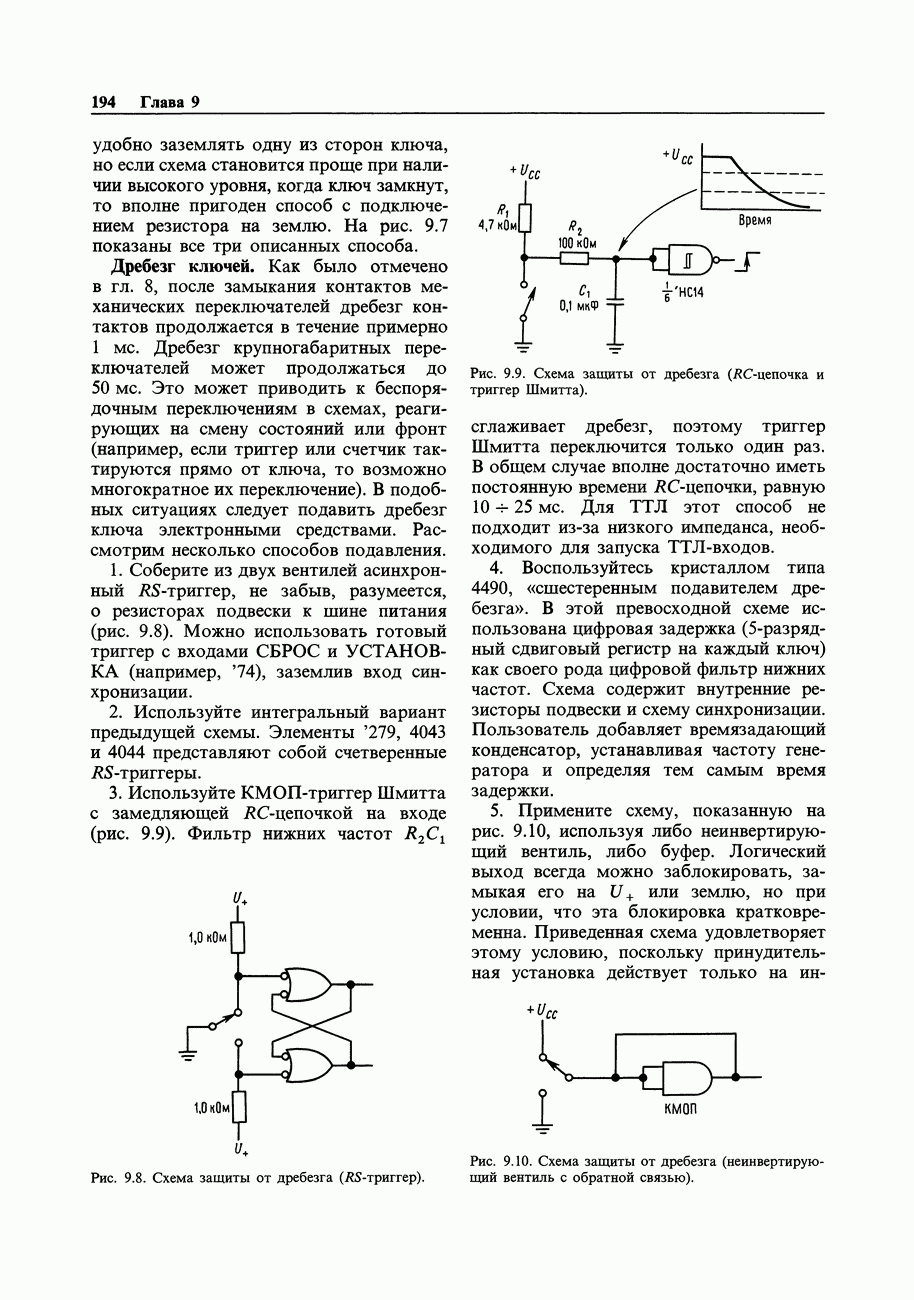
- 9.04. Управление КМОП-и ТТЛ-входами
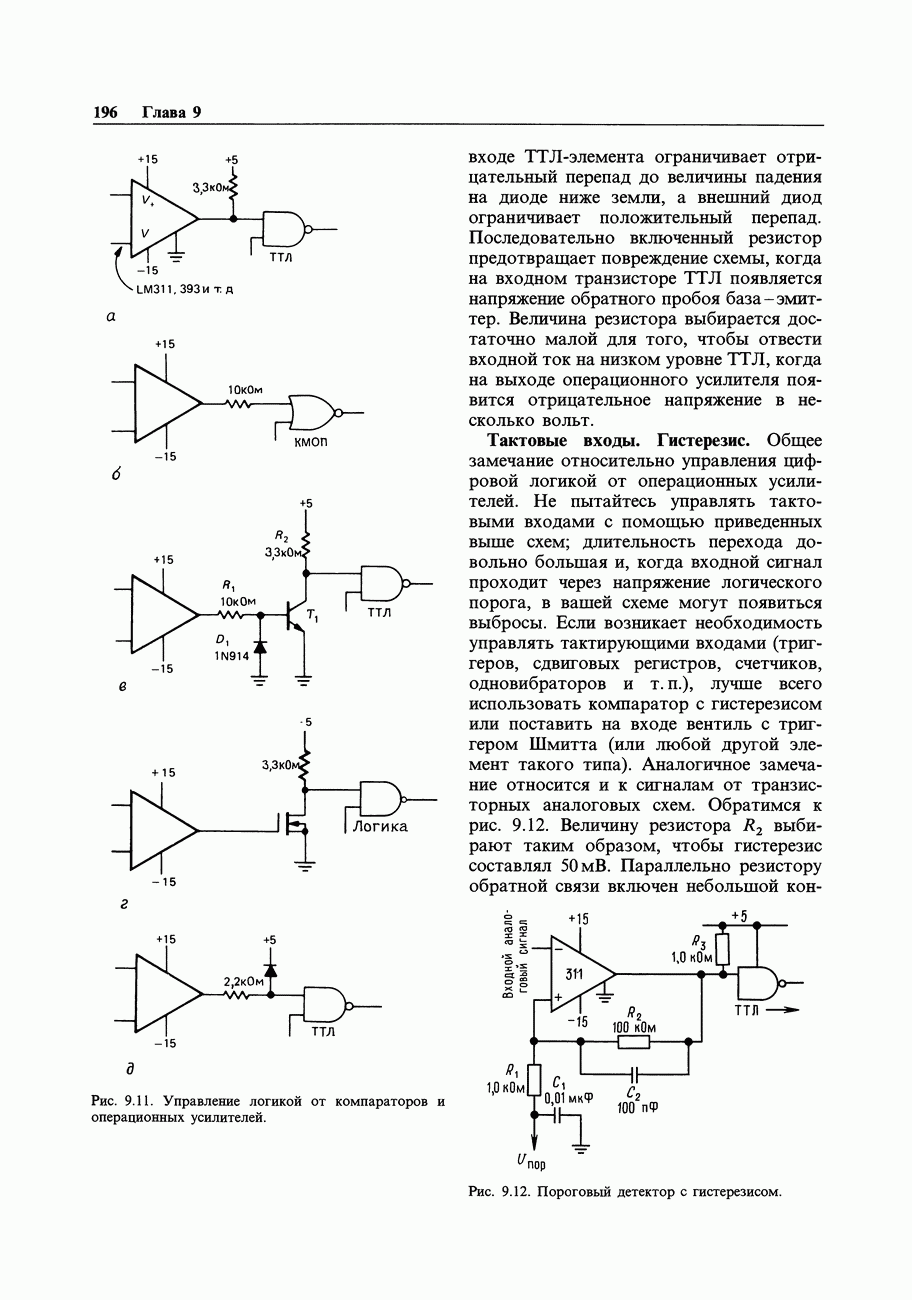
- 9.05. Управление цифровой логикой от компараторов и операционных усилителей
- 9.06. Некоторые замечания, касающиеся логических входов
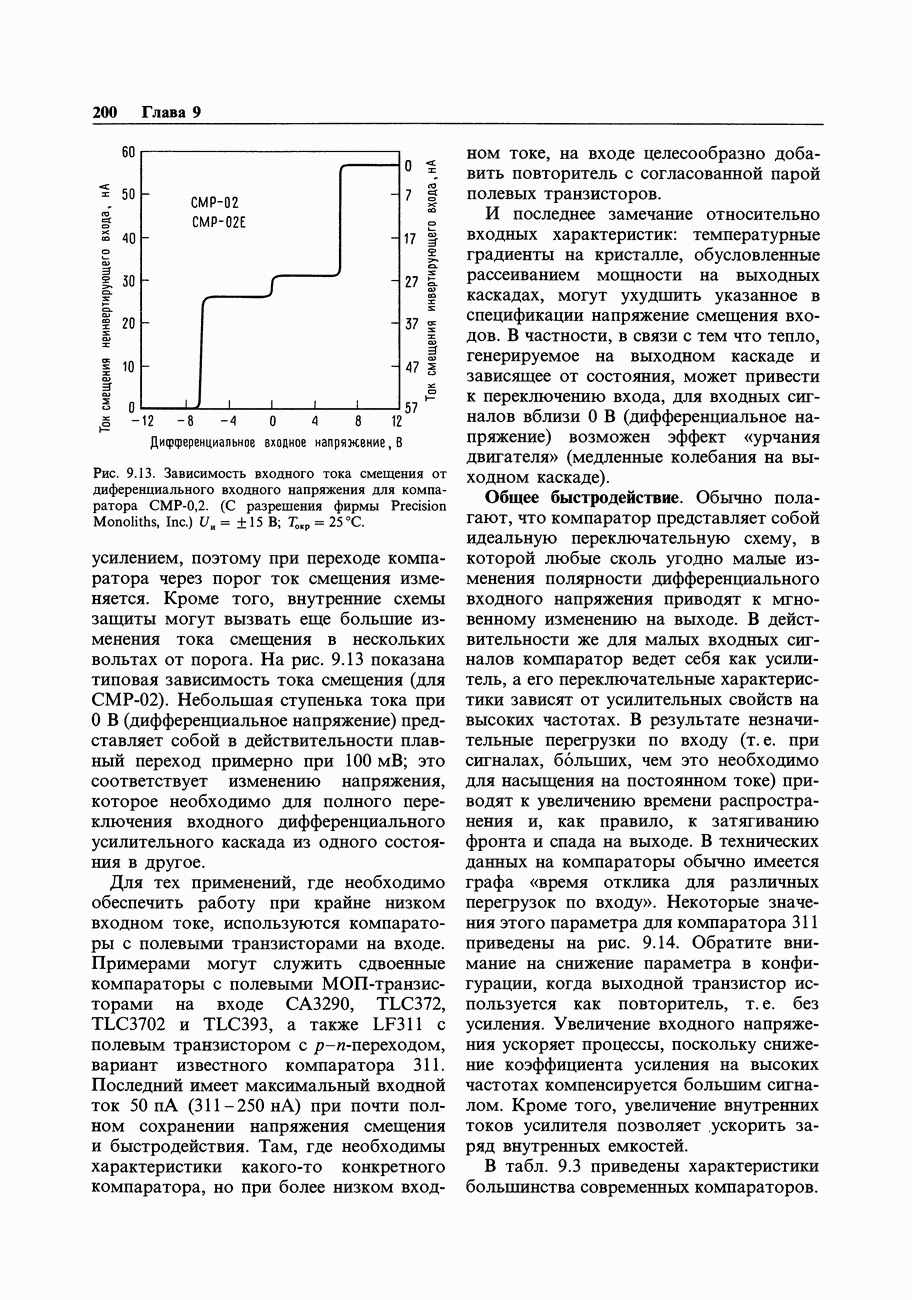
- 9.07. Компараторы
- 9.08. Управление внешней цифровой нагрузкой от КМОП- и ТТЛ-элементов
- 9.09. Сопряжение n-МОП БИС
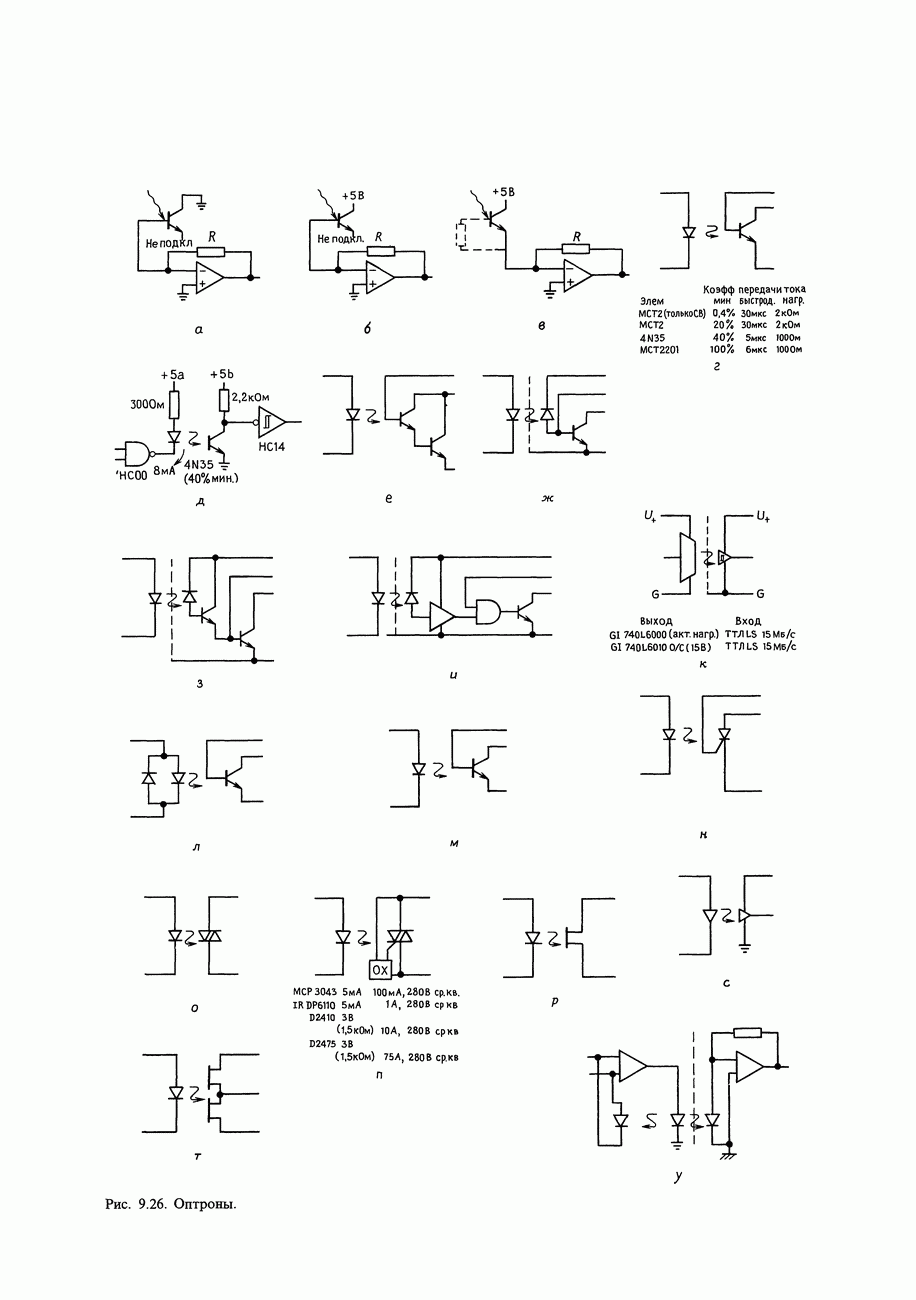
- 9.10. Оптоэлектроника
- ЦИФРОВЫЕ СИГНАЛЫ И ДЛИННЫЕ ЛИНИИ
- 9.11. Внутриплатные соединения
- 9.12. Межплатные соединения
- 9.13. Шины данных
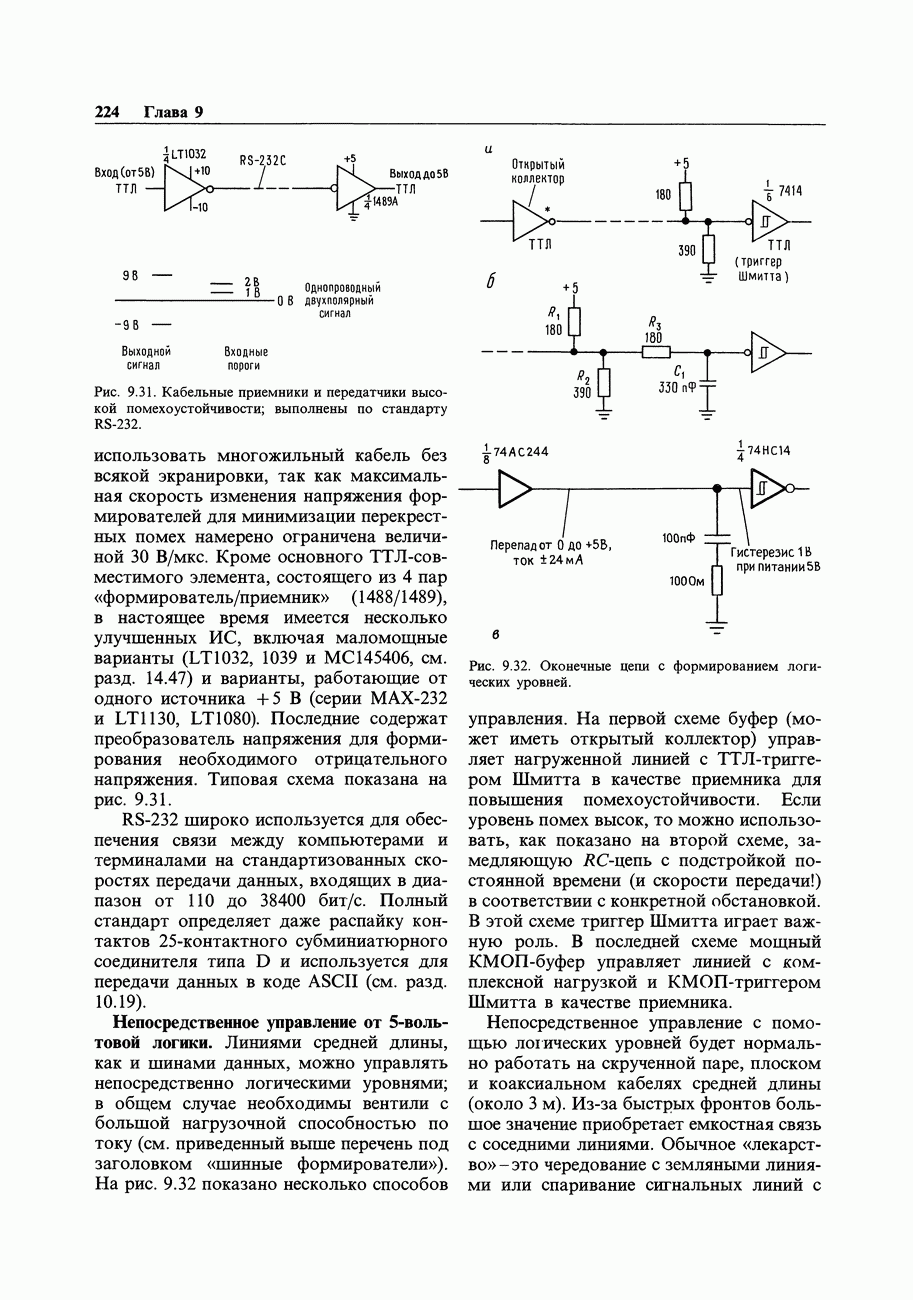
- 9.14. Кабельные связи
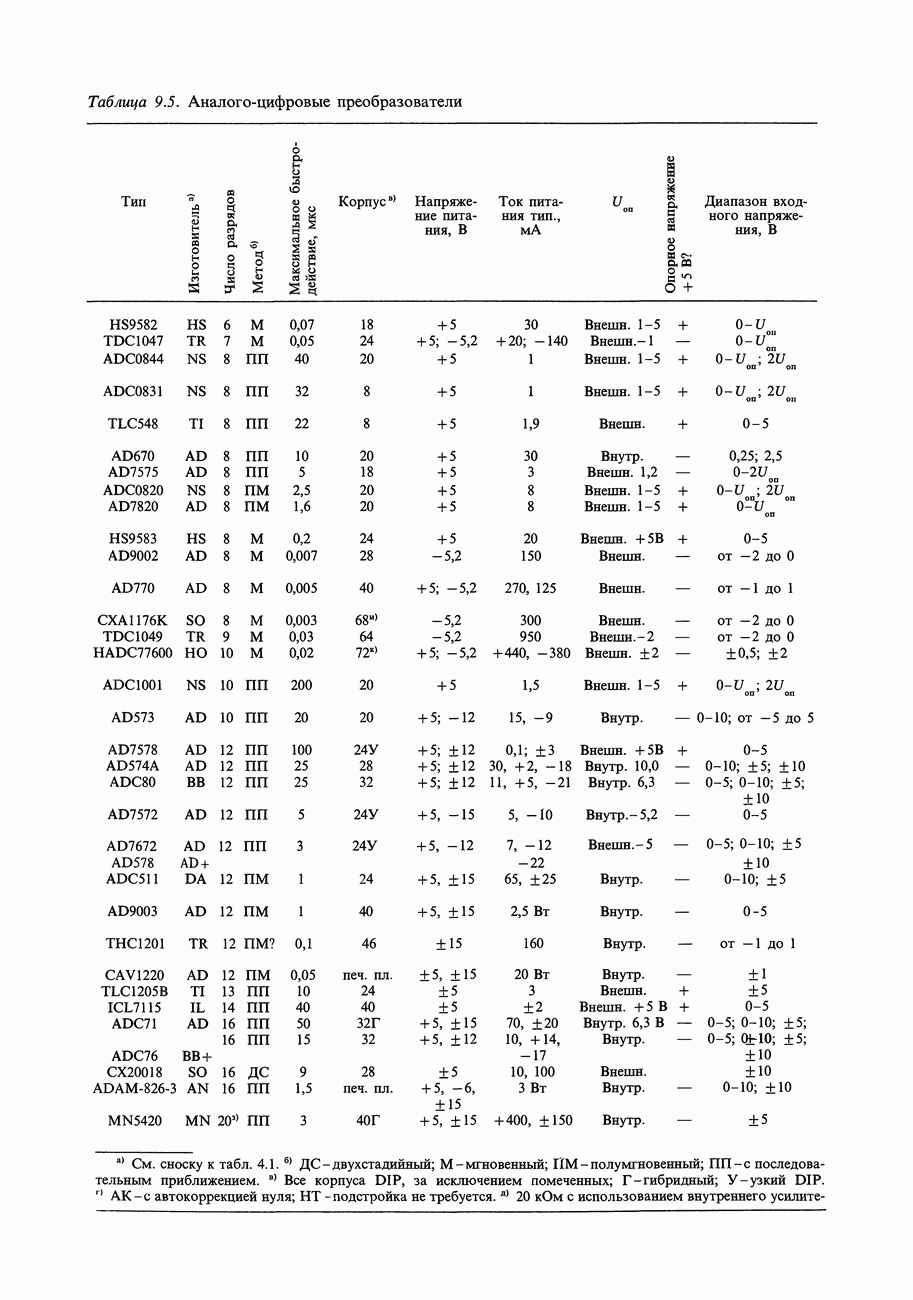
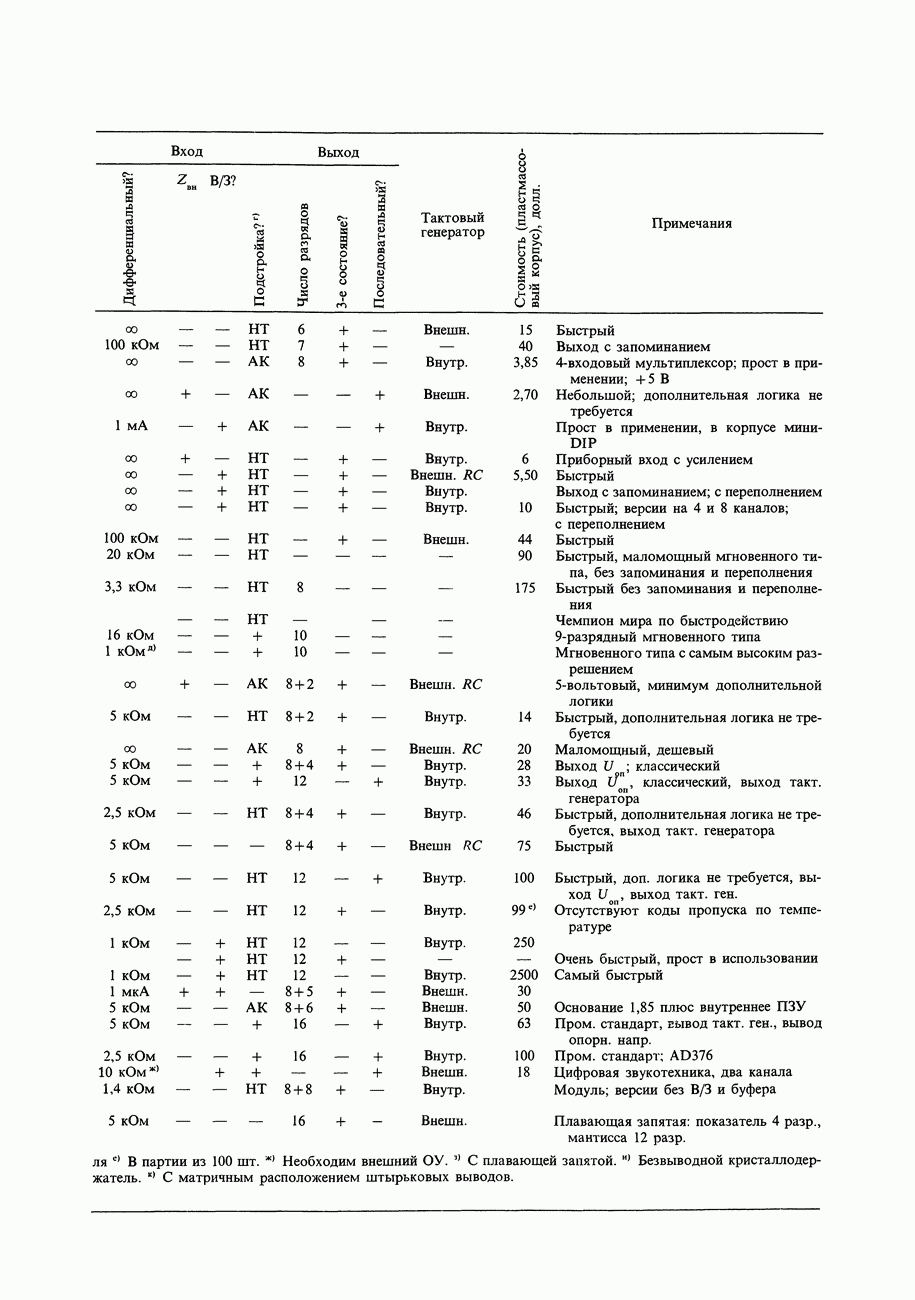
- АНАЛОГО-ЦИФРОВОЕ ПРЕОБРАЗОВАНИЕ
- 9.15. Введение в аналого-цифровое преобразование
- 9.16. Цифро-аналоговые преобразователи (ЦАП)
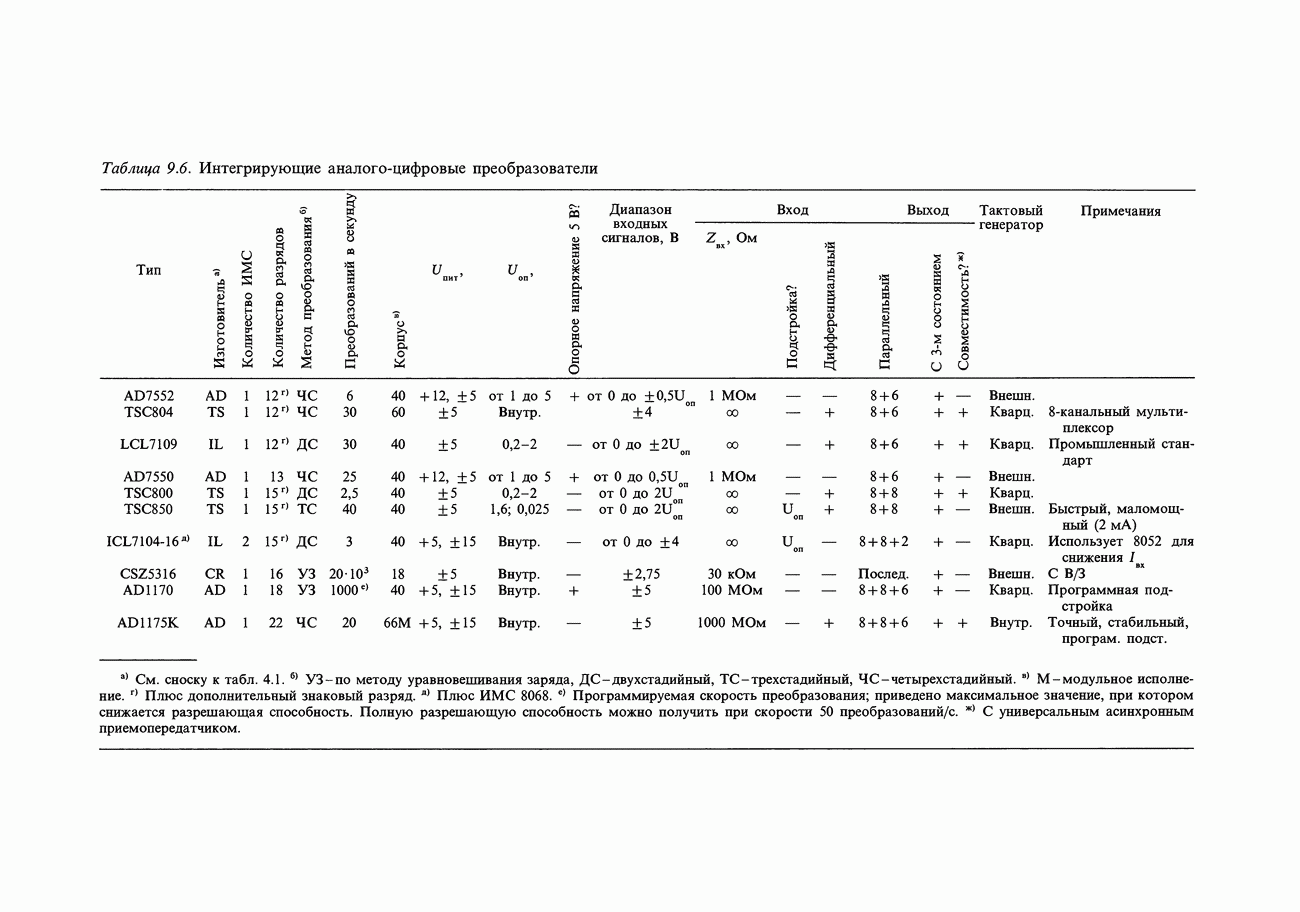
- 9.17. Интегрирующие ЦАП
- 9.18. ЦАП с умножением
- 9.19. Выбор ЦАП
- 9.20. Аналого-цифровые преобразователи
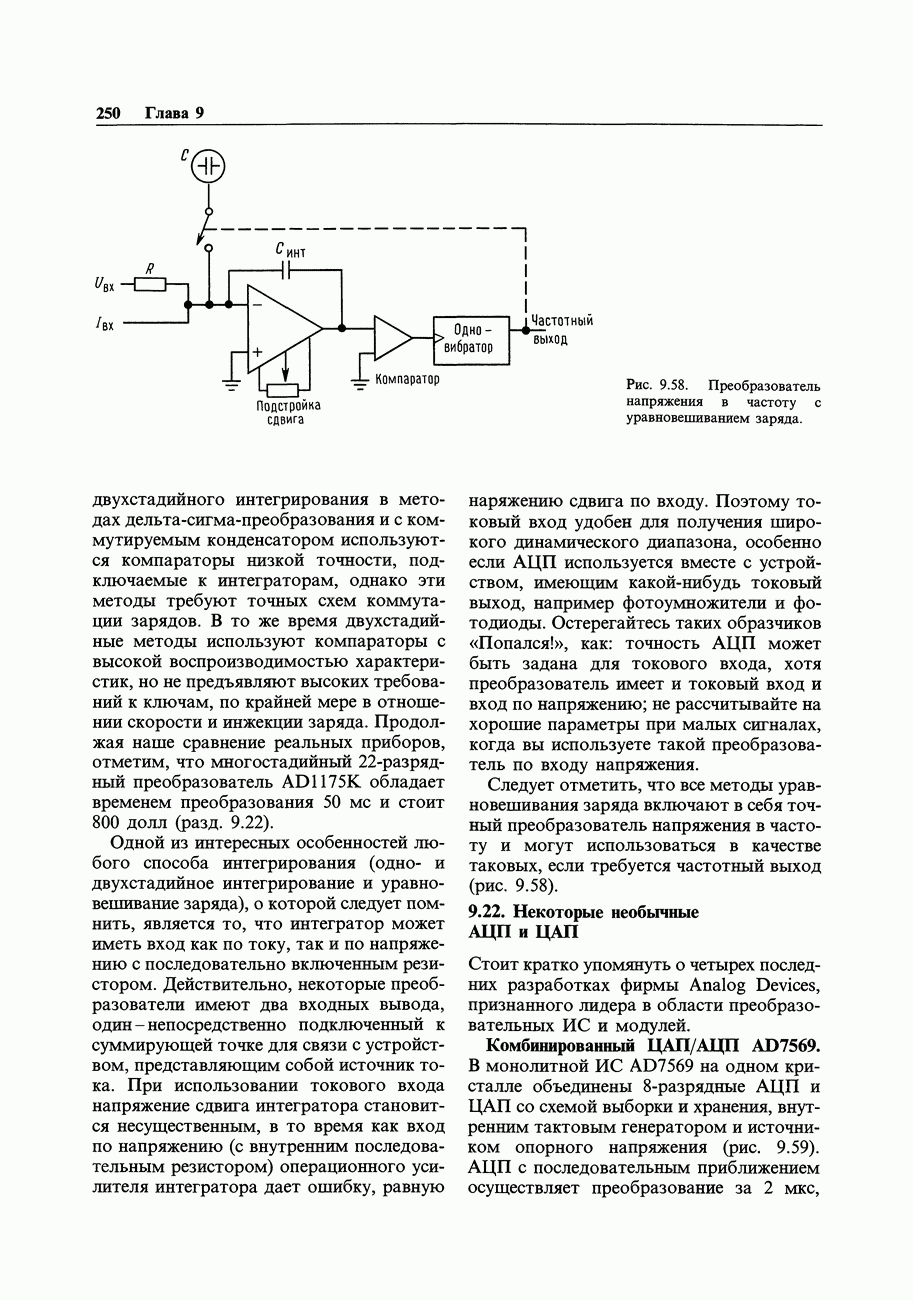
- 9.21. Методы уравновешивания заряда
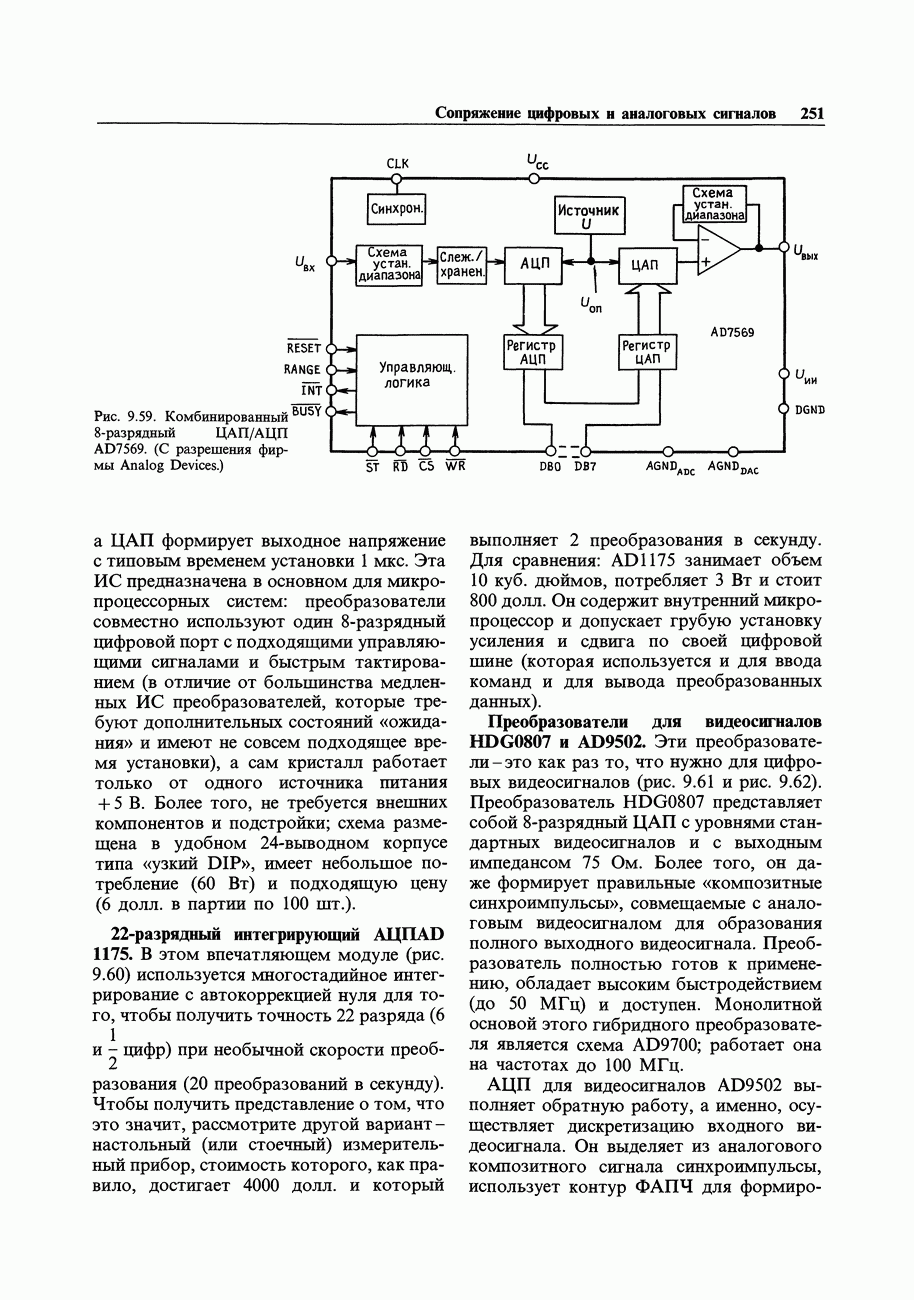
- 9.22. Некоторые необычные АЦП и ЦАП
- 9.23. Выбор АЦП
- ПРИМЕРЫ А/Ц-ПРЕОБРАЗОВАНИЯ
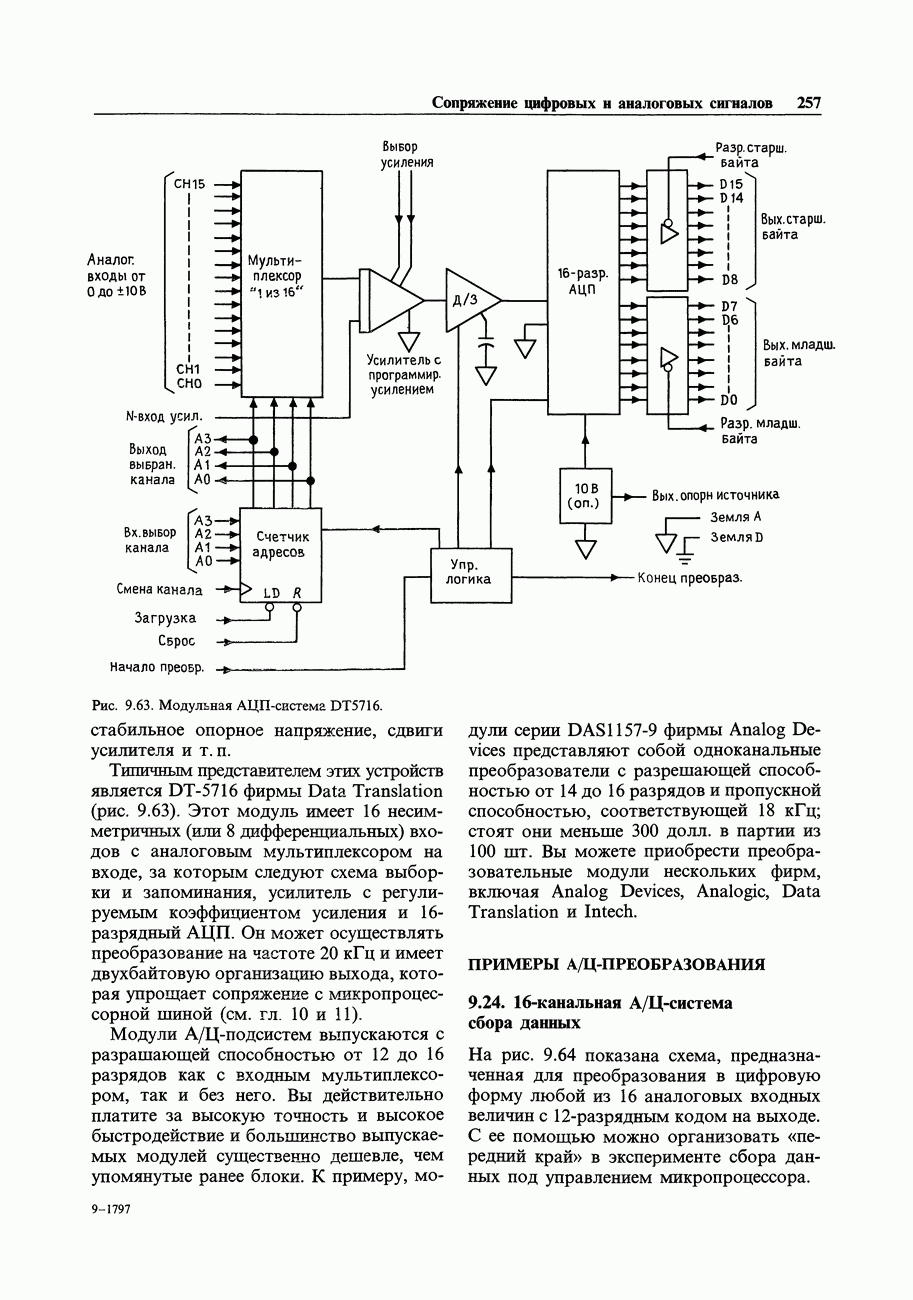
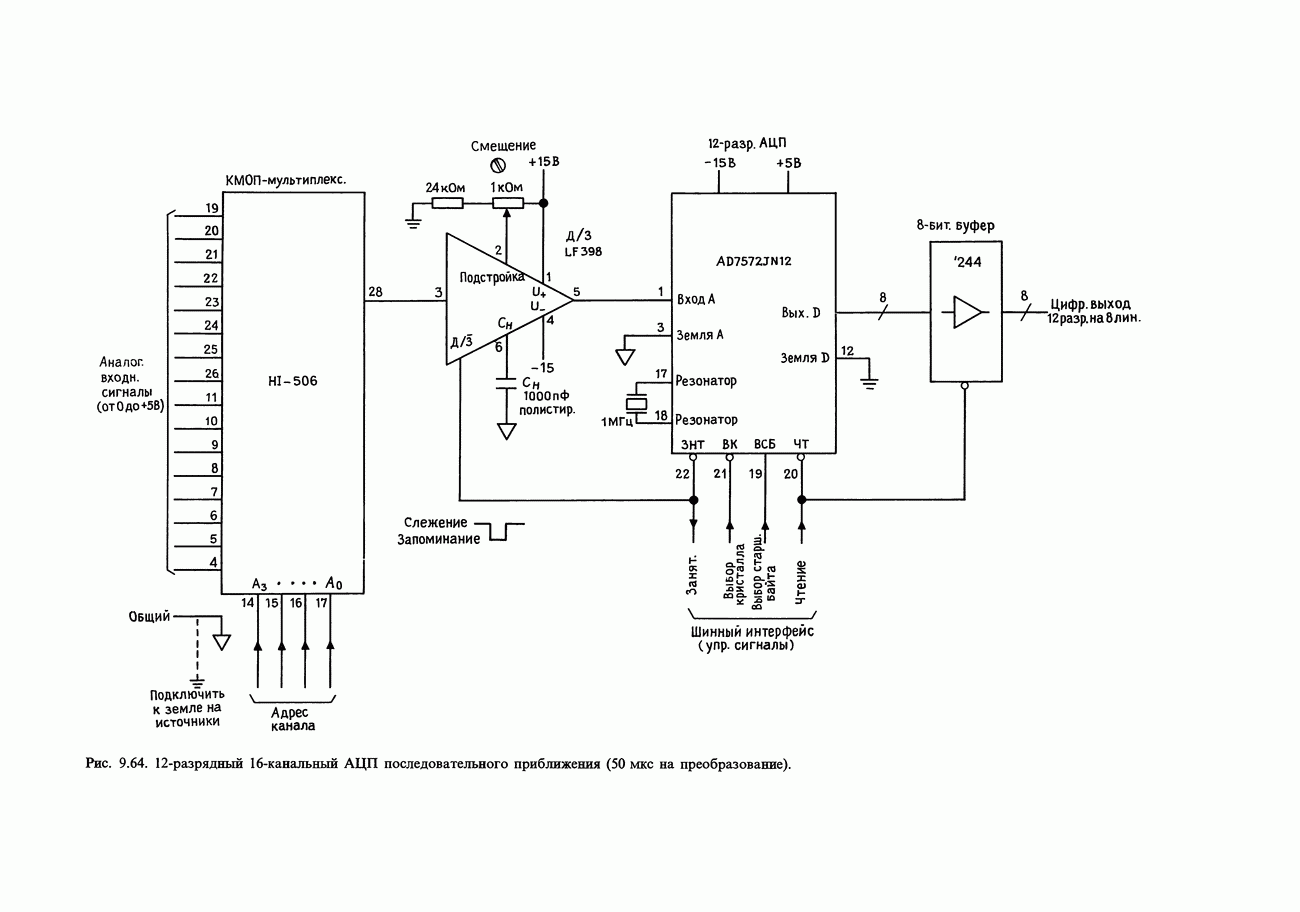
- 9.24. 16-канальная А/Ц-система сбора данных
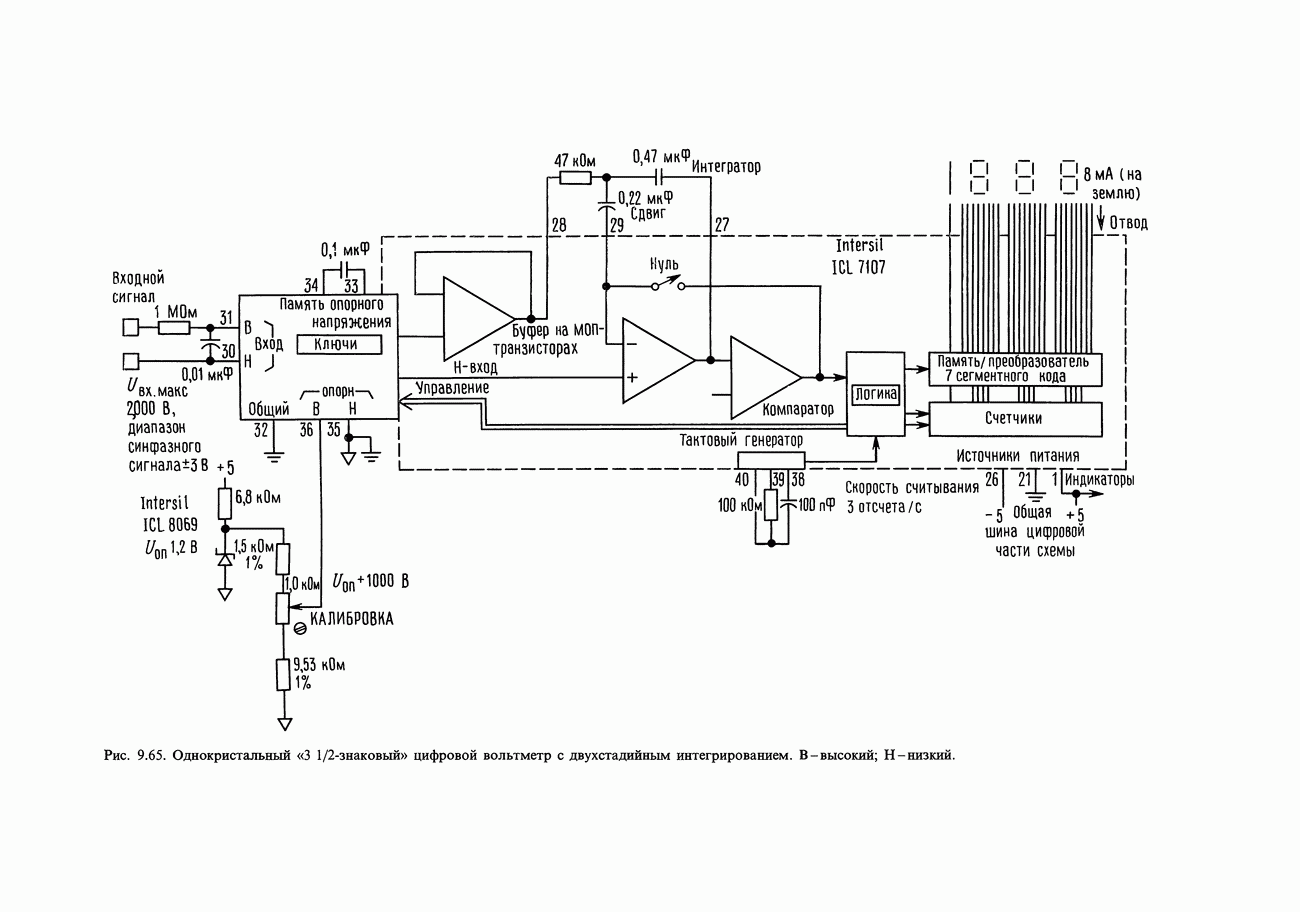
- 9.25. 3 1/2 — знаковый цифровой вольтметр
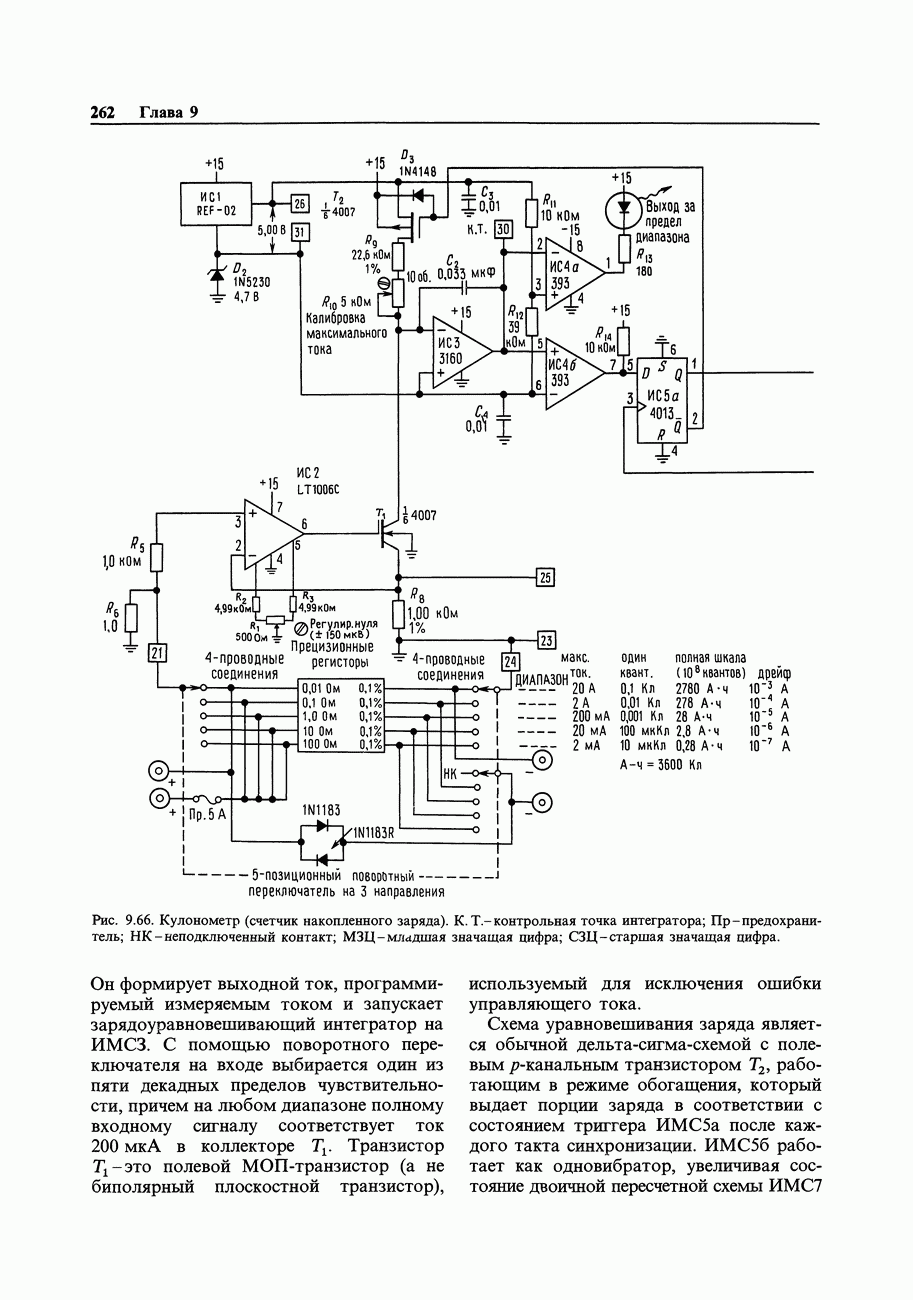
- 9.26. Кулонометр
- СХЕМЫ ФАЗОВОЙ АВТОПОДСТРОЙКИ ЧАСТОТЫ
- 9.28. Проектирование ФАПЧ
- 9.29. Пример разработки: умножитель частоты
- 9.30. Захват и слежение в системе ФАПЧ
- 9.31. Некоторые примеры применения систем ФАПЧ
- ПСЕВДОСЛУЧАЙНЫЕ ДВОИЧНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ГЕНЕРАТОРЫ ШУМА
- 9.32. Цифровые методы генерации шума
- 9.33. Последовательности, генерируемые регистрами сдвига с обратными связями
- 9.34. Формирование аналогового шума с использованием последовательностей максимальной длины
- 9.35. Энергетический спектр последовательности, сформированной при помощи регистра сдвига
- 9.36. Низкочастотная фильтрация
- 9.37. Краткое заключение
- 9.38. Цифровые фильтры
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 10. МИКРОЭВМ
- МИНИ-ЭВМ, МИКРОЭВМ И МИКРОПРОЦЕССОРЫ
- 10.01. Архитектура микроЭВМ
- НАБОР КОМАНД КОМПЬЮТЕРА
- 10.02. Язык ассемблера и язык машинных кодов
- 10.03. Упрощенный набор команд процессора Intel 8086/8
- 10.04. Программный пример
- СИГНАЛЫ МАГИСТРАЛИ И ЕЕ ФУНКЦИОНИРОВАНИЕ
- 10.05. Основные сигналы магистрали: данные, адрес, синхронизация
- 10.06. Программируемый ввод-вывод: вывод данных
- 10.07. Программируемый ввод-вывод: ввод данных
- 10.08. Программируемый ввод-вывод: регистры состояний
- 10.09. Прерывания
- 10.10. Обработка прерываний
- 10.11. Прерывания в целом
- 10.12. Прямой доступ в память
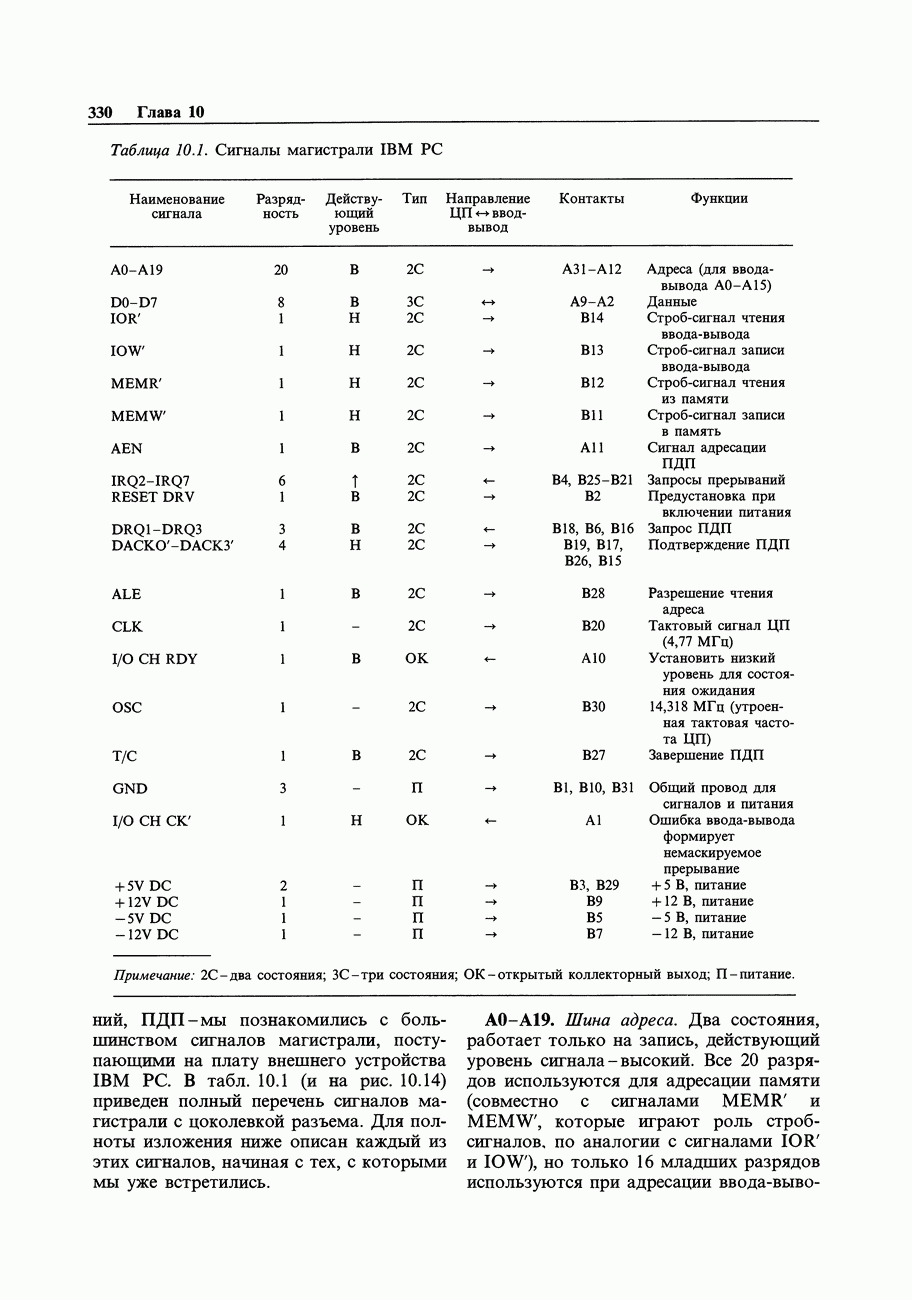
- 10.13. Сводный перечень сигналов магистрали IBM PC
- 10.14. Синхронный и асинхронный протоколы магистрали
- 10.15. Магистрали других микрокомпьютеров
- 10.16. Подключение к компьютеру периферийных устройств
- СИСТЕМНЫЕ КОНЦЕПЦИИ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
- 10.17. Программирование
- 10.18. Операционные системы, файлы и использование памяти
- ПРИНЦИПЫ ПЕРЕДАЧИ ДАННЫХ
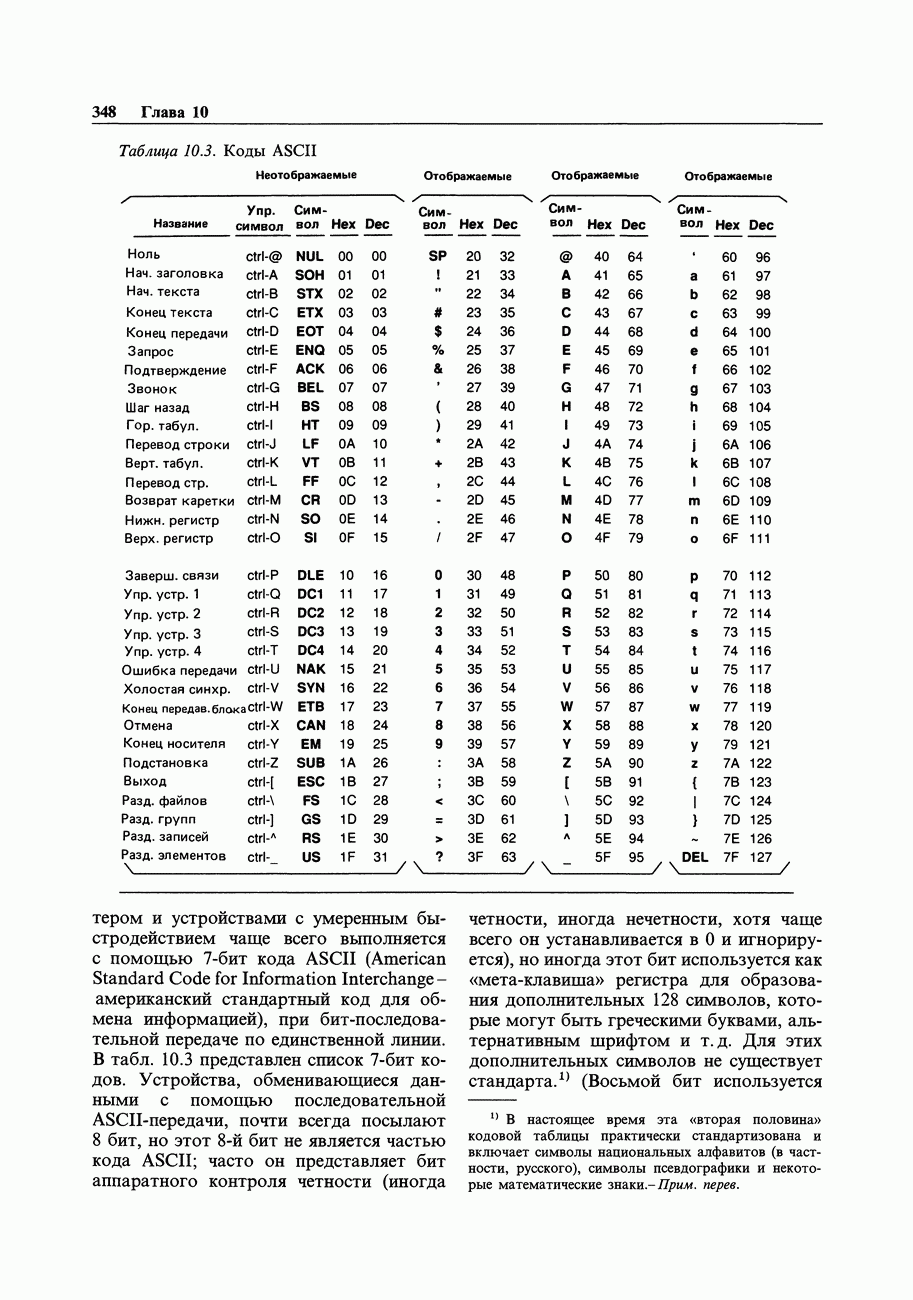
- 10.19. Последовательная связь и коды ASCII
- 10.20. Параллельная связь
- 10.21. Локальные вычислительные цепи
- 10.22. Пример интерфейса: аппаратная упаковка данных
- 10.23. Форматы чисел