| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9.03. Сопряжение логических семейств
Поскольку существуют ситуации, когда вам приходится смешивать различные типы логических семейств, важно знать, каким образом можно обеспечить «общение» различных семейств друг с другом. Например, многие представляющие интерес кристаллы БИС созданы на основе  -МОП-технологии с ТТЛ-совместимыми выходными уровнями (ВЫСОКИЙ - около
-МОП-технологии с ТТЛ-совместимыми выходными уровнями (ВЫСОКИЙ - около  ), но их нельзя сразу же подключать к
), но их нельзя сразу же подключать к  . Другой пример, вам захотелось использовать превосходную серию счетчиков
. Другой пример, вам захотелось использовать превосходную серию счетчиков  в существующей схеме, построенной на
в существующей схеме, построенной на  . Или вам понадобилась
. Или вам понадобилась  -вольтовая логика по периферии
-вольтовая логика по периферии  -вольтовой КМОП-системы для того, чтобы обеспечить соединение с внешними ТТЛ-совместимыми сигналами, или для питания кабелей.
-вольтовой КМОП-системы для того, чтобы обеспечить соединение с внешними ТТЛ-совместимыми сигналами, или для питания кабелей.

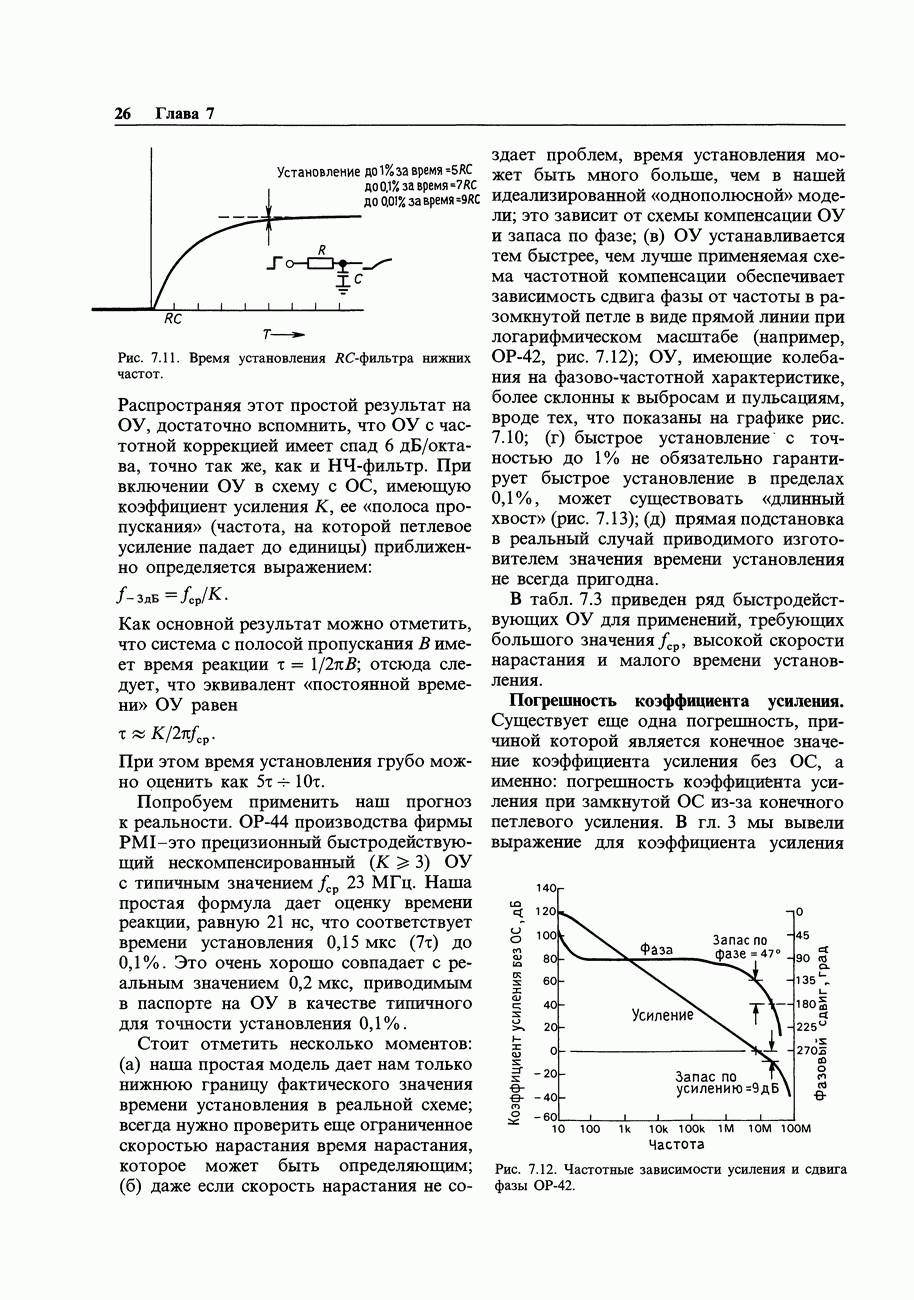
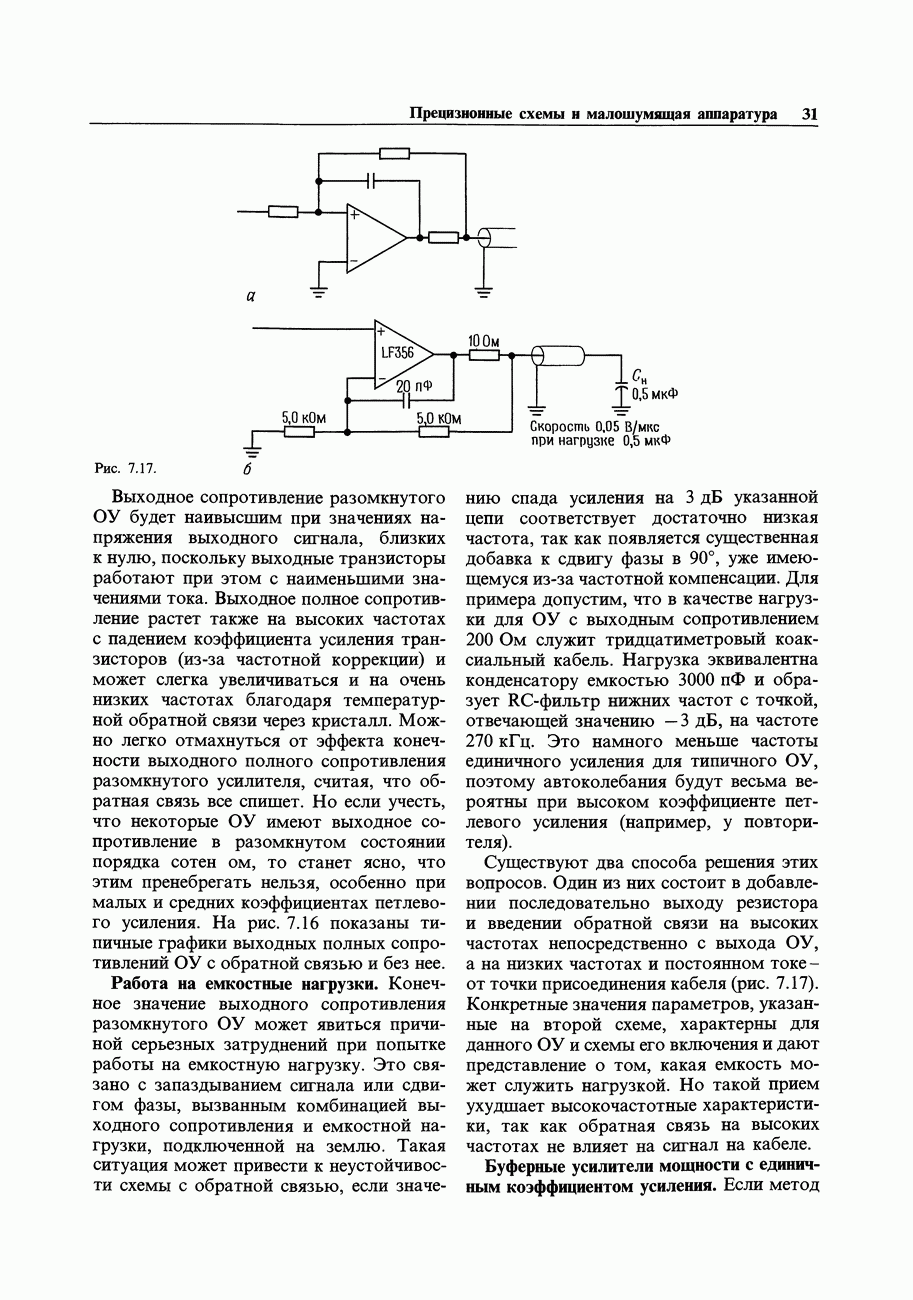
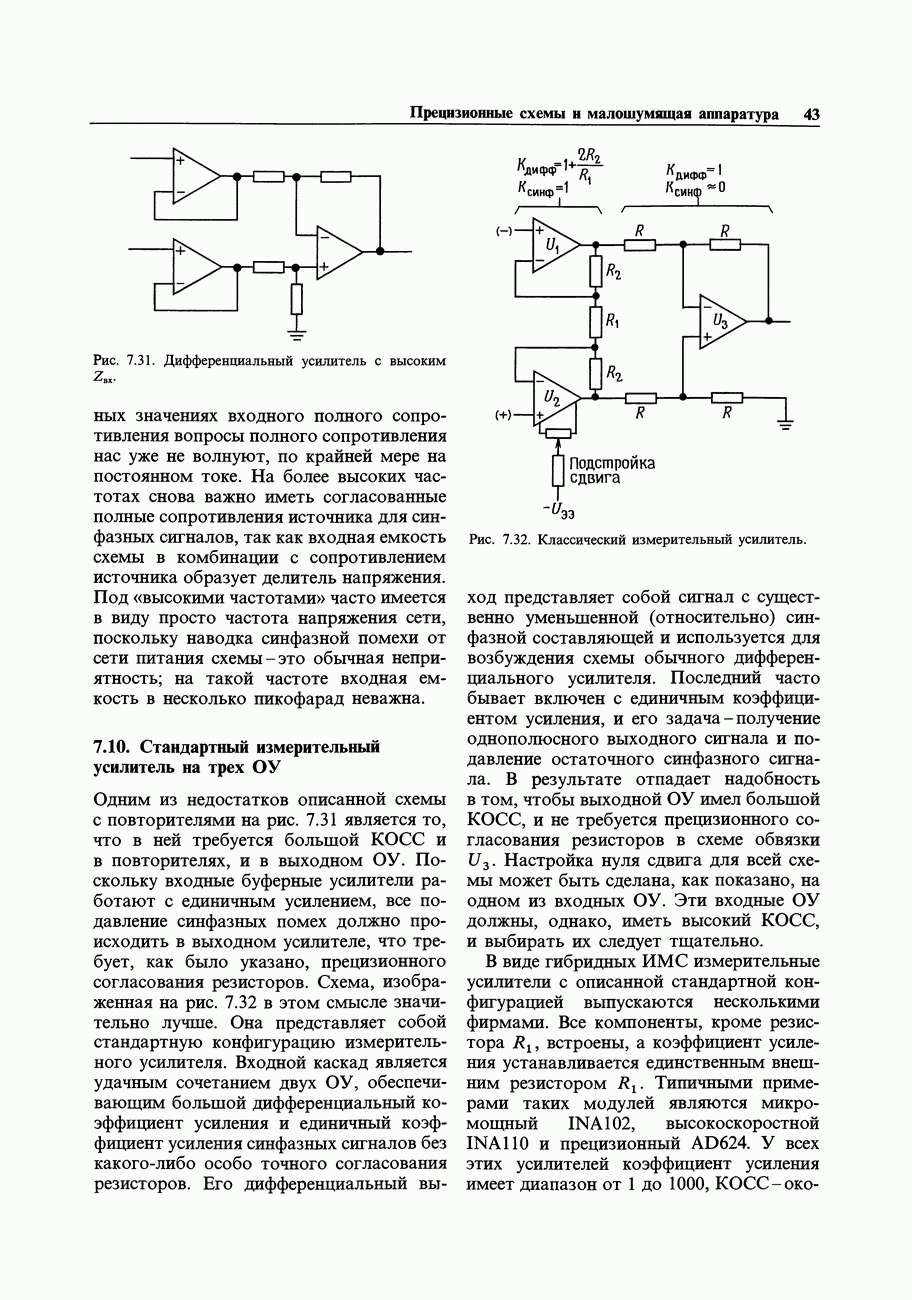
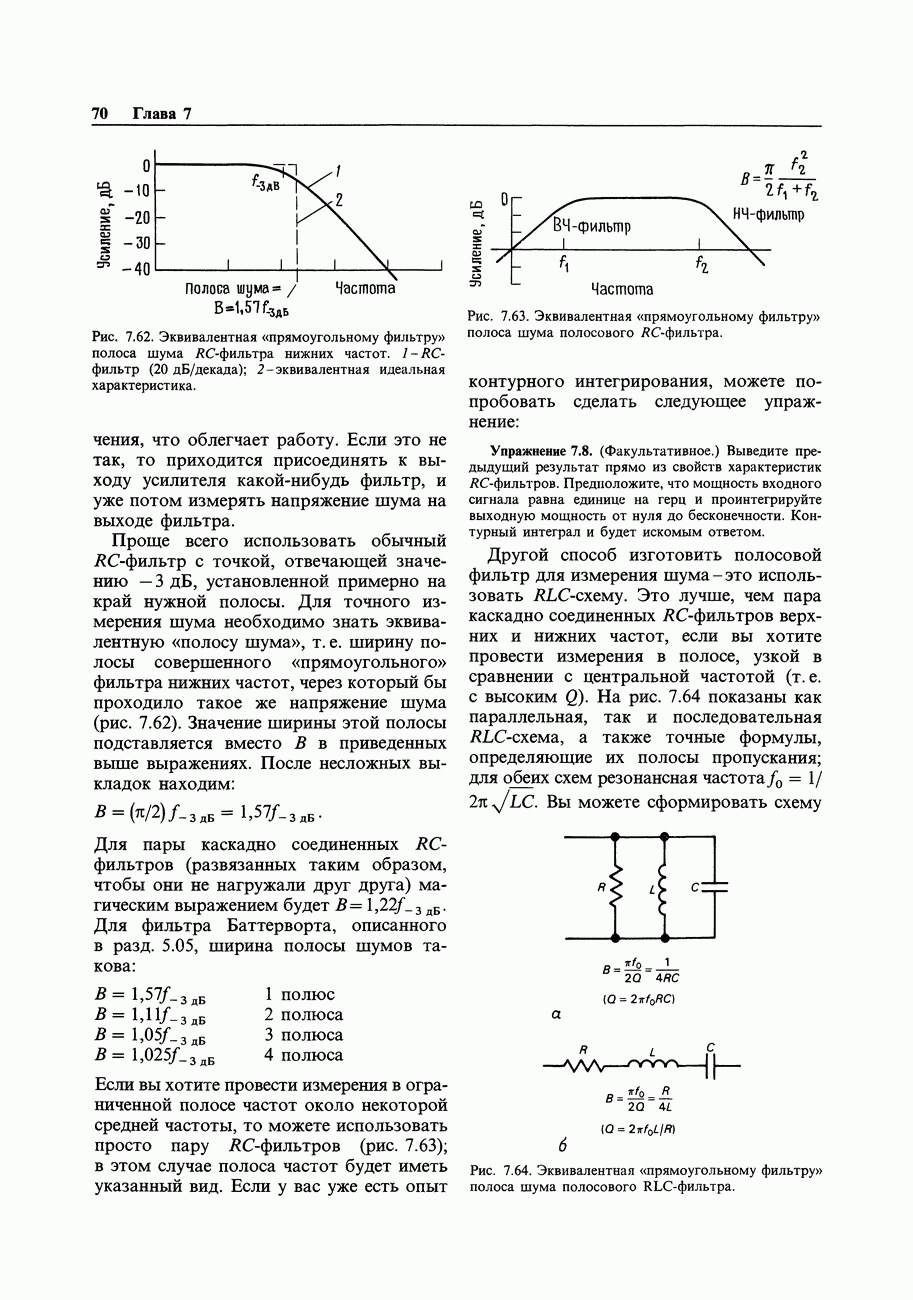
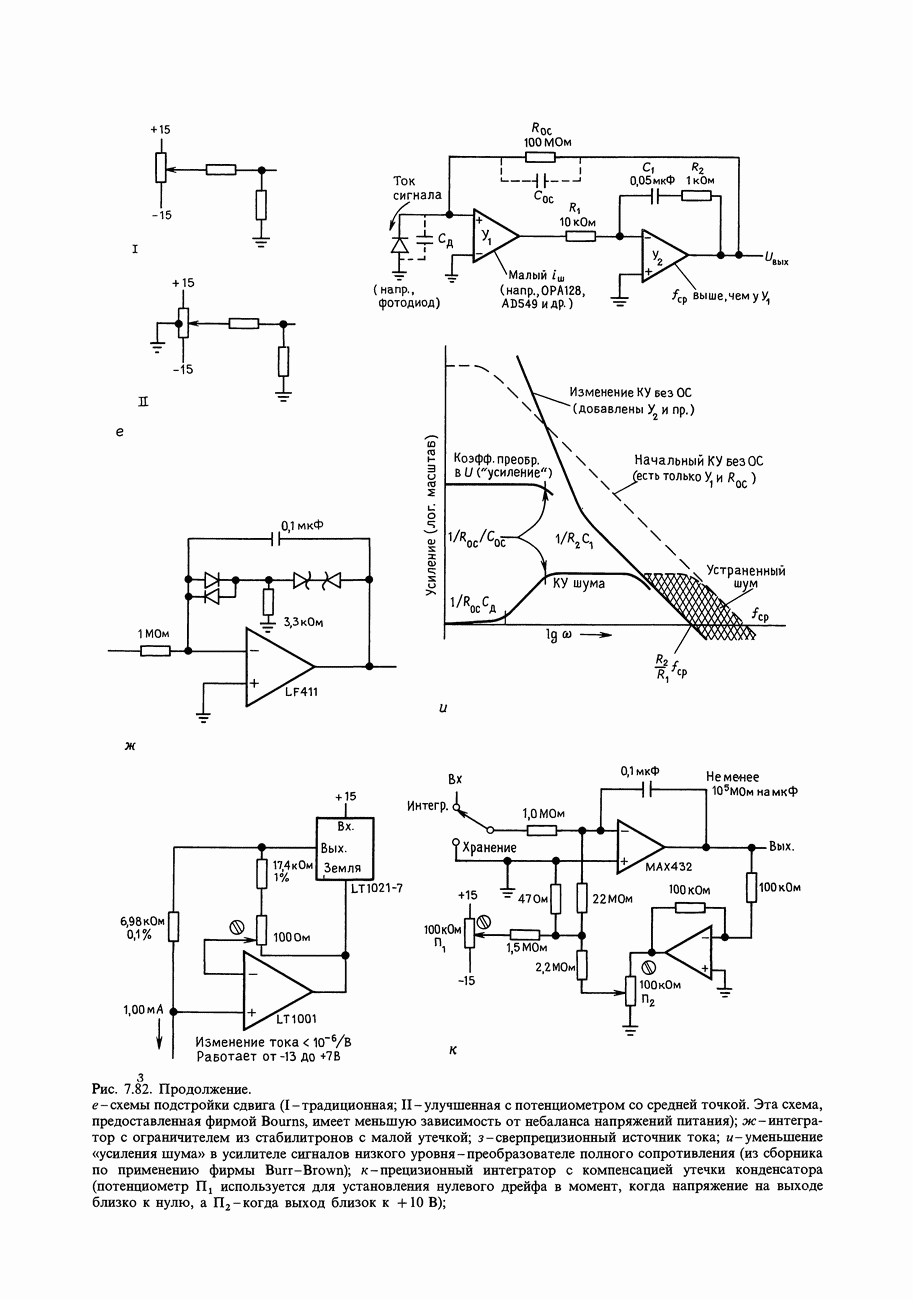
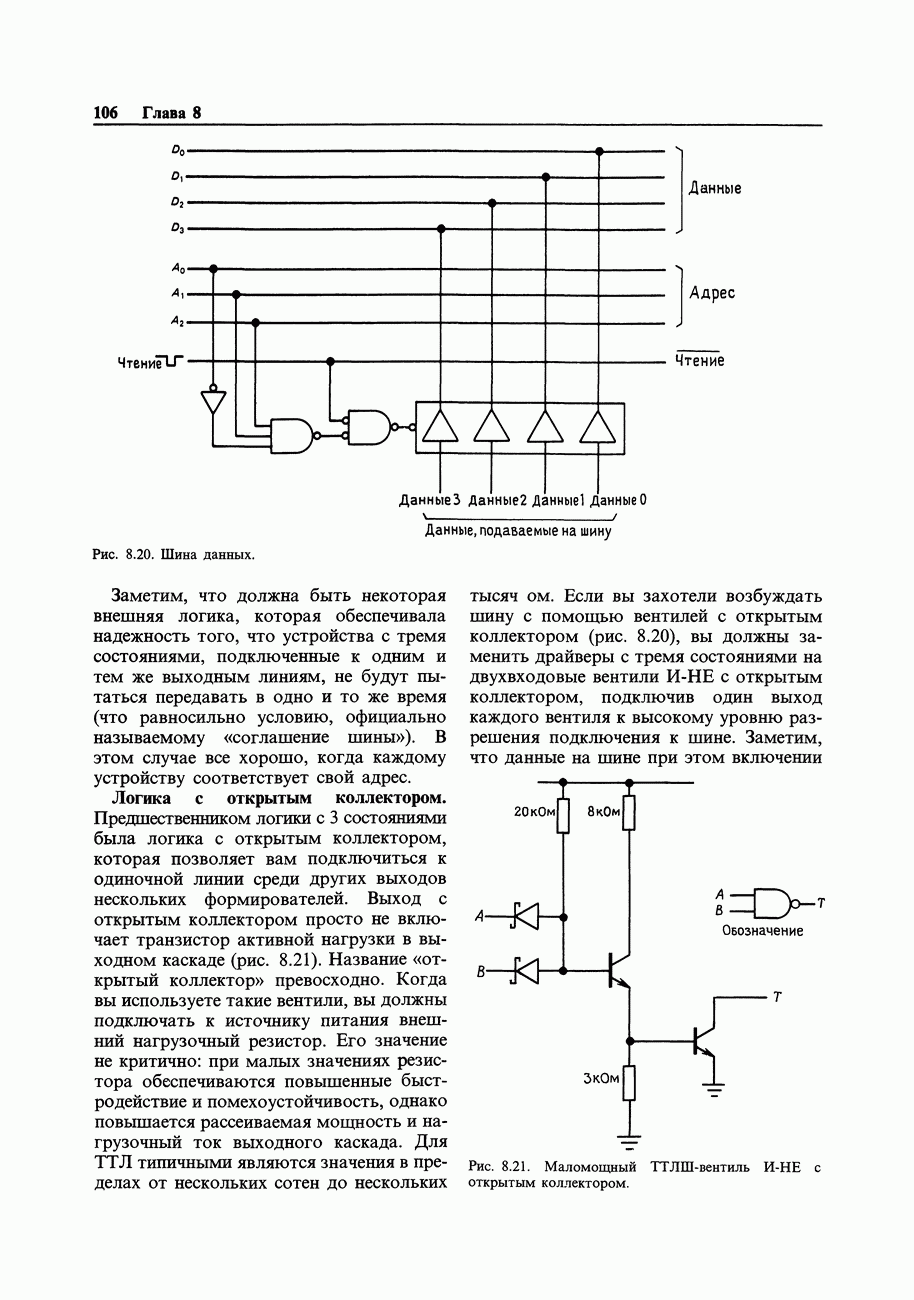
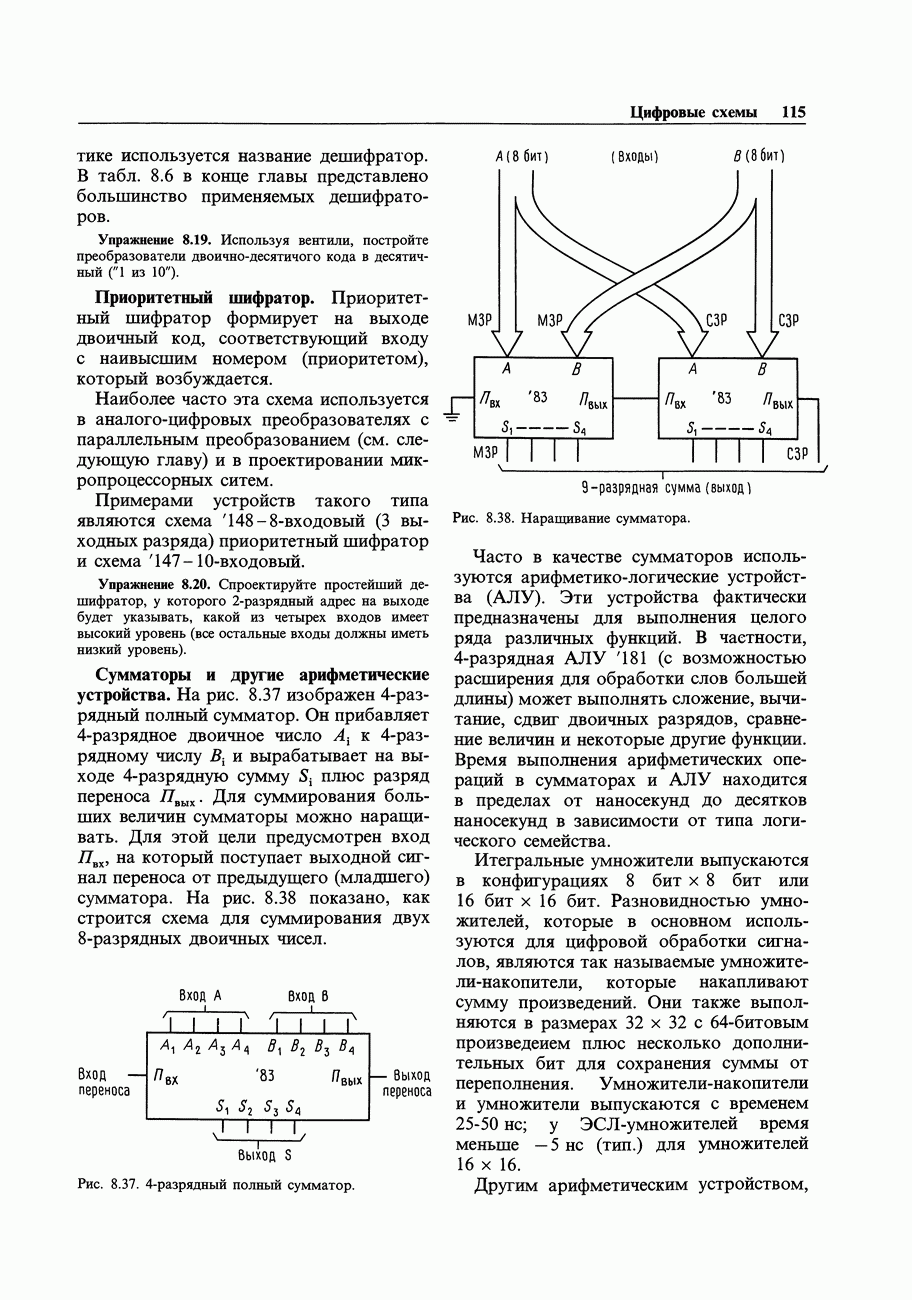
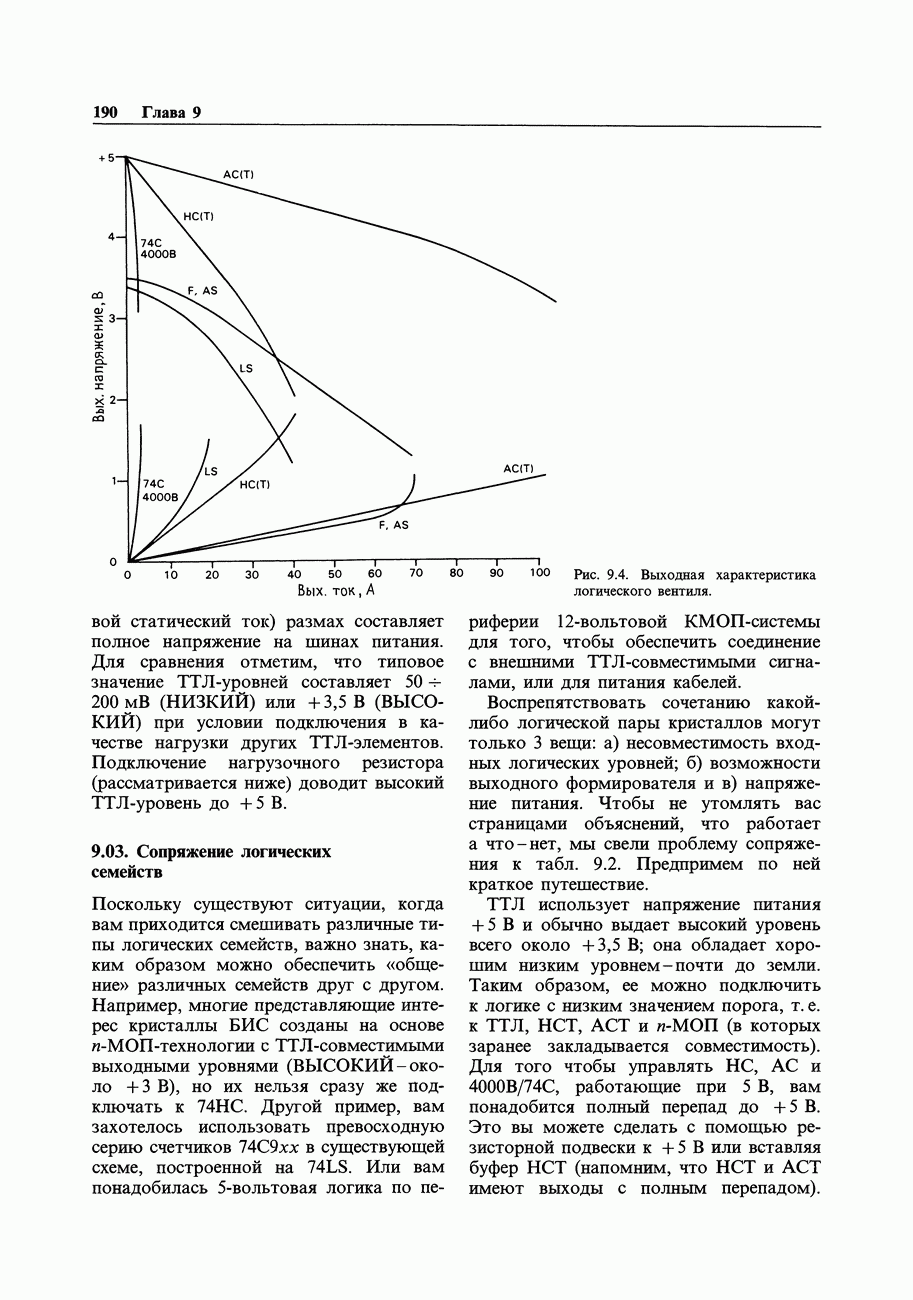
Рис. 9.4. Выходная характеристика логического вентиля.
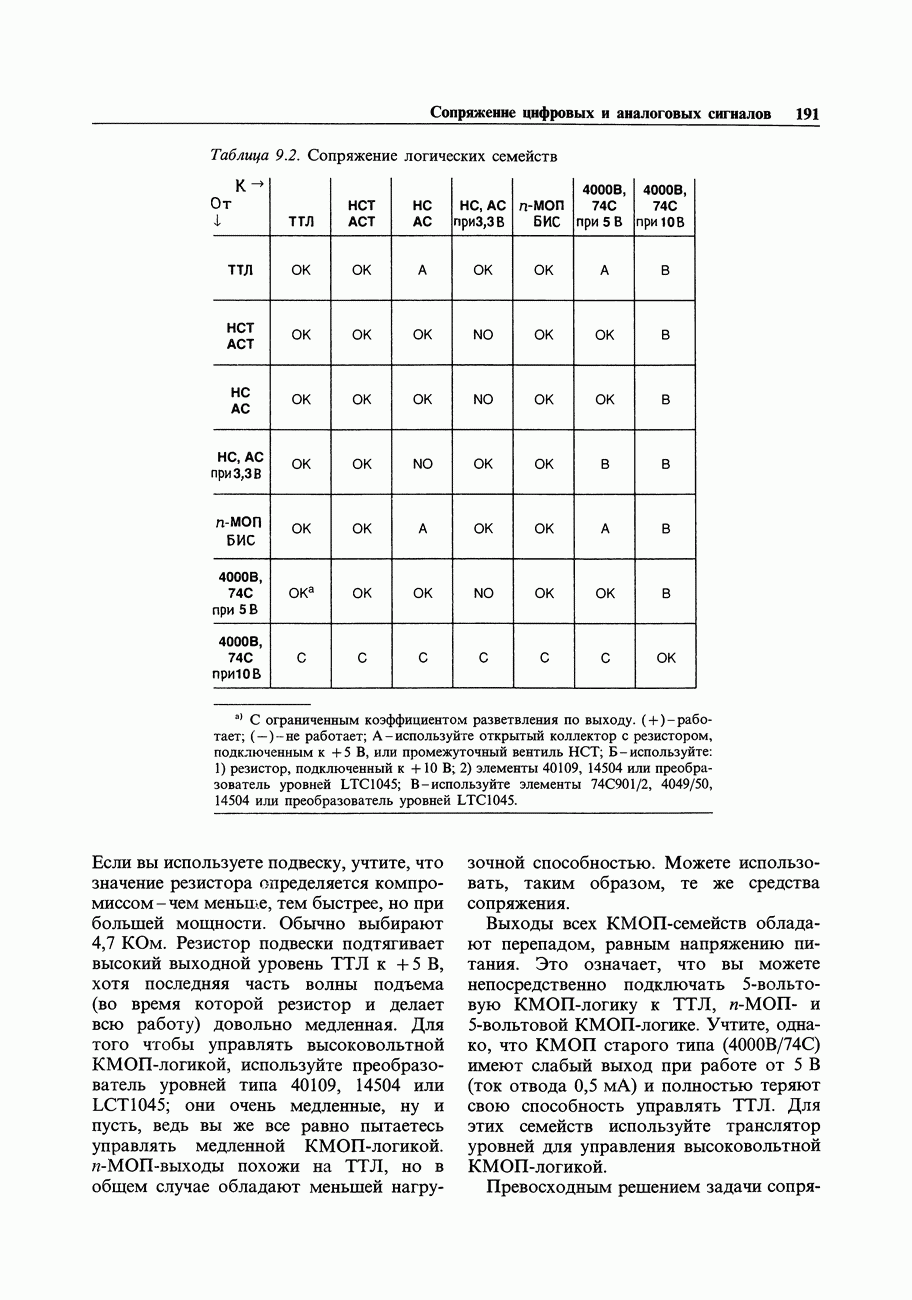
Воспрепятствовать сочетанию какой-либо логической пары кристаллов могут только 3 вещи: а) несовместимость входных логических уровней; б) возможности выходного формирователя и в) напряжение питания. Чтобы не утомлять вас страницами объяснений, что работает а что - нет, мы свели проблему сопряжения к табл. 9.2. Предпримем по ней краткое путешествие.
ТТЛ использует напряжение питания  и обычно выдает высокий уровень всего около
и обычно выдает высокий уровень всего около  ; она обладает хорошим низким уровнем - почти до земли. Таким образом, ее можно подключить к логике с низким значением порога, т. е. к ТТЛ, НСТ, ACT и
; она обладает хорошим низким уровнем - почти до земли. Таким образом, ее можно подключить к логике с низким значением порога, т. е. к ТТЛ, НСТ, ACT и  -МОП (в которых заранее закладывается совместимость). Для того чтобы управлять НС, АС и
-МОП (в которых заранее закладывается совместимость). Для того чтобы управлять НС, АС и  , работающие при 5 В, вам понадобится полный перецад до
, работающие при 5 В, вам понадобится полный перецад до  . Это вы можете сделать с помощью резисторной подвески к
. Это вы можете сделать с помощью резисторной подвески к  или вставляя буфер НСТ (напомним, что НСТ и ACT имеют выходы с полным перепадом).
или вставляя буфер НСТ (напомним, что НСТ и ACT имеют выходы с полным перепадом).
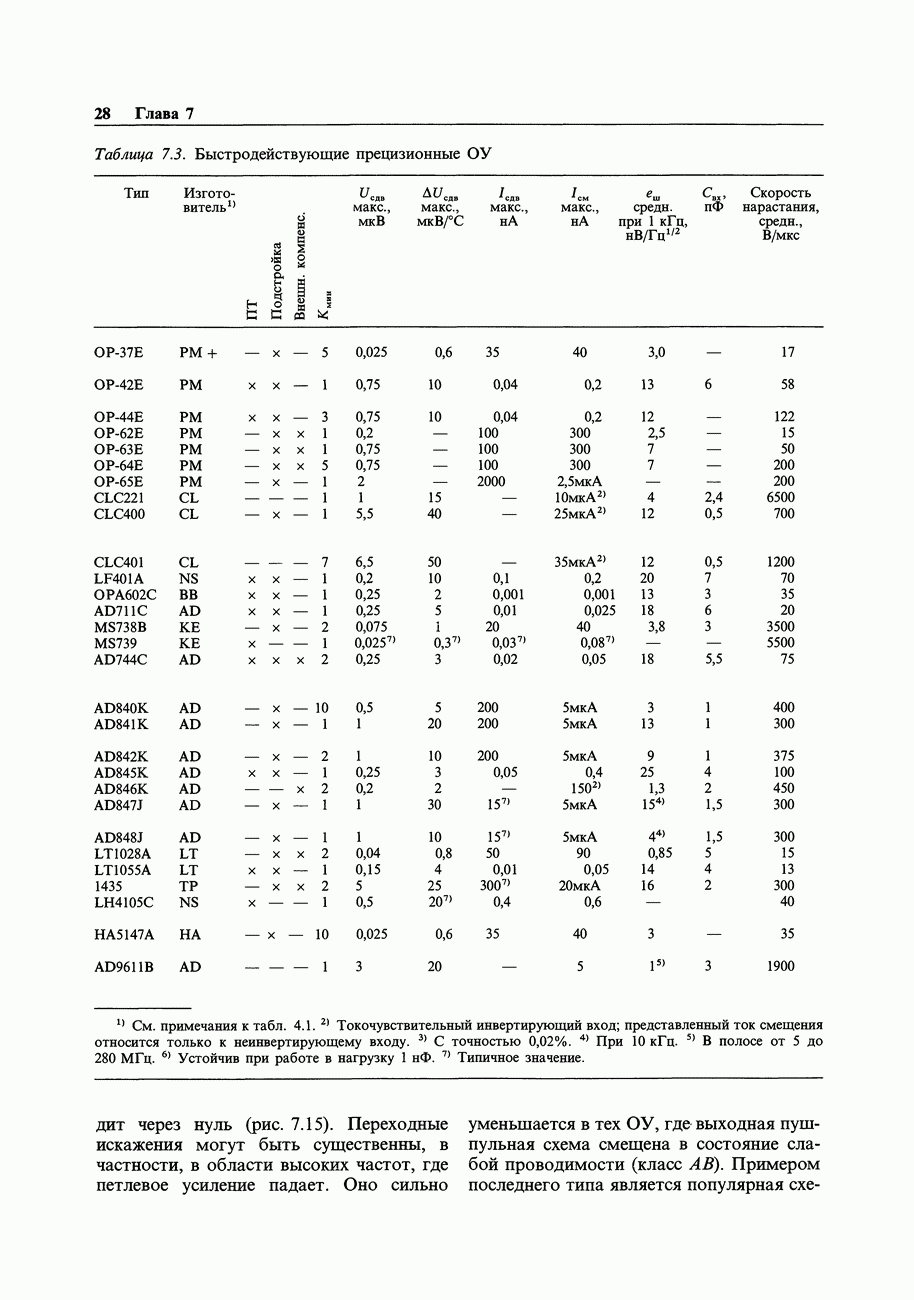
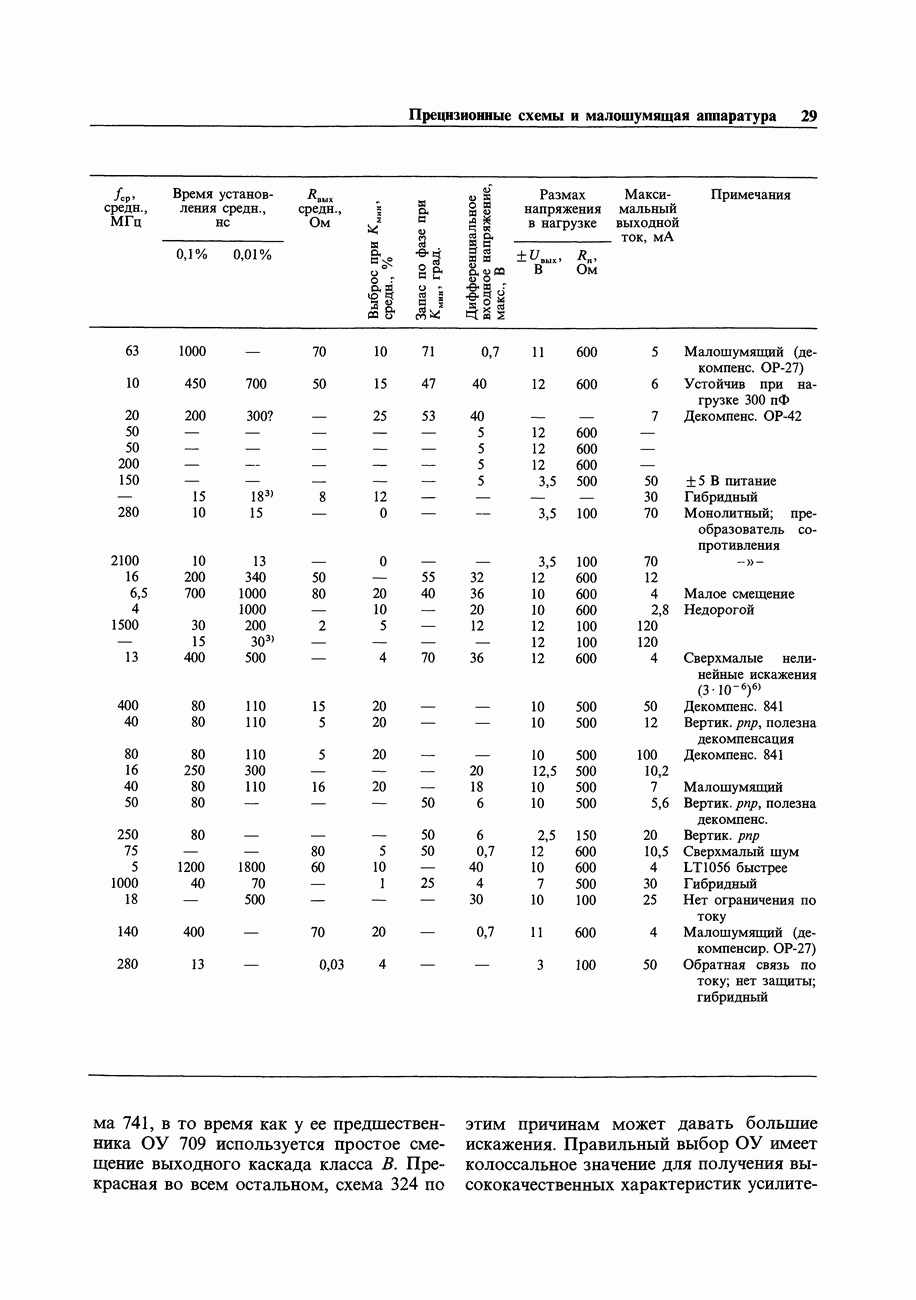
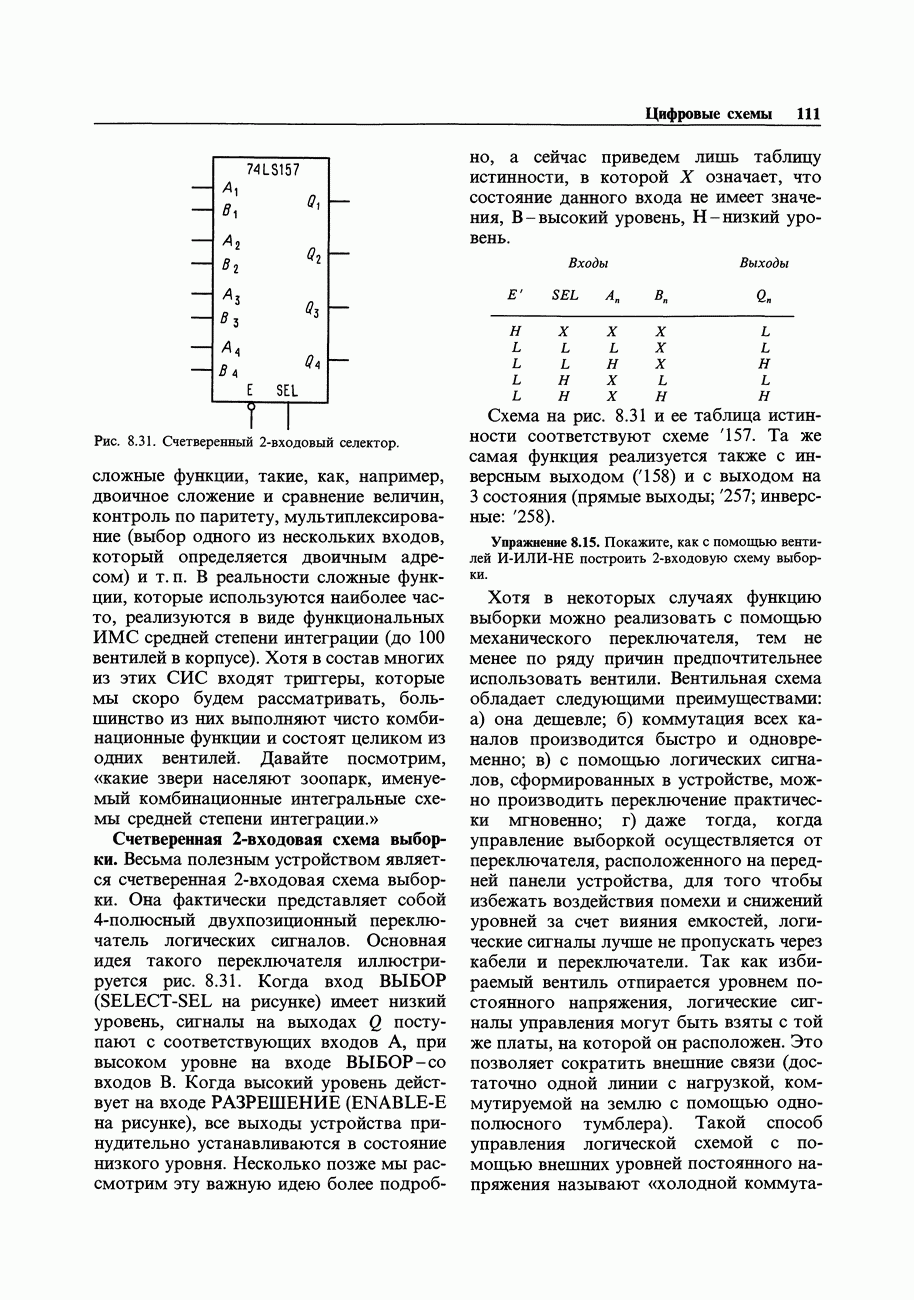
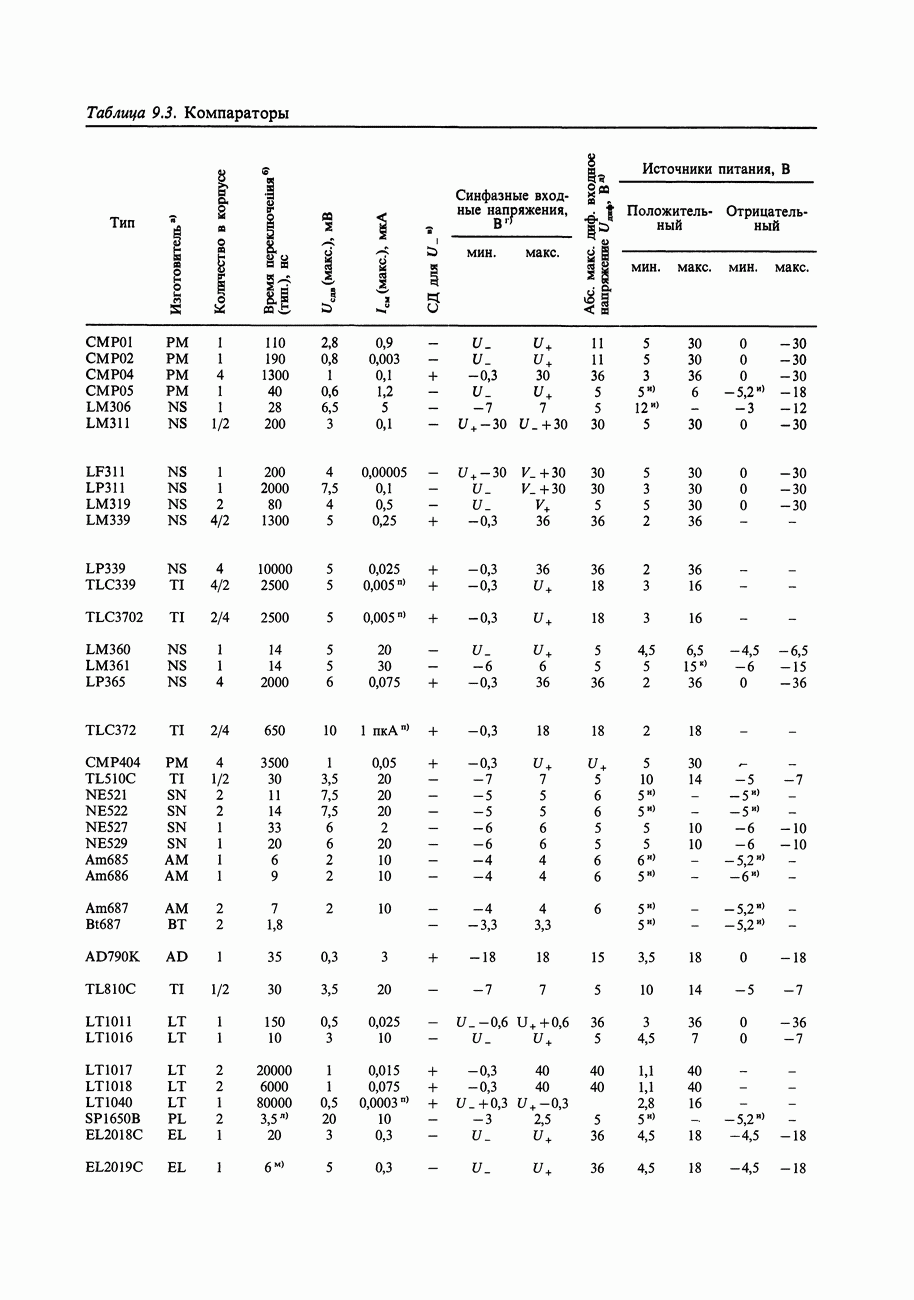
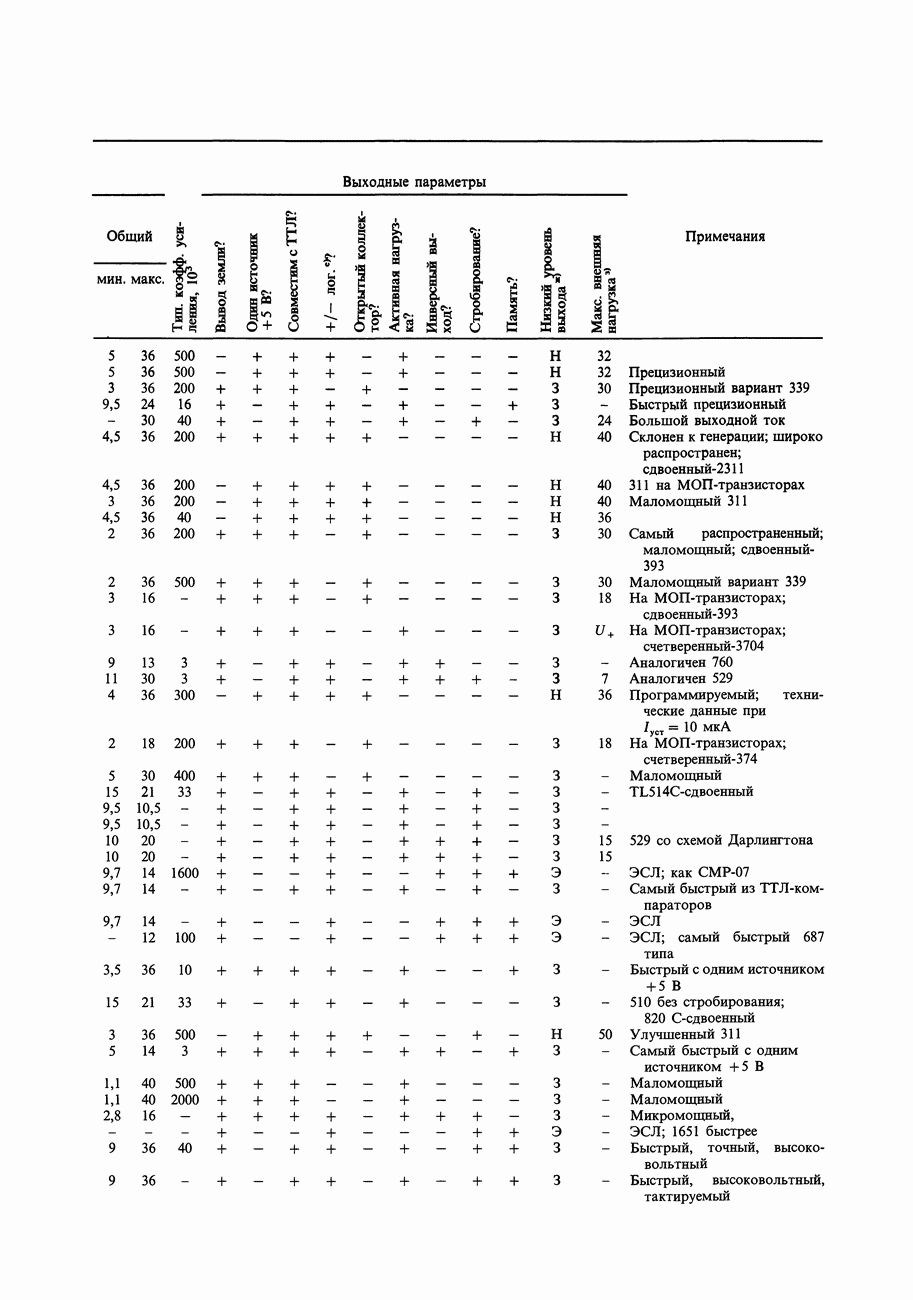
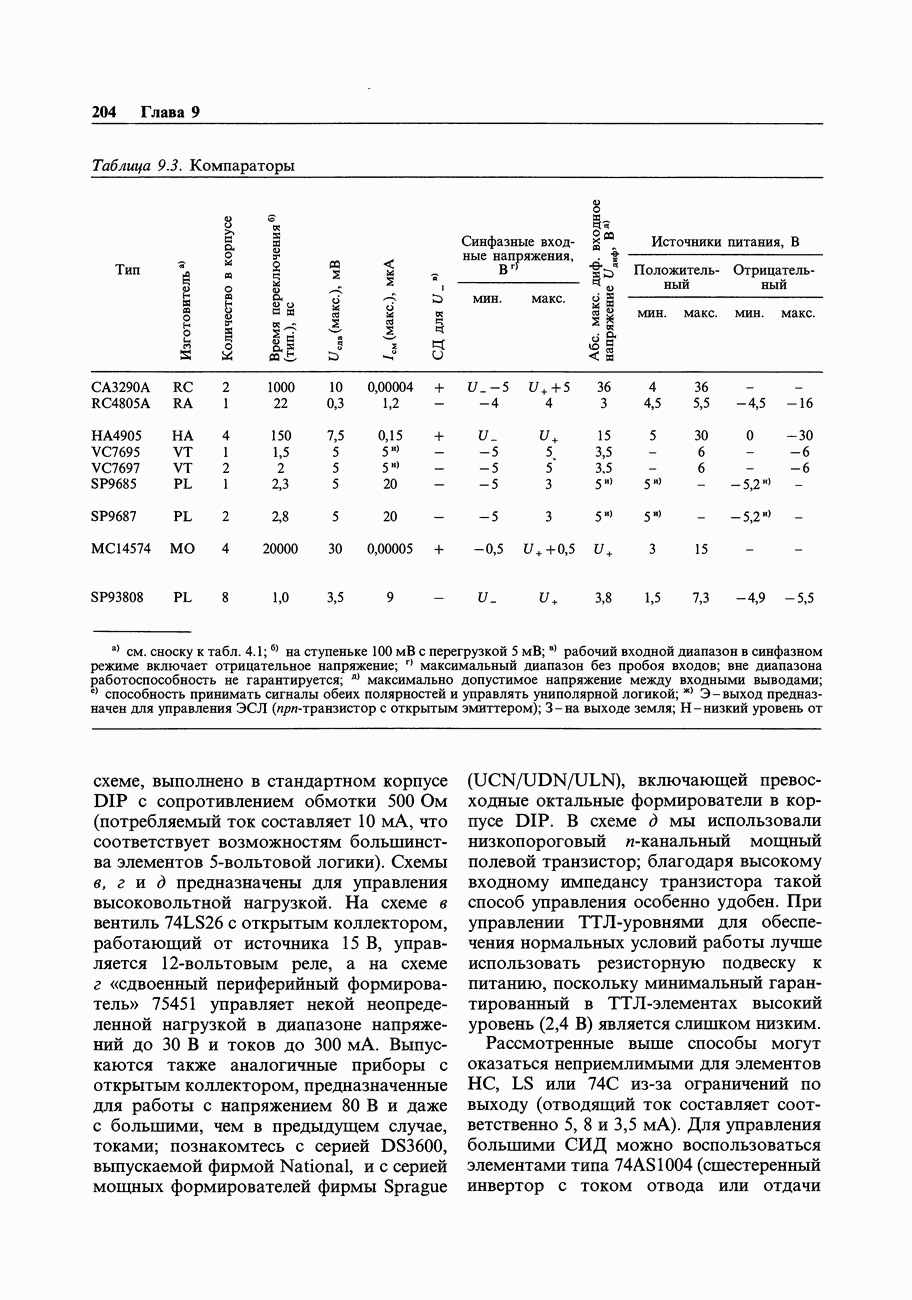
Таблица 9.2. Сопряжение логических семейств

Если вы используете подвеску, учтите, что значение резистора определяется компромиссом - чем меньше, тем быстрее, но при большей мощности. Обычно выбирают 4,7 КОм. Резистор подвески подтягивает высокий выходной уровень ТТЛ к  , хотя последняя часть волны подъема (во время которой резистор и делает всю работу) довольно медленная. Для того чтобы управлять высоковольтной КМОП-логикой, используйте преобразователь уровней типа 40109, 14504 или
, хотя последняя часть волны подъема (во время которой резистор и делает всю работу) довольно медленная. Для того чтобы управлять высоковольтной КМОП-логикой, используйте преобразователь уровней типа 40109, 14504 или  они очень медленные, ну и пусть, ведь вы же все равно пытаетесь управлять медленной КМОП-логикой. n-МОП-выходы похожи на ТТЛ, но в общем случае обладают меньшей нагрузочной способностью. Можете использовать, таким образом, те же средства сопряжения.
они очень медленные, ну и пусть, ведь вы же все равно пытаетесь управлять медленной КМОП-логикой. n-МОП-выходы похожи на ТТЛ, но в общем случае обладают меньшей нагрузочной способностью. Можете использовать, таким образом, те же средства сопряжения.
Выходы всех КМОП-семейств обладают перепадом, равным напряжению питания. Это означает, что вы можете непосредственно подключать  -вольто-вую КМОП-логику к ТТЛ,
-вольто-вую КМОП-логику к ТТЛ,  -МОП- и
-МОП- и  -вольтовой КМОП-логике. Учтите, однако, что КМОП старого типа
-вольтовой КМОП-логике. Учтите, однако, что КМОП старого типа  имеют слабый выход при работе от 5 В (ток отвода
имеют слабый выход при работе от 5 В (ток отвода  ) и полностью теряют свою способность управлять ТТЛ. Для этих семейств используйте транслятор уровней для управления высоковольтной КМОП-логикой.
) и полностью теряют свою способность управлять ТТЛ. Для этих семейств используйте транслятор уровней для управления высоковольтной КМОП-логикой.
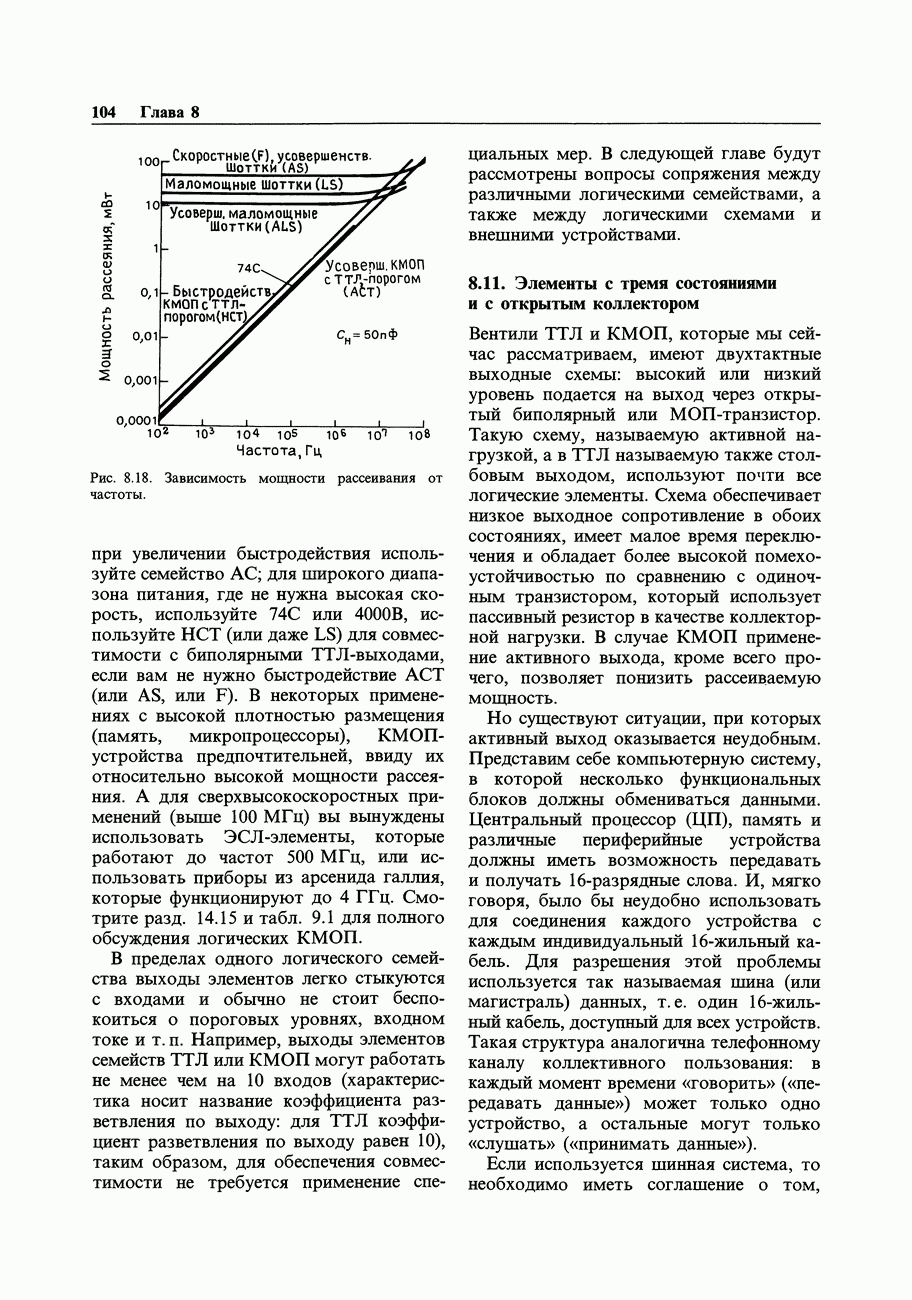
Превосходным решением задачи сопряжения КМОП-ТТЛ/n-МОП является использование КМОП при уменьшенном напряжении питания; по стандарту JEDEC Standard № 8 напряжение питания составляет  , при этом входной порог располагается вблизи обычного ТТЛ-порога 1,4 В. Таким образом, ТТЛ может непосредственно управлять НС/АС при питании 3,3 В и наоборот. В качестве дополнительного вознаграждения работа при 3,3 В снижает динамическую мощность потребления (см. разд. 8.10, 14.16 и рис. 8.18 и рис. 14.38) на 55% относительно мощности при 5 В при увеличении задержек распространения почти на 40%. Учтите, однако, что вы не можете подключать (и в том и в другом направлении)
, при этом входной порог располагается вблизи обычного ТТЛ-порога 1,4 В. Таким образом, ТТЛ может непосредственно управлять НС/АС при питании 3,3 В и наоборот. В качестве дополнительного вознаграждения работа при 3,3 В снижает динамическую мощность потребления (см. разд. 8.10, 14.16 и рис. 8.18 и рис. 14.38) на 55% относительно мощности при 5 В при увеличении задержек распространения почти на 40%. Учтите, однако, что вы не можете подключать (и в том и в другом направлении)  -вольтовую КМОП к другим КМОП, работающим при 5 В.
-вольтовую КМОП к другим КМОП, работающим при 5 В.
Упражнение 9.1. Объясните, почему последнее утверждение истинно.
Наконец, высоковольтная КМОП-логика может управлять  -вольтовой логикой, если для формирования
-вольтовой логикой, если для формирования  -вольтового выходного перепада вы поставите преобразователь уровней
-вольтового выходного перепада вы поставите преобразователь уровней  или 4049/4050). Можно управлять LS ТТЛ-элементами непосредственно от высоковольтной КМОП-логики, поскольку там нет диодов, защищающих входы, и входное напряжение пробоя обычно превышает 10 В; однако в соответствии с техническими условиями на LS (абсолютное максимальное входное напряжение 7 В) необходимо использовать преобразователь уровней.
или 4049/4050). Можно управлять LS ТТЛ-элементами непосредственно от высоковольтной КМОП-логики, поскольку там нет диодов, защищающих входы, и входное напряжение пробоя обычно превышает 10 В; однако в соответствии с техническими условиями на LS (абсолютное максимальное входное напряжение 7 В) необходимо использовать преобразователь уровней.
Предостережение. Хотя статические логические уровни могут не вызывать беспокойства, иногда возникает занимательная динамическая несовместимость, если вы пытаетесь управлять фронтовыми входами (например, входы синхронизации счетчиков) НС или АС от выходов более медленной логики типа  или
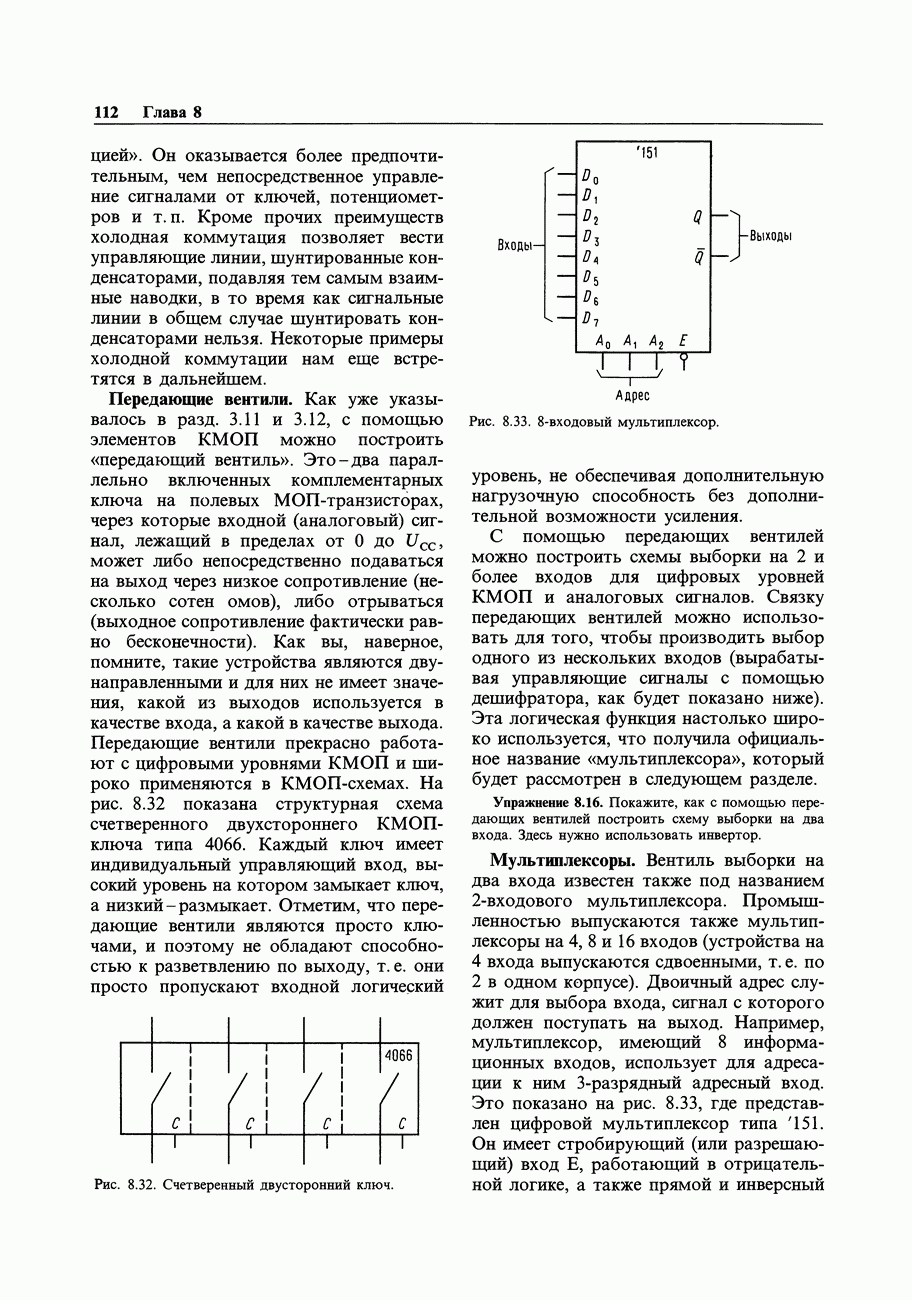
или  . На рис. 9.5 изображены многократные переходы, которые вы могли часто наблюдать; иногда кристалл НС совсем отказывается считать до тех пор, пока вы не прикоснетесь щупом осциллографа (или небольшой
. На рис. 9.5 изображены многократные переходы, которые вы могли часто наблюдать; иногда кристалл НС совсем отказывается считать до тех пор, пока вы не прикоснетесь щупом осциллографа (или небольшой  )! По-видимому, виновником этого является комбинация большого времени перехода и относительно высокого выходного импеданса медленной КМОП.
)! По-видимому, виновником этого является комбинация большого времени перехода и относительно высокого выходного импеданса медленной КМОП.

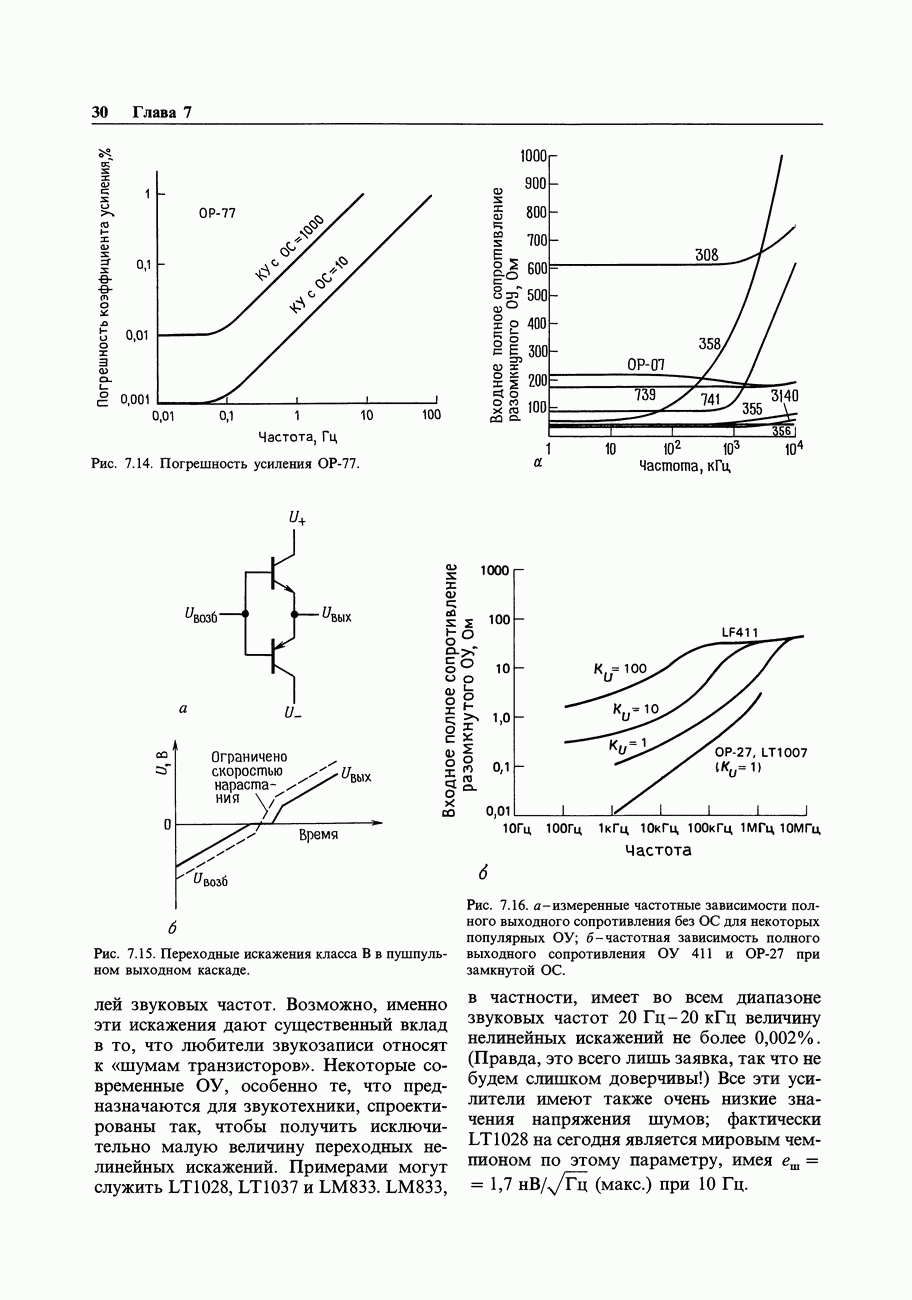
Рис. 9.5. Быструю фронтовую логику нельзя запускать медленными сигналами (например, от узлов с медленной логикой).
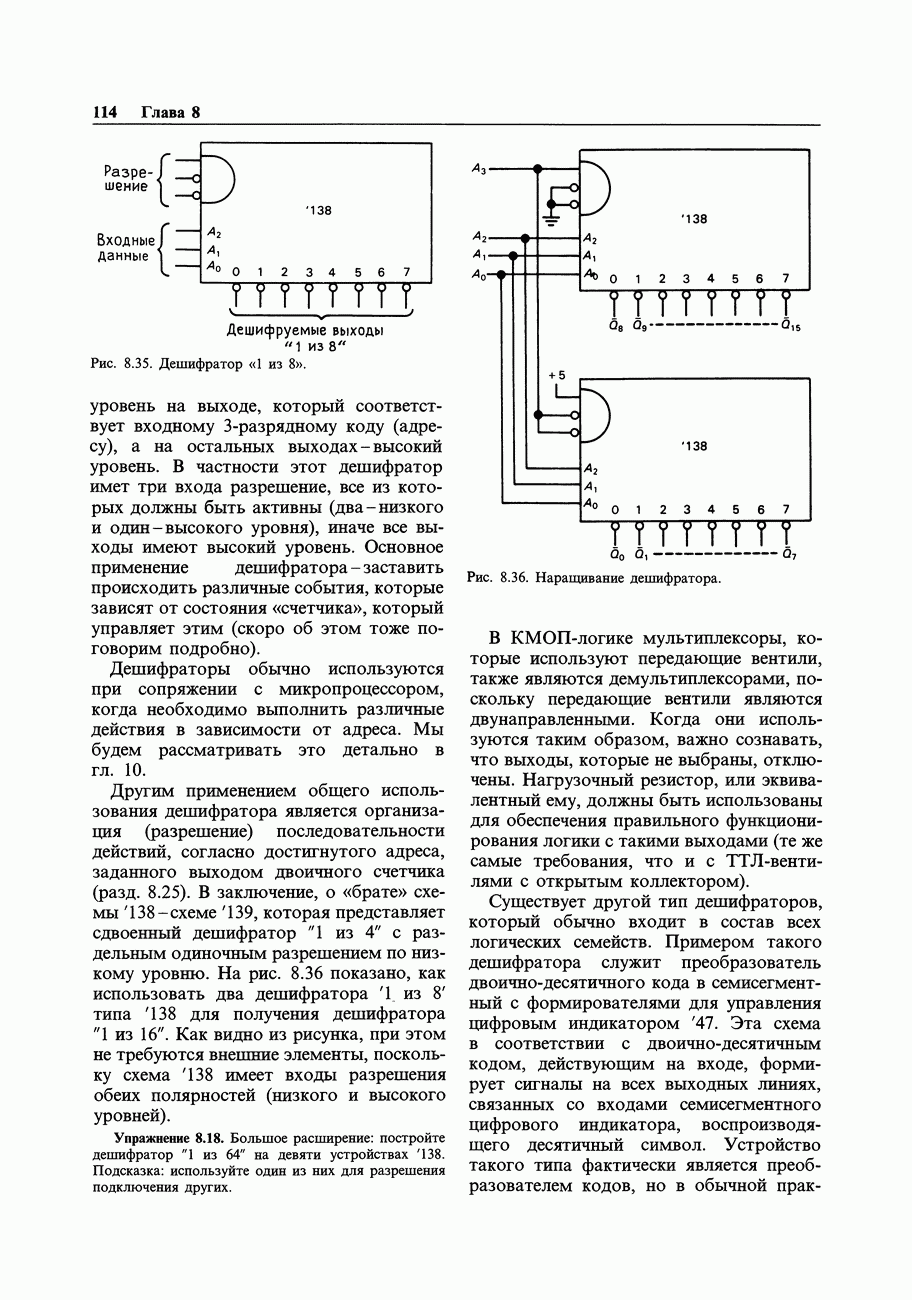
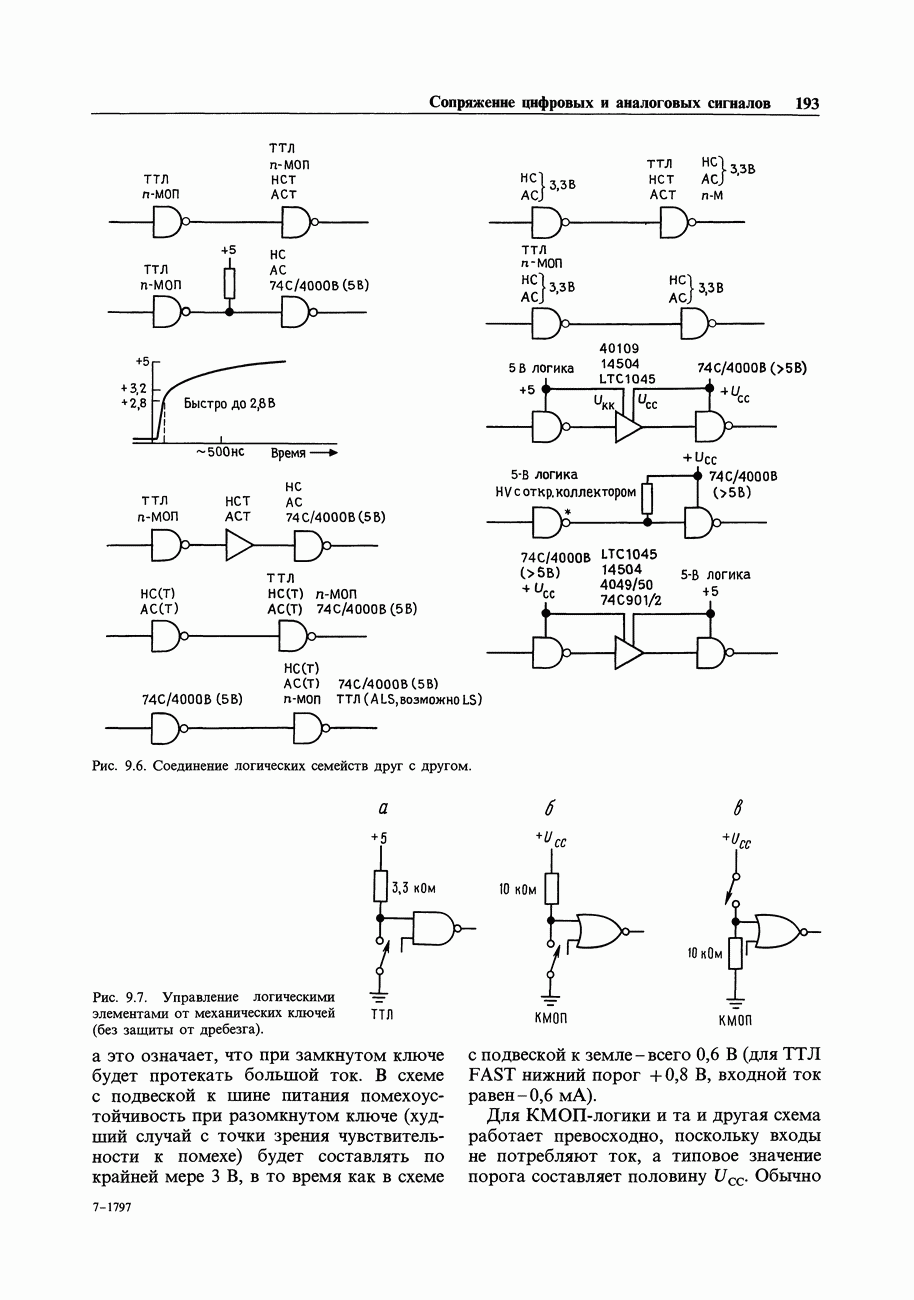
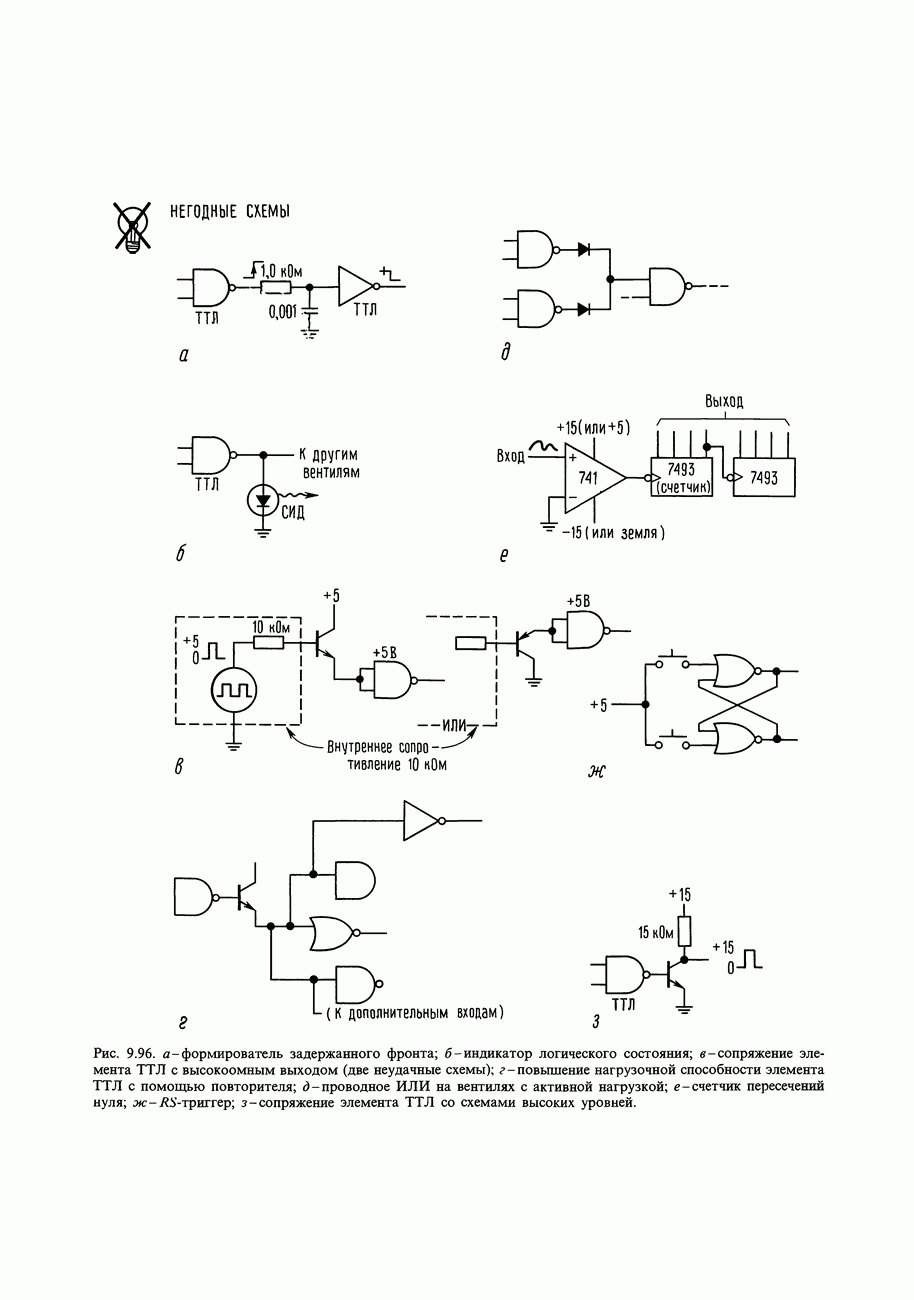
На рис. 9.6 приведены несколько сочетаний семейств, с которыми вам, вероятно, доводилось встречаться.
| << Предыдущий параграф | Следующий параграф >> |
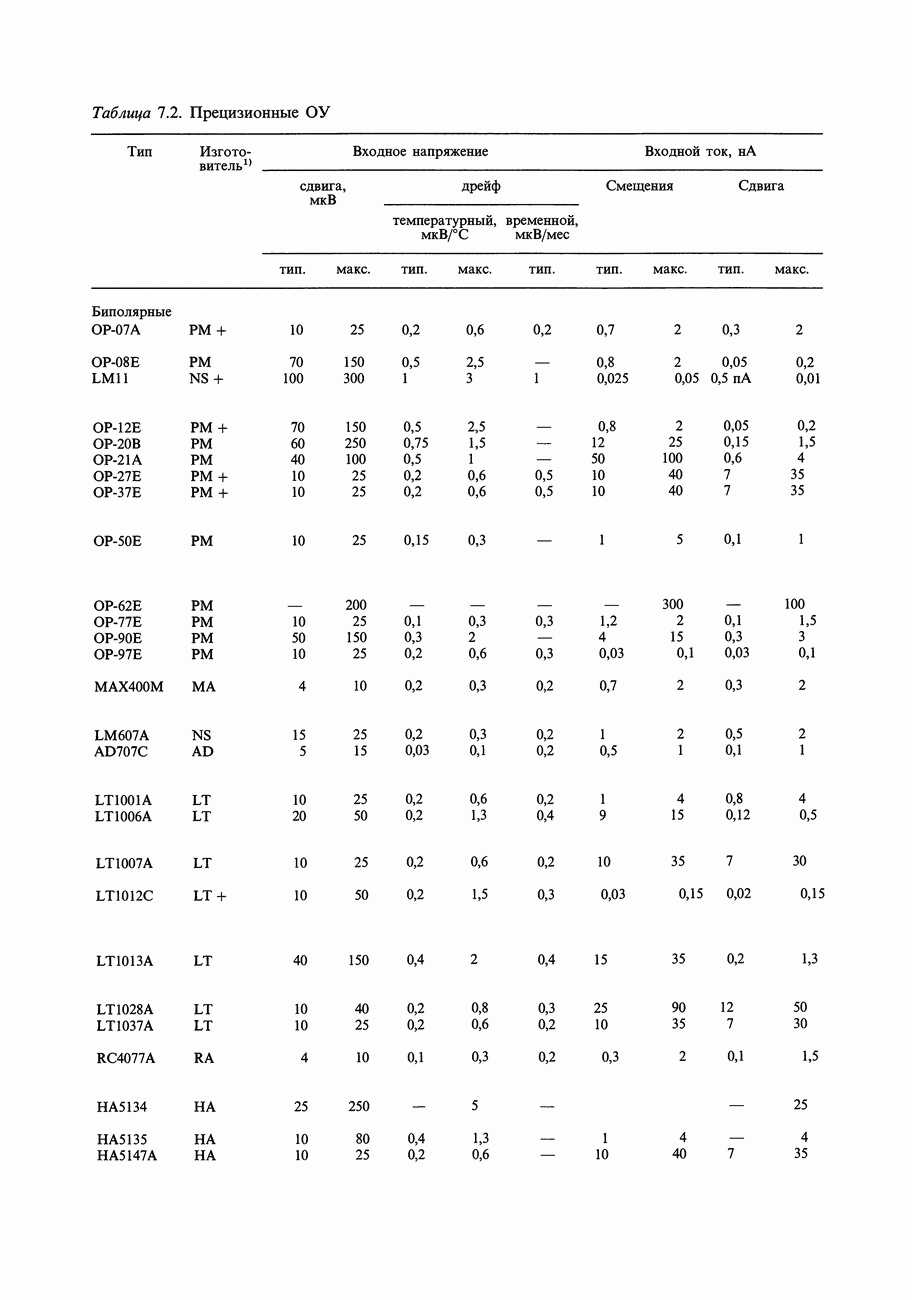
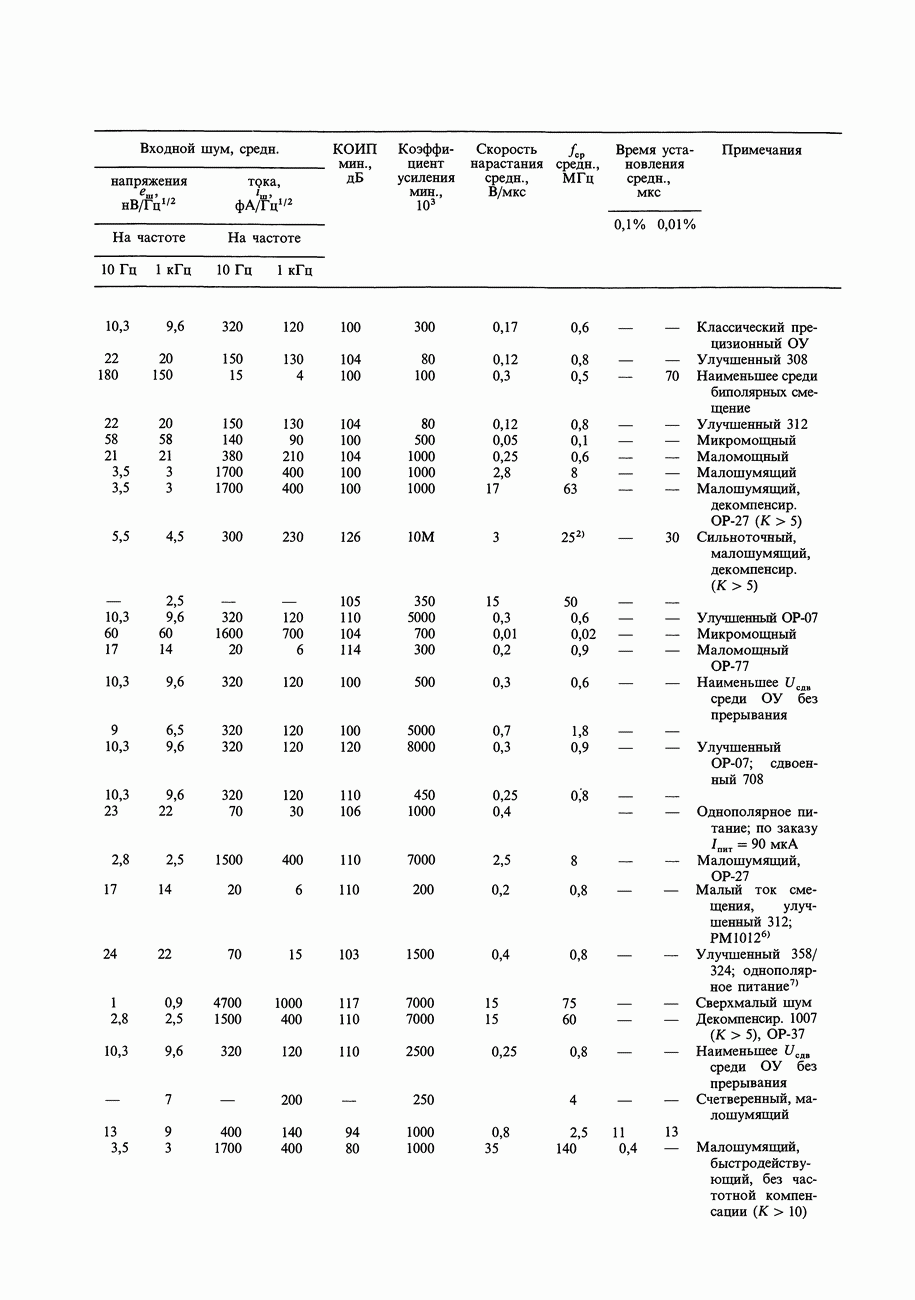
- ГЛАВА 7. ПРЕЦИЗИОННЫЕ СХЕМЫ И МАЛОШУМЯЩАЯ АППАРАТУРА
- 7.01. Соотношение точности и динамического диапазона
- 7.02. Бюджет погрешностей схемы
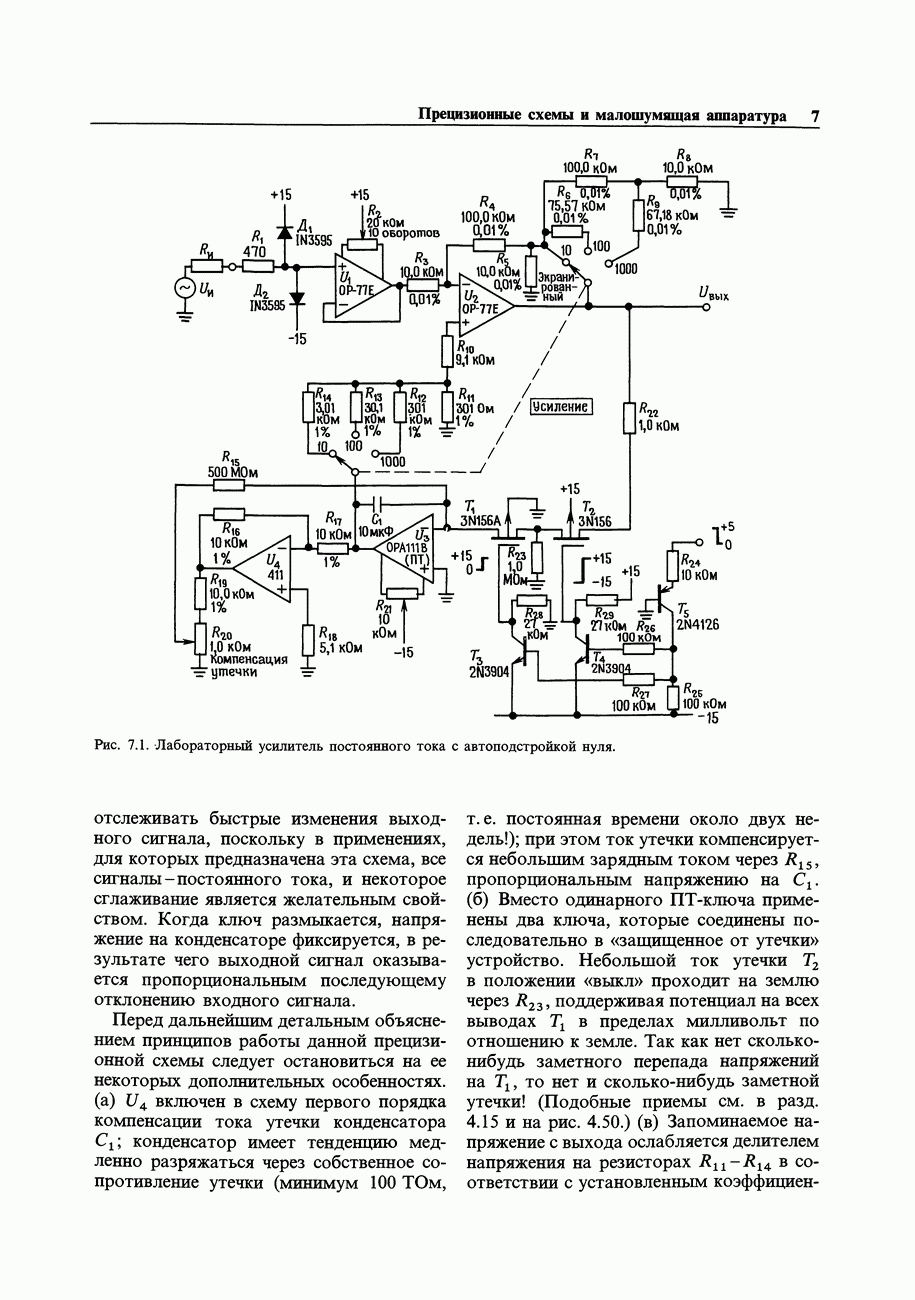
- 7.03. Пример схемы: прецизионный усилитель с автоматическим выбором нуля
- 7.04. «Бюджет погрешностей» при проектировании прецизионной схемы
- 7.05. Погрешности внешних цепей
- 7.06. Входные погрешности усилителя
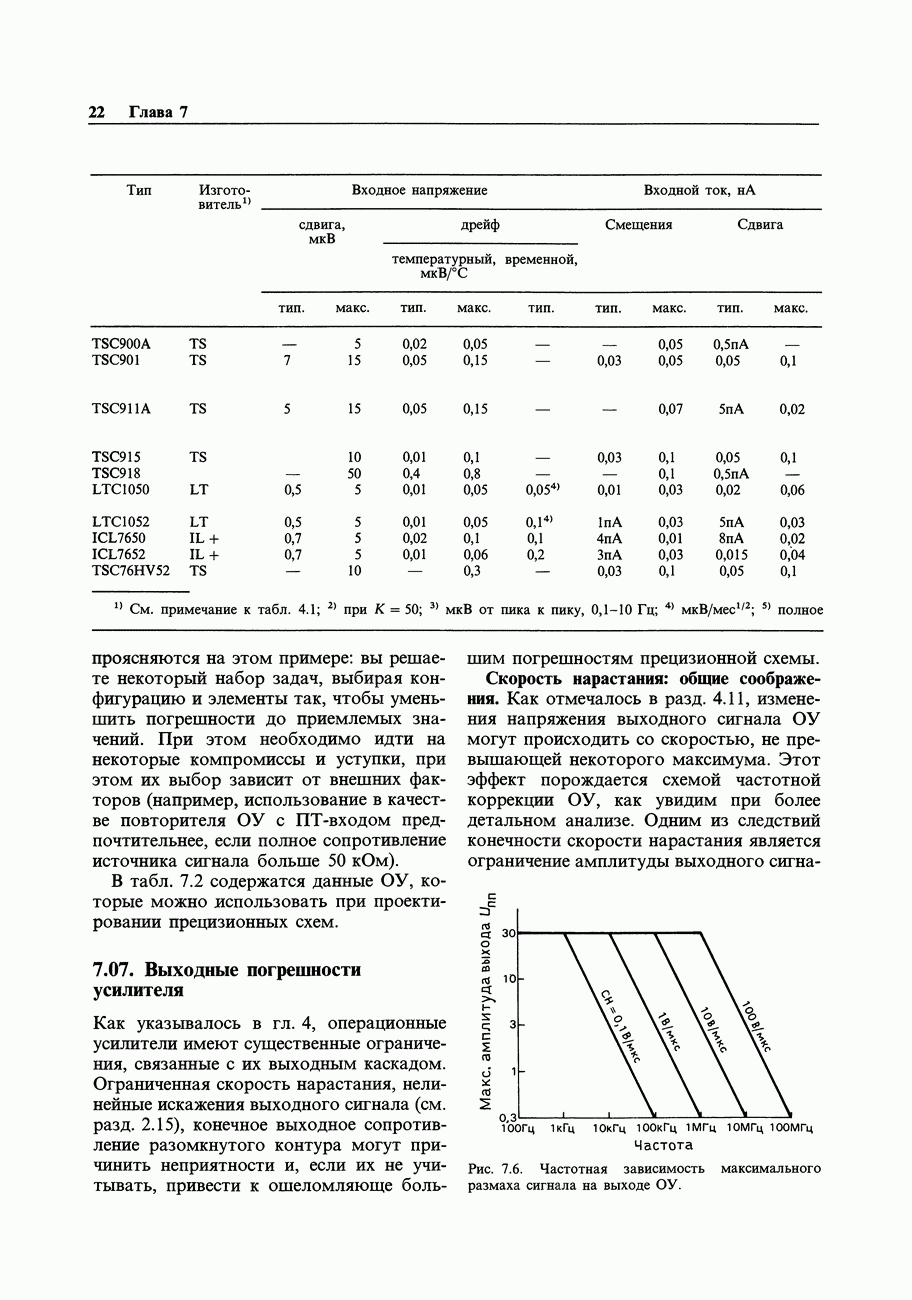
- 7.07. Выходные погрешности усилителя
- 7.08. Усилители с автоподстройкой нуля (стабилизированные прерыванием)
- Кое-что еще о схемах с прерыванием
- ДИФФЕРЕНЦИАЛЬНЫЕ И ИЗМЕРИТЕЛЬНЫЕ УСИЛИТЕЛИ
- 7.09. Простой разностный усилитель
- 7.10. Стандартный измерительный усилитель на трех ОУ
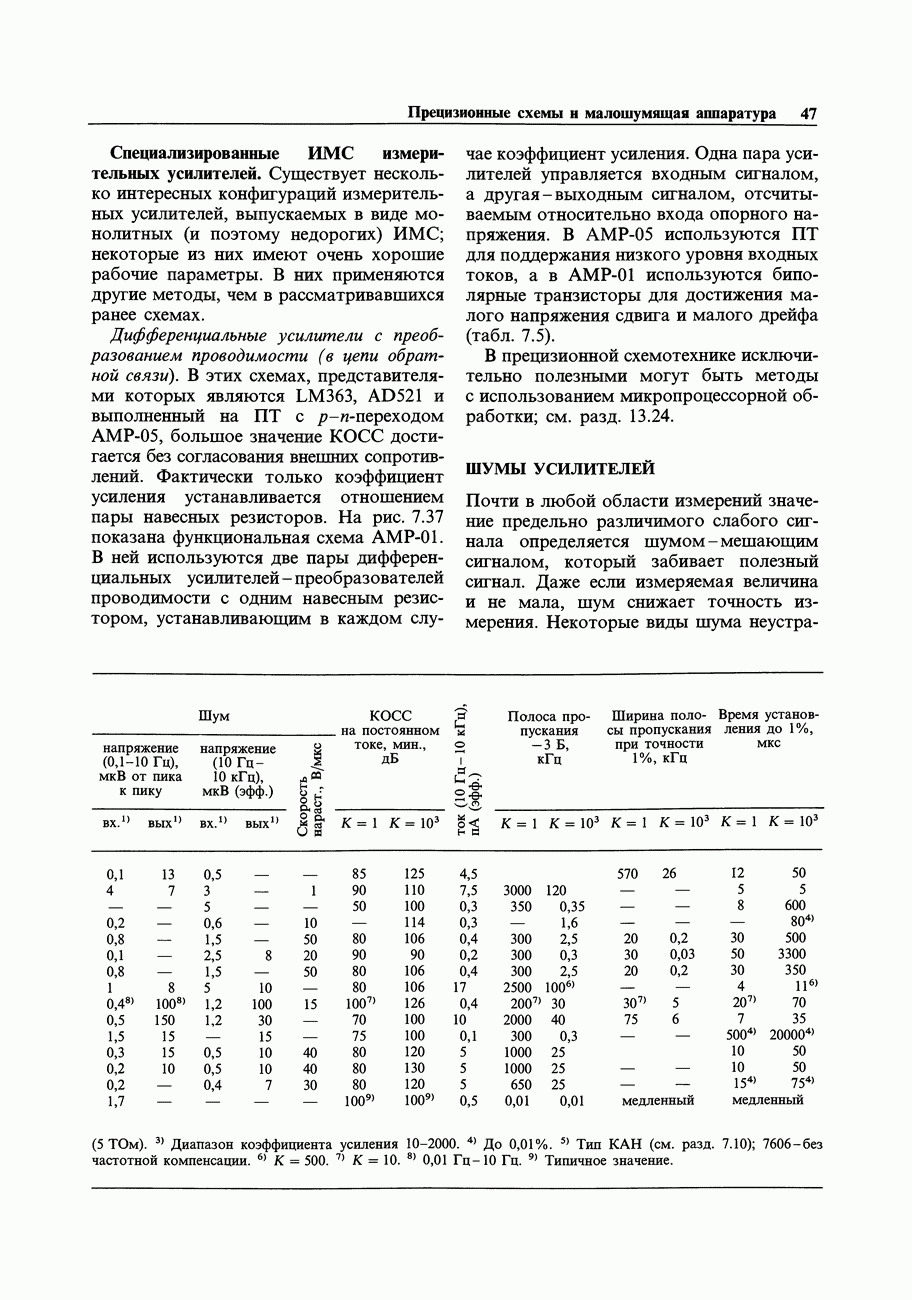
- ШУМЫ УСИЛИТЕЛЕЙ
- 7.11. Происхождение и виды шумов
- 7.12. Отношение сигнал/шум и коэффициент шума
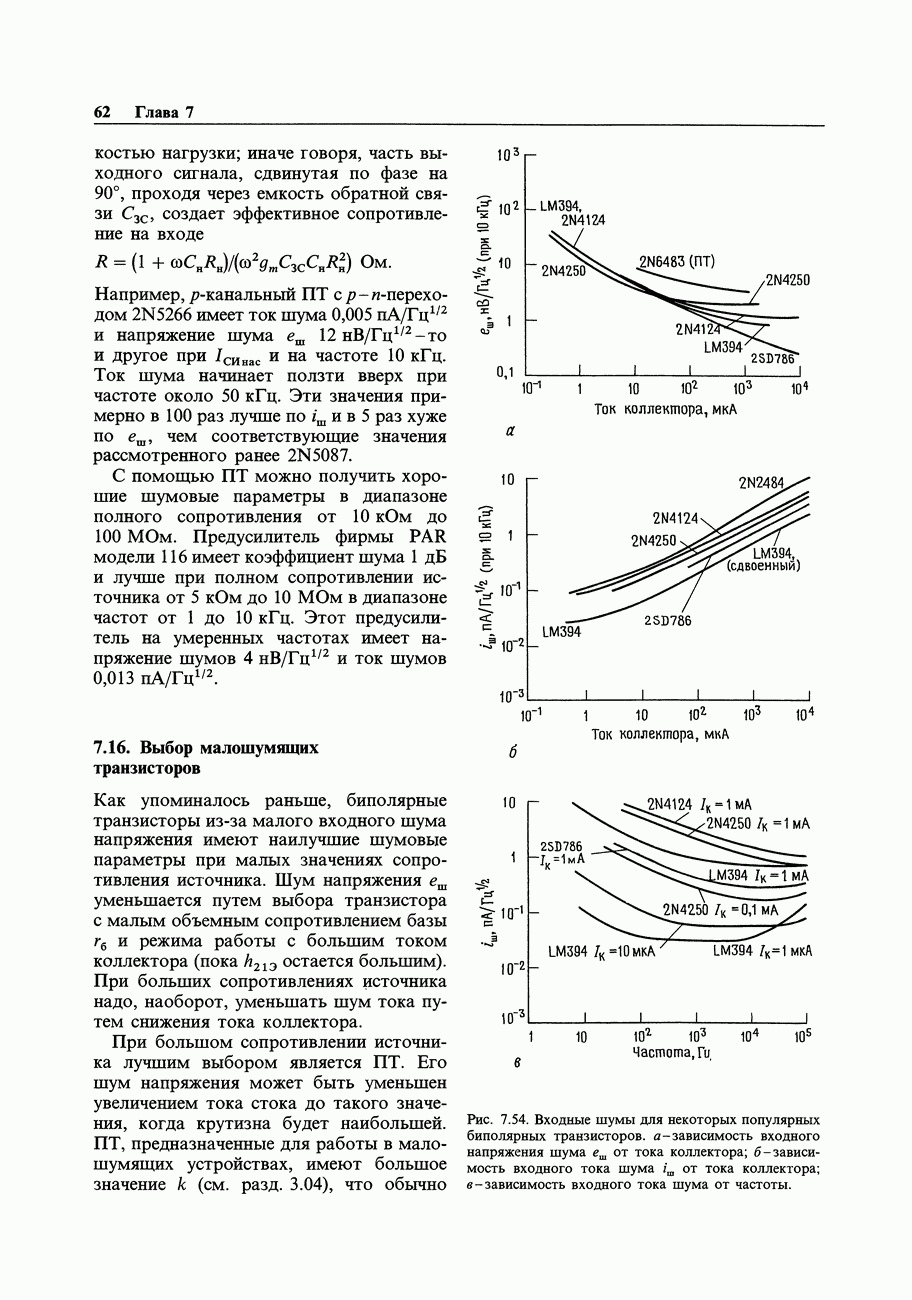
- 7.13. Шум тока и напряжения транзисторного усилителя
- 7.14. Проектирование малошумящих схем на биполярных транзисторах
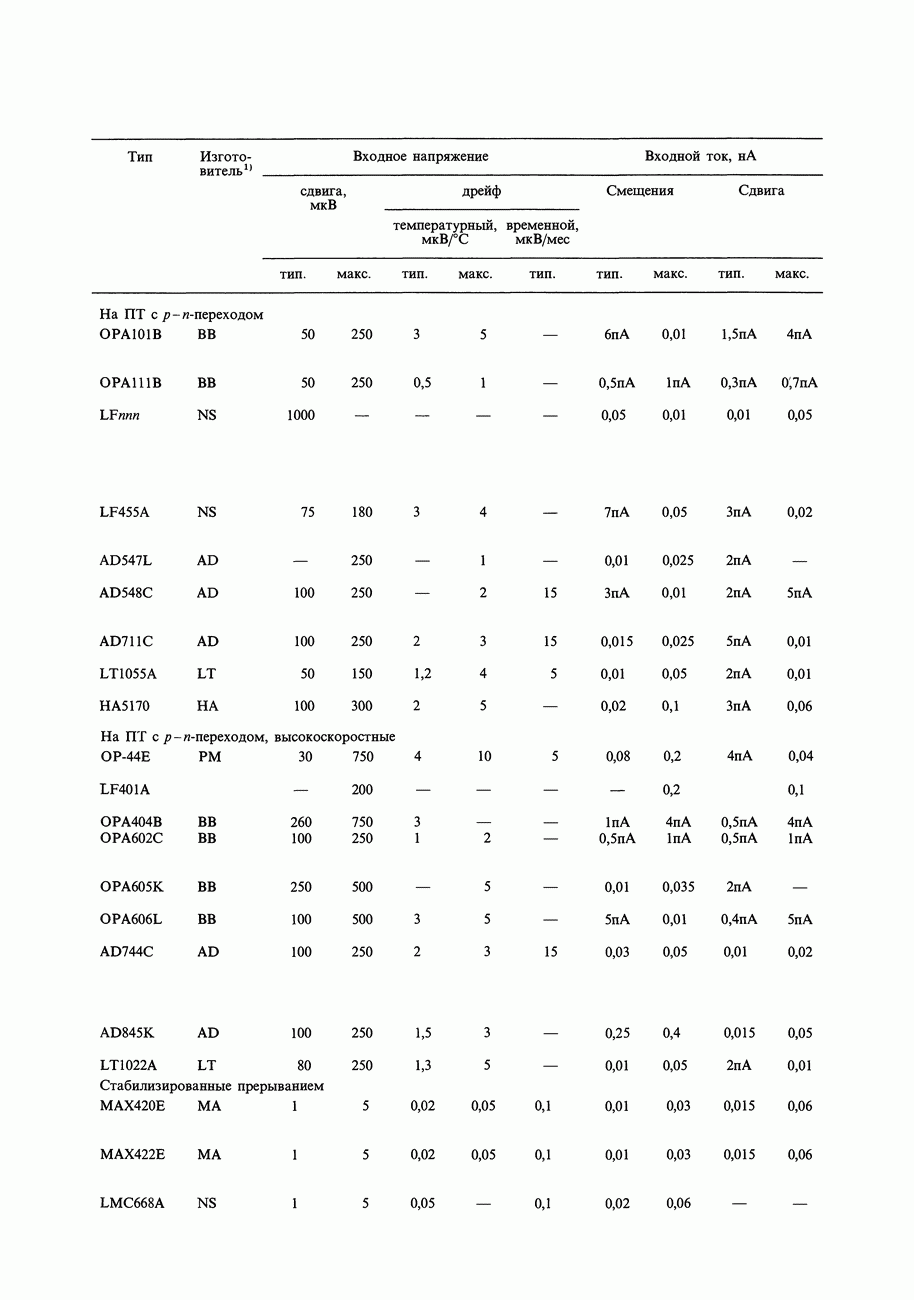
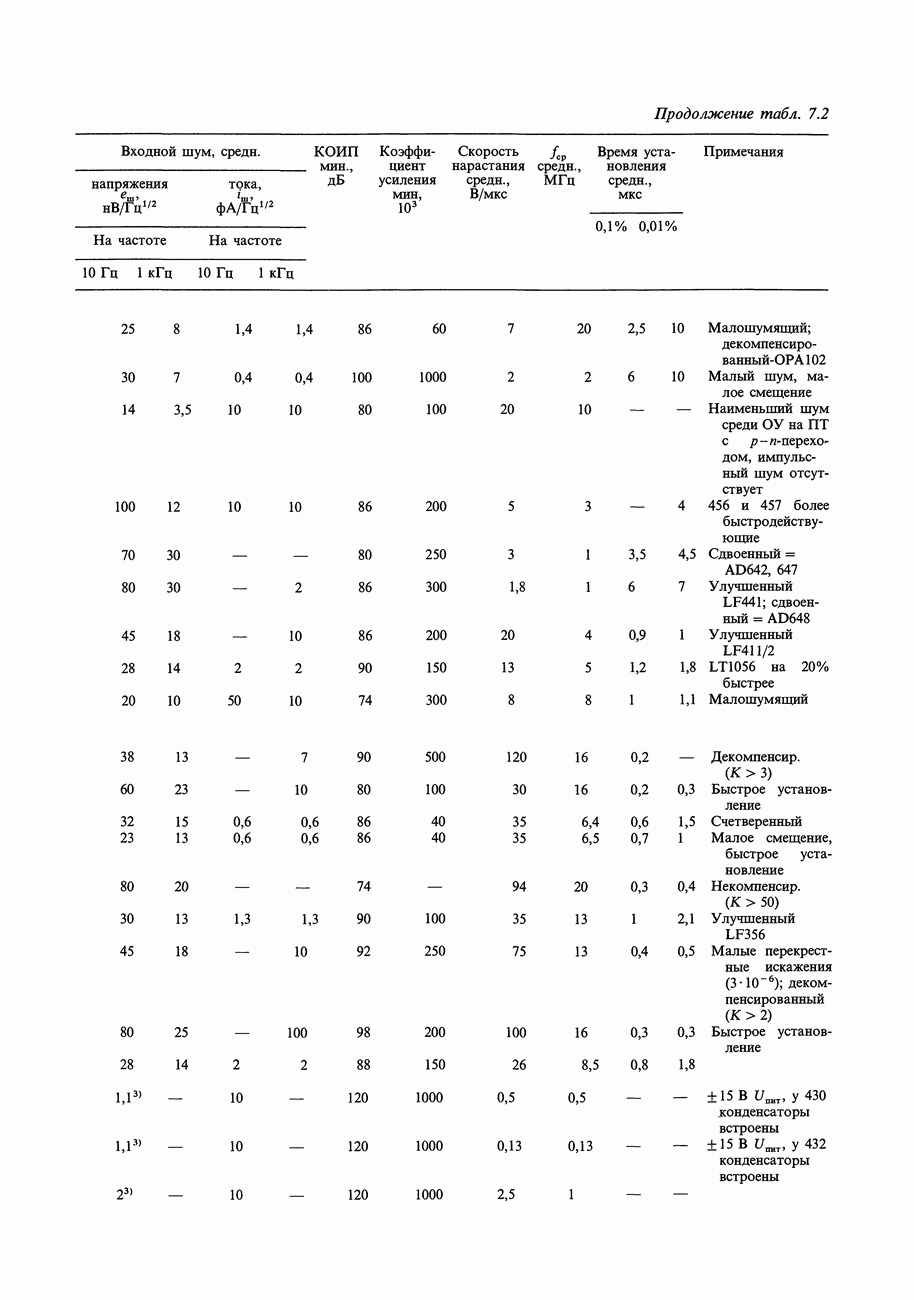
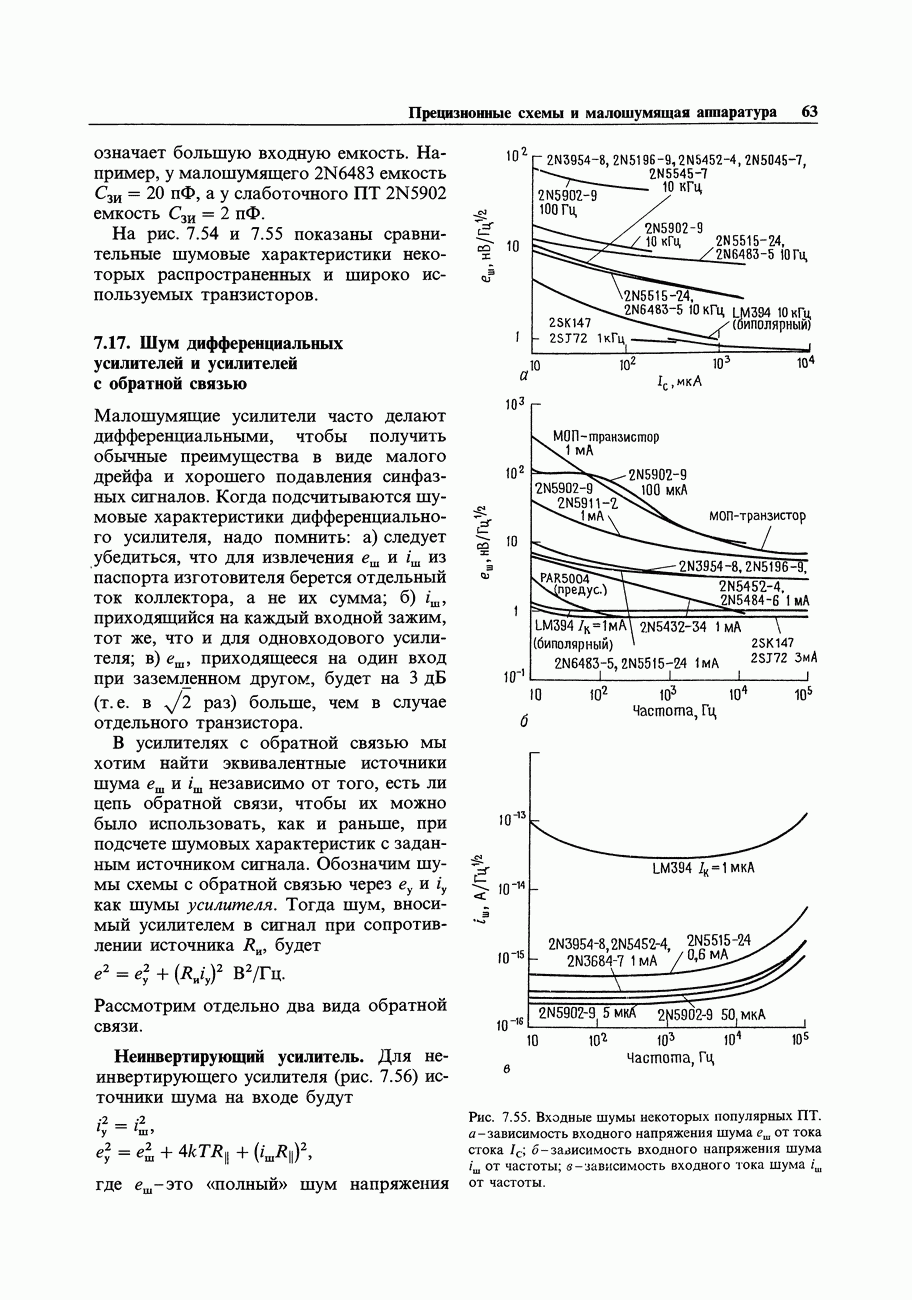
- 7.15. Шум ПТ
- 7.16. Выбор малошумящих транзисторов
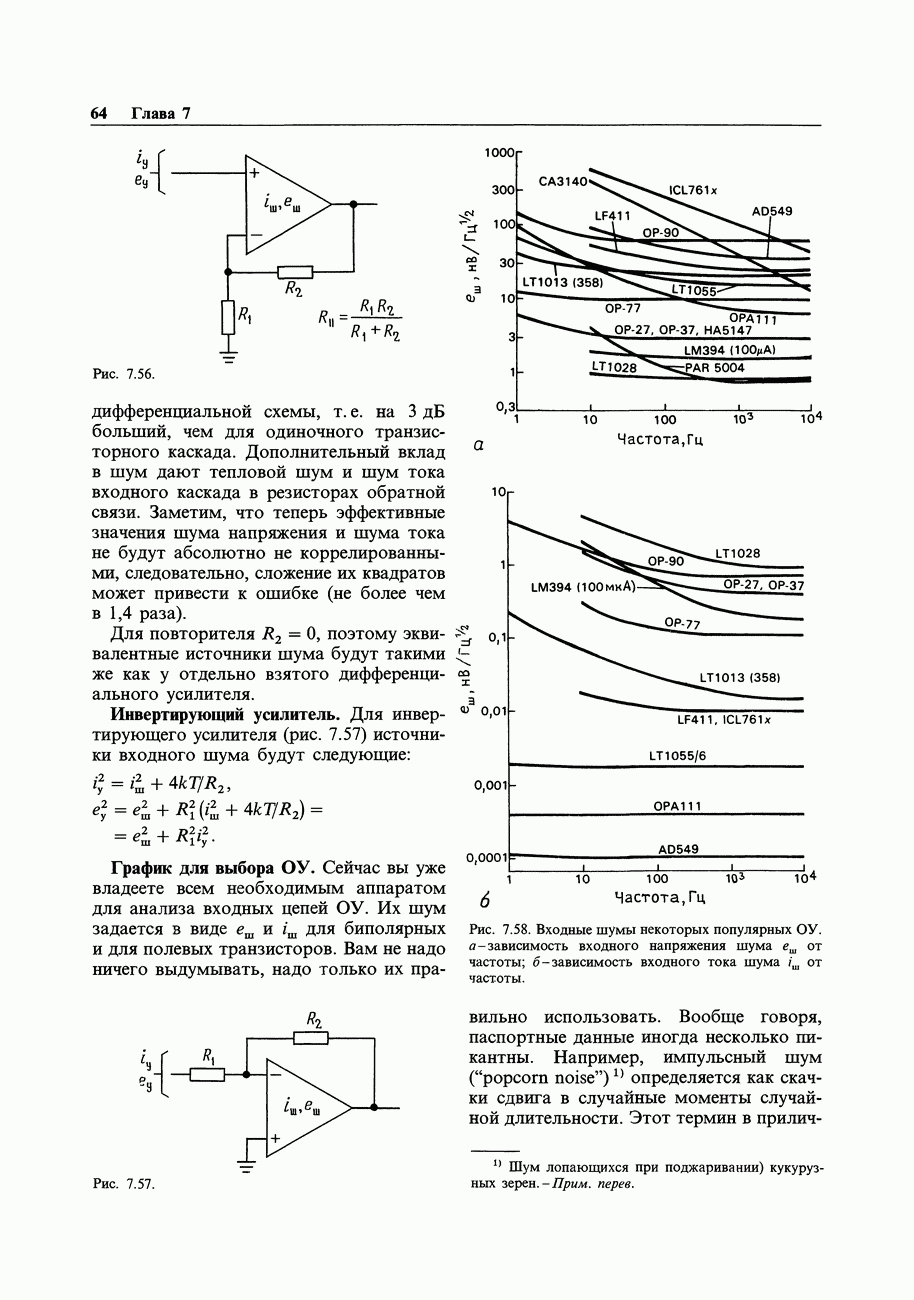
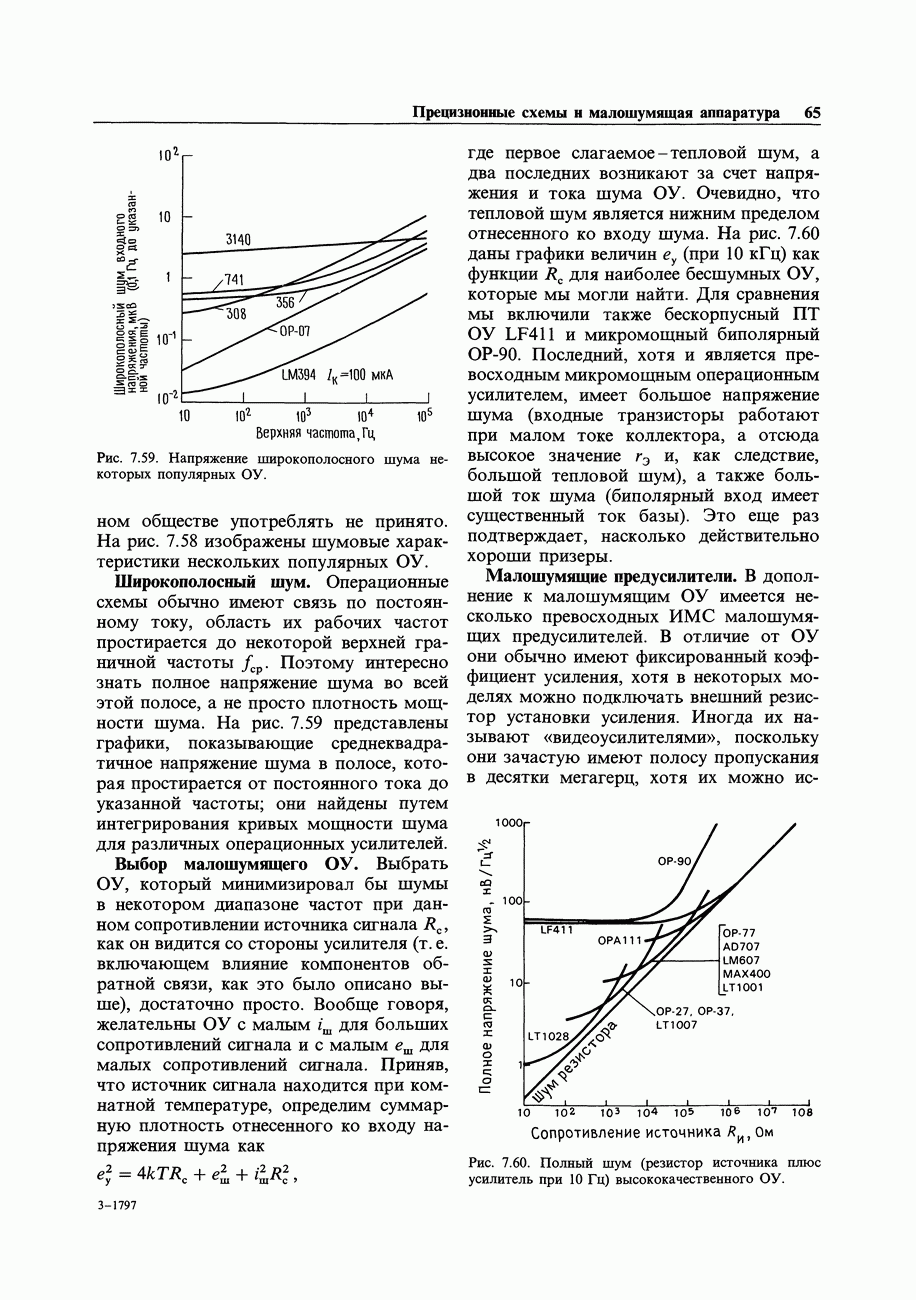
- 7.17. Шум дифференциальных усилителей и усилителей с обратной связью
- ИЗМЕРЕНИЕ ШУМА И ИСТОЧНИКИ ШУМА
- 7.18. Измерение без источника шума
- 7.19. Измерение с источником шума
- 7.20. Генераторы шумов и сигналов
- 7.21. Ограничение полосы частот и измерение среднеквадратичного (эффективного) напряжения
- 7.22. Попурри на тему шумов
- ПОМЕХИ: ЭКРАНИРОВАНИЕ И ЗАЗЕМЛЕНИЕ
- 7.23. Помехи
- 7.24. Сигнальное заземление
- 7.25. Межприборное заземление
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 8. ЦИФРОВЫЕ СХЕМЫ
- 8.01. Цифровые и аналоговые сигналы
- 8.02. Логические состояния
- ЛОГИЧЕСКИЕ УРОВНИ
- 8.03. Числовые коды
- 8.04. Вентили и таблицы истинности
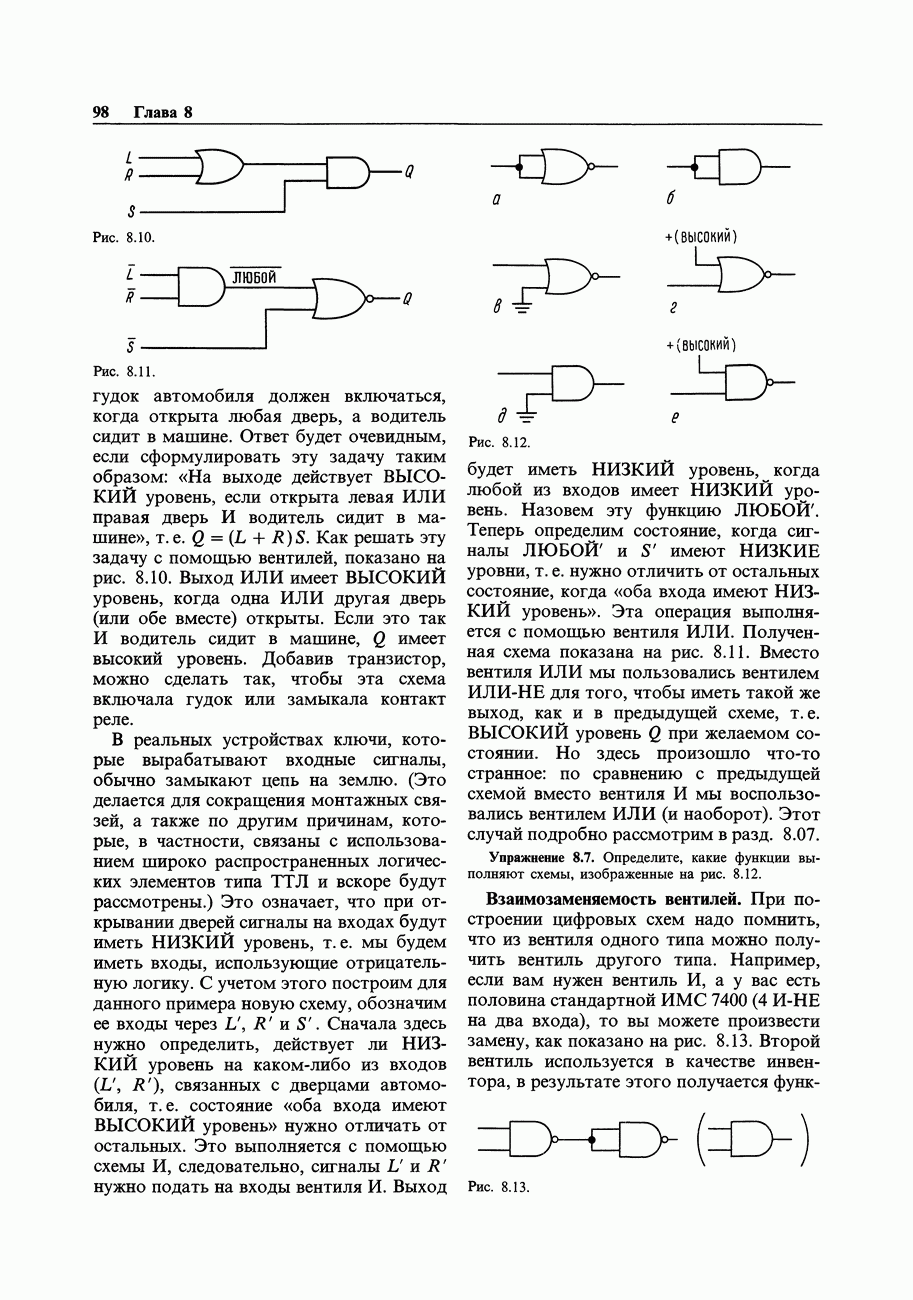
- 8.05. Схемы вентилей на дискретных элементах
- 8.06. Пример схемы с вентилями
- 8.07. Логические обозначения при заданных уровнях
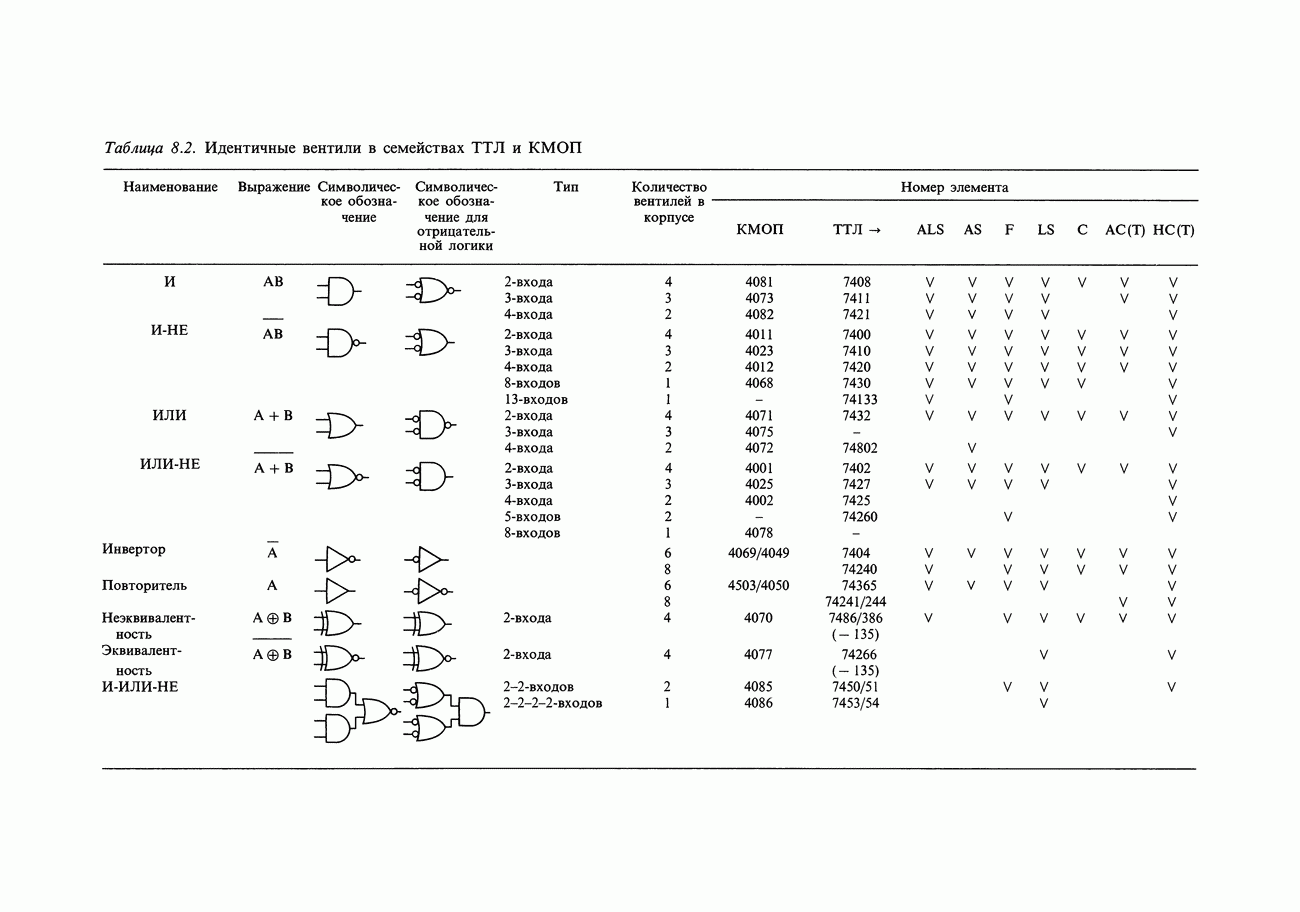
- 8.08. Каталог идентичных вентилей
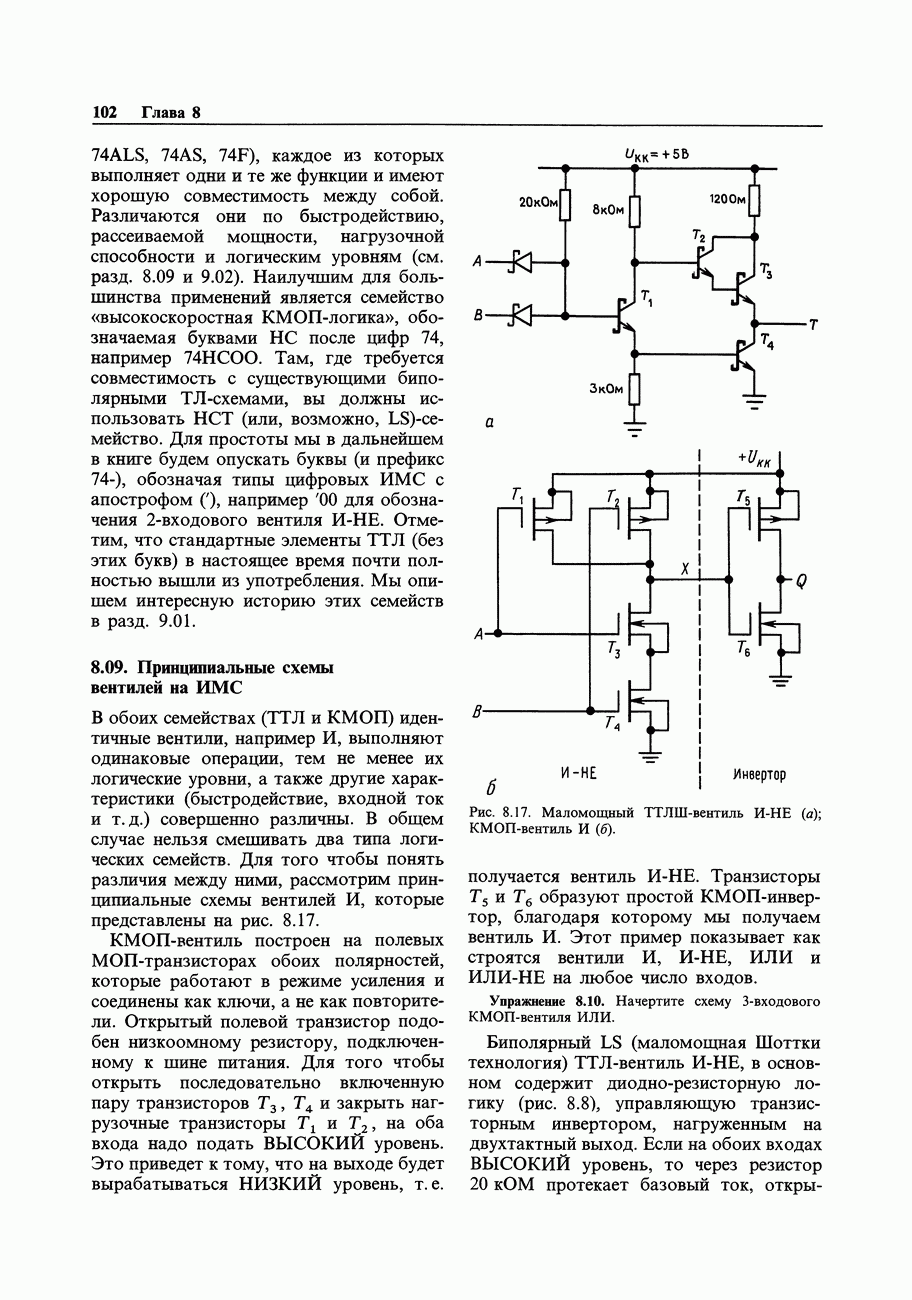
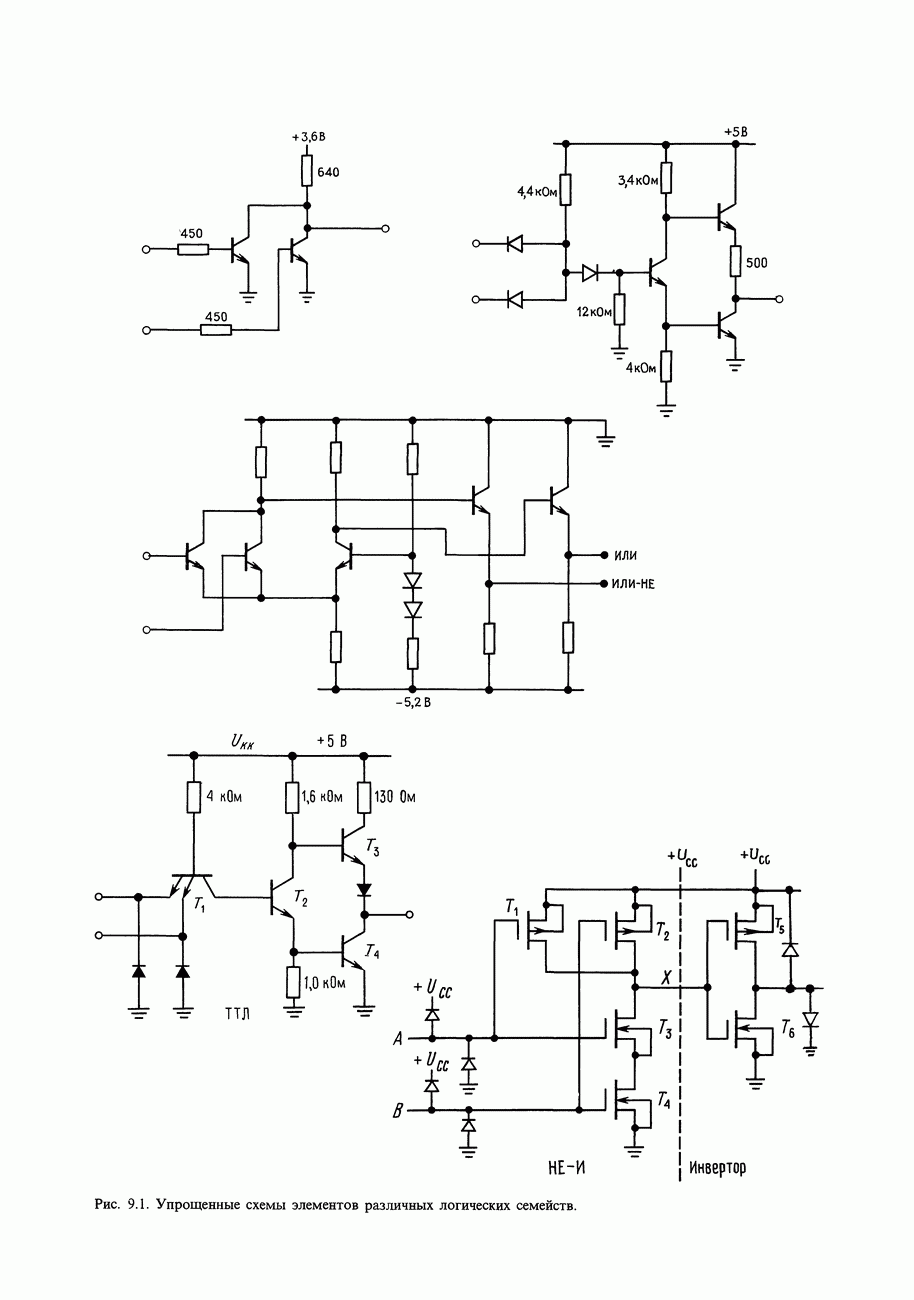
- 8.09. Принципиальные схемы вентилей на ИМС
- 8.10. Характеристики ТТЛ и КМОП
- 8.11. Элементы с тремя состояниями и с открытым коллектором
- КОМБИНАЦИОННАЯ ЛОГИКА
- 8.12. Логические тождества
- 8.13. Минимизация и карты Карно
- 8.14. Комбинационные функциональные схемы, реализованные на стандартных ИМС
- 8.15. Реализация произвольных таблиц истины
- ПОСЛЕДОВАТЕЛЬНОСТНАЯ ЛОГИКА
- 8.16. Устройства с памятью: триггеры
- 8.17. Тактируемые триггеры
- 8.18. Последовательностная логика-объединение памяти и вентилей
- 8.19. Синхронизатор
- МОНОСТАБИЛЬНЫЕ МУЛЬТИВИБРАТОРЫ
- 8.20. Характеристики одновибраторов
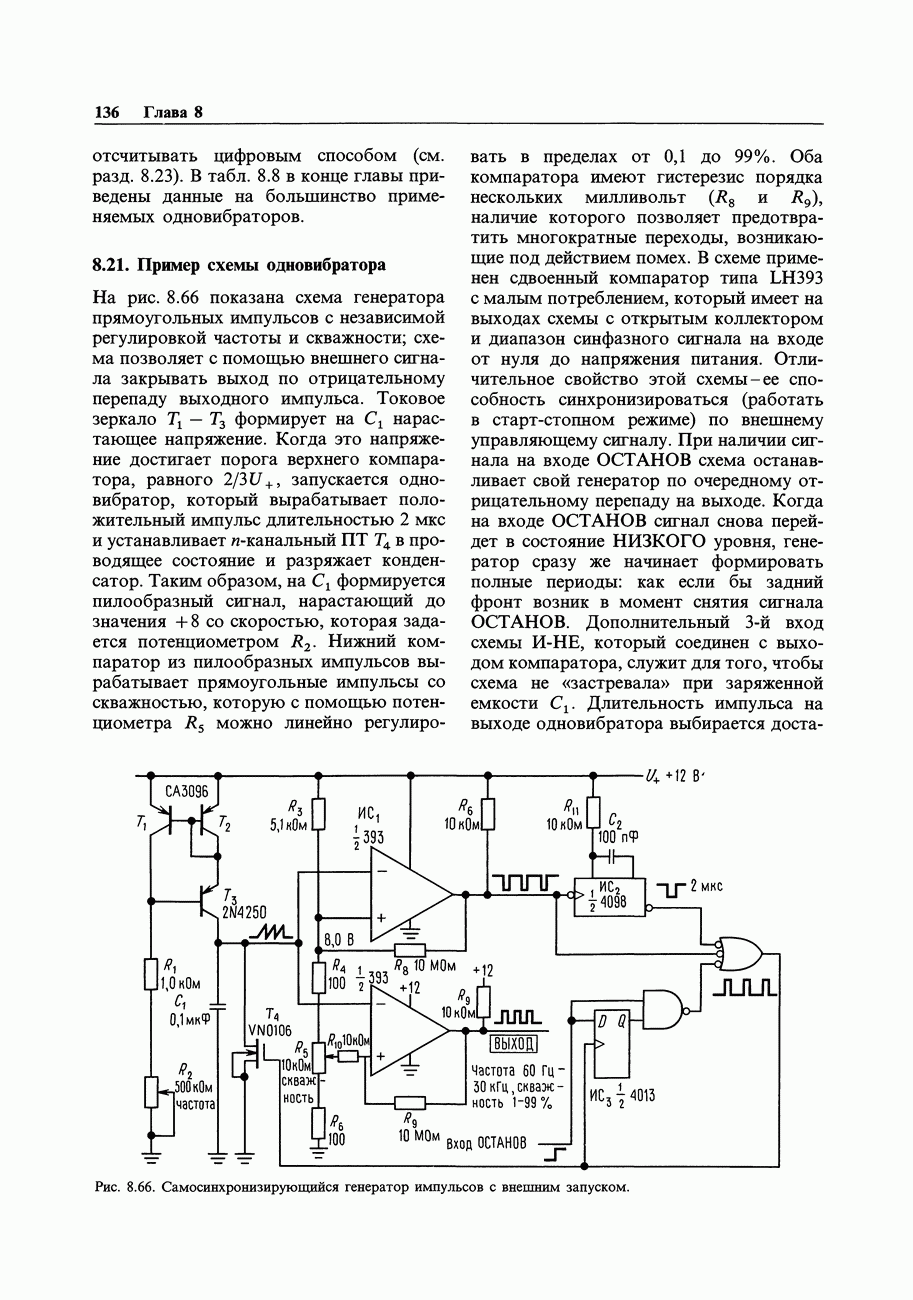
- 8.21. Пример схемы одновибратора
- 8.22. Предостережения относительно одновибраторов
- 8.23. Получение выдержки времени с помощью счетчиков
- ПОСЛЕДОВАТЕЛЬНОСТНЫЕ ФУНКЦИИ, РЕАЛИЗУЕМЫЕ НА СТАНДАРТНЫХ ИМС
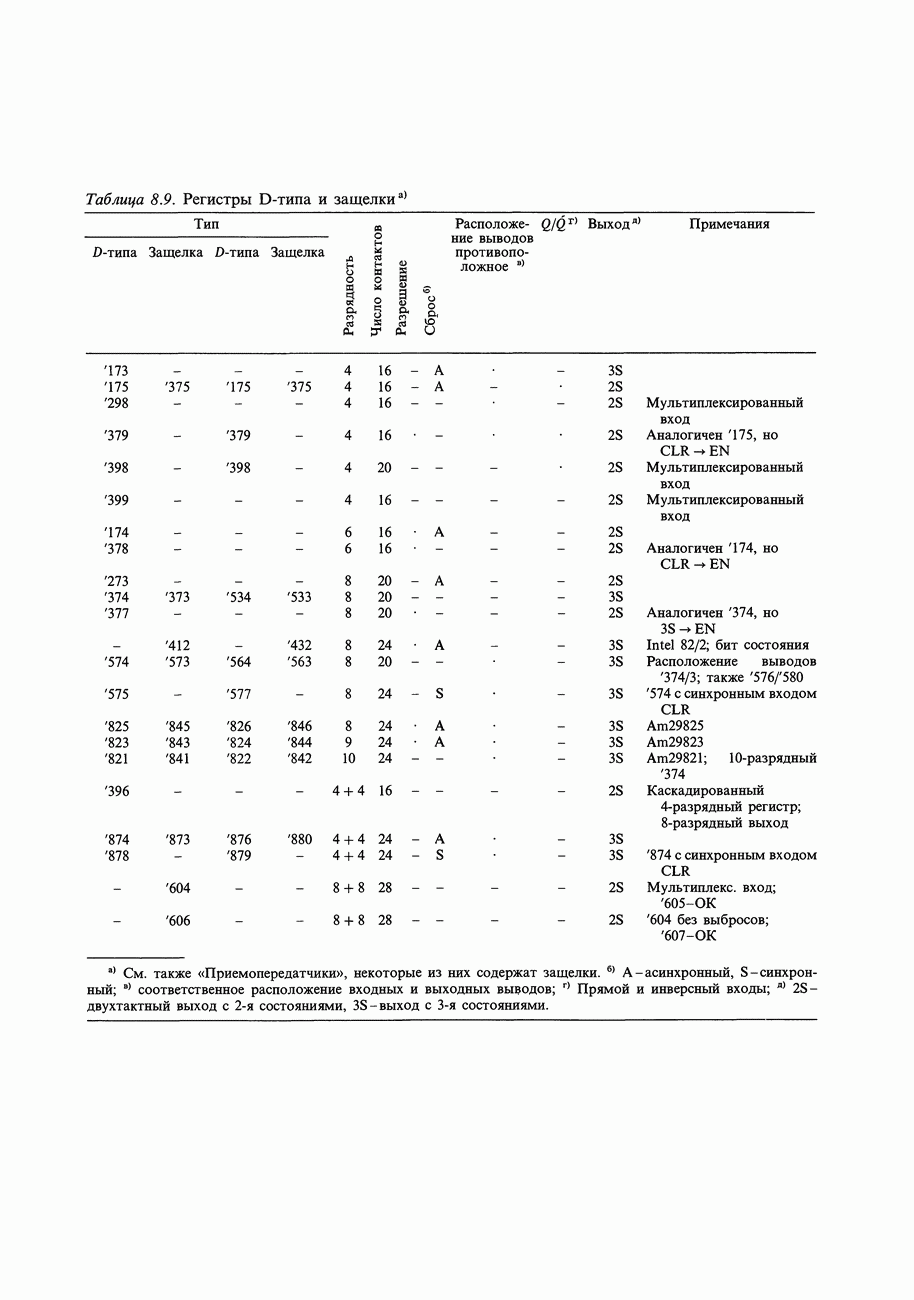
- 8.24. Фиксирующие схемы-защелки и регистры
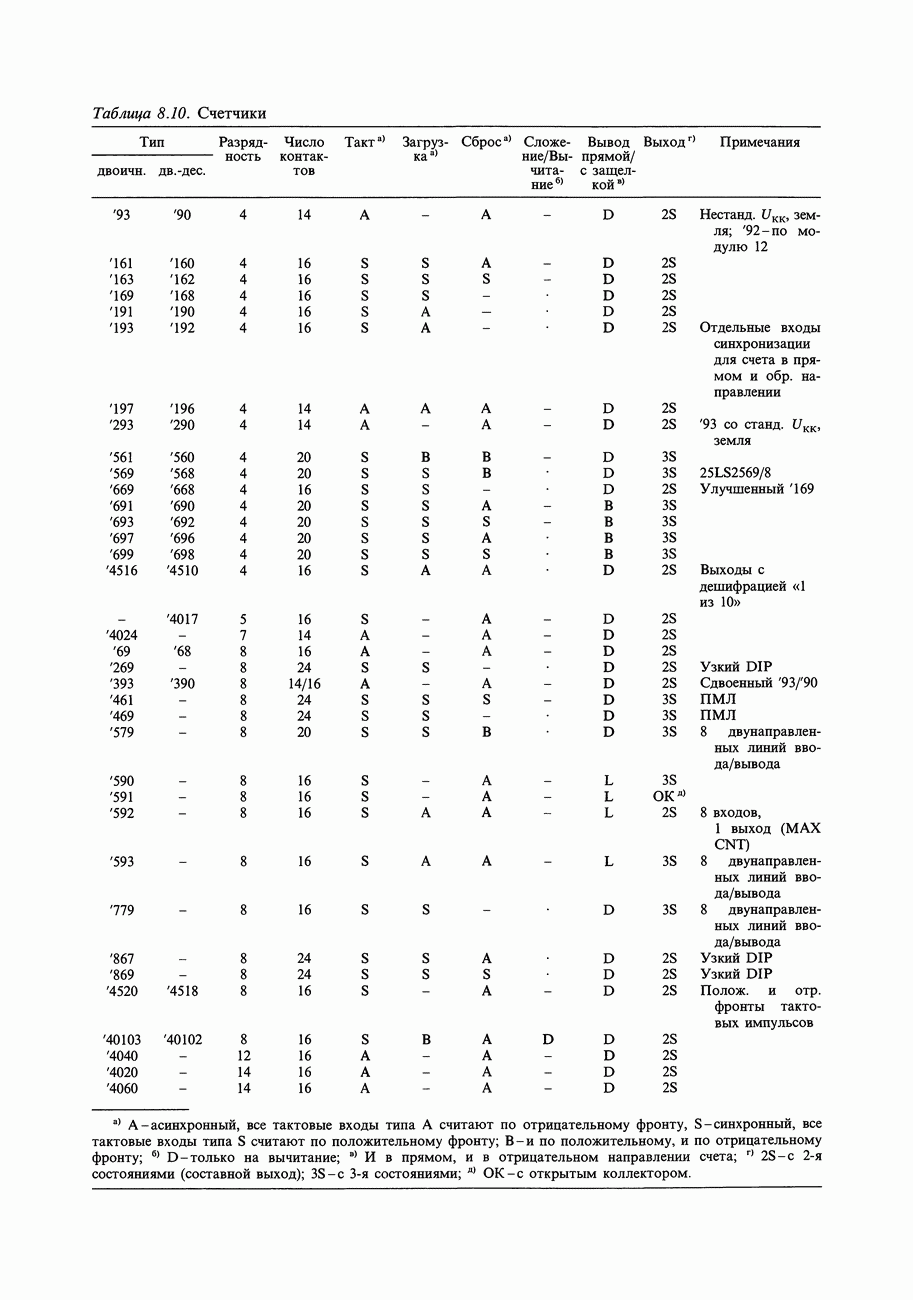
- 8.25. Счетчики
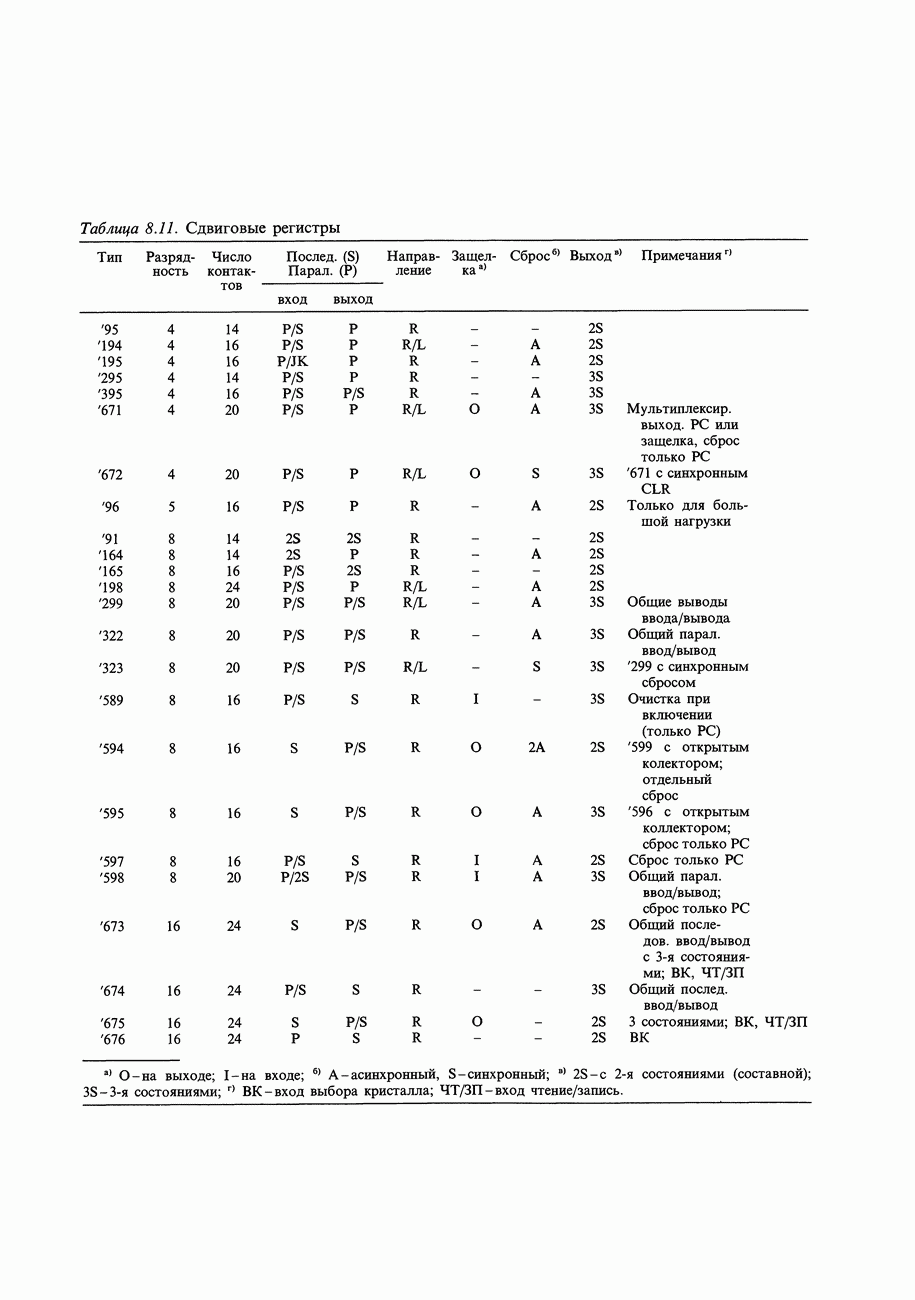
- 8.26. Регистры сдвига
- 8.27. Последовательностные ПМЛ
- Возможные применения программируемых логических интегральных схем (ПЛИС)
- 8.28. Разнообразные последовательностные схемы
- НЕКОТОРЫЕ ТИПОВЫЕ ЦИФРОВЫЕ СХЕМЫ
- 8.29. Счетчик по модулю n
- 8.30. Мультиплексируемый цифровой индикатор на светодиодах
- 8.31. Привод звездного телескопа
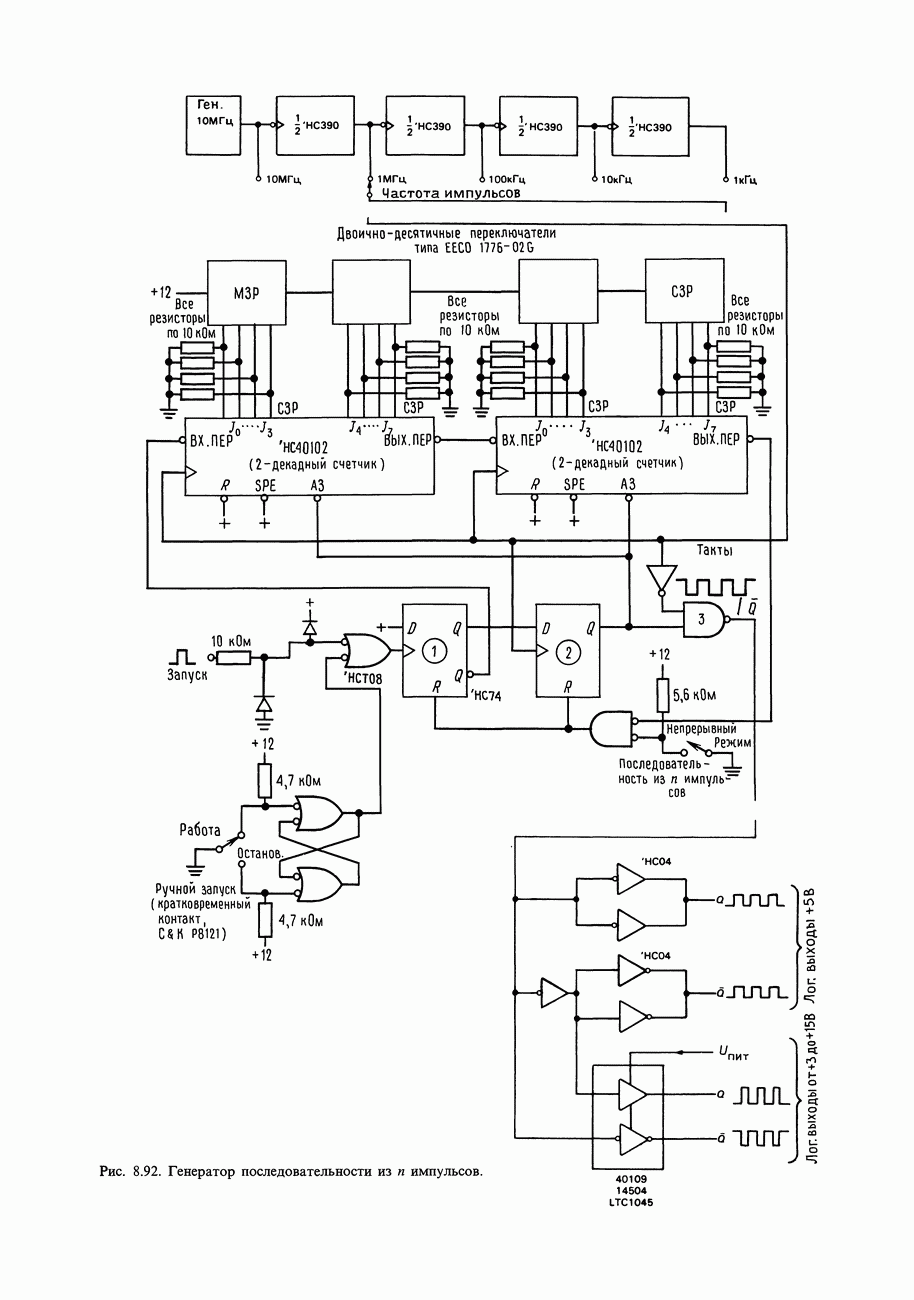
- 8.32. Генератор последовательности из n импульсов
- ПАТОЛОГИЯ В ЛОГИЧЕСКИХ СХЕМАХ
- 8.33. Проблемы статических режимов
- 8.34. Проблемы при переключениях
- 8.35. Прирожденные недостатки ТТЛ и КМОП
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 9. СОПРЯЖЕНИЕ ЦИФРОВЫХ И АНАЛОГОВЫХ СИГНАЛОВ
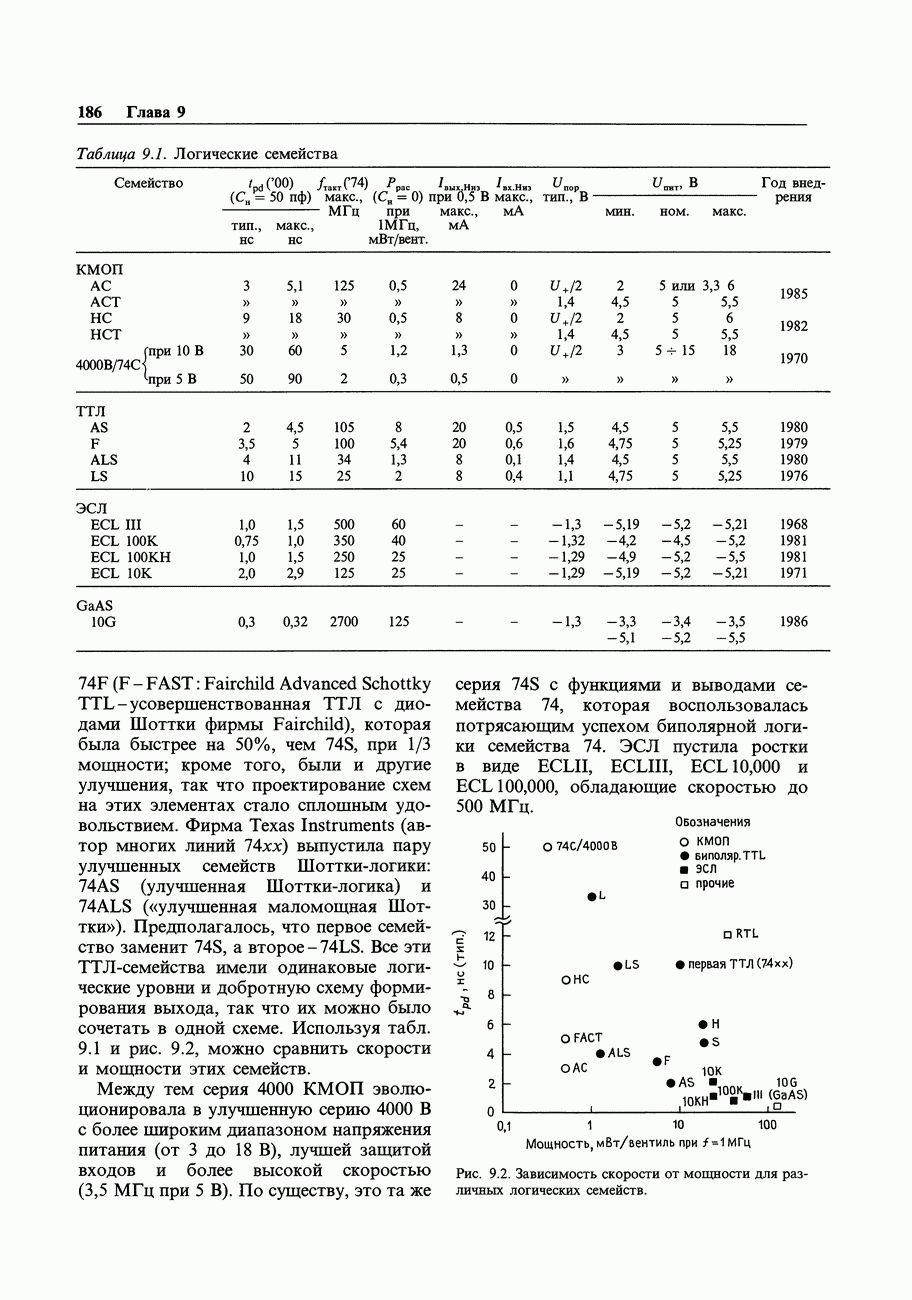
- 9.01. Хронология логических семейств
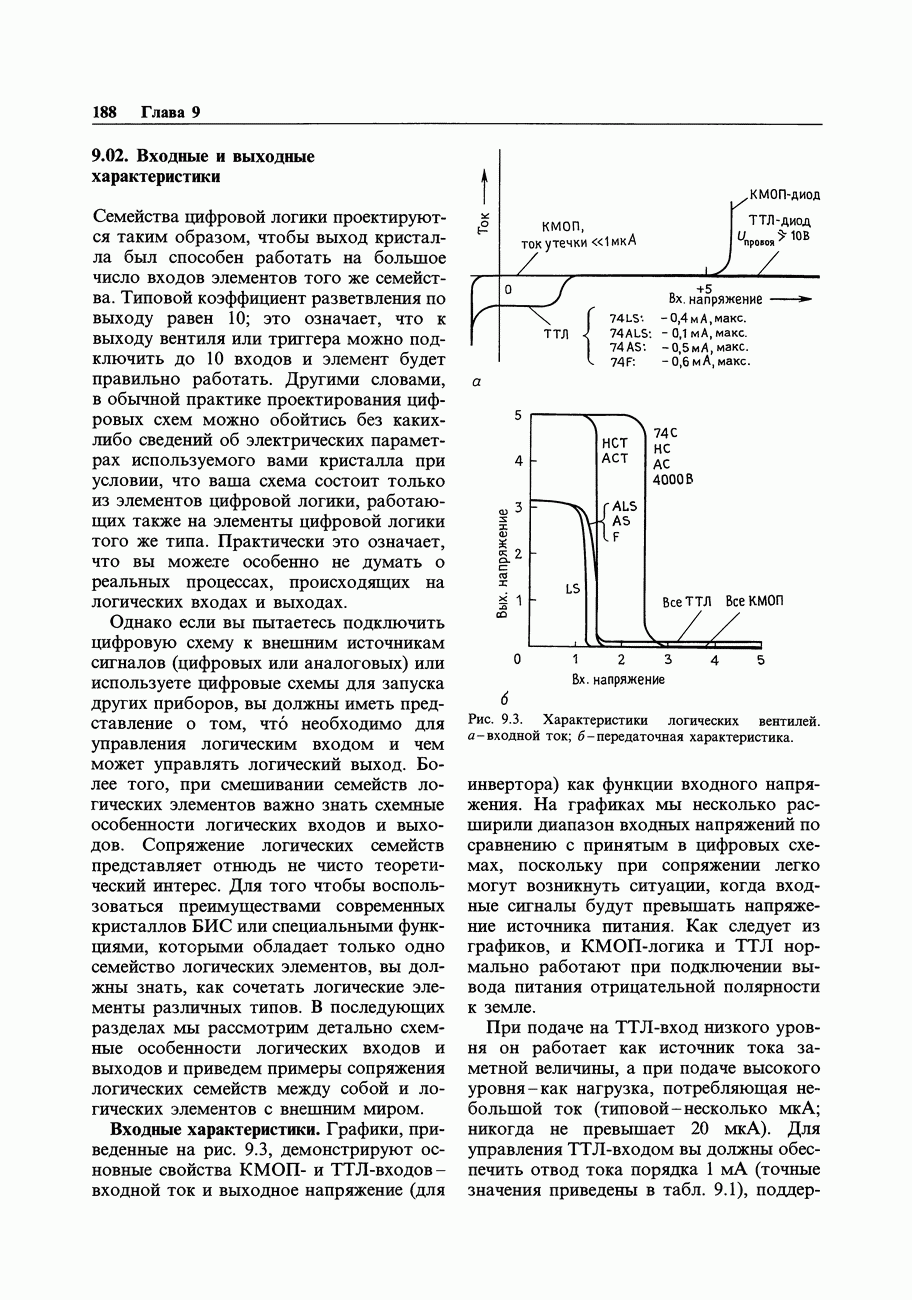
- 9.02. Входные и выходные характеристики
- 9.03. Сопряжение логических семейств
- 9.04. Управление КМОП-и ТТЛ-входами
- 9.05. Управление цифровой логикой от компараторов и операционных усилителей
- 9.06. Некоторые замечания, касающиеся логических входов
- 9.07. Компараторы
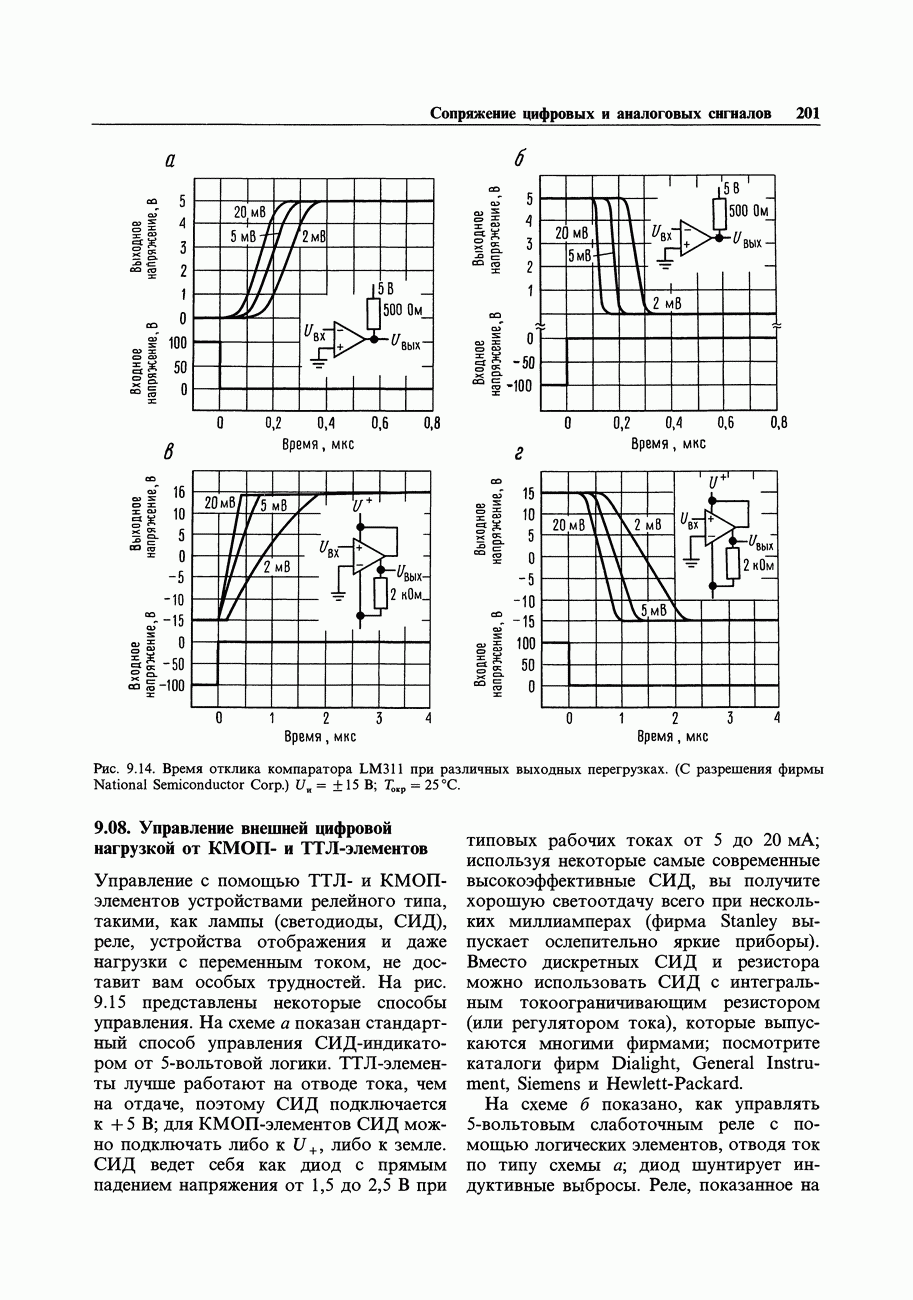
- 9.08. Управление внешней цифровой нагрузкой от КМОП- и ТТЛ-элементов
- 9.09. Сопряжение n-МОП БИС
- 9.10. Оптоэлектроника
- ЦИФРОВЫЕ СИГНАЛЫ И ДЛИННЫЕ ЛИНИИ
- 9.11. Внутриплатные соединения
- 9.12. Межплатные соединения
- 9.13. Шины данных
- 9.14. Кабельные связи
- АНАЛОГО-ЦИФРОВОЕ ПРЕОБРАЗОВАНИЕ
- 9.15. Введение в аналого-цифровое преобразование
- 9.16. Цифро-аналоговые преобразователи (ЦАП)
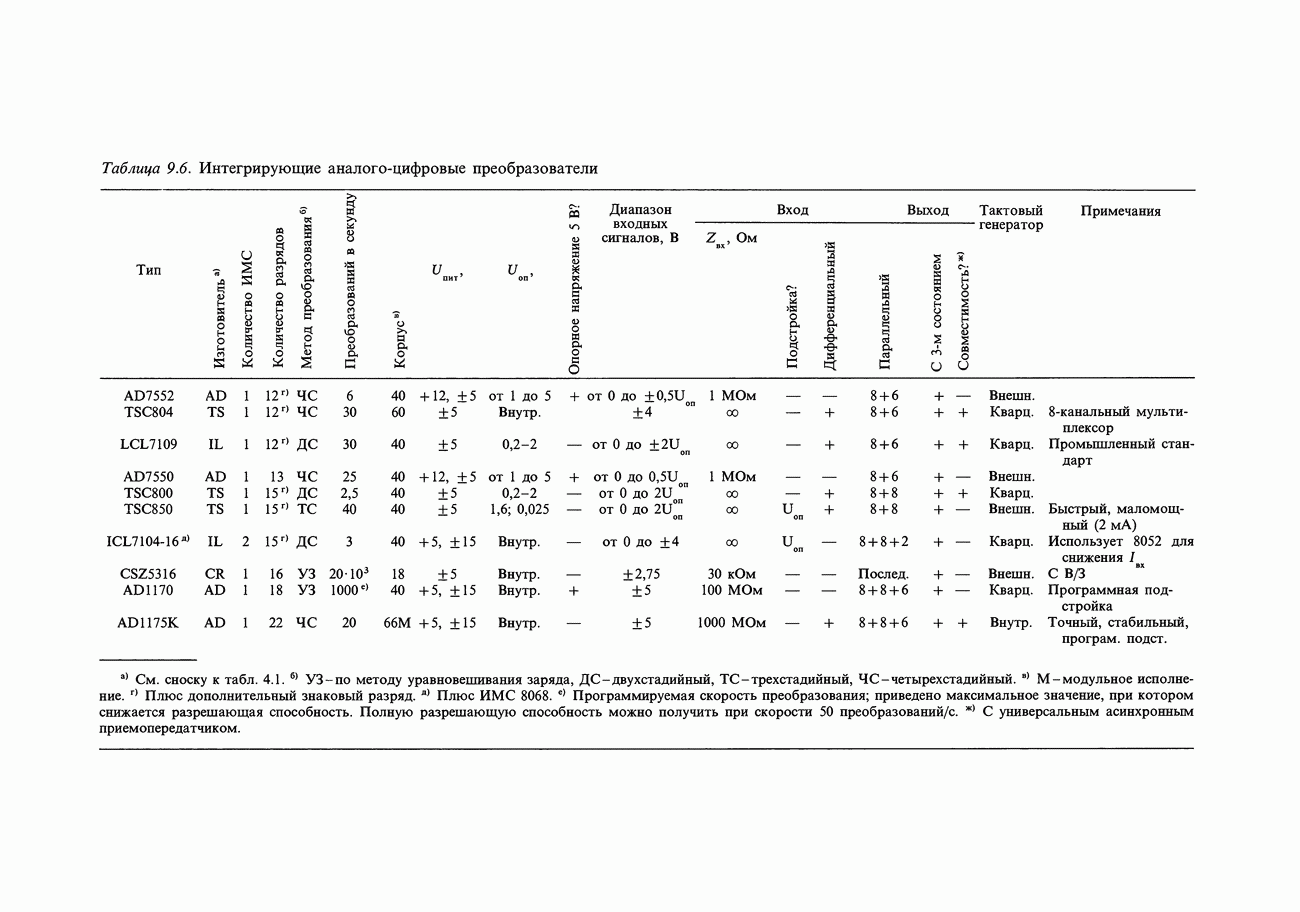
- 9.17. Интегрирующие ЦАП
- 9.18. ЦАП с умножением
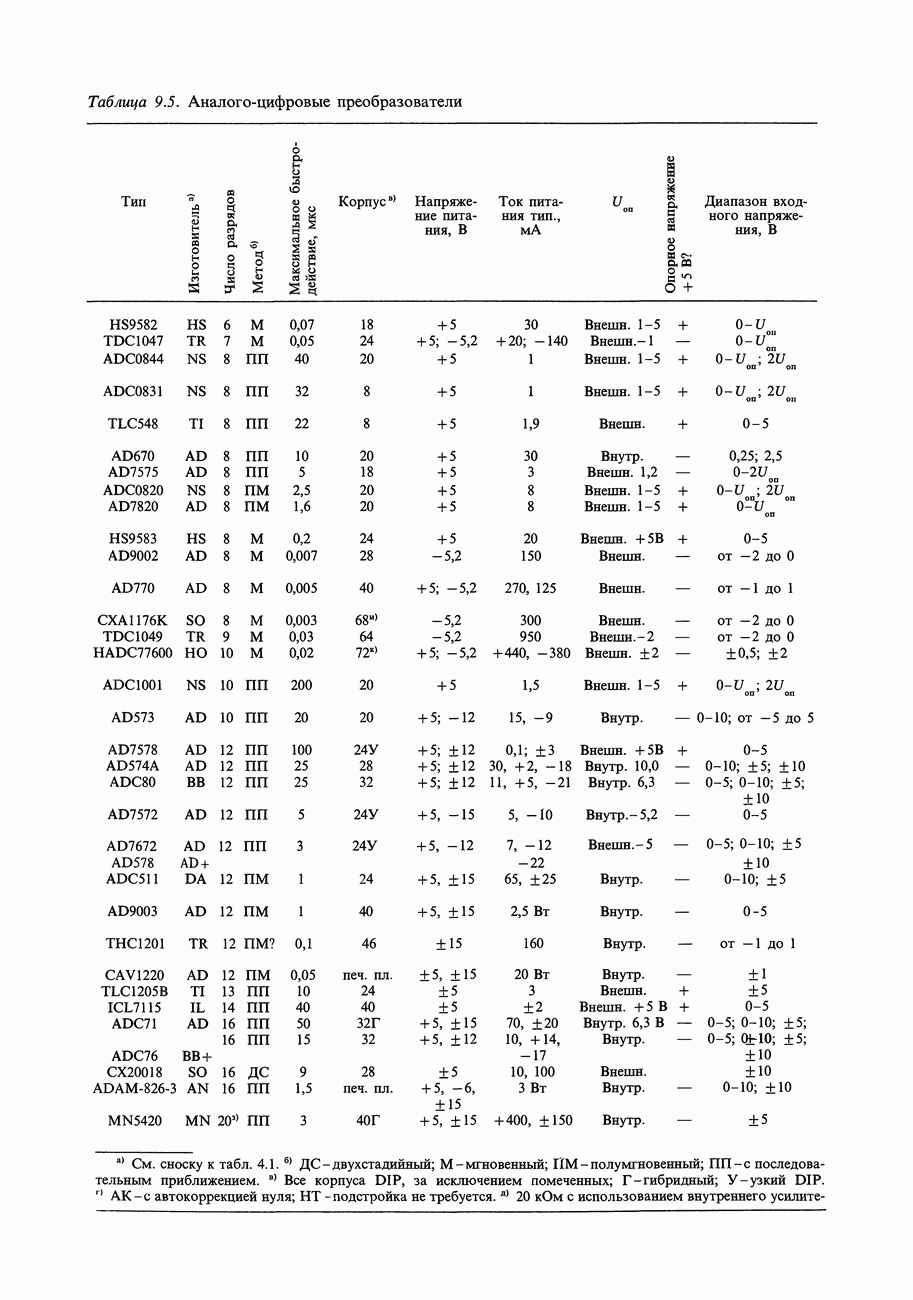
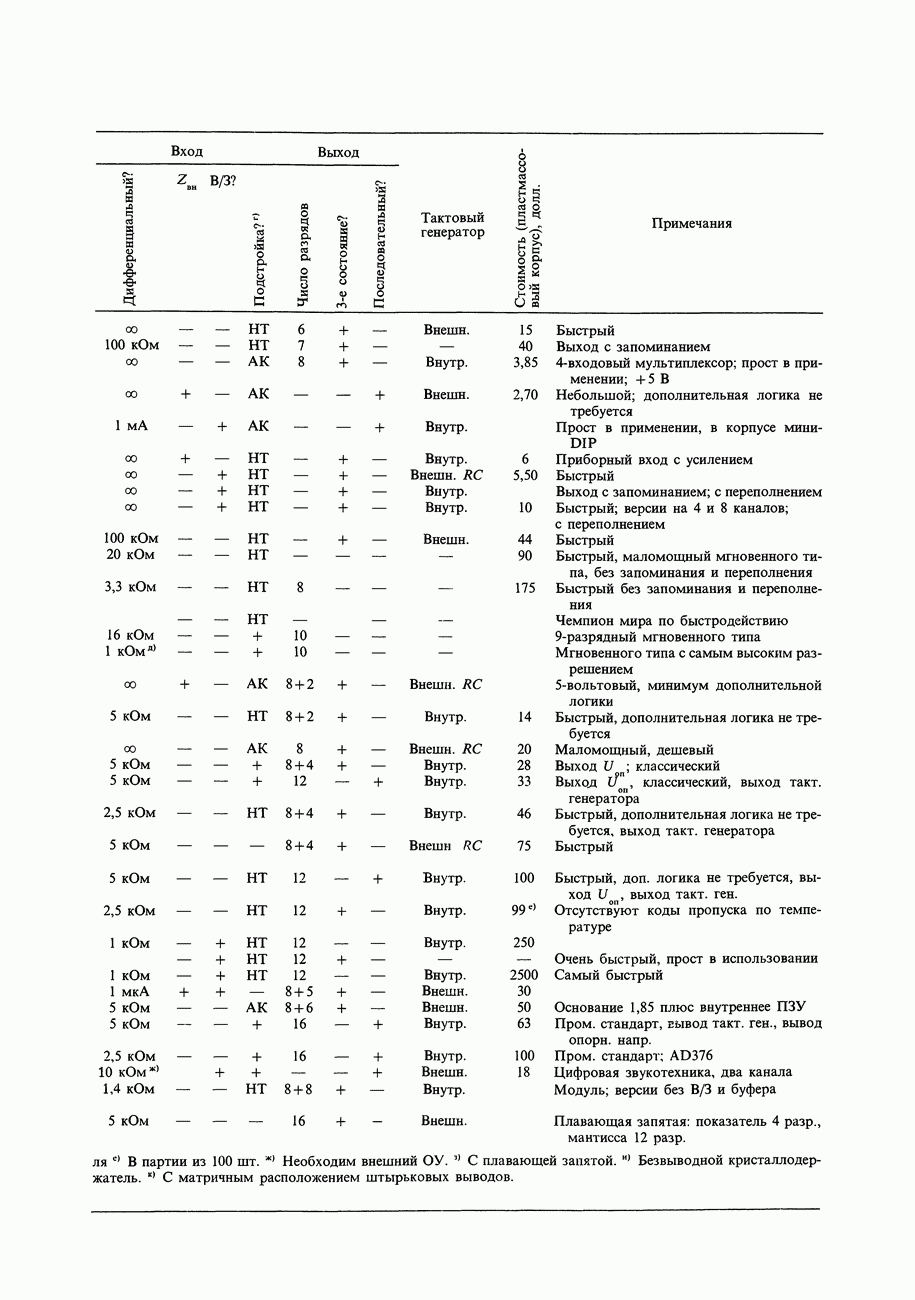
- 9.19. Выбор ЦАП
- 9.20. Аналого-цифровые преобразователи
- 9.21. Методы уравновешивания заряда
- 9.22. Некоторые необычные АЦП и ЦАП
- 9.23. Выбор АЦП
- ПРИМЕРЫ А/Ц-ПРЕОБРАЗОВАНИЯ
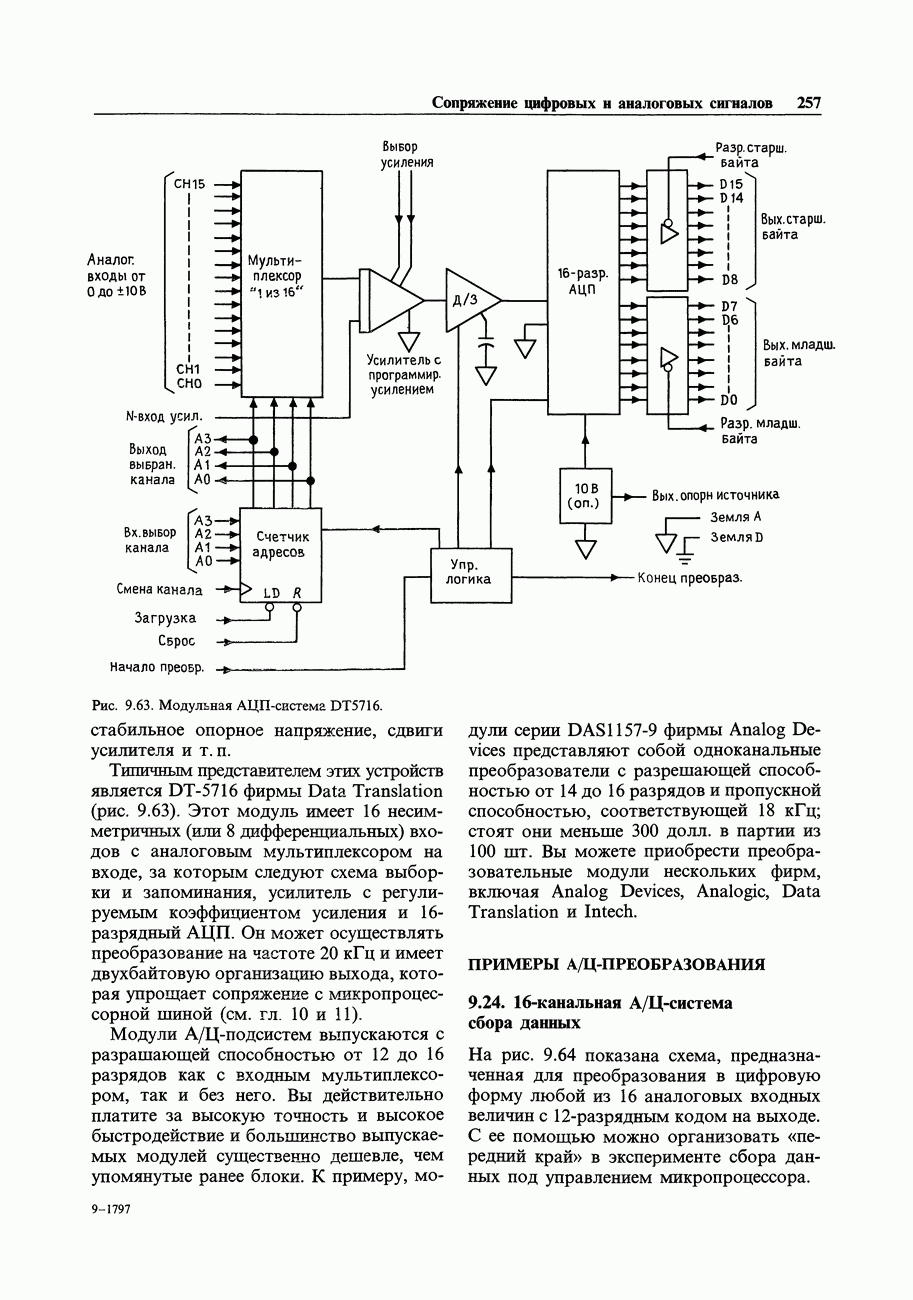
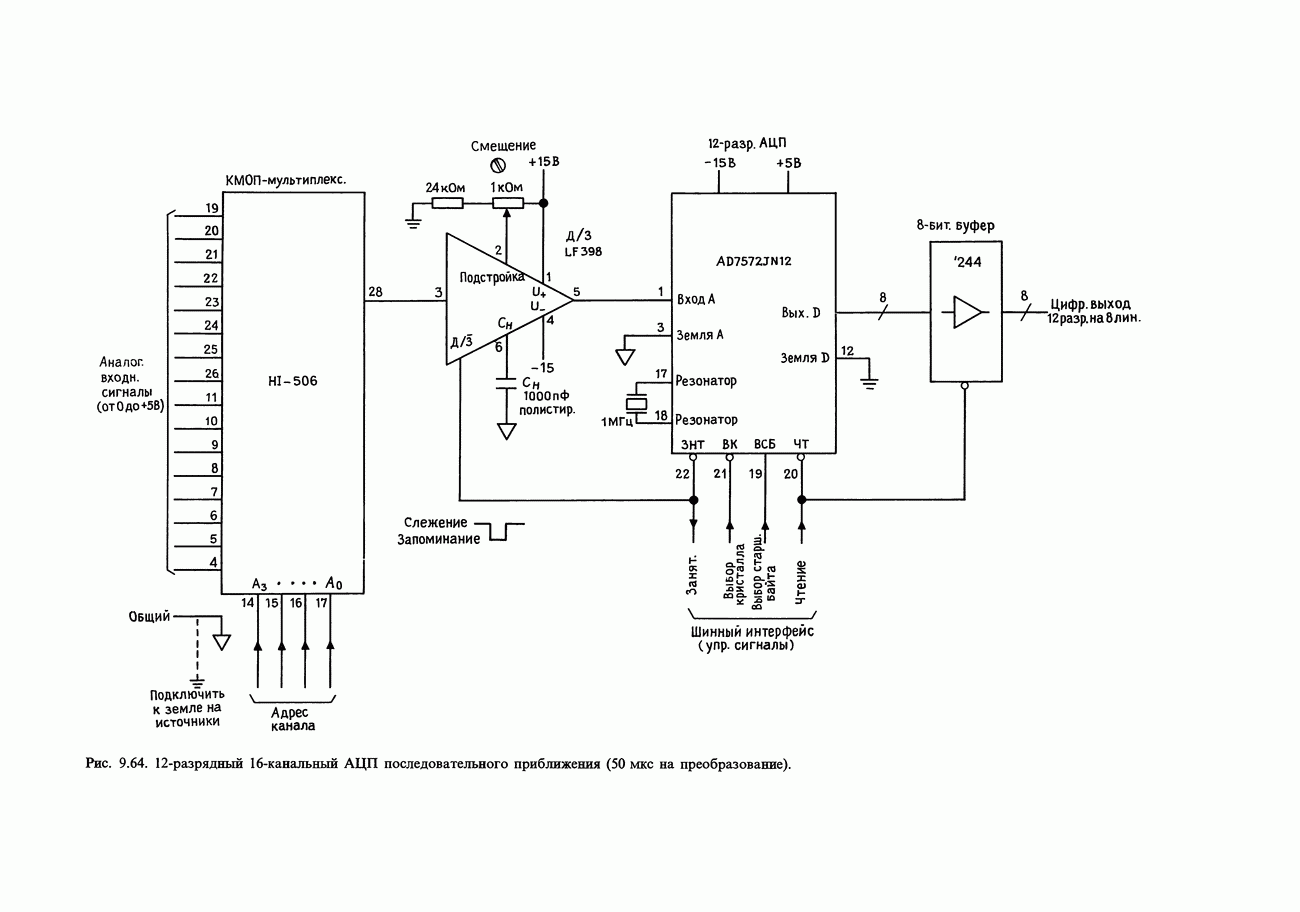
- 9.24. 16-канальная А/Ц-система сбора данных
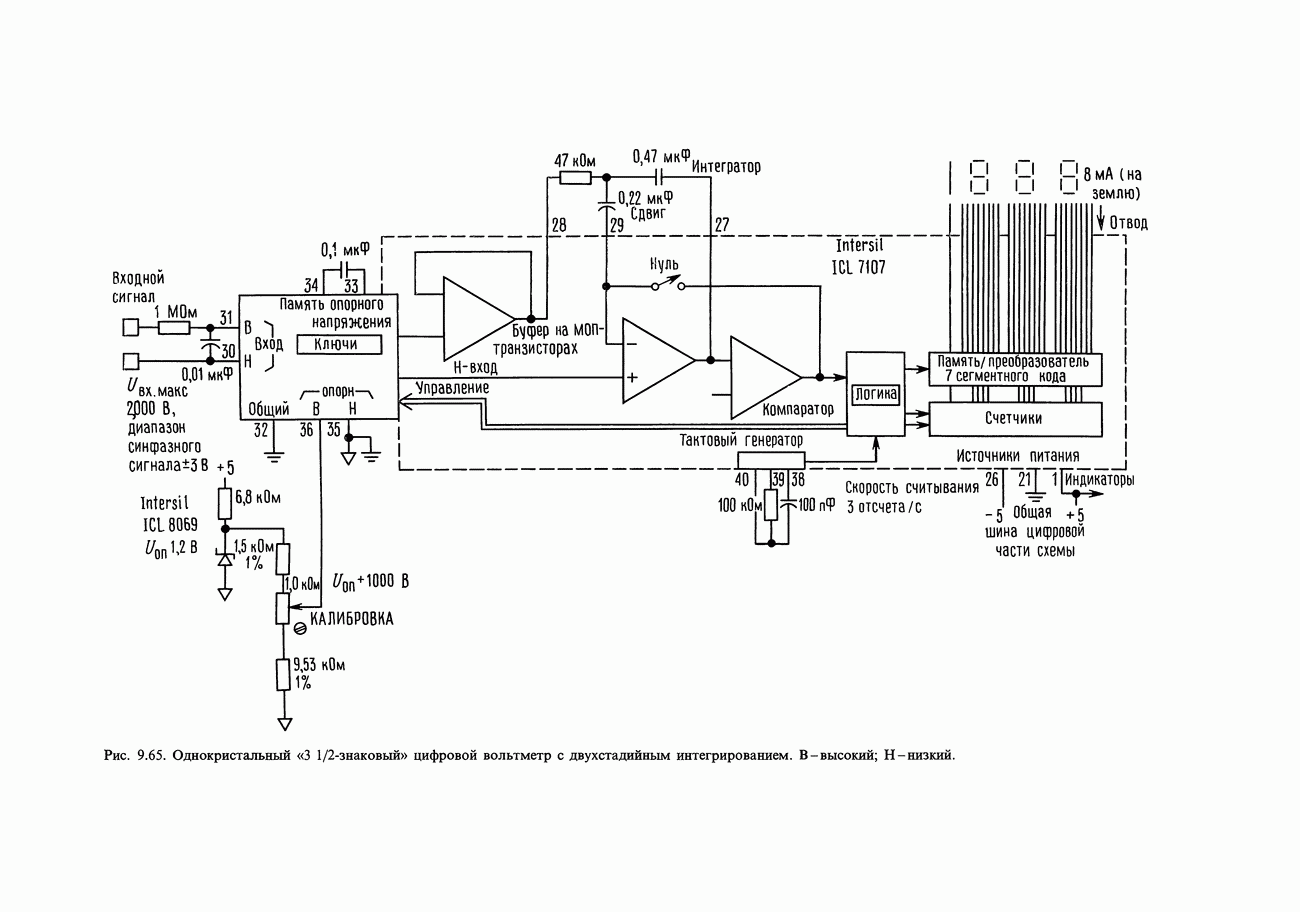
- 9.25. 3 1/2 — знаковый цифровой вольтметр
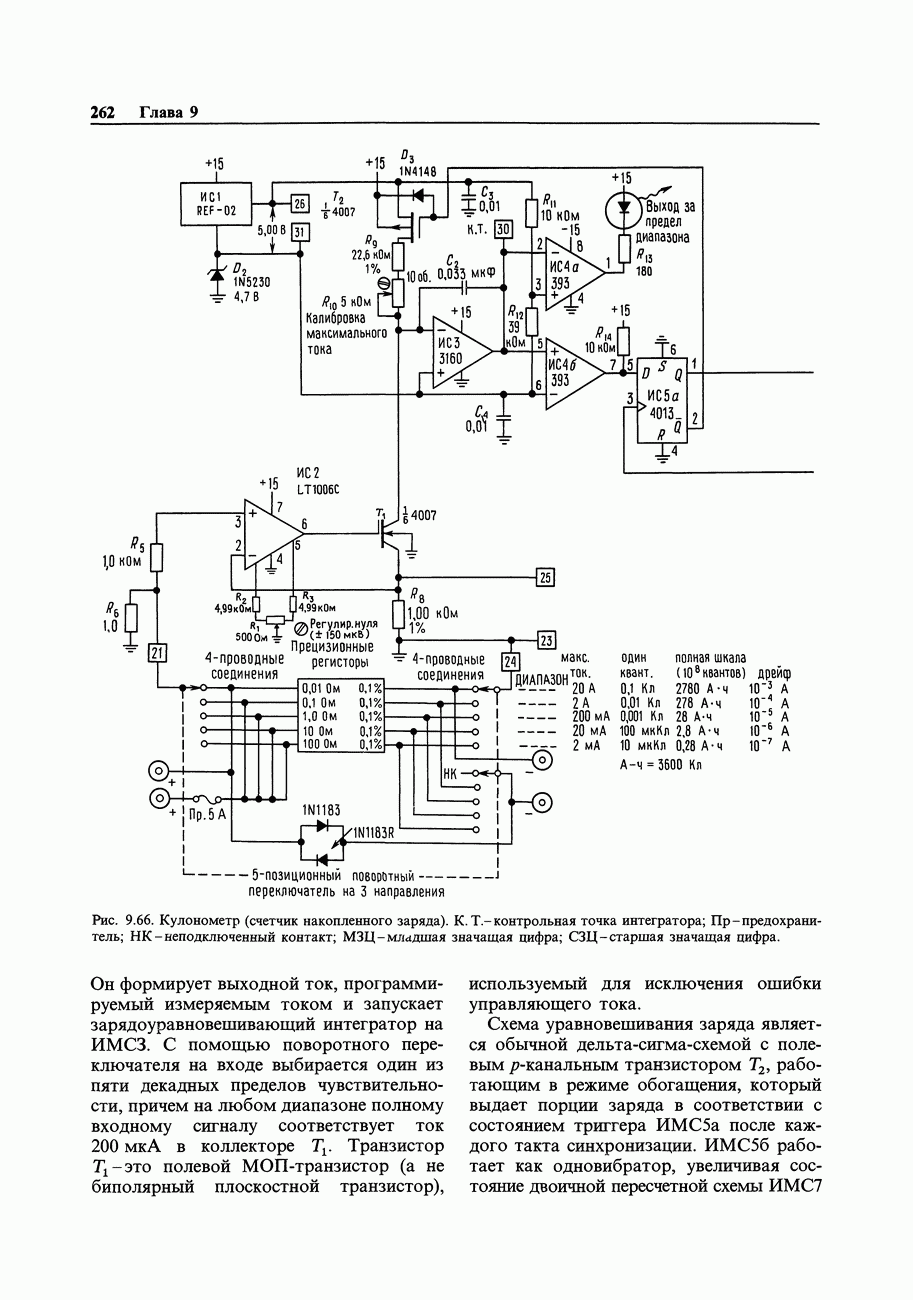
- 9.26. Кулонометр
- СХЕМЫ ФАЗОВОЙ АВТОПОДСТРОЙКИ ЧАСТОТЫ
- 9.28. Проектирование ФАПЧ
- 9.29. Пример разработки: умножитель частоты
- 9.30. Захват и слежение в системе ФАПЧ
- 9.31. Некоторые примеры применения систем ФАПЧ
- ПСЕВДОСЛУЧАЙНЫЕ ДВОИЧНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ГЕНЕРАТОРЫ ШУМА
- 9.32. Цифровые методы генерации шума
- 9.33. Последовательности, генерируемые регистрами сдвига с обратными связями
- 9.34. Формирование аналогового шума с использованием последовательностей максимальной длины
- 9.35. Энергетический спектр последовательности, сформированной при помощи регистра сдвига
- 9.36. Низкочастотная фильтрация
- 9.37. Краткое заключение
- 9.38. Цифровые фильтры
- СХЕМЫ, НЕ ТРЕБУЮЩИЕ ПОЯСНЕНИЙ
- ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
- ГЛАВА 10. МИКРОЭВМ
- МИНИ-ЭВМ, МИКРОЭВМ И МИКРОПРОЦЕССОРЫ
- 10.01. Архитектура микроЭВМ
- НАБОР КОМАНД КОМПЬЮТЕРА
- 10.02. Язык ассемблера и язык машинных кодов
- 10.03. Упрощенный набор команд процессора Intel 8086/8
- 10.04. Программный пример
- СИГНАЛЫ МАГИСТРАЛИ И ЕЕ ФУНКЦИОНИРОВАНИЕ
- 10.05. Основные сигналы магистрали: данные, адрес, синхронизация
- 10.06. Программируемый ввод-вывод: вывод данных
- 10.07. Программируемый ввод-вывод: ввод данных
- 10.08. Программируемый ввод-вывод: регистры состояний
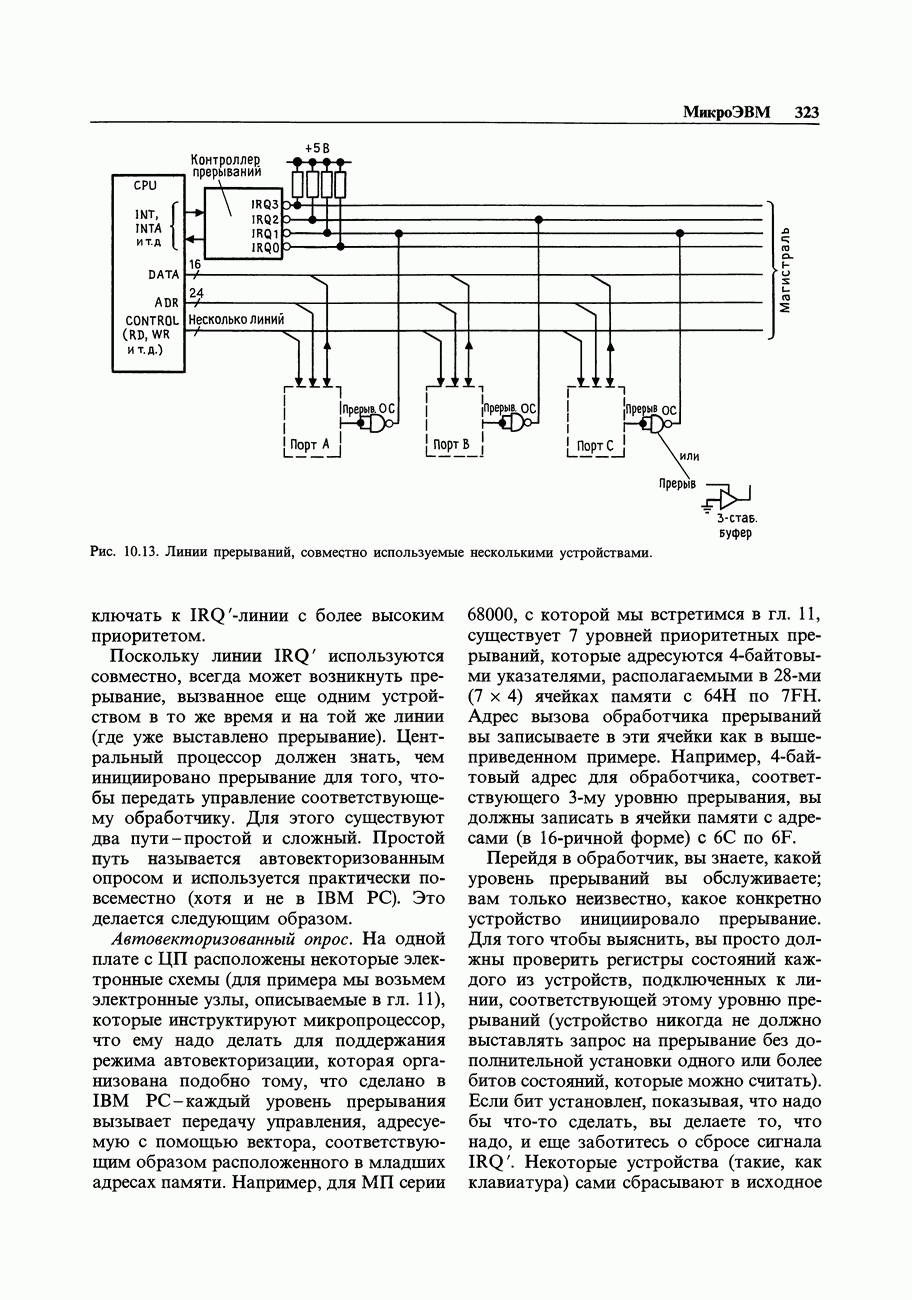
- 10.09. Прерывания
- 10.10. Обработка прерываний
- 10.11. Прерывания в целом
- 10.12. Прямой доступ в память
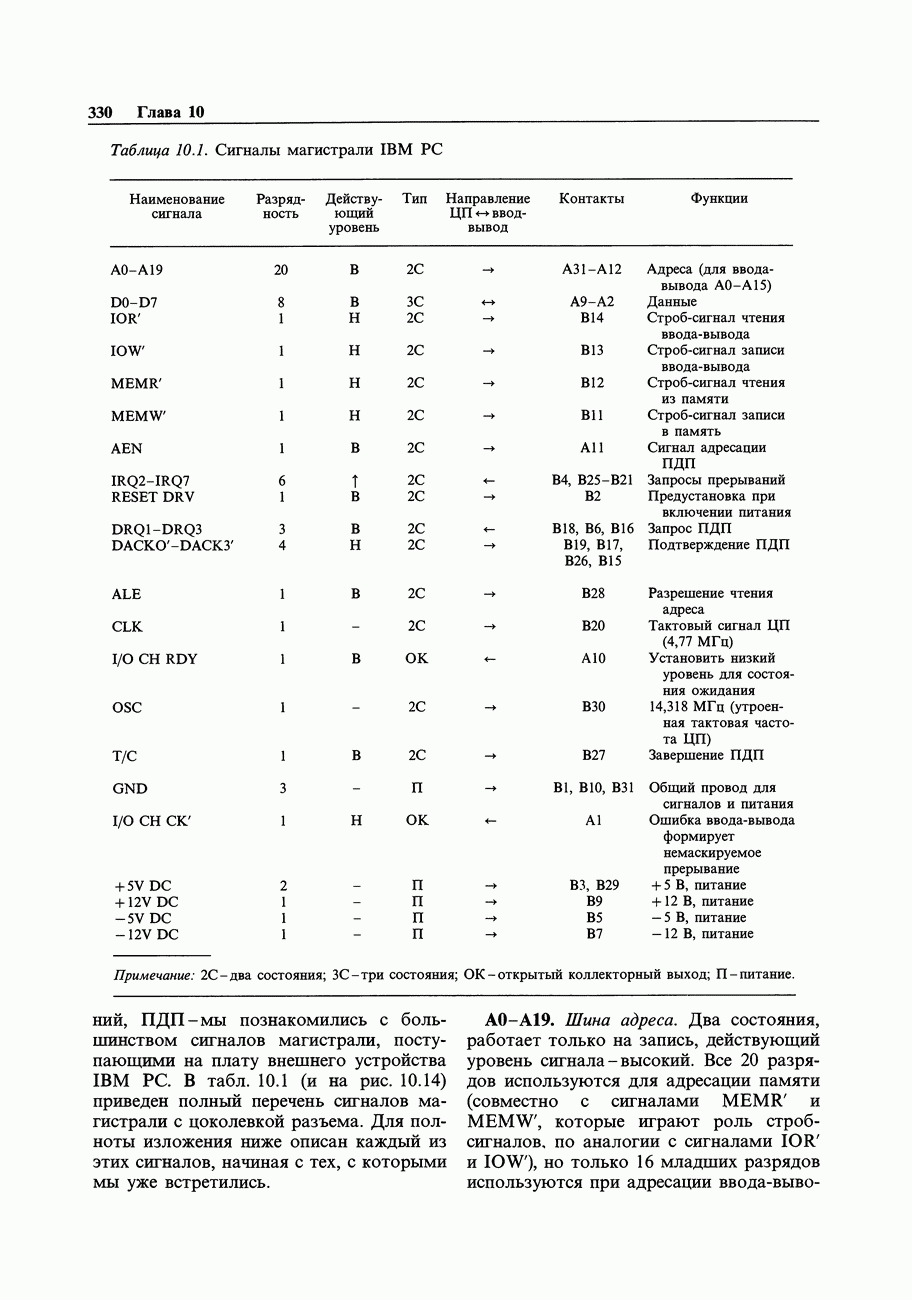
- 10.13. Сводный перечень сигналов магистрали IBM PC
- 10.14. Синхронный и асинхронный протоколы магистрали
- 10.15. Магистрали других микрокомпьютеров
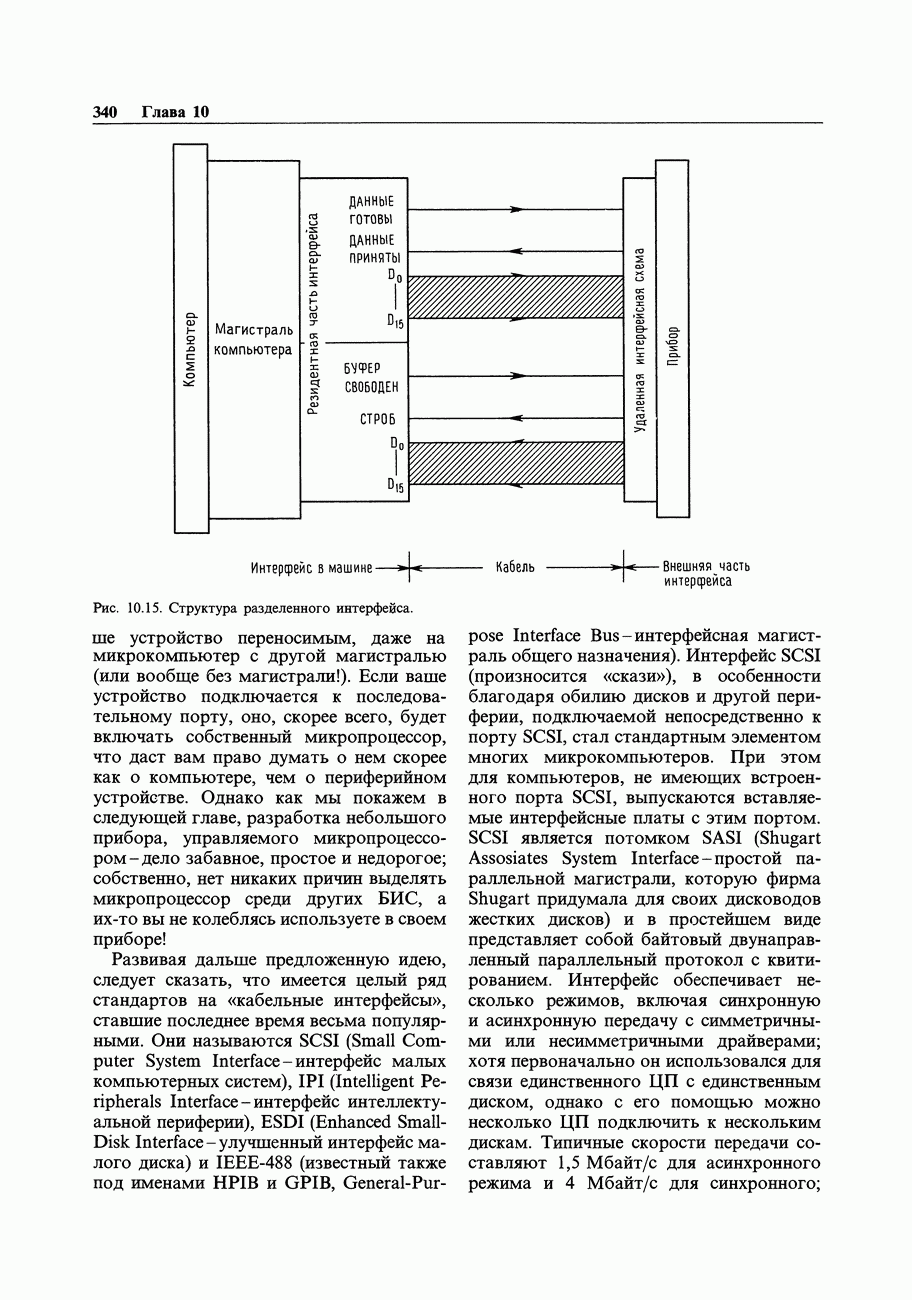
- 10.16. Подключение к компьютеру периферийных устройств
- СИСТЕМНЫЕ КОНЦЕПЦИИ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
- 10.17. Программирование
- 10.18. Операционные системы, файлы и использование памяти
- ПРИНЦИПЫ ПЕРЕДАЧИ ДАННЫХ
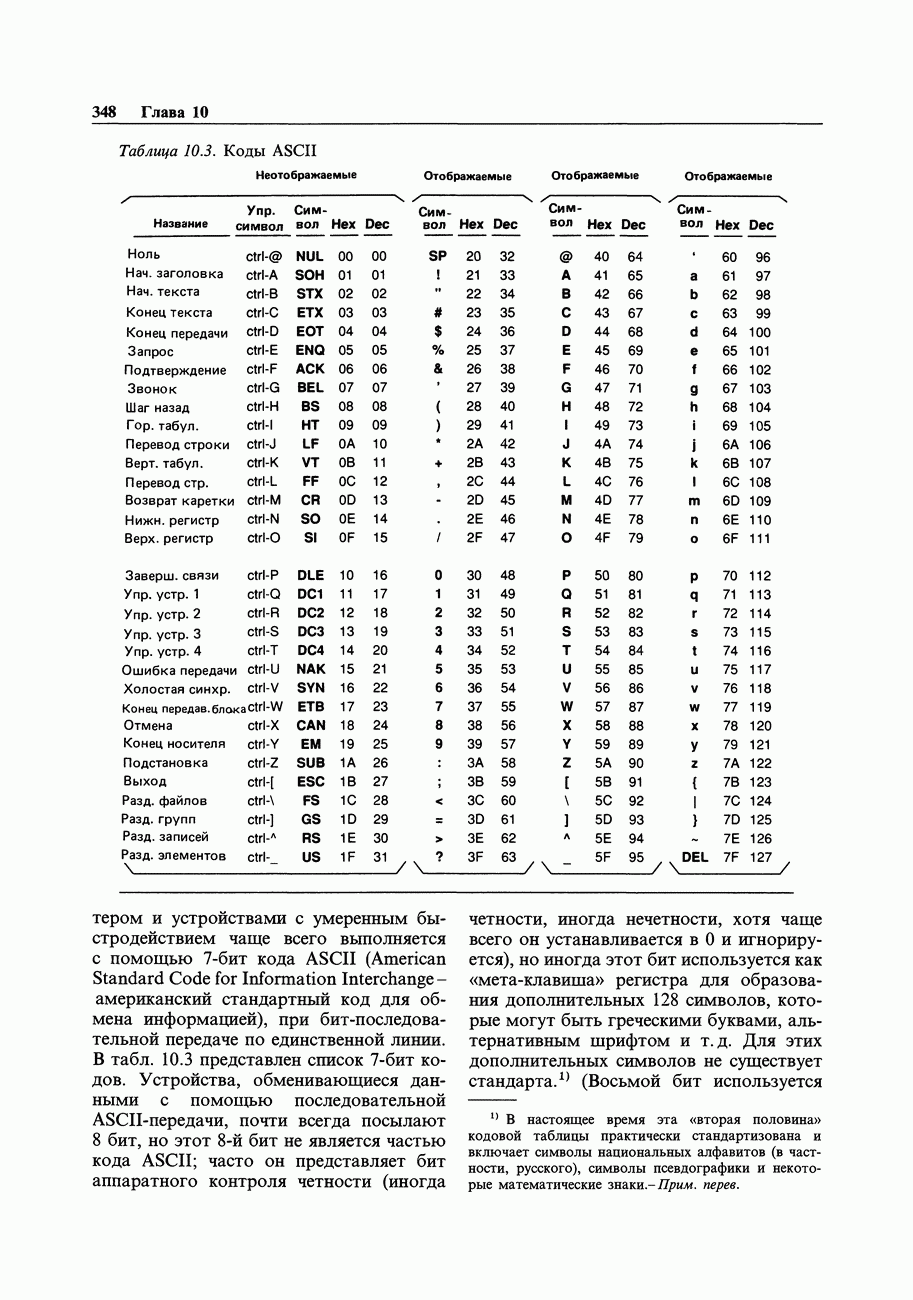
- 10.19. Последовательная связь и коды ASCII
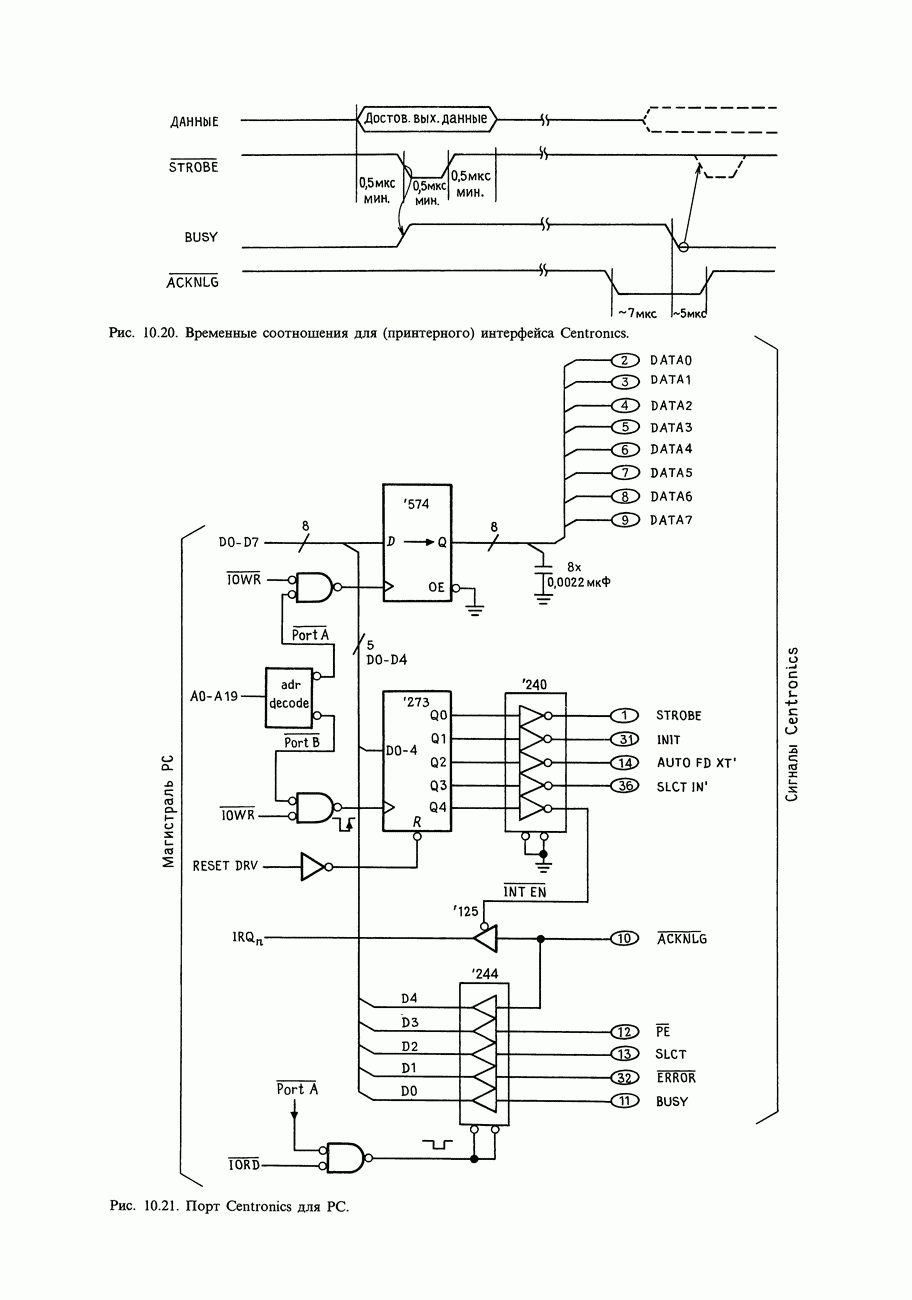
- 10.20. Параллельная связь
- 10.21. Локальные вычислительные цепи
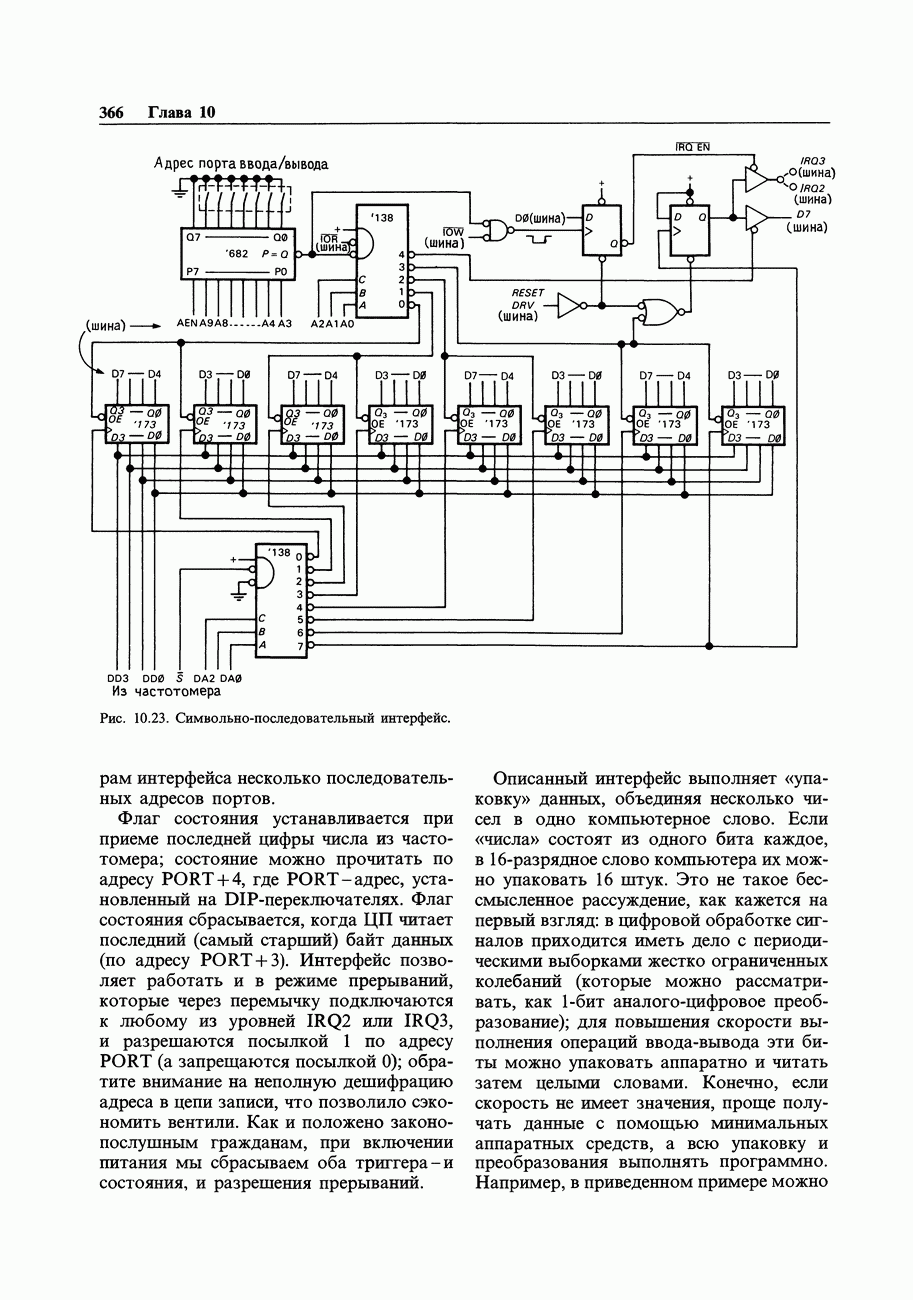
- 10.22. Пример интерфейса: аппаратная упаковка данных
- 10.23. Форматы чисел